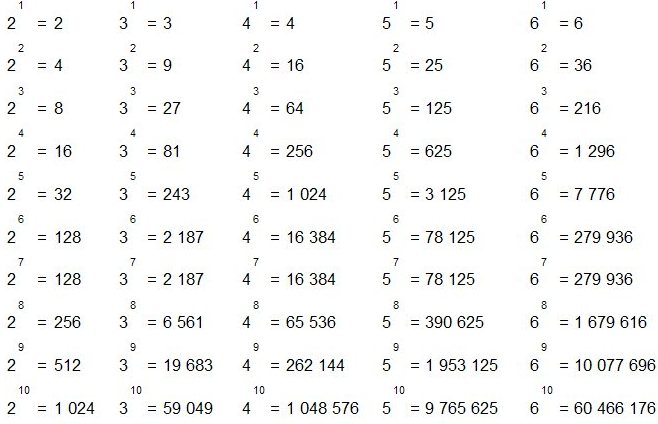
Как найти 2 степени N? – Обзоры Вики
Другое решение состоит в том, чтобы продолжать делить число на два, т. е. сделать n = n/2 итеративно. На любой итерации, если n%2 становится ненулевым и n не равно 1, то n не является степенью числа 2. Если n становится равным 1, то это степень числа 2.
Какая степень числа 2 равна 32? Степени двойки, показатели которых являются степенями двойки
| n | 2 n |
|---|---|
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
Как найти 2 в степени 100? Ответ: Значение 2100 = 1.2676506002 × 1030. 2100 = 1.
2676506002 × 1030.
Во-вторых, как вы рассчитываете мощность в ваттах? Формула расчета мощности: W (джоулей в секунду) = V (джоулей на кулон) x A (кулонов в секунду) где W — ватты, V — вольты, A — ток в амперах. На практике мощность — это мощность, производимая или используемая в секунду. Например, 60-ваттная лампочка потребляет 60 джоулей в секунду.
Что такое степени 2?
Степень двойки — это номер формы 2n в котором n — целое число, то есть результат возведения в степень с числом два в качестве основания и целым числом n в качестве показателя степени.
тогда как решить 2 в 100 степени? Ответ: Значение 2100 = 1.2676506002 × 1030. 2100 = 1.2676506002 × 1030.
Какой показатель у 5?
Степени и экспоненты
| базовый номер | 2-я степень | 5-я степень |
|---|---|---|
| 3 | 9 | 243 |
| 4 | 16 | 1,024 |
| 5 | 25 | 3,125 |
| 6 | 36 | 7,776 |
Что такое e в математике? Число e, также известное как число Эйлера, равно математическая константа, приблизительно равная 2.
71828, и может быть охарактеризован многими способами. Это основание натуральных логарифмов. Это предел (1 + 1/n)n когда n приближается к бесконечности, это выражение возникает при изучении сложных процентов.
Что значит 3²?
3 в квадрате 3² = 3 × 3 = 9. 4 в квадрате равно 4² = 4 × 4 = 16. 5 в квадрате равно 5² = 5 × 5 = 25. 6 в квадрате равно 6² = 6 × 6 = 36. 7 в квадрате равно 7² = 7 × 7 = 49.
Какая целая степень числа 2 равна 1024? 1024 это степень два:210 (2 в десятой степени). Это ближайшая степень двойки от десятичной 1000 и десятой 10000.6 (десятичное число 1296).
Какое значение имеет 2 Power 50?
2 в 50-й степени равно 1,125,899,906,842,624.
Что такое 2 в степени 4?
Таблицы экспонент и паттерны
| Полномочия 2 | Полномочия 3 | Полномочия 4 |
|---|---|---|
| 21 = 2 | 31 = 3 | 41 = 4 |
| 22 = 4 | 32 = 9 | 42 = 16 |
| 23 = 8 | 33 = 27 | 43 = 64 |
| 24 = 16 | 34 = 81 | 44 = 256 |
Что такое формула электроэнергии? В формуле P = VI, p обозначает мощность, V обозначает разность потенциалов, а I обозначает ток.
У закона Ома также есть вариант, который звучит как P = r × l2 или V2/R, это формула для электрической мощности. … Формула P = E / t, где P означает мощность, E означает энергию, а t означает время в секундах.
Как считать кВт? Киловатт — это просто мера того, сколько энергии потребляет электроприбор — 1,000 ватт, если быть точным. Вы можете быстро преобразовать ватты (Вт) в киловатты (кВт), уменьшив мощность на 1,000: 1,000 Вт 1,000 = 1 кВт.
Какой показатель у 4?
Таблицы экспонент и паттерны
| Полномочия 2 | Полномочия 3 | Полномочия 4 |
|---|---|---|
| 24 = 16 | 34 = 81 | 44 = 256 |
| 25 = 32 | 35 = 243 | 45 = 1024 |
| 26 = 64 | 36 = 729 | 46 = 4096 |
| 27 = 128 | 37 = 2187 | 47 = 16384 |
Какой показатель у 36? 62=6×6=36 .
(Помните, это не просто 6×2.) 6 — основание, а 2 — показатель степени. Это также называется «6 в квадрате»; это площадь квадрата со стороной 6.
Какое значение имеет 3 степени против 6?
Следовательно, число 3 в шестой степени равно 729.
Что такое e в калькуляторе? На дисплее калькулятора E (или e) означает для показателя степени 10, и за ним всегда следует другое число, которое является значением показателя степени. Например, калькулятор покажет число 25 триллионов как 2.5E13 или 2.5E13. Другими словами, E (или e) — это сокращенная форма научного обозначения.
Как вы делаете полномочия?
Как решить степени в физике? Мощность равна работе (Дж), разделенной на время (с). Единицей СИ для мощности является ватт (Вт), который равен 1 джоулю работы в секунду (Дж/с). Мощность может быть измерена в единице, называемой лошадиной силой.
Одна лошадиная сила — это количество работы, которую лошадь может выполнить за 1 минуту, что равно 745 ваттам мощности.
Как вы набираете экспоненты?
Нажмите Клавиши «Shift» и «6» для ввода символа вставки. Или введите две звездочки подряд. Введите показатель степени.
2 В степени 2018 последняя цифра • Вэб-шпаргалка для интернет предпринимателей!
Нахождение последней цифры в записи степени натурального числа.
После изучения темы “Степень с натуральным показателем” была предложена такая задача: найти последнюю цифру степеней:
Мы заметили, что в первом случае показатели степеней составные числа, а во втором случае показатели степеней простые числа. В обоих случаях есть основания четные и нечетные. Мы сначала попробовали представить степени в виде произведения степеней с тем же основанием и одинаковыми показателями, затем воспользовались со свойствами степеней с натуральными показателями
Просмотр содержимого документа«Последняя цифра степени числа»
Последняя цифра степени.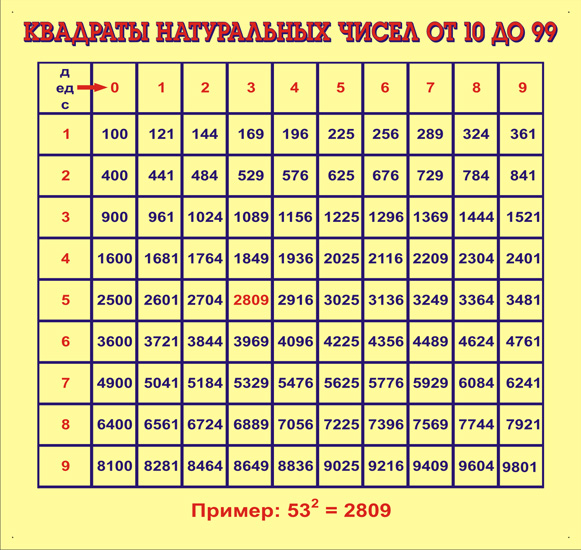
Приведем небольшое исследование: выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа 2 n , где n – натуральное число, с изменением показателя n. Для этого рассмотрим таблицу:
Мы видим, что через каждые четыре шага последняя цифра повторяется. Заметив это, нетрудно определить последнюю цифру степени 2 n для любого показателя n.
В самом деле, возьмем число 2 100 . Если бы мы продолжили таблицу, то оно попало бы в столбец, где находятся степени 2 4 , 2 8 , 2 12 , показатели которых кратны четырем. Значит, число 2 100 , как и эти степени, оканчивается цифрой 6.
Возьмем к примеру, 2 22 , если проверить, просто посчитав, то получится 4194304 – последняя цифра 4.
Теперь попробуем пользоваться таблицей, но в таблице 4 числа, а показатель степени 22, однако, после последнего числа этот «круг» начинается заново. Поэтому, показатель степени 22 делим на 4, получаем число 5 и остаток 2 т.е мы сделаем 5 «кругов», и отсчитаем ещё 2 в перед, а второе число – это 4, значит, таблица работает.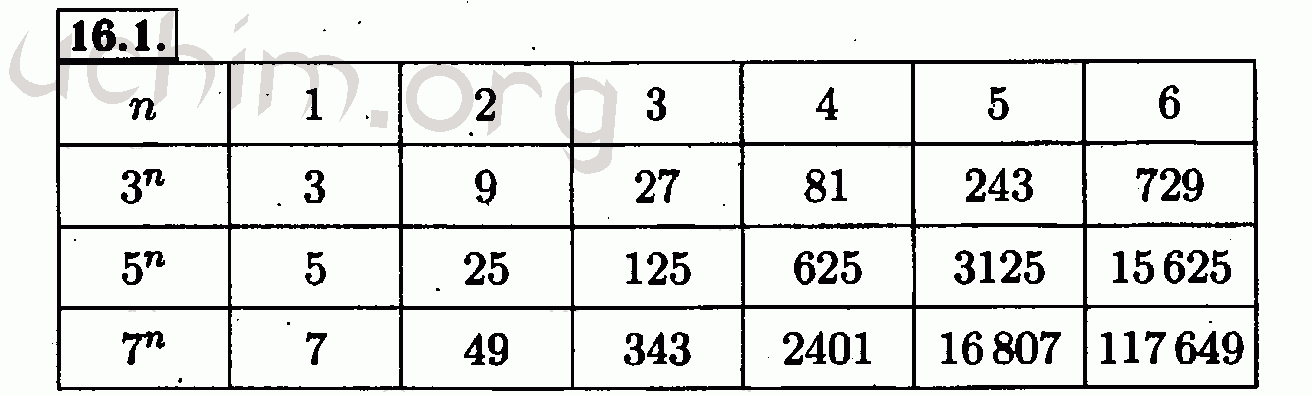
А теперь посмотрим, можно ли составить таблицы для остальных чисел. Все описывать не буду, лишь скажу, что у меня получилось составить таблицу для всех чисел от 1 до 10, а далее будет повторяться, допустим, у 12 последние числа будут такие же, как и у 2, а у 25 – так же, как и у 5.
Закономерности возведения в степень:
Запись числа, являющегося полным квадратом, может оканчиваться только цифрами 0, 1, 4, 5, 6 или 9.
Если запись числа оканчивается цифрой 0, 1, 5 или 6,то возведение в любую степень не изменит последние цифры.
При возведении любого числа в пятую степень его последняя цифра не изменится.
Если число оканчивается цифрой 4 (или 9), то при возведении в нечетную степень последняя цифра не изменяется, а при возведении в четную степень изменится на 6 (или 1 соответственно).
Если число оканчивается цифрой 2, 3, 7 или 8, то при возведении в степень возможны четыре различных цифры.
Две последних цифры степени.
Мы теперь знаем, что последняя цифра рано или поздно будет повторяться.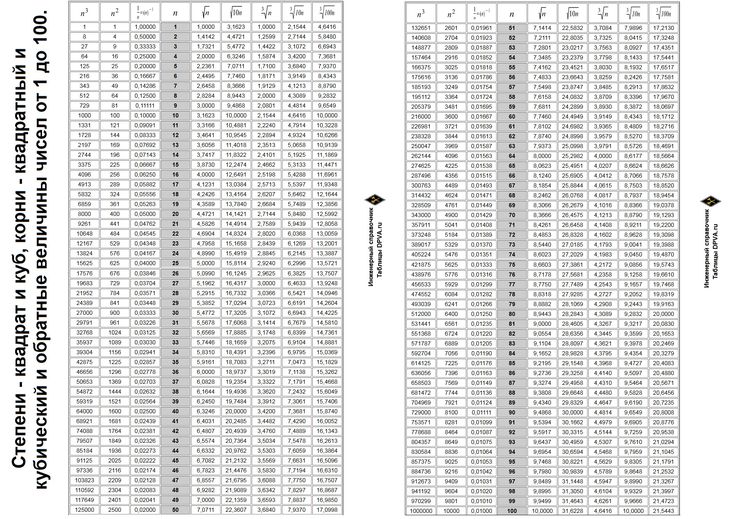
Но как же обстоит дело с 2-мя последними цифрами? Я осмелюсь предположить, что не только 2, но и 3 и более последних цифр будут повторяться. Что ж проверим это, так же я заметила, что периоды из прошлой таблицы просто увеличились в 5 раз, кроме чисел 5 и 10, а про число 1 я писать не стала, так как результат всегда будет 1.
Степень
04
05
08
09
10
«Математику уже затем учить следует,
что она ум в порядок приводит»
Эти слова раскрывают сущность предмета математика, так как именно она, прежде всего, учит нас мыслить, рассуждать, анализировать, делать выводы, умозаключения и подводить итоги. Математика является одним из основных школьных предметов, потому, что все перечисленные качества необходимы не только математику, но и представителю любой другой науки. Развитием этих качеств занимается, прежде всего, математика. Существуют специальные задачи, которые направлены на формирование названных умений.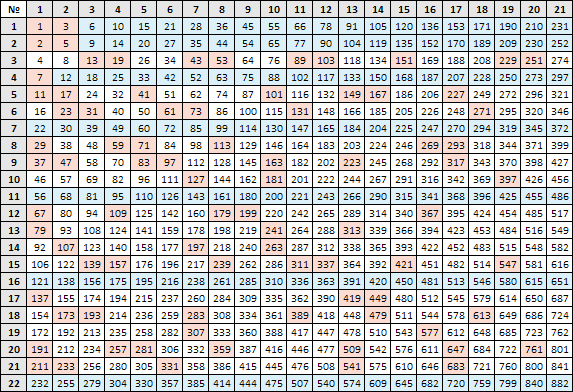
Готовясь к различным математическим конкурсам, мы столкнулись с таким заданием « Какой будет последняя цифра числа ?» На первый взгляд эта задача может показаться достаточно сложной и я принялся за вычисления…
В ходе решения этой задачи возникла идея исследовать, а какой будет последняя цифра любого натурального числа в любой степени, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа?
Составить опорную таблицу «Последние цифры степени», найти закономерности в них, научится вычислять последние цифры степеней.
Актуальность темы исследования обусловлена насущной необходимостью поиска быстрых алгоритмов решения практически важных задач, отработки навыков устного счета.
2. Последняя цифра степени
Выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа , где N , n – натуральные числа, с изменением показателя n. Для этого составим таблицу:
Для наглядности составим таблицу, где будут записаны цифры, которыми оканчиваются записи натуральных чисел:
Заполняя столбики получаем такой результат: пятая и девятая и т.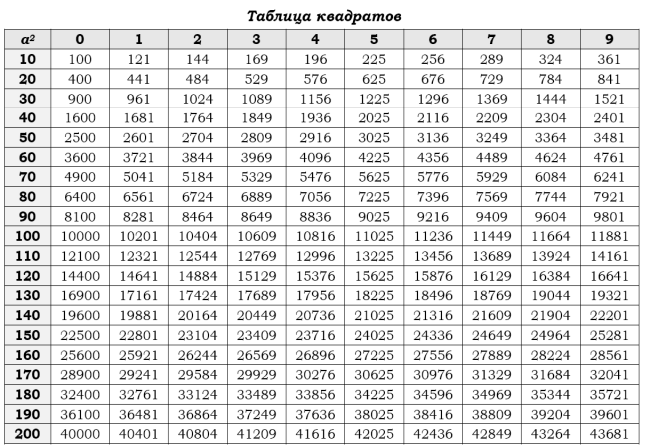
д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.
3. Закономерности возведения в степень
Результаты в таблице повторяются через каждые четыре столбца.
Про числа 1 и 10 писать не будем, т.к. результат всегда будет 1 или 0 соответственно.
Любая степень чисел 5 и 6 оканчивается соответственно на 5 и на 6.
Последние цифры степеней чисел 4 и 9 повторяются через каждые два шага, при возведении в четную степень последняя цифра не меняется, будет соответственно 4 или 9, при возведении в нечетную степень изменится на 6 или 1 соответственно.
Квадрат любого натурального числа может оканчиваться на 0, 1,4, 5, 6 и 9,
Куб натурального числа может оканчиваться любой цифрой
Используя полученные результаты попробуем найти последние цифры степени по остатку от деления её показателя на 4
Если остаток равен 0 и основание нечетное, то число будет оканчиваться на 1(кроме чисел оканчивающихся на цифру 5), если основание четное (кроме круглых чисел), то числа будут оканчиваться на цифру 6.
Теперь будем подбирать такие числа, что при делении показателя степени на 4 будут давать остатки 1, 2, 3
45:4=11 (остаток 1)
102:4=25 (остаток 2)
Если остаток равен 1, то последняя цифра степени будет равна последней цифре в записи основания степени;
Если остаток равен 2, то последняя цифра степени будет равна последней цифре в записи квадрата основания;
Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.
Значит чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4.
Последние цифры степеней чисел 2 , 12, 22 и т. д. (3, 13, 23 и т.д.) и т. д. будут совпадать.
4. Последние две цифры степени
Мы видим, что последняя цифра рано или поздно будет повторяться, а как будет обстоять дело с 2-мя и 3-мя последними цифрами ? Вероятно, они тоже будут повторяться. Для наглядности составим таблицу, где будут записаны две цифры, которыми оканчиваются записи натуральных чисел:
Глядя на таблицу, замечаем что последние две цифры тоже повторяются, только период повторения увеличивается, кроме того у некоторых чисел 1-е не входит в период, так например:
Но начиная с 21 степени по 40 последние две цифры будут повторяться.
Последние цифры чисел 3,13 и 8 тоже будут повторятся с периодом 20, но последние две цифры чисел 3 и 13 совпадать не будут, не будут совпадать последние две цифры для степеней чисел 4 и 14 и т.д.
Последние цифры чисел 4 и 9 будут повторяться с периодом 10,последние цифры числа 6 будут повторятся с периодом 5, но число 6 не входит в период, последние цифры числа 7 будут повторятся с периодом – 4. Любая степень числа 5 (начиная со 2 –ой) и 25 будет оканчиваться на 25, а число 15 в четной степени будет оканчиваться на 25, а в нечетной на 75. Период чисел 11, тоже будет равен 10, но здесь есть еще одна закономерность:
Для числа 11 в степени – число десятков будет равно показателю степени
Для числа 21 – период равен 4, а число десятков будет равно числу, полученному , если число 2 умножить на показатель степени
5. Заключение
Определить последнюю цифру степени числа не сложно, мы легко составили алгоритм, для двух последних цифр степени числа такой алгоритм уже не составишь, закономерности есть , но их меньше.
41 .
(8+3=11, последняя цифра 1)
Найдите последнюю цифру суммы степеней числа 2 с показателями, равными 32, 69, 469, 1995, 19951995.
(6+2+2+8+8=26 последняя цифра 6)
В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (− 1). Не опечатка ли это?
(опечатка. Число 23021 337 оканчивается единицей Поэтому последняя цифра числа (23021 337 − 1) равна 0, а значит, это число делится на 10 и потому составное.)
Делится ли число+ на 10 ?
(Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 Значит, их сумма оканчивается на 0 и потому делится на 10.)
Найдите последнюю цифру числа . Степени считаются сверху вниз: =
Последние две цифры числа 7 7 образуют число 43 (это можно вычислить непосредственно, отбрасывая при каждом умножении все цифры результата, кроме последних двух). Значит, число 7 7 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени).
Найдите 2 последние цифры числа 8 1989 .
В таблице 2-х последних цифр, у числа 8 период 20, (1989:20=99 остаток 9 , число 8 в 9 степени оканчивается цифрами 28, последние 2 цифры числа 8 1989 – 28).
На контрольной работе по перекрашиванию юный хамелеон перекрашивается по очереди из красного -> в желтый -> зелёный -> синий -> фиолетовый -> красный -> жёлтый -> зелёный и т.д. перекрасился он 2010 раз и начав с красного он в конце стал синим, но известно что он допустил ошибку, покраснел в тот момент, когда должен был приобрести другой цвет. Какого он был цвета перед этим покраснением?
(Заметим, что здесь период повторения цветов равен 5. Красный цвет будет встречаться на числах оканчивающихся на 0 и 5. Значит и должен он был закончить снова на красном.
Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов?
(У часов период повторения равен 24, значит число 102938475 разделить на 24 = 4289103,12… 102938475 — (4289103 * 24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов, через 102938475 часы будут показывать 13:00).
11. Доказать, что число кратно 2.
12. Доказать, что -1 кратно 5 (при натуральном n).
13. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n. 14. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?
7.
Использованная литература
1. «Все задачи «Кенгуру» 1994-2008- Санкт-Петербург, 2008.
2. «Задачи для подготовки к олимпиадам. Математика 5-8 классы» сост. Н.В. Заболотнева. – Волгоград: Учитель, 2007.- 99с.
3. Лихтарников Л.М. Занимательные логические задачи. (Для учащихся начальной школы) Оформление С. Григорьева — СПб.: Лань, МИК, 1996.- 125с.
4. Л.М.Лоповок 1000 проблемных задач по математике. Книга для учащихся Москва : Просвещение, 1995
5. Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
6. Чулков П.В. Математика. Школьные олимпиады: методическое пособие. 5- кл./ П.В. Чулков.- М.: Издательство НЦ ЭНАС, 2007.- 88с. (Портфель учителя).
7. Шуба М.Ю. Занимательные задачи в обучении математике: Книга для учителя. — 2-е изд.-М.: Просвещение, 1995.- 22с.
МОУ «Шербакульская средняя общеобразовательная школа №1»
Научное сообщество учащихся «Поиск»
Тема: « Последняя цифра степени.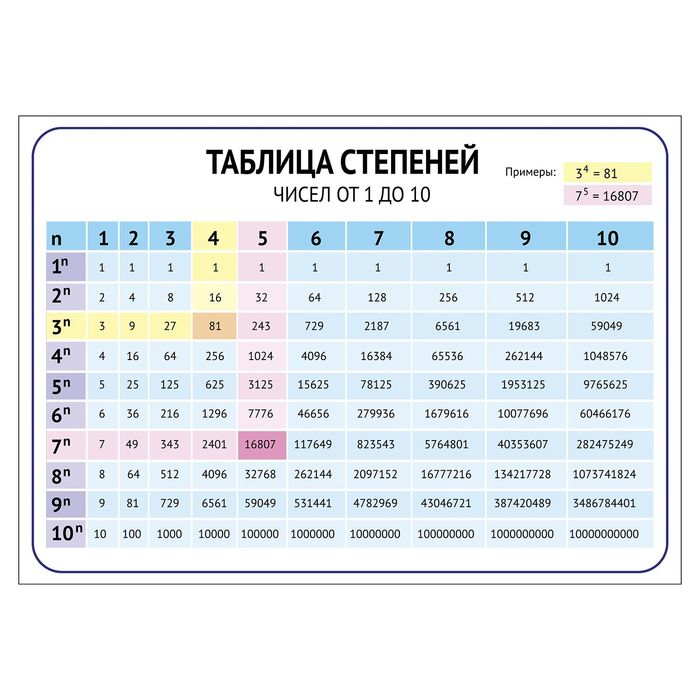
»
Выполнила: ученица 7 «б» класса
Руководитель: Пушило Т.Л.
2010 – 2011 уч. год
· Последняя цифра степени.
· Закономерности возведения в степень
· Две последних цифры степени.
Однажды, листая страницы книги «Тысяча проблемных задач по математике», я увидела с первого взгляда очень трудную задачу, точнее сказать пример надо было найти последнюю цифру суммы
1 1989 + 2 1989 + 3 1989 + 4 1989 + 5 1989 +…+ 1989 1989 .
Потом я подумала, а ведь должен же быть, какой-нибудь рациональный способ вычисления и тут я принялась считать…
Гипотеза: Можно ли сказать какой будет последняя цифра у любой степени?
· Узнать, можно ли построить таблицу последних цифр различных степеней.
· Найти закономерность в них.
· Используя таблицу практиковаться на более легких задачах и решить вышеупомянутый пример и если получится более сложные.
Последняя цифра степени.
Приведем небольшое исследование: выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа 2 n , где n – натуральное число, с изменением показателя n . Для этого рассмотрим таблицу:
| 2 1 = 2 2 5 = 32 2 9 = 512 | 2 2 = 4 2 6 = 64 2 10 = 1024 | 2 3 = 8 2 7 = 128 2 11 = 2048 | 2 4 = 16 2 8 = 256 2 12 = 4096 |
Мы видим, что через каждые четыре шага последняя цифра повторяется. Заметив это, нетрудно определить последнюю цифру степени 2 n для любого показателя n .
В самом деле, возьмем число 2 100 . Если бы мы продолжили таблицу, то оно попало бы в столбец, где находятся степени 2 4 , 2 8 , 2 12 , показатели которых кратны четырем. Значит, число 2 100 , как и эти степени, оканчивается цифрой 6.
Возьмем к примеру, 2 22 , если проверить, просто посчитав, то получится 4194304 – последняя цифра 4.
Теперь попробуем пользоваться таблицей, но в таблице 4 числа, а показатель степени 22, однако, после последнего числа этот «круг» начинается заново.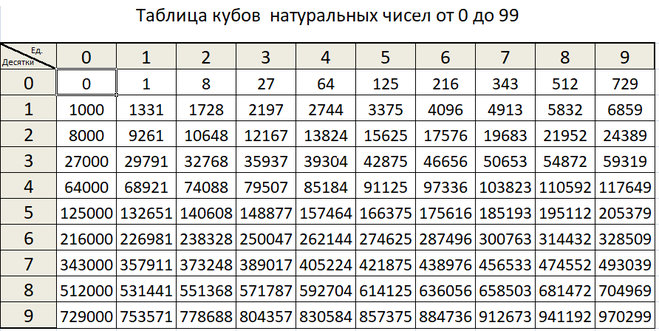
Поэтому, показатель степени 22 делим на 4, получаем число 5 и остаток 2 т.е мы сделаем 5 «кругов», и отсчитаем ещё 2 в перед, а второе число – это 4, значит, таблица работает.
А теперь посмотрим, можно ли составить таблицы для остальных чисел. Все описывать не буду, лишь скажу, что у меня получилось составить таблицу для всех чисел от 1 до 10, а далее будет повторяться, допустим, у 12 последние числа будут такие же, как и у 2, а у 25 – так же, как и у 5.
Закономерности возведения в степень:
- Запись числа, являющегося полным квадратом, может оканчиваться только цифрами 0, 1, 4, 5, 6 или 9.
- Если запись числа оканчивается цифрой 0, 1, 5 или 6,то возведение в любую степень не изменит последние цифры.
- При возведении любого числа в пятую степень его последняя цифра не изменится.
- Если число оканчивается цифрой 4 (или 9), то при возведении в нечетную степень последняя цифра не изменяется, а при возведении в четную степень изменится на 6 (или 1 соответственно).
- Если число оканчивается цифрой 2, 3, 7 или 8, то при возведении в степень возможны четыре различных цифры.
Две последних цифры степени.
Два в сотой степени: удивительный ответ
Ответ:
Ну… прежде чем я смогу дать вам ответ, вам нужно немного справочная информация… Длина городского квартала вам наверняка знакома.
с.  Представьте, что вы идете на целый квартал. 
около 3 минут.
Представьте себе 100 блоков от начала до конца. Это длина большой город, вроде Миннеаполиса, где я живу. 20 минут езды от одного конца города до другого, если не было ни пробок, ни красных светофоров, чтобы ждать.  Пешком расстояние займет 5 часов.
Однако свет может пройти из одного конца Миннеаполиса в другой за
менее одной десятитысячной секунды. Свет — самый быстрый
вещь есть.  Нет ничего быстрее.
Расстояние через Соединенные Штаты примерно в 200 раз превышает длину
город, так что ходить без остановок, даже без перерыва на горшок, потребовалось бы
1000 часов или почти 42 дня. Свет проходит это расстояние за
чуть больше 1/100 секунды. Страна очень большая,
но свет очень, очень быстро.
Расстояние от Земли до Луны почти в 100 раз больше ширины США.  Потребуется всего около 11 лет, чтобы дойти до Луна. Свет проходит от Земли до Луны менее чем за 1,3 секунды.
По сравнению с любым расстоянием на Земле Луна ужасно далека.  Но свет преодолевает расстояние за одно сердцебиение.
Плутон — самая далекая из известных планет в нашей Солнечной системе: подробнее
чем в 15 000 раз дальше от Земли, чем Луна.
гораздо больший скачок в масштабе, чем любое из предыдущих повышений.
потребуется 167 000 лет, чтобы добраться до Плутона.
летать!  Даже свету требуется 5,5 часов, чтобы достичь Плутона.
  По крайней мере,
хорошо знакомый период времени.  Но по сравнению с
1,3 секунды, чтобы свет достиг Луны, Плутон ужасно далеко.
Ближайшая к нашей Солнечной системе звезда — Проксима Центавра. 4,2 световых года, а это значит, что его свет проходит через 4,2 года. добраться сюда.  Это в 6700 раз дальше, чем Плутон.  Еще один огромный скачок в масштабе — например, гораздо больший, чем скачок в 200 раз от ширина города равна ширине Соединенных Штатов.  Вы можете довольно легко дождаться 5,5 часов, которые требуются для того, чтобы свет прошел от Солнца до Плутон, но ожидание 4,2 года, которое требуется свету, чтобы добраться сюда. Проксима требует гораздо больше терпения. звезда невероятно далека.
Звезды тонко разбросаны по большей части нашей галактики, Млечный
Way.  Хотя ближайшая к Земле звезда находится на расстоянии 4,2 световых года от нас,
среднее расстояние между ближайшими соседними звездами составляет около
10 световых лет.
Поскольку в
Млечный Путь, галактика должна быть невообразимо большой.
видимый диск оценивается в 100 000 световых лет в диаметре. 
Это более чем в 20 000 раз превышает расстояние до Проксимы.
Самый большой скачок в масштабе.
Вы можете ждать 4,2 года, пока свет доберется до Земли от Проксимы. Центавра, но 100 000 лет намного длиннее, чем прожили люди. выращивание продовольственных культур или строительство постоянных укрытий. времени, которое невозможно пережить и, вероятно, нельзя постигли.  Это предполагает, что расстояние через Млечный Путь тоже за гранью понимания.
Ближайшая к нам крупная галактика — знаменитая Галактика Андромеды. 
Он очень похож по размеру и форме на Млечный Путь и является
другой крупный компонент Местной группы галактик.
самая далекая вещь, которую можно увидеть невооруженным глазом.  Свет
от Андромеды проделал путь в 3 миллиона световых лет, чтобы добраться до нас. 
Это в 30 раз больше диаметра Млечного Пути.
 Когда звездный свет
из Андромеды, которую мы видим сейчас, начали свой путь на Землю люди
еще не существовало.  Наши предки еще не научились делать
каменные инструменты.
Самая далекая галактика, которую когда-либо видели непосредственно (открыта в 1999 г.),
красное смещение 6,68, что указывает на то, что его свет был испущен, когда
Возраст Вселенной составлял всего 5% от ее нынешнего возраста. Если Вселенная сейчас
Свету 13,7 миллиарда лет, свет прошел 13 миллиардов световых лет.
чтобы добраться до нас.  Это в 4300 раз больше расстояния до Андромеды
Галактика. Еще один огромный скачок в масштабе. 13 миллиардов лет назад
облако пыли и газа, из которого должна была сформироваться наша Солнечная система,
еще не существует.
Максимально возможное расстояние — это расстояние, на которое свет может
путешествие от начала Вселенной до Большого Взрыва.  Все
свет от этого события был немедленно поглощен (и переизлучен,
и много раз повторно поглощались), но спустя 380 000 лет температура
упал достаточно, чтобы образовались атомы водорода, в результате чего Вселенная
стать прозрачным.
  Это позволило свету беспрепятственно распространяться. 
Свет от горячей молодой Вселенной достигает нас сейчас, сильно смещенный в красную сторону,
как космическое микроволновое фоновое излучение.
Фоновое излучение преодолело почти 13,7 миллиардов световых лет. или в 4600 раз больше расстояния до Галактики Андромеды.
Хорошо. Теперь ответ на вопрос.
Вы помните вопрос:
          Какой толщины будет стопка бумаги после того, как
          разрежет ее пополам и уложит в стопку 100 раз?
Каждый раз, когда вы разрезаете стопку бумаги на две части, количество удвоения:  2 x 2 x 2…  сто раз, или два до Сотая степень, обозначенная как 2 100 .
Два в сотой степени равно 1 267 650 600 228 229 401 496 703 205 376.
В системе наименования номеров США это один нониллион, 267 октиллионов,
650 септиллионов, 600 секстиллионов, 228 квинтиллионов, 229 квадриллионов, 401
триллион 496 миллиардов 703 миллиона 205 тысяч 376.
С помощью калькулятора, который показывает достаточное количество цифр, вы можете получить это число. просто перемножая двойки менее чем за минуту.
Умножение на толщину бумаги в миллиметрах (0,1 мм) дает высоту стопки в миллиметрах. Деление результата на 1000 дает высоту стопки в метрах.  Разделив это на количество метров в световом году (9 460 536 000 000 000) дает высота стека в световых годах.
Начав с листа бумаги толщиной 0,1 миллиметра, удвоив толщина в сто раз приводит к стопке 13,4 миллиарда световых лет высотой.   Он будет простираться от Земли до самая далекая галактика, которую мы можем увидеть с помощью самых мощных телескопов. почти на краю наблюдаемой Вселенной.
Часть космического телескопа Хаббла Deep Field — север.  Почти каждое пятно света представляет собой галактику.
Если вам трудно поверить, что всего 100 разрезов бумаги
заставит стек вырасти до такой высоты, вот
93-8
Сколько будет 2 в 33-й степени?
Итак, вы хотите знать, сколько будет 2 в 33-й степени, не так ли? В этой статье мы объясним, как именно выполнить математическую операцию под названием «возведение числа 2 в степень 33».
Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Что такое возведение в степень?
Давайте сначала зафиксируем наши термины, а затем посмотрим, как вычислить число 2 в 33-й степени.
Когда мы говорим об возведении в степень, все, что мы на самом деле имеем в виду, это то, что мы умножаем число, которое мы называем основанием (в данном случае 2) само по себе определенное количество раз. Показатель степени — это количество раз, которое нужно умножить на 2, что в данном случае составляет 33 раза.
2 в степени 33
Есть несколько способов, как это может быть выражено, и наиболее распространенными способами, которые вы увидите, являются:
- 2 33 9) для обозначения показателя степени. Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса.
«Сколько будет 2 в 33-й степени?». VisualFractions.com . По состоянию на 16 октября 2022 г. http://visualfractions.com/calculator/exponent/what-is-2-to-the-33rd-power/.
«Сколько будет 2 в 33-й степени?». VisualFractions.com , http://visualfractions.com/calculator/exponent/what-is-2-to-the-33rd-power/. По состоянию на 16 октября 2022 г.
Сколько будет 2 в 33-й степени?. VisualFractions.com. Получено с http://visualfractions.com/calculator/exponent/what-is-2-to-the-33rd-power/.
Итак, мы упомянули, что возведение в степень означает умножение базового числа само на себя для получения показателя степени число раз.
Давайте посмотрим на это более наглядно:
2 в 33-й степени = 2 x … x 2 (33 раза)
Итак, каков ответ?
Теперь, когда мы объяснили теорию, стоящую за этим, давайте посчитаем числа и выясним, чему равно 2 в 33-й степени:
2 в степени 33 = 2 33 = 8 589 934 592
Почему мы вообще используем возведение в степень, такое как 2 33 ? Что ж, нам намного проще писать умножения и выполнять математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.
Надеюсь, эта статья помогла вам понять, как и почему мы используем возведение в степень, и дала вам ответ, который вы изначально искали. Теперь, когда вы знаете, сколько будет 2 в 33-й степени, вы можете продолжить свой веселый путь.
Не стесняйтесь поделиться этой статьей с другом, если вы считаете, что она поможет ему, или перейдите вниз, чтобы найти еще несколько примеров.
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
