Sin 40 Градусов
Таблица синусов от 1 до 3. Таблица синусов в градусах от 1 до 3. В таблице синусов точность значений синуса составляет четыре знака после запятой. В тригонометрической таблице синусов углы даны в градусах. Таблица синусов начинается со значения синуса одного градуса.
Синус нуля градусов равен нулю. Таблица синусов применяется при решении самых разных математических, физических, инженерных задач. Значения синусов используются в расчетах самых разных величин в физике и других науках. Если вам нужен синус таблица от 3. Если у вас угол альфа в пределах от 3. Значения синусов этих двух углов равны, поскольку в тригонометрии для синуса (и не только для него, а для всех тригонометрических функций) существует равенство: sin (.
Таблица синусов начинается со значения синуса одного градуса. Синус нуля sin 40 градусов это сколько — 0,6428 вот сколько! Онлайн-сервис для перевода градусов в радианы, а также для перевода радианов в градусы.
По таблице синусов очень удобно смотреть, чему равен sin 5, sin 6, sin 2.
В этой же таблице можно посмотреть ответ на вопрос . В тригонометрии, и не только в тригонометрии, но и во всей нашей математике, угол пи радиан равен 1.
Вот эти самые 1. 80 градусов и нужно разделить на 1. Поскольку 1. 80/1.
По- украински это будет звучать так: таблиця значень тригонометричних функц. Вы не поверите, но в Украине тоже есть блондинки. И им тоже нужна математика для блондинок и тригонометрия для блондинок.
Кроме всех прочих достоинств этой таблицы синусов, в ней есть sin угла 7 градусов, который многие хотят видеть. Если вам интересно, как находить косинус синус угла 7. Синус угла 7. 5 градусов смотрите в строчечке напротив угла в 7. Во всех таблицах внешний вид одинаковый и сделаны они по одному принципу. Найти значение: Значение sin 5. Синус угла найти — значения синусов угла вы без труда найдете в очень красивой таблице на картинке.
Синус 1. 5 градусов равен — 0,2. Проверьте по таблице, я могу наврать. Синус пи/1. 2 — равен синусу 1.
Смотрите выше.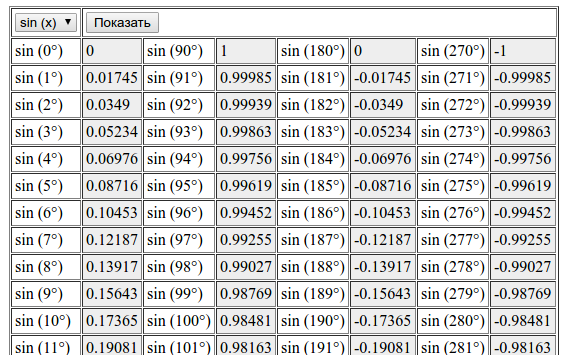
sin 3- х градусов — равен 0,0. Таблица синусов по физике — для физики больше подойдет эта таблица. Физики — люди серьезные и в сокращение дробей не играют.
Добавлена таблица значений синусов, таблица синусов от 0 до 360 градусов, полная таблица синусов. Тригонометрические функции, тригонометрия. Синус, sin 40 градусов, sin 40. Синус, sin 40 радиан. На ‘Знаниях’ вы найдёте миллионы ответов, правильность которых подтвердили активные участники сообщества, но Проверенные ответы — это лучшие из лучших.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513. Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла. Пользоваться таблицей очень просто — найдите нужный угол и в той же строке увидите синус и косинус этого угла. Для примера возьмем угол, равный 30 градусам. Таблица синусов, она-же таблица косинусов. Углы в угловых градусах и минутах.
Исчисление— Первообразная от $\sin{x}$, когда $x$ задано в степенях
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 972 раза
$\begingroup$
Я знаю, что вычисления обычно выполняются в радианах и что $\int{\sin{x}}$ ${dx}=-\cos{x}+C$ при работе с ними.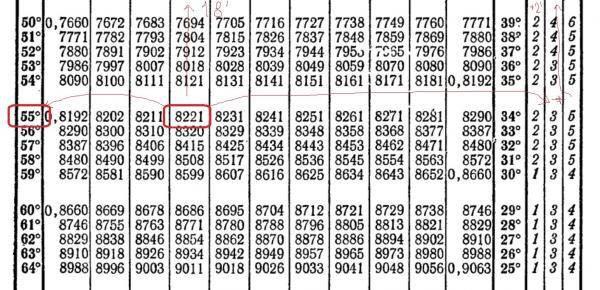
9{30}{\sin{x}}$ ${dx} =7,676178925$, если $x$ указано в градусах? Я заметил, что $\frac{7,676178925\pi}{180}\прибл.1339745962$, но не уверен, какое значение это имеет для этой проблемы, кроме того факта, что это $7,676178925$ градусов в радианах.
- исчисление
- интегрирование
- тригонометрия
3
$\begingroup$
9{30} \sin \frac {\pi x}{180}\;dx\приблизительно 7,676$$, где аргумент $\sin$ теперь выражен в радианах. Обратите внимание, что результатом интеграла является чистое число, а не градусы или радианы.$\endgroup$
1
$\begingroup$
Чтобы найти интеграл в градусах, лучше — для ясности, а не обязательно по какой-либо формальной причине — начать в радианах с преобразования в градусы в функции синуса.
то есть 9b f(x)dx = F(b)-F(a)$) также применимо и здесь. Просто не забудьте убедиться, что $a,b$ также указаны в градусах. Кроме того, первообразная в основном такая же, как в радианах.
Что касается вашего второго вопроса, то смысл любого интеграла, по сути, один и тот же: площадь со знаком под кривой подынтегральной функции между двумя точками, выбранными в качестве границ. Обратите внимание, что он не будет использовать те же единицы измерения, что и подынтегральная функция, то есть он не будет выражаться в градусах.
$\endgroup$
1
$\begingroup$
Первообразная не меняется вместе с единицами, пока единицы в первообразной и исходной одинаковы. Другими словами, если sin(x) оценивается в градусах, то первообразная по-прежнему равна -cos(x)+C, где x по-прежнему выражается в градусах. Если вы хотите, чтобы одно или другое значение выражалось в радианах, вам нужно всего лишь составить $\frac{\pi}{180}$, чтобы значение x изменилось на радианы.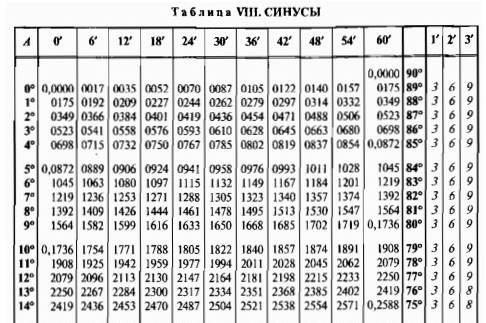
$\endgroup$
0
$\begingroup$
Я немного запутался в некоторых ответах на этот вопрос. Я считаю, что большая часть путаницы восходит к тому факту, что функция «синус» в радианах и градусах не является одной и той же функцией (в дальнейшем я буду обозначать первую через $\sin$, а вторую через $\operatorname{ грех}$). 9\circ}\pi \operatorname{Cos}(x) \right)= \operatorname{Sin}(x)$$ функций синуса и косинуса в градусах. Обратите внимание, что первообразная синуса в градусах действительно имеет единицы степени.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 9°)} \,=\, 0$
Синус угла ноль градусов может быть получен в математике двумя различными геометрическими подходами.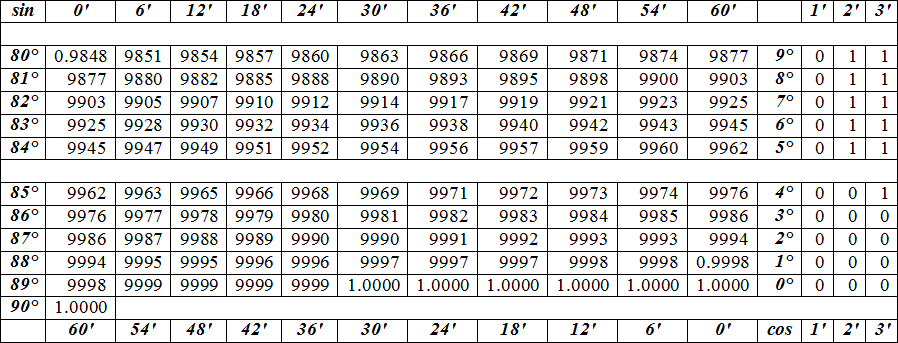
Теперь настало ваше время научиться математически вычислять синус угла, равный нулю, в радианах.
Фундаментальный метод
Синус угла ноль градусов можно получить теоретически, рассматривая геометрическое свойство стороны в прямоугольном треугольнике с нулевым градусом. Теперь представьте себе прямоугольный треугольник, угол которого равен нулю градусов. $\Delta RPQ$ является примером прямоугольного треугольника с нулевым углом. 9°)}$ $\,=\,$ $0$
Экспериментальный метод
Грех угла ноль градусов доказывается также практически с помощью геометрических средств путем построения прямоугольного треугольника с углом ноль градусов. Теперь давайте начнем процесс построения прямоугольного треугольника с углом ноль градусов.
- Проведите горизонтальную прямую из точки $A$ на плоскости.
- Возьмите транспортир и начертите линию с нулевым углом, совместив точку $A$ с ее средней точкой, а также совместив правую базовую линию с горизонтальной линией.
