Статья «Задачи на составление уравнений с помощью таблиц»
УДК 51-3
Задачи на составление уравнений с помощью таблиц
Оплачко О.В.
Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа №2
Аннотация. В статье представлены различные типы решения задач на составление уравнений с помощью таблиц, а именно, задачи на работу, на сплавы, на движение.
Ключевые слова: математика, задачи через пусть х, табличный способ.
Tasks for composing equations using tables
Oplachko O. V.
Municipal state educational institution secondary school №2
Annotation. The article presents various types of solving problems for drawing up equations using tables, namely, tasks for work, for alloys, for movement.
Keywords: mathematics,
problems through let x, tabular way.
Задачи на составление уравнений встречаются в кимах ОГЭ, ЕГЭ, ВПР как по математике, так и по другим предметам. Но многие из обучающихся не приступают к выполнению данных заданий. Возникает вопрос, что вызывает трудность? Почему ребята не решают такие задания и теряют баллы при поступлении? Каждому учителю математики очень интересна данная проблема и пути её решения.
В результате опроса среди обучающихся 5-11 классов были получены следующие данные: более 30% учеников не могут перевести текст задачи на математический язык, 53 % — не знают формул, которые помогают решить задачи на работу, концентрацию и движение, 68% — не понимают, какое выражение больше, из какого выражения нужно вычитать другое.
Таким образом, целью исследования является выявление наиболее эффективного способа решения задач на составление уравнений, который смогут освоить не только отличники.
Рассмотрим
некоторые понятия, которыми будем пользоваться, при решении таких задач.
Уравнение – это равенство, которое содержит в себе переменную (переменные), значения которых требуется найти.
Корень уравнения – это значение переменной, при подстановке которого уравнение обращается в верное числовое равенство.
Решить уравнение – значит найти все значения переменных, входящих в него, которые обращают это уравнение в верное числовое равенство, или установить, что данное уравнение решений не имеет.
Система уравнений – это несколько уравнений, объединенных фигурной скобкой, в которых одни и те же переменные обозначают одни и те же числа.
Решением системы уравнений является набор значений всех входящих в него переменных, который обращает каждое уравнение системы в верное числовое равенство.
Решить систему уравнений
Табличный
способ решения задач – это способ, который
заключается в построении таблицы, строки которой соответствуют элементам одного из рассматриваемых в
условии задачи множеств, столбцы — элементам другого, пересечение
строки и столбца — комбинации двух элементов разных множеств.
Решить задачу – значит найти последовательность понятий, формул, правил, которая приводит к ответу.
На уроках алгебры, факультативах, внеурочных занятиях ребятам восьмых классов были предложены различные способы решения данных задач. Лучше всех справились с контрольной работой ученики того класса, с которыми был отработан табличный метод. Более 73 % из тех, кто писал контрольную работу, смогли решить задачи. 85 % обучающихся этого класса правильно составили уравнение к условию задачи (на ОГЭ заработали бы один из двух баллов). Среди этих 85 % были и те ученики, у которых в четверти стоит тройка. Кроме того, как только с ребятами другого класса был отработан этот же метод решения задач, качество знаний при написании аналогичных вариантов контрольной работы выросло на 61 %.
Рассмотрим некоторые примеры задач ОГЭ и ЕГЭ на составления уравнений, которые решим табличным способом. При заполнении таблицы к каждой задаче нужно задавать наводящие вопросы.
Задача
1.
Катер прошёл 16 км по течению реки и 30 км против течения, затратив на весь путь 1 час 30 мин. Найдите собственную скорость катера, если скорость течения реки составляет
1км/ч [3, с. 198].
Перед тем, как заполнить таблицу, ученикам было предложено решить данную задачу. С данным заданием справились только 36 %. После одного разобранного примера следующую задачу табличным методом решало 93% и справились с ней 68% обучающихся.
Ученикам задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Что обозначим за х? Каким выражением будем обозначать скорость по течению и против течения? Чему равен путь по течению и против течения? Как выразить время через скорость и путь? Какую вы знаете формулу? Как только ребята отвечают на вопросы, параллельно заполняется таблица. С помощью такого метода обучающиеся начинают рассуждать и понимают принцип решения задач.
Решение: пусть х км/ч – собственная скорость катера
| v | s | t |
по течению | х+1 | 16 | |
против течения | х-1 | 30 |
При решении данных задач нужно пояснять, что при нахождении
скорости против течения, необходимо из скорости катера вычитать скорость
течения реки.
Составим и решим уравнение
Перенесем из левой части уравнения в правую с противоположным знаком, приведем дроби к общему знаменателю и выполним арифметические действия.
Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель отличен от нуля
Умножим первое уравнение на минус один, получим следующую систему:
не удовлетворяет условию задачи, так как скорость не может быть отрицательным числом.
Ответ: 31км/ч – собственная скорость катера.
Задача
2. Во дворе Николая Павловича расположен
бассейн, подача воды обеспечивается двумя насосами. Один из них, работая
самостоятельно, наполняет бассейн за 30 минут, а другой – за 20 минут. За
сколько минут оба насоса наполнят бассейн, работая одновременно [2, с.
53].
Решение: в задачах на работу часто объём работы обозначают за единицу, В – время, П – производительность, Р – работа.
В=Р:П, Р=П*В, П=Р:В (1)Перед тем, как заполнить таблицу, ученикам было предложено решить данную задачу. С данным заданием справились только 29 %. После одного разобранного примера следующую задачу табличным методом решало 78% и справились с ней 52% обучающихся.
Ученикам задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Какие величины будем обозначать переменными? Чему равна в данном случае работа? Как выразить время наполнения бассейна первого насоса, второго насоса, время их совместной работы? Как только ребята отвечают на вопросы, параллельно заполняется таблица.
| П | Р | В |
Первый насос | 1 | 30 | |
Второй насос | у | 1 | 20 |
Первый насос + второй насос | х + у | 1 | ? |
Пользуясь формулами (1), выразим время работы первого, второго
насоса и их совместное время.
В выражение вместо х и у подставим выражения, полученные на предыдущем шаге
приведем дроби к общему знаменателю, сложим их и выполним деление
Ответ: за 12 минут оба насоса наполнят бассейн, работая одновременно.
Задача 3. Имеются два сосуда, содержащие 25 кг и 21 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 39 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 42 % кислоты. Сколько кг кислоты содержится в первом растворе? [1, с. 88]
Решение: Перед тем, как заполнить таблицу, ученикам было предложено решить данную задачу. С данным заданием справились только 17 %. После одного разобранного примера следующую задачу табличным методом решало 62% и справились с ней 41% обучающихся.
Ученикам
задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Какие
величины будем обозначать переменными? Чему равны массы первого, второго
раствора, их совместная масса? Как найти массу кислоты для каждого из данных
случаев? Как только ребята отвечают на вопросы, параллельно заполняется
таблица.
| mр-ра | % кислоты | mкислоты |
1 раствор | 25 | а | 25а*0,01 |
2 раствор | 21 | в | 21в*0,01 |
1 раствор+2 раствор | 25+21=46 | 39 | 0,39*46 |
Равные
массы обозначим 1, так как при решении уравнения эти массы сократятся. | |||
1 раствор | 1 | а | 1*а*0,01 |
2 раствор | 1 | в | 1*в*0,01 |
1 раствор+2 раствор | 1+1 | 42 | 0,42*2 |
Составим и решим систему уравнений
Умножим оба уравнения системы на 100, чтобы избавиться от десятичных дробей
Выразим из второго уравнения системы переменную а через переменную в и подставим во второе уравнение
Раскроем скобки во втором уравнении системы, приведем подобные слагаемые, найдем значения переменных и а
(кг) кислоты в 1
растворе.
Ответ: 1,875 кг
В заключение следует отметить, что табличный способ решения задач позволяет структурировать текстовую информацию, является более наглядным и понятным для многих учеников, позволяет оформить задачу более компактно, не требует написания большого текста и экономит время, что является немаловажным фактом на экзаменах. Кроме того, исследование показало, что табличный метод позволил повысить процент правильности выполнения данных задач, а именно, задачи на движение – на 32 % , задачи на работу – на 23 % , задачи на смеси и сплавы – на 24%.
Список литературу
1) Лысенко Ф.Ф. Математика. 9-й класс. Подготовка к ОГЭ – 2021. 40 тренировочных вариантов по демоверсии 2021 года: учебно-методическое пособие / под ред. Ф.Ф. Лысенко, С.О. Иванова. – Ростов н /Д.:Легион,2020.-384 с.
2)
Лысенко Ф.Ф. Математика. Подготовка к ЕГЭ
– 2021. 40 тренировочных вариантов по демоверсии 2021 года: учебно-методическое
пособие / под ред.
Ф.Ф. Лысенко, С.О. Иванова. – Ростов н /Д.:Легион,2020.-400
с.
3) Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В..Полонский, М.С. Якир. – М:Вентана –Граф, 2013. – 256 с.
ФИО (полностью) | Оплачко Ольга Владимировна |
Ученая степень, звание | Нет |
Должность и место работы (полное название организации по Уставу ОО) | Учитель математики и информатики муниципального казенного общеобразовательного учреждения средней общеобразовательной школы №2 |
Муниципальное образование (район, город), в котором располагается ОО | Город Острогожск, Воронежская область |
olia. | |
Телефон для связи | 8-952-559-60-33 |
Адрес проживания с индексом | 397853, Воронежская область, город Острогожск, улица Комсомольская, д.62, кв. 45.
|
12. Сводная таблица видов частных решений для различных видов правых частей
Таблица 1.
N | Правая часть дифф. уравнения | Корни Характеристического уравнения | Виды частного Решения |
I. | 1. Число не является корнем характеристического уравнения | ||
2. Число – корень характеристического уравнения кратности | |||
II. | 1. Число не является корнем характеристического уравнения | ||
2. Число является корнем характеристического уравнения кратности | |||
III. | 1. Числа не являются корнями характеристического уравнения кратности | ||
2. Числа являются корнями характеристического уравнения кратности | |||
IV. | 1. Числа не являются корнями характеристического уравнения кратности | ||
2. Числа являются корнями характеристического уравнения кратности |
Пример. Найти общее решение уравнения
.
Решение. Общее решение данного уравнения складывается из общего решения соответствующего ему однородного уравнения и частного решения данного уравнения, т.
е. .
Найдем общее решение соответствующего однородного уравнения
.
Составим характеристическое уравнение и найдем его корни.
Поэтому общее решение однородного уравнения будет
2.Найдем частное решение данного уравнения. Так как в правой части его дан квадратный многочлен , и ноль не является корнем характеристического уравнения, то частное решение надо искать в виде (см. табл.1, случай I)
Где — неизвестные коэффициенты, которые нужно определить.
Так как выражение для является решением данного уравнения, то функция и ее производные будучи подставлены в это уравнение удовлетворяют тождеству, т. е. сохраняют знак равенства в данном уравнении.
Найдем производные
Подставим эти выражения в данное уравнение и сгруппируем члены равенства по степеням :
.
Так как многочлены равны, то, следовательно, равны соответственные коэффициенты при одинаковых степенях , поэтому
Следовательно, частное решение будет иметь вид , а общее решение данного уравнения будет
Пример.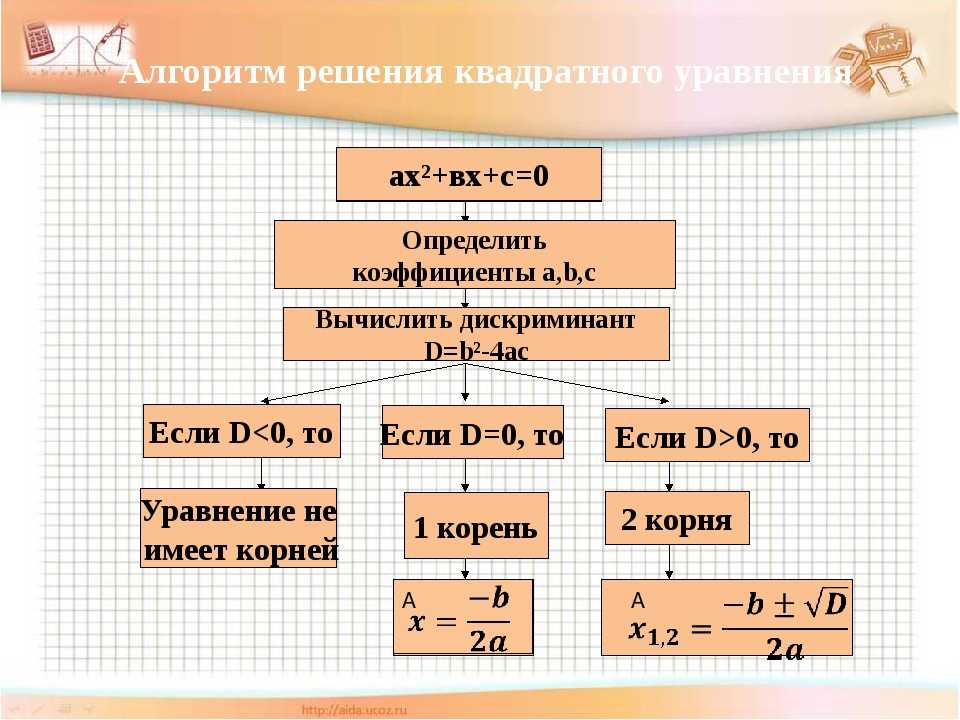
Найти общее решение уравнения .
Решение. Общее решение данного уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения :
1. Определим . Запишем соответственное уравнение . Через характеристическое уравнение находим его общее решение.
Поэтому
2.Определим частное решение .
Представим правую часть данного уравнения в виде (*):
Где — одночлен нулевой степени (вещественное число), а — одночлен первой степени (см. табл.1, случай III(1)). Так как не является корнем характеристичского уравнения, а То частное решение данного уравнения ищем в виде
Тогда
.
Так как является решением данного уравнения, то будучи подставленной в это уравнение вместе со своими производными она удовлетворяет равенству.
Подставим 1 в данное уравнение и сгруппируем по и , будем иметь
Или
Приравниваем коэффициенты в силу равенства выражений при и . Коэффициент при в правой части равен нулю, а при равен , поэтому будем иметь
Так как многочлены равны, то, следовательно, равны их коэффициенты при одинаковых степенях .
Приравнивая коэффициенты левых и правых частей равенств, получим систему относительно :
.
Частное решение запишется
Общее решение данного уравнения
Рассмотрим случай, когда неоднородное уравнение имеет вид
. (6)
Для отыскания частного решения такого уравнения используется теорема:
Если — частное решение уравнения , а — частное решение уравнения , то есть частное решение уравнения (6).
Пример. Проинтегрировать уравнение
Решение. Общее решение данного уравнения
,
Где — общее решение соответственного данному однородного уравнения, — частное решение данного уравнения, где — частное решение уравнения А — частное решение уравнения
1. Определим общее решение для уравнения
Общим решением уравнения будет
2. Определим частное решение уравнения .
Представим правую часть в виде (*)
.
Частное решение ищем в виде (см. табл.1, случай III (2)), так как число является корнем характеристического уравнения кратности :
,
Где и- некоторые вещественные числа и , которые нужно определить.
Итак, частное решение запишется выражением
Тогда
Из тождества которое получится после подстановки И в уравнение , определим и :
Приравниваем коэффициенты при И левой и правой части.
3. Определим частное решение Уравнения
В правой части имеем выражение вида , где . Частное решение Уравнения ищем в виде (см. табл.1, случай II(1)):
,
вычислим производные
Из тождества, полученного после подстановки и В уравнение , определим коэффициенты :
Сократим на
.
Приравняем коэффициенты при одинаковых степенях левой и правой частей равенства.
, решая систему, получим .
Получили
Следовательно, общее решение данного уравнения
| < Предыдущая | Следующая > |
|---|
Написание уравнения для описания таблицы — Задача 2
Чтобы написать функцию для описания таблицы значений, сначала посмотрите, есть ли какие-либо шаблоны, которые появляются сразу.
Если нет, то рассмотрите форму пересечения наклона линии y=mx+b, где m = наклон и b = пересечение y. Точка пересечения с осью Y — это точка пересечения прямой с осью Y. В этой точке точки координат будут иметь значение x, равное 0. Следовательно, в таблице значений, если есть пара значений, в которых x равно 0, то эта упорядоченная пара представляет собой точку, которую пересекает график функции. ось y или точка пересечения y, которая равна «b». Затем, чтобы найти наклон, используйте формулу наклона и подставьте значения из двух упорядоченных пар из таблицы значений в качестве значений x1, y1 и x2, y2. Поскольку наклон, по сути, представляет собой изменение значения x по сравнению с изменением значения y, вы также можете найти наклон, определив единицу изменения для x и y. Как только вы найдете значение наклона, вставьте его в форму пересечения наклона линии. Результатом является функция, описывающая отношения в заданной таблице значений. Убедитесь, что оно равно f(x).
функция склон ты перехватываешь шаблон
Эта задача немного сложна, потому что, когда вы смотрите на это количество ящиков, вы видите, что оно уменьшается.
Я начинаю с 1, 2, 3, 4, умножить на 4. Я начинаю с 16 ящиков, затем сокращаю до 12, затем 8, а затем 4. Так что это немного отличается от некоторых задач, которые вы, возможно, видели. потому что эти числа уменьшаются, а не увеличиваются. Картинки становятся меньше.
Итак, что я хочу сделать, так это поискать какие-то шаблоны, посмотреть, смогу ли я увидеть что-нибудь, что я могу признать математическим шаблоном, с которым я знаком. Например, чтобы помочь мне организовать это, я собираюсь сделать таблицу, в которой у меня будет номер изображения, а затем количество ящиков, и это поможет мне искать закономерности. Как и на моей картинке, числа 0, 1, 2, 3 и 4, 0, 1, 2, 3 и 4, а затем, если вы посчитаете, сколько ящиков в 16, то у нас есть 12, затем у нас есть 8, а затем 4 и тогда на этой четвертой картинке нет ящиков. Это немного странно, что мы разберемся с этим, когда доберемся до этого.
Итак, это просто еще один способ представления той же информации, и мне нужно найти уравнение, описывающее это.
Итак, я начну с написания уравнения словами, а через секунду переделаю его в математические символы. Количество ящиков будет равно чему-то.
Я заметил одну вещь: я начинаю с 16, моя нулевая группа начиналась с 16, а оттуда она уменьшается. Итак, я собираюсь сказать, что 16 уберут что-то, чего я еще не знаю, что там будет. Тогда давайте посмотрим, насколько он снижается. Каждый раз, когда я вычитаю 4 ячейки, как раньше у меня было четыре строки по четыре или четыре столбца по четыре, теперь у меня есть только три столбца по четыре, это тот, который был удален.
Здесь я снова убираю колонку из 4 клеток с предыдущей картинки. Происходит то, что я вычитаю 4 каждый раз. Вы можете увидеть это здесь, уберите 4, уберите 4 и так далее и так далее. Таким образом, способ написания этого шаблона будет в 4 раза больше номера изображения, номера изображения. Вот как я написал бы это словами, или, если бы я хотел использовать математические символы, я бы убрал в 4 раза это правило, или это уравнение описывает, сколько клеток есть в каждом номере изображения.
Опять же, это немного странно, потому что вместо того, чтобы увеличиваться, картинки становятся меньше, но вы все еще можете использовать свои техники узоров. Посмотрите, с чего вы начинаете, а затем посмотрите, насколько сильно вы меняетесь. Мы начали с 16, а затем каждый раз уменьшаем на четыре.
Как найти уравнение по таблице чисел
Обновлено 2 ноября 2020 г.
Автор: Мариекор Аграванте
Математические уравнения — это, по сути, соотношения. Уравнение линии описывает взаимосвязь между значениями x и y , найденными на координатной плоскости. Уравнение прямой записывается как y=mx + b , где константа m — наклон линии, а b — .0025 г -перехват. Один из часто задаваемых алгебраических проблемных вопросов заключается в том, как найти уравнение прямой из набора значений, например таблицы чисел, соответствующих координатам точек. Вот как решить эту алгебраическую задачу.
Понимание значений в таблице
Числа в таблице часто представляют собой значения x и y , которые верны для линии, что означает x и Значения y соответствуют координатам точек на прямой.
Учитывая, что линейное уравнение равно y=mx + b , значения x и y — это числа, которые можно использовать для получения неизвестных, таких как наклон и точка пересечения с осью y.
Найти уклон
Наклон линии, представленный м , измеряет ее крутизну. Кроме того, наклон дает ключ к пониманию направления линии в координатной плоскости. Наклон постоянен в линии, что объясняет, почему его значение можно рассчитать. Наклон можно определить по 9Значения 0025 x и y представлены в данной таблице. Помните, что значения x и y соответствуют точкам на линии. В свою очередь, для вычисления наклона линейного уравнения необходимо использовать две точки, такие как точка A ( x 1 , y 1 ) и точка B ( x 2 ). , г 2 ). Уравнение для нахождения уклона:
м = \frac{y_2-y_1}{x_2-x_1}
для определения члена м .
Обратите внимание, что из этого уравнения наклон представляет собой изменение значения y на единицу изменения значения x . Давайте возьмем в качестве примера первую точку, А, являющуюся (2, 5), и вторую точку, В, являющуюся (7, 30). Уравнение, которое нужно решить для уклона, тогда принимает вид
После определения наклона следующим неизвестным, который нужно найти, является член b , что является пересечением y . Точка пересечения y определяется как значение, при котором линия пересекает ось y на графике. Чтобы получить точку пересечения y линейного уравнения с известным наклоном, подставьте значения x и y из таблицы. Поскольку предыдущий шаг выше показал, что наклон равен 5, подставьте значения точки A (2, 5) в уравнение линии, чтобы найти значение b . Таким образом, y=mx + b становится
5=(5 × 2)+b =10+b
, так что значение b равно −5.