Сколько градусов в полном углу: Полный угол – градус

Содержание

Отсчёт углов на тригонометрическом круге. Положительные и отрицательные углы. Распределение углов по четвертям. Измерение углов Могут ли градусы быть отрицательными

Угол: ° π rad =

Преобразовать в: радианы градусы 0 — 360° 0 — 2π положительное отрицательное Вычислять

Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами .

На картинке видны 4 разных угла, образованных пересечением прямых AB и CD

Обычно углы измеряются в градусах, что обозначается как °. Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°). Таким образом, градус — это $\frac{1}{360}$ круга.

Углы больше 360 градусов

Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов

Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.

В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.

Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)

Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360. Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.

Пример 3
1. Найти соответствующий положительный угол

a) -35°
b) -60°
c) -180°
d) — 670°

2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°

2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°

Радиан

Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.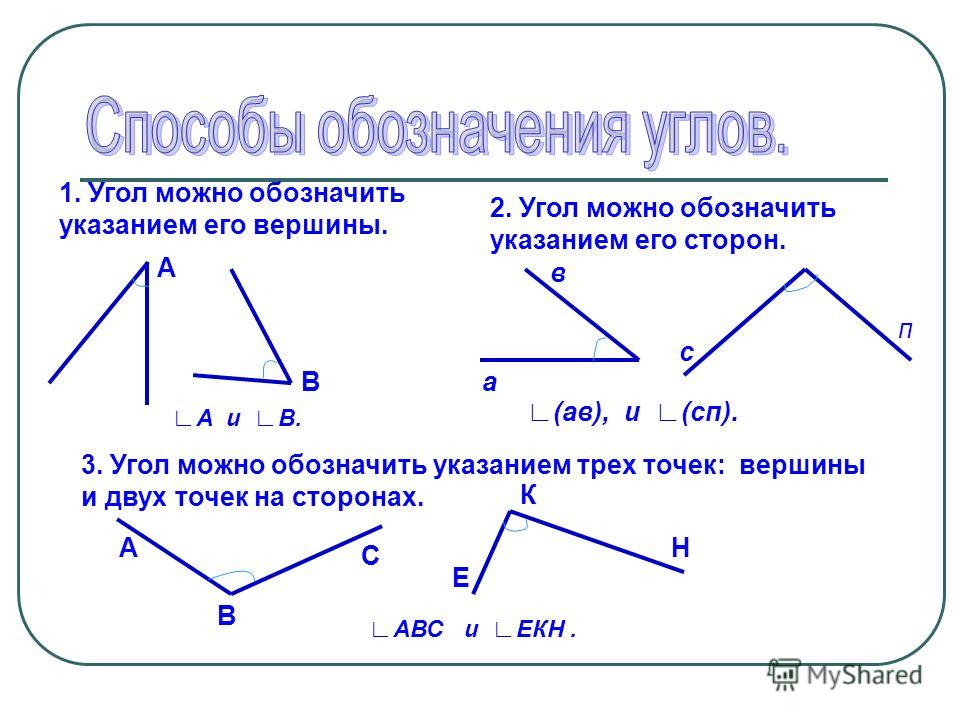

{\circ}$
c) 1 рад = 57.3°
$2.4 = \frac{2.4 \times 57.3}{1} = 137.52$

Отрицаетльные углы и углы больше, чем $2\pi$ радиан

Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.

Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.

Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$

$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$

Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.

Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$

Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.

b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки

c) $\frac{7}{2}\pi=3.5\pi=2\pi+1.5\pi$, $1.5\pi$ равно три четверти цикла $(\frac{1.5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки

Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.

Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.

В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.

Основные величины тригонометрии

Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.

В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.

Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:

Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.

Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

Итак, не трудно догадаться, что 2π – это полная окружность или 360°.

Свойства тригонометрических функций: синус и косинус

Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.

Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:

Синусоида	Косинусоида
y = sin x	y = cos x
ОДЗ [-1; 1]	ОДЗ [-1; 1]
sin x = 0, при x = πk, где k ϵ Z	cos x = 0, при x = π/2 + πk, где k ϵ Z
sin x = 1, при x = π/2 + 2πk, где k ϵ Z	cos x = 1, при x = 2πk, где k ϵ Z
sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z	cos x = — 1, при x = π + 2πk, где k ϵ Z
sin (-x) = — sin x, т. е. функция нечетная	cos (-x) = cos x, т. е. функция четная
	функция периодическая, наименьший период — 2π
sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk)	cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk)
возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk]	возрастает на промежутке [-π + 2πk, 2πk]
убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk]	убывает на промежутках
производная (sin x)’ = cos x	производная (cos x)’ = — sin x

Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.

Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:

Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.

Свойства тангенсоиды и котангенсоиды

Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.

Y = tg x.
Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
Наименьший положительный период тангенсоиды равен π.
Tg (- x) = — tg x, т. е. функция нечетная.
Tg x = 0, при x = πk.
Функция является возрастающей.
Tg x › 0, при x ϵ (πk, π/2 + πk).
Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
Производная (tg x)’ = 1/cos 2 ⁡x .

Рассмотрим графическое изображение котангенсоиды ниже по тексту.

Основные свойства котангенсоиды:

Y = ctg x.
В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
Наименьший положительный период котангенсоиды равен π.
Ctg (- x) = — ctg x, т. е. функция нечетная.
Ctg x = 0, при x = π/2 + πk.
Функция является убывающей.
Ctg x › 0, при x ϵ (πk, π/2 + πk).
Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
Производная (ctg x)’ = — 1/sin 2 ⁡x Исправить

Пара различных лучей Оа и Оb, выходящих из одной точки О, называется углом и обозначается символом (а, b). Точка О называется вершиной угла, а лучи Оа u Оb — сторонами угла. Если А и В — две точки лучей Оа и Оb, то (а, b) обозначается также символом АОВ (рис. 1.1).

Угол (а, Ь) называют развернутым, если лучи Оа и Ob, выходящие из одной точки, лежат на одной прямой и не совпадают (т. е. противоположно направлены).

Рис.1.1

Два угла считаются равными, если один угол можно наложить на другой так, чтобы стороны углов совпадали. Биссектрисой угла называется луч с началом в вершине угла, делящий угол на два равных угла.

Говорят, что луч ОС, исходящий из вершины угла АОВ, лежит между его сторонами, если он пересекает отрезок АВ (рис. 1.2). Говорят, что точка С лежит между сторонами угла, если через эту точку можно провести луч с началом в вершине угла, лежащий между сторонами угла. Множество всех точек плоскости, лежащих между сторонами угла, образует внутреннюю область угла (рис. 1.3). Множество точек плоскости, не принадлежащих внутренней области и сторонам угла, образует внешнюю область угла.

Угол (а, b) считают больше угла (c, d), если угол (с, d) можно наложить на угол (а, b) так, что после совмещения одной пары сторон вторая сторона угла (с, d) будет лежать между сторонами угла (а, b). На рис. 1.4 АОВ больше АОС.

Пусть луч с лежит между сторонами угла (а, b) (рис. 1.5). Пары лучей а, с и с, b образуют два угла. Об угле (а, b) говорят, что он является суммой двух углов (а, с) и (с, b), и пишут: (а, b) = (а, с) + (с, b).

Рис.1.3

Обычно в геометрии имеют дело с углами, меньшими развернутого. Однако в результате сложения двух углов может получиться угол, больший развернутого. В этом случае ту часть плоскости, которая считается внутренней областью угла, отмечают дугой. На рис. 1.6 внутренняя часть угла АОВ, полученного в результате сложения углов АОС и СОВ и большего развернутого, отмечена дугой.

Рис.1.5

Существуют также углы большие 360°. Такие углы образуются, например, вращением пропеллера самолета, вращением барабана, на который наматывается канат, и т. д.

В дальнейшем при рассмотрении каждого угла условимся считать одну из сторон этого угла его начальной стороной, а другую — конечной стороной.

Любой угол, например угол АОВ (рис. 1.7), можно получить в результате вращения подвижного луча вокруг вершины О от начальной стороны угла (ОА) до его конечной стороны (ОВ). Мы будем измерять этот угол, учитывая полное количество оборотов, сделанных при этом вокруг точки О, а также и направление, в котором происходило вращение.

Положительные и отрицательные углы.

Пусть мы имеем угол, образованный лучами ОА и ОВ (рис.1.8). Подвижный луч, вращаясь вокруг точки О от своего начального положения (ОА), может занять конечное положение (ОВ) при двух различных направлениях вращения. Эти направления показаны на рисунке 1.8 соответствующими стрелками.

Рис.1.7

Подобно тому, как на числовой оси одно из двух направлений считается положительным, а другое отрицательным, различают и два различных направления вращения подвижного луча. Условились считать положительным направлением вращения то направление, которое противоположно направлению вращения часовой стрелки. Направление вращения, совпадающее с направлением вращения часовой стрелки, считается отрицательным.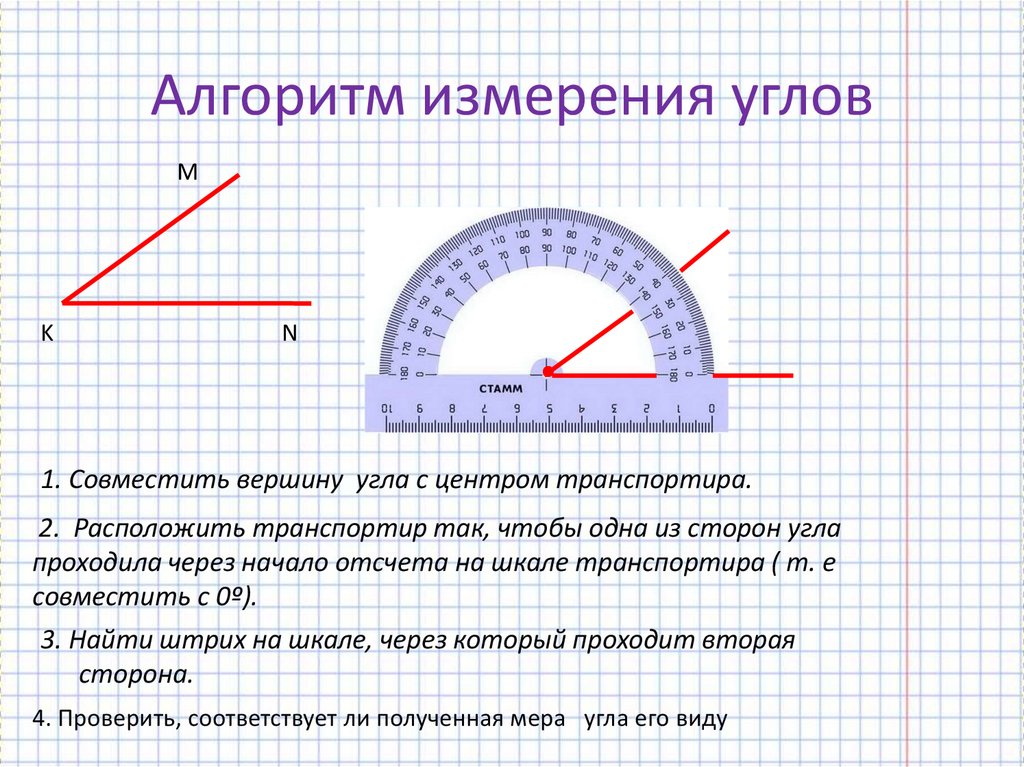

В соответствии с этими определениями углы также подразделяются на положительные и отрицательные.

Положительным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в положительном направлении.

На рисунке 1.9 даны некоторые положительные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)

Отрицательным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в отрицательном направлении.

На рисунке 1.10 изображены некоторые отрицательные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)

Но два совпадающих луча могут также образовать и углы +360°п и -360°п (п = 0,1,2,3,…). Обозначим через б наименьший возможный неотрицательный угол поворота, переводящий луч ОА в положение ОВ. Если теперь луч ОВ совершит дополнительно полный оборот вокруг точки О, то получим другую величину угла, а именно: АВО = б + 360°.

Измерение углов дугами окружности.

Единицы измерения дуг и углов

В ряде случаев оказывается удобным измерять углы при помощи дуг окружности. Возможность такого измерения основа на известном предложении планиметрии о том, что в одном круге (или в равных кругах) центральные углы и соответствующие им дуги находятся в прямой пропорциональной зависимости.

Пусть некоторая дуга данной окружности принята за единицу измерения дуг. Соответствующий этой дуге центральный угол примем за единицу измерения углов. При таком условии любая дуга окружности и соответствующий этой дуге центральный угол будут содержать одно и то же число единиц измерения. Поэтому, измеряя дуги окружности, можно определять и величину соответствующих этим дугам центральных углов.

Рассмотрим две наиболее распространенные системы измерения дуг и углов.

Градусная мера измерения углов

При градусном измерении углов в качестве основной единицы измерения углов (эталонного угла, с которым сравниваются различные углы) берется угол в один градус (обозначается 1?). Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).

Радианная мера измерения углов

Наряду с градусной мерой измерения углов в геометрии и тригонометрии употребляется и другая мера измерения углов, называемая радианной. Рассмотрим окружность радиуса R с центром О. Проведем два радиуса О А и ОВ так, чтобы длина дуги АВ была равна радиусу окружности (рис. 1.12). Получившийся при этом центральный угол АОВ будет углом в один радиан. Угол в 1 радиан принимается за единицу измерения радианной меры измерения углов. При радианном измерении углов развернутый угол равен р радиан.

Градусная и радианная единицы измерения углов связаны равенствами:

1 радиан =180?/р57° 17″ 45″; 1?=р/180 радиана0,017453радиана;

1″=р/180*60 радиана0,000291 радиана;

1″»=р/180*60*60 радиана0,000005 радиана.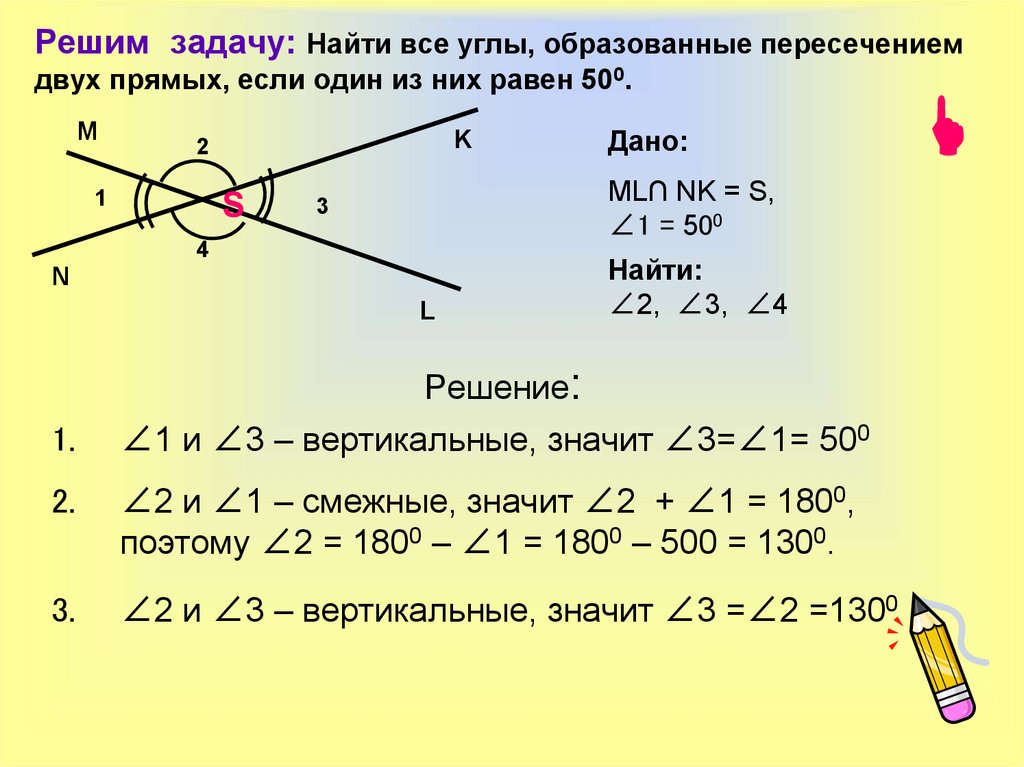

Градусную (или радианную) меру угла также называют величиной угла. Величину угла АОВ иногда обозначают /

Классификация углов

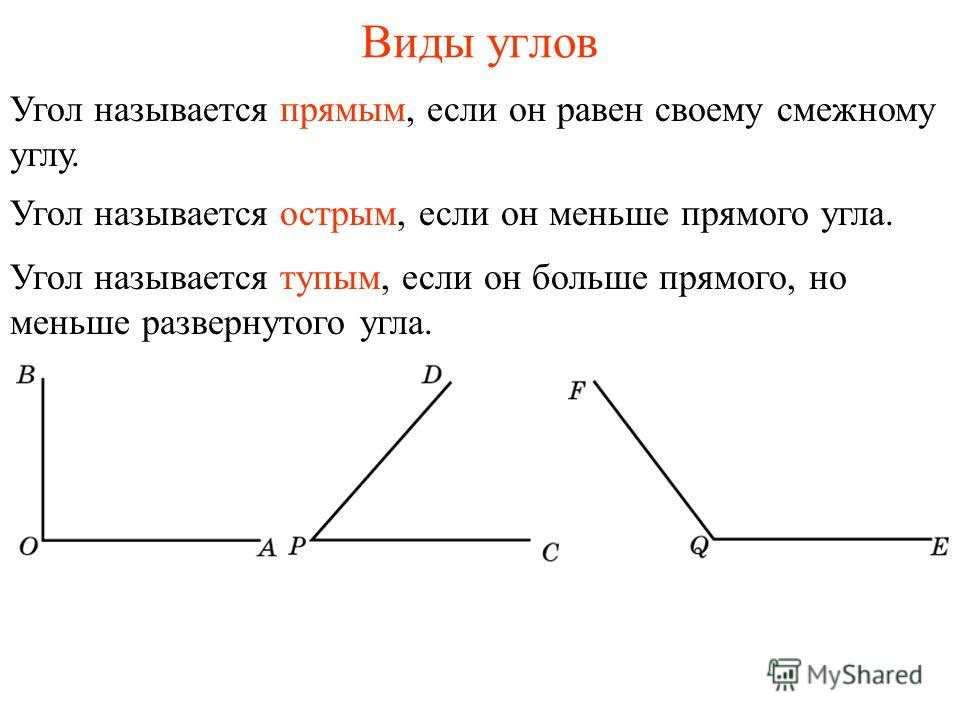
Угол, равный 90°, или в радианной мере р/2, называется прямым углом; его часто обозначают буквой d. Угол, меньший 90°, называется острым; угол, больший 90°, но меньший 180°, называется тупым.

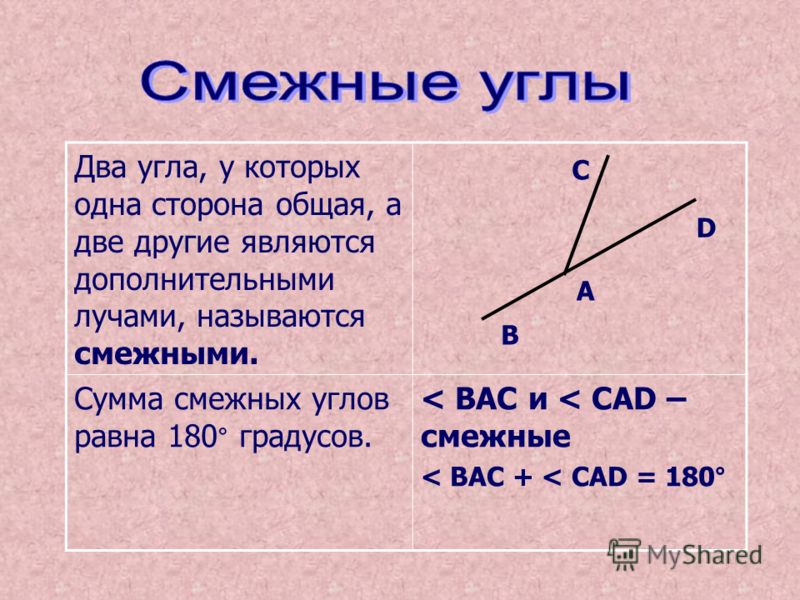
Два угла, имеющие одну общую сторону и в сумме составляющие 180°, называются смежными углами. Два угла, имеющие одну общую сторону и в сумме составляющие 90°, называются дополнительными углами.

Отсчёт углов на тригонометрическом круге.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Он почти такой, как в предыдущем уроке. Есть оси, окружность, угол, всё чин-чинарём. Добавлены номера четвертей (в уголках большого квадрата) — от первой, до четвёртой. А то вдруг кто не знает? Как видите, четверти (их ещё называют красивым словом «квадранты») нумеруются против хода часовой стрелки. Добавлены значения угла на осях. Всё понятно, никаких заморочек.

И добавлена зелёная стрелка. С плюсом. Что она означает? Напомню, что неподвижная сторона угла всегда прибита к положительной полуоси ОХ. Так вот, если подвижную сторону угла мы будем крутить по стрелке с плюсом , т.е. по возрастанию номеров четвертей, угол будет считаться положительным. Для примера на картинке показан положительный угол +60°.

Если будем откладывать углы в обратную сторону, по ходу часовой стрелки, угол будет считаться отрицательным. Наведите курсор на картинку (или коснитесь картинки на планшете), увидите синюю стрелку с минусом. Это — направление отрицательного отсчёта углов. Для примера показан отрицательный угол (- 60°). А ещё вы увидите, как поменялись циферки на осях… Я их тоже перевёл в отрицательные углы. Нумерация квадрантов не меняется.

Вот тут, обычно, начинаются первые непонятки. Как так!? А если отрицательный угол на круге совпадёт с положительным!? Да и вообще, получается что, одно и то же положение подвижной стороны (или точки на числовой окружности) можно обозвать как отрицательным углом, так и положительным!?

Да.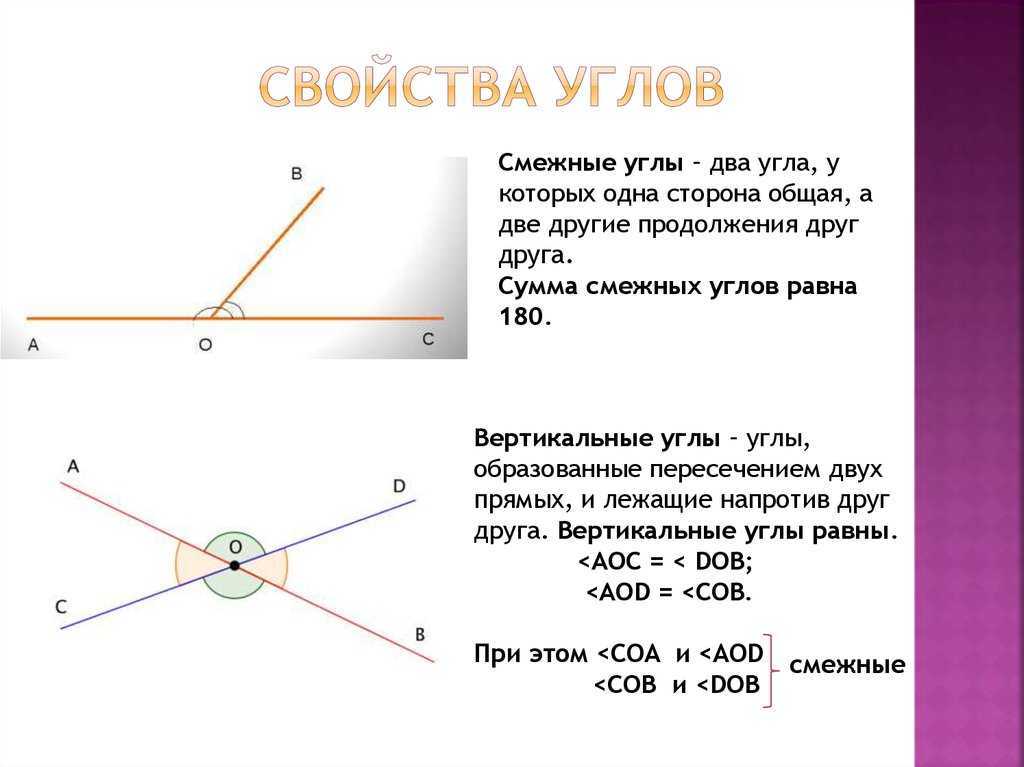 Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.

Не вопрос. Всяко правильно.) Выбор положительного или отрицательного исчисления угла зависит от условия задания. Если в условии ничего не сказано открытым текстом про знак угла, (типа «определить наименьший положительный угол» и т.д.), то работаем с удобными нам величинами.

Исключением (а как без них?!) являются тригонометрические неравенства, но там мы эту фишку освоим.

А теперь вопрос вам. Как я узнал, что положение угла 110° совпадает с положением угла -250°?
Намекну, что это связано с полным оборотом. В 360°… Непонятно? Тогда рисуем круг. Сами рисуем, на бумаге. Отмечаем угол примерно 110°. И считаем , сколько остается до полного оборота. Останется как раз 250°…

Уловили? А теперь — внимание! Если углы 110° и -250° занимают на круге одно и то же положение, то что? Да то, что у углов 110° и -250° совершенно одинаковые синус, косинус, тангенс и котангенс!
Т.е. sin110° = sin(-250°), ctg110° = ctg(-250°) и так далее. Вот это уже действительно важно! И само по себе — есть масса заданий, где надо упростить выражения, и как база для последующего освоения формул приведения и прочих премудростей тригонометрии.

Понятное дело, 110° и -250° я взял наобум, чисто для примера. Всё эти равенства работают для любых углов, занимающих одно положение на круге. 60° и -300°, -75° и 285°, ну и так далее. Отмечу сразу, что углы в этих парочках — разные. А вот тригонометрические функции у них — одинаковые.

Думаю, что такое отрицательные углы вы поняли. Это совсем просто. Против хода часовой стрелки — положительный отсчёт. По ходу — отрицательный. Считать угол положительным, или отрицательным зависит от нас . От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.

Углы больше 360°.

Займемся углами которые больше 360°. А такие бывают? Бывают, конечно. Как их нарисовать на круге? Да не проблема! Допустим, нам надо понять, в какую четверть попадёт угол в 1000°? Легко! Делаем один полный оборот против хода часовой стрелки (угол-то нам дали положительный!). Отмотали 360°. Ну и мотаем дальше! Ещё оборот — уже получилось 720°. Сколько осталось? 280°. На полный оборот не хватает… Но угол больше 270° — а это граница между третьей и четвёртой четвертью. Стало быть наш угол в 1000° попадает в четвёртую четверть. Всё.

Как видите, это совсем просто. Ещё раз напомню, что угол 1000° и угол 280°, который мы получили путём отбрасывания «лишних» полных оборотов — это, строго говоря, разные углы.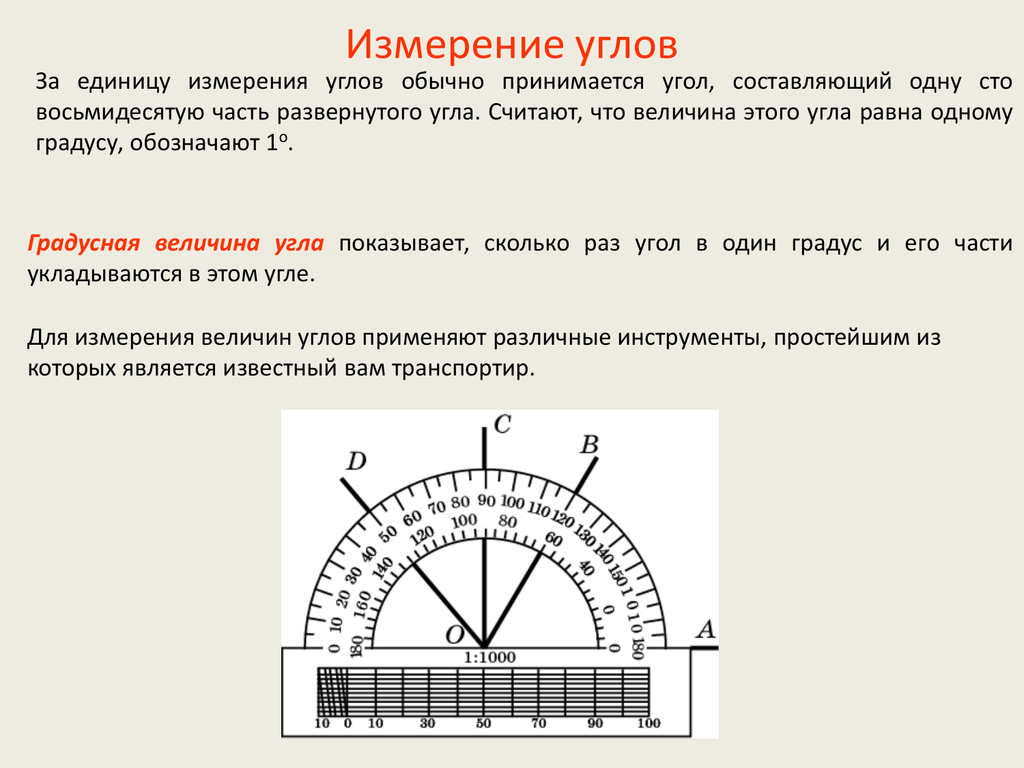 Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…

Зачем всё это нужно? Зачем нам переводить углы из одного в другой? Да всё за тем же.) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)

Ну что, потренируемся?)

Отвечаем на вопросы. Сначала простые.

1. В какую четверть попадает угол -325° ?

2. В какую четверть попадает угол 3000° ?

3. В какую четверть попадает угол -3000° ?

Есть проблемы? Или неуверенность? Идём в Раздел 555, Практическая работа с тригонометрическим кругом. Там, в первом уроке этой самой «Практической работы…» всё подробненько… В таких вопросах неуверенности быть не должно!

4. Какой знак имеет sin555° ?

5. Какой знак имеет tg555° ?

Определили? Отлично! Сомневаетесь? Надо в Раздел 555.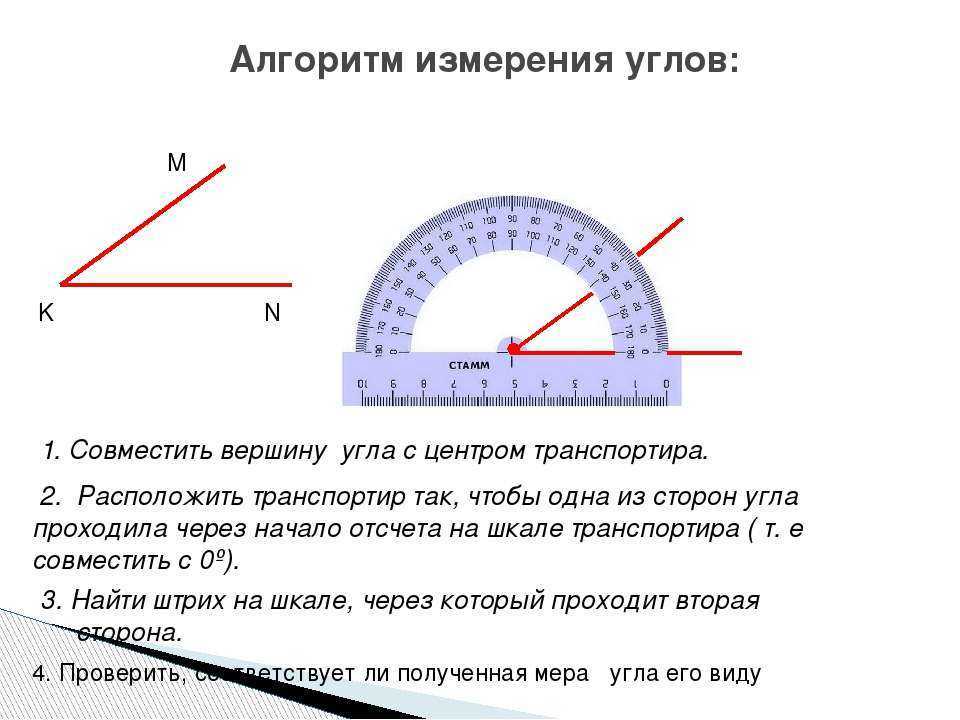 .. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.

А теперь вопросы помудрёнее.

6. Привести выражение sin777° к синусу наименьшего положительного угла.

7. Привести выражение cos777° к косинусу наибольшего отрицательного угла.

8. Привести выражение cos(-777°) к косинусу наименьшего положительного угла.

9. Привести выражение sin777° к синусу наибольшего отрицательного угла.

Что, вопросы 6-9 озадачили? Привыкайте, на ЕГЭ и не такие формулировочки встречаются… Так и быть, переведу. Только для вас!

Слова «привести выражение к…» означают преобразовать выражение так, чтобы его значение не изменилось, а внешний вид поменялся в соответствии с заданием. Так, в задании 6 и 9 мы должны получить синус, внутри которого стоит наменьший положительный угол. Всё остальное — не имеет значения.

Ответы выдам по порядку (в нарушение наших правил). А что делать, знака всего два, а четверти всего четыре… Не разбежишься в вариантах.

6. sin57°.

7. cos(-57°).

8. cos57°.

9. -sin(-57°)

Предполагаю, что ответы на вопросы 6 -9 кое-кого смутили. Особенно -sin(-57°) , правда?) Действительно, в элементарных правилах отсчёта углов есть место для ошибок… Именно поэтому пришлось сделать урок: «Как определять знаки функций и приводить углы на тригонометрическом круге?» В Разделе 555. Там задания 4 — 9 разобраны. Хорошо разобраны, со всеми подводными камнями. А они тут есть.)

В следующем уроке мы разберёмся с загадочными радианами и числом «Пи» . Научимся легко и правильно переводить градусы в радианы и обратно. И с удивлением обнаружим, что этой элементарной информации на сайте уже хватает , чтобы решать некоторые нестандартные задачки по тригонометрии!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас. )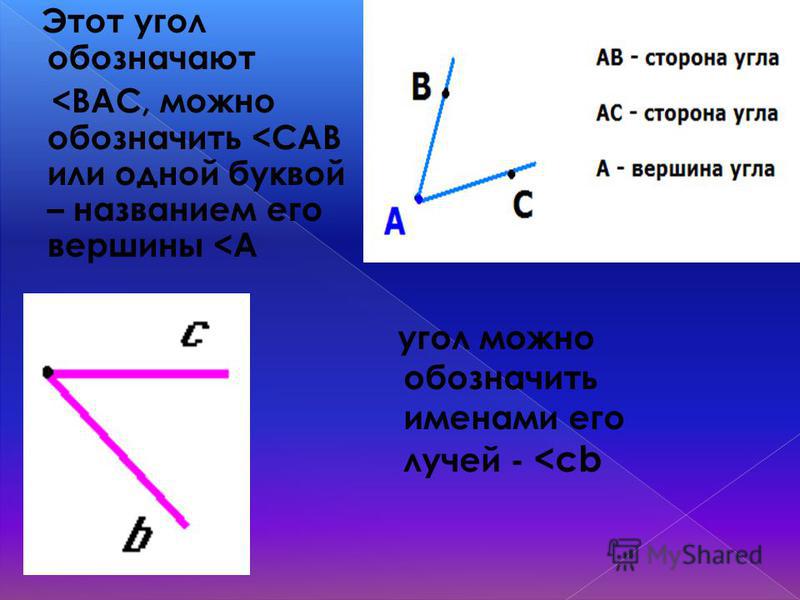

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В тригонометрии важным понятием является угол поворота . Ниже мы последовательно будем давать представление о повороте, и вводить все сопутствующие понятия. Начнем с общего представления о повороте, скажем о полном обороте. Далее перейдем к понятию угла поворота и рассмотрим его основные характеристики, такие как направление и величина поворота. Наконец, дадим определение поворота фигуры вокруг точки. Всю теорию по тексту будем снабжать поясняющими примерами и графическими иллюстрациями.

Навигация по странице.

Что называют поворотом точки вокруг точки?

Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.

Введем понятие поворота точки вокруг точки .

Сначала дадим определение центра поворота.

Определение.

Точку, относительно которой осуществляется поворот, называют центром поворота .

Теперь скажем, что получается в результате поворота точки.

В результате поворота некоторой точки A относительно центра поворота O получается точка A 1 (которая в случае некоторого количества может совпадать с A ), причем точка A 1 лежит на окружности с центром в точке O радиуса OA . Иными словами, при повороте относительно точки O точка A переходит в точку A 1 , лежащую на окружности с центром в точке O радиуса OA .

Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.

Также стоит отметить, что поворот точки А вокруг точки O стоит рассматривать как перемещение в результате движения точки А по окружности с центром в точке O радиуса OA .

Для наглядности приведем иллюстрации поворота точки А вокруг точки O , на рисунках, расположенных ниже, перемещение точки А в точку А 1 покажем при помощи стрелки.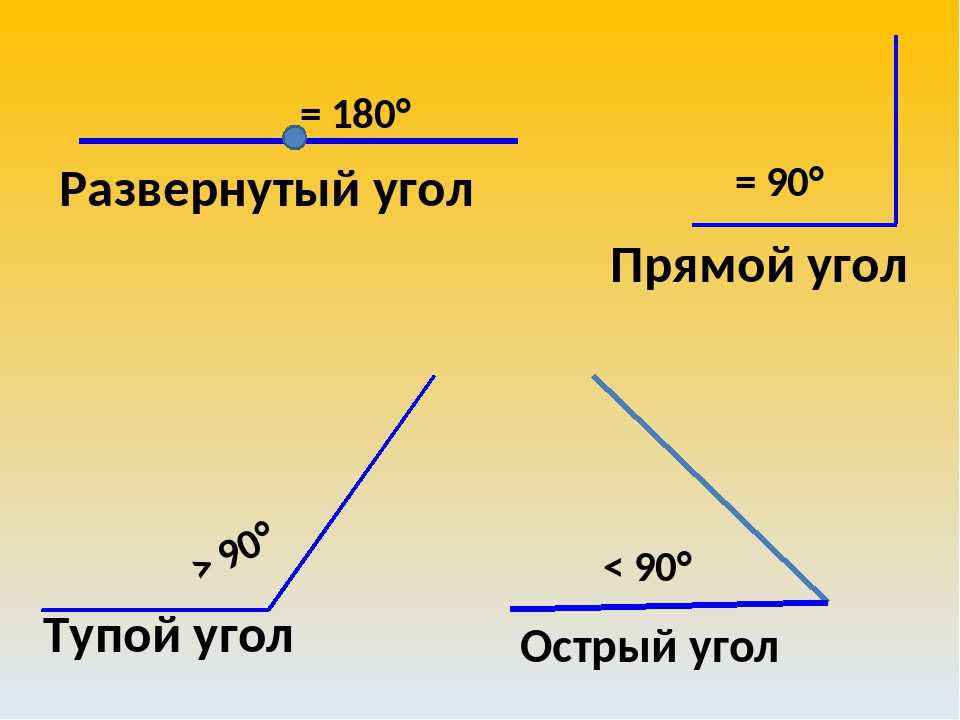

Полный оборот

Можно выполнить такой поворот точки A относительно центра поворота O , что точка А , пройдя все точки окружности, окажется на прежнем месте. При этом говорят, что точка А совершила вокруг точки O .

Дадим графическую иллюстрацию полного оборота.

Если же не останавливаться на одном обороте, а продолжать движение точки по окружности, то можно выполнить два, три и так далее полных оборотов. На чертеже ниже справа показано, как могут быть произведены два полных оборота, а слева — три оборота.

Понятие угла поворота

Из введенного в первом пункте понятия поворота точки понятно, что существует бесконечное множество вариантов поворота точки А вокруг точки O . Действительно, любую точку окружности с центром в точке O радиуса OA можно рассматривать как точку A 1 , полученную в результате поворота точки А . Поэтому, чтобы отличать один поворот от другого, вводится понятие угла поворота .

Одной из характеристик угла поворота является направление поворота . По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.

Другой характеристикой угла поворота является его величина . Углы поворота измеряются в тех же единицах, что и : наиболее распространены градусы и радианы. Здесь стоит заметить, что угол поворота может выражаться в градусах любым действительным числом из промежутка от минус бесконечности до плюс бесконечности, в отличие от угла в геометрии, величина которого в градусах положительна и не превосходит 180 .

Для обозначения углов поворота обычно используются строчные буквы греческого алфавита: и т.д. Для обозначения большого количества углов поворота часто применяют одну букву с нижними индексами, к примеру, .

Теперь поговорим о характеристиках угла поворота подробнее и по порядку.

Направление поворота

Пусть на окружности с центром в точке O отмечены точки A и A 1 . В точку А 1 можно попасть из точки A , выполнив поворот вокруг центра O либо по часовой стрелке, либо — против часовой стрелки. Эти повороты логично считать различными.

Проиллюстрируем повороты в положительном и отрицательном направлении. На чертеже ниже слева показан поворот в положительном направлении, а справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, отличной от центра поворота, полностью определяется указанием его величины, с другой стороны, по величине угла поворота можно судить о том, как этот поворот был осуществлен.

Как мы уже упоминали выше, величина угла поворота в градусах выражается числом от −∞ до +∞ . При этом знак плюс соответствует повороту по часовой стрелке, а знак минус – повороту против часовой стрелки.

Теперь осталось установить соответствие между величиной угла поворота и тем, какому повороту она соответствует.

Начнем с угла поворота, равного нулю градусам. Этому углу поворота отвечает перемещение точки А в себя. Другими словами, при повороте на 0 градусов вокруг точки O точка А остается на месте.

Переходим к повороту точки А вокруг точки O , при котором поворот происходит в пределах половины оборота. Будем считать, что точка А переходит в точку А 1 . В этом случае абсолютная величина угла AOA 1 в градусах не превосходит 180 . Если поворот происходил в положительном направлении, то величина угла поворота считается равной величине угла AOA 1 , а если поворот происходил в отрицательном направлении, то его величина считается равной величине угла АОА 1 со знаком минус. Для примера приведем рисунок, показывающий углы поворота в 30 , 180 и −150 градусов.

Углы поворота большие 180 градусов и меньшие −180 градусов определяются на основе следующего достаточно очевидного свойства последовательных поворотов : несколько последовательных поворотов точки A вокруг центра O равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Приведем пример, иллюстрирующий данное свойство. Выполним поворот точки А относительно точки O на 45 градусов, а затем еще повернем эту точку на 60 градусов, после чего повернем эту точку на −35 градусов. Обозначим промежуточные точки при этих поворотах как A 1 , A 2 и A 3 . В эту же точку А 3 мы могли попасть, выполнив один поворот точки A на угол 45+60+(−35)=70 градусов.

Итак, углы поворота, большие 180 градусов, мы будем представлять как несколько последовательных поворотов на углы, сумма величин которых дает величину исходного угла поворота. Например, угол поворота 279 градусов соответствует последовательным поворотам на 180 и 99 градусов, или на 90 , 90 , 90 и 9 градусов, или на 180 , 180 и −81 градус, или на 279 последовательных поворотов по 1 градусу.

Аналогично определяются и углы поворота, меньшие −180 градусов. К примеру, угол поворота −520 градусов можно интерпретировать как последовательные повороты точки на −180 , −180 и −160 градусов.

Подведем итог . Мы определили угол поворота, величина которого в градусах выражается некоторым действительным числом из промежутка от −∞ до +∞ . В тригонометрии мы будем работать именно с углами поворота, хотя слово «поворот» часто опускают, и говорят просто «угол». Таким образом, в тригонометрии мы будем работать с углами произвольной величины, под которыми будем понимать углы поворота.

В заключение этого пункта отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 градусов (или 2·π радианов), а в отрицательном – углу поворота в −360 градусов (или −2·π рад). При этом удобно большие углы поворота представлять как некоторое количество полных оборотов и еще один поворот на угол величиной от −180 до 180 градусов. Для примера возьмем угол поворота 1 340 градусов. Несложно 1 340 представить как 360·4+(−100) . То есть, исходному углу поворота отвечают 4 полных оборота в положительном направлении и последующий поворот на −100 градусов. Другой пример: угол поворота −745 градусов можно интерпретировать как два оборота против часовой стрелки и последующий поворот на −25 градусов, так как −745=(−360)·2+(−25) .

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко расширяется на поворот любой фигуры вокруг точки на угол (речь идет о таком повороте, что и точка, относительно которой осуществляется поворот, и фигура, которую поворачивают, лежат в одной плоскости).

Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.

В качестве примера приведем иллюстрацию следующему действию: выполним поворот отрезка AB на угол относительно точки O , это отрезок при повороте перейдет в отрезок A 1 B 1 .

Список литературы.

Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- isbn 5-09-002727-7
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Измерение углов. Транспортир. Видеоурок. Математика 5 Класс

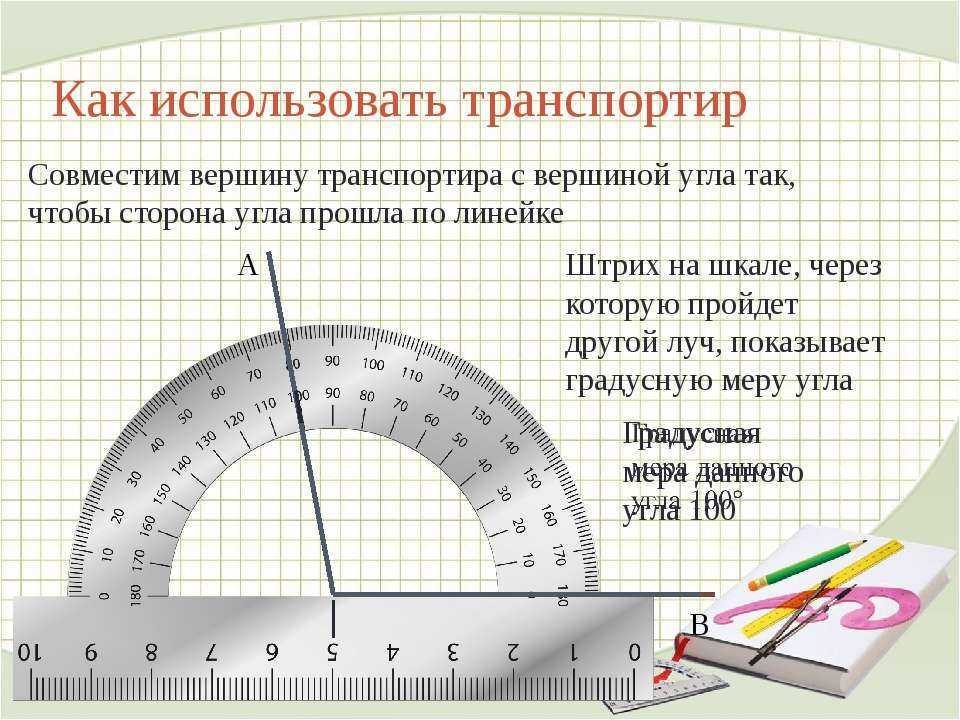
Транспортир — это простой и удобный инструмент для измерения и построения углов. В основном распространены транспортиры полукруглой формы, хотя существуют и круглые транспортиры, рассчитанные на 360 градусов. Если вы впервые столкнулись с транспортиром и не знаете, как им пользоваться, прочитайте эту статью! Это совсем несложно: несколько простых шагов, и вы как следует освоите этот полезный инструмент.

Транспортиром пользуются для измерения углов.

Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой. На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».

Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.

На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю. Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).

Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.

Что такое транспортир?

Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

Образовательные:

познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
научить пользоваться транспортиром.

Развивающие:развивать внимание, мышление учащихся;развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;развивать познавательный интерес к предмету.Воспитательные:воспитывать чувство взаимоуважения;воспитывать у учащихся навыки учебного труда.
I. Организационный момент

II. Вступительное слово учителя

Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны. Будем учиться не только математике, но и умению общаться, уважению друг к другу. Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:

Правила пользования

В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.

Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.

Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.

Измеряем угол

Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:

Острый. Таким называют угол до 90 градусов.
Прямым является угол, равный 90 градусам.
Тупой угол варьируется в диапазоне от 90 до 180 градусов.
Развёрнутый угол представляет собой прямую линию или 180 градусов.
Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.

Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.

Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

Набор школьника

Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.

Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.

Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.

Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!

Итог

На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира. Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок и

Метр, дюйм, аршин — это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд — это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах — время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).

Рис. 1. Окружность, разделенная на 360 равных углов

Один такой маленький угол назовем углом в 1° (см. Рис. 2).

Рис. 2. 1 градус

Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).

Рис. 3. Углы равны

Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).

Рис. 4. Более явный пример равенства углов

Величина любого угла — это сколько раз в него умещается угол в 1°.

Вот мы видим угол 13° (см. Рис. 5).

Рис. 5. Угол 13°

Понятно, что полный угол

состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).

Рис. 6. Полный угол

Развернутый угол

— это половина полного угла. Он равен (см. Рис. 7).

Рис. 7. Развернутый угол

Прямой угол

является половиной развернутого и равен 90° (см. Рис. 8).

Рис. 8. Прямой угол

Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый — на 180, или прямой — на 90.

Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).

Рис. 9. Транспортир

Единицы измерения на ней — градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, — это 180°, развернутый.

Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.

1. Измерим пару углов.

Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, — 54° (см. Рис. 10, 11).

Рис. 10. Измерение угла

Проделаем то же самое со вторым углом, 137°.

Рис. 11. Измерение угла

Если сторона угла не достает до шкалы, то ее нужно сначала продлить.

2. Начертим углы 29°, 81° и 140°.

Сначала чертим одну сторону угла по линейке (см. Рис. 12).

Рис. 12. Построение одной стороны угла

Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла — 29° (см. Рис. 13).

Рис. 13. Использование транспортира для построения углов

Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).

Рис. 14. Угол 29°

Точно так же строим два других угла (см. Рис. 15).

Рис. 15. Построение углов

Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус

— это полного угла.

Инструментом для измерения и построения углов является транспортир.

Можно не использовать названия углов — полный, развернутый, прямой. Мы можем просто говорить — 360 градусов, 180 или 90 градусов.

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину — скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода — 5 км/ч, 5 минут — это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

Точно по такому же принципу устроена другая единица измерения расстояния — световой год. Световой год — расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения — это измерять вес в килограммах. На самом деле килограмм — единица измерения массы, а вес — это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения — градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

Получим величину угла , которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

Рис. 16. Тангенс

Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Существуют и другие единицы измерения углов.

1.
Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.

Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.

Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда — уже очень маленькая величина, но ее тоже можно делить дальше.

Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.

2.
Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.

3.
Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).

Рис. 17. Радианы

Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад — дуга 1 см, угол 2 рад — длина дуги 2 см.

Список литературы

Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013.
Виленкин Н.Я. и др. Математика. 5 кл. — М.: Мнемозина, 2013.
Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. — М.: Мнемозина, 2013.

Shkolo.ru ().
Cleverstudents.ru ().
Festival.1september.ru ().

Домашнее задание

Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013. Стр. 144 № 522.
Начертите углы: 23°, 167°, 84°.
Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) — 2010. Стр. 163 № 3.

Пусть в результате тщательного и искусного наблюдения та или шая цель вами найдена. Очевидно, этого еще мало: нужно определись местоположение цели, чтобы наша артиллерия знала, куда стрелять. Как это сделать?

Местоположение цели определяют обычно по отношению к ориентиру, — именно по отношению к тому ориентиру, который находится ближе всего к цели. Достаточно знать две координаты цели — ее дальность, то-естъ расстояние от наблюдателя или от орудия до цели, и угол, под которым цель видна нам правее или левее ориентира, — и тогда местоположение цели будет определено достаточно точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до этого ориентира нам известно заранее. Пусть оно равно 1000 метрам. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром. Чем же и как артиллеристы измеряют углы?

В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не толшо измерять углы, но и быстро в уме по угловым величинам находить линейные величины и, наоборот, — по линейным величинам находить угловые. Пользоваться в таких случаях градусной системой измерения углов неудобно. Поэтому артиллеристы приняли совсем иную меру углов. Мера эта — «тысячная», или, как ее называют иначе, деление угломера.

Представим себе окружность, разделенную на 6000 равных частей.

Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

Известно, что радиус (R

) любой окружности укладывается по ее длине приблизительно 6 раз, следовательно, можно считать, что длина окружности равна 6
R
. Мы же разделили окружность на 6000 равных частей; отсюда 6
R
= 6000 частей окружности. Теперь легко узнать, какую часть радиуса будет составлять одна шеститысячная часть окружности. Очевидно, что она будет в 6000 раз меньше величины 6
R
, то-есть будет равна или одной тысячной радиуса . Поэтому-то артиллерийская мера углов — деление угломера — и носит название «тысячной» (рис. 212). Такой мерой пользоваться для измерения углов очень удобно. {243}

Вспомните, что в поле зрения бинокля вы видели сетку с делениями, то-есть короткие и длинные черточки, которые расположены вправо, влево и вверх от перекрестия, находящегося в центре поля зрения бинокля (рис. 213). Эти деления и есть «тысячные». Маленькое деление сетки (между короткой и длинной черточками) равно 5 «тысячным», а большое деление (между длинными черточками) — 10 «тысячным».

На рис. 213 эти деления обозначены не просто числами 5 и 10, а с приставленными слева нолями — 6-05. и 0-10. Так пишут и произносят артиллеристы все угловые величины в «тысячных», чтобы избежать ошибок в командах. Например, если нужно передать в команде угол, равный 185 «тысячным» или 8 «тысячным», то произносят эти числа как номер телефона: «один восемьдесят пять» или «ноль ноль восемь», и соответственно пишут 1-85 или 0-08.

Зная теперь, как устроена сетка бинокля, вы можете измерить по ней угол между двумя предметами (точками местности), которые ввдны с вашего наблюдательного пункта. Взгляните опять на рис. 213. Вы видите, что между перекрестком дорог, куда направлено перекрестие, и отдельно стоящим деревом (вправо от перекрестка дорог) укладывается два больших деления и одно маленькое, то-есть 25 «тысячных» или 0-25. Это и есть угол между перекрестком дорог и деревом. Точно так же вы можете определить угол между перекрестком дорог и домиком (влево от перекрестка дорог). Он равен 0-40. {244}

Сетка с делениями, примерно такая же как в бинокле, имеется и в поле зрения стереотрубы. Но у стереотрубы для измерения углов есть еще угломерная шкала снаружи.

На рис. 214 показаны те части стереотрубы (лимб и барабан лимба), при помощи которых можно более точно, чем по сетке, измерять горизонтальные углы.

Окружность лимба разделена на 60 частей, и поворот стереотрубы на одно деление лимба соответствует таким образом 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и при полном обороте барабана стереотруба поворачивается всего только на одно деление лимба (т. е. на 100 «тысячных»). Следовательно, деление барабана соответствует не 100 «тысячным», а всего лишь одной «тысячной». Это позволяет уточнять показания лимба в 100 раз и дает возможность измерять углы с точностью до одной «тысячной».

Чтобы измерить угол между двумя точками, пользуясь лимбом и барабаном, совмещают перекрестие стереотрубы сначала с правой тачкой; для этого, подведя указатель лимба к делению 30 и деление барабана 0 к его указателю (рис. 215), поворачивают трубу в нужную сторону при помощи маховичка точной наводки (см. рис. 214). Затем, вращая барабан лимба, совмещают перекрестие стереотрубы с левой точкой. При этом указатель лимба передвинется и покажет новый отсчет. Разность между полученным отсчетом и первоначальной установкой (30-00) и будет равна искомому углу (рис. 215).

Но не только при помощи этих сложных приборов можно измерять углы.

Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы запомните, сколько в них заключается «тысячных» или, как говорят артиллеристы, какова «цена» ладони и пальцев. Хотя разные люди имеют разную ширину ладони и пальцев, но все же «цена» их не будет сильно отличаться от указанной на рис. 216. Вытянув перед собой руку на полную ее длину, вы можете быстро измерить угол между любыми точками местности (рис. 217). Чтобы не делать больших ошибок при измерении углов таким приемом, надо проверить «цену» своих пальцев. Для этого нужно вытянуть руку на уровне {245}

глаз и заметить, какую часть пространства закрыл собой палец (или ладонь руки), а затем измерить это пространство при помощи стереотрубы, поставленной на то же место.

Понятно, что подобным же простейшим «угломером» может служить всякий предмет, «цену» которого вы заблаговременно определили. На рис. 218 показаны такие предметы и их примерная «цена» в «тысячных».

Ознакомившись с приемами измерения углов, вы можете теперь убедиться в том, что, пользуясь «тысячными», можно весьма просто по угловым величинам определять линейные величины, а по линейным величинам — угловые. Для этого рассмотрим два примера. {246}

Первый пример (рис. 219). С наблюдательного пункта вы видите впереди проволочные заграждения противника; они протянулись полосой от мельницы влево до сухого дерева. Расстояние до мельницы, а следовательно, и до проволочных заграждений вы определили по карте; оно равно 1500 метрам. Вам поставлена задача — узнать длину наблюдаемой полосы проволочных заграждений. Как это сделать? Карта здесь вам не поможет, так как на ней нет сухого дерева, на ней есть только мельница.

Чтобы решить данную задачу, вы прежде всего определяете угол, под которым видна с наблюдательного пункта полоса проволочных заграждений, то-есть угол между направлениями на мельницу и на сухое дерево. Вы измерили этот угол по сетке бинокля; он оказался рашым 100 «тысячным», или 1-00.

Дальше задача решается просто. Надо лишь представить себе, что ваш наблюдательный пункт — это центр той окружности, которая описана радиусом, равным расстоянию от вас до мельницы. Радиус этот равен 1500 метрам. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 1,5 метра. А так как угол между мельницей и сухим деревом равен не одной, а 100 «тысячным», то значит расстояние между мельницей и сухим деревом равно не 1,5 метра, а 150 метрам. Это и будет длина полосы проволочных заграждений {247}

Второй пример (рис. 220). В канаве около шоссе вы обнаружили пулемет, по которому решили открыть огонь. Вам надо вычислить расстояние до пулемета или, что то же, — до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна — она равна 6 метрам. Измерьте теперь по вертикальной сетке бинокля угол, под которым вы видите телеграфный столб (угол между верхним концом столба и его основанием). Тогда вы будете иметь все данные для определения расстояния.

Допустим, что этот угол оказался равен 3 «тысячным». Очевидно, что если углу 3 «тысячных» с этого расстояния соответствует 6 метров на местности, то одной «тысячной» будет соответствовать 2 метра, а всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2000 метрам.

На рассмотренных примерах вы убедились, что принятая в артиллерии мера для измерения углов позволяет без всякого труда находить одну «тысячную» от любой величины расстояния. Для этого только надо в числе, выражающем величину расстояния, отделить справа три знака. Все это проделывается очень быстро в уме.

А вот что получилось бы, если за меру углов принять не «тысячную», а обычную, применяемую в геометрии меру углов: один градус или одну минуту. Углу в один градус соответствовала бы линейная величина, равная 1/60 радиуса, а углу в одну минуту — 1/3600 радиуса; следовательно, при решении любой из приведенных задач пришлось бы делить числа, выражающие расстояния до целей, не на 1000, а на 60 или на 3600.

Попробуйте проделать это деление с любым выбранным наугад числом и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись. Вот почему артиллерийская мера углов практически является несравненно более удобной. {248}

Измерить угол

— значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус

— это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Где еще используются

Очень часто при проведении ремонтных работ, составления таблиц в журналах и тетрадях, создании различных изделий мастерами различных профессий, домохозяйками, рабочими применяется данный инструмент. Для чего нужна линейка, например, бухгалтеру? При занесении данных из листов в компьютер накладывает линейку на ту строку, с которой нужно работать. Так он не потеряет место, где остановился.

Вот такие полезные свойства у линейки и траспортира! А стоят они недорого и доступны каждому.

Процессор – системный блок — предназначен для вычислений, обработки информации и управления работой компьютера. 2 типа корпуса Desctop — настольный вариант Tower — башня Кнопки: power (вкл/выкл), reset (перезагрузка) Индикаторы: power (вкл/выкл), hdd (ЖД)

Монитор — устройство визуального представления данных. Его потребительские параметры: 1. Размер – по диагонали: 17, 20, 21 дюйм 2. Шаг маски – шаг между отверстиями специальной панели: 0,25-0,27 мм 3. Частота регенерации –обновление изображения, частота кадров: от 100 Гц 4. Класс защиты – стандарт техники безопасности

Устройства системного блока Внутренние Внешние — устройства, находящиеся внутри системного блока. — устройства, подключаемые к системному блоку снаружи. — блок питания — материнская плата — видеокарта — сетевая плата — дисководы ЖМД — монитор — клавиатура — принтер — мышь — сканер — модем — колонки

Задание 5, стр. 55 Информация — сведения об интересующем вас предмете. Компьютер — универсальное программно управляемое устройство для обработки информации. Процессор — устройство, предназначенное для вычислений, обработки информации и управления работой компьютера. Оперативная память — информация в ней находиться только во время работы компьютера. Жёсткий диск — используется для длительного хранения информации.

Задание 5, стр. 55 Клавиатура — устройство для ввода информации путём нажатия клавиш. Монитор — устройство визуального отображения информации. Мышь — устройство для быстрого перемещения по экрану и выбору нужной информации. Принтер — устройство для печати информации на бумаге. Данные — информация, представленная в форме, пригодной для обработки компьютером. Аппаратное обеспечение — совокупность всех устройств компьютера.

Транспортир представляет собой геометрический инструмент, используемый для измерения углов.

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

теодолит;
оптический транспортир в строительной промышленности и геодезии;
инклинометр для определения уклонов и косвенной альтиметрии;
секстант для навигации.

Назначение линейки

Линейка — это длинная узкая прямоугольная полоса с нанесенной по верхнему краю (на некоторых линейках и по нижнему) шкалой и цифрами.

Для чего нужна линейка человеку? Во-первых, для измерения небольших расстояний, длины, высоты и ширины различных предметов; во-вторых, для проведения ровных прямых линий при помощи карандаша, ручки, фломастера. То есть линейка имеет две основные функции: измерение и проведение ровных линий. Нередко используются сразу обе, например, нужно нарисовать прямоугольник со сторонами 5 см и 7 см. Берем линейку, прикладываем на лист в нужном месте сначала горизонтально, карандашом проводим от 0 до 7 см, затем рисуем перпендикулярные стороны по концам по 5 см и завершаем верхнюю сторону 7 см.

С другой стороны, линейка используется не для построений, а просто для измерений. Например, вам нужно измерить длину ручки, чтобы понять, поместится она в миниатюрную карандашницу или нет.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Инструкция

Если под рукой нет ничего кроме листа бумаги и карандаша, то можно обойтись даже этими принадлежностями. Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.
Можно начертить угол с помощью прямоугольных треугольников, которые могут быть разными – с углами 90°, 45°, 45° и 90°, 60°, 30°. Возьмите треугольник (с углами 90°, 45°, 45°) и обведите на листе бумаги острый угол в 45°. Если имеется только треугольник с углами 90°, 60°, 30°, то на другом листе бумаги обведите прямой угол, вырежьте его, сложите пополам и обведите на нужном чертеже. Это и будет угол в 45°.
Самым точным будет вариант построения, при котором используется транспортир. Начертите на листе бумаги линию, отметьте на ней угловую точку, приложите транспортир и отметьте точкой 45° , после чего соедините их между собой.
Интересно, что даже с помощью циркуля можно также изобразить угол в 45° . Для этого достаточно иметь перед собой изображенный угол в 90° (например, с помощью прямоугольного треугольника или путем сгибания бумаги вчетверо). Затем от угловой точки циркулем проведите окружность.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Ответ

Пошаговое объяснение:

Для начала надо иметь в руках транспортир, примерно такой, как на фото. Этот почти антиквариат — из СССР — 8 копеек стоит.

Действие первое — нужно иметь изображение угла, который мы хотим измерить. Угол — это два луча исходящие из одной точки.

При обозначении угла из трех букв обозначение вершины — это центральная буква. Например,∠АОС — вершина О и два луча ОА и ОС.

Действие второе: Совместить вершину угла О с центром транспортира, а его развернутый угол с одним из лучей.

Действие третье, самое сложное: Определить значение самого угла. Находим показание транспортира — место где второй луч пересекает шкалу транспортира. Возможно для этого понадобится продлить луч до пересечения со шкалой. На шкале транспортира две шкалы, одна на увеличение — от 0° до 180°, другая — на уменьшение — от 180° до 0°.

На рисунке это и +140° и -40°. Думаем: какое показание взять за результат. Просто думаем.

В приложении и второй рисунок: 20°, 25° и 70°.

Как пользоваться транспортиром

По тому месту, где вторая сторона угла пересекает угломерную шкалу транспортира, определяется величина угла.

Введение

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.

Измерение угла транспортиром

Оцените, к какому типу относится интересующий вас угол. Углы можно разделить на три класса: острые, тупые и прямые.

Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу). Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира. На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы

. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Размер матрицы и угол обзора объектива фотоаппарата

Экскурс в историю

Раньше, в пленочную эпоху, широчайшее распространение имела пленка формата 35 мм — обычная фотопленка, знакомая каждому человеку. Она использовалась повсеместно, начиная от простейших компактных фотоаппаратов (пожалуй, у каждого была пленочная “мыльница”), заканчивая серьезной профессиональной техникой. Поскольку все аппараты имели одинаковую площадь светочувствительного элемента (пленочного кадра), на всех аппаратах объективы с одинаковым фокусным расстоянием давали одинаковый угол обзора. К примеру, на любом фотоаппарате, работающем с 35-мм пленкой, объектив с фокусным расстоянием 50 мм имел угол обзора 45°. Напомним, что и в современных полнокадровых цифровых камерах используется сенсор, по размеру равный кадру фотопленки — 24х36 мм.

Угол обзора объектива и размер матрицы

Сегодня же ситуация изменилась. Матрицы в цифровых фотоаппаратах бывают разного размера.

Современные форматы матриц фотоаппаратов

Поэтому при одинаковых фокусных расстояниях объектива на разных камерах угол обзора будет зависеть еще и от того, каков размер матрицы фотоаппарата. Взглянем на схему:

Чем меньше матрица фотоаппарата, тем уже угол обзора объектива при том же фокусном расстоянии

Получается, что если на полнокадровой матрице (или на пленочном кадре) объектив с фокусным расстоянием 50 мм обеспечит угол обзора 45°, то на матрице формата APS-C — уже 35°. На фотокамере системы Nikon 1 с еще более компактной матрицей формата 1” тот же объектив даст угол обзора всего лишь 15°. Чем меньше в фотоаппарате матрица, тем сильнее объектив с тем же фокусным расстоянием будет “приближать”. Один и тот же объектив, будучи установленным на разные фотоаппараты, будет давать совершенно разную картинку. Это нужно учитывать при выборе оптики.

Кроп-фактор и эквивалентное фокусное расстояние

Поскольку сегодня в различных камерах установлены матрицы совершенно разного размера, легко запутаться с тем, какой угол обзора даст объектив с тем или иным фокусным расстоянием на той или иной фотокамере.

Фотографам старой закалки, привыкшим к работе с пленочной фототехникой и к классическим значениям фокусных расстояний, четко ассоциируют их с конкретными углами обзора. Чтобы разобраться с тем, какому фокусному расстоянию соответствует тот или иной угол обзора объектива на современных аппаратах, было введено два понятия: кроп-фактор и эквивалентное фокусное расстояние.

Эквивалентное фокусное расстояние (ЭФР)

Данная характеристика не нужна новичкам, тем кто купил свою первую фотокамеру — ему цифры эквивалентного фокусного расстояния ни о чем не скажут. А вот опытным фотографам, привыкшим к пленочной фототехнике, эта характеристика окажется полезной. Также она будет полезна тем, кто задумался о покупке новой фотокамеры с матрицей другого размера и хочет выбрать подходящую для нее оптику, узнать, как на новой камере будут работать его старые объективы.

Эквивалентное фокусное расстояние позволяет узнать, какое фокусное расстояние будет иметь объектив с таким же углом обзора на полнокадровой (или пленочной) фотокамере. Эта характеристика позволяет сравнивать объективы, всех типов камер, в том числе и компактных. В характеристиках объектива, рассчитанного не под полнокадровую камеру, зачастую можно найти пункт “эквивалентное фокусное расстояние” или “фокусное расстояние в 35-мм эквиваленте”. Этот пункт нужен для того, чтобы фотограф, смог разобраться с тем, какой угол обзора даст данный объектив. К примеру, для объектива с фокусным расстоянием 50 мм, установленного на камеру с матрицей APS-C эквивалентными фокусным расстоянием будет 75 мм. Крохотное фокусное расстояние 4,3 мм, используемое в объективе компактной камеры, соответствует по углу обзора 24-мм объективу на полном кадре.

Как рассчитать самому эквивалентное фокусное расстояние? Для этого нужно знать кроп-фактор. Это условный множитель, отражающий изменение угла обзора объектива при его использовании с матрицами меньшего размера. Этот множитель выводится при сопоставлении диагоналей матриц цифровых аппаратов с пленочным кадром 24х36 мм. Слово “кроп-фактор” происходит от английских слов crop — “обрезать” и factor — “множитель”.

Например, диагональ матрицы формата APS-C меньше полнокадровой примерно в 1,5 раза. Так что кроп-фактор для матрицы APS-C будет равен 1,5. А вот диагональ матрицы формата Nikon CX меньше полнокадровой в 2,7 раз. Поэтому ее кроп-фактор будет равняться 2,7. Теперь, зная кроп-фактор, мы сможем рассчитать и эквивалентное фокусное расстояние для объектива. Для этого нужно фактическое фокусное расстояние объектива умножить на кроп-фактор. Допустим, нам необходимо узнать эквивалентное фокусное расстояние для объектива 35 мм, если он будет установлен на камеру с матрицей APS-C. 35х1,5=50мм. Итак, эквивалентное фокусное расстояние такого объектива будет равно 50 мм. То есть на любительской зеркалке 35-мм объектив будет вести себя так же, как классический “полтинник” на полном кадре.

Фотография, сделанная полнокадровым аппаратом и объективом с фокусным расстоянием 20 мм. Что будет, если тот же объектив установить на камеру с матрицей APS-C или на аппарат семейства Nikon-1? Угол обзора станет уже. В кадр войдут только области, показанные на картинке.

В дальнейших уроках мы будем изучать, какими объективами пользуются при съемке различных сюжетов, укажем их фокусные расстояния как для фотокамер с матрицей APS-C, так и для полнокадровых аппаратов.

Размеры матриц и кроп-фактор фототехники Nikon

В современных системных зеркальных и беззеркальных фотокамерах Nikon применяется всего три стандарта матриц различного размера. В них легко разобраться.

Полнокадровые матрицы (Nikon FX). Имеют физический размер 36х24 мм, то есть равны по размерам кадру с 35-мм пленки. На такие фотоаппараты рассчитано большинство современных объективов. И на них они могут раскрыть весь свой потенциал. Среди современных аппаратов Nikon, полнокадровыми матрицами оснащаются: Nikon D610, Nikon D750, Nikon D800/D800E, Nikon D810, Nikon D4/D4s, Nikon Df. Поскольку матрица таких фотоаппаратов равна по размерам пленочному кадру, то и понятие кроп-фактора и ЭФР для таких аппаратов не нужно.

Матрицы формата APS-C (Nikon DX). Имеют физический размер 25,1х16,7 мм и кроп-фактор 1,5. Такая матрица незначительно меньше полнокадровой, но зато значительно дешевле. Подобные матрицы иногда называют “кропнутыми” (обрезанными). Такой размер матриц используют почти все производители цифровых зеркальных фотоаппаратов. Среди современных аппаратов Nikon матрицы APS-C имеют камеры Nikon D3300, Nikon D5300, Nikon D5500, Nikon D7100. С ними по-прежнему можно использовать полнокадровую оптику, однако, все объективы будут значительно сильнее “приближать”, что не всегда удобно, ведь некоторые объективы рассчитаны на сугубо определенный вид съемки и потеря ими нужного угла обзора не позволяет их использовать по назначению. Прежде всего это касается широкоугольной, портретной и репортажной оптики. Полнокадровая широкоугольная оптика теряет свое главное достоинство — большой угол обзора; портретные полнокадровые объективы на “кропе” начинают слишком сильно приближать, и на них становится сложно снимать, приходится очень далеко отходить. Например, установив классический портретный объектив с фокусным расстоянием 85 мм на кропнутую камеру, придется отойти от фотографируемого человека на 5-7 метров, чтобы снять хотя бы портрет по пояс. Полнокадровая репортажная оптика (прежде всего зум-объективы с фокусным расстоянием 24-70 мм) получает на кропе неудобные углы обзора, не очень подходящие на практике для быстрой, динамичной репортажной съемки.

Чтобы создать подходящие для этих задач объективы, для “кропа” выпускают специально разработанные объективы. В системе Nikon такие объективы маркируются буквами “DX” в названии. Поскольку такие объективы рассчитываются для использования на меньшей по размеру матрице, они и сами становятся компактнее и дешевле своих полнокадровых собратьев.

Важно иметь в виду, что на DX-объективах (рассчитанных на камеры с матрицей APS-C) указывается реальное, а не эквивалентное фокусное расстояние

По этой же причине они не смогут корректно работать на полнокадровых матирцах. Что будет, если установить “кропнутый” объектив на полнокадровую камеру? В отличие от фотоаппаратов Canon, у Nikon есть такая возможность. В таком случае будет получаться очень сильное затемнение по краям кадра. Кстати, современные полнокадровые аппараты Nikon могут распознавать “кропнутую” оптику в случае ее установки, они автоматически обрезают кадр до размеров матрицы APS-C. Такую настройку можно включить или выключить в меню камеры.

Фото сделано на полнокадровую фотокамеру объективом с фокусным расстоянием 85мм.

NIKON D810 / 85.0 mm f/1.4 УСТАНОВКИ: ISO 80, F1.4, 1/1250 с, 85.0 мм экв.

Фото сделано на фотокамеру с матрицей APS-C тем же объективом и с той же дистанции. Как видите, объектив на кропе дал более узкий угол обзора.

NIKON D5300 / 85.0 mm f/1.4 УСТАНОВКИ: ISO 100, F1.4, 1/1600 с

Фотографии сделаны одним и тем же объективом с одинаковой дистанции. Как видите, вариант, сделанный на “кропнутую” камеру имеет более узкий угол обзора, в кадр вошло меньше деталей.

Nikon CX — формат матриц для беззеркалок семейства Nikon 1. Физический размер — 13,2х8,8 мм. Имеют кроп-фактор 2,7. Столь небольшая матрица обеспечивает всей системе компактность. Для нее разрабатывается своя оптика: она компактна и практична. Через специальный переходник (Nikon FT-1) на камерах Nikon 1 можно использовать и объективы для полнокадровых и APS-C аппаратов.

Через переходник Nikon FT-1 можно устанавливать объективы от зеркалок на фотокамеры семейства Nikon 1.

У других производителей встречаются матрицы и других размеров, а значит и с другим кроп-фактором. Например, широко известен стандарт матриц micro 4/3, используемый сразу несколькими производителями. Этот стандарт имеет кроп-фактор 2. Это не очень крупные матрицы, со всеми вытекающими плюсами и минусами. Камеры, оборудованные такими матрицами компактны, как и разработанная для них оптика. Однако, аппаратам с таким сенсором очень сложно тягаться в качестве изображения с полнокадровыми аппаратами — площадь матрицы различается в четыре раза.

Итоги

Если вы собираетесь покупать новую фотокамеру или выбираете новую оптику к старой и хотите выполнить примерный расчет угла обзора объектива, узнайте кроп-фактор установленной в ней матрицы. Исходя из этого выбирайте и технику. Если ваш фотоаппарат имеет кроп-фактор 1,5, знайте, что вам потребуется более короткофокусная оптика, чем для полнокадровых фотоаппаратов. В следующем уроке мы поговорим о том, объективы с каким фокусным расстоянием подойдут для тех или иных видов съемки, какой подойдет объектив для съемки портретов, а какой — для съемки пейзажей.

Математика. Градусы между стрелками. Логические задачи, головоломки, тесты на интеллект, логические игры. Часы в задачах

В некоторых школьных играх, викторинах, а так же в учебниках по алгебре и геометрии можно встретить задания, в которых вам потребуется определить какой угол образуют стрелки часов, часовая и минутная. На самом деле сделать это довольно просто. Правильные ответы на задания по алгебре представлены ниже.

Так же на картинке вы можете увидеть наглядно углы, которые образуют стрелки. Минутная стрелка — красная, а часовая стрелка — синяя. Для того чтобы самим высчитать углы можно воспользоваться небольшой хитростью. Нужно просто запомнить, что расстояние между минутной и часовой стрелкой в одно деление — это угол в 30 градусов. Так, если между стрелками будет два деления, то между ними будет образован угол в 60 градусов. Если три деления, то образуется угол в 90 градусов. Если 6 делений, то стрелки часов уже образуют угол в 180 градусов.

а) в 3 ч — 90 градусов;
б) в 5 ч — 150 градусов;
в) в 10 ч — 60 градусов;
г) в 11 ч — 30 градусов;
д) в 2 ч 30 мин — 120 градусов;
е) в 5 ч 30 мин — 30 градусов;
ж) в 6 ч — 180 градусов;
з) в 3 ч 45 мин — 180 градусов;
и) в 4 ч — 120 градусов.

Попробуйте теперь отгадать сами. Какой угол образует минутная стрелка если она стоит на числе 12, а часовая стрелка показывает 1 час? А, какой угол образует часовая стрелка, если она стоит на 7, а минутная стрелка стоит на 3? А, какой угол образует минутная и часовая стрелка если обе они показывают на число 12?

Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 8 часов?

Решение задачи

Данный урок показывает, как использовать свойства окружности в задачах с циферблатом (определение углов между часовой и минутной стрелками). При решении задачи используем свойство окружности: полный оборот окружности составляет 360 градусов. Учитывая, что циферблат делится на 12 равных часов, можно легко определить, сколько градусов соответствует одному часу. Дальнейшее решение сводится правильному определению разности часов между минутной и часовой стрелками, и выполнению простейшего умножения. При решении задач следует четко понимать, что мы рассматриваем положение часовой и минутной стрелок относительно их положения к отсечкам часов, т.е. от 1 до 12.

Решение данной задачи рекомендовано для учащихся 7-х классов при изучении темы «Треугольники» («Окружность. Типовые задачи»), для учащихся 8-х классов при изучении темы «Окружность» («Взаимное расположение прямой и окружности», «Центральный угол. Градусная мера дуги окружности»), для учащихся 9-х классов при изучении темы «Длина окружности и площадь круга» («Окружность, описанная около правильного многоугольника»). При подготовке к ОГЭ урок рекомендован при повторении тем «Окружность», «Длина окружности и площадь круга».

Комментарии:

KReoN, 2010-03-05

Я сначала попался, подумав что 0. Сдает недостаток терпения)

Кристина, 2010-03-05

0
между ними четверть часа.
360/12/4 = 15/2
Задача хорошая, но слишком легая. Кстати, а как там может получится 0?
360/(12*4)=7.5

x_ler, 2010-03-06

90 градусов!
представте картинку и между 3 и 15 половина круга,а целый 180 градусов,значит половина равна 90.

Леха, 2010-03-07

X_ler, что тут сказать, ты дибил!
Попей Викадин..
Ты полный даун..
Вообще то между стрелками 367.5 градусов!

skadi, 2010-03-08

7,5
352,5
ану для тупих еще разок!!!=))) они же на одной линии!!!

an-96, 2010-03-08

Леха, сам ты даун. КАКИХ 367,5 градусов??
2 an-96 ну на самом деле 367.5 градусов == 7.5 градусов (alfa == alfa % 2*pi). Ну это так, к слову

an-96, 2010-03-09

Я понимаю, но с таким же успехом можно сказать 727,5

firemen, 2010-03-10

А кто скажет, во сколько минут, того же 4-го часа стрелки совпадут?
минутная стрелка находится на 1 четверти циферблата, а часовая уже ушла вперед от цифры 3 на 1/4 часа, а всего на циферблате 12 часов или 360градусов. На 1 час приходится 30 град, следовательно на 1/4 часа придется 7,5 градуса.
Ответ: 7,5 градуса

гоша, 2010-03-11

Я чето галюнул и сделал в вда раза меньше — -3.75)))

Yrik0914, 2010-03-13

данияр, 2010-03-14

Я думаю, что между стрелками на часах 45 градусов., если 360 делить на 2, то полочиться 180, а если 180 делить на 2 то плучиться 90. А 90 делить на 2 = 45!!!

арина, 2010-03-14

Я думала о

вася, 2010-03-14

7,5 град

Hawaiian, 2010-03-23

360/12*4=7,5

Dita Kim, 2010-04-04

И снова: задачка простая, а в ответе решение сложнее, чем когда решала я… Радует, что ответ совпал и люди, оставляющие комменты, решали так же, как и я=)

Stblnger, 2010-04-05

Я плохо учился в школе!!! объясните по-человечески, почему так…. почему не ноль градусов?
хочется понять

Stblnger, 2010-04-05

Тьфу ты… понял. отбой

Саша, 2010-04-16

Вася, 2010-03-14
7,5 град
при полном обороте минутной стрелки(60 мин) часовая проходит растояние между двумя соседними цифрами, а это пять минутных делений. Одно деление соответствует 6 град.(360:60).
Когда минутная проходит одно деление, часовая проходит в 12 раз меньшее растояние.
Сколько делний пройдет часовая стрелка за 15 мин? Правильно, она пройдет 15/12, или 1,25 деления. т.к. деление у нас равно 60 град, то 1/4(что соответствует 0,25)деления — это 1,5 град. И выходит, что когда минутная стрелка будет на 15 минутах, то часовая пройдет растояние равное 1,25 минутных делений и в пересчете на градусы это будет соответствовать 6+1,5=7,5 град.
Вася,Красавчик,обьяснил непонятливым

Ilgar96, 2010-04-22

360

15 ч 16 м 21(81) с

Слабо вычислить?

иВАСЯ, 2010-07-01

Ага а 7 градусов 30 минут не хотите!!! 7,5 — тоже мне!!)))))

Слава, 2010-08-23

Правильный ответ 0), потому что в это время между стрелками нет угла а значит 0. Ну Архимеды накрутили тут градусов))))))
7.5 чо так сложно?

Егор, 2010-11-03

7,5 потомучто часовая стрелка проходит 360 градусов за 12 ровных частей т. е. одна пятиминутка 360/12=30 градусов,а 30 /4=7,5 вот и ответ

Marex, 2010-11-05

Юрий, 2010-05-11
Интересный вопрос задали выше:
а во сколько времени того же часа угол будет равен нулю?

15 ч 16 м 21(81) с

Слабо вычислить?

Легко, якщо виразити рух стрілок через хвилинні відмітки (далі Х/В).
Приймаємо час 15:15 за початкову відмітку. Тоді хвилинна стрілка знаходиться на позначці 0 Х/В, годинна — на позначці 5/4 Х/В. Час переміщення хвилинної стрілки Тх і годинної Тг буде однаковий. Швидкість переміщення хвилинної стрілки — 1/60 Х/В за сек., годинної — 1/720 Х/В за сек. Виражаємо Тх і Тг через відповідні значення швидкості і переміщення і прирівнюємо вирази. Отримуємо систему рівнянь: 60*Sг=720*Sх; Sг=Sх-5/4. Отже 60*(Sг+5/4)=720Sг, Sг=5/44, Sх=15/11~1.36(хв.)~1хв., 21,6 сек. При початковій умові точки відліку отримаємо час 15 год., 16 хв., 22 сек

sava, 2010-11-06

Можно подождать когда на часах будет 3.15(на механических) тогда ответ=0

Viola, 2010-11-08

Между стрелками 7. 5 град
0

Schiki, 2010-12-03

Легко слишком

Юля, 2011-02-15

Не нуль. Тому що велика стілка не стоїть на місці а рухається тільки помалу. Отже 1\4 години)))

w2w, 2011-02-25

Сильно удивили ответы о нуле градусов. Граждане, на часы посмотрите, или это так сложно? Или реальность уже не может подсказать рационального решения и надо все «мысленно» делать? Особенно если это «мысленно» ни в какие ворота.

Алексей, 2011-02-26

Оригинальный ответ — сидел смотрел на часы, дождался 15:14 и ломанулся к часам с транспортиром и замерил угол.
0

zara, 2011-03-15

0 градус

Михаил, 2011-04-21

Слава, Алексей и Виктория ЛОХИ!
на цыферблате 12 цыфр угол между которыми 30 град(360\12)
за 15 мин стрелка часовая проходит 1\4 растояния между соседними цыфрами а минутная находиться на отметке 3
следовательно угол между стрелками 30\4=7,5

Но почему разделили на 4?

Витек, 2011-05-28

Денис, 2011-07-10

Честно — отстой задачка.
есть и покруче

Сергей, 2011-08-12

Какие градусы вы о чем?
Они на одной прямой.
Ответ ноль О
Механические часы посмотрите.
.И если вы так считаете то почему теже 30 градусов вы сново делите на 4?

Сергей, 2011-08-12

А понял в где собака зарыта там не совсем на одной прямой)))
1 час = 12 пятиминуток,
1 час = 360 градусов
одна пятиминутка — 360 / 12 = 30 градусов.

юлик, 2011-09-07

30 градусов

A ya srazu rewil xotya mne 12))))

Вадим, 2011-09-26

А какой угол спрашивается: внешний или внутренний?))
решал так: 360 градусов разделить на 12 часов и разделить на 4 пятнадцатиминутки = 7,5 градусов
==============
но сначала начал со сложного способа: 12 часов * 60 минут = 720 минут, 720 минут / 360 градусов = 2 минуты (это 1 градус). 3ч15мин = 195 минут, 195/2=97,5 градуса (угол между началом отсчёта и часовой стрелкой). 97,5-90=7,5 градуса
Задача немного некорректна… Я сразу подумал, если есть подвох, он связан с временем. На самом деле, если по логике автора рассуждать, ответов может быть уйма…(1 час или 3 разн. нет, вычтем обороты)
1 час = 60 min. = 360 гр = 2П = 0 градусов
15 мин. = (1\4) часа = (1\4)*0 = 0 градусов. Ответ 0 градусов. У кого ответ был 0 не расстраивайтесь, вы тоже правы

анит@, 2011-10-27

Эй люди вы чево совсем подурели когда часы показуют 15 минут — минутная стрелко стоит на цыфре 3.

Тимофей, 2011-10-30

А мне почему-то кажется что 24,я внимательно смотрел на часы,и между стрелками расстояние ровно 4 минуты…вот и одна минута это 6 градусов,и поэтому я считаю что 24 градуса,разве это не так?
Люди, те у кого ответ вышел «0», как вы считаете так странно??? Между ними есть угол, хоть и маленький. Ведь часовая стрелка не может быть ровно направленна на «3» так как прошло уже 15 минут, а это четверть часа. Она с каждой минутой отклоняется от тройки в сторону четверки. То как же у вас в 15 минут она так и остается стоять на цифре 3??? Она заржавела у вас что ли? Правильный ответ 7. 5

Омар, 2011-12-02

Вы что вообще 0 будет

«Часы» в задачах

Введение

Единицы измерения отрезков времени – час, минута, секунда и ее доли созданы самим человеком. Люди издавна воспринимали течение времени, наблюдая постоянную смену дня и ночи и ряд других систематически повторяющихся явлений природы. Но измерять время они научились значительно позднее. Теперь из всех известных приборов, самыми распространенными являются часы, которыми мы постоянно пользуемся, и не только в быту, но и в науке и технике, без них невозможно представить жизнь.

Человеку часто приходится решать задачи, связанные с часами. Например, как поставить точное время, если твои часы остановились, как определить страны света пользуясь часами, и т. д. Мне стало интересно, какие задачи существуют, связанные с часами, и я решил систематизировать их. Итак, цель моей работы : исследовать и систематизировать задачи, в которых говорится о часах, выявить методы их решения. В связи с этим я поставил такие задачи :

1. изучить соответствующую литературу;

2. подобрать задачи, в условиях которых говорится о часах;

3. определить уровень их сложности и найти их решения;

4. предложить найденные задачи учителям математики для использования в своей работе.

Просмотрев различные пособия, я выяснил, что многие задачи, такие как задачи на движения, на параметры, на решение уравнений собранны в один сборник, а задач о часах не так уж и много, и отдельно ни кем не рассмотрены. Поэтому моя подборка по данной теме имеет признаки новизны. Решения любых задач актуальны, носят исследовательский характер, в том числе и задач о часах.

Объектом исследования являются задачи, а предметом — задачи о часах

Основное содержание

Задачи на разделения.

Первые задачи, которые встречаются в начальных классах – это задачи о разделении циферблата часов на 2 части, на 3 части прямой линией (одной, двумя), так чтобы суммы чисел в каждой части были равными и определить эту сумму. Разделить на 6 частей. [ 1. стр.23]

http://pandia.ru/text/78/135/images/image002_236.gif»>Решения (см рис.) Сумма все чисел на циферблате – 78. х >12– сумма, а у >1 – число частей, тогда х·у = 78. Воспользуемся тем, что 78 = 2 · 3 · 13.

Варианты: 1) х = 39, у = 2;

2) х = 26, у = 3; 3) х = 13, у = 6.

2. Разделить циферблат часов на части так, чтобы суммы чисел в каждой части, составили прогрессии.

Решения (см рис) Получаются прогрессии: 6, 15, 24, 33 и 15, 18, 21, 24.

Задачи на нахождения углов между стрелками

1. Какие углы составляют между собой стрелки часов, если они показывают 7 часов и 9 часов 30 минут?

Решение: а) Стрелки показывают 7 часов..gif»>.

б) Стрелки показывают 9 часов 30 минут. Дуга между их концами содержит двенадцатых доли полной окружности или , что составляет 1050.

2. Ежедневно Он подходил к городским часам в 4 часа. Она же приходила туда, когда воображаемая биссектриса между часовой и минутной стрелками проходила через цифру 6. Когда приходила Она?

Решение. По условию углы 1 и 2 равны (рис. 1). Так как часовая стрелка показывает время между 4 и 5 часами, то минутная стрелка расположена между цифрами 7 и 8, то есть искомое время между 4 ч 35 мин и 4 ч 40 мин…gif»>ч.. В силу симметрии для показания t минутной стрелки получим следующее неравенство:

35 + 5 · t

рис 1. Ответ : в 4 часа 38 минут.

4. (Задача аналогична задаче 2, но способ решения другой). Через сколько минут после полудня биссектриса между часовой и минутной стрелками укажет на 13 мин?

Решение. Пусть А – угол между 12:00 и часовой стрелкой, В – угол между 12:00 и минутной стрелкой. Тогда угол между 12:00 и биссектрисой угла равен = 6° · 13 (за 1 мин положение стрелки изменяется на 6°)..gif»>ч, или 24 мин. Ответ: через 24 мин.

5. Сейчас стрелки часов совпадают, через сколько минут угол между ними будет 180°?

Решение. Пусть скорость часовой стрелки – х , тогда скорость минутной стрелки – 12х , а скорость удаления стрелок друг от друга – 11х , у – время в минутах, при котором выполняется равенства 11ху = 30 мин. Найдем, чему равно значение 12ху , то есть сколько времени потребовалось минутной стрелке, чтобы преодолеть угол в 180°.

12ху = . 30 = мин, что составляет 32мин. Ответ: через 32мин.

6. Совпадение часовых стрелок. Сколько раз в сутки стрелки часов совпадают?

Решение. 1 способ. Начнем с положения 12:00 или 00:00. В течение первого часа минутная стрелка, пройдя круг, ни разу не совпадает с часовой. Затем минутная стрелка будет совпадать с часовой один раз в течение каждого часа (примерно в 13:50, в 14:10 и т. д.). За двенадцатый час минутная стрелка совпадает с часовой лишь в 12:00, но эту точку мы отнесли к следующему кругу. Значит, всего стрелки совпадают лишь одиннадцать раз за полный оборот часовой стрелки, а в сутки – 22 раза. Ответ : 22 раза.

Решение: 2 способ. Мы можем воспользоваться уравнениями, выведенными при решении задачи А. Мошковского (смотри задачу 2 раздел «Испорченные часы»): ведь если часовая и минутная стрелки совместились, то их можно обменять местами – от этого ничего не изменится. При этом обе стрелки прошли одинаковое число делений от цифры 12, т. е. х = у. Таким образом, из рассуждений, относящихся к предыдущей задаче, мы выводим уравнение , где m – целое число от 0 до 11. Из этого уравнения находим . Из 12 возможных значений для m (от 0 до 11), мы получаем не 12, а только 11 различных положений стрелок, так как при m = 11 мы находим х = 60, т. е. обе стрелки прошли 60 делений и находятся на цифре 12; это же получим при m = 0.

7. Сколько раз в сутки стрелки часов направлены противоположно (то есть угол между ними равен 180°)?

Решение. Начиная с 6:00 стрелки направлены противоположно первый раз в 6:00, во второй раз, около 7:05, третий раз, около 4:54, в двенадцатый раз – 6:00, но этого уже было первый раз. Итого: одиннадцать раз за 12 часов, а в сутки – 22 раза. Ответ: 22 раза.

8. Сколько раз в сутки стрелки часов перпендикулярны?

Решение. Пусть по кратчайшей дуге стрелки удаляются (минутная стрелка дальше по ходу стрелок). Тогда, начиная с 12:00, стрелки перпендикулярны в первый раз, когда часовая стрелка расположена в промежутке от 12:00 до 1:00, во второй раз – от 1:00 до 2:00 и т. д.; всего 11 раз за полный оборот часовой стрелки, то есть в сутки – 22 раза.

Пусть наоборот стрелки часов сближаются. Рассуждая аналогично, получим – 22 раза в сутки. В итоге: 44 раза стрелки перпендикулярны. Ответ: 44 раза.

1. Сколько раз в сутки угол между стрелками часов равен данному углу α?

Решение. 1. Случай, когда α = 0 (стрелки совпадают), рассмотрен в задаче 4.

2. Случай, когда α = 180°, рассмотрен в задаче 5.

3. Рассмотрим случай, когда α отличается от крайних значений, то есть 0 α

а) Пусть по кратчайшей дуге стрелки удаляется (минутная стрелка дальше по ходу). Тогда (начиная с 12:00) угол между стрелками между ними будет равен α в первый раз, когда часовая стрелка расположена в промежутке от 12:00 до 1:00, во второй раз от 1:00 до 2:00 и т. д., всего 11 раз за оборот часовой стрелки, или 22 раза в сутки.

б) Пусть, наоборот, стрелки часов сближаются. Рассуждая аналогично, получим еще 22 раза в сутки.

В итоге, всего за сутки угол между стрелками будет равен α 44 раза. Частный случай этой задачи рассмотрен в задаче 6.

Ответ: 22 раза при α равном 0 или 180° и 44 раза при других значениях α.

Задачи на догонялки

1. Узнать, через сколько минут после того, как часы показывали ровно 9 часов, минутная стрелка догонит часовую.

Решение: Для того, чтобы минутная стрелка догнала часовую, ей надо пройти на 45 минутных делений больше часовой. Поскольку часовая стрелка проходит одно минутное деление на 12 минут меньше, то она за каждую минуту проходит минутного деления, и, следовательно, минутная стрелка нагоняет часовую за каждую минуту на минутных делений, а на 45 минутных делений потребуется: http://pandia. ru/text/78/135/images/image026_46.gif»> оборота в час. За х ч минутная стрелка пройдет х оборотов, а часовая оборота, но для того, чтобы стрелки совпали, путь, пройденный минутной стрелкой, должен быть на оборота больше..gif»>, решив которое найдем х = ч, то есть мин, или 10мин.

3. Стрелки обходят циферблат. Ровно в 12 часов дня минутная и часовая стрелки совпадают. Затем минутная стрелка вырывается впереди через некоторое время, обойдя часовую на целый круг, вновь накрывает ее. В какой момент это происходит?

Решение: 1 способ . К 12 часам ночи часовая стрелка сделает 1 оборот, а минутная – 12, следовательно, минутная обгонит часовую на 11 кругов. Значит, за это время минутная стрелка обходила часовую11 раз, а на один круг она ее обгоняла за ч

http://pandia.ru/text/78/135/images/image015_88.gif»>ч.

Задачи « Испорченные часы»

1. Часы показывают в некоторый момент на 2 минуты меньше, чем следует, хотя и идут вперед. .gif»> суток..gif»> суток..gif»> служит решением задачи.

2. Задача А. Мошковского для А. Эйнштейна. «Возьмем положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы все же правильные показания. Но в другие моменты, — например, в 6 часов, взаимный обмен стрелками, привел бы к абсурду , к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. возникает вопрос: когда и как часто стрелки часов занимают такие положения, что замена одной другою дает новое положение, тоже возможное на правильных часах?»

Решение: Будем измерять расстояния стрелок по кругу циферблата от точки, где стоит цифра 12, в 60-х долях окружности.

Пусть одно из требуемых положений стрелок наблюдалось тогда, когда часовая стрелка отошла от цифры 12 на х делений, а минутная на у делений. Так как часовая стрелка проходит 60 делений за 12 часов, т. е. 5 делений в час, то х делений она прошла за http://pandia.ru/text/78/135/images/image040_28.gif»> часов. Минутная стрелка прошла х делений за у минут, т. е. за часов тому назад, или через http://pandia.ru/text/78/135/images/image043_29.gif»> полных часов. Это число тоже является целым (от 0 до 11). Имеем систему уравнений , где m и n – целые числа, которые могут меняться от 1 до 11. Из этой системы находим: . Давая m и n значения от 0 до 11, мы определим все требуемые положения стрелок. Так как каждое из 12 значений m можно сопоставить с каждым из 12 значений n , то казалось бы, число всех решений равно 12 · 12 = 144. Но в действительности оно равно 143, потому, что при m = 0, n = 0 и при m = 11, n = 11 получается одно и то же положение стрелок. При m = 11, n = 11 имеем х = 60, у = 60, т. е. часы показывают 12, как и в случае m = 0, n = 0. Всех возможных положений мы рассматривать не будем. Возьмем лишь один случай: m = 1, n = 1. , т. е..gif»> с. Ответ: 66 секунд.

2. Когда секундная стрелка на часах прошла 1 с, минутная стрелка прошла 6 мин. Тем не менее часы исправны. Как это объяснить?

Решение. Речь идет о секунде времени и угловых минутах. Действительно, за 1 ч минутная стрелка проходит 360°, за мин — 6°, за 1 с в 60 раз меньше, то есть 6 угловых минут.

3. Одни часы отстают на 6 мин, а другие спешат на 3 мин в сутки. Сейчас их показания совпадают. Через сколько суток они снова совпадут?

Решение. Одни часы отстают на 6 мин, другие спешат на 3 мин в сутки. Значит, за одни сутки расхождение увеличивается на 9 мин и через некоторое время составит 12 ч и не будет распознано. Чтобы узнать, когда это произойдет, нужно 12 ч разделить на 9 мин, результат – 80 суток. Ответ: через 80 суток.

4. Электронные часы показывают время ab:cd:ef, a-f – произвольные цифры от нуля до девяти. Сколько раз в сутки показания часов представлены двумя цифрами, каждая из которых повторяется три раза?

Решение . 1–й случай. Варианты этого случая: 00:ХХ:ХХ, 11:ХХ:ХХ, Х – неизвестная цифра. Первые две цифры зафиксированы, третья цифра (0,1 или 2) может расположиться в четырех позициях, и так как 1 ≤ Х

2–й случай. Теперь рассмотрим варианты ab :ХХ:ХХ, где а є {0;1}, 6 ≤ b ≤ 9; таких вариантов восемь, в каждом только одна комбинации ab: ab: ab , так как цифра больше 5 не может представлять десятки минут или секунд.

3–й случай. Все остальные варианты (их 13): ab :ХХ:ХХ, где є {0;1;2}, 0

ab:aa:bb; ab:ab:ab; ab:ab:ba;

ab:ba:ab; ab:ab:ba; ab:bb:aa;

Всего возможно 6 · 13 = 78 вариантов. Таким образом, общее количество вариантов составляет 60 + 8 + 78, или 1вариантов.

Заключение

Изучив соответствующую литературу, подобрав задачи, в условиях которых говорится о часах, я разделил их на группы: задачи на разделения, задачи на нахождения углов между стрелками, задачи на «догонялки», « Испорченные часы» и разные задачи. При поисках решения задач я пытался найти разные варианты и способы решения, некоторые из которых описал в работе. Интересным мне показался графический способ решения задач на «догонялки» и задачи на определения положения стрелок. Найдены некоторые закономерности движения стрелок относительно друг друга. Все это облегчает решение рассматриваемых задач. Включенные в эту работу задачи можно использовать при проведении занятий кружков, предложить в виде элективного курса интересующимся этими вопросами школьникам, т. е они могут иметь практическое применении.

Использованная литература

Депман. И.Я. За страницами учебника математики, М, «Просвешение», 1989.с. 289 Еленский Щ. По следам Пифагора. М., Детгиз, 1961, с 483. Перельман алгебра. – Д., ВАП, 1994, с. 200 Сивашинский по математике для внеклассных занятий.(9-10 классы). М., «Просвещение», 1968. с.311. Уляшева Л. «Еще идут старинные часы». Математика в школе, №7, 2007.

Приложение

Сборник задач «О часах»

В какие моменты между 12 часов дня и 12 часов ночи стрелки образуют а) развернутый угол; б) прямой угол; в) угол в 200? Имеются песочные часы на 3 мин и на 5 мин. Отмерьте с их помощью промежуток времени в 1 мин.

Решение. Запустим часы одновременно. Когда пройдут 3 мин, перевернем эти часы, начнем новый отсчет времени. Когда пройдут 5 мин, на трехминутных часах к этому времени останется песка ровно на 1 мин. Конец отчета времени – когда «остановятся» трехминутные часы. Действительно, 2 · 3 – 5 = 1.

Замечание. Можно рассмотреть эту задачу в общем виде: пусть первые часы на х мин, вторые – на у мин. Отмерить z мин. Решение этой задачи сводится к решению уравнения z = nx – my.

3. Минутную стрелку обломили так, что она перестала отличаться от часовой. Сколько раз в сутки можно ошибочно считать время с часов с такими стрелками, если при этом не разрешается наблюдать за ходом часов?

Разобьем циферблат на 12 часовых секторов (рис. 4). Пусть α – угол между часовой стрелкой и лучом, направленных к началу стрелка, β – угол между минутной стрелкой и лучом, направленных к началу сектора, в котором находится минутная стрелка; оба угла измеряется в долях от величины сектора в 30°, значения α и β находятся в интервале бывает на третьем месте по 10 мин каждый час; в) в остальные 50 мин часа еще по 5 мин – на четвертом месте. Итого, по 15 мин в каждый из 18 часов, то есть 4 ч 30 мин. Всего получаем 4 + 2 + 4.5 = 10.5 ч. Рассуждая аналогично, получим время показана цифры на табло для всех случаев.

Ответ : для цифры 2 – 10.5 ч; 0 и 1 – по 16 ч; 3 – 8.25 ч; 4 и 5 – по 7.5 ч; для остальных – по 4.2 ч. [ 5.]

Как измерить острый угол транспортиром. Измерение углов. Транспортир

Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор — транспортир :

У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком » , a секунды — знаком «» . Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

50°34» 19«»

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB :

Луч OD делит его на два угла: ∠AOD и ∠DOB . Таким образом, ∠AOB = ∠AOD + ∠DOB .

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

Представим себе окружность, разделенную на 6000 равных частей.

Известно, что радиус (R ) любой окружности укладывается по ее длине приблизительно 6 раз, следовательно, можно считать, что длина окружности равна 6R . Мы же разделили окружность на 6000 равных частей; отсюда 6R = 6000 частей окружности. Теперь легко узнать, какую часть радиуса будет составлять одна шеститысячная часть окружности. Очевидно, что она будет в 6000 раз меньше величины 6R , то-есть будет равна или одной тысячной радиуса . Поэтому-то артиллерийская мера углов — деление угломера — и носит название «тысячной» (рис. 212). Такой мерой пользоваться для измерения углов очень удобно. {243}

Вспомните, что в поле зрения бинокля вы видели сетку с делениями, то-есть короткие и длинные черточки, которые расположены вправо, влево и вверх от перекрестия, находящегося в центре поля зрения бинокля (рис. 213). Эти деления и есть «тысячные». Маленькое деление
сетки (между короткой и длинной черточками) равно 5 «тысячным», а большое деление (между длинными черточками) — 10 «тысячным».

Но не только при помощи этих сложных приборов можно измерять углы.

Еще в школе каждый человек сталкивался с такой вещью, как транспортир. Но, к сожалению, далеко не каждый, как в школьное время, так и уже в старшем возрасте, знает, как правильно им пользоваться. Данная инструкция научит каждого правильно пользоваться этим предметом.

Начнем, пожалуй, с того, что же такое транспортир. Транспортир – это инструмент для измерения градусного значения углов. Чаще всего такой инструмент имеет полукруглую форму. Но есть и исключения, а именно транспортиры, которые имеют полностью круглую форму (360 градусов).

Как правильно пользоваться транспортиром

Для начала необходимо понять, что представляет из себя данный инструмент. Он являет собой полукруглый предмет (как уже было сказано выше, может быть и круглый) с небольшим отверстием в середине, которое называется точкой отсчета. Именно последнее (точку отсчета) нужно совместить с вершиной треугольника.
Дальше для измерения необходимого угла, необходимо основание транспортира разместить параллельно стороне угла или катету треугольника. Для этого нужно выбрать сторону треугольника (она будет базовой, именно с этой стороной нужно совместить основание транспортира). Не стоит путать базовую линию угла и основание транспортира (это совершенно разные вещи).
Как только вы совместили точку отсчета с вершиной угла, а основание транспортира с катетом, можно смело измерить угол. Тогда второй катет треугольника будет указывать на шкалу с цифрами на полуокружности транспортира. Главное – это не запутаться с цифрами, ведь сделав это, вы допустите ошибку в измерении необходимого угла.
Стоит понимать, что чем больше (тупее) угол, тем больше его градусное значение. Угол максимально может составить 180 градусов.
Самые маленькие (острые) углы могут составлять только меньше 90 градусов, все, которые будут больше этого значения уже считаются большими (тупыми).

Как правильно измерить градусное значение угла транспортиром

Для этого необходимо сделать следующие действия:

Центральную точку (точку отсчета) необходимо совместить с вершиной угла, который необходимо измерить. Транспортир необходимо зафиксировать на данном месте с помощью ручки, карандаша или любого другого предмета. После этого его необходимо повернуть таким образом, чтобы одна из сторон угла совпала с основанием транспортира (полуокружность с градусной шкалой должна смотреть вверх).
Теперь необходимо посмотреть, на какое число на полуокружности указывает вторая сторона угла (она должна пересекать полуокружность транспортира). Необходимо посмотреть, через какое число проходит эта линия.
Если линию продлить невозможно (она все равно не доходит до полуокружности транспортира), следует взять кусочек бумаги или линейку и совместить ее с той стороной, которая не доходит до полуокружности. В таком случае, линейка должна “продлить” вторую сторону угла до пересечения с полуокружностью, на которую указаны градусы.

Как правильно начертить угол при помощи транспортира

Для начала необходимо начертить линию с помощью транспортира. Такая линия будет базовой. Именно по ней вы будете ориентироваться, чтобы начертить вторую. Для лучшего удобства ее нужно расположить горизонтально.
На этой линии необходимо отметить точку, которая будет вершиной вашего угла. Такую точку необходимо совместить с точкой отсчета на транспортире.
Далее необходимо совместить базовую линию угла с основанием транспортира. После этого следует посмотреть на полуокружность транспортира и выбрать необходимое градусное значение. На бумаге следует нарисовать точку рядом с этим значением. К такой точке необходимо будет провести вторую линию из вершины угла.
После этого можно смело отложить транспортир в сторону.
Теперь нужно взять в руки линейку и соединить вершину угла и точку, которая уже была нарисована возле нужного вам градусного значения.

Дело сделано! Вы получили угол с необходимым для вас градусным значением. В итоге, хотелось бы сказать, что пользоваться транспортиром достаточно просто, если грамотно использовать все эти советы. Но если же вам удалось немного запутаться с градусными шкалами, стоит помнить, что они абсолютно одинаковы, только идут в противоположных направлениях для удобства использования транспортира.

Транспортир представляет собой геометрический инструмент, используемый для измерения углов.

Как выглядит транспортир

Основные и обязательные части транспортира — два ключевых элемента. Первый из них — линейка, разделенная на сантиметровые деления. При этом такая линейка обычно снабжена обозначением точки начала отсчета, которая используется в процессе измерений. Второй элемент транспортира — угломерная шкала, представляющая собой полукруг, обыкновенно включающий деления от 0 до 180°. При этом существуют модифицированные модели транспортиров, которые имеют полную круговую шкалу, то есть позволяют измерять углы величиной от 0 до 360° градусов.

Каждая угломерная шкала содержит линейку значений величины углов как в прямом, так и в обратном направлении. Это позволяет использовать транспортир для измерения как острых, так и тупых углов.

Материалы, применяемые для изготовления транспортиров, могут быть самыми различными. Самыми распространенными вариантами таких материалов являются пластик и металл. Дерево в настоящее время используется для этих целей несколько реже, поскольку такие транспортиры обычно имеют большую толщину и несколько менее удобны в использовании.

Точность измерений каждого инструмента находится в прямой зависимости от его размера. Так, более крупные транспортиры позволяют измерять углы с большей точностью, а небольшие инструменты дают лишь приблизительное представление о величине измеряемого угла.

Как использовать транспортир

При помощи транспортира можно решать две основные задачи: измерение углов и построение углов. Так, для измерения угла необходимо поместить его вершину в точку начала отсчета, обозначенную на линейке транспортира. Затем необходимо обратить внимание на то, чтобы сторона угла, направленная на угломерную шкалу, пересекала ее. В случае, если длина этой стороны оказывается недостаточной, следует продлить ее до пересечения угломерной шкалы.

После этого нужно посмотреть, на каком значении сторона угла пересекает указанную шкалу. В случае, если измерению подвергается острый угол, искомое значение будет меньше 90°, а при измерении тупого угла следует пользоваться той частью шкалы, которая содержит деления, превышающие 90°.

Аналогичным образом осуществляется построение углов при помощи транспортира. Сначала следует провести линию, которая будет представлять собой одну из сторон, а ее , которое станет вершиной, поместить в точку отсчета. Затем на угломерной шкале точкой нужно отметить нужную величину угла, который может быть как острым, так и тупым. После этого, убрав транспортир, соедините вершину будущего угла с проставленной точкой: в результате вы получите искомый угол.

Назад Вперёд

Цели:

Образовательные :
- познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
- научить пользоваться транспортиром.
Развивающие :
- развивать внимание, мышление учащихся;
- развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;
- развивать познавательный интерес к предмету.
Воспитательные :
- воспитывать чувство взаимоуважения;
- воспитывать у учащихся навыки учебного труда.

ХОД УРОКА

I. Организационный момент

II. Вступительное слово учителя

Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны.
Будем учиться не только математике, но и умению общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:

III. Устная работа

Какие из углов, изображенных на рисунке, являются:

а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?

О каком угле мы с вами еще не вспомнили? [О развернутом]
Какой угол называется развернутым? Острым? Прямым? Тупым?

Мы знаем, что два угла можно сравнивать друг с другом.
Какой способ для этого мы использовали? [Наложение]

Но углы, также как и отрезки, можно сравнивать не только наложением, но и с помощью измерения.

IV. Изучение нового материала

Для построения и измерения углов используют специальный прибор. Как он называется, вы узнаете, отгадав кроссворд.

1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие угол.
4. Угол, который образуют два дополнительных друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину развернутого угла.
7. Инструмент, который используют для построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше развернутого.
10. Результат умножения.
11. Результат вычитания.

Учитель демонстрирует учащимся транспортир или показывает на плакате:

– Для измерения углов применяют транспортир. Положите перед собой транспортиры. Вы видите, какие они разные, но у всех есть нечто общее, о чем мы сейчас будем говорить.

Слайд 5. Итак, шкала транспортира. Она расположена на полуокружности и пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет слева направо и справа налево.

Слайд 6. Также есть круглые транспортиры, шкала идет по кругу от 0 до 360, но она также разделена на две полуокружности.

Центр этой полуокружности отмечен на транспортире точкой или черточкой. Найдите на своем транспортире центр и покажите его.

Штрихи шкалы транспортира делят полуокружность на 180 равных частей. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен доле развернутого угла. Такие углы называют градусами.

Слайд 7. Итак, градусом называют долю развернутого угла. Градусы обозначают знаком °. Каждое деление шкалы транспортира равно 1°.

Историческая справка

Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут , а минуту – на 60 секунд :

Объяснение учителя (с демонстрацией на доске), как с помощью транспортира можно измерить угол.

– Как измеряют углы с помощью транспортира ?

1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть величина этого угла.

Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.

V. Практическая работа

Каждому ученику выдается набор углов: острый, прямой, тупой и развернутый.

Задания

Выберите из предложенных вам углов острый, тупой, прямой, развернутый.
Измерьте их градусную меру и запишите в тетрадях эти данные.
Сделайте вывод о градусной мере:

а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.

Вывод:

VI. Физкультурная пауза

Покажите руками угол 90°, 180°.
Покажите руками острый угол, тупой угол.
Покажите рукой, где вокруг нас есть прямые углы.
Повернитесь на 180°. А теперь на 90°.

Продолжаем работать.

Задание: Начертите в тетради угол любой величины. Предложите соседу по парте его измерить.

VII. Работа по карточкам

У всех учеников карточки с одинаковым заданием.

Задание: Измерьте углы и запишите результаты измерений в тетрадях.

Слайд11.

Задание: Выполняется устно с использованием модели часов.

Какой угол образуют часовая и минутная стрелки часов:

а) в 3 ч; в) в 10 ч; д) в 2 ч 30 мин;
б) в 5 ч; г) в 6 ч; е) в 5 ч 30 мин?

Задача №1652

Луч ОС лежит внутри угла АОВ, причем АОС = 37°, ВОС = 19°?.

Чему равен угол АОВ°

Слайды 13, 14, 15.

VIII. Итог урока

IX. Задание на дом

п. 42, №1651, №1683, №1672.

Чему равен угол поворота.

Документ без названия. Вопросы и задания для самоконтроля

В городе есть новая игра, в которой хочет Фред. Это своего рода физическая игра быстрого мышления, требующая рефлексов и знаний о углах вращения. Хорошо, эта игра еще не существует. Основная идея включает в себя углы поворота. Оказывается, существует как минимум четыре способа описания углов поворота. Все четыре пути имеют смысл и понятны. Позвольте Фреду помочь в этой игре.

Скажем, вы стоите лицом к стене и делаете один полный поворот. Вы все еще стоите перед стеной, так? У нас может быть половина хода, четверть оборота и любая другая часть хода. Что нам нужно во всех это поворот, является ссылкой. Ссылка — это начальное место, из которого мы поворачиваемся. Да, да, и нам также нужно направление. Это может быть поворот по часовой стрелке или против часовой стрелки.

Навигация по странице.

Что называют поворотом точки вокруг точки?

Введем понятие поворота точки вокруг точки .

Сначала дадим определение центра поворота.

Представьте, что полный поворот разделен на четыре части, называемые квадрантами. Затем каждый из этих квадрантов равномерно делится на 100 гонок. Первые 100 гонок предназначены для первого квадранта. Затем для второго квадранта выбраны от 101 до 200. Таким образом, полный оборот имеет 400 гонок.

Пример

Мы могли бы также использовать 2π радиан для полного хода. Как насчет в общей сложности 200 гонок? Есть 360 градусов в полный ход. Прежде чем мы разворачиваем Фреда на игру, давайте попробуем измерить некоторые углы. Точка, где встречаются две стороны, является вершиной угла. Один из способов проверить ваше понимание — определить угол поворота в следующих примерах, прежде чем смотреть на ответ и объяснение. Мы можем выполнять эти угловые измерения с некоторыми отношениями преобразования.

Определение.

Точку, относительно которой осуществляется поворот, называют центром поворота .

Теперь скажем, что получается в результате поворота точки.

Давайте начнем с того, как Фред сидит у вершины и просматривает положительный х-окс. Где Фред ухаживает за ним, он завершает следующие угловые повороты. Вращаться против часовой стрелки на 100 га. Вращение по часовой стрелке является отрицательным углом относительно эталона.

Фред любит эту игру и полностью понимает, как измерить и нарисовать угол поворота четырьмя различными способами. Но вся эта ротация оставила ему головокружение. Полный поворот — это полный поворот, который начинается и заканчивается в том же месте. Фракции полного поворота относительно ссылки допускают частичное вращение. Другой мерой угла поворота является угол, в котором 100 гонов соответствует одному квадранту. Исходная сторона является начальной стороной для вращения, а сторона терминала — стороной после того, как было выполнено вращение.

Точка, где встречаются две стороны, — это вершина. На этих уроках мы узнаем. Что такое вращение, как рисовать повернутое изображение объекта, заданного центром, угол и направление вращения. как найти угол поворота с учетом объекта, его изображения и центра вращения. как вращать точки и формы на плоскости координат относительно начала координат. Преобразование, в котором объект вращается вокруг неподвижной точки. Направление вращения может быть по часовой стрелке или против часовой стрелки.

Фиксированная точка, в которой происходит поворот, называется центром вращения. Количество произведенного вращения называется углом поворота. Для любого вращения нам нужно указать центр, угол и направление вращения. Учитывая центр вращения и угол поворота, мы можем определить повернутое изображение объекта.

Полный оборот

Повернуть точки на плоскости координат

Теперь мы рассмотрим, как точки и формы вращаются на координатной плоскости. Будет полезно отметить шаблоны координат, когда точки вращаются вокруг начала координат под разными углами. Вращение геометрии Вращение представляет собой изометрическое преобразование: исходная фигура и изображение являются конгруэнтными. Ориентация изображения также остается неизменной, в отличие от отражений. Для выполнения геометрического вращения сначала нужно знать точку поворота, угол поворота и направление. Вращение также совпадает с композицией отражений по пересекающимся линиям.

Дадим графическую иллюстрацию полного оборота.

Вопросы и задания для самоконтроля

На следующих диаграммах показано вращение 90 °, 180 ° и 270 ° относительно начала координат. Прокрутите страницу вниз для получения дополнительных примеров и решений. Как вращать точки на плоскости координат? Следующие видеоролики показывают вращение по часовой стрелке и против часовой стрелки 0˚, 90˚, 180˚ и 270˚ о происхождении. Также исследуется структура координат. Состав преобразований Отражение в пересекающихся линиях Теорема.

Два отражения в параллельных линиях = перевод. Два отражения в пересекающихся линиях = вращение. Пример: Ниже представлена композиция из двух отражений в пересекающихся линиях. Изучая фигуры и фигуры, мы сталкиваемся с симметричными и асимметричными изображениями. Симметричные формы имеют линию, по обе стороны которой фигура подобна. Эта линия известна как линия симметрии. Можно сказать, что фигура с одной стороны линии симметрии является зеркальным отображением другого.

Понятие угла поворота

Здесь мы узнаем о вращательной симметрии. Вращательная симметрия идентифицируется как угол, в то время как мы поворачиваем фигуру в ее среднюю точку. Вращательная симметрия заключается в том, что точка перемещается по объектам и прилегает к себе более одного раза в 360 градусов. Изучать фигуры, движущиеся вокруг точки, называют центром вращения. Вращательная симметрия имеет более чем один порядок вращательной симметрии, объекты могут поместиться в пределах 360 градусов.

Если фигура находит два одинаковых совпадения за один оборот, тогда она известна как. Аналогично, если объект обладает тремя одинаковыми совпадениями в одном полном вращении, то говорят, что он имеет вращательную симметрию порядка 3 и т.д. В объекте, после вращательной симметрии, этот объект оказывается одинаковым после вращения исправления или определенного числа вращений. Объекты могут содержать более одной вращающейся симметрии. Точка вращательной симметрии должна быть повернута так, чтобы она была похожа на другую вершину или сторону.

Это не может быть аналогичная вершина или сторона. Подробнее о вращательной симметрии. Число местоположений, в которых форма умеет вращаться, не внося никаких изменений в метод, который он первоначально ищет, — это известный порядок вращательной симметрии.

Вышеуказанная форма не изменяется даже после того, как форма повернута. Поэтому он имеет вращательную симметрию. Картинка имеет вращательную симметрию, если она выглядит точно так же после поворота на 1/2 оборота или меньше. Если форма совпадает с собой много раз, поскольку она изогнута в точке, тогда предполагается, что она содержит вращательную симметрию.

Теперь поговорим о характеристиках угла поворота подробнее и по порядку.

Заказать 1 объекты вращательной симметрии.

Равнобедренные треугольные объекты имеют порядок 1 вращения симметрии.
Объекты скалярного треугольника имеют порядок 1 вращения симметрии.
Равнобедренные трапециевидные объекты имеют порядок 1 вращения симметрии.
Объекты трапеции имеют порядок 1 вращения симметрии.
Кайт-объекты имеют порядок 1 вращения симметрии.

Порядок 2 вращения объектов симметрии.

Что называют поворотом точки вокруг точки?

Объекты прямоугольника имеют порядок 2 вращения симметрии.
Объекты параллелограмма имеют порядок 2 вращения симметрии.
Объекты ромба имеют порядок 2 вращения симметрии.
Объекты эллипса имеют порядок 2 вращения симметрии.

Порядок 3 вращения объектов симметрии.

Направление поворота

Объекты равносторонних треугольников имеют порядок 3 вращения симметрии. Порядок 4 вращения объектов симметрии. Квадратные объекты имеют порядок 4 вращения симметрии. Порядок 5 вращений объектов симметрии. Обычные пятиугольные объекты имеют порядок 5 вращения симметрии.

Вращательная симметрия зависит от типа треугольника. Треугольник классифицируется как: треугольник треугольника, равнобедренный треугольник и равносторонний треугольник, основанный на длине сторон треугольников. Скальные треугольники: треугольник со всеми тремя неравными сторонами. Треугольник будет иметь вращательную симметрию при завершении одного круга, а его порядок вращательной симметрии равен 1. Искомый треугольник. Треугольник, который имеет две стороны и два угла одной и той же меры. Порядок симметрии будет равен 1, а угол вращательной симметрии равен 360 градусам.

Величина угла поворота, угол произвольной величины

Треугольник треугольника: равносторонний треугольник, мы имеем в виду, что треугольник имеет все три отрезка одной и той же меры. Угол поворота вращательной симметрии равен 120 градусам, а порядок симметрии для равностороннего треугольника будет равен 3. Порядок вращательной симметрии заключается в том, сколько раз форма будет соответствовать себе во время одного полного вращения. при повороте на угол 180 градусов или меньше по центру, рисунок выравнивается с самим собой. Каждый день мы видим много логотипов компании.

У площади есть вращательная симметрия?

Эти логотипы часто имеют симметрию. Появляется какая-то геометрическая фигура, как если бы она находилась в исходном положении, выполняя одно полное вращение на 360 градусов. Да, квадрат имеет вращательную симметрию. Квадрат имеет 4 стороны, а измерение вращения составляет 90 градусов. Таким образом, квадратные объекты имеют порядок 4 вращения симметрии.

Да, объекты прямоугольника имеют порядок 2 вращения симметрии. Прямоугольник представляет собой особый вид четырехугольника, который имеет равные противоположные стороны, а все углы прямоугольника имеют угол 90 градусов. Прямоугольник имеет 2 линии симметрии.

Параллелограмма имеет вращательную симметрию?

У трапеции есть вращательная симметрия

Нет, трапеция не имеет вращательной симметрии, потому что если мы повернем трапецию на 90 градусов, 180 градусов и 270 градусов, она никогда не получит точного положения. Существует ли у Пентагона вращательная симметрия. Да, обычные объекты пятиугольника имеют порядок 5 вращения симметрии. В правильной пятиугольной стороне все стороны имеют одинаковую длину, и все внутренние углы одинаковы. Порядок вращательной симметрии пятиугольника равен 5, поскольку порядок симметрии зависит от равного количества сторон.

Поворот фигуры вокруг точки на угол

Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.

Список литературы.

Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- isbn 5-09-002727-7
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Движение тела по окружности можно описывать тем же способом, которым пользуются при описании прямолинейного движения. Но часто более удобным оказывается другой способ, с которым мы сейчас ознакомимся.

Представим себе, что некоторое тело движется по окружности радиусом (рис. 65). Проведем из центра О окружности радиус

к какой-нибудь течке тела А и будем следить не только за самим телом, но за радиусом, проведенным к нему. Мы увидим, что, по мере того как тело движется, радиус поворачивается. Если, например, тело за промежуток времени переместилось из точки А в точку В, то за это же время радиус повернулся на угол Этот угол мы будем называть углом поворота радиуса. О движении тела можно, следовательно, сказать, во-первых, что тело за промежуток времени прешло путь по дуге окружности, во-вторых, что оно совершило перемещение в, модуль которого равен длине хорды и, в-третьих, что радиус, проведенный к телу, совершил псвсрот на угол

Если бы тело двигалось по окружности другого радиуса (см. рис. 65), то длина пройденного пути была бы больше. Большей была бы и длина перемещения Угол же поворота ради в обоих случаях остается одним и тем же. Так, конец минутной стрелки маленьких ручных часов за 15 мин проходит путь длиной сколо 1,5 см. За это же время конец минутной стрелки огромных башенных часов (например, часов Спасской башни Кремля) проходит путь длиной в несколько метров. Но минутные стрелки всех часов в мире за четверть часа поворачиваются на один и тот же угол — 50° (рис. 66).

Если мы снова Еернемся к рисунку 65, то увидим, что у тел, движущихся по окружностям с радиусами равны не только угли псссрсга. В обоих случаях одинаковы и отношения длины дуги к радиусу:

По какой бы окружности ни двигалось тело, при равных углах поворота радиуса равны и отношения длины дуги к радиусу. Поэтому и сами углы можно измерять величиной этого отношения

При таком измерении углов за единицу измерения угла удобно принять не градус, а угол, соответствующий дуге, длина которой I равна радиусу потому что тогда угол будет равен единице. Такая единица измерения угла сейчас общепринята в науке, и называют ее радианом (сокращенно рад).

Радиан — это угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу.

Легко установить связь между градусом и радианом.

Когда тело (или точка) совершит один полный оборот по окружности радиусом то длина пройденной дуги будет равна Поэтому величина угла в радианах равна:

Следэзательно, один оборот — это поворот радиуса на угол рад. В градусной мере этот же угол равен Отсюда

Таким образом, длина дуги, пройденной телом, и угол поворота радиуса, проведенного к нему, связаны формулой

Скорость равномерного движения тела по окружности тоже можно выражать в угловых единицах. Для этого используют понятие угловой скорости.

Под угловой скоростью мы будем понимать отношение угла поворота радиуса, проведенного к телу, к промежутку времени, в течение которого совершен этот поворот. Угловую скорость обозначают греческой буквой со (омега), так что

Так как здесь угол выражен в радианах, а время в секундах, то угловая скорость со измеряется в радианах в секунду (рад/сек).

В отличие от угловой скорости скорость измеряемую отношением длины пути ко времени и выражаемую в метрах в секунду, называют линейной скоростью. Между угловой скоростью со и линейной скоростью очень простая связь. Если в выражение для угловой скорости подставить вместо его значение то мы получим:

Так как в свою очередь то или

Упражнение 15

1. Что такое угловая скорость? В каких единицах ее измеряют?

2. Как связаны между собой угловая и линейная скорость?

3. Вычислите угловую и линейную скорость движения Земли вокруг Солнца. Радиус орбиты Земли считать равным 150 000.000 км.

4. Какова линейная скорость конца минутной стрелки часов на Спасской башне Московского Кремля, если длина стрелки 3,5 м? Сравните угловую скорость этой стрелки с угловой скоростью минутной стрелки ручных часов.

Полный угол — определение, формирование, примеры

LearnPracticeDownload

Полный угол — это тип угла, который измеряется в 360°. Угол образуется, когда две линии пересекаются в точке и измеряют расстояние между этими двумя линиями. Существуют различные типы углов, такие как прямой угол, острый угол, тупой угол и так далее. Полный угол соответствует одному полному обороту на 360°. Давайте узнаем больше об этой интересной концепции полных углов и решим несколько примеров.

1.	Определение полного угла
2.	Представление полного угла
3.	Формирование полного угла
4.	Часто задаваемые вопросы о полном угле

Определение полного угла

Если после одного полного оборота последний луч совпадает с падающим или начальным лучом, то образованный таким образом угол называется полным углом. Другими названиями являются полный угол и круглый угол. Угол равен 2π радиан = 360 градусов, что соответствует центральному углу всей окружности. Четыре прямых угла или два прямых угла составляют полный угол. Угол похож на нулевой угол, но разница заключается в степени вращения.

Представление полного угла

Полный угол может быть представлен в трех различных системах измерения углов, а именно:

Полный угол представлен как 360° в шестидесятеричной системе счисления.
Полный угол представлен как 2π в круговой системе.
Полный угол представлен как 400 ^g в сотенной системе.

Формовка полного угла

Полный угол можно составить двумя способами:

Полный угол линией

Рассмотрим луч AD, расположенный на плоскости. Когда луч AD поворачивается на угол 360° для достижения того же положения, создается другой луч AC. Угол, под которым луч достигает своего конечного положения от своего начального положения, равен ∠CAD, а требуемый угол поворота равен 360°. Следовательно, ∠CAD = 360° и является полным углом.

Полный угол между двумя линиями

Рассмотрим два луча PQ и PR, два луча образуют один и тот же угол, однако угол между двумя лучами составляет полный угол. Угол между двумя лучами записывается как ∠RPQ = 360°, так как он совершает полный оборот.

Связанные темы

Ниже перечислены несколько интересных тем, связанных с полными углами, посмотрите.

Пары уголков
Внутренние уголки
Дополнительные уголки
Дополнительные углы

Примеры полных углов

Пример 1: Сэм совершает утреннюю пробежку по прямоугольному парку, начиная с точки А и заканчивая точкой А. За один раунд он проходит 4 прямых угла. Определить степень.
Решение: Так как Сэм завершает весь раунд, начиная с точки A и заканчивая в той же точке, покрывая 4 прямых угла, он завершает угол. Это означает, что градус, покрываемый Сэмом, составляет 360°, что делает его полным углом.
Пример 2: Белла пытается обойти квадратный блок из секции D, чтобы вернуться в ту же начальную точку. Но она останавливается на полпути в секции F. Можете ли вы определить градус и угол, который она охватывает?
Решение: Чтобы завершить раунд, начиная с секции D и обратно в секцию D, Белла должна совершить полный оборот. Это означает, что ей нужно пройти полный угол, охватывающий 360°. Поскольку она останавливается на полпути, она может пройти только половину пути, т. е. останавливается на 180°. Таким образом, получается прямой угол.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

Часто задаваемые вопросы о полных углах

Что такое полный угол?

Когда угол завершает свой полный оборот, начиная с 0 градусов и заканчивая 360 градусами, он называется полным углом. Его измерение равно 360 градусам.

Каковы 6 типов углов?

6 типов углов: прямые углы, острые углы, тупые углы, прямые углы, рефлекторные углы и полные углы.

Что такое полный или полный угол?

Угол, который завершает полный оборот, т. е. 1 полный оборот с началом и окончанием в одной и той же точке, называется полным или полным углом. Градус полного угла равен 360° или 2π.

Как выглядит полный угол?

Полный угол охватывает весь поворот, начинающийся и заканчивающийся в одной и той же точке. Это полный круг с вращением на 360°.

В чем разница между полным углом и рефлекторным углом?

Полный угол представляет собой полный круг с поворотом на 360°. Принимая во внимание, что угол рефлекса — это тип угла, который измеряет более 180 °, но менее 360 °. Например, 192°, 250°, 178° и т. д. — это все углы рефлекса.

Как сделать полный угол?

Полный угол можно построить двумя способами: сначала с помощью линий, а затем с помощью двух линий. Линия может построить полный угол с помощью луча, который совершает полный оборот на 360 °, при этом луч является постоянным плоскостью. Построение полного угла между двумя линиями осуществляется путем повторного использования двух лучей на одной плоскости с теми же точками, которые совершают полный оборот.

Скачать БЕСПЛАТНЫЕ учебные материалы

Угловые рабочие листы

Математические рабочие листы и
наглядная учебная программа

Угол 360 градусов — построение, определение, шаги по рисованию и измерению

LearnPracticeDownload

Угол 360 градусов — это полный угол или полный угол, поскольку он образует окружность вокруг точки. Это ровно вдвое больше прямого угла (угол 180 градусов). Если говорить о реальном примере угла в 360 градусов, то прекрасным примером является угол между двумя стрелками часов в положении 12 часов. Угол между двумя стрелками часов составляет 360°, потому что они образуют полный оборот или круг. Обе руки будут перекрывать друг друга под углом 12, что представляет собой угол в 360 градусов.

1.	Что такое угол 360 градусов?
2.	Угол 360 градусов Название
3.	Как нарисовать угол 360 градусов?
4.	Часто задаваемые вопросы

Что такое угол 360 градусов?

Угол в 360 градусов является полным углом и равен обороту. Его еще называют полным углом. Два плеча угла, составляющего 360 градусов, перекрывают друг друга из общей вершины. Угол в 360 градусов не меняет направление точки или линии. Посмотрите на изображение, приведенное ниже, показывает, как выглядит угол 360 градусов.

Из изображения выше видно, что угол в 360 градусов образует полный круг. Это шесть раз угол 60 градусов, четыре раза прямой угол и дважды прямой угол.

Угол 360 градусов Название

Угол, равный 360 градусам, называется полным углом . Всякий раз, когда мы строим угол в 360 градусов, он всегда образует круг, поэтому он известен как полный угол. Существуют разные названия углов разных измерений. Например, половина угла в 360 градусов, то есть угол в 180 градусов, известен в геометрии как прямой угол. Точно так же одна четвертая часть 360 градусов, то есть 9Угол 0 градусов известен как прямой угол. Углы, которые меньше 360 градусов, но больше 180 градусов, относятся к категории рефлекторных углов.

Как нарисовать угол 360 градусов?

Угол 360 градусов можно нарисовать с помощью транспортира и циркуля.

Рисование угла в 360 градусов с помощью транспортира

Чтобы нарисовать угол в 360 градусов с помощью транспортира, имеется транспортир на 360 градусов круглой формы. У него есть центр посередине, который можно проследить, чтобы нарисовать угол в 360 градусов.

Построение угла в 360 градусов с помощью компаса

Выполните указанные действия, чтобы построить угол в 360 градусов с помощью компаса.

Шаг 1: Начертите с помощью линейки луч и назовите его AB.
Шаг 2: Поместите кончик компаса в точку A и выберите подходящую ширину на компасе.
Шаг 3: Поместите кончик карандаша где-нибудь между A и B на луче AB и начните рисовать дугу.
Шаг 4: Остановитесь, когда снова достигнете той же точки. Это необходимый угол 360°.

Важные примечания

Угол в 360 градусов также называют полным углом.
Угол вокруг центральной точки окружности составляет 360 градусов.

Связанные статьи об угле 360 градусов

Ознакомьтесь с этими интересными статьями, посвященными углам 360 градусов.

Угол 45 градусов
Уголки
Угол 60 градусов
Тупой угол
Угол 180 градусов
Угол рефлекса
Угол 30 градусов
Угол 90 градусов

Примеры угла 360 градусов

Пример 1: Можете ли вы помочь Джозефу найти разницу между углом 180° и углом 360°?
Решение: Угол в 180 градусов представляет собой прямую линию, известную как полуокружность. Он изменяет направление линии или луча. Угол в 360 градусов образует круг. Два плеча угла, образующего 360 градусов, перекрывают друг друга.
Пример 2: Если угол в 360 градусов разделить на четыре части так, что сумма трех частей равна 270 градусам, то чему равен четвертый угол?
Решение: Пусть неизвестный угол равен x.
сумма трех других углов + x = 360°
270° + х = 360°
х = 360° — 270° = 90°
Следовательно, четвертый угол равен 90°. Это прямой угол.
Пример 3: Есть три угла, образующие вместе полный угол: угол A, угол B и угол C. Если угол A = 130 градусов, угол B = 90 градусов, то какова величина угла C?
Решение: Мы знаем, что полный угол равен 360 градусам. Это означает, что угол A + угол B + угол C = 360 градусов.
130° + 90° + С = 360°
C = 360° — (90° + 130°) = 140°
Таким образом, угол C равен 140 градусам.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по углу 360 градусов

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле 360 градусов

Как называется угол 360 градусов?

Угол в 360 градусов называется полным углом, полным углом или полным поворотом. Он образует круг вокруг точки. Прекрасным примером угла в 360 градусов являются две стрелки часов в положении 12 часов.

Как выглядит угол 360 градусов?

Угол в 360 градусов выглядит как круг, поскольку он совершает полный оборот вокруг точки.

Как нарисовать угол 360 градусов?

Чтобы построить угол в 360 градусов, нарисуйте луч с помощью линейки. Поместите кончик циркуля в конечную точку и нарисуйте дугу, начинающуюся и заканчивающуюся в одной и той же точке луча. Этот угол и будет искомым.

Сколько прямых углов составляют угол 360 градусов?

Прямой угол равен 90 градусам. Чтобы найти количество прямых углов, необходимых для угла в 360 градусов, нам нужно разделить 360 на 90. Итак, 360/90 = 4. Следовательно, 4 прямых угла составляют угол в 360 градусов.

Как нарисовать угол 360 градусов с помощью транспортира?

Транспортир на 360 градусов имеет форму круга. Итак, чтобы составить угол в 360 градусов с помощью транспортира, нарисуйте линию, луч или отрезок. Поместите центральную точку этого транспортира в любую конечную точку линии. Проследите окружность, заданную в центре, вокруг конечной точки. Это и будет искомый угол 360 градусов.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочие листы для угла 360 градусов

Рабочие листы по математике и
наглядный учебный план круг.

В радианах полный угол равен $2\pi$ радианам.

$360$ Углы в градусах играют важную роль в математике, включая геометрию и тригонометрию, и в естественных науках, включая астрономию и физику. Они также важны в инженерии, архитектуре и дизайне.

Перед тем, как перейти к этому разделу, ознакомьтесь с углами и типами углов.

В этом разделе рассматриваются:

Что такое угол 360 градусов?
Угол 360 градусов против нулевого угла
Определение угла 360 градусов
Примеры полного угла

Угол 360 Что такое 360?

Угол в 360$ градусов — это полный оборот или «полный угол». Это также мера внутреннего угла окружности и сумма внутренних углов четырехугольника.

В радианах полный угол равен $2\pi$ радианам.

Поворот объекта на $360$ градусов возвращает его в исходное положение и первоначальную ориентацию.

Угол 360 градусов и нулевой угол

Угол 360 градусов и нулевой угол могут выглядеть одинаково. Это связано с тем, что если объект поворачивается на ноль градусов или на $360$ градусов, конечный результат будет таким же.

Процесс отличается. В одном случае ничего не сдвинулось. В другом случае объект совершил полный круг.

Однако из-за этого факта тригонометрические функции являются $2\pi$ циклическими. То есть их значения повторяются через каждые $2\pi$ или $360$ градусов. То есть свойства угла в 360$ будут такими же, как и у угла в 0$.

Угол 360 градусов Определение

Угол в 360$ градусов — это полный оборот. Он равен $2\pi$ радианам или внутреннему углу окружности.

Примеры полного угла

Наиболее классическим примером полного угла является единичный круг.

Это круг радиусом в единицу с центром в начале координат. Такой круг имеет длину окружности $2\pi$, а длина дуги любого участка окружности равна длине радиана.

Эти круги используются в тригонометрии, потому что в этом круге легко нарисовать прямоугольные треугольники, которые имеют простые размеры, что упрощает поиск тригонометрических соотношений.

Суммарный угол единичной окружности равен $360$ градусам. При работе с углами, превышающими $360$, отношения находятся путем вычитания $360$ градусов или $2\pi$ радианов столько раз, сколько необходимо, пока не получится число $k$, большее или равное $0$ и меньшее, чем $360. $. Тогда отношение для начального угла равно отношению при $k$.

Примеры

В этом разделе рассматриваются распространенные примеры задач на полные углы и их пошаговые решения.

Пример 1

Докажите, что сумма внутренних углов четырехугольника равна $360$ градусов.

Решение

Есть несколько способов сделать это. Один из способов заключается в том, чтобы узнать, что сумма внутренних углов треугольника равна $180$ градусам или мере прямой линии.

Этот факт известен с древности и может быть доказан без измерения углов. Фактически, у Евклида есть доказательство этого факта в его Элементы в предложении 32.

Но соединение двух треугольников дает четырехугольник.

Следовательно, сумма внутренних углов четырехугольника должна быть равна сумме внутренних углов двух треугольников. То есть сумма внутренних углов должна быть равна мере двух прямых.

Но две прямые — это полный угол. Следовательно, внутренний угол четырехугольника равен $360$ градусам или $2\pi$ радианам.

Пример 2

Найдите угол, который больше или равен $0$ градусов и меньше $360$, что эквивалентно $567$ градусам. Классифицируйте этот угол.

Решение

Полный угол и угол, равный нулю градусов, лежат на одной прямой и указывают в одном направлении. В этот момент углы сбрасываются. Следовательно, угол $360$ действует так же, как угол $0$. Точно так же угол в 361$ градус обладает теми же свойствами, что и угол в 1$ градус.

Таким образом, чтобы найти угол с теми же свойствами, нужно многократно вычитать из угла $360$ градусов или $3\pi$, пока разница не станет числом от $0$ до $360$.

В этом случае $567-360 = 207$. Таким образом, угол с мерой $567$ градусов будет иметь те же свойства, что и рефлекторный угол $207$ градусов.

Пример 3

Аналоговые часы показывают 4 часа. Какое время будет после того, как минутная стрелка сделает оборот на 360 долларов? На сколько градусов повернется часовая стрелка за это же время?

Решение

Когда минутная стрелка делает поворот на 360$ градусов, она возвращается в исходное положение. Поскольку начальное время было 4 часа, минутная стрелка начиналась с двенадцати. После поворота он вернется на двенадцать.

Когда минутная стрелка совершает полный оборот за сутки, это означает, что прошел один час. Таким образом, часовая стрелка переместится из положения, находящегося прямо на четвёрке, прямо на пятерке. Это означает, что часовая стрелка переместится на $\frac{1}{12}$-й круг. В градусах это $\frac{360}{12} = 30$ градусов. В радианах это $\frac{2\pi}{12} = \frac{\pi}{6}$ радиан.

Пример 4

Круг имеет радиус $4$. Найдите длину отрезка окружности, длина дуги которого равна $360$ градусов.

Решение

Длина дуги отрезка — это длина окружности окружности, заключенной под заданным углом, образованным центром окружности и двумя радиусами.

Длина дуги $360$ градусов означает, что угол, образованный двумя радиусами, является полным углом. Но это также полный внутренний угол круга. Следовательно, длина отрезка окружности, содержащегося в этом угле, равна полной окружности.

Длина окружности этого круга равна $8\times\pi = 8\pi$.

Пример 5

Покажите, что сумма внутреннего угла и соответствующего ему внешнего угла в многоугольнике составляет полный угол.

Решение

Внутренний угол многоугольника равен наименьшему из двух возможных углов. Другой угол, который будет углом рефлекса, представляет собой тот же угол, измеренный в противоположном направлении (по часовой стрелке или против часовой стрелки).

Эти два угла вместе образуют круг. Следовательно, их угловая мера составляет $360$ градусов или $2\pi$ радиан, то же, что и полный угол.

Дополнительные примеры и пояснения

Докажите, что если к треугольнику добавить четырехугольник так, что две прямые четырехугольника лежат на одной линии с двумя линиями сторон треугольника, а другая сторона четырехугольника равна третья сторона, то новая фигура представляет собой треугольник.
Часовая стрелка на часах поворачивается на $360$ градусов. Что такое новое время и на сколько градусов повернулась минутная стрелка?

Ключ ответа

Треугольник и четырехугольник с одной общей стороной образуют фигуру с $3+4-2 = 5$ сторонами и углами. Суммарная мера его внутреннего угла составит $540$ градусов.
Однако этот пятиугольник имеет два прямых угла, потому что две стороны четырехугольника лежат на одной линии с двумя сторонами треугольника. Каждый прямой угол в многоугольнике фактически уменьшает его на одну сторону. В этом случае общее количество сторон будет $5-2 = 3$. Следовательно, полученная фигура будет треугольником.
Если часовая стрелка повернется на $360$ градусов, значит, прошло двенадцать часов. Это означает, что время то же самое, но изменилось время AM или PM. Например, если начальное время было 8:00, новое время — 20:00.
Поскольку минутная стрелка совершает оборот на $360$ один раз в час, она сделала оборот на $360 \× 12 = 4320$ градусов.

Иллюстрации/математические объекты, созданные с помощью GeoGebra.

Как найти угол в процентах от окружности

Все ресурсы по геометрии среднего уровня

8 диагностических тестов 250 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Промежуточная геометрия Помощь » Плоская геометрия » Круги » Сектора » Как найти угол в процентах от окружности

Сколько градусов в окружности?

Возможные ответы:

Правильный ответ:

Объяснение:

В круге есть градусы, поэтому уравнение, которое нужно решить, превращается в простую процентную задачу:

Сообщить об ошибке

Сектор содержит круг. Чему равен центральный угол сектора?

Возможные ответы:

Правильный ответ:

Объяснение:

Целый круг . Таким образом, сектор, принадлежащий кругу, имеет центральный угол, равный .

Следовательно, наш центральный угол равен

Сообщить об ошибке

Если у вас есть процент от круга, какой угол в градусах образует эту область?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Теперь нужно преобразовать в десятичное число.

Если вы умножите 360 на 0,667, вы получите градусную меру, соответствующую проценту, который равен 240.

Сообщить об ошибке тот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Сначала преобразуйте в десятичное число.

Если умножить 360 на 0,20, получится градусная мера, соответствующая проценту, который равен 72.

Сообщить об ошибке что создает этот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Чтобы начать эту задачу, нам нужно преобразовать проценты в десятичные числа.

Если умножить 360 на 0,30, получится градусная мера, соответствующая проценту, который равен 108.

Сообщить об ошибке что создает этот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляют 360 градусов.

Сначала преобразуйте проценты в десятичные числа.

Теперь, если вы умножите 360 на 0,35, вы получите градусную меру, соответствующую проценту, который равен 126.

Сообщить об ошибке , что создает этот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Сначала преобразуйте проценты в десятичные числа.

Если умножить 360 на 0,90, получится градусная мера, соответствующая проценту, который равен 324.

Сообщить об ошибке что создает этот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Сначала нам нужно преобразовать проценты в десятичные числа.

Если умножить 360 на 0,45, получится градусная мера, соответствующая проценту, который равен 162.

Сообщить об ошибке что создает этот регион?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Чтобы решить эту задачу, нам сначала нужно преобразовать процент в десятичную дробь.

Если вы умножите 360 на 0,375, вы получите градусную меру, соответствующую проценту, который равен 135.

Сообщить об ошибке

Если у вас есть круг, под каким углом в градусах создается эта область?

Возможные ответы:

Правильный ответ:

Объяснение:

Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.

Сначала нам нужно преобразовать проценты в десятичные числа.

Если вы умножите 360 на 0,70, вы получите градусную меру, соответствующую проценту, который равен 252.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все промежуточные ресурсы по геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Почему геометрия не измеряется? Почему 360 градусов, а не 1, 10, 100 или даже 1000? | Примечания и вопросы

Категории
Укромные уголки
Прошлый год
Семантические загадки
Тело красивое
Бюрократия, белая ложь
Спекулятивная наука
Этот остров со скипетром
Корень зла
Этические загадки
Эта спортивная жизнь
Сцена и экран
Птицы и пчелы

СПЕКУЛЯТИВНАЯ НАУКА

Почему геометрия не была «измерена»? Почему 360 градусов, а не 1, 10, 100 или даже 1000?

Дэвид Хьюз, Торонто, Канада

Потому что одна из основных переменных в геометрии — число три. Например, если число три равно 180, это означает, что в равностороннем треугольнике углы равны 60 градусов. Какими были бы их углы в метрической системе?
Питер Брук, Кинмак Шотландия

Было; есть единица измерения, называемая град, из которых 100 — прямой угол (90 условных градусов, или пи/2 радиана). Он возник во Франции как «класс» наряду с другими метрическими единицами. Я знаю только, что французская артиллерия действительно использовала его.
Эндрю Уокер, Лестер, Англия

На самом деле градусы были «метрически», в технике углы часто измеряются в радианах, при этом длина окружности выражается как 2Π радиан.
Угловое измерение в градусах или радианах дано по отношению к окружности, 360 градусов или 2 пи радиана являются мерой одного полного оборота. Если бы мы разделили окружность на что-либо, отличное от 360 градусов, нам пришлось бы изменить и наши календари — древние греки выяснили, что в году 360 дней, и что, следовательно, мы продвигаемся вокруг солнца со скоростью один градус в секунду. день — они были довольно близко, учитывая, что они работали по наблюдению в одиночку!
Питер Кларк, Кембридж, Великобритания

Градус — произвольная единица; в основном любое деление круга будет работать как система измерения. Градус имеет то преимущество, что 360 делится без остатка на 2, 3, 4, 5, 6, 8, 9 и 10, что упрощает вычисление угла в уме; действительно, это главное преимущество всех старых имперских единиц. Есть более фундаментальная единица, называемая радианом. Это угол, образуемый дугой окружности, длина которой равна ее радиусу. Поскольку длина окружности равна 2 х пи х радиус один, в круге 2 пи, или 6,283 радиана. Это хорошо для расчетов углового движения, но трудно работать в уме.
Рэй Галлахер, Белфаст, Северная Ирландия

Мы унаследовали 360 градусов от вавилонян, но многие древние общества очень интересовались астрономией, а в некоторых (мегалитическая Британия?) было 366 градусов по окружности. Это логично, так как Земля обращается вокруг своей оси 366 раз в год. Их измерения кажутся взаимосвязанными, а не произвольными, как метрически разделенный круг. Вавилоняне, вероятно, сократили это число до 360, так как оно намного легче делится на множество факторов.
Вивьен, Лондон, Великобритания

Во время археологических раскопок недалеко от Рима мне однажды дали установить теодолит. После некоторого времени, пытаясь заставить его работать, я заметил, что шкала, по которой измерялись горизонтальные углы, показывает 400 градусов, а не 360. Мой руководитель сказал мне, что это была старая часть оборудования, когда-то являвшаяся частью попытки измерить окружность. . Я не уверен, была ли это чисто итальянская инициатива или нет!
Крис Лайес, Хангерфорд, Великобритания

Вавилоняне дали нам круг на 360 градусов. Это число оказывается наименьшим, чье частное представляет собой целое число при делении на любое целое число от 1 до 10 (кроме 7, которое, возможно, добавляло семерке статус «магического числа»). Я слышал, что (по крайней мере, в вооруженных силах США) артиллерийские батареи используют круг в 1000 градусов для большей точности, так что — если это правда — по крайней мере, это начало.
Том Эмис, Ванкувер, Вашингтон, США

И вавилоняне, и китайцы использовали шестидесятеричную систему счисления, что означает, что у них было 59 цифр, а не 9 (ноль был изобретен намного позже). Хотя у них действительно была цифра 10, поэтому их число 11 по-прежнему записывалось как цифра 10 рядом с цифрой 1. Происхождение этого точно неизвестно, хотя на них явно повлияла астрономия и тот факт, что существуют (почти) 360 дней в году. Они также придумали шестьдесят минут в часе, 24 часа в сутки. Это всего лишь еще один пример отставания от школьных стандартов, когда мы ожидаем, что школьники будут знать только 9цифры (и ноль)
Камьяр, Самос Греция

Потому что обычно вы хотите знать, как далеко вы находитесь по окружности, и вы можете разделить 360 на множество более полезных дробей. Действительно, единицей, которую предпочитают математики, является не градус, а радиан. Дважды пи (6,2831853…) радиан равняется 360 градусам. Таким образом, вместо 90 градусов вы говорите «пи больше двух радиан».
Джонатан С., Херефорд Англия

Градиан, грейд, град или гон — метрическая угловая единица, разработанная в послереволюционной Франции как часть метрической системы (наряду с 10-дневной неделей, 10-часовым днем, 100-минутным часом и 100-минутной секундой). В прямом угле 100 град, или в 360 градусах 400 град. Он до сих пор используется французскими военными, а карманные калькуляторы имеют градусы, радианы и градианы для тригонометрических функций.
Марк Манзокки, Абердин, Великобритания

Градиенты в небольшой степени используются во Франции и других странах. На прямой угол 100 град, на полный круг 400. Аксессуар-калькулятор, поставляемый с операционной системой Windows, позволяет вам работать в градусах, а не в градусах или радианах.
Ник Роуз, Пламптон-Грин, Великобритания

В то время как математики довольны градусами или чаще радианами, поскольку математика становится более продвинутой, другие действительно делят углы на 100. Градиан или град — это единица измерения, которая получается путем разделения прямого угла (90 градусов) на 100 частей. Военным нравится эта форма измерения угла, и легко получить компас, настроенный таким образом. Я предполагаю, что используются и другие — в конце концов, 360 градусов являются чисто произвольными и историческими пережитками вавилонской шестидесятеричной системы счисления, а не преднамеренным выбором.
Хейден Риссбрук, Уолтемстоу, Великобритания

В то время как математики довольны градусами или чаще градами, по мере того, как математика становится более продвинутой, другие действительно делят углы на 100. Градиан или град — это единица измерения, которая получается путем разделения прямого угла (90 градусов) на 100 частей. Военным нравится эта форма измерения угла, и легко получить компас, настроенный таким образом. Я предполагаю, что используются и другие, в конце концов, 360 градусов являются чисто произвольными и историческими пережитками вавилонской шестидесятеричной системы счисления, а не преднамеренным выбором.
Хейден Риссбрук, Уолтемстоу, Великобритания

360 имеет гораздо больше делителей, чем 10, 100, 1000 и т. д. Поэтому круг легче разделить на множество различных равных частей — 2,3,4,5,6,8,9,10…… Попробуйте сделать это со 100 или 1000.
Льюис, Лондон, Великобритания

Использование 400 гон вместо 360 градусов также можно найти в землеустройстве. Некоторые теодолиты будут иметь возможность выбора градусов или гонов, и многие теодолиты, сделанные в бывшем восточном блоке, использовали эту систему.
Хэмиш, Ипсвич, Великобритания

Добавьте свой ответ

Разница между поворотами на 180 и 360

Возможно, вы помните, что в средней школе учили геометрии, что в окружности 360 градусов. Углы измеряются в градусах с вершиной, расположенной в центре круга. Это означает, что прямой угол, образующий четверть круга, равен 90 градусам, а горизонтальная линия, образующая основание теоретического полукруга, равна 180 градусам.

(Неизвестно, как древние математики остановились на 360 как на количестве градусов в окружности, но некоторые историки отмечают, что это приблизительно соответствует количеству дней в календарном году и что окружность смутно совпадает с эллиптической орбитой Тот факт, что многие числа без остатка делятся на 360, также может иметь какое-то отношение к этому.)

Корявый.

Градусы выражают углы поворота, поэтому мы говорим о них, когда говорим о петлях, наклонах, трюках на скейтборде, маневрах на сноуборде и баскетбольных данках. Полное путешествие по краю круга составляет 360 градусов, а это означает, что если вы завершите вращение вокруг центральной оси своего тела, в конечном итоге вы окажетесь в том же направлении, что и в начале.

Полуоборота составляет 180 градусов, что вокруг той же центральной оси поместит вас в положение, противоположное тому, где вы смотрели изначально. Чарльз Линдберг, 19 лет27, использовал один-восемьдесят и три-шестьдесят для описания воздушных маневров, которые использовали половину и полные обороты соответственно.

Во второй половине 20-го века один-восемьдесят использовалось идиоматично для описания любого изменения направления, подобно по кругу или его французскому эквиваленту, по направлению .

Я пускаю «Пинто» в скоростной дрифт на всех четырех колесах через поток машин и выезжаю на грунтовую дорогу, ведущую к кладбищу, затем сделал один-восемьдесят , чтобы посмотреть, что меня ждет в другом направлении.
— Г. Гордон Лидди, Уилл , 1980

Естественно, фраза (иногда произносимая как поворот на 180 градусов ) может относиться к образному изменению направления, делая противоположное тому, что делали раньше:

«У иранского режима есть выбор. Она может либо развернуться на 180 градусов и действовать как нормальная страна, либо увидеть, как ее экономика рухнет… Мы надеемся, что новое соглашение с Ираном возможно».
— Майк Помпео, цитата из New York Magazine , 6 ноября 2018 г.
Работают, и не просто, не быстро. Но когда загорается лампочка, они делают один-восемьдесят . Внезапно они начинают говорить о том, чтобы заплатить вперед, вернуться в один прекрасный день и сами стать наставниками.
— Кен Морган, цитата из Macomb Daily (Clinton Township, Mich.), 25 сентября 2015 г.
14 сентября Тигры проиграли DeSales 40-14. Это было их четвертое поражение подряд, причем все они были как минимум на 19 очков больше.точки. Три из этих поражений были домашними. С тех пор команда Джоша Абелла совершила разворот на 180 градусов , одержав семь побед подряд.
— Джейсон Фрейкс и Стив Биттенбендер, The Courier Journal (Луисвилл, Кентукки), 10 ноября 2018 г.

Когда три-шестьдесят используется с точки зрения физических движений, это относится к полному вращению:

«Сделай три-шестьдесят !» — крикнул кто-то с трибун, и Кори побледнел:0371 три шестьдесят ? Я убью себя. Но ладно», и он исполнил великолепный вращательный данк.
— Дарси Фрей, Последний выстрел , 1994
Он сломал одного ныряльщика, сломался влево, а совершил разворот на 360 градусов, чтобы сбить с толку другого ныряльщика из Небраски.
— Аарон Макманн, MLive.com , 22 сентября 2018 г.

Но иногда писатели забывают то, чему они научились в геометрии, и берутся за все 360 , когда на самом деле они имеют в виду, конечно, изменение курса, то есть 180 :

Тайгер Вудс неудачно стартовал на чемпионате PGA, проиграв первые две лунки дважды. Но судьба Тайгера после этого сделала 360 , чему, возможно, способствовала смена рубашки. То есть, если вы верите тому, что читаете в Твиттере.
— Golf.com , 9 августа 2018 г.

Если бы Тайгер Вудс совершил физический разворот на 360 градусов, он бы смотрел в том же направлении, что и в начале. Расширьте это до фигуративного направления, и его состояние не изменилось бы, и он все еще был бы призраком на протяжении всего курса. Вместо этого 180 предполагает поворот судьбы, который автор предлагает здесь.

««Выполнение одной восьмидесяти» подразумевает поворот, например: «С тех пор, как она перешла на прозак, вся ее личность сделала одну восемьдесят». К гардеробу, я думаю, не относится… Конечно, «сделать три-шестьдесят» гораздо хуже. «Вольтефейс» намного лучше, но его больше никто не использует».
— Кейт Кристенсен, Джереми Трейн , 2001

Есть несколько объяснений этой простой ошибке. Во-первых, возникает искушение думать, что удвоение числа просто подчеркивает или преувеличивает, а не изменяет его значение, подобно тому, как кто-то выкладывается на невозможные 110 процентов.

Углы больше 360 градусов

Радиан

Отрицаетльные углы и углы больше, чем $2\pi$ радиан

Основные величины тригонометрии

Тригонометрический круг

Свойства тригонометрических функций: синус и косинус

Свойства тангенсоиды и котангенсоиды

Положительные и отрицательные углы.

Измерение углов дугами окружности.

Классификация углов

Отсчёт углов на тригонометрическом круге.

Углы больше 360°.

Что называют поворотом точки вокруг точки?

Полный оборот

Понятие угла поворота

Направление поворота

Величина угла поворота, угол произвольной величины

Поворот фигуры вокруг точки на угол

Измерение углов. Транспортир. Видеоурок. Математика 5 Класс

Что такое транспортир?

Презентация к уроку

Правила пользования

Измеряем угол

Вывод

Набор школьника

Итог

История изобретения

Где еще используются

Разновидности и использование

Назначение линейки

Измерение градусов угла

Инструкция

Построение угла

Ответ

Как пользоваться транспортиром

Введение

Измерение угла транспортиром

Теорема Пифагора

Размер матрицы и угол обзора объектива фотоаппарата

Читайте также:

Экскурс в историю

Угол обзора объектива и размер матрицы

Кроп-фактор и эквивалентное фокусное расстояние

Эквивалентное фокусное расстояние (ЭФР)

Размеры матриц и кроп-фактор фототехники Nikon

Итоги

Математика. Градусы между стрелками. Логические задачи, головоломки, тесты на интеллект, логические игры. Часы в задачах

Решение задачи

Как измерить острый угол транспортиром. Измерение углов. Транспортир

Измерение углов транспортиром

Свойства измерения углов

Как правильно пользоваться транспортиром

Как правильно измерить градусное значение угла транспортиром

Как правильно начертить угол при помощи транспортира

Как выглядит транспортир

Как использовать транспортир

Чему равен угол поворота.

Что называют поворотом точки вокруг точки?

Пример

Полный оборот

Повернуть точки на плоскости координат

Вопросы и задания для самоконтроля

Понятие угла поворота

Что называют поворотом точки вокруг точки?

Направление поворота

Величина угла поворота, угол произвольной величины

У площади есть вращательная симметрия?

Параллелограмма имеет вращательную симметрию?

У трапеции есть вращательная симметрия

Поворот фигуры вокруг точки на угол

Полный угол — определение, формирование, примеры

Определение полного угла

Представление полного угла

Формовка полного угла

Полный угол линией

Полный угол между двумя линиями

Примеры полных углов

Часто задаваемые вопросы о полных углах

Что такое полный угол?

Каковы 6 типов углов?