Сколько комбинаций из 10 цифр: Сколько комбинаций из 10 цифр по 4?

4=10000. Из этого числа вычтем количество запрещенных комбинаций (т. к. пин-коды из 4 одинаковых цифр запрещены).

Как посчитать сколько будет комбинаций?

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n! (n−k)!

Сколько комбинаций из 4 цифр и 2 букв?

Ответ: 1.

Сколько комбинаций можно составить из 4 букв?

Ответ: 456976 комбинаций.

Сколько комбинаций из 12 букв?

Итого, получили 12 букв. Комбинаций цифр 999.

Сколько может быть комбинаций автомобильных номеров?

Номер автомобиля состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 10 цифр и алфавит в 30 букв. Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.

Сколько можно составить автомобильных номеров в пределах одного региона?

По ГОСТу максимальное число комплектов номеров, которое можно изготовить для региона, составляет 1 726 272, так как есть ограничения — например, не может быть регистрационного знака с тремя нулями.

Сколько комбинаций можно составить из 5 цифр?

Сколько всего возможных комбинаций из пяти чисел 12345, да 120, надо лишь эти числа между собой перемножить 1*2*3*4*5=120, но есть одно «но» нужно подсчитать еще и такие варианты как например 11234, 11123, 11112, 12234, 12333, 12222, 12344 и т.

Сколько вариантов чисел из 6 цифр?

То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.

Сколько возможных комбинаций из цифр 1 2 3?

Рассмотрим комбинации из трёх цифр 1,2,3 с повторениями. Всего – 27 комбинаций.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5?

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? И сколько из них с неповторяющимися цифрами? = 5× 4×3 = 60.

Сколько трехзначных чисел можно составить из цифр 0 2 4?

Сколько трёхзначных чисел можно составить из цифр 0, 2, 4? Всем трям, то есть здравствуйте. 🙂 Я по жизни оптимист, натуралист, огородник-г… Ответ: 18 трёхзначных чисел.

Сколько трехзначных чисел можно составить из цифр 1 4 5 9?

Сколько трёхзначных чисел можно составить их цифр 1 4 5 и 9 простите, нечаянно нажала не ту кнопку. можно составить 3•3•4 = 36 чисел. Поскольку число трехзначное, и если бы цифр всего было 3, получилось бы 3•3 = 9 комбинаций.

Сколько чисел от 100 до 199?

Все решения Всего чисел: 200 – 99 = 101 – нечетное количество. От 100 до 199 будет 100 чисел – половина из них (50 штук) будут четные и плюс еще 1 четное число 200, всего получится 51 четное число.

Сколько всего существует натуральных чисел?

Всего есть 9 натуральных однозначных чисел (0 не считается натуральным). Двузначных (количество чисел от 1 до 99, минус однозначные): 99 — 9 = 99. И есть трехзначных (количество чисел от 1 до 999, минус однозначные и двузначные):

Сколько комбинаций из 3 чисел возможно? – Обзоры Вики

Есть ровно 1,000 возможных комбинаций для 3-значного кода. Для 10,000-значного кода возможно 4 XNUMX комбинаций.

Отсюда, как решить 10 факториалов? равно 362,880 10. Попробуйте посчитать 10! XNUMX! знак равно 10×9!

Сколько существует комбинаций из 6 чисел? Сколько существует различных комбинаций из 6 чисел? Для любой группы из 6 цифр и букв возможно 720 различных перестановок или комбинации, которые можно сделать.

Дополнительно Сколько комбинаций из 4 предметов можно составить из 6 предметов? – 6 предметов образуют одну и только одну комбинацию. — 6 предметов, взятых по 2 или 4 за раз, форма: C(6, 2) = C(6, 4) = 6!/(2!* 4!) = 15 комбинации.

Сколько существует комбинаций из 8 чисел? Количество возможных комбинаций с 8 номерами равно 255.

Что означает n в математике?

Натуральные числа, подсчет чисел. Буква (N) — это символ, используемый для обозначения натуральных чисел. Натуральные числа также известны как счетные числа, и они начинаются с цифры 1 и продолжаются до бесконечности (никогда не заканчиваются), что обозначается тремя точками (…).

Отменяются ли факториалы? Вы можете отменить, но вы должны быть осторожны, как вы это делаете. Например: к! (к+1)! можно уменьшить до 1k+1, отменив часть факториала сверху, но вы НЕ МОЖЕТЕ отменить, например: k! (к+1)!

Как вы делаете факториалы в Python? Использование встроенной функции

1. # Программа Python для поиска.
2. # факториал заданного числа.
3. импортная математика.
4. дефакт (сущ):
5. возврат (математика. факториал (п))
6. num = int(input(«Введите число:»))
7. f = факт (число)
8. print(«Факториал», num, «is», f)

Сколько существует перестановок 5 чисел?

(Для k = n, _nP_k = п! Таким образом, на 5 объектов приходится 5! знак равно 120 аранжировок.)

Также Сколько существует комбинаций из 9 чисел? Следовательно, общее количество возможностей равно 9×9! знак равно3265920. Следовательно, 9-значные числа из разных цифр могут быть образованы 3265920 способами. 4, что является 90,000 различных комбинаций.

Сколько существует комбинаций из 8 чисел с повторами?

Примечание: всего 8 элементов 40,320 различных комбинаций.

Сколько комбинаций может быть из 9 цифр? Следовательно, путем умножения вариантов мы получаем общее количество возможностей, равное 9×9×8×7×6×5×4×3×2=3265920. Следовательно, 9-значные числа из разных цифр могут быть образованы 3265920 способами.

Сколько существует комбинаций из 12 чисел? Количество возможных комбинаций с 12-значным числом равно 4,095.

Ноль — это действительное число?

На самом деле настоящие числа — это практически любые числа, которые вы можете придумать. … Действительные числа могут быть положительными или отрицательными, и включить число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел.

Пи действительное число? Вкратце, пи, которое записывается как греческая буква р или π, представляет собой отношение длины окружности любого круга к диаметру этого круга. … Цель пи — иррациональное число, что означает, что его десятичные формы не заканчиваются (например, 1/4 = 0.25) и не повторяются (например, 1/6 = 0.166666…).

Что такое R * в математике?

В математике обозначение R * представляет два разных значения. В системе счисления R * определяет набор всех ненулевых действительных чисел, который образует группу по операции умножения. В функциях R* определяет рефлексивно-транзитивное замыкание бинарного отношения «R» в множестве. 4 (4)

Для чего придумали факториал? Использование! был основан Кристианом Крампом в 1808 г.. Хотя они могут показаться очень простыми, использование факториальной записи для неотрицательных целых чисел и дробей немного сложно. Приложения варьируются от простой алгебры до исчисления, и он также используется для определения вероятностей.

Что такое заглавная гамма в математике?

В математике гамма-функция (обозначаемая буквой Γ, заглавной буквой гамма из греческого алфавита) является одним из часто используемых расширений функции гаммы. факториальная функция комплексных чисел. Гамма-функция определена для всех комплексных чисел, кроме неположительных целых чисел.

Комбинаторика

— Сколько различных телефонных номеров возможно в пределах кода города?

спросил 8 лет, 3 месяца назад

Изменено 6 лет, 3 месяца назад

Просмотрено 137 тысяч раз

$\begingroup$

Телефонный номер состоит из 10 цифр. Первые три — это код города, а остальные 7 — это местный телефонный номер, который не может начинаться с 0. Сколько разных телефонных номеров может быть в одном коде города?

• комбинаторика

$\endgroup$

2

$\begingroup$

Из Википедии http://en.

wikipedia.org/wiki/North_American_Numbering_Plan:

Каждый трехзначный код города может содержать до 7 919 900 уникальных телефонных номеров:

• NXX может начинаться только с цифр [2–9] , предоставляя базу из 8 миллионов чисел: ( 8 x 100 x 10000 ) .
• Однако последние две цифры NXX не могут быть равны 1 во избежание путаницы с кодами N11 (вычтите 80 000).
• Несмотря на широкое использование NXX «555» для вымышленных телефонных номеров — см. 555 (номер телефона) — сегодня единственными такими номерами, специально зарезервированными для вымышленного использования, являются «555-0100» до «555-0199», а остальные « 555-дюймовые номера, выпущенные для фактического назначения в качестве информационных номеров (вычтите 100).
• В кодах отдельных географических зон несколько других префиксов NXX, как правило, не назначаются: код(ы) домашней зоны, коды соседних внутренних зон и наложения, коды зон, зарезервированные для использования поблизости в будущем, коды отраслевых испытаний (обычно NXX 958 и 959) и коды специальных услуг (например, NXX 950 и 976).
  Вычтите для 911 411и т. д. экстренных и информационных номеров

$\endgroup$

1

$\begingroup$

Если мы визуализируем номер телефона как имеющий три «слота»: один для кода города, один для первой цифры и последний, состоящий из шести оставшихся цифр, по принципу умножения есть 1 способ заполнить первый слот. , 9{10}}$D) $10!$

Ответ

Подтверждено

234,6 тыс.+ просмотров

Подсказка: Сначала создадим 10 пустых мест, которые необходимо заполнить цифрами 1 и 2. Затем мы напишем возможность и способы заполнения каждого из пробелов по отдельности, а затем перемножим эти способы, чтобы получить требуемый ответ.

Полный пошаговый ответ:
Нам нужно составить 10-значное число.
Следовательно, наш номер будет выглядеть примерно так: __ __ __ __ __ __ __ __ __ __.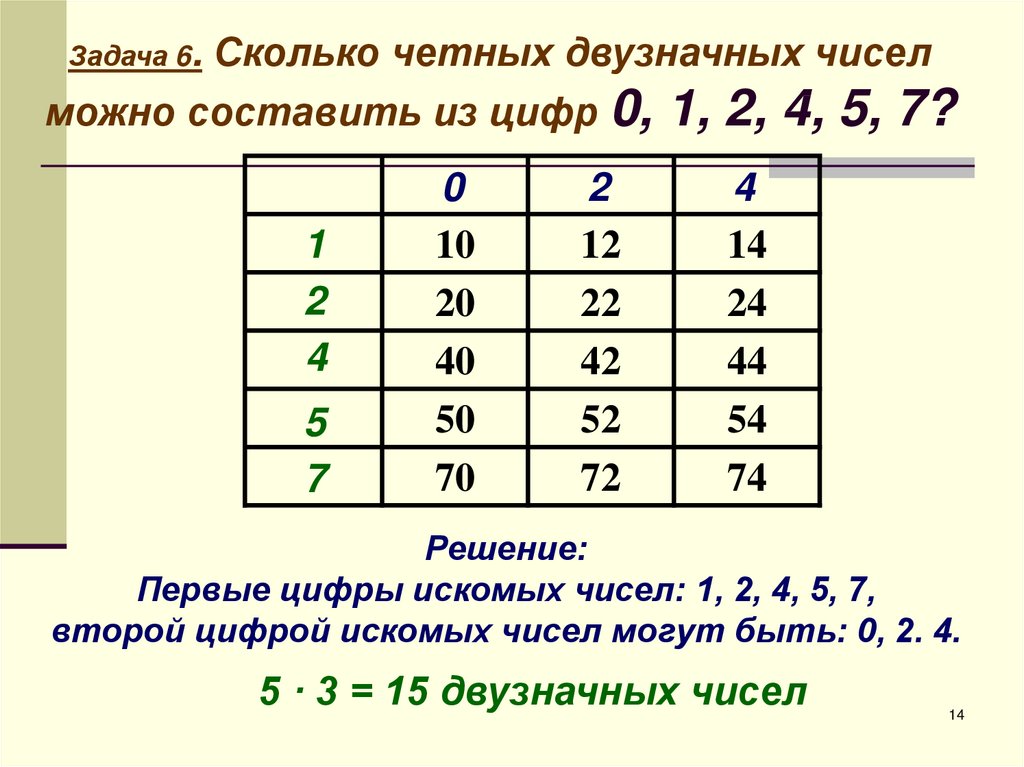
В приведенном выше представлении есть 10 пробелов, которые необходимо заполнить цифрами 1 и 2.
Очевидно, нам нужно повторить наши цифры.
Итак, первое место можно заполнить как цифрами 1, так и цифрами 2. Следовательно, первое место можно заполнить двумя способами.
Аналогично, второе место можно заполнить, используя как цифры 1, так и 2. Следовательно, второе место можно заполнить двумя способами.
Точно так же и третье место можно заполнить, используя как цифры 1, так и 2. Следовательно, третье место можно заполнить двумя способами.

Точно так же четвертое место можно заполнить, используя как цифры 1, так и 2. Следовательно, четвертое место можно заполнить двумя способами.
Аналогично, пятое место можно заполнить, используя как цифры 1, так и 2. Следовательно, пятое место можно заполнить двумя способами.
Точно так же шестое место можно заполнить, используя как цифры 1, так и 2. Следовательно, шестое место можно заполнить двумя способами.
Аналогично, седьмое место можно заполнить, используя как цифры 1, так и 2.