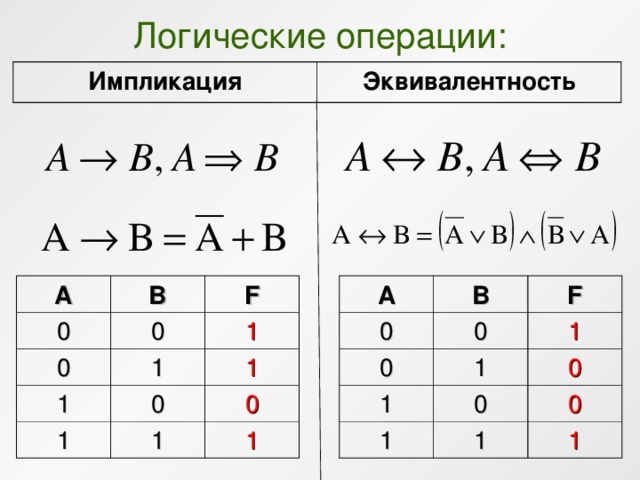
Основы логики. Логические операции и таблицы истинности
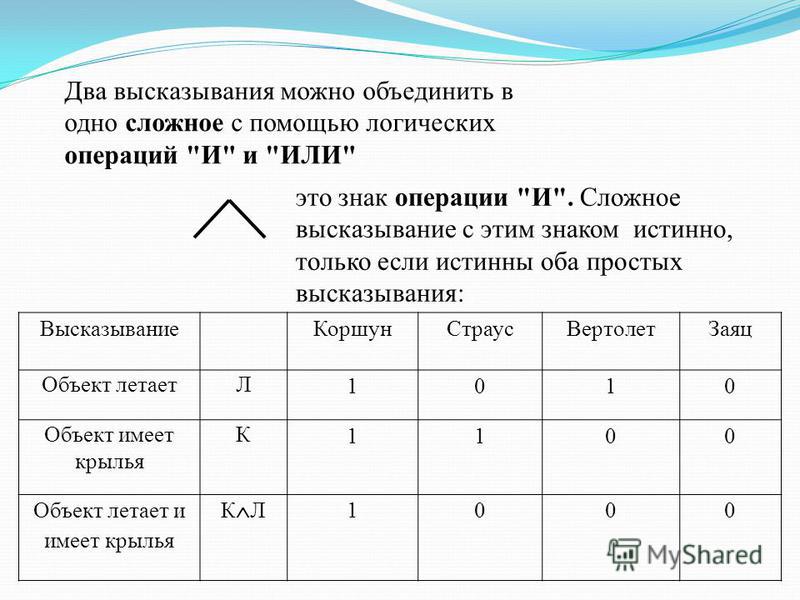
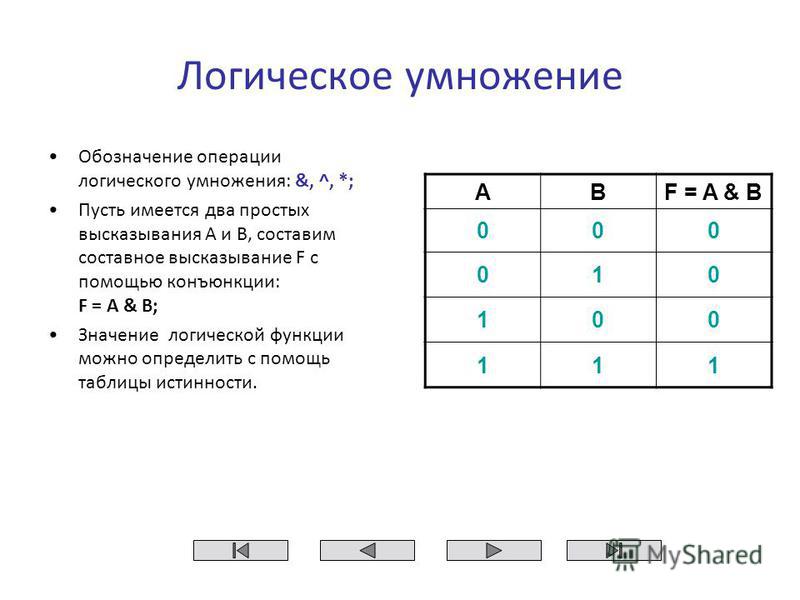
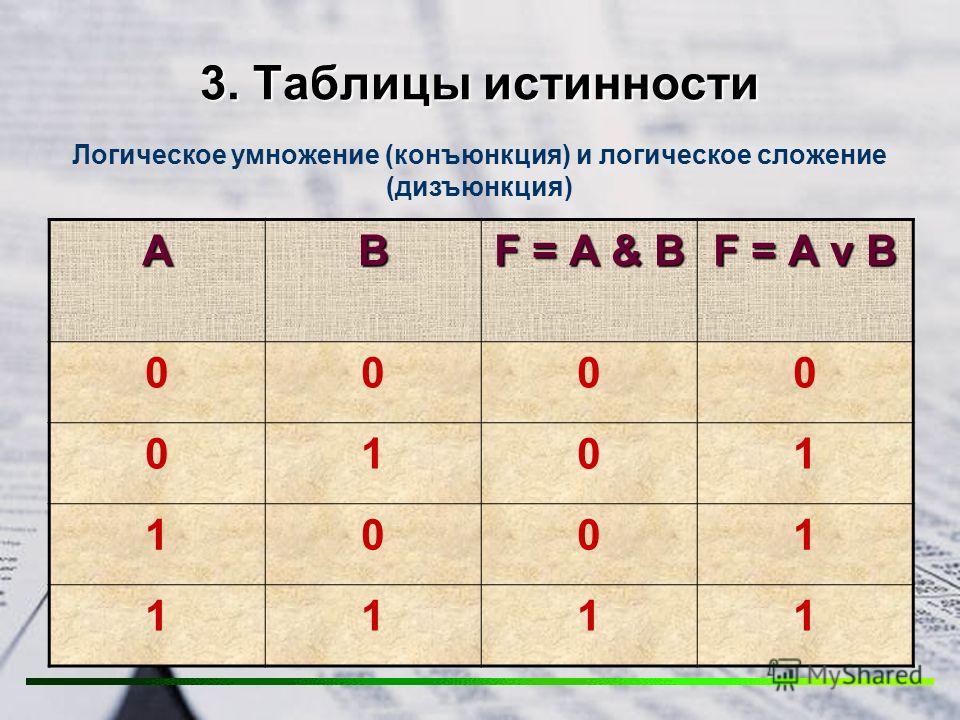
Основы логики. Логические операции и таблицы истинности На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции. Глоссарий, определения логики Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)). Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий. Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций. Логические операции и таблицы истинности 1) Логическое умножение или конъюнкция: Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно. Обозначение: F = A & B. Таблица истинности для конъюнкции
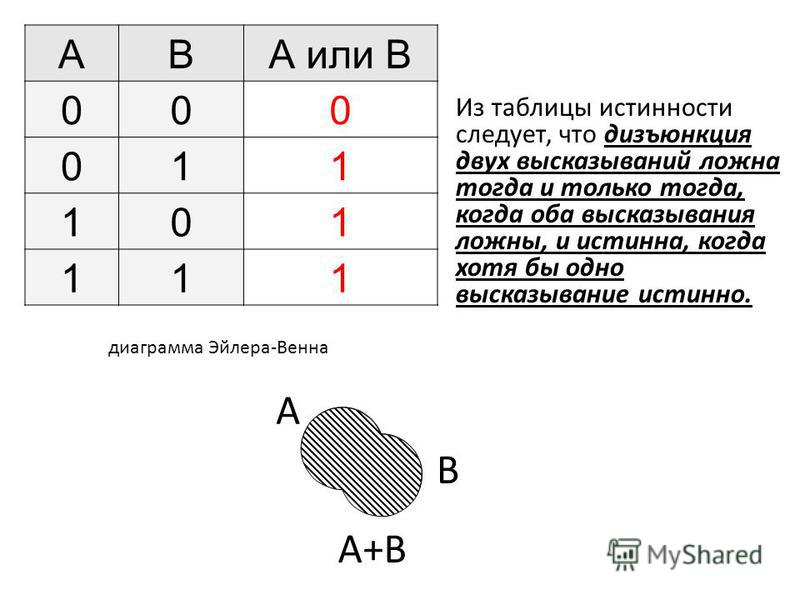
2) Логическое сложение или дизъюнкция: Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны. Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия: Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. Обозначение: F = ¬A. Таблица истинности для инверсии
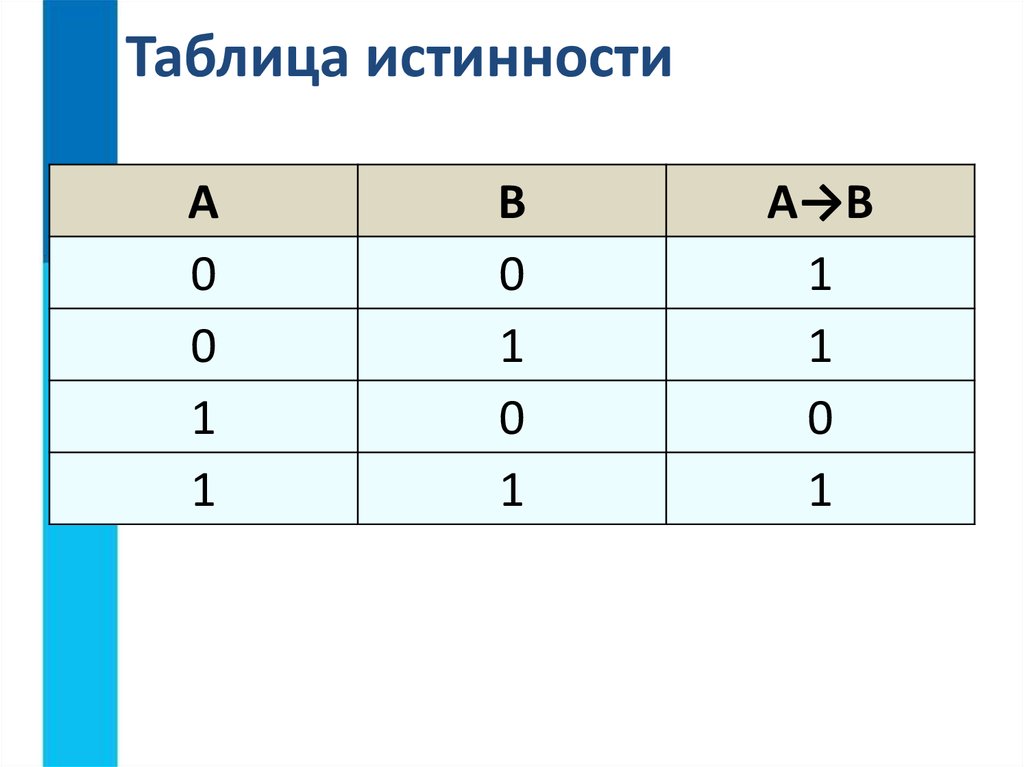
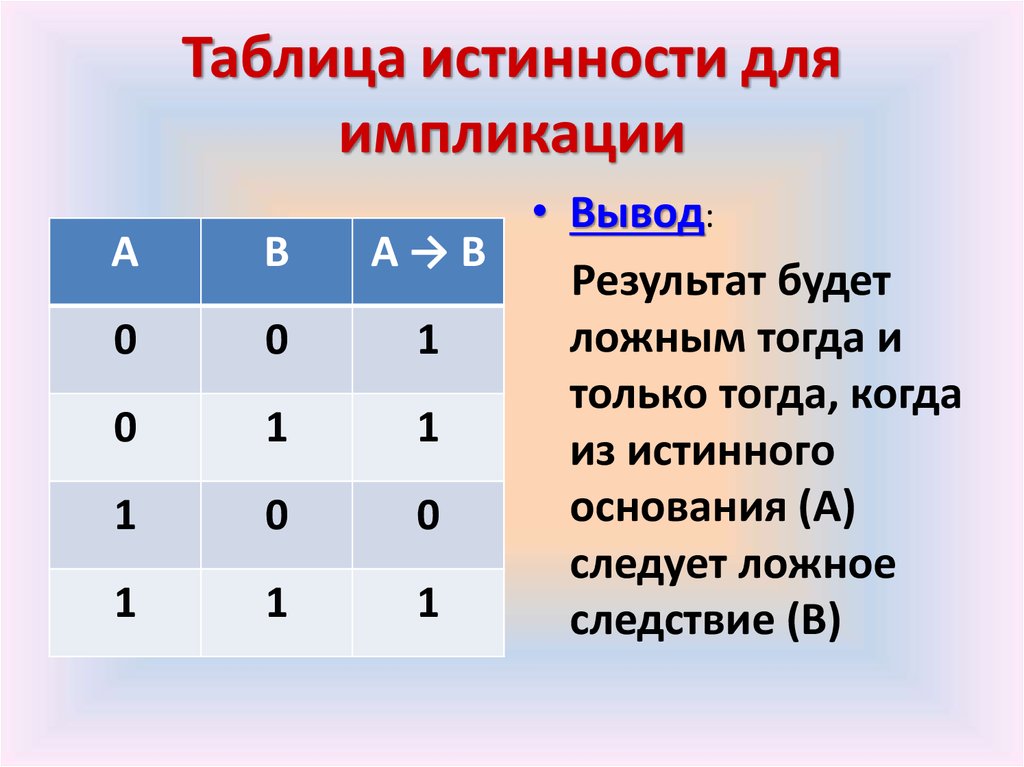
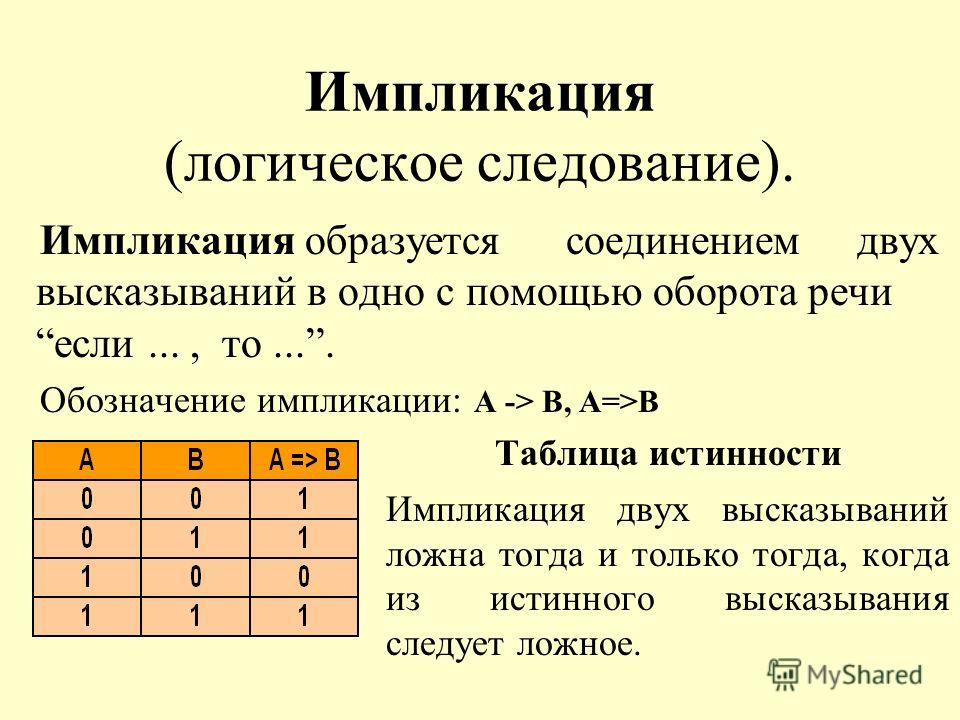
4) Логическое следование или импликация: Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. «A → B» истинно, если из А может следовать B. Обозначение: F = A → B. Таблица истинности для импликации
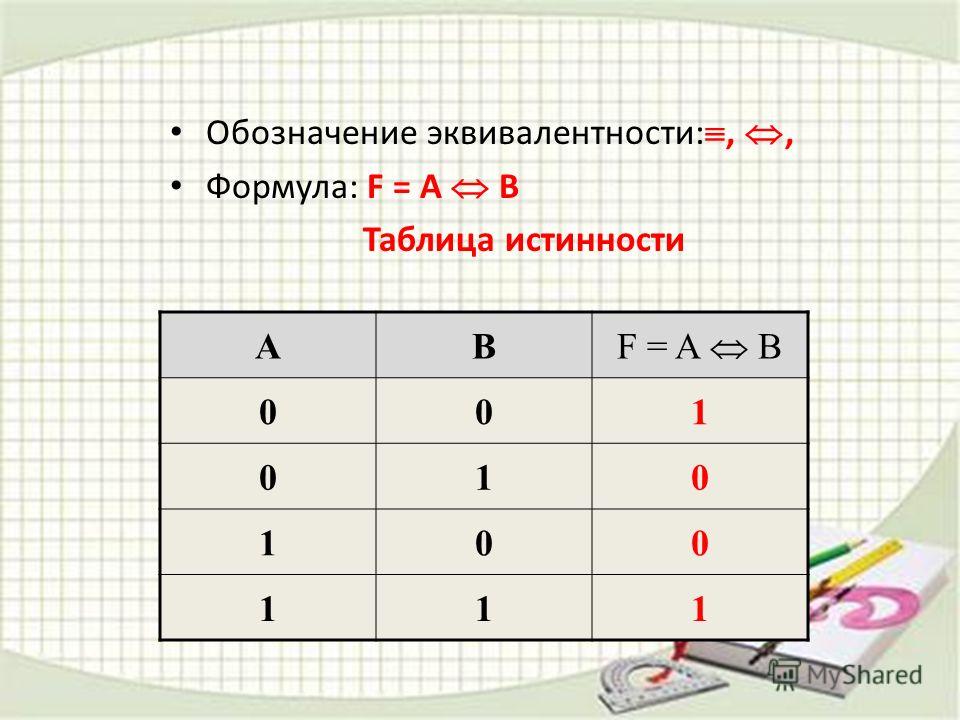
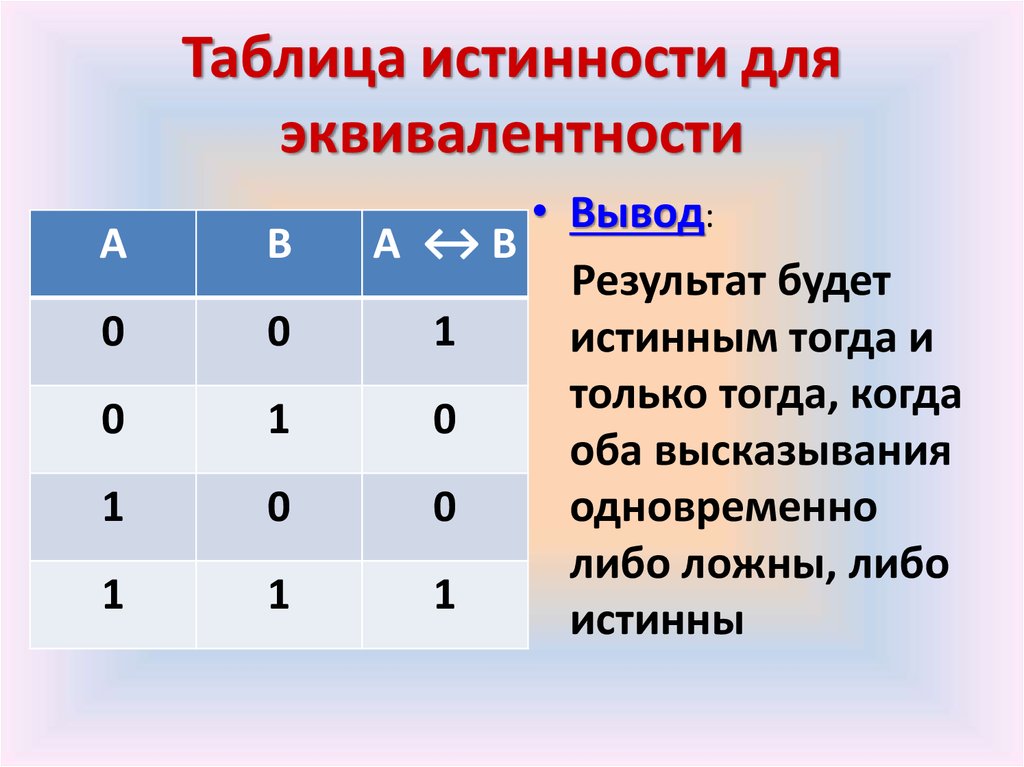
5) Логическая равнозначность или эквивалентность: Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность. «A ↔ B» истинно тогда и только тогда, когда А и B равны.
6) Операция XOR (исключающие или) «A ⊕ B» истинно тогда, когда истинно А или B, но не оба одновременно. Обозначение: F = A ⊕ B.
Порядок выполнения логических операций в сложном логическом выражении1. Для изменения указанного порядка выполнения логических операций используются скобки. Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…). В общем случае таблицы истинности имеют размер 2N строк комбинаций для N независимых логических переменных.
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения. Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности. Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Так, заменить операцию импликации можно в соответствии со следующим правилом: A → B = ¬A \/ BДля замены операции эквивалентности существует два правила: В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств. Логические выражения и множества На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула
Решим уравнение: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1 методом подстановки.
Ответ 2 вариант [3,11] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Основы логики. Логические операции и таблицы истинности
Содержание:
- Глоссарий, определения логики
- Логические операции и таблицы истинности
- Порядок выполнения логических операций в сложном логическом выражении
На данной странице будут рассмотренны 5 логических операций:
конъюнкция,
дизъюнкция,
инверсия,
импликация и
эквивалентность,
которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных
логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам
воспользоваться нашими программами для решения задач по математике,
геометрии и
теории вероятности.
Помоми большого количества программ для решения задач на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Также мы рассмотрим порядок выполнения данных логических операций в сложных
логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам
воспользоваться нашими программами для решения задач по математике,
геометрии и
теории вероятности.
Помоми большого количества программ для решения задач на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами,
обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать
одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать
одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины
следует ложь.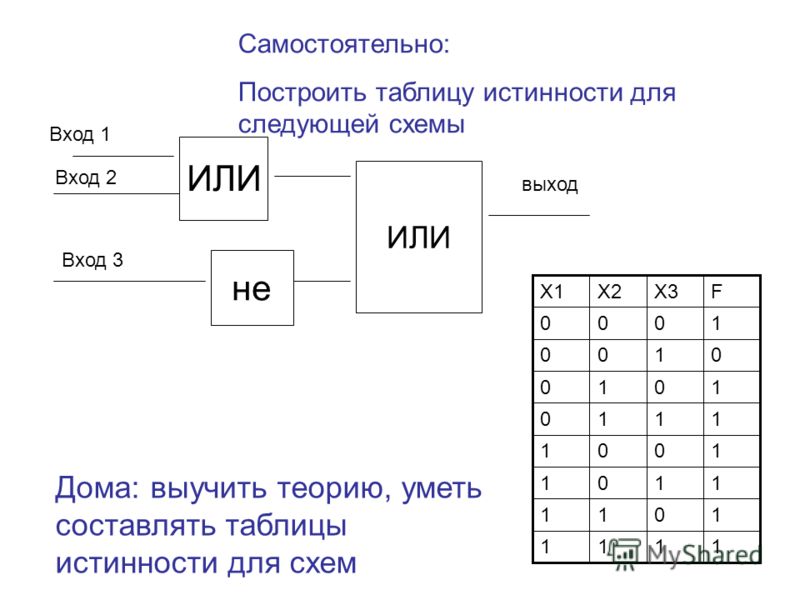 Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
а второе (В) является следствием.
Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1.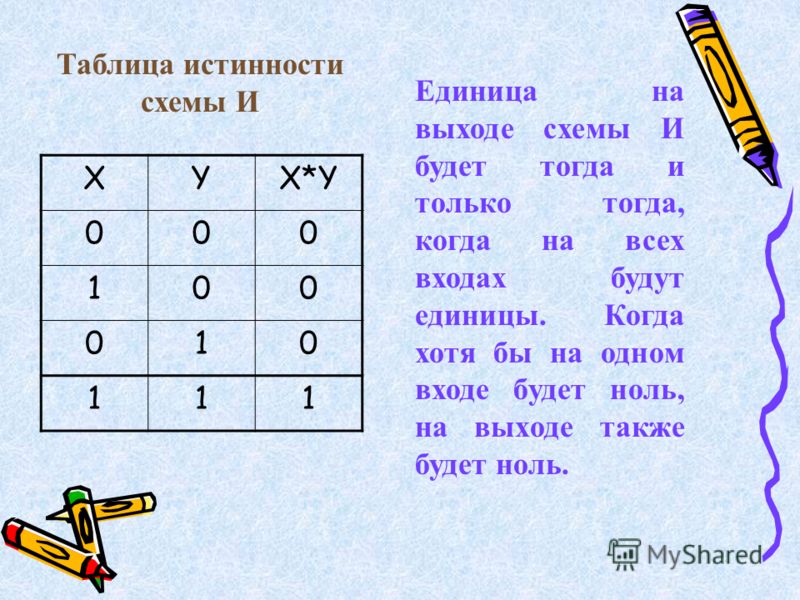 Инверсия;
Инверсия;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Логические операции: определения, обозначения, таблицы истинности
В данной публикации мы рассмотрим 5 логических операций: приведем их определения, способы записи (если он есть), а также соответствующие им таблицы истинности.
- Основные термины
- Логические операции и таблицы истинности
- Умножение (конъюнкция)
- Сложение (дизъюкция)
- Отрицание (инверсия)
- Следование (импликация)
- Равнозначность (эквивалентность)
Основные термины
Высказывание – предложение, которое выражает некоторое суждение, по которому определяется, истинно оно (обозначается цифрой “1”) или ложно (пишется как “0”).
Логическая операция – действие в уме, в результате которого меняется содержание или объем понятий, а также, образуются новые понятия.
Логическое выражение – устное или письменное утверждение, в котором присутствуют как постоянные величины, так и переменны. В зависимости от принимаемых переменными значений, логическое выражение может быть либо истинным (1), либо ложным (0).
Сложное логическое выражение – это составное выражение, которое включает одно или несколько простых и/или сложных логических выражений, связанных между собой логическими операциями.
Логические операции и таблицы истинности
Умножение (конъюнкция)
Конъюкция – это сложное логическое выражение, являющееся истинным исключительное в том случае, если оба простых выражения, из которых оно состоит, являются истинными. В противном случае, оно ложно.
Обозначается таким образом: F = A & B.
Таблица истинности для конъюнкции
Сложение (дизъюкция)
Дизъюкция – сложное логическое выражение, считающееся истинными, если хотя бы одно из простых логических выражений является истинным. Соответственно, ложно оно только в том случае, если оба простых выражения, также, являются ложными.
Соответственно, ложно оно только в том случае, если оба простых выражения, также, являются ложными.
Записывается так: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Отрицание (инверсия)
Инверсия – это сложное логическое выражение, получаемое следующим образом:
- Если исходное логическое выражение истинно, то результат отрицания считается ложным.

- Если исходное выражение ложно, то результатом отрицания будет истина.
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
Следование (импликация)
Импликация – сложное логическое выражение, связывающее два простых выражения. При этом первое является условием (A), а второе – следствием (B). Выражение истинно всегда, за исключением случаев, когда из истины следует ложь.
При этом первое является условием (A), а второе – следствием (B). Выражение истинно всегда, за исключением случаев, когда из истины следует ложь.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Равнозначность (эквивалентность)
Эквивалентность – сложное логическое выражение, считающееся истинным исключительно тогда, когда оба простых выражения одинаковы истинны.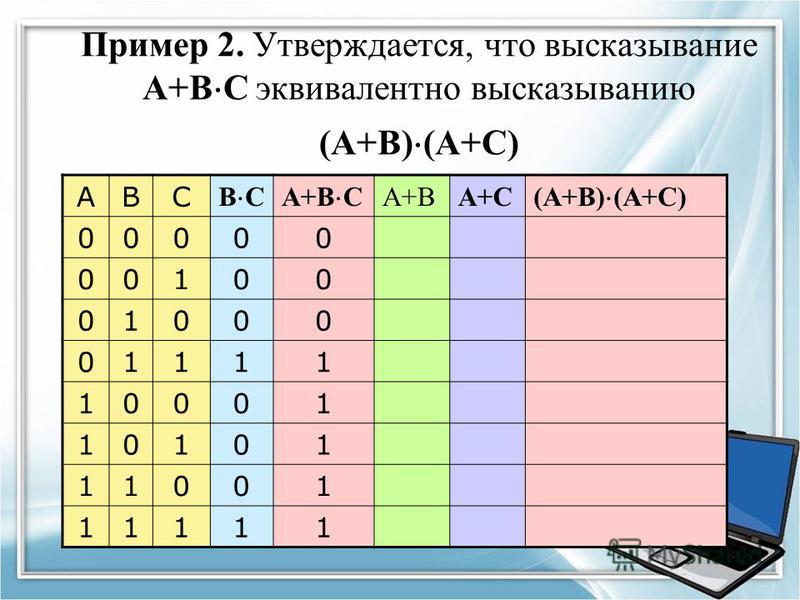
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Примечание: Операции в сложном логическом выражении выполняются в следующем порядке:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность
Чтобы изменить данный порядок, необходимо использовать скобки.
Логические операции и таблицы истинности
Похожие презентации:
Основы логики. Таблица истинности. Равносильные логические выражения
Логические операции
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
Основы программирования на языке Python. Логическая операция
Алгебра логики и таблицы истинности. (лекция 4)
Логические операции
Логические операции
Логические операции компьютеров
Элементарные логические операции
Элементы математической логики
1. Логические операции и таблицы истинности
Учитель информатикиПоборцева Елена Валентиновна
2. КОНЪЮНКЦИЯ
F = A & B.
Логическое умножение
КОНЪЮНКЦИЯ — это
новое сложное выражение
будет истинным только
тогда, когда истинны оба
исходных простых
выражения.
Конъюнкция определяет
соединение двух
логических выражений с
помощью союза И.
A
B
F
1
1
1
1
0
0
0
1
0
0
0
0
3.
 Примеры:
Примеры:10
10
10
10
делится на
не делится
делится на
не делится
2 и 5 больше 3
на 2 и 5 больше 3
2 и 5 не больше 3
на 2 и 5 не больше 3
► F=A&B
Задание: Определить, чему будет равно значение F
для каждого выражения.
4. ДИЗЪЮНКЦИЯ
F=A+BЛогическое сложение –
ДИЗЪЮНКЦИЯ — это
новое сложное выражение
будет истинным тогда и
только тогда,
когда истинно хотя бы
одно из исходных (простых)
выражений.
► Дизъюнкция определяет
соединение двух
логических выражений с
помощью союза ИЛИ
A
B
F
1
1
1
1
0
1
0
1
1
0
0
0
5. Примеры:
► 10делится на
► 10 не делится
► 10 делится на
► 10 не делится
2 или 5 больше 3
на 2 или 5 больше 3
2 или 5 не больше 3
на 2 или 5 не больше 3
F=AVB
Задание: Определить, чему будет равно значение F для
каждого выражения.
6. ИНВЕРСИЯ
Логическое отрицание :
ИНВЕРСИЯ — если исходное
выражение истинно, то
результат отрицания будет
ложным, и наоборот, если
исходное выражение ложно,
то результат отрицания будет
истинным/
Данная операция означает,
что к исходному логическому
выражению добавляется
частица НЕ или слова
НЕВЕРНО, ЧТО
A
_
F=A
1
0
0
1
► Пример:
► Луна
— спутник Земли (А).
► Луна — не спутник Земли (не A)
_
F= A
8. Логическое следование (импликация)
Логическое следование (Импликация) образуется
соединением двух высказываний в одно с помощью союза
«если… то…».
Импликация записывается как посылка следствие; (остриё
всегда указывает на следствие).
F = A B, составное высказывание, образованное с помощью
операции: логическое следование (импликация)
Суждение, выражаемое импликацией, выражается также
следующими способами:
1. Посылка является условием, достаточным для выполнения следствия;
2. Следствие является условием, необходимым для истинности посылки.
9. «Житейский» смысл импликации.
«Житейский» смыслимпликации.
Для более лёгкого понимания смысла импликации и
запоминания ее таблицы истинности может
пригодиться житейская модель:
А — начальник. Он может приказать «работай» (1) или
сказать «делай что хочешь» (0).
В — подчиненный. Он может работать (1) или
бездельничать (0).
В таком случае импликация — не что иное, как
послушание подчиненного начальнику.
По таблице истинности легко проверить, что
послушания нет только тогда, когда начальник
приказывает работать, а подчиненный бездельничает.
10. ИМПЛИКАЦИЯ
Логическое
следование: ИМПЛИКАЦИЯ связывает два простых логических
выражения, из которых первое
является условием (А), а второе
(В)– следствием из этого условия.
Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда,
когда условие А истинно, а
следствие В ложно.
Обозначается A B
символом «следовательно» и
выражается словами ЕСЛИ … ,
ТО …
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1
11. Примеры:
Если данный четырёхугольник квадрат, то около него
можно описать окружность
Если данный четырёхугольник не квадрат, то около
него можно описать окружность
Если данный четырёхугольник квадрат, то около него
нельзя описать окружность
Если данный четырёхугольник не квадрат, то около
него нельзя описать окружность
A B
Задание: Определить, чему будет равно значение F для каждого
выражения.
12. Порядок выполнения логических операций
► 1.инверсия
► 2. конъюнкция
► 3. дизъюнкция
► 4. импликация
Для изменения указанного порядка
выполнения операций используются
скобки.
13. Пример задания 1:
Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
►Какое
1) ¬X ¬Y ¬Z
X
Y
Z
F
1
0
0
1
0
0
0
1
1
1
1
0
выражение соответствует F?
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z
14. Решение :
нужно для каждой строчки подставить заданные
значения X, Y и Z во все функции, заданные в
ответах, и сравнить результаты с соответствующими
значениями F для этих данных
если для какой-нибудь комбинации X, Y и Z результат
не совпадает с соответствующим значением F,
оставшиеся строчки можно не рассматривать,
поскольку для правильного ответа все три результата
должны совпасть со значениями функции F
первое выражение, равно 1 только при X=Y=Z=0 , поэтому это
неверный ответ (первая строка таблицы не подходит)
второе выражение, равно 1 только при X=Y=Z=1, поэтому это
неверный ответ (первая и вторая строки таблицы не подходят)
третье выражение, равно нулю при X=Y=Z=0, поэтому это
неверный ответ (вторая строка таблицы не подходит)
наконец, четвертое выражение, равно нулю только тогда, когда
X=Y=Z=1, а в остальных случаях равно 1, что совпадает с
приведенной частью таблицы истинности
X
Y
Z
F
таким образом, правильный ответ – 4
1) ¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
1
0
0
1
0
0
0
1
1
1
1
0
4) ¬X ¬Y ¬Z
16.
 Пример задания 2:
Пример задания 2:Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
X
Y
Z
F
1
0
0
1
0
0
0
0
1
1
1
0
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X ¬Y ¬Z
4) X ¬Y ¬Z
17. Решение :
В столбце F есть единственная единица
для комбинации X=1, Y=Z=0,
простейшая функция, истинная (только)
для этого случая, имеет вид , она есть
среди приведенных ответов (ответ 3)
таким образом, правильный ответ – 3.
18. Пример задания 3:
Дан фрагмент таблицы
истинности выражения F
(см. таблицу справа).
Какое выражение
соответствует F?
1) (X ¬Y)→ Z
2) (X Y)→ ¬Z
X
Y
Z
F
0
0
0
0
0
1
1
1
1
0
0
1
3) X (¬Y → Z)
4) X Y ¬Z
19. Ответ к заданию 3:
► Найдиправильный ответ:
English Русский Правила
Простейшие логические функции — МегаЛекции
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
A B F
1 1 1
1 0 0
0 1 0
0 0 0
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
A B F
1 1 1
1 0 1
0 1 1
0 0 0
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
A неА
1 0
0 1
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь.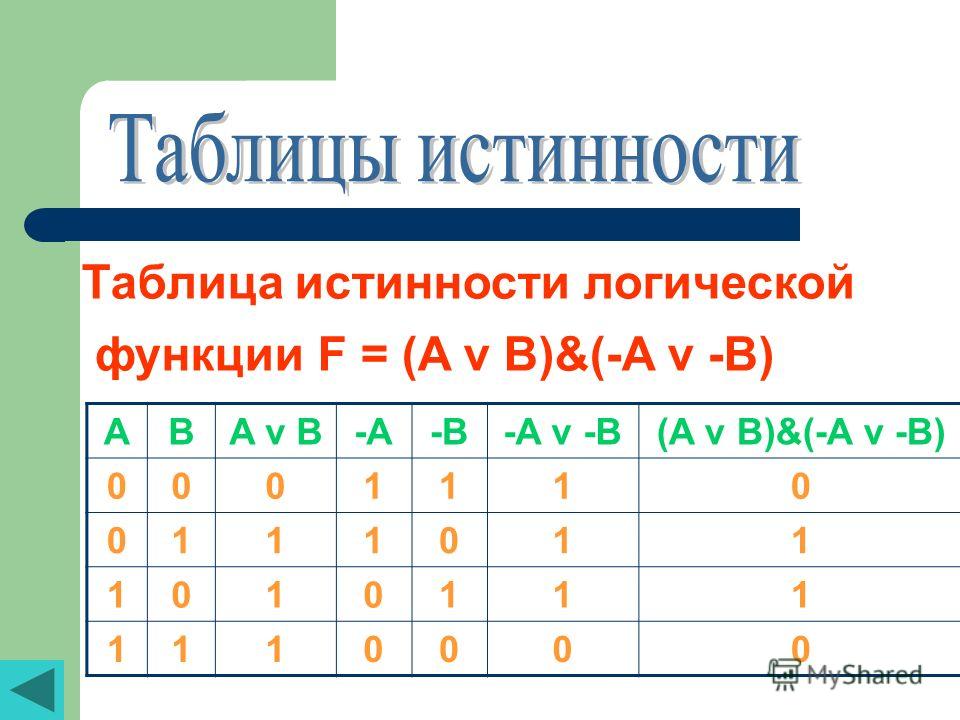 Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
A B F
1 1 1
1 0 0
0 1 1
0 0 1
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
A B F
1 1 1
1 0 0
0 1 0
0 0 1
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Таблица истинности для функции двух переменных
F1 – const 0 – постоянная 0
F2 – логическое умножение – конъюнкция (А И В).
F3 – отрицание логического следствия — НЕ (ЕСЛИ А ТО В).
F4 – аргумент А.
F5 – отрицание обратного логического следствия — НЕ (ЕСЛИ В ТО А).
F6 – аргумент В.
F7 – отрицание логической равнозначности — НЕ (А тогда и только тогда, когда В).
F8 – логическое сложение — дизъюнкция (А ИЛИ В).
F9 – отрицание логического умножения – НЕ (А И В).
F10 – логическая равнозначность — эквиваленция (А тогда и только тогда, когда В).
F11 – логическое отрицание аргумента B – инверсия (НЕ В).
F12 – обратное логическое следствие — импликация (ЕСЛИ В ТО А)
F13 – логическое отрицание аргумента А – инверсия (НЕ А).
F14 – логическое следствие — импликация (ЕСЛИ А ТО В).
F15 – отрицание логического сложения — НЕ (А ИЛИ В).
F16 – const 1 – постоянная 1
КНФ и ДНФ
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.
Алгоритм построения ДНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: Закон двойного отрицания, Закон де Моргана, Дистрибутивность.
Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: Закон двойного отрицания, Закон де Моргана, Дистрибутивность.
Алгоритм построение см. ДНФ
СКНФ и СДНФ
СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причем единственная.
СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных букв
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Правила преобразования
А + В = В + А АВ = ВА
(А + В) + С = (А + С) + В (АВ)С = (АС)В
А(В + С) = АВ + АС А + (ВС) = (А + В)(А +С)
А + В = `А ×`В А × В = `А +`В
А + А = А А А = А
А = А А +`АВ = А + В
А + АВ = А А×(А + В) = А
А +`А = 1 А ×`А = 0
А + 0 = А А × 0 = 0
А + 1 = 1 А × 1 = А
Таблица истинности
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо 1, либо 0).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Карта Карно
Комбинационная логика
В теории цифровых устройств комбинационной логикой называют логику функционирования устройств комбинационного типа. У комбинационных устройств состояние выхода однозначно определяется набором входных сигналов. Это отличает комбинационную логику от секвенциальной логики, в рамках которой выходное значение зависит не только от текущего входного воздействия, но и от предыстории функционирования цифрового устройства. Другими словами, секвенциальная логика предполагает наличие памяти, которая в комбинационной логике не предусмотрена.
Характеристика
Комбинационная логика используется в вычислительных цепях для формирования входных сигналов и для подготовки данных, которые подлежат сохранению. На практике вычислительные устройства обычно сочетают комбинационную и секвенциальную логику. у, дизъюнкция хVу и отрицание х_ . В комбинационных схемах используются логические элементы: конъюнктор, дизъюнктор, инвертор, а также производные элементы: И-НЕ, ИЛИ-НЕ и «Равнозначность». Наиболее известные комбинационные устройства — это сумматор, полусумматор, шифратор, дешифратор, мультиплексор и демультиплексор.
у, дизъюнкция хVу и отрицание х_ . В комбинационных схемах используются логические элементы: конъюнктор, дизъюнктор, инвертор, а также производные элементы: И-НЕ, ИЛИ-НЕ и «Равнозначность». Наиболее известные комбинационные устройства — это сумматор, полусумматор, шифратор, дешифратор, мультиплексор и демультиплексор.
Временные гонки»
Воспользуйтесь поиском по сайту:
Как следует построить таблицу истинности логического выражения, алгоритм и примеры
Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.
Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.
Содержание:
- Алгебраические преобразования логических выражений
- Отрицание
- Конъюнкция
- Дизъюнкция
- Импликация и эквивалентность
- Прочие логические функции
- Построение таблиц истинности
- Примеры
- Штрих Шеффера
- Стрелка Пирса
- Определение эквивалентности
Алгебраические преобразования логических выражений
Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина. Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.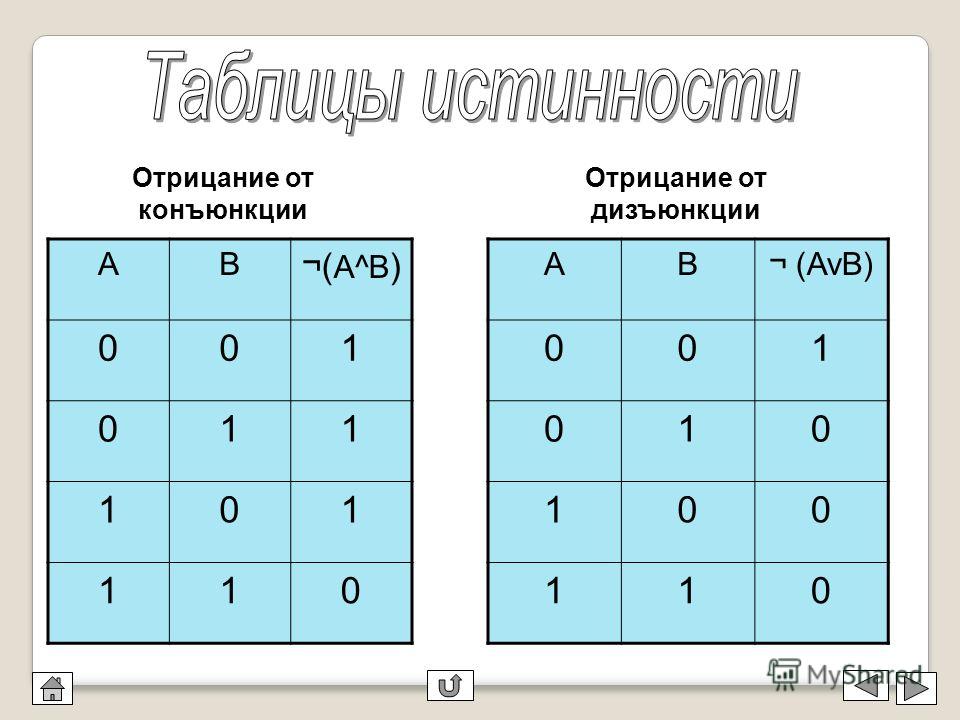
Отрицание
Отрицание и инверсия — самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.
Таблица истинности для отрицания будет такова:
| А | не А |
| Л | И |
| И | Л |
Конъюнкция
Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией. То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно.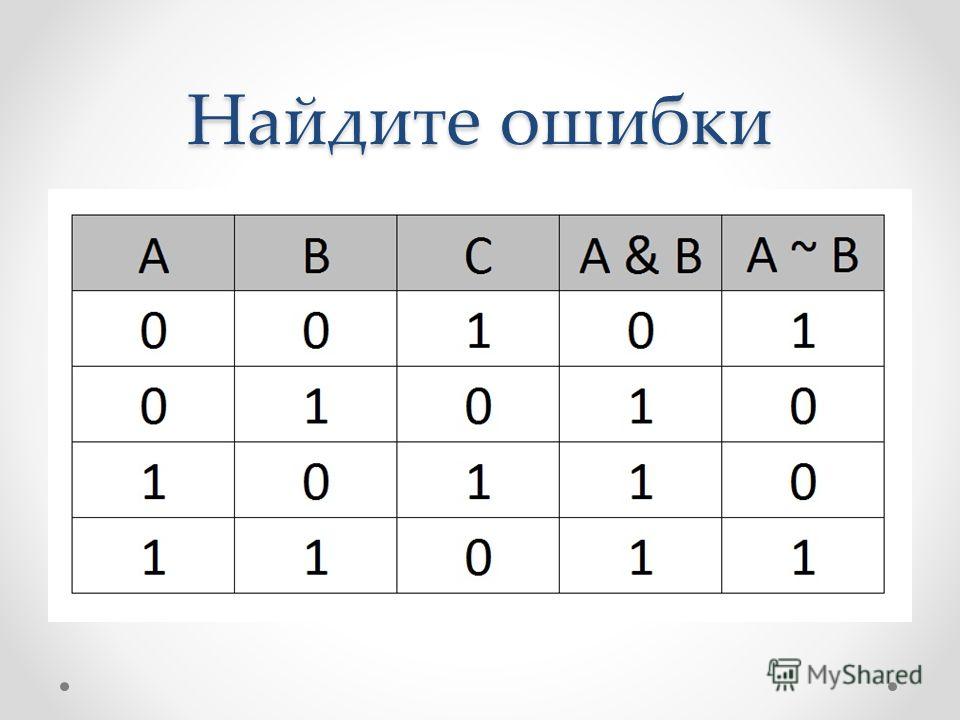 Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.
Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.В таблице это будет выглядеть так:
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Строгую дизъюнкцию или сложение по модулю также называют «исключающим или».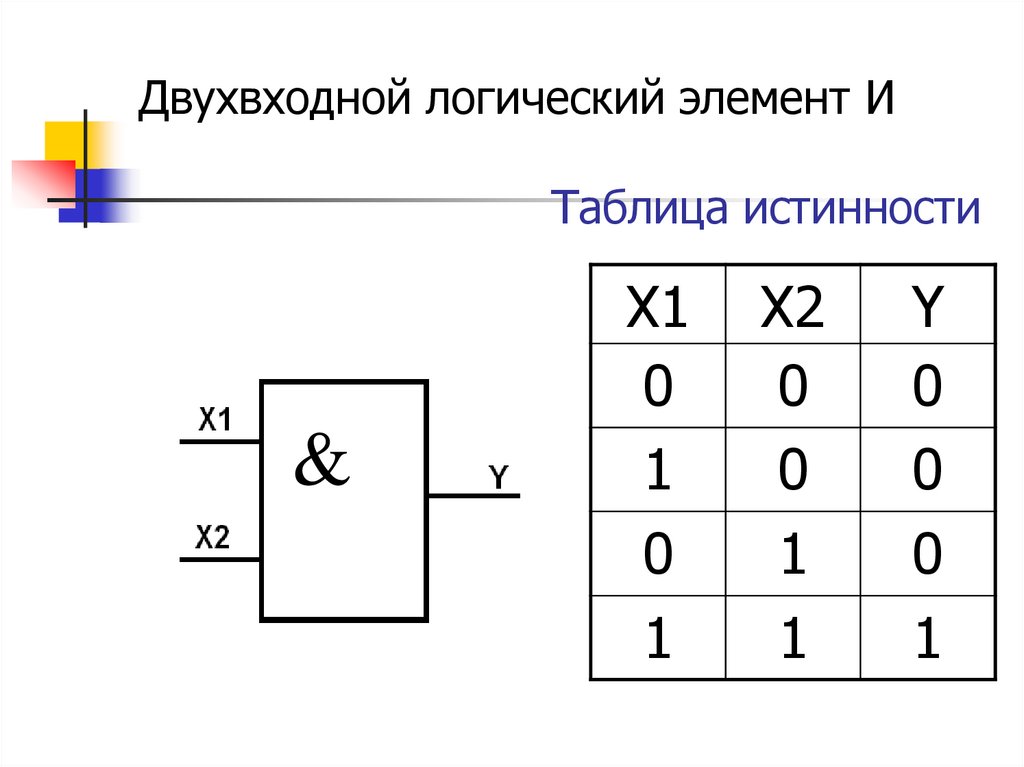 Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.
Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б». Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.
Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.
В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть. То есть Б необходимо для А, но не достаточно.
Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| И | Л | Л |
| И | И | И |
Логическая операция эквивалентность, по сути, является взаимной импликацией.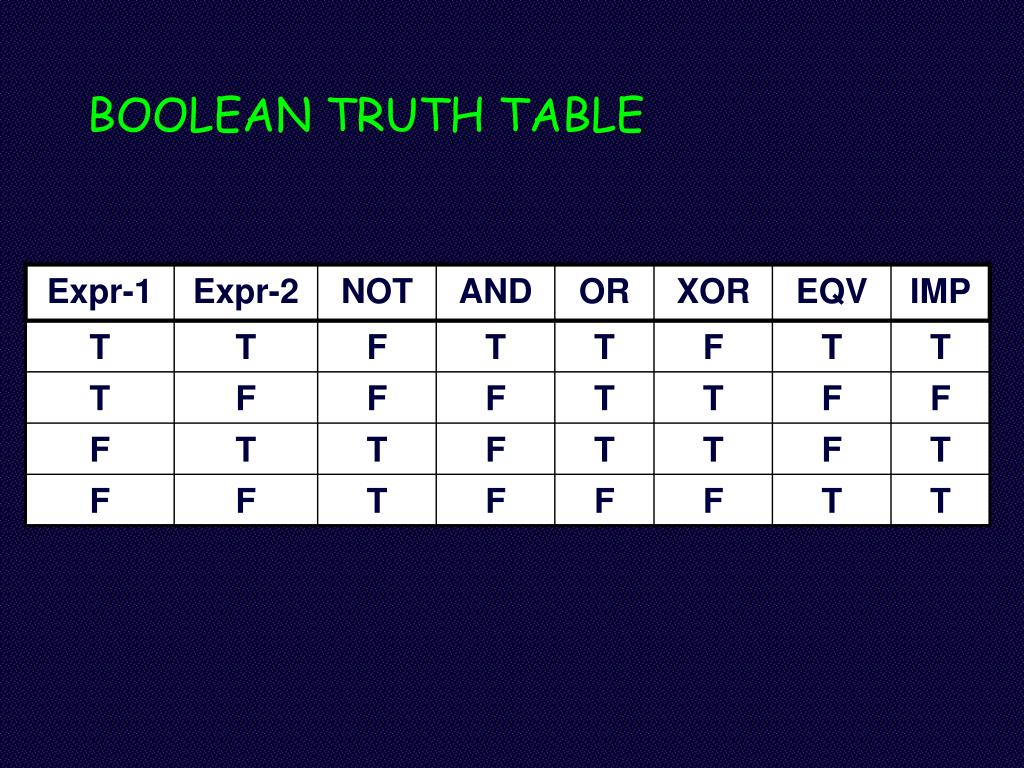 «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
«А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
В математике эквивалентность используется для определения необходимого и достаточного условия. Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А. Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак».
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
- Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
- Стрелка Пирса представляет сбой отрицание дизъюнкции.
Построение таблиц истинности
Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:
- Разбить выражение на простые утверждения и обозначить каждое из них как переменную.
- Определить логические преобразования.
- Выявить порядок действий этих преобразований.
- Сосчитать строки в будущей таблице. Их количество равно два в степени N, где N — число переменных, плюс одна строка для шапки таблицы.
- Определить число столбцов. Оно равно сумме количества переменных и количества действий. Можно представлять результат каждого действия в виде новой переменной, если так будет понятней.

- Шапка заполняется последовательно, сначала все переменные, потом результаты действий в порядке их выполнения.
- Заполнение таблицы надо начать с первой переменной. Для неё количество строк делится пополам. Одна половина заполняется нулями, вторая — единицами.
- Для каждой следующей переменной нули и единицы чередуются вдвое чаще.
- Таким образом заполняются все столбцы с переменными и для последней переменной значение меняется в каждой строке.
- Потом последовательно заполняются результаты всех действий.
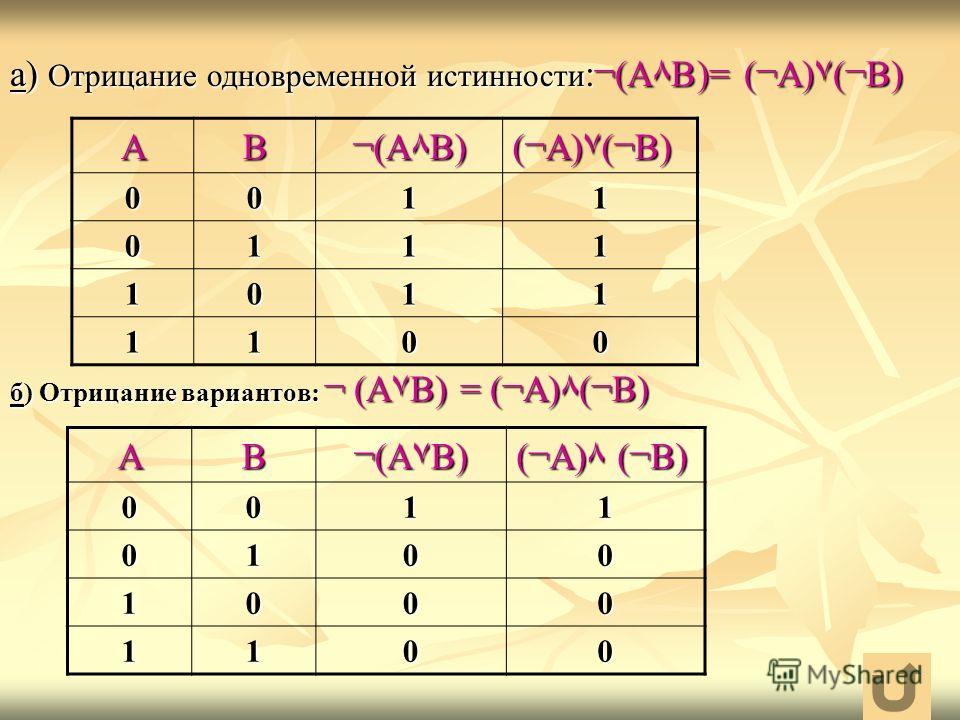
В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.
Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:
- выражения в скобках;
- отрицание или инверсия;
- конъюнкция;
- строгая и обычная дизъюнкция;
- импликация;
- эквивалентность.

Примеры
Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:
- Штрих Шеффера.
- Стрелка Пирса.
- Определение эквивалентности.
Штрих Шеффера
Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:
| А | Б | А и Б | не (А и Б) |
| Л | Л | Л | И |
| Л | И | Л | И |
| И | Л | Л | И |
| И | И | И | Л |
Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
Стрелка Пирса
Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:
| А | Б | А или Б | не (А или Б) |
| Л | Л | Л | И |
| Л | И | И | Л |
| И | Л | И | И |
| И | И | И | Л |
| А | Б | не А | не Б | не А и не Б |
| Л | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | И |
| И | И | Л | Л | Л |
Значения выражений совпали.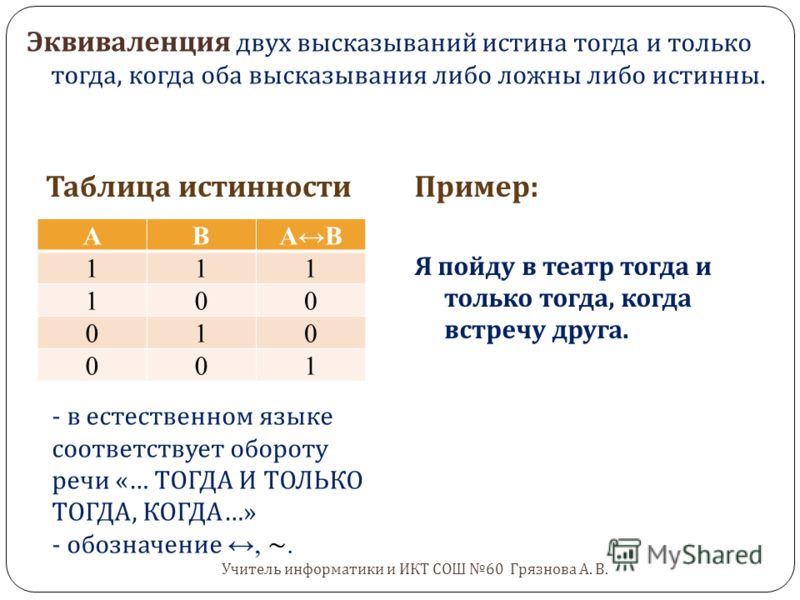 Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.
Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.
Определение эквивалентности
Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».
Здесь две переменных и пять действий. Строим таблицу:
| А | Б | В = (из А следует Б) | Г = (из Б следует А) | Д = А эквивалентно Б | Е = В и Г | Д эквивалентно Е |
| Л | Л | И | И | И | И | И |
| Л | И | И | Л | Л | Л | И |
| И | Л | Л | И | Л | Л | И |
| И | И | И | И | И | И | И |
В последнем столбце все значения истинные.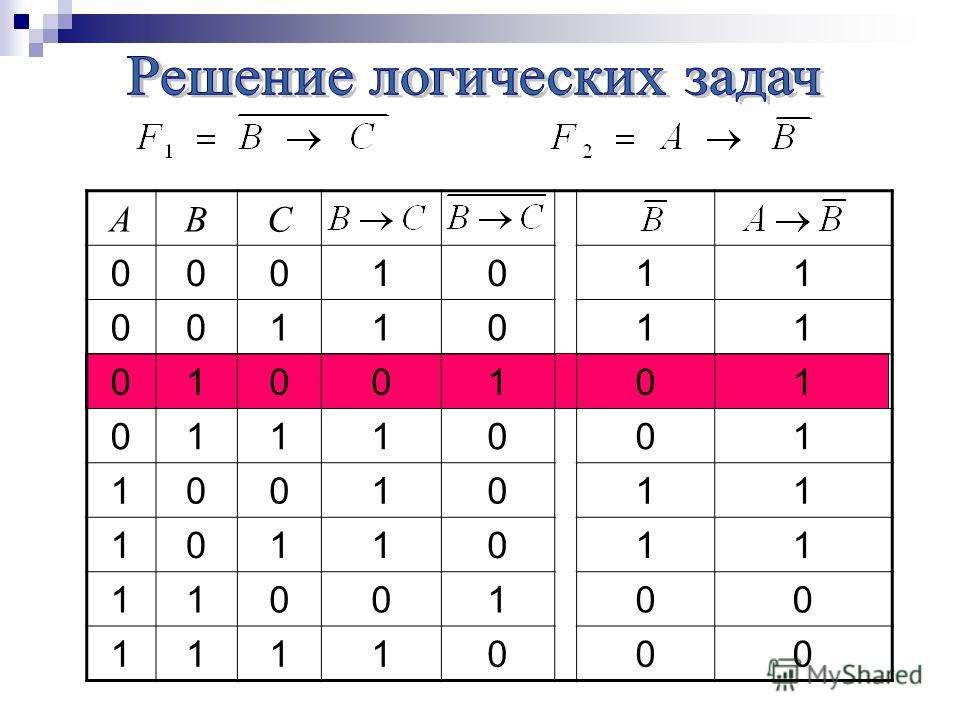 Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
для цифровой логики Таблицы истинности
для цифровой логикиТаблица истинности показывает, как выход логической схемы реагирует на различные комбинации входов, используя логическую 1 для истинного и логический 0 для ложного. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
| Индекс Концепции электроники Цифровые схемы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


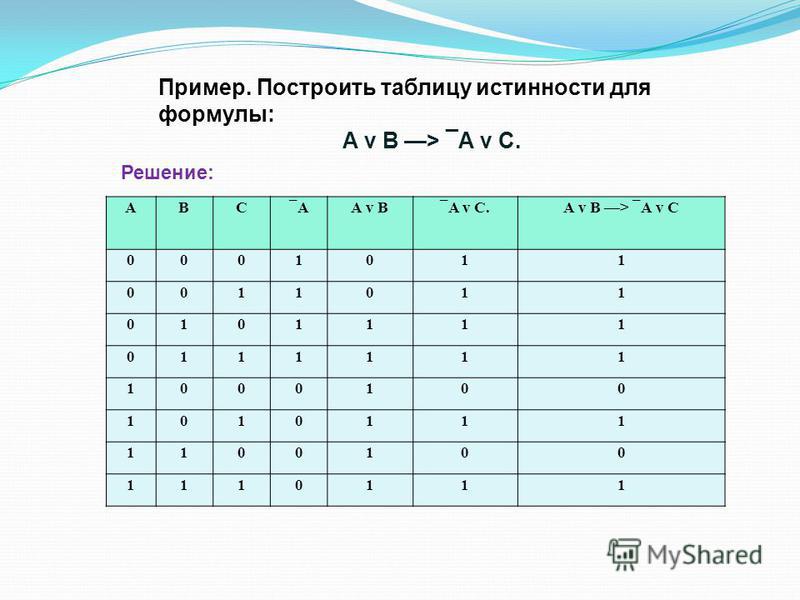
 То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.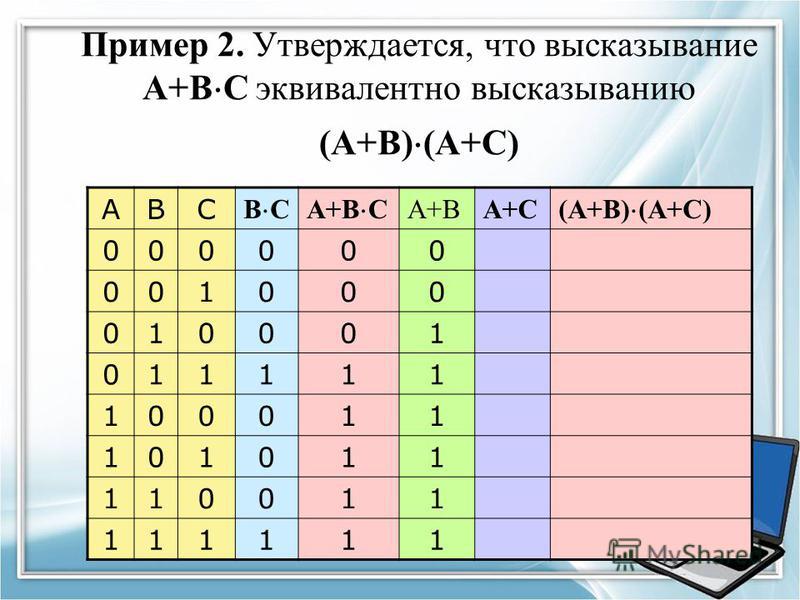
 Инверсия;
Инверсия;
 Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.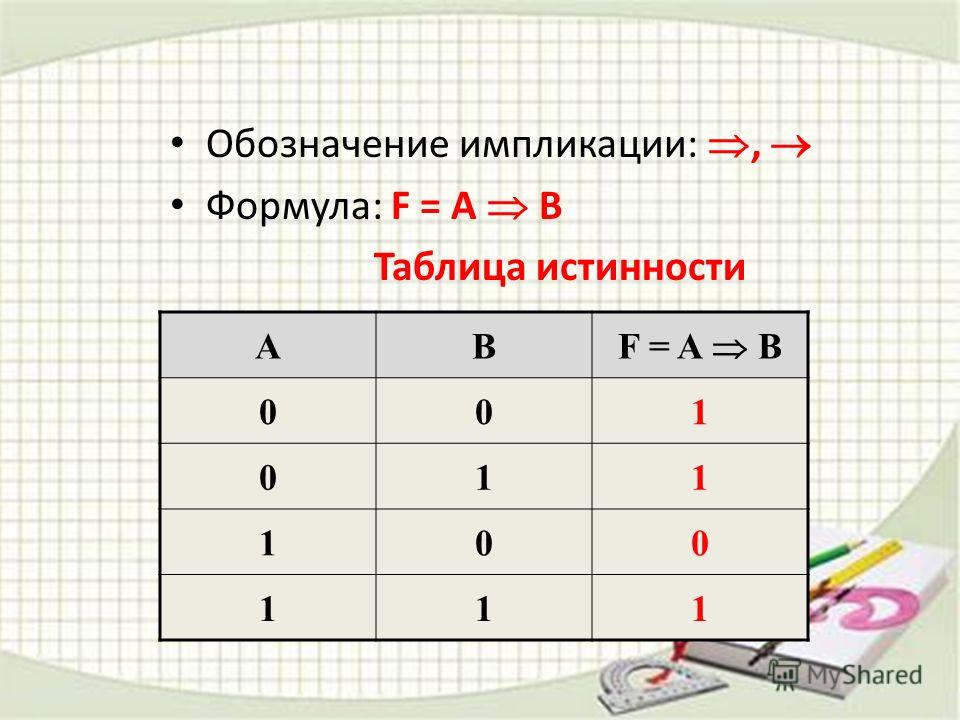


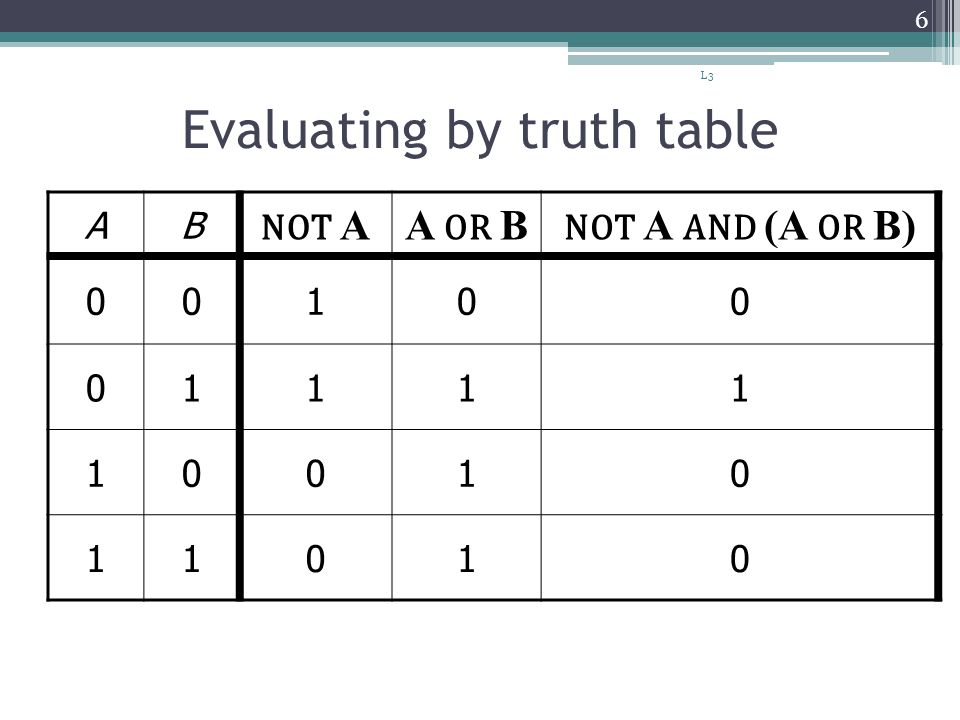 Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.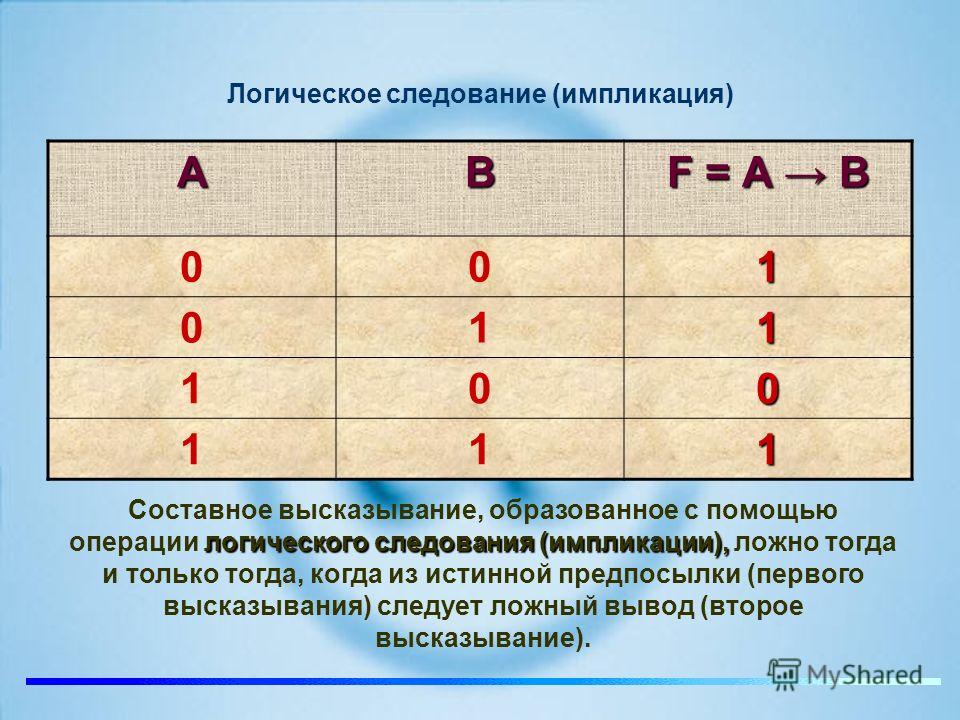 0360 соединение исходных заявлений. Мы используем символ ∧\клин ∧ для обозначения конъюнкции. Если ppp и qqq — два простых утверждения, то p∧qp \wedge qp∧q обозначает конъюнкцию ppp и qqq и читается как «ppp и qqq». □_\квадрат□
0360 соединение исходных заявлений. Мы используем символ ∧\клин ∧ для обозначения конъюнкции. Если ppp и qqq — два простых утверждения, то p∧qp \wedge qp∧q обозначает конъюнкцию ppp и qqq и читается как «ppp и qqq». □_\квадрат□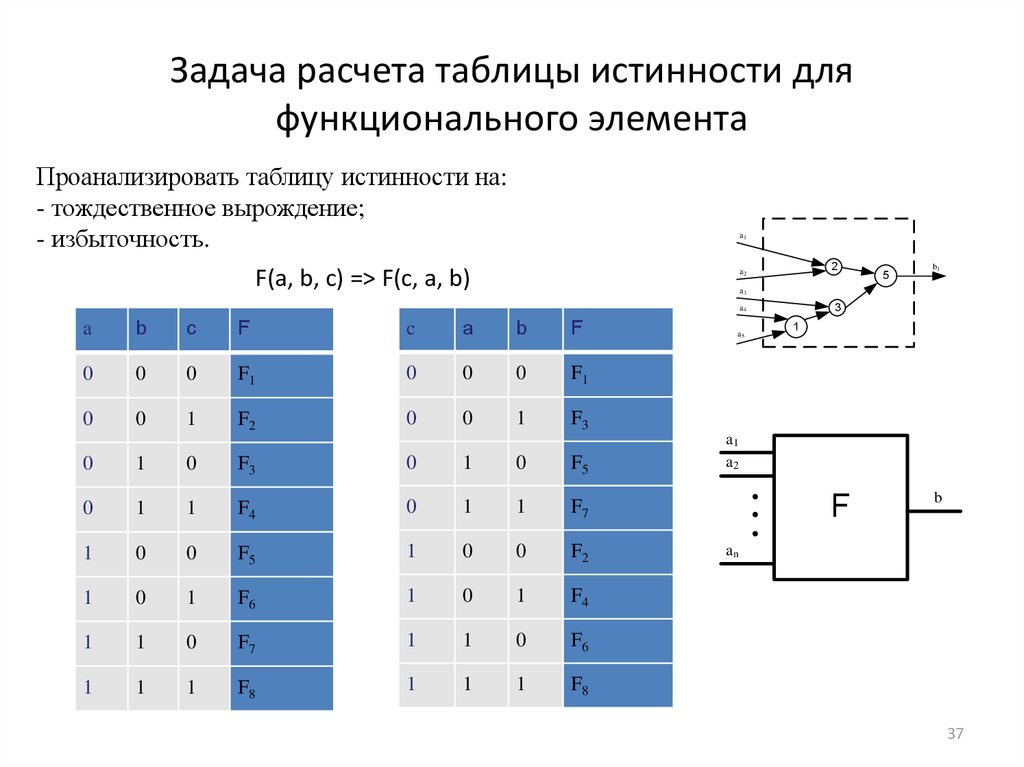 □_\квадрат□
□_\квадрат□ \neg (p \клин q) = {\neg p} \vee {\neg q}.¬(p∧q)=¬p∨¬q .
\neg (p \клин q) = {\neg p} \vee {\neg q}.¬(p∧q)=¬p∨¬q .
 Единственный возможный вывод — ¬b\neg b¬b, где Альфред не самый старший. Из утверждения 1, a→ba \rightarrow ba→b, поэтому по modus tollens, ¬b→¬a\neg b \rightarrow \neg a¬b→¬a. Следовательно, Чарльз является самым старшим из .
Единственный возможный вывод — ¬b\neg b¬b, где Альфред не самый старший. Из утверждения 1, a→ba \rightarrow ba→b, поэтому по modus tollens, ¬b→¬a\neg b \rightarrow \neg a¬b→¬a. Следовательно, Чарльз является самым старшим из . Поскольку c→dc \rightarrow dc→d из утверждения 2, по modus tollens, ¬d→¬c\neg d \rightarrow \neg c¬d→¬c. Следовательно, Эрик — самый младший .
Поскольку c→dc \rightarrow dc→d из утверждения 2, по modus tollens, ¬d→¬c\neg d \rightarrow \neg c¬d→¬c. Следовательно, Эрик — самый младший . Это сочетает в себе оба следующих:
Это сочетает в себе оба следующих: Проще всего, но не всегда лучше решить их, разбив их на небольшие составные таблицы истинности.
Проще всего, но не всегда лучше решить их, разбив их на небольшие составные таблицы истинности. Вот несколько:
Вот несколько: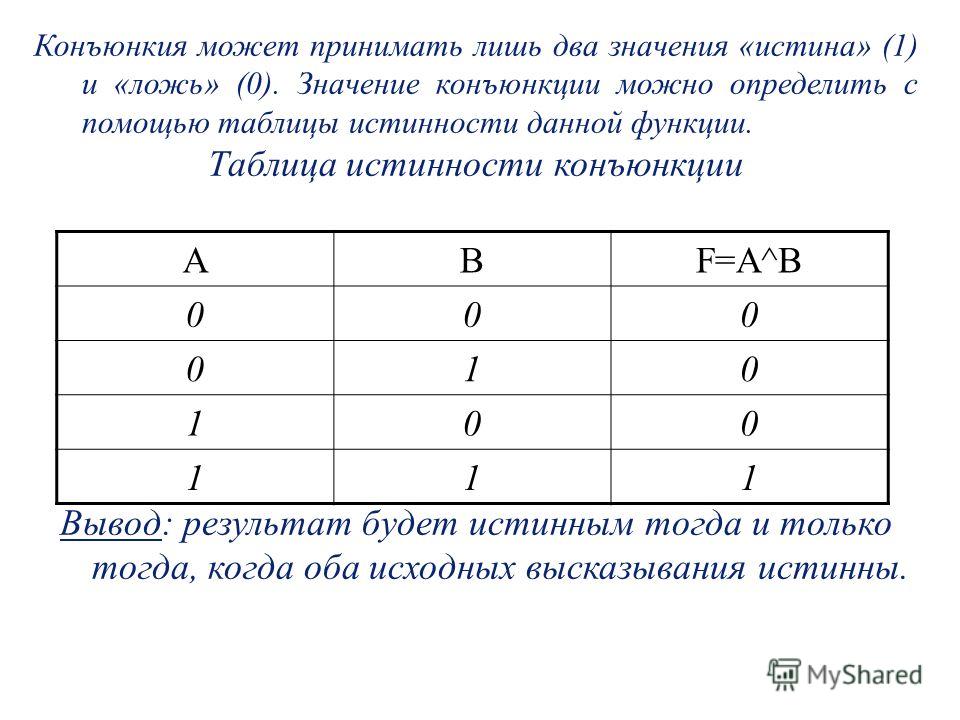

 Наша цель — использовать переведенные формулы для определения достоверности аргументов. Для этого воспользуемся инструментом, называемым таблицей истинности. По сути, таблица истинности — это список всех различных комбинаций значений истинности, которые может иметь предложение или набор предложений.
Наша цель — использовать переведенные формулы для определения достоверности аргументов. Для этого воспользуемся инструментом, называемым таблицей истинности. По сути, таблица истинности — это список всех различных комбинаций значений истинности, которые может иметь предложение или набор предложений.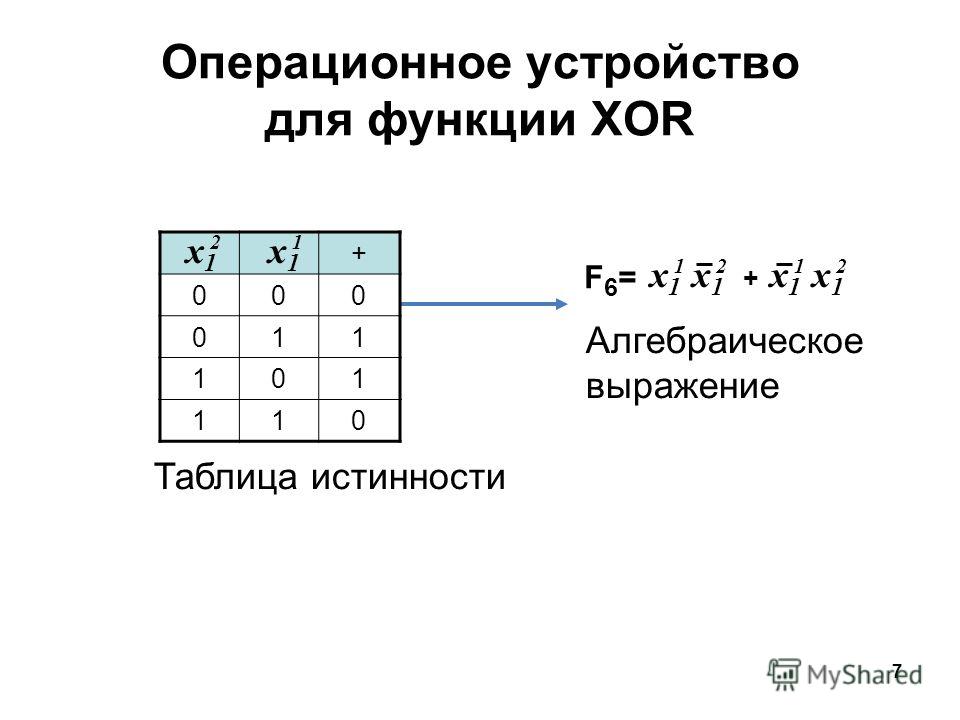 В этом случае у нас есть только одна буква, и она может быть как истинной, так и ложной.
В этом случае у нас есть только одна буква, и она может быть как истинной, так и ложной. Во-первых, они оба могут быть правдой.
Во-первых, они оба могут быть правдой.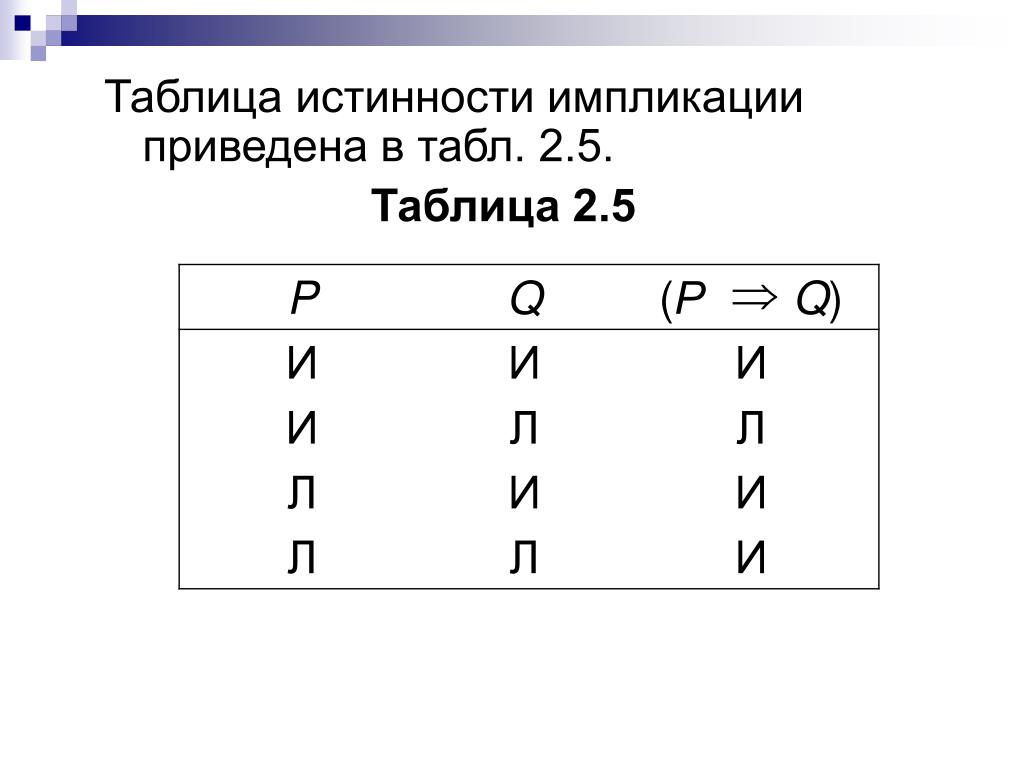 Помните, что дизъюнкции истинны, если хотя бы одна дизъюнкция истинна, и ложны в противном случае. Таким образом, дизъюнкция ложна только в нижней строке.
Помните, что дизъюнкции истинны, если хотя бы одна дизъюнкция истинна, и ложны в противном случае. Таким образом, дизъюнкция ложна только в нижней строке.
 Затем мы перейдем к следующему столбцу и поставим четыре Т и четыре F.
Затем мы перейдем к следующему столбцу и поставим четыре Т и четыре F.
 Я сделаю это смелым, чтобы быть ясным. Наша полная таблица истинности со всеми столбцами выглядит так:
Я сделаю это смелым, чтобы быть ясным. Наша полная таблица истинности со всеми столбцами выглядит так: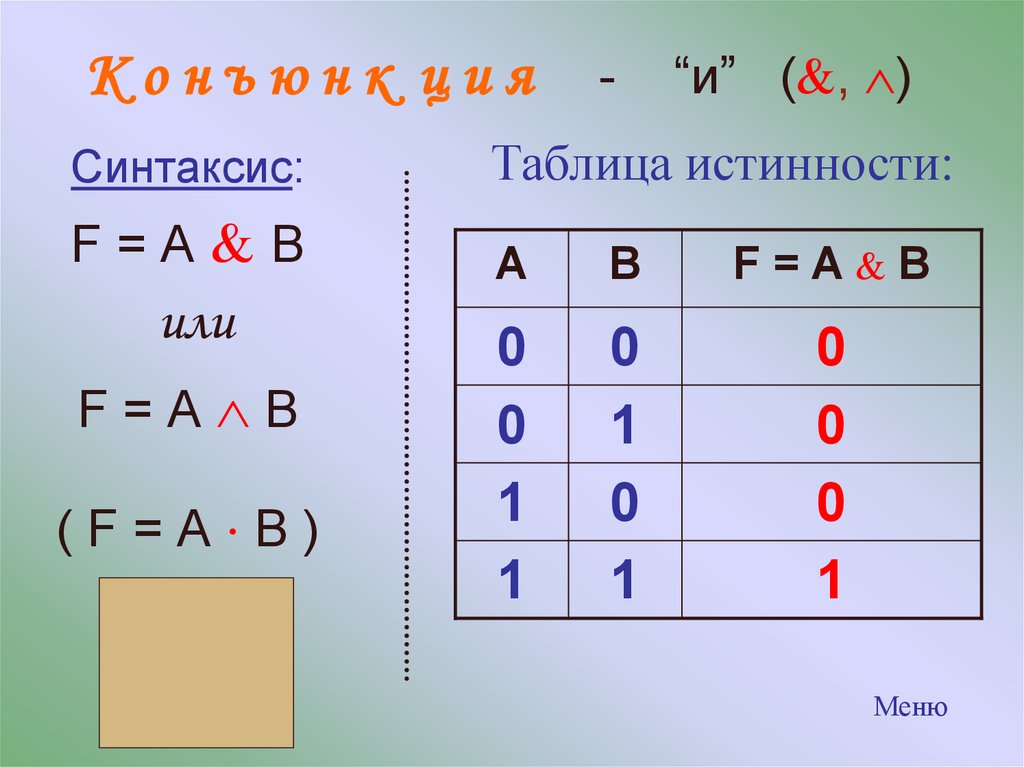
 Первый по существу утверждает, что это не так, что P и Q оба верны, а второй утверждает, что хотя бы одно из них ложно. Это всего лишь два способа сказать одно и то же.
Первый по существу утверждает, что это не так, что P и Q оба верны, а второй утверждает, что хотя бы одно из них ложно. Это всего лишь два способа сказать одно и то же.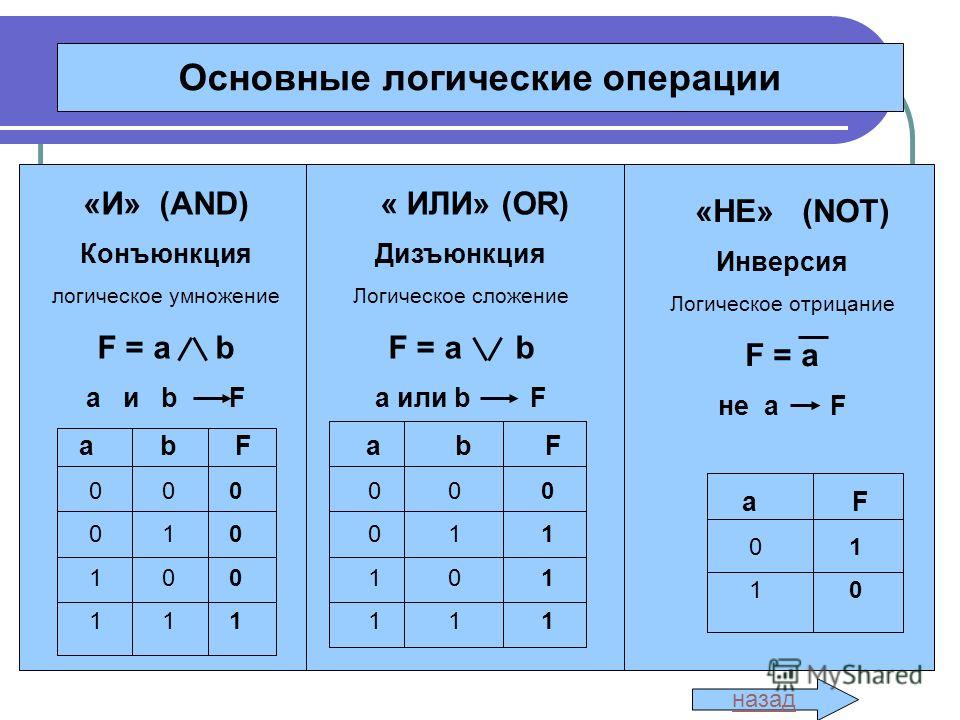
 Итак, этот аргумент действителен.
Итак, этот аргумент действителен. Итак, я знаю, что нет ряда, в котором были бы все истинные предпосылки и ложный вывод.
Итак, я знаю, что нет ряда, в котором были бы все истинные предпосылки и ложный вывод. Таким образом, этот аргумент недействителен. На самом деле, это настолько распространенный неверный аргумент, что у него есть название: «Предположение о следствии».
Таким образом, этот аргумент недействителен. На самом деле, это настолько распространенный неверный аргумент, что у него есть название: «Предположение о следствии». Это называется «Отрицание прошлого».
Это называется «Отрицание прошлого». Итак, вторая посылка также верна. Третья посылка ложна, так как является отрицанием истинной конъюнкции. Наконец, вывод верный.
Итак, вторая посылка также верна. Третья посылка ложна, так как является отрицанием истинной конъюнкции. Наконец, вывод верный.

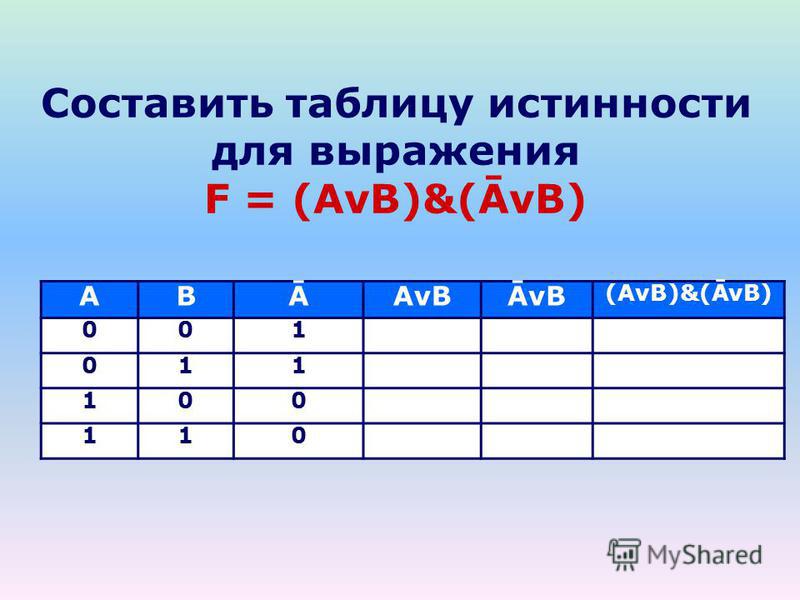
 Мы ищем что-то вроде буквы, которая имеет разные значения истинности, или ложную дизъюнктуру с истинной дизъюнкцией. Здесь каждая буква имеет одинаковое значение истинности, где бы она ни встречалась. У нас есть соединение с двумя истинными соединениями, два ложных дизъюнкции, оба с двумя ложными дизъюнкциями, ложное условное предложение с истинным антецедентом и ложным следствием и истинное отрицание с ложным отрицанием предложения. Все выглядит нормально, а значит возможно, чтобы аргумент имел истинные посылки и ложный вывод, и определенно недействителен. Проблемной строкой будет та, в которой A верно, B верно, C ложно и D ложно. Это будет строка 4 всей таблицы истинности.
Мы ищем что-то вроде буквы, которая имеет разные значения истинности, или ложную дизъюнктуру с истинной дизъюнкцией. Здесь каждая буква имеет одинаковое значение истинности, где бы она ни встречалась. У нас есть соединение с двумя истинными соединениями, два ложных дизъюнкции, оба с двумя ложными дизъюнкциями, ложное условное предложение с истинным антецедентом и ложным следствием и истинное отрицание с ложным отрицанием предложения. Все выглядит нормально, а значит возможно, чтобы аргумент имел истинные посылки и ложный вывод, и определенно недействителен. Проблемной строкой будет та, в которой A верно, B верно, C ложно и D ложно. Это будет строка 4 всей таблицы истинности.
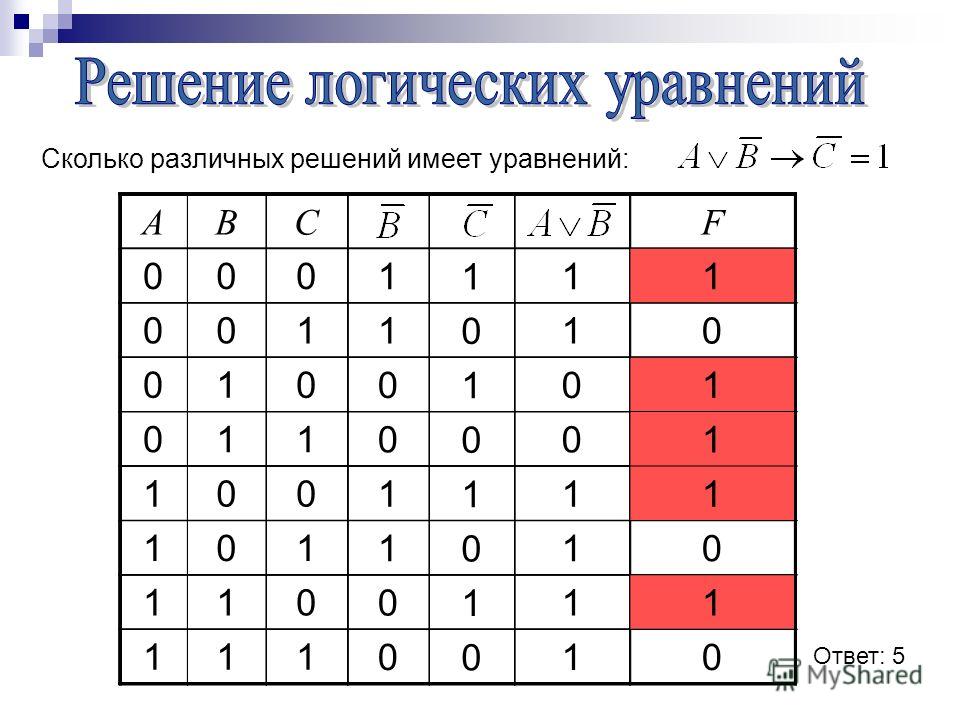 Обратите внимание, что у нас есть истинные условия с ложными последствиями. Это означает, что оба антецедента должны быть ложными.
Обратите внимание, что у нас есть истинные условия с ложными последствиями. Это означает, что оба антецедента должны быть ложными.
 ↩︎
↩︎
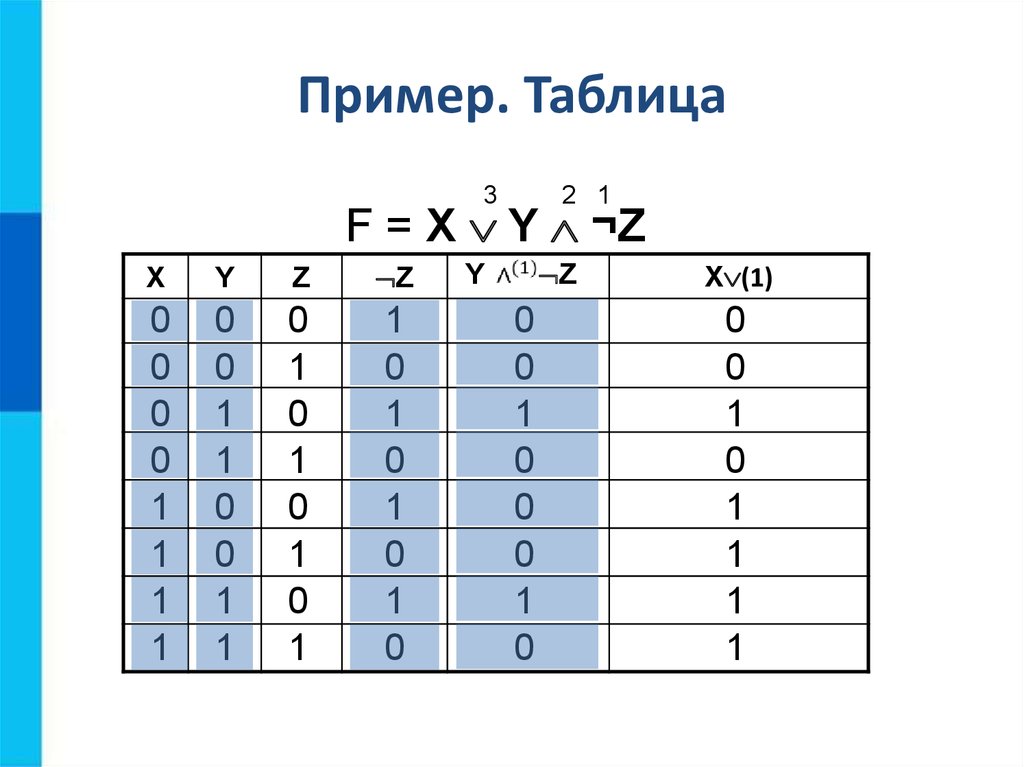 [latex]A\wedge{B}[/latex] – это элементы, существующие в обоих наборах, в [latex]A\cap{B}[/latex]. Точно так же [latex]A\vee{B}[/latex] будет элементами, которые существуют в любом наборе, в [latex]A\cup{B}[/latex].
[latex]A\wedge{B}[/latex] – это элементы, существующие в обоих наборах, в [latex]A\cap{B}[/latex]. Точно так же [latex]A\vee{B}[/latex] будет элементами, которые существуют в любом наборе, в [latex]A\cup{B}[/latex]. 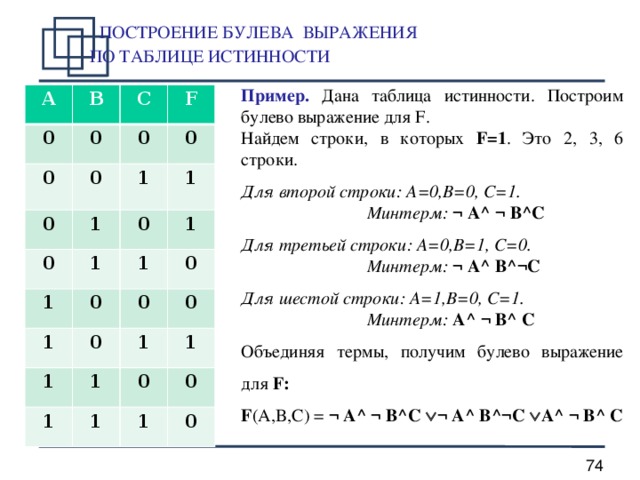
 Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.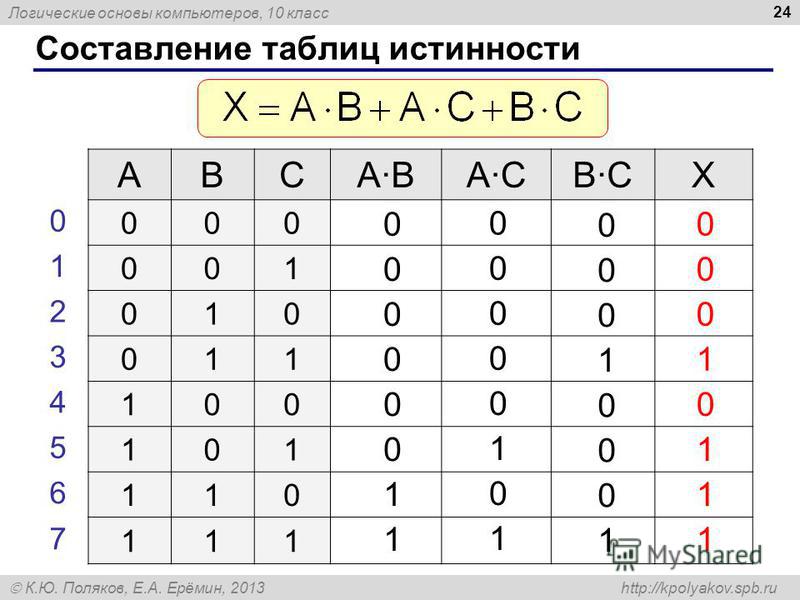


 Сначала идет операция деления или умножения? Поэтому мы используем круглые скобки для уточнения: \(4 \div (2 \times 2) = 1\), но \((4 \div 2) \times 2 = 4\).
Сначала идет операция деления или умножения? Поэтому мы используем круглые скобки для уточнения: \(4 \div (2 \times 2) = 1\), но \((4 \div 2) \times 2 = 4\).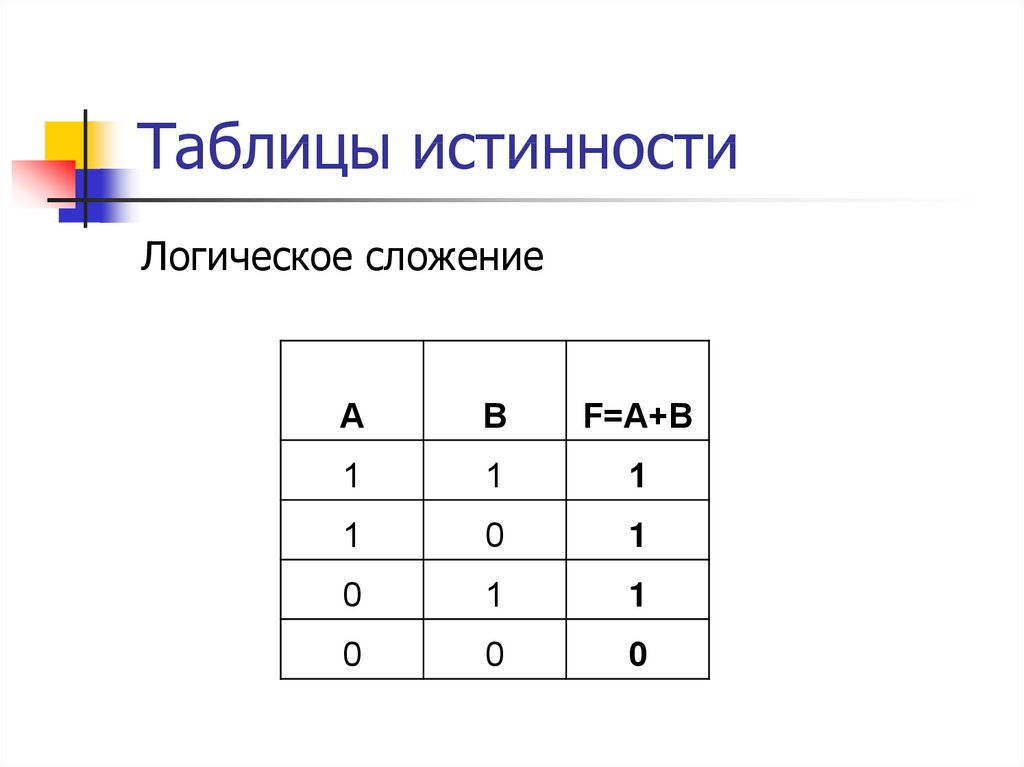
 Но все становится загроможденным и трудным для чтения, если мы добавляем круглые скобки вокруг каждого отрицания. Таким образом, у нас есть особое понимание \(\neg\) для поддержания порядка.
Но все становится загроможденным и трудным для чтения, если мы добавляем круглые скобки вокруг каждого отрицания. Таким образом, у нас есть особое понимание \(\neg\) для поддержания порядка.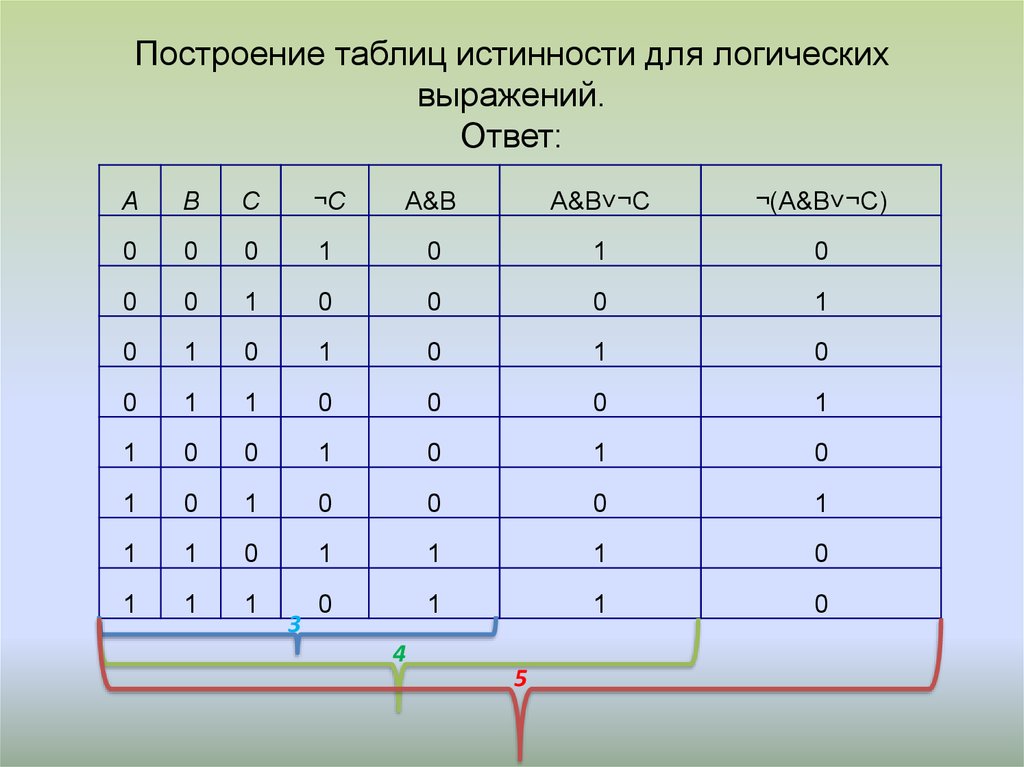 Поскольку каждое из этих утверждений может быть либо истинным, либо ложным, необходимо рассмотреть \(2 \times 2 = 4\) возможных ситуаций.
Поскольку каждое из этих утверждений может быть либо истинным, либо ложным, необходимо рассмотреть \(2 \times 2 = 4\) возможных ситуаций.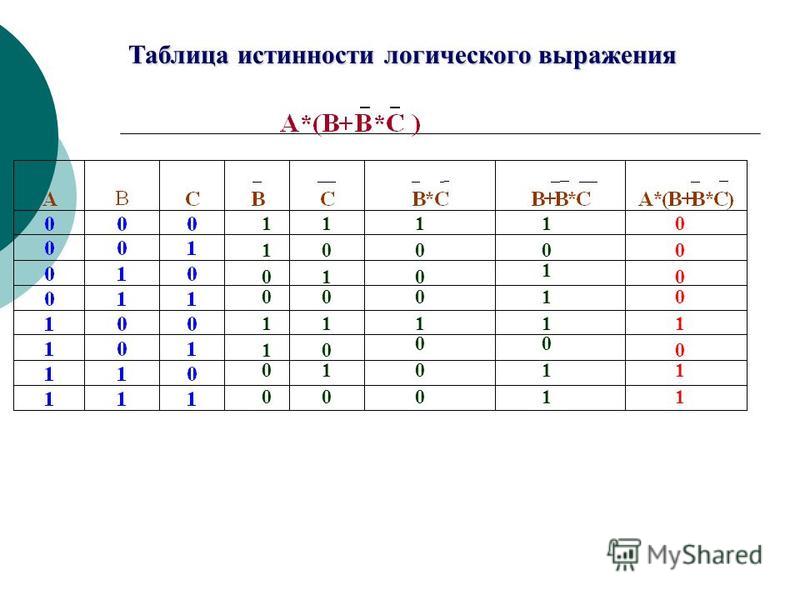 Но почему это правда, когда обе стороны верны? Разве «Либо \(A\), либо \(B\)» не означает, что всего один из этих верный?
Но почему это правда, когда обе стороны верны? Разве «Либо \(A\), либо \(B\)» не означает, что всего один из этих верный? \]
Это просто очень явный способ сказать: либо одно, либо другое, но не то и другое.
\]
Это просто очень явный способ сказать: либо одно, либо другое, но не то и другое. Чтобы заполнить столбец для \(\neg(A \wedge B)\), мы обращаемся к столбцу для \(A \wedge B\) и применяем правила из таблицы для \(\neg\):
Чтобы заполнить столбец для \(\neg(A \wedge B)\), мы обращаемся к столбцу для \(A \wedge B\) и применяем правила из таблицы для \(\neg\):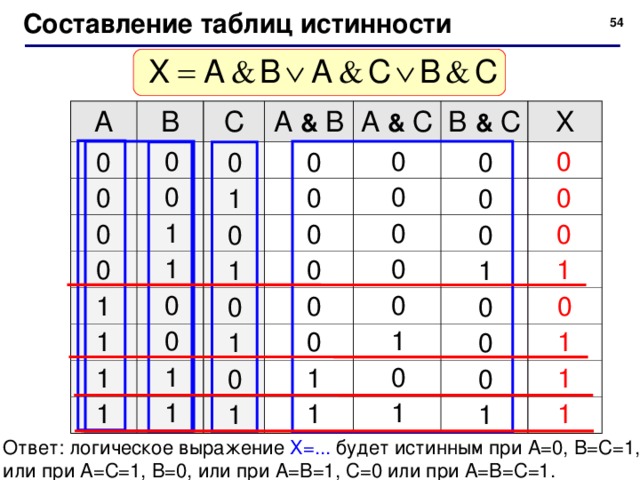 С практикой они быстро становятся рутиной.
С практикой они быстро становятся рутиной.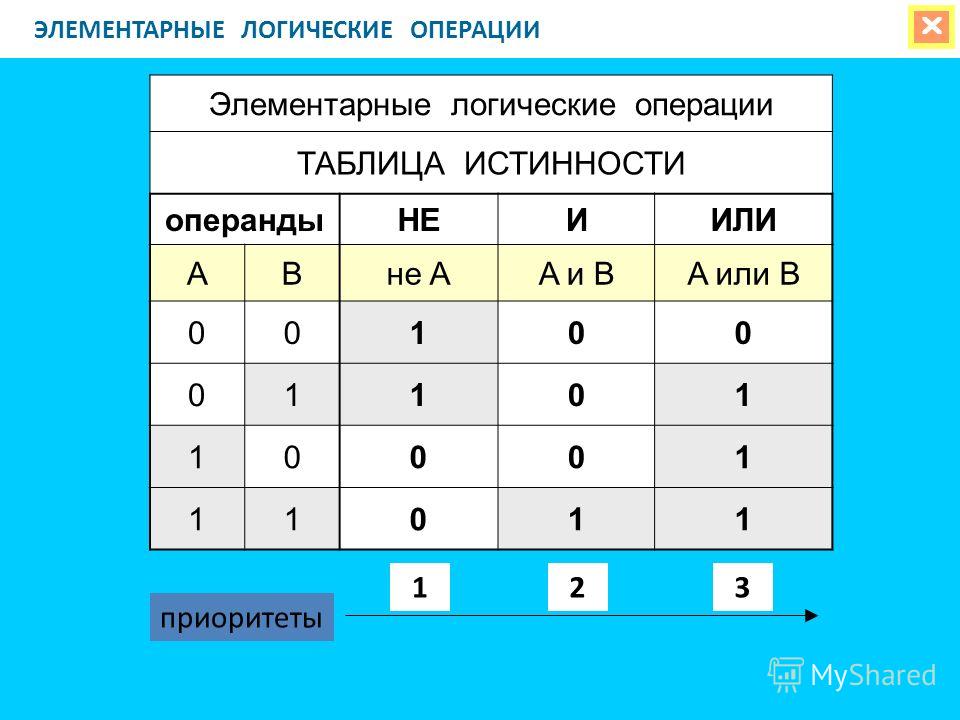
 5 Включение и эквивалентность
5 Включение и эквивалентность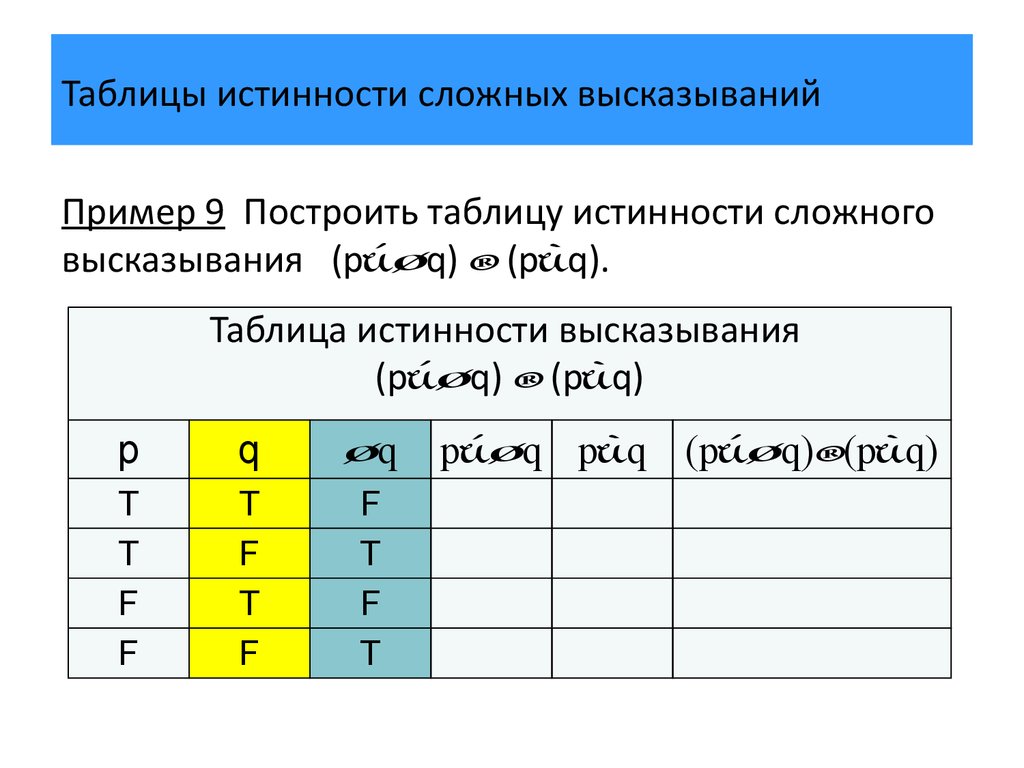
 Итак, еще раз таблица истинности говорит нам, что этот аргумент действителен.
Итак, еще раз таблица истинности говорит нам, что этот аргумент действителен.