ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения.  § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  Круг кривизны§ 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  Криволинейный интеграл от линейной формы по произвольной кривой.4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
1.4. Сложение колебаний одного направления
Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.
Сложение колебаний с одинаковыми частотами
Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:
|
|
(1. |
34)где x1, x2— переменные, описывающие колебания, A1, A2— их амплитуды, а , — начальные фазы. Результирующее колебание
удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.
Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону
|
|
(1. |
35)Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).
Рис. 1.12. Векторная диаграмма для общего решения (1.23)
Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А1 и А2 Возьмем их векторную сумму (рис. 1.13)
Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты
Проекция вектора А1 на ось 0x равна сумме проекций соответствующих векторов
Таким образом, вектор А представляет собой результирующее колебание.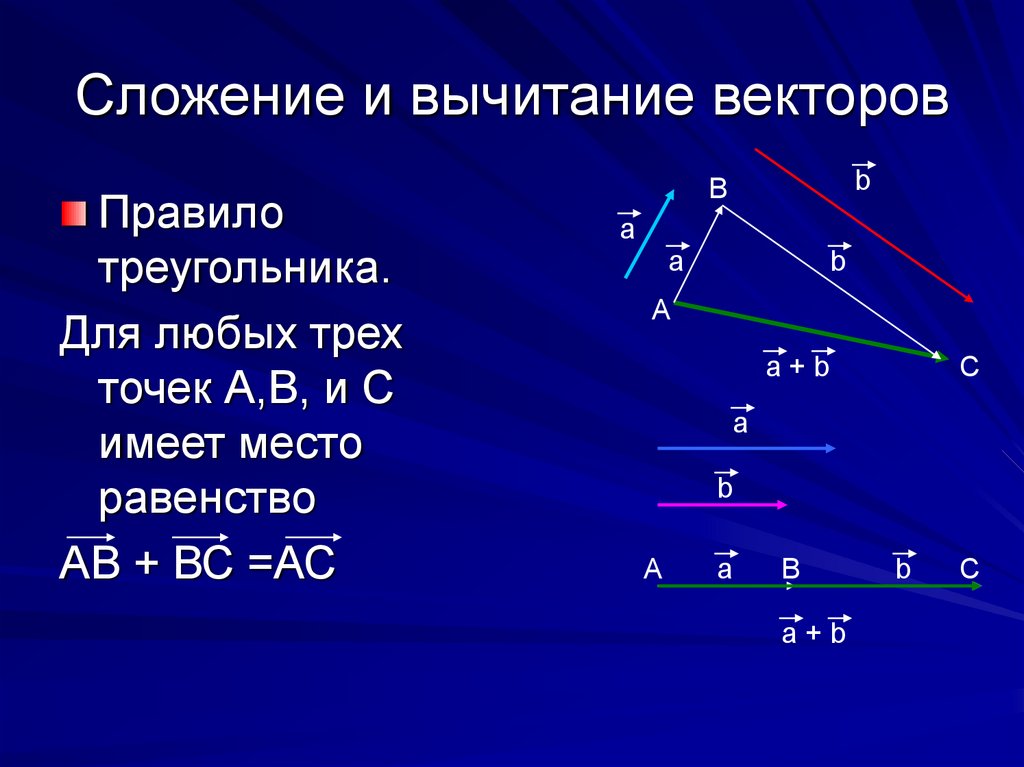
Этот вектор вращается с той же угловой скоростью , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой A и начальной фазой a. Согласно теореме косинусов:
|
|
(1.36) |
В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную (то есть ), то амплитуда результирующего колебания равна сумме амплитуд
Если же складываемые колебания находятся в противофазе (то есть ), то
Биения
В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте.
Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.
|
Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами. |
Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно, и . Итак,
|
|
(1.37) |
Складываем эти выражения и учитываем известную формулу тригонометрии:
|
|
(1. |
38)Если то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:
|
|
(1.39) |
Кроме того, множитель в скобках меняется медленно по сравнению с . Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой w, эффективная амплитуда которого изменяется со временем по закону (1.40) (рис. 1.14):
|
|
(1. |
40)Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону , причем все три его параметра: строго постоянны во времени.
Рис. 1.14. Биения при сложении колебаний с близкими частотами
Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен
|
|
(1.41) |
Видео 1.12 Биения на экране осциллографа
Видео 1.13 Биения: осциллограф и динамик
Видео 1.
14 «Двойной» маятник: запись песком картины биений
Колебания двух связанных осцилляторов
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<<k. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).
Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается
Тогда в положении равновесия координаты грузов равны
При колебаниях координаты равны, соответственно, x1(t), x2(t). Удлинения пружин записываются как
Мы имеем дело с системой с двумя степенями свободы.
Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная
и сила со стороны пружины K, равная
На второй груз действуют аналогичные силы
и
Соответственно, уравнения движения имеют вид
|
|
(1.42) |
Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x1оказывают влияния колебания x2и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными колебаниями (модами)).
Именно, введем новые переменные x1 и x2:
|
|
(1.43) |
Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат
В этих переменных уравнения (1.42) принимают вид:
|
|
(1.44) |
Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:
|
|
(1. |
45)Первое уравнение описывает гармонические колебания с частотой
совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой
Так как K<<k, имеем
|
|
(1.46) |
Соответственно, мы получаем общее решение системы уравнений:
|
|
(1. |
47)Общее решение для координат х1 и х2 колеблющихся точек следуют из (1.47) и (1.43):
|
|
(1.48) |
Для примера рассмотрим случай, когда первая масса смещается на расстояние от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:
|
|
(1.49) |
Этому соответствуют следующие начальные значения нормальных координат:
|
|
(1. |
50)Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид
|
|
(1.51) |
Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:
|
|
(1.52) |
Графики функций x1(t), x2(t) показаны на рис.
1.16. Видна характерная картина биений.
Рис. 1.16. Биения в системе двух связанных осцилляторов
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту первый маятник колеблется с максимальной амплитудой, а второй покоится.
На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.
Рис. 1.17. Биения в системе связанных маятников
Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x1), то A2 = 0 и, как следует из общего решения (1.
48),
|
|
(1.53) |
Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов
Возбуждение только второй (x2) нормальной моды означает, что A1 = 0:
|
|
(1. |
54)В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.
В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.
Дополнительная информация
http://allphysics.ru/feynman/bieniya — Фейнмановские лекции по физике.
Биения.
Линейная алгебра
— математически строгий способ описания двух векторов, которые имеют одинаковые компоненты, но не равны.
$\begingroup$
В линейной алгебре нас учат, что векторы могут быть представлены как сложение скалярного произведения базисных векторов. Например, если $\hat \imath, \hat \jmath$ — единичные векторы, $$\vec v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = v_1\hat \imath + v_2\hat \jmath$$ Возможно ли, что некоторый вектор $\vec v_*$ также равен $\begin{bmatrix} v_1 \\ v_2 \end{bmatrix}$, но их выражение через базис делает его таким, что $ \vec v \neq \vec v_*$, например, если последний имеет другой базис s.t. $\vec v_* = v_1\шляпа r + v_2\шляпа p$? Каково точное описание этой ситуации? Я не думаю, что достаточно сказать, что у них разные базы, так как, может быть, мы могли бы построить одну базу из другой. Они не могут использовать одно и то же векторное пространство или что-то в этом роде? Должны ли мы с самого начала объявлять какое-то свойство $\vec v_*$?
Я думаю, такая ситуация может возникнуть, если векторы используют разные системы координат, но как это описать?
- линейная алгебра
- векторные пространства
- векторы
$\endgroup$
$\begingroup$
вектора можно представить как сложение скалярного умножения базисных векторов.
Я думаю, вы имеете в виду, что вектор может быть выражен как линейная комбинация базисных векторов (если дан базис для нашего векторного пространства). 9*$ относительно $\beta_2$.
$\endgroup$
5
$\begingroup$
Дано векторное пространство $V$ и вектор $v\in V$.
Пусть есть два упорядоченных базиса $U=\{u_1,u_2,…u_n\}$ и $W=\{w_1,w_2,…w_n\}$ и пусть представление $v$ в упорядоченном базисе $U$ и $W$ равны $$[v]_U=\begin{bmatrix} c_1 \\ c_2 \\.\\.\\.\\c_n \end{bmatrix}$$ и $$[ v]_W=\begin{bmatrix} c’_1 \\ c’_2 \\.\\.\\.\\c’_n \end{bmatrix}$$ 9{-1}=A_{W\rightarrow U}$
PS: Если хотите, могу обсудить метод нахождения матрицы перехода.
$\endgroup$
4
Скалярное произведение двух векторов: определение, формула и свойства
Векторы — это величины, которые имеют как величину, так и направление, а операции, которые можно выполнять над векторами, — это сложение и умножение.
Умножение векторов можно выполнить двумя способами, а именно скалярным произведением векторов и перекрестным произведением векторов. Скалярное произведение — это один из способов умножения двух или более векторов. Результат скалярного произведения векторов является скалярной величиной. Следовательно, скалярное произведение векторов также известно как скалярное произведение. Скалярное произведение векторов имеет различные приложения в геометрии, механике, технике, астрономии и т. д.
Скалярное произведение двух векторов равно произведению величины и направления и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов, лежащих в одной плоскости двух векторов. Скалярный продукт двух векторов может быть положительным действительным числом, отрицательным действительным числом или нулем.
В векторной алгебре, если два вектора заданы как \(x=(x_{1},x_{2},x_{3},….
.,x_{n})\) и \(y= (y_{1},y_{2},y_{3},…..,y_{n})\), то их скалярное произведение равно: 9{n}x_{i}y_{i}\)
Определение скалярного произведения векторов можно дать двумя способами: алгебраическим и геометрическим. Алгебраическим способом скалярное произведение является суммой произведений соответствующих элементов двух последовательностей чисел. С геометрической точки зрения скалярное произведение — это произведение евклидовой величины двух векторов и косинуса угла между ними.
Проекция векторов: Скалярное произведение векторов полезно при определении компонента одного вектора в направлении другого вектора. Проекция одного вектора на другой вектор — это ширина тени представленного вектора на другой вектор.
Проекция векторов достигается путем умножения величины представленных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Предположим, OA = x , OB = y , два вектора и \(\theta\) угол между x и y .
Проведите линию AL перпендикулярно OB.
Из прямоугольного треугольника OAL,
\(cos\theta=\frac{OL}{OA}\)
\(OL=OA cos\theta=\left|x\right|cos\theta\)
OL указывает на векторную проекцию x на y .
x \(\cdot\) y = \(\left|x\right|\left|y\right|cos\theta\)
x \(\cdot\) y = \(\left|y\right|OL\)
x \(\cdot\) y = \(\left|y\right|\) (проекция x на y ) .
Таким образом, проекция х на y = \(\frac{x\cdot y}{\left|y\right|}\).
Аналогично, проекция y на x = \(\frac{x\cdot y}{\left|x\right|}\).
Скалярное произведение формулы двух векторовПредположим, что x и y — два ненулевых вектора, а \(\theta\) — это угол между двумя векторами, затем скалярное произведение (или скалярное произведение) двух векторов обозначается как x \(\cdot\) y , что определяется как
x \(\cdot\) y = \(\left|x\right|\left|y\right|cos\theta\),
где
- \(\left|x\right |\) = величина x ,
- \(\left|y\right|\) = величина y ,
- \(\theta\) = угол между векторами x и y .
Примечание. \(\theta\) не определено, если величина любого из векторов равна нулю, т. е. a = 0 или b = 0.
Узнайте о скалярном тройном произведении
Как найти скалярное произведение двух векторов?Предположим, что если два вектора выражаются через единичные векторы i, j, k вдоль осей x, y и z, то скалярное произведение двух векторов получается следующим образом:
Шаг 1: Если \(x=x_{1}\шляпа{i}+x_{2}\шляпа{j}+x_{3}\шляпа{k}\) и \(y=y_{1}\шляпа{i} +y_{2}\hat{j}+y_{3}\hat{k}\), то скалярное произведение x и y равно
x \(\cdot\) y = \((x_{1}\шляпа{i}+x_{2}\шляпа{j}+x_{3}\шляпа{k})\cdot(y_{1}\шляпа{i}+y_{ 2}\шляпа{j}+y_{3}\шляпа{k})\).
Шаг 2: x \(\cdot\) y = \((x_{1}y_{1})(\hat{i}\cdot\hat{i})+(x_{ 1}y_{2})(\шляпа{i}\cdot\шляпа{j})+(x_{1}y_{3})(\шляпа{i}\cdot\шляпа{k})+(x_{ 2}y_{1})(\шляпа{j}\cdot\шляпа{i})+(x_{2}y_{2})(\шляпа{j}\cdot\шляпа{j})+(x_{ 2}y_{3})(\шляпа{j}\cdot\шляпа{k})+(x_{3}y_{1})(\шляпа{k}\cdot\шляпа{i})+(x_{ 3}y_{2})(\шляпа{k}\cdot\шляпа{j})+(x_{3}y_{3})(\шляпа{k}\cdot\шляпа{k})\).
Шаг 3: Точечное отношение единичных векторов вдоль трех осей выглядит следующим образом шляпа{k}\cdot\шляпа{i}=0\) и
\(\шляпа{i}\cdot\шляпа{i}=\шляпа{j}\cdot\шляпа{j}=\шляпа{k}\cdot\шляпа{k}=1\).
Шаг 4: Используя точечное отношение единичных векторов, мы имеем
x \(\cdot\) y = \(x_{1}y_{1}+x_{2}y_{2} +x_{3}y_{3}\).
Примеры скалярного произведения двух векторовНиже приведены некоторые примеры скалярного произведения двух векторов:
- Скалярное произведение двух единичных векторов: Скалярное произведение двух единичных векторов равно единице. Предположим, что для двух единичных векторов 9{\circ}\) = ab (0) = 0.
Рассмотрим a , b и c — действительные векторы, ‘x’ y’ является скаляром, то скалярное произведение удовлетворяет следующим свойствам:
Свойство 1: Коммутативное свойство: Скалярное произведение векторов коммутативно, т.
е. a \(\cdot\) b = b \ (\cdot\) a,
Это следует из определения (\(\theta\) угол между a и b ):
a \(\cdot\) b = \(\left|a\right|\left|b\right|cos\theta=\left|b\right |\left|a\right|cos\theta\) = b \(\cdot\) a .
Свойство 2: Распределительное свойство: Скалярное произведение векторов является дистрибутивным по отношению к сложению векторов, т. е. \) б + а \(\cdot\) в.
Свойство 3: Билинейность Свойство: Скалярное произведение векторов является билинейным, т.е. ) b ) + ( a \(\cdot\) c ).
Свойство 4: скалярное умножение Свойство: Скалярное умножение векторов задается формулой ) б ).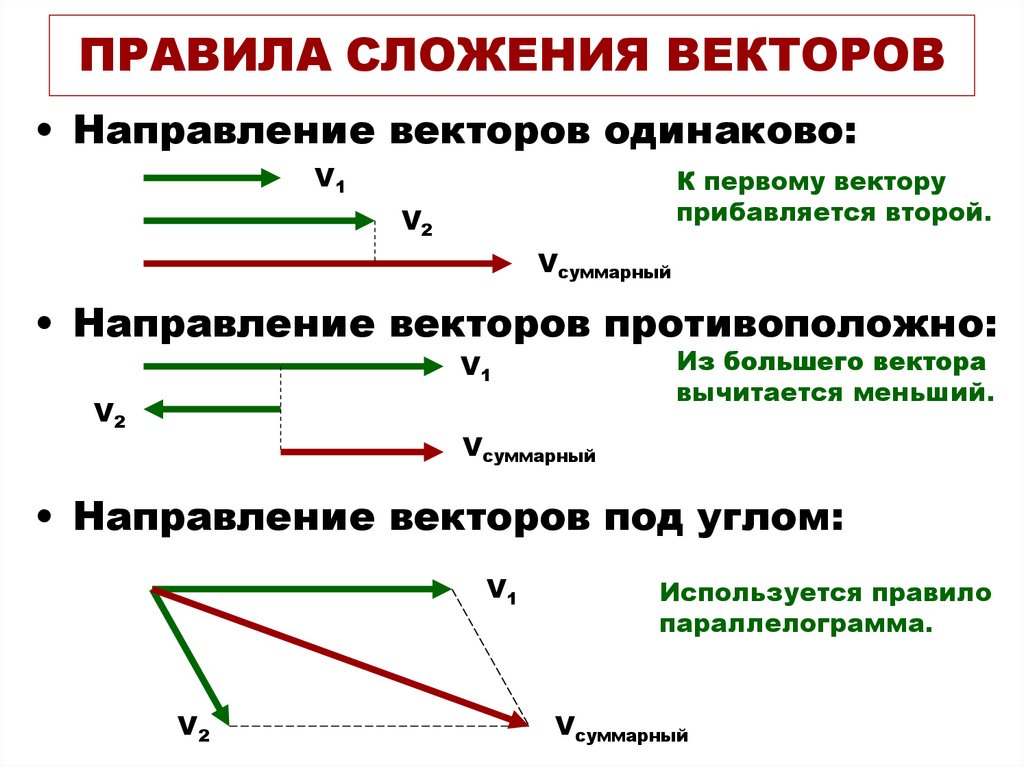
Свойство 5: Неассоциативность Свойство: Скалярное произведение векторов неассоциативно, потому что скалярное произведение между скаляром ( a \(\cdot\) b ) и вектором ( c ) не определено, это означает, что выражения ( a \(\cdot\) b )\(\cdot\) c или a \(\cdot\)( b \(\cdot\) c ) не определены. Свойство скалярного умножения иногда называют «ассоциативным законом для скаляра и скалярного произведения» или «скалярное произведение ассоциативно по отношению к скалярному умножению», потому что c( a \(\cdot\) b ) = (c a )\(\cdot\) b = a \(\cdot\)(c b ).
Свойство 6: Ортогональность Свойство: Два ненулевых вектора a и b ортогональны тогда и только тогда, когда a \(\cdot\) b = 0,
Произведение разности между 9057 иВекторы и векторное произведение векторов
Скалярное произведение двух векторов
- Скалярное произведение двух векторов A и B определяется как скалярная величина AB\(\cos\theta\), где \(\theta\) — угол между ними, такой что \(0\leq \theta \leq \pi\) .
- Обозначается A \(\cdot\) B путем помещения между векторами точки.
- Итак, у нас есть уравнение A \(\cdot\) B = AB\(\cos\theta\).
- Скалярное произведение векторов также известно как скалярное произведение двух векторов.
Перекрестное произведение двух векторов
- Перекрестное произведение двух векторов A и B определяется как AB\(\sin\theta\) с направлением, перпендикулярным A и в правой системе, где \(\theta\) — угол между ними такой, что \(0\leq \theta \leq \pi\).
- Обозначим A \(\times\) B , поставив знак креста между векторами. 9{\circ}\)
= (2)(3)(1/2)
= 3.
Пример 2: Вычислить скалярное произведение двух векторов a = (1, 2, 3) и б = (4, -5, 6).
Решение: Даны векторы a = (1, 2, 3) и b = (4, -5, 6) соответственно.
a \(\cdot\) b = (1, 2, 3)\(\cdot\)(4, -5, 6)
a \(\cdot\) b = (1)(4)+(2)(-5)+(3)(6)
a \(\cdot\) b = 4 – 10 + 18
a \(\cdot\) b = 12.
Мы надеемся, что приведенная выше статья поможет вам понять и сдать экзамен. приготовления. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о скалярном произведении двух векторовВ.1 Что такое скалярное произведение двух взаимно перпендикулярных векторов? 9{2}\).
Q.
