Сложение вычитание умножение и деление чисел с разными знаками: Сложение и вычитание целых чисел с разными знаками

Вычитание чисел с разными знаками

В курсе арифметики установлено, что вычитание есть действие, обратное сложению, при помощи которого по данной сумме и по одному слагаемому находят другое слагаемое.

Пользуясь этим определением, мы должны разобрать, как надо выполнять вычитание относительных чисел.

Пусть надо из (+8) вычесть (–3), т. е. пусть надо

Первое данное число выражает данную сумму, второе – данное слагаемое, а над найти другое слагаемое (для него оставлено место после знака равенства), т. е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:

(?) + (–3) = +8.

Но сразу этот вопрос решить трудно, а поэтому сначала решим более простой, вспомогательный вопрос: какое число надо сложить с (–3), чтобы в сумме получился нуль ?, т. е.

(?) + (–3) = 0.

На этот вопрос ответ ясен: надо взять для неизвестного слагаемого число, имеющее ту же абсолютную величину, как и данное слагаемое, но обратный знак, – в данном случае надо для неизвестного слагаемого взять число +3. Теперь перейдем к решению главного вопроса: мы взяли для неизвестного слагаемого число + 3 и в сумме получился нуль, но нам надо получить в сумме число +8, поэтому надо чтобы и в другое слагаемое вошло это же число +8. Следовательно, неизвестное слагаемое должно состоять: 1) из +3, чтобы в сумме получился нуль и 2) из +8, чтобы эту сумму «нуль» довести до требуемой +8. Поэтому на месте неизвестного слагаемого пишем + 3 + 8:

(+ 8) – (– 3) = + 3 + 8 = + 11.

Последнее (= + 11) написано на том основании, что числа + 3 и + 8 надо соединить в одно или сложить.

Вот еще примеры:

(– 7) – (+ 5) = – 5 – 7 = – 12.

Искомое слагаемое должно состоять: 1) из –5, чтобы в сумме получился нуль и 2) из –7, чтобы дополнить этот нуль до требуемой суммы, до –7. Сложив числа –5 и –7, получим –12.

(– 3) – (– 8) = + 8 – 3 = + 5.

Искомое слагаемое должно состоять: 1) из +8, чтобы в сумме получился нуль и 2) из –3, чтобы дополнить этот нуль до требуемой суммы, до –3. Сложив числа +8 и –3, получим +5.

(+7) – (+9) = –9 + 7 = –2.

Искомое слагаемое должно состоять: 1) из –9, чтобы в сумме получился нуль и 2) +7, чтобы дополнить этот нуль до требуемой суммы, до +7; сложив числа –9 и +7, получим –2.

Из этих примеров видим, что вычитание в алгебре состоит лишь в умении раскрывать скобки: надо второе число (данное слагаемое или вычитаемое) написать с обратным знаком, а первое число (данную сумму или уменьшаемое) написать с тем же знаком. После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.

Так как сумма не изменяется от перестановки слагаемых, то можно числа, полученные в разобранных примерах после раскрытия скобок, переставить, чтобы порядок был согласен с порядком данных чисел:

(+ 8) – (– 3) = + 8 + 3; (– 7) – (+ 5) = – 7 – 5;
– 3 – (– 8) = – 3 + 8; (+ 7) – (+ 9) = + 7 – 9.

Итак,

чтобы раскрыть скобки при вычитании, надо первое число (уменьшаемое) написать без изменения и приписать к нему второе число (вычитаемое) с обратным знаком.

Заметим еще, что при обозначении вычитания первое число пишется часто без скобок, а если оно положительное, то, как уже известно, знак + можно впереди не писать.

Например,

– 3 – (– 5) = – 3 + 5 = + 2; 1 – (– 6) = 1 + 6 = 7;
3 – (+ 3) = 3 – 3 = 0.

14. Примеры на сложение и вычитание. Пусть требуется вычислить:

1 – {3 + [5 – (3 – 5 – 6)]}.

Мы станем руководствоваться следующим порядком: если внутри какой-либо пары скобок нет других скобок и нет действия, то эти скобки можно раскрыть; если же внутри этих скобок есть действие (сложение), то надо сначала его выполнить. В нашем примере такой порядок: сначала выполним сложение чисел, написанных внутри маленьких скобок, потом надо эти скобки раскрыт, выполнить сложение внутри квадратных скобок, раскрыть квадратные скобки, выполнить сложение внутри витых скобок, раскрыть эти скобки и, наконец, сложить полученные числа:

1 – {3 + [5 – (3 – 5 – 6)]} = 1 – {3 + [5 – (– 8)]} = 1 – {3 + [5 + 8]} =
= 1 – {3 + [+13]} = 1 – {3 + 13} = 1 – {+ 16} = 1 – 16 = – 15.

Конечно, при навыке можно сразу выполнять несколько действий и, следовательно, укоротить вычисление.
Еще пример:

Пусть еще требуется вычислить выражение:

a – {(b – c) – [d + (e + f)]} при a = – 3; b = 1; c = 4; d = – 5; e = – 7; f = 2.

Выполним вычисления по действиям:

1) b – c = + 1 – (+ 4) = 1 – 4 = – 3;

2) e + f = (– 7) + (+ 2) = – 7 + 2 = – 5;

3) d + (– 5) = – 5 + (– 5) = – 5 – 5 = – 10;

4) (– 3) – (– 10) = – 3 + 10 = + 7;

5) – 3 – (+ 7) = – 3 – 7 = – 10.

Примеры для упражнений:

Если взять число нуль и прибавлять к нему по +1, то получим ряд постепенно увеличивающихся целых чисел:

0, +1, +2, +3, +4, +5, …..

Этот ряд совпадает (см. конец п. 10) с натуральным рядом чисел, т. е. с

0, 1, 2, 3, 4, 5 …..

Если мы, взяв число нуль, вычтем из него (+1), затем еще раз вычтем (+1) и т. д., то, согласно с тем, как мы это понимали в арифметике по отношению к натуральному ряду чисел, мы теперь признаем, что и здесь станем получать все уменьшающиеся целые числа:

1) 0 – (+ 1) = – 1; 2) (– 1) – (+ 1) = – 1 – 1 = – 2;
3) (– 2) – (+ 1) = – 3 и т. д.

Получим, идя от нуля налево, ряд уменьшающихся относительных чисел:

….., – 5, – 4, – 3, – 2, – 1, 0.

Соединяя этот ряд с предыдущим, получим полный ряд относительных чисел:

….., – 6, – 5, – 4, – 3, – 2, – 1, 0, +1, +2, +3, +4, +5, +6 …..

Этот ряд и вправо и влево идет без конца.

Всякое число в этом ряду больше другого, которое стоит левее и меньше любого, стоящего правее его. Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.

В промежутках между целыми числами этого ряда можно вставить бесконечно много дробных чисел.

правила, примеры, решения, арифметические действия с рациональными числами

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных.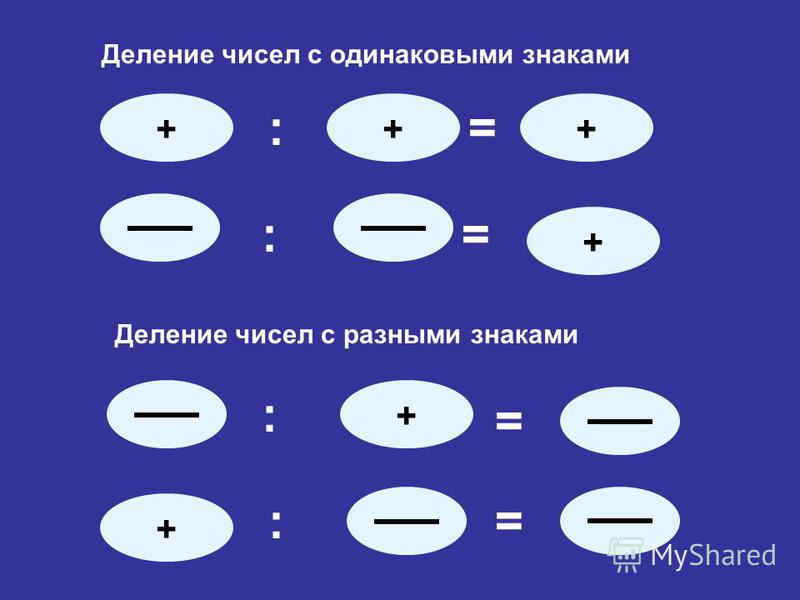 Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Определение 1

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a.

Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.

Сложение противоположных рациональных чисел

Определение 2

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).

К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Пример 1

Необходимо произвести сложение рациональных чисел: 0,6 и 59.

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.

Осуществим сложение дробей с разными знаменателями:

610+59= 5490+ 5090= 10490=1745

Ответ: 0,6 + 59= 1745.

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Определение 3

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.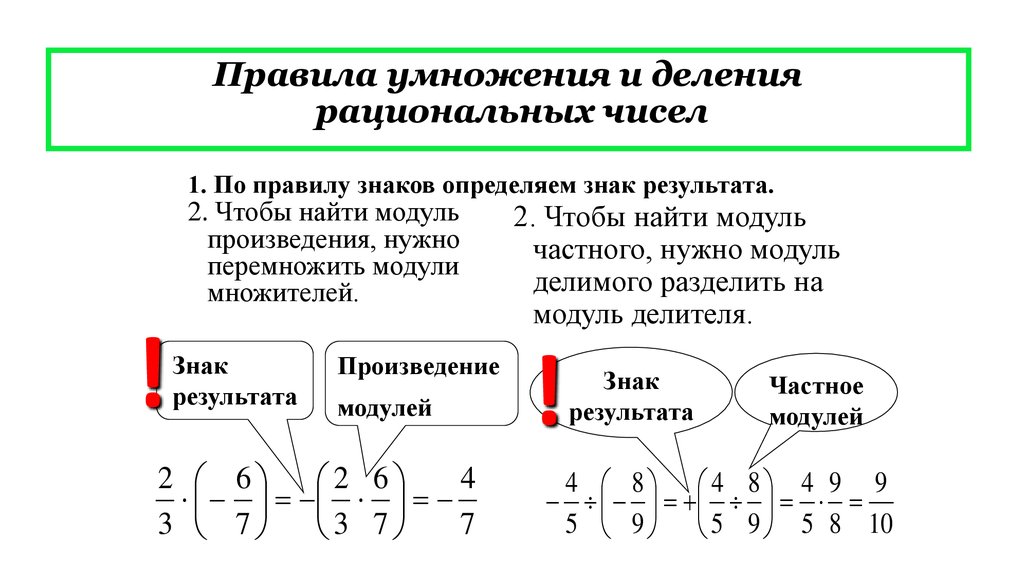

Пример 2

Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей — рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8,2-234= 8210- 234= 59 20.

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.

Сложение отрицательных рациональных чисел

Определение 4

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Пример 3

Необходимо произвести сложение чисел: -4,0203 и -12,193.

Решение

Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:

​​​​​​

Полученному результату присваиваем знак минус: -16,2133.

Ответ: (-4,0203)+(-12,193) =-16,2133.

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, что a-b=c и a-c=b. И наоборот: из равенств a-b =c и a-c=b следует, что c+b=a.

Определение 5

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Пример 4

Необходимо вычислить разность рациональных чисел: 4,(36)– 15.

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955

Ответ: 4,(36)-15= 4955

Определение 6

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a–b=a+(-b).

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.

Пример 5

Необходимо из рационального числа 27 вычесть рациональное число 537

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537

Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517

Ответ:27+-537=-517

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Определение 7

Произведение любого рационального числа a на нуль есть нуль.

Т.е. a·0=0.

Используя переместительное свойство умножения, получим: 0·а=0.

К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0.

Умножение на единицу

Определение 8

Умножение любого рационального числа a на 1 дает число a.

Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.

Умножение взаимообратных чисел

Определение 9

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.

К примеру, результатом произведения чисел 56 и 65 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Пример 6

Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.

Решение

Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.

Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.

Ответ: 0,5 ·625= 325

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Пример 7

Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2,121 · 3,4 = 7,2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Определение 10

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Пример 8

Необходимо найти произведение чисел: -338и 212

Решение

Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212

Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716

Ответ: -338·212=-8716

Умножение отрицательных рациональных чисел

Определение 11

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Пример 9

Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.

Решение: модули заданных чисел соответственно равны 3,146 и 56.

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: (-3,146) · (-56) = 176,176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, что b·c=a.

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Определение 12

Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство a : b = a · b-1.

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Пример 10

Необходимо выполнить действие деления 313:-116

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.

Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267

Ответ: 313:-116=-267

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Презентация на тему Статья Методическая разработка урока по теме Математическое путешествие по материкам и островам. Этот урок желательно проводить в курсе математики 6–ого класса при рассмотрении темы сложение и вычитание , умножение и деление отрицательных чисел и чисе

Слайд 1Текст слайда:

Статья «Методическая разработка урока по теме «Математическое путешествие по материкам и островам». Этот урок желательно проводить в курсе математики 6–ого класса при рассмотрении темы сложение и вычитание , умножение и деление отрицательных чисел и чисел с разными знаками.

Тип урока: обобщающий урок- самостоятельная работа.
Цели и задачи урока:
Образовательные:
-закрепить и проконтролировать уровень знаний, умений и навыков сложения , вычитания умножения и деления отрицательных чисел с разными знаками.
Развивающие:
-создать у школьников положительную мотивацию к предмету;
-повысить общую культуру учащихся;
-расширить кругозор учащихся , помочь школьникам лучше понять роль математики в истории общества.
Воспитательные:
-воспитать у школьников честность, ответственность и аккуратность;
-формирование умений у учащихся работать в коллективе.
Оборудование урока:
Иллюстративный и раздаточный материал (листы с заданиями, с ответами), интерактивная доска, мультимедийный проектор, компьютер).

---

Слайд 2Текст слайда:

Ход урока

Класс разбивается на 4 варианта по пять человек. Учитель сообщает, что получив › 12балов каждый вариант может получить путевку в виртуальное путешествие на один из пяти материков или на остров. У каждого варианта лист с 18 заданиями. За каждый правильно решенный пример каждый вариант получает 1 бал. После отведенного времени решения самостоятельной работы каждый вариант получает лист с ответами и буквами на разброс в таблице. Ученики сами проверяют ответы и считают баллы, собирают из букв имя материка или острова и узнают ,что интересное они узнают во время путешествия.
Организационный момент.
Сообщение учителя.
Сегодня на уроке мы обобщим и повторим тему «Сложение и вычитание , умножение и деление отрицательных чисел и чисел с разными знаками». У нас необычный урок. Мы отправимся с вами в виртуальное путешествие по пяти материкам и островам.
1.Объяснение условий урока , распределение на 4 варианта (5мин.).
2. Самостоятельная работа (25 мин.).
3.Физкультминутка (3 мин.).
4.Проверка (5мин).
(› 12-примеров -5, 10-12 примеров -4, 6-9 примеров-3).
5.Вопросы и ответы (5 мин.).
6.Выставление оценок (1мин.).
7.Домашнее задание (1мин. ).
Дать домашнее задание тем учащимся, которые получили оценки ниже «5».
№ 1491(а, б, в, д, е, з).

---

Слайд 3Текст слайда:

Приложение №1 Математическое путешествие по материкам и островам.

Антарктида

Евразия

Северная Америка

Африка

Южная Америка

Австралия

---

Слайд 4Текст слайда:

Приложение №2 1 вариант

1-вопрос

2-вопрос

---

Слайд 5Текст слайда:

Приложение №3 2 вариант

1 вопрос

2 вопрос

---

Слайд 6Текст слайда:

Приложение №4 3 вариант

1 вопрос

2 вопрос

---

Слайд 7Текст слайда:

Приложение №5 4 вариант

2 вопрос

1 вопрос

---

Слайд 8Текст слайда:

Приложение №6 Дополнительный вариант.

---

Слайд 9Текст слайда:

Приложение №7 Физкультминутка

Утром гномы в лес пошли.  (шаг на месте) По дороге гриб нашли. (наклон вперёд, выпрямиться, руки на поясе) А за ним-то раз, два, три - (наклоны туловища из стороны в сторону) Показались ещё три!  (руки вперёд, затем в сторону) И пока грибы срывали,  (наклоны вперёд, руки к полу) Гномы в школу опоздали.  (руки к щекам и покачать головой из стороны в сторону) Побежали, заспешили (бег на месте) И грибы все уронили! (присесть)

---

Слайд 10Текст слайда:

1 вопрос

2 вопрос

Приложение №8
Ответы
1 вариант

---

Слайд 11Текст слайда:

Приложение №9 Ответы 2 вариант

1-вопрос

2-вопрос

---

Слайд 12Текст слайда:

Приложение №10 Ответы 3 вариант

2-вопрос

1-вопрос

---

Слайд 13Текст слайда:

Приложение №11 Ответы 4 вариант

2-вопрос

1-вопрос

---

Слайд 14Текст слайда:

Дополнительный вариант.

Приложение №12
Ответы

---

Слайд 15Текст слайда:

Приложение №13 Вопросы и Ответы 1 вариант

1. Какие страны расположены одновременно на двух материках?
В Африке и Евразии –Египет в Сев. и Южн. Америке- Панама.
2. Я самая длинная и могучая река в мире, как меня зовут?
Нил- в центральной Африке.

---

Слайд 16Текст слайда:

Приложение №14 Вопросы и Ответы 2 вариант

3.Назовите имя острова, который «прыгает».
Кенгуру
4.Что означает название этого «прыгающего» острова?
Не понимаю.
Первые европейцы, увидев это животное, спросили у аборигенов о его названии, те ответили «кенгуру», что означало «не понимаю» . Так в результате недоразумения животное получило свое имя.

---

Слайд 17Текст слайда:

Приложение №15 Вопросы и Ответы 3 вариант

5.Какой остров похож на крокодила?
Остров Куба.
6.Какую страну можно «носить на голове?
Панама.

---

Слайд 18Текст слайда:

Приложение №16 Вопросы и Ответы 4 вариант

8.Народная мудрость гласит- Держи ноги в холоде, а голову в тепле. В какой стране?
Аргентина
9.Какой остров утверждает , что имеет отношение к спортивной одежде?
Я майка

---

Слайд 19Текст слайда:

Приложение №17 Дополнительные вопросы и ответы.

10.Какая страна расположена в двух полушариях и омывается двумя океанами.
Колумбия
11.Самая древняя столица мира?
Дамаск в Сирии.
12.Самый маленький остров?
Ямал.

---

Слайд 20Текст слайда:

Приложение №18 Спасибо за урок.

---

Слайд 21Текст слайда:

Приложение №19 Литература 1.Е. Н. Селищев «География для любознательных, или о чем не узнаешь на уроке» 2. А.С. Чесноков, К.И. Нешков «Дидактические материалы по математике» 6 класс

---

Скачать презентацию

Операции с числами со знаком

Операции с числами со знаком

Операции с подписанными номерами
Дополнение Вычитание     Умножение Подразделение

 

 

Дополнение Правила	Примеры
Когда добавив два числа с одинаковыми знаками, сложите значения и сохраните общее знак.	1. (+3) + (+5) = + 8 2. 4 + 6 = 10 3.  (-3) + (-5) = — 8 4.   — 4 + (- 6 ) = -10
Когда сложив два числа с разными знаками, вычесть значения и использовать знак большего числа.	1. (+3) + (-5) = -2 2. (-3) + (+5) = +2 3. 4 + (- 6 ) = -2 4.   — 4 + 6 = 2
Дополнение Вычитание     Умножение Дивизион верх
Вычитание Правила	Примеры
Изменить оператор вычитания для сложения и изменения знака числа что сразу следует. Соблюдайте правила добавления изложенные выше. (т.е. добавить противоположное)	1. (+3) — (-5) =     (+3) + (+5) = 8 2. (-3) — (+5) =      (-3) + (-5) = — 8 3. 4 — (- 6 ) =         4 + (+ 6 ) = 10 4.   — 4 — 6 =       — 4 + (- 6) = — 10
Дополнение Вычитание     Умножение Дивизион верх
Умножение Правила	Примеры
Когда при умножении двух чисел с одинаковым знаком произведение положительно.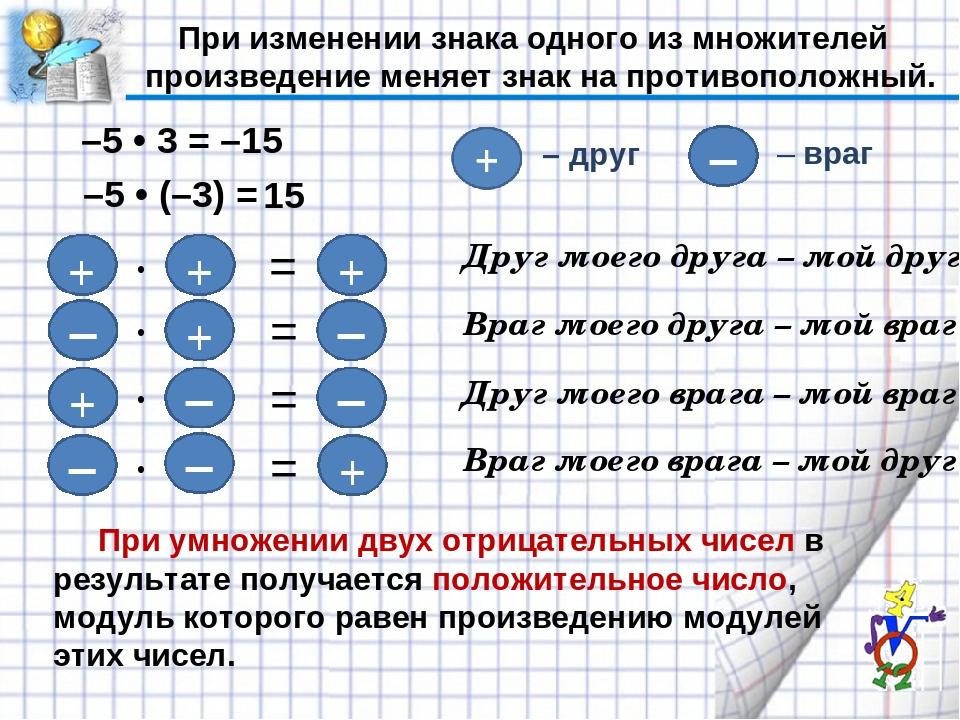 (+)(+) = +        (-)(-) = +	1. (+3) (+5) = +15 2.  (4)( 6) = 24 3.  (-3) + (-5) = +15 4.  — 4(- 6 ) = 24
Когда при умножении двух чисел с разными знаками произведение отрицательно. (+)(-) = —          (-)(+) = —	1. (+3) (-5) = -15 2. 4 (-6 ) = 24 3. (-3) (+5) = -15 4.   — 4 ( 6 ) = -24
Дополнение Вычитание     Умножение Подразделение верх
Отдел Правила	Примеры
Когда при делении двух чисел с одинаковым знаком частное положительно. (+)/(+) = +          (-)/(-) = +	1. (+3) (+5) = +15 2.  (4)( 6) = 24 3. (-3) + (-5) = +15 4.  — 4(- 6 ) = 24
Когда разделяющий два числа с разными знаками частное отрицательно. (+)/(-) = —          (-)/(+) = —	1. (+15) / (-5) = -3 2. 24 / (-6 ) = 4 3. (-15) /(+3) = -5 4. — 24 /( 6 ) = -4
Примечание : Правила деления такие же, как и правила умножения.
Дополнение Вычитание     Умножение Подразделение верх

Числовой ряд и сложение, вычитание, умножение и деление

Автор: Марк Зегарелли и

Обновлено: 26 марта 2016 г.

Базовая математика и предварительная алгебра для чайников

Книга 9036

Числовая строка — это просто строка с числами, отмеченными через равные промежутки времени. Вы, вероятно, увидели свой первый числовой ряд, когда учились считать до десяти. Вы можете использовать этот надежный инструмент для выполнения операций Большой четверки (сложение, вычитание, умножение и деление) над относительно небольшими числами.

Числовая строка может быть полезным инструментом для сложения и вычитания небольших чисел:

• При сложении переместите вверх по числовой строке вправо.

• При вычитании переместите вниз по числовой строке влево.

Чтобы умножить на числовой прямой, начните с 0 и посчитайте первое число в задаче столько раз, сколько указано вторым числом .

Чтобы разделить на числовой прямой, сначала заблокируйте сегмент числовой строки от 0 до первый номер в задаче. Затем разделите этот отрезок поровну на количество частей, указанное вторым числом . Длина каждой части — это ответ на деление.

Примеры вопросов

1. Добавьте 6 + 7 в числовой строке.

   13. Выражение 6 + 7 означает, что начинается с 6, до 7, , что приводит к 13.

2. Вычтите 12 – 4 в числовой строке.

   8. Выражение 12 — 4 означает, что начинается с 12, вниз на 4, , что приводит к 8.

3. Умножьте 2 x 5 на числовой прямой.

   10. Начиная с 0, сосчитайте двойками всего пять раз, чтобы получить 10.

4. Разделите 12 / 3 на числовой прямой.

   4. Выделите отрезок числовой прямой от 0 до 12. Теперь разделите этот отрезок поровну на три меньшие части. Каждая из этих частей имеет длину 4, так что это ответ на задачу.

Практические вопросы

1. Добавьте в числовую строку следующие числа:

   а. 4 + 7 = ?

   б. 9 + 8 = ?

   г. 12 + 0 = ?

   д. 4 + 6 + 1 + 5 = ?

2. Вычтите из числовой строки следующие числа:

   а. 10 – 6 = ?

   б. 14 – 9 = ?

   г. 18 – 18 = ?

   д. 9 – 3 + 7 – 2 + 1 = ?

3. Умножьте следующие числа на числовой прямой:

   а. 2 х 7 = ?

   б. 7 х 2 = ?

   г. 4 х 3 = ?

   д. 6 х 1 = ?

   эл. 6 х 0 = ?

   ф. 0 х 10 = ?

4. Разделите следующие числа на числовой прямой:

   а. 8 / 2 = ?

   б. 15/5 = ?

   г. 18/3 = ?

   д. 10/10 = ?

   эл. 7 / 1 = ?

   ф. 0 / 2 = ?

Ответы на практические вопросы следующие:

1. Добавить в числовую строку.

   а. 4 + 7 = 11 . Выражение 4 + 7 означает, что начинается с 4, до 7, , что приводит к 11.

   б. 9 + 8 = 17 . Выражение 9 + 8 означает, что начинается с 9, до 8, , что приводит к 17.

   г. 12 + 0 = 12 . Выражение 12 + 0 означает, что начинается с 12, до 0, , что приводит к 12.

   д. 4 + 6 + 1 + 5 = 16 . Выражение 4 + 6 + 1 + 5 означает, что начинается с 4, до 6, до 1, до 5, , что приводит к 16.

2. Вычитание в числовой строке.

   а. 10 – 6 = 4 . Выражение 10 – 6 означает, что начинается с 10, уменьшается на 6, , что приводит к 4.

   б. 14 – 9 = 5 . Выражение 14 – 9 означает, что начинается с 14, вниз на 9, , что приводит к 5.

   г. 18 –18 = 0 . Выражение 18 – 18 означает, что начинается с 18, уменьшается на 18, , что приводит к 0,

   д. 9 – 3 + 7 – 2 + 1 = 12 . Выражение 9 – 3 + 7 – 2 + 1 означает, что начинается с 9, вниз 3, вверх 7, вниз 2, вверх 1, , что приводит к 12.

3. Умножение на числовом ряду.

   а. 2 х 7 = 14 . Начиная с 0, посчитайте двойками семь раз, в результате чего вы получите 14.

   б. 7 х 2 = 14 . Начиная с 0, сосчитайте по семеркам два раза, в результате чего вы получите 14.

   г. 4 х 3 = 12 . Начиная с 0, посчитайте по четыре в общей сложности три раза, что приведет вас к 12.

   д. 6 х 1 = 6 . Начиная с 0, сосчитайте до шести один раз, и вы получите 6.

   эл. 6 х 0 = 0 . Начиная с 0, сосчитайте по шесть ноль раз, что приведет к 0.

   ф. 0 х 10 = 0 . Начиная с 0, сосчитайте нулями десять раз, чтобы получить 0.

4. Разделить по числовой прямой.

   а. 8 / 2 = 4 . Заблокируйте отрезок числовой прямой от 0 до 8. Теперь разделите этот отрезок поровну на две меньшие части. Каждая из этих частей имеет длину 4, так что это ответ на задачу.

   б. 15/5 = 3 . Заблокируйте отрезок числовой прямой от 0 до 15. Разделите этот отрезок поровну на пять меньших частей. Каждая из этих частей имеет длину 3, так что это ответ на задачу.

   г. 18/3 = 6 . Заблокируйте отрезок числовой прямой от 0 до 18 и разделите этот отрезок поровну на три меньшие части. Каждая часть имеет длину 6, ответ на задачу.

   д. 10/10 = 1 . Заблокируйте отрезок числовой прямой от 0 до 10 и разделите этот отрезок поровну на десять меньших частей. Каждая из этих частей имеет длину 1,

   эл. 7 / 1 = 7 . Отгородите отрезок числовой прямой от 0 до 7 и разделите этот отрезок поровну на 1 часть (то есть вообще не делите). Этот кусок по-прежнему имеет длину 7.

   ф. 0 / 2 = 0 . Заблокируйте отрезок числовой прямой от 0 до 0. Длина этого отрезка равна 0, поэтому он не может быть меньше. Это показывает вам, что 0 разделить на любое число равно 0.

Об этой статье

Эту статью можно найти в категории:

• Базовая математика,

Базовое сложение, вычитание, умножение и деление

Все математические ресурсы верхнего уровня SSAT

6 диагностических тестов 311 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

Справка по математике верхнего уровня SSAT » Понятия и операции с числами » Основное сложение, вычитание, умножение и деление

Какова сумма двух процентов в десятичной форме?

7 процентов и 135 процентов

Возможные ответы:

Правильный ответ:

Объяснение:

Сложите проценты и получите 142 процента. Чтобы преобразовать проценты в десятичные числа, вы делите на 100, поэтому ответ равен 1,42.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Выполните выражение в скобках, и вы получите . Затем вы делаете  и получаете . Затем вы делаете  и получаете . Потом добавляешь.

Сообщить об ошибке

Если Сюзи купила пару туфель за , рубашку за и пару брюк за . Сколько всего она потратила?

Возможные ответы:

Правильный ответ:

Объяснение:

Сложите все три значения и получите .

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала преобразуйте в десятичное число.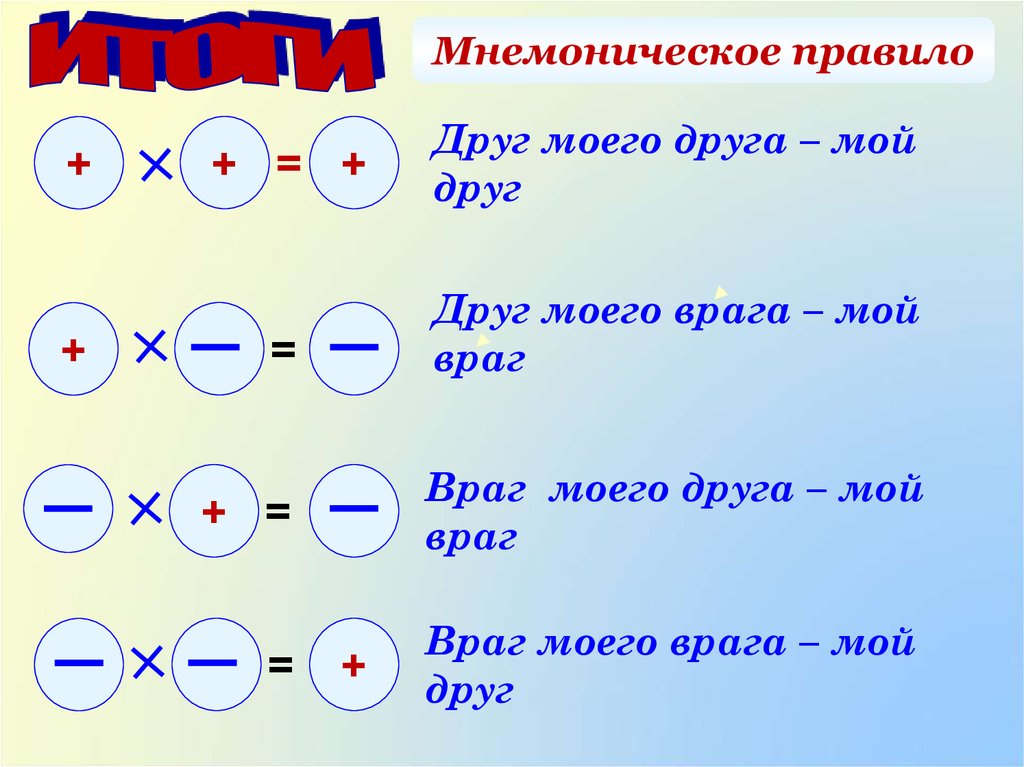 У нас осталось

Теперь сложите три числа, стараясь точно выровнять десятичные точки. Складываем справа налево:

1) 4 и 5 = 9

2) 5, 2 и 2 = 9

3) 2 стоит одна = 2

Остается 2,99 для окончательного ответа.

Сообщить об ошибке

 и  являются простыми целыми числами:  и . Сколько возможных значений  есть?

Возможные ответы:

Восемь

Пять

Семь

Шесть

Четыре

Пять 7 7 Пояснение:

 может быть равно любому из простых чисел от 45 до 55, из которых два — 47 или 53.

 может быть равно любому из простых чисел от 15 до 25, из которых три — 17, 19, и 23.

Их сумма может быть любой из следующих:

Это дает пять возможных сумм.

Сообщить об ошибке

 и  являются простыми целыми числами.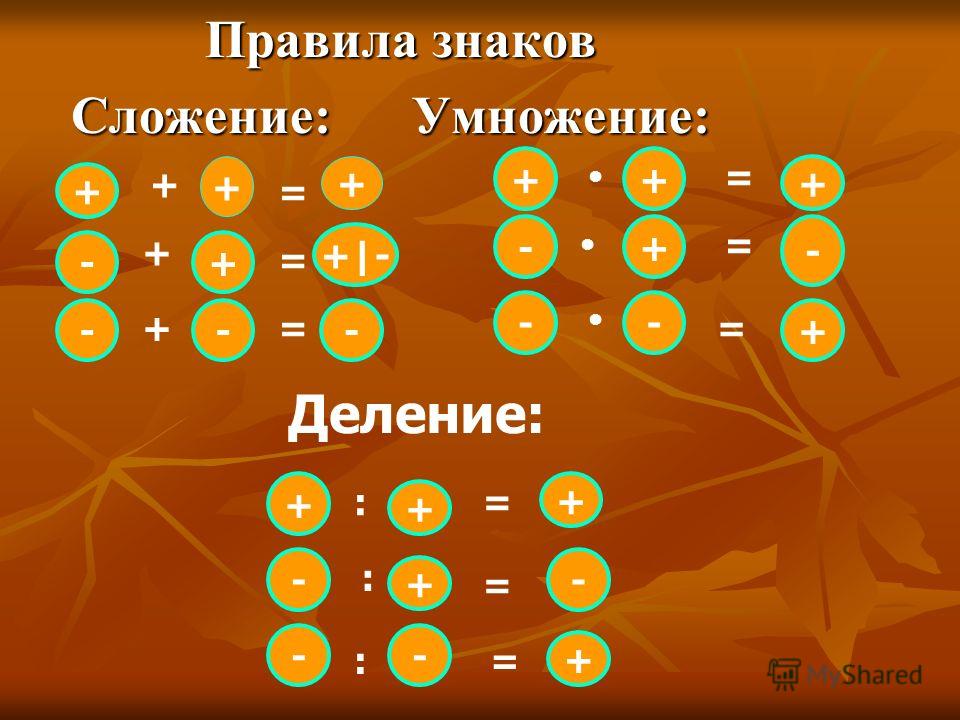 а также . Каково максимально возможное значение  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти максимально возможное значение , прибавьте максимально возможное значение к максимально возможному значению . Это происходит, когда  равно наибольшему простому числу между 35 и 45, то есть 43, и когда  равно наибольшему простому числу между 85 и 9.5, что равно 89. Сложите два числа:

Сообщить об ошибке

В соревновании по математике команда школы Линкольн Хай состояла из пяти учащихся: Мелани, Неда, Оливии, Филлис и Куинн. Мелани опередила Неда на 12 очков; Нед опередил Куинна на 19 очков; Филлис опередила Неда на 45 очков и Оливию на 20 очков. Кто занял третье место среди пятерки?

Возможные ответы:

Нед

Филлис

Куинн

Мелани

Оливия

Правильный ответ:

Мелани

Объяснение:

Поскольку это рассуждение справедливо независимо от фактических результатов, предположим, что Куинн набрала 100 баллов. Тогда Нед набрал на 19 баллов больше, чем Куинн, или 119, а Мелани набрала на 12 баллов больше, чем Нед, или 131. Филлис набрала на 45 баллов больше, чем Нед, или 164, а Оливия набрала на 20 очков меньше, чем Филлис, или 144. Получается порядок от большего к меньшему:

Филлис, Оливия, Мелани, Нед, Куинн

Мелани заняла третье место среди пяти.

Сообщить об ошибке

Какой из следующих углов является дополнительным к углу, равному 45 градусам?

Возможные ответы:

Правильный ответ:

Пояснение:

Дополнительные углы в сумме дают 180 градусов. Учитывая это , правильный ответ – 135. 

Сообщить об ошибке

  

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте порядок операций, чтобы сначала выполнить операцию в скобках, что даст вам .