Случайная величина x задана функцией распределения f x найти плотность: Плотность распределения непрерывной случайной величины. Теория вероятностей

Плотность распределения вероятностей — f(x)

Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так .

Плотностью вероятностей случайной величины называют первую производную от интегральной функции распределения вероятностей

откуда дифференциал

Поскольку прирост определяют зависимости

куплена плотности вероятностей на прирост случайной величины соответствует вероятность того, что случайная величина содержаться в промежутке где .

Геометрически на графике плотности вероятностей соответствует площадь прямоугольника с основанием и высотой

Свойства плотности вероятностей

1. Плотность вероятностей принимает положительные значения . Это свойство следует из определения первой производной от функции распределения , которая в свою очередь является неубывающей функцией.

2. Условие нормирования случайной величины

3.Вероятность попадания случайной величины в промежуток определяется зависимостью

4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием

—————————————

Рассмотрим задачи для закрепления материала на практике.

Пример 1. Закон распределения случайной величины заданы функцией

Найти плотность распределения вероятностей и построить графики обеих функций . Вычислить вероятность того, что случайная величина принадлежит промежутку

Решение. Вычисляем функцию плотности вероятностей

Графики функций изображены на рисунках

 

 

Вероятность события вычислим по формуле

Согласно приведенной выше формулы получим

На этом задача решена.

———————————————

Пример 2. По заданной функцией плотности распределения вероятностей

установить параметры и функцию распределения вероятностей . Построить графики функций.

Решение. Значение постоянной определяем из условия нормировки

При найденном значении плотность вероятностей будет иметь вид

Функция распределения вероятностей определяется интегрированием:

Записываем общий вид функции ,

Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже

 

 

 

—————————————

Пример 3. Случайная величина имеет закон распределения вероятностей в виде треугольника

Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график и вычислить .

Решение. На промежутках и плотность вероятностей меняется по линейному закону вида

для первого и второго участки соответственно. Для нахождения неизвестных констант установим ординаты вершины треугольника . Используем условие нормирования, согласно которому площадь треугольника равна единице:

При известных координатах всех вершин находим уравнение прямых

Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат , то уравнение прямой которая через эту точку проходит следующее

где – ордината пересечения с осью . Подстановкой второй точки прямой находят неизвестную константу . Для заданных точек получим

Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение

а ее функция примет вид

Функцию распределения вероятностей находим интегрированием:

а) на промежутке :

2) на промежутке

Следовательно, функция распределения вероятностей такая

Ее график приведен ниже

Вычисляем вероятность события согласно формуле

или

Следовательно, вероятность равна

————————-

Хорошо проанализируйте приведенные примеры — это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.

Непрерывная случайная величина, функция распределения и плотность

• Определение непрерывной случайной величины и её связь с вероятностью
• Функция распределения непрерывной случайной величины и плотность вероятности

Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.

Примерами непрерывных случайных величин могут служить: диаметр детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.

Так как для непрерывных случайных величин функция F(x), в отличие от дискретных случайных величин

, нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Это значит, что для непрерывной случайной величины бессмысленно говорить о распределении вероятностей между её значениями: каждое из них имеет нулевую вероятность. Однако в некотором смысле среди значений непрерывной случайной величины есть «более и менее вероятные». Например, вряд ли у кого-либо возникнет сомнение, что значение случайной величины — роста наугад встреченного человека — 170 см — более вероятно, чем 220 см, хотя и одно, и другое значение могут встретиться на практике.

В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.

Итак, функцией распределения случайной величины (как дискретной, так и непрерывной) или интегральной функцией называется функция , которая определяет вероятность, что значение случайной величины X меньше или равно граничному значению х.

Для дискретной случайной величины в точках её значений x1, x2, …, xi,… сосредоточены массы вероятностей p1, p2, …, pi,…, причём сумма всех масс равна 1. Перенесём эту интерпретацию на случай непрерывной случайной величины. Представим себе, что масса, равная 1, не сосредоточена в отдельных точках, а непрерывно «размазана» по оси абсцисс Оx с какой-то неравномерной плотностью. Вероятность попадания случайной величины на любой участок Δ

x будет интерпретироваться как масса, приходящаяся на этот участок, а средняя плотность на этом участке — как отношение массы к длине. Только что мы ввели важное понятие теории вероятностей: плотность распределения.

Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:

.

Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:

вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:

или

.

При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x):

.

График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).

Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.

Свойства функции плотности вероятности непрерывной случайной величины

1. Вероятность того, что случайная величина примет какое-либо значение из интервала (и площадь фигуры, которую ограничивают график функции f(x

) и ось Ох) равна единице:

2. Функция плотности вероятности не может принимать отрицательные значения:

,

а за пределами существования распределения её значение равно нулю

---

Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.

Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.

Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение

C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.

Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.

Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:

Найти функцию f(x) плотности вероятности непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8: .

Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:

График функции F(x) — парабола:

График функции f(x) — прямая:

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:

.

Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:

Вычислить коэффициент C. Найти функцию F(x) распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5: .

Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:

Таким образом, функция плотности вероятности непрерывной случайной величины:

Интегрируя, найдём функцию F(x) распределения вероятностей. Если x < 0, то F(x) = 0. Если 0 < x < 10, то

.

x > 10, то F(x) = 1.

Таким образом, полная запись функции распределения вероятностей:

График функции f(x):

График функции F(x):

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:

.

Пример 3. Плотность вероятности непрерывной случайной величины X задана равенством , при этом . Найти коэффициент А, вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[, функцию распределения непрерывной случайной величины X.

Решение. По условию приходим к равенству

.

Но

Следовательно, , откуда . Итак,

.

Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:

Теперь получим функцию распределения данной случайной величины:

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пример 4. Найти плотность вероятности непрерывной случайной величины X, которая принимает только неотрицательные значения, а её функция распределения .

Решение. По определению плотности вероятности получаем

при и при , поскольку F(x) для этих значений x постоянна (равна нулю).

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пройти тест по теме Теория вероятностей и математическая статистика

Пример 5. Плотность распределения непрерывной случайной величины задана формулой:

(при x > 0)

(a — положительный коэффициент).

1) найти функцию распределения непрерывной случайной величины;

2) найти вероятность того, что непрерывная случайная величина примет значение, лежащее между 1 и 2.

Решение.

1) При x < 0 f(x) = 0, значит . При x > 0 . Первый интеграл равен нулю. Второй . Итак, функция распределения данной непрерывной случайной величины имеет вид:

2) вероятность попадания непрерывной случайной величины на участок между 1 и 2 вычислим как приращение функции распределения на этом участке:

Пример 6. Непрерывная случайная величина имеет плотность

при .

1) найти вероятность попадания непрерывной случайной величины на участок от 0 до π/4;

2) функцию распределения непрерывной случайной величины.

Решение.

1) находим вероятность:

.

2) находим функцию распределения непрерывной случайной величины:

Пример 7. Плотность распределения непрерывной случайной величины задана формулой

.

Найти вероятность попадания непрерывной случайной величины на участок (-1; +1)

Решение.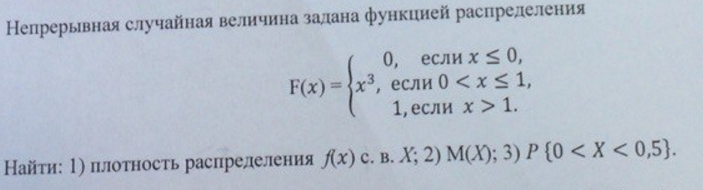

.

Назад

Листать

Вперёд>>>

Пройти тест по теме Теория вероятностей и математическая статистика

К началу страницы

Начало темы «Теория вероятностей»

Действия над вероятностями

Различные задачи на сложение и умножение вероятностей

Формула полной вероятности

Формула Байеса

Независимые испытания и формула Бернулли

Распределение вероятностей дискретной случайной величины

Математическое ожидание и дисперсия случайной величины

Биномиальное распределение дискретной случайной величины

Распределение Пуассона дискретной случайной величины

Равномерное распределение непрерывной случайной величины

Нормальное распределение непрерывной случайной величины

Функция плотности вероятности | PDF

← предыдущая

следующая →

---

Чтобы определить распределение дискретной случайной величины, мы можем указать ее PMF или CDF. Для непрерывные случайные величины, CDF четко определен, поэтому мы можем предоставить CDF. Тем не менее, PMF делает не работают для непрерывных случайных величин, потому что для непрерывной случайной величины $P(X=x)=0$ для всех $x \in \mathbb{R}$. Вместо этого мы обычно можем определить функцию плотности вероятности (PDF) 9+} \frac{P(x

Таким образом, у нас есть следующее определение PDF непрерывных случайных величин:

Определение
Рассмотрим непрерывную случайную величину $X$ с абсолютно непрерывной CDF $F_X(x)$. Функция $f_X(x)$, определяемая формулой $$f_X(x)=\frac{dF_X(x)}{dx}=F’_X(x), \hspace{20pt} \textrm{если }F_X(x) \textrm{ дифференцируемо в }x$$ называется функцией плотности вероятности (PDF) $X$.

Найдем PDF равномерной случайной величины $X$, обсуждавшейся в Пример 4.1. Этот случайный Говорят, что переменная имеет распределение $Uniform(a,b)$. Функция CDF $X$ представлена ​​в уравнении 4.1. Взяв производная, получаем \begin{уравнение} f_X(x) = \слева\{ \begin{массив}{л л} \frac{1}{b-a} & \quad a b \end{массив} \right. \end{уравнение} Заметим, что CDF не дифференцируема в точках $a$ и $b$. Тем не менее, как мы обсудим позже, это не важно. На рис. 4.2 показана плотность вероятности $X$. Как видим, значение PDF постоянно в интервал от $a$ до $b$. Вот почему мы говорим, что $X$ равномерно распределено по $[a,b]$.

Рис.4.2 — PDF для непрерывной случайной величины, равномерно распределенной по $[a,b]$.

Равномерное распределение — это простейшая непрерывная случайная величина, которую вы можете себе представить. Для других типов непрерывных случайных величин PDF неравномерна. Обратите внимание, что для малых значений $\delta$ мы можем написать $$P(x f_X(x_2)$, мы можем сказать $P(x_1 P(x_2)

---

Поскольку PDF является производной CDF, CDF может быть получен из PDF путем интегрирования (при условии абсолютной непрерывности): $$F_X(x)=\int_{-\infty}^{x} f_X(u)du. $$ Кроме того, у нас есть $$P(а 9{-x} & \quad x \geq 0\\ 0 & \quad \text{иначе} \end{массив} \right. \end{уравнение} где $c$ — положительная константа.

1. Найдите $c$.
2. Найдите CDF для X, $F_X(x)$.
3. Найти $P(1)

• Решение

---

Диапазон

Диапазон случайной величины $X$ — это множество возможных значений случайной величины. Если $X$ является непрерывной случайной величиной, мы можем определить диапазон $X$ как множество действительных чисел $x$, для которых PDF больше нуля, т.е. $$R_X=\{х | f_X(x)>0\}.$$ Набор $R_X$, определенный здесь, может не точно отображать все возможные значения $X$, но разница практически неважно. 9\alpha}\,dx = \begin{case} \infty,& 0<\alpha\leq 1 \\ \frac{\alpha x_0}{\alpha-1},& \alpha > 1 \end{cases}$$

Чаевые: В то время как функция распределения должна быть определена на всей $\mathbb{R}$, функция плотности вероятности не должна быть определена на всей $\mathbb{R}$, но она все же должна быть определена почти везде на $\mathbb{R}$.

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

	$$f_X(x)=\lim_{\Delta \rightarrow 0} \frac{F_X(x+\Delta)-F_X(x)}{\Delta}$$
	$$=\frac{dF_X(x)}{dx}=F’_X(x), \hspace{20pt} \textrm{если }F_X(x) \textrm{ дифференцируемо в }x.$$