Cредняя линия треугольника, средняя линия трапеции. Средняя линия трапеции Средняя линия трапеции атанасян презентация
Определение: средней линией треугольника называется отрезок, соединяющий середины двух его сторон. АК = КС ВЕ = СЕ КЕ – средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины боковых её сторон. А ВС К Н Е АН = НВ КЕ = СЕ НЕ – средняя линия АВСК А В С К Е Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
Средняя линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А С В М К Дано: АВС, МК – средняя линия Доказательство: Т. к. по условию МК – средняя линия, то АМ = МВ = ½ АВ, СК = КВ = ½ ВС, Значит, ВМ АВ ВК ВС 1 2 В – общий для АВС и МВК, значит, АВС и МВК подобны по второму признаку подобия, следовательно, ВМК = А, значит, МК АС. Доказать: МК АС, МК = ½ АС МК АС 1 2 Из подобия треугольников также следует, что, т. е. МК = ½ АС.
Реши задачу F R N ? А В
Доказательство: Проведём А 1 В 1 А В С А1А1 В1В1 О С1С1 По условию АА 1, ВВ 1 – медианы значит, ВА 1 = СА 1, АВ 1 = СВ 1, т. е. А 1 В 1 – средняя линия. Значит, А 1 В 1 АВ, поэтому 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны по двум углам. Значит, их стороны пропорциональны: АО ВО АВ А1ОА1О В1ОВ1О А1В1А1В1 По свойству средней линии треугольника АВ = 2 А 1 В 1, т. е. АО ВО АВ А1ОА1О В1ОВ1О А1В1А1В1 2 1 Аналогично, СО С1ОС1О 2 1 Получим: С1ОС1О АОВОСО А1ОА1ОВ1ОВ1О 2 1
Средняя линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме. А В С К М Р Дано: АВСК – трапеция МР – средняя линия Доказать: МР АК, МР ВС МР = Доказательство: О Проведём через точку М прямую МЕ АК, докажем, что МЕ пройдёт через Р. Т. к. АВСК – трапеция, то ВС АК, а, значит, ВС МЕ АК Т. к. МР – средняя линия, то АМ= МВ, КР = СР Е Следовательно, МР лежит на МЕ, значит, МР АК, МР ВС.
«Урок площадь трапеции» — В прямоугольной трапеции основания 5см. и 17см., а меньшая боковая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто получил 5, 4, 3 балла? В каждом случае формулируют теорему, которую доказали. Решение поставленной задачи. Как вычислить площадь трапеции? Какие элементы плоских фигур используются в формулах площадей?
«Задачи на теорему Пифагора» — №21 Найти: Х. №18 Найти: Х. №27 Найти: Х. Задачи на готовых чертежах («Теорема Пифагора»). №23 Найти: Х. №25 Найти: Х. №26 Найти: Х. №13 Найти: Х. №20 Найти: Х. №19 Найти: Х. №14 Найти: Х. Вы справились со всеми предложенными заданиями. №29 Найти: Х. №28 Найти: Х. №30 Найти: Х. №22 Найти: Х.
«Теорема Фалеса» — Фалес широко известен как геометр. Астрономия. Милетский материалист.
«Теорема синусов» — Стороны треугольника пропорциональны синусам противолежащих углов. Решение: Устная работа: Ответы к задачам по чертежам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:
«Урок теорема Пифагора» — Определить вид треугольника: Знакомства с теоремой. Доказательство теоремы. Разминка. Теорема Пифагора. И обрете лестницу долготою 125стоп. План урока: Исторический экскурс. Показ картинок. Решение простейших задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить вид четырехугольника KMNP.
«Теорема Пифагора 8 класс» — ФИГУРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катеты с- гипотенуза.
краткое содержание других презентаций
«Построение правильных многоугольников» — ?=60?. ·180?. Геометрия. ?=. n. n — 2. Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
«Теорема Фалеса» — Теорема Фалеса. Именем Фалеса названа геометрическая теорема. Астрономия. Проведем через точку В2 прямую ЕF, параллельную прямой А1А3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии Ученицы 9 «А» класса Сорогиной Полины. Милетский материалист. Геометрия. По свойству параллелограмма А1А2=FВ2, А2А3=В2Е. Фалес широко известен как геометр. И так как А1А2=А2А3, то FВ2=В2Е.
«Разложение вектора по двум неколлинеарным» — Пусть р коллинеарен b . Доказательство: Разложение вектора по двум неколлинеарным векторам.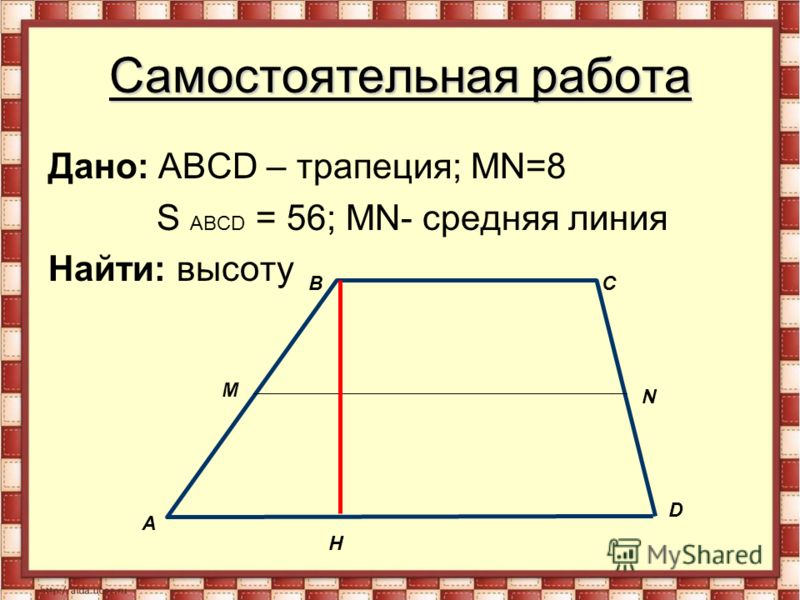 Доказательство: Пусть а и b — неколлинеарные векторы. Лемма: Если векторы а и b коллинеарны и а? 0, то существует такое число k, что b = ka. Докажем, что любой вектор р можно разложить по векторам а и b. Геометрия 9 класс. Тогда р = уb , где у – некоторое число.
Доказательство: Пусть а и b — неколлинеарные векторы. Лемма: Если векторы а и b коллинеарны и а? 0, то существует такое число k, что b = ka. Докажем, что любой вектор р можно разложить по векторам а и b. Геометрия 9 класс. Тогда р = уb , где у – некоторое число.
«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе. Луковникова Н.М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 г.Томск-2007. Правильные многоугольники.
«Симметрия фигур» — Прямая а называется осью симметрии фигуры. D. Одна фигура получена из другой преобразованием. Оглавление. Преобразование, обратное движению, также является движением. А1. Выполнил:Пантюков Е. А. Существует множество различных видов симметрии. М1. Преобразование фигур.
«Симметрия относительно прямой» — Фигура может иметь одну или несколько осей симметрии. Симметрия в природе. Савченко Миша, 9В класс. Угол. Кто же изображен на фотографии оригинале? Л.С. Атанасян «Геометрия 7-9». Равнобедренная трапеция.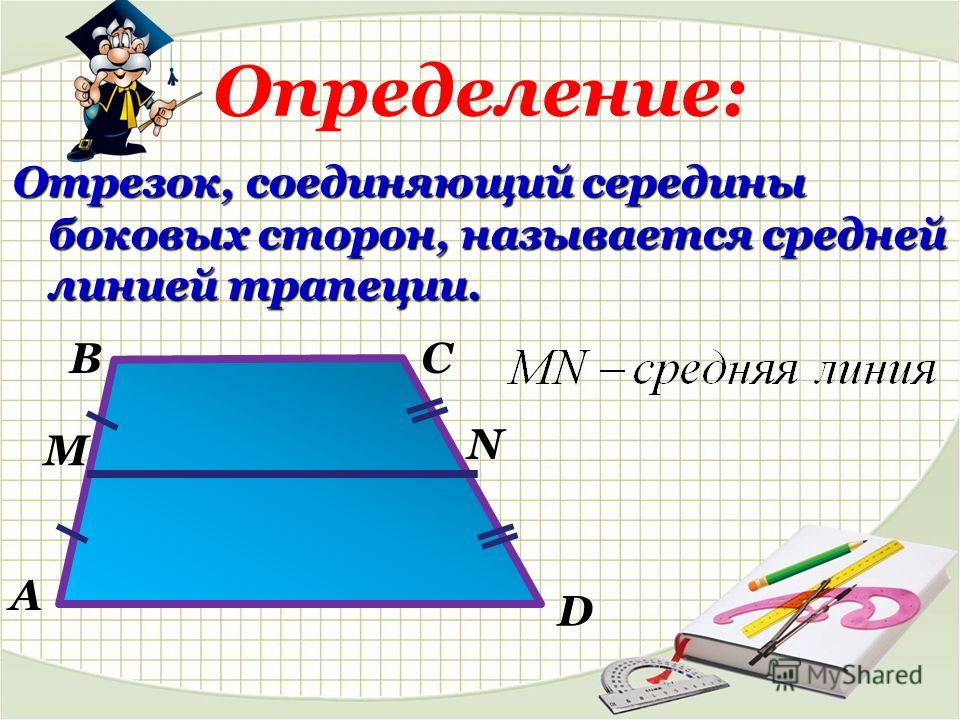 Построить отрезок А1В1 симметричный отрезку АВ относительно прямой. Сколько осей симметрии имеет каждая фигура? Прямоугольник.
Построить отрезок А1В1 симметричный отрезку АВ относительно прямой. Сколько осей симметрии имеет каждая фигура? Прямоугольник.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Средняя линия (8 класс)
Средняя линия треугольника
Средняя линия треугольника. Определение: Отрезок, соединяющий середины двух сторон треугольника, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. т.е.: КМ ║ АС КМ = ½ АС A B C K M
Решить задачу устно: A B C K M 7 см Дано: M К – сред. линия Найти: АС?
Работа в парах:
Решим задачу: Дано: MN – сред. линия Найти: P ∆ АВС M N A B C 3 4 3, 5
Работа в парах:
Средняя линия трапеции
Вспомним: Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны A D B C BC || AD — основания AB łł CD – боковые стороны
Средняя линия трапеции. Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. A D B C M N MN – средняя линия трапеции ABCD
Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. A D B C M N MN – средняя линия трапеции ABCD
Теорема о средней линии трапеции Средняя линия трапеции параллельна её основаниям и равна их полусумме. т.е.: М N ║ВС║А D М N = ½ (ВС+А D) M N A D B C
Решить устно: M N A D B C 6,3 см 18,7 см?
Решить устно в парах: Дано: AB = 16 см; CD = 1 8 см; М N = 15 см Найти: P ABCD = ? M N A D B C
Самостоятельная работа Задача: Средняя линия трапеции равна 5 см. Найти основания трапеции, если известно, что нижнее основание больше верхнего основания в 1,5 раз. Решение: A D B C 5 см Пусть BC = Х см тогда AD = 1.5X см BC+AD = 10 см X + 1.5X = 10 X = 4 Значит: BC = 4 см AD = 6 см
СПАСИБО ЗА УРОК!!!
Презентация разработана учителем математики ГБОУ СОШ №467 Г. Санкт-Петербурга, Колпинского района Лугвиной Натальей Анатольевной
По теме: методические разработки, презентации и конспекты
Урок обобщения и закрепления знаний по теме «Средняя линия треугольника.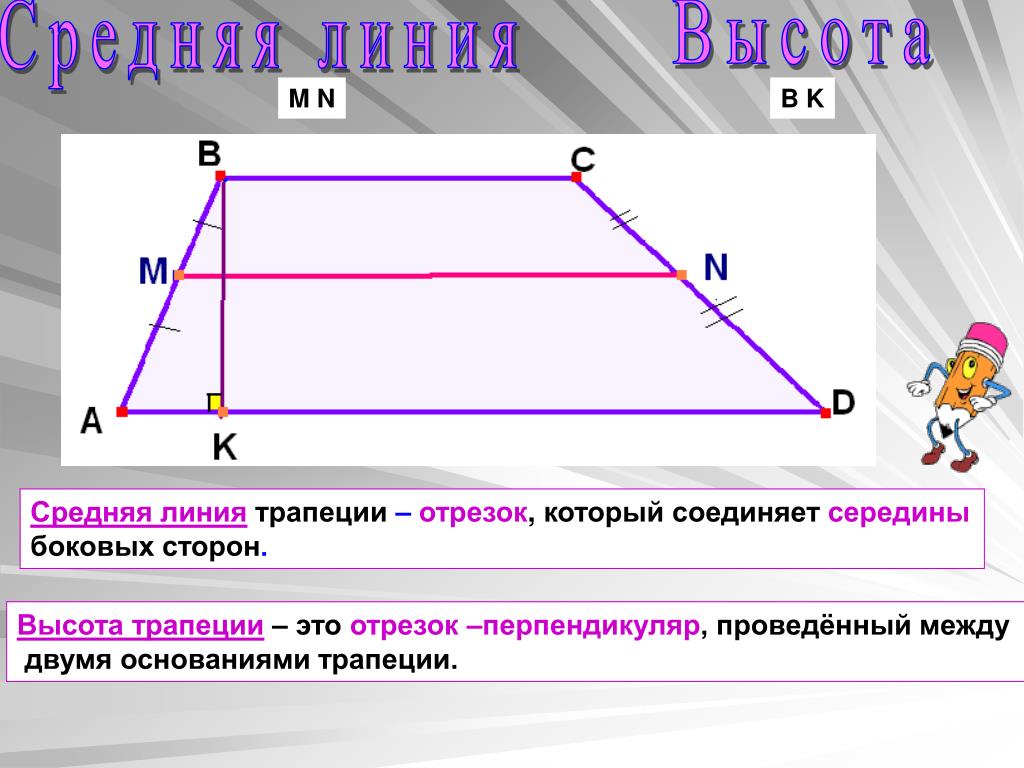 Средняя линия трапеции» в 8 классе с использованием ИКТ….
Средняя линия трапеции» в 8 классе с использованием ИКТ….
Рабочая тетрадь — это индивидуальное творческое задание ученика. которое предполагает самостоятельную работу с текстом по теме «Трапеция. Средняя линия трапеции», применение знаний при решении задач. …
Тема «Средняя линия трапеции» относится к одной из важных тем курса геометрии. Данная фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные этой темы часто встречаются в итоговых контрольных и аттестационных работах. Знание по данной теме могут также пригодиться при обучении в средних и высших заведениях.
Хотя и в теме заявлена фигура трапеция, но рассмотрение данной темы может проходить в период изучения темы «Векторы» и «Применение векторов при решении задач». Это можно понять, глядя на слайд презентации.
Автор здесь определяет среднюю линию, как отрезок, который соединяет середины боковых сторон. Более того, здесь же отмечено, что средняя линия трапеции параллельна ее основаниям, а также равна их полусумме.
слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)
Если внимательно рассмотреть, то в двух случаях получается сложение противоположных векторов, дающих в результате нуль. Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащий основания. Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, равен половине суммы векторов, содержащих основания. Теперь идет сравнение векторов. Получается, что все эти векторы одинаково направленные. Это значит, что знаки векторов можно смело опускать.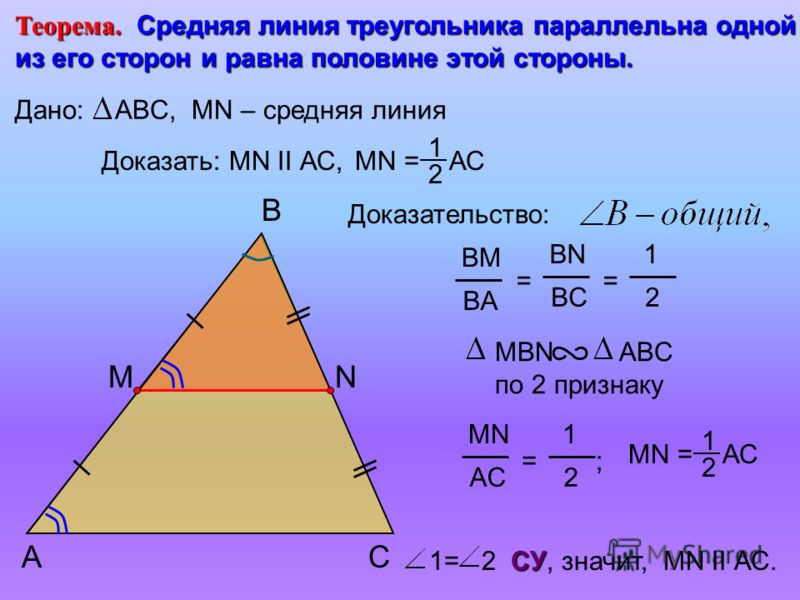
Презентация содержит единственный слайд, который несет в себе большое количество информации. Здесь дано определение средней линии трапеции, а также указано ее основное свойство. В курсе геометрии это свойство является теоремой. Так здесь доказана теорема с использованием знаний понятия векторов и действий над ними.
Учитель может данную презентацию дополнить своими примерами и задачами, но все, что требуется для среднего уровня знаний по данному предмету здесь опубликовано. Более того, так автор оставил возможность учителю пофантазировать, доработать то, что ему самому захочется для того,чтобы создать соответствующую атмосферу на уроке. Не стоит забывать и про сам настрой на урок. Тогда с помощью данной презентации точно можно добиться желаемого результата.
Cредняя линия треугольника, средняя линия трапеции
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Cредняя
линия
треугольн
ика,
средняя
линия
трапеции.
Определение: средней линией треугольника называется
отрезок, соединяющий середины двух его сторон.
С
К
АК = КС
ВЕ = СЕ
Е
А
КЕ – средняя линия
АВС
Сколько средних линий в треугольнике ?
Определение: средней линией трапеции называется
отрезок, соединяющий середины боковых её сторон.
В
Н
А
С
АН = НВ
КЕ = СЕ
Е
К
Сколько средних линий в трапеции ?
НЕ – средняя линия
АВСК
Средняя линия треугольника
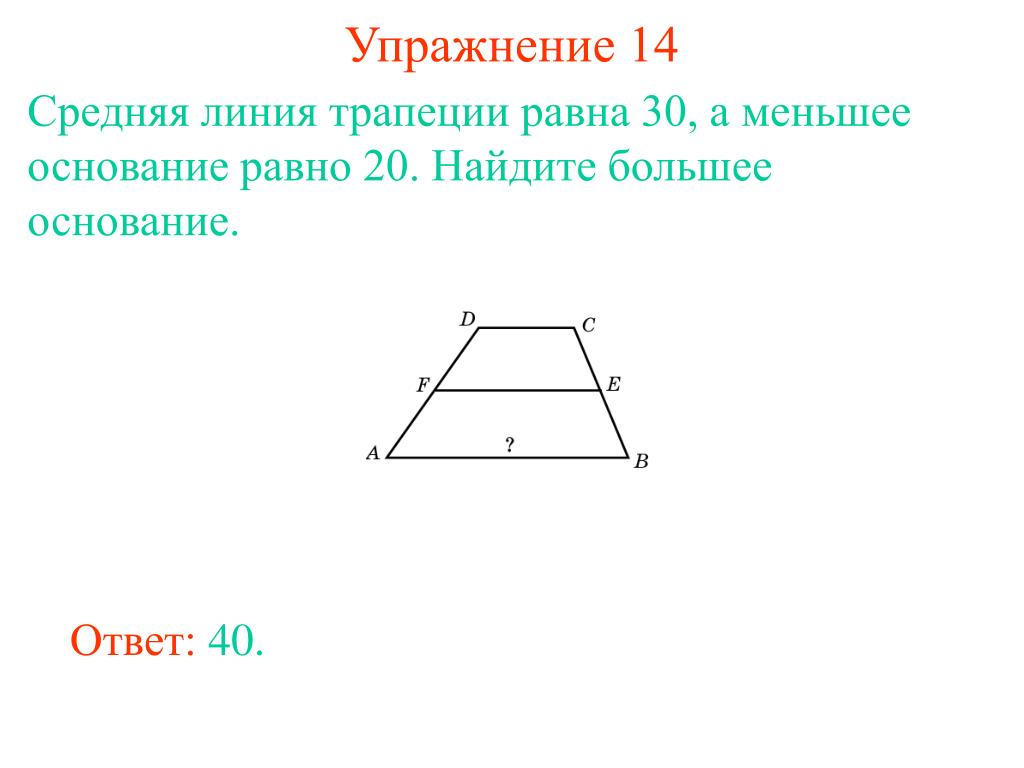
Теорема.
 Средняя линия треугольника параллельна одной из его сторон
Средняя линия треугольника параллельна одной из его сторони равна половине этой стороны.
В
Дано: АВС, МК – средняя линия.
Доказать: МК
М
К
А
Доказательство:
С
ВМ
АС, МК = ½ АС.
Т. к. по условию МК – средняя линия,
то АМ = МВ = ½ АВ, СК = КВ = ½ ВС.
ВК
1
В – общий для АВС и
МВК,
,
2
АВ
ВС
значит, АВС и МВК подобны по второму признаку подобия,
Значит,
следовательно,
ВМК =
А, значит, МК АС.
Из подобия треугольников также следует, что
МК
АС
1
, т. е. МК = ½ АС.
2
Реши задачу
1.
R
А
F
?
В
18
N
Реши задачу
2.
С
К
?
В
2,7
М
А
Реши задачу
3.
А
К
Р
Дано: АВ = 1 дм,
АС = 6 см,
АК = КС,
АР = РВ.
Найти: КР.
С
В
Нужное свойство медиан треугольника
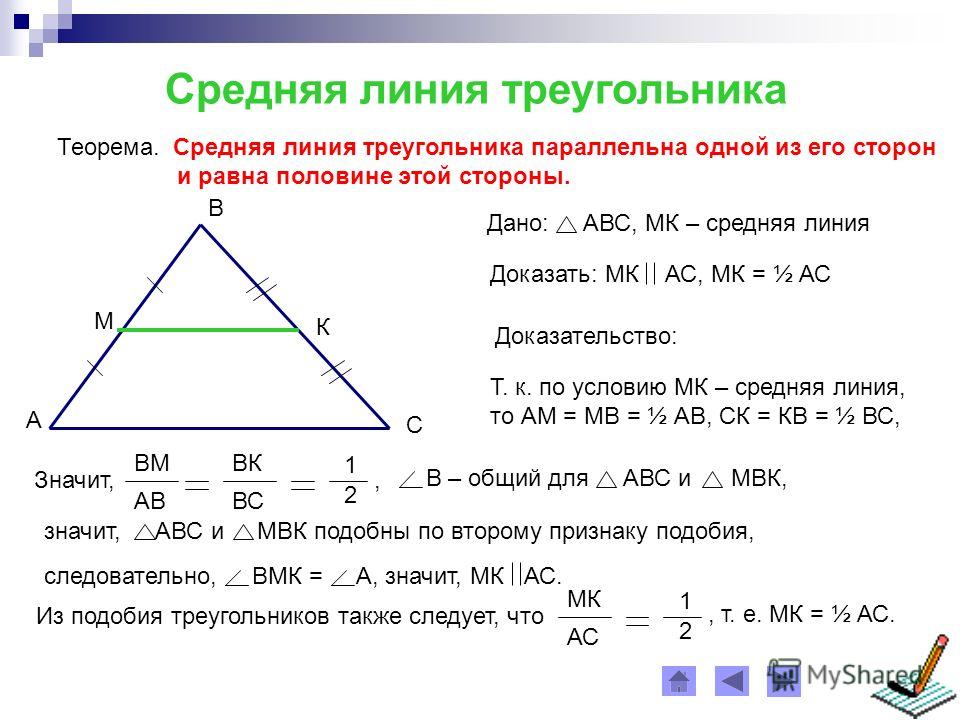
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1,
считая от вершины.
В
А1
С1
С
О
В1
А
Дано: АВС,
АА1, ВВ1, СС1 –
медианы.
АО
А1О
Доказать:
ВО
В1О
СО
С1О
2
1
Доказательство:
С
Проведём А1В1.
В1
4
3
1
А
А1
2
О
По условию АА1, ВВ1 – медианы значит,
С1
ВА1 = СА1, АВ1= СВ1, т. е. А1В1 – средняя линия.
В
Значит, А1В1 АВ, поэтому
1=
2,
3=
4.
Следовательно, треугольники АОВ и А1ОВ1 подобны по двум углам.
Значит, их стороны пропорциональны:
АО
А1О
ВО
В1О
По свойству средней линии треугольника АВ = 2 А1В1 , т. е.
АО
А1О
ВО
В1О
Аналогично,
Получим:
СО
С1О
АО
А1О
АВ
А1В1
2
1
ВО
В1О
2
1
СО
С1О
2
1
АВ
А1В1
Средняя линия трапеции
Теорема. Средняя линия трапеции параллельна основаниям
и равна их полусумме.
В
Дано: АВСК – трапеция,
МР – средняя линия.
С
Р
М
Е
Доказать: МР
АК, МР
О
МР =
К
А
Проведём через точку М прямую МЕ
Т.
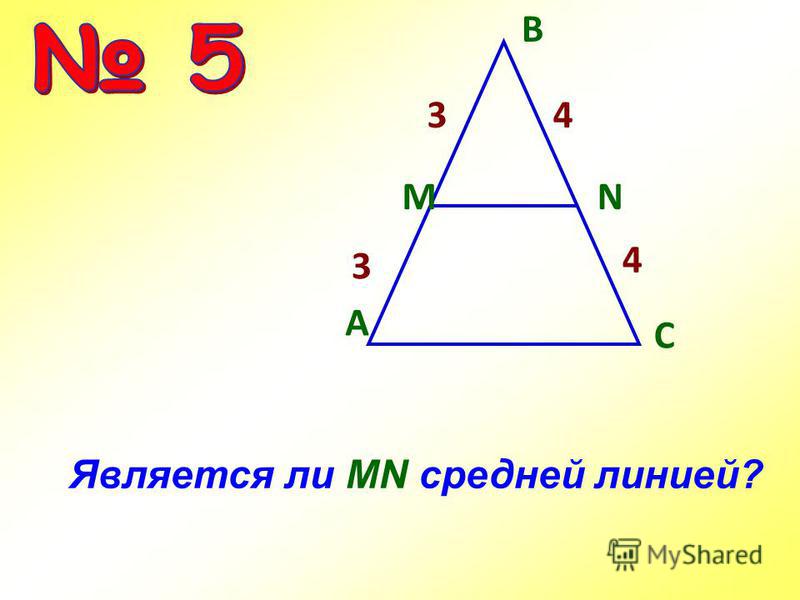 к. АВСК – трапеция, то ВС
к. АВСК – трапеция, то ВСДоказательство:
AK BC
2
АК, докажем, что МЕ пройдёт через Р.
АК, а, значит, ВС
МЕ
АК.
Т. к. МР – средняя линия, то АМ= МВ, КР = СР.
Следовательно, МР лежит на МЕ, значит, МР АК, МР ВС.
Проведём ВК. По теореме Фалеса О – середина ВК, значит,
МО – средняя линия
ВС,
АВК, ОР – средняя линия
ВСК.
AK BC
МР = МО + ОР = ½ АК + ½ ВС = ½ ( АК + ВС) =
2
По теореме Фалеса
МЕ пересечёт СК
в середине СК,
т. е. в точке Р.
Реши задачу
Найти длину средней линии ОЕ трапеции АВСК
по данным на чертеже:
В
7
О
А
С
Е
15
К
Реши задачу
Найти длину верхнего основания трапеции
УСРН по данным на чертеже:
С
Р
9
А
У
В
4
Н
Реши задачу
Найти площадь трапеции УСРН по данным на
чертеже:
К
С
Р
6
9
А
У
В
Н
Решение задачи
B ромбе АBСD О- точка пересечения диагоналей, Е и F — середины
сторон ВС и DС.
 Докажите, что ЕF = ВО, ЕF АС
Докажите, что ЕF = ВО, ЕF АСДано:
E
АВСD — ромб,
B
C
О– точка пересечения диагоналей,
Е — середина ВС,
F
F — середина DС.
O
Доказать:
ЕF = ВО, ЕF АС.
A
D
Доказательство:
Так как АВСD — ромб, то ВО = ОD = ½ ВD, ВD АС.
Рассмотрим ВСD. Так как Е–середина ВС, F — середина DС,
то ЕF- средняя линия ВСD,
значит, ЕF = ½ ВD, и, следовательно, ЕF = ВО.
Пo свойству средней линии треугольника: ЕF ВD,
a по доказанному ВD
АС, значит, и ЕF
АС, что и т. д.
Михайлова Л. П.
ГОУ ЦО № 173.
English Русский Правила
«Средняя линия треугольника и трапеции»
Урок геометрии в 8-м классе на тему
«Средняя линия треугольника и трапеции»
Цели урока:
Образовательные:
- повторение определений средней линии треугольника и трапеции;
- применение свойств средней линии при решении задач;
- формирование умения анализировать знания о средней линии треугольника и трапеции и приведение их в систему.

Развивающие:
- развитие геометрического мышления обучающихся при решении геометрических задач, интереса к предмету, познавательной и творческой деятельности учащихся, математической речи, памяти, внимания;
- обучение учащихся учиться математике, самостоятельной добыче знаний.
Воспитательные:
- воспитание у учащихся ответственного отношения к учебному труду, воли;
- формирование эмоциональной культуры и культуры общения
Тип урока: у — повторение
Оборудование: листы оценивания, стикеры, плакаты, маркеры, конверты для рефлексии, презентация физминутки.
Просмотр содержимого документа
«»Средняя линия треугольника и трапеции»»
Урок геометрии в 8-м классе на тему
«Средняя линия треугольника и трапеции»
Цели урока:
Образовательные:
повторение определений средней линии треугольника и трапеции;
применение свойств средней линии при решении задач;
формирование умения анализировать знания о средней линии треугольника и трапеции и приведение их в систему.

Развивающие:
развитие геометрического мышления обучающихся при решении геометрических задач, интереса к предмету, познавательной и творческой деятельности учащихся, математической речи, памяти, внимания;
обучение учащихся учиться математике, самостоятельной добыче знаний.
Воспитательные:
Тип урока: у — повторение
Оборудование: листы оценивания, стикеры, плакаты, маркеры, конверты для рефлексии, презентация физминутки.
План урока:
Этап урока | Форма взаимодействия | Время | Идеи 7 модулей 6, 7 |
ПОБУЖДЕНИЕ | У-у | 5 мин | 1,3 |
Эмоциональная атмосфера Мотивация | У-у | 3 мин | Новые подходы в обучении Диалоговое обучение |
Лист самооценивания | У-у | 2 мин | Оценивание |
ПРЕЗЕНТАЦИЯ | У-у | 8 мин | 1,2,3 |
Правила в группах | у-у | 3 мин | Формативное оценивание |
Проверка д\з | У-у | 5 мин | Диалоговое обучение |
ПРИМЕНЕНИЕ | у-у | 24 мин | 1,2,5 |
Инсерт | у | 2 мин | Критическое мышление |
Выполнение проекта | у-у | 5 мин | Саморегуляция |
Защита проекта | у-у | 6 мин | Диалоговое обучение Критическое мышление Работа с одаренными детьми |
Оценивание | у-у У-у | 4 мин | Формативное и суммативное оценивание |
Физминутка | У-у | 2 мин | |
Дифференцированная с. | у-у | 5 мин | Работа с одаренными детьми |
РЕФЛЕКСИЯ | У-у | 8 мин | 1,2,3,5 |
Синквейн | У-у | 2 мин | |
Домашнее задание | У-у | 1 мин | Работа с одаренными детьми |
Оценивание | у | 1 мин | Оценивание |
Ход урока:
Деятельность учителя | Деятельность обучающихся | ||||
1. | |||||
Приветствие учителя Ребята, послушайте, какая тишина! Это в школе начались уроки. Мы не будем тратить время зря, И приступим все к работе. Мы сюда пришли учиться, Не лениться, а трудиться. Работаем старательно, Слушаем внимательно. Мотивация урока. Сегодня мы продолжим путешествие по прекрасной стране Геометрия. Лучше разглядим ее красоту и совершенство. Девизом нашего урока будет: «С любовью к ее величеству — науке геометрии». Для того, чтобы работа каждого была сегодня замечена, я предлагаю вам заполнить лист оценивания. Здесь будут отмечаться ваши оценки за каждый вид работ. Вашу работу буду оценивать я, командир команды и вы сами. В итоге выведите среднюю отметку за урок. | Обучающиеся приветствуют учителя вставанием. Дети настроены на урок. Готовы к получению знаний. Дети заполняют лист в начале урока. | ||||
2. ПРЕЗЕНТАЦИЯ 8’ | |||||
Работа в группах. Сегодня вы будете работать в группах. Поэтому, для того, чтобы ваша совместная работа была плодотворной, необходимо разработать правила, по которым вы будете работать. Давайте обговорим, какие, по-вашему мнению, должны быть правила? | Дети отвечают: каждый в группе обязан работать, соблюдение дисциплины, помогать друг другу, мнение каждого ценно и т.д. Оформляют на листе. Оцениваются с помощью стикеров. Лучшие правила берутся за основу. Распределяют обязанности в группе: таймкипер, секретарь, докладчик, председатель, генерал, новатор. | ||||
Проверка домашнего задания. | |||||
Вопросы учителя | Ответы обучающихся | ||||
Какое определение было задано на повторение? | Определение средней линии треугольника и трапеции | ||||
Как разделить отрезок на несколько равных частей? | с помощью линейки, циркуля, с применением теоремы Фалеса | ||||
Какое значение имеет средняя линия в геометрии? | Зная определение мы можем решать задачи, представить практическое применение линий в строительстве, инженерии | ||||
Какое место в геометрии занимает изучение средней линии? | Изучение средней линии является одной из основных тем, и ее понятие формирует базовые представления о геометрии | ||||
3. | |||||
1.Работа в группе. 10’ Используя материал учебника обучаемые (по методике «Инсерт») выделяют самое главное и составляют презентацию по теме: «Средняя линия треугольника и трапеции» в виде: 1. Разговор с подругой. 2. Статья в научный журнал. 3. Репортаж с урока. 4. Объяснение родителям | Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине. Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. Средняя линия трапеции параллельная основаниям и равна их полусумме. | ||||
2.Защита проекта. | Выступают докладчики от каждой группы. | ||||
3.Оценивание. Оценки заполняются в таблицу учителем | С учетом критериев, которые были разработаны на предыдущем уроке с помощью учителя:
| ||||
№ группы Критерии | 1 группа | 2 группа | 3 группа | 4 группа | |
Содержательность (3 б) | 3 | 3 | 3 | 2 | |
Эстетическое оформление (2 б) | 1 | 1 | 2 | 2 | |
Защита проекта (3 б) | 3 | 2 | 3 | 2 | |
Время (1 б) | 1 | 1 | 1 | 1 | |
Итого мах = 9 б | 8 | 7 | 9 | 7 | |
Дети наклеивают стикеры с пожеланиями. Капитаны команд в листах оценивания отмечают работу каждого в группе. | |||||
4.Физкультминутка. Одолела вас дремота, (Зеваем.) Шевельнуться неохота? Ну-ка, делайте со мною Упражнение такое: Вверх, вниз потянись, (Руки вверх, потянулись.) Окончательно проснись. Руки вытянуть пошире. (Руки в стороны.) Раз, два, три, четыре. Наклониться — три, четыре (Наклоны туловища.) И на месте поскакать. (Прыжки на месте.) На носок, потом на пятку. Все мы делаем зарядку. | Дети выполняют физминутку. Есть пассивные наблюдатели. | ||||
Решение задач по готовым чертежам.
| Решение задач на скорость. Кто первый решит – тот выходит к доске с кратким решением. Работа его оценивается учителем в листе оценивания. | ||||
4.РЕФЛЕКСИЯ 8’ | |||||
1. Выводы. Вот и подошел к концу наш урок. Давайте подведем итоги в виде синквейна по теме. | Дети составляют синквейн по теме средняя линия. Средняя линия Параллельная, делящая Проводится, делит, лежит Средняя линия есть у треугольника и у трапеции. Половина основания | ||||
2. Оценивание. Посчитайте свою среднюю отметку за урок. Поднимите, кто получил сегодня «5», «4», «3». Поставьте свои оценки в дневник. Листы оценивания сдайте командиру команды. Он сдаст их мне. 3. Свое настроение нарисуйте на листке и положите в соответствующий конверт. 4.Домашнее задание: повторить Теорему Пифагора, вопросы с.47, решить № 78. Спасибо за урок! | Сдают листы оценивания командиру команды Рисуют смайлик и кладут в соответствующий конверт. | ||||
Средняя часть трапеции | Облегчение синдрома спешки
CCSS-M-G-CO.C.10
Доказывать теоремы о треугольниках. Теоремы включают: меры внутренних углов треугольника в сумме дают 180°; углы при основании равнобедренных треугольников равны; отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и равен половине длины ; медианы треугольника сходятся в одной точке.
Что вы делаете, когда стандарт на день указывает, что вы хотите, чтобы учащиеся изучали и выясняли самостоятельно?
Я договорился со своим администратором о публикации стандарта процесса на день (Математическая практика) вместо стандарта содержания.
На многих уроках геометрии наши учебные цели включают поиск и использование структуры и поиск и выражение регулярности в повторяющихся рассуждениях .
Мы определили средний сегмент:
Средний сегмент треугольника — это отрезок, концы которого являются серединами двух сторон треугольника.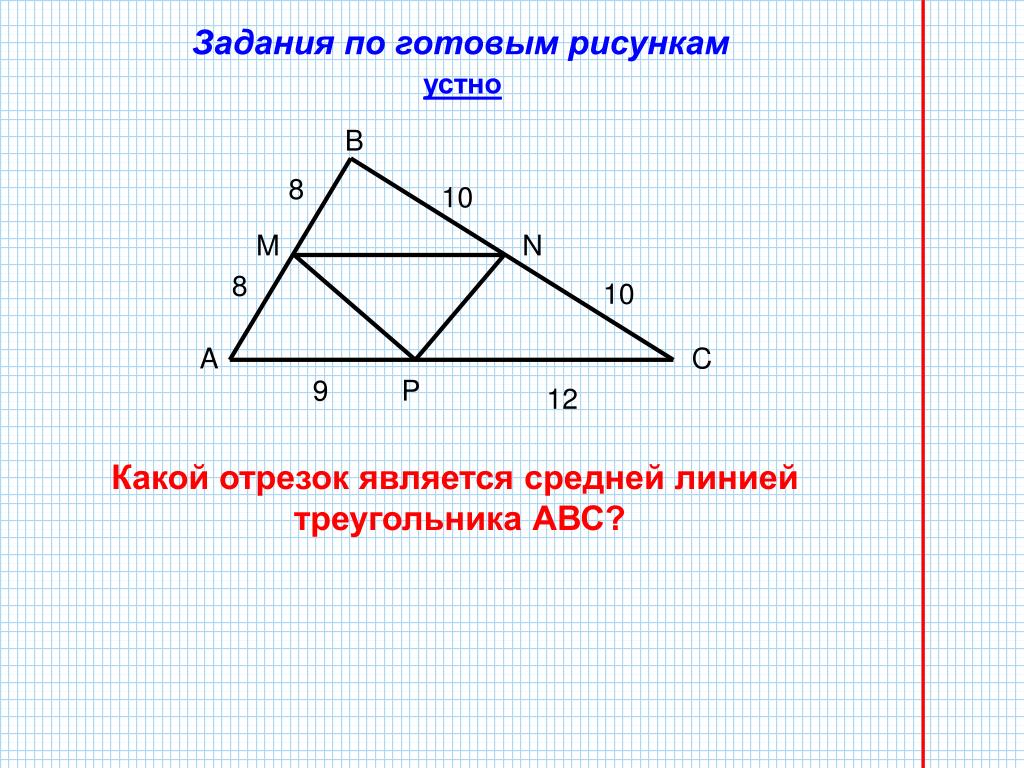
Средняя часть трапеции — это отрезок, концы которого являются серединами непараллельных сторон.
Затем мы построили среднюю часть трапеции. Учащиеся наблюдали за трапецией, когда я изменил трапецию.
Я отправил быстрый опрос: что, по-вашему, верно в отношении середины трапеции?
Создает треугольник и трапецию. 1
все середины образуют подобный треугольник 1
mn параллелен yx 2
((1)/(2)) размер исходной точки 1
параллельно основанию треугольника 1
все средние сегменты образуют подобный перевернутый треугольник 1
параллельно основанию 1 Δ0 0
0 cre8
cre8
и ловушка 1
создает треугольник и трапецию 1
Она образует сторону треугольника, аналогичную исходной. 1
Средний отрезок параллелен стороне, не участвующей в образовании среднего отрезка. 1
Это будет медиана 1
мн, параллельно YX 1
Параллельно основанию 1
мн параллельно YX 1
мн параллель в ловушку и tri 1
все сегменты образуют треугольник, аналогичный исходному 1
все соединенные середины образуют треугольник, аналогичный исходному 1
создает ∆ сверху + ловушку. внизу 1
внизу 1
Треугольник XMN подобен треугольнику XYZ.
Линия MN параллельна линии YX. 1
2/3 наибольшая сторона 1
2/3 o 1
сторона, параллельная середине, является 1
образует треугольник, а тра mon 1
Чтобы немного изменить ситуацию, я быстро распечатал предположения студентов, разрезал их и раздал по несколько штук каждой команде. Теперь вы решаете, верны ли высказанные вами предположения. И если да, то почему?
Я использовал Class Capture, чтобы следить за тем, как ученики разговаривают и работают (и играют/исследуют за рамками заданных догадок).
Затем я спросил, что они выяснили с помощью быстрого опроса:
seg mn параллельно обеим seg ab и seg dc 1
параллельно обоим основаниям на dc и ab 2
Трапеция ABCD аналогична ABNM.
Линии AB и CD параллельны середине отрезка. 1
MN параллелен AB и DC 1
Создает линию, параллельную основаниям, и формирует две трапеции. 1
1
n-отрезок параллелен верхней и нижней сторонам 1
((AB+DC)/(2)) 2
он будет параллелен сторонам над и под ним 1
MN параллелен DC и AB 1
(AB+DC)/(2)=MN 1
параллельно DC 1
Образует две трапеции 1
// 2 ab и dc 1
образует две трапозоиды 1
Параллелен сторонам над и под ним. 1
делает 2 ловушки. 1
Получается аналогичная трапеция. 1
они образуют 2 трапеции, ab+dc/2 1
параллельно основанию трапеции 1
ab ll to mn ll to dc. когда параллелограмм образует 2 конгруэнтных трапеции 1
трапеция ABNM подобна трапеции MNCD 1
все средние сегменты образуют диалу 1
А потом мы говорили о том, как они узнали, что эти заявления верны.
У Джамерии было много измерений трапеции. Я сделал ее Ведущей в прямом эфире. Какие предположения мы можем сделать, используя эту информацию?
Я сделал Джареда ведущим.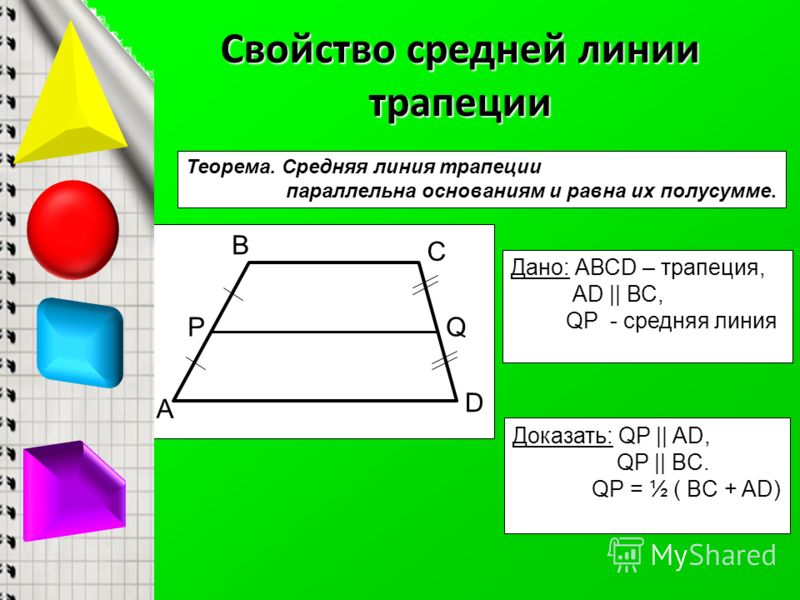
Что математически дает нам вспомогательная линия Джареда?
Я сделал Лэндона ведущим.
Какие предположения мы можем сделать, используя эту информацию?
Я отправил экспресс-опрос, чтобы определить, могут ли учащиеся использовать сделанное нами предположение о длине среднего отрезка по сравнению с длиной основания трапеции.
А как насчет средних сегментов треугольника?
А почему?
Мы еще не начали наш модуль по дилатациям, поэтому в одном из последующих уроков мы поговорим о том, почему.
И так путешествие продолжается, даже заключая сделки с моими администраторами по мере необходимости, чтобы создать класс, где учащиеся могут выдвигать, проверять и доказывать свои собственные предположения вместо того, чтобы получать теоремы из нашего учебника для доказательства.
Теги: CCSS-M G-CO.C.10, Class Capture, формирующая оценка, Live Presenter, ищите и используйте структуру, Ищите регулярность в повторяющихся рассуждениях, Средняя часть трапеции, Средняя часть треугольника , публикация целей урока в классе, быстрый опрос, TI-Nspire Navigator
[решено] 9 КЛАСС — | Курс Герой
9 КЛАСС —
Транскрипция текста
МАТЕМАТИКА 9
Имя:
Класс и раздел:
Свидание:
УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ ЛИСТ
Доказательство теоремы о средней линии.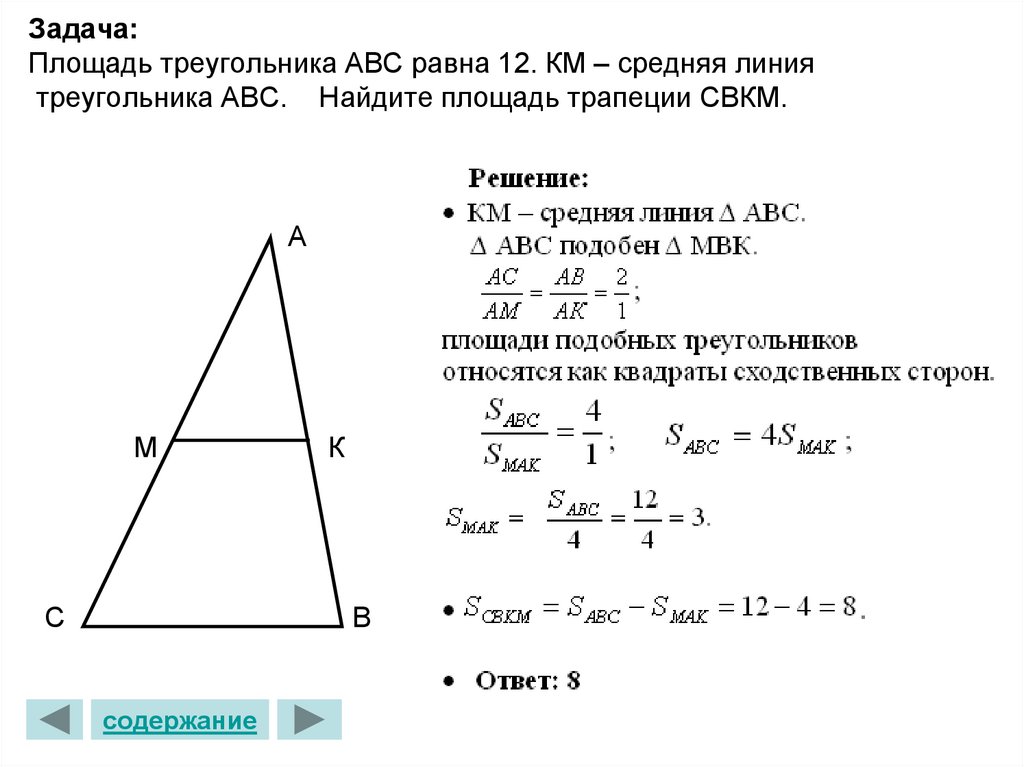 I. Исходная информация для учащихся
Эти рабочие листы служат вашим руководством для самообучения и облегчат урок по доказательству
теорема о средней линии.
Доказательство теоремы о средней линии очень полезно для понимания некоторых понятий в
геометрия особенно в связи с трапецией и подобия. Чтобы доказать теорему о средней линии,
давайте сначала узнаем, что такое теорема о средней линии.
ТЕОРЕМА СРЕДНЕЙ ЛИНИИ:
В AABC, D и E
Сегмент, который соединяется
являются серединами АВ и АС
Е
середины двух сторон одной
соответственно. Эти средние точки
треугольник параллелен третьей стороне
при соединении образует сегмент
и вдвое короче.
DE
С
Следующие определения некоторых важных терминов могут быть вам полезны:
Определение средней точки — точка на линии
Определение средней точки |AM =
отрезок, который делит его на две равные части.
М
Е
Середина отрезка.
SAS (Side-Angle-Side) постулат конгруэнтности
— утверждает, что если две стороны и включенный
Постулат Сторона-Угол-Сторона
углы одного треугольника равны
Если: 2 стороны и прилежащий угол
соответствующие две стороны и включены
конгруэнтны
угол другого треугольника, то треугольники
конгруэнтны
Теорема AIP — если
две линии образуют конгруэнтную чередующуюся внутреннюю часть
углы с секущей, то прямые равны
АИП
параллельно.
I. Исходная информация для учащихся
Эти рабочие листы служат вашим руководством для самообучения и облегчат урок по доказательству
теорема о средней линии.
Доказательство теоремы о средней линии очень полезно для понимания некоторых понятий в
геометрия особенно в связи с трапецией и подобия. Чтобы доказать теорему о средней линии,
давайте сначала узнаем, что такое теорема о средней линии.
ТЕОРЕМА СРЕДНЕЙ ЛИНИИ:
В AABC, D и E
Сегмент, который соединяется
являются серединами АВ и АС
Е
середины двух сторон одной
соответственно. Эти средние точки
треугольник параллелен третьей стороне
при соединении образует сегмент
и вдвое короче.
DE
С
Следующие определения некоторых важных терминов могут быть вам полезны:
Определение средней точки — точка на линии
Определение средней точки |AM =
отрезок, который делит его на две равные части.
М
Е
Середина отрезка.
SAS (Side-Angle-Side) постулат конгруэнтности
— утверждает, что если две стороны и включенный
Постулат Сторона-Угол-Сторона
углы одного треугольника равны
Если: 2 стороны и прилежащий угол
соответствующие две стороны и включены
конгруэнтны
угол другого треугольника, то треугольники
конгруэнтны
Теорема AIP — если
две линии образуют конгруэнтную чередующуюся внутреннюю часть
углы с секущей, то прямые равны
АИП
параллельно.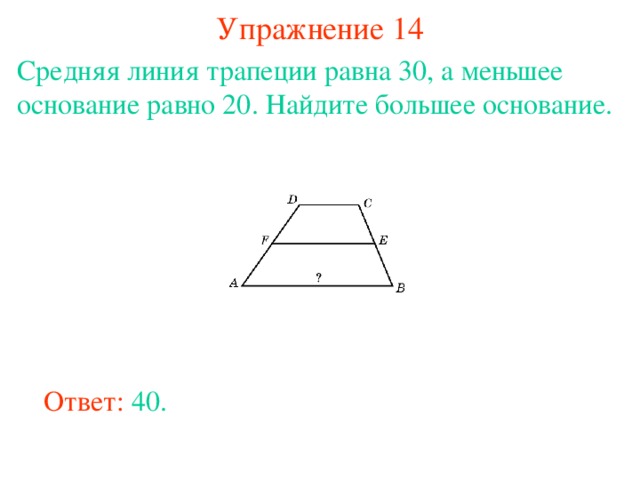 CPCTC — Соответствующие части конгруэнтности
Треугольники конгруэнтны
Вертикальные углы — два несмежных угла
СПКТС
образован двумя пересекающимися линиями.
Транзитивное свойство конгруэнтности —
AB = CD и CD = EF, тогда AB
р
~ ЭФ
АКСИЗ . АТРС
Постулат сложения сегментов — утверждает, что если
нам даны две точки на прямой
отрезке А и С третья точка В лежит на
отрезок AC тогда и только тогда, когда расстояния
между точками соответствуют требованиям
Вертикальные углы или
уравнения AB + BC = AC.
(Вы также можете ознакомиться с определением других терминов,
АВ + ВС = АС
алгебраические свойства, постулаты и теоремы
которые могут помочь вам выполнить данные действия.)
14
CPCTC — Соответствующие части конгруэнтности
Треугольники конгруэнтны
Вертикальные углы — два несмежных угла
СПКТС
образован двумя пересекающимися линиями.
Транзитивное свойство конгруэнтности —
AB = CD и CD = EF, тогда AB
р
~ ЭФ
АКСИЗ . АТРС
Постулат сложения сегментов — утверждает, что если
нам даны две точки на прямой
отрезке А и С третья точка В лежит на
отрезок AC тогда и только тогда, когда расстояния
между точками соответствуют требованиям
Вертикальные углы или
уравнения AB + BC = AC.
(Вы также можете ознакомиться с определением других терминов,
АВ + ВС = АС
алгебраические свойства, постулаты и теоремы
которые могут помочь вам выполнить данные действия.)
14
… Показать больше
Транскрипция изображения текста
ил. Учебная компетенция: Доказывает теорему о средней линии (для треугольников). (M9GE-Иллд-1)
ЗАДАНИЕ 1: Это Папереллеграмма!
Позвольте трем членам семьи или друзьям присоединиться к вам, когда вы выполняете задание. Подготовьте необходимые материалы.
Выполните процедуру и ответьте на поставленные вопросы.
Материалы: 4 листа короткой высокосортной бумаги, карандаш, линейка, клейкая лента, транспортир и ножницы.
Процедура:
1. Каждый член должен начертить и вырезать треугольник из связи.
бумага. (равносторонний треугольник, прямоугольный треугольник, тупоугольный треугольник и остроугольный треугольник
он не равноугольный)
2. Выберите третью сторону треугольника. Отметьте каждую середину двух других сторон
затем соедините средние точки, чтобы сформировать сегмент.
3. Измерьте нарисованный отрезок и третью выбранную вами сторону.
В: Сравните длины нарисованных отрезков и третьей стороны, которую вы
выбрал. Что вы заметили?
4. Разрежьте треугольник по нарисованному отрезку.
В: Какие две фигуры образуются после разрезания треугольника по отрезку
нарисовано?
5. Используйте клейкую ленту, чтобы снова соединить треугольник с другой фигурой таким образом.
таким образом, чтобы их общая вершина была средней точкой, а конгруэнтные сегменты
образованные средней точкой совпадают.
Подготовьте необходимые материалы.
Выполните процедуру и ответьте на поставленные вопросы.
Материалы: 4 листа короткой высокосортной бумаги, карандаш, линейка, клейкая лента, транспортир и ножницы.
Процедура:
1. Каждый член должен начертить и вырезать треугольник из связи.
бумага. (равносторонний треугольник, прямоугольный треугольник, тупоугольный треугольник и остроугольный треугольник
он не равноугольный)
2. Выберите третью сторону треугольника. Отметьте каждую середину двух других сторон
затем соедините средние точки, чтобы сформировать сегмент.
3. Измерьте нарисованный отрезок и третью выбранную вами сторону.
В: Сравните длины нарисованных отрезков и третьей стороны, которую вы
выбрал. Что вы заметили?
4. Разрежьте треугольник по нарисованному отрезку.
В: Какие две фигуры образуются после разрезания треугольника по отрезку
нарисовано?
5. Используйте клейкую ленту, чтобы снова соединить треугольник с другой фигурой таким образом.
таким образом, чтобы их общая вершина была средней точкой, а конгруэнтные сегменты
образованные средней точкой совпадают.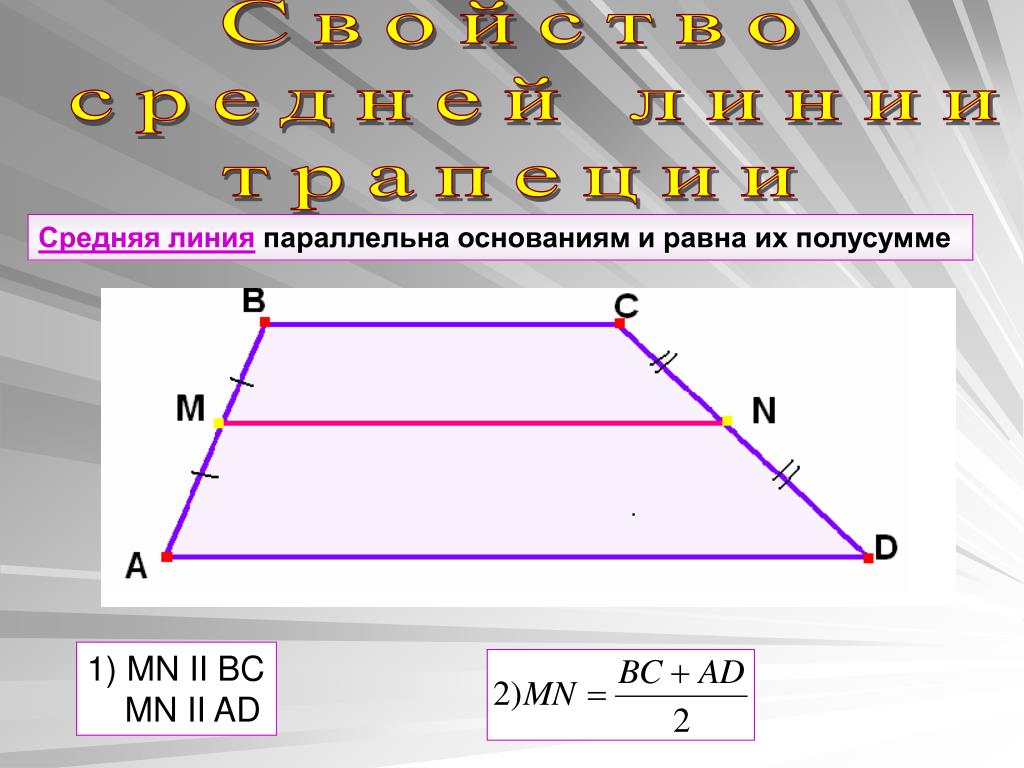 В: После повторного соединения вырезов, какая фигура образуется новой фигурой? Почему?
В: Что вы можете сказать о своих выводах по отношению к выводам вашей семьи?
участники/друзья?
В: Считаете ли вы, что результаты применимы ко всем видам треугольников? Почему?
ЗАДАНИЕ 2: Покажи мне!
Указания: Чтобы доказать теорему о средней линии, проанализируйте приведенную ниже ситуацию и укажите причины.
к данным утверждениям, которые следуют. Вы можете выбрать правильный ответ из поля выбора на
право.
ТЕОРЕМА СРЕДНЕЙ ЛИНИИ:
Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей
сторона и половина длины.
Дано: AHNS, O — середина HN,
E — середина NS
Докажите: ОЕ | ГС, ОЭ = = ГС
15
Н
В: После повторного соединения вырезов, какая фигура образуется новой фигурой? Почему?
В: Что вы можете сказать о своих выводах по отношению к выводам вашей семьи?
участники/друзья?
В: Считаете ли вы, что результаты применимы ко всем видам треугольников? Почему?
ЗАДАНИЕ 2: Покажи мне!
Указания: Чтобы доказать теорему о средней линии, проанализируйте приведенную ниже ситуацию и укажите причины.
к данным утверждениям, которые следуют. Вы можете выбрать правильный ответ из поля выбора на
право.
ТЕОРЕМА СРЕДНЕЙ ЛИНИИ:
Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей
сторона и половина длины.
Дано: AHNS, O — середина HN,
E — середина NS
Докажите: ОЕ | ГС, ОЭ = = ГС
15
Н
… Показать больше
Транскрипция текста
Доказательство:
Заявления
Причины
ВЫБОР
1. AHNS, O – середина HN,
1.Дано
E — середина NS
а. Значение
2. Когда Of расширен. Eсть
2. В прямой ровно одна точка между
параллелограмм.
точка T такая, что OE = ET
два других момента, которые считаются
середина линии. И эти две точки
б. САС
равноудален от середины
Конгруэнтность
3. ЭН = ЭП
3.
Постулат
4. 42 = 23
4. Вертикальные углы равны
5. АОНЭ = АТСЕ
5.
в. Параллелогра
6. 21 = 24
6.ЦПКТС
м Недвижимость.
7. ГН II СТ
7.
д. Определение
8. ОН = ВКЛ.
8. Определение средней точки
средней точки
9. ВКЛ = ТС
9. УПКТС (утверждение 5)
10. ОН = СТ
10.
е. Замена
11. Четырехугольник
ГОРЯЧИЕ
является
а
11.
[утверждение
параллелограмм.
(СН) 2]
12. ДЭ II ГС
12.0E на стороне OT of HOTS
13. ОЕ + ЕТ = ОТ
13. Постулат сложения сегментов (SAP)
F. Дополнение
14. ОЕ + ОЕ = ОТ
14.
15. 20Э = ОТ
15.
грамм. По АИП
Теорема
16. ГС II ОТ
16.
17. 20Э = ГС
17. По замене
час Замена
18. OF = =HS(Отрезок, соединяющий
18.
(СН 14 и 15)
середины двух сторон одной
треугольник вдвое короче третьего
я. переходный
сторона.
Имущество
Поздравляем! Вы только что завершили доказательство теоремы о средней линии. Эту теорему можно
применяется для решения задач. Попробуйте следующее упражнение.
ЗАНЯТИЕ 3: Действуйте!
Направления: В AMCG A и I являются серединами MG и CG соответственно.
И эти две точки
б. САС
равноудален от середины
Конгруэнтность
3. ЭН = ЭП
3.
Постулат
4. 42 = 23
4. Вертикальные углы равны
5. АОНЭ = АТСЕ
5.
в. Параллелогра
6. 21 = 24
6.ЦПКТС
м Недвижимость.
7. ГН II СТ
7.
д. Определение
8. ОН = ВКЛ.
8. Определение средней точки
средней точки
9. ВКЛ = ТС
9. УПКТС (утверждение 5)
10. ОН = СТ
10.
е. Замена
11. Четырехугольник
ГОРЯЧИЕ
является
а
11.
[утверждение
параллелограмм.
(СН) 2]
12. ДЭ II ГС
12.0E на стороне OT of HOTS
13. ОЕ + ЕТ = ОТ
13. Постулат сложения сегментов (SAP)
F. Дополнение
14. ОЕ + ОЕ = ОТ
14.
15. 20Э = ОТ
15.
грамм. По АИП
Теорема
16. ГС II ОТ
16.
17. 20Э = ГС
17. По замене
час Замена
18. OF = =HS(Отрезок, соединяющий
18.
(СН 14 и 15)
середины двух сторон одной
треугольник вдвое короче третьего
я. переходный
сторона.
Имущество
Поздравляем! Вы только что завершили доказательство теоремы о средней линии. Эту теорему можно
применяется для решения задач. Попробуйте следующее упражнение.
ЗАНЯТИЕ 3: Действуйте!
Направления: В AMCG A и I являются серединами MG и CG соответственно. Рассмотрим каждое данное
информацию и ответьте на следующие вопросы.
1. Дано: Al=5,5
Вопрос: Какова мера МС?
2. Учитывая GC = 8
Вопрос: Что является мерой КИ?
3. Учитывая GI = 4 и MA = 5
Вопрос: Что является мерой MG? ГК? МГ + ГК?
4. Учитывая Al = 17
Вопрос: Какова мера Al + MC?
16
Рассмотрим каждое данное
информацию и ответьте на следующие вопросы.
1. Дано: Al=5,5
Вопрос: Какова мера МС?
2. Учитывая GC = 8
Вопрос: Что является мерой КИ?
3. Учитывая GI = 4 и MA = 5
Вопрос: Что является мерой MG? ГК? МГ + ГК?
4. Учитывая Al = 17
Вопрос: Какова мера Al + MC?
16
… Показать еще
Транскрипция текста
РУБРИКА ЗАДАНИЕ 1: Это Папереллелограмма!
4 балла
3 балла
2 балла
1 балл
Полный ответ на
|Хороший твердый ответ
Объяснение
является
Пропускает
ключ
Понимание
вопросы с подробным
с
Чисто
неясно.
точки.
объяснение.
объяснение.
Шоу
полный
Ответ показывает
Ответ показывает
Шоу
существенный
Продемонстрировано
понимание
понимание
немного
полное отсутствие
вопросы
из
знания
понимание
математические идеи и
проблема, идеи и
понимание
процессы.
задание.
процессы
задачи
Не встречается
Идет
вне
в
Встречает
в
Вряд ли встречается
в
Требования
требования
принадлежащий
требования
требования
требования
задача.
задача
задание.
задание
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
ОТРАЖЕНИЕ
Брайант, М. Л., Булалайао, Л.Е., Калланта, М.М., Круз,
Д.Д., Де Вера Р.Ф., Гарсия Г.Т., Хавьер С.Е., Лазаро Р.А.,
Какова ваша "линия Hugot" к
Местерио, BJ & Саладино, RHA, (2014),
Материал для учащихся по математике 9, типография ФЭФ.
выражать свои чувства во время
https://ncalculators.com/geometry/mid-points-
отвечая на деятельность.
калькулятор.htm
https://virtualnerd.com/geometry/congruent-
треугольники/доказательство-sss-sas/определение-sas-треугольник-
постулат конгруэнтности
https://slideplayer.com/slide/14709210/
https://www.learner.org/series/learning-math-
геометрия/рассечения-и-доказательство/часть-c-средней линии-
теорема-55 минут/
15.f
Д’9Т
11.2
14,6
2,4
18.1
!’ОТ
1.11
отличаться)
Мероприятие 3:
Действие 2:
1. МГ=10
Действие 1:
Ключ ответа
8:09(Ответы могут
Приготовленный:
КРИСТИН Р. ОПИАНА
Писатель
17
Л., Булалайао, Л.Е., Калланта, М.М., Круз,
Д.Д., Де Вера Р.Ф., Гарсия Г.Т., Хавьер С.Е., Лазаро Р.А.,
Какова ваша "линия Hugot" к
Местерио, BJ & Саладино, RHA, (2014),
Материал для учащихся по математике 9, типография ФЭФ.
выражать свои чувства во время
https://ncalculators.com/geometry/mid-points-
отвечая на деятельность.
калькулятор.htm
https://virtualnerd.com/geometry/congruent-
треугольники/доказательство-sss-sas/определение-sas-треугольник-
постулат конгруэнтности
https://slideplayer.com/slide/14709210/
https://www.learner.org/series/learning-math-
геометрия/рассечения-и-доказательство/часть-c-средней линии-
теорема-55 минут/
15.f
Д’9Т
11.2
14,6
2,4
18.1
!’ОТ
1.11
отличаться)
Мероприятие 3:
Действие 2:
1. МГ=10
Действие 1:
Ключ ответа
8:09(Ответы могут
Приготовленный:
КРИСТИН Р. ОПИАНА
Писатель
17
… Показать больше
Транскрипция текста
МАТЕМАТИКА 9
Имя:
Класс и раздел:
Свидание:
УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ ЛИСТ
ДОКАЗАТЕЛЬСТВО ТЕОРЕМ О ТРАПЕЦИЯХ
I.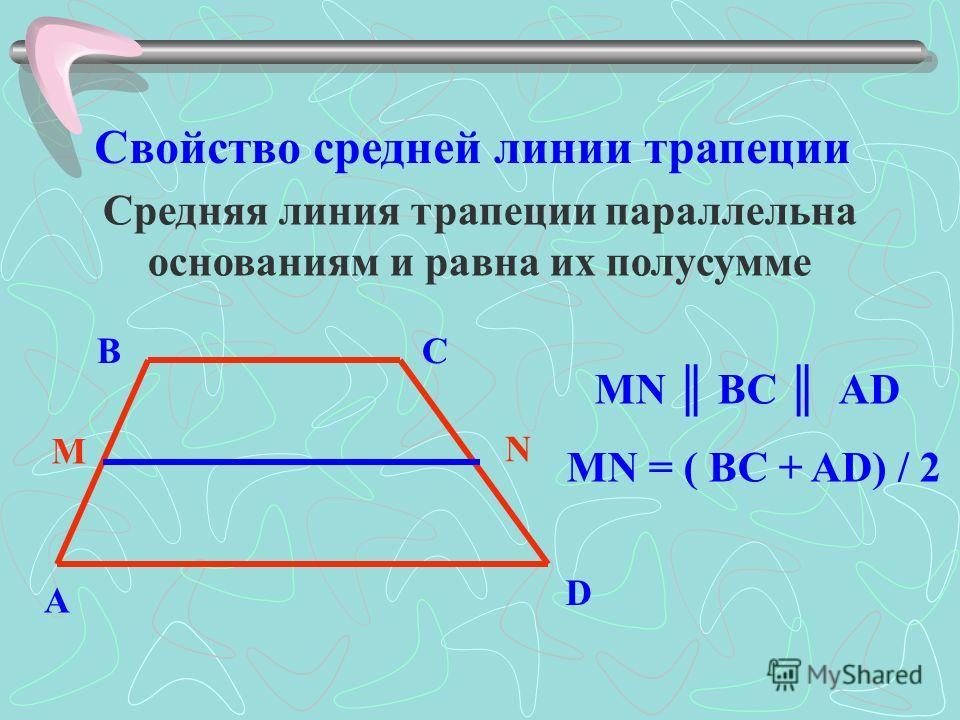 Исходная информация для учащихся
Эти листы учебных заданий служат вашим руководством по самообучению. Он содержит мероприятия, которые
предназначен для облегчения понимания урока по процессу доказательства теорем о трапециях.
Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон. Непараллельные стороны это
называются катетами, а углы называются углами при основании. Если стороны трапеции равны, то
трапеция — это равнобедренная трапеция. Давайте посмотрим на цифры ниже.
А
база
нога
нога
диагональ
диагональ
база
Д’
Рис.1 Трапеция с ее частями
Рис.2 Равнобедренная трапеция с конгруэнтными катетами
Теорема о средней линии треугольника аналогична теореме для трапеций, называемой
Теорема о середине (медиане) трапеции. Медиана или середина трапеции – это линия
отрезок, соединяющий середины двух непараллельных сторон (катетов) трапеции.
ТЕОРЕМА О СРЕДНЕМ СЕГМЕНТЕ (МЕДИАНЕ)
ТРАПЕЦИЯ:
Линия, соединяющая середины
М
два катета трапеции параллельны
основания, а его длина равна половине
Д
сумма длин оснований.
Исходная информация для учащихся
Эти листы учебных заданий служат вашим руководством по самообучению. Он содержит мероприятия, которые
предназначен для облегчения понимания урока по процессу доказательства теорем о трапециях.
Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон. Непараллельные стороны это
называются катетами, а углы называются углами при основании. Если стороны трапеции равны, то
трапеция — это равнобедренная трапеция. Давайте посмотрим на цифры ниже.
А
база
нога
нога
диагональ
диагональ
база
Д’
Рис.1 Трапеция с ее частями
Рис.2 Равнобедренная трапеция с конгруэнтными катетами
Теорема о средней линии треугольника аналогична теореме для трапеций, называемой
Теорема о середине (медиане) трапеции. Медиана или середина трапеции – это линия
отрезок, соединяющий середины двух непараллельных сторон (катетов) трапеции.
ТЕОРЕМА О СРЕДНЕМ СЕГМЕНТЕ (МЕДИАНЕ)
ТРАПЕЦИЯ:
Линия, соединяющая середины
М
два катета трапеции параллельны
основания, а его длина равна половине
Д
сумма длин оснований.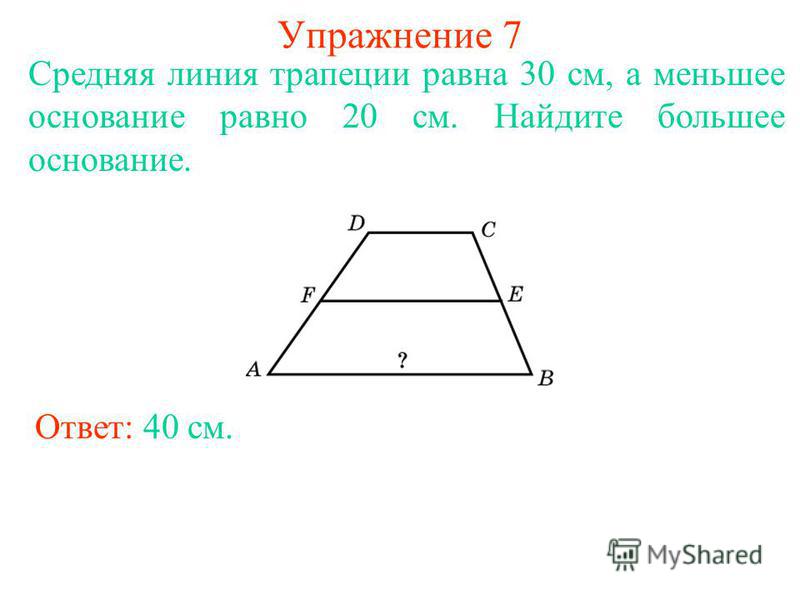 MN — средний сегмент или медиана
MN = (4B +CD) ипезоид ABCD, где
Остальные теоремы о трапеции относятся к равнобедренной трапеции. Первая теорема касается
углы основания равнобедренной трапеции.
Теорема 1. Углы при основании равнобедренной трапеции равны
конгруэнтный.
У равнобедренной трапеции ABCD две пары углов при основании.
ZA = 2B и ZD = ZC
Вторая теорема касается пары противоположных углов равнобедренной трапеции.
Теорема 2. Противолежащие углы равнобедренной трапеции равны
дополнение
дополнительный.
У равнобедренной трапеции ABCD две пары противоположных углов.
ЗА + 2С = 180
<D+2B=180"
18
MN — средний сегмент или медиана
MN = (4B +CD) ипезоид ABCD, где
Остальные теоремы о трапеции относятся к равнобедренной трапеции. Первая теорема касается
углы основания равнобедренной трапеции.
Теорема 1. Углы при основании равнобедренной трапеции равны
конгруэнтный.
У равнобедренной трапеции ABCD две пары углов при основании.
ZA = 2B и ZD = ZC
Вторая теорема касается пары противоположных углов равнобедренной трапеции.
Теорема 2. Противолежащие углы равнобедренной трапеции равны
дополнение
дополнительный.
У равнобедренной трапеции ABCD две пары противоположных углов.
ЗА + 2С = 180
<D+2B=180"
18
… Показать больше
Транскрипция текста
В равнобедренной трапеции ABCD две диагонали равны: AC = BD
Теорема 3. Диагонали равнобедренной трапеции равны
конгруэнтный.
Вам могут помочь определения некоторых важных терминов:
Теорема о средней линии. Отрезок, соединяющий середины
М
Мидлина
две стороны треугольника параллельны третьей стороне и
вдвое короче.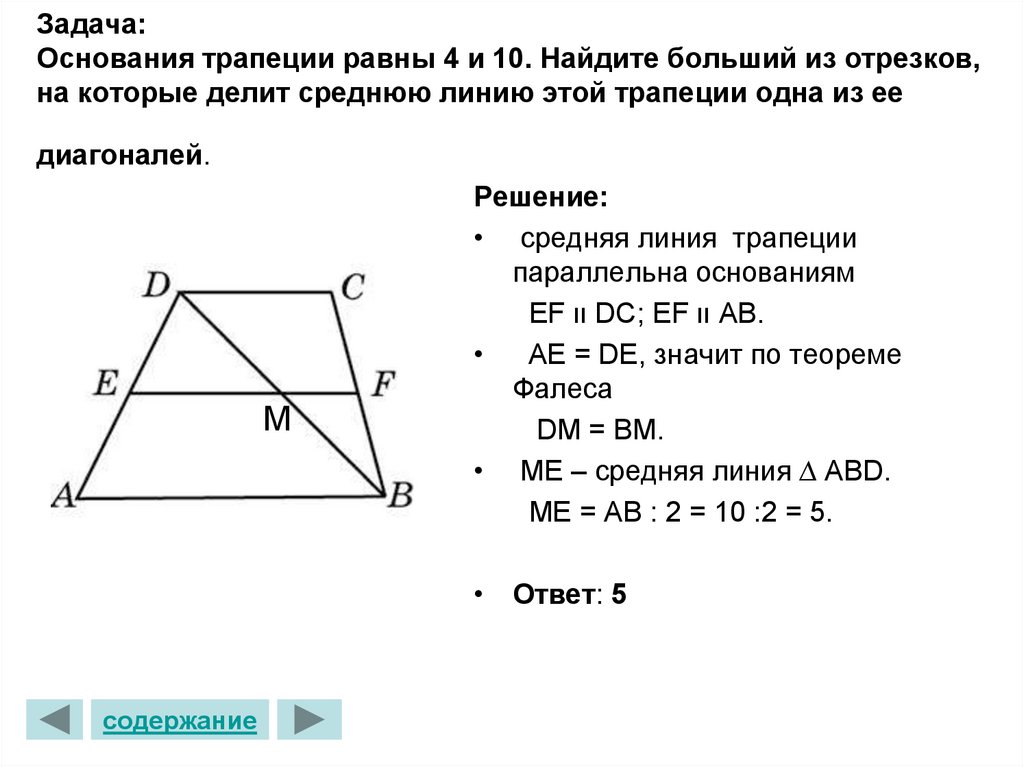 МН/БК
Миннесота – Австралия
Определение параллелограмма — четырехугольник с
две пары противоположных сторон, которые параллельны
Замена- Когда две вещи равны, мы можем заменить одну на другую, и мы знаем
что уравнение по-прежнему будет верным.
Распределительное свойство: a(b+c) = ab+ac
Постулат о параллельности. Утверждает, что через любую заданную точку, не лежащую на прямой, проходит ровно
одну прямую, параллельную этой прямой в той же плоскости.
Симметричное свойство конгруэнтности — если AB = CD, то CD = AB или если ZABC=ZDEF, то
ZDEF = ZABC.
Теорема о внутренних углах с одинаковой стороной. Если две параллельные прямые пересечены секущей, то
те же боковые внутренние углы являются дополнительными.
Определение равнобедренного треугольника — треугольник с двумя равными сторонами.
Теорема о равнобедренном треугольнике: если две стороны треугольника равны, то углы, лежащие против
эти стороны равны.
(Вы также можете ознакомиться с определениями других терминов, алгебраических свойств, постулатов и теорем.
МН/БК
Миннесота – Австралия
Определение параллелограмма — четырехугольник с
две пары противоположных сторон, которые параллельны
Замена- Когда две вещи равны, мы можем заменить одну на другую, и мы знаем
что уравнение по-прежнему будет верным.
Распределительное свойство: a(b+c) = ab+ac
Постулат о параллельности. Утверждает, что через любую заданную точку, не лежащую на прямой, проходит ровно
одну прямую, параллельную этой прямой в той же плоскости.
Симметричное свойство конгруэнтности — если AB = CD, то CD = AB или если ZABC=ZDEF, то
ZDEF = ZABC.
Теорема о внутренних углах с одинаковой стороной. Если две параллельные прямые пересечены секущей, то
те же боковые внутренние углы являются дополнительными.
Определение равнобедренного треугольника — треугольник с двумя равными сторонами.
Теорема о равнобедренном треугольнике: если две стороны треугольника равны, то углы, лежащие против
эти стороны равны.
(Вы также можете ознакомиться с определениями других терминов, алгебраических свойств, постулатов и теорем.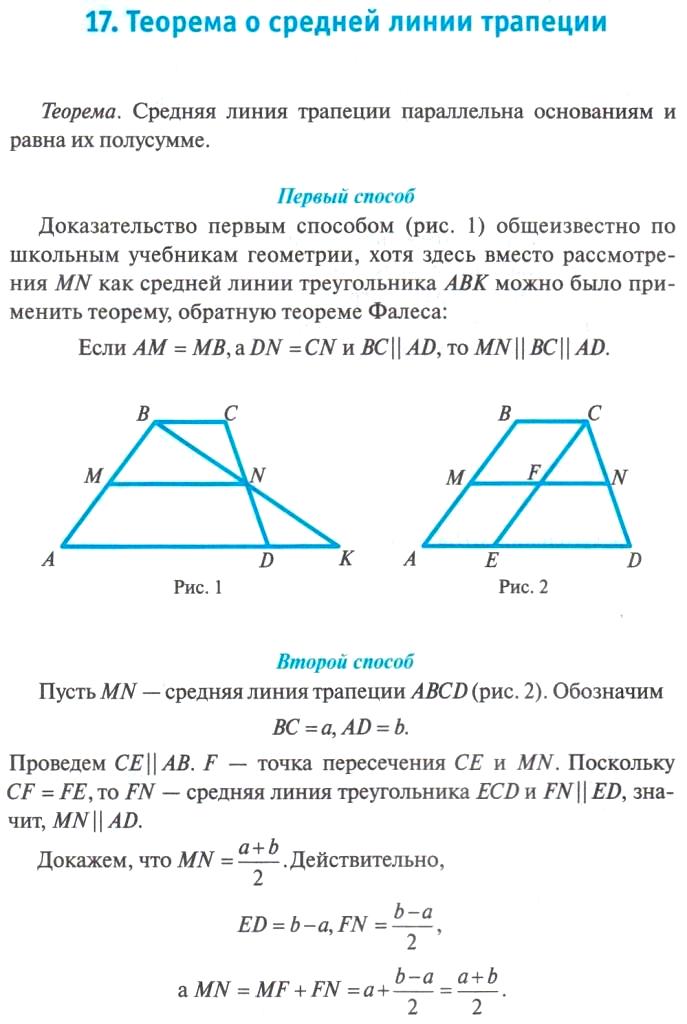 которые могут помочь вам выполнить данные действия.)
Ил. Учебная компетенция: Доказывает теоремы о трапециях и воздушных змеях. (М9GE-Illd-2)
ЗАДАНИЕ 1: Покажи мне!
ТЕОРЕМА О СРЕДНЕМ СЕГМЕНТЕ (МЕДИАНЕ) НА ТРАПЕЦИЯХ:
Прямая, соединяющая середины двух катетов трапеции, параллельна
основания, а его длина равна половине суммы длин оснований.
Указания: Докажите теорему о среднем отрезке (медиане), проанализировав приведенную ниже ситуацию и
предоставление причин для данных заявлений, которые следуют. Вы можете выбрать правильный ответ из
поле выбора справа.
Дано: Трапеция МИНС с медианным TR
Докажите: ТР II ИН, ТР МС, ТР = = (МС + ИН)
М
19
которые могут помочь вам выполнить данные действия.)
Ил. Учебная компетенция: Доказывает теоремы о трапециях и воздушных змеях. (М9GE-Illd-2)
ЗАДАНИЕ 1: Покажи мне!
ТЕОРЕМА О СРЕДНЕМ СЕГМЕНТЕ (МЕДИАНЕ) НА ТРАПЕЦИЯХ:
Прямая, соединяющая середины двух катетов трапеции, параллельна
основания, а его длина равна половине суммы длин оснований.
Указания: Докажите теорему о среднем отрезке (медиане), проанализировав приведенную ниже ситуацию и
предоставление причин для данных заявлений, которые следуют. Вы можете выбрать правильный ответ из
поле выбора справа.
Дано: Трапеция МИНС с медианным TR
Докажите: ТР II ИН, ТР МС, ТР = = (МС + ИН)
М
19
… Показать больше
Транскрипция текста
Доказательство:
Заявления
Причины
1. ТР = =МС + = В
1. Дано
ВЫБОР
2. Нарисуйте IS с точкой P в качестве середины.
2. Две точки определяют ровно одну прямую.
а. Средняя линия
3.ТП = =МС и ТП | РС
3. Теорема о средней линии треугольника IMS
Теорема о
треугольник ИНС
4.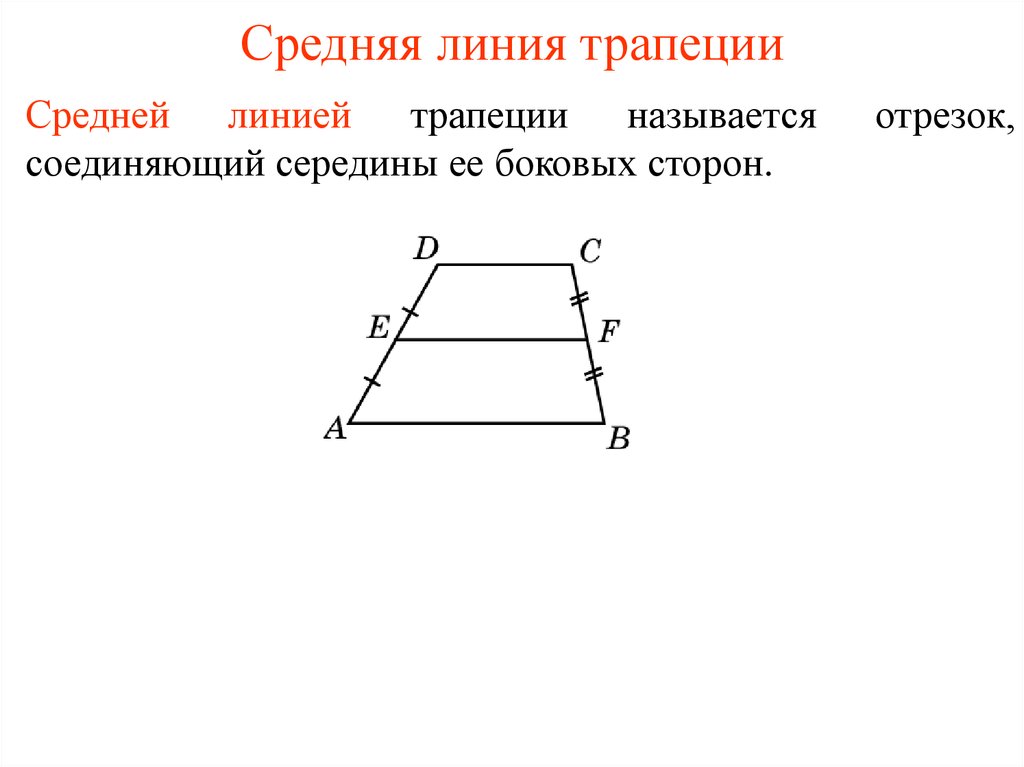 ПР = = В и ПР I| В
б. Значение
5. ВХОД MSI
5 .
Трапеция
в. Если 2 строки | |
6. ТП II ИН
к той же строке,
7.TP и PR параллельны IN.
|7.TP и PR либо параллельны, либо совпадают
они | | к
Таким образом, T, P и R коллинеарны.
линия (определение параллели). Поскольку они содержат
друг друга.
общую точку P, то TP и PR равны
д. Сегмент
содержится в одной строке.
Постулат сложения
8.ТР = ТП + ПР
8.
е. Распределительный
9. ТР = =МС + =ВХ
9. Замена
свойство
равенство
10. ТР = =(МС + ИН)
10.
Давайте сделаем упражнение V.1!
Инструкция: Ответьте на следующие вопросы. См. рисунок справа.
С
1. Если BA=24см и DC=26см, найдите длину KF?
2. Если BA=10 см и DC=12 см, найдите длину KF?
3. Найдите длину среднего основания трапеции, у которой
размеры параллельных оснований 14 см и 46 см.
4. Предположим, что DC=26см и KF=25см. Что такое
мера БА?
ЗАДАНИЕ 2: Покажи мне!
Теорема 1: углы при основании равнобедренной трапеции равны.
Указания: Проанализируйте данную ситуацию и объясните причины приведенных ниже утверждений.
ПР = = В и ПР I| В
б. Значение
5. ВХОД MSI
5 .
Трапеция
в. Если 2 строки | |
6. ТП II ИН
к той же строке,
7.TP и PR параллельны IN.
|7.TP и PR либо параллельны, либо совпадают
они | | к
Таким образом, T, P и R коллинеарны.
линия (определение параллели). Поскольку они содержат
друг друга.
общую точку P, то TP и PR равны
д. Сегмент
содержится в одной строке.
Постулат сложения
8.ТР = ТП + ПР
8.
е. Распределительный
9. ТР = =МС + =ВХ
9. Замена
свойство
равенство
10. ТР = =(МС + ИН)
10.
Давайте сделаем упражнение V.1!
Инструкция: Ответьте на следующие вопросы. См. рисунок справа.
С
1. Если BA=24см и DC=26см, найдите длину KF?
2. Если BA=10 см и DC=12 см, найдите длину KF?
3. Найдите длину среднего основания трапеции, у которой
размеры параллельных оснований 14 см и 46 см.
4. Предположим, что DC=26см и KF=25см. Что такое
мера БА?
ЗАДАНИЕ 2: Покажи мне!
Теорема 1: углы при основании равнобедренной трапеции равны.
Указания: Проанализируйте данную ситуацию и объясните причины приведенных ниже утверждений.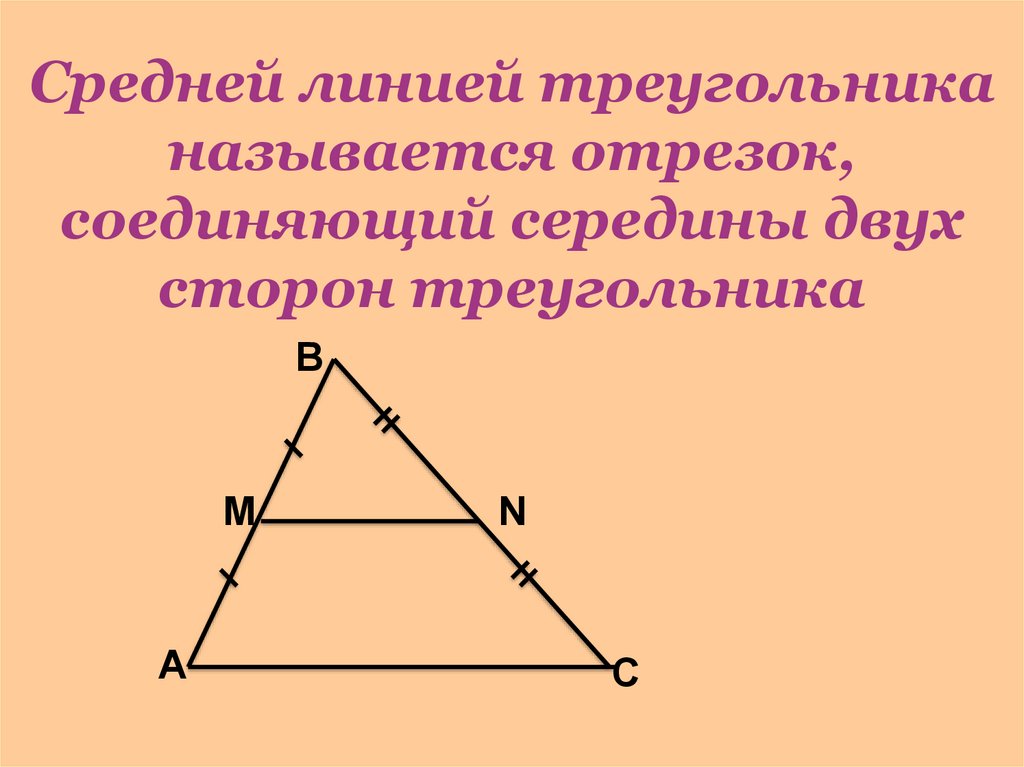 Выбирать
правильные ответы из поля выбора справа.
Дано: Равнобедренная трапеция AMOR , MO |I AR
Докажите: ZA =ZR, ZAMO =20
Доказательство:
Заявления
Причины
1. Равнобедренный
Трапеция
1. Дано
ВЫБОР
АМОР, Миссури || дополненная реальность
2.AM = ИЛИ; МО | | дополненная реальность
2 .
a.Симметричное свойство
3. Из M нарисуйте ME |1
3.Постулат о параллельности
б.Замена
ИЛИ где E лежит на AR.
c. Углы при основании равнобедренной трапеции равны =
БОЛЕЕ
является
а
4. Определение
из
г. Определение равнобедренного треугольника
параллелограмм.
параллелограмм
e. Свойство параллелограмма
ф. Определение равнобедренной трапеции
g-добавки равных углов равны =
Выбирать
правильные ответы из поля выбора справа.
Дано: Равнобедренная трапеция AMOR , MO |I AR
Докажите: ZA =ZR, ZAMO =20
Доказательство:
Заявления
Причины
1. Равнобедренный
Трапеция
1. Дано
ВЫБОР
АМОР, Миссури || дополненная реальность
2.AM = ИЛИ; МО | | дополненная реальность
2 .
a.Симметричное свойство
3. Из M нарисуйте ME |1
3.Постулат о параллельности
б.Замена
ИЛИ где E лежит на AR.
c. Углы при основании равнобедренной трапеции равны =
БОЛЕЕ
является
а
4. Определение
из
г. Определение равнобедренного треугольника
параллелограмм.
параллелограмм
e. Свойство параллелограмма
ф. Определение равнобедренной трапеции
g-добавки равных углов равны =
… Показать больше
Транскрипция текста
5.ME = ИЛИ
5 .
6.ИЛИ = Я
6. Симметричное свойство
7.AM = Я
7. Переходное свойство (утверждения 2 и 6)
8.AAME — равнобедренный треугольник
8.
9,41 = Z
9 .
10,21 = 2р
10.Соответственные углы равны
11.2R = ЗА
11.
12.ЗА = ЗР
12.
13. ЗА и ЗАМО — дополнительные углы.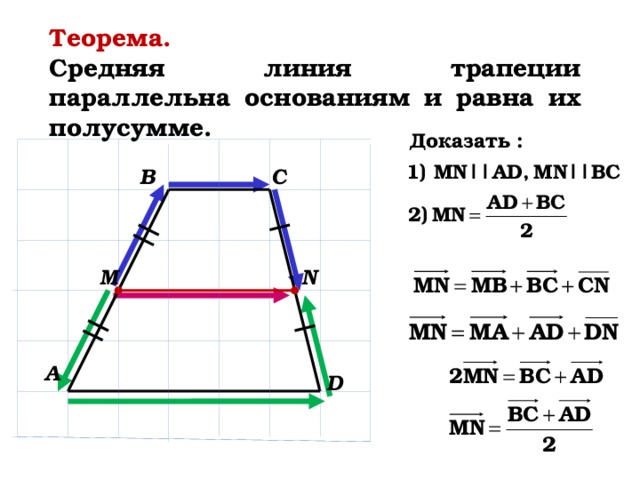 13.Внутренние углы, МО | | дополненная реальность
20 и ZR — дополнительные углы.
14.ЗАМ0 = 20
14 .
Давайте сделаем упражнение V.2!
Инструкция: Применим теорему о равнобедренной трапеции, ответив на следующие вопросы.
1. В равнобедренной трапеции ЛОВУШКА, если градусная мера
р
ZP = 60 градусов. Какова мера ZA?
1750
2. См. ЛОВУШКУ равнобедренной трапеции. Мера
LT составляет 115 градусов, какова мера ZR?
3. См. ЛОВУШКУ равнобедренной трапеции.
Если мера ЗП 35 градусов, то мера
ZA является
4. Если LP составляет 30 градусов, какой из других углов
также измеряет 30 градусов?
ЗАДАНИЕ 3: Покажи мне!
Теорема 2: Противоположные углы равнобедренной трапеции дополнительные.
Дано: Равнобедренная трапеция ARTS
Докажите: ZART и 25 являются дополнительными
ВЫБОР
а. Определение равнобедренного сустава
ZA и ZT являются дополнительными
трапеция
Доказательство:
b. свойство параллелограмма
c.теорема о равнобедренном треугольнике
d. углы основания равнобедренного
Заявления
Причины
треугольники равны
1.Равнобедренная трапеция ИСКУССТВА
1.
13.Внутренние углы, МО | | дополненная реальность
20 и ZR — дополнительные углы.
14.ЗАМ0 = 20
14 .
Давайте сделаем упражнение V.2!
Инструкция: Применим теорему о равнобедренной трапеции, ответив на следующие вопросы.
1. В равнобедренной трапеции ЛОВУШКА, если градусная мера
р
ZP = 60 градусов. Какова мера ZA?
1750
2. См. ЛОВУШКУ равнобедренной трапеции. Мера
LT составляет 115 градусов, какова мера ZR?
3. См. ЛОВУШКУ равнобедренной трапеции.
Если мера ЗП 35 градусов, то мера
ZA является
4. Если LP составляет 30 градусов, какой из других углов
также измеряет 30 градусов?
ЗАДАНИЕ 3: Покажи мне!
Теорема 2: Противоположные углы равнобедренной трапеции дополнительные.
Дано: Равнобедренная трапеция ARTS
Докажите: ZART и 25 являются дополнительными
ВЫБОР
а. Определение равнобедренного сустава
ZA и ZT являются дополнительными
трапеция
Доказательство:
b. свойство параллелограмма
c.теорема о равнобедренном треугольнике
d. углы основания равнобедренного
Заявления
Причины
треугольники равны
1.Равнобедренная трапеция ИСКУССТВА
1. Дано
е.замена
2.АР = ТС; РТ = АС
f. определение дополнительных
углы
3. Из R нарисуйте RE || TS, где E |3.
лежит на АС.
g. Внутренние углы с одной и той же стороны
4.REST — параллелограмм
4. Определение параллелограмма
Теорема
постулат сложения h.angle
5.ТС = РЕ
5.
i.теорема о сумме внутренних углов
6.АР = РЕ
6. Переходное свойство
на треугольнике
j.определение равнобедренного сустава
7.AARE — равнобедренный треугольник.
7
треугольник
8,23 = ЗА
8.
k.параллельный постулат
21
Дано
е.замена
2.АР = ТС; РТ = АС
f. определение дополнительных
углы
3. Из R нарисуйте RE || TS, где E |3.
лежит на АС.
g. Внутренние углы с одной и той же стороны
4.REST — параллелограмм
4. Определение параллелограмма
Теорема
постулат сложения h.angle
5.ТС = РЕ
5.
i.теорема о сумме внутренних углов
6.АР = РЕ
6. Переходное свойство
на треугольнике
j.определение равнобедренного сустава
7.AARE — равнобедренный треугольник.
7
треугольник
8,23 = ЗА
8.
k.параллельный постулат
21
… Показать больше
Транскрипция текста
9.m21 + m23 + mZA
9 .
10,23 = 22
10. Альтернативные внутренние углы равны.
11.ЗА = 25
11.
12.мз1 + мз2 + мзс
12. Замена (утверждение 9,10 и 11)
13.21 + 22 = ЗАРТ
13.
14.myART + мзС
14.
15.мЗС + мзТ
15
16.мЗА+мзТ
16. Замена
18. ZART и 2S дополняют друг друга
17.
ZA и ZT являются дополнительными
Давайте сделаем упражнение V.3!
Инструкция: Применим теорему о равнобедренной трапеции, ответив на следующие вопросы.
1. В равнобедренной трапеции TRAP градусная мера
1150
ZP= 60 градусов.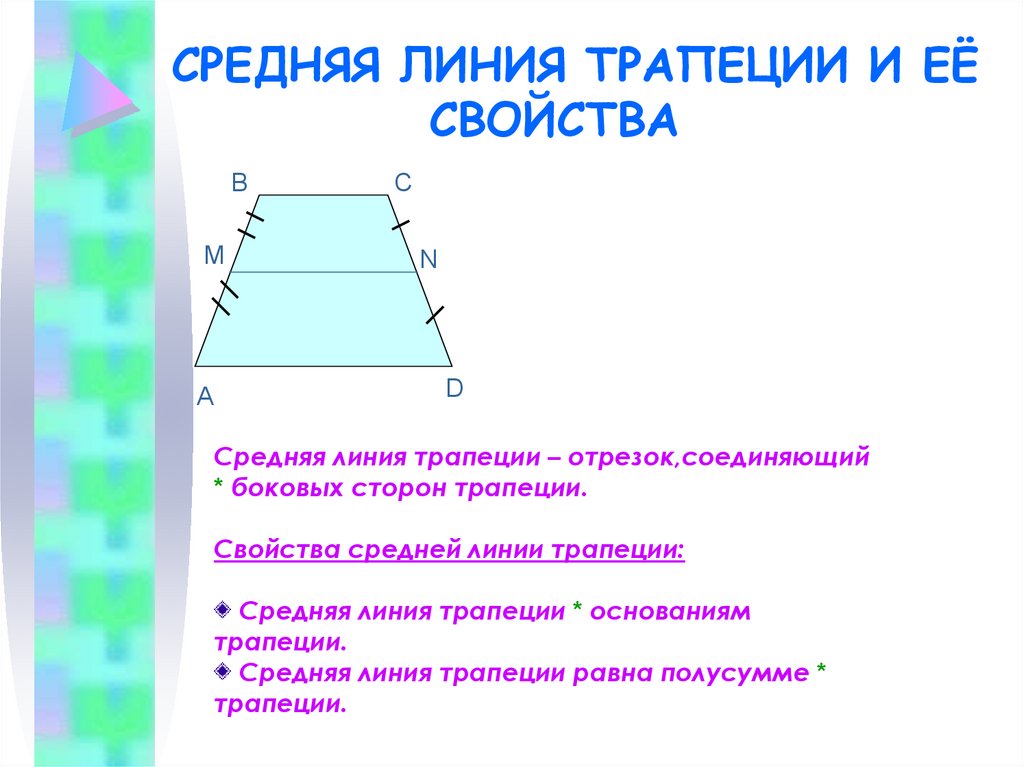 Что является мерой ZR?
2.В равнобедренной трапеции ЛОВУШКА, если градусная мера
ZT = 120 градусов. Какова мера ZA?
1. Найдите меру x на приведенном ниже рисунке справа.
72quot;
4. В градусах найдите меру суммы углов x и y на приведенном ниже рисунке.
1209ЗАДАНИЕ 4: Покажи мне!
Теорема 3. Диагонали равнобедренной трапеции конгруэнтны.
Дано: Равнобедренная трапеция ROMA
Докажите: RM = АО
Доказательство:
Заявления
Причины
ВЫБОР
Заявления:
1.
1. Дано
a.Равнобедренная трапеция ROMA
2.ИЛИ = МА
2.
б.АРОМ = ААМО
Причины:
3.ЗРОМ = ЗАМО
3.
а. определение равнобедренного сустава
4.0M = МО
4.
трапеция
5.
5. Постулат конгруэнтности SAS
б. СПКТС
в. углы основания равнобедренного
6.РМ = АО
6.
треугольники равны
д. возвратное свойство
22
Что является мерой ZR?
2.В равнобедренной трапеции ЛОВУШКА, если градусная мера
ZT = 120 градусов. Какова мера ZA?
1. Найдите меру x на приведенном ниже рисунке справа.
72quot;
4. В градусах найдите меру суммы углов x и y на приведенном ниже рисунке.
1209ЗАДАНИЕ 4: Покажи мне!
Теорема 3. Диагонали равнобедренной трапеции конгруэнтны.
Дано: Равнобедренная трапеция ROMA
Докажите: RM = АО
Доказательство:
Заявления
Причины
ВЫБОР
Заявления:
1.
1. Дано
a.Равнобедренная трапеция ROMA
2.ИЛИ = МА
2.
б.АРОМ = ААМО
Причины:
3.ЗРОМ = ЗАМО
3.
а. определение равнобедренного сустава
4.0M = МО
4.
трапеция
5.
5. Постулат конгруэнтности SAS
б. СПКТС
в. углы основания равнобедренного
6.РМ = АО
6.
треугольники равны
д. возвратное свойство
22
… Показать больше
Транскрипция текста
Давайте сделаем упражнение V.4!
Инструкция: Применим теорему о равнобедренной трапеции, ответив на следующие вопросы.
Обратитесь к данному рисунку справа.
1. В равнобедренной трапеции ROMA, какова мера АО
если RM измеряет 20 см?
2. Какова мера AE, если RM измеряет 20 см и OE
размер 15см?
3. Какова мера RM, если AE измеряет 8 см, а OE
размер 12см?
4. Какова мера OE, если RM измеряет 22 см и AE
размер 9см?
Поздравляем! Вы завершили доказательство теорем о трапециях.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
ОТРАЖЕНИЕ
Брайант, М.Л., Булалайао, Л.Е., Калланта, М.М., Круз, Дж.Д., Де Вера, Р.Ф.,
Напишите короткую лирику из определенного
Гарсия, Г.Т., Хавьер, С.Е., Лазаро, Р.А., Местерио, Б.Дж. Саладино,
песня, которая представляет ваши чувства
RHA, (2014), Материал для учащихся по математике 9, типография ФЭФ.
при ответе на действия.
https://www.wyzant.com/resources/lessons/math/geometry/quad
Нотралы/трапеции и воздушные змеи
https://www.onlinemathlearning.com/trapezoid-median.html
https://www.ck12.org/geometry/properties-of-equality-and-
конгруэнтность/урок/Свойства-равенства и-конгруэнтности-BSC
ГЕОМ/
https://mathbitsnotebook.com/Geometry/Quadrilaterals/QDTropki
4.1209 4. 13см
4. ЗА
4. 24см
3. 108 3. 20см
3. 35
3. 30см
te.html4: ".
Какова мера AE, если RM измеряет 20 см и OE
размер 15см?
3. Какова мера RM, если AE измеряет 8 см, а OE
размер 12см?
4. Какова мера OE, если RM измеряет 22 см и AE
размер 9см?
Поздравляем! Вы завершили доказательство теорем о трапециях.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
ОТРАЖЕНИЕ
Брайант, М.Л., Булалайао, Л.Е., Калланта, М.М., Круз, Дж.Д., Де Вера, Р.Ф.,
Напишите короткую лирику из определенного
Гарсия, Г.Т., Хавьер, С.Е., Лазаро, Р.А., Местерио, Б.Дж. Саладино,
песня, которая представляет ваши чувства
RHA, (2014), Материал для учащихся по математике 9, типография ФЭФ.
при ответе на действия.
https://www.wyzant.com/resources/lessons/math/geometry/quad
Нотралы/трапеции и воздушные змеи
https://www.onlinemathlearning.com/trapezoid-median.html
https://www.ck12.org/geometry/properties-of-equality-and-
конгруэнтность/урок/Свойства-равенства и-конгруэнтности-BSC
ГЕОМ/
https://mathbitsnotebook.com/Geometry/Quadrilaterals/QDTropki
4.1209 4. 13см
4. ЗА
4. 24см
3. 108 3. 20см
3. 35
3. 30см
te.html4: ".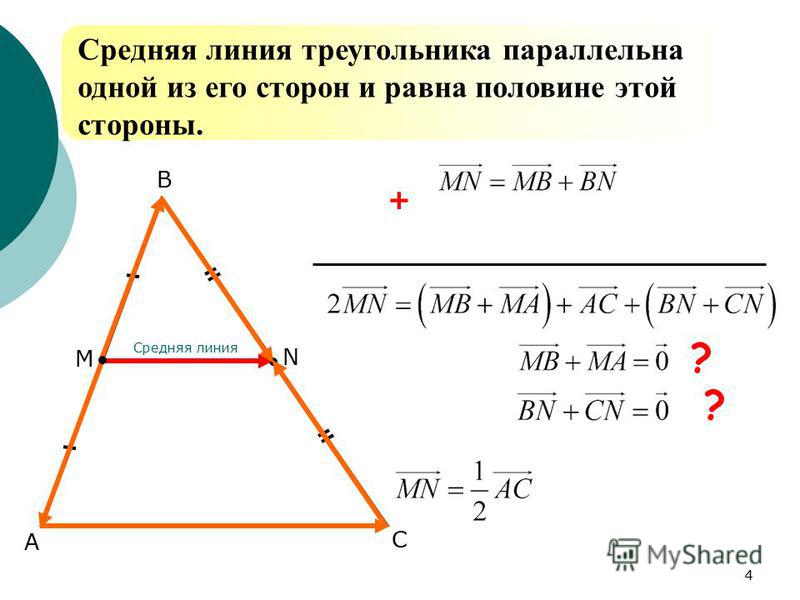 text=DEFINITIONX34%20AnX20равнобедренный*20трапециевидныйx
2. 6092. 5см
2. 115
2. 11см
20is.its: 20is%20an* 20равнобедренный* 20трапеция.
1. 1209 1. 20см
1. 60
1. 25см
https://sciencestruck.com/geometry-terms
Т.4
Т.3
Т.2
В.1!
https://www.nagwa.com/en/worksheets/723150624896/0. ~:текст=
Давайте сделаем некоторые упражнения
Truex: 20or% 20Falsex 34%:20TheX: 20midse
Причины: 2.а; 3.в; 4.г; 6.б
0of 20thex 20trapezoid.&text=%FOX90%90%84%20%FOX9090
Утверждения: 1.а;5.б
85%20%FOX9090%8620%FOX9090%87%20ис.%FOX90x90
Действие 4:
15 г; 17.f
DX690% 86%20.
2.а; 3.к; 5.б; 7.к; 8.в; 9.1; 11.г; 13.ч; 14.д;
Мероприятие 3:
https://www.freemathhelp.com/feliz-trapezoids.html
2. ф; 5. д; 8. д; 9. в; 11. б; 12. а; 14. г
Действие 2:
4.а; 5. б; 6. в; 8. д; 10. е
Действие 1:
Ключ ответа
Приготовленный:
КРИСТИН Р. ОПИАНА
23
text=DEFINITIONX34%20AnX20равнобедренный*20трапециевидныйx
2. 6092. 5см
2. 115
2. 11см
20is.its: 20is%20an* 20равнобедренный* 20трапеция.
1. 1209 1. 20см
1. 60
1. 25см
https://sciencestruck.com/geometry-terms
Т.4
Т.3
Т.2
В.1!
https://www.nagwa.com/en/worksheets/723150624896/0. ~:текст=
Давайте сделаем некоторые упражнения
Truex: 20or% 20Falsex 34%:20TheX: 20midse
Причины: 2.а; 3.в; 4.г; 6.б
0of 20thex 20trapezoid.&text=%FOX90%90%84%20%FOX9090
Утверждения: 1.а;5.б
85%20%FOX9090%8620%FOX9090%87%20ис.%FOX90x90
Действие 4:
15 г; 17.f
DX690% 86%20.
2.а; 3.к; 5.б; 7.к; 8.в; 9.1; 11.г; 13.ч; 14.д;
Мероприятие 3:
https://www.freemathhelp.com/feliz-trapezoids.html
2. ф; 5. д; 8. д; 9. в; 11. б; 12. а; 14. г
Действие 2:
4.а; 5. б; 6. в; 8. д; 10. е
Действие 1:
Ключ ответа
Приготовленный:
КРИСТИН Р. ОПИАНА
23
… Показать больше
Ответ и объяснение
Решено проверенным экспертом
Рейтинг Helpful
или nec facilis.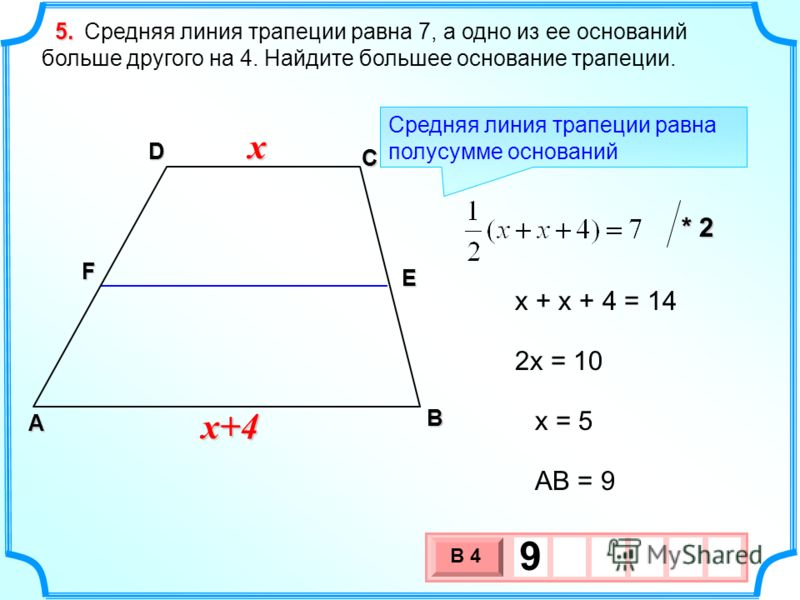 Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Начни лекцию
Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Начни лекцию
Итур Лаореет. Нам р
, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacini
Получите полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
Пошаговое объяснение
6 Вложения
jpg
jpg
jpg
jpg
jpg
jpg
Отзывы учащихся
100% (1 оценка)
Средняя линия треугольника, средняя линия трапеции. Средняя линия трапеции Средняя линия трапеции atanasyan презентация
Определение: Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. АК = КС БЭ = СЕ КЕ — средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A BC K N E AH = HB KE = CE NOT — средняя линия ABC A B C K E Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
A BC K N E AH = HB KE = CE NOT — средняя линия ABC A B C K E Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
Средняя линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А С В М К Дано: АВС, МК — средняя линия Доказательство: Так как по условию МК — средняя линия, то АМ = МБ = ½ АВ, СК = КВ = ½ ВС, Значит, ВМ АВ ВК ВС 1 2 В — общее для АВС и МВК, значит, АВС и МВК подобны по второму признаку подобия, следовательно, ВМК = А, а значит, МК АС. Докажите: МК AS, MK = ½ AS MK AS 1 2 Из подобия треугольников также следует, что, то есть MK = ½ AS.
Решить проблему F R N? А Б
Доказательство: Проведем А 1 В 1 А В С А1А1 В1В1 О С1С1 По условию АА 1, ВВ 1 — средние средние, БА 1 = СА 1, АВ 1 = СВ 1, т.е. А 1 В 1 — средние линия. Отсюда А 1 В 1 АВ, следовательно, 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны в двух углах. Это означает, что их стороны пропорциональны: AO VO AB A1OA1O B1OB1O A1B1A1B1 По свойству средней линии треугольника AB = 2 A 1 B 1 , т.е.
Это означает, что их стороны пропорциональны: AO VO AB A1OA1O B1OB1O A1B1A1B1 По свойству средней линии треугольника AB = 2 A 1 B 1 , т.е.
Средняя линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме. А В С К М Р Дано: АВСК — трапеция МР — средняя линия Докажите: МР АК, МР ВС МР = Доказательство: О Проведите прямую МЭ АК через точку М, докажите, что МЭ пройдет через Р.Т.К. АБСК — трапеция, тогда ВС АК, а, следовательно, ВС МЕ АК. Так как МР — средняя линия, то АМ = МВ, КР = СР Е Следовательно, МР лежит на МЕ, а значит, МР АК, МР ВС. Запустим ВК. По теореме Фалеса О — середина ВК, значит, МО — средняя линия АВК, ОП — средняя линия ВСК МР = МО + ОП = ½ АК + ½ ВС = ½ (АК + ВС ) = По теореме Фалеса МЭ пересечет СК в середине СК т.е. в точке Р.
«Площадь занятия трапецией» — В прямоугольной трапеции основания 5см. и 17см., а меньшая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто набрал 5, 4, 3 балла? В каждом случае сформулируйте доказанную теорему. Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?
Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?
«Задачи на теорему Пифагора» — №21 Находка: Х. №18 Находка: Х. №27 Находка: X. Задачи на готовые рисунки («Теорема Пифагора»). №23 Находка: Х. №25 Находка: Х. №26 Находка: Х. №13 Находка: Х. №20 Находка: Х. №19Находка: Х. №14 Находка: Х. Вы выполнили все предложенные задания. №29 Находка: Х. №28 Находка: Х. №30 Находка: Х. №22 Находка: Х.
Теорема Фалеса — Фалес широко известен как геометр. Астрономия. Милетский материалист. Проведем через точку В2 прямую ЕF, параллельную линии А1А3. Из равенства треугольников следует равенство сторон В1В2 = В2В3. Теорема Фалеса. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Треугольники B2B1F и B2B1E равны по второму знаку равенства треугольников.
«Теорема синусов» — Стороны треугольника пропорциональны синусам противоположных углов. Решение: Устная работа: Ответы на задания по рисункам: Проверка домашнего задания.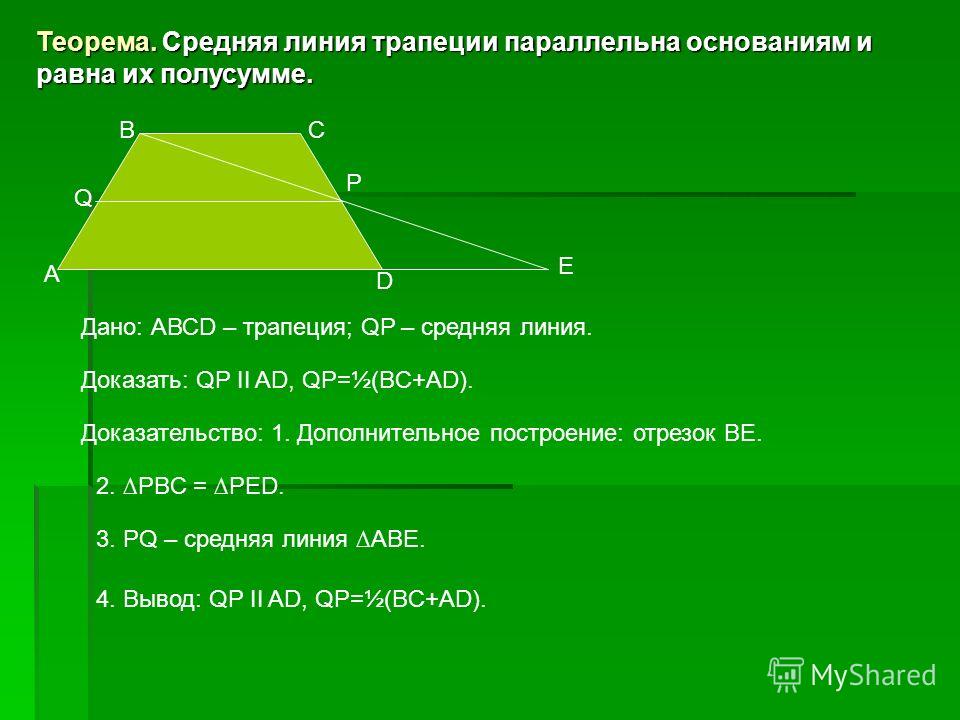 Тема урока: Теорема синусов. Теорема синусов:
Тема урока: Теорема синусов. Теорема синусов:
«Урок по теореме Пифагора» — Определить вид треугольника: Знакомство с теоремой. Доказательство теоремы. Разогревать. Теорема Пифагора. И вы найдете лестницу длиной 125 футов. План урока: Историческая справка. Отображение картинок. Решение простейших задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить тип четырехугольника КМНП.
«Теорема Пифагора 8 класс» — ЦИФРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катет c- гипотенуза. Высота. Доказательство Бхаскари. Открытия пифагорейцев в математике. Дано: Треугольник прямоугольный, а, b — катеты, с — гипотенуза Докажите: с2 = а2 + b2. Меньшая сторона прямоугольного треугольника.
резюме других презентаций
«Построение правильных многоугольников» -? = 60?. ? 180. Геометрия. ? =. н. п — 2. Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
«Теорема Фалеса» — Теорема Фалеса. Геометрическая теорема названа в честь Фалеса. Астрономия. Проведем через точку В2 прямую ЕF, параллельную линии А1А3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии ученицы 9 «А» класса Сорогиной Полины. Милетский материалист. Геометрия. По свойству параллелограмма A1A2 = FB2, A2A3 = B2E. Фалес широко известен как геометр. А так как А1А2=А2А3, то FB2=B2E.
Геометрическая теорема названа в честь Фалеса. Астрономия. Проведем через точку В2 прямую ЕF, параллельную линии А1А3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии ученицы 9 «А» класса Сорогиной Полины. Милетский материалист. Геометрия. По свойству параллелограмма A1A2 = FB2, A2A3 = B2E. Фалес широко известен как геометр. А так как А1А2=А2А3, то FB2=B2E.
«Разложение вектора на два неколлинеарных» — Пусть p коллинеарно b. Доказательство: Разложение вектора на два неколлинеарных вектора. Доказательство. Пусть a и b — неколлинеарные векторы. Лемма: Если векторы a и b коллинеарны и a? 0, то существует число k такое, что b = ka. Докажем, что любой вектор p можно разложить по векторам a и b. Геометрия 9 класс. Тогда p = yb, где y — некоторое число.
«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе. Луковникова Н.М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 Томск-2007г.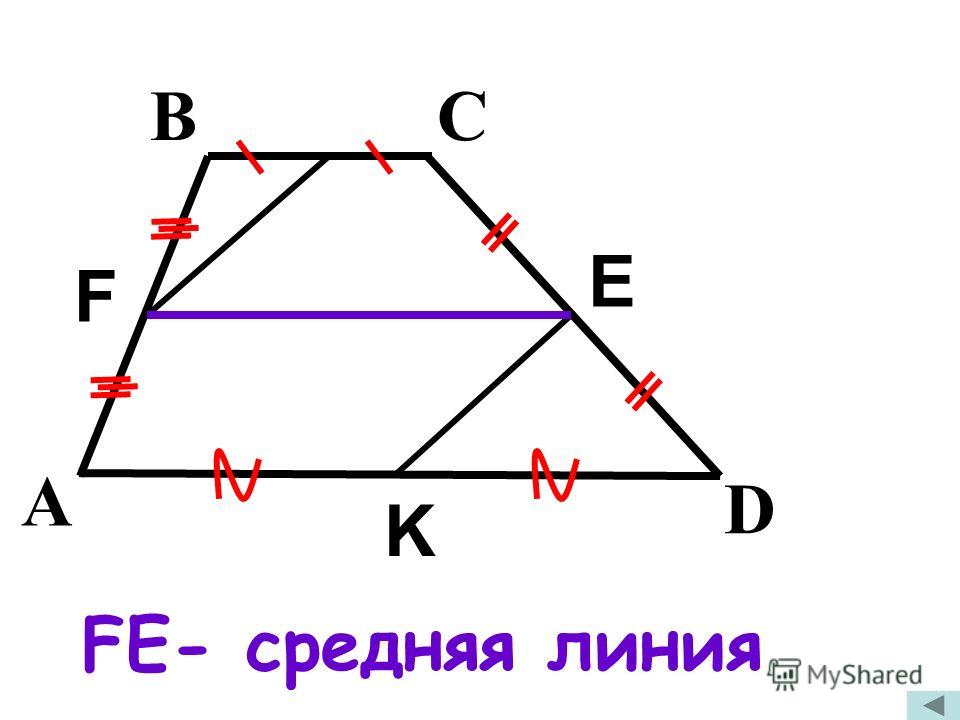 Правильные многоугольники.
Правильные многоугольники.
«Симметрия фигур» — Линия а называется осью симметрии фигуры. D. Одна форма получается из другой путем трансформации. Оглавление. Обратное преобразование движения есть тоже движение. А1. Выполнил: Пантюков Е. А. Существует множество различных типов симметрии. М1. Трансформация фигур.
«Симметрия относительно прямой» — Фигура может иметь одну или несколько осей симметрии. Симметрия в природе. Савченко Миша, 9Б класс. Угол. Кто изображен на оригинальном фото? Л.С. Атанасяна «Геометрия 7-9». Равнобедренная трапеция. Постройте отрезок А1В1, симметричный отрезку АВ относительно прямой. Сколько осей симметрии у каждой фигуры? Прямоугольник.
Для использования предварительного просмотра презентаций создайте себе учетную запись Google (аккаунт) и войдите в it: https://accounts.google.com
Подписи к слайдам:
Средняя линия (8 класс)
Средняя линия треугольника
Средняя линия треугольника Определение: Отрезок, соединяющий середины Две стороны треугольника называются СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА. 0003
0003
Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. то есть: КМ ║ АС КМ = ½ АС А Б В К М
Решить задачу устно: А Б В К М 7 см Дано: М К — среднее. Строковый поиск: AU?
Работая в парах:
Решим задачу: Дано: MN — ср. линия Найти: P ∆ ABC M N A B C 3 4 3, 5
Работая в парах:
Средняя линия трапеции
Напомним: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны A D B C BC || AD — основания AB łł CD — стороны
Средняя линия трапеции. Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A D B C M N MN — средняя линия трапеции ABCD
Теорема о средней линии трапеции Средняя линия трапеции параллельна ее основаниям и равна их полусумме. то есть: M N ║BC║A D M N = ½ (ВС + А D) M N A D B C
Решить устно: M N A D B C 6,3 см 18,7 см?
Решите устно в парах: Дано: АВ = 16 см; CD = 18 см; М Н = 15 см. Найти: Р ABCD = ? М Н А Д Б В
Найти: Р ABCD = ? М Н А Д Б В
Самостоятельная работа Задача: Средняя линия трапеции равна 5см. Найдите основания трапеции, если известно, что нижнее основание в 1,5 раза больше верхнего. Решение: A D B C 5 см Пусть ВС = Х см тогда AD = 1,5Х см ВС + AD = 10 см Х + 1,5Х = 10 Х = 4 Значит: ВС = 4 см AD = 6 см
СПАСИБО ЗА УРОК!!!
Презентацию разработала Лугвина Наталья Анатольевна Лугвина, учитель математики, СОШ № 467 г. Санкт-Петербурга, Колпинский район
По теме: методические разработки, презентации и конспекты
Урок обобщения и закрепления знаний по теме «Средняя линия треугольника. Средняя линия трапеции» в 8 классе с использованием ИКТ….
Рабочая тетрадь – индивидуальное творческое задание учащегося. который предполагает самостоятельную работу с текстом по теме «Трапеция. Средняя линия трапеции», применение знаний при решении задач. …
Тема «Средняя линия трапеции» является одной из важных тем курса геометрии. Эта фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные по этой теме, часто встречаются в выпускных экзаменах и аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.
Задания, содержащие данные по этой теме, часто встречаются в выпускных экзаменах и аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.
Хоть в теме и заявлена фигура трапеция, но рассмотрение данной темы может проходить в ходе изучения темы «Векторы» и «Использование векторов при решении задач». Понять это можно, взглянув на слайд презентации.
Здесь автор определяет срединную линию как отрезок, соединяющий середины сторон. Причем здесь также отмечено, что средняя линия трапеции параллельна ее основаниям, а также равна их полусумме. Именно в ходе доказательства этого утверждения и пригодятся знания, связанные с векторами. Применяя правила сложения векторов по рисунку, приведенному в качестве иллюстрации условия, получаются равенства. Эти равенства имеют одну и ту же левую часть, и это средняя линия трапеции в виде вектора. Складывая эти равенства, мы получаем большое выражение в правой части равенства.
слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)
Если внимательно рассмотреть, то в двух случаях получается сложение противоположных векторов, в результате чего получается ноль . Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащих основания. Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, составляет половину суммы векторов, содержащих основания. Теперь векторы сравниваются. Получается, что все эти векторы имеют одинаковое направление. Это означает, что знаки векторов можно смело опускать. И тогда получается, что самая средняя линия трапеции равна полусумме оснований.
Презентация содержит один слайд, несущий много информации. Здесь дано определение средней линии трапеции и указано ее основное свойство. В курсе геометрии это свойство является теоремой. Вот как доказывается теорема, используя знание понятия векторов и действий над ними.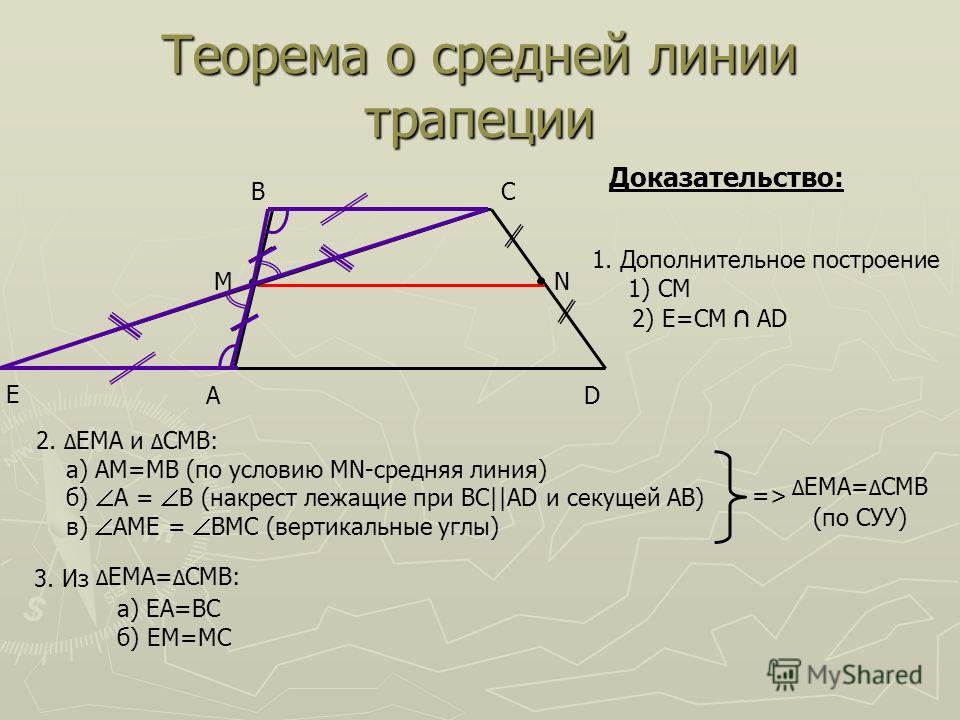

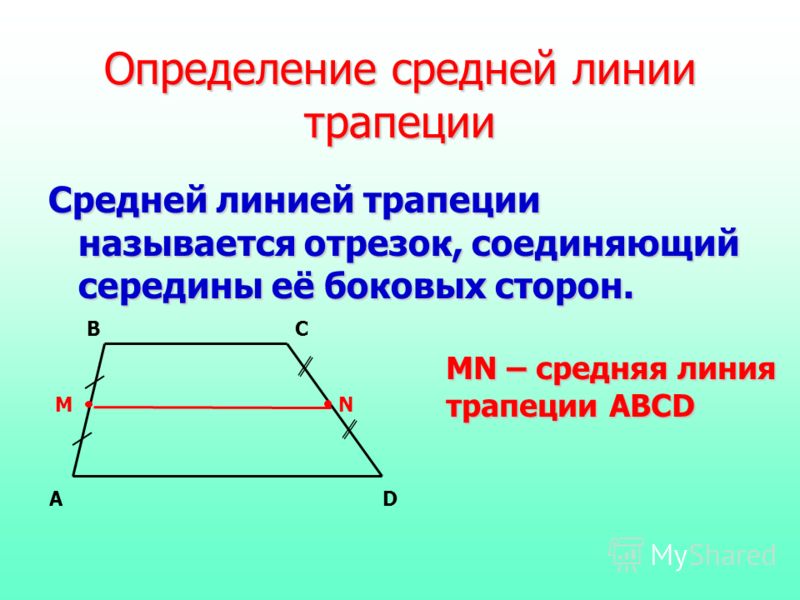
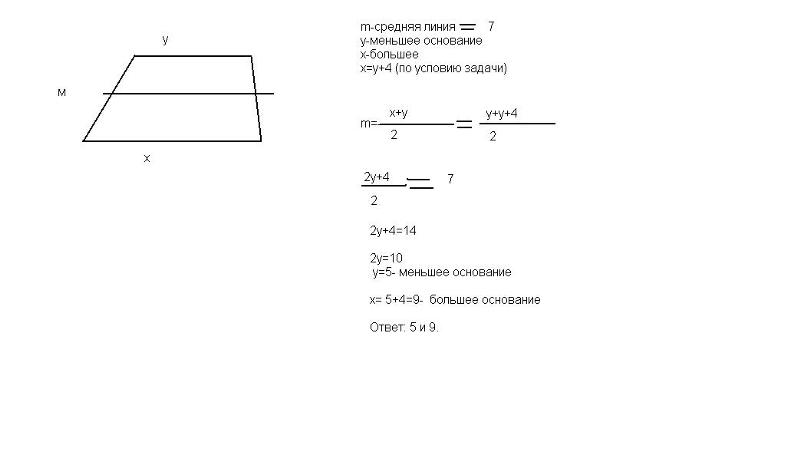
 р
р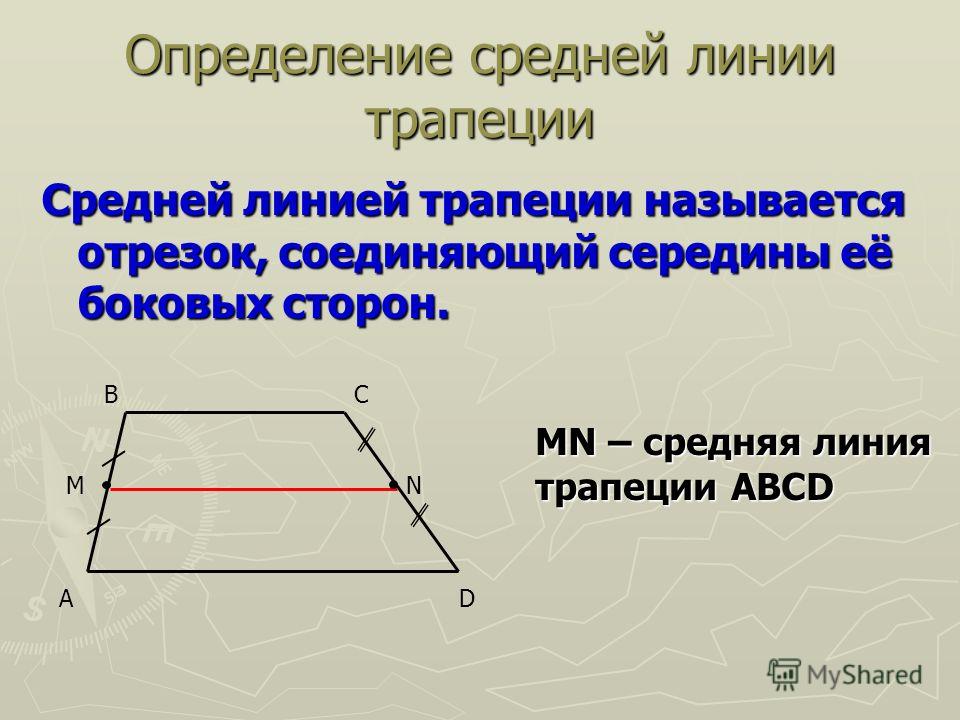 ПОБУЖДЕНИЕ 5’
ПОБУЖДЕНИЕ 5’
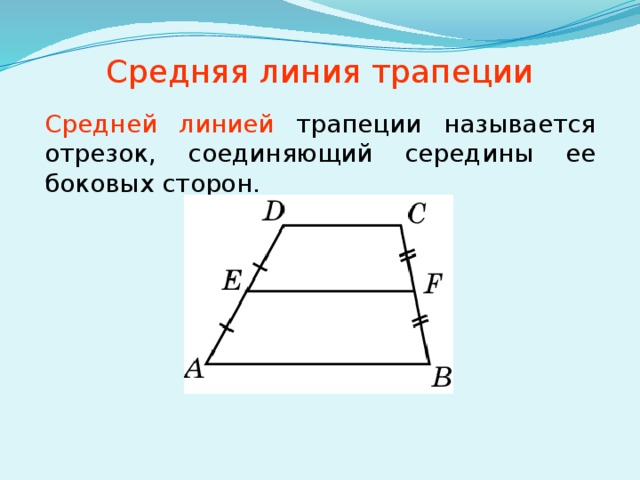
 ПРИМЕНЕНИЕ 24’
ПРИМЕНЕНИЕ 24’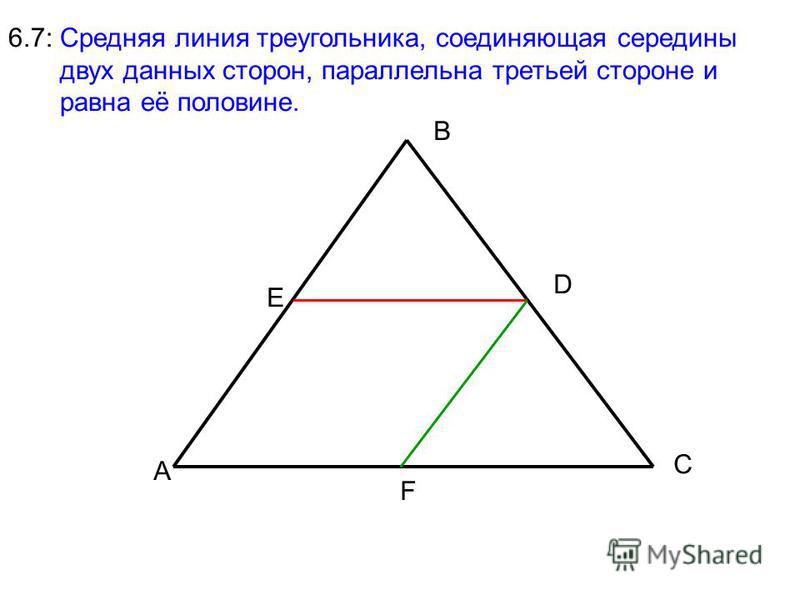 1 группа представляет доклад как разговор подружек, 2 группа – как статья в научный журнал, 3 группа как репортаж с урока, 4 группа – как объяснение родителям.
1 группа представляет доклад как разговор подружек, 2 группа – как статья в научный журнал, 3 группа как репортаж с урока, 4 группа – как объяснение родителям.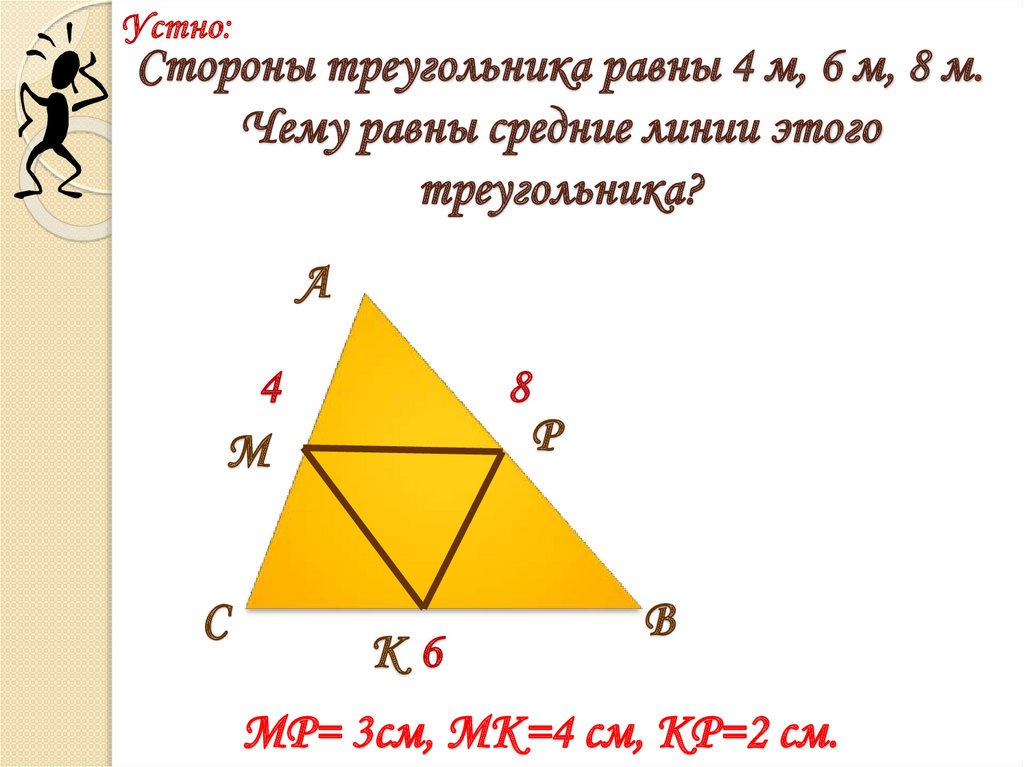 Формативное оценивание.
Формативное оценивание.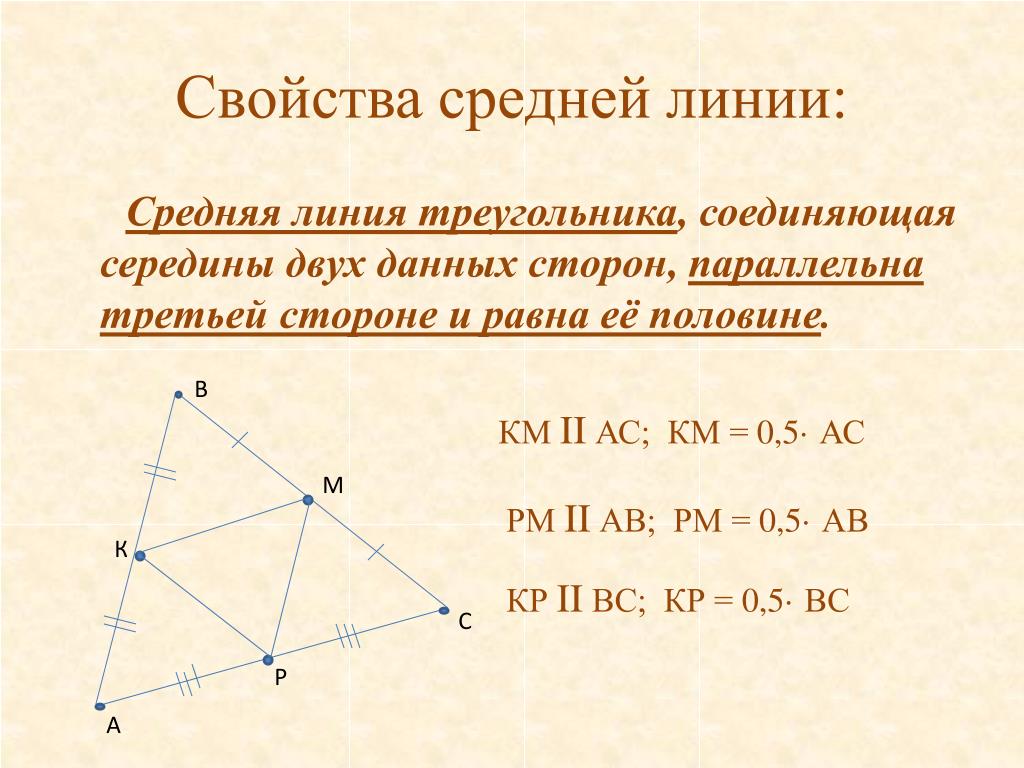
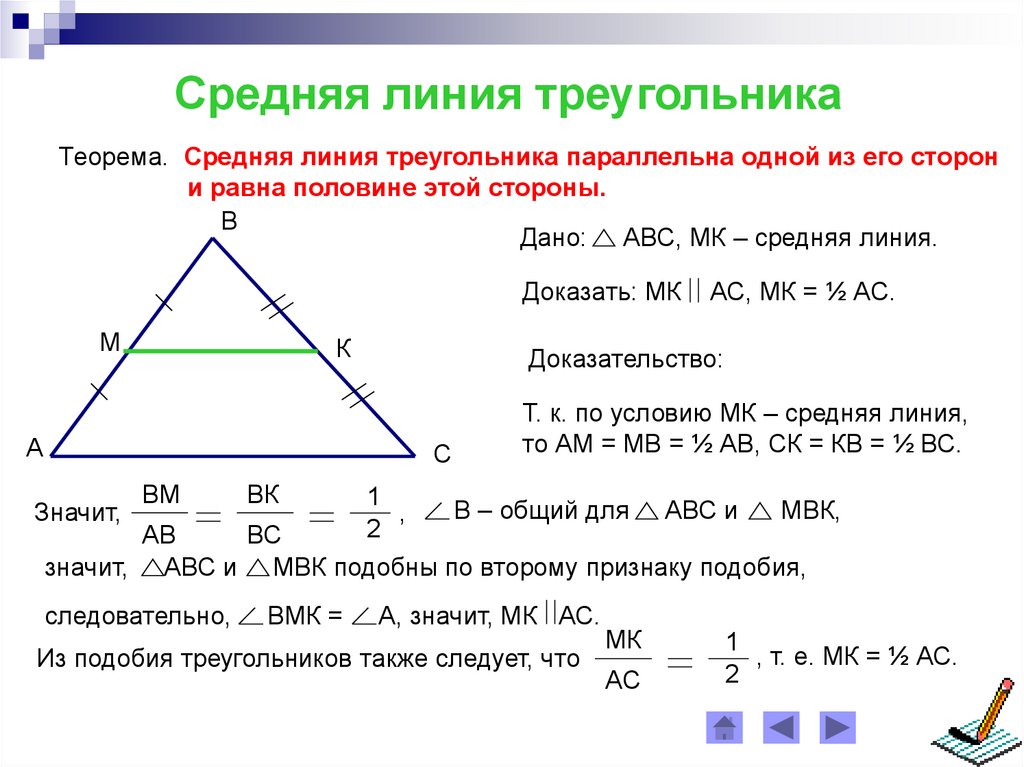
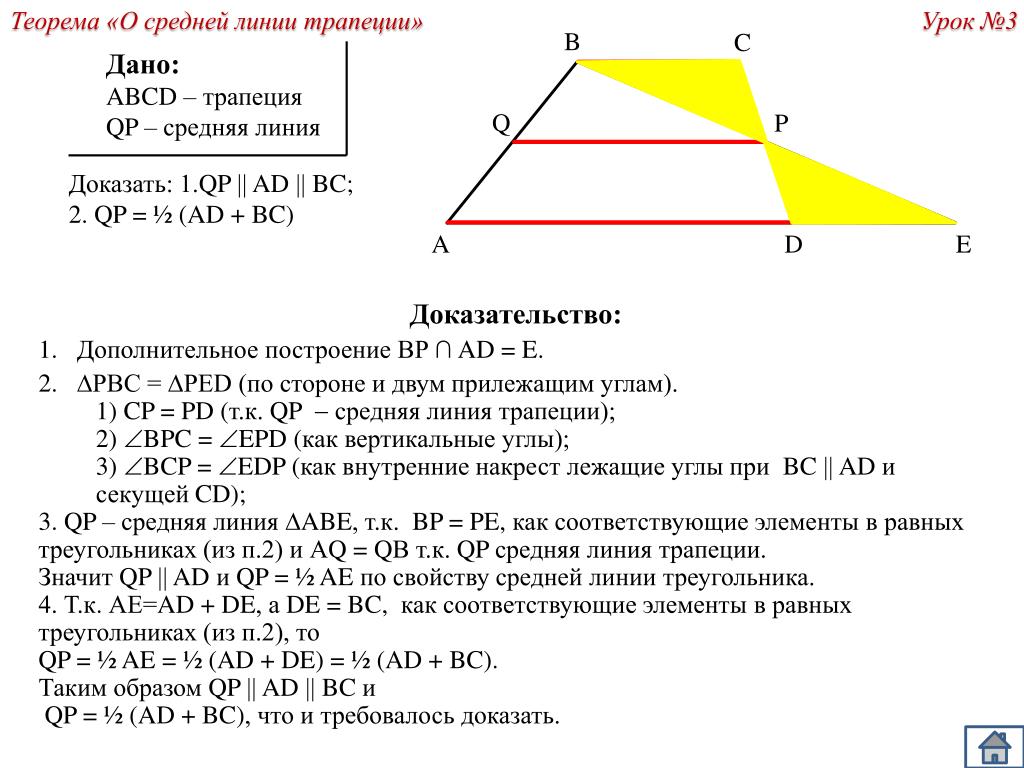 Записывают д\з в дневник.
Записывают д\з в дневник.