Медиана в статистике
Медиана вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).
* не важно, дискретного или интервального, генеральной совокупности или выборочной.
Медиану можно отыскать несколькими способами. Если даны первичные данные, то сортируем их по возрастанию либо убыванию и находим середину ранжированного ряда: . Почему именно 13-я варианта? Потому что перед ней находится 12 чисел и после неё тоже 12 чисел, таким образом, значение разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически:
– если совокупность содержит нечётное количество вариант (наш случай), то делим её объём пополам: и округляем полученное значение в бОльшую сторону: 13 – получая тем самым номер искомой варианты;
– если совокупность содержит чётное количество вариант, например 20, то делаем то же самое: и медианное значение рассчитываем как среднее
арифметическое 10-й и следующей варианты: .
Подчёркиваю, что изложенная выше инструкция работает для упорядоченного (по возрастанию либо убыванию) ряда. Но есть и
более быстрый путь, где ничего не нужно сортировать. Это использование стандартной функции Экселя:
– забиваем в любую свободную ячейку =МЕДИАНА(, выделяем мышью все варианты, закрываем скобку ) и жмём Enter. Попробуйте самостоятельно. Этот способ удобен, когда вам дано много чисел.
Следует отметить, что в Экселе существуют и отдельные функции для вычисления средней (=СРЗНАЧ), моды (=МОДА) и ещё много чего, но я против использования этих функций в учебном курсе, за исключением случаев, где это действительно целесообразно. …Почему против? Потому что они не помогают понять суть показателей. Так, среднюю гораздо вразумительнее рассчитывать следующим образом:
=СУММ(выделяем мышью диапазон) / объем совокупности. Вычисления рекомендую опробовать лично (ссылка выше).
Ситуация вторая. Когда составлен либо изначально дан готовый дискретный ряд. Тут
можно поступить «по любительски» – начать отсчитывать примерно равное количество вариант по краям ряда:
после чего мысленно либо на черновике их отбрасывать, в данном случае отбросим по 8 штук сверху и снизу:
откуда становится ясно, что медианное значение:
Или в более солидном стиле, находим относительные накопленные
частоты:
и ту варианту, у которой «перевалила» за
отметку 0,5 (50% упорядоченной совокупности). Для варианты успело накопиться (32% совокупности), а вот для – уже (64%). Таким образом, отметка в 50% пройдена именно здесь, и, стало быть, .
Запишем красивый ответ:
И тут возникает следующий закономерный вопрос: а зачем вообще нужна мода с медианой? –
ведь есть средняя.
А дело в том, что в ряде случаев среднее значение неудовлетворительно характеризует центральную
тенденцию совокупности:
Пример 9
Известны результаты продаж пиджаков в универмаге города:
где – количество пуговиц на пиджаке, – число продаж.
Обратите внимание, что в условии задачи ничего не сказано о том, генеральная ли это совокупность или выборочная, и в подобной ситуации я не рекомендую ничего додумывать – среднюю просто обозначаем через , без подстрочного индекса.
Задание: вычислить среднюю. В экселевском файле уже забиты исходные данные и приведена краткая инструкция. Если под пальцами нет Экселя, считаем на калькуляторе. Ну а если вам не нравятся пиджаки, то представьте какие-нибудь шляпки с цветочками:)
….Есть? Какие мысли на счёт полученного значения ? …С такой статистикой магазин разорится.
Ещё хуже в этом смысле ситуация с медианой, продолжаем решать задачу в Экселе либо в тетради. Особо зоркие читатели, медиану углядят устно.
И, конечно, важнейший показатель здесь мода: . Потому что такая мода 🙂 Более того, в прикладных исследованиях рассматривают несколько модальных значений, в частности, ещё одной модой можно считать варианту . Но это уже «попсовая» статистика, которую я не буду развивать в настоящем курсе.
Теперь надеваем пиджаки / шляпы и возвращаемся на фабрику, где бухгалтер Петрова вычислила генеральную среднюю заработную плату рабочих: денежных единиц. Здесь мы плавно переходим к интервальному ряду, который целесообразно составлять для «денежных» показателей.
Что будет, если к совокупности добавить руководящий персонал и директора Петрова? Средняя зарплата немного увеличится: , и это уже будет несколько искажённая картина.
А вот если сюда добавить олигарха Петровского, то полученная средняя вообще вызовет широкое возмущение общественности.
Поэтому если в статистической совокупности есть «аномальные» отклонения в ту или иную сторону, то в качестве оценки центрального значения как нельзя лучше подходит медиана, которая в нашем условном примере будет равна, скажем, . Ниже этой планки зарабатывает ровно половина сотрудников фабрики и выше – другая половина, включая Петрова и Петровского. …Главное только, чтобы они наняли правильного статистика 🙂
3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?
3.1.2. Мода
| Оглавление |
Азбука медицинской статистики. Глава I. C чего начинается статистический анализ?
Вся статистика — это изучение того, как один параметр влияет на другой, как они соизменяются
Досье КС
Константин Кравчик
Математик-аналитик. Специалист в области статистических исследований в медицине и гуманитарных науках
Москва
На сегодняшний день существует огромное количество статей по клиническим исследованиям.
Клиницист, стремящийся к глубоким знаниям, наверняка знает про базы медицинских статей, например, pubmed, eMedicine World Medical Library, National Library of Medicine — National Institutes of Health и так далее. Статьи в этих базах написаны строгим научным языком, с указанием методов статистического анализа. Читатель, не искушенный в статистике, встречается с большим количеством неясных ему терминов, например: «анализ мощности» и «расчет количества выборки», «критерии сравнения средних», «корреляции», «отношения шансов», «пропорциональные риски» и так далее. Если читатель не понимает, что это такое, то он или закроет статью, или не сможет оценить, адекватно ли автор применил статистические методы для анализа эмпирических данных и можно ли доверять полученным выводам. Итак, начнем с азов.
Медиана, мода, среднее, разброс
Рассмотрим пример: исследование охватило 200 человек с ожирением. Вес участников исследования колебался от 105 до 203 кг. Это разброс значений, или дисперсия.
Средний вес составил 120 кг — это среднее значение веса в выборке. К примеру, 30 из 200 человек имели вес 115 кг. Остальные весили по‑разному, поэтому 115 — оказалось самым «популярным» значением веса в выборке, то есть модой веса.
Даже на базе этих данных мы можем составить представление о том, как выражен изучаемый признак: большинство участников исследования весило ближе к 100 кг, и только немногие весили около 200. Кроме определения «чистого» веса можно, например, ранжировать (разделить) пациентов по индексу массы тела — ИМТ. Например, 1 — ожирение первой степени (ИМТ 30–35), 2 — ожирение второй степени (ИМТ 35–40), 3 — ожирение третьей степени (ИМТ более 40). И тут мы плавно подходим к понятию шкал переменных.
Какие бывают шкалы
Для справки
Медиана — значение, которое делит ряд чисел (распределение) ровно пополам, так что одна половина больше этого значения, а вторая меньше. Например, семерка для ряда чисел 2, 3, 3, 4, 7, 5, 6, 9, 9. Если в выборке чётное число элементов, медиану чаще всего высчитывают как полусумму двух соседних значений.
Например, медиану набора {1, 3, 5, 7} принимают равной 4.
Мода — значение во множестве наблюдений, которое встречается наиболее часто. Мода достаточно редко встречается в медицинских исследованиях, однако является базовым понятием статистики.
Общепринято использовать классификацию шкал измерения, предложенную американским психологом Стенли Стивенсоном еще в 1946 году.
1. Номинативная (категориальная) шкала
Это шкала классификации каких‑то категорий. Например, пациентов можно разделить по полу, по уровню холестерина в крови (высокий, низкий, средний), степеням ожирения, как в приведенном примере, и т. п.
С этой шкалой нельзя производить никаких математических действий (сложение, деление, вычитание, умножение). Номинативные переменные часто называют группирующими, они нужны, для того чтобы разбить выборку на осмысленные категории.
2. Порядковая (ранговая) шкала
Показывает степень выраженности признака, когда приписывается ранг от «очень слабо выражен» до «очень сильно выражен».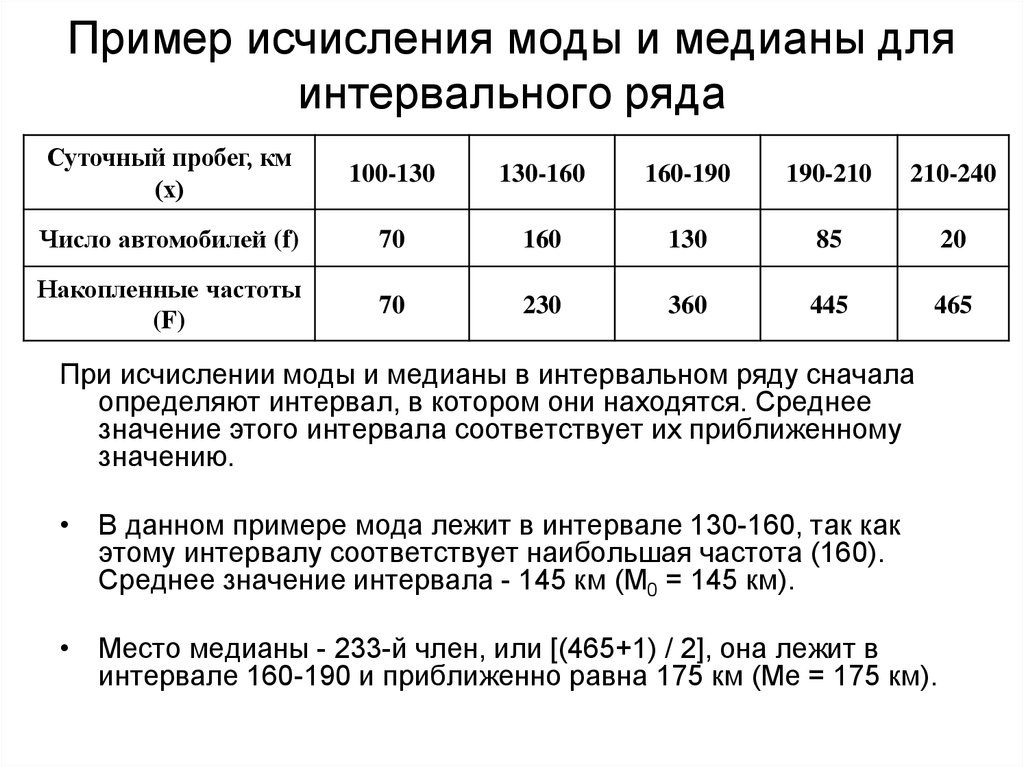
Частный случай ранговой шкалы — это шкала суммарных оценок Лайкерта, которая часто используется в опросниках.
Например, в Болевом опроснике Мак-Гилла есть вопрос:
Как Вы оцениваете свою боль? Ответы: слабая, умеренная, сильная, сильнейшая, невыносимая.
Если пациент Петров описал свою степень боли как сильную, а пациент Иванов как невыносимую, мы понимаем, что Иванову скорее всего больнее, чем Петрову, условно говоря, на 2 пункта. Однако ранги — это неметрическая шкала, которая не несет количественной информации.
Еще к специфичным ранговым шкалам можно отнести шкалу Жана Стэпела. Это 10‑балльная шкала без нулевой точки, которая позволяет оценить, насколько верно или неверно каждое утверждение описывает вопрос. Например, вопрос к пациенту: «Вы считаете, что терапия этим лекарством Вам помогла?».
Да, терапия эффективна:
– 5, – 4, – 3, – 2, – 1, 1, 2, 3, 4, 5
Нет, терапия неэффективна:
– 5, – 4, – 3, – 2, – 1, 1, 2, 3, 4, 5.
Чем выше число, тем больше согласие с утверждением.
С помощью ранговых шкал мы можем, во-первых, высчитать меру разброса, моду и медиану, а во‑вторых, сравнивать признак в нескольких выборках, например, у мужчин и женщин, в группе вмешательства и группе плацебо. Данные методы будут рассмотрены в следующих выпусках журнала.
Среднее обычно не используется для ранговых шкал. Если мы сравниваем ранги между группами (например, до курса лечения и после), мы сравниваем медианы. Однако для шкал Лайкерта и Стэпела мы можем высчитать среднее значение.
3. Метрическая шкала
К ней относятся непрерывная шкала и шкала отношений (абсолютная шкала).
В непрерывной шкале значения лежат в диапазоне от минус бесконечности до плюс бесконечности. Классический пример — это температура по Цельсию. В этой шкале 0 («ноль») не означает отсутствие признака, например, температура воды в 0 ºС не означает, что у воды нет температуры.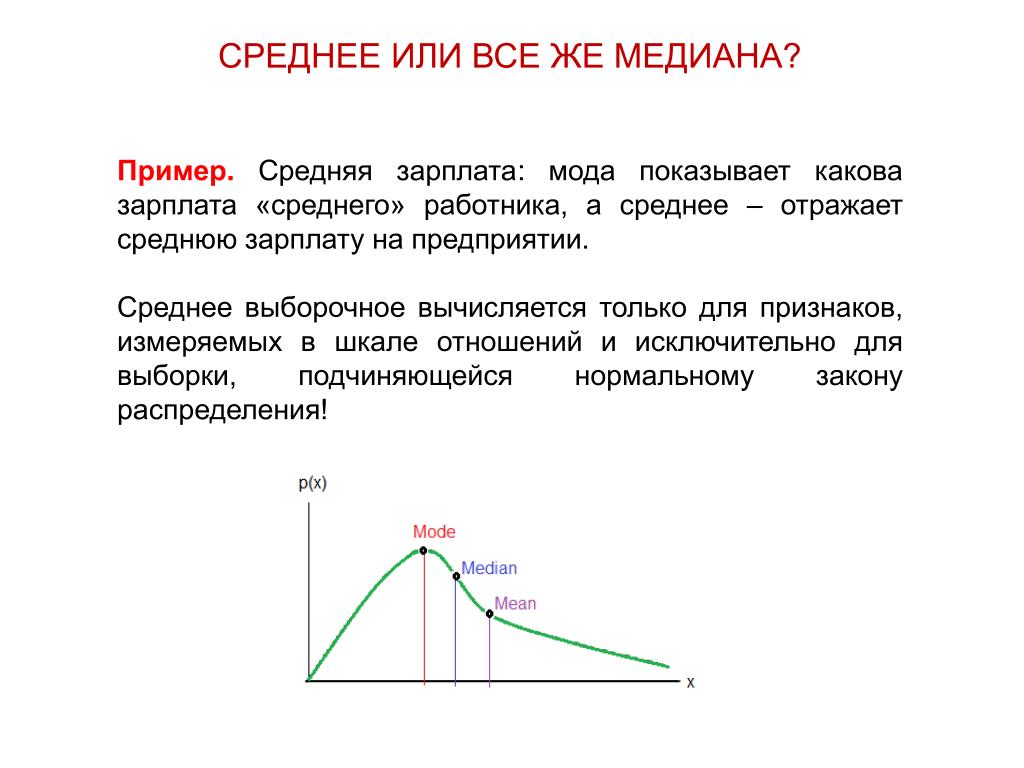
В этой шкале мы можем сказать, насколько больше или меньше выражен признак.
Шкала отношений такая же, как и непрерывная, но в ее случае 0 означает отсутствие признака. К примерам такой шкалы относятся рост, вес, возраст, т. к. не может быть роста минус 1,5 метра или веса в минус 50 килограмм.
К метрическим шкалам больше применимо среднее значение, медиана, а также мода. Однако со средним значением следует быть осторожным, т. к. оно чувствительно к крайне высоким и крайне низким значениям. Некорректное применение среднего значения иллюстрирует анекдот о средней температуре по больнице: у одних температура 40 °С, в морге уже остыли, но в среднем — 36,6°С.
М±SD
Часто в научных статьях мы видим такие понятия, как дисперсия, стандартное отклонение, размах. Это одни из самых важных понятий в статистике, и обозначают они меру разброса значений изучаемого признака.
Разброс — показатель того, насколько значения признака отклоняются от его среднего значения.
К каждой шкале применима своя мера разброса. Например, уровень гемоглобина — это метрическая шкала. Для такой шкалы характерная мера разброса — это дисперсия, показатель разнородности значений признака. Дисперсия (D) измеряется в квадратных единицах признака, в случае гемоглобина — (г/л)2, поэтому для удобства изучения можно извлечь корень из дисперсии √D и получить стандартное отклонение (standart diviation — SD), которое обозначают буквой σ (сигма). Стандартное отклонение характеризует разброс в обе стороны от среднего значения.
Для меры разброса ранговых шкал более применим размах, разница между максимальным значением признака и минимальным: max — min.
Для шкалы Лайкерта можно использовать стандартное отклонение.
Тем не менее иногда в статьях и диссертациях можно заметить, что размах используется совместно со стандартным отклонением для метрических переменных.
Среднее обозначают буквой µ (Мю) или М. Таким образом, если средний уровень гемоглобина µ=96, а стандартное отклонение σ=20, то диапазон значений лежит в пределах µ±σ (М±SD), или, в нашем случае, 96±20, то есть диапазон от 76 до 116.
Важно помнить, что в этом диапазоне будет лежать 68 % значений признака в случае нормального распределения, 95 % значений лежат в пределах двух сигм и 99 % лежат в пределах трех сигм, но об этом в следующем номере.
Как найти медиану для набора данных
Все ресурсы статистики AP
4 Диагностические тесты 140 практических тестов Вопрос дня Карточки Learn by Concept
AP Статистика Справка » Данные » Одномерные данные » Одномерные дескрипторы данных » Как найти медиану для набора данных
Шесть домов выставлены на продажу и имеют следующую долларовую стоимость в тысячах долларов:
535
155
305
720
315
214
Какова средняя стоимость шести домов?
Возможные ответы:
Правильный ответ:
Объяснение:
Медиана определяется путем упорядочения значений в группе от наименьшего к наибольшему: 155, 214, 305, 315, 535, 720.
Значение, находящееся непосредственно посередине, является медианой. Например, если есть пять чисел, третье является медианой. Здесь у нас четное количество значений, поэтому непосредственно посередине нет значения. Чтобы найти медиану при отсутствии самого среднего значения, найдите среднее значение двух средних значений. Среднее значение определяется путем сложения двух значений и деления на два (число в группе):
Сообщить об ошибке
Найти медиану множества.
Возможные ответы:
Правильный ответ:
Объяснение:
Медиана — это среднее значение набора в порядке возрастания.
В этом наборе из 11 записей медианой является 6-й элемент набора в порядке возрастания, или 6.
Сообщить об ошибке
Найти медиану набора
Возможные ответы:
Правильный ответ:
Объяснение:
Медиана — это среднее значение набора в порядке возрастания.
В этом наборе из 6 (или любого четного числа) записей медиана – это среднее значение двух средних записей набора в порядке возрастания
или
Сообщить об ошибке целое число.
Найдите медиану множества.
Возможные ответы:
Правильный ответ:
Объяснение:
Медиана — это среднее значение набора в порядке возрастания.
В этом наборе из 8 (или любого четного числа) элементов медиана – это среднее значение двух средних элементов набора в порядке возрастания
или
Сообщить об ошибке шесть игр и набирает следующие очки: 69, 78, 82, 69, 98, 85. Найдите медиану.
Возможные ответы:
69
82
75,5
80
Правильный ответ:8000 Объяснение:
Чтобы найти медиану выборки с четным размером выборки, упорядочите значения от наименьшего к наибольшему, возьмите два средних значения, сложите их и разделите на ноль.
69, 78, 82, 69, 98, 85
69, 69, {78, 82} 85, 98
(78+82) / 2 = 80
Сообщить об ошибке
Уведомление об авторских правах
Все статистические ресурсы AP
4 Диагностические тесты 140 практических тестов Вопрос дня Карточки Learn by Concept
Метод Python Statistics.median()
❮ Статистические методы
Пример
Вычислить медиану (среднее значение) заданных данных:
# Библиотека статистики импорта
статистика импорта
# Вычисление средних значений
print(statistics.median([1, 3, 5, 7, 9, 11, 13])) , 11]))
Попробуйте сами »
Определение и использование
statistics.median( ) Метод вычисляет медиану (среднее значение) заданных данных
набор. Этот метод также сортирует данные в порядке возрастания перед вычислением медианы.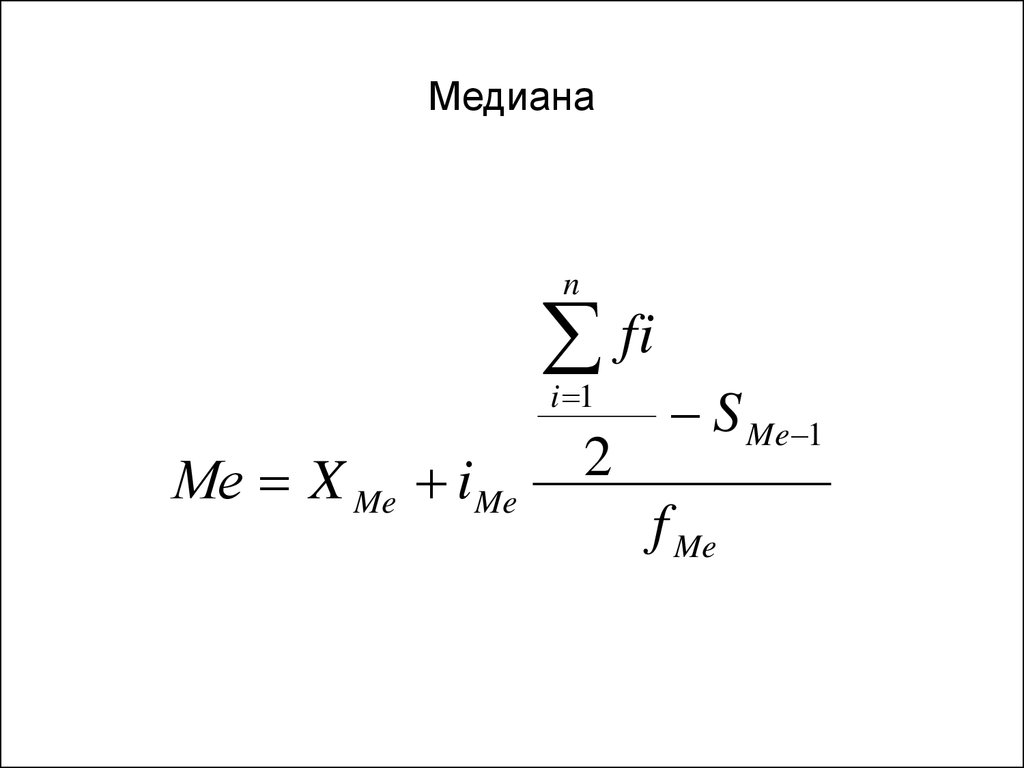
Совет: Математическая формула для медианы: Медиана = {(n + 1) / 2}-е значение, где n — количество значений в наборе данных. Для того, чтобы вычислить медиану, данные нужно сначала отсортировать по возрастанию. медиана — это число в середине.
Примечание: Если число значений данных нечетное, возвращается точное среднее значение. Если число значений данных четное, возвращается среднее из двух средних значений.
Синтаксис
статистика.медиана( данные )
Значения параметров
| Параметр | Описание |
|---|---|
| данные | Обязательно. Используемые значения данных (могут быть любой последовательностью, списком или итератор) |
Примечание: Если данные пусты, возвращается ошибка StatisticsError.
Технические детали
| Возвращаемое значение: | A поплавок 9Значение 0184, представляющее медиану
(среднее значение) заданных данных |
|---|---|
| Версия Python: | 3,4 |
❮ Статистические методы
ВЫБОР ЦВЕТА
Лучшие учебники
Учебник HTMLУчебник CSS
Учебник JavaScript
Учебник How To
Учебник SQL
Учебник Python
Учебник W3.
CSS Учебник Bootstrap
Учебник PHP
Учебник Java
Учебник C++
Учебник по jQuery
Основные ссылки
Справочник по HTMLСправочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery
Top8s Примеры HTML
Примеры CSS
Примеры JavaScript
Примеры How To
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery
FORUM | О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.