Приведение определителя к треугольному виду
Определитель вида называется треугольным (все элементы ниже главной диагонали равны нулю)
.
Треугольный определитель равен произведению элементов главной диагонали.
Определитель, в котором все элементы ниже побочной диагонали, равны нулю, изменением порядка столбцов на обратный сводится к треугольному:
При вычислении иногда удобно, используя свойства определителей 1-6, привести его к треугольному виду и найти произведение элементов главной диагонали.
Решение систем уравнений с помощью определителей (по формулам Крамера) Основные теоретические сведения
, |
|
, , – определитель системы.
Определитель – определитель, полученный заменой столбца при неизвестном на столбец свободных членов.
Формулы Крамера: ; .
Если , система имеет единственное решение: .
Если , то система имеет множество решений (эти решения будем искать методом Гаусса).
Если и хотя бы один из определителей , , отличен от нуля, то система не имеет решений (несовместна).
Пусть , тогда систему можно решать по формулам Крамера.
Решение системы запишем в виде:
; ; .
Для запоминания порядка коэффициентов при неизвестных нарисуем такую “вертушку”:
Для неизвестного – в определители записываем коэффициенты при и ; для неизвестного – двигаясь по часовой стрелке, коэффициенты при и ; для неизвестного – коэффициенты при и .
Примеры решения задач
Задача 1. Вычислить определители:
а)
;
б) ;
в) .
Задача 2. Вычислить определитель следующими способами:
а) по правилу треугольников:
;
б) разложением по первой строке (по определению):
;
в) разложением по второму столбцу:
.
Задача 3. Вычислить, используя свойства определителей:
а)
;
б)
;
в)
.
Задача 4. Вычислить определитель Вандермонда и выяснить, при каких значениях , , этот определитель равен нулю:
.
Определитель равен нулю при равенстве какой-либо пары чисел из , , .
Задача 5. Доказать, что
а) .
Решение.
;
б) .
Решение.
.
Задача 6. Решить уравнение:
а) .
Решение.
, , по теореме Виета: , ;
б) .
Решение.
, , , по теореме Виета: , ;
в) .
Решение. При определитель равен нулю при любых . Если , то
,
, .
Или, преобразуя определитель и складывая первую строку со второй и третьей, получаем
, .
Задача 7. Привести определитель к треугольному виду и вычислить:
1) .
Решение. Используя свойство линейности, вычтем первую строку из второй, прибавим первую строку к третьей, вычтем первую строку, умноженную на 2, из четвертой
.
2) .
Решение.
.
Задача 8. Вычислить определитель разложением по первой строке (по определению) и какому-либо ряду:
.
а) вычисление определителя разложением по первой строке:
;
б) вычисление определителя по первому столбцу:
.
Задача 9. Вычислить определители:
а) ; б) .
Решение:
а) применим разложение по четвертой строке:
.
б) .
Заметим, что первая и третья строки пропорциональны, поэтому .
Задача 10. Решить системы:
1)
Решение.
Определитель данной системы: отличен от нуля, следовательно, она имеет единственное решение:
, .
Таким образом, ; ;
2)
Решение.
Составим определитель системы и вычислим его:
.
Определитель , следовательно, формулы Крамера применимы.
Вычислим остальные определители:
; ;
; .
Итак, ; ; ;
. Проверить постановкой в любое уравнение системы.
Задачи для самостоятельного решения
Вычислить определители:
1. | 2. . |
3. . | 4. . |
5. . | 6. . |
7. . | 8. . |
9. . | 10. . |
Ответ: 1. 144; 2. 1; 3. ; 4. ; 5. –117; 6. 144; 7. 0; 8. –155; 9. ; 10. 1.
Решить систему уравнений:
1. | 2. |
3. | 4. |
5. | 6. |
7. |
Ответ: 1. ; 2. Система
несовместна; 3. Система
несовместна; 4.
; 5. , , ; 6.
, , ;7. .
Система
несовместна; 4.
; 5. , , ; 6.
, , ;7. .
Страница не найдена — ПриМат
По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.
Искать:© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2),
линейная алгебра — использование операций со строками для вычисления следующего определителя 3×3
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 6к раз
$\begingroup$
Используйте операции со строками для вычисления следующего определителя $\begin{bmatrix}3&3&-3\\3&4&-4\\2&-3&-5\end{bmatrix}$
Я знаю, как легко вычислить определитель, используя метод $i — j + k$. .. Проблема в том, что я поместил матрицу в LTF (нижняя треугольная форма), а затем использовал произведение диагонали. Итак, я сделал:
.. Проблема в том, что я поместил матрицу в LTF (нижняя треугольная форма), а затем использовал произведение диагонали. Итак, я сделал:
$R_2 \leftarrow R_1 + (-1)R_2$
$R_3 \leftarrow 2R_1 + (-3)R_3$
$R_3 \leftarrow 15R_2 + R_3$
чтобы получить матрицу в LTF $\begin{bmatrix}3&3&-3\\0&-1&1\\0&0&23\end{bmatrix} \имплицитно \det(A) = (3)(-1)(23) = -69$ Я знаю, что так как я использовал этими операциями я поменял определитель, как именно можно исправить обратно? Я также знаю, что $\det(A)$ должно быть $= -24$ .
- линейная алгебра
- определитель
$\endgroup$
3
$\begingroup$
Окончательная матрица должна быть $$ \begin{bmatrix} 3 и 3 и -3 \\ 0 и -1 и 1 \\ 0 и 0 и 24 \end{bmatrix} $$ Однако вы умножили определитель на $-1$ с помощью первой операции и на $-3$ со второй, так что вы получаете $$ \frac{3\cdot(-1)\cdot24}{(-1)\cdot(-3)}=-24 $$
Я использую другой метод, уменьшая развороты до $1$:
\начать{выравнивать}
\begin{bmatrix}
3 и 3 и -3 \\
3 и 4 и -4 \\
2 и -3 и -5
\end{bmatrix}
&\к
\begin{bmatrix}
1 и 1 и -1 \\
3 и 4 и -4 \\
2 и -3 и -5
\end{bmatrix} && R_1\gets\color{red}{\frac{1}{3}}R_1
\\[6px]
&\к
\begin{bmatrix}
1 и 1 и -1 \\
0 и 1 и -1 \\
2 и -3 и -5
\end{bmatrix} && R_2\получает R_2-R_1
\\[6px]
&\к
\begin{bmatrix}
1 и 1 и -1 \\
0 и 1 и -1 \\
0 и -5 и -3
\end{bmatrix} && R_3\получает R_3-2R_1
\\[6px]
&\к
\begin{bmatrix}
1 и 1 и -1 \\
0 и 1 и -1 \\
0 и 0 и -8
\end{bmatrix} && R_3\получает R_3+5R_2
\\[6px]
&\к
\begin{bmatrix}
1 и 1 и -1 \\
0 и 1 и -1 \\
0 и 0 и 1
\end{bmatrix} && R_3\gets \color{red}{-\frac{1}{8}}R_3
\end{выравнивание}
Красные цифры говорят о том, что определитель был умножен на
$$
-\фракция{1}{24}
$$
так что это $-24$.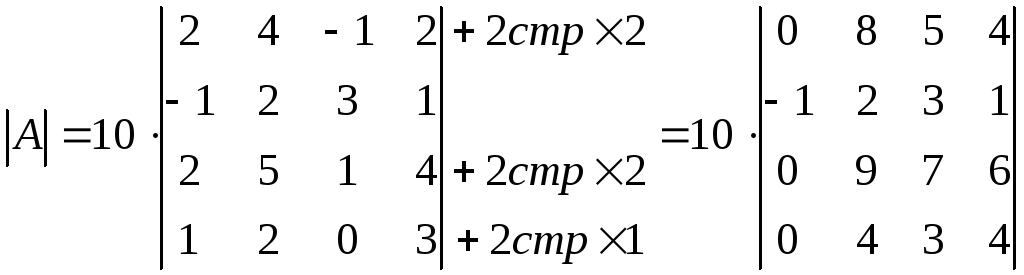
$\endgroup$
$\begingroup$
Умножение любой строки на $\lambda$ приводит к умножению определителя на $\lambda$.
Добавление любого числа, кратного строке, к другой строке не изменяет определитель.
Так
$R_2 \leftarrow R_1 + (-1)R_2$
умножает определитель на $-1$ (поскольку умножение $R_2$ на $-1$ умножает определитель на $-1$, а добавление $R_1$ к $R_2$ ничего не делает с определителем).
$R_3 \leftarrow 2R_1 + (-3)R_3$
умножает определитель на $-3$.
$R_3 \leftarrow 15R_2 + R_3$
умножает определитель на $1$ (т.е. ничего не делает).
Суммарный определитель умножен на коэффициент $-1\times-3\times1=3$. Таким образом, деление нового определителя на $3$ даст исходный определитель.
$\endgroup$
$\begingroup$
Проблема в том, что операции, которые вы выполняли, были не элементарными операциями со строками, а скорее составными операциями, включающими умножение отдельных строк перед выполнением операции со строками.

 .
.