Степени с одинаковыми основаниями при умножении: Умножение степеней с одинаковыми основаниями — урок. Алгебра, 7 класс.

Умножение и деление степеней с одинаковыми основаниями | План-конспект урока по алгебре:

Тема урока: Умножение и деление степеней с одинаковыми основаниями

Учитель: Порутчикова А.М.

Место работы, должность: учитель математики МБОУ СОШ №6 с.Вольное МО Успенский район

Класс: 7 класс

Предмет: Алгебра

Учебник:  Ю.Н. Макарычев «Алгебра. 7 класс».

Цель урока: вывести  правила умножения и деления степеней с одинаковыми основаниями; дать определение нулевой степени числа, не равного нулю; формировать умение выполнять указанные действия со степенями.

Задачи  урока:

1. Образовательные задачи урока (формирование познавательных УУД):

• познакомить учащихся со степенью с натуральным показателем;
• тренировать способность к использованию выведенного алгоритма;
• организовать деятельность учащихся по приобретению необходимых умений и навыков;
• повторить и закрепить;

1. Воспитательные задачи урока ( формирование коммуникативных и личностных УУД):

• содействовать развитию познавательного интереса учащихся к предмету;
• прививать учащимся навыки организации самостоятельной работы;
• умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

3. Развивающие задачи урока: (формирование регулятивных УУД)

• развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;

 Тип урока: 

Урок изучения и первичного закрепления новых знаний

 

Используемые учебники и учебные пособия: 

Учебник для общеобразовательных учреждений /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковскогоей С.А. Теляковского 

Используемое оборудование: 

Презентация,  раздаточный материал; лист целеполагания (Приложение 1.) и лист самоконтроля (Приложение 2.).

I  Организационный момент. Мотивационный момент.

Здравствуйте ребята! Садитесь!

Прежде чем начать урок мне бы хотелось рассказать одну притчу:

«Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому вопрос. У первого спросил: «Что ты делал целый день». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?». И тот ответил: «А я добросовестно выполнял свою работу». Третьему человеку задал свой вопрос мудрец и в ответ услышал: «А я принимал участие в строительстве храма!»

Желаю и вам ребята сегодня принять участие в строительстве храма ваших знаний.

II.Актуализация знаний и фиксация затруднения в деятельности (актуализировать учебный материал необходимый для изучения нового, зафиксировать затруднения в деятельности)

1. Проверка домашнего задания.

СЛАЙД 2

Откройте тетради, запишите число и классная работа.

Что было задано на дом?(№377, 386 (а,в), 388(а-г), 400)

Проверка домашнего задания.

№ 388.

Решение:

а) –13 + (–2)3 = –1 + (–8) = –9;

б) –62 – (–1)4 = –36 – 1 = –37;

в) –83 + (–3)3 = –512 + (–27) = –539;

г) 10 – 5 · 24 = 10 – 5 · 16 = 10 – 80 = –70;

 Поменяйтесь тетрадями с партнёром по плечу, оцените работу партнёра с решением, которое представлено на доске.

2. Устная работа

СЛАЙДЫ 3-5

Для дальнейшей работы по этой теме, нам нужно будет вспомнить элементарные правила степеней.

• Ответьте на вопросы.        

1. Что такое степень? 

2. Чему равна степень отрицательного числа с четным показателем?

 3. Чему равна степень отрицательного числа с нечетным показателем?

3. Что получится при возведении в степень с натуральным показателем числа нуль?

СЛАЙД 6

• Вычислите:

а) 32;    б) ;        в) ;                г) (–0,1)4;                д) ;        е) –(–7)2;        

ж) –(–2)3;                з) 016;                        и) (–1)18;                к) –(–1)23.

СЛАЙД 7

• Проверочная работа.

Найдите значение выражения.

а)  – (0,5)2;                б) 3000 · (0,2)3 – (–2)6.

        СЛАЙД 8

• Работа в парах:

 Вычислите:

                      

(возникает затруднение при выполнении последних двух заданий)

Выход на проблему и постановка учебной задачи на урок. (задачу на урок ставят сами дети)

III.Постановка цели и задач урока. Мотивация учебной деятельности.

СЛАЙД 9

Построение проекта выхода из затруднения и открытие нового знания

Записывают тему урока и разрабатываю план действий:

— представить степени в виде произведения

— вычислить значение степени

— провести анализ полученного затруднения

— записать формулу в общем виде

— сформулировать соответствующее правило

Работа с учебником (стр.99-101)

Свойство 1. При умножении степеней с одинаковыми основаниями  основание  оставляют  прежним,  а  показатели  степеней складывают.

по сочетательному свойству умножения
по определению степени с натуральным показателем
= 25 Итак,  22 · 23 = 22 + 3	= am + n

Свойство 2.  При делении степеней с одинаковыми основаниями, основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

5 > 3 35 : 33 =	m > n, a ≠ 0 am : an =
запишем частное в виде дроби
сократим дробь
по определению степени с натуральным показателем
= 32 Итак, 35 : 33 = 35 – 3	= am – n

---

            Замечаем, что  am : am = am – m = a0 = 1.

Определение. Степень числа а, не равного нулю, с нулевым показателем равна единице.

 

СЛАЙДЫ 10-11

Вернемся к тем заданиям, где возникли затруднения в ходе устной работы

IV.Усвоение новых знаний и способов действий.

 Первичное закрепление

Учебник «Алгебра 7 класс» автор Макарычев Ю.Н.

№ 403 (а, е, ж,з), № 405 (а-г), № 407, 409 (а,в,д,е), 410 (а,в,д), 411(а-г), 414(а,в,з). 416(а,б,в),417(а,б)

1. № 403.

Решение:

а) x5x8 = x5 + 8 = x13;                        е) yy12 = y1 + 12 = y13;

ж) 2624 = 26 + 4 + 210;                        з) 757 = 75 + 1 = 76.

2. № 405.

Решение:

а) a15 = a6 + 9 = a6 ∙  a9;                   б) a15 = a9 + 6 = a9 ∙  a6;

в) a15 = a2 + 13 = a2 ∙  a13;                г) a15 = a14 + 1 = a14 ∙  a = a ∙  a14.

3. № 407.

Решение:

Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:

6 = 1 + 5;                6 = 2 + 4;                6 = 3 + 3.

Значит,  a6 = a ∙  a5;    a6 = a2 ∙  a4;    a6 = a3 ∙  a3.

4. № 409.

Решение:

а) m3m2m8 = m3 + 2 + 8 = m13;                в) xx4x4x = x1 + 4 + 4 + 1 = x10;

д) 78 ∙  7 ∙  74 = 78 + 1 + 4 = 713;                е) 5 ∙  52 ∙  53 ∙  55 = 51 + 2 + 3 + 4 = 511.

5. № 410.

При выполнении этого упражнения ученики сами определяют основание степени, которое будет являться общим для двух степеней.

Решение:

а) 58 ∙  25 = 58 ∙  52 = 58 + 2 = 510;

в) 615 ∙  36 = 615 ∙  62 = 615 + 2 = 617;

д) 0,45 ∙  0,16 = 0,45 ∙  0,42 = 0,45 + 2 = 0,47;

е) 0,001 ∙  0,14 = 0,13 ∙  0,14 = 0,13 + 4 = 0,17.

6. № 411.

Решение:

а) 24 ∙  2 = 24 + 1 = 25 = 32;

б) 26 ∙  4 = 26 ∙  22 = 26 + 2 = 28 = 256;

в) 8 ∙  27 = 23 ∙  27 = 23 + 7 = 210 = 1024;

г) 16 ∙  32 = 24 ∙  25 = 24 + 5 = 29 = 512.

1. № 414.

Решение:

а) x5 : x3 = x5 – 3 = x2;

в) a21 : a = a21 – 1 = a20;

з) 0,79 : 0,74 = 0,79 – 4 = 0,75.

2. № 416.

Решение:

а) 56 : 54 = 56 – 4 = 52 = 25;

б) 1015 : 1012 = 1015 – 12 = 103 = 1000;

в) 0,510 : 0,57 = 0,510 – 7 = 0,53 = 0,125;

г) ;

д) 2,7313 : 2,7312 = 2,7313 – 12 = 2,73;

е) .

3. Используя правила умножения и деления степеней, упростите выражение.

а) x8 ∙  x3 : x5;                        б) x20 : x10 ∙  x;

в) x7 : x3 : x3;                        г) x14 : x9 ∙  x5.

Решение:

а) x8 ∙  x3 : x5 = x8 + 3 : x5 = x11 : x5 = x11 – 5 = x6;

б) x20 : x10 ∙  x = x20 – 10 ∙  x = x10 ∙  x = x10 + 1 = x11;

в) x7 : x3 : x3 = x7 – 3 : x3 = x4 : x3 = x4 – 3 = x;

г) x14 : x9 ∙  x5 = x14 – 9 ∙  x5 = x5 ∙  x5 = x5 + 5 = x10.

4. № 417.

Решение:

а) = 86 : 84 = 86 – 4 = 82 = 64;

б) = 0,87 : 0,84 = 0,87 – 4 = 0,83 = 0,512;

в) = (–0,3)5 : (–0,3)3 = (–0,3)5 – 3 = (–0,3)2 = 0,09;

V.Физкультминутка

VI. Контроль и самоконтроль знаний и способов действий

Самостоятельная работа (по вариантам) Раздается каждому учащемуся, решение можно выполнять прямо на листочках. После выполнения работы проверяются в классе, и каждый ученик оценивает себя сам.

Вариант 1.

Вариант 2.

VII. Включение в систему знаний и повторение.

        СЛАЙДЫ 12-13

         Задача «определить во сколько раз масса земного шара больше массы всего окружающего его воздуха».

Решение. Чтобы убедиться, насколько облегчаются практические вычисления при пользовании степенным изображением больших чисел, выполним такой расчет: определим, во сколько раз масса земного шара больше массы всего окружающего его воздуха.

На каждый кв. сантиметр земной поверхности воздух давит, мы знаем, с силой около килограмма. Это означает, что вес того столба атмосферы, который опирается на 1 кв. см, равен 1 кг. Атмосферная оболочка Земли как бы составлена вся из таких воздушных столбов; их столько, сколько кв. сантиметров содержит поверхность нашей планеты; столько же килограммов весит вся атмосфера. Заглянув в справочник, узнаем, что величина поверхности земного шара равна 510 млн. кв. км, т. е. 51 × 107 кв. км.

Рассчитаем, сколько квадратных сантиметров в квадратном километре. Линейный километр содержит 1000 м, по 100 см в каждом, т. е. равен 105 см, а кв. километр содержит (105)2 = 1010 кв. сантиметров. Во всей поверхности земного шара заключается поэтому

51 × 107× 1010 = 51 × 1017

кв. сантиметров. Столько же килограммов весит и атмосфера Земли. Переведя в тонны, получим:

51 × 1017 : 1000 = 51 × 1017 : 103=51 × 1017-3 = 51 × 1014.

Масса же земного шара выражается числом

6 × 1021 тонн.

Чтобы определить, во сколько раз наша планета тяжелее ее воздушной оболочки, производим деление:

6 × 1021 : 51 × 1014 ≈ 106,

т. е. масса атмосферы составляет примерно миллионную долю массы земного шара

VIII.Рефлексия учебной деятельности на уроке, подведение итогов.

– Дайте определение степени с натуральным показателем.

– Сформулируйте правило возведения отрицательного числа в четную степень, в нечетную степень.

– Какой знак имеет результат возведения любого числа в квадрат?

– Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.

– Чему равно значение выражения 20; (–1)1?

 Заполнить  пункты «знаю» и «умею» таблицы целеполагания.

Заполнение листов самоконтроля.

Пожалуйста, поделитесь  своими мыслями о сегодняшнем занятии (хотите одним предложением).

Вам для этого помогут слова

1. Сегодня на уроке я закрепил…..
2. На что мне нужно обратить внимание…….

IX. Информация о домашнем задании.

СЛАЙД 14

П.16 выучить правила.

Решить задания: I уровень: №404, 408, 415, 418;   II уровень: №406, 412, 419 (б,г,е), 533.

Выразить массу Земли и Луны в различных единицах массы (в граммах, килограммах, в центнерах и тоннах)

Приложение 1.

Лист целеполагания

Ф.И.___________________________________________

Вопросы	Знаю	Не знаю	Хочу знать
Что такое степень с натуральным показателем?
Как возвести отрицательное число  Степень ?
Как умножать степени с одинаковыми основаниями?
Как делить степени с одинаковыми основаниями?
Как возвести число в степень с нулевым показателем?

 

Приложение 2.

Лист самоконтроля

Ф.И.________________________________________________

№	Виды работ	Оценка
1.	Проверка домашнего задания
2.	Устная работа
3.	Работа в парах
4.	Самостоятельная работа по вариантам
5.	Решение задачи
	Средняя оценка:

Повторяем и систематизируем школьный курс алгебры и начал анализа

Повторяем и систематизируем школьный курс алгебры и начал анализа

Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с. В книге в конспективной форме изложен теоретический материал по алгебре и началам анализа. К каждому пункту теоретического материала приведены упражнения с решениями и упражнения трех уровней сложности для самостоятельного решения. Она может быть использована при подготовке к экзаменам в высшие учебные заведения. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а 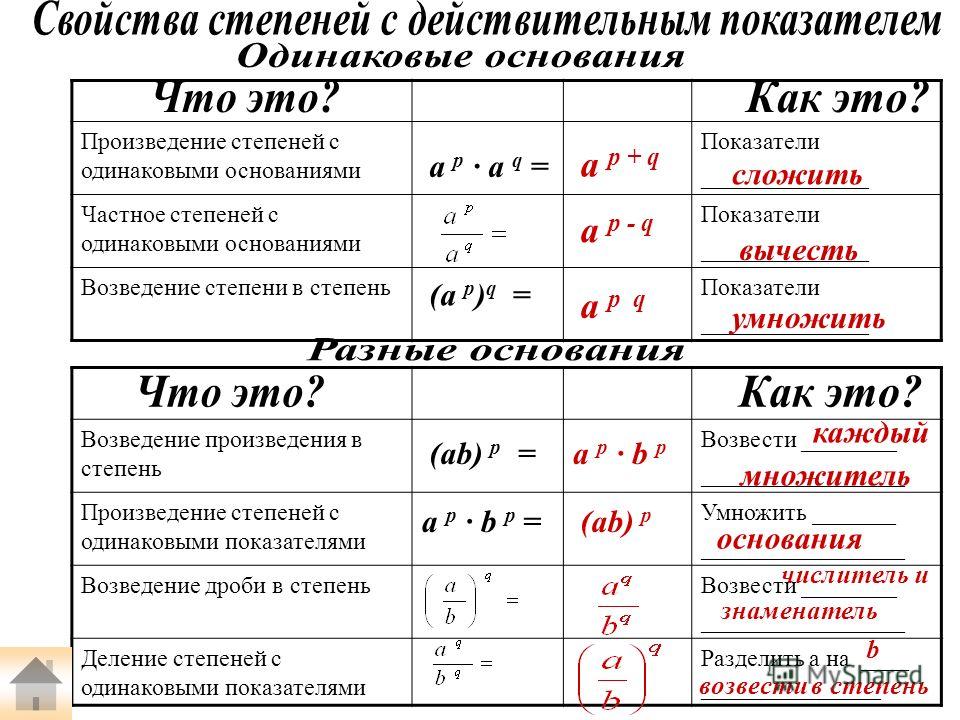§ 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление

Умножение показателей степени с одинаковым основанием

• Математические сомнения
• Индексы
• Операции
• Умножение

Две или более степени с одинаковым основанием часто участвуют в умножении в математике. Невозможно напрямую умножать показатели степени с одним и тем же основанием, но концепция возведения в степень применяется при выполнении умножения показателей степени с одним и тем же основанием для получения их произведения.

Вот пошаговая процедура для начинающих, которая поможет вам умножить индексы с одним и тем же основанием. 99$

Тот же математический подход применяется к любому количеству показателей степени с одним и тем же основанием для их умножения, а также для легкого получения их произведения.

Сложите показатели степени и запишите их сумму как показатель степени основания, когда в математике умножаются два или более показателей степени с одинаковым основанием. На основе этого правило сложения показателей степени разработано в общем виде для использования его в качестве формулы в математике.

• Предыдущий

• Следующие

Экспоненты и умножение — Произведение свойств степеней — Упрощено

В вашем браузере отключен JavaScript.

Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

• Математика
• Алгебра 1
• Экспоненты
• Экспоненты и умножение — произведение свойств степеней

Рейтинг

Ø 5,0 / 3 балла

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти в Google

Авторы

Сьюзен Сайфан

Основы по теме

Экспоненты и умножение – Произведение степеней Свойство

Если вы решаете задачи на умножение в степени, записывая уравнения в длинной форме, возможно, у вас сводит пальцы, вы используете много-много бумаги и снова и снова точите карандаш.

Чтобы узнать, как сохранить пальцы и некоторые деревья, посмотрите это видео. Вместо того, чтобы записывать задачи на умножение на экспоненту в длинной форме, используйте правило произведения степеней, чтобы облегчить решение задач и быстрее закончить работу.

Правило произведения степеней гласит: для одинаковых основных показателей сложите показатели, а затем упростите. Итак, для задачи 2, возведенной в 20-ю степень, умноженной на 2, возведенную в 10-ю степень — вместо того, чтобы выписывать все эти двойки — поскольку основания одинаковы, вы можете просто добавить показатели степени. Ответ: 2 в 30-й степени. Вау, это было очень быстро, и ни одно дерево не должно было погибнуть!

Теперь, когда вы так быстро закончили домашнюю работу по умножению на степень, что вы можете сделать со всем оставшимся временем? Что ж, так как ваши пальцы больше не будут судорожными, вы можете заняться вязанием, пока вы смотрите больше видео по алгебре I на диване. Что бы вы ни решили делать, получайте удовольствие от обучения, и вы удивитесь, насколько весело решать математические задачи!

Интерпретировать структуру выражений.

CCSS.MATH.CONTENT.HSA.SSE.A.1

Стенограмма

Экспоненты и умножение — свойство произведения степеней

Пока Итан расслабляется на диване, он болтает с другом. О, нет! Давайте посмотрим на задание и посмотрим, что нужно сделать Итану… Ему нужно написать сочинение для своего класса по английскому языку . Учитель английского языка Итана, который также является энтузиастом математики, дал ученикам 10² дней, чтобы написать 10³ слов КАЖДЫЙ ДЕНЬ около 9 дней. 0179 мужество . Итан не думает, что это так уж плохо. Он прав?

Экспоненты и умножение

Используя экспоненты и умножение , давайте поможем Итану вычислить, сколько слов ему нужно писать в день. Чтобы облегчить себе жизнь при умножении показателей, вы можете использовать правило произведения степеней. Когда у вас есть число, возведенное в степень, например, aⁿ , умноженное на другое число с тем же основанием, aᵐ, вы можете записать его в длинной форме как «а», умноженное на «n», умноженное на «а». умножить ‘m’ раз. Все вместе мы можем записать это произведение как «а», умноженное на «n» плюс «m» раз.

Сложите и упростите

Или просто aⁿ⁺ᵐ . Чтобы умножить показатели степени с одинаковым основанием, добавьте показателей степени, затем упростите . Итак… чтобы рассчитать количество слов, которые Итан должен написать за два дня, умножьте количество дней, в течение которых учитель поручил написать эссе, на количество слов, которые должен написать Итан. (10²)(10³) Если хотите, вы можете записать все десятки в длинной форме, как мы показывали вам раньше.

Произведение правила Пауэрса

Как видите, число 10 умножается на 2 + 3 или упрощается в 5 раз. Мы можем записать это как 10⁵ …. или вы можете использовать правило произведения степеней и просто добавить показатели степени, поскольку основание одинаково для чисел, которые мы хотим умножить. В любом случае ответ будет 10⁵… или 100 000 слов. Это слова, а не символов .

О, это больше, чем ожидал Итан. Когда он получил задание, количество слов казалось небольшим. Чувствуя себя немного подавленным, он начинает писать. Через несколько часов он понимает, что может писать 1024 или 2¹⁰ слов в час, и на данный момент он написал около 25 000 слов. У него еще есть 2⁴, или 16, часов. Сможет ли он выучить 100 000 слов вовремя? Чтобы решить эту проблему, вычислить (2⁴)(2¹⁰). Вы можете перечислить двойки в длинной форме, а затем умножить, если это поможет.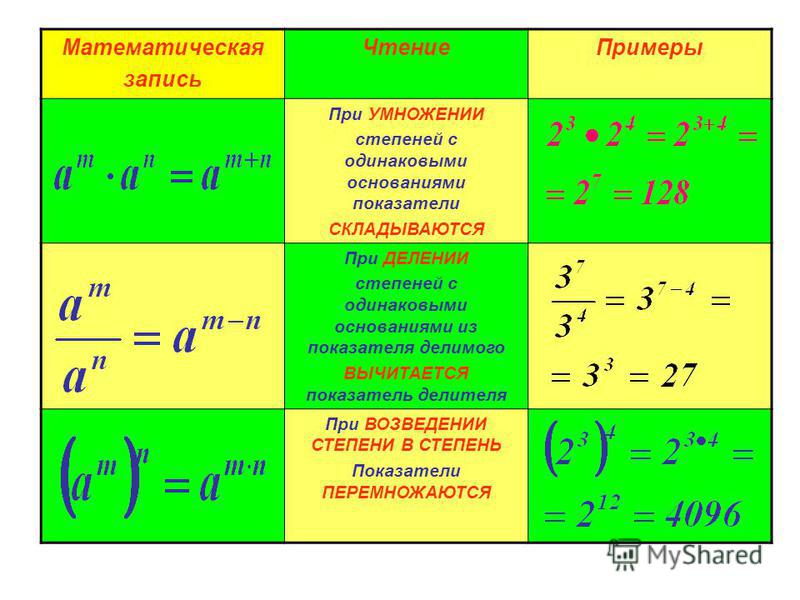

Те же основания

Как видите, 2 умножается на 10 + 4, или просто в 14 раз. Вы можете записать это как 2¹⁴… или, поскольку 90 179 оснований 90 180 совпадают, вы можете снова использовать правило произведения степеней. (2¹⁰)(2⁴) = 2¹⁴… и это равно 16 384 словам. Мы также можем записать это как 1.6384E4. Е4? Вам может быть интересно, что, черт возьми, такое E4 ? Это сокращение от 10⁴. Теперь Итан понимает, как использовать правило произведения степеней, но это не решает его проблему…

Решите задачу

За то время, что у него осталось, чтобы написать, у него будет около 40 000 слов. О, нет! Он будет коротким на 60 000 слов, но у Итана есть идея — это наверняка мощное движение … Сработает ли это? Наверное, не будет, но кто знает? Может быть…, только может быть…

Экспоненты и умножение — произведение свойств в степени. Упражнение

Хотели бы вы применить полученные знания? Вы можете просмотреть и потренироваться с заданиями к видео 93=8}$

$8$ Лебеди прошли мимо Итана, пока он отдыхал.

Опишите, как умножать мощности с одним и тем же основанием в соответствии со свойством «Сила произведений».

Подсказки

Каждую степень можно записать как произведение.

Вот пример правила.

Решение

Мы проиллюстрировали произведение свойств полномочий ниже. Это свойство можно использовать при умножении чисел с одинаковым основанием, возведенных в степень. 9{20}}$

Еще видео по теме Экспоненты

Нулевые и отрицательные экспоненты

Экспоненты и умножение — произведение степеней Свойство

Экспоненты и деление — свойство отношения степеней

Степени произведений и частных

Чтение и запись научной нотации

Операции с числами в научной записи

Экспоненциальный рост и упадок

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический

• Условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Свяжитесь с нами!

help@sofatutor.