Матрицы и действия над ними
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Тема 1. «Матрицы и действия над ними»
Основные понятия:
1. Определение матрицы
2. Виды матриц
3. Действия над матрицами
4. Перестановочные матрицы
1. Определение матрицы
Прямоугольная таблица чисел вида
à11
à
21
À
…
àm1
à12
à22
…
àm 2
… à1n
… à2 n
… …
… àmn
называется матрицей.
àij- элементы матрицы.
Размер матрицы
Главная диагональ матрицы
Побочная диагональ матрицы
2. Виды матриц
• Прямоугольная
• Квадратная
• Нулевая
• Единичная
• Диагональная
• Симметричная
• Вырожденная
• Равные
• Треугольная
• Квазитреугольная (ступенчатая или трапециевидная)
• Матрица-строка или строчная матрица
• Матрица-столбец или столбцевая матриц
Матрица называется прямоугольной, если количество ее
строк не совпадает с количеством столбцов:
1
À
0
2
3
2
0
3
5
Матрица называется квадратной, если количество ее строк
совпадает с количеством столбцов:
7 45
À
1 0
Матрица называется нулевой, если все ее элементы нулевые :
0 0 0
À
0 0 0
Квадратная матрица называется единичной, если элементы
по главной диагонали единицы, а остальные элементы
нулевые :
1 0 0
À 0 1 0
0 0 1
Квадратная матрица называется диагональной, если
элементы по главной диагонали отличны от нуля, а
остальные элементы нулевые:
2 0 0
À 0 3 0
0 0 1
Квадратная матрица называется симметричной, если
относительно главной диагонали для всех ее элементов
выполняется условие aij a ji :
1 0 1
À 0 2 77
1 77 3
Квадратная матрица называется вырожденной, если ее
определитель равен нулю.

Матрицы А и В (одинаковых размерностей) называются
равными, если
:
aij bij
1 3
À 13 0
2 7
1 3
B 13 0
2 7
Квадратные матрицы вида
a11
a
n1
a1n
или
0
называются треугольными.
1 2 3
À 4 5 0
6 0 0
a11
0
1
0
À
0
0
a1n
ann
4
7
9
0 0 10
2 3
5 6
0 8
Прямоугольная матрица вида
0
0
a12
a1m
a22
a2 m
0
amm
a1n
a2 n
amn
называется квазитреугольной (ступенчатая или
трапециевидная)
1
À 0
0
2
2
1
2
0
3
3
1
0
3
3
1
1
0
5
Матрица, состоящая из одной строки называется матрицейстрокой или строчной матрицей.
À 1 2 3 0
Матрица, состоящая из одного столбца называется
матрицей-столбцом или столбцевой матрицей
2
À 0
2
Операции над матрицами
Линейные:
1) Сумма (разность) матриц;
2) Произведение матрицы на число.

Нелинейные:
1) Транспонирование матрицы;
2) Умножение матриц;
3) Нахождение обратной матрицы.
Суммой (разностью) двух матриц одинаковой
размерности называется матрица, элементы которой
равны сумме (разности) соответствующих элементов
матриц слагаемых.
Например:
à11 à12 à13
b11 b12 b13
À
, B
à21 à22 à23
b21 b22 b23
à11 b11 à12 b12 à13 b13
A B
à21 b21 à22 b22 à23 b23
Произведением матрицы на число называется матрица,
полученная из данной умножением всех ее элементов на
число.
Например:
à11 à12 à13
À
à21 à22 à23
à11 à12 à13
à21 à22 à23
Линейные операции обладают следующими свойствами:
1) A B B A
2) A B C A B C
3) A 0 A
4) A A 0
5) 1 A A
6) A A
7) A B A B
8) A A A
Матрица, полученная из данной заменой каждой ее
строки столбцом с тем же номером, называется
матрицей, транспонированной относительно данной.
Например:
à11 à12 à13
À
,
à21 à22 à23
à11 à21
T
A à12 à22
à
à
23
13
Умножение матриц определяется для согласованных матриц.

Произведением матрицы Àm n àij на матрицу
Bn k bij называется матрица Cm k cij , для
которой cij ai1 b1 j ai 2 b2 j … ain, bnj
т.е. каждый элемент матрицы С равен сумме
произведений элементов i-й строки матрицы А на
соответствующие элементы j-го столбца матрицы В.
Например:
b11
à11 à12 à13
b21
à21 à22 à23 b
31
à11 b11 à12 b21 à13 b31
à21 b11 à22 b21 à23 b31
В случае, когда АВ=ВА, матрицы А и В называют
перестановочными или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
1 2
À
0 3
Пример 2. Найти все перестановочные матрицы к матрице
2 4
À
1 0
Свойства операции транспонирования:
1) A
T T
A
2) A B A B
T
T
3) A B B A
T
T
T
T
Матрица А называется согласованной с
матрицей В, если число столбцов матрицы А
равно числу строк матрицы В:
Например:
1)
Àm n ,
Bn k
2)
À2 4 ,
B4 1
3)
Àm 2 ,
B2 k
Свойства операции умножение матриц:
1.
 Свойство сочетательности или ассоциативности
Свойство сочетательности или ассоциативностиAB C A BC
2.
AB A B A B
3.
Свойство распределительности (дистрибутивности)
справа и слева относительно сложения матриц
A B C AC BC
C A B CA CB
Решение (Пример 1):
1) B a
b общий вид всех перестановочных матриц
c d
2) Применим определение перестановочных матриц
AB=BA:
1 2 a b a 2c b 2d
ÀB
3d
0 3 c d 3c
a b 1 2 a 2a 3b
BA
c d 0 3 c 2c 3d
Получаем: a 2c
3c
b 2d a 2a 3b
3d c 2c 3d
3) По определению равных матриц
a 2c a
a R
b 2d 2a 3b b a d
3c c
c 0
3d 2c 3d
d R
4) Общий вид всех перестановочных матриц
a a d
B
0
d
English Русский Правила
новый вид пирамиды или грамотная стратегия
Матричный маркетинг – один из самых противоречивых способов продвижения. Стратегия матрицы – явление не новое, ему уже более 15 лет. В основе лежит учетная таблица (матрица), в которой отражено количество совершенных сделок или иных достигнутых результатов и порядок оплаты работы дистрибьюторов.
Сходство с сетевым маркетингом и страх перед финансовыми пирамидами рождают множество негативных ассоциаций и предубеждений. Существует стереотип, согласно которому при помощи такой стратегии можно только продавать и только косметику. Но самые смелые компании используют этот инструмент для продвижения своих идей – и именно они оказываются впереди.
При построении матрицы вы получаете максимально широкий охват аудитории за счет постоянного привлечения людей и роста числа дистрибьюторов. Продвигайте практически любой продукт и воплощайте самые технологически смелые проекты: сфера применения матричного маркетинга не имеет границ. Кроме того, стратегию отличает простота восприятия – значит, ваша идея будет принята с легкостью.
Основное стратегическое направление – информационный охват максимального количества людей и одновременное снижение затрат на продвижение. Стоит отметить, что заполнение матрицы – по большей части командная работа. Чем больше людей вы привлечете к продвижению продукта, и чем более они будут активны, тем быстрее будут расти информационные показатели.
Отличия матричного маркетинга от сетевого
У гораздо более известного сетевого и матричного маркетинга есть несколько различий. В сетевом маркетинге акцент делается на личные связи, доход зависит исключительно от персональных продаж, а узнаваемость продукта или услуги не растет быстро.
Матричные проекты отличаются многоуровневой системой получения прибыли. Это означает, что ваш доход, ваша узнаваемость, уровень продаж зависит не только от вас самих и людей, которых вы смогли увлечь своей идеей, но и от тех, кому рассказали об этом ваши участники.
В основе матричного маркетинга стратегии лежит ступенчатая организация работы: от одного человека до сотен дистрибьюторов. Это и есть матрица. Различают три основных типа:
Линейная матрица: число мест не ограничено и каждый участник проекта может привлекать любое количество рефералов.
Бинарная матрица: здесь количество мест ограничено – один человек может зарегистрировать определенное число новых участников.
Если лимит регистраций для человека исчерпан, но кто-то хочет стать участником и регистрируется по его партнерской ссылке, то новичок автоматически переходит либо участнику на уровень выше (так называемому спонсору, создавая «переливы снизу»), либо на уровень ниже (к рефералу, «переливы сверху»).
Шахматная матрица: в этом случае определяется порядок (например, четный либо нечетный) по которому новый участник автоматически отправляется в команду не того, кто его пригласил, а спонсора последнего – таким образом, каждый участник дарит часть рефералов своему спонсору, а сам получает новых членов команды от своих приглашенных.
Более жесткие стратегии подразумевают беспрекословное соблюдение условий заполнения матрицы. В таком случае при заполнении всех ячеек дистрибьютор может «передать» кому-либо следующего лично привлеченного участника, при этом непосредственная связь с этим человеком у дистрибьютора заканчивается. Более комфортный вариант матричного плана дает дистрибьютору право пригласить несколько человек дополнительно, и в том случае, если какая-то из ячеек матрицы остается невостребованной, ее место заполняет «партнер для подстраховки».
Есть и другой тип различия матриц: делящиеся, неделящиеся, статичные, динамические, форсированные. Делящаяся матрица наполняется членами команды слева направо и сверху вниз. В момент заполнения она разделяется, и каждый участник стратегии матрицы продвигается вверх. Ранее пришедший участник (также называемый спонсор) получает предназначенный бонус и возможность вырасти на уровень вверх. При форсированной матрице на каждом уровне количество участников должно быть четко определено.
В маркетинге, который связан с продуктами, бывают матрицы 2×2, 3×3, 5×5 и т.д. Например, в матрице 5×5 дистрибьютору нужно привлечь для начала 5 партнеров, каждому из них необходимо пригласить также по 5 партнеров, следом – еще по 5 и т.д., чтобы вся матрица была заполнена. Пока это не случится, никакой денежной компенсации дистрибьютор не получает.
Модели матричного маркетинга
Существуют две модели, по которым работает матричный маркетинг: увеличение продаж и рост количества участников схемы.
В основе первой модели лежит план продаж, который работает как мотивация к действию. Стоимость продукта для вас, как для участника стратегии, и для итогового покупателя обычно различается. При вступлении для вас указывается рекомендованная цена, завышать которую вы можете, но не факт, что вы сможете реализовать товар с большой наценкой. Маржа в некоторых случаях достигает 40%. Достаточно известные корпорации, предлагающие свой продукт матричным способом, успешно функционируют.
При втором способе продвижения услуги или продукта вы направляете усилия на то, чтобы привлекать новых рекрутов в ряды компании, создавая свой уровень (ступень). Достигнуть цели этим способом не всегда получается, потому что для людей всегда остается важным заработать максимум, не прикладывая при этом много усилий.
Привлечение новых членов не гарантирует вам их активности при продвижении товара и подписке новых дистрибьюторов, поэтому вы рискуете остаться на том же уровне дохода, с которого начинали.
Любому бизнесу стоит присмотреться к матрице. Такая маркетинговая стратегия редко используется в чистом виде и ценится именно за редкость использования. При грамотном сочетании с другими методами продвижения идей она способствует достижению целей за более короткий срок и с меньшими затратами.
Корпоративные мастер-классы
Повышайте компетенции своей команды, не выходя из офиса
Мастер-классы от bigtime-ventures – это концентрированная информация по 13 элементам развития бизнеса, сформированная под цели и задачи именно вашей компании.
Подробнее
Бесплатный пошаговый онлайн-решатель матриц
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор Якобиана
Чтобы найти матрицу Якобиана, выберите переменные, введите функции в соответствующие поля ввода и нажмите кнопку вычислить с помощью калькулятора Якобиана
Калькулятор Якобиана используется для нахождения матрицы Якобиана и определитель после взятия производной данной функции. Этот калькулятор матрицы Якоби находит матрицу для функций с двумя и тремя переменными.
Этот калькулятор матрицы Якоби находит матрицу для функций с двумя и тремя переменными.
Что такое матрица Якоби?
В векторном исчислении матрица Якоби функций многих переменных — это матрица всех ее частных производных 1-го порядка.
Матрица Якоби принимает на вход равное количество строк и столбцов, т. е. 2×2, 3×3 и т. д. Другими словами, входные значения должны быть квадратной матрицей. Определитель матрицы Якоби называется определителем Якоби.
Обозначается J и записью (i, j), например J i ,j = ∂f i / ∂x j
Формула матрицы Якоби
Ниже приведена общая формула для нахождения матрицы Якоби.
Как рассчитать матрицу Якоби?
Ниже приведен решенный пример матрицы Якоби.
Пример
Найдите матрицу Якоби x = x 2 + 2y 2 & y = 3x – 2y относительно x&y.
Решение
Шаг 1: Запишите заданные функции в виде матрицы.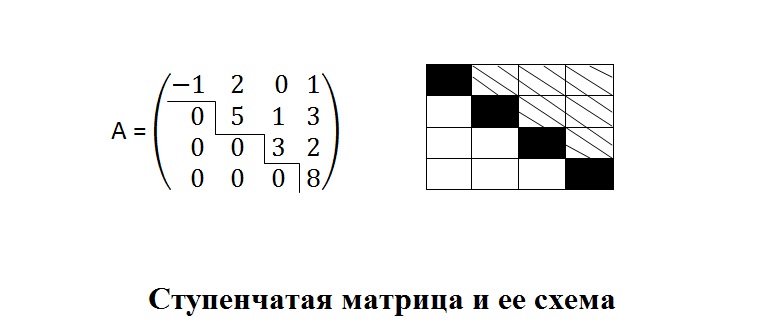
x = x 2 + 2y 2
y = 3x — 2y
Шаг 2: Найдите частичный производство колонны 1 W.R.R.T «x x’ x ’x’ x ’x’ x ’x’ h ’hails . .
∂/∂x (x 2 , 3x) = 2x, 3
∂/∂y (2y 2 , -2y) = 4y, -2
Шаг 3: Запишите члены в матрицу форма.
Это требуемая матрица Якоби 2×2 заданных функций.
Определитель этой матрицы равен -4x -12y
Матрица Якоби = -4x – 12y
Как найти якобиан матрицы 3×3
– z 2 , y = 5x – 3y + 6z и z = x + y + z относительно x,y&z.Решение
Чтобы найти матрицу Якоби 3×3, выполните следующие действия.
Шаг 1: Запишите заданные функции в виде матрицы.
x = 3x 3 + 4y 2 — z 2
y = 5x — 3y + 6z
z = x + y + z
Шаг 2:
.

