Таблица значений критерия Стьюдента (t-критерия)
Skip to contentArtman Таблицы
p — доверительной вероятности и f — числа степеней свободы
(коэффициент стьюдента находим по таблице)
| f | p | |||||||
| 0.80 | 0.90 | 0.95 | 0.98 | 0.99 | 0.995 | 0.998 | 0.999 | |
| 1 | 3.0770 | 6.3130 | 12.7060 | 31.820 | 63.656 | 127.656 | 318. | 636.619 |
| 2 | 1.8850 | 2.9200 | 4.3020 | 6.964 | 9.924 | 14.089 | 22.327 | 31.599 |
| 3 | 1.6377 | 2.35340 | 3.182 | 4.540 | 5.840 | 7.458 | 10.214 | 12.924 |
| 4 | 1.5332 | 2.13180 | 2.776 | 3.746 | 4.604 | 5.597 | 7.173 | 8.610 |
| 5 | 1. 4759 | 2.01500 | 2.570 | 3.649 | 4.0321 | 4.773 | 5.893 | 6.863 |
| 6 | 1.4390 | 1.943 | 2.4460 | 3.1420 | 3.7070 | 4.316 | 5.2070 | 5.958 |
| 7 | 1.4149 | 1.8946 | 2.3646 | 2.998 | 3.4995 | 4.2293 | 4.785 | 5.4079 |
| 8 | 1.3968 | 1.8596 | 2.3060 | 2.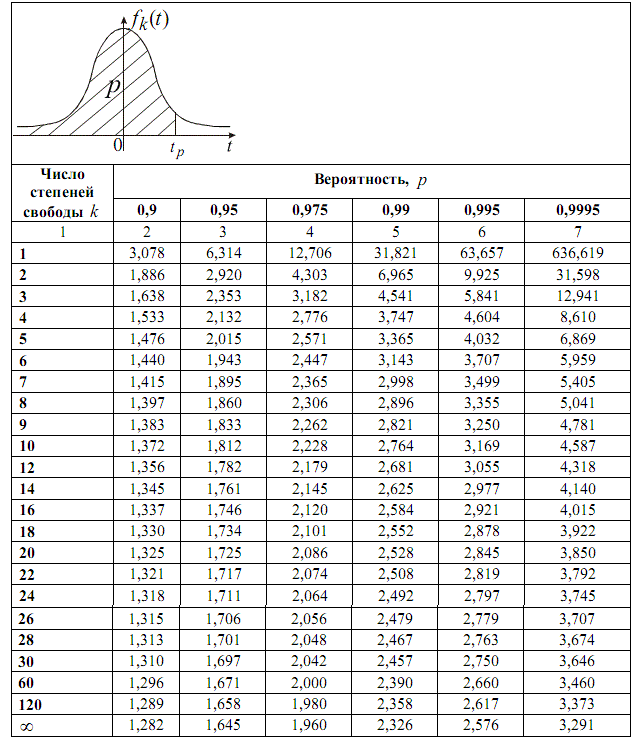 8965 | 3.3554 | 3.832 | 4.5008 | 5.0413 |
| 9 | 1.3830 | 1.8331 | 2.2622 | 2.8214 | 3.2498 | 3.6897 | 4.2968 | 4.780 |
| 10 | 1.3720 | 1.8125 | 2.2281 | 2.7638 | 3.1693 | 3.5814 | 4.1437 | 4.5869 |
| 11 | 1.363 | 1.795 | 2.201 | 2.718 | 3.105 | 3.496 | 4. 024 | 4.437 |
| 12 | 1.3562 | 1.7823 | 2.1788 | 2.6810 | 3.0845 | 3.4284 | 3.929 | 4.178 |
| 13 | 1.3502 | 1.7709 | 2.1604 | 2.6503 | 3.1123 | 3.3725 | 3.852 | 4.220 |
| 14 | 1.3450 | 1.7613 | 2.1448 | 2.6245 | 2.976 | 3.3257 | 3.787 | 4.140 |
| 15 | 1.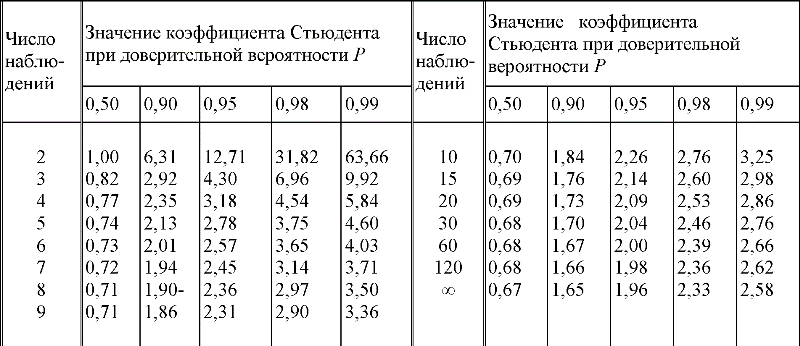 3406 | 1.7530 | 2.1314 | 2.6025 | 2.9467 | 3.2860 | 3.732 | 4.072 |
| 16 | 1.3360 | 1.7450 | 2.1190 | 2.5830 | 2.9200 | 3.2520 | 3.6860 | 4.0150 |
| 17 | 1.3334 | 1.7396 | 2.1098 | 2.5668 | 2.8982 | 3.2224 | 3.6458 | 3.965 |
| 18 | 1.3304 | 1.7341 | 2.1009 | 2. 5514 | 2.8784 | 3.1966 | 3.6105 | 3.9216 |
| 19 | 1.3277 | 1.7291 | 2.0930 | 2.5395 | 2.8609 | 3.1737 | 3.5794 | 3.8834 |
| 20 | 1.3253 | 1.7247 | 2.08600 | 2.5280 | 2.8453 | 3.1534 | 3.5518 | 3.8495 |
| 21 | 1.3230 | 1.7200 | 2.2.079 | 2.5170 | 2.8310 | 3.1350 | 3. 5270 | 3.8190 |
| 22 | 1.3212 | 1.7117 | 2.0739 | 2.5083 | 2.8188 | 3.1188 | 3.5050 | 3.7921 |
| 23 | 1.3195 | 1.7139 | 2.0687 | 2.4999 | 2.8073 | 3.1040 | 3.4850 | 3.7676 |
| 24 | 1.3178 | 1.7109 | 2.0639 | 2.4922 | 2.7969 | 3.0905 | 3.4668 | 3.7454 |
| 25 | 1. | 1.7081 | 2.0595 | 2.4851 | 2.7874 | 3.0782 | 3.4502 | 3.7251 |
| 26 | 1.315 | 1.705 | 2.059 | 2.478 | 2.778 | 3.0660 | 3.4360 | 3.7060 |
| 27 | 1.3137 | 1.7033 | 2.0518 | 2.4727 | 2.7707 | 3.0565 | 3.4210 | 3.6896 |
| 28 | 1.3125 | 1.7011 | 2.0484 | 2. 4671 | 2.7633 | 3.0469 | 3.4082 | 3.6739 |
| 29 | 1.3114 | 1.6991 | 2.0452 | 2.4620 | 2.7564 | 3.0360 | 3.3962 | 3.8494 |
| 30 | 1.3104 | 1.6973 | 2.0423 | 2.4573 | 2.7500 | 3.0298 | 3.3852 | 3.6460 |
| 32 | 1.3080 | 1.6930 | 2.0360 | 2.4480 | 2.7380 | 3.0140 | 3.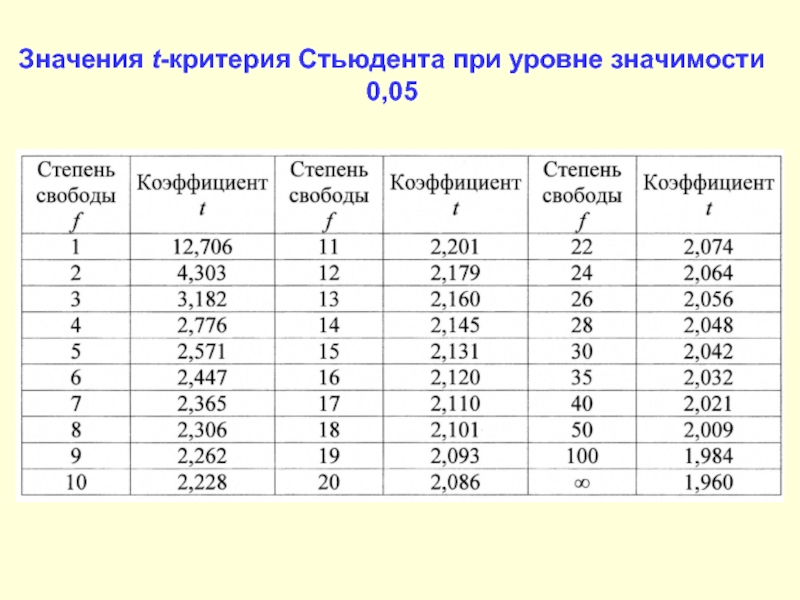 3650 | 3.6210 |
| 34 | 1.3070 | 1.6909 | 2.0322 | 2.4411 | 2.7284 | 3.9520 | 3.3479 | 3.6007 |
| 36 | 1.3050 | 1.6883 | 2.0281 | 2.4345 | 2.7195 | 9.490 | 3.3326 | 3.5821 |
| 38 | 1.3042 | 1.6860 | 2.0244 | 2.4286 | 2.7116 | 3.9808 | 3.3190 | 3.5657 |
| 40 | 1.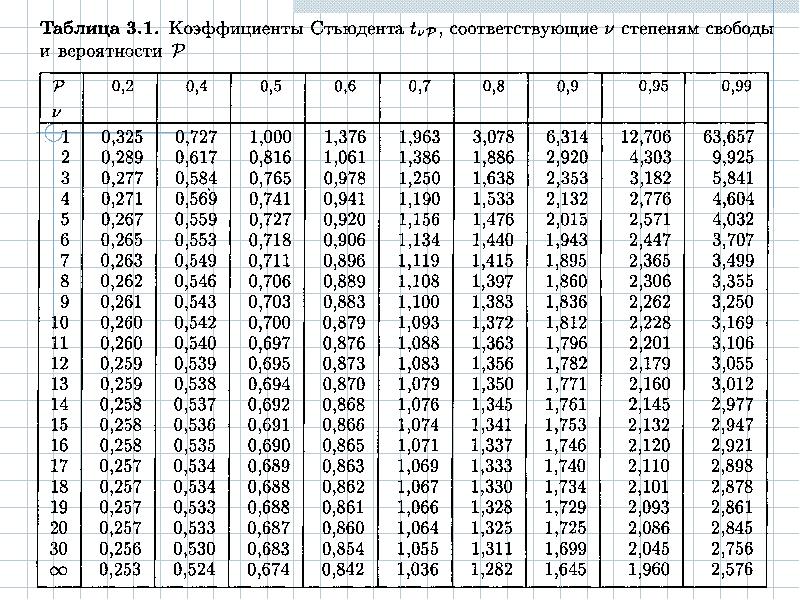 303 | 1.6839 | 2.0211 | 2.4233 | 2.7045 | 3.9712 | 3.3069 | 3.5510 |
| 42 | 1.320 | 1.682 | 2.018 | 2.418 | 2.6980 | 2.6930 | 3.2960 | 3.5370 |
| 44 | 1.301 | 1.6802 | 2.0154 | 2.4141 | 2.6923 | 3.9555 | 3.2861 | 3.5258 |
| 46 | 1.300 | 1.6767 | 2.0129 | 2. 4102 | 2.6870 | 3.9488 | 3.2771 | 3.5150 |
| 48 | 1.299 | 1.6772 | 2.0106 | 2.4056 | 2.6822 | 3.9426 | 3.2689 | 3.5051 |
| 50 | 1.298 | 1.6759 | 2.0086 | 2.4033 | 2.6778 | 3.9370 | 3.2614 | 3.4060 |
| 55 | 1.2997 | 1.673 | 2.0040 | 2.3960 | 2.6680 | 2.9240 | 3. 2560 | 3.4760 |
| 60 | 1.2958 | 1.6706 | 2.0003 | 2.3901 | 2.6603 | 3.9146 | 3.2317 | 3.4602 |
| 65 | 1.2947 | 1.6686 | 1.997 | 2.3851 | 2.6536 | 3.9060 | 3.2204 | 3.4466 |
| 70 | 1.2938 | 1.6689 | 1.9944 | 2.3808 | 2.6479 | 3.8987 | 3.2108 | 3.4350 |
| 80 | 1. 2820 | 1.6640 | 1.9900 | 2.3730 | 2.6380 | 2.8870 | 3.1950 | 3.4160 |
| 90 | 1.2910 | 1.6620 | 1.9867 | 2.3885 | 2.6316 | 2.8779 | 3.1833 | 3.4019 |
| 100 | 1.2901 | 1.6602 | 1.9840 | 2.3642 | 2.6259 | 2.8707 | 3.1737 | 3.3905 |
| 120 | 1.2888 | 1.6577 | 1.9719 | 2. 3578 | 2.6174 | 2.8598 | 3.1595 | 3.3735 |
| 150 | 1.2872 | 1.6551 | 1.9759 | 2.3515 | 2.6090 | 2.8482 | 3.1455 | 3.3566 |
| 200 | 1.2858 | 1.6525 | 1.9719 | 2.3451 | 2.6006 | 2.8385 | 3.1315 | 3.3398 |
| 250 | 1.2849 | 1.6510 | 1.9695 | 2.3414 | 2.5966 | 2.8222 | 3. 1232 | 3.3299 |
| 300 | 1.2844 | 1.6499 | 1.9679 | 2.3388 | 2.5923 | 2.8279 | 3.1176 | 3.3233 |
| 400 | 1.2837 | 1.6487 | 1.9659 | 2.3357 | 2.5882 | 2.8227 | 3.1107 | 3.3150 |
| 500 | 1.2830 | 1.6470 | 1.9640 | 2.3330 | 2.7850 | 2.8190 | 3.1060 | 3.3100 |
Методы статистики
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента.
Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
1. История разработки t-критерия
Данный критерий был разработан Уильямом Сили Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
3. В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение.
Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
4. Как рассчитать t-критерий Стьюдента?
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М1 — средняя арифметическая первой сравниваемой совокупности (группы), М2 — средняя арифметическая второй сравниваемой совокупности (группы), m1 — средняя ошибка первой средней арифметической, m2 — средняя ошибка второй средней арифметической.
5. Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать.
Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
6. Пример расчета t-критерия Стьюдента
Для изучения эффективности нового препарата железа были выбраны две группы пациентов с анемией. В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо.
После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа.
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
После выполнения расчетов, значение t-критерия оказалось равным 4,51. Находим число степеней свободы как (34 + 40) — 2 = 72. Сравниваем полученное значение t-критерия Стьюдента 4,51 с критическим при р=0,05 значением, указанным в таблице: 1,993. Так как рассчитанное значение критерия больше критического, делаем вывод о том, что наблюдаемые различия статистически значимы (уровень значимости р<0,05).
Таблицы активности Ruckus | Продукты
Создание адаптируемых учебных пространств
Таблицы активности Ruckus позволяют пользователям быстро переходить от интерактивной к целенаправленной работе. С легкостью расставляйте и переставляйте столы, чтобы участвовать в совместных или традиционных макетах учебного пространства. Выбирайте из десяти динамических форм — клевер, D-образная форма, ромб, подкова, почка, воздушный змей, прямоугольник, круг, звездочка, квадрат — различных размеров и высот.
Просмотреть все изображения
Особенности
- Таблицы активности Ruckus обеспечивают гибкость настройки и мобильность, что позволяет использовать различные стили преподавания и обучения.
- Доступно множество размеров десяти динамических форм: клевер, D-образная форма, ромб, почка, воздушный змей, подкова, прямоугольник, круг, квадрат, звездочка.
- Пол с регулируемой высотой (12–19 дюймов) доступен для восьми форм рабочих столов; все столы также доступны с регулируемой высотой сидя (20-33 дюйма), регулируемой высотой сидя-стойки (29-42 дюйма) и фиксированной высотой (29»).
- Варианты основания включают подпятники, ролики или одновременно подпятники и ролики.
- Доступны десятки цветов рамы, цвета ламината, цвета кромки.
Конструкция
- Столешницы толщиной 1-¼ дюйма со склеенной кромкой 74P и поверхностью из ламината высокого давления (столы Kite и Diamond также предлагаются со столешницей ¾ дюйма с кромкой 73P).
- Рамы имеют наружный диаметр 1-¾ дюйма. Стальная труба 14-го калибра с блестящим никель-хромовым или порошковым покрытием.
- Столы с регулируемой высотой регулируются с шагом в 1 дюйм.
- Направляющие и ролики одинаковой высоты можно менять в полевых условиях, сохраняя высоту поверхности.
Посмотреть брошюру и техническую документацию
Особенности продукта
Многочисленные формы и размеры столешниц Столы для занятий Ruckus доступны в 10 динамических формах: клевер, D-образная форма, ромб, подкова, почка, воздушный змей, прямоугольник, круг, звездочка и квадрат, которые предлагаются в различных размерах.
Выберите один из четырех вариантов высоты стола: фиксированная высота 29 дюймов, регулируемая высота пола (12–19 дюймов), регулируемая высота сидя (20–33 дюйма) или регулируемая высота сидя-стоя (29–42 дюйма). «). Базовые варианты включают скольжения, ролики или как ролики, так и скольжения. Взаимозаменяемые ролики и опоры одинаковой высоты можно быстро заменить в полевых условиях, сохраняя при этом первоначальную высоту поверхности.
Стили прочных кромокЗакругленные или квадратные углы доступны с кромкой 73P и 74P, которая обеспечивает влагостойкость и защиту от несанкционированного доступа. Обе кромки предлагаются в широком диапазоне стандартных цветов.
Цена по прейскуранту начинается с
$ 684 – $ 1,497
Время выполнения заказа
6* Недель
*Если количество заказа превышает 200 единиц, свяжитесь со службой поддержки для уточнения времени выполнения заказа.
Запросить цену
Чтобы запросить цену на этот продукт, заполните форму ниже, и представитель KI свяжется с вами в ближайшее время.
Аналогичные продукты
Стойки Ruckus для ног Рабочие столы Ruckus Опорные столы Столы для пируэтовДополнительные продукты
Стул Рукус Белые доски Ruckus Рикошетный табурет Имаджиназиум БлипсРабочие столы Ruckus | Продукты | KI
Адаптируемый. Мобильный. Прочный.
Рабочие столы Ruckus подходят для различных конфигураций учебных помещений и отвечают строгим требованиям рабочих мест, медиацентров, научных лабораторий и обычных классов.
Просмотреть все изображения
Особенности
- Съемные рабочие поверхности без инструментов облегчают перемещение через узкие дверные проемы
- Размеры столов для различных планировок помещений: 30 x 54 дюйма, 48 x 54 дюйма и 60 x 54 дюйма (при высоте 36 дюймов)
- Материалы рабочей поверхности: ламинат, деревянный брусок или фенольная смола
- Варианты хранения: отделение для хранения вещей или вместительная сумка с запирающимися дверцами или без них
- Дополнительные модули питания, крючки для сумок и съемные полки
Конструкция
- Испытано на статическую нагрузку до 2000 фунтов
- Основание представляет собой прочную стальную конструкцию, окрашенную порошковой краской – основания и дверцы могут быть окрашены в разные цвета
- Стойки основания и рамы имеют сварные стальные усиливающие элементы 18 калибра для повышенной прочности
- Запирающиеся 3-дюймовые ролики промышленного класса обеспечивают мобильность и надежность Модули питания
- имеют 120 В переменного тока и беспроводную зарядку USB-A, USB-C и/или Qi
Посмотреть брошюру и техническую документацию
Особенности продукта
Варианты прочной поверхности Три различных рабочих поверхности способствуют активному обучению: деревянный брусок, ламинат или фенольная смола.
Хранение в базе позволяет хранить учебные материалы под рукой и поддерживать порядок в учебных помещениях. Ящики и ящики для хранения вещей доступны с запирающимися дверцами или без них. Блоки с дверьми предлагаются с опциональными контрастными цветами.
Легко вставляется в дверные проемыСъемные рабочие поверхности без инструментов и двухкомпонентные основания облегчают перемещение.
Цена по прейскуранту начинается с
$ 1,686 – $ 5,494
Срок поставки
6* недель
*Для рабочих столов Ruckus с цифровыми замками или разделочными блоками срок поставки составляет 7 недель. Для рабочих столов Ruckus со столешницами из фенольной смолы время выполнения заказа составляет 8 недель.
Запросить цену
Чтобы запросить цену на этот продукт, заполните форму ниже, и представитель KI свяжется с вами в ближайшее время.