После разложения общий член ряда записывается следующим образом:
$$ a_n =\frac{1}{(2n+1)(2n+3)}=\frac{1}{2} \frac{1}{2n+1} — \frac{1}{2} \frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) $$
$$ a_2 = \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) $$
$$ a_3 = \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=\frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) $$
$$ a_n = \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) $$
| Замечание |
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) + \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) + \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) + … $$
$$ … + \frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) + \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) = $$
Выносим дробь одну вторую $ \frac{1}{2} $ за скобки:
$$ = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9} … + $$
$$ + … \frac{1}{2n-1} — \frac{1}{2n+1} + \frac{1}{2n+1} — \frac{1}{2n+3} \bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $.
Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=\lim_{n\to\infty} S_n = \lim_{n\to\infty} \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = $$
$$ = \frac{1}{2} \lim_{n\to\infty} \bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} $$
Сумма ряда | это… Что такое Сумма ряда?
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).
Содержание
|
Определение
Пусть — числовой ряд.
Число называется n-ой частичной суммой ряда .
Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
Сходимость числовых рядов
Свойство 1. Если ряд
- (1.1)
сходится и его сумма равна S, то ряд
- (1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
- ,
а их суммы равны и соответственно, то сходятся и ряды
- ,
причём сумма каждого равна соответственно .
Необходимый признак сходимости ряда
Ряд может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:
Это необходимый признак сходимости ряда (но не достаточный!).
Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Примеры
- где — сумма геометрической прогрессии, в частности
- .
- — гармонический ряд расходится.
- — телескопический ряд.
См. также
- Действия с числовыми рядами
Обобщения числовых рядов
- Ряд Тейлора
- Ряд Фурье
- Степенной ряд
- Функциональный ряд.
Признаки сходимости
- Логарифмический признак сходимости
- Признак Абеля
- Признак Гаусса
- Признак Дирихле
- Признак Ермакова
- Признак Лобачевского
- Признак Раабе
- Признак сходимости д’Аламбера
- Признаки Коши:
- Радикальный признак Коши
- Интегральный признак Коши
- Теорема Лейбница о сходимости знакочередующихся рядов
Литература
- Выгодский М. Я. Справочник по высшей математике.
— 12-е изд. — М.: Наука, 1977. - Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
- Савельева Р. Ю. Высшая математика. Теория рядов.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
— 12-е изд. — М.: Наука, 1977.Примечания
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Указ. соч., глава 11.
Формула бесконечного ряда — изучите формулу для вычисления бесконечного ряда
Формула бесконечного ряда используется для нахождения суммы последовательности, в которой количество членов бесконечно. Существуют различные типы бесконечных рядов. В этом разделе мы обсудим сумму бесконечных арифметических рядов и сумму бесконечных геометрических рядов. Арифметический ряд — это последовательность, в которой разница между каждым последующим членом постоянна на всем протяжении, а геометрический ряд — это ряд, в котором отношение последовательных членов к предыдущему везде одинаково.
Формула бесконечного ряда — удобный инструмент для очень быстрого вычисления суммы. Давайте узнаем больше о формуле бесконечного ряда вместе с решенными примерами.
Что такое формула бесконечного ряда?
Формула суммы бесконечного геометрического ряда используется для нахождения суммы ряда, простирающегося до бесконечности. Это также известно как сумма бесконечных GP. Находя сумму GP, мы обнаруживаем, что сумма сходится к значению, хотя ряд имеет бесконечные члены. Формула бесконечного ряда, если −1 Где, Примечание. Если r > 1, сумма не существует, так как сумма не сходится. Давайте теперь посмотрим на несколько решенных примеров с использованием формулы бесконечного ряда. Отличное обучение в старшей школе с использованием простых подсказок Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами. Забронировать бесплатный пробный урок Пример 1: Используя формулу бесконечного ряда, найдите сумму бесконечных рядов: 1/4 + 1/16 + 1/64 + 1/256 +⋯ 
Дано: a = ¼
r = (1/16) / (1/4) = (1/64) / (1/16) = ¼
Чтобы найти: Сумма заданного бесконечного ряда
Если r<1, то сумма определяется как Сумма = a/(1-r)
Применяя значения к формуле бесконечного ряда, мы получаем
Сумма=( 1/4)/(1-1/4)
Сумма=(1/4)/(3/4)
Сумма=4/(3*4)
Сумма=1/3
Ответ: Сумма 1/4+1/16+1/64+1/256+⋯ равна 1/3
Пример 2.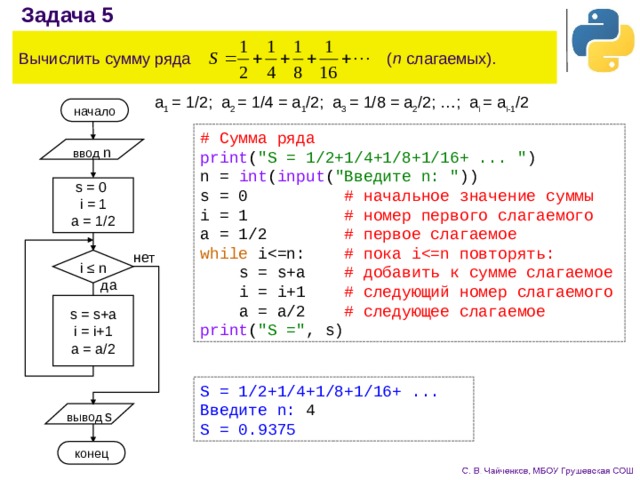
Используя формулу бесконечного ряда, найдите сумму бесконечного ряда: 1/2 + 1/ 6 + 1/18 + 1/54 + ⋯
Решение:
Дано: a = 1/2
r = (1/6) / (1/2) = (1/18) / (1/6) = 1/3
Найти : Сумма данного бесконечного ряда
Если r<1, то сумма задается как Сумма = a/(1-r)
Применяя значения к формуле бесконечного ряда, мы получаем
Сумма=(1/2)/(1-1/3)
Сумма=(1/2)/(2/3)
Сумма=3/( 2*2)
Сумма=3/4
Ответ: Сумма 1/2 + 1/6 + 1/18 + 1/54 + ⋯ равна 3/4
Пример 3: Оценка 3 + 7 + 11 + …….Решение:
a = 3, d = 4 и n = ∞
Здесь разница > 0,
Итак, сумма = + ∞
Ответ: 3 + 7 + 11 + ……. = + ∞
Часто задаваемые вопросы о формуле бесконечного ряда
Что такое сумма бесконечных членов?
Бесконечный ряд состоит из бесконечного числа членов. Сумма первых n слагаемых S n называется частичной суммой.
Если S n стремится к пределу, когда n стремится к бесконечности, предел называется суммой ряда до бесконечности. Сумма бесконечных арифметических рядов равна либо +∞, либо -∞. Сумма бесконечного геометрического ряда, когда обыкновенное отношение <1, тогда сумма сходится к a/(1-r), что является формулой бесконечного ряда бесконечного GP. Здесь a — первое слагаемое, r — обыкновенное отношение.
Что такое формула бесконечного ряда?
Сумма бесконечных арифметических рядов равна либо +∞, либо -∞. Сумма формулы бесконечного геометрического ряда также известна как сумма бесконечного GP. Формула бесконечного ряда, если значение r таково, что −1 Сумма = a/(1-r) Где, При нахождении суммы данного бесконечного геометрического ряда Если r<1, то сумма определяется как Sum = a/(1-r). Эту бесконечную ЗП можно записать как 3/10 + 3/100 + 3/1000+……… Здесь мы находим, что первый член a = 3/10, а r = 3/100 ÷ 3/10 = 1/10 Поскольку r < 1, сумма должна сходиться к a/ (1-r) как по формуле бесконечного ряда для бесконечного GP. Таким образом, сумма до бесконечности = (3/10) ÷ (1 — 1/10) Сумма = 3/10 ÷ 9/10 = 1/3 Таким образом, сумма сходится к 1/3. 0,3+ 0,33+ 0,333+…. = 1/3 Бесконечный
геометрический ряд
это сумма бесконечного
геометрическая последовательность
. В этой серии не будет последнего члена. Общий вид бесконечного геометрического ряда таков:
а
1
+
а
1
р
+
а
1
р
2
+
а
1
р
3
+
. Мы можем найти сумму всех конечных геометрических рядов. Но в случае бесконечного геометрического ряда, когда
обыкновенное отношение
больше единицы, члены последовательности будут становиться все больше и больше, и если вы добавите большие числа, вы не получите окончательного ответа. Единственным возможным ответом будет бесконечность. Таким образом, мы не имеем дело с обыкновенным отношением больше единицы для бесконечного геометрического ряда. Если обычное отношение
р
лежит между
−
1
к
1
, мы можем иметь сумму бесконечного геометрического ряда. То есть сумма выходит за
|
р
| <
1
. Сумма
С
бесконечного геометрического ряда с
−
1 <
р
<
1
дается формулой, С
«=»
а
1
1
−
р Бесконечный ряд, имеющий сумму, называется сходящимся рядом, а сумма
С
н
называется частичной суммой ряда. Вы можете использовать сигма-нотацию для представления бесконечного ряда. Например,
∑
н
«=»
1
∞
10
(
1
2
)
н
−
1
представляет собой бесконечный ряд. Символ бесконечности, расположенный над обозначением сигмы, указывает на то, что ряд бесконечен. Чтобы найти сумму вышеупомянутого бесконечного геометрического ряда, сначала проверьте, существует ли сумма, используя значение
р
. Здесь значение
р
является
1
2
. С
|
1
2
| <
1
, сумма выходит. Теперь воспользуемся формулой суммы бесконечного геометрического ряда. С
«=»
а
1
1
−
р Заменять
10
для
а
1
и
1
2
для
р
. Что такое a и r в формуле бесконечного ряда?
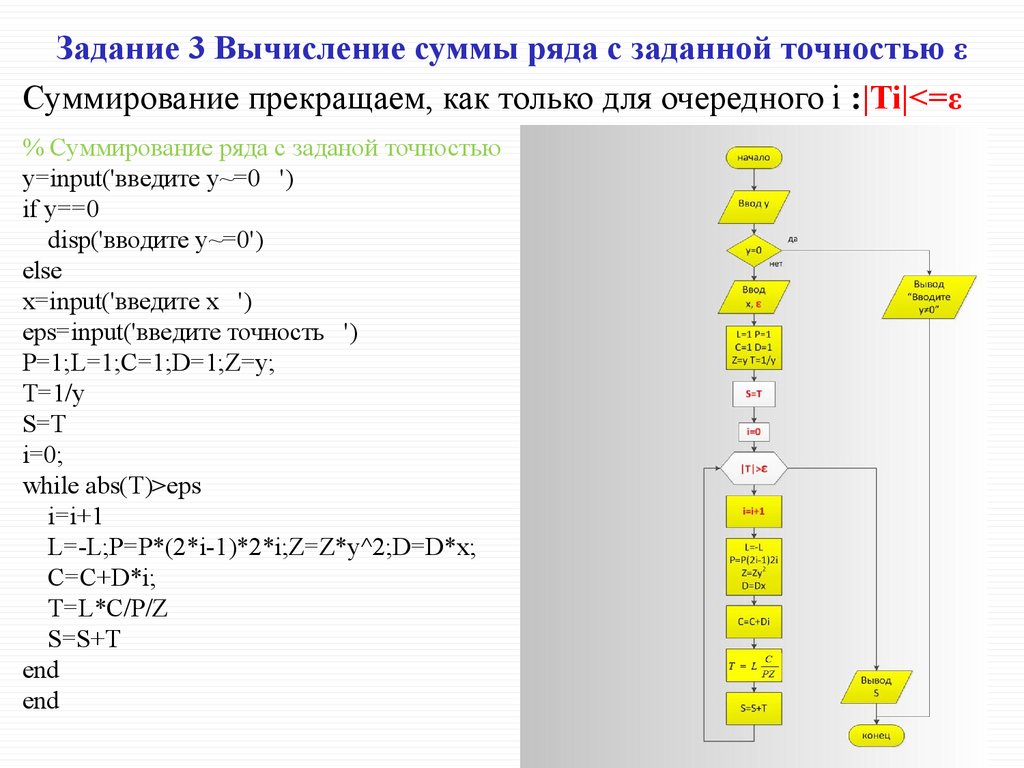В этой формуле бесконечного ряда a = первый член ряда, r = обыкновенное отношение между двумя последовательными членами и −1 Найдите сумму бесконечной ЗП 0.3+ 0.33+ 0.333+….
Бесконечный геометрический ряд
Горячая математика
