Где тангенс положительный. Свойства синуса, косинуса, тангенса и котангенса угла
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.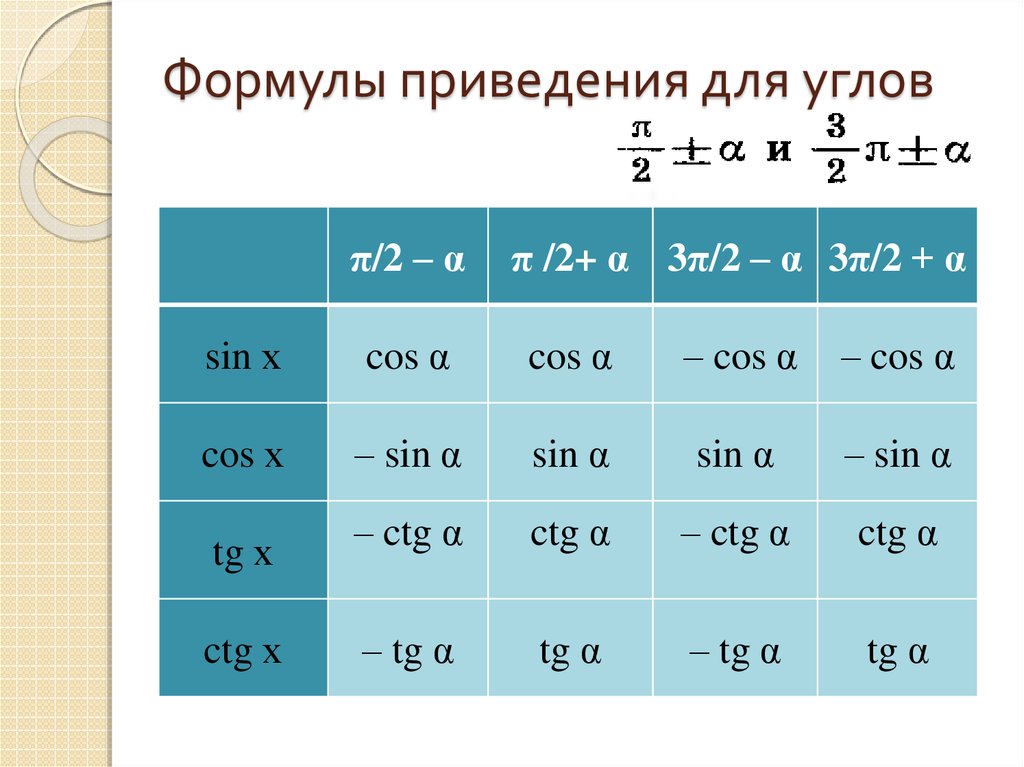
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Yandex.RTB R-A-339285-1
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)
Вновь обратимся к единичной окружности.
Точка A 1 (x , y) — результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , — y) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая — (x , — y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Отсчёт углов на тригонометрическом круге.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Он почти такой, как в предыдущем уроке. Есть оси, окружность, угол, всё чин-чинарём. Добавлены номера четвертей (в уголках большого квадрата) — от первой, до четвёртой. А то вдруг кто не знает? Как видите, четверти (их ещё называют красивым словом «квадранты») нумеруются против хода часовой стрелки. Добавлены значения угла на осях. Всё понятно, никаких заморочек.
Добавлены значения угла на осях. Всё понятно, никаких заморочек.
И добавлена зелёная стрелка. С плюсом. Что она означает? Напомню, что неподвижная сторона угла всегда
Если будем откладывать углы в обратную сторону, по ходу часовой стрелки, угол будет считаться отрицательным. Наведите курсор на картинку (или коснитесь картинки на планшете), увидите синюю стрелку с минусом. Это — направление отрицательного отсчёта углов. Для примера показан отрицательный угол (- 60°). А ещё вы увидите, как поменялись циферки на осях… Я их тоже перевёл в отрицательные углы. Нумерация квадрантов не меняется.
Вот тут, обычно, начинаются первые непонятки. Как так!? А если отрицательный угол на круге совпадёт с положительным!? Да и вообще, получается что, одно и то же положение подвижной стороны (или точки на числовой окружности) можно обозвать как отрицательным углом, так и положительным!?
Да.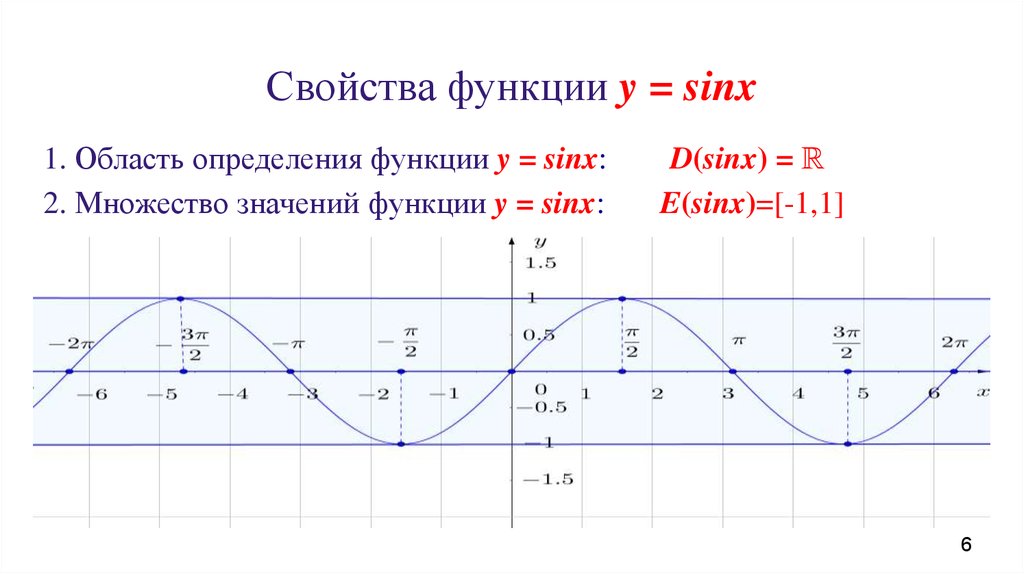 Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Не вопрос. Всяко правильно.) Выбор положительного или отрицательного исчисления угла зависит от условия задания. Если в условии ничего не сказано открытым текстом про знак угла, (типа «определить наименьший положительный угол» и т.д.), то работаем с удобными нам величинами.
Исключением (а как без них?!) являются тригонометрические неравенства, но там мы эту фишку освоим.
А теперь вопрос вам. Как я узнал, что положение угла 110° совпадает с положением угла -250°?
Намекну, что это связано с полным оборотом. В 360°… Непонятно? Тогда рисуем круг. Сами рисуем, на бумаге. Отмечаем угол
 Останется как раз 250°…
Останется как раз 250°…Уловили? А теперь — внимание! Если углы 110° и -250° занимают на круге одно и то же положение, то что? Да то, что у углов 110° и -250° совершенно одинаковые синус, косинус, тангенс и котангенс!
Т.е. sin110° = sin(-250°), ctg110° = ctg(-250°) и так далее. Вот это уже действительно важно! И само по себе — есть масса заданий, где надо упростить выражения, и как база для последующего освоения формул приведения и прочих премудростей тригонометрии.
Понятное дело, 110° и -250° я взял наобум, чисто для примера. Всё эти равенства работают для любых углов, занимающих одно положение на круге. 60° и -300°, -75° и 285°, ну и так далее. Отмечу сразу, что углы в этих парочках — разные. А вот тригонометрические функции у них — одинаковые.
Думаю, что такое отрицательные углы вы поняли. Это совсем просто. Против хода часовой стрелки — положительный отсчёт. По ходу — отрицательный. Считать угол положительным, или отрицательным зависит от нас . От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.
От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.
Углы больше 360°.
Займемся углами которые больше 360°. А такие бывают? Бывают, конечно. Как их нарисовать на круге? Да не проблема! Допустим, нам надо понять, в какую четверть попадёт угол в 1000°? Легко! Делаем один полный оборот против хода часовой стрелки (угол-то нам дали положительный!). Отмотали 360°. Ну и мотаем дальше! Ещё оборот — уже получилось 720°. Сколько осталось? 280°. На полный оборот не хватает… Но угол больше 270° — а это граница между третьей и четвёртой четвертью. Стало быть наш угол в 1000° попадает в четвёртую четверть. Всё.
Как видите, это совсем просто. Ещё раз напомню, что угол 1000° и угол 280°, который мы получили путём отбрасывания «лишних» полных оборотов — это, строго говоря, разные углы. Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…
Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…
Зачем всё это нужно? Зачем нам переводить углы из одного в другой? Да всё за тем же.) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)
Ну что, потренируемся?)
Отвечаем на вопросы. Сначала простые.
1. В какую четверть попадает угол -325° ?
2. В какую четверть попадает угол 3000° ?
3. В какую четверть попадает угол -3000° ?
Есть проблемы? Или неуверенность? Идём в Раздел 555, Практическая работа с тригонометрическим кругом. Там, в первом уроке этой самой «Практической работы…» всё подробненько… В таких вопросах неуверенности быть не должно!
4. Какой знак имеет sin555° ?
5. Какой знак имеет tg555° ?
Определили? Отлично! Сомневаетесь? Надо в Раздел 555. .. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.
.. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.
А теперь вопросы помудрёнее.
6. Привести выражение sin777° к синусу наименьшего положительного угла.
7. Привести выражение cos777° к косинусу наибольшего отрицательного угла.
8. Привести выражение cos(-777°) к косинусу наименьшего положительного угла.
9. Привести выражение sin777° к синусу наибольшего отрицательного угла.
Что, вопросы 6-9 озадачили? Привыкайте, на ЕГЭ и не такие формулировочки встречаются… Так и быть, переведу. Только для вас!
Слова «привести выражение к…» означают преобразовать выражение так, чтобы его значение не изменилось, а внешний вид поменялся в соответствии с заданием. Так, в задании 6 и 9 мы должны получить синус, внутри которого стоит наменьший положительный угол. Всё остальное — не имеет значения.
Ответы выдам по порядку (в нарушение наших правил). А что делать, знака всего два, а четверти всего четыре. .. Не разбежишься в вариантах.
.. Не разбежишься в вариантах.
6. sin57°.
7. cos(-57°).
8. cos57°.
9. -sin(-57°)
Предполагаю, что ответы на вопросы 6 -9 кое-кого смутили. Особенно -sin(-57°) , правда?) Действительно, в элементарных правилах отсчёта углов есть место для ошибок… Именно поэтому пришлось сделать урок: «Как определять знаки функций и приводить углы на тригонометрическом круге?» В Разделе 555. Там задания 4 — 9 разобраны. Хорошо разобраны, со всеми подводными камнями. А они тут есть.)
В следующем уроке мы разберёмся с загадочными радианами и числом «Пи» . Научимся легко и правильно переводить градусы в радианы и обратно. И с удивлением обнаружим, что этой элементарной информации на сайте уже хватает , чтобы решать некоторые нестандартные задачки по тригонометрии!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Урок по алгебре в 9 классе по теме «Свойства синуса, косинуса, тангенса и котангенса»
Применение кейсовой технологии на уроках.
Урок по алгебре в 9 классе
по теме «Свойства синуса, косинуса, тангенса и котангенса»
Цель урока: сформировать умение учащихся определять знаки тригонометрических функций в каждой четверти, какие функции четные, нечетные; знать изменяются ли значения тригонометрических функций при изменении угла.
Оборудование урока: тригонометр, таблицы: четных и нечетных функций; таблицы значений тригонометрических функций для углов в 0°, 30°, 45°, 60°, 90°; таблица Брадиса, дидактический материал на каждого ученика.
Ход урока.
Вводно-мотивационный этап: постановка плана и цели урока, мотивация учебной деятельности, организация учебной работы на уроке, создание эмоционального настроя.
Операционный этап:
Определение тригонометрических функций sin α, cos α, tg α, ctg α при помощи рисунка; рассматривается единичная окружность. Учащиеся вспоминают, что sin α=y/r , cos α=x/r. tg α=y/x, ctg α=x/y и затем формулируются определения данных функций с учетом того, что r=1, т. е. sin α=y, cos α=x, tg α= sin α/cos α, а ctg α= cos α/ sin α.
е. sin α=y, cos α=x, tg α= sin α/cos α, а ctg α= cos α/ sin α.
2. Повторение значения функций в первой четверти и заполнение таблицы у себя в тетради.
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа №1. У каждого ученика на столе имеется текст задания. Учащимся необходимо записать только ответы. И сразу же проверяются ответы. Учитель открывает скрытые ответы, записанные на доске. Учащиеся сами оценивают выполненную работу.
У каждого ученика на столе имеется текст задания. Учащимся необходимо записать только ответы. И сразу же проверяются ответы. Учитель открывает скрытые ответы, записанные на доске. Учащиеся сами оценивают выполненную работу.
Операционный этап:
Самостоятельная работа №1
Вычислите:
А) 2 х sin 30° — 4 х tg45° = 2 х ½ — 4 х 1= -3;
Б) 2 х sin 45° + 6 cos 60°= 2 х√2/2 + 6 х½= √2 +3;
В) tg45° х tg60°= 1 х√3=;
Г) tg30° х ctg30°= √3/3х √3=;
Учитель предлагает кейс с теоритическим материалом учащиеся думают и отвечают на вопрос какой знак будет иметь sin α, cos α, tg α, ctg α в каждой четверти, если:
а) α=48°;
б) α=137°;
в) α=200°;
г) α=306°.
Учащиеся делают вывод, после чего вывешивается таблица
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем проводится блиц-самостоятельная работа №2 с последующей проверкой.
Самостоятельная работа №2
Какой знак имеют:
А) sin 179° Б) cos280° В) tg 175° Г) ctg 359°.
Следующей свойство рассматривают учащиеся вместе с учителем, выясняют зависимость между sin α, cos α, tg α, ctg α противоположных углов, делаются соответствующие рисунки и выводы: cos (-α)= cos α; tg (-α)= -tg α; ctg (-α)= -ctg α; sin(- α)=- sin α.
Какие функции являются четными, какие не четными?
Закрепляются новое свойство решением примера из учебника, и выполняем самостоятельную работу №3.
Самостоятельная работа №3
Найдите:
А) sin (-60°)= -√3/2;
Б) cos(-90)°=0;
В) tg (-45°)=-1;
Г) ctg (-30°)=√3.
Последнее свойство тригонометрических функций обсуждается учителем вместе с учащимися при решении следующего примера.
sin 30°= sin (30°+360°)= sin (30°-360°)= sin (30°+360°х2)= sin (30°-360°х2)= …½
Учащиеся делают вывод о том, что значение sin α, cos α, tg α, ctg α при изменении угла на целое число оборотов не изменяются.
Закрепление: решение упражнения из учебника.
Рефлексивно-оценочный этап:
Рефлексия. внимание учащихся обращается на применение тригонометра и таблицы Брадиса при нахождении тригонометрических функций от 0°до 90°.
В заключении подводится итог уроку. Формулируются все три свойства тригонометрических функций рассмотренных на данном уроке. Учитель оценивает работу учащихся, учитывая самооценку каждого в течение урока и выставляет общую отметку.
Домашнее задание.
Синус, косинус, тангенс, котангенс
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $\alpha $:
Мы видим, что острый угол $\alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $\alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $\alpha $.
Тогда:
Определение 1. Синус угла $\alpha $ — это отношение противолежащего катета к гипотенузе:
\[\sin \alpha =\frac{\text{противолежащий катет}}{\text{гипотенуза}}=\frac{a}{c}\]
Определение 2.
Косинус угла $\alpha $ — это отношение прилежащего катета к гипотенузе:
\[\cos \alpha =\frac{\text{прилежащий катет}}{\text{гипотенуза}}=\frac{b}{c}\]
Определение 3. Тангенс угла $\alpha $ — это отношение противолежащего катета к прилежащему:
\[\operatorname{tg}\alpha =\frac{\text{противолежащий катет}}{\text{прилежащий катет}}=\frac{a}{b}\]
Определение 3. Котангенс угла $\alpha $ — это отношение прилежащего катета к противолежащему:
\[\operatorname{ctg}\alpha =\frac{\text{прилежащий катет}}{\text{противолежащий катет}}=\frac{b}{a}\]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $\alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $\alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
\[\begin{align}\sin \alpha& =\frac{BC}{AC}=\frac{5}{4} \\ \cos \alpha& =\frac{AB}{AC}=\frac{3}{5} \\ \operatorname{tg}\alpha& =\frac{BC}{AB}=\frac{4}{3} \end{align}\]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
\[\operatorname{ctg}\alpha =\frac{1}{\operatorname{tg}\alpha }\]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $\alpha $.
{2}}=1+1=2 \\ AC & =\sqrt{2} \\ \end{align}\]
Теперь найдём синус, косинус и тангенс:
\[\begin{align}\sin \alpha &=\frac{BC}{AC}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} \\ \cos \alpha &=\frac{AB}{AC}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} \\ \operatorname{tg}\alpha&=\frac{BC}{AB}=\frac{1}{1}=1 \end{align}\]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $\alpha $. Найдите $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
Решение.
\[\begin{align}\sin \alpha &=\frac{5}{13} \\ \cos \alpha &=\frac{12}{13} \\ \operatorname{tg}\alpha &=\frac{5}{12} \\ \end{align}\]
Задача 4.
{2}}=4-1=3 \\ l &=\sqrt{3} \\ \end{align}\]
Синус, косинус и тангенс:
\[\begin{align}\sin \alpha&=\frac{1}{2} \\ \cos \alpha&=\frac{\sqrt{3}}{2} \\ \operatorname{tg}\alpha&=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3} \\ \end{align}\]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $\alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $\alpha $. \circ \] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
\circ \] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
\[\Delta ABC\sim \Delta AMN\]
Из подобия треугольников следует двойное равенство
\[\frac{AB}{AM}=\frac{BC}{MN}=\frac{AC}{AN}\]
Выпишем второе равенство — получим пропорцию
\[\frac{BC}{MN}=\frac{AC}{AN}\]
Попробуем выразить $\sin \alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
\[BC\cdot AN=MN\cdot AC\]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
\[\begin{align}\frac{BC\cdot AN}{AN\cdot AC} &=\frac{MN\cdot AC}{AN\cdot AC} \\ \frac{BC}{AC} &=\frac{MN}{AN} \end{align}\]
Однако по определению синуса имеем:
\[\begin{align}\sin BAC &=\frac{BC}{AC} \\ \sin MAN &=\frac{MN}{AN} \\ \end{align}\]
Получается, что $\sin BAC=\sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $\alpha $ мы всегда будем получать одно и то же значение $\sin \alpha $.
То же самое касается и $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ — они зависят лишь от градусной меры угла $\alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
- Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.
 \circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:
\[\sin \alpha =\sin A=\frac{BC}{AB}=\frac{3}{5}=0,6\]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод.
 \circ $. Но когда $\sin \alpha =0,6$, мы уже не можем назвать угол $\alpha $ (хотя всегда можем построить такой угол).
\circ $. Но когда $\sin \alpha =0,6$, мы уже не можем назвать угол $\alpha $ (хотя всегда можем построить такой угол).С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $\alpha $:
Выразим синус, косинус:
\[\sin \alpha =\frac{a}{c};\quad \cos \alpha =\frac{b}{c}\]
А теперь выразим тангенс и заметим, что
\[\operatorname{tg}\alpha =\frac{a}{b}=\frac{a}{c}\cdot \frac{c}{b}=\frac{\sin \alpha }{\cos \alpha }\]
Точно так же можно выразить и котангенс:
\[\operatorname{ctg}\alpha =\frac{b}{a}=\frac{b}{c}\cdot \frac{c}{a}=\frac{\cos \alpha }{\sin \alpha }\]
Более того, сам тангенс и котангенс тоже связаны:
\[\operatorname{tg}\alpha \cdot \operatorname{ctg}\alpha =\frac{a}{b}\cdot \frac{b}{a}=1\]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
\[\operatorname{tg}\alpha =\frac{\sin \alpha }{\cos \alpha };\quad \operatorname{ctg}\alpha =\frac{\cos \alpha }{\sin \alpha };\quad \operatorname{tg}\alpha \cdot \operatorname{ctg}\alpha =1\]
Эти формулы нужно знать наизусть.
 \circ $, поэтому $\sin \alpha \gt 0$. Следовательно
\circ $, поэтому $\sin \alpha \gt 0$. Следовательно\[\sin \alpha =\frac{7}{\sqrt{113}}\]
Найдём $\operatorname{tg}\alpha $:
\[\operatorname{tg}\alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{7}{\sqrt{113}}\cdot \frac{\sqrt{113}}{8}=\frac{7}{8}\]
Окончательный ответ:
\[48\operatorname{tg}\alpha =48\cdot \frac{7}{8}=6\cdot 7=42\]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $\alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52\cos \alpha $ для острого угла $\alpha $, если $\sin \alpha =\frac{5}{13}$.
 {2}}\alpha = \\ & =1-\frac{1}{26}=\frac{25}{26} \\ \sin \alpha&=\pm \frac{5}{\sqrt{26}} \end{align}\]
{2}}\alpha = \\ & =1-\frac{1}{26}=\frac{25}{26} \\ \sin \alpha&=\pm \frac{5}{\sqrt{26}} \end{align}\]Поскольку $\sin \alpha \gt 0$ для острых $\alpha $, выбираем
\[\sin \alpha =\frac{5}{\sqrt{26}}\]
Считаем $\operatorname{tg}\alpha $:
\[\operatorname{tg}\alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{5}{\sqrt{26}}\cdot \frac{\sqrt{26}}{1}=5\]
Откуда
\[1+2\operatorname{tg}\alpha =1+2\cdot 5=11\]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11.
 Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Найдите тангенс угла $ABC$, изображённого на координатной сетке:Решение. Дополнительное построение: $AH\bot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
\[\operatorname{tg}ABC=\frac{AH}{BH}=\frac{3}{4}=0,75\]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AH\bot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
\[\operatorname{tg}ABC=\frac{AH}{BH}=\frac{2}{4}=\frac{1}{2}\]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.

Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
\[\operatorname{tg}MNK=\frac{HK}{HN}=\frac{\sqrt{2}}{2\sqrt{2}}=\frac{1}{2}=0,5\]
Здесь мы предположили, что сторона квадрата сетки равна 1.
 Но с тем же успехом можно считать, что сторона квадрата $a$:
Но с тем же успехом можно считать, что сторона квадрата $a$:\[\operatorname{tg}MNK=\frac{HK}{HN}=\frac{a\sqrt{2}}{2a\sqrt{2}}=\frac{1}{2}=0,5\]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $\operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
\[\operatorname{tg}DEF=\frac{a\sqrt{10}}{a\sqrt{10}}=1\]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.

К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2
Синус, косинус, тангенс, котангенс — 10 класс, урок и презентация
Дата публикации: .

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.Скачать:Синус и косинус (PPTX)
Что будем изучать:
1. Определение синуса и косинуса.
2. Определение тангенса и котангенса.
3. Основное тригонометрическое тождество.
4. Таблица значений синуса, косинуса, тангенса, котангенса.
5. Основные свойства.
6. Синус и косинус в жизни.
7. Примеры и задачи.Синус и косинус. Определения
Ребята, давайте отметим на числовой окружности точку $Р$. Посмотрите на рисунок, наша точка $Р$ соответствует некоторому числу $t$ числовой окружности, тогда абсциссу точки $Р$ будем называть косинусом числа $t$ и обозначать $cos(t)$, а ординату точки $Р$ назовем синусом числа $t$ и обозначим $sin(t)$.
А как будет выглядеть запись синуса и косинуса на математическом языке?
Наша точка $Р(t) = Р(x,y)$. 2=1$.
2=1$.Значения синуса, косинуса, тангенса, котангенса в четвертях окружности:
Значения синуса, косинуса, тангенса, котангенса в четвертях окружности:
Таблица значений синуса, косинуса, тангенса, котангенса
не сущ. – не существует значение, т.к. на 0 делить нельзя.Основные свойства синуса и косинуса
Для любого числа $t$ справедливы равенства:
$sin(-t) = -sin(t)$.
$cos(- t) = cos(t)$.
$tg(- t) = -tg(t)$.
$ctg(- t) = -ctg(t)$.$sin(t + 2π*k) = sin(t)$.
$cos(t +2π*k ) = cos(t)$.$sin(t + π ) = -sin(t)$.
$cos(t +π ) = -cos(t)$.$tg(t + π*k ) = tg(t)$.
$ctg(t +π*k ) = ctg(t)$.$sin(t + \frac{π}{2}) = cos(t)$.
$cos(t + \frac{π}{2}) = -sin(t)$.Синус и косинус в жизни
Для чего нужны синусы и косинусы в обычной жизни?
На практике синусы и косинусы применяются во всех инженерных специальностях, особенно в строительных. Их используют моряки и летчики в расчетах курса движения. Не обходятся без синусов и косинусов геодезисты и даже путешественники. В географии эти понятия применяют для измерения расстояний между объектами и в спутниковых навигационных системах.
Не обходятся без синусов и косинусов геодезисты и даже путешественники. В географии эти понятия применяют для измерения расстояний между объектами и в спутниковых навигационных системах.
Пример 1.
Вычислить синус и косинус $t$, при $t=\frac{53π}{4}$.Решение:
Поскольку, числам $t$ и $t+2π*k$, $k$ – целое число, соответствует одна точка числовой окружности, то:
$\frac{53π}{4}=(12 + \frac{5}{4})*π = 12π + \frac{5π}{4}=\frac{5π}{4} + 2π*6$.
Воспользуемся свойством: $sin(t + 2π*k ) = sin(t)$, $cos(t +2π*k)= cos(t)$.
$sin(\frac{5π}{4} + 2π*6) = sin(\frac{5π}{4}) = sin(\frac{π}{4} + π)$.
$cos(\frac{5π}{4} + 2π*6) = cos(\frac{5π}{4})=cos(\frac{π}{4} + π)$.
Воспользуемся свойством: $sin(t + π ) = -sin(t)$, $cos(t+π) =-cos(t)$.
$sin(\frac{π}{4} + π)=-sin(\frac{π}{4})$.
$cos(\frac{π}{4} + π)=-cos(\frac{π}{4})$.
Из таблицы значений синуса и косинуса получаем: $sin(\frac{53π}{4})=-\frac{\sqrt{2}}{2}$; $cos(\frac{53π}{4})=-\frac{\sqrt{2}}{2}$.Пример 2.

Вычислить синус и косинус $t$, при $t=-\frac{49π}{3}$.Решение:
Поскольку, числам $t$ и $t+2π*k$, $k$ – целое число, соответствует одна точка числовой окружности, тогда:
$-\frac{49π}{3}=-(16 + \frac{1}{3})*π =-16π +(-\frac{π}{3}) = (-\frac{π}{3}) + 2π*(-8)$.
Воспользуемся свойством: $sin(t + 2π*k ) = sin(t)$, $cos(t +2π*k)= cos(t)$.
$sin(-\frac{π}{3} + 2π*(-8) )=sin(-\frac{π}{3} )$.$cos(-\frac{π}{3} + 2π*(-8) )=cos(-\frac{π}{3} )$.
Воспользуемся свойством: $sin(- t) = -sin(t)$, $cos(- t) = cos(t)$.
$sin(-\frac{π}{3})=-sin(\frac{π}{3})$.
$cos(-\frac{π}{3})=cos(\frac{π}{3})$.
Из таблицы значений синуса и косинуса получаем: $sin(-\frac{49π}{3})=-\frac{\sqrt{3}}{2}$; $cos(-\frac{49π}{3})=\frac{1}{2}$.
Пример 3.
Решите уравнение и неравенство:
а) $sin(t)=\frac{\sqrt{3}}{2}$.
б) $sin(t)>\frac{\sqrt{3}}{2}$.Решение:
$sin(t)$ – это ордината точки числовой окружности (из определения).
Значит на числовой окружности нужно найти точки с ординатой $\frac{\sqrt{3}}{2}$. Пусть, это будут точки F и G. Определим, каким значениям $t$ соответствуют точки $F$ и $G$ на рисунке.
Пусть, это будут точки F и G. Определим, каким значениям $t$ соответствуют точки $F$ и $G$ на рисунке.
а) Точки $F$ и $G$ имеют координаты: $\frac{π}{3} +2 π*k$ и $\frac{2π}{3}+2 π*k$.
б) Точки, которые удовлетворяют неравенству $sin(t)>\frac{\sqrt{3}}{2}$, расположены на дуге FG.
Тогда: $\frac{π}{3} +2 π*k<t<\frac{2π}{3} +2 π*k$.
Ответ :
a) $t=\frac{π}{3}+2 π*k$ и $t= \frac{2π}{3} +2 π*k$.
б) $\frac{π}{3}+2 π*k<t<\frac{2π}{3} +2 π*k$.Пример 4.
Решить уравнение и неравенство:
а) $cos(t)=\frac{1}{2}$.
б) $cos(t)>\frac{1}{2}$.Решение:
$cos(t)$ – это абсцисса точки числовой окружности (из определения).
Значит, на числовой окружности необходимо найти точки с абсциссой равной $\frac{1}{2}$. Пусть это будут точки F и G (см. рисунок). Надо определить, каким значениям $t$, они соответствуют.
а) Точки F и G имеют координаты: $-\frac{π}{3}+2π*k$ и $\frac{π}{3}+2π*k$.
б) Точки, которые удовлетворяют неравенству $cos(t)>\frac{1}{2}$, расположены на дуге FG.
Тогда: $-\frac{π}{3}+2π*k<t<\frac{π}{3}+2π*k$.Ответ:
a) $-\frac{π}{3}+2π*k$ и $\frac{π}{3}+2π*k$.б) $-\frac{π}{3}+2π*k<t<\frac{π}{3}+2π*k$.
Пример 5.
Вычислить тангенс и котангенс $t$, при: $t=-\frac{7π}{3}$.
Решение:Числам $t$ и $t+2π*k$, где k – целое число, соответствует одна точка числовой окружности, тогда:
$-\frac{7π}{3} = -(2 + \frac{1}{3})*π = -2π +(-\frac{π}{3}) = (-\frac{π}{3}) + 2π$.Воспользуемся свойством: $tg(x+ π*k) = tg(x)$, $ctg(x+π*k) = ctg(x)$.
$tg((-\frac{π}{3}) + 2π ) = tg(-\frac{π}{3})$.
$сtg((-\frac{π}{3}) + 2π ) = сtg(-\frac{π}{3})$.
Воспользуемся свойством: $tg(-x) = -tg(x)$, $ctg(-x) = -ctg(x)$.
$tg(-\frac{π}{3})=-tg(\frac{π}{3})$.
$сtg(-\frac{π}{3})=-сtg(\frac{π}{3})$.
Из таблицы значений получаем: $tg(-\frac{7π}{3}) =-tg(\frac{π}{3}) = -\sqrt{3}$.
$сtg(-\frac{7π}{3}) = -сtg(\frac{π}{3}) =-\frac{\sqrt{3}}{3}$.Примеры для самостоятельного решения:
1) Вычислить синус и косинус $t$, при
а) $t=\frac{61π}{6}$,
б) $t= -\frac{52π}{3}$.
2) Решите уравнения:
a) $sin(t)=-\frac{1}{2}$;
б) $sin(t) >-\frac{1}{2}$;
в) $sin(t) 3) Решите уравнения:
a) $cos(t)=-\frac{1}{2}$;
б) $cos(t) >-\frac{1}{2}$;
в) $cos(t) 4) Вычислить тангенс и котангенс $t$, при
а) $t= \frac{19π}{6}$;
б) $t=\frac{41π}{4}$.Тригонометрические функции с примерами решения и образцами выполнения
Оглавление:
Тригонометрические функции — служат прежде всего для описания разнообразных периодических процессов. С периодически повторяющимися ситуациями человек сталкивается повсюду. Его жизнь сопровождают различные астрономические явления — восход и заход Солнца, изменение фаз Луны, чередование времен года, положение звезд на небе, затмения и движения планет. Человек давно заметил, что все эти явления возобновляются периодически. Жизнь на Земле тесно связана с ними, и поэтому неудивительно, что астрономические наблюдения явились источником многих математических открытий.

Биение сердца, цикл в жизнедеятельности организма, вращение колеса, морские приливы и отливы, заполненность городского транспорта, эпидемии гриппа — в этих многообразных примерах можно найти общее: эти процессы периодичны.
Открывая утром газету, мы часто читаем сообщение об очередном запуске искусственного спутника Земли. Обычно в сообщении указываются наименьшее и наибольшее расстояния спутника от поверхности Земли и период его обращения. Если сказано, что период обращения спутника составляет 92 мин, то мы понимаем, что его положение относительно Земли в какой-то момент времени и через каждые 92 мин с этого момента будет одинаковым. Так мы приходим к понятию периодической функции как функции, обладающей периодом, т. е. таким числом Т, что значения функции при значениях аргумента, отличающихся на Т, 2Т, ЗТ и т. д., будут одинаковыми.
Астрономия, которая дает нам наиболее наглядное представление о периодических процессах, определяет положение объектов в небесной сфере с помощью углов.
 Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов.
Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов.Область определения и множество значений тригонометрических функций
Вы знаете, что каждому действительному числу х соответствует единственная точка единичной окружности, получаемая
поворотом точки (1; 0) на угол х радиан. Для этого угла
определены sin х и cos х. Тем самым каждому действительному числу х поставлены в соответствие числа sin х и cos х, т. е. на множестве R всех действительных чисел определены функцииy = sin x и у = cos x.
Таким образом, областью определения функций y = sin x и
у = cos x является множество R всех действительных чисел.
Чтобы найти множество значений функции y = sin х, нужно
выяснить, какие значения может принимать у при различных значениях х, т. е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение
е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение
sin x = a имеет корни, если , и не имеет корней, если
|а |> 1 .Томсон Уильям, лорд Кельвин (1824— 1907) — английский физик, президент Лондонского королевского общества. Дал одну из формулировок второго начала термодинамики, предложил абсолютную шкалу температур (шкалу Кельвина).
Следовательно, множеством значений функции у = sin x
является отрезокАналогично множеством значений функции у = сos x также
является отрезокЗадача:
Найти область определения функции
Найдем значения х, при которых выражение —
не имеет смысла, т. е. значения х, при которых знаменатель равен
нулю. Решая уравнение sin x + cos х = 0, находим tg x = — 1,
Следовательно, областью определения данной функции являются все значенияЗадача:
Найти множество значений функции y = 3 + sin х cos х.

Нужно выяснить, какие значения может принимать у при
различных значениях х, т. е. установить, для каких значений а
уравнение 3 + sin х cos х = а имеет корни. Применяя формулу
синуса двойного угла, запишем уравнение так:откуда sin2x = 2a — 6. Это уравнение имеет корни, если
|2а — 6| = 1, т. е. если , откудаСледовательно, множеством значений данной функции является промежуток
Функция y = tg x определяется формулой
Эта функция определена при тех значениях х, для которых
Известно, что cos x = 0 приСледовательно, областью определения функции y = tg х является множество чисел
Так как уравнение tg x = a имеет корни при любом
действительном значении а, то множеством значений функции
y = tg х является множество R всех действительных чисел.
Функции y = sin x, у = cos x, y = tg x называются
тригонометрическими функциями.Задача:
Найти область определения функции y = sin Зх + tg 2х.
Нужно выяснить, при каких значениях х выражение
sin 3x + tg 2х имеет смысл. Выражение sin Зх имеет смысл при
любом значении х, а выражение tg 2х — при т. е. приСледовательно, областью определения данной функции является множество действительных чисел
Задача:
Найти множество значений функции
у = 3 sin x + 4 cos х.Выясним, при каких значениях а уравнение 3 sin x + 4 cos x = a имеет корни. Поделим уравнение на
Так как то очевидно найдется такой угол первой четверти , что (этот угол )
Тогда откуда
так как . Уравнение примет вид т. e. Это уравнение имеет корни, если
Уравнение примет вид т. e. Это уравнение имеет корни, еслиОтвет.
Четность, нечетность, периодичность тригонометрических функций
Вы знаете, что для любого значения х верны равенства
sin ( — x ) = — sin x, cos ( — x) = — cos x.Следовательно, y = sin х — нечетная функция, а у = cos х —
четная функция. Так как для любого значения х из области
определения функции y — tg x верно равенство tg (— х)= — tg х,
то y = tg х — нечетная функция.Задача:
Выяснить, является ли функция
четной или нечетной.
Используя формулу приведения, запишем данную функцию
так:Имеем , т. е. данная функция является четной. ▲
Известно, что для любого значения х верны равенства
Из этих равенств следует, что значения синуса и косинуса
периодически повторяются при изменении аргумента на
Такие функции называются периодическими с периодомФункция f (x) называется периодической, если существует такое число что для любого х из области определения этой функции выполняется равенство f (х — T) = f (x) = f( x+ T ).

Число 7 называется периодом функции f (х).
Из этого определения следует, что если х принадлежит области определения функции f (х), то числа х + T , х — Т и вообще
числа х + Tn , также принадлежат области определения
этой периодической функции и f (х + Tn ) = f (х),Покажем, что число является наименьшим положительным периодом функции у = cos х.
Пусть T > 0 — период косинуса, т. е. для любого х выполняется равенство cos (х + T) = cos х. Положив х = 0, получим
cos T = 1 . ОтсюдаТак как T > 0 , то T может принимать значения … и поэтому период не может быть меньше
Можно доказать, что наименьший положительный период функции у = sin х также равен
Задача:
Доказать, что f (x) = sin 3 x — периодическая
функция с периодомЕсли функция f (х) определена на всей числовой оси, то для
того, чтобы убедиться в том, что она является периодической
с периодом T, достаточно показать, что для любого х верно
равенство f (х + T ) = f (х). Данная функция определена для всех и
Данная функция определена для всех иПокажем, что функция tg х является периодической с периодом
Если х принадлежит области определения этой функции, т. е. то по формулам приведения получаем:
Таким образом,
Следовательно, — период функции tg х.
Покажем, что — наименьший положительный период функции tg х.
Пусть T — период тангенса, тогда tg ( x + T ) = tg x , откуда
при х = 0 получаем:Так как наименьшее целое положительное k равно 1, то —
наименьший положительный период функции tg х.Задача:
Доказать, что периодическая функция
с периодомТак как то — периодическая функция с периодом
Периодическими функциями описываются многие физические
процессы (колебания маятника, вращение планет, переменный
ток и т. д.).
На рисунке 34 изображены графики некоторых периодических функций.
Отметим, что на всех последовательных отрезках числовой
прямой, длина которых равна периоду, график периодической
функции имеет один и тот же вид.Функция у = cos x, ее свойства и график
Напомним, что функция у = cos х определена на всей числовой прямой и множеством ее значений является отрезок [— 1; 1].
Следовательно, график этой функции расположен в полосе между прямыми у = — 1 и у = 1.
Так как функция у = cos х периодическая с периодом , то
достаточно построить ее график на каком-нибудь промежутке длиной , например на отрезке тогда на
промежутках, получаемых сдвигами выбранного отрезка на график будет таким же.
Функция у = cos х является четной. Поэтому ее график симметричен относительно оси Оу. Для построения графика на отрезке достаточно построить его для а затем симметрично отразить относительно оси Оу.
Прежде чем перейти к построению графика, покажем, что
функция у = cos х убывает на отрезкеВ самом деле, при повороте точки Р (1; 0) вокруг начала координат против часовой стрелки на угол от 0 до абсцисса точки,
т. е. cos х, уменьшается от 1 до — 1. Поэтому если то (рис. 35). Это и означает, что функция у = cos х убывает на отрезке .Используя свойство убывания функции y = cos x на отрезке и найдя несколько точек, принадлежащих графику,
построим его на этом отрезке (рис. 36).
Пользуясь свойством четности функции у = cos х, отразим
построенный на отрезке график симметрично относительно оси Оу, получим график этой функции на отрезке (рис. 37).Так как у = cos х — периодическая функция с периодом
и ее график построен на отрезке длиной, равной периоду, распространим его по всей числовой прямой с помощью сдвигов на и т. д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).
д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).Итак, график функции у = cos x: построен геометрически на
всей числовой прямой, начиная с построения его части на отрезке
. Поэтому свойства функции у = cos х можно получить,
опираясь на свойства этой функции на отрезке . Например, функция y = cosx возрастает на отрезке так как она убывает на отрезке и является четной.
Перечислим основные свойства функции у = cos х;
1) Область определения — множество R всех действительных
чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = cos х периодическая с периодом .
4) Функция у = cos х четная.
5) Функция у = cos х принимает:
— значение, равное 0, при
— наибольшее значение, равное 1, при
— наименьшее значение, равное — 1, при
— положительные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на …;
— отрицательные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на …;
6) Функция у = cos х:
— возрастает на отрезке и на отрезках, получаемых
сдвигами этого отрезка на , … ;
— убывает на отрезке и на отрезках, получаемых
сдвигами этого отрезка на , … .
Задача:
Найти все корни уравнения
принадлежащие отрезку
Построим графики функций у = сos х и — на данном
отрезке (рис. 39). Эти графики пересекаются в трех точках,
абсциссы которых являются корнями уравненияНа отрезке корнем уравнения является число . Из рисунка видно, что точки и симметричны относительно оси Оу, т. е. а
.Ответ.
Задача:
Найти все решения неравенства принадлежащие отрезку
Из рисунка 39 видно, что график функции у = cos x лежит
выше графика функции на промежутках иОтвет.
Функция y=sin x, ее свойства и график
Функция y = sin x определена на всей числовой прямой, является нечетной и периодической с периодом . Ее график можно
построить таким же способом, как и график функции у = cos x,
начиная с построения, например, на отрезке . Однако проще воспользоваться следующей формулой:
Однако проще воспользоваться следующей формулой:Эта формула показывает, что график функции у = sin х можно
получить сдвигом графика функции у = соs х вдоль оси абсцисс
вправо на (рис. 40).График функции у = sin х изображен на рисунке 41.
Кривая, являющаяся графиком функции у = sin х, называется
синусоидой.Так как график функции у = sin х получается сдвигом графика функции у = соs х, то свойства функции у = sin х можно получить из свойств функции у = соs x.
Перечислим основные свойства функции у = sin х :
1) Область определения — множество Я всех действительных чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = sin x периодическая с периодом .
4) Функция у = sin х нечетная.5) Функция y = sin x принимает:
— значение, равное 0 , при
— наибольшее значение, равное 1, при
— наименьшее значение, равное — 1, при
— положительные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на , … ;
— отрицательные значения на интервале и на
интервалах, получаемых сдвигами этого интервала
на , … .
6) Функция у = sin х:
— возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на и на отрезках, получаемых сдвигами этого отрезка на , …
Задача:Найти все корни уравнения
принадлежащие отрезкуПостроим графики функций у = sin х и — на данном
отрезке (рис. 42). Эти графики пересекаются в двух точках,
абсциссы которых являются корнями уравненияНа отрезке уравнение имеет корень
Второй корень так как
Ответ .
Задача:
Найти все решения неравенства
принадлежащие отрезкуИз рисунка 42 видно, что график функции y = sin x лежит
ниже графика функции на промежутках иОтвет.
Функция y=tg x, ее свойства и график
Напомним, что функция y = tg x определена при является нечетной и периодической с периодом .
 Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .
Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .Наконец, используя периодичность, построить график функции
y = tgx на всей области определения.Прежде чем строить график функции на промежутке ,
покажем, что на этом промежутке функция y = tg x возрастает.Пусть Покажем, что т. е.
По условию откуда по свойствам функции
у = sin х, имеем а по свойствам функции
y = cos x имеем откудаПеремножив неравенства и получим
Используя свойство возрастания функции y = tg x на промежутке и найдя несколько точек, принадлежащих графику, построим его на этом промежутке (рис. 43).
Пользуясь свойством нечетности функции y = tg x, отразим
построенный на промежутке график симметрично относительно начала координат; получим график этой функции на интервалеНапомним, что при функция y = tg x не определена.

Если и х приближается к , то sin х приближается к 1,
a cos х, оставаясь положительным, стремится к 0. При этом дробь неограниченно возрастает, и поэтому график функцииу = tg х приближается к вертикальной прямой . Аналогично при отрицательных значениях х, больших и приближающихся к , график функции y = tg x приближается к вертикальной прямой .
Перейдем к построению графика функции у = tg х на всей области определения. Функция y = tg х периодическая с периодом .
Следовательно, график этой функции получается из ее графика
на интервале (рис. 44) сдвигами вдоль оси абсцисс
на (рис. 45).Итак, весь график функции у = tg х строится с помощью
геометрических преобразований его части, построенной на
промежутке .Поэтому свойства функции y = tg x можно получить, опираясь
на свойства этой функции на промежутке . Например,
Например,
функция y = tg x возрастает на интервале , так как
эта функция возрастает на промежутке и является
нечетной.
Перечислим основные свойства функции y = tg x:
1) Область определения — множество всех действительных
чисел2) Множество значений — множество R всех действительных
чисел.
3) Функция у = tg х периодическая с периодом
4) Функция y = tg x нечетная.
5) Функция у = tg x принимает:
— значение, равное 0, при
— положительные значения на интервалах — отрицательные значения на интервалах
6) Функция у = tg х возрастает на интервалахЗадача:
Найти все корни уравнения tg х = 2, принадлежащие отрезку
Построим графики функций y = tg х и у = 2 на данном отрезке (рис. 46, а) . Эти графики пересекаются в трех точках, абсциссы которых являются корнями уравнения tg x = 2.

На интервале уравнение имеет корень
Так как функция у = tg х периодическая с периодом , тоОтвет.
Задача:
Найти все решения неравенства
принадлежащие отрезкуИз рисунка 46, а видно, что график функции y = tg х лежит
не выше прямой у = 2 на промежуткахи .
Ответ.
Задача:
Решить неравенство tg х > 1.
Построим графики функций y = tg x и у = 1 (рис. 46, б).
Рисунок показывает, что график функции y = tgx лежит выше
прямой у = 1 на промежутке , а также на промежутках,
полученных сдвигами его на и т. д.Ответ.
Тригонометрические функции широко применяются в математике, физике и технике. Например, многие процессы, такие, как колебание струны, колебание маятника, напряжение в цепи
Углы и их измерение
переменного тока и т. д., описываются функцией, которая задается формулой Такие процессы называют
гармоническими колебаниями, а описывающие их функции —
гармониками (от греческого harmonikos — соразмерный). График
График
функции получается из синусоиды y = sin x
сжатием или растяжением ее вдоль координатных осей и
сдвигом вдоль оси Ох. Обычно гармоническое колебание является
функцией времени: где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.Геометрический угол — это часть плоскости, ограниченная двумя лучами, выходящими из одной точки, вершины угла. Чтобы сравнивать углы, удобно закрепить их вершины в одной точке и вращать стороны.
Как измеряют углы? В качестве единицы измерения геометрических углов принят градус часть развернутого угла.
Конкретные углы удобно измерять в градусах с помощью транспортира. Многие оптические приборы также используют градусную меру угла. Углы, получающиеся при непрерывном вращении, удобно измерять не в градусах, а с помощью таких чисел, которые отражали бы сам процесс построения угла, т.
 е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.
е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.Представим себе, что зафиксирована не только вершина угла, но и один из образующих его лучей. Заставим второй луч вращаться вокруг вершины. Ясно, что получающиеся углы будут зависеть от скорости вращения и времени. Можно считать, что вращение происходит равномерно (с постоянной угловой скоростью). Тогда поворот будет определяться путем, который пройдет какая-либо фиксированная точка подвижного луча.
Если расстояние точки от вершины равно /?, то при вращении точка движется по окружности радиуса R. Отношение пройденного пути к радиусу R не зависит от радиуса и может быть взято за меру угла. Численно она равна пути, пройденному точкой по окружности единичного радиуса.
Итак, пусть угол получен вращением подвижного луча от некоторого начального положения. Его величина численно равна пути, который пройдет точка этого луча, находящаяся на единичном расстоянии от вершины.

Развернутый угол измеряется половиной длины единичной окружности. Это число обозначается буквой л. Число я было известно людям с глубокой древности и с довольно большой точностью. Первые десятичные знаки этого числа таковы:
π = 3,14159265358….
Угол величиной π часто используется как самостоятельная единица измерения углов — прямой угол равен угол в равностороннем треугольнике равен .
Часто встречаются записи меры углов в виде и т. д. Угол, мера которого равна числу 1, называют радианом. Он соответствует некоторому углу, чуть меньшему, чем , ведь ≈ 1,047.
АННА ВОВК u715078663 ДЕЛАЕТ АЛГЕБРУ №2 (дополнительная)
Гаусс Карл Фридрих
(1777—1855) — немецкий математик, астроном и физик. Еще студентом написал «Арифметические исследования», определившие развитие теории чисел до нашего времени. В 19 лет определил, какие правильные многоугольники можно построить циркулем и линейкой. Занимался геодезией и вычислительной астрономией.
 Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.
Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.Так как на практике приходится иметь дело как с градусной, так и с радианной мерой, то на микрокалькуляторе обычно есть рычажок, регулирующий способ измерения используемого в вычислениях угла. Фактически микрокалькулятор умеет переводить градусы в радианы и обратно.
Выведем формулы для этого перевода. Достаточно сравнить меры одного и того же угла, например прямого:
Откуда
Обратно можно выразить единицу (т. е. один радиан) в градусной мере:
В географии, астрономии и других прикладных науках используют доли градуса — минуту и секунду. Минута — это градуса, а секунда — минуты. Запишем соотношения между различными единицами измерения углов:
Заметим еще, что обозначение градуса (минуты, секунды) нельзя пропускать в записи, а обозначение радиана опускают. С физической точки зрения угол — безразмерная величина, поэтому имеют смысл записи: а = 0,23, а = 3,14, а=0,01. Во всех этих записях подразумевается, что угол а измерен в радианах.
 Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.
Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.Движение точки по окружности во многом аналогично движению точки по прямой. Чтобы определить положение точки на прямой, недостаточно знать путь, пройденный ею от начальной точки, нужно указать еще направление движения. Обычно на прямой фиксируют положительное направление, а положение точки определяют одним числом, которое может быть не только положительным (как путь), но и отрицательным.
Аналогично поступают и с вращательным движением. В качестве положительного направления движения по окружности выбирается движение против часовой стрелки. Угол задают числом t (которое может принимать произвольное значение). Чтобы построить угол t, на единичной окружности от неподвижной точки откладывают путь, равный|t|, в направлении, определяемом знаком числа t. Таким образом, для произвольного числа t мы построили угол t, определяемый двумя лучами — неподвижным и тем, который проходит через построенную точку (рис.
 84).
84).При таком обобщении понятия угла постепенно отходят от его геометрического образа как части плоскости, лежащей между двумя лучами. Фактически слово «угол» становится для нас синонимом слова «число». Угол t (т. е. произвольное число t) может выступать у нас в качестве аргумента тригонометрических функций. Изображать угол t нам будет удобно не в виде пары лучей, а в виде точки единичной окружности. Для этого мы подробно рассмотрим вращательное движение.
Вращательное движение и его свойстваПредставим себе маленький шарик, который равномерно вращается по единичной окружности в положительном направлении (т. е. против часовой стрелки). Будем считать, что в момент времени t = О шарик находился в положении А и что за время t = 1 он проходит по окружности расстояние, равное 1. Половину окружности шарик проходит за время, равное π, а всю окружность — за время 2 π.
Обозначим через Pt точку на окружности, в которой шарик находится в момент времени t.
 Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t <0. Рассмотрим примеры.
Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t <0. Рассмотрим примеры.1.Пусть t=. Отложим по окружности от точки Р0 в положительном направлении путь длиной .
Так как длина всей окружности равна 2 π, то точка является серединой дуги АВ (рис. 85).
2. Пусть . Отложим от точки Р0 путь длиной
Заметим, что Пройдя путь длиной 2 π, мы опять попадаем в точку А. Пройдя оставшийся путь, мы попадаем в середину дуги АВ. Таким образом, точка совпадает с точкой .
3. Найдем теперь точку Для этого нам необходимо пройти в отрицательном направлении путь длиной
Таким образом, мы для каждого значения t можем построить точку Рt. На языке механики аргумент t — это время, на языке геометрии t — это угол.
Оси координат делят плоскость на четыре части. В зависимости от того, в какую часть плоскости попадает точка Рt, говорят о том, в какую четверть попадает угол t.
 При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения.
При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения.Свойство 1. Для всякого целого числа k точка Рt совпадает с точкой Это свойство выражает периодичность вращательного движения: если моменты времени отличаются на число, кратное 2 π, то шарик в эти моменты времени занимает одно и то же положение.
Свойство 2. Если , то найдется такое целое число k, что
Свойство 3. Для всякого значения t точки Рt и Рt+π диаметрально противоположны.Свойство 4. Для всякого значения t точки Рt и Р_t симметричны друг другу относительно оси абсцисс.
Свойство 5. Для всякого значения t точки Рt и Р_t+π симметричны относительно оси ординат.
Свойство 6. Для всякого значения t точки Рt и симметричны друг другу относительно биссектрисы первого и третьего координатных углов.
Эти свойства легко объяснить с помощью рисунка 86. Сделаем лишь пояснение к свойству 6. Возьмем две точки Р0 и
Они симметричны друг другу относительно биссектрисы первого и третьего координатных углов.
 Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку , надо на такое же
Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку , надо на такое жерасстояние двигаться от точки , но в противоположном направлении. Ясно, что при этом точки Рt и при всяком t будут
оставаться симметричными друг другу относительно указанной прямой.
Определение тригонометрических функций
Тригонометрические функции определяются с помощью координат вращающейся точки. Рассмотрим на координатной плоскости ху единичную окружность, т. е. окружность единичного радиуса с центром в начале координат. Обозначим через Ро точку единичной окружности с координатами (1; 0) (рис. 87). Точку Ро будем называть начальной точкой. Возьмем произвольное число t. Повернем начальную точку на угол t. Получим точку на единичной окружности, которую обозначим через Рt.
Определение. Синусом числа t называется ордината точки Pt, косинусом числа t называется абсцисса точки Pt, где Р, получается поворотом начальной точки единичной окружности на угол t.

Если обозначить координаты точки Р, через х и у, то мы получим x = cost y = sint или можно записать, что точка Рt имеет координаты (cos t; sin t).
Так как координаты точки Р, (х; у), лежащей на единичной окружности, связаны соотношением х2 + у2 = 1, то sin t и cos t связаны соотношением
которое называют основным тригонометрическим тождеством.
Определение. Тангенсом числа t называется отношение синуса числа t к его косинусу, т. е. по определению
Котангенсом числа t называется отношение косинуса числа t к его синусу, т. е. по определению
Тангенс числа t определен для тех значений t, для которых cos t ≠ 0. Котангенс числа t определен для тех значений t, для которых sin t ≠ 0.
ПериодичностьТригонометрические функции являются периодическими функциями.
Теорема:
Число 2π является периодом синуса и косинуса.
Доказательство.
 Необходимо доказать тождества
Необходимо доказать тождестваЗначения тригонометрических функций определяются с помощью координат вращающейся точки. Так как точки Pt и Рt+2π совпадают, то совпадают и их координаты, т. е. cos t = cos (t + 2π) и sin t = sin (t + 2π), что и требовалось доказать.
Следствие:
Верны тождества
Действительно, Аналогично доказывается и второе тождество. Это означает, что 2π является одним из периодов тангенса и котангенса.
Равенство sin (t + 2π) = sin t верно при всех значениях t. Подставляем в это равенство вместо t число t+2π, получаем цепочку равенств sin(t+ 2 π +2 π ) = sin (t + 2 π ) = sin t, т. е. равенство sin (t + 4 π ) = sin t также верно при всех значениях t. Аналогично, подставляя вместо t число t— 2 π , получим тождество sin (t —2 π ) = sin t. Можно сказать так, что раз 2 π является периодом синуса, то и 2-2 π , —2 π также являются его периодами. Получаем, что всякое число вида 2πk {k ∈ Z) является периодом синуса.
Число 2π выделяется тем, что это наименьший положительный период синуса.
Знаки тригонометрических функций Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.
Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.Знаки тригонометрических функций определяются в зависимости от того, в какой четверти лежит рассматриваемый угол.
Синус числа t есть ордината точки Рt. Поэтому синус положителен в первой и второй четвертях и отрицателен в третьей и четвертой.
Косинус числа t как абсцисса точки Рt положителен в первой и четвертой четвертях и отрицателен во второй и третьей.Тангенс и котангенс являются отношением координат. Поэтому они положительны тогда, когда эти координаты имеют одинаковые
Четность
знаки (первая и третья четверти), и отрицательны, когда разные (вторая и четвертая четверти). Знаки тригонометрических функций по четвертям приведены на рисунке 88.Теорема:
Синус — нечетная функция, т. е. при всех t выполнено равенство sin (— t) = — sin t.

Косинус — четная функция, т. е. при всех t выполнено равенство cos ( — t) =cos t.
Доказательство:
Действительно, мы знаем, что для всякого значения t точки Р, и Р_( симметричны друг другу относительно оси абсциссы (т. е. cos t = cos ( — t)), а ординаты противоположны (т. е. sin t=— sin ( — t)), что и требовалось доказать.
Следствие. Тангенс и котангенс — нечетные функции.
Действительно, . Аналогично доказывается нечетность котангенса.
Формулы приведенияЗначения тригонометрических функций острых углов можно вычислить по таблицам или с помощью прямоугольного треугольника. Их вычисление для любого значения аргумента можно привести к вычислению значений для аргумента
Соответствующие формулы так и называются — формулы приведения. Они основаны на симметрии вращательного движения.
Основные формулы:
Формула (1) —это запись в координатной форме свойства 3 вращательного движения, формула (2) — это запись свойства 5, а формула (3) — запись свойства 6.

С помощью периодичности и формул (1) — (3) можно привести вычисление синуса и косинуса любого числа t к их вычислению для t, лежащего между 0 и .
Из основных формул (1) — (3) можно вывести и другие формулы приведения:
Доказательство:
Аналогично выводятся формулы
Формулы приведения для тангенса и котангенса получаются как следствие аналогичных формул для синуса и косинуса. Например:
Мнемоническое правило для запоминания формул приведения следующее:
1) Название функции не меняется, если к аргументу левой части добавляется — π или + π, и меняется, если добавляется число ± или
2) Знак правой части определяется знаком левой, считая, что
Примеры.
1.Вычислить sin . Представим так:
Далее,
Значения тригонометрических функцийВычисление значений тригонометрических функций имеет длинную историю. Потребности точных астрономических наблюдений вызвали к жизни появление огромных таблиц, позволявших производить вычисления с четырьмя, пятью и даже семью и более знаками.
 На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности.
На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности.Некоторые соображения о значениях тригонометрических функций надо помнить всегда, так как они облегчают вычисления.
1) С помощью формул приведения вычисление значения тригонометрической функции любого числа можно свести к вычислению функции угла, лежащего в первой четверти.
2) Достаточно знать значение лишь одной из тригонометрических функций. С помощью основных тождеств и зная четверть, в которой лежит значение аргумента, легко найти значения остальных функций.
Примеры:
3) Полезно помнить значения тригонометрических функций для углов двух «знаменитых» прямоугольных треугольников —для равнобедренного и для треугольника с углами 30° () и 60° ().
 Эти значения обычно записывают с помощью радикалов и при необходимости эти радикалы заменяют их приближенными значениями
Эти значения обычно записывают с помощью радикалов и при необходимости эти радикалы заменяют их приближенными значениямиСведем их в таблицу, дополнив ее значениями t = 0 и t=.
Решение простейших тригонометрических уравненийДля решения некоторых,особенно простых, но важных уравнений достаточно вспомнить определение тригонометрической функции.
Примеры:
- sin t = 0. Вращающаяся точка Рt имеет нулевую ординату в моменты времени t—0, π, 2 π, …, а также t— π, —2 π…..В общем виде множество этих значений можно записать в виде t=πk, k ∈ Z. Таким образом, решением уравнения sin t = 0 будут числа t = πk, k ∈ Z.
Запишем кратко решения еще нескольких уравнений, правильность которых предлагается проверить самостоятельно.
Все рассмотренные уравнения имеют бесчисленное множество решений. Эти решения записываются в виде бесконечных серий с помощью переменной (в наших примерах к), которая может принимать любые целые значения.
Теперь легко доказать, что 2π является наименьшим положительным периодом синуса и косинуса.
 Действительно, формула 3 показывает, что значение 1 синус принимает только в точках
Действительно, формула 3 показывает, что значение 1 синус принимает только в точкахРасстояние между соседними точками этой последовательности равно 2 π, поэтому синус не может иметь положительный период, меньший 2 π. Рассуждения для косинуса аналогичны.
Исследование тригонометрических функций
Основные свойства синуса и косинусаПри введении тригонометрических функций мы обозначали аргумент буквой t, так как буквы х и у были заняты — они обозначали координаты вращающейся точки Рt. Сейчас при исследовании мы вернемся к обычным обозначениям: х — аргумент, у — функция.
Рассмотрим функции y = sinx и y = cosx.
1) Область определения. Синус и косинус числа х задаются как координаты точки Рх, получающейся из точки Ро (1; 0) поворотом на угол х. Так как поворот возможен на любой угол, то областью определения синуса и косинуса является множество R всех вещественных чисел.
2) Промежутки монотонности. Проследим за характером изменения координат точки Рх, движущейся по окружности.
 При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= точка займет положение Р (0; 1). Итак, в первой четверти синус (ордината) возрастает от 0 до 1, а косинус (абсцисса) убывает от 1 до 0.
При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= точка займет положение Р (0; 1). Итак, в первой четверти синус (ордината) возрастает от 0 до 1, а косинус (абсцисса) убывает от 1 до 0.Когда точка переходит во вторую четверть, ордината начинает убывать от 1 до 0. Абсцисса становится отрицательной и растет по абсолютной величине, значит, косинус продолжает убывать от 0 до — 1. В третьей четверти синус становится отрицательным и убывает от 0 до —1, а косинус начинает возрастать от — 1 до 0.
Наконец, в четвертой четверти синус возрастает от — 1 до 0 и косинус возрастает от 0 до 1. Монотонность синуса и косинуса по четвертям показана на схеме VIII.
3) Точки экстремума. Координаты вращающейся точки меняются между —1 и +1. Эти числа являются наименьшими и наибольшими значениями синуса и косинуса. Если требуется указать абсциссы точек экстремума, то надо решить уравнения sin х = ±1 и cos х= ± 1.

4) Промежутки постоянного знака и корни функции. Мы повторим их еще раз при построении графика.
5) Множество значений. Синус и косинус принимают любые значения от —1 до +1, так как являются координатами точки, движущейся по единичной окружности.
Графики синуса и косинусаДля приближенного построения синусоиды можно поступить так. Разделим первую четверть на 8 равных частей и на столько же частей разделим отрезок [0; ]оси абсцисс. Удобно при этом начертить окружность слева, как на рисунке 89. Перенесем значения синуса (проекции на ось у точек деления окружности) к соответствующим точкам оси х. Получим точки, лежащие на синусоиде, которые нужно плавно соединить и продолжить кривую дальше, пользуясь симметрией.
Так мы получим график синуса на промежутке [0;]. Так
как sin (—х = sin +x). то график синуса должен быть
симметричен относительно прямой x=. Это позволяет построить
график синуса на отрезке [-; π].
 Воспользовавшись нечетностью
Воспользовавшись нечетностьюсинуса, получим график синуса на отрезке [ — π; 0] симметричным отражением построенной части синусоиды относительно начала координат. Так как отрезок [— π; π] имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельными переносами построенной кривой.
График синуса мы построили, воспользовавшись его свойствами. При этом к определению синуса мы обращались только при построении графика на отрезке [0; ].
Построение графика на всей оси потребовало знания симметрии вращательного движения (формулы приведения, нечетность, периодичность). После того как график построен, полезно вернуться к свойствам синуса и посмотреть, как они проявляются на графике.
Функция y = sin х имеет период 2 π. На графике это свойство отражается следующим образом: если мы разобъем ось х на отрезки длиной 2 π, например, точками… —4 π, —2 π, 0, 2 π, 4 π, …, то весь график разобьется на «одинаковые» части, получающиеся друг из друга параллельным переносом вдоль-оси х.
 При этом видно, что 2 π — наименьший положительный период синуса.
При этом видно, что 2 π — наименьший положительный период синуса.Функция y = sin x: нечетна. На графике это свойство проявляется так: синусоида симметрична относительно начала координат.
Функция y = sin x обращается в нуль при х = πk, k ∈ Z. На графике это точки пересечения синусоиды с осью абсцисс.
Функция y = sin x положительна при и отрицательна при или третьей-четвертой четвертям (sin х<0).
Функция y = sin х возрастает при и убывает при
Указанные отрезки соответствуют четвертой-первой и второй-третьей четвертям.
Множеством значений функции y = sinx является отрезок [— 1; 1]. Действительно, проекции вращающейся точки на ось заполняют отрезок [—1; 1]. На графике это свойство проявляется так: синусоида расположена в полосе и при этом проекции точек графика на ось у целиком заполняют отрезок [— 1; 1].
График косинуса можно построить так же, как и график синуса. Возможен и другой путь. Формулы приведения показывают, что синус и косинус связаны между собой простыми соотношения-
ми. Воспользуемся, например, формулой cosx = sin (x+)
Воспользуемся, например, формулой cosx = sin (x+)
Эта формула показывает, что график косинуса получается сдвигом синусоиды на влево по оси х (схема VIII).Если изображать графики синуса и-косинуса в системе координат с одинаковым масштабом по осям, то синусоида получается очень растянутой. Однако на практике величины х и у, связанные с помощью тригонометрических функций, имеют различные единицы измерения и необязательно изображать их в одном масштабе.
Если аргумент умножить на некоторое число, то синусоида будет, как гармоника, сжиматься и растягиваться по оси х. Примеры такого преобразования приведены на рисунке 90.
Если значение синуса умножить на число, то будет происходить растяжение (сжатие) по оси у.
Графики функций вида у = А sin ( ω х + а) при различных А, ω, а являются синусоидами. Эти функции описывают так называемые гармонические колебания — движение проекции вращающегося шарика на ось или колебания конца упругой пружины.
Постоянные величины А, ω, а, задающие колебания, имеют наглядный физический смысл: А — амплитуда колебания, ω — его частота, а — начальная фаза.
Исследование тангенса и котангенса
Если свойства синуса и косинуса мы получили, рассматривая свойства движения точки по окружности, то для исследования тангенса и котангенса нам нет необходимости возвращаться к механической модели.
По определению тангенс числа х задается как отношение sin х и cos х. Изучим свойства тангенса.
1.Областью определения функции является
множество всех вещественных чисел, за исключением тех, в которых косинус обращается в нуль. Мы запишем это множество следующим образом:
2. Тангенс — периодическая функция с периодом π:
3. Тангенс — нечетная функция, т. е. tg ( — х)= — tg х.
4. Функция y = tg x обращается в нуль одновременно с синусом, т. е. при x=πk, k ∈ Z.
5. Функция у= tg x: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
Выберем для дальнейшего изучения тангенса какой-либо промежуток числовой оси длиной, равной периоду, т. е. числу π. Можно было бы выбрать отрезок от 0 до π, но это неудобно, так как внутри этого отрезка есть точка x= в которой тангенс не определен.
 Лучше выбрать промежуток ( —; ).
Лучше выбрать промежуток ( —; ).6. Тангенс возрастает в первой четверти. Действительно, пусть
Тогда (возрастание синуса) и (убывание косинуса). Так как значения косинуса положительны, то по свойству неравенств имеем
Умножим это неравенство на неравенство с положительными членами: sin х1<sin х2. Получим tg x1<tg x2.
Тангенс возрастает также и в четвертой четверти. Действительно, пусть Тогда имеем
Теперь числа (— х2) и ( — х1) лежат в первой четверти, и мы можем воспользоваться тем, что в первой четверти тангенс возрастает: tg (— x2)<tg (— x1). Но так как тангенс — нечетная функция, получим:
На промежутке (—; 0 ] тангенс отрицателен и возрастает. На тангенс становится положительным и возрастает.
В итоге тангенс возрастает на промежутке (-; ).
7. Какие же значения принимает тангенс? Когда х возрастает от 0 до тангенс возрастает. При этом когда х приближается к синус х близок к единице, а косинус близок к нулю. Поэтому отношение становится сколь угодно большим.
 То, что любое вещественное число может быть значением тангенса, видно из рисунка 91. Построим ось, параллельную оси ординат с началом в точке Ро. Возьмем на этой оси точку, соответствующую произвольно выбранному числу а. Соединим 0 с а. Получим точку Р на окружности. Пусть х — число, принадлежащее и такое, что (cos х; sin х) — координаты Р. Тогда
То, что любое вещественное число может быть значением тангенса, видно из рисунка 91. Построим ось, параллельную оси ординат с началом в точке Ро. Возьмем на этой оси точку, соответствующую произвольно выбранному числу а. Соединим 0 с а. Получим точку Р на окружности. Пусть х — число, принадлежащее и такое, что (cos х; sin х) — координаты Р. ТогдаМы показали, что областью значений тангенса является вся числовая ось R.
Вообще на этой оси, которую часто называют осью тангенсов, можно проследить все свойства тангенса.
8. Построим график тангенса. На промежутке график
тангенса можно построить по точкам, учтя, что тангенс строго возрастает, в нуле обращаясь в нуль, а при приближении к становится сколь угодно большим (рис. 92).Отразив построенную часть графика относительно начала координат (тангенс — нечетная функция), получим график тангенса на промежутке . Для построения полного графика
разобьем числовую ось на отрезки, перенося вправо
и влево на π, 2 π, З π и т. д.
д.График тангенса распадается на отдельные, не связанные между собой части. Это вызвано тем, что в точках тангенс не определен.
Замечание (о монотонности тангенса).
Мы доказали, что функция тангенс возрастает на .Можно ли сказать, что тангенс возрастает на всей области определения? Нет. Достаточно посмотреть на график. Если взять
Хотя х1 <х2, но tg х1 >tg х2.
Нарушение монотонности связано с тем, что между точками х1 и х2 лежала точка х = в которой тангенс не определен.
Однако можно сказать, что тангенс возрастает на каждом промежутке, который целиком попадает в его область определения.
Свойства котангенса получаются так же, как и свойства тангенса. Перечислим кратко эти свойства, оставляя их доказательство для самостоятельной работы.
1.Функция определена при
2. Функция у = ctg х периодична. Ее периодом является число π:
3. Функция у = ctg x нечетна: ctg ( — х)= — ctg х.
4. Функция у = ctg х обращается в нуль одновременно с косинусом, т.
 е. при х = + лk, k ∈ Z.
е. при х = + лk, k ∈ Z.5. Функция у = ctgx: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
6. Функция y=ctgx убывает на промежутке (0; π). Перенося его на kπ, получаем, что котангенс убывает на каждом промежутке ( πk; π + πk).
7. Область значений котангенса — множество R всех вещественных чисел.
8. График котангенса изображен на рисунке 93.
Производные тригонометрических функцийПусть точка А движется с единичной скоростью . по окружности радиуса 1 с центром в начале координат О в положительном направлении. Координаты точки А в момент времени t равны cos t и sin t. Вектор мгновенной скорости точки А в момент времени t направлен по касательной к окружности в точке А (рис. 94), и в силу теоремы о перпендикулярности касательной к радиусу, проведенному в точку касания, вектор перпендикулярен вектору .
Вычислим координаты вектора . Отложив от точки О вектор , мы получим вектор , координаты которого равны координатам вектора .
 Далее, так как движение точки А по окружности происходит с единичной скоростью, то длина вектора и равна 1, поэтому длина вектора также равна 1. Следовательно, точка В лежит на окружности.
Далее, так как движение точки А по окружности происходит с единичной скоростью, то длина вектора и равна 1, поэтому длина вектора также равна 1. Следовательно, точка В лежит на окружности.Вектор перпендикулярен вектору, поэтому если A = Pt,
то . Таким образом, координаты вектора = равны
С другой стороны, координаты скорости являются производными от координат точки А, следовательно,
Найдем производную функции y = A sin ( ωt + а):
Рассмотрим примеры.
Вычислим теперь производную функции y = tgx. Так как то по теореме о производной частного получаем:
Следовательно,
Аналогично
Таким образом,
Примеры:
Приближенные формулыГлавная приближенная формула: вблизи нуля sin t ≈ t.
Доказательство. Дифференциал функции y = sin х равен dy = cos х dx. Найдем dy при х = 0. Так как cos 0=1, то при х = 0 dy = dx. Найдем приращение функции:
∆y = sin ∆х — sin 0 = sin ∆х.

Так как ∆y ≈ dy, то получим ∆y = sin ∆х ≈ dy=dx = ∆х. Вместо ∆х можно написать t и получить sin t ≈ t.
Эта формула дает тем точнее значение синуса, чем ближе t к нулю. Возможность заменять sin t на t при маленьких значениях угла t широко употребляется в приближенных вычислениях. Можно дать различные интерпретации этой приближенной формулы.
1. — это запись того, что отношение приращения
функции к его главной части стремится к единице при стремлении к нулю приращения аргумента.
2. Рассмотрим единичный круг. Пусть для простоты t>0. Тогда длина дуги АВ равна t, а длина отрезка ВС равна sin t. Удвоим дугу АВ и отрезок ВС — дуга BD имеет длину 2t, а хорда BD — длину 2 sin t. Соотношение sin t ≈ t означает, что отношение длины хорды к длине стягиваемой ею дуги стремится к единице, когда дуга стягивается в точку (рис. 95).
3. Рассмотрим касательную к синусоиде в начале координат. Так как (sin x)’=cos х, a cos 0= 1, то уравнение этой касательной у — х.
 Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.
Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.Для получения других приближенных формул выпишем дифференциалы тангенса и косинуса:
При x = 0 получим приближенное значение тангенса:
Применяя этот же прием к косинусу, мы получим, что дифференциал косинуса при x=0 равен —sin0 • dx т. е. равен 0. Это означает, что главная часть приращения косинуса равна нулю и в первом приближении cos x ≈ cos 0 = 1. Можно получить более точную формулу таким путем. Запишем cos х так:
Заменим в этой формуле sin х на х и воспользуемся приближенной формулой для квадратного корня:
Полученная приближенная формула для косинуса вблизи точки x = 0 весьма точна.
Более точные приближения можно получить с помощью формул
Примеры:
- Вычислить приближенно sin 0,03 • tg 0,12. sin 0,03 ≈ 0,03, tg 0,12 ≈ 0,12, sin 0,03 • tg 0,12 ≈ 0,0036 ≈ 0,004.

- Вычислить приближенно sin 2°. Переводим 2° в радианную меру: 2° ≈ 0,034. sin 2° ≈ 0,034.
Тождественные преобразования
Формулы сложенияТригонометрические функции связаны между собой многочисленными соотношениями. Первая серия тождеств описывает связь между координатами точки окружности — это так называемые основные соотношения. Эти соотношения позволяют выразить значения одних функций через другие (при одном и том же значении аргумента). Вторая серия тождеств происходит от симметрии и периодичности в движении точки по окружности. Отсюда мы получаем формулы приведения. Третий источник тригонометрических формул — это изучение поворотов. Поворот точки на угол а + β можно составить из композиции двух поворотов — на угол а и на угол β. Есть простые формулы, связывающие координаты точек Эти формулы называются формулами сложения.
Нашей целью является вывод формул, связывающих sin (а ± β), cos (а ± β), tg (а ± β), ctg (а ± β) с тригонометрическими функциями углов а и β.
 Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.
Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.Теорема. Косинус разности двух углов равен произведению косинусов этих углов, сложенному с произведением синусов:
cos (а — β) =cos а cos β + sin а sin β.
Доказательство. Построим углы а и β помощью единичной окружности, т. е. точки Ра и Рβ , такие, что векторы образуют углы а и β с положительным направлением оси абсцисс. Угол между векторами равен а — β (рис. 96).
Вычислим скалярное произведение этих векторов. По определению скалярного произведения
(так как векторы имеют длину, равную 1).
Теперь вычислим это же скалярное произведение с помощью координат:
Сравнивая результаты вычислений, получаем требуемую формулу:
Доказательство теоремы закончено. Выведем остальные формулы.
Косинус суммы. Сумму а + β представим как разность а — ( — β) и подставим в формулу для косинуса разности:
Воспользуемся тем, что cos( —p) = cos p (четность косинуса), a sin( —p)=—sin p (нечетность синуса).
 Получим:
Получим:Синус суммы. Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности получим:
Окончательно
В качестве примера вычислим sin 15°. Представим 15° как разность 45° —30°. Получим sin 15° = sin (45° — 30°) = sin 45° cos 30°
Тангенс суммы и разности. По определению tg(a + β) формулам синуса и косинуса суммы имеем:
Разделив числитель и знаменатель этой дроби на cos a cos β, получим:
Заменяя β на ( — β) и пользуясь нечетностью тангенса, получаем:
Формулы удвоенияФормулы сложения являются одними из основных формул, связывающих тригонометрические функции. Из них можно вывести различные следствия. Полагая а = р, получим так называемые формулы удвоения.
Тригонометрические функции половинного угла
Заметим, что в формуле для cos 2a можно заменить на 1 — или на 1 — . Получим две новые формулы:Из формул двойных углов можно получить формулы для синуса и косинуса половинного угла.
 Сначала запишем:
Сначала запишем:Затем в этих формулах подставив вместо а, получим:
Извлекая корень, получим:
(Для того чтобы раскрыть модули, надо знать, в какой четверти лежит угол ).
Обилие тригонометрических формул связано с тем, что между основными тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом — есть соотношения, которые позволяют по-разному написать одно и то же выражение. Возникает вопрос: нельзя ли выбрать одну какую-то функцию и через нее выражать все остальные? Если в качестве такой функции мы выберем синус, то во многих формулах появятся квадратные корни. Так, например, выражая sin 2а через sin а, мы получим sin 2а = 2 sin а cos а = 2 sin а . Такие формулы неудобны.
Оказывается, что все тригонометрические функции от аргумента х (и от nх при целом n) выражаются через тангенс угла рационально, без квадратных корней. Выведем эти полезные формулы.
Напишем формулы двойного угла для исходного угла
Представим число 1 в виде и поделим на 1 правые части последних формул
Поделим теперь числитель и знаменатель каждой дроби на
Пользуясь этими формулами, можно функцию вида у = а sin x + b cos x + c представить в виде рациональной функции от tg .

Пример. Выразить у = 2 sin х + З cos х — 1 в виде функции от tg .
Преобразование суммы тригонометрических функций в произведение и обратные преобразованияПусть требуется преобразовать сумму sin a + sin β в произведение. Используем следующий искусственный прием: напишем тождества
заменим а и β выражениями, стоящими справа, в формулах для синуса суммы и разности:
Аналогично выводятся еще три формулы:
Выпишем подряд четыре формулы сложения:
Вычитая почленно из четвертого равенства третье, получим:
Складывая третье и четвертое равенства, получим:
Складывая два первых равенства, получим:
Мы рассмотрели различные тождества, связывающие тригонометрические функции. Все их запомнить трудно, и приходится обращаться к таблицам и справочникам. Важнее запомнить не сами формулы, а то, какие функции между собой они связывают, что с их помощью можно получить.
Тригонометрические уравнения
Простейшим тригонометрическим уравнением называется уравнение вида sinx=a, где cos x=a, tgx=a, где a — некоторое действительное число.
Арксинус
Рассмотрим уравнение sin x = a. Так как областью значений синуса является отрезок [—1; 1], то это уравнение не имеет решений при |a| > 1. Пусть теперь |а|< 1. Построим на одном чертеже графики у = а и y = sin x (рис. 97).
По рисунку ясно, что прямая у = а пересечет синусоиду бесконечно много раз. Это означает, что при |a| ≤ 1 уравнение sin x = a имеет бесконечно много корней. Так как синус имеет период 2π, то достаточно найти все решения в пределах одного периода. По графику видно, что при |a| < 1 на отрезке [0; 2π] есть два числа, или, можно сказать, два угла, синус которых равен а.
Если один из таких углов а, то другой π—а. Все другие решения уравнения sin х = а, где |a| < 1, получаются из двух найденных с помощью свойства периодичности синусa.
Итак, пусть а — какое-либо решение уравнения sin х = а, где |a| < 1. Тогда все решения этого уравнения получаются по формулам
Эти две серии решений иногда записываются одной формулой:
Пример.
 Решить уравнение
Решить уравнениеОдно решение этого уравнения Все остальные решения получаются по формулам
Как мы уже выяснили, уравнение sinx=a при |а| ≤ 1 имеет бесконечно много решений. Для одного из них имеется специальное название — арксинус.
Определение. Пусть число а по модулю не превосходит единицы. Арксинусом числа а называется угол х, лежащий в пределах от , синус которого равен а.
Обозначение: х = arcsin а.
Итак, равенство x = arcsin a равносильно двум условиям: sin z = a и
Обратим еще раз внимание на то, что arcsin а существует лишь, если |а|≤ 1.
Примеры:
Теперь решения уравнения sin х = а (при |а| ≤ 1) можно записать так: х = arcsin а+2πk, х= π — arcsin а+2πk, или в виде одной формулы:
Запишем некоторые тождества для арксинуса.
- sin arcsin а = а.
Это тождество вытекает из определения арксинуса (arcsin а — это такой угол х, что sin х=а).

Действительно, обозначим sin х через а. Тогда наше тождество будет равносильно определению арксинуса: arcsin а = х, если и sinx = a. Заметим, что выражение arcsin (sin х) имеет смысл при любом х, однако при оно не равно х.
Действительно, синусы от правой и левой частей равны: sin (arcsin ( —а)) = —а и sin ( — arcsin а)= —sin (arcsin а)= —а. В то же время правая часть доказываемого равенства — это угол, принадлежащий отрезку . Поэтому левая и правая части равны между собой.
АрккосинусТак же как и в предыдущем пункте, при |а|>1 уравнение cosx = a решений не имеет; если |а| ≤ 1 то решений уравнения бесконечно много.
Если a — какое-либо решение уравнения cos х=а, то —а также есть решение этого уравнения, так как cos a = cos ( — a). По графику или на единичном круге видно, что при |а|< 1 в пределах одного периода уравнение cos х=а имеет два решения.
Если a — одно из решений уравнения cos х = а, то все решения исчерпываются двумя сериями:
Эти серии обычно записывают в виде одной формулы:
Пример.
 Решить уравнение
Решить уравнениеОдно решение находится легко: .
Запишем все решения так:
Так же как и для синуса, выделяется одно определенное решение уравнения cos х = а и ему дается специальное название — арккосинус.
Определение. Пусть а — число, по модулю не превосходящее единицы. Арккосинусом числа а называется угол х, лежащий в пределах от 0 до π, косинус которого равен а.
Обозначение: х= arccos а.
Равенство x = arccos a равносильно двум условиям: cos x = a и 0 ≤ х ≤ π. Арккосинус числа а существует лишь при |а| ≤ 1 .
Пример:
Решение уравнения cos х=а (при |а| ≤ 1) можно записать теперь в общем виде:
По каким причинам для значений арксинуса был выбран отрезок , а для арккосинуса отрезок [0; π]?
Это объясняется тем, что на этих отрезках, во-первых, синус и косинус принимают все возможные значения от — 1 до 1 и, во-вторых, каждое значение принимается ровно один раз. Отрезков с этими условиями бесконечно много, но при этом выбраны отрезки «поближе к нулю».

Для арккосинуса можно вывести ряд тождеств.
- cos (arccos а) = а.
Это тождество следует из определения арккосинуса.
Обозначим cos x = а. Получим определение арккосинуса: arccos а = х, если x ∈ [0; π ] и cos х = а.
Сначала вычислим косинус от левой и правой частей:
Если равны косинусы двух чисел, то это еще не означает, что равны сами числа. Проверим, что правая часть принадлежит отрезку [0; π]. (Так как левая часть тоже принадлежит этому отрезку, то из равенства косинусов двух чисел теперь уже будет следовать равенство самих чисел.) Итак, надо доказать, что π —arccos а принадлежит [0; π]. Действительно, arccos а ∈ [0; π — arccos а ∈ [ — π ; 0], π— arccos а ∈ [0; π], что и требовалось доказать.
АрктангенсОбласть значений тангенса (котангенса) — вся числовая ось. Поэтому уравнения tgx = a, ctg х — а имеют решения при любом а. В пределах одного периода π тангенс и котангенс принимают каждое значение ровно один раз.
 Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:
Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:где a — какое-либо решение соответствующего уравнения. Примеры. Решить уравнения:
Определения арктангенса и арккотангенса вводятся аналогично определениям арксинуса и арккосинуса, поэтому мы проведем его короче.
Определение. Арктангенсом числа а называется угол тангенс которого равен а. Арккотангенсом числа а называется угол x ∈ (0; π), котангенс которого равен а.
Обозначения: х = arctg а и x = arcctg а. Примеры.
2. Решить уравнения:
Тождества:
Решение тригонометрических уравненийТригонометрические уравнения встречаются в задачах, в которых из соотношений между тригонометрическими функциями требуется найти неизвестные углы. Основными, чаще всего встречающимися тригонометрическими уравнениями являются уравнения простейшего типа sin х — а, cos х = а, tg х = а и ctg х = а, которые уже рассмотрены в предыдущих пунктах.
 Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.
Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.Более сложные тригонометрические уравнения обычно решаются сведением их к простейшим с помощью различных алгебраических и тригонометрических формул и преобразований. Рассмотрим некоторые приемы решения тригонометрических уравнений.
а) Уравнения, алгебраические относительно одной из тригонометрических функций.
Примеры решения уравнений.
Это уравнение является квадратным относительно sin х. Корни этого квадратного уравнения и sin x= — 2. Второе из полученных простейших уравнений не имеет решений, так как |sinx| ≤ 1, решение первого можно записать так:
Если в уравнении встречаются разные тригонометрические функции, то надо пытаться заменить их все через какую-нибудь одну, используя тригонометрические тождества.
Так как квадрат синуса легко выражается через косинус, то, заменяя sin2 х на 1 —cos2 х и приводя уравнение к квадратному относительно cos х, получим 2 (1 —cos2 х) — 5 cos х — 5 = 0, т.
 е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которого
е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которогоУравнение решений не имеет. Решения уравнения cos x= — 1 запишем в виде
Заменив ctg x на и приведя к общему знаменателю, получим квадратное уравнение , корни которого tg x=l, tg х = 3, откуда
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используют формулы, выражающие синус и косинус через тангенс половинного угла, т. е.
Делая замену, получаем уравнение относительно
Квадратное уравнение имеет корни откуда
б) Уравнения, решаемые понижением их порядка.
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры решения уравнений.
- Решить уравнение
Можно заменить cos 2х на 2 — 1 и получить квадратное уравнение относительно cos х, но проще заменить на и получить линейное уравнение относительно cos 2х:
2.
 Решить уравнение
Решить уравнениеПодставляя вместо их выражение через cos 2x, получим:
в) Уравнения, решаемые после преобразований с помощью тригонометрических формул.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы преобразования суммы в произведение.
Примеры решения уравнений.
Преобразуем произведение синусов в сумму:
Полученное уравнение можно решить разными способами. Можно воспользоваться формулами сложения и преобразовать в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 2х и 6х:
Получим два уравнения:
Проверьте, что решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче:
г) Однородные уравнения.
Решим уравнение
Если считать, что sin х и cos х — члены первой степени, то каждое слагаемое имеет вторую степень. Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
Гармонические колебания Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.)
Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.)Гармонические колебания — это процесс, который может быть описан функцией вида у = A sin (ω + а).
Примеры:
1) Колебания упругой пружины. Конец упругой пружины (точка Р) при ее сжатии или растяжении описывает колебательные движения. Если на прямой, по которой движется точка Р, ввести координату х так, чтобы в положении равновесия xр = 0, оттянуть конец пружины в положительном направлении на расстояние A и в момент времени t = 0 отпустить его, то зависимость координаты точки Р от времени t (рис. 98) будет иметь следуюший вид: , где ω — некоторый коэффициент, характеризующий упругость пружины.
2) Электрический колебательный контур. Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора С и катушки индуктивности L (рис.
 99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени.
99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени.Таким образом, гармоническое колебание у=А sin (ωt + a) определяется тремя параметрами: амплитудой A>0, угловой скоростью ω>0 и так называемой начальной фазой а. Часто вместо угловой скорости ω говорят о частоте колебаний v, которая связана с угловой скоростью ω (или иначе круговой частотой) формулой ω = 2πv. Функция у периодична. Ее основной период равен
Колебания приходится складывать. В механике это связано с тем, что на точку может действовать несколько сил, каждая из которых вызывает гармонические колебания.
 В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функций
В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функцийесть функция того же вида:
Достаточно научиться складывать функции вида у = A1 sin ωt и
y = A2 cos ωt. Для их сложения применяется прием введения вспомогательного угла. Итак, рассмотрим выражение у = A1 sin ωt + A2 cos ωt. Оно похоже на формулу синуса суммы: sin (ωt + a) = sin ωt cos a+ cos ωt sin a. Числа A1 и A2 нельзя считать косинусом и синусом, однако если их разделить на число то тогда это будет возможно. Введем угол а с помощью соотношении
Сделаем преобразование:
Примеры:
Периодические функцииТригонометрические функции являются периодическими. В общем виде функция y = f(x) называется периодической, если существует такое число Т ≠ О, что равенство f (x+T)=f (х) выполняется тождественно при всех значениях х.

Обычно среди периодов периодической функции можно выделить наименьший положительный период, который часто называют основным периодом. Все другие периоды функции являются целыми кратными основного. График периодической функции состоит из повторяющихся кусков, поэтому достаточно построить его на отрезке изменения аргумента длиной, равной основному периоду. На рисунке 100 изображены графики различных периодических функций.
Приведем пример одной интересной периодической функции. Всякое число х можно представить в виде суммы его целой и дробной частей. Целая часть числа х определяется как наибольшее целое число, не превосходящее х, и обозначается [х]. Например, [3]=3; [3,14]=3; [ — 3,14]=— 4. Дробная часть обозначается {x} и равна по определению x — [x]. Функция у — {х)=х — [х] является периодической с основным периодом, равным единице. Ее график изображен на рисунке 101.
Если функция y — f (х) периодична и ее периодом является число Т, то и функция y=f (kx) будет периодической, причем ее пе-риодом будет число Действительно, рассмотрим функцию y=g(x), где g(x) = f{kx).
 Вычислим
ВычислимСдвиг аргумента не меняет период функции. Отсюда следует, что функция у=А sin (ωt + а), задающая гармоническое колебание, имеет период
Если Т является общим периодом двух функций f и g, то Т остается периодом их суммы, произведения, частного. Правда, как мы видим на примере тангенса, если Т является основным периодом f и g, то это может быть не так для новых функций, полученных из f и g арифметическими операциями.
Сумма двух функций с различными периодами необязательно будет периодической. Интересен случай сложения двух функций с различными, но очень близкими периодами. Рассмотрим, например, сумму функций близки друг к другу. Складывая синусы, получим
Так как
Поэтому при маленьких значениях t и
Однако с ростом t множитель будет убывать.
«Ровное» гармоническое колебание типа у1 заменится «биением», график которого изображен на рисунке 102. Можно представить себе, что «биение» — это колебание, амплитуда которого медленно (и тоже периодически) меняется.
Разложение на гармоники Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.
Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.Чистый звуковой тон представляет собой колебание с некоторой постоянной частотой. Музыка, которую мы слышим, представляет собой наложение различных чистых тонов, т. е. получается сложением колебаний с различными частотами. Преобладание звука той или иной частоты (скажем, низких звуков или высоких) связано с амплитудой соответствующих колебаний. Это знакомое нам разложение звуков на чистые тона часто встречается при изучении различных колебательных процессов.
Можно сказать так: простейшие гармонические колебания являются теми кирпичиками, из которых складывается любое колебание. На языке математики это означает, что любую периодическую функцию можно представить с наперед заданной точностью как сумму синусов.

Эйлер Леонард
(1707—1783) — швейцарский математик и механик, академик Петербургской Академии наук, автор огромного количества научных открытий во всех областях математики. Эйлер первым применил средства математического анализа в теории чисел, положил начало топологии.
«Математика, вероятно, никогда не достигла бы такой высокой степени совершенства, если бы древние не приложили столько усилий для изучения вопросов, которыми сегодня многие пренебрегают из-за их мнимой бесплодности».
Л. ЭйлерЭтот замечательный факт обнаружен еще в XVIII в. Д. Бернулли при решении задачи о колебании струны. Это показалось удивительным и невозможным по отношению к любой функции даже такому гениальному математику, как Л. Эйлер, который, кстати, является автором всей современной символики тригонометрии. Систематически разложения периодических функций в сумму синусов (или, как говорят, на гармоники) изучал в начале XIX в.
 французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.
французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.В качестве примера на рисунке 103 изображено приближение к периодической функции y = {x) в виде суммы нескольких гармоник. Разложение произвольного периодического сигнала на гармоники является главным математическим аппаратом радиотехники.
Тригонометрические и обратные тригонометрические функции
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
2.
 1: Графики функций косинуса и синуса
1: Графики функций косинуса и синуса- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7104
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
- Каковы графики и важные свойства графиков \(y = \cos(x)\) и \(y = \sin(x)\)?
- Каковы области определения функций синуса и косинуса? Каковы диапазоны функций синуса и косинуса?
- Каковы периоды функций синуса и косинуса? Что означает период?
- Что такое амплитуда? Как амплитуда влияет на график синуса или косинуса?
- Сравните это с графиком из части (1). В чем сходство? Каковы различия?
- Найдите четыре отдельных значения \(t\), где график функции синуса пересекает ось \(t\). Такие значения называются \(t\) — пересечений функции синуса (или корней или нулей ).
- Судя по графикам, это максимальное значение \(\sin(t)\). Определите два различных значения \(t\), которые дают это максимальное значение \(\sin(t)\).
- Судя по графикам, это минимальное значение \(\sin(t)\). Определите два различных значения \(t\), которые дают это минимальное значение \(\sin(t)\).

- Ответить
На график нанесены не все точки, но ниже приведен график одного полного периода \(y = \cos(t)\) для \(0 \leq t \leq 2\pi\).

- Сравните график на рисунке \(\PageIndex{2}\) с графиком из упражнения \(\PageIndex{1}\). В чем сходство? Каковы различия?
- Найдите четыре отдельных значения \(t\), где график функции косинуса пересекает ось \(t\). Такие значения называются \(t\)- пересечений функции косинуса (или корней или нулей ).
- Судя по графикам, это максимальное значение \(\cos(t)\). Определите два различных значения \(t\), которые дают это максимальное значение \(\cos(t)\).
- Судя по графикам, это минимальное значение \(\cos(t)\). Определите два различных значения \(t\), которые дают это минимальное значение \(\cos(t)\).
- Ответить
- Разница в том, что график на рисунке \(\PageIndex{2}\) показывает три полных периода \(y = \cos(t)\) на интервале \([-2\pi, 4\pi] \).

- График \(y = \cos(t)\) имеет \(t\)-пересечения в точках \(t = -\dfrac{3\pi}{2}, t = -\dfrac{\pi}{ 2}, t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}, t = \dfrac{5\pi}{2}\) и \(t = \dfrac {7\пи}{2}\)
- Максимальное значение \(y = \cos(t)\) равно \(1\). График достигает этого максимума при \(t = -2\pi, t = 0, t = 2\pi\) и \(t = 4\pi\).
- Минимальное значение \(y = \cos(t)\) равно \(-1\). График достигает этого минимума при \(t = -\pi, t = \pi\) и \(t = 3\pi\)
- Разница в том, что график на рисунке \(\PageIndex{2}\) показывает три полных периода \(y = \cos(t)\) на интервале \([-2\pi, 4\pi] \).
- Ответить
График \(y = \sin(t)\) имеет \(t\)-пересечения \(t = 0, t = \pi\) и \(t = 2\pi\) в интервале \([0, 2\пи]\).
Если мы добавим период \(2\pi\) к каждому из этих \(t\)-отрезков и вычтем период \(2\pi\) из каждого из этих \(t\)-отрезков, мы увидим что график \(y = \sin(t)\) имеет \(t\)-пересечения \(t = -2\pi, t = -\pi, t = 0, t = \pi, t = 2\pi, t = 3\pi\) и \(t = 4\pi\) в интервале \([-2\pi, 4\pi]\).
Мы можем определить другие \(t\)-отрезки \(y = \sin(t)\), многократно добавляя или вычитая период \(2\pi\). Например, есть \(t\)-перехват по адресу:
.- \(t = 3\pi + 2\pi = 5\pi\)
- \(т = 5\пи + 2\пи = 7\пи\)
Однако, если мы более внимательно посмотрим на график \(y = \sin(t)\), мы увидим, что \(t\)-отрезки разнесены на \(\pi\) единиц. Это означает, что мы можем сказать, что \(t = 0 + k\pi\), где \(k\) — некоторое целое число, является \(t\)-перехватом \(y = \sin(t)\) .
- Нарисуйте графики \(y = \sin(t)\), \(y = \dfrac{1}{2} \sin(t)\) и \(y = 2\sin(t)\), \(y = -\sin(t)\) и \(y = 2\sin(t)\) на одном и том же оси. Убедитесь, что ваша графическая утилита находится в радианном режиме и используйте \(-2\pi \leq x \leq 2\pi\) и \(-2.5 \leq x \leq 2.5\).
- Используйте апплет Geogebra Амплитуда синусоиды по следующему веб-адресу: http://gvsu.
 edu/s/LM
edu/s/LM - Ответить
- С помощью графической утилиты нарисуйте график \(y = 3,6\cos(t)\), используя окно просмотра, указанное до этого теста выполнения.
- Используйте графическую утилиту для построения графика \(y = -2,75\sin(t)\).
- Ответить
1.
2.
- Нарисуйте график \(y = \cos(-x)\), используя \(0 \leq x \leq 2 \Пи\). График должен быть идентичен графику \(y = \cos(x)\).
- Нарисуйте график \(y = \sin(-x)\), используя \(0 \leq x \leq 2\pi\). График должен быть идентичен графику \(y = \sin(x)\).

- Важные характеристики синусоидальных функций вида \(y = A\sin(t)\) или \(y = A\cos(t)\) показано в таблице 2.
 1.
1. - Информации в Таблице 2.1 может показаться, что нужно запомнить много, и на самом деле в следующих разделах мы получим намного больше информации о синусоидальных волнах. Таким образом, вместо того, чтобы пытаться запомнить все из таблицы 2.1, лучше запомнить основные формы графиков, как показано на рисунке \(\PageIndex{7}\) и рисунке \(\PageIndex{8}\).
- Один из способов запомнить положение делений на оси \(t\) – запомнить, что расстояние между этими делениями составляет четверть периода, а период – \(2\).
 Пи\). Таким образом, интервал \(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
Пи\). Таким образом, интервал \(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\). - Функция \(f\) является четной функцией 9н\). Таким образом, граф симметричен относительно начала координат. Вот почему мы используем термин четные функции для тех функций \(f\), для которых \(f(-x) = f(x)\), и мы используем термин нечетные функции для тех функций, для которых \(f( —х) = —f(x)\).
Эта страница под названием 2.1: Графики функций косинуса и синуса распространяется под лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- четная функция
- нечетная функция
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
Тригонометрические тождества, свойства и графики
Косинус является одним из основных математических тригонометрических соотношений . Функция косинуса определяется как отношение длин сторон, прилегающих к углу и гипотенузе прямоугольного треугольника . Математически формула функции косинуса относительно сторон прямоугольного треугольника записывается так: cosx = смежная сторона/гипотенуза = основание/гипотенуза, где x — острый угол между основанием и гипотенузой.
Обозначается cosx, где x — угол. Cosx является периодической функцией и имеет период 2π. 9Функция косинуса 0050
используется для отображения некоторых сценариев реальной жизни, таких как радиоволны, приливы, звуковые волны, электрические токи, музыкальные тона и т. д.Подробнее: Введение в тригонометрию Содержание
- Функция косинуса
- Тождества функции косинуса
- Свойства функции косинуса
- График функции косинуса
- Things to Remember
- Sample Questions
Key Takeaways: Cosine Function, Cosine function identities, Cosine Function Graph, Cosine Values Table
Cosine Function
Функция косинуса
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Рассмотрим единичную окружность с центром в начале координат плоскости.
 Точка P перемещается на окружность окружности. Из данного рисунка мы увидим, что P присутствует в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикулярное падение из точки P на горизонтальную ось. Затем из точек O, P и Q образуется треугольник, где QO — основание, PQ — высота треугольник . Формула косинуса для вышеуказанного условия будет записана как: cosx = OQ/OP. Здесь х — острый угол, образованный между основанием и гипотенузой.
Точка P перемещается на окружность окружности. Из данного рисунка мы увидим, что P присутствует в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикулярное падение из точки P на горизонтальную ось. Затем из точек O, P и Q образуется треугольник, где QO — основание, PQ — высота треугольник . Формула косинуса для вышеуказанного условия будет записана как: cosx = OQ/OP. Здесь х — острый угол, образованный между основанием и гипотенузой.Функция косинуса из единичного круга
также прочитал: Применение тригонометрии
Тригонометирование
[Нажмите здесь для выборки. решать различные математические задачи, связанные с функцией косинуса. Это:
- cosx = 1/secx
- cos- 1 x = arccos x, где x лежит между [-1, 1]
- sin 2 x + cos 2 x + 1 cos y) = cosx cosy — sinx siny
- cos(x-y) = cosx cosy + sinx siny
- cos2x = cos 2 x — sin 2 x = 2cos 2 x — 1 = 1 — 9858 in 2 90 x
- Производная от cosx: d(cosx)/dx = -sinx
- Интеграл функции косинуса: ∫cosx dx = sinx + c, где c — постоянная интегрирования
- cosx является четной функцией, потому что cos(-x) = cosx
- Функция, обратная косинусу, является секущей.
- Область функции косинуса представляет собой действительные числа и диапазон [-1, 1].
- График cosx повторяется через 2π, поэтому функция является периодической с периодом 2π.
- Разложение функции косинуса в ряд по степеням равно cos x = ∑ ∞ n=0 (-1)n x 2n /(2n)!
- Косинус — периодическая функция с периодом 2π. Домен cosx равен (-∞, ∞) с диапазоном [-1, 1].
- График косинуса помогает узнать среднесуточную температуру в любом месте. Он похож на синусоидальный график.
- Основное различие между графиками синуса и косинуса заключается в том, что график синуса начинается с 0, тогда как график косинуса начинается с 90*.
- График cos обычно начинается с 1 и падает до -1, а затем снова начинает расти. Это движение дает кривую вверх и вниз.

- Тригонометрические функции и значения всегда имеют дело с отношением к прямоугольному треугольнику. Авиация, криминология, морская биология и навигация и т. д. используют тригонометрию во всех аспектах.
Algebra 2 Digital MEGA Bundle плюс печатные формы
Цифровой меганабор Algebra 2 из более чем 70 интерактивных заданий с Google® Slides, безбумажной и не требующей подготовки для вас, и будет увлекательным и увлекательным обучением для ваших учеников.
 Это дополняет почти каждую учебную программу по алгебре 2, и многие мероприятия и ресурсы включают в себя печатные версии. INCL
Это дополняет почти каждую учебную программу по алгебре 2, и многие мероприятия и ресурсы включают в себя печатные версии. INCL71
Продукты
$ 187,50PRICE $ 187,50 $ 267,84RIGINAT Печатные формы
Вашим учащимся понравится каждое задание в этом наборе из 20 интерактивных заданий для предварительного исчисления с Google® Slides. Они безбумажны и не требуют подготовки для вас, но при этом интересны и сложны для ваших учеников. Эти мероприятия станут отличным дополнением к вашей учебной программе Trigonometry или Precalculus I
20
Продукты
$ 57,50PRICE $ 57,50 $ 81,25 ЦЕНЫ $ 81,25 SAVE $ 23,75
VIEW BUCKER
914SAVE $ 23,75PreCalculus First Semester Digital Bundle plus Printables
Независимо от того, какую учебную программу вы используете для PreCalculus, эти цифровые ресурсы дополнят ваши занятия, привлекут и бросят вызов вашим ученикам.
 Многие ресурсы также включают версии и компоненты для печати. Включены различные виды деятельности, а также задания для самостоятельной оценки и оценки. Каждый
Многие ресурсы также включают версии и компоненты для печати. Включены различные виды деятельности, а также задания для самостоятельной оценки и оценки. Каждый74
Продукты
$ 199,00PRICE 199,00 $ 273,25ORIGINAT0032
Этот мега-цифровой набор включает более 160 интерактивных цифровых заданий, которые будут увлекательными и увлекательными для ваших учеников. Многие ресурсы имеют версию для печати. С таким большим количеством учителей, обучающих как алгебру, 2, так и Precalculus I объединили как алгебру 2 цифровые мега, так и TH
166
Продукты
$ 399,98PRICE $ 399,98 $ 615.09.ORIGINAT Тригонометрические функции плюс цифровой пакет
Этот модуль PreCalculus Unit 4, Тригонометрические функции (тригонометрия Unit 1), Super Bundle включает в себя пошаговые заметки, задания, домашние задания, викторины, органайзеры, редактируемые оценки и многое другое, ПЛЮС цифровые задания и цифровые оценки, которые улучшат ваши уроки PreCalculus и привлечь свой
39
Продукты
$ 109,50PRICE $ 109,50 $ 147,50 ЦЕНЫ $ 147.
 50S 38,00
50S 38,00View Bundle
Algebra 1 Algebra 2 Algebra 2 Megbo Digital Combo.0032
Так как многие учителя преподают как Алгебру 1, так и Алгебру 2, я создал этот МегаКомбо-Набор Цифровых Упражнений, который включает в себя Мега-Набор Цифровых Упражнений по Алгебре 1 для Google™ Drive и Алгебра 2 MEGA-Набор Упражнений GOOGLE™, созданных для Google® Диска. , мероприятия —
134
Продукты
$ 347.50price $ 347,50 $ 493.09.Original Цена $ 493,09save $ 145,59
View Back
ГРАФИК0032
Вашим учащимся понравится изучать графическое построение синуса и косинуса с помощью ресурсов в этом новом цифровом наборе тем. (Многие ресурсы имеют версии для печати.) Включены заметки, цифровые лабиринты, цифровые органайзеры, флип-книги, сопоставление и редактируемые задания для самостоятельной оценки, некоторые с Prin
7
Продукты
14,75 долл.
 США Цена 14,75 долл. США 21,50 долл. 6,75 долл. США
США Цена 14,75 долл. США 21,50 долл. 6,75 долл. СШАView Bundle
- PDF со ссылками на продукт. Вам не нужно предоставлять TpT доступ к вашему Диску Google™ или Диску Google вашей школы, чтобы использовать этот продукт.
- Подробные иллюстрированные инструкции по доступу к этому ресурсу и совместному использованию этого ресурса с вашими учащимися для занятий с Google™ Classroom и без него. 2022)
- Дополнительный лист для печати
- Клавиши ответов
- Это периодические функции с периодом.

- Домен каждой функции и диапазон.
- График симметричен относительно начала координат, потому что это нечетная функция.
- График симметричен относительно оси, потому что это четная функция.
- Это периодические функции с периодом.
- Область определения каждой функции равна ( − ∞ , ∞ ), а диапазон равен.
- График y = sin x y = sin x симметричен относительно начала координат, потому что это нечетная функция.
Пусть sin( x ) = y .

Если 2 k π − π/2 ≤ x ≤ 2 k π + π/2 для некоторого целого числа k , тогдаx = arcsin( y ) + 2 k π.
Если (2 k + 1)π − π/2 ≤ x ≤ (2 k + 1)π + π/2 для некоторого целого числа k , тогда
x = (2 k + 1)π − arcsin( y ).
Пусть cos( x ) = y .
Если 2 k π ≤ x ≤ 2 k π + π для некоторого целого числа k , тогдаx = arccos( y ) + 2 k π.
Если (2 k + 1)π ≤ x ≤ (2 k + 1)π + π для некоторого целого числа k , тогда
x = (2 k + 2)π − arccos( y ).
Пусть tan( x ) = y .
Если k π − π/2 < x < k π + π/2 для некоторого целого числа k , тогдаx = arctan( y ) + k π.

Пусть cotan( x ) = y .
If k π < x < k π + π для некоторого целого числа k , тогдаx = arccotan( y ) + к π.
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Начальное занятие
Самая простая форма рисования графика функции — это построение точек. Используйте значения в данной таблице, чтобы нанести точки на график \(y = \sin(x)\), а затем нарисуйте график \(y = \sin(t)\) для \(0 < t < 2\пи\). Примечание : по оси \(t\) линии сетки отстоят друг от друга на \(\dfrac{\pi}{12}\) единиц, а по оси \(y\) линии сетки отстоят на 0,1 единицы. отдельно.
Используйте значения в данной таблице, чтобы нанести точки на график \(y = \sin(x)\), а затем нарисуйте график \(y = \sin(t)\) для \(0 < t < 2\пи\). Примечание : по оси \(t\) линии сетки отстоят друг от друга на \(\dfrac{\pi}{12}\) единиц, а по оси \(y\) линии сетки отстоят на 0,1 единицы. отдельно.
| \(т\) | \(\sin(t)\) | \(\sin(t)\) (приблизительно) |
|---|---|---|
| 0 | 0 | 0 |
| \(\dfrac{\pi}{6}\) | \(\dfrac{1}{2}\) | 0,5 |
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | 0,707 |
| \(\dfrac{\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | 0,866 |
| \(\dfrac{\pi}{2}\) | 1 | 1 |
| \(\dfrac{2\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | 0,866 |
| \(\dfrac{3\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | 0,714 |
| \(\dfrac{5\pi}{6}\) | \(\dfrac{1}{2}\) | 0,5 |
| \(\пи\) | 0 | 0 |
| \(\dfrac{7\pi}{6}\) | \(-\dfrac{1}{2}\) | -0,5 |
| \(\dfrac{5\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | -0,707 |
| \(\dfrac{4\pi}{3}\) | \(-\dfrac{\sqrt{3}}{2}\) | -0,866 |
| \(\dfrac{3\pi}{2}\) | -1 | -1 |
| \(\dfrac{5\pi}{3}\) | \(-\dfrac{\sqrt{3}}{2}\) | -0,866 |
| \(\dfrac{7\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | -0,707 |
| \(\dfrac{11\pi}{6}\) | \(-\dfrac{1}{2}\) | -0,5 |
| \(2\пи\) | 0 | 0 |
Мы также можем использовать графический калькулятор или другое графическое устройство, чтобы нарисовать график синусоидальной функции. Убедитесь, что устройство настроено на радианный режим, и используйте его для построения графика \(y = \sin(t)\), используя \(-2\pi \leq t \leq 4\pi\) и \(-1.2 \leq t \leq 1.2\). Примечание : Многие графические утилиты требуют использования \(x\) в качестве независимой переменной. Для таких устройств нам нужно использовать \(y = \sin(x)\). Это никак не отразится на графике функции.
Убедитесь, что устройство настроено на радианный режим, и используйте его для построения графика \(y = \sin(t)\), используя \(-2\pi \leq t \leq 4\pi\) и \(-1.2 \leq t \leq 1.2\). Примечание : Многие графические утилиты требуют использования \(x\) в качестве независимой переменной. Для таких устройств нам нужно использовать \(y = \sin(x)\). Это никак не отразится на графике функции.
Периоды функций синуса и косинуса
Одна вещь, которую мы можем наблюдать на графиках функции синуса в начальном упражнении, заключается в том, что график, кажется, имеет форму «волны», и что эта «волна» повторяется по мере нашего продвижения вперед. горизонтальная ось. Мы видим, что часть графика между 0 и \(2\pi\) кажется идентичной части графика между \(2\pi\) и \(4\pi\) и части графика между \(-2\pi\) и 0. График функции синуса демонстрирует то, что известно как периодическое свойство. На рис. 2.1 показан график \(y = \sin(t)\) для трех циклов.
Рисунок \(\PageIndex{1}\): График \(y = \sin(t)\) с \(-2\pi \leq t \leq 4\pi\)
Мы говорим, что функция синуса является периодической функцией . Такие функции часто используются для моделирования повторяющихся явлений, таких как раскачивание маятника вперед и назад, груз, прикрепленный к пружине, и вибрация гитарной струны.
Причина, по которой график \(y = \sin(t)\) повторяется, заключается в том, что значение \(\sin(t)\) представляет собой координату y точки, когда она движется по единичной окружности. Поскольку длина окружности единичного круга составляет \(2\pi\) единиц, дуга длины \((t + 2\pi)\) будет иметь ту же конечную точку, что и дуга длины t. Поскольку \(\sin(t)\) является координатой y этой точки, мы видим, что \(\sin(t + 2\pi) = \sin(t)\). Это означает, что период функции синуса равен \(2\pi\). Ниже приводится более формальное определение периодической функции.
Поскольку длина окружности единичного круга составляет \(2\pi\) единиц, дуга длины \((t + 2\pi)\) будет иметь ту же конечную точку, что и дуга длины t. Поскольку \(\sin(t)\) является координатой y этой точки, мы видим, что \(\sin(t + 2\pi) = \sin(t)\). Это означает, что период функции синуса равен \(2\pi\). Ниже приводится более формальное определение периодической функции.
Определение
Определение. Функция \(f\) является периодической с периодом \(p\), если \(f(t + p) = f(t)\) для всех \(t\) в области определения \(f\) а \(р\) — наименьшее положительное число, обладающее этим свойством.
Обратите внимание, что если \(f\) — периодическая функция с периодом \(p\), то если мы добавим 2\(p\) к \(t\), мы получим \[f(t + 2p) = f((t+p)+p) = f(t + p) =f(t).\]
Мы можем продолжить повторять этот процесс и увидеть, что для любого целого числа \(k\), \[f( t + kp) = f(t).\]
До сих пор мы обсуждали только функцию синуса, но аналогичное поведение мы получаем и с функцией косинуса. Напомним, что функция обтекания оборачивает числовую прямую вокруг единичного круга таким образом, что это повторяется в сегментах длины \(2\pi\). Это периодическое поведение, и оно приводит к периодическому поведению функций как синуса, так и косинуса, поскольку значением синуса является \(y\)-координата точки на единичной окружности, а значением косинуса является \ (x\)-координата одной и той же точки на единичной окружности, функции синуса и косинуса повторяются каждый раз, когда мы делаем один оборот вокруг единичной окружности. То есть \[\cos(t + 2\pi) = \cos(t) \space и \space \sin(t + 2\pi) = \sin(t).\]
Напомним, что функция обтекания оборачивает числовую прямую вокруг единичного круга таким образом, что это повторяется в сегментах длины \(2\pi\). Это периодическое поведение, и оно приводит к периодическому поведению функций как синуса, так и косинуса, поскольку значением синуса является \(y\)-координата точки на единичной окружности, а значением косинуса является \ (x\)-координата одной и той же точки на единичной окружности, функции синуса и косинуса повторяются каждый раз, когда мы делаем один оборот вокруг единичной окружности. То есть \[\cos(t + 2\pi) = \cos(t) \space и \space \sin(t + 2\pi) = \sin(t).\]
Важно понимать, что \(2\pi\) — это наименьшее число, при котором это происходит. Следовательно, функции косинуса и синуса периодичны с периодом \(2\pi\).
Упражнение \(\PageIndex{1}\)
Конечно, мы можем использовать графическую утилиту для построения графика функции косинуса. Тем не менее, это помогает понять график, если мы на самом деле нарисуем график вручную, как мы делали это для функции синуса в начальном упражнении.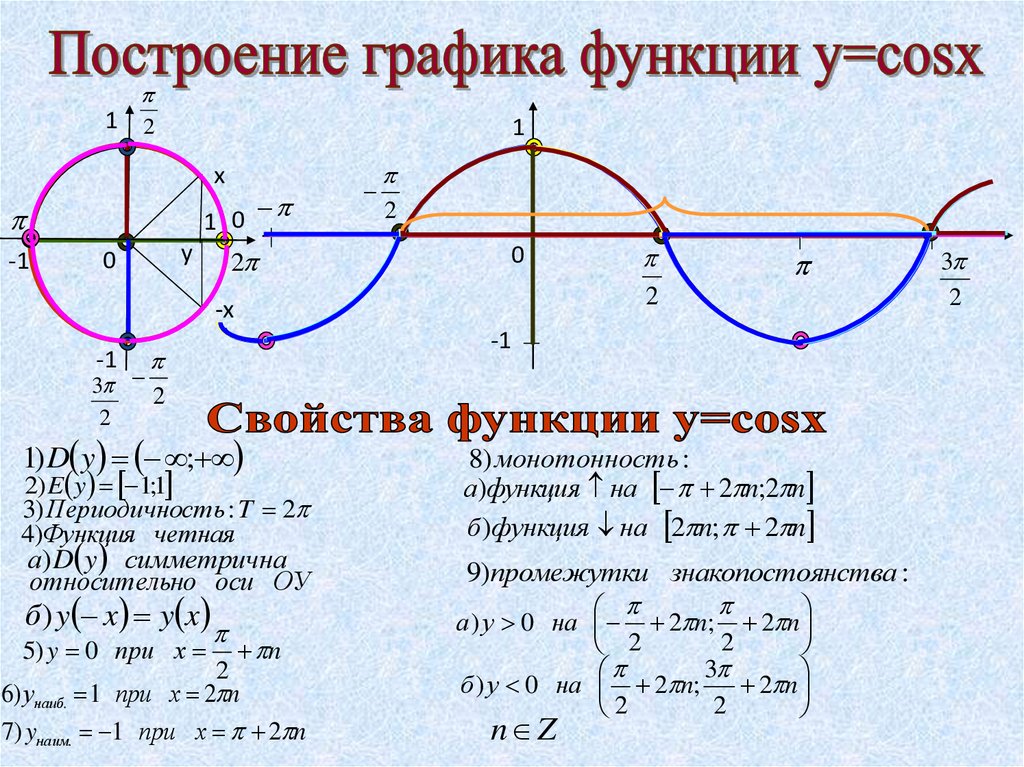 Используйте значения в данной таблице, чтобы нанести точки на график \(y = \cos(t)\), а затем нарисуйте график \(y = \cos(t)\) для \(0 \leq t \leq 2\pi\).
Используйте значения в данной таблице, чтобы нанести точки на график \(y = \cos(t)\), а затем нарисуйте график \(y = \cos(t)\) для \(0 \leq t \leq 2\pi\).
| \(т\) | \(\cos(t)\) | \(\cos(t)\) (приблизительно) |
|---|---|---|
| \(0\) | \(1\) | \(1\) |
| \(\dfrac{\pi}{6}\) | \(\dfrac{\sqrt{3}}{2}\) | \(0,866\) |
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | \(0,707\) |
| \(\dfrac{\pi}{3}\) | \(\dfrac{1}{2}\) | \(0,5\) |
| \(\dfrac{\pi}{2}\) | \(0\) | \(0\) |
| \(\dfrac{2\pi}{3}\) | \(-\dfrac{1}{2}\) | \(-0,5\) |
| \(\dfrac{3\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-0,714\) |
| \(\dfrac{5\pi}{6}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-0,866\) |
| \(\пи\) | \(-1\) | \(-1\) |
| \(\dfrac{7\pi}{6}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-0,866\) |
| \(\dfrac{5\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-0,714\) |
| \(\dfrac{4\pi}{3}\) | \(-\dfrac{1}{2}\) | \(-0,5\) |
| \(\dfrac{3\pi}{2}\) | \(0\) | \(-1\) |
| \(\dfrac{5\pi}{3}\) | \(\dfrac{1}{2}\) | \(0,5\) |
| \(\dfrac{7\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(0,707\) |
| \(\dfrac{11\pi}{6}\) | \(\dfrac{\sqrt{3}}{2}\) | \(-0,866\) |
| \(2\пи\) | \(1\) | \(1\) |
Рисунок \(\PageIndex{2}\): График \(y = \cos(t)\) с \(-2\pi \leq t \leq 4\pi\)
Упражнение \( \PageIndex{2}\)
Задание 2.3 (Графики функций синуса и косинуса).
Теперь мы построили график функций синуса и косинуса, нанеся точки и используя графическую утилиту. Мы сможем лучше понять эти графики, если увидим, как эти графики связаны с определениями единичного круга \(\sin(t)\) и \(\cos(t)\). Мы будем использовать два апплета Geogebra, чтобы помочь нам сделать это.
Первый апплет называется Генератор синусоидальных графиков . Веб-адрес: gvsu. edu/s/Ly
edu/s/Ly
. Для начала просто переместите ползунок на \(t\), пока не получите \(t = 1\), и посмотрите на полученное изображение. Слева будет копия единичного круга с нарисованной дугой длиной \(1\). Также будет отображаться \(y\)-координата конечной точки этой дуги (\(0,84\) с округлением до сотых). Горизонтальная линия будет соединена с точкой \((1, 0,84)\) на графике \(y = \sin(t)\). По мере того, как значения \(t\) изменяются с помощью ползунка, таким образом на графике \(y = \sin(t)\) будет отображаться больше точек.
Другой апплет называется Генератор синусоидальных графиков и работает аналогично Генератору синусоидальных графиков . Веб-адрес этого апплета: http://gvsu.edu/s/Lz
Свойства графиков функций синуса и косинуса
Графики \(y = \sin(t)\) и \(y = \cos(t)\) называются синусоидальными волнами , а функции синуса и косинуса называются синусоидальными функциями . Обе эти синусоидальные волны имеют период \(2\pi\). График за один период называется цикл графика . Как и в случае с другими функциями в нашем предыдущем изучении алгебры, еще одним важным свойством графиков являются их точки пересечения, в частности, горизонтальные точки пересечения или точки пересечения графика с горизонтальной осью. Одно большое отличие от алгебры состоит в том, что функции синуса и косинуса имеют бесконечно много точек пересечения по горизонтали.
График за один период называется цикл графика . Как и в случае с другими функциями в нашем предыдущем изучении алгебры, еще одним важным свойством графиков являются их точки пересечения, в частности, горизонтальные точки пересечения или точки пересечения графика с горизонтальной осью. Одно большое отличие от алгебры состоит в том, что функции синуса и косинуса имеют бесконечно много точек пересечения по горизонтали.
В упражнении \(\PageIndex{2}\) мы использовали рисунок \(\PageIndex{2}\) и определили, что \(-\dfrac{\pi}{2}, \dfrac{\pi}{2 }, \dfrac{3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{7\pi}{2}\) являются \(t\)-перехватами на графике \( у = \cos(t)\). В частности, в интервале \([0, 2\pi]\) единственными \(t\)-перехватами \(y = \cos(t)\) являются \(t = \dfrac{\pi} {2}\) и \(t = \dfrac{3\pi}{2}\).
Конечно, есть и другие \(t\)-перехваты, и здесь период \(2\pi\) полезен. Мы можем сгенерировать любой другой \(t\)-отрезок \(y = \cos(t)\), добавив к этим двум значениям целое число, кратное периоду \(2\pi\). Например, если мы добавим \(6\pi\) к каждому из них, мы увидим, что \(t = \dfrac{13\pi}{2}\) и \(t = \dfrac{15\pi}{ 2}\) являются \(t\) точками пересечения \(y = \cos(t)\).
Например, если мы добавим \(6\pi\) к каждому из них, мы увидим, что \(t = \dfrac{13\pi}{2}\) и \(t = \dfrac{15\pi}{ 2}\) являются \(t\) точками пересечения \(y = \cos(t)\).
Упражнение \(\PageIndex{3}\)
Используйте график для определения \(t\)-отрезков \(y = \sin(t)\) в интервале \([0, 2\pi ]\). Затем используйте свойство периода функции синуса, чтобы определить \(t\)-отрезки \(y = \sin(t)\) в интервале \([-2\pi, 4\pi]\). Сравните этот результат с графиком на рис. 2.1. Наконец, определите два \(t\)-отрезка \(y = \sin(t)\), которые не лежат в интервале \([-2\pi, 4\pi]\).
Упражнение 2.5 (Изучение графиков синусоидальных функций)
Выполните одно из следующих действий:
Выражение для \(g(t)\) можно изменить, но оставить равным \(g(t) = \sin(t)\). Ползунок можно перемещать, чтобы изменить значение A, и будет построен график \(y = A\sin(t)\). Изучите эти графики, изменив значения A, убедившись, что вы используете отрицательные значения A, а также положительные значения A. (Можно изменить это на \(g(t) = \cos(t)\) и исследовать графики \(y = A\sin(t)\).
Амплитуда функций синуса и косинуса
Графики функций из упражнения 2.5 должны были выглядеть как один из графиков на рисунке 2.3. Оба графика являются графиками из \(y = A\sin(t)\), но слева — для \(A > 0\), а справа — для \(A < 0\). Обратите внимание, что когда \( А < 0\), \(—А > 0\). Еще одной важной характеристикой синусоидальной волны является амплитуда. Амплитуда каждого из графиков на рис. 2.3 представлена длиной штриховых линий, и мы видим, что эта длина равна \(|A|\).
Определение: амплитуда
Амплитуда синусоидальной волны равна половине расстояния между максимальным и минимальным функциональными значениями.
\[\text{Амплитуда} = \dfrac{1}{2}|(\text{максимальная координата y}) — (\text{минимальная координата y})|\]
Рисунок \(\ PageIndex{3}\): Графики \(y = A\sin(t)\)
Упражнение \(\PageIndex{4}\)
Нарисуйте графики \(y = A\cos(t)\) для \(A > 0\) и для \(A <0\) аналогично графикам для \(y = A\sin(t)\) на рисунке \(\PageIndex{3}\).
Использование графической утилиты
Мы часто используем графическую утилиту для построения графика синусоидальной функции. При этом рекомендуется использовать амплитуду, чтобы установить соответствующее окно просмотра. Основная идея состоит в том, чтобы на экране графической утилиты отображалось чуть больше одного периода синусоиды. Например, если мы пытаемся нарисовать график \(y = 3,6\cos(t)\), мы могли бы использовать следующее окно просмотра. \[-0.5 \leq x \leq 6.5 \space and \space -4 \leq y \leq 4.\] Если возможно, установите \(x\)-галочки равными всем \(\dfrac{\pi {4}\) или \(\dfrac{\pi}{2}\) единиц.
Упражнение \(\PageIndex{5}\)
Симметрия и отрицательные тождества
Изучите график \(y = \cos(t)\), показанный на рис. 2.2. Если мы сосредоточимся на той части графика между \(-2\pi\) и \(2\pi\), мы можем заметить, что левая часть графика является «зеркальным отражением» правой части графика. . Чтобы увидеть это лучше, используйте апплет Geogebra Симметрия графика из \(y = \cos(t)\) по следующей ссылке: http://gvsu.edu/s/Ot
Рисунок \(\PageIndex{4}\): График Демонстрация симметрии \(y = \cos(t)\)
На рисунке \(\PageIndex{4}\) показано типичное изображение из этого апплета. Поскольку вторая координата точки на графике является значением функции в первой координате, этот рисунок (и апплет) указывает, что \(b = \cos(t)\) и \(b = \cos(- т)\).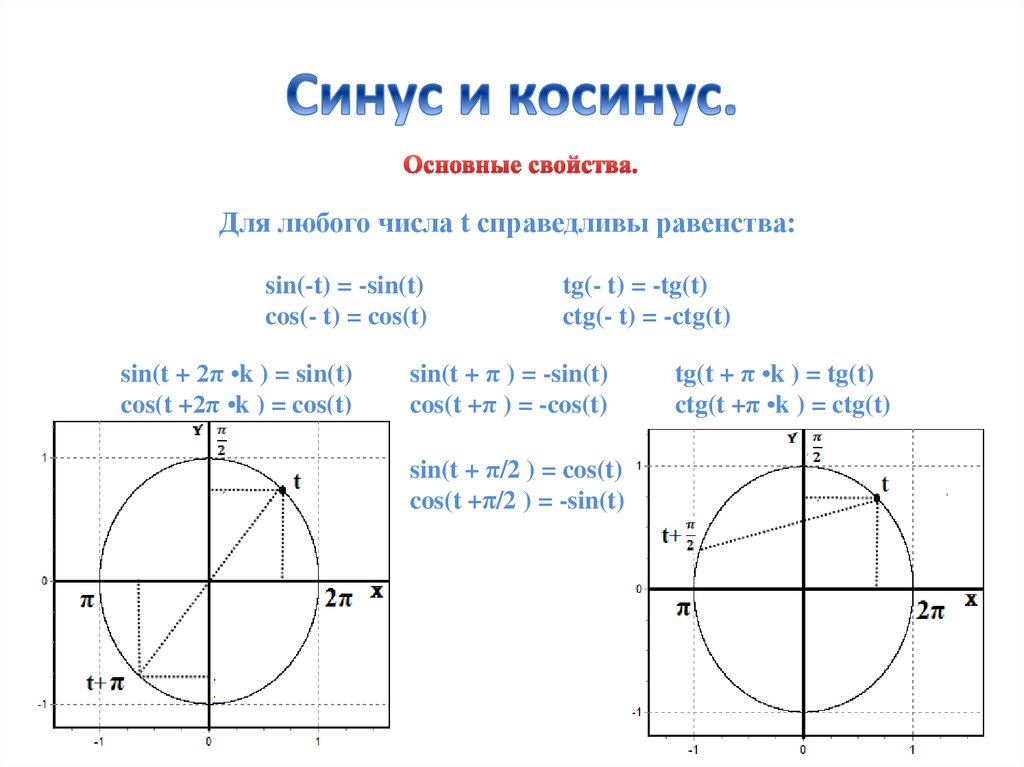 То есть это иллюстрирует тот факт, что \(\cos(-t) = \cos(t)\). Следующее задание дает объяснение, почему это так.
То есть это иллюстрирует тот факт, что \(\cos(-t) = \cos(t)\). Следующее задание дает объяснение, почему это так.
Упражнение 2.8: Положительная и отрицательная дуги
В этом упражнении мы будем использовать апплет Geogebra под названием Рисование положительной дуги и отрицательной дуги на единичной окружности . Ссылка на этот апплет: http://gvsu.edu/s/Ol
Поскольку в апплете используется ползунок \(t\), дуга длины t будет нарисована синим цветом, а дуга длины \ (-t\) будет нарисовано красным цветом. Кроме того, будут отображаться координаты конечных точек обеих дуг \(t\) и \(-t\). Изучите координаты этих двух точек при различных значениях \(t\). Что вы наблюдаете? Имея в виду, что координаты этих точек также могут быть представлены как \[(\cos(t), \sin(t))\space и \space (\cos(-t), \sin(-t)), \]
Что они говорят о взаимосвязи между \(\cos(-t)\) и \(\cos(t)\)? Как насчет отношения между \(\sin(-t)\) и \(\sin(t)\)?
На рисунке \(\PageIndex{5}\) показана типичная ситуация, проиллюстрированная в Упражнении 2. 8. На единичной окружности проведены дуга и соответствующая ей отрицательная дуга. То, что мы видели
8. На единичной окружности проведены дуга и соответствующая ей отрицательная дуга. То, что мы видели
Рисунок \(\PageIndex{5}\): Дуга и отрицательная дуга на единичной окружности
состоит в том, что если конечной точкой дуги \(t\) является \((a , б)\), то в силу симметрии окружности мы видим, что конечной точкой дуги \(-t\) является \((a, -b)\). Итак, диаграмма иллюстрирует следующие результаты, которые иногда называют отрицательные идентификаторы дуги .
Определение: тождества отрицательной дуги
Для каждого действительного числа \(t\), \[\sin(-t) = -\sin(t) \space \cos(-t) = \cos(t).\ ]
Для дальнейшей проверки тождеств отрицательных дуг для синуса и косинуса используйте графическую утилиту для:
Эти тождества с отрицательными дугами дают нам возможность взглянуть на симметрию графиков функций косинуса и синуса. Мы уже проиллюстрировали симметрию функции косинуса на рисунке \(\PageIndex{4}\). Из-за этого мы говорим, что график \(y = \cos(t)\) симметричен относительно оси y .
А как насчет симметрии графика синуса? На рисунке \(\PageIndex{6}\) показано, что отрицательное тождество \(\sin(-t) = \sin(t)\) подразумевает симметрию \(y = \sin(t)\). В этом случае мы говорим, что график \(y = \sin(t)\) равен симметрично относительно начала координат .
Рисунок \(\PageIndex{6}\): График, показывающий симметрию \(y = \sin(t)\).
Чтобы лучше увидеть симметрию графика синуса, используйте апплет Geogebra Symmetry of the Graph of \(y = \sin(t)\) по следующей ссылке: http://gvsu.edu/s/ Ou
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
| \(у = А\sin(t)\) | \(у = А\cos(t)\) | |
|---|---|---|
| Все действительные числа | домен | Все действительные числа |
| \(2\пи\) | период | \(2\пи\) |
| \(|А|\) | амплитуда | \(|А|\) |
| \((0, 0)\) | \(y\)-перехват | \((0, А)\) |
| \(t = 0\) и \(t = \pi\) | \(t\)-перехват в \([0, 2\pi)\) | \(t = \dfrac{\pi}{2}\) и \(t = \dfrac{3\pi}{2}\) |
| \(|А|\) | максимальное значение | \(|А|\) |
| \(-|А|\) | минимальное значение | \(-|А|\) |
| Интервал \([-|A|, |A|]\) | диапазон | Интервал \([-|A|, |A|]\) |
| \(t = \dfrac{\pi}{2}\) | , когда \(A > 0\), максимум приходится на | \(t = 0\) |
| \(t = \dfrac{3\pi}{2}\) | , когда \(A > 0\), максимум приходится на | \(т = \пи\) |
| \(t = \dfrac{3\pi}{2}\) | , когда \(A < 0\), максимум приходится на | \(т = \пи\) |
| \(t = \dfrac{\pi}{2}\) | , когда \(A < 0\), максимум приходится на | \(t = 0\) |
| происхождение | симметрия по отношению к | ось \(y\) |
Рисунок \(\PageIndex{7}\): Графики \(y = A\sin(t)\).
Рисунок \(\PageIndex{8}\): Графики \(y = A\cos(t)\).
Дополнительный материал – четные и нечетные функции
Существует более общий математический контекст для этих типов симметрии, и он связан с так называемыми четными и нечетными функциями.
Определения: четные и нечетные функции
Подробнее: Отношения и тождества в тригонометрии
Свойства функций косинуса
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Функция косинуса, обладающая особыми тригонометрическими свойствами.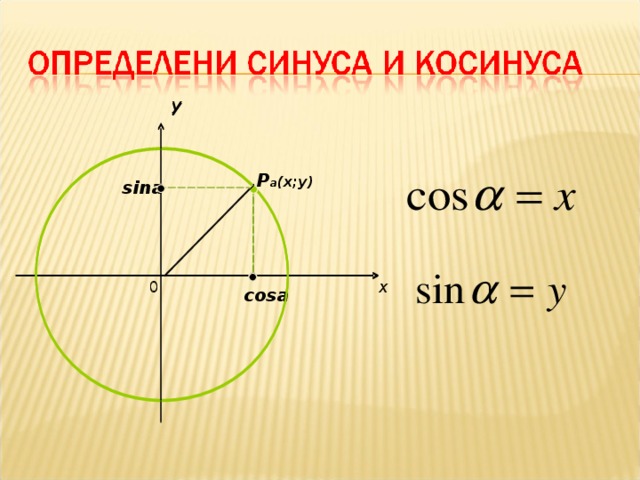 Некоторые из них перечислены ниже:
Некоторые из них перечислены ниже:
Подробнее: Область определения и диапазон тригонометрической функции
Графики функции косинуса
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Из приведенного выше изображения видно, что cosx = OQ/OP 1 = ОК. Из-за изменения x значение косинуса также меняется в зависимости от вариант по длине OQ. Ниже приведены некоторые случаи вариации:
Вариации функции косинуса
Случай 1: Изменение OQ в первом квадранте
Предположим, что изначально P находится на горизонтальной оси.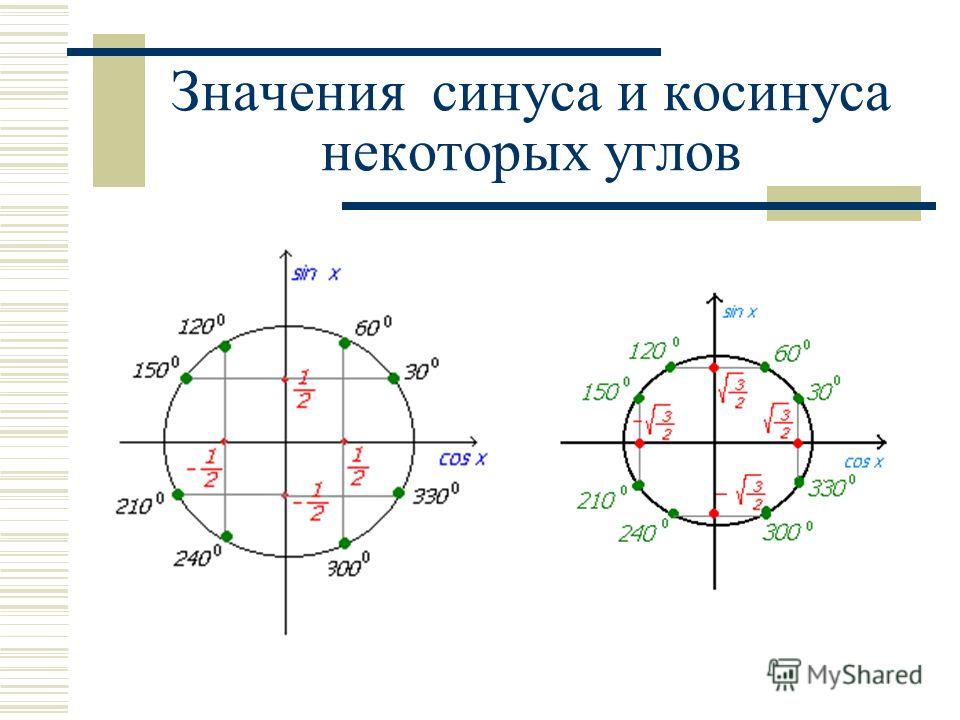 Рассмотрим движение P на 90° или π/2 рад. Длина OQ уменьшилась с начального значения 1 (если значение x равно 0 рад) до конечного значения 0 (если значение x равно π/2 рад).
Рассмотрим движение P на 90° или π/2 рад. Длина OQ уменьшилась с начального значения 1 (если значение x равно 0 рад) до конечного значения 0 (если значение x равно π/2 рад).
Случай 2: Изменение OQ во втором квадранте
В этом случае P перемещается из положения 90° в положение 180°. В этой фазе длина OQ увеличивается, а значение косинуса уменьшается от значения 0° при 90° до минимума -1 при 180°.
Подробнее: Значение log1 до 10
Случай 3. Изменение OQ в третьем квадранте
В этом случае P перемещается от 180° до 270°, поэтому длина OQ уменьшается. Поскольку направление вдоль отрицательной оси y, фактическое значение cosx увеличивается с -1 до 0. Таким образом, значение косинуса для угла x увеличивается.
Случай 4: изменение OQ в четвертом квадранте
В этом случае P изменяется от 270* до 360*, поэтому OQ увеличивается с 0 до 1. Длина OQ увеличивается с увеличением алгебраического значения OQ. Таким образом, значение косинуса для угла x увеличивается.
Таким образом, значение косинуса для угла x увеличивается.
Эти варианты можно изобразить на графике. Горизонтальная ось представляет входную переменную x как угол, а вертикальная ось представляет значение функции косинуса для x. Итак, график строится так, как показано ниже:
График функции косинуса
Подробнее: Формула и интеграция
Вещи. основание/гипотенуза.
Читайте также: Введение в тригонометрию: отношения, тождества и дополнительные углы
Примеры вопросов
Вопросы. Как косинус помогает в тригонометрии? (2 балла)
Отв. В прямоугольном треугольнике синус угла равен длине стороны, противоположной длине гипотенузы. При этом косинус угла будет равен длине прилежащего катета гипотенузы.
Вопрос. Мужчина застрял на вершине горящего здания. Спасатели приставили к зданию лестницу, которая составляет угол 60° с землей. Длина лестницы 70 футов. На каком расстоянии лестница от стены? (2 балла)
Отв. Так как cos 60* = 1/2,
Лестница будет считаться гипотенузой.
Итак, По формуле cosx = прилежащая сторона/гипотенуза = основание/гипотенуза, где x угол
cos 60* = основание/70
1/2 = база/70
база = 35 шт.
Вопросы. Докажите значение cos 60* = 1/2, используя формулу косинуса cos 2 x. (2 балла)
Отв. Чтобы доказать, мы будем использовать формулу косинуса двойного угла, которая задается как cos2x = 2cos2x-1 и значение косинуса для угла 30 *. Отсюда имеем
cos 60* = cos(2×30*)
cos 60* = 2cos 2 (30*)-1
cos 60* = 2(√3/2) 2 -1 as cos 30* = √3/2
cos 60* = 3/2 — 1
cos 60* = 1/2
Таким образом, мы доказали cos60* = 1/2.
Вопрос. Найдите значение x, если cos -1 (√3/3) = x, используя формулу арккосинуса. (2 балла)
Отв. Согласно вопросу,
cox = смежная сторона/гипотенуза
cos-1 является обратной функцией cosx
Как мы знаем,
cos(π/9) = √3/3
Так как π /9 ∈ [0, π], cos-1(√3/3) = π/9
Итак, значение x равно π/9.
Вопрос. Найдите cos -1 , если (-1/2). (2 балла)
Отв. Как мы знаем,
cos-1(-x) = cos-1x
Следовательно, cos -1 (-1/2) = π-cos-11/2
cos -1 ( -1/2) = π-π/3
cos -1 (-1/2) = 2π/3
Итак, значение cos -1 равно 2π/3.
Вопрос. Прилежащая сторона косинуса прямоугольного треугольника равна 24 см. Гипотенуза равна примерно 30 см. Чему равен угол косинуса треугольника? (2 балла)
Отв. дан, смежная сторона = основание = 24 см
Гипотеназа = 30 см
cosθ = соседняя сторона/гипотенуза = основание/гипотенуза
cosθ = 24/30
cosθ = 0,8
cosθ = 4/5032
vduct -14/5
Вопрос. Докажите sin 2 θ + cos 2 θ = 1. (3 балла)
(3 балла)
Ответ. Пусть a, b, c — длины прямоугольного треугольника
sinθ = b/c = противолежащая сторона/гипотенуза
cosθ = a/c = смежная сторона/гипотенуза
sin 2 θ + cos 2 θ = b 2 90 8 8 9098 2 /C 2
SIN 2 θ + COS 2 θ = A 2 + B 2 /C 2
от Pith -PithagastaS 2
от PitHAGASAS 2
от PitHAGASAS 2
. 2 + б 2
а 2 + б 2 /с 2 = 1
Следовательно, sin 2 θ + cos 2 θ = 1
Таким образом, мы доказали вышеприведенное тригонометрическое тождество.
Вопрос. Является ли функция косинуса четной или нечетной и какова область определения функции косинуса? (2 балла)
Отв. Функция f(x) определяется как четная функция, если f(-x) = f(x) для всех x, и как нечетная, если f(-x) = -f(x) для всех x. Функция косинуса является четной функцией, потому что cos(-x) = cosx.
Функция f(x) определяется как четная функция, если f(-x) = f(x) для всех x, и как нечетная, если f(-x) = -f(x) для всех x. Функция косинуса является четной функцией, потому что cos(-x) = cosx.
Областью определения функции косинуса являются все действительные числа, так как cosx определен для всех действительных чисел R.
Периодические свойства синуса и косинуса Сопоставление в цифровой плюс печати
Добавить в список желаний
Джоан Кесслер
5,4 тыс. подписчиков
Включает Google Apps™
Учитель-автор указал, что этот ресурс включает ресурсы из Google Workspace (например, документы, слайды и т. д.).
Также входит в комплект
VIEW BUCKERLY
1014SAVE $ 23,75View Buckerly
1014 10.75View Buckerly
1014 10.75.0032
Этот набор безбумажных упражнений и тестов по тригонометрии привлечет и бросит вызов вашим ученикам и станет отличным дополнением к учебной программе по тригонометрии или предварительному исчислению.
39
Продукты
110,25 $Цена 110,25 $148,00Первоначальная цена 148,00$Сэкономьте 37,75 $0032
Независимо от того, какую учебную программу вы используете для PreCalculus, этот цифровой набор для Unit 4 Trigonometric Functions дополнит ваши занятия, а также заинтересует и бросит вызов вашим ученикам. Поскольку учебные программы различаются между школами и районами, я перечислил темы ниже в алфавитном порядке, чтобы сделать это Easie
18
Продукты
$ 48,95PRICE $ 48,95 $ 65,25. Действия и оценки с помощью PRINTABLES
Независимо от того, какую учебную программу вы используете для PreCalculus, этот безбумажный цифровой мега-набор из 131 заданий и тестов NO PREP дополнит ваши занятия, заинтересует и бросит вызов вашим ученикам в течение всего года и идеально подходит для дистанционного обучения. Click on the links above to see full descr
131
Products
$438.03Price $438.03$486.70Original Price $486.70Save $48.67
View Bundle
Описание
Стандарты
1
Обзоры
20
Q & A
1
больше от Joan Kessler. навыки, необходимые для достижения успеха. Деятельность носит аналитический характер и не включает в себя построение графиков. Учащиеся сортируют и сопоставляют функции синуса и косинуса с их периодом , амплитудой и фазовым сдвигом. На каждом слайде 6 задач, одна из которых синусоидальная, а другая косинусоидальная. Таким образом, учащиеся могут сортировать и сопоставлять 24 элемента головоломки на слайде с помощью функции перетаскивания этого интерактивного ресурса Google®. Включена черно-белая версия для печати.
Теперь вы можете назначить оба слайда или задать им сначала синус, а затем косинус. Студенты могут работать индивидуально или в группах. Некоторые задачи похожи друг на друга, что усложняет задачу. Части имеют буквенные коды для облегчения оценки.
Части имеют буквенные коды для облегчения оценки.
В комплекте:
____________________________________________________________________
Вам также может понравиться:
★ График. GOOGLE Slides
★ Trig: Графики и свойства функций тангенса, котангенса, секанса и косеканса Задание для самостоятельной оценки с помощью Google Forms™
★ Загадка идентификации TRIG с Google Slides
★ Интерактивный блок кружок Google Slides Ресурс
★ Интерактивный ноутбук TRIG. Синусно-косинусного лабиринта плюс HW
Синусно-косинусного лабиринта плюс HW
★ Дополнительные цифровые интерактивные ресурсы
★ Набор складных и интерактивных страниц блокнота для Trig и PreCalculus
_______________________________________________________
⇒ Нажмите здесь , чтобы стать подписчиком и первыми узнавать о моих бесплатных предложениях, распродажах и новых продуктах, разработанных, чтобы помочь вам преподавать, экономить время и вовлекать своих учеников. Знаете ли вы, , что вы можете вернуть 5% на будущие покупки, оставив отзыв? Ваше мнение очень ценится.
Если у вас есть какие-либо вопросы или комментарии, пожалуйста, свяжитесь со мной по электронной почте: [email protected].
УСЛОВИЯ ЛИЦЕНЗИИ: Покупка лицензии на этот ресурс предназначена для использования одним учителем только для его или ее учеников. Никакая часть этого ресурса не может быть передана коллегам или использована всем отделом, школой или округом без приобретения надлежащего количества лицензий. Пожалуйста, уважайте мой труд и не делитесь им.
Пожалуйста, уважайте мой труд и не делитесь им.
УСЛОВИЯ АВТОРСКОГО ПРАВА: © Джоан Кесслер, 2018–2021 гг. (distancemath.com™). Этот ресурс нельзя загружать в Интернет в любой форме, включая классные/личные веб-сайты или сетевые диски, если только сайт не защищен паролем и доступен только вашим учащимся.
#TpTdigital
CCSSHSF-TF.B.5
Выберите тригонометрические функции для моделирования периодических явлений с заданной амплитудой, частотой и средней линией.
Каковы свойства функций синуса и косинуса? – Sluiceartfair.com
по Вопросы пользователей
Мелл
Какими свойствами обладают функции синуса и косинуса?
Функции синуса и косинуса имеют несколько различных характеристик:
Какими свойствами обладает косинус?
Косинус — это тригонометрическая функция угла. Он обладает рядом свойств, таких как периодичность и четность. В контексте треугольника для указанного угла косинус — это отношение длины стороны, СМЕЖНОЙ к углу, к длине наибольшей стороны или ГИПОТЕНУЗЫ треугольника.
В чем разница между синусом, косинусом и тангенсом?
Косинус (часто сокращенно «cos») — это отношение длины стороны, примыкающей к углу, к длине гипотенузы. А тангенс (часто сокращенно «тан») — это отношение длины стороны, противоположной углу, к длине стороны, примыкающей. SOH → sin = «противоположное» / «гипотенуза»
Как узнать, когда использовать синус или косинус?
Правило синусов используется, когда нам даны либо а) два угла и одна сторона, либо б) две стороны и не заключенный между ними угол. Правило косинусов используется, когда нам даны либо а) три стороны, либо б) две стороны и угол между ними.
Правило косинусов используется, когда нам даны либо а) три стороны, либо б) две стороны и угол между ними.
Каковы характеристики функции синуса?
Функции синуса и косинуса имеют несколько отличительных характеристик: Это периодические функции с периодом 2π. Область определения каждой функции — (−∞, ∞), а диапазон — [−1,1]. График y = sin x симметричен относительно начала координат, потому что это нечетная функция.
Как преобразовать sin в cos?
Все треугольники имеют 3 угла, сумма которых составляет 180 градусов. Следовательно, если один угол равен 90 градусам, мы можем вычислить Sin Theta = Cos (90 – Theta) и Cos Theta = Sin (90 – Theta).
Что такое синус?
В математике синус — это тригонометрическая функция угла. Синус острого угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (гипотенуза ).
Для чего вы используете правило синусов?
Чтобы решить треугольник, нужно найти длины каждой из его сторон и всех его углов. Правило синусов используется, когда нам даны либо а) два угла и одна сторона, либо б) две стороны и не заключенный между ними угол. Правило косинусов используется, когда нам даны либо а) три стороны, либо б) две стороны и угол между ними.
Каковы характеристики графиков синуса и косинуса?
Функции синуса и косинуса имеют несколько отличительных характеристик:
Как построить график функции синуса?
Поскольку график синусоидальной функции строится на плоскости x–y, вы перепишете это как f(x) = sin x, где x — мера угла в радианах. Найдите значения домена и диапазона. Вычислите x-перехваты графика. Вычислите максимальную и минимальную точки графика. Нарисуйте график функции.
Найдите значения домена и диапазона. Вычислите x-перехваты графика. Вычислите максимальную и минимальную точки графика. Нарисуйте график функции.
Какое уравнение для косинуса?
В тригонометрии закон косинусов, также известный как формула косинуса или правило косинуса, связывает длины сторон треугольника с косинусом одного из его углов. Формула косинуса: cos θ = смежная / гипотенуза. а 2 = б 2 + с 2 — 2bc.cosA.
Какое уравнение составляет синусоидальный график?
Общее уравнение синусоидального графика: y = A sin(B(x – D)) + C. Общее уравнение косинусного графика: y = A cos(B(x – D)) + C. Пример : Имея преобразованный график синуса или косинуса, определите возможное уравнение.
Что означают sin cos и Tan?
Sin означает синус, cos означает косинус, а tan означает тангенс. Они используются в тригонометрии для нахождения длин сторон.
youtube.com/embed/EfdYqqIt1Lc?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Репетитор по математике — Функции — Теория
Репетитор по математике — Функции — Теория — Элементарные функцииЗдесь мы предполагаем, что вы знакомы с углами и как они измерено, в частности, с радиан . Если вы не уверены, вы можете посмотри на это примечание.
Существует несколько способов определения тригонометрических функций. Мы кратко вспомните два из них, основанные на геометрических представлениях. Тогда мы посмотрим на характеристики тригонометрических функций, вспомните некоторые триггер тождества, попробуйте сделать некоторые смысл их инверсий и заключаем с краткое примечание относительно секанса и косеканса.
Геометрические определения
Единица измерения. Пусть α — любой угол.
Рассмотрим единичный круг на плоскости и луч, идущий
от начала под углом α . Пусть ( x , y ) координаты пересечения луча и
единичный круг.
Затем мы определяем
Пусть ( x , y ) координаты пересечения луча и
единичный круг.
Затем мы определяем
Конечно, некоторые определения не имеют смысла, если x = 0, соответственно. г = 0,
Ясно, что тогда мы имеем
Функции sec( α ) (секанс) и csc( α ) (косеканс) был очень популярен в старые времена, когда людям еще приходилось вычислять вещи сами по себе, так как они упростили вычисления с помощью триггера функции. Сегодня они в основном забыты, и мы включаем их сюда для ради полноты. Мы вернемся к ним в конце этого раздела.
Обратите внимание, что при таком определении все эти функции 2π-периодический, при ближайшем рассмотрении тангенс и котангенс равны π-периодический.
Прямоугольный треугольник. Пусть α — угол от интервал (0,π/2). Рассмотрим произвольный прямоугольный треугольник с другой угол равен α . Тогда у нас есть следующие определения:
Эти функции связаны теми же формулами, что и выше. Как мы продлеваем
эти определения под любым углом α ? Сначала мы определяем
sin(0)=0,cos(0)=1,sin(π/2)=1,cos(π/2)=0,
Как мы продлеваем
эти определения под любым углом α ? Сначала мы определяем
sin(0)=0,cos(0)=1,sin(π/2)=1,cos(π/2)=0,
Для α от [π/2,π] мы определяем sin( α ) = sin(π − α ) а также cos( α ) = -cos(π — α ).
Для α от [п, 2п] мы определяем sin( α ) = -sin( α — π) а также cos( α ) = -cos(2π — α ).
Таким образом, мы получаем синус и косинус на [0,2π], то расширяем их для всех углов, повторяя этот основной период. Остальные функции могут быть все определяется с помощью синуса и косинуса и приведенных выше формул.
В заключение мы напомним значения синуса и косинуса для популярные ракурсы:
Eсть простой способ запомнить их, используя левая рука.
Еще одно практическое замечание, вместо того, чтобы писать
[sin( x )] n мы обычно пишем
sin n ( x ), аналогично для других триггерных функций.
Свойства тригонометрических функций
г. Синус. Домен:
D (грех) = &реал;.
График:
Функция непрерывна в своей области определения, 2π-периодический, ограниченный, и симметричным, а именно нечетным, так как имеем sin(- x ) = -sin( x ). У нас также есть
sin( x + π) = −sin( x ), sin( x + π/2) = cos( x ), sin( x — π/2) = −cos( x ).
Из периодичности имеем
sin( x + 2 k π) = sin( x ), sin( x + (2 k + 1)π) = −sin( x ).
Нулевыми точками синуса являются точки вида k π, где k — любое целое число; это также точки перегиба. Локальные экстремумы находятся в точках π/2 + k π.
Что касается пределов на концах области, пределов синуса на бесконечности и
отрицательной бесконечности не существует.
Производная:
[sin( x )]′ = cos( x ).
Косинус. Домен:
D (cos) = &реал;.
График:
Функция непрерывна в своей области определения, 2π-периодическая, ограниченная, и симметричным, а именно четным, так как имеем cos(− x ) = cos( x ). У нас также есть
cos( x + π) = −cos( x ), cos( x + π/2) = −sin( х ), cos( x — π/2) = sin( x ).
Из периодичности имеем
cos( x + 2 k π) = cos( x ), cos( x + (2 k + 1)π) = −cos( x ).
Нулевые точки косинуса — это точки вида π/2 + k π, где k — любое целое число; это тоже точки перегиб. Локальные экстремумы находятся в точках к π.
Что касается пределов на концах области, пределов косинуса на бесконечности
и отрицательной бесконечности не существует.
Производная:
[cos( x )]′ = −sin( x ).
Тангенс. Домен:
График:
Функция непрерывна в своей области определения, π-периодическая, неограниченная, и симметричным, а именно нечетным, так как имеем загар (− x ) = −загар ( x ). У нас также есть
загар( x + π) = загар( x ), тангенс (π — x ) = -тангенс ( х ).
Нулевыми точками касательной являются точки вида к π, где к любое целое число; это также точки перегиба. нет местных экстремумы.
Что касается пределов на концах области, пределов касательной в бесконечности и отрицательная бесконечность не имеют смысла, так как домен не включает никаких окрестности бесконечности или отрицательной бесконечности. Пределы на конечных точках домена не существует, но у нас там односторонние лимиты:
Производная:
[tan( x )]’ = 1/cos 2 ( x ).
Котангенс. Домен:
График:
Функция непрерывна в своей области определения, π-периодическая, неограниченная, и симметричным, а именно нечетным, так как имеем детская кроватка (− x ) = − кроватка ( x ). У нас также есть
детская кроватка( x + π) = детская кроватка( x ), раскладушка (π − х ) = — раскладушка ( х ).
Нулевыми точками котангенса являются точки вида π/2 + k π, где k — любое целое число; это также точки перегиба. Локальных экстремумов нет.
Что касается пределов на концах области, пределов котангенса на бесконечности и отрицательная бесконечность не имеют смысла, так как домен не включает никаких окрестности бесконечности или отрицательной бесконечности. Пределы на конечных точках домена не существует, но у нас там односторонние лимиты:
Производная:
[кот( х )]’ = -1/sin 2 ( х ).
Триггерные идентификаторы
Сначала некоторые популярные тождества для синуса и косинуса.
Следующие тождества менее популярны, но иногда они очень полезны.
Синус и косинус также можно получить (или даже определить) с помощью экспонент и комплексные числа.
Наконец, иногда этот трюк тоже полезен.
У нас очевидная проблема, когда C 2 = 0. Тогда мы можем взять φ = π/2 если C 2 > 0 а также φ = −π/2 если C 2 < 0,
Теперь некоторые популярные тождества для тангенса и котангенса.
Поскольку синус и косинус могут быть выражены с помощью комплексных экспонент, то одно и то же верно для тангенса и котангенса.
Наконец, мы покажем некоторые формулы, связывающие синус/косинус и тангенс.
Обратные тригонометрические функции
Когда мы смотрим на графики выше, мы сразу видим, что ни один из четырех основные триггерные функции 1-1, поэтому у них нет инверсий. С другой стороны, с практической точки зрения было бы чрезвычайно полезно нечто обратное, и действительно, люди приписывали углы сторонам треугольников задолго до математики придумали понятие обратного. Для этого правильно, мы используем обычный трюк, мы ограничим триггерные функции до интервалы, на которых они уже 1-1. Выберем интервалы так, чтобы они как можно больше (чтобы они покрывали весь диапазон), а также чтобы они давали «разумные» углы, т.е. около 0. Действительно, больше Практично узнать, что угол в треугольнике равен 30 градусам, а затем узнать что это 750 градусов (на самом деле мы должны использовать радианы, но градусы легче представить и напечатать в Интернете, поэтому здесь я сделал исключение).
Обратные тригонометрические функции. Они определяются следующим образом. Сначала мы ограничиваем четыре тригонометрические функции интервалами, как указано.
Сначала мы ограничиваем четыре тригонометрические функции интервалами, как указано.
Затем рассмотрим обратные к этим ограничениям. Они называются дуги синус (обозначается арксинус), арккосинус (обозначается арккосинус), арккосинус тангенс (обозначается arctan) и арккотангенс (обозначается arccot). Графики этих функций здесь:
Перечислим теперь основные свойства этих обратных триггерных функций. Они есть все непрерывны, монотонны и ограничены.
Примечание: Многие авторы (и большинство производителей калькуляторов) на самом деле используют
другое обозначение, а именно sin -1 ( x ), cos -1 ( x ) и т. д. Это обозначение чрезвычайно вводит в заблуждение и
многие студенты действительно видят, по общему признанию, сильное сходство между
sin −1 ( x ) и, скажем,
грех 2 ( x ) для квадрата
синуса; логически они затем ожидают, что
sin −1 ( x ) равно
на самом деле 1/sin( x ). Конечно, обратному синусу и
1/sin( x )
это совсем разные функции. Хотя есть достаточно хороший
обоснование этого обозначения (см. наше изложение
обратные функции в теории —
Реальные функции), очень жаль из-за этих недоразумений.
Поскольку существует вполне приемлемая альтернатива, которая также широко известна,
а именно эти дуги, мы всегда будем использовать их здесь.
Конечно, обратному синусу и
1/sin( x )
это совсем разные функции. Хотя есть достаточно хороший
обоснование этого обозначения (см. наше изложение
обратные функции в теории —
Реальные функции), очень жаль из-за этих недоразумений.
Поскольку существует вполне приемлемая альтернатива, которая также широко известна,
а именно эти дуги, мы всегда будем использовать их здесь.
Примечание: Вернемся к исходному вопросу: нам дано число х , и мы хотим найти число х , удовлетворяющее, скажем, sin( x ) = y . Если это x из региона в которое мы только что ограничили синусом, то у нас есть решение x = arcsin( y ). Но что, если по какой-то причине нам нужно х из другой части реальной линии? Или взято из другую точку зрения, если мы ограничим синус другим разумным интервала, какова будет формула обратной функции к такому ограниченный синус? (И, конечно, косинус и т. д.) Следующие формулы верны:
Есть очень интересные формулы, связывающие триг-функции и их инверсии. Они редко используются, но они такие милые, что мы не можем не поставить их здесь.
Секанс и косеканс
Мы лишь кратко рассмотрим их свойства. Графики:
Производные:
Гиперболические функции
Назад к теории — Элементарно
функции
Основные свойства тригонометрических функций — x-engineer.org 92(\alpha)=1\]
Далее мы рассмотрим значения тригонометрических функций для некоторых основных углов: 30°, 45° и 60°. °.
°.
Сначала возьмем квадрат со стороной 1. Единица измерения длины стороны в данном примере не имеет значения.
Изображение: Квадрат со стороной 1
Если провести диагональ из точки А в точку С, то получится прямоугольный треугольник (ADC). Гипотенуза имеет длину квадратного корня из 2. Мы находим это, применяя теорему Пифагора: 9\circ)&=\frac{\text{смежный}}{\text{напротив}}&=\frac{AD}{CD}=1
\end{split} \end{equation*} \]
Для углы 30° и 60°, будем использовать равносторонний треугольник со стороной 1. То же самое, для данного конкретного примера единица измерения длины стороны не имеет значения.
Изображение: Квадрат со стороной 1
Проведя высоту треугольника, отрезок BD, мы получим два равных отрезка, AD и DC, которые имеют длину 1/2.
9\circ)&=\frac{\text{смежный}}{\text{напротив}}&=\frac{BD}{CD}=\sqrt{3}\end{split} \end{equation*} \ ]
Углы 30°, 45° и 60° очень распространены в геометрии, поэтому очень важно знать, как вычислять для них тригонометрические функции.

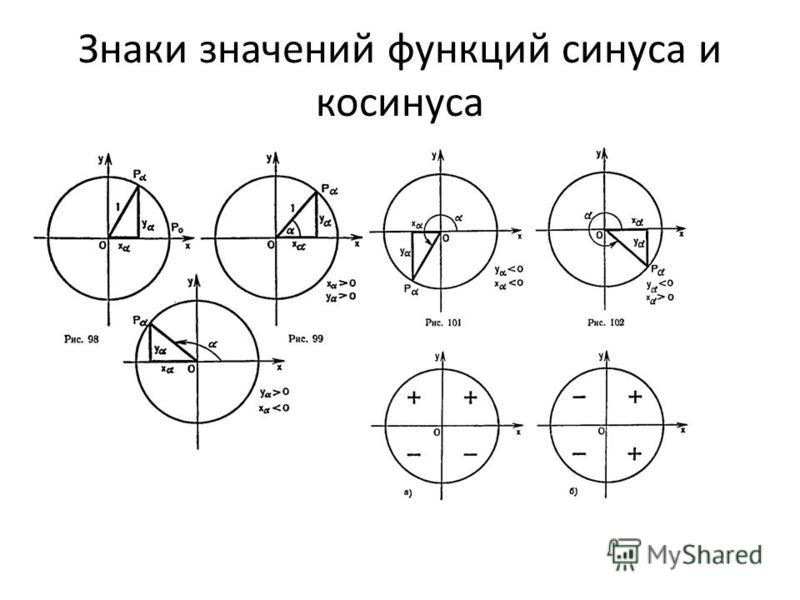 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.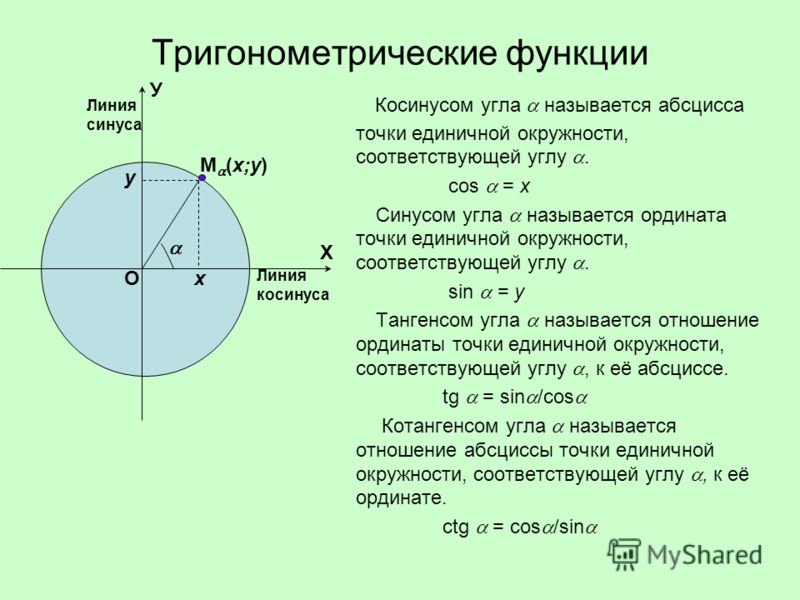 д.
д.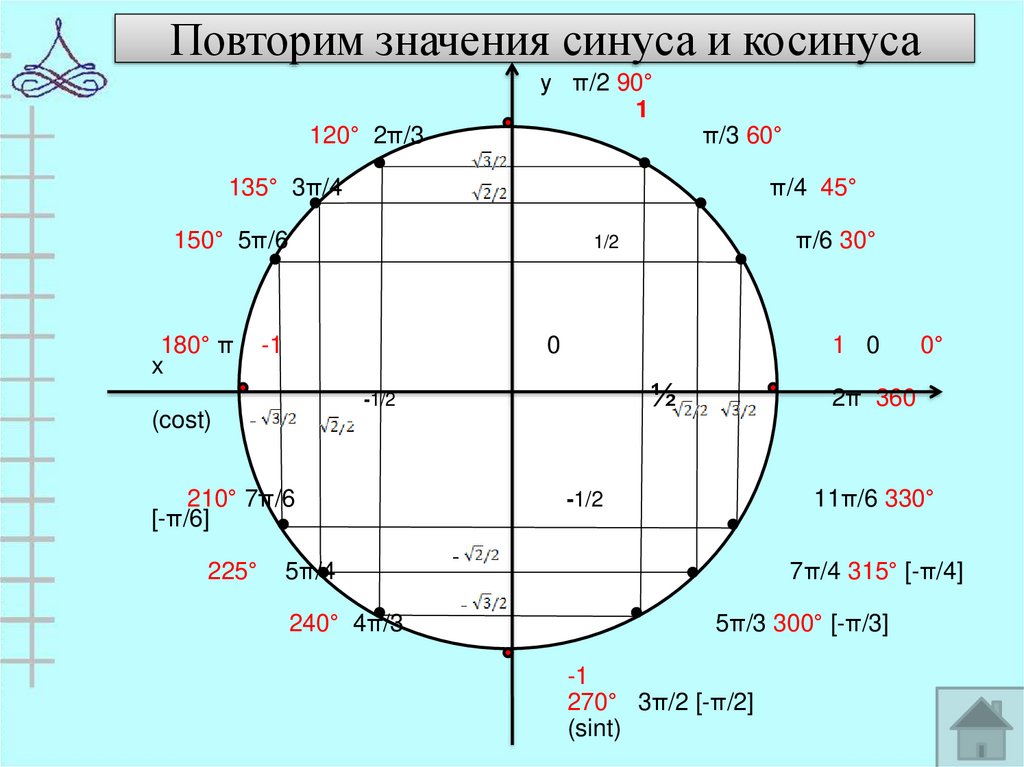 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Косинус угла $\alpha $ — это отношение прилежащего катета к гипотенузе:
Косинус угла $\alpha $ — это отношение прилежащего катета к гипотенузе:
 {2}}=1+1=2 \\ AC & =\sqrt{2} \\ \end{align}\]
{2}}=1+1=2 \\ AC & =\sqrt{2} \\ \end{align}\] {2}}=4-1=3 \\ l &=\sqrt{3} \\ \end{align}\]
{2}}=4-1=3 \\ l &=\sqrt{3} \\ \end{align}\] \circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти. \circ $. Но когда $\sin \alpha =0,6$, мы уже не можем назвать угол $\alpha $ (хотя всегда можем построить такой угол).
\circ $. Но когда $\sin \alpha =0,6$, мы уже не можем назвать угол $\alpha $ (хотя всегда можем построить такой угол). \circ $, поэтому $\sin \alpha \gt 0$. Следовательно
\circ $, поэтому $\sin \alpha \gt 0$. Следовательно {2}}\alpha = \\ & =1-\frac{1}{26}=\frac{25}{26} \\ \sin \alpha&=\pm \frac{5}{\sqrt{26}} \end{align}\]
{2}}\alpha = \\ & =1-\frac{1}{26}=\frac{25}{26} \\ \sin \alpha&=\pm \frac{5}{\sqrt{26}} \end{align}\] Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Найдите тангенс угла $ABC$, изображённого на координатной сетке: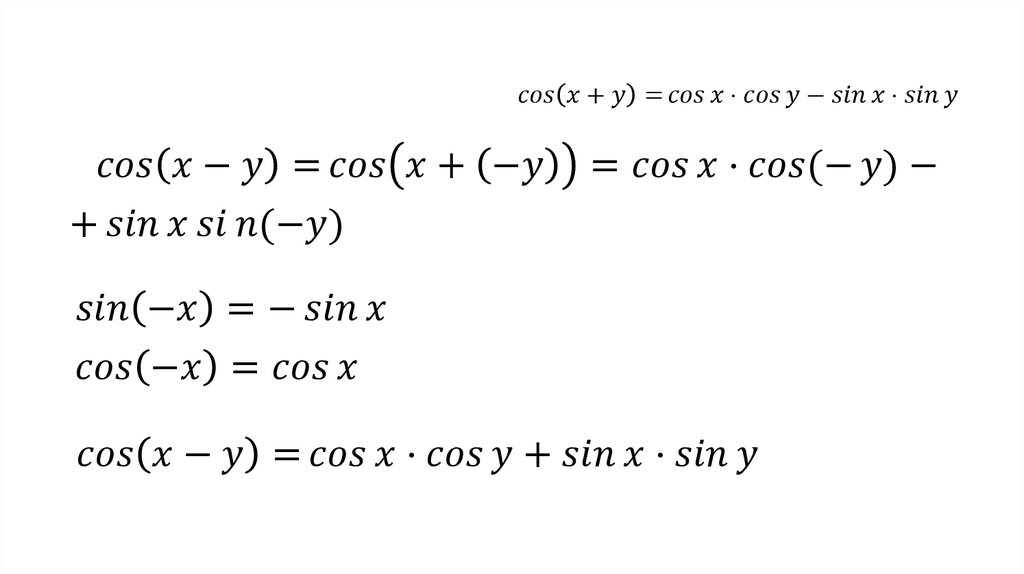
 Но с тем же успехом можно считать, что сторона квадрата $a$:
Но с тем же успехом можно считать, что сторона квадрата $a$: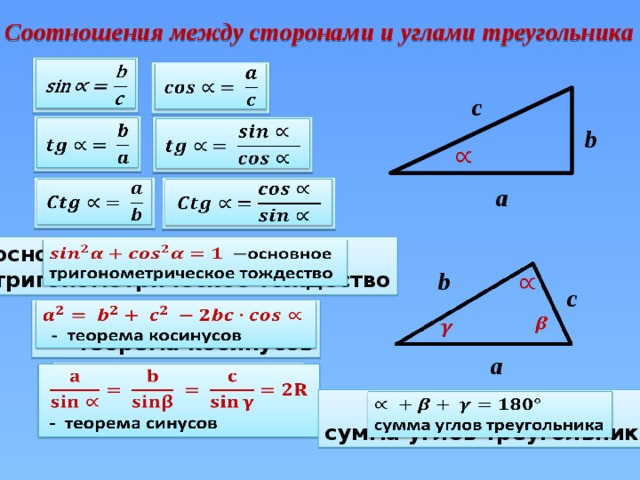

 2=1$.
2=1$. Не обходятся без синусов и косинусов геодезисты и даже путешественники. В географии эти понятия применяют для измерения расстояний между объектами и в спутниковых навигационных системах.
Не обходятся без синусов и косинусов геодезисты и даже путешественники. В географии эти понятия применяют для измерения расстояний между объектами и в спутниковых навигационных системах. 
 Пусть, это будут точки F и G. Определим, каким значениям $t$ соответствуют точки $F$ и $G$ на рисунке.
Пусть, это будут точки F и G. Определим, каким значениям $t$ соответствуют точки $F$ и $G$ на рисунке.
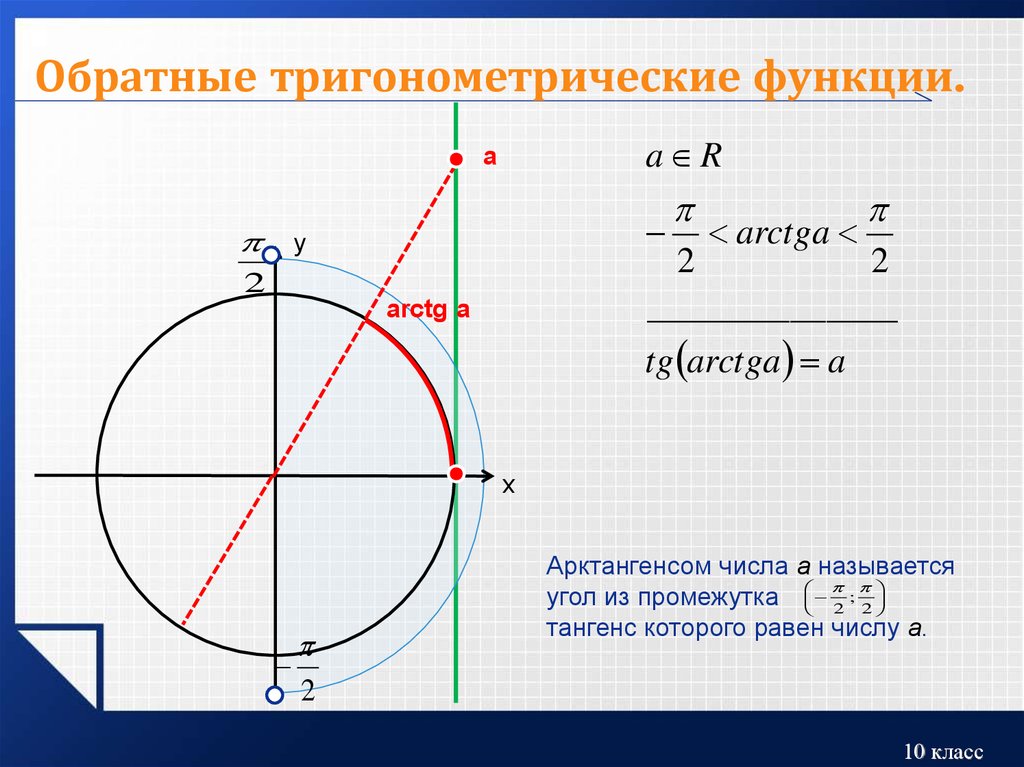

 Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов.
Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов. е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение
е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение 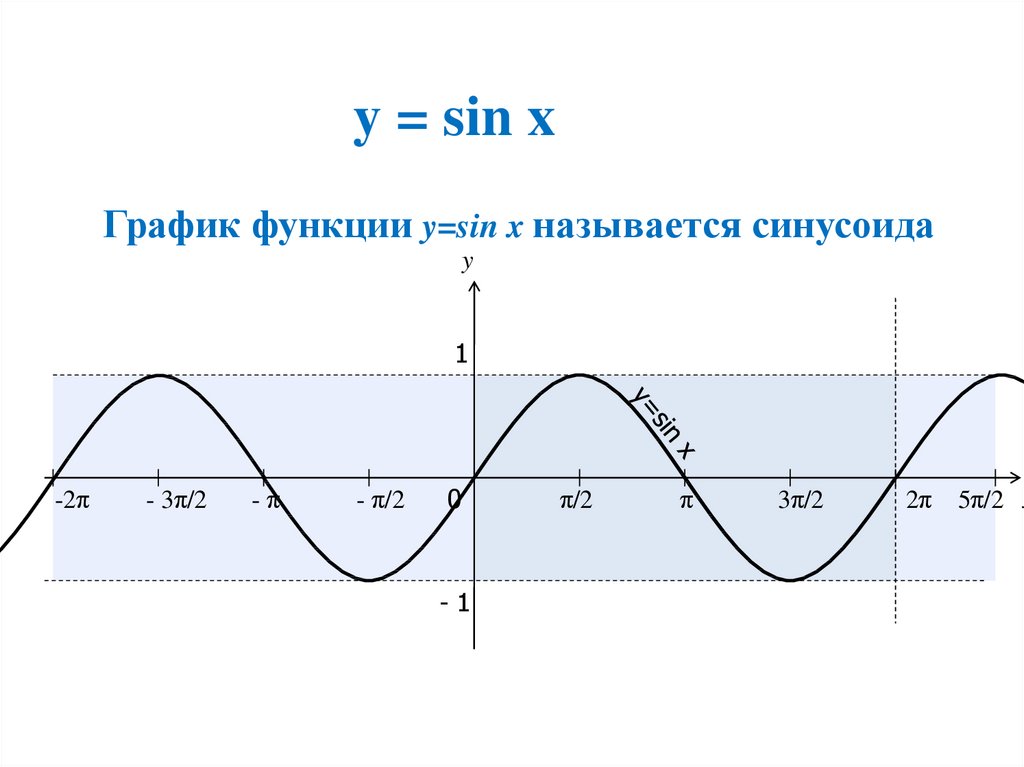

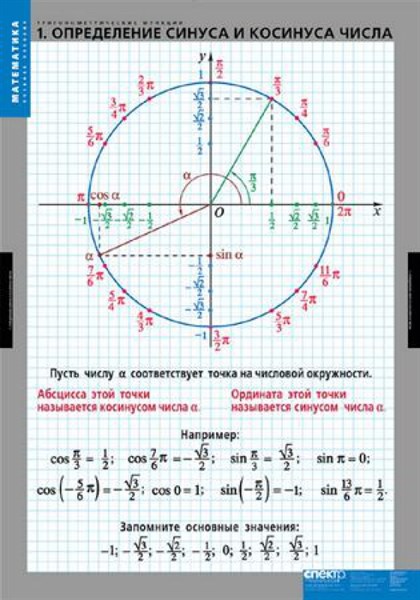 Уравнение примет вид т. e. Это уравнение имеет корни, если
Уравнение примет вид т. e. Это уравнение имеет корни, если
 Данная функция определена для всех и
Данная функция определена для всех и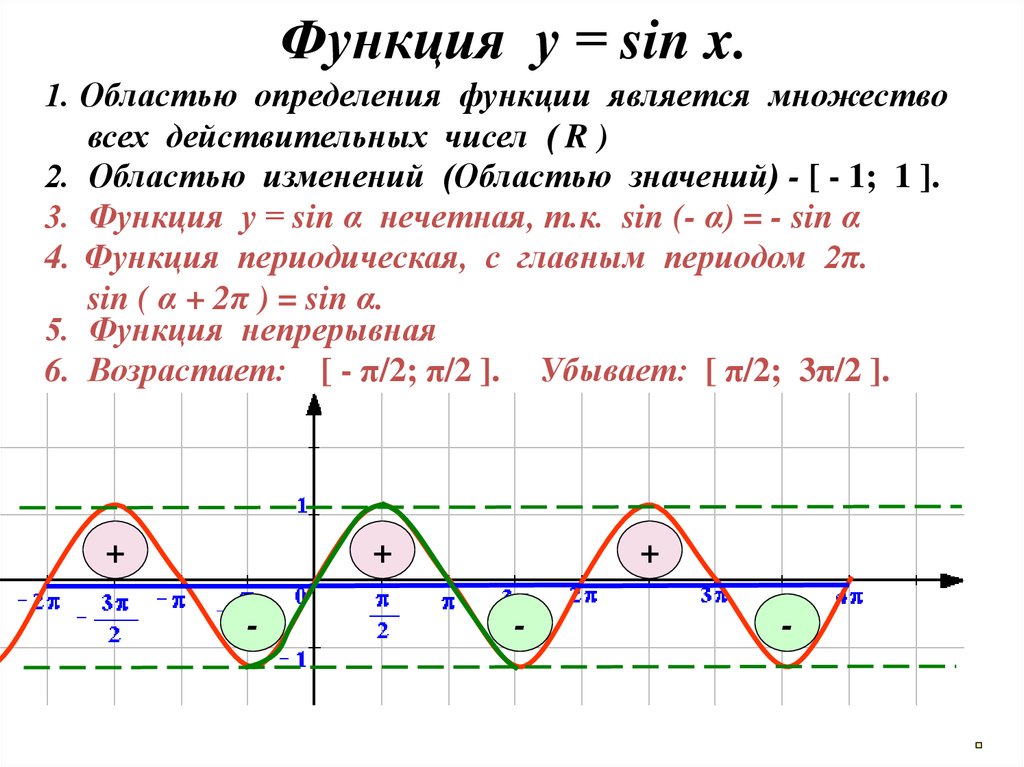

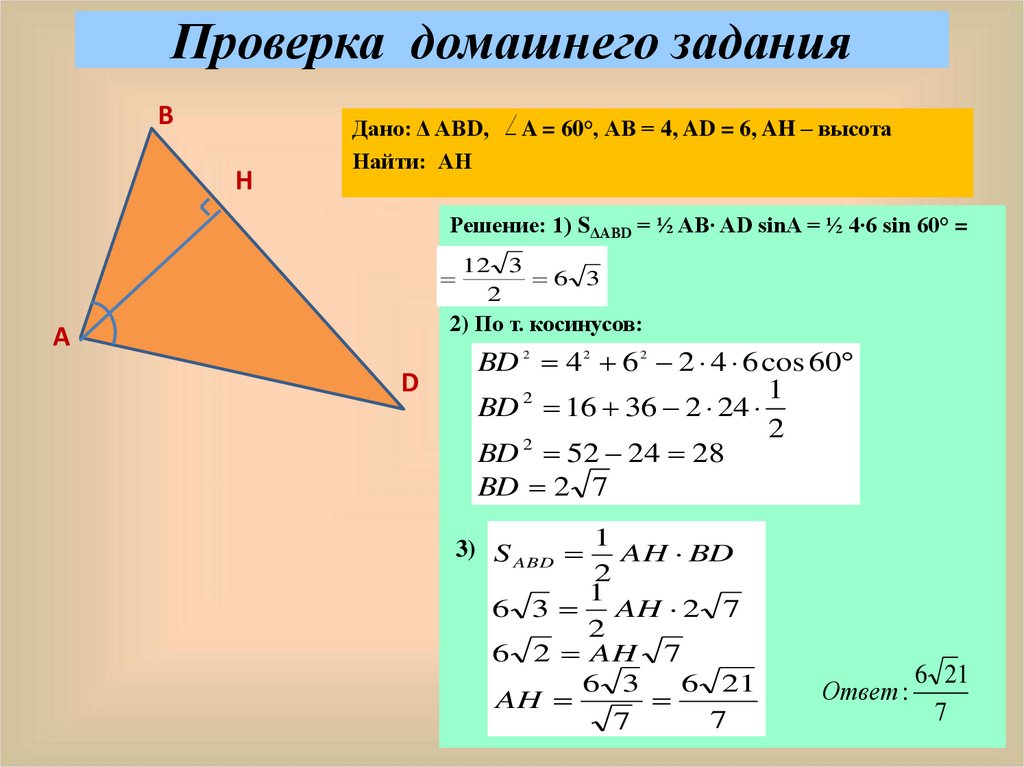 д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).
д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).
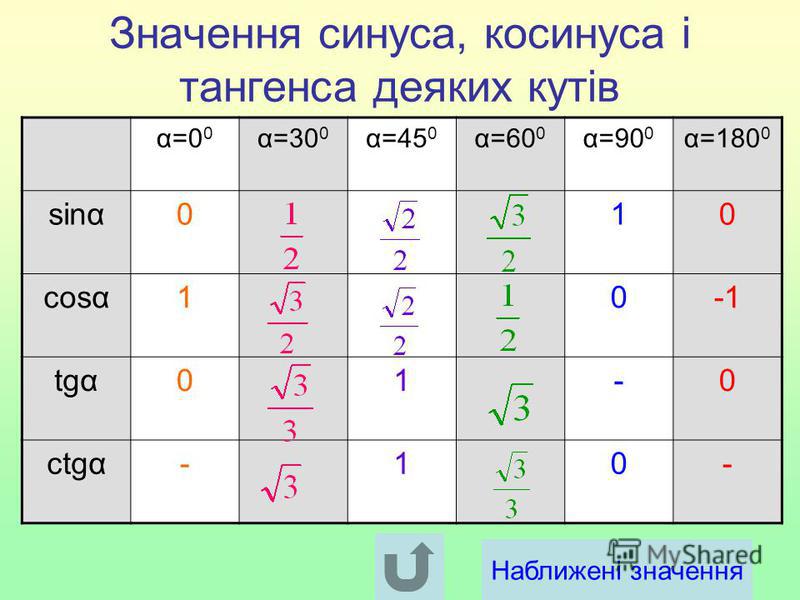 Однако проще воспользоваться следующей формулой:
Однако проще воспользоваться следующей формулой:
 Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .
Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .
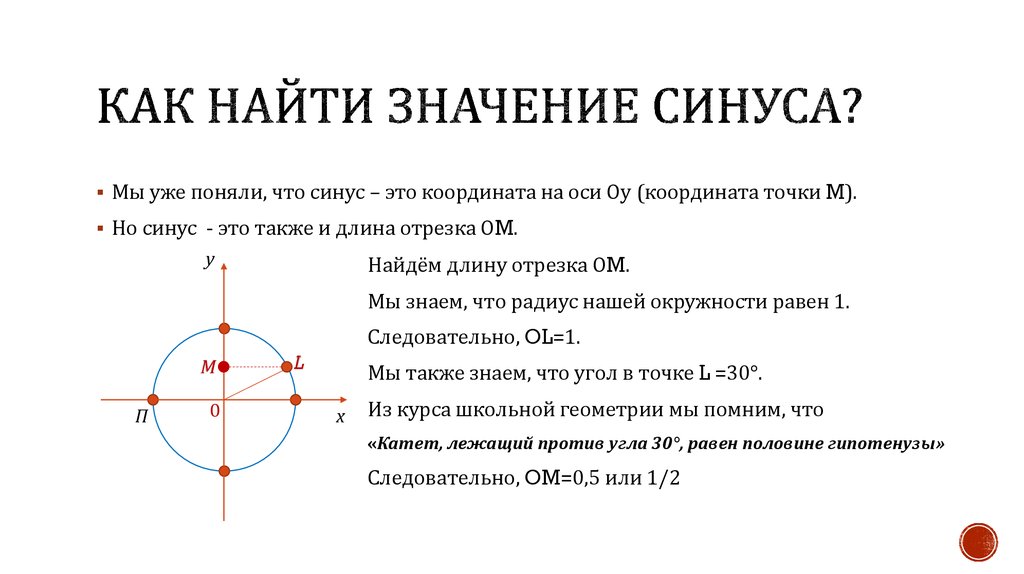 Например,
Например,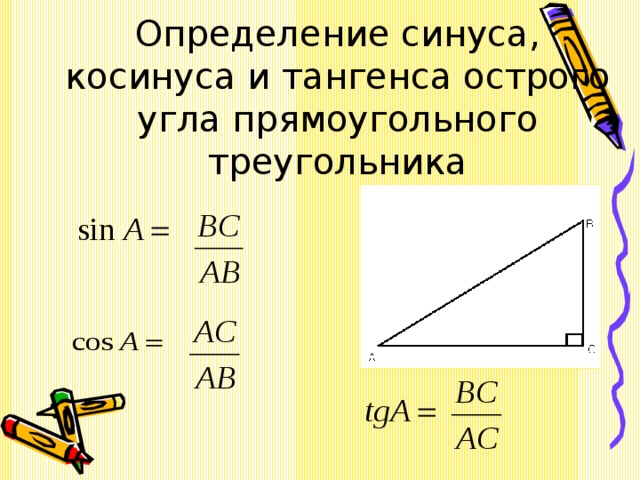
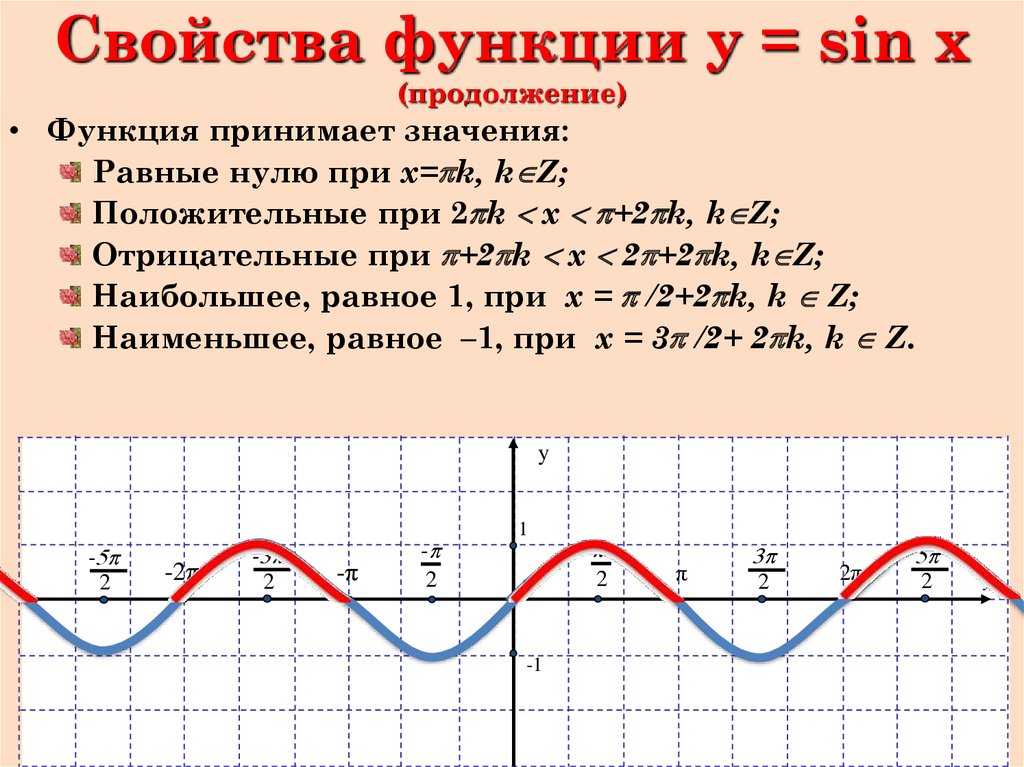 График
График 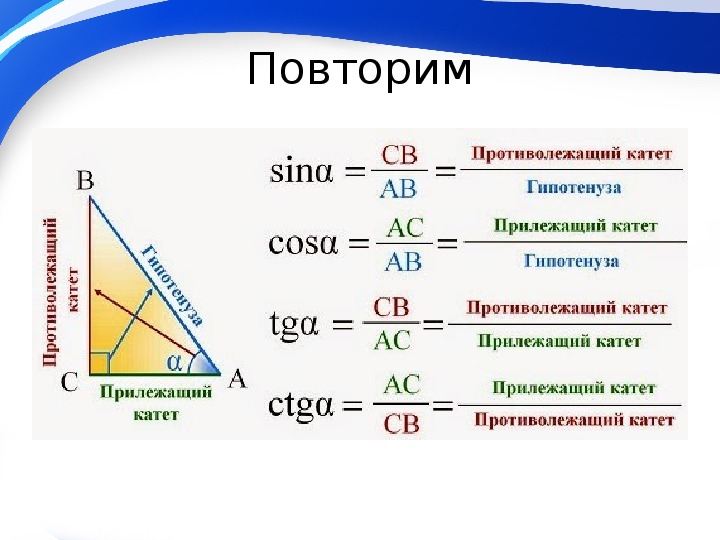 е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.
е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.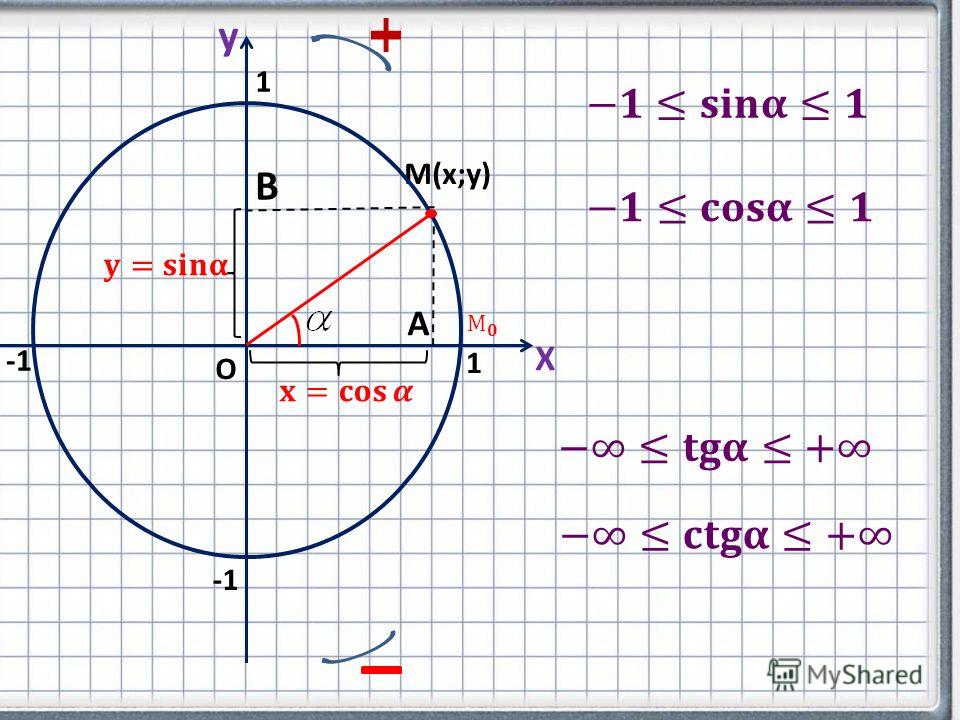
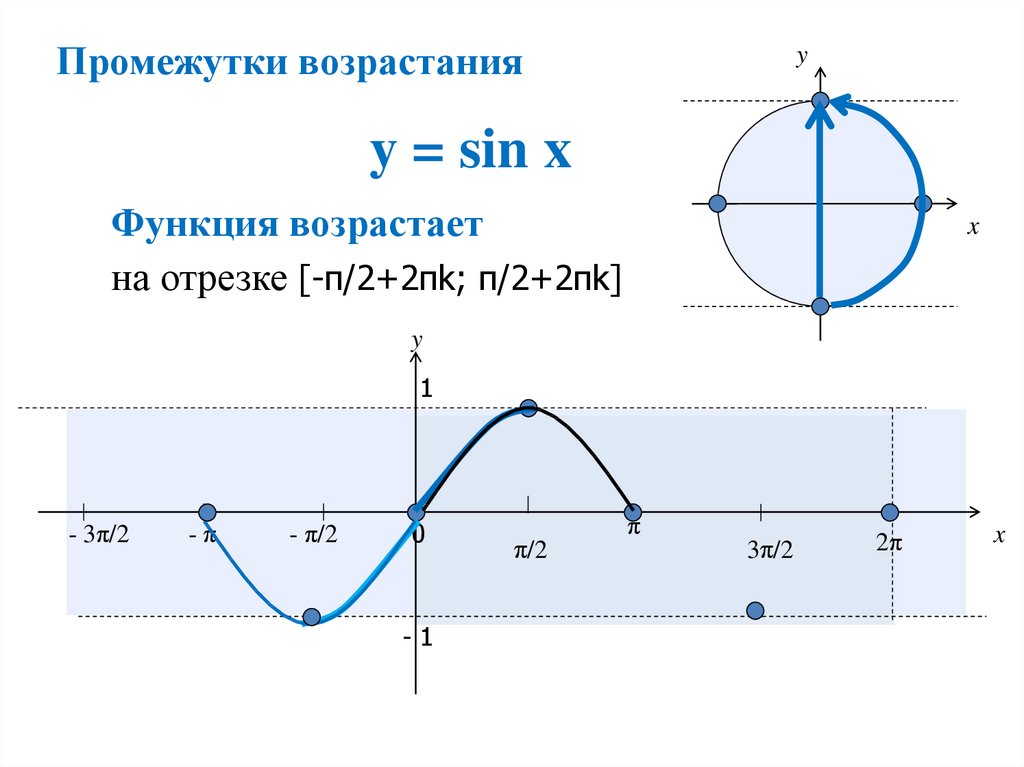 Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.
Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии. Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.
Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.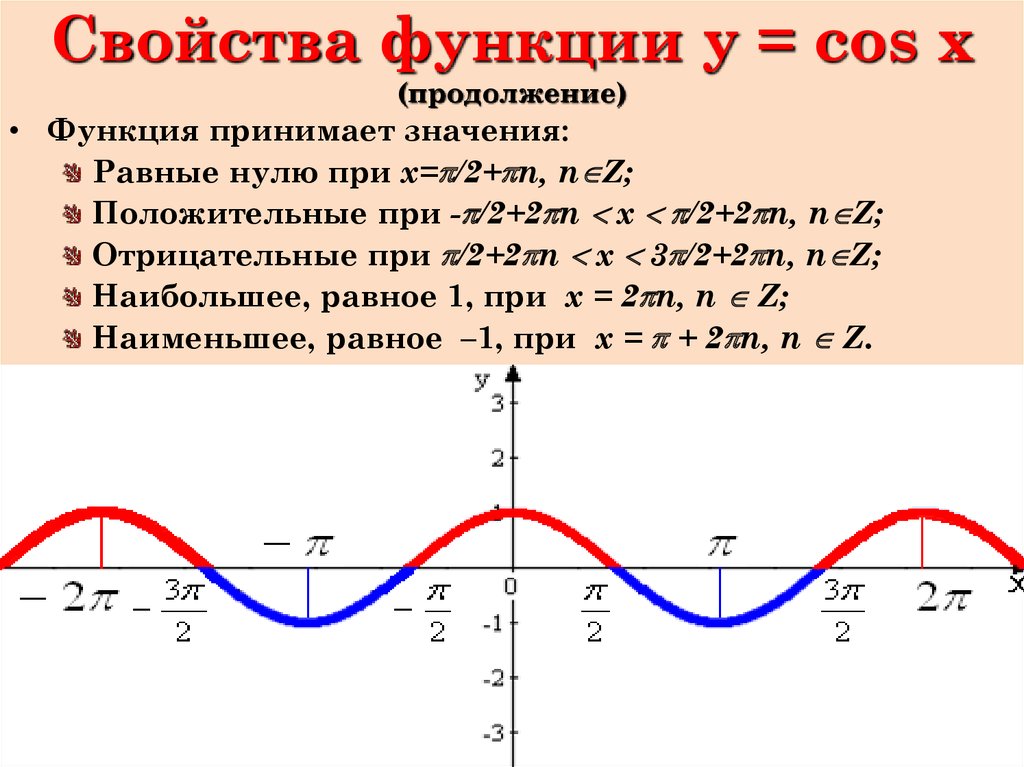 84).
84).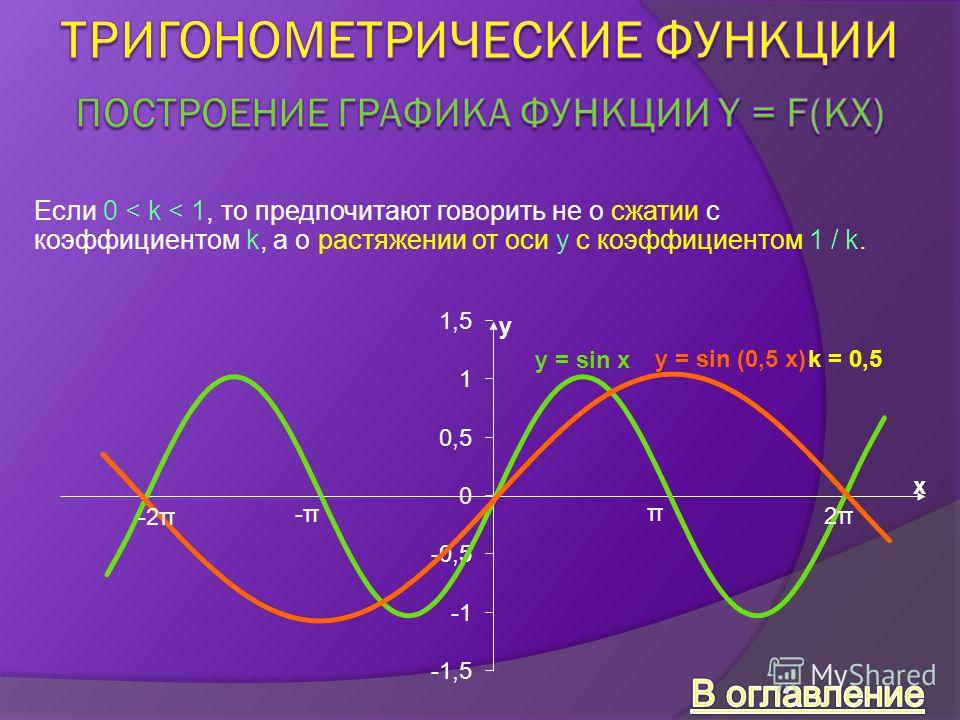 Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t <0. Рассмотрим примеры.
Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t <0. Рассмотрим примеры. При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения.
При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения. Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку , надо на такое же
Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку , надо на такое же
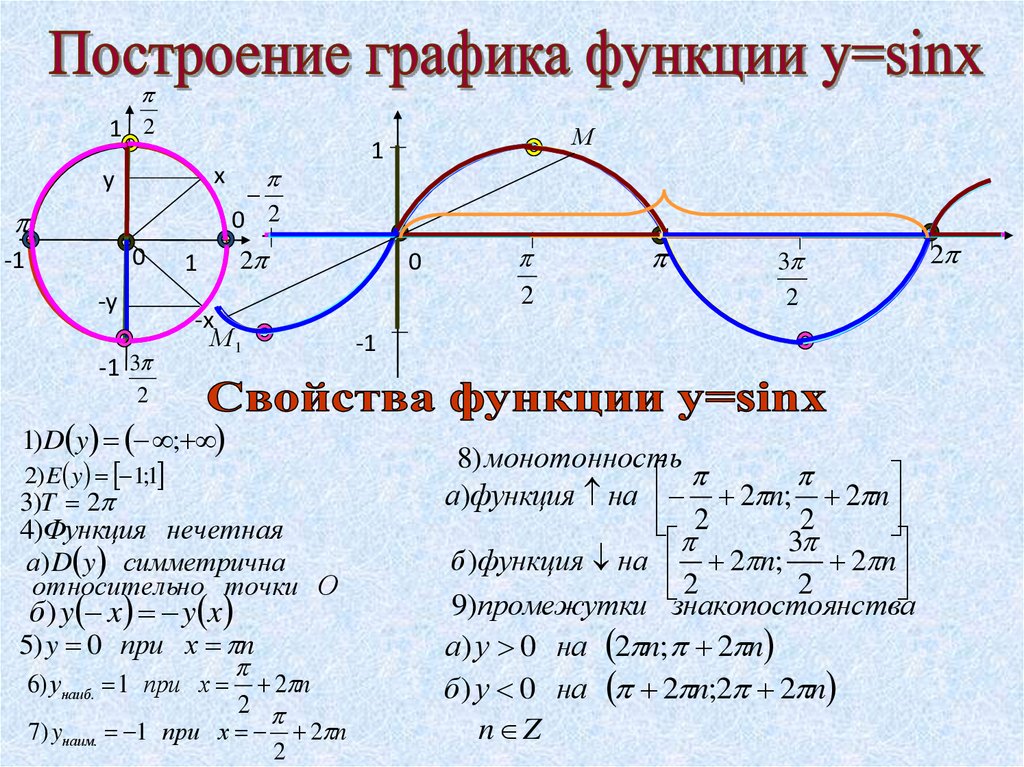 Необходимо доказать тождества
Необходимо доказать тождества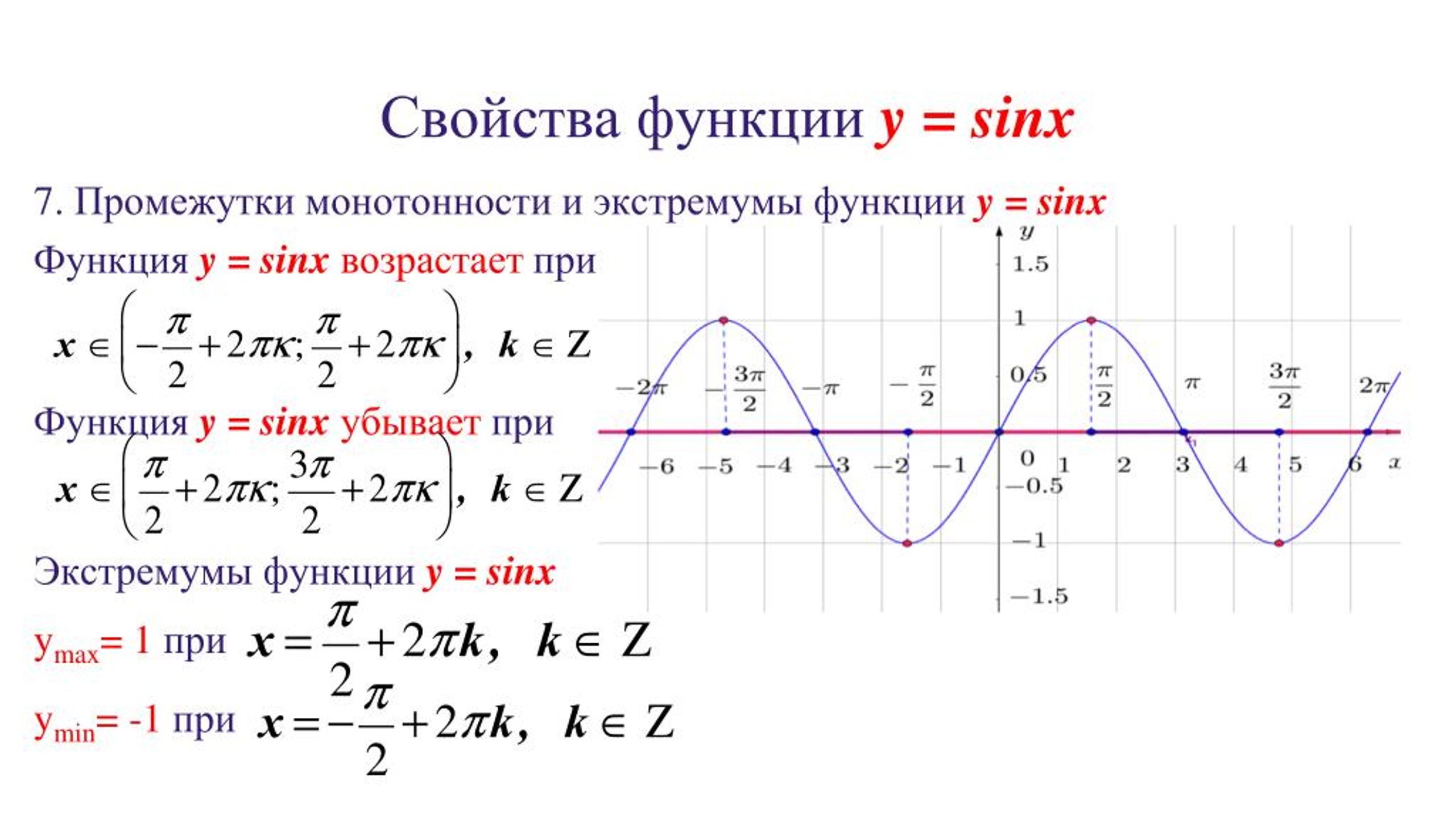 Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.
Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.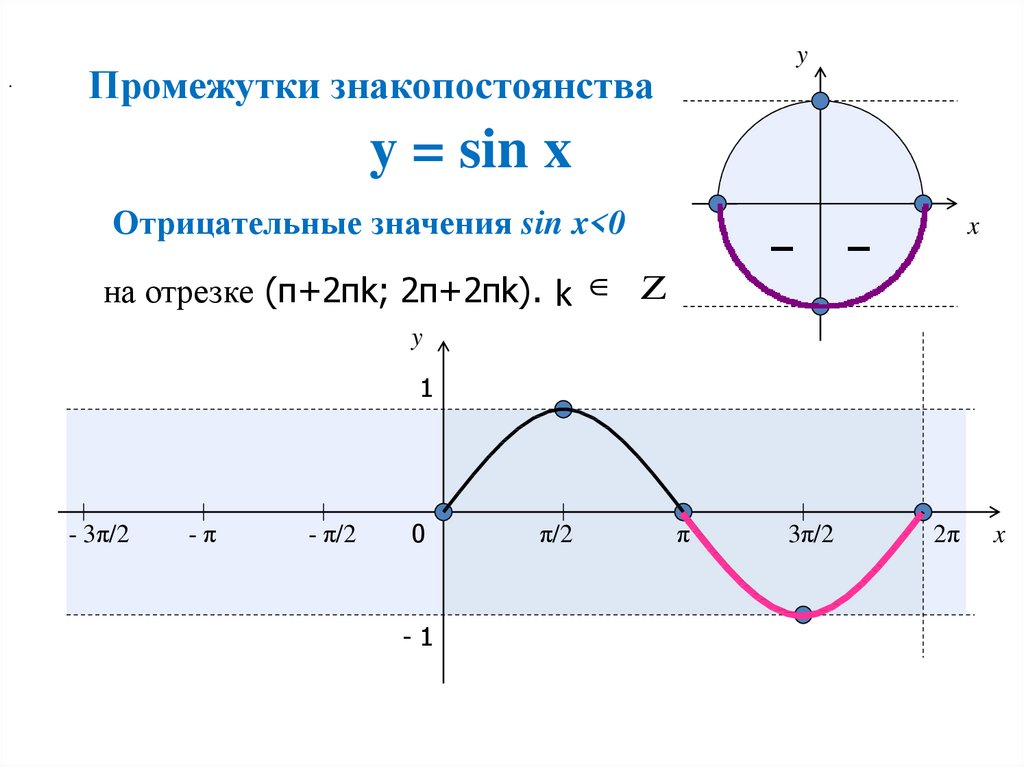

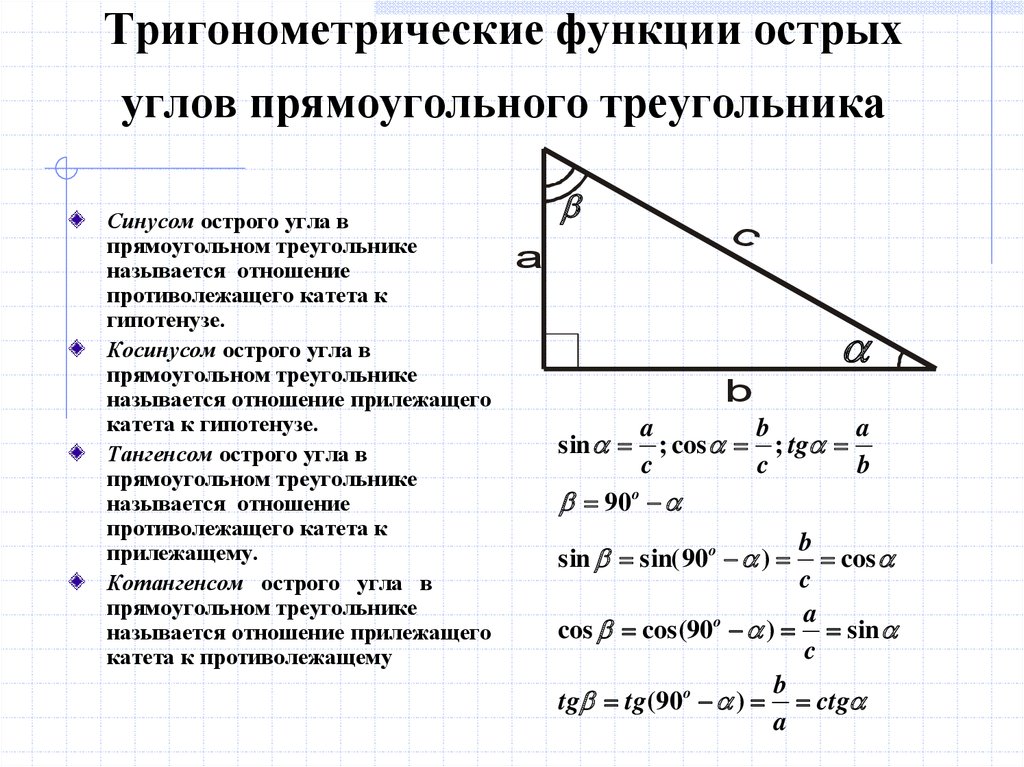 На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности.
На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности. Эти значения обычно записывают с помощью радикалов и при необходимости эти радикалы заменяют их приближенными значениями
Эти значения обычно записывают с помощью радикалов и при необходимости эти радикалы заменяют их приближенными значениями Действительно, формула 3 показывает, что значение 1 синус принимает только в точках
Действительно, формула 3 показывает, что значение 1 синус принимает только в точках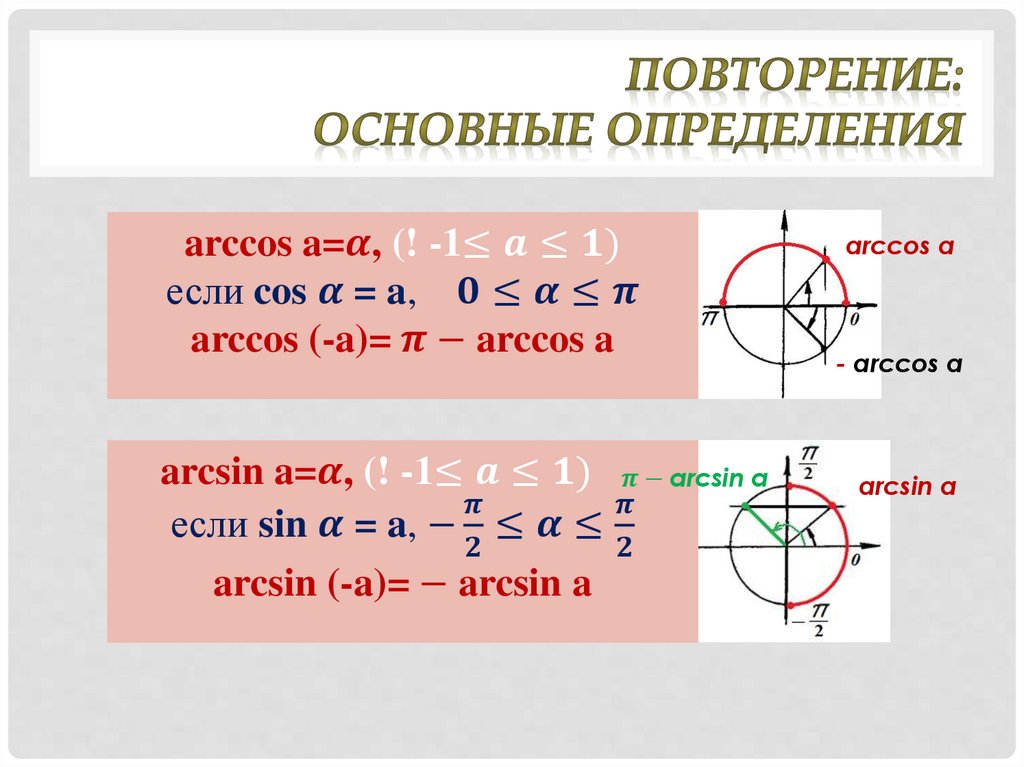 При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= точка займет положение Р (0; 1). Итак, в первой четверти синус (ордината) возрастает от 0 до 1, а косинус (абсцисса) убывает от 1 до 0.
При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= точка займет положение Р (0; 1). Итак, в первой четверти синус (ордината) возрастает от 0 до 1, а косинус (абсцисса) убывает от 1 до 0.
 Воспользовавшись нечетностью
Воспользовавшись нечетностью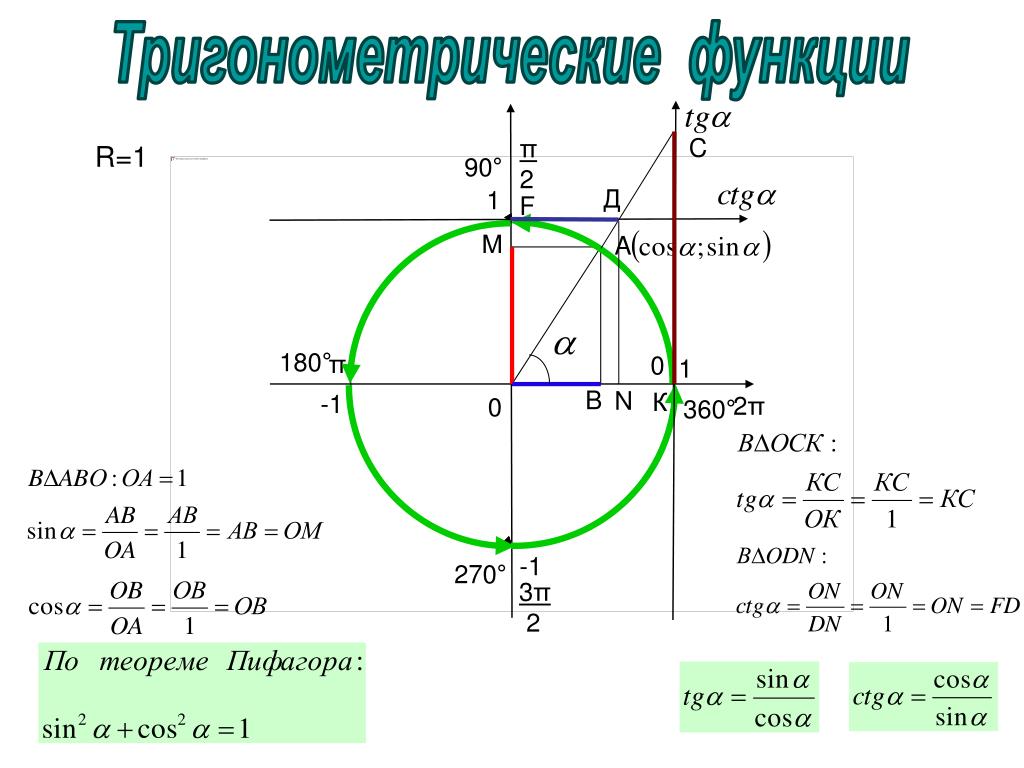 При этом видно, что 2 π — наименьший положительный период синуса.
При этом видно, что 2 π — наименьший положительный период синуса. Воспользуемся, например, формулой cosx = sin (x+)
Воспользуемся, например, формулой cosx = sin (x+)
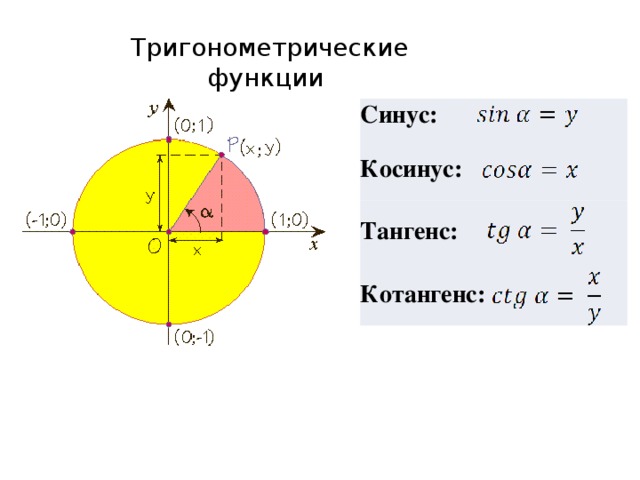 Лучше выбрать промежуток ( —; ).
Лучше выбрать промежуток ( —; ). То, что любое вещественное число может быть значением тангенса, видно из рисунка 91. Построим ось, параллельную оси ординат с началом в точке Ро. Возьмем на этой оси точку, соответствующую произвольно выбранному числу а. Соединим 0 с а. Получим точку Р на окружности. Пусть х — число, принадлежащее и такое, что (cos х; sin х) — координаты Р. Тогда
То, что любое вещественное число может быть значением тангенса, видно из рисунка 91. Построим ось, параллельную оси ординат с началом в точке Ро. Возьмем на этой оси точку, соответствующую произвольно выбранному числу а. Соединим 0 с а. Получим точку Р на окружности. Пусть х — число, принадлежащее и такое, что (cos х; sin х) — координаты Р. Тогда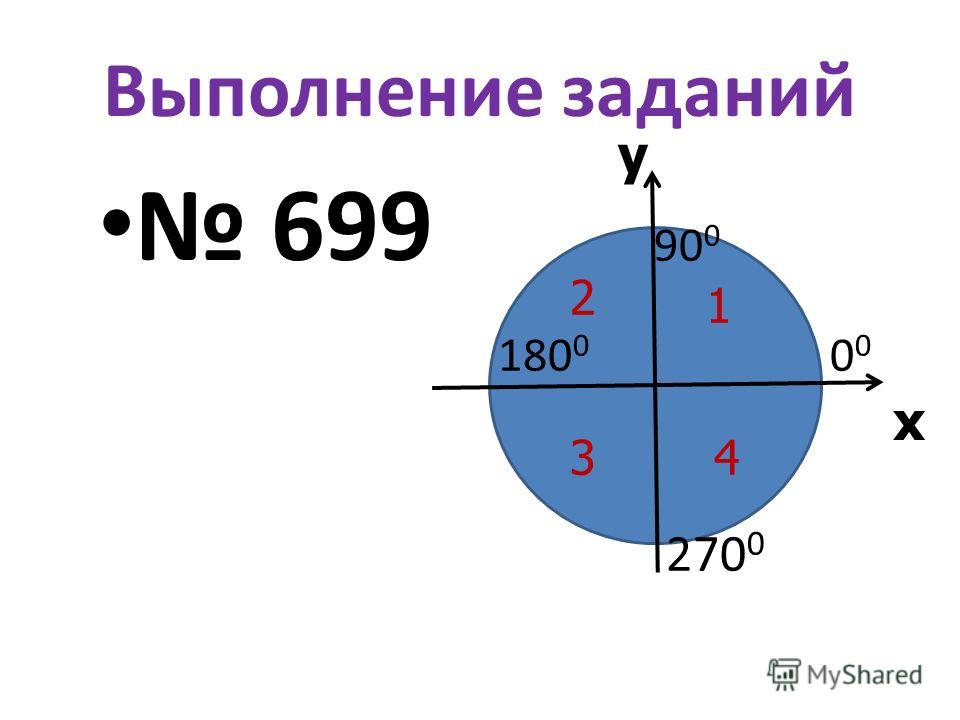 д.
д.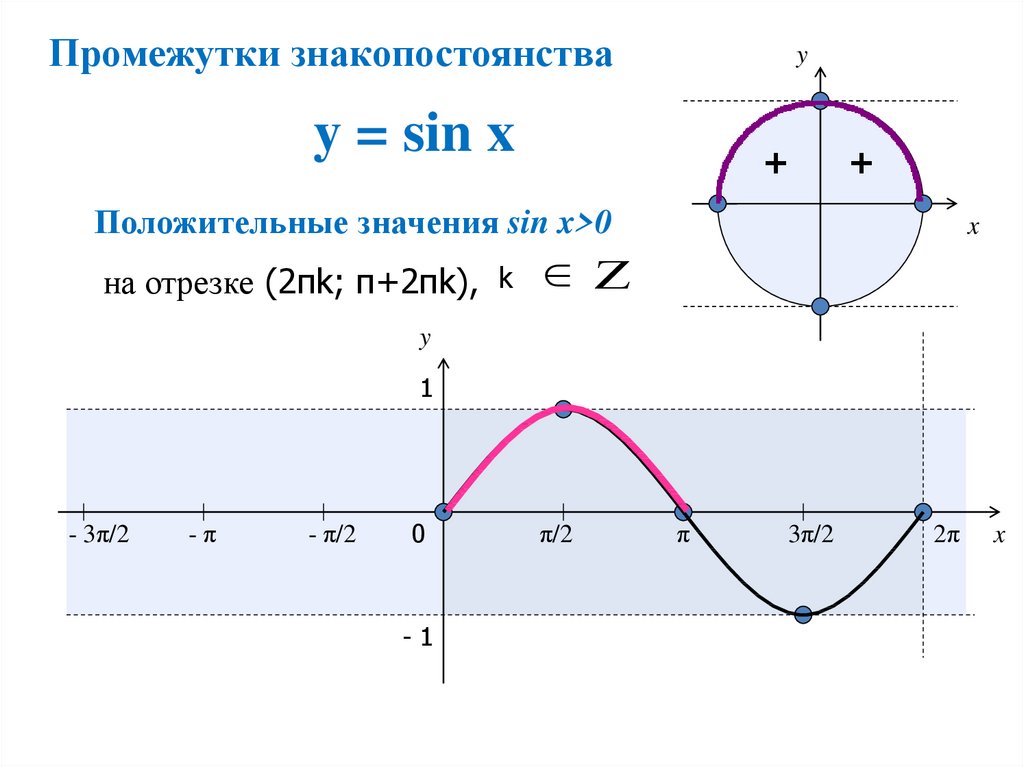 е. при х = + лk, k ∈ Z.
е. при х = + лk, k ∈ Z.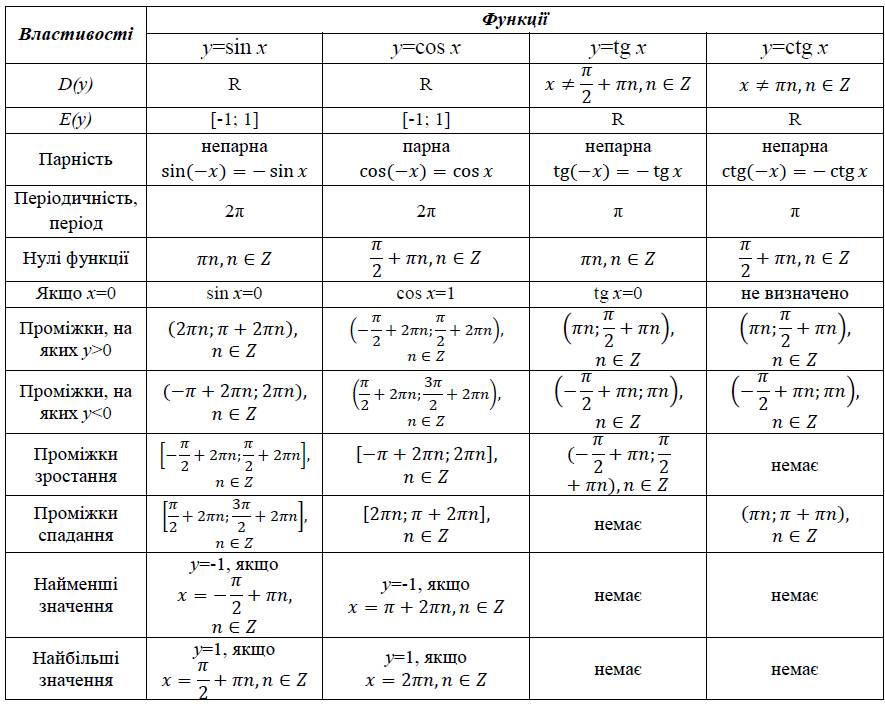 Далее, так как движение точки А по окружности происходит с единичной скоростью, то длина вектора и равна 1, поэтому длина вектора также равна 1. Следовательно, точка В лежит на окружности.
Далее, так как движение точки А по окружности происходит с единичной скоростью, то длина вектора и равна 1, поэтому длина вектора также равна 1. Следовательно, точка В лежит на окружности.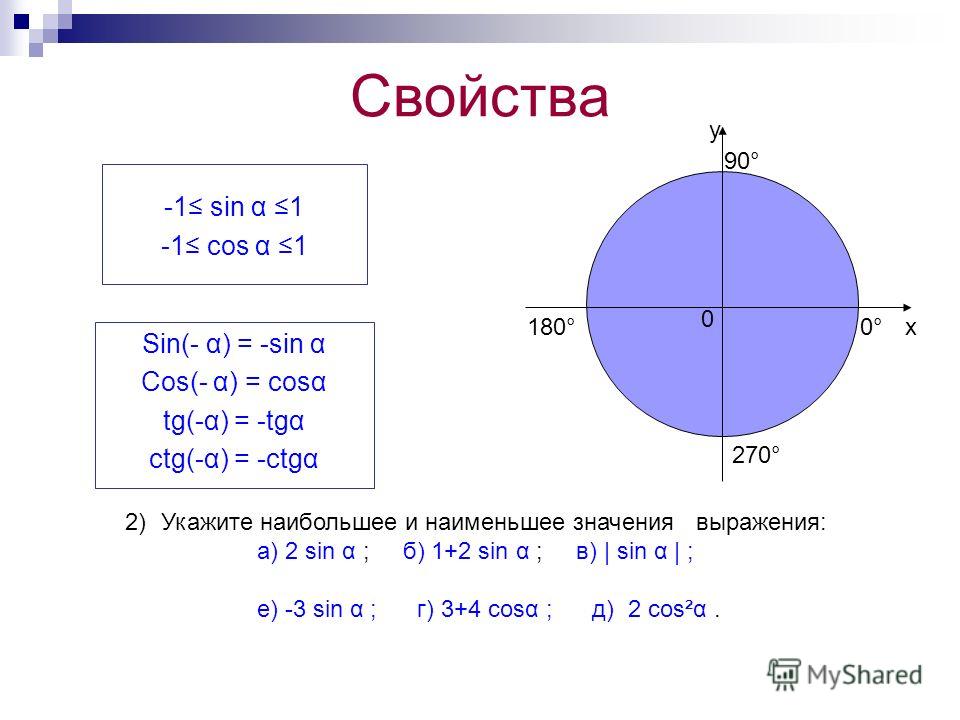
 Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.
Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.
 Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.
Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.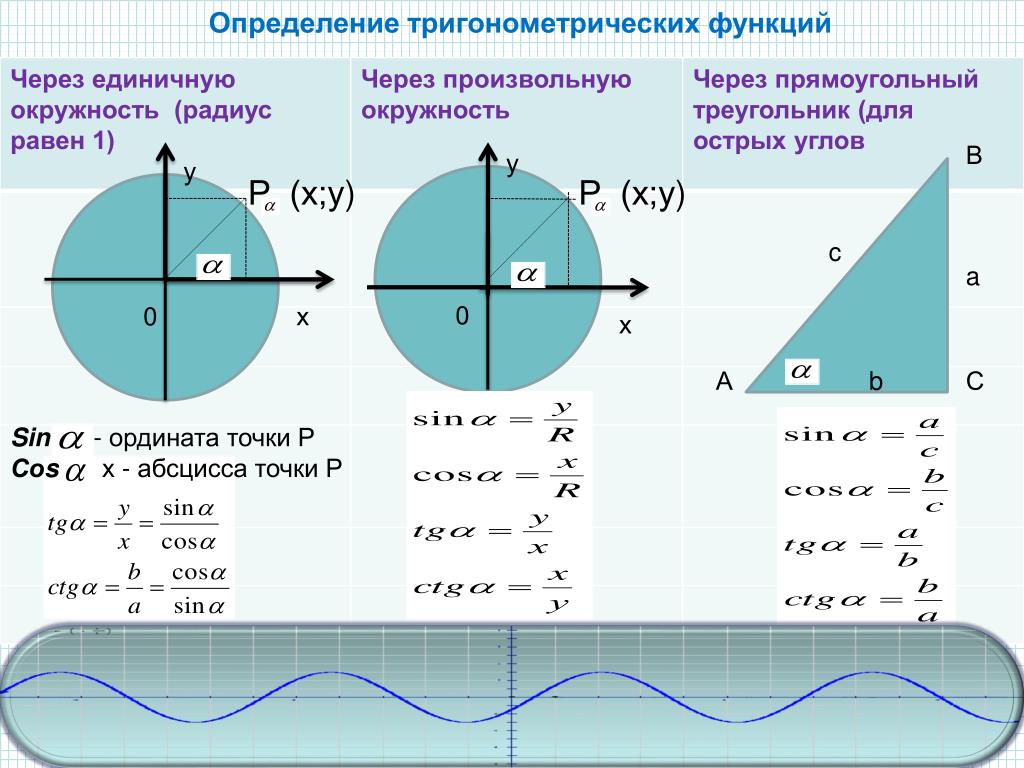 Получим:
Получим: Сначала запишем:
Сначала запишем: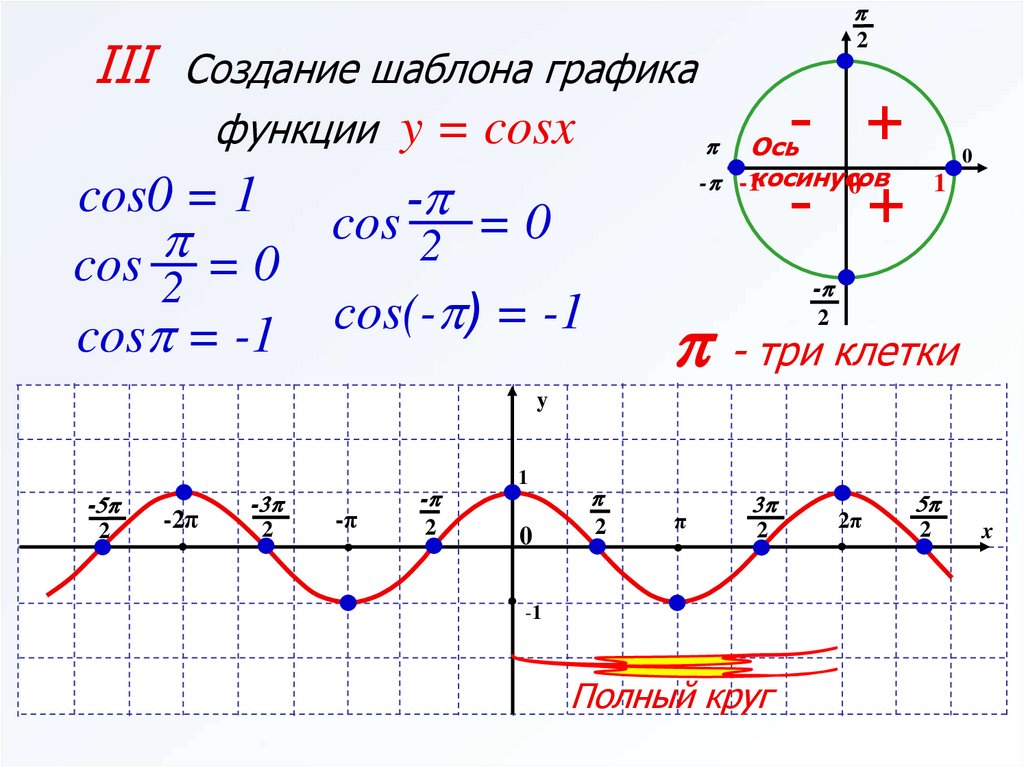
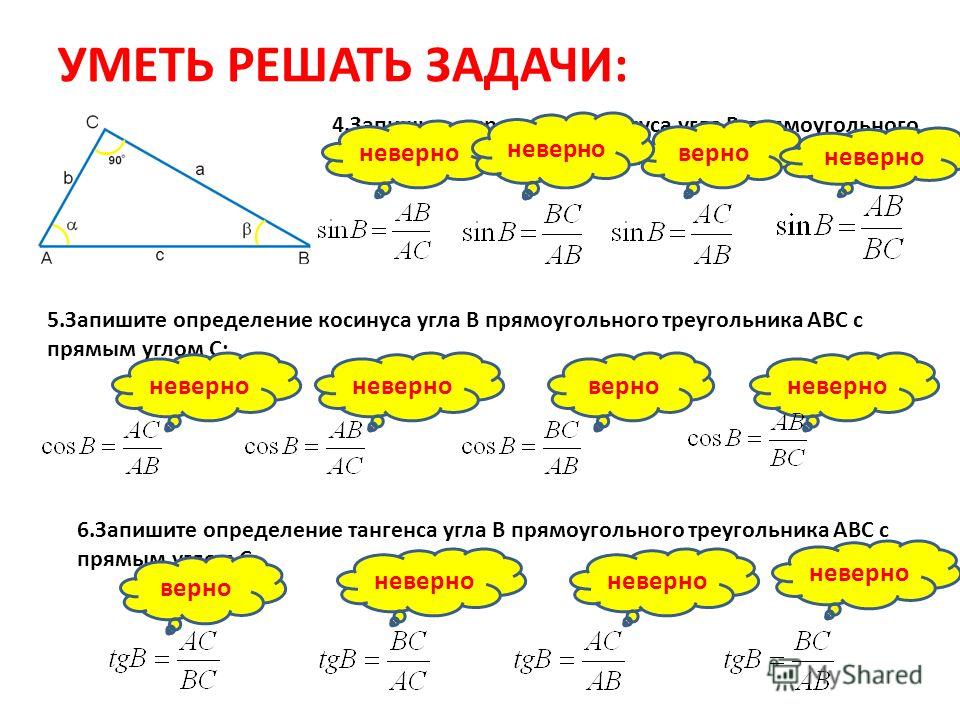
 Решить уравнение
Решить уравнение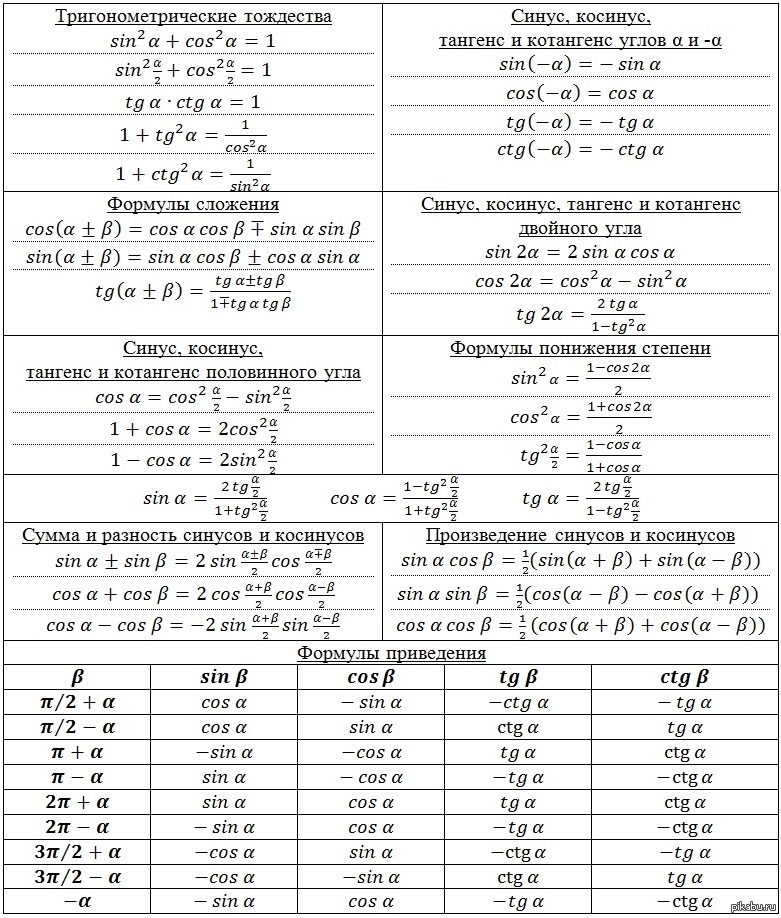
 Решить уравнение
Решить уравнение
 Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:
Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода: Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.
Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения. е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которого
е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которого Решить уравнение
Решить уравнение Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.)
Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.) 99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени.
99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени. В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функций
В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функций
 Вычислим
Вычислим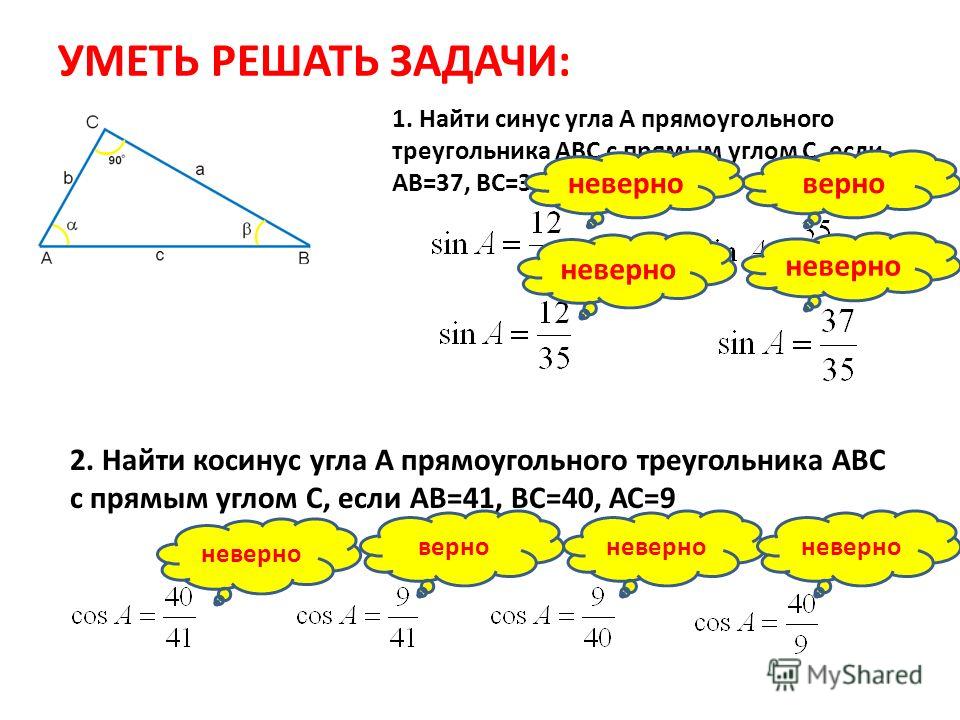 Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.
Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.
 французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.
французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.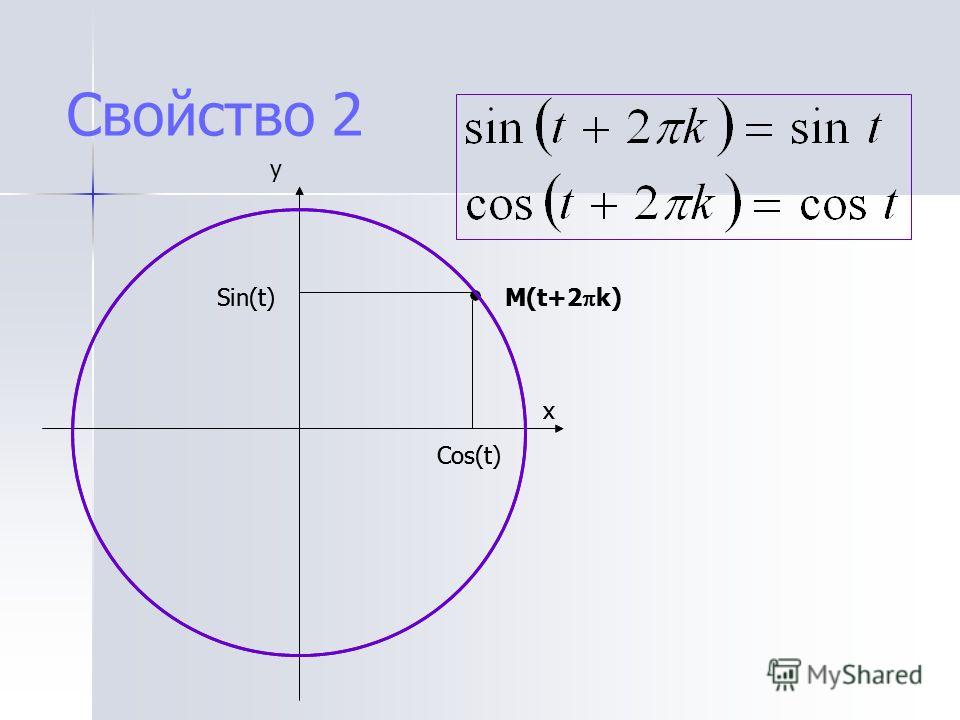 1: Графики функций косинуса и синуса
1: Графики функций косинуса и синуса
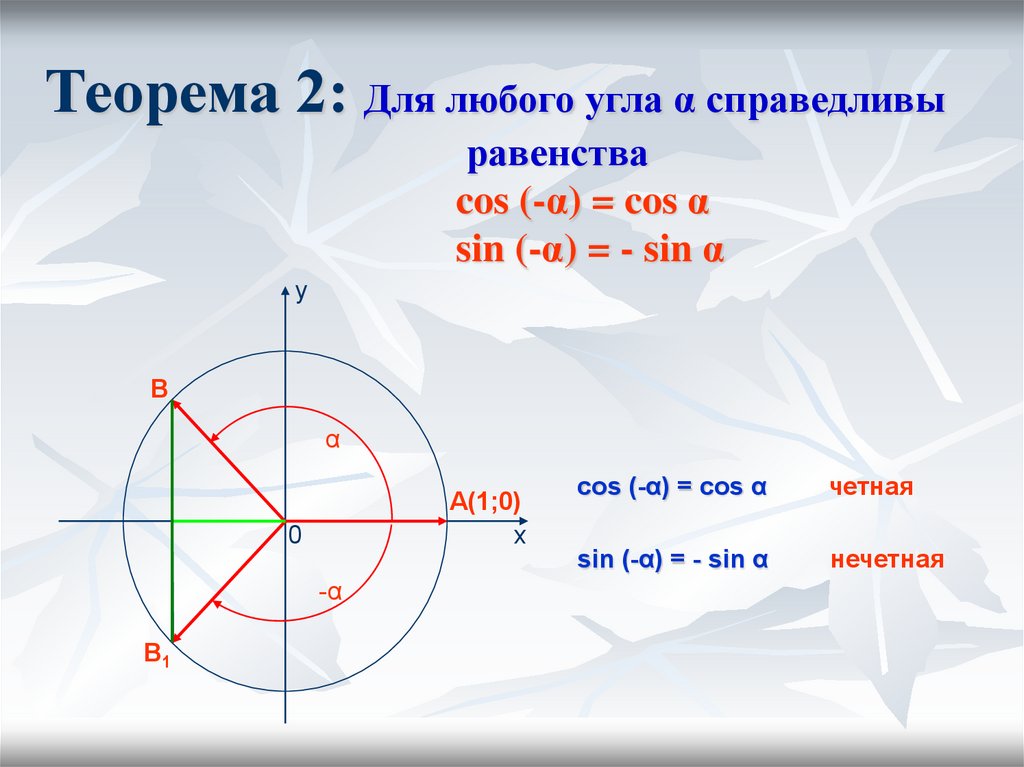
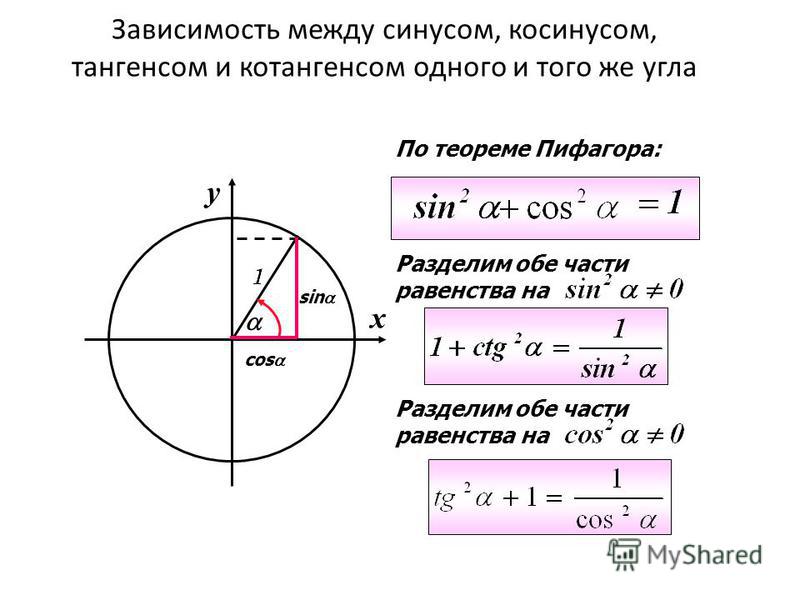

 edu/s/LM
edu/s/LM
 1.
1. Пи\). Таким образом, интервал \(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
Пи\). Таким образом, интервал \(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
 gvsu.edu/books/12
gvsu.edu/books/12 Точка P перемещается на окружность окружности. Из данного рисунка мы увидим, что P присутствует в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикулярное падение из точки P на горизонтальную ось. Затем из точек O, P и Q образуется треугольник, где QO — основание, PQ — высота треугольник . Формула косинуса для вышеуказанного условия будет записана как: cosx = OQ/OP. Здесь х — острый угол, образованный между основанием и гипотенузой.
Точка P перемещается на окружность окружности. Из данного рисунка мы увидим, что P присутствует в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикулярное падение из точки P на горизонтальную ось. Затем из точек O, P и Q образуется треугольник, где QO — основание, PQ — высота треугольник . Формула косинуса для вышеуказанного условия будет записана как: cosx = OQ/OP. Здесь х — острый угол, образованный между основанием и гипотенузой.