Таблица функции лапласа для нормального распределения: 23. Функция Лапласа

Дифференциальное и интегральное исчисления для втузов, т.2

Дифференциальное и интегральное исчисления для втузов, т.2

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Второй том включает разделы: дифференциальные уравнения, кратные и криволинейные интегралы, интегралы по поверхности, ряды, уравнения математической физики, операционное исчисление, элементы теории вероятностей и математической статистики, матрицы. Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII. (n) = f(x) § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14. 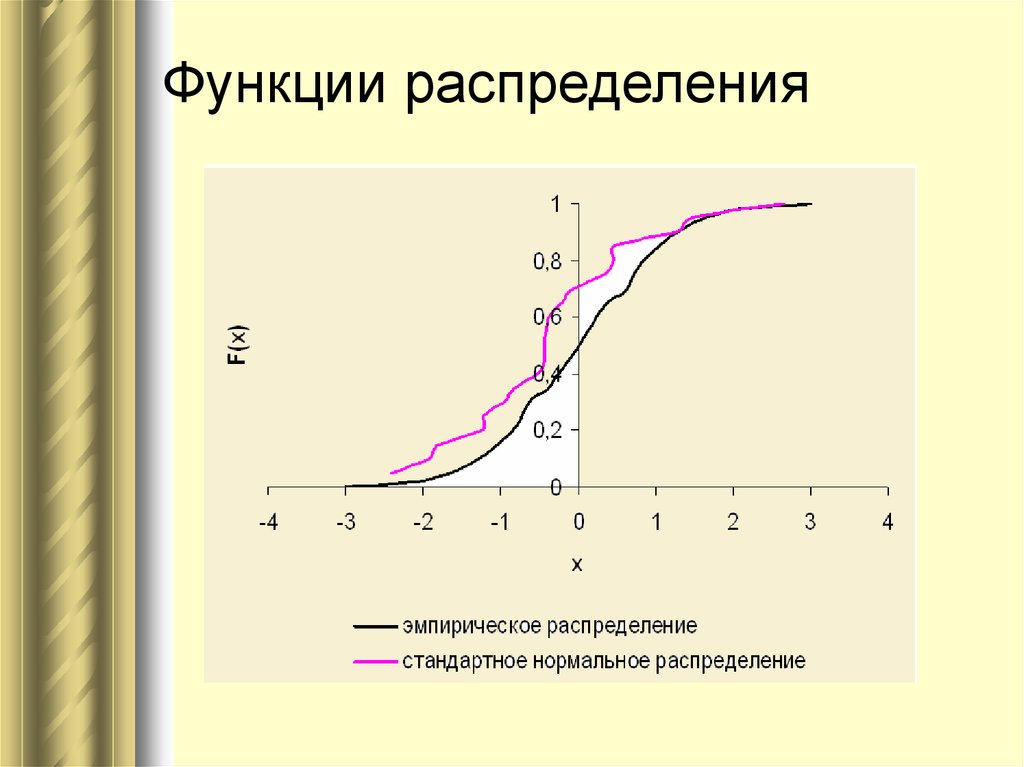Момент инерции и координаты центра масс тела § 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13. Степенные ряды. Интервал сходимости § 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4. Ряды Фурье для четных и нечетных функций § 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи § 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. Дифференцирование изображения § 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей § 2. Классическое определение вероятности и непосредственный подсчет вероятностей § 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15. Нормальный закон распределения. Математическое ожидание нормального распределения § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27. 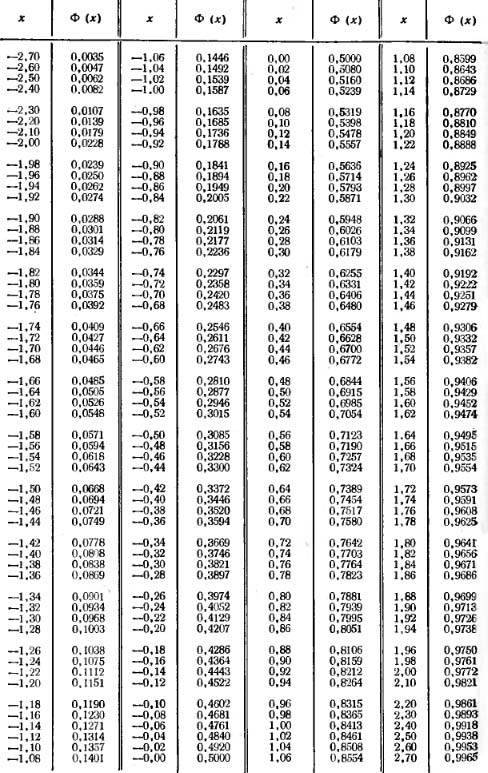Задачи математической статистики. Статистический материал § 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому § 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ

17.Функция Лапласа

Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

где а и s—некоторые постоянные, называемые параметрами нормального распределения.

Функция распределения F(x) в рассматриваемом случае принимает вид

Использование формул f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим формулам можно упростить, если от нормального распределения с произвольными параметрами а и s перейти к нормальному распределению с параметрами а=0, s = 1.

Функция плотности нормального распределения f(x) с параметрами а=0, s =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

Функция плотности и интегральная функция стандартной нормальной случайной величины(СВ) будут иметь вид:

Для вычисления вероятности попадания СВ в интервал (a, b) воспользуемся функцией Лапласа:

_{Перейдем к стандартной нормальной случайной величине}

_Тогда

Значения функции Ф(u) необходимо взять из таблицы приложений «Таблица значений функции Ф(х)» .

18.Правило трех сигм

Вычислим вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит .

Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую в качестве подставим : .Таким образом, вероятность того, что отклонение случайной величины по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит , составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных событий, можно считать практически невозможным. Вывод (правило трех сигм): если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

т.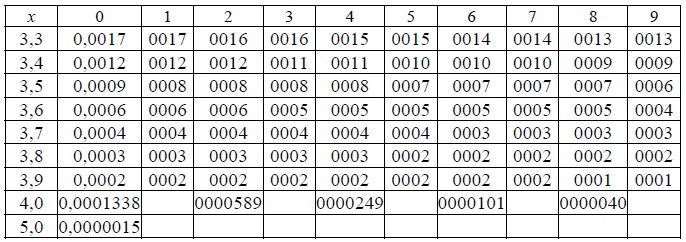 е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:

19.Контрольный листок

Какая бы задача не стояла перед системой, объединяющей последовательность применения статистических методов, всегда начинают со сбора исходных данных, на базе которых затем применяют тот или иной инструмент.

Контрольный листок (или лист) — это инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации.

Обычно контрольный листок представляет собой бумажный бланк, на котором заранее напечатаны контролируемые параметры, согласно которым можно заносить в листок данные с помощью пометок или простых символов. Он позволяет автоматически упорядочить данные без их последующего переписывания. Таким образом, контрольный листок — хорошее средство регистрации данных.

Число различных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным. Например, график температуры больного — один из возможных типов контрольных листков. В качестве другого примера можно привести контрольный листок, применяемый для фиксирования отказавших деталей в телевизорах (см. рисунок 3.2.).

Рис.  Контрольный листок.

   Дата_______  Смена____ Цех________  Бригада____ Изделие______

Границы интервала	Группа данных	Кол–во
30,011-30,020	/ / / /	4
30,021-30,030	/ / / /  / / / /    / / /	13
30,031-30,040	/ / / /  / / / /  / / / /  / / / /  / / / / / / / /  / / / /	34
30,041-30,050	/ / / /  / / / /  / / / /  / / / /  / / / /  / / / /  / / /	33
30,051-30,060	/ / / / / / / / / /	12
30,061-30,070	/ / / /	4
Итого		100

              Объем партии ________  Контролер_____________

При составлении контрольных листков следует обратить внимание на то, чтобы было указано, кто, на каком этапе процесса и в течение какого времен собирал данные, а также чтобы форма листка была простой и понятной без дополнительных пояснений. Важно и то, чтобы все данные добросовестно фиксировались, и собранная в контрольном листке информация могла быть использована для анализа процесса.

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

• Катализируемое родием [2π + 2π + 2π]-циклоприсоединение алкиниламидов и сероуглерода к индолотиопиранов тионам ()

  Бенджамин Дассонневиль, Феликс Хинкель, Хайнер Детерт

  Международный журнал органической химии Том 13 № 1, 14 марта 2023 г.

  DOI: 10.4236/ijoc.2023.131003 10 загрузок  53 просмотров

• Синхронная папиллярная карцинома щитовидной железы и почечная эпителиоидная ангиомиолипома с метастазами в печень или сочетанием: клинико-патологические характеристики и исход ()

  Дук Тхань Ле, Тхи Ван Нгуен, Туан Ань До, Чин Трунг Ву, Кхоа Хонг Фам, Ту Ван Дао, Чу Ван Нгуен

  Журнал библиотеки открытого доступа Том 10 №3, 14 марта 2023 г.

  DOI: 10.4236/oalib.1109736 3 загрузки  23 просмотра

• Гангрена Фурнье у ребенка, госпитализированного в педиатрическое отделение неотложной помощи клинической больницы имени Габриэля Туре ()

  Дембеле Адама, Сиссе Мохамед Эльмулуд, Того Пьер, Таль Курейсси, Майга Белко, Кейта Дженеба, Думбия Абдул Карим, Кулибали Умар, Исса Амаду, Амаду Ибрагим, Кулибали Бакари, Траоре Калиру, Того Бубакар

  Открытый журнал педиатрии Том 13 № 2, 14 марта 2023 г.

  DOI: 10.4236/ojped.2023.132027 5 загрузок  29 просмотров

• Систематический обзор и метаанализ рандомизированных контрольных испытаний для проверки роли нестероидных противовоспалительных препаратов в качестве защитного фактора у субъектов с болезнью Альцгеймера ()

  Акаш Астана, Шашанк Трипати, Рахна Агарвал

  Успехи в лечении болезни Альцгеймера Том 12 № 1, 14 марта 2023 г.

  DOI: 10.4236/aad.2023.121001 8 загрузок  53 просмотров

• Влияние хитина, биоугля и навоза на урожай и качество баклажанов и зеленого перца ()

  Джордж Ф. Антониус, Анудж Чилувал, Анджан Непал

  Сельскохозяйственные науки Том 14 №3, 14 марта 2023 г.

  DOI: 10.4236/as.2023.143024 7 загрузок  37 просмотров

• Изучение генетической структуры и разнообразия маниоки ( Manihot esculenta ) Зародышевая плазма для африканской мозаики маниоки и выход корней при хранении в свежем виде()

  Джанату Вероника Сесай, Айя Лебби, Ричард Уодсворт, Эфраим Нуваманья, Сулейман Бадо, принц Эммануэль Норман

  Открытый журнал генетики Том 13 № 1, 14 марта 2023 г.

  DOI: 10.4236/ojgen.2023.131002 7 загрузок  28 просмотров

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Бесплатные информационные бюллетени SCIRP

Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.

Вершина

Нормальное распределение | Гауссово распределение | Кривая Белла | Нормальная кривая

Что такое нормальное распределение?

Нормальное распределение, также известное как распределение Гаусса (названное в честь немецкого математика Карла Гаусса, впервые описавшего его), представляет собой непрерывное распределение вероятностей, в котором появление данных более сгруппировано вблизи среднего значения, чем появление данных далеко от среднего.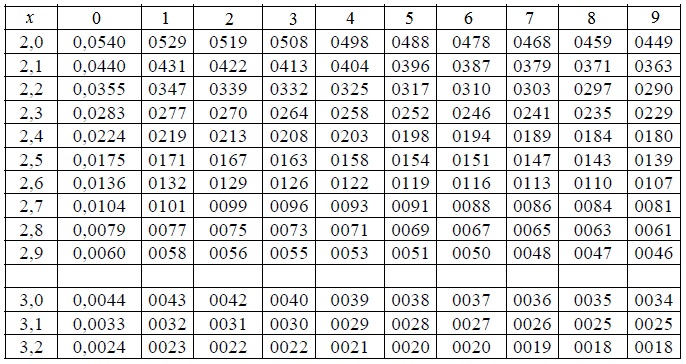 Эта характеристика придает нормальному распределению колоколообразную форму, симметричную относительно среднего значения. Нормальное распределение является одним из наиболее распространенных типов моделей распределения, используемых в статистике и реальной жизни.

Примеры нормального распределения

Пример 1: Нормальное распределение результатов тестов

Нормальное распределение можно наблюдать, анализируя результаты тестов студентов по любому конкретному курсу. Большое количество студентов наберет средний балл (скажем, 65 из 100), в то время как некоторые наберут около 50 или 80 баллов, и меньшее число студентов не сдаст тест или получит высший балл. Если бы баллы этих студентов отображались на графике, он имел бы форму кривой нормального распределения.

Пример 2: Нормальное распределение веса новорожденных

Из приведенного выше рисунка видно, что средний вес новорожденного ребенка близок к 3,5 кг, и многие из них весят от 3 до 4 кг.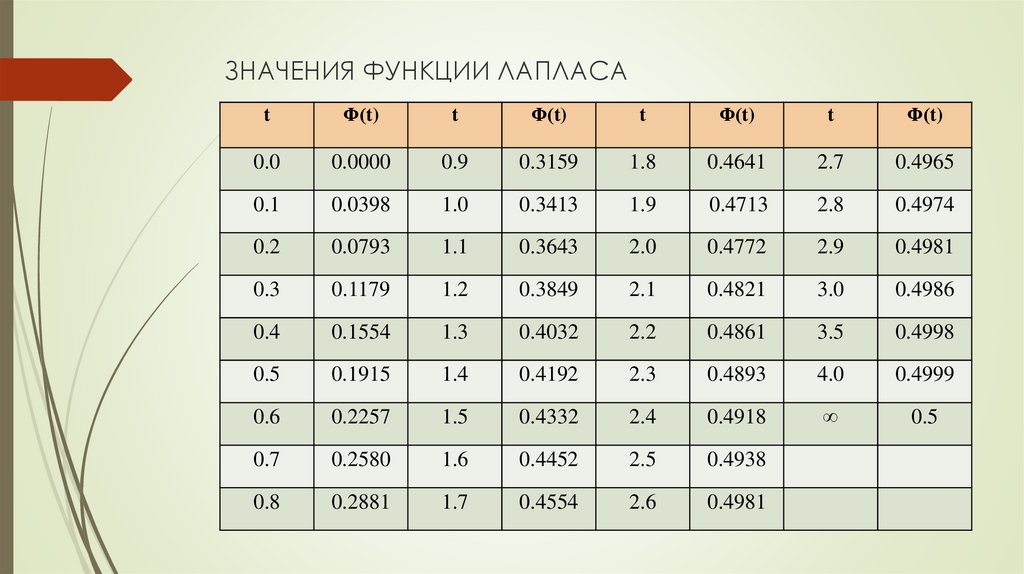 Но по мере того, как мы удаляемся от среднего, мы обнаруживаем, что очень немногие младенцы весят 2 или 5 килограммов, и еще меньше детей весят 1 или 6 килограммов. Говорят, что такое распределение соответствует кривой нормального распределения или нормальному распределению 9.0003

Другими распространенными примерами нормального распределения, которые мы можем наблюдать вокруг себя ежедневно, являются:

• Рост девочек, принадлежащих к определенной возрастной группе.
• Результаты SAT или GRE.
• Заработная плата сотрудников, работающих в одной организации.

График нормального распределения и его характеристики

1. Площадь под кривой нормального распределения представляет вероятность, а общая площадь под кривой равна 1.

График нормального распределения

2. Нормальное распределение симметрично по обе стороны от среднего, т. е. значения распределены равномерно, образуя одинаковые половины по обе стороны от среднего.

3. Для нормального распределения среднее значение, медиана и мода равны

4. В графе нормального распределения, чем дальше значение от среднего, тем меньше вероятность его возникновения и тем меньше вероятность того, что оно произойдет, и те, которые группируются вокруг среднего происходят с большей вероятностью.

5. Хвосты нормально распределенного графа приближаются к оси X, но никогда не касаются ее.

Что такое функция плотности вероятности?

Функция плотности вероятности (PDF) — это статистическая функция в теории вероятностей, значение которой в пространстве выборки в любой заданной точке или выборке можно интерпретировать как обеспечивающее относительную вероятность того, что значение случайной величины будет равно этой выборке.

Функция плотности вероятности определяет вероятность того, что случайная величина примет значение, связанное между заданными интервалами. В теории статистики PDF широко известен тем, что помогает нам вычислять вероятности, связанные со случайными величинами.

Свойства функции плотности вероятности

Рассмотрим непрерывную случайную величину x с функцией плотности f(x), тогда функция плотности вероятности должна удовлетворять следующим условиям:

• Функция плотности всегда неотрицательна, т. е. f (x) > 0, для всех возможных значений x
• Площадь под кривой равна 1, т. е. ∫f(x)dx = 1 (x принадлежит ∞, −∞)

Функция плотности вероятности Нормальное распределение

Функция плотности вероятности (PDF) для нормального распределения с непрерывной случайной величиной x, со средним значением µ , дисперсией σ   ² и стандартным отклонением σ  задается как:

Функция плотности. ) нормального распределения

Среднее значение нормального распределения — это центроид функции плотности вероятности, а стандартное отклонение σ — это мера дисперсии нескольких случайных величин вокруг среднего значения. Поскольку нормальные распределения определяются средним значением и стандартным отклонением, давайте более подробно рассмотрим их оба.

Что означает ?

В нормальном распределении среднее значение представляет собой центральную тенденцию и пик распределения, вокруг которого концентрируется большинство значений. Доказано, что среднее значение является важной мерой при изучении теории вероятностей, поскольку оно включает в себя все значения данных, полученные от населения, и дает нам представление о поведенческих моделях набора данных.

Например, чтобы узнать, сколько среднестатистический житель Нью-Йорка платит ежемесячную арендную плату «в среднем» , лучший способ — найти набор данных, содержащий информацию о ежемесячной арендной плате, выплачиваемой лицами, проживающими в Нью-Йорке, сложив все значения арендной платы и разделив их на количество лиц, включенных в это исследование.

Аналогично, когда речь идет о более сложных наборах данных, чтобы найти среднее значение, мы суммируем все значения данных и делим его на размер набора данных. Он представлен символом μ (греческий алфавит «Му»).

Если мы построим набор данных, в котором значения распределены нормально, мы получим что-то, известное как нормальная кривая (кривая Белла), где пик кривой представляет наше среднее значение, а набор данных представляет собой нормальное распределение.

Что такое стандартное отклонение

Стандартное отклонение — это мера того, насколько разбросаны значения данных ниже кривой, и обозначается символом σ (греческая буква «сигма»). Он представляет собой дисперсию значений данных, принадлежащих набору данных, по отношению к его среднему значению. Это означает, что чем меньше стандартное отклонение, тем ближе значения данных к среднему, и чем выше стандартное отклонение, тем дальше и разбросаны значения данных от среднего.

Существует два типа стандартных отклонений, а именно: стандартное отклонение выборки и стандартное отклонение генеральной совокупности. Задается по формулам:

Формулы стандартного отклонения

где

σ – стандартное отклонение генеральной совокупности

S – стандартное отклонение выборки

N – численность генеральной совокупности

x _i – каждое значение данных генеральной совокупности

x̅ – среднее значение населения

Стандартное отклонение и правило 68-95-99,7

Правило 68-95-99,7 для нормального распределения

Правило 68-95-99,7, также известное как эмпирическое правило нормального распределения, введенное Абрахамом де Муавром, гласит, что для стандартного нормального распределения:

• 68% всех значений находятся в пределах одного стандартного отклонения от среднего
• 95 % всех значений находятся в пределах двух стандартных отклонений от среднего
• 99,7 % всех значений или почти все значения находятся в пределах трех стандартных отклонений от среднего

Поскольку нормальное распределение по своей природе симметрично, Эмпирическое правило также может быть продемонстрировано как:

Эмпирическое правило симметрично разделено на две части средним значением

Нормальное лечение | Кривая Белла

Кривая нормального распределения также известна как нормальная кривая или «кривая Белла». Название происходит от того факта, что кривая, используемая для изображения нормального распределения, напоминает форму колокола. Колоколообразная кривая симметрична, так как половина данных будет располагаться слева от среднего значения, а другая половина — справа. Термины нормальное распределение, нормальная кривая и колоколообразная кривая часто используются в статистике как синонимы.

Использование нормального распределения

Замечено, что многие природные явления следуют типу «кривой Белла» модели данных и распределения вероятностей. Специалисты по данным наблюдают за существованием нормально распределенных шаблонов данных в наиболее распространенных областях, где данные интенсивно используются, таких как бизнес, медицинский анализ, частные организации и государственные органы. Вот несколько примеров:

• Мы наблюдаем, как нормальное распределение широко используется производителями, чтобы понять склонность потребителей к определенному продукту. Это помогает им понять психологию потребителей, а также помогает им улучшить отношения между потребителем и покупателем.
• Университеты могут использовать нормальное распределение для разработки своих тестов.
• Страховые компании прогнозируют вероятность несчастных случаев, включая различные параметры о застрахованном лице, чтобы обеспечить им премию.
• Организации по производству лекарств используют нормальное распределение для проверки своих клинических исследований и улучшения лекарств, вызывающих меньше побочных эффектов.
• Отделы маркетинга будут собирать информацию о вероятности спроса на их продукцию в различных ценовых категориях, чтобы определить правильную цену.
• Электронные схемы со слабыми сигналами (радиоприемники или микрофонные предусилители) чувствительны к тепловому шуму, и эти сигналы имеют нормальное распределение. Следовательно, вычисление таких факторов, как «коэффициент битовых ошибок» или «коэффициент ложных срабатываний», становится проще.

Стандартное нормальное распределение

Стандартное нормальное распределение (SND) — это нормальное распределение со средним нулем и стандартным отклонением 1. Оно центрировано на нуле (среднее) и имеет интервалы, отстоящие на 1 стандартное отклонение друг от друга по обе стороны от Значение.

Любое нормальное распределение с любым средним значением и любым стандартным отклонением может быть преобразовано в стандартное нормальное распределение, где у вас есть нулевое среднее значение и стандартное отклонение 1, посредством известного преобразования и стандартизации .

Формула плотности вероятности для стандартного нормального распределения.0006  ) из 1 упрощается до:

Функция плотности вероятности для стандартного нормального распределения

Z-показатели или стандартные показатели

Каждое число на горизонтальной оси кривой стандартного нормального распределения соответствует Z-показателю, также обычно известному как стандарт Счет.

Z-Score сообщает нам, сколько стандартных отклонений наблюдения от среднего значения μ. Например, Z-показатель 2,5 (положительный Z-показатель) указывает, что значение находится на 2,5 стандартных отклонения справа от среднего, тогда как Z-показатель -1 (отрицательный Z-показатель) указывает, что значение 1 стандартное отклонение слева от среднего, и если Z-показатель равен 0, то это указывает на то, что Z-показатель эквивалентен среднему.

Преимущество стандартизации заключается в том, что с помощью таблицы Z-Score мы можем легко рассчитать точные площади для любой данной нормально распределенной популяции с любым средним значением или стандартным отклонением, а также это позволяет нам сравнивать две оценки, полученные из разных выборок, которые могут иметь разные средние значения и стандартные отклонения.

Для стандартизации или для получения стандартной оценки мы используем формулу Z-Score:

Z-Score Formula

Z Table или Standard Normal Table

Z-оценка позволяет нам рассчитать, с какой областью связана конкретная Z-оценка, и мы можем узнать эту точную область с помощью «Таблицы Z-оценки», также известной как «Стандартная таблица норм».

Значения, которые меньше среднего (нуля), соответствуют отрицательной оценке в Z-таблице и лежат слева от среднего значения, как показано на рисунке выше. Чтобы рассчитать Z-оценку этих отрицательных значений, мы обращаемся к таблице отрицательных Z-оценок.

Аналогично, значения, превышающие среднее (ноль), дают положительную оценку в Z-таблице и лежат справа от среднего на графике. Следовательно, для расчета Z-оценки этих положительных значений мы обращаемся к таблице положительных Z-оценок.

Как использовать Z-таблицу

Давайте разберемся, как использовать формулу Z-оценки и Z-таблицу с помощью нескольких примеров:

Пример 1: Результаты тестов 50 учеников в классе имеет нормальное распределение со средним значением = 65 и стандартным отклонением = 8. Какая доля учащихся набрала менее 46 баллов?

Решение: Пусть X обозначает долю учащихся, набравших менее 46 баллов, P (X < 46).

Используя формулу Z-Score, мы получаем,

= P (Z < X – μ / σ)

= P (Z < 46 – 65/8)

= P (Z < -2,37)

Следовательно, P (X < 46) = P (Z < -2,37)

Чтобы отобразить то же самое в Z-таблице, нам нужно выбрать соответствующую Z-таблицу (отрицательную или положительную) в зависимости от того, является ли наша Z-оценка отрицательной или положительной.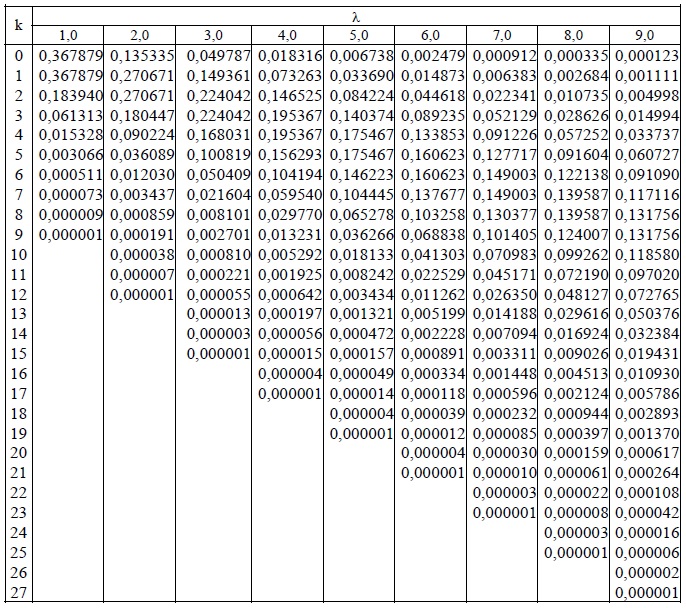 В нашем случае показатель Z равен -2,37, поэтому будет использоваться отрицательная таблица Z.

Чтобы найти площадь под кривой для -2,37, сначала мы проходим в горизонтальном направлении вдоль крайнего левого столбца по оси Y, чтобы найти значение первых двух цифр Z Score (-2,3 на основе нашего примера)

После этого нам нужно пройти вдоль оси X самой верхней строки, чтобы найти значение цифр во втором десятичном разряде (0,07 в нашем примере)

Теперь сопоставьте эти два значения с Z-таблицей и найдите пересечение строки первых двух цифр и столбца второго десятичного значения в таблице. И вуаля! пересечение этих двух и есть наш ответ.

По таблице Z-Score получаем Следовательно P(x<46) = P(Z<-2,37) = 0,00889, что указывает только на 0,88 % (0,00889X 100) студентов набрали менее 46 .

Пример 2: Тестовый балл 50 учащихся в классе нормально распределен со средним значением 65 и стандартным отклонением 8. Какая доля учащихся набрала более 75 баллов.

Решение: Пусть X обозначает долю учащихся которые набрали более 75 баллов, P (X > 75).

Используя формулу Z-Score, получаем,0003

т. е. P (X > 75) = P (Z > 1,25)

По таблице Z-Score получаем P (Z < 1,25) = 0,8944 (область слева от Z-Score), это указывает 89,44% студентов набрали менее 75 баллов.

Но нам нужно найти долю студентов, набравших более 75 баллов, P (Z > 1,25), которая находится справа от рассчитанного Z-показателя.

Самое важное, что нужно понимать при расчете площади под кривой справа от Z-показателя:

Площадь (справа) = 1 – Площадь (слева)

Таким образом, P (Z > 1,25) = 1 – 0,8944 = 0,1056

Только 10,56% учащихся набрали за тест более 75 .

История нормального распределения

Признание открытия нормального распределения неоднозначно. Некоторые авторы приписывают заслугу Аврааму де Муавру, а некоторые авторы приписывают заслугу Карлу Фридриху Гауссу.

Абрахам Де Муавр

Де Муавр опубликовал исследование коэффициентов в биномиальном разложении (a+b) ⁿ во втором издании своего учебника по вероятности «Доктрина шансов» в 1738 году.

Карл Фридрих Гаусс

Тогда как Гаусс ввел нормальное распределение вместе с другими важными математическими понятиями, такими как метод наименьших квадратов, в своей монографии, опубликованной как «». Theoria motus corporum coelestium in sectionibus conicis solem ambientium ». Следовательно, нормальное распределение также было взаимозаменяемо известно как распределение Гаусса на протяжении многих лет.

Пьер-Симон Лаплас

Пьеру-Симону Лапласу также приписывают значительный вклад в нормальное распределение, поскольку он первым поставил проблему агрегирования наблюдений. Однако это привело его к созданию собственного двойного экспоненциального распределения в качестве решения, известного как распределение Лапласа. Именно Лаплас, а не Гаусс, доказал центральную предельную теорему, которая служит теоретической основой для нормального распределения.

Роберт Адриан

Менее известный факт заключается в том, что ирландский математик по имени Роберт Адриан опубликовал в 1809 годудва вывода нормального закона вероятности, полностью независимые от работы Гаусса, которые были заново открыты метеорологом из Кливленда Кливлендом Эббом лишь позже, в 1871 году. Ниже приведены названия, взаимозаменяемо используемые для нормального распределения:0011 Закон Гаусса

Второй закон Лапласа

Нормальная кривая

Закон вероятности ошибок

Кривая нормального распределения

Закон ошибки

Гаусс сказал, что использовал термин «нормальные» по отношению к «нормальным уравнениям» подразумевая техническое значение слова «ортогональный», а не «обычный». Это привело к путанице, поскольку многие статистики, как студенты, так и преподаватели использовали слово «нормальный» в качестве прилагательного, подразумевая его как «обычный», «обычный», «типичный» и, следовательно, «нормальный». На самом деле именно Карл Пирсон в 20-м веке дал термину «нормальный» его законное обозначение для дистрибутива и того, каким он должен быть, и популяризировал его.

No related posts.