математика / Тест-Центр.РФ
тест
ТЕСТ: Сложение трех слагаемых (сложность 0) версия:1 ⇑
создано: 29 апреля 2022 г. 21:18
Выполнено 10 раз
Ключевые слова:
0 0 0
статья
СТАТЬЯ: Таблица умножения⇐
14 марта 2017 г. 22:14
Башков А.А.
Таблица умножения 10 на 10
0 0 0
тест
Башков А.А.
ТЕСТ: Квадраты натуральных чисел (1-100) версия:1 ⇑
создано: 11 марта 2017 г. 23:27
Выполнено 327 раз
Ключевые слова:
0 0 0
статья
СТАТЬЯ: Таблица квадратов натуральных чисел от 1 до 1000⇐
1 сентября 2015 г. 22:14
Башков А.А.
Таблица квадратов натуральных чисел от 1 до 1000
0 0 0
статья
СТАТЬЯ: Таблица квадратных корней от 1 до 100⇐
1 сентября 2015 г. 21:23
Башков А.А.
Таблица квадратных корней для натуральных чисел от 1 до 100
0 0 0
статья
СТАТЬЯ: Таблица квадратных корней⇐
23 мая 2015 г. 00:16
00:16
Башков А.А.
Таблица квадратных корней для чисел от 1 до 1000
0 0 0
тест
Башков А.А.
ТЕСТ: Сложение целых чисел (сложность 0) версия:1 ⇑
создано: 30 декабря 2014 г. 16:47
Выполнено 77 раз
Ключевые слова:
0 0 0
тест
Башков А.А.
ТЕСТ: Сложение целых чисел (сложность: 1) версия:1 ⇑
создано: 30 декабря 2014 г. 13:17
Выполнено 23 раза
Ключевые слова:
0 0 0
тест
Башков А.А.
ТЕСТ: Сложение целых чисел (сложность 2) версия:1 ⇑
создано: 30 декабря 2014 г. 12:54
Выполнено 19 раз
Ключевые слова:
0 0 0
тест
Башков А.А.
ТЕСТ: Умножение чисел (сложность: 5) версия:1 ⇑
создано: 12 сентября 2014 г. 22:56
Выполнено 29 раз
Ключевые слова: устный счет,умножение целых чисел
0 0 0
тест
Башков А.А.
ТЕСТ: Умножение чисел (сложность: 4) версия:1 ⇑
создано: 12 сентября 2014 г. 22:55
Выполнено 11 раз
Ключевые слова: устный счет,умножение целых чисел
0 0 0
тест
Башков А.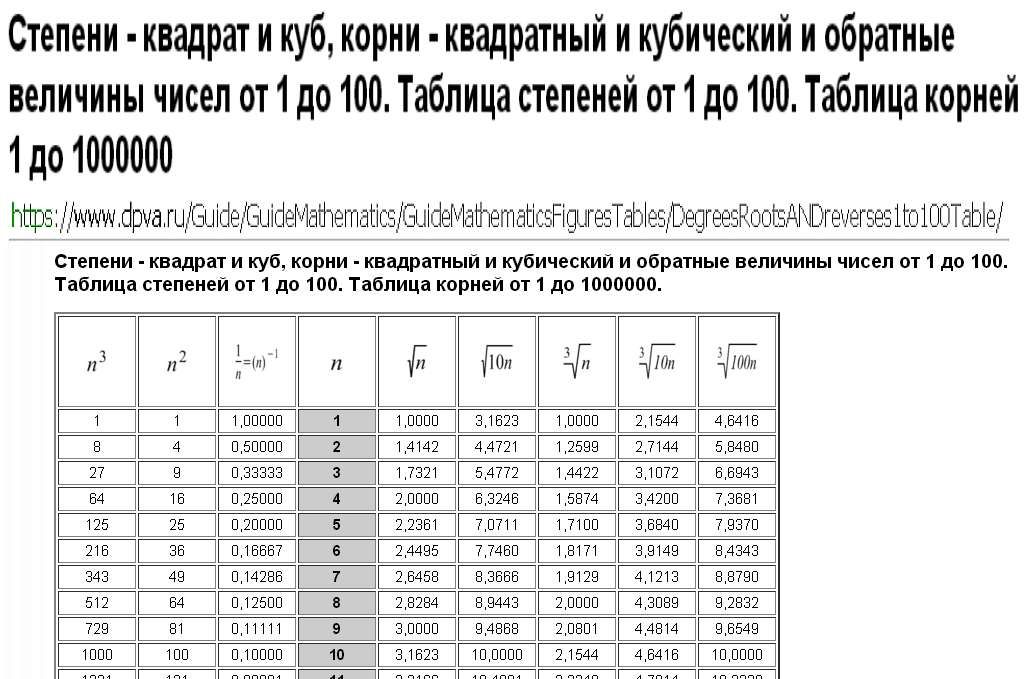 А.
А.
ТЕСТ: Умножение чисел (сложность: 3) версия:1 ⇑
создано: 12 сентября 2014 г. 22:54
Выполнено 10 раз
Ключевые слова: устный счет,умножение целых чисел
0 0 0
тест
Башков А.А.
ТЕСТ: Умножение чисел (сложность: 2) версия:1 ⇑
создано: 12 сентября 2014 г. 22:52
Выполнено 17 раз
Ключевые слова: устный счет,умножение целых чисел
0 0 0
тест
Башков А.А.
ТЕСТ: Умножение чисел (сложность: 1) версия:1 ⇑
создано: 12 сентября 2014 г. 22:51
Выполнено 23 раза
Ключевые слова: устный счет,умножение целых чисел
0 0 0
тест
Башков А.А.
ТЕСТ: Пропорции (сложность: 3) версия:1 ⇑
создано: 12 сентября 2014 г. 19:39
Выполнено 2 раза
Ключевые слова: устный счет,уравнения вида пропорции
0 0 0
тест
Башков А.А.
ТЕСТ: Пропорции (сложность: 2) версия:1 ⇑
создано: 12 сентября 2014 г. 19:35
Выполнено 4 раза
Ключевые слова: устный счет,уравнения вида пропорции
0 0 0
тест
Башков А.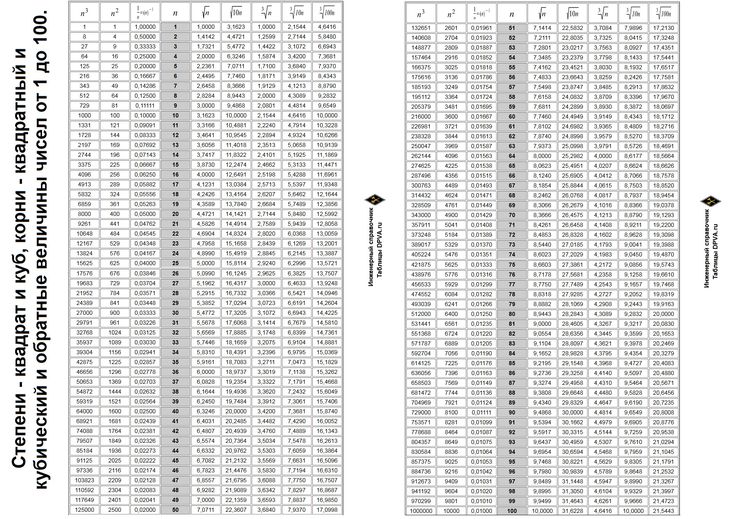 А.
А.
ТЕСТ: Пропорции (сложность: 1) версия:1 ⇑
создано: 12 сентября 2014 г. 18:58
Выполнено 17 раз
Ключевые слова: устный счет,уравнения вида пропорции
0 0 0
тест
Башков А.А.
ТЕСТ: Умножение целых чисел (сложность: 4) версия:1 ⇑
создано: 11 сентября 2014 г. 23:33
Выполнено 4 раза
Ключевые слова:
0 0 0
тест
Башков А.А.
ТЕСТ: Таблица квадратных корней 1-1000 версия:1 ⇑
создано: 10 сентября 2014 г. 23:13
Выполнено 40 раз
Ключевые слова: Устный счет
0 0 0
тест
Башков А.А.
ТЕСТ: Квадратные уравнения (сложный) версия:1 ⇑
создано: 5 сентября 2014 г. 21:54
Выполнено 10 раз
Ключевые слова: Квадратные уравнения
0 0 0
тест
Башков А.А.
ТЕСТ: Таблица квадратных корней 1-10000 версия:1 ⇑
создано: 25 августа 2014 г. 23:11
Выполнено 4 раза
Ключевые слова: Устный счет
0 0 0
тест
Башков А.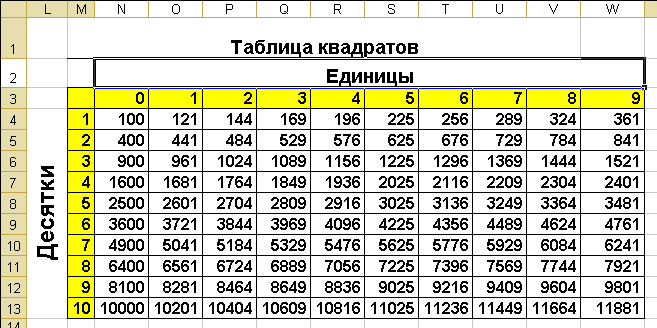 А.
А.
ТЕСТ: Таблица квадратных корней 1-100 версия:2 ⇑
создано: 20 августа 2014 г. 19:30
Выполнено 33 раза
Ключевые слова: Устный счет
0 0 0
тест
Башков А.А.
ТЕСТ: Таблица умножения версия:1 ⇑
создано: 15 декабря 2013 г. 11:42
Выполнено 435 раз
Ключевые слова: Устный счет
0 0 0
квадратных и кубических. Как пользоваться таблицей, примеры
Содержание:
- Что такое корень в математике
-
Таблица корней
- Кубические корни
- Специфические характеристики применения таблицы квадратных и кубических корней
- Как пользоваться таблицей
- Примеры
Содержание
- Что такое корень в математике
-
Таблица корней
- Кубические корни
- Специфические характеристики применения таблицы квадратных и кубических корней
- Как пользоваться таблицей
- Примеры
Что такое корень в математике
Корень n-степени из определенного числа x характеризуется в качестве определенной величины y, то есть \(y^{n}=x\).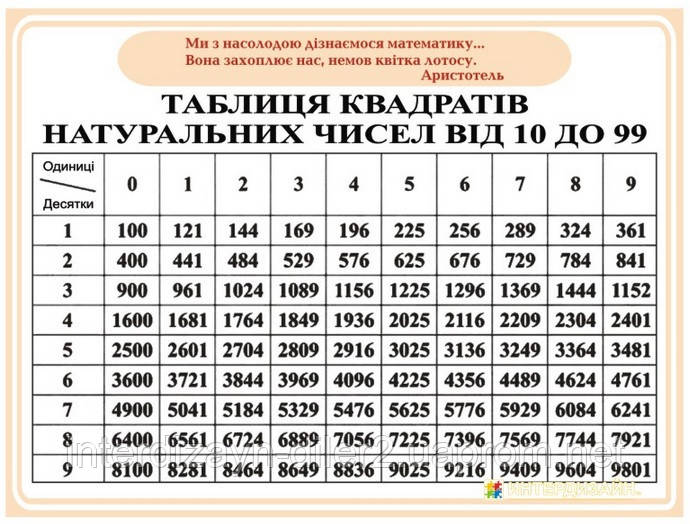 В данном уравнении n является натуральной величиной, которая носит название степень корня (показатель, именно на эту величину необходимо совершать возведение в степень). Обычно величина степени корня эквивалентна 2 или же является величиной, что больше 2. Вариант, при котором n=1 не интересен для математического сообщества, результат не изменится.
В данном уравнении n является натуральной величиной, которая носит название степень корня (показатель, именно на эту величину необходимо совершать возведение в степень). Обычно величина степени корня эквивалентна 2 или же является величиной, что больше 2. Вариант, при котором n=1 не интересен для математического сообщества, результат не изменится.
Такой вариант написания часто используется в алгебре: \(y=\sqrt[n]{x}\). Обозначение в виде корневого знака \(\sqrt{}\) носит название радикала. Величина x является подкоренной величиной. Обычно данное число является либо комплексным, либо вещественным. Также возможно внесение под корень более сложных алгебраических явлений, например матриц, вычетов, операторов и других.
Вот такие математические действия можно совершать с величинами, которые являются корнями:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- умножение;
- деление;
- возведение в степень.

Основные особенности корней:
- Только положительная величина, которая точно определена, способна быть корнем нечетной степени, рассчитанным из положительного значения: \(\sqrt[n]{x}=y\), где \(x,y>0\), показатель n является нечетным значением. Приведем пример: \(\sqrt[3]{125}=5, \sqrt[5]{32}=2, \sqrt[15]{1}=1\).
- Только отрицательная величина, которая точно определена, способна стать корнем нечетной степени, рассчитанным из отрицательного значения: \(\sqrt[n]{x}=y\), где x,y<0, показатель n является нечетным значением. Приведем пример: \(\sqrt[3]{-8}=-2\), \(\sqrt[5]{-243}=-3\), \(\sqrt[7]{-1}=-1\).
- Две величины с двумя разными знаками получится, если рассчитывать корень четной степени из величины без отрицательного знака. Оба полученных значения несмотря на то, что будут разные по своему знаку, но будут эквиваленты по собственному модулю. \(\pm{\sqrt[n]{x}}=\pm{y},\) где \(x,y>0\), показатель n является четным значением.
 Приведем пример: \(\pm{\sqrt{4}}=\pm{2}\).
Приведем пример: \(\pm{\sqrt{4}}=\pm{2}\). - Невозможно извлечь корень из числа со знаком «минус» четной степени — такой величины просто нет в сфере вещественных величин, потому что в процессе возведения каждого вещественного значения в степень четной величины итогом можно считать только число без знака «минус». Но корни подобного типа возможно вычленять, но в системе, которая намного шире обычный корневой — множестве комплексных чисел. В таком случае величины корня будут являться комплексными значениями. \(\sqrt[n]{x}\) нельзя найти в сфере вещественных значений при условии x<0, показатель n является четным.
- Стоит запомнить, что при вычислении корня всех натуральных степеней из нуля будет все равно ноль. \(\sqrt[0]{0}\).
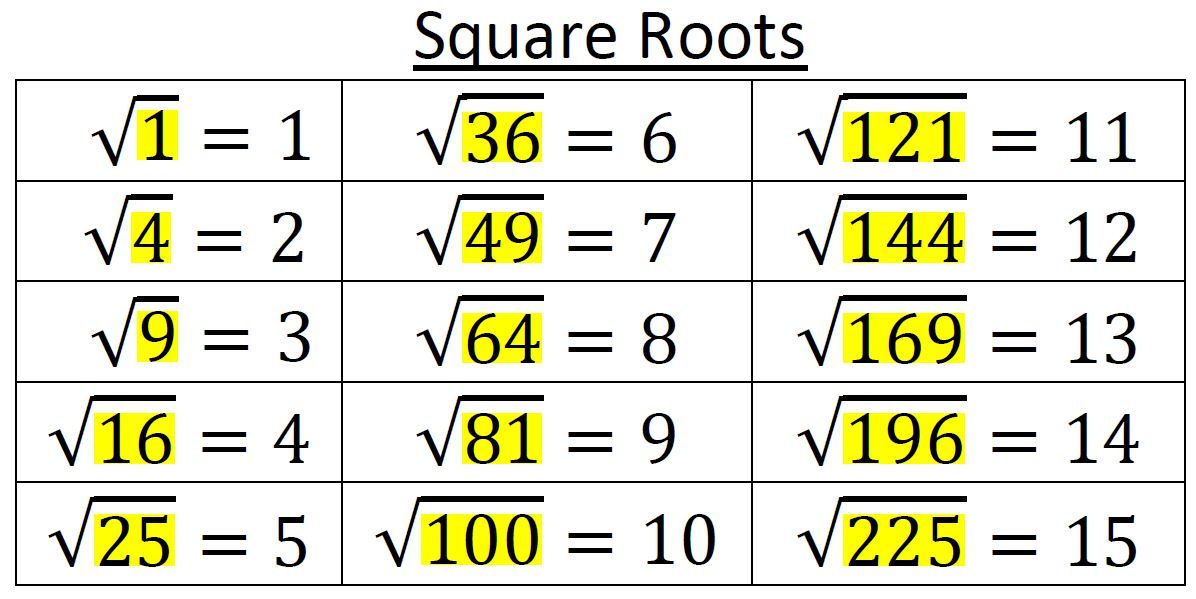
Таблица корней
Математический корень в квадрате, рассчитанный из положительной величины x будет всегда положительной величиной y, квадратное значение которого будет эквивалентно значению x. Возможно выразить данное соотношение при помощи следующего выражения: \(y^{2}=x\)
Есть методы, используя которые возможно рассчитать корень положительной величины самостоятельно.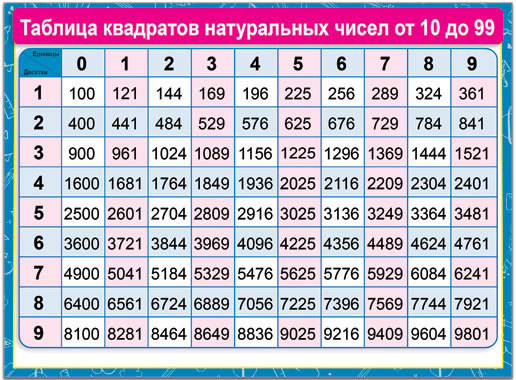 К примеру, возможно разложить значение на разные множители в квадрате, а потом рассчитать корневые значения этих величин. Но стоит понимать, что подобный вариант решения задач не всегда справедлив для большого количества чисел — у некоторых значений корневой итог станет не натуральной величиной. Для таких случаев и пользуются либо таблицей корней, либо специальными вычислительными приборами, к примеру калькулятором.
К примеру, возможно разложить значение на разные множители в квадрате, а потом рассчитать корневые значения этих величин. Но стоит понимать, что подобный вариант решения задач не всегда справедлив для большого количества чисел — у некоторых значений корневой итог станет не натуральной величиной. Для таких случаев и пользуются либо таблицей корней, либо специальными вычислительными приборами, к примеру калькулятором.
Так выглядит калькулятор:
Источник: office-planet.ruПри помощи таблицы корней возможно рассчитать корень каждого значения, которое попадает в промежуток от 0 до 99. Заметьте, что в строчках у таблицы прописываются десятки, тогда как в столбиках таблицы прописывают единицы. Ячейка в таблице, в которой соприкасаются необходимые величины, будет считаться числом, которое требовалось найти по задаче.
Так выглядит таблица квадратных корней:
Источник: wiki.fenix.helpКубические корни
Корень в кубической степени из величины x будет величиной y, что в процессе возведения в третью степень будет равняться x.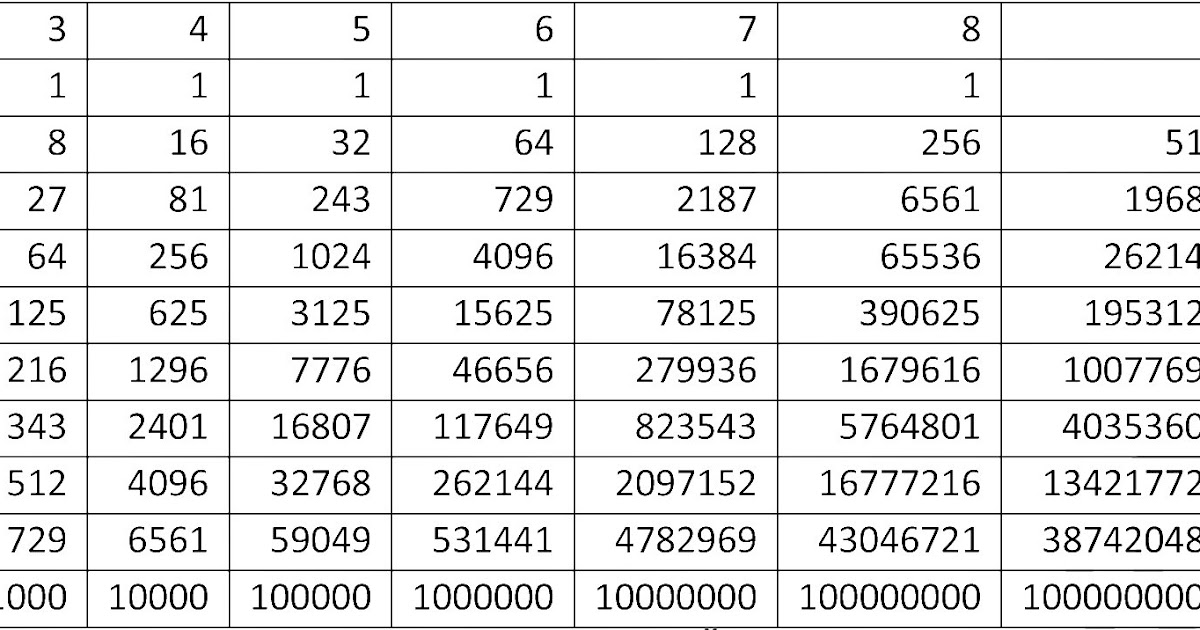 {3}=x\).
{3}=x\).
Главная особенность корня в кубе (то есть в третьей степени) заключается в том, что в процессе вычленения значения из него получится только один вариант ответа. При условии положительности изначального значения корень также будет неотрицательным. При условии отрицательности изначального значения корень также будет отрицательным.
Для расчета корней в кубе существуют такие же таблицы, как и для квадратных корней. Вариантов очень много, но больше всего используют таблицы для чисел в промежутке от 0 до 99. В таблице кубических корней также в строчках находятся десятки, а в столбиках находятся единицы.
Так выглядит таблица кубических корней:
Источник: wiki.fenix.helpКроме таблиц, в которых представлена только вторая и третья варианты степеней, есть таблицы, в которых представлены нестандартные значения — выше 2 и 3. Но часто математики не используют подобные таблицы.
Примечание
В таблицах двух видов, которые приведены выше, можно заметить, что не отображается целых величин — все величины округляются вплоть до пятого знака после запятой. Из-за этого для уточнения вычислений необходимо использовать калькулятор или любой другой прибор для вычисления.
Из-за этого для уточнения вычислений необходимо использовать калькулятор или любой другой прибор для вычисления.
Специфические характеристики применения таблицы квадратных и кубических корней
Таблицы корней в кубе и в квадрате применяются совершенно одинаково. Но из-за того, что степени могут быть как четные, так и нечетные, появляются определенные отличия в расчете значений подобных корней.
Исходя из дефиниции термина «квадратный корень» получается, что число, которое находится под корнем, никогда не является неположительным числом. Данную особенность стали использовать потому, что требовалось привести к однозначности термин «корень в квадрате». Но существует расширенная дефиниция корня в квадрате в математике.
Согласно ей корень в квадрате является корнем, возведенным во вторую степень. Для подобного вида корня не нужно вычленять неотрицательное выражение, а также положительную величину непосредственно корня.
В процессе работы со всеми таблицами стоит понимать, что за корень в квадрате необходимо рассчитать — корень алгебраический или же корень арифметический.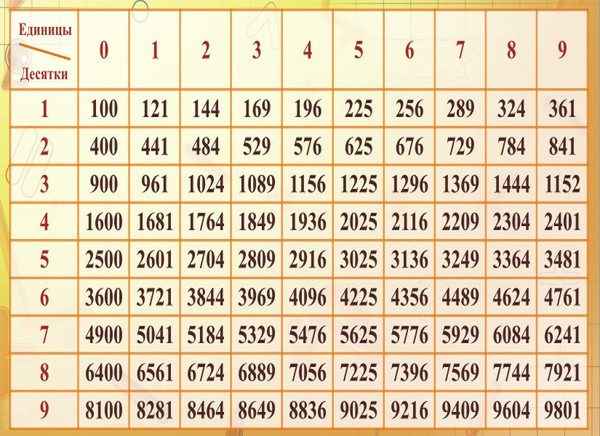 В случае арифметического корня необходимо нужно брать величину из корневой таблицы, не совершая никаких иных операций.
В случае арифметического корня необходимо нужно брать величину из корневой таблицы, не совершая никаких иных операций.
В случаях, когда совершаются операции с алгебраическим вариантом корня, итог будет основываться на величине, величине, которая находится под корнем. В случае, когда величина под корнем является величиной более нуля, тогда корней в результате получится два корня — один неотрицательный, а другой отрицательный. В случае, когда величина, которую возвели в степень, является неположительной, тогда у уравнения не будет никаких вариантов решения. Четной будет вторая степень, потому что не существует подобной величины, что при возведении в квадрат привело бы к неположительному значению.
Пример
\(\sqrt{47}=\pm6.85565\)
Величина 47 является величиной, которая не равняется нулю, из-за этого корня будет два: 6.85565 и -6.85565. \(\sqrt{-35}\neq5.91608\), \(\sqrt{-35}\neq-5.91608\). -35 является величиной неположительной, из-за этого решения не будет.
Для того чтобы быстрее, точнее рассчитывать величины-ответы на задачи, изобрели корневую таблицу, в которой возможно найти рассчитанные ранее корни. В корневой таблице в строчке находятся единицы, в столбиках находятся десятки. Приведем пример использования таблицы: нужно рассчитать корень в квадрате величины 54. Для начала нужно взглянуть на столбики, ищем нужное нам число, то есть 5, потом необходимо взглянуть на строчку, найти там нужное число, то есть 4. После необходимо рассмотреть место, в котором эти цифры пересекаются. В этой ячейке располагается необходимый для задачи результат, то есть 6,7082.
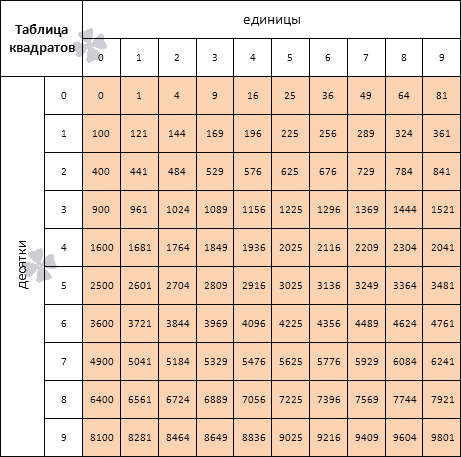
Существует также таблица квадратов — ее нельзя сопоставлять с корневой таблицей. Таблица квадратов выглядит таким образом:
Источник: reshit.ruТаблицей квадратов уместно пользоваться в тех случаях, когда необходимо рассчитать величину двухзначной величины, возведенной в квадрат. Приведем пример: необходимо возвести в двойную степень число 89.
Значения в таблице достаточно быстро запоминаются, поэтому возможно после продолжительного времени использования этой таблицы, перестать использовать ее.
Примеры
Приведем немного примеров расчета корней при помощи таблицы кубических и квадратных корней.
Задача 1
Необходимо рассчитать значение, которое получится после извлечения корня из значения 13824. \(\sqrt[3]{13824}\). Посмотрим на кубическую корневую таблицу:
Источник: wiki.fenix.helpВ таблице необходимо найти данное число, рассматриваем, в какой строчке и в каком столбце они соприкасаются. Строчка — 4, столбик — 2. Получается, что значение будет — 24. Таким образом, ответ будет \(\sqrt[3]{13824}=24\).
Задача 2
Необходимо рассчитать значение, которое получится после извлечения корня из значения 5.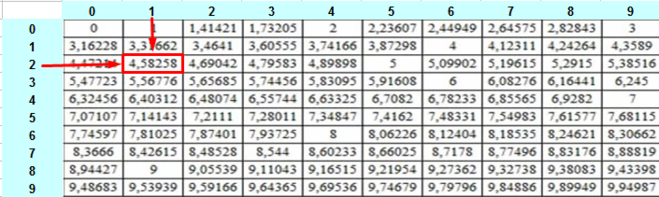 \(\sqrt[3]{5}\). Посмотрим на кубическую корневую таблицу.
\(\sqrt[3]{5}\). Посмотрим на кубическую корневую таблицу.
В таблице необходимо найти данное число, рассматриваем, в какой строчке и в каком столбце они соприкасаются. Строчка — 5, столбик — 0. Получается, что значение будет — 1,70998.
Ответ: \(\sqrt[3]{5}=1,70998.\)
Задача 3
Необходимо рассчитать значение, которое получится после извлечения корня из значения \(\sqrt{64}\). Посмотрим на квадратную корневую таблицу.
Источник: wiki.fenix.helpВ таблице необходимо найти данное число, рассматриваем, в какой строчке и в каком столбце они соприкасаются. Строчка — 6, столбик — 4. Получается, что значение будет — 6,78233.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Стол квадратного корня Hidden Treasuresсо стеклянной столешницей от Hammary
Выбранная комбинация опций недоступна.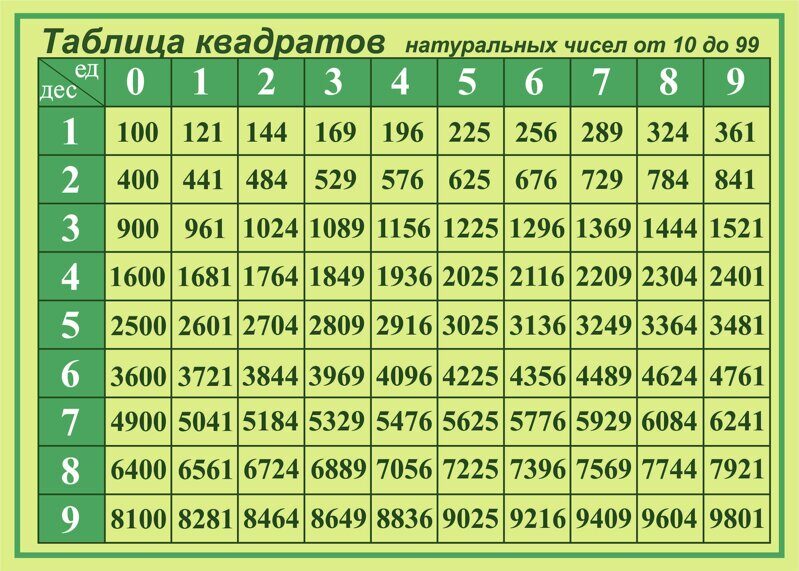
Товар успешно добавлен в корзину.
Наша цена: Наша распродажа: $ 1661,00
+ Бесплатная доставка
- Краткое описание:
- Коллекция Hidden Treasures — это невероятный ассортимент единственных в своем роде акцентных предметов, вдохновленных лучшими дизайнерскими решениями мебели со всего мира. Каждый выбор — настоящее сокровище, богатое иконами и традициями Старого Света.
Предполагаемая дата доставки:
Предполагаемый день доставки:
- Описание
Стол Hidden Treasures Square Root со стеклянной столешницей от Hammary
Коллекция Hidden Treasures — это невероятный ассортимент уникальных акцентных предметов, вдохновленных лучшими дизайнерскими решениями мебели со всего мира.
Особенности:
- Изготовлен из натурального пня камфорного дерева.
О производителе
В октябре 1943 года, после восьми лет работы с производителями мебели в Каролине и Вирджинии в качестве торгового представителя Reliance Varnish Company и Central Glass Company, Гамильтон Лоуден Брюс решил попробовать свои силы в производстве мебели. Арендовав небольшое здание за 15 долларов в месяц, он нанял двух помощников и начал производить садовые стулья с брезентовым покрытием. Производство составляло 24 стула в сутки. Компания получила свое название от Гамильтона и его жены Мэри, поэтому Hammary.
В конце 1947 года г-н Брюс отказался от линии шезлонгов и начал производить группу журнальных столиков. С портфелем, полным дизайнерских эскизов, г-н Брюс быстро обошел восточные магазины мебели и вернулся домой с заказами на 200 000 долларов. .. и это еще до того, как на заводе были изготовлены первые образцы столов. В 1948 году компания начала производить столы из красного дерева и резины с кожаной столешницей и столешницей из красного дерева, а в следующем году перешла на кожаные столешницы исключительно из настоящего красного дерева Гондураса.
.. и это еще до того, как на заводе были изготовлены первые образцы столов. В 1948 году компания начала производить столы из красного дерева и резины с кожаной столешницей и столешницей из красного дерева, а в следующем году перешла на кожаные столешницы исключительно из настоящего красного дерева Гондураса.
Сегодня Hammary предлагает различные стили: столики для особых случаев, стулья и предметы для поиска сокровищ. Группы столов содержат ассортимент таких предметов, как коктейльные столики, столики с лампами и диванные столики с деревянными или стеклянными столешницами на выбор. В дополнение к столам, изготовленным из различных пород дерева, Hammary также предлагает столы, изготовленные из металлов, таких как кованое железо, чугун или литой алюминий, с деревянными, стеклянными или мраморными столешницами.
Размеры:
Габаритные размеры: 54″ Ш x 28″ Г x 19″ H
Стеклянная столешница: толщина 1 дюйм
Общий вес продукта: 60
Требуется сборка: Нет
Таблица квадратного корня и кубического корня
Общие калькуляторы
- Квадратный корень и кубический корень
- Температура плавления металлов
- Перейти на главную страницу
Калькулятор находит кубический корень, квадратный корень, куб и квадрат для заданного значения
| Enter Number | Square | Cube | Square Root | Cube Root |
Table shows the square, cube,square root and cube root of the numbers starting from 1 to 50.
| Номер | квадрат | Куб | Квадратный корень | Кубический корень | |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0083 | 1.000 | 1.000 |
| 2 | 4 | 8 | 1.414 | 1.260 | |
| 3 | 9 | 27 | 1.732 | 1.442 | |
| 4 | 16 | 64 | 2.000 | 1.587 | |
| 5 | 25 | 125 | 2.236 | 1.710 | |
| 6 | 36 | 216 | 2.449 | 1.817 | |
| 7 | 49 | 343 | 2.646 | 1.913 | |
| 8 | 64 | 512 | 2.828 | 2.000 | |
| 9 | 81 | 729 | 3.000 | 2.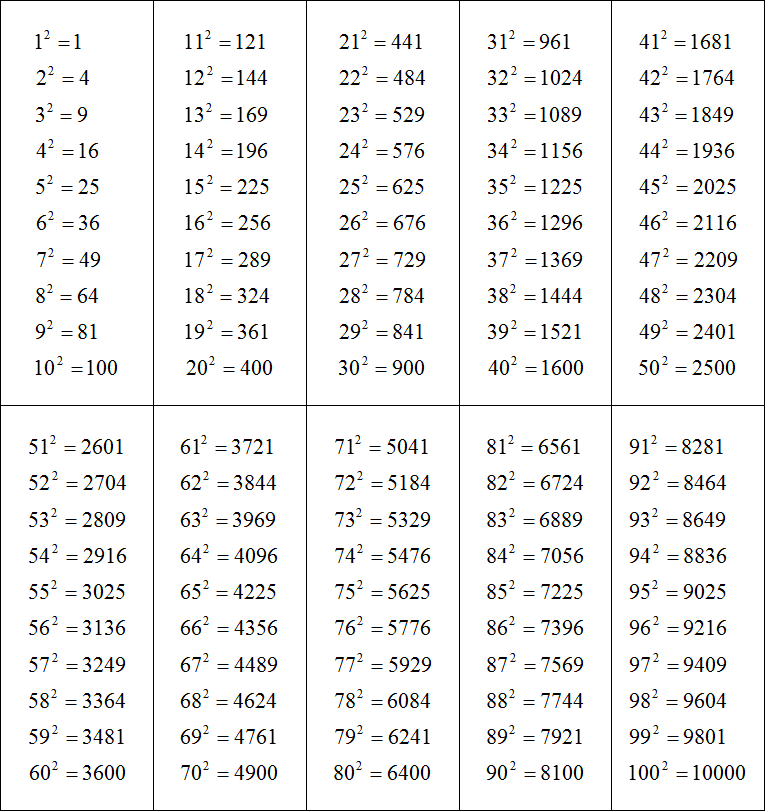 080 080 | |
| 10 | 100 | 1000 | 3.162 | 2.154 | |
| 11 | 121 | 1331 | 3.317 | 2.224 | |
| 12 | 144 | 1728 | 3.464 | 2.289 | |
| 13 | 169 | 2197 | 3.606 | 2.351 | |
| 14 | 196 | 2744 | 3.742 | 2.410 | |
| 15 | 225 | 3375 | 3.873 | 2.466 | |
| 16 | 256 | 4096 | 4.000 | 2.520 | |
| 17 | 289 | 4913 | 4.123 | 2.571 | |
| 18 | 324 | 5832 | 4.243 | 2.621 | |
| 19 | 361 | 6859 | 4.359 | 2.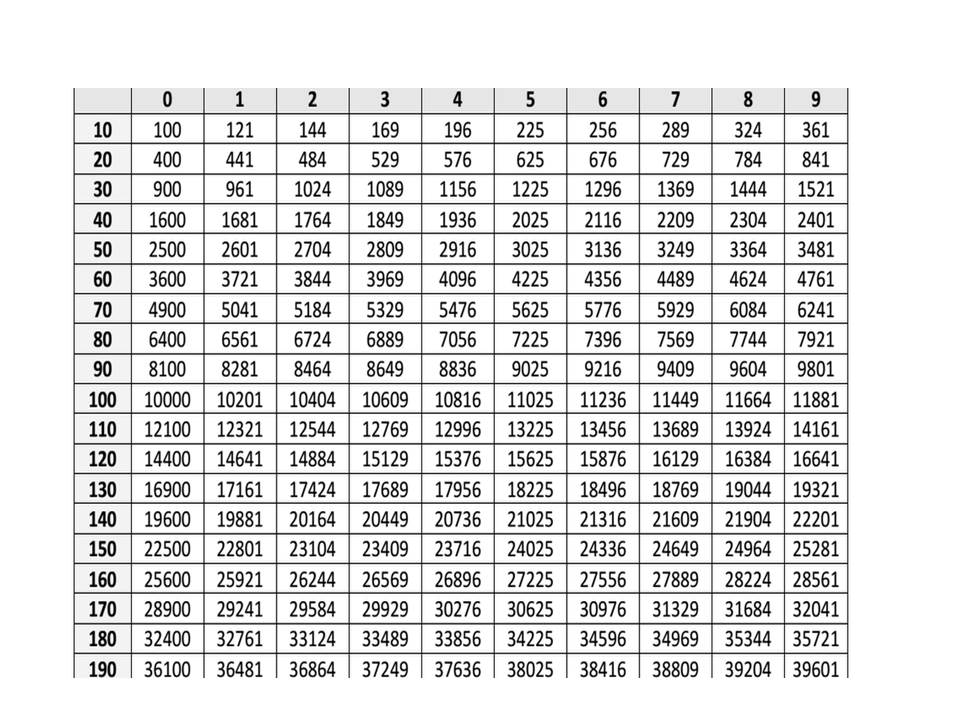 668 668 | |
| 20 | 400 | 8000 | 4.472 | 2.714 | |
| 21 | 441 | 9261 | 4.583 | 2.759 | |
| 22 | 484 | 10648 | 4.690 | 2.802 | |
| 23 | 529 | 12167 | 4.796 | 2.844 | |
| 24 | 576 | 13824 | 4.899 | 2.884 | |
| 25 | 625 | 15625 | 5.000 | 2.924 | |
| 26 | 676 | 17576 | 5.099 | 2.962 | |
| 27 | 729 | 19683 | 5.196 | 3.000 | |
| 28 | 784 | 21952 | 5.292 | 3.037 | |
| 29 | 841 | 24389 | 5. 385 385 | 3.072 | |
| 30 | 900 | 27000 | 5.477 | 3.107 | |
| 31 | 961 | 29791 | 5.568 | 3.141 | |
| 32 | 1024 | 32768 | 5.657 | 3.175 | |
| 33 | 1089 | 35937 | 5.745 | 3.208 | |
| 34 | 1156 | 39304 | 5.831 | 3.240 | |
| 35 | 1225 | 42875 | 5.916 | 3.271 | |
| 36 | 1296 | 46656 | 6.000 | 3.302 | |
| 37 | 1369 | 50653 | 6.083 | 3.332 | |
| 38 | 1444 | 54872 | 6.164 | 3,362 | .0092 |
| 39 | 1521 | 59319 | 6. |


 Приведем пример: \(\pm{\sqrt{4}}=\pm{2}\).
Приведем пример: \(\pm{\sqrt{4}}=\pm{2}\).