Таблица критерия Пирсона χ2 (хи-квадрат) онлайн. Теория вероятностей и математическая статистика
Ниже представлена таблица значений критических точек распределения χ2 (хи-квадрат) критерия Пирсона, широко используемые в задачах математической статистики, таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание.
| Число степеней свободы k | Уровень значимости α | |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,6 | 5 | 3,8 | 0,0039 | 0,00098 | 0,00016 |
| 2 | 9,2 | 7,4 | 6 | 0,103 | 0,051 | 0,02 |
| 3 | 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 |
| 6 | 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 |
| 7 | 18,5 | 16 | 14,1 | 2,17 | 1,69 | 1,24 |
| 8 | 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19 | 16,9 | 3,33 | 2,7 | 2,09 |
| 10 | 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 |
| 11 | 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 23,3 | 21 ,0 | 5,23 | 4,4 | 3,57 |
| 13 | 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 27,5 | 25 | 7,26 | 6,26 | 5,23 |
| 16 | 32 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 28,9 | 9,39 | 8,23 | 7,01 | |
| 19 | 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,9 |
| 22 | 40,3 | 36,8 | 33,9 | 12,3 | 11 | 9,54 |
| 23 | 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | |
| 24 | 43 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 45,7 | 42,6 | 17,7 | 16 | 14,3 |
| 30 | 50,9 | 47 | 43,8 | 18,5 | 16,8 | 15 |
Таблица критических точек распределения Пирсона хи-квадрат
Таблица критических точек распределения Пирсона «хи-квадрат»)
| k /α | 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 |
| 1 | 6,63490 | 5,02389 | 3,84146 | 0,00393 | 0,00098 | 0,00016 |
| 2 | 9,21034 | 7,37776 | 5,99146 | 0,10259 | 0,05064 | 0,02010 |
| 3 | 11,34487 | 9,34840 | 7,81473 | 0,35185 | 0,21580 | 0,11483 |
| 4 | 13,2767 | 11,14329 | 9,48773 | 0,71072 | 0,48442 | 0,29711 |
| 5 | 15,08627 | 12,8325 | 11,0705 | 1,14548 | 0,83121 | 0,55430 |
| 6 | 16,81189 | 14,44938 | 12,59159 | 1,63538 | 1,23734 | 0,87209 |
| 7 | 18,47531 | 16,01276 | 14,06714 | 2,16735 | 1,68987 | 1,23904 |
| 8 | 20,09024 | 17,53455 | 15,50731 | 2,73264 | 2,17973 | 1,64650 |
| 9 | 21,66599 | 19,02277 | 16,91898 | 3,32511 | 2,70039 | 2,08790 |
| 10 | 23,20925 | 20,48318 | 18,30704 | 3,94030 | 3,24697 | 2,55821 |
| 11 | 24,72497 | 21,92005 | 19,67514 | 4,57481 | 3,81575 | 3,05348 |
| 12 | 26,21697 | 23,33666 | 21,02607 | 5,22603 | 4,40379 | 3,57057 |
| 13 | 27,68825 | 24,7356 | 22,36203 | 5,89186 | 5,00875 | 4,10692 |
| 14 | 29,14124 | 26,11895 | 23,68479 | 6,57063 | 5,62873 | 4,66043 |
| 15 | 30,57791 | 27,48839 | 24,99579 | 7,26094 | 6,26214 | 5,22935 |
| 16 | 31,99993 | 28,84535 | 26,29623 | 7,96165 | 6,90766 | 5,81221 |
| 17 | 33,40866 | 30,19101 | 27,58711 | 8,67176 | 7,56419 | 6,40776 |
| 18 | 34,80531 | 31,52638 | 28,86930 | 9,39046 | 8,23075 | 7,01491 |
| 19 | 36,19087 | 32,85233 | 30,14353 | 10,11701 | 8,90652 | 7,63273 |
| 20 | 37,56623 | 34,16961 | 31,41043 | 10,85081 | 9,59078 | 8,26040 |
| 21 | 38,93217 | 35,47888 | 32,67057 | 11,59131 | 10,2829 | 8,89720 |
| 22 | 40,28936 | 36,78071 | 33,92444 | 12,33801 | 10,98232 | 9,54249 |
| 23 | 41,63840 | 38,07563 | 35,17246 | 13,09051 | 11,68855 | 10,19572 |
| 24 | 42,97982 | 39,36408 | 36,41503 | 13,84843 | 12,40115 | 10,85636 |
| 25 | 44,31410 | 40,64647 | 37,65248 | 14,61141 | 13,11972 | 11,52398 |
| 26 | 45,64168 | 41,92317 | 38,88514 | 15,37916 | 13,84391 | 12,19815 |
| 27 | 46,96294 | 43,19451 | 40,11327 | 16,15140 | 14,57338 | 12,87850 |
| 28 | 48,27824 | 44,46079 | 41,33714 | 16,92788 | 15,30786 | 13,56471 |
| 29 | 49,58788 | 45,72229 | 42,55697 | 17,70837 | 16,04707 | 14,25645 |
| 30 | 50,89218 | 46,97924 | 43,77297 | 18,49266 | 16,79077 | 14,95346 |
| 31 | 52,19139 | 48,23189 | 44,98534 | 19,28057 | 17,53874 | 15,65546 |
| 32 | 53,48577 | 49,48044 | 46,19426 | 20,07191 | 18,29076 | 16,36222 |
| 33 | 54,77554 | 50,72508 | 47,39988 | 20,86653 | 19,04666 | 17,07351 |
| 34 | 56,06091 | 51,96600 | 48,60237 | 21,66428 | 19,80625 | 17,78915 |
| 35 | 57,34207 | 53,20335 | 49,80185 | 22,46502 | 20,56938 | 18,50893 |
| 36 | 58,61921 | 54,43729 | 50,99846 | 23,26861 | 21,33588 | 19,23268 |
| 37 | 59,89250 | 55,66797 | 52,19232 | 24,07494 | 22,10563 | 19,96023 |
| 38 | 61,16209 | 56,89552 | 53,38354 | 24,8839 | 22,87848 | 20,69144 |
| 39 | 62,42812 | 58,12006 | 54,57223 | 25,69539 | 23,65432 | 21,42616 |
| 40 | 63,69074 | 59,34171 | 55,75848 | 26,5093 | 24,43304 | 22,16426 |
| 41 | 64,95007 | 60,56057 | 56,94239 | 27,32555 | 25,21452 | 22,90561 |
| 42 | 66,20624 | 61,77676 | 58,12404 | 28,14405 | 25,99866 | 23,65009 |
| 43 | 67,45935 | 62,99036 | 59,30351 | 28,96472 | 26,78537 | 24,39760 |
| 44 | 68,70951 | 64,20146 | 60,48089 | 29,78748 | 27,57457 | 25,14803 |
| 45 | 69,95683 | 65,41016 | 61,65623 | 30,61226 | 28,36615 | 25,90127 |
| 46 | 71,20140 | 66,61653 | 62,82962 | 31,43900 | 29,16005 | 26,65724 |
| 47 | 72,44331 | 67,82065 | 64,00111 | 32,26762 | 29,95620 | 27,41585 |
| 48 | 73,68264 | 69,02259 | 65,17077 | 33,09808 | 30,75451 | 28,17701 |
| 49 | 74,91947 | 70,22241 | 66,33865 | 33,93031 | 31,55492 | 28,94065 |
| 50 | 76,15389 | 71,42020 | 67,50481 | 34,76425 | 32,35736 | 29,70668 |
Обычно такая точность (5 знаков после запятой) не требуется. 2) = \alpha $$
2) = \alpha $$
Значения χ2 критерия Пирсона — таблица
| k | $$P({\chi ^2} > \chi _{}^2) = \alpha $$ | ||||||
| 0,995 | 0,99 | 0,975 | 0,95 | 0,9 | 0,75 | 0,5 | |
| 1 | 0,000039 | 0,00016 | 0,00098 | 0,0039 | 0,016 | 0,102 | 0,455 |
| 2 | 0,01 | 0,02 | 0,051 | 0,103 | 0,211 | 0,575 | 1,39 |
| 3 | 0,072 | 0,115 | 0,216 | 0,352 | 0,584 | 1,21 | 2,37 |
| 4 | 0,207 | 0,297 | 0,484 | 0,711 | 1,06 | 1,92 | 3,36 |
| 5 | 0,412 | 0,554 | 0,831 | 1,15 | 1,61 | 2,67 | 4,35 |
| 6 | 0,676 | 0,872 | 1,24 | 1,64 | 2,2 | 3,45 | 5,35 |
| 7 | 0,989 | 1,24 | 1,69 | 2,17 | 2,83 | 4,25 | 6,35 |
| 8 | 1,34 | 1,65 | 2,18 | 2,73 | 3,49 | 5,07 | 7,34 |
| 9 | 1,73 | 2,09 | 2,7 | 3,33 | 4,17 | 5,9 | 8,34 |
| 10 | 2,16 | 2,56 | 3,25 | 3,94 | 4,87 | 6,74 | 9,34 |
| 11 | 2,6 | 3,05 | 3,82 | 4,57 | 5,58 | 7,58 | 10,3 |
| 12 | 3,07 | 3,57 | 4,4 | 5,23 | 6,3 | 8,44 | 11,3 |
| 13 | 3,57 | 4,11 | 5,01 | 5,89 | 7,04 | 9,3 | 12,3 |
| 14 | 4,07 | 4,66 | 5,63 | 6,57 | 7,79 | 10,2 | 13,3 |
| 15 | 4,6 | 5,23 | 6,26 | 7,26 | 8,55 | 11 | 14,3 |
| 16 | 5,14 | 5,81 | 6,91 | 7,96 | 9,31 | 11,9 | 15,3 |
| 17 | 5,7 | 6,41 | 7,56 | 8,67 | 10,1 | 12,8 | 16,3 |
| 18 | 6,26 | 7,01 | 8,23 | 9,39 | 10,9 | 13,7 | 17,3 |
| 19 | 6,84 | 7,63 | 8,91 | 10,1 | 11,7 | 14,6 | 18,3 |
| 20 | 7,43 | 8,26 | 9,59 | 10,9 | 12,4 | 15,5 | 19,3 |
| 21 | 8,03 | 8,9 | 10,3 | 11,6 | 13,2 | 16,3 | 20,3 |
| 22 | 8,64 | 9,54 | 11,0 | 12,3 | 14,0 | 17,2 | 21,3 |
| 23 | 9,26 | 10,2 | 11,7 | 13,1 | 14,8 | 18,1 | 22,3 |
| 24 | 9,89 | 10,9 | 12,4 | 13,8 | 15,7 | 19,0 | 23,3 |
| 25 | 10,5 | 11,5 | 13,1 | 14,6 | 16,5 | 19,9 | 24,3 |
| 26 | 11,2 | 12,2 | 13,8 | 15,4 | 17,3 | 20,8 | 25,3 |
| 27 | 11,8 | 12,9 | 14,6 | 16,2 | 18,1 | 21,7 | 26,3 |
| 28 | 12,5 | 13,6 | 15,3 | 16,9 | 18,9 | 22,7 | 27,3 |
| 29 | 13,1 | 14,3 | 16,0 | 17,7 | 19,8 | 23,6 | 28,3 |
| 30 | 13,8 | 15 | 16,8 | 18,5 | 20,6 | 24,5 | 29,3 |
| k | $$P({\chi ^2} > \chi _{}^2) = \alpha $$ | ||||||
| 0,995 | 0,99 | 0,975 | 0,95 | 0,9 | 0,75 | 0,5 | |
| 1 | 0,000039 | 0,00016 | 0,00098 | 0,0039 | 0,016 | 0,102 | 0,455 |
| 2 | 0,01 | 0,02 | 0,051 | 0,103 | 0,211 | 0,575 | 1,39 |
| 3 | 0,072 | 0,115 | 0,216 | 0,352 | 0,584 | 1,21 | 2,37 |
| 4 | 0,207 | 0,297 | 0,484 | 0,711 | 1,06 | 1,92 | 3,36 |
| 5 | 0,412 | 0,554 | 0,831 | 1,15 | 1,61 | 2,67 | 4,35 |
| 6 | 0,676 | 0,872 | 1,24 | 1,64 | 2,2 | 3,45 | 5,35 |
| 7 | 0,989 | 1,24 | 1,69 | 2,17 | 2,83 | 4,25 | 6,35 |
| 8 | 1,34 | 1,65 | 2,18 | 2,73 | 3,49 | 5,07 | 7,34 |
| 9 | 1,73 | 2,09 | 2,7 | 3,33 | 4,17 | 5,9 | 8,34 |
| 10 | 2,16 | 2,56 | 3,25 | 3,94 | 4,87 | 6,74 | 9,34 |
| 11 | 2,6 | 3,05 | 3,82 | 4,57 | 5,58 | 7,58 | 10,3 |
| 12 | 3,07 | 3,57 | 4,4 | 5,23 | 6,3 | 8,44 | 11,3 |
| 13 | 3,57 | 4,11 | 5,01 | 5,89 | 7,04 | 9,3 | 12,3 |
| 14 | 4,07 | 4,66 | 5,63 | 6,57 | 7,79 | 10,2 | 13,3 |
| 15 | 4,6 | 5,23 | 6,26 | 7,26 | 8,55 | 11 | 14,3 |
| 16 | 5,14 | 5,81 | 6,91 | 7,96 | 9,31 | 11,9 | 15,3 |
| 17 | 5,7 | 6,41 | 7,56 | 8,67 | 10,1 | 12,8 | 16,3 |
| 18 | 6,26 | 7,01 | 8,23 | 9,39 | 10,9 | 13,7 | 17,3 |
| 19 | 6,84 | 7,63 | 8,91 | 10,1 | 11,7 | 14,6 | 18,3 |
| 20 | 7,43 | 8,26 | 9,59 | 10,9 | 12,4 | 15,5 | 19,3 |
| 21 | 8,03 | 8,9 | 10,3 | 11,6 | 13,2 | 16,3 | 20,3 |
| 22 | 8,64 | 9,54 | 11,0 | 12,3 | 14,0 | 17,2 | 21,3 |
| 23 | 9,26 | 10,2 | 11,7 | 13,1 | 14,8 | 18,1 | 22,3 |
| 24 | 9,89 | 10,9 | 12,4 | 13,8 | 15,7 | 19,0 | 23,3 |
| 25 | 10,5 | 11,5 | 13,1 | 14,6 | 16,5 | 19,9 | 24,3 |
| 26 | 11,2 | 12,2 | 13,8 | 15,4 | 17,3 | 20,8 | 25,3 |
| 27 | 11,8 | 12,9 | 14,6 | 16,2 | 18,1 | 21,7 | 26,3 |
| 28 | 12,5 | 13,6 | 15,3 | 16,9 | 18,9 | 22,7 | 27,3 |
| 29 | 13,1 | 14,3 | 16,0 | 17,7 | 19,8 | 23,6 | 28,3 |
| 30 | 13,8 | 15 | 16,8 | 18,5 | 20,6 | 24,5 | 29,3 |
Как пользоваться таблицей Пирсона
k — число степеней свободы, определяется по формуле:
k=n−r−1
где
m — количество признаков;
r — количество оцениваемых параметров распределения случайной величины.
Для нормального распределения число степеней свободы находится по формуле
k=ι−3
Уровень значимости α берется из условия задачи.
Например α=0,01, k=12, тогда
Получаем значение Fтабл=26,2
6908
Корреляция Пирсона — Учебные пособия по SPSS
Постановка задачи
Возможно, вы захотите проверить, существует ли статистически значимая линейная зависимость между двумя непрерывными переменными, весом и ростом (и, соответственно, сделать вывод, является ли связь значимой в популяции). Вы можете использовать двумерную корреляцию Пирсона, чтобы проверить, существует ли статистически значимая линейная зависимость между ростом и весом, а также определить силу и направление связи.
Перед тестом
В примере данных мы будем использовать две переменные: «Рост» и «Вес». Переменная «Высота» представляет собой непрерывную меру роста в дюймах и имеет диапазон значений от 55,00 до 84,41 ( Анализ > Описательный Статистический > Описательный ). Переменная «Вес» представляет собой непрерывную меру веса в фунтах и имеет диапазон значений от 101,71 до 350,07.
Переменная «Вес» представляет собой непрерывную меру веса в фунтах и имеет диапазон значений от 101,71 до 350,07.
Прежде чем мы рассмотрим корреляции Пирсона, мы должны взглянуть на диаграммы рассеяния наших переменных, чтобы получить представление о том, чего ожидать. В частности, нам нужно определить, разумно ли предположить, что наши переменные имеют линейные отношения. Нажмите Графики > Устаревшие диалоговые окна > Разброс/точка . В окне Scatter/Dot нажмите Simple Scatter , затем нажмите Define . Переместите переменную «Высота» в поле «Ось X» и переместите переменную «Вес» в поле «Ось Y». Когда закончите, нажмите OK .
Чтобы добавить линейную аппроксимацию, как показано на рисунке, дважды щелкните график в средстве просмотра вывода, чтобы открыть редактор диаграмм. Щелкните Элементы > Подогнать линию к сумме . В окне «Свойства» убедитесь, что для параметра «Метод подгонки» установлено значение 9. 0019 Линейный , затем нажмите Применить . (Обратите внимание, что добавление линии тренда линейной регрессии также добавит значение R-квадрата на поля графика. Если мы возьмем квадратный корень из этого числа, оно должно совпадать со значением полученной нами корреляции Пирсона.)
0019 Линейный , затем нажмите Применить . (Обратите внимание, что добавление линии тренда линейной регрессии также добавит значение R-квадрата на поля графика. Если мы возьмем квадратный корень из этого числа, оно должно совпадать со значением полученной нами корреляции Пирсона.)
Из На диаграмме рассеяния мы видим, что по мере увеличения роста вес также имеет тенденцию к увеличению. Кажется, что есть некоторая линейная зависимость.
Запуск теста
Чтобы запустить двумерную корреляцию Пирсона, нажмите Анализ > Сопоставление > Двумерный . Выберите переменные Высота и Вес и переместите их в поле Переменные. В области Коэффициенты корреляции выберите Pearson . В области Test of Significance выберите нужный тест значимости, двусторонний или односторонний. В этом примере мы выберем двусторонний тест значимости. Установите флажок рядом с Пометить существенные корреляции .
Нажмите OK , чтобы запустить двумерную корреляцию Пирсона. Выходные данные для анализа будут отображаться в средстве просмотра выходных данных.
Выходные данные для анализа будут отображаться в средстве просмотра выходных данных.
Синтаксис
КОРРЕЛЯЦИИ /VARIABLES=Вес Рост /PRINT=ДВА ХВОСТА /ОТСУТСТВУЕТ=ПАРА.
Вывод
Таблицы
Результаты будут отображать корреляции в таблице с пометкой Корреляции .
Корреляция высоты с самой собой (r=1) и количество непропущенных наблюдений высоты (n=408).
B Корреляция роста и веса (r=0,513), на основе n=354 наблюдений с попарно непропущенными значениями.
C Корреляция роста и веса (r=0,513), на основе n=354 наблюдений с попарно непропущенными значениями.
D Корреляция веса с самим собой (r=1) и количеством непропущенных наблюдений для веса (n=376).
Важными ячейками, которые мы хотим рассмотреть, являются либо B, либо C. (Ячейки B и C идентичны, потому что они содержат информацию об одной и той же паре переменных.) Ячейки B и C содержат коэффициент корреляции для корреляции между ростом и вес, его p-значение и количество полных парных наблюдений, на которых основан расчет.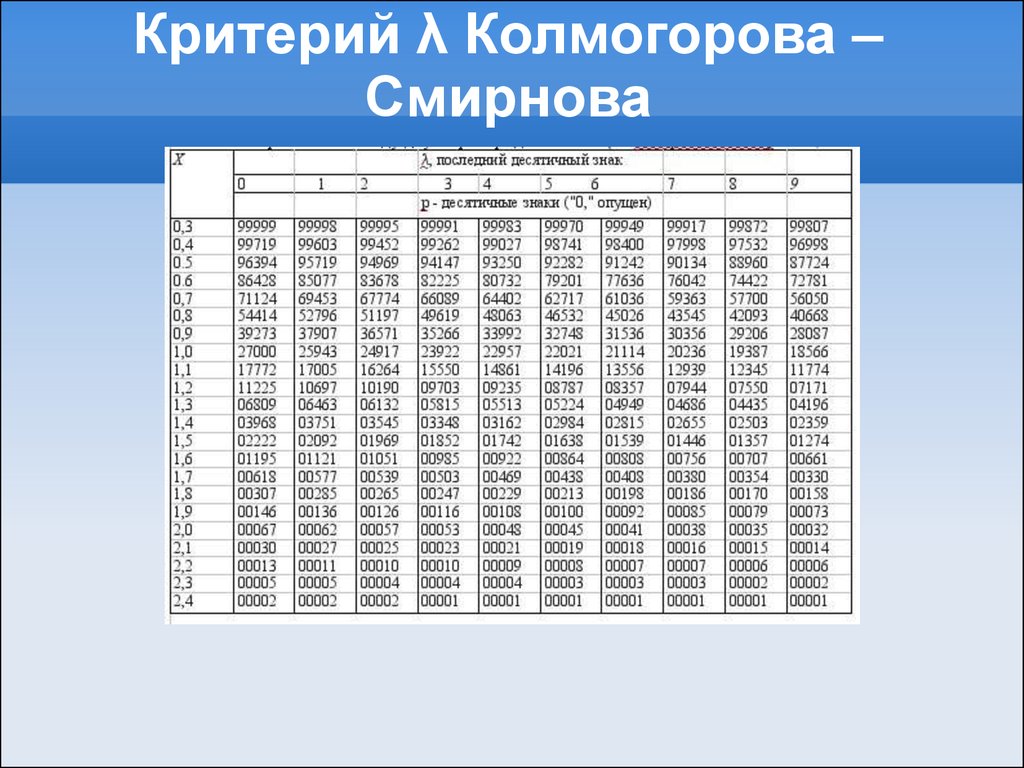
Все корреляции на главной диагонали (ячейки A и D) равны 1. Это потому, что переменная всегда идеально коррелирует сама с собой. Обратите внимание, однако, что размеры выборки отличаются в ячейке A ( n = 408) по сравнению с ячейкой D ( n = 376). Это связано с отсутствующими данными — для переменной Weight пропущено больше наблюдений, чем для переменной Height.
Если вы выбрали пометку значимых корреляций, SPSS отметит уровень значимости 0,05 одной звездочкой (*) и уровень значимости 0,01 двумя звездочками (0,01). В ячейке B (повторяется в ячейке C) мы видим, что коэффициент корреляции Пирсона для роста и веса составляет 0,513, что является значимым ( p < 0,001 для двустороннего теста), на основе 354 полных наблюдений (т. е. случаев с неотсутствующими значениями как для роста, так и для веса).
Решение и выводы
На основании полученных результатов можно констатировать следующее:
- Вес и рост имеют статистически значимую линейную зависимость ( r = 0,513, p < 0,001).

- Направление связи положительное (т. е. рост и вес имеют положительную корреляцию), что означает, что эти переменные имеют тенденцию к совместному увеличению (т. е. больший рост связан с большим весом).
- Величина или сила ассоциации приблизительно умеренная (0,3 < | r | < 0,5).
КОКТЕЙЛЬНЫЙ СТОЛ PEARSON SQUARE
КОКТЕЙЛЬНЫЙ СТОЛ PEARSON SQUAREБЕРКШИР
КОКТЕЙЛЬНЫЙ СТОЛ PEARSON SQUARE
Артикул №: 011-911
Посмотреть всю коллекцию
История American Drew восходит к 19 годам.27. Коллекция Berkshire воплощает богатый опыт в свежем выражении повседневного европейского традиционного стиля.
Об этой коллекции
Габаритные размеры
| Высота: | 18. 00 00 |
| Ширина: | 42.00 |
| Длина: | 42.00 |
Элементы дизайна и функции
Уход и очистка
Уход и очистка/Уход за отделкой. Отделка по своей природе устойчива к незначительным повседневным опасностям или несчастным случаям, однако для сохранения красоты деревянной мебели необходимы некоторые меры предосторожности. (1) Протрите пыль мягкой тканью, слегка смоченной водой. Всегда трите в направлении волокон древесины. (2) Не ставьте напитки прямо на мебель. (3) Мебель не должна находиться под прямыми солнечными лучами. (4) Немедленно удаляйте любые разливы или пятна.
(1) Протрите пыль мягкой тканью, слегка смоченной водой. Всегда трите в направлении волокон древесины. (2) Не ставьте напитки прямо на мебель. (3) Мебель не должна находиться под прямыми солнечными лучами. (4) Немедленно удаляйте любые разливы или пятна.
Другие детали
Hickory Veneers & Select Hardwoods
Скачать
Скачать
СкачатьСОРТИРОВАТЬ ПО По умолчанию от новых к старым от самых старых к новейшим
ВЫСОТА
ТИП МЕБЕЛИСПАЛЬНИ
ГОСТИНАЯ
КОМНАТ
СТОЛОВАЯ
КОМНАТ
АКЦЕНТЫ
- Среднее пятно
- В наличии
ОБЕДЕННЫЙ СТУЛ АННЕТ
ПИСЬМЕННЫЙ СТОЛ BERKSHRE
БУФЕТ КОНКОРД
АЛМАЗНОЕ КРЕСЛО
АЛМАЗНЫЙ КРЕСЛО
ПАНЕЛЬ EASTBROOK ИЗГОЛОВЬЕ КРОВАТИ 5/0
ПАНЕЛЬ EASTBROOK ИЗГОЛОВЬЕ КРОВАТИ 6/6
ЭДМИСТЕН СУНДУК ДЛЯ МОЛОДЧИКОВ
СТОЛ ДЛЯ НОГ ERVIN
ИЗголовье кровати GLENDALE UPH SHELTER 5/0
ИЗГОЛОВЬЕ КРОВАТИ GLENDALE UPH SHELTER 6/6
КРУГЛЫЙ ОБЕДЕННЫЙ СТОЛ HILLCREST В КОМПЛЕКТЕ
ПАНЕЛЬНАЯ КРОВАТЬ KING EASTBROOK В КОМПЛЕКТЕ
КРОВАТЬ-КРОВАТЬ KING GLENDALE UPH В КОМПЛЕКТЕ
ТУМБА МАРТИН
КОМОД MAYVIEW
ЗЕРКАЛО MAYVIEW
ЖУРНАЛЬНЫЙ СТОЛИК PEARSON
ПРЯМОУГОЛЬНЫЙ СТОЛ PEARSON С ВЫДВИЖНЫМ ЯЩИКОМ
ТОРЦЕВОЙ КРУГЛЫЙ СТОЛ PEARSON
ДИВАННЫЙ СТОЛ PEARSON
КОКТЕЙЛЬНЫЙ СТОЛ PEARSON SQUARE
КОМОД ПЕНЛИ
ПАНЕЛЬНАЯ КРОВАТЬ QUEEN EASTBROOK В КОМПЛЕКТЕ
QUEEN GLENDALE UPH SHELTER BED COMPLETE
Коэффициент корреляции Пирсона: бесплатные примеры
Что такое коэффициент корреляции Пирсона? Коэффициент корреляции Пирсона или коэффициент корреляции Пирсона или r Пирсона определяется в статистике как измерение силы взаимосвязи между двумя переменными и их связи друг с другом.
Проще говоря, коэффициент корреляции Пирсона вычисляет эффект изменения одной переменной при изменении другой переменной.
Например: До определенного возраста (в большинстве случаев) рост ребенка будет увеличиваться по мере увеличения его/ее возраста. Конечно, его/ее рост зависит от различных факторов, таких как гены, местонахождение, диета, образ жизни и т. д.
Этот подход основан на ковариации и, таким образом, является лучшим методом измерения взаимосвязи между двумя переменными.
Создать бесплатную учетную запись
Что делает тест коэффициента корреляции Пирсона? Корреляция коэффициента Пирсона имеет высокую статистическую значимость. Он рассматривает взаимосвязь между двумя переменными. Он стремится провести линию через данные двух переменных, чтобы показать их взаимосвязь. Взаимосвязь переменных измеряется с помощью калькулятора коэффициента корреляции Пирсона. Эта линейная зависимость может быть положительной или отрицательной.
Например:
- Положительная линейная зависимость: В большинстве случаев доход человека увеличивается по мере увеличения его/ее возраста.
- Отрицательная линейная зависимость: Если транспортное средство увеличивает скорость, время, затрачиваемое на поездку, уменьшается, и наоборот.
Из приведенного выше примера видно, что коэффициент корреляции Пирсона, r, пытается выяснить две вещи – силу и направление взаимосвязи из заданных размеров выборки.
Формула коэффициента корреляции ПирсонаФормула коэффициента корреляции определяет связь между переменными. Он возвращает значения от -1 до 1. Используйте приведенный ниже калькулятор корреляции коэффициента Пирсона, чтобы измерить силу двух переменных.
Формула коэффициента корреляции Пирсона:
Где:
N = количество пар оценок
Σxy = сумма произведений парных оценок
Σx = сумма баллов x
Σy = сумма баллов y
Σx2 = сумма квадратов баллов x
Σy2 = сумма квадратов баллов y
Коэффициент корреляции Пирсона 3 пошаговое руководство по расчету коэффициента корреляции Пирсона: Шаг первый: Создайте таблицу коэффициентов корреляции Пирсона.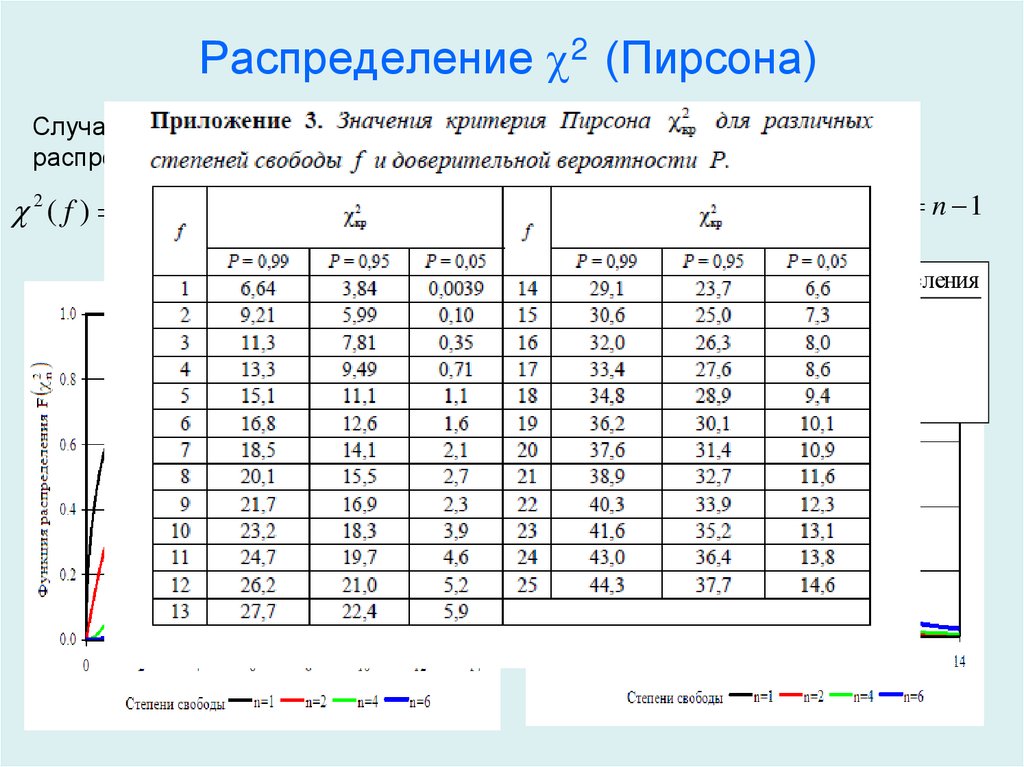 2). Обратитесь к этой простой диаграмме данных.
2). Обратитесь к этой простой диаграмме данных.
Шаг второй: Используйте базовое умножение, чтобы заполнить таблицу.
Шаг третий: Сложите все столбцы снизу вверх.
Шаг четвертый: Используйте формулу корреляции, чтобы подставить значения.
Если результат отрицательный, между двумя переменными существует отрицательная корреляционная связь. Если результат положительный, то существует положительная корреляционная связь между переменными. Результаты также могут определять силу линейной зависимости, т. е. сильную положительную связь, сильную отрицательную связь, среднюю положительную связь и т. д.
Определение силы коэффициента корреляции «произведение-момент» Пирсона Коэффициент корреляции «произведение-момент» Пирсона или просто коэффициент корреляции Пирсона или коэффициент корреляции Пирсона r определяет силу линейной зависимости между двумя переменными. Чем сильнее связь между двумя переменными, тем ближе ваш ответ будет склоняться к 1 или -1.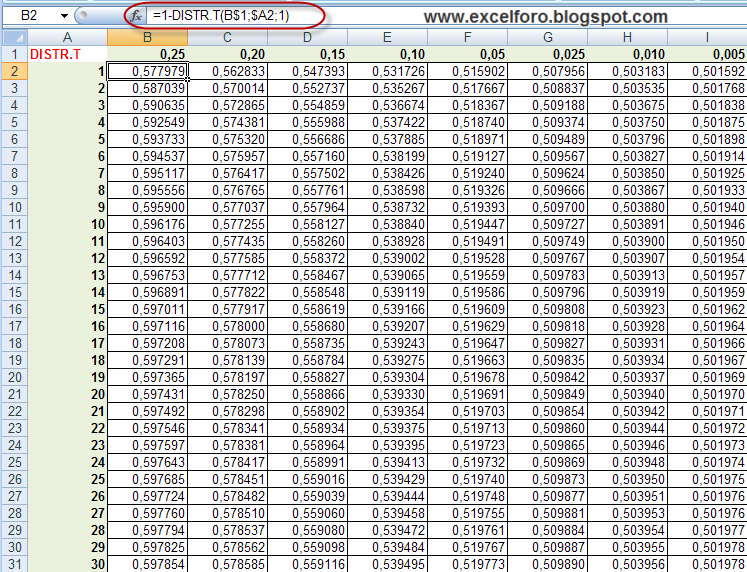 Достижение значений 1 или -1 означает, что все точки данных нанесены на прямую линию «наилучшего соответствия». Это означает, что изменение факторов любой переменной не ослабляет корреляцию с другой переменной. Чем ближе ваш ответ к 0, тем больше вариация переменных.
Достижение значений 1 или -1 означает, что все точки данных нанесены на прямую линию «наилучшего соответствия». Это означает, что изменение факторов любой переменной не ослабляет корреляцию с другой переменной. Чем ближе ваш ответ к 0, тем больше вариация переменных.
Ниже приведены предлагаемые рекомендации по интерпретации коэффициента корреляции Пирсона:
Обратите внимание, что сила связи переменных зависит от того, что вы измеряете, и размеров выборки.
На графике можно заметить взаимосвязь между переменными и сделать предположения еще до их расчета. Диаграммы рассеяния, если они близки к линии, показывают сильную связь между переменными. Чем ближе диаграммы рассеяния лежат рядом с линией, тем сильнее взаимосвязь переменных. Чем дальше они отходят от линии, тем слабее становятся отношения. Если линия почти параллельна оси x из-за случайно расположенных на графике диаграмм рассеяния, можно с уверенностью предположить, что между двумя переменными нет корреляции.
Термины «сила» и «направление» имеют статистическую значимость. Вот простое объяснение двух слов:
- Сила: Сила означает корреляцию отношений между двумя переменными. Он означает, насколько последовательно будет меняться одна переменная за счет изменения другой. Значения, близкие к +1 или -1, указывают на сильную связь. Эти значения достигаются, если точки данных попадают на линию или очень близко к ней. Чем дальше точки данных удаляются, тем слабее сила линейной зависимости. Когда нет практического способа провести прямую линию, потому что точки данных разбросаны, сила линейной зависимости самая слабая.
- Направление: Направление линии указывает на положительную линейную или отрицательную линейную зависимость между переменными. Если линия имеет восходящий наклон, переменные имеют положительную связь. Это означает, что увеличение значения одной переменной приведет к увеличению значения другой переменной.
 Отрицательная корреляция изображает нисходящий наклон. Это означает, что увеличение количества одной переменной приводит к уменьшению значения другой переменной.
Отрицательная корреляция изображает нисходящий наклон. Это означает, что увеличение количества одной переменной приводит к уменьшению значения другой переменной.
Создать бесплатную учетную запись
Примеры коэффициента корреляции ПирсонаДавайте рассмотрим несколько наглядных примеров, которые помогут вам интерпретировать таблицу коэффициентов корреляции Пирсона:
- Большая положительная корреляция:6
На приведенном выше рисунке показана корреляция почти +1.
Диаграммы рассеяния построены почти на прямой линии.
Наклон положительный, что означает, что если одна переменная увеличивается, другая переменная также увеличивается, показывая положительную линейную линию.
Это означает, что изменение одной переменной прямо пропорционально изменению другой переменной.
Примером большой положительной корреляции может быть: По мере того, как дети растут, растут и размеры их одежды и обуви.
Давайте рассмотрим несколько наглядных примеров, которые помогут вам интерпретировать таблицу коэффициентов корреляции Пирсона:
- Средняя положительная корреляция:
На рисунке выше показана положительная корреляция.
Корреляция выше +0,8, но ниже 1+.
Он показывает довольно четкую линейную картину подъема.
Примером средней положительной корреляции может быть: По мере увеличения количества автомобилей увеличивается потребность в топливной переменной.
- Малая отрицательная корреляция
На приведенном выше рисунке графики рассеяния не так близки к прямой линии по сравнению с более ранними примерами
На ней показана отрицательная линейная корреляция приблизительно -0,5
Изменение одной переменной обратно пропорционально изменению другой переменной так как наклон отрицательный.
Примером небольшой отрицательной корреляции может быть: чем больше кто-то ест, тем меньше он голоден.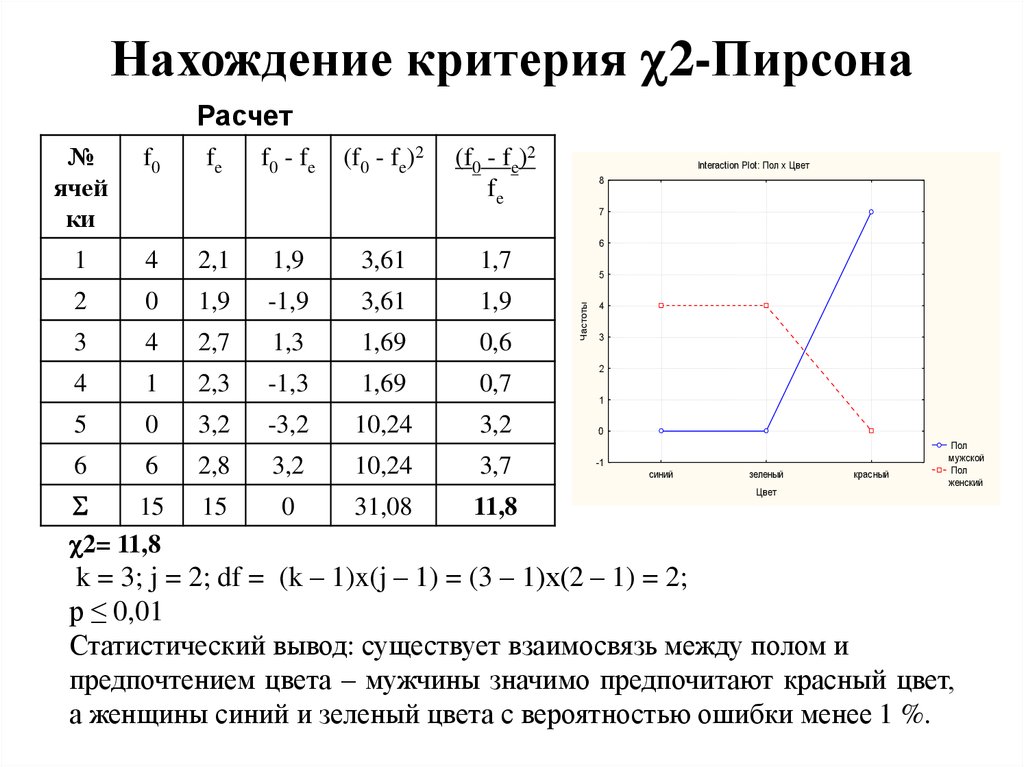


 Отрицательная корреляция изображает нисходящий наклон. Это означает, что увеличение количества одной переменной приводит к уменьшению значения другой переменной.
Отрицательная корреляция изображает нисходящий наклон. Это означает, что увеличение количества одной переменной приводит к уменьшению значения другой переменной.