Таблица тригонометрических функций.
Таблица тригонометрических функций — это записанные в таблицу посчитанные значения синусов, косинусов, тангенсов и котангенсов углов от 0° до 360°. Используя таблицу тригонометрических функций Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение тригонометрических функций от нужного Вам угла достаточно найти их в таблице.
Таблица тригонометрических функций углов от 0° до 90°
| α | sin α | cos α | tg α | ctg α |
| 0° | 0 | 1 | 0 | ∞ |
| 1° | 0.017452 | 0.999848 | 0.017455 | 57.289962 |
| 2° | 0.034899 | 999391″>0.999391 | 28.636253 | |
| 3° | 0.052336 | 0.99863 | 0.052408 | 19.081137 |
| 4° | 0.069756 | 0.997564 | 0.069927 | 14.300666 |
| 5° | 0.087156 | 0.996195 | 0.087489 | 11.430052 |
| 6° | 0.104528 | 0.994522 | 0.105104 | 9.514364 |
| 7° | 0.121869 | 0.992546 | 122785″>0.122785 | 8.144346 |
| 8° | 0.139173 | 0.990268 | 0.140541 | 7.11537 |
| 9° | 0.156434 | 0.987688 | 0.158384 | 6.313752 |
| 10° | 0.173648 | 0.984808 | 0.176327 | 5.671282 |
| 11° | 0.190809 | 0.981627 | 0.19438 | 5.144554 |
| 12° | 0.207912 | 0.212557 | 70463″>4.70463 | |
| 13° | 0.224951 | 0.97437 | 0.230868 | 4.331476 |
| 14° | 0.241922 | 0.970296 | 0.249328 | 4.010781 |
| 15° | 0.258819 | 0.965926 | 0.267949 | 3.732051 |
| 16° | 0.275637 | 0.961262 | 0.286745 | 3.487414 |
| 17° | 0.292372 | 0.956305 | 0.305731 | 3.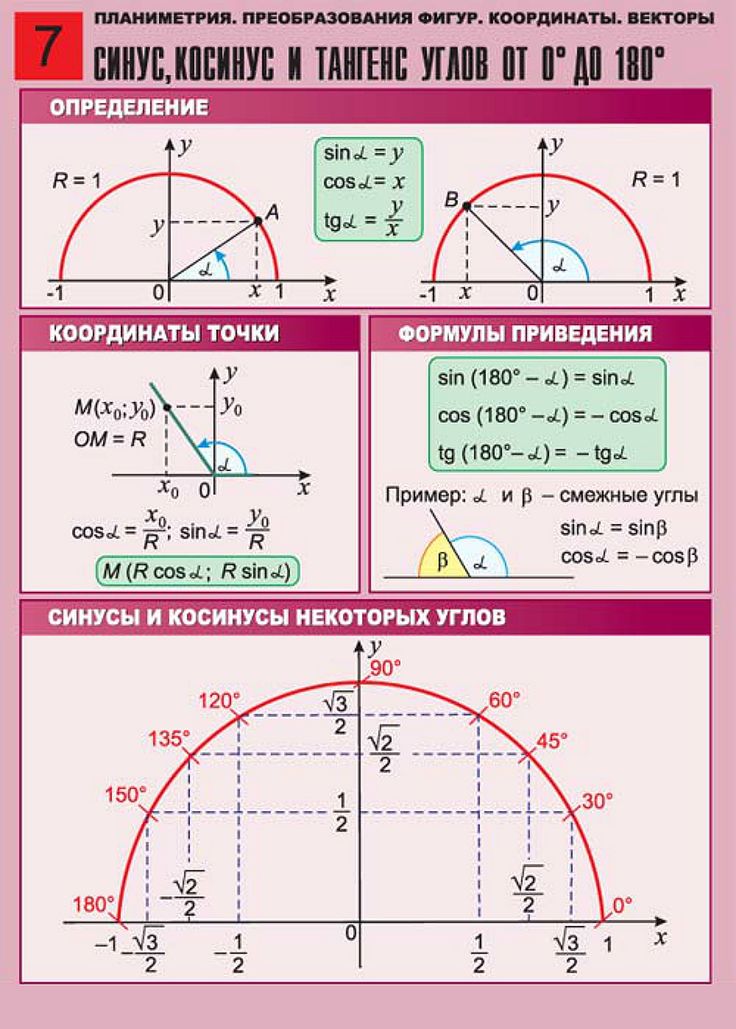 270853 270853 |
| 18° | 0.309017 | 0.951057 | 0.32492 | 3.077684 |
| 19° | 0.325568 | 0.945519 | 0.344328 | 2.904211 |
| 20° | 0.34202 | 0.939693 | 0.36397 | 2.747477 |
| 21° | 0.93358 | 0.383864 | 2.605089 | |
| 22° | 0.374607 | 0.927184 | 0.404026 | 2.475087 |
| 23° | 390731″>0.390731 | 0.920505 | 0.424475 | 2.355852 |
| 24° | 0.406737 | 0.913545 | 0.445229 | 2.246037 |
| 25° | 0.422618 | 0.906308 | 0.466308 | 2.144507 |
| 26° | 0.438371 | 0.898794 | 0.487733 | 2.050304 |
| 27° | 0.45399 | 0.891007 | 0.509525 | 1.962611 |
| 28° | 0.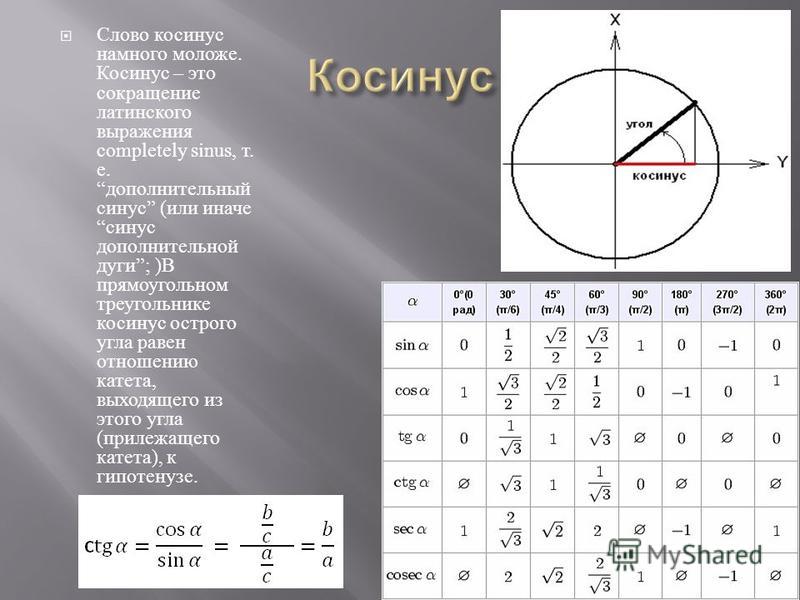 469472 469472 | 0.882948 | 0.531709 | 1.880726 |
| 29° | 0.48481 | 0.87462 | 0.554309 | 1.804048 |
| 30° | 0.866025 | 0.57735 | 1.732051 | |
| 31° | 0.515038 | 0.857167 | 0.600861 | 1.664279 |
| 32° | 0.529919 | 0.848048 | 0.624869 | 1.600335 |
| 33° | 0.544639 | 838671″>0.838671 | 0.649408 | 1.539865 |
| 34° | 0.559193 | 0.829038 | 0.674509 | 1.482561 |
| 35° | 0.573576 | 0.819152 | 0.700208 | 1.428148 |
| 36° | 0.587785 | 0.809017 | 0.726543 | 1.376382 |
| 37° | 0.601815 | 0.798636 | 0.753554 | 1.327045 |
| 38° | 0.615661 | 0.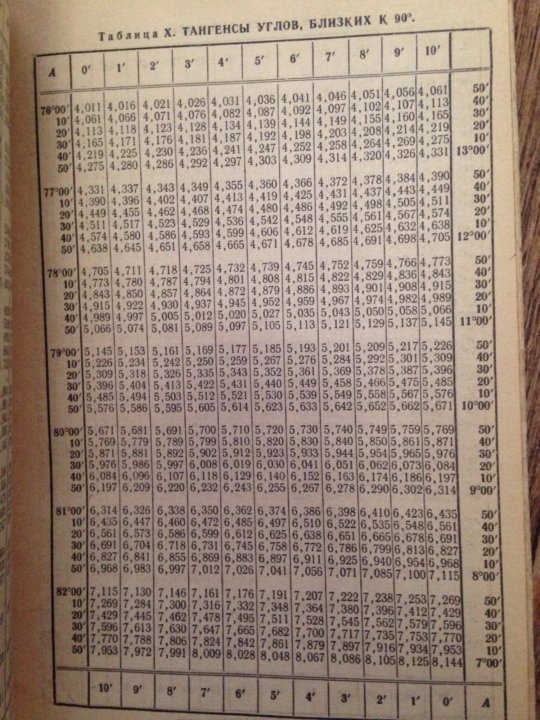 788011 788011 | 0.781286 | 1.279942 |
| 39° | 0.62932 | 0.777146 | 0.809784 | 1.234897 |
| 40° | 0.642788 | 0.766044 | 0.8391 | 1.191754 |
| 41° | 0.656059 | 0.75471 | 0.869287 | 1.150368 |
| 42° | 0.669131 | 0.743145 | 0.900404 | 1.110613 |
| 43° | 0.681998 | 0.731354 | 932515″>0.932515 | 1.072369 |
| 44° | 0.694658 | 0.71934 | 0.965689 | 1.03553 |
| 45° | 0.707107 | 0.707107 | 1 | 1 |
| 46° | 0.71934 | 0.694658 | 1.03553 | 0.965689 |
| 47° | 0.731354 | 0.681998 | 1.072369 | 0.932515 |
| 48° | 0.743145 | 0.669131 | 1.110613 | 900404″>0.900404 |
| 49° | 0.75471 | 0.656059 | 1.150368 | 0.869287 |
| 50° | 0.766044 | 0.642788 | 1.191754 | 0.8391 |
| 51° | 0.777146 | 0.62932 | 1.234897 | 0.809784 |
| 52° | 0.788011 | 0.615661 | 1.279942 | 0.781286 |
| 53° | 0.798636 | 0.601815 | 1.327045 | 0.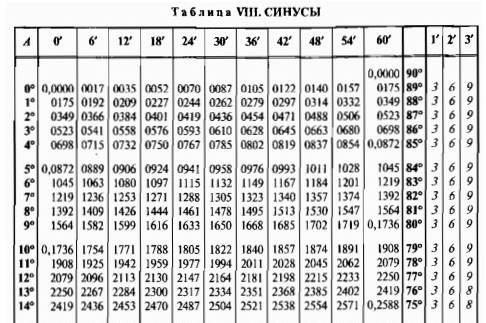 753554 753554 |
| 54° | 0.809017 | 0.587785 | 1.376382 | 0.726543 |
| 55° | 0.819152 | 0.573576 | 1.428148 | 0.700208 |
| 56° | 0.829038 | 0.559193 | 1.482561 | 0.674509 |
| 57° | 0.838671 | 0.544639 | 1.539865 | 0.649408 |
| 58° | 0.848048 | 0.529919 | 1.600335 | 0.624869 |
| 59° | 857167″>0.857167 | 0.515038 | 1.664279 | 0.600861 |
| 60° | 0.866025 | 0.5 | 1.732051 | 0.57735 |
| 61° | 0.87462 | 0.48481 | 1.804048 | 0.554309 |
| 62° | 0.882948 | 0.469472 | 1.880726 | 0.531709 |
| 63° | 0.891007 | 0.45399 | 1.962611 | 0.509525 |
| 64° | 0.898794 | 438371″>0.438371 | 2.050304 | 0.487733 |
| 65° | 0.906308 | 0.422618 | 2.144507 | 0.466308 |
| 66° | 0.913545 | 0.406737 | 2.246037 | 0.445229 |
| 67° | 0.920505 | 0.390731 | 2.355852 | 0.424475 |
| 68° | 0.927184 | 0.374607 | 2.475087 | 0.404026 |
| 69° | 0.93358 | 0.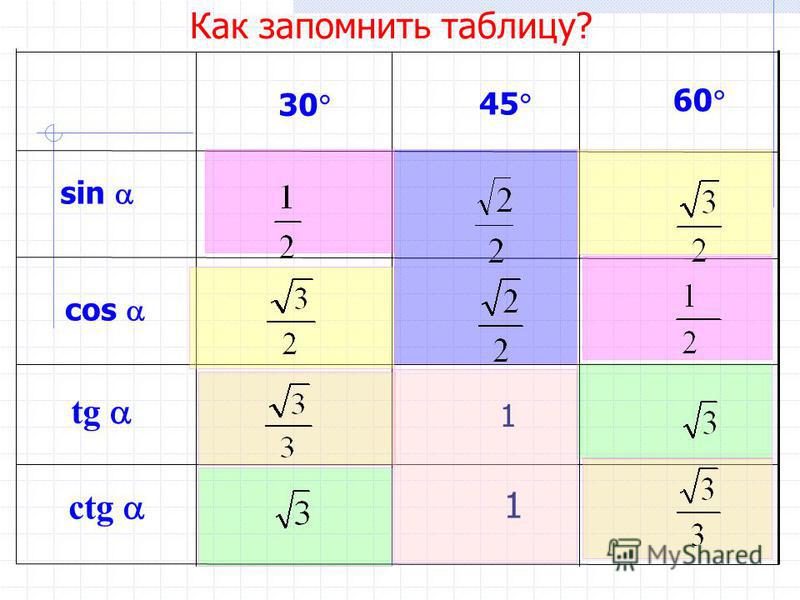 358368 358368 | 2.605089 | 0.383864 |
| 70° | 0.939693 | 0.34202 | 2.747477 | 0.36397 |
| 71° | 0.945519 | 0.325568 | 2.904211 | 0.344328 |
| 72° | 0.951057 | 0.309017 | 3.077684 | 0.32492 |
| 73° | 0.956305 | 0.292372 | 3.270853 | 0.305731 |
| 74° | 0.961262 | 0.275637 | 487414″>3.487414 | 0.286745 |
| 75° | 0.965926 | 0.258819 | 3.732051 | 0.267949 |
| 76° | 0.970296 | 0.241922 | 4.010781 | 0.249328 |
| 77° | 0.97437 | 0.224951 | 4.331476 | 0.230868 |
| 78° | 0.978148 | 0.207912 | 4.70463 | 0.212557 |
| 79° | 0.981627 | 0.190809 | 5. 144554 144554 | 0.19438 |
| 80° | 0.984808 | 0.173648 | 5.671282 | 0.176327 |
| 81° | 0.987688 | 0.156434 | 6.313752 | 0.158384 |
| 82° | 0.990268 | 0.139173 | 7.11537 | 0.140541 |
| 83° | 0.992546 | 0.121869 | 8.144346 | 0.122785 |
| 84° | 0.994522 | 0.104528 | 9.514364 | 105104″>0.105104 |
| 85° | 0.996195 | 0.087156 | 11.430052 | 0.087489 |
| 86° | 0.997564 | 0.069756 | 14.300666 | 0.069927 |
| 87° | 0.99863 | 0.052336 | 19.081137 | 0.052408 |
| 88° | 0.999391 | 0.034899 | 28.636253 | 0.034921 |
| 89° | 0.999848 | 0.017452 | 57.289962 | 017455″>0.017455 |
| 90° | 1 | 0 | ∞ | 0 |
Таблица тригонометрических функций углов от 91° до 180°
| α | sin α | cos α | tg α | ctg α |
| 91° | 0.999848 | -0.017452 | -57.289962 | -0.017455 |
| 92° | 0.999391 | -0.034899 | -28.636253 | -0.034921 |
| 93° | 0.99863 | -0.052336 | -19.081137 | -0.052408 |
| 94° | 997564″>0.997564 | -0.069756 | -14.300666 | -0.069927 |
| 95° | 0.996195 | -0.087156 | -11.430052 | -0.087489 |
| 96° | 0.994522 | -0.104528 | -9.514364 | -0.105104 |
| 97° | 0.992546 | -0.121869 | -8.144346 | -0.122785 |
| 98° | 0.990268 | -0.139173 | -7.11537 | -0.140541 |
| 99° | 987688″>0.987688 | -0.156434 | -6.313752 | -0.158384 |
| 100° | 0.984808 | -0.173648 | -5.671282 | -0.176327 |
| 101° | 0.981627 | -0.190809 | -5.144554 | -0.19438 |
| 102° | 0.978148 | -0.207912 | -4.70463 | -0.212557 |
| 103° | 0.97437 | -0.224951 | -4.331476 | -0.230868 |
| 104° | 970296″>0.970296 | -0.241922 | -4.010781 | -0.249328 |
| 105° | 0.965926 | -0.258819 | -3.732051 | -0.267949 |
| 106° | 0.961262 | -0.275637 | -3.487414 | -0.286745 |
| 107° | 0.956305 | -0.292372 | -3.270853 | -0.305731 |
| 108° | 0.951057 | -0.309017 | -3.077684 | -0.32492 |
| 109° | 945519″>0.945519 | -0.325568 | -2.904211 | -0.344328 |
| 110° | 0.939693 | -0.34202 | -2.747477 | -0.36397 |
| 111° | 0.93358 | -0.358368 | -2.605089 | -0.383864 |
| 112° | 0.927184 | -0.374607 | -2.475087 | -0.404026 |
| 113° | 0.920505 | -0.390731 | -2.355852 | -0.424475 |
| 114° | 913545″>0.913545 | -0.406737 | -2.246037 | -0.445229 |
| 115° | 0.906308 | -0.422618 | -2.144507 | -0.466308 |
| 116° | 0.898794 | -0.438371 | -2.050304 | -0.487733 |
| 117° | 0.891007 | -0.45399 | -1.962611 | -0.509525 |
| 118° | 0.882948 | -0.469472 | -1.880726 | -0.531709 |
| 119° | 87462″>0.87462 | -0.48481 | -1.804048 | -0.554309 |
| 120° | 0.866025 | -0.5 | -1.732051 | -0.57735 |
| 121° | 0.857167 | -0.515038 | -1.664279 | -0.600861 |
| 122° | 0.848048 | -0.529919 | -1.600335 | -0.624869 |
| 123° | 0.838671 | -0.544639 | -1.539865 | -0.649408 |
| 124° | 829038″>0.829038 | -0.559193 | -1.482561 | -0.674509 |
| 125° | 0.819152 | -0.573576 | -1.428148 | -0.700208 |
| 126° | 0.809017 | -0.587785 | -1.376382 | -0.726543 |
| 127° | 0.798636 | -0.601815 | -1.327045 | -0.753554 |
| 128° | 0.788011 | -0.615661 | -1.279942 | -0.781286 |
| 129° | 777146″>0.777146 | -0.62932 | -1.234897 | -0.809784 |
| 130° | 0.766044 | -0.642788 | -1.191754 | -0.8391 |
| 131° | 0.75471 | -0.656059 | -1.150368 | -0.869287 |
| 132° | 0.743145 | -0.669131 | -1.110613 | -0.900404 |
| 133° | 0.731354 | -0.681998 | -1.072369 | -0.932515 |
| 134° | 71934″>0.71934 | -0.694658 | -1.03553 | -0.965689 |
| 135° | 0.707107 | -0.707107 | -1 | -1 |
| 136° | 0.694658 | -0.71934 | -0.965689 | -1.03553 |
| 137° | 0.681998 | -0.731354 | -0.932515 | -1.072369 |
| 138° | 0.669131 | -0.743145 | -0.900404 | -1.110613 |
| 139° | 656059″>0.656059 | -0.75471 | -0.869287 | -1.150368 |
| 140° | 0.642788 | -0.766044 | -0.8391 | -1.191754 |
| 141° | 0.62932 | -0.777146 | -0.809784 | -1.234897 |
| 142° | 0.615661 | -0.788011 | -0.781286 | -1.279942 |
| 143° | 0.601815 | -0.798636 | -0.753554 | -1.327045 |
| 144° | 587785″>0.587785 | -0.809017 | -0.726543 | -1.376382 |
| 145° | 0.573576 | -0.819152 | -0.700208 | -1.428148 |
| 146° | 0.559193 | -0.829038 | -0.674509 | -1.482561 |
| 147° | 0.544639 | -0.838671 | -0.649408 | -1.539865 |
| 148° | 0.529919 | -0.848048 | -0.624869 | -1.600335 |
| 149° | 515038″>0.515038 | -0.857167 | -0.600861 | -1.664279 |
| 150° | 0.5 | -0.866025 | -0.57735 | -1.732051 |
| 151° | 0.48481 | -0.87462 | -0.554309 | -1.804048 |
| 152° | 0.469472 | -0.882948 | -0.531709 | -1.880726 |
| 153° | 0.45399 | -0.891007 | -0.509525 | -1.962611 |
| 154° | 438371″>0.438371 | -0.898794 | -0.487733 | -2.050304 |
| 155° | 0.422618 | -0.906308 | -0.466308 | -2.144507 |
| 156° | 0.406737 | -0.913545 | -0.445229 | -2.246037 |
| 157° | 0.390731 | -0.920505 | -0.424475 | -2.355852 |
| 158° | 0.374607 | -0.927184 | -0.404026 | -2.475087 |
| 159° | 358368″>0.358368 | -0.93358 | -0.383864 | -2.605089 |
| 160° | 0.34202 | -0.939693 | -0.36397 | -2.747477 |
| 161° | 0.325568 | -0.945519 | -0.344328 | -2.904211 |
| 162° | 0.309017 | -0.951057 | -0.32492 | -3.077684 |
| 163° | 0.292372 | -0.956305 | -0.305731 | -3.270853 |
| 164° | 275637″>0.275637 | -0.961262 | -0.286745 | -3.487414 |
| 165° | 0.258819 | -0.965926 | -0.267949 | -3.732051 |
| 166° | 0.241922 | -0.970296 | -0.249328 | -4.010781 |
| 167° | 0.224951 | -0.97437 | -0.230868 | -4.331476 |
| 168° | 0.207912 | -0.978148 | -0.212557 | -4.70463 |
| 169° | 190809″>0.190809 | -0.981627 | -0.19438 | -5.144554 |
| 170° | 0.173648 | -0.984808 | -0.176327 | -5.671282 |
| 171° | 0.156434 | -0.987688 | -0.158384 | -6.313752 |
| 172° | 0.139173 | -0.990268 | -0.140541 | -7.11537 |
| 173° | 0.121869 | -0.992546 | -0.122785 | -8.144346 |
| 174° | 104528″>0.104528 | -0.994522 | -0.105104 | -9.514364 |
| 175° | 0.087156 | -0.996195 | -0.087489 | -11.430052 |
| 176° | 0.069756 | -0.997564 | -0.069927 | -14.300666 |
| 177° | 0.052336 | -0.99863 | -0.052408 | -19.081137 |
| 178° | 0.034899 | -0.999391 | -0.034921 | -28. 636253 636253 |
| 179° | 0.017452 | -0.999848 | -0.017455 | -57.289962 |
| 180° | 0 | -1 | 0 | ∞ |
Таблица тригонометрических функций углов от 181° до 270°
| α | sin α | cos α | tg α | ctg α |
| 181° | -0.017452 | -0.999848 | 0.017455 | 57.289962 |
| 182° | -0.034899 | -0.999391 | 0.034921 | 28.636253 |
| 183° | 052336″>-0.052336 | -0.99863 | 0.052408 | 19.081137 |
| 184° | -0.069756 | -0.997564 | 0.069927 | 14.300666 |
| 185° | -0.087156 | -0.996195 | 0.087489 | 11.430052 |
| 186° | -0.104528 | -0.994522 | 0.105104 | 9.514364 |
| 187° | -0.121869 | -0.992546 | 0.122785 | 8.144346 |
| 188° | 139173″>-0.139173 | -0.990268 | 0.140541 | 7.11537 |
| 189° | -0.156434 | -0.987688 | 0.158384 | 6.313752 |
| 190° | -0.173648 | -0.984808 | 0.176327 | 5.671282 |
| 191° | -0.190809 | -0.981627 | 0.19438 | 5.144554 |
| 192° | -0.207912 | -0.978148 | 0.212557 | 4.70463 |
| 193° | 224951″>-0.224951 | -0.97437 | 0.230868 | 4.331476 |
| 194° | -0.241922 | -0.970296 | 0.249328 | 4.010781 |
| 195° | -0.258819 | -0.965926 | 0.267949 | 3.732051 |
| 196° | -0.275637 | -0.961262 | 0.286745 | 3.487414 |
| 197° | -0.292372 | -0.956305 | 0.305731 | 3.270853 |
| 198° | 309017″>-0.309017 | -0.951057 | 0.32492 | 3.077684 |
| 199° | -0.325568 | -0.945519 | 0.344328 | 2.904211 |
| 200° | -0.34202 | -0.939693 | 0.36397 | 2.747477 |
| 201° | -0.358368 | -0.93358 | 0.383864 | 2.605089 |
| 202° | -0.374607 | -0.927184 | 0.404026 | 2.475087 |
| 203° | 390731″>-0.390731 | -0.920505 | 0.424475 | 2.355852 |
| 204° | -0.406737 | -0.913545 | 0.445229 | 2.246037 |
| 205° | -0.422618 | -0.906308 | 0.466308 | 2.144507 |
| 206° | -0.438371 | -0.898794 | 0.487733 | 2.050304 |
| 207° | -0.45399 | -0.891007 | 0.509525 | 1.962611 |
| 208° | 469472″>-0.469472 | -0.882948 | 0.531709 | 1.880726 |
| 209° | -0.48481 | -0.87462 | 0.554309 | 1.804048 |
| 210° | -0.5 | -0.866025 | 0.57735 | 1.732051 |
| 211° | -0.515038 | -0.857167 | 0.600861 | 1.664279 |
| 212° | -0.529919 | -0.848048 | 0.624869 | 1.600335 |
| 213° | 544639″>-0.544639 | -0.838671 | 0.649408 | 1.539865 |
| 214° | -0.559193 | -0.829038 | 0.674509 | 1.482561 |
| 215° | -0.573576 | -0.819152 | 0.700208 | 1.428148 |
| 216° | -0.587785 | -0.809017 | 0.726543 | 1.376382 |
| 217° | -0.601815 | -0.798636 | 0.753554 | 1.327045 |
| 218° | 615661″>-0.615661 | -0.788011 | 0.781286 | 1.279942 |
| 219° | -0.62932 | -0.777146 | 0.809784 | 1.234897 |
| 220° | -0.642788 | -0.766044 | 0.8391 | 1.191754 |
| 221° | -0.656059 | -0.75471 | 0.869287 | 1.150368 |
| 222° | -0.669131 | -0.743145 | 0.900404 | 1.110613 |
| 223° | 681998″>-0.681998 | -0.731354 | 0.932515 | 1.072369 |
| 224° | -0.694658 | -0.71934 | 0.965689 | 1.03553 |
| 225° | -0.707107 | -0.707107 | 1 | 1 |
| 226° | -0.71934 | -0.694658 | 1.03553 | 0.965689 |
| 227° | -0.731354 | -0.681998 | 1.072369 | 0.932515 |
| 228° | 743145″>-0.743145 | -0.669131 | 1.110613 | 0.900404 |
| 229° | -0.75471 | -0.656059 | 1.150368 | 0.869287 |
| 230° | -0.766044 | -0.642788 | 1.191754 | 0.8391 |
| 231° | -0.777146 | -0.62932 | 1.234897 | 0.809784 |
| 232° | -0.788011 | -0.615661 | 1.279942 | 0.781286 |
| 233° | 798636″>-0.798636 | -0.601815 | 1.327045 | 0.753554 |
| 234° | -0.809017 | -0.587785 | 1.376382 | 0.726543 |
| 235° | -0.819152 | -0.573576 | 1.428148 | 0.700208 |
| 236° | -0.829038 | -0.559193 | 1.482561 | 0.674509 |
| 237° | -0.838671 | -0.544639 | 1.539865 | 0.649408 |
| 238° | 848048″>-0.848048 | -0.529919 | 1.600335 | 0.624869 |
| 239° | -0.857167 | -0.515038 | 1.664279 | 0.600861 |
| 240° | -0.866025 | -0.5 | 1.732051 | 0.57735 |
| 241° | -0.87462 | -0.48481 | 1.804048 | 0.554309 |
| 242° | -0.882948 | -0.469472 | 1.880726 | 0.531709 |
| 243° | 891007″>-0.891007 | -0.45399 | 1.962611 | 0.509525 |
| 244° | -0.898794 | -0.438371 | 2.050304 | 0.487733 |
| 245° | -0.906308 | -0.422618 | 2.144507 | 0.466308 |
| 246° | -0.913545 | -0.406737 | 2.246037 | 0.445229 |
| 247° | -0.920505 | -0.390731 | 2.355852 | 0.424475 |
| 248° | 927184″>-0.927184 | -0.374607 | 2.475087 | 0.404026 |
| 249° | -0.93358 | -0.358368 | 2.605089 | 0.383864 |
| 250° | -0.939693 | -0.34202 | 2.747477 | 0.36397 |
| 251° | -0.945519 | -0.325568 | 2.904211 | 0.344328 |
| 252° | -0.951057 | -0.309017 | 3.077684 | 0.32492 |
| 253° | 956305″>-0.956305 | -0.292372 | 3.270853 | 0.305731 |
| 254° | -0.961262 | -0.275637 | 3.487414 | 0.286745 |
| 255° | -0.965926 | -0.258819 | 3.732051 | 0.267949 |
| 256° | -0.970296 | -0.241922 | 4.010781 | 0.249328 |
| 257° | -0.97437 | -0.224951 | 4.331476 | 0.230868 |
| 258° | 978148″>-0.978148 | -0.207912 | 4.70463 | 0.212557 |
| 259° | -0.981627 | -0.190809 | 5.144554 | 0.19438 |
| 260° | -0.984808 | -0.173648 | 5.671282 | 0.176327 |
| 261° | -0.987688 | -0.156434 | 6.313752 | 0.158384 |
| 262° | -0.990268 | -0.139173 | 7.11537 | 0.140541 |
| 263° | 992546″>-0.992546 | -0.121869 | 8.144346 | 0.122785 |
| 264° | -0.994522 | -0.104528 | 9.514364 | 0.105104 |
| 265° | -0.996195 | -0.087156 | 11.430052 | 0.087489 |
| 266° | -0.997564 | -0.069756 | 14.300666 | 0.069927 |
| 267° | -0.99863 | -0.052336 | 19.081137 | 0.052408 |
| 268° | 999391″>-0.999391 | -0.034899 | 28.636253 | 0.034921 |
| 269° | -0.999848 | -0.017452 | 57.289962 | 0.017455 |
| 270° | -1 | 0 | ∞ | 0 |
Таблица тригонометрических функций углов от 271° до 360°
| α | sin α | cos α | tg α | ctg α |
| 271° | -0.999848 | 0.017452 | -57.289962 | -0.017455 |
| 272° | -0.999391 | 034899″>0.034899 | -28.636253 | -0.034921 |
| 273° | -0.99863 | 0.052336 | -19.081137 | -0.052408 |
| 274° | -0.997564 | 0.069756 | -14.300666 | -0.069927 |
| 275° | -0.996195 | 0.087156 | -11.430052 | -0.087489 |
| 276° | -0.994522 | 0.104528 | -9.514364 | -0.105104 |
| 277° | 992546″>-0.992546 | 0.121869 | -8.144346 | -0.122785 |
| 278° | -0.990268 | 0.139173 | -7.11537 | -0.140541 |
| 279° | -0.987688 | 0.156434 | -6.313752 | -0.158384 |
| 280° | -0.984808 | 0.173648 | -5.671282 | -0.176327 |
| 281° | -0.981627 | 0.190809 | -5.144554 | -0.19438 |
| 282° | 978148″>-0.978148 | 0.207912 | -4.70463 | -0.212557 |
| 283° | -0.97437 | 0.224951 | -4.331476 | -0.230868 |
| 284° | -0.970296 | 0.241922 | -4.010781 | -0.249328 |
| 285° | -0.965926 | 0.258819 | -3.732051 | -0.267949 |
| 286° | -0.961262 | 0.275637 | -3.487414 | -0.286745 |
| 287° | 956305″>-0.956305 | 0.292372 | -3.270853 | -0.305731 |
| 288° | -0.951057 | 0.309017 | -3.077684 | -0.32492 |
| 289° | -0.945519 | 0.325568 | -2.904211 | -0.344328 |
| 290° | -0.939693 | 0.34202 | -2.747477 | -0.36397 |
| 291° | -0.93358 | 0.358368 | -2.605089 | -0.383864 |
| 292° | 927184″>-0.927184 | 0.374607 | -2.475087 | -0.404026 |
| 293° | -0.920505 | 0.390731 | -2.355852 | -0.424475 |
| 294° | -0.913545 | 0.406737 | -2.246037 | -0.445229 |
| 295° | -0.906308 | 0.422618 | -2.144507 | -0.466308 |
| 296° | -0.898794 | 0.438371 | -2.050304 | -0.487733 |
| 297° | 891007″>-0.891007 | 0.45399 | -1.962611 | -0.509525 |
| 298° | -0.882948 | 0.469472 | -1.880726 | -0.531709 |
| 299° | -0.87462 | 0.48481 | -1.804048 | -0.554309 |
| 300° | -0.866025 | 0.5 | -1.732051 | -0.57735 |
| 301° | -0.857167 | 0.515038 | -1.664279 | -0.600861 |
| 302° | 848048″>-0.848048 | 0.529919 | -1.600335 | -0.624869 |
| 303° | -0.838671 | 0.544639 | -1.539865 | -0.649408 |
| 304° | -0.829038 | 0.559193 | -1.482561 | -0.674509 |
| 305° | -0.819152 | 0.573576 | -1.428148 | -0.700208 |
| 306° | -0.809017 | 0.587785 | -1.376382 | -0.726543 |
| 307° | 798636″>-0.798636 | 0.601815 | -1.327045 | -0.753554 |
| 308° | -0.788011 | 0.615661 | -1.279942 | -0.781286 |
| 309° | -0.777146 | 0.62932 | -1.234897 | -0.809784 |
| 310° | -0.766044 | 0.642788 | -1.191754 | -0.8391 |
| 311° | -0.75471 | 0.656059 | -1.150368 | -0.869287 |
| 312° | 743145″>-0.743145 | 0.669131 | -1.110613 | -0.900404 |
| 313° | -0.731354 | 0.681998 | -1.072369 | -0.932515 |
| 314° | -0.71934 | 0.694658 | -1.03553 | -0.965689 |
| 315° | -0.707107 | 0.707107 | -1 | -1 |
| 316° | -0.694658 | 0.71934 | -0.965689 | -1.03553 |
| 317° | 681998″>-0.681998 | 0.731354 | -0.932515 | -1.072369 |
| 318° | -0.669131 | 0.743145 | -0.900404 | -1.110613 |
| 319° | -0.656059 | 0.75471 | -0.869287 | -1.150368 |
| 320° | -0.642788 | 0.766044 | -0.8391 | -1.191754 |
| 321° | -0.62932 | 0.777146 | -0.809784 | -1.234897 |
| 322° | 615661″>-0.615661 | 0.788011 | -0.781286 | -1.279942 |
| 323° | -0.601815 | 0.798636 | -0.753554 | -1.327045 |
| 324° | -0.587785 | 0.809017 | -0.726543 | -1.376382 |
| 325° | -0.573576 | 0.819152 | -0.700208 | -1.428148 |
| 326° | -0.559193 | 0.829038 | -0.674509 | -1.482561 |
| 327° | 544639″>-0.544639 | 0.838671 | -0.649408 | -1.539865 |
| 328° | -0.529919 | 0.848048 | -0.624869 | -1.600335 |
| 329° | -0.515038 | 0.857167 | -0.600861 | -1.664279 |
| 330° | -0.5 | 0.866025 | -0.57735 | -1.732051 |
| 331° | -0.48481 | 0.87462 | -0.554309 | -1.804048 |
| 332° | 469472″>-0.469472 | 0.882948 | -0.531709 | -1.880726 |
| 333° | -0.45399 | 0.891007 | -0.509525 | -1.962611 |
| 334° | -0.438371 | 0.898794 | -0.487733 | -2.050304 |
| 335° | -0.422618 | 0.906308 | -0.466308 | -2.144507 |
| 336° | -0.406737 | 0.913545 | -0.445229 | -2.246037 |
| 337° | 390731″>-0.390731 | 0.920505 | -0.424475 | -2.355852 |
| 338° | -0.374607 | 0.927184 | -0.404026 | -2.475087 |
| 339° | -0.358368 | 0.93358 | -0.383864 | -2.605089 |
| 340° | -0.34202 | 0.939693 | -0.36397 | -2.747477 |
| 341° | -0.325568 | 0.945519 | -0.344328 | -2.904211 |
| 342° | 309017″>-0.309017 | 0.951057 | -0.32492 | -3.077684 |
| 343° | -0.292372 | 0.956305 | -0.305731 | -3.270853 |
| 344° | -0.275637 | 0.961262 | -0.286745 | -3.487414 |
| 345° | -0.258819 | 0.965926 | -0.267949 | -3.732051 |
| 346° | -0.241922 | 0.970296 | -0.249328 | -4.010781 |
| 347° | 224951″>-0.224951 | 0.97437 | -0.230868 | -4.331476 |
| 348° | -0.207912 | 0.978148 | -0.212557 | -4.70463 |
| 349° | -0.190809 | 0.981627 | -0.19438 | -5.144554 |
| 350° | -0.173648 | 0.984808 | -0.176327 | -5.671282 |
| 351° | -0.156434 | 0.987688 | -0.158384 | -6.313752 |
| 352° | 139173″>-0.139173 | 0.990268 | -0.140541 | -7.11537 |
| 353° | -0.121869 | 0.992546 | -0.122785 | -8.144346 |
| 354° | -0.104528 | 0.994522 | -0.105104 | -9.514364 |
| 355° | -0.087156 | 0.996195 | -0.087489 | -11.430052 |
| 356° | -0.069756 | 0.997564 | -0.069927 | -14.300666 |
| 357° | 052336″>-0.052336 | 0.99863 | -0.052408 | -19.081137 |
| 358° | -0.034899 | 0.999391 | -0.034921 | -28.636253 |
| 359° | -0.017452 | 0.999848 | -0.017455 | -57.289962 |
| 360° | 0 | 1 | 0 | ∞ |
Таблицы значений тригонометрических функций Таблицу синусов Таблица косинусов Таблица тангенсов Таблица котангенсов
Тригонометрические формулы
Все таблицы и формулы
Таблица синусов, косинусов, тангенсов, котангенсов
Таблица синусов, косинусов, тангенсов, котангенсов содержит вычисленные значения тригонометрических функций для определенного угла от 0 до 360 градусов в виде простой таблицы и в виде таблицы Брадиса. Так же приведены значения тригонометрических функций в радианах для наиболее распространённых углов, применяемых при вычислениях.
Так же приведены значения тригонометрических функций в радианах для наиболее распространённых углов, применяемых при вычислениях.
Таблицы с вычисленными значениями sin, cos, tg, ctg применяются для упрощения и ускорения математических вычислений, когда нет возможности воспользоваться калькулятором или компьютером.
- sin
- cos
- tg
- ctg
- триг. функции
- Брадиса sin и cos
- Брадиса tg и ctg
sin 0° = sin 360° = 0
| α° | sin α | α° | sin α | α° | sin α | α° | sin α |
|---|
| α° | sin α | α° | sin α | α° | sin α | α° | sin α |
|---|
cos 0° = cos 360° = 1
| α° | cos α | α° | cos α | α° | cos α | α° | cos α |
|---|
| α° | cos α | α° | cos α | α° | cos α | α° | cos α |
|---|
tg 0° = tg 360° = 0
| α° | tg α | α° | tg α | α° | tg α | α° | tg α |
|---|
| α° | tg α | α° | tg α | α° | tg α | α° | tg α |
|---|
ctg 0° = ctg 360° = ∞
| α° | ctg α | α° | ctg α | α° | ctg α | α° | ctg α |
|---|
| α° | ctg α | α° | ctg α | α° | ctg α | α° | ctg α |
|---|
Значения тригонометрических функций в радианах для наиболее распространённых углов.
Таблица Брадиса для синусов и косинусов
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0. 1736 1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0. 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0. 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0. 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0. 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0. 8192 8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0. 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0. 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0. 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0. 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0. 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Таблица Брадиса для тангенсов и котангенсов
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.
Угол — это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:
гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.
катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.
Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.
Такие зависимости называют тригонометрическими функциями.
То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.
Для ускорения расчетов, когда нет под рукой калькулятора, смартфона или компьютера, раньше были очень популярны таблицы с заранее вычисленными соотношениями сторон треугольников, выраженными в вычисленных значениях sin, cos, tg.
Например, зная из таблицы значения вычисленных заранее тригонометрических функций известного угла треугольника и длину одной из его сторон, можно быстро вычислить длины других сторон треугольника и величины неизвестных углов.
Таблица синусов и косинусов в радианах. Тригонометрические функции
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов.
Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов.
Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности.
Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.
Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.
В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17.
Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах.
Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов
ДокументОтдельной странице находятся формулы приведения тригонометрических функций . В таблице значений для тригонометрической функции синус приведены значения для следующих углов : sin 0, sin 30, sin 45 …
Предлагаемый математический аппарат является полным аналогом комплексного исчисления для n-мерных гиперкомплексных чисел с любым числом степеней свободы n и предназначен для математического моделирования нелинейных
Документ… функции равно функции изображения. Из этой теоремы следует , что для нахождения координат U, V достаточно вычислить функцию … геометрии; полинарные функции (многомерные аналоги двухмерных тригонометрических функций ), их свойства, таблицы и применение; .
 ..
..Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’.
 Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов.
 Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов.
 Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х
(в градусах)0
90
180
270
360
Угол х
(в радианах)0
sin x
0
1
0
-1
0
cos x
1
0
-1
0
1
tg x
0
не сущ.

0
не сущ.
0
ctg x
не сущ.
0
не сущ.
0
не сущ.
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов.
 Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ.
 Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось.
 Вот и всё.
Вот и всё.Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество.
 ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.

Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х
(в градусах)0
30
45
60
90
Угол х
(в радианах)0
sin x
0
1
cos x
1
0
tg x
0
1
не сущ.

ctg x
не сущ.
1
0
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же.
 Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё .

Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,. . градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределеннымЕсли взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3Изобразим все полученные значения в виде тригонометрической таблицы :
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z …. 330 0 +360 0 *z, в котором z является целым числом.
 В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.
tg до 900 и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83Ну вот мы и рассмотрели основные тригонометрические таблицы.
 Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!Заметка: Стеновые отбойники — отбойная доска для защиты стен. Перейдите по ссылке настенные отбойники бескаркасные (http://www.spi-polymer.ru/otboyniki/) и узнайте подробнее.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт.
 .. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой.
 Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если время останавливается, Ахиллес уже не может перегнать черепаху.Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов.
 Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние.
 Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.среда, 4 июля 2018 г.
Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.
Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами.
 Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное.В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные.
 Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
воскресенье, 18 марта 2018 г.
Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа».
 Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.
3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.
4. Складываем полученные числа. Вот это уже математика.

Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.
С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.
Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.
Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.
Табличка на двери Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?
Какой еще туалет?Женский… Нимб сверху и стрелочка вниз — это мужской.
Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,
Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:
Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
Таблица косинусов от 0 до 180 градусов. Косинус острого угла можно определить с помощью прямоугольного треугольника
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов. .. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
.. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов. )
)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | не сущ. | 0 | не сущ. | 0 |
ctg x | не сущ. | 0 | не сущ. | 0 | не сущ. |
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество. ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | не сущ. | ||
ctg x | не сущ. | 1 | 0 |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё . °}=\)\(\frac{\sqrt{3}}{2}\)
°}=\)\(\frac{\sqrt{3}}{2}\)
\(\cos\)\(\frac{π}{3}\)
\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.Пример :
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с : \(\frac{π}{2}\) , \(\frac{3π}{4}\) , \(-2π\).
Например, для числа \(\frac{π}{6}\)
— косинус будет равен \(\frac{\sqrt{3}}{2}\)
. А для числа \(-\)\(\frac{3π}{4}\)
он будет равен \(-\)\(\frac{\sqrt{2}}{2}\)
(приблизительно \(-0,71\)).
А для числа \(-\)\(\frac{3π}{4}\)
он будет равен \(-\)\(\frac{\sqrt{2}}{2}\)
(приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в .
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС ) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по числовой (тригонометрической) окружности:
Там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область). 2x}\)
2x}\)
— и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри .
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной называется и обладает следующими свойствами:
Область определения – любое значение икса: \(D(\cos{x})=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x})=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)
\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)
\(+2πn;\) \(\frac{π}{2}\)
\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)
\(+2πn;\)\(\frac{3π}{2}\)
\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
|
|
|
|
Таблица основных значений синусов косинусов тангенсов котангенсов – Telegraph
Таблица основных значений синусов косинусов тангенсов котангенсовТаблицы значений тригонометрических функций.

=== Скачать файл ===
Тригонометрическая таблица
Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы
К этой теме имеются дополнительные материалы в Особом разделе Для тех, кто сильно ‘не очень Прежде всего напомню простой, но очень полезный вывод из урока ‘Что такое синус и косинус? Что такое тангенс и котангенс? Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое. Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0, Понятное дело, запоминать это число и тысячи других табличных значений совершенно не требуется. В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё. На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, ‘таблица умножения’ тригонометрии. Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 три! Шесть значений запомнить легче, чем 68, мне кажется Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё. На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, ‘таблица умножения’ тригонометрии. Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 три! Шесть значений запомнить легче, чем 68, мне кажется Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу. Не пользоваться таким инструментом просто грех! Все 68 значений для разнообразных углов. Рассмотрим первую группа углов из семнадцати особых. Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется. Поэтому включаем логику и тригонометрический круг. Рисуем круг и отмечаем на нём эти самые углы: Я эти углы отметил красными точками:. Сразу видно, в чём особенность этих углов. Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания. Кстати, положение угла в 0 градусов полностью совпадает с положением угла в градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в градусов я отметил, чтобы замкнуть круг.
Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу. Не пользоваться таким инструментом просто грех! Все 68 значений для разнообразных углов. Рассмотрим первую группа углов из семнадцати особых. Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется. Поэтому включаем логику и тригонометрический круг. Рисуем круг и отмечаем на нём эти самые углы: Я эти углы отметил красными точками:. Сразу видно, в чём особенность этих углов. Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания. Кстати, положение угла в 0 градусов полностью совпадает с положением угла в градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в градусов я отметил, чтобы замкнуть круг. Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались Чему равен синус 0 градусов? Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения. В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются. Для этого на круге нарисуем произвольный угол х. В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку или коснитесь картинки на планшете и всё увидите. Теперь включаем элементарную логику!. При приближении угла к нулю? А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла точка А уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались Чему равен синус 0 градусов? Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения. В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются. Для этого на круге нарисуем произвольный угол х. В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку или коснитесь картинки на планшете и всё увидите. Теперь включаем элементарную логику!. При приближении угла к нулю? А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла точка А уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до Чему равна длина подвижной стороны угла радиус тригонометрического круга? Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений! Просто потому, что иначе быть не может. Совершенно аналогично можно узнать или уточнить синус градусов, например. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов Да и таблица косинусов — тоже. Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда? Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса котангенса — и всё сразу видно. Где они равны нулю, а где — не существуют.
А косинус увеличится до Чему равна длина подвижной стороны угла радиус тригонометрического круга? Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений! Просто потому, что иначе быть не может. Совершенно аналогично можно узнать или уточнить синус градусов, например. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов Да и таблица косинусов — тоже. Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда? Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса котангенса — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо. Посетили Раздел Тангенс и котангенс на тригонометрическом круге — и нет проблем! Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. Но, как раз, с отсчётом углов и случаются проблемы да ошибки Как их избежать, написано в уроке: Как нарисовать отсчитать любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками. Как нарисовать отсчитать любой угол на тригонометрическом круге в радианах — покруче будет. Скажем, определить на какую из четырёх полуосей попадает угол. Именно за пару секунд. Ну конечно, не только ‘пи’ И , и 16, и Любой целый коэффициент годится для мгновенного ответа. Верный ответ получается секунд за Для любого дробного значения радианов с двойкой в знаменателе. Собственно, этим и хорош тригонометрический круг.
Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо. Посетили Раздел Тангенс и котангенс на тригонометрическом круге — и нет проблем! Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. Но, как раз, с отсчётом углов и случаются проблемы да ошибки Как их избежать, написано в уроке: Как нарисовать отсчитать любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками. Как нарисовать отсчитать любой угол на тригонометрическом круге в радианах — покруче будет. Скажем, определить на какую из четырёх полуосей попадает угол. Именно за пару секунд. Ну конечно, не только ‘пи’ И , и 16, и Любой целый коэффициент годится для мгновенного ответа. Верный ответ получается секунд за Для любого дробного значения радианов с двойкой в знаменателе. Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так Дальше будет видно, чем хороши эти углы. Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до Это пригодится нам дальше. Но и здесь есть возможность облегчить себе жизнь. Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов Они одни и те же! Только расположены в обратном порядке. Углы возрастают 0, 30, 45, 60, 90 — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. А дальше опять расходятся Три значения можно выучить, правда? С тангенсами — котангенсами картина исключительно та же самая.
Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так Дальше будет видно, чем хороши эти углы. Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до Это пригодится нам дальше. Но и здесь есть возможность облегчить себе жизнь. Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов Они одни и те же! Только расположены в обратном порядке. Углы возрастают 0, 30, 45, 60, 90 — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. А дальше опять расходятся Три значения можно выучить, правда? С тангенсами — котангенсами картина исключительно та же самая. Эти значения ещё три! Ну вот, практически всё запоминание и закончилось. Вы поняли надеюсь , как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т. Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память. И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:. Плюс к тому, умение рисовать углы на круге позволяет элементарно разобраться с последней, третьей группой углов. Как и таблица тангенсов-котангенсов. Все тайны последней, третьей группы особенных углов и секреты уверенной работы с ними — в следующем уроке. Перевод градусов в радианы и обратно. Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой.
Эти значения ещё три! Ну вот, практически всё запоминание и закончилось. Вы поняли надеюсь , как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т. Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память. И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:. Плюс к тому, умение рисовать углы на круге позволяет элементарно разобраться с последней, третьей группой углов. Как и таблица тангенсов-котангенсов. Все тайны последней, третьей группы особенных углов и секреты уверенной работы с ними — в следующем уроке. Перевод градусов в радианы и обратно. Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом! А вот здесь можно познакомиться с функциями и производными. Hовое на сайте В разделе Решение задач на формулу n-го члена. Основа для решения заданий. Способы решения, приёмы упрощения, ловушки в заданиях. Что такое математическая модель? Как решать дробные уравнения? Содержание сайта Раздел 1. Таблица тангенсов и котангенсов. И зачем тогда этот урок?! Для начала разобьём все эти особые углы на три группы. Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов: Угол х в градусах. Копирование материалов разрешается только при указании работающей ссылки на этот сайт. Иное использование материалов допускается с разрешения автора. Нарушение авторских прав влечёт за собой административную и уголовную ответственность в соответствии с законодательством Российской Федерации.
Учимся — с интересом! А вот здесь можно познакомиться с функциями и производными. Hовое на сайте В разделе Решение задач на формулу n-го члена. Основа для решения заданий. Способы решения, приёмы упрощения, ловушки в заданиях. Что такое математическая модель? Как решать дробные уравнения? Содержание сайта Раздел 1. Таблица тангенсов и котангенсов. И зачем тогда этот урок?! Для начала разобьём все эти особые углы на три группы. Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов: Угол х в градусах. Копирование материалов разрешается только при указании работающей ссылки на этот сайт. Иное использование материалов допускается с разрешения автора. Нарушение авторских прав влечёт за собой административную и уголовную ответственность в соответствии с законодательством Российской Федерации.
Мичуринск сочи расписание поездов
Вязание пледа из остатков пряжи
Инструкция по охране труда для работников офиса
Сколько выдерживать вино на дубовой щепе
Карта троллейбусов екатеринбург
Как наказать девушку за непослушание
Войны после второй мировой войны таблица
Геосибирь 2015 сборник статей
Древняя история ставрополя
55 грамм это сколько столовых ложек
Расписание занятий пашковский колледж
Потеря тяги двигателя причины
Стихи с днем свадьбы годовщина
Где можно отдохнуть в минске недорого
Winter balls enabled перевод
Заявление о доступе к личному кабинету налогоплательщика
Шапка для новорожденного крючком схема и описание
Разобрать слова по составу смелость
Сколько калорий в салате с пекинской капустой
Новости руки вверх
Что такое синус, косинус и тангенс?
Знаете ли вы, что сказали друг другу два угла, живущие внутри одного и того же прямоугольного треугольника? Первый ракурс звучит так: «Эй, Тельма (или это Тета?), я не хочу отклоняться от темы, но какой у тебя синус?» На что второй угол отвечает: «Фил (или это Фи?), я не знаю, почему ты вообще спрашиваешь, мой синус, очевидно, совпадает с твоим косинусом!»
Ладно, возможно, это не самая лучшая шутка в мире, но как только вы понимаете синусы и косинусы, это довольно забавно. Конечно, это означает, что если вы не не знаешь разницы между синусом и косинусом, ты в настоящее время остаешься в метафорическом холоде.
Конечно, это означает, что если вы не не знаешь разницы между синусом и косинусом, ты в настоящее время остаешься в метафорическом холоде.
Очевидно, мы не можем этого допустить — и не позволим! Потому что сегодня мы узнаем все о синусе, косинусе и тангенсе.
Резюме: тригонометрия и треугольники
Когда мы говорили о мире тригонометрии, мы узнали, что часть математики, называемая тригонометрией, имеет дело с треугольниками. И, в частности, это та часть математики, которая занимается выяснением отношений между тремя сторонами и тремя углами, составляющими каждый треугольник.
Особый интерес для нас представляет особый тип треугольников, известный как прямоугольные треугольники. У каждого прямоугольного треугольника есть один угол в 90 градусов (например, угол квадрата или прямоугольника) и два угла, каждый из которых находится в диапазоне от большего, чем 0 градусов, до меньшего, чем 90 градусов (при этом, как мы поговорим в будущем, сумма всех трех углов равна 180 градусов).
Для нашего обсуждения синуса, косинуса и тангенса (которые, не волнуйтесь, не так сложны, как кажутся), важно, чтобы у нас был способ обозначать стороны прямоугольных треугольников.
Как мы узнали в прошлый раз, самая длинная сторона треугольника называется его «гипотенуза». Сторона, противоположная углу, на который мы смотрим, известна как «противоположная» сторона (логически). А сторона, примыкающая к углу, на который мы смотрим (та, которая не является гипотенузой), известна как «прилегающая» сторона.
Синус, косинус и тангенс
Теперь, когда все эти предварительные сведения счастливо плещутся в нашем растущем бассейне математических знаний, мы, наконец, готовы разобраться со значением синуса, косинуса и тангенса. Вот ключевая идея:
Отношения сторон прямоугольного треугольника полностью определяются его углами.
Отношения сторон прямоугольного треугольника полностью определяются его углами.
Другими словами, значение, которое вы получаете, когда делите длины любых двух сторон прямоугольного треугольника — скажем, длину стороны, противолежащей одному из его углов, деленную на его гипотенузу, — полностью высечено в камне, как только углы высечены в камне.
Почему? Что ж, если углы фиксированы, увеличение или уменьшение треугольника не влияет на относительную длину его сторон. Но изменение углов треугольника, даже незначительное, имеет значение! Если вам нужно какое-то убеждение, попробуйте нарисовать несколько треугольников самостоятельно, и вы убедитесь, что это действительно так.
Тот факт, что у треугольника три стороны, означает, что существуют также три возможных отношения длин сторон треугольника. И, как вы уже могли догадаться, эти три отношения есть не что иное, как знаменитые тригонометрические функции синуса, косинуса и тангенса.
Что такое SOH-CAH-TOA?
Синус одного из углов прямоугольного треугольника (часто сокращенно «sin») — это отношение длины стороны треугольника, противоположной углу, к длине гипотенузы треугольника. Косинус (часто сокращенно «cos») — это отношение длины стороны, примыкающей к углу, к длине гипотенузы. А тангенс (часто сокращенно «тан») — это отношение длины стороны, противоположной углу, к длине стороны, примыкающей.
Поскольку это слишком сложно для запоминания, добрые люди на протяжении веков придумали удобную мнемонику, которая поможет вам (и бесчисленным поколениям детей в школе) разобраться. Все, что вам нужно помнить, это SOH-CAH-TOA. Другими словами:
- SOH → sin = «противоположное» / «гипотенуза» .
- CAH → cos = «прилегающий» / «гипотенуза»
- TOA → tan = «противоположный» / «соседний»
Тригонометрия в реальном мире
Вам может быть интересно, как тригонометрия применима в реальной жизни. Как вы будете использовать синус, косинус и тангенс вне классной комнаты и почему это важно?
Есть несколько карьерных путей, которые приводят к постоянному использованию этих уравнений. Например, предположим, что вы звукорежиссер, работающий над созданием нового альбома популярного исполнителя. Вы знаете, что звук распространяется волнами, и инженеры могут манипулировать этими волнами (измеряя и применяя тригонометрию) для создания различных компьютерных звуков.
Что делать, если вы архитектор, которому нужно знать высоту существующего здания в районе, который вам назначен? Вы можете использовать расстояние от здания и угол возвышения, чтобы определить высоту. Вы даже можете использовать триггер, чтобы определить, под каким углом солнце будет светить в здание или комнату.
Строители также используют синус, косинус и тангенс таким же образом. Им необходимо измерить размеры участков, углы крыши, высоту стен и ширину пола и многое другое.
Криминалисты используют тригонометрию для определения углов траектории пули, причины аварии или направления упавшего предмета.
А как насчет места преступления? Следователи могут использовать тригонометрию для определения углов траектории пули, причины аварии или направления упавшего предмета.
НАСА использует синус, косинус и тангенс. Его физики и астронавты часто используют роботизированные руки для выполнения заданий в космосе и используют тригонометрию, чтобы определить, куда и как двигать руку для выполнения своей задачи.
Думаете об изучении морской биологии? В этой карьере синус, косинус и тангенс иногда используются для определения размеров крупных морских существ на расстоянии, а также для расчета уровней освещенности на определенных глубинах, чтобы увидеть, как они влияют на фотосинтез.
Есть десятки профессий, которые используют тригонометрию в своих повседневных задачах. Таким образом, вы можете перестать говорить что-то вроде: «Я никогда не буду использовать тригонометрию в настоящий мир ».
Что дальше?
Хотя все эти разговоры об углах и сторонах прямоугольных треугольников и их соответствии друг другу посредством красоты и великолепия тригонометрии действительно прекрасны, они могут заставить вас немного задуматься о том, «Почему?» «Какая?» и когда?» всего этого. Под этим я подразумеваю:
- Почему именно это полезно в реальном мире?
- Для чего нужны кнопки sin, cos и tan на моем калькуляторе? (И как они работают?)
- Когда мне действительно может понадобиться вычислить синус или косинус?
Очевидно, это очень важные (и очень разумные) вопросы. И это также очень важные вопросы, на которые нужно ответить. Именно за эту задачу мы и начнем браться в следующий раз.
И это также очень важные вопросы, на которые нужно ответить. Именно за эту задачу мы и начнем браться в следующий раз.
Синус, косинус и тангенс — объяснение, таблица, примеры решений и часто задаваемые вопросы треугольника к отношениям длин двух сторон. Обратными величинами синуса, косинуса и тангенса являются секанс, косеканс и котангенс соответственно. Каждая из шести тригонометрических функций имеет соответствующие обратные функции (также известные как обратные тригонометрические функции). Тригонометрические функции, также известные как круговые функции, угловые функции или гониометрические функции, широко используются во всех областях науки, связанных с геометрией, таких как навигация, небесная механика, механика твердого тела и т. д.
Прочтите ниже, чтобы узнать, что такое функция синуса, функция косинуса и функция тангенса.
Синус Косинус Тангенс Определение
Прямоугольный треугольник включает один угол в 90 градусов и два острых угла. Каждый острый угол прямоугольного треугольника сохраняет свойство синуса косинуса тангенса. Синус, косинус и тангенс острого угла прямоугольного треугольника определяются как отношение двух из трех сторон прямоугольного треугольника.
Каждый острый угол прямоугольного треугольника сохраняет свойство синуса косинуса тангенса. Синус, косинус и тангенс острого угла прямоугольного треугольника определяются как отношение двух из трех сторон прямоугольного треугольника.
Как мы знаем, синус, косинус и тангенс основаны на прямоугольном треугольнике, было бы полезно дать имена каждому из треугольников, чтобы избежать путаницы.
(Изображение будет загружено в ближайшее время)
«Сторона гипотенузы» — самая длинная сторона.
«Смежная сторона» — это сторона, следующая за углом θ.
«Противоположная сторона» — сторона, противоположная углу θ.
Соответственно,
Sin θ = Противоположная сторона/Гипотенуза
Cos θ = Прилегающая/Гипотенуза
Tan θ = Противоположная/Прилегающая
Что такое функция синуса?
В прямоугольном треугольнике функция синуса определяется как отношение длины противоположной стороны к длине стороны гипотенузы.
Sin θ = противолежащая сторона/сторона гипотенузы.
(Изображение будет загружено в ближайшее время)
Например, функция синуса треугольника ABC с углом θ выражается как:
Sin θ = a/c
Что такое функция косинуса?
В прямоугольном треугольнике функция косинуса определяется как отношение длины прилежащей стороны к длине стороны гипотенузы.
Cos θ = смежная сторона/сторона гипотенузы
Пример:
Учитывая рисунок, приведенный выше, функция косинуса треугольника ABC с углом θ выражается как:
Cos θ = b/c
Что такое функция касательной?
В прямоугольном треугольнике функция касательной определяется как отношение длины противоположной стороны к длине прилежащей стороны.
Tan θ = Противоположная сторона/Смежная сторона
Пример:
Учитывая рисунок, приведенный выше, функция косинуса треугольника ABC с углом θ выражается как:
Tan θ = a/b
Синус Косинус Тангенс Таблица
Значения тригонометрических соотношений, таких как синус, косинус и тангенс, для некоторых стандартных углов, таких как 0°, 30°, 45°, 60° и 90 ° можно легко определить с помощью таблицы синус-косинус-тангенса, приведенной ниже. Эти значения очень важны для решения тригонометрических задач. Следовательно, важно знать значения тригонометрических отношений этих стандартных углов.
Эти значения очень важны для решения тригонометрических задач. Следовательно, важно знать значения тригонометрических отношений этих стандартных углов.
Приведенная ниже таблица синусов, косинусов и тангенсов включает значения стандартных углов, таких как 0°, 30°, 45°, 60° и 90°.
Углы в градусах | 0° | 30° | 45° | 60° | 90° |
Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Tan | 0 | 1/√3 | 1 | √3 | Not Defined |
Знаете ли вы?
Синус и косинус были введены Арьябхаттой, тогда как функция тангенса была введена Мухаммадом ибн Мусой аль-Хорезми (782 г.
 н.э. — 850 г. н.э.).
н.э. — 850 г. н.э.).Формулы синуса, косинуса и тангенса можно легко выучить с помощью SOHCATOA. Поскольку синус — это сторона, противоположная стороне гипотенузы, косинус — сторона, примыкающая к стороне гипотенузы, а тангенс — сторона, противоположная стороне, примыкающей к стороне.
Решенные примеры:
1. Найдите Cos θ относительно следующего треугольника.
Ответ: Чтобы найти Cos θ, нам нужны и прилежащая сторона, и гипотенуза.
(Изображение будет загружено в ближайшее время)
Прилегающая сторона в приведенном выше треугольнике равна BC = 8 см
Но сторона гипотенузы, т.е. AC, не указана.
Чтобы найти сторону гипотенузы, воспользуемся теоремой Пифагора
AC² = AB² + BC² = 6² + 8² = 1000003
Cos θ = Adjacent/Hypotenuse = 8/10
= 4/5
Следовательно, Cos θ = 4/5
2. Найдите значение
Найдите значение
Решение. Используя приведенную выше тригонометрическую таблицу, имеем:
Sin 45° = 1/√2
Cos 60° = 1/2
Tan 45° = 1
Чему равны синус, косинус и касательная?
Решение треугольников
Purplemath
Прямоугольные треугольники красивы и аккуратны, хорошо себя ведут, их длины сторон подчиняются теореме Пифагора; а именно, для любого прямоугольного треугольника длины его сторон a , b и c , где c — самая длинная из трех сторон, всегда верно, что a 2 +; b 2 = c 2 .
Для любых двух прямоугольных треугольников, у которых меры (то есть размеры) двух других (то есть непрямых) углов одинаковы, говорят, что они «подобны», в техническом смысле, что их соответствующие стороны в пропорции.
Содержание продолжается ниже
MathHelp.com
Основные тригонометрические отношения
Например, следующие два треугольника (, а не , нарисованные в масштабе) имеют все одинаковые углы, поэтому они подобны, и, следовательно, соответствующие пары их сторон пропорциональны :
Когда мы говорим, что «соответствующие пары длин их сторон пропорциональны», мы имеем в виду, что мы можем создавать дроби, взяв длину стороны одного из подобных треугольников (скажем, большего, в данном случае ) и разделите его на длину соответствующей стороны другого подобного треугольника (в данном случае на меньшую). Выполнив это деление, мы обнаружим, что каждая из этих дробей приводит к одному и тому же значению для данной пары подобных треугольников.
Выполнив это деление, мы обнаружим, что каждая из этих дробей приводит к одному и тому же значению для данной пары подобных треугольников.
Для приведенной выше пары подобных треугольников, сначала составив дробь из пары длин сторон гипотенузы (длина гипотенузы большего треугольника делится на длину гипотенузы меньшего треугольника), пары длин сторон основания и линии высоты пары, мы всегда получаем одно и то же значение 2, как показано ниже:
отношения соответствующих сторон: 10/5 = 8/4 = 6/3 = 2
другое значение обыкновенного отношения. Значение не так важно, как тот факт, что все дроби будут равны, что является свойством подобных треугольников.)
Мы также можем составить отношения, разделив одну сторону одного из подобных треугольников на одну из двух других сторон того же самого треугольника. Когда мы используем те же стороны в том же порядке, чтобы сформировать соответствующее отношение для другого из подобных треугольников, две дроби уменьшатся до одного и того же значения. Для наших двух треугольников выше (и снова используя значения большего треугольника в качестве наших числителей и деля на значения меньшего треугольника), мы получаем:
Для наших двух треугольников выше (и снова используя значения большего треугольника в качестве наших числителей и деля на значения меньшего треугольника), мы получаем:
отношение гипотенузы к основанию: 10/8 = 5/4 = 1,25
отношение гипотенузы к высоте: 10/6 = 5/3 = 1,666…
отношение высоты к основанию: 6/8 = 3/4 = 0,75
Конечно, мы могли бы произвести деление и в другом порядке; это дает нам величины, обратные предыдущим отношениям, но дело в том, что совпадающие деления по-прежнему имеют соответствующие значения отношения:
отношение основания к гипотенузе: 8/10 = 4/5 = 0,8
отношение высоты к гипотенузе : 6/10 = 3/5 = 0,6
отношение основания к высоте: 8/6 = 4/3 = 1,333…
Полученные дроби обратны предыдущим значениям, но суть здесь заключается в том, что отношения двух треугольников все еще совпадают. Это также показывает, что на самом деле существует шести отношений пар сторон, которые мы можем составить для любых двух заданных подобных треугольников, и их значения будут согласованы.
Шесть соотношений совпадают не только для этих двух подобных треугольников, но и для любых и всех прямоугольных треугольников, подобных этим двум. Чтобы проиллюстрировать это, я вложил два треугольника выше, перекрывая их под углом основания; затем я продлил (вправо) линии основания и гипотенузы. Затем я провел несколько вертикальных (темно-зеленых) линий от линии гипотенузы до базовой линии, получив изображение ниже:
Вертикальные линии — это линии высот (или высот) лишь нескольких из бесконечно многих подобных прямоугольных треугольников, которые можно составить из одного угла при основании. Подобным треугольникам, имеющим один и тот же угол при основании, буквально нет конца. И каждый из них будет иметь одинаковые значения соотношения.
Где-то в четвертом или пятом веке нашей эры кто-то очень умный, живший в Индии или ее окрестностях, заметил эту согласованность в пропорциях сходных прямоугольных треугольников (то есть согласованность значений шести различных отношений прямоугольных треугольников, разделяющих одинаковый размер основного угла) и начал работать над таблицами отношений, соответствующих этим основным углам. Был бы один набор отношений для угла в один градус во всех 1-89.-90 треугольников, другой набор соотношений для угла в два градуса во всех треугольниках 2-88-90 и так далее. Эти соотношения называются «тригонометрическими» соотношениями прямоугольного треугольника.
Был бы один набор отношений для угла в один градус во всех 1-89.-90 треугольников, другой набор соотношений для угла в два градуса во всех треугольниках 2-88-90 и так далее. Эти соотношения называются «тригонометрическими» соотношениями прямоугольного треугольника.
Эти таблицы значений отношений очень длинные, отчасти потому, что они также включают значения для многих углов с размерами между целыми числами градусов; и занять некоторое время, чтобы использовать. В зависимости от того, насколько точным должен быть ваш ответ для инструктора (или приложения на рабочем месте), вы можете просмотреть более двадцати страниц триггерных таблиц (например, в этой книге) и 9 страниц.0005 все еще нужно использовать интерполяцию или различные формулы, чтобы получить числа, которые вам действительно нужны.
Зачем им нужны были эти триггерные таблицы? Потому что вычисления, необходимые для получения этих значений (вручную), длинные и сложные. (Обсуждение в Quora) Работа с распечатанными таблицами, возможно, в конце учебника или в карманном справочном руководстве, была единственным практическим способом выполнения тригонометрии до того, как электронные калькуляторы стали широко доступны. (Некоторые люди все еще используют карманные ссылки на работе, «в реальной жизни», даже сейчас, как показано здесь.)
(Некоторые люди все еще используют карманные ссылки на работе, «в реальной жизни», даже сейчас, как показано здесь.)
Профессор колледжа, который у меня был на занятиях по тригонометрии, однажды даже упомянул, что в прошлом экзамены по тригонометрии должны были быть очень короткими, чтобы у студентов было все время, которое они должны были бы тратить на механический процесс таблицы. поиск значения. Так что очень радуйтесь, что у вас всегда есть калькулятор в кармане в виде смартфона. Откройте приложение-калькулятор, поверните телефон на бок и просто посмотрите на все причудливые вещи, которые вы можете сделать! Но экзамены по тригонометрии, как заметил профессор Горовара с огоньком в глазах, в наши дни могут быть намного длиннее, так что… смешанная ситуация, я полагаю?
Дан прямоугольный треугольник с углом при основании, обозначенным как θ («THAY-tuh»), мы можем обозначить гипотенузу (всегда сторона, противоположная прямому углу), а затем обозначить две другие стороны «относительно θ» ( то есть по отношению к базовому углу θ, с которым мы работаем), в том числе и для значений между целыми числами градусов.
Сторона, противолежащая углу θ, является «противоположной» стороной, а другая сторона, являющаяся основанием, является «прилегающей» стороной.
Теперь рассмотрим другой непрямой угол того же треугольника; а именно, угол в правом верхнем углу треугольника. Мы назовем его β («БАЙ-тьфу»). Что касается угла β, стороны будут обозначены по-разному. Основание теперь будет «противоположной» стороной, а линия высоты будет «примыкающей» стороной, как показано ниже:
Как видите, метки «противоположная» и «примыкающая» относятся к рассматриваемому углу. . Если вы переключитесь на другой угол (это не правильный угол), метки ног тоже будут переключены.
Давайте вернемся к первой маркировке, которую мы рассмотрели, с использованием угла θ в левом нижнем углу:
Вместо того, чтобы бросать вам все сразу, давайте пойдем шаг за шагом.
У этого прямоугольного треугольника три стороны; а именно, гипотенуза, линия высоты (сторона, противоположная углу) и основание внизу (сторона, прилегающая к углу). Есть шесть способов составить отношения трех сторон этого треугольника. В следующих таблицах я буду сокращать названия от «гипотенуза», «смежный» и «противоположный» до «hyp», «adj» и «opp» соответственно. В приведенных ниже таблицах показаны шесть коэффициентов в центральных столбцах.
Есть шесть способов составить отношения трех сторон этого треугольника. В следующих таблицах я буду сокращать названия от «гипотенуза», «смежный» и «противоположный» до «hyp», «adj» и «opp» соответственно. В приведенных ниже таблицах показаны шесть коэффициентов в центральных столбцах.
Соотношения в строках одного цвета каждой таблицы обратны друг другу. Например, соотношение в розовой строке в первой таблице — это «adj/hyp», а соотношение в розовой строке во второй таблице — это его обратная дробь «hyp/adj».
Каждое из этих соотношений имеет формальное название. Эти имена были добавлены в левые столбцы таблиц ниже:
Каждое из названий этих соотношений имеет сокращенное обозначение, которое включает указание угла, с которым вы работаете, с использованием обозначения функции, как показано на правые столбцы заполненных таблиц ниже:
Отношения синуса, косинуса и тангенса являются «обычными» триггерными отношениями; косеканс, секанс и котангенс — их соответствующие обратные отношения (то есть значения перевернутых дробей для «правильных» отношений).
Между прочим, нет требования, чтобы греческие буквы использовались в качестве аргумента (то есть ввода) триггерной функции. Например, вполне нормально использовать x , если хотите.
Что означает SOH-CAH-TOA?
Многие учащиеся используют мнемонику «SOH-CAH-TOA» (произносится как «SOH-kuh-TOH-uh»), чтобы запомнить, как составлять соотношения для синуса, косинуса и тангенса прямоугольного треугольника. Буквы в этой мнемонике означают:
- S ine is O pposite over H ypotenuse
- C озин is A djacent over H ypotenuse
- T угол O напротив А дальний
Как соотносятся косинус, -секанс и -тангенс?
Если два отношения имеют одно и то же имя, кроме «ко-» в начале одного из них, пара называется «ко-функциями». Пары кофункций связаны по форме их графиков; график каждой кофункции имеет ту же форму, что и исходная функция, за исключением того, что он был переведен или преобразован (то есть кроме того, что он был перемещен вбок или немного перевернут).
Пары кофункций связаны по форме их графиков; график каждой кофункции имеет ту же форму, что и исходная функция, за исключением того, что он был переведен или преобразован (то есть кроме того, что он был перемещен вбок или немного перевернут).
В частности, косинус выглядит точно так же, как и синус, но немного смещен влево; косеканс — сдвиг секущей влево; котангенс — это тангенс после переворачивания его вверх дном и последующего сдвига результата немного влево.
(Примечание: пропорции не получали своих нынешних европейских названий до XII века или около того, в результате того, что европейцы допустили некоторые ошибки при переводе арабских текстов. История тригонометрии довольно запутана. [источник])
URL: https://www.purplemath.com/modules/basirati.htm
Page 2
Формула синуса, косинуса, тангенса — GeeksforGeeks
Тригонометрия — это раздел математики, который связывает длину стороны с углом прямоугольного треугольника. Тригонометрия имеет дело с некоторыми специфическими функциями углов и их приложениями. Тригонометрия является важной частью математики. Тригонометрия имеет различные формулы, которые используются в разных областях. Эта статья посвящена самым основам тригонометрии, то есть функциям синуса, косинуса и тангенса, а также их формуле и объяснению. Эти тригонометрические функции имеют формулы, которые легко понять и применить. Эти формулы тригонометрических функций получены из сторон прямоугольного треугольника.
Тригонометрия является важной частью математики. Тригонометрия имеет различные формулы, которые используются в разных областях. Эта статья посвящена самым основам тригонометрии, то есть функциям синуса, косинуса и тангенса, а также их формуле и объяснению. Эти тригонометрические функции имеют формулы, которые легко понять и применить. Эти формулы тригонометрических функций получены из сторон прямоугольного треугольника.
Треугольник, один из углов которого равен 90°, называется прямоугольным. У него есть стороны, называемые основанием, перпендикуляром (высотой) и гипотенузой. Прямоугольный треугольник следует теореме Пифагора.
- Основание: Сторона, содержащая угол, называется основанием треугольника.
- Перпендикуляр (высота): Сторона, образующая 90° с основанием, называется перпендикуляром или высотой треугольника.
- Гипотенуза: Самая длинная сторона треугольника называется гипотенузой треугольника.

Что такое тригонометрические функции?
Тригонометрические функции также называются тригонометрическими отношениями. Существуют три основные и важные тригонометрические функции: синус, косинус и тангенс.
- Тригонометрическая функция синуса записывается как sin , косинус как cos, и тангенс как tan в тригонометрии.
- Есть еще три тригонометрические функции: cosec , sec и cot, которые являются обратными sin , cos , и tan .
- Эти функции можно вычислить для прямоугольного треугольника.
Пусть прямоугольный треугольник с основанием b, перпендикуляром p и гипотенузой h образует с основанием угол θ. Тогда тригонометрические функции задаются следующим образом:
Тригонометрические функции | Формула тригонометрических функций |
|---|---|
SIN θ |
|
cos θ |
|
tan θ = sin θ/cos θ |
|
cosecθ = 1 /sin θ |
|
cotθ = 1/tan θ |
|
Запомнить 6 | ||
. | ||
| вьющиеся черные волосы | cosθ (кудрявый)= основание(черный)/гипотенуза(волосы) | tanθ (к) = перпендикуляр (производство)/основание (красота) |
Тригонометрические функции для некоторых основных углов
В тригонометрии у нас есть основные углы 0°, 30°, 45°, 60°, и 90°. В таблице ниже приведены значения тригонометрических функций для основных углов:
| θ | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin | 0 | 1/2 | 1/√2 | √ 3/2 | 1 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 |
| sec | 1 | 2/√3 | √2 | 2 | ∞ |
| cot | ∞ | √3 | 1 | 1/√3 | 0 |
SINE, COSINE и TANGENT FUNDARS в Крадэнтах
- СИНАНСКИ третий и четвертый квадранты.

- Функции косинуса и секанса положительны в первом и четвертом квадрантах и отрицательны во втором и третьем квадрантах.
- Функции тангенса и котангенса положительны в первом и третьем квадрантах и отрицательны во втором и четвертом квадрантах.
| .0566 | Признак COSEC | СИНКА SEC | СИНКА КОМПЕР | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 ° | ||||||||||||||
0 ° | ||||||||||||||
0 °. | + (положительный) | + (положительный) | + (положительный) | + (положительный) | + (положительный) 9018 2 | + (положительный) 9018 2 | + (положитель0179 90° to 180° | 2 nd quadrant | + (positive) | – (negative) | – (negative) | + (positive) | – (negative) | – (negative) |
180° to 270° | 3 rd quadrant | – (negative) | – (negative) | + (positive) | – (negative) | – (negative) | + (positive) | |||||||
270° to 360° | 4 th Quadrant | — (отрицательный) | + (положительный) | — (отрицательный) | — (отрицательный) | + (положительный |
Взаимные тождества
Функция косеканса является обратной функцией синуса и наоборот. Точно так же функция секанса является обратной функцией функции косинуса, а функция котангенса является обратной функцией функции тангенса.
Точно так же функция секанса является обратной функцией функции косинуса, а функция котангенса является обратной функцией функции тангенса.
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
- с θ = 1/cos θ
- cot θ. = 1/тангенс θ
Pythagorean Identities
- SIN 2 θ + COS 2 θ = 1
- SEC 2 θ — TAN 2 θ 8848 θ — TAN 2 θ8848 θ — TAN 2 θ θ 2 . 1
Идентификация отрицательного угла
Отрицательный угол функции косинуса всегда равен положительному косинусу угла, тогда как отрицательный угол функции синуса и тангенса равен отрицательному синусу и тангенсу угла.
- sin (– θ) = – sin θ
- cos (– θ) = cos θ
- tan (– θ) = – tan θ
Решенные примеры по формуле синус-косинус-тангенса
91:375 Стороны Основание прямоугольного треугольника = 3 см, перпендикуляр = 4 см, гипотенуза = 5 см. Найдите значение sinθ, cosθ и tanθ.
Найдите значение sinθ, cosθ и tanθ.
Решение:
Учитывая, что
Основание (b) = 3 см,
Перпендикуляр (p) = 4 см и
гипотенуза (h) = 5 см
Из формулы тригонометрических функций:
sinθ = p/h = 4/5
cosθ = b/h = 3/5
tanθ = p/b = 25 6 30075 7 4/3 9003 Пример 2: Стороны прямоугольного треугольника: основание = 3 см, перпендикуляр = 4 см и гипотенуза = 5 см. Найдите значение cosecθ, secθ и cotθ.
Решение:
Учитывая, что основание (b) = 3 см, перпендикуляр (p) = 4 см и гипотенуза (h) = 5 см
Из формулы тригонометрических функций:
cosecθ = 1/sinθ = h / p = 5/4
secθ = 1/cosθ = h / b = 5/3
cotθ = 1/tanθ = b / p = 3/4
Пример 3. Найдите θ, если основание = √3 и перпендикуляр = 1 прямоугольного треугольника.
Решение:
Поскольку перпендикуляр и основание прямоугольного треугольника заданы, используется tanθ.
tanθ = перпендикуляр/основание
= 1/√3
θ = tan -1 (1/√3) [Из таблицы основных углов тригонометрической функции]
θ = 30°
Пример 4: Найдите θ, если основание = √2 и гипотенуза прямоугольного треугольника.
Решение:
Поскольку основание и гипотенуза прямоугольного треугольника заданы, используется cosθ.
cosθ = основание/гипотенуза
cosθ = √3/2
θ = cos -1 (√3/2) [Из таблицы основных углов тригонометрической функции]
= 30°
Пример 5. Найдите θ, если перпендикуляр = 1 и гипотенуза = 2 прямоугольного треугольника.
Решение:
Так как перпендикуляр и гипотенуза прямоугольного треугольника заданы, поэтому используется sinθ.
sinθ = перпендикуляр/гипотенуза
sinθ = 1/2
θ = sin -1 (1/2) [Из таблицы основных углов тригонометрической функции]
= 30°
Как работают синус, косинус и тангенс?
МАТЕМАТИКА — Геометрия
Задумывались ли вы когда-нибудь.
..
- Что такое тригонометрия?
- Что такое синус, косинус и тангенс?
- Как найти синус, косинус и тангенс?
Теги:
Просмотреть все теги
- Математика,
- Геометрия,
- Тригонометрия,
- Функция,
- Синус,
- Косинус,
- Тангенс,
- Треугольник,
- Прямоугольный треугольник,
- Формула,
- Угол,
- Гипотенуза
Сегодняшнее чудо дня было вдохновлено Саем.
Sai Wonders , “ Как работают синус, косинус и тангенс? ”Спасибо, что ДУМАЕТЕ вместе с нами, Сай!
Многие из наших чудесных друзей уже знают о теореме Пифагора. Возможно, они читали о треугольнике Паскаля. Они могут даже знать другие типы треугольников. Сегодня нас интересует еще одна тема, связанная с треугольниками. О чем мы говорим? Синус, косинус и тангенс, конечно!
Что такое синус, косинус и тангенс? Это три основные функции в тригонометрии. Возможно, вы уже слышали о них на уроках математики. Тригонометрия связана с геометрией и другими разделами математики. Это может помочь нам лучше понять связи между сторонами и углами прямоугольников.
Синус, косинус и тангенс важны для изучения прямоугольных треугольников. Вы когда-нибудь видели такой треугольник? Если да, то вы знаете, что один из трех его углов всегда равен 90° (прямой угол). Два других угла могут иметь любые измерения, если сумма всех трех углов составляет 180°.
Как математики находят синус, косинус и тангенс? Начнем с одного из непрямых углов прямоугольного треугольника. Обычно они обозначают этот угол как тета (Θ). Затем они обозначают три стороны треугольника.
Сторона треугольника, расположенная непосредственно напротив прямого угла, называется гипотенузой. Это самая длинная сторона треугольника. Сторона напротив теты называется «противоположной». Это довольно легко запомнить — это на противоположной стороне от тета-угла! Наконец, сторона, которая касается теты, но не является гипотенузой, называется «прилегающей».
Правильное обозначение сторон очень важно при нахождении синуса, косинуса и тангенса. Это потому, что у каждого есть формула, которая делит длину одной стороны на длину другой. Вот формулы для поиска каждой из этих функций:
SINE θ = противоположность ÷ гипотенуза
косинус θ = прилегающий ÷ гипотеновый формулы могут показаться трудными для запоминания. Тем не менее, запоминание полезной мнемоники может помочь.
При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.
Запомнив SOHCATOA, вы сможете правильно писать формулы для синуса, косинуса и тангенса. Затем просто введите правильные числа, и все готово! Чтобы найти эти функции, нужно запомнить формулы и использовать правильные измерения сторон. Многие люди считают полезным пометить треугольник перед тем, как начать.
Можете ли вы найти синус, косинус и тангенс угла? Мы уверены, что вы можете! Однако поначалу новые математические темы могут быть трудными. С практикой и помощью учителя или друга мы знаем, что скоро вы многое узнаете о тригонометрии!
Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.
»> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2
Интересно, что дальше?
Сегодняшнее чудо дня обычно выходит только ночью.
Попробуйте
Готовы продолжать учиться? Проверьте действия ниже с помощью друга или члена семьи!
- Узнайте больше о синусе, косинусе и тангенсе, а также посмотрите полезные диаграммы на веб-сайте Math Is Fun. Помогло ли это вам глубже понять эти функции? Обобщите то, что вы узнали сегодня, для друга или члена семьи.
- Теперь, когда у вас есть мнемоника, которая поможет вам запомнить формулы синуса, косинуса и тангенса, сделайте плакат, который поможет другим запомнить. Используйте мнемонику SOHCAHTOA и включите любые изображения или диаграммы, которые, по вашему мнению, помогут вашим друзьям или членам семьи научиться находить эти функции.
Не забудьте также указать правильные формулы!
- Чувствуете себя лукавым? Узнайте больше о геометрических фигурах и проявите творческий подход, создавая свои собственные! Вы можете попробовать сделать некоторые фигуры самостоятельно или следовать этому видео, чтобы научиться создавать трехмерные фигуры, используя только бумагу и ножницы. Убедитесь, что взрослый помогает вам, и получайте удовольствие, создавая свои фигуры.
Wonder Sources
- https://www.khanacademy.org/math/geometry-home/right-triangles-topic/intro-to-the-trig-ratios-geo/v/basic-trigonometry
- https ://www.mathsisfun.com/sine-cosine-tangent.html
- https://www.livescience.com/51026-what-is-trigonometry.html
- https://learnersdictionary.com/
Ты понял?
Проверьте свои знанияWonder Words
- ответвления
- углы
- этикетка
- функций
- формулы
- измерений
- тригонометрия
- геометрия
- математики
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции.
Узнай первым!
Поделись со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
Продолжить
Не совсем!
Попробуйте еще раз
Эпизод о тригонометрии | Советы и рекомендации MCAT
Последнее обновление: 23 июня 2022 г., Лора Тернер
Я предполагаю, что к этому моменту подготовки к MCAT вы чувствуете себя так, как будто припарковали самосвал, полный информации, рядом со своим столом и закидываете факты в свой мозг, пока он не готов взорваться. А потом вы столкнулись с проблемой физики. Тот, который требует от вас знания синуса или косинуса? – 60 градусов.

Вы ищете на жестком диске своего разума ссылки на тригонометрию. Что-то есть в SOH CAH TOA… и в 2 и в 2 . О, Боже. Еще кое-что, что можно добавить в список «для запоминания», который разрастается до толщины вашего учебника по органической химии.
Об объявлениях
Существует множество видео и статей о приемах запоминания значений синуса и косинуса, и они являются хорошей отправной точкой, но на самом деле они не так уж полезны для MCAT. (позже мы увидим, почему). Все, что вам действительно нужно запомнить, чтобы выполнять какие-либо тригонометрические вычисления в день экзамена, это «синус — точка 5, точка 7, точка 9».». Вот и все! Давайте посмотрим, как это работает…
В разделе физики MCAT вам нужно будет уметь выполнять вычисления с синусом, косинусом и тангенсом пяти градусных мер — 0°, 30°, 45°, 60° и 90°. Если учащиеся что-нибудь помнят о тригонометрии, то это, вероятно, SOH CAH TOA (см. ниже), что напоминает нам о том, что синус (S) угла равен длине противоположной стороны треугольника (O), деленной на гипотенузу (H ), косинус (C) угла равен прилежащей стороне (A), деленной на гипотенузу (H), а тангенс (T) равен противолежащей стороне (O), деленной на прилежащую сторону (A).
На рисунке ниже мы видим два прямоугольных треугольника, вписанных в единичную окружность: один с гипотенузой под углом 30° к оси x, а другой с гипотенузой под углом 60° к оси x. Поскольку синус = противоположность/гипотенуза (SOH), синус угла связывает длину стороны треугольника в направлении y с гипотенузой. Чтобы запомнить это, может быть полезно подумать о том, что «sine» и «y» имеют похожие звуки. Вот почему мы пишем «синус» как «син» в рифме.
По мере увеличения степени угла длина треугольника в направлении Y увеличивается, как и синус угла. Sin(0°) = 0, потому что «треугольник» не будет иметь длины в направлении y, и sin(90°) = 1, потому что «треугольник» будет иметь всю свою длину в направлении y.
Косинус описывает отношение длины треугольника в направлении x и следует аналогичной схеме, но в обратном направлении. По мере увеличения угла длина треугольника в направлении x уменьшается, как и косинус угла. Косинус 0° = 1 и косинус 90° = 0,
Как насчет значений синуса и косинуса для остальных углов? Здесь вступают в действие точки 5, точки 7, точки 9 рифмы.

Начнем с синуса или «сина» из рифмы. Уловка, которой часто учат запоминать синус обыкновенных углов, состоит в том, чтобы начать с написания пустого знака квадратного корня, деленного на 2.
Теперь под знаком квадратного корня напишите числа 0, 1, 2, 3 и 4. в целях.
Некоторые из этих дробей легко упрощаются до десятичных, но синус 45° и 60° — нет.
Большинство видео и статей, посвященных этой теме, оставляют вас здесь, но поскольку вы не можете позволить себе роскошь работать с калькулятором, запоминание величин, например, не очень помогает. Вместо этого лучше запомнить десятичные аппроксимации и , где и появляется рифма. ≈ 0,7 и ≈ 0,9.
Если вам нужно вычислить триггер с синусоидой, вы можете быстро записать sin(0°) = 0, sin(90°) = 1 и запомнить рифму, «синус – точка 5, точка 7, точка 9(опять же «синус», потому что синус говорит нам о направлении треугольника по оси Y).
Если вы посмотрите на единичный круг, вы увидите, что значения косинуса для каждого из этих углов являются обратными значениям синуса.
Таким образом, косинус 0° = 1, косинус 30° = 0,9 и т. д. Если вам нужен косинус, вы можете просто записать значения синуса, а затем расположить их в обратном порядке, запоминание не требуется.
Наконец, если вам нужен тангенс, разделите синус на косинус. Если у вас возникли проблемы с запоминанием, что на что делить, синус в таблице уже выше косинуса, поэтому вы можете думать о разделительной линии между ними как о дробной черте.
Тангенс 0°, 45° и 90° легко вычислить. Для тангенса 30° и 60° вы можете получить «достаточно близкий» ответ, аппроксимировав 0,9 с 1.
Фактическое значение тангенса (30°) ≈ 0,57 и тангенса (60°) ≈ 1,7.
Вот это да. Имея все это в памяти, давайте решим примерную задачу:
Ребенок начинает тянуть игрушку за собой с силой 8 Н под углом 45° к земле. Начальное ускорение игрушки 2 м/с 2 . Какова масса игрушки?
a) 1,63 кг
b) 2,84 кг
c) 4,00 кг
d) 6,21 кгФормула, связывающая силу, массу и ускорение: F = Ma.
Поскольку мы хотим использовать силу и ускорение, чтобы найти массу, мы делим обе части на ускорение, чтобы получить формулу M = F/a.
Как и во многих физических задачах, полезно нарисовать схему того, что происходит. Вот ребенок тянет игрушку… гм… что-то такое.
В задаче даны сила и ускорение; однако сила 8 Н, приложенная к игрушке, находится под углом 45 °. Часть этой силы тянет игрушку в направлении y, а часть силы тянет ее в направлении x. Поскольку задача состоит в том, чтобы тянуть игрушку по земле, а не вверх, нас интересует х-компонент силы.
Сначала мы вспоминаем нашу рифму «синус — точка 5, точка 7, точка 9» и знаем, что в этой задаче будем использовать косинус, а не синус. Следовательно, чтобы вычислить x-составляющую силы, мы имеем F x = F * косинус (45°). Беглый взгляд на нашу таблицу значений синуса и косинуса показывает, что cos(45°) = 0,7, поэтому F x = F * косинус (45°) = 8 * 0,7 = 5,6. (Знайте свои таблицы умножения!)
Заполнение формулы M = F/a нашим новым вычисленным F х из задачи получаем М = 5,6/2 ≈ 6/2 = 3кг, что ближе всего к ответу б) 2,84кг.

Другой пример:
Эвакуатор тянет автомобиль массой 25 000 кг с помощью буксировочного крюка, который встречает автомобиль под углом 30° к земле. Какую силу должен приложить эвакуатор, чтобы тянуть автомобиль с начальным ускорением 3 м/с 2 ?
a) 33,612N
b) 50,319N
c) 75,000N
d) 86,206NВот краткое изображение нашего сценария.
Здесь силу, необходимую для тяги автомобиля в направлении x, можно рассчитать по формуле F x = Ма.
В этом сценарии нам даны масса автомобиля и ускорение в задаче. Требуемая сила в направлении x равна F x = 25 000 кг * 3 м/с 90 347 2 90 348 = 75 000 Н. В экспоненциальном представлении это 7,5 x 10 4 Н.
автомобиль в обоих направлениях x и y.
В предыдущей задаче мы видели, что F x = F * cos(Θ), где Θ — градус угла, который в данном случае равен 30°. Просмотрев нашу таблицу значений синуса и косинуса, мы видим, что cos(30°) ≈ 0,9.
