| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.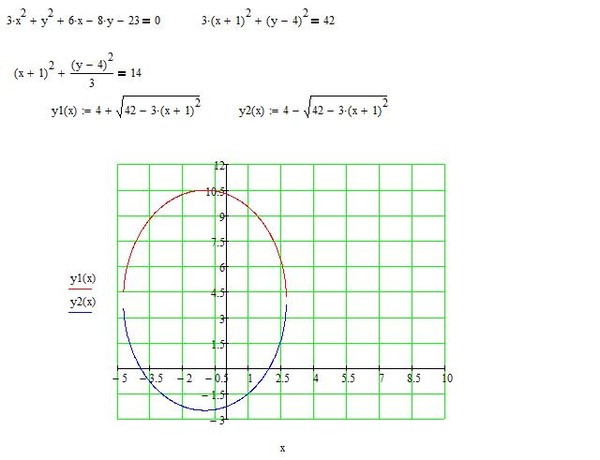 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.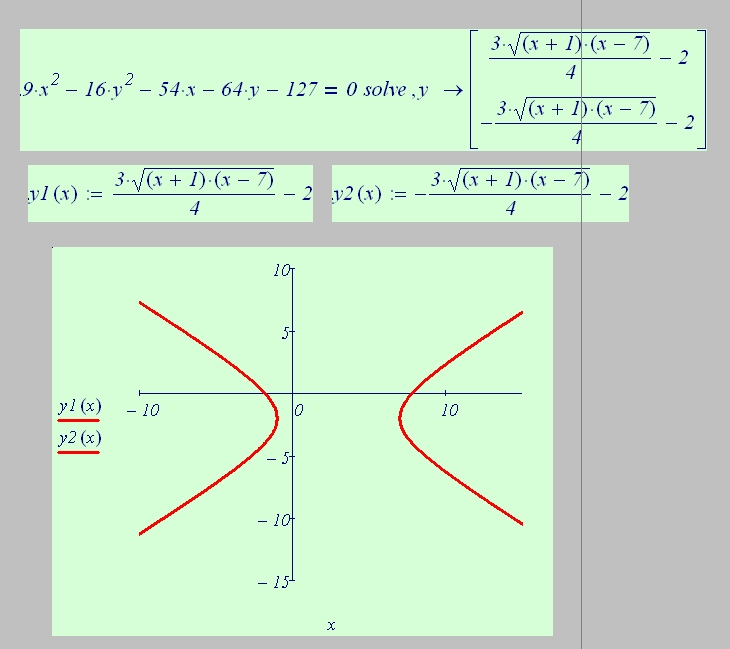 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.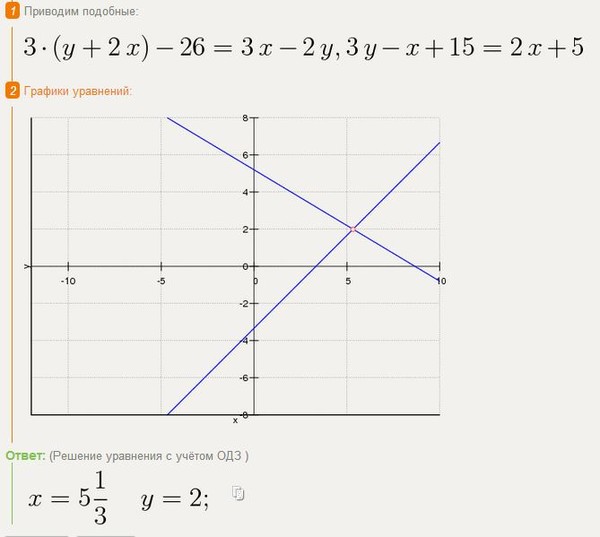 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.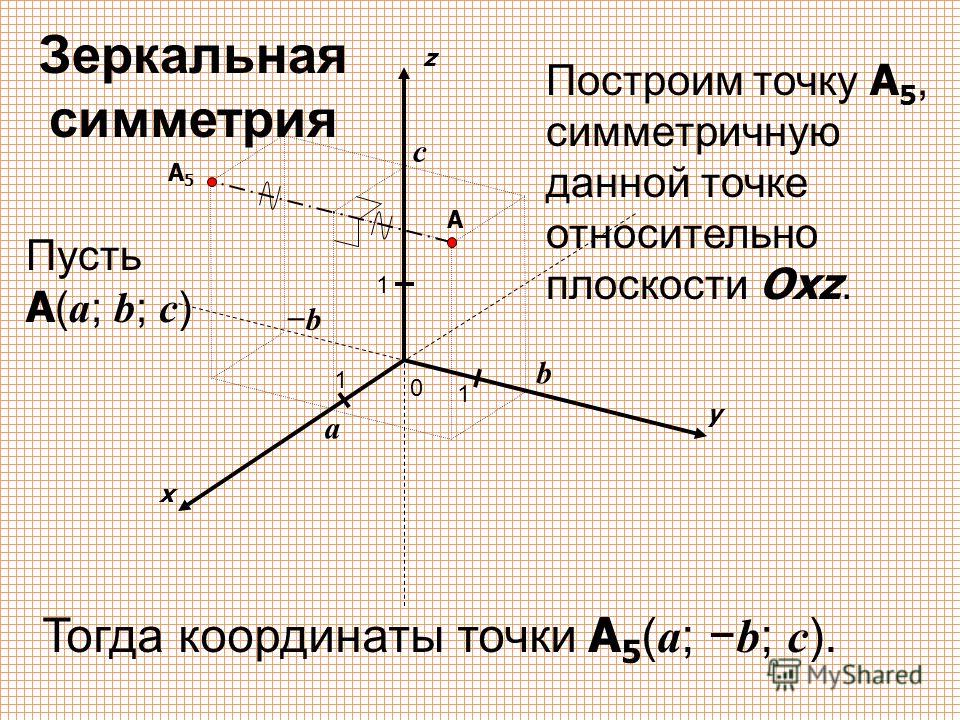 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.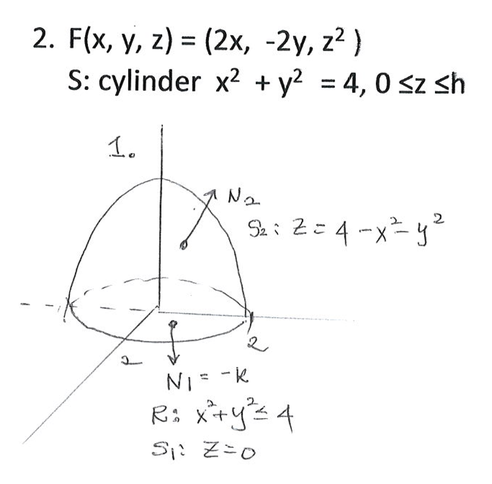 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. 2 2 |
Maxima – максимум свободы символьных вычислений
Впервые было опубликовано в «Linux Format» №11 (85), ноябрь 2006 г.
«А рисовать вы тоже умеете?» — «Рисовать? Кого-нибудь привлечем»
Как мы уже говорили в прошлый раз, количество различных функций в
Maxima разработчики постарались свести к минимуму, а широту размаха
каждой конкретной функции, соответственно, к максимуму. Соблюдается
эта тенденция и в функциях построения графиков: основных таких функций
всего две, с очевидными, как всегда, названиями — plot2d и plot3d (одно из значений
слова plot — график, а аббревиатуры 2d и 3d переводятся как двумерный и трехмерный). Если говорить точнее, возможности графической
отрисовки не встроены в Maxima, а реализованы посредством внешних
программ, в чем и прослеживается пресловутый Unix-way: «одна задача —
одна программа». По умолчанию, построением графиков
занимается gnuplot, но кроме него есть разрабатываемый
вместе с Maxima и идущий в ее же пакете openmath. Gnuplot
необходимо установить (вручную либо автоматически — как зависимость
Maxima) из пакета
Gnuplot
необходимо установить (вручную либо автоматически — как зависимость
Maxima) из пакета gnuplot-nox, либо
просто gnuplot, а для работы openmath нужен
командный интерпретатор wish, входящий обычно в
пакет tk; и, начиная с версии 5.10.0, еще и xMaxima.
Теперь кратко — о возможностях. Начнем
с plot2d. Кратчайший вариант ее вызова
такой: plot2d(выражение, [символ, начало, конец]), где
выражение задает функцию, график которой нужно построить, символ —
неизвестное (он, понятное дело, должен быть единственным
неопределенным символом, входящим в выражение), а начало и конец
задают отрезок оси Y в таком варианте записи выбирается автоматически,
исходя из минимума и максимума функции на заданном
промежутке. Обратите внимание, что неизвестное и концы промежутка
нужно задавать не тремя отдельными параметрами, как, скажем,
в integrate, а в виде списка. Это связано с тем,
что
Это связано с тем,
что plot2d может принимать еще и дополнительные
аргументы — в таком случае они перечисляются следом за таким списком,
что исключает всякую путаницу.
После вызова функции plot2d в таком варианте откроется
окно gnuplot, в котором будет отображен затребованный
график. Никакой интерактивной работы с полученным
изображением gnuplot не предусматривает, кроме
автоматического его масштабирования при изменении размеров
окна. Насмотревшись вдоволь, можно закрыть окно с графиком
клавишей Q, либо, в случае работы с Maxima в редакторе
TeXmacs или wxMaxima, просто переключиться обратно в интерфейс,
оставив окно gnuplot открытым, и продолжить работу:
В некоторых случаях автоматический подбор отображаемого xучастка
вертикальной оси может нас не устроить. Например, он работает не очень
хорошо, если функция имеет на заданном промежутке точку разрыва, хотя
бы один из односторонних пределов в которой равен бесконечности: тогда
промежуток по оси Y будет выбран слишком большим.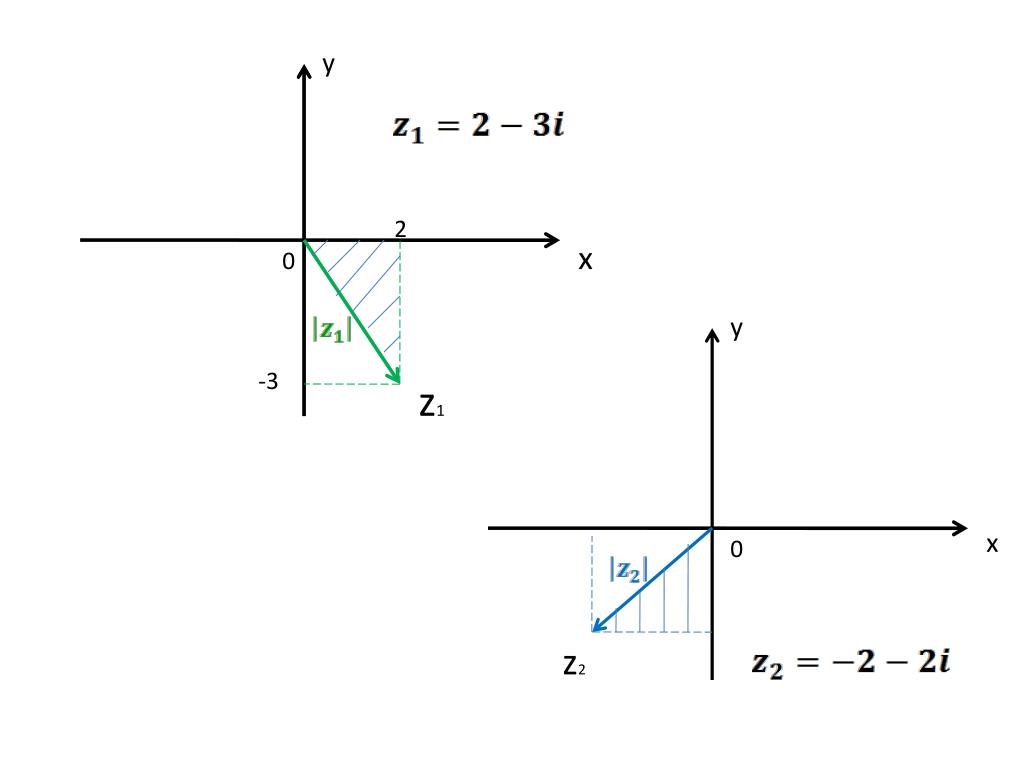 Да и в
других случаях может понадобиться изменить умолчательное
поведение. Для этого предусмотрен такой вариант вызова
функции:
Да и в
других случаях может понадобиться изменить умолчательное
поведение. Для этого предусмотрен такой вариант вызова
функции: plot2d(выражение, [символ, начало, конец],
[y, начало, конец]). Здесь буква y используется в
качестве обозначения вертикальной оси, а остальные два параметра имеют
тот же смысл, что и выше.
Как видите, умолчательный вид графиков в gnuplot достаточно прост и даже аскетичен, но здесь можно очень и очень многое
менять с помощью дополнительных опций. Некоторые из которых будут
освещены чуть ниже, а остальные можно изучить по документации
к gnuplot.
Чтобы построить на одной и той же картинке одновременно два графика
(или больше), просто передайте функции plot2d вместо
отдельного выражения их список:
Здесь [x, 0.01, 5] вместо [x, 0, 5] я
написал «по привычке» — Maxima 5.9.x выдавала ошибку, если заданная
функция была не определена на одном из концов интервала. В 5.10.0 мне
эту ошибку воспроизвести не удалось; так что есть основания полагать,
что поведение в таких случаях поправили.
В 5.10.0 мне
эту ошибку воспроизвести не удалось; так что есть основания полагать,
что поведение в таких случаях поправили.
Может plot2d строить и графики параметрически заданных
функций. Для этого используется список с ключевым
словом parametric: plot2d([parametric, x-выражение, y-выражение,
[переменная, начало, конец],
[nticks, количество]]). Здесь x-выражение и y-выражение задают зависимость координат от параметра,
то есть, по сути, это две функции
вида x(t), y(t), где t —
переменная параметризации. Эта же переменная должна фигурировать в
следующем аргументе-списке, а
параметры начало, конец, как и в двух других
рассмотренных случаях, задают отрезок, в пределах которого этот
параметр будет изменяться. Последний аргумент-список, с ключевым
словом nticks, задает количество кусочков, на которые
будет разбит интервал изменения параметра при построении графика.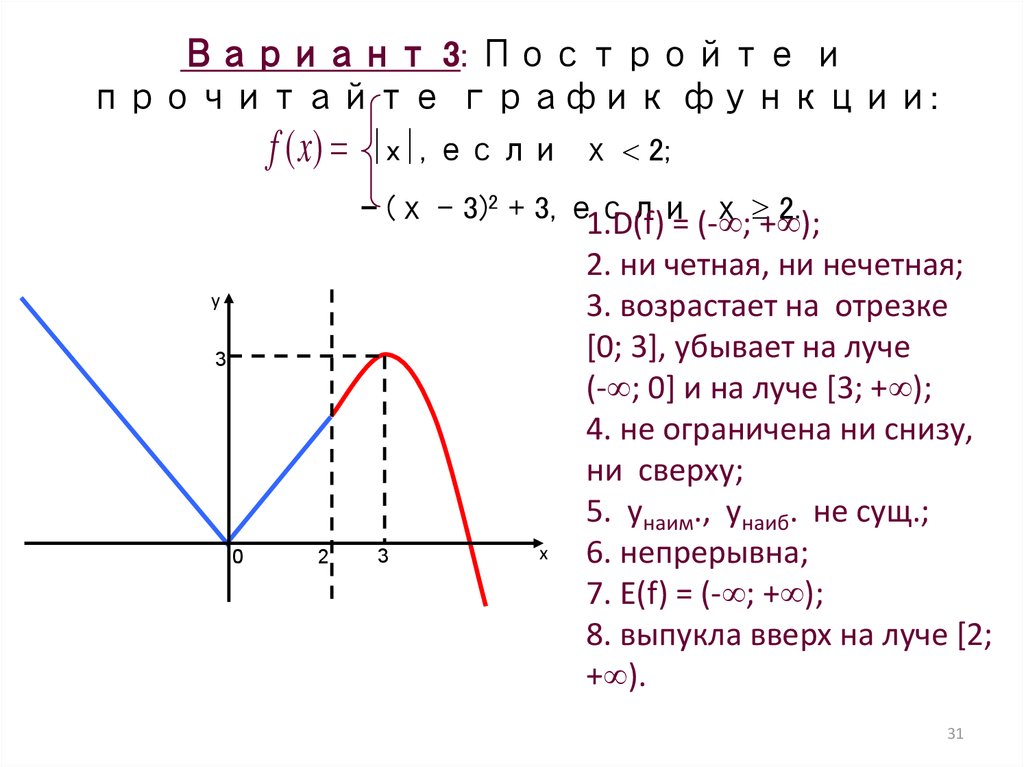 Этот
аргумент опционален, но на практике он нужен почти всегда:
умолчательное значение
Этот
аргумент опционален, но на практике он нужен почти всегда:
умолчательное значение nticks равно 10;
согласитесь, редко бывает нужно в качестве графика получить ломаную из
10 отрезков. Вот пример построения графика параметрической
функции:
Кроме parametric, функция plot2d понимает
еще одно ключевое слово: discrete. Предназначено оно, как
нетрудно догадаться, для отображения на плоскости дискретных множеств;
точнее говоря, конечных наборов точек. По записи аргументов такой
вариант распадается еще на
два: plot2d([discrete, x-список, y-список]) и plot2d([discrete, [x, y]-список]). В первом варианте
координаты задаются как два отдельных списка [x1, x2, …, xn],
[y1, y2, ,…, yn], а во втором — как список пар координат
отдельных точек [[x1, y1], [x2, y2], …, [xn, yn]].
Если мы, к примеру, имеем набор статистических значений, зависящих от номера, мы можем отобразить его, задав в качестве x-координат сами эти номера, то есть натуральные числа:
По умолчанию множество отображается в виде ломаной с вершинами в
заданных точках; такое поведение можно изменить и получить вывод, к
примеру, в виде отдельных точек. Это достигается использованием
специальных опций, применимых как к
Это достигается использованием
специальных опций, применимых как к plot2d, так и
к plot3d, поэтому давайте перейдем к рассмотрению
последней.
Придаем объем
Функция plot3d имеет два варианта вызова: один для
явного задания функции и один для параметрического. В обоих случаях
функция принимает три аргумента. Для явно заданной
функции: plot3d(выражение, [переменная1, начало, конец],
[переменная2, начало, конец]); аргументы
аналогичны plot2d, с той разницей, что здесь независимых
переменных две.
Построение нескольких поверхностей на одном графике не
поддерживается — потому, вероятно, что на таком рисунке проблематично
было бы что-либо разглядеть. Посему для параметрически заданной
функции ключевое слово parametric не требуется: вызов с первым
аргументом-списком уже не с чем перепутать. График параметрически
заданной функции строится
так: plot3d([выражение1, выражение2, выражение3],
[переменная1, начало, конец], [переменная2, начало, конец]),
где выражения отвечают, по
порядку, x(u, v), y(u, v), z(u, v).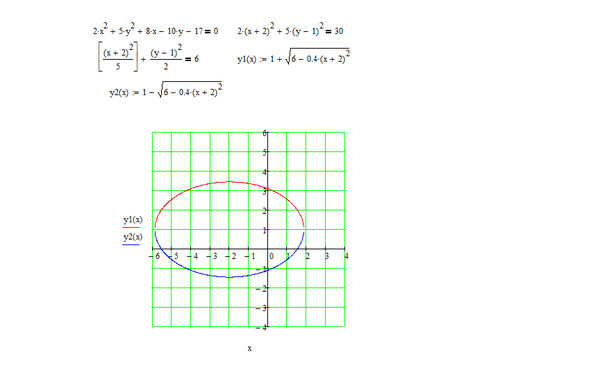
С помощью параметрической формы можно строить и пространственные кривые. Для этого просто нужно задать второй, фиктивный, параметр, чтобы Maxima не ругалась на неправильный синтаксис вызова функции:
И отсюда мы плавно переходим к опциям функций построения графиков,
посредством использованной выше опции grid. Каждая опция
имеет некоторое умолчательное значение, а изменить его можно, добавив
к аргументам список вида [имя-опции, значение]. Строго
говоря, рассмотренные выше y и nticks также
являются опциями; в предпоследнем примере мы задали
опции nticks значение 120, а в примере перед
ним в качестве значения опции y использовалась пара
чисел 0, 5. В документации к Maxima
символ x, выступавший в примерах выше в качестве
обязательного параметра, также приводится как опция; на самом деле
опцией он является только в случае parametric и действует
тогда так же, как и опция y, только по другой
оси.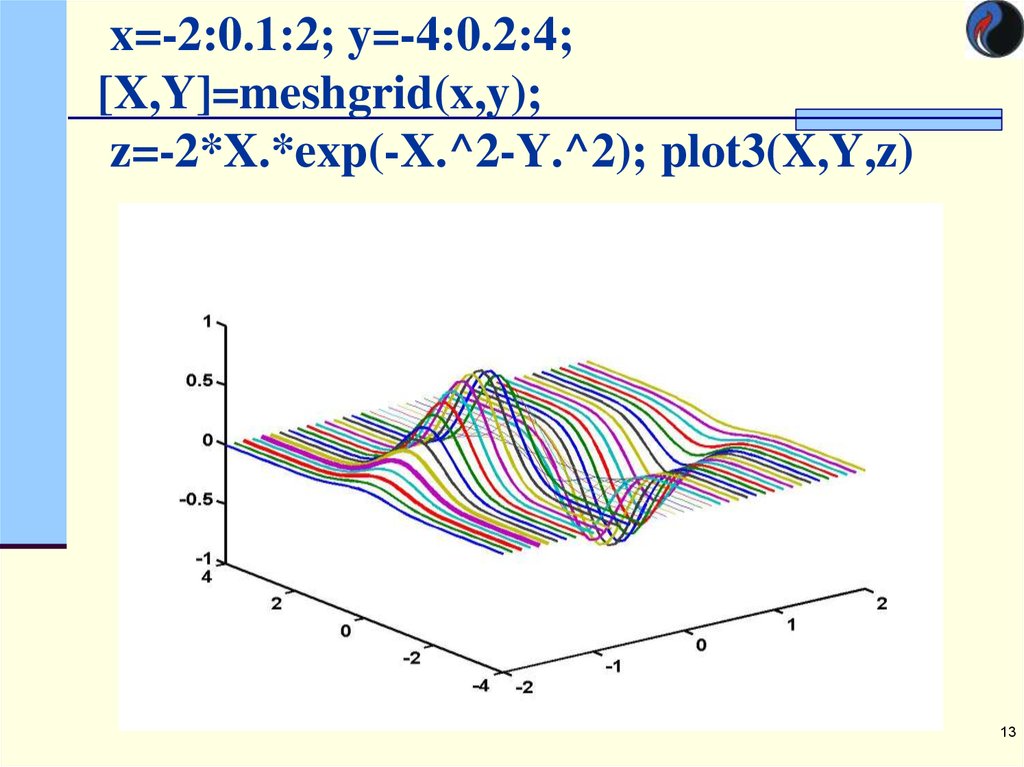 Опция
Опция grid, использованная выше, применима к
трехмерным графикам вместо опции nticks, используемой для
двумерных. Она, также как и y, задается в виде двух целых
значений, которые для поверхностей задают размер ячеек сетки, в виде
которой отображается поверхность; первое число — вдоль
оси X, второе — вдоль оси Y; либо, в случае
параметрического задания, по первому и по второму параметру
соответственно. Для кривых из этих параметров действует только один,
но писать нужно опять же оба, дабы не нарушать синтаксис; и здесь этот
параметр имеет в точности тот же смысл, что nticks для
кривых на плоскости. Но перейдем к другим опциям.
С претензией на красоту
Первая опция, которую мы рассмотрим, задает формат вывода
результата; так она и называется: plot_format. Формат
может принимать одно из четырех значений, первое из которых действует
по умолчанию: gnuplot, mgnuplot, openmath и ps. В умолчательном варианте
(значение
В умолчательном варианте
(значение gnuplot) данные для отображения передаются
напрямую программе gnuplot, которая сама по себе имеет
достаточно гибкое управление, и параметры ей можно передавать прямо из
Maxima с помощью дополнительных опций
функций plot2d/3d. Параметров этих настолько
много, что gnuplot могла бы стать темой отдельной статьи;
так что обращайтесь за ними к документации по gnuplot. В
противовес своим богатым возможностям, gnuplot имеет
перед следующими двумя интерфейсами (если откровенно — скорее, лишь
перед одним из них) только один недостаток: она генерирует статичное
изображение, тогда как mgnuplot и openmath позволяют в
реальном времени масштабировать и передвигать картинку,
а plot3d — еще и вращать линию или поверхность в разные
стороны в пространстве.
Следующий вариант — mgnuplot — является дополнительным
интерфейсом к gnuplot, написанным на Tcl/Tk, но динамика
у него настолько «задумчивая», а остальные возможности настолько
бедны, что я не вижу смысла останавливаться на нем подробнее.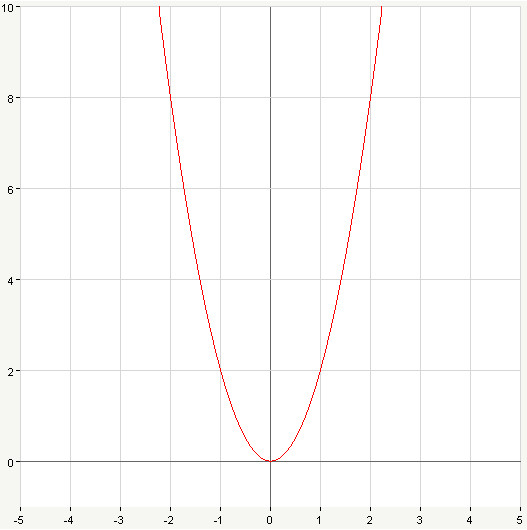
И перехожу сразу к openmath. Он тоже не очень-то
поддается управлению, зато предоставляет хорошую интерактивность,
особенно ценную в трехмерном варианте: после того, как объект
сгенерирован, его можно масштабировать и очень динамично вращать,
разглядывая со всех сторон. Особенно это помогает для сложных
поверхностей, когда, глядя на статичную «сетку» gnuplot,
непросто понять форму поверхности. Справедливости ради нужно отметить,
что gnuplot позволяет задавать точку обзора трехмерного
объекта в качестве одного из многочисленных параметров, то есть хотя
картинка и статична, но с какой стороны на нее смотреть, мы можем
указать произвольно.
Ну и последнее значение опции plot_format подталкивает
Maxima к непосредственной генерации PostScript-документа с
изображением. Но и здесь надо сказать: генерировать PostScript-вывод
умеет и все тот же gnuplot.
Большинство остальных опций относятся только к формату
вывода gnuplot. А мы рассмотрим еще одну универсальную,
пригодную для всех форматов и преобразующую не результирующее
изображение, а сам процесс построения графика; точнее, систему
координат. Называется эта опция
А мы рассмотрим еще одну универсальную,
пригодную для всех форматов и преобразующую не результирующее
изображение, а сам процесс построения графика; точнее, систему
координат. Называется эта опция transform_xy, по
умолчанию она равна false. Передавать ей нужно выражение,
сгенерированное функцией make_transform([x, y, z], f1(x, y, z),
f2(x, y, z), f3(x, y, z)). Кроме того, существует одно
встроенное преобразование, известное как polar_xy и
соответствующее make_transform([r, th, z], r*cos(th), r*sin(th),
z), то есть переходу к полярной цилиндрической системе
координат. В качестве примера использования transform_xy приведу преобразование к полярным сферическим координатам, раз уж во
встроенном виде его нет:
Обратите внимание: в первом аргументе-списке к make_transform последним должен идти зависимый символ, то есть тот, который будет выступать функцией от двух других.
Если вам нужно постоянно работать со сферическими координатами,
можете задать, скажем, spherical_xy:make_transform([t, f, r],
r*sin(f)*sin(t), r*cos(f)*sin(t), r*cos(t)), и затем при
построении графиков писать [transform_xy, spherical_xy].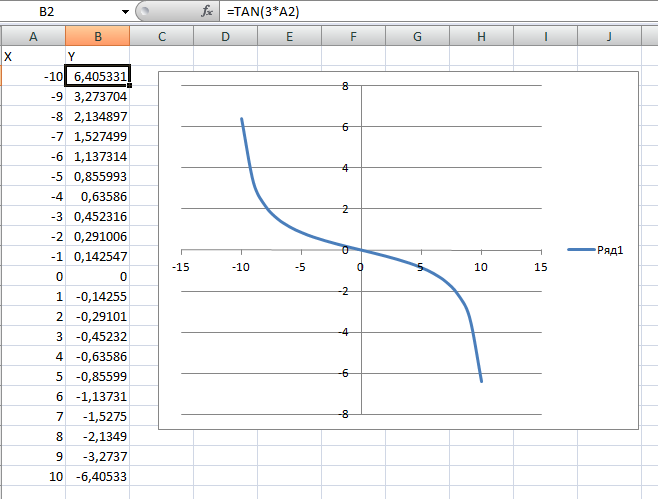 Ветвитесь и
повторяйтесь До сих пор мы двигались только по прямой, а теперь
поговорим о средствах «изменения траектории»: условном операторе и
циклах.
Ветвитесь и
повторяйтесь До сих пор мы двигались только по прямой, а теперь
поговорим о средствах «изменения траектории»: условном операторе и
циклах.
Начнем с условия. В Maxima, в отличие от большинства «традиционных»
процедурных и объектных языков программирования, где существует так
называемый условный оператор, привычная
связка if—then—else является не
синтаксической конструкцией, а самым настоящим оператором. По своему
действию он больше всего похож на тернарный оператор языка C, только с
более «человеческим»
синтаксисом: if условие then выражение1 else выражение2. При
выполнении «условия» из двух «выражений» вычисляется только первое и
возвращается как результат оператора; в противном случае выполняется
только второе и оно же является значением всего
выражения if—then—else. Часть
конструкции else выражение2, как и в большинстве языков
программирования, опциональна. Если ее нет, а условие все-таки не
выполнилось, результат оператора if будет
равен false.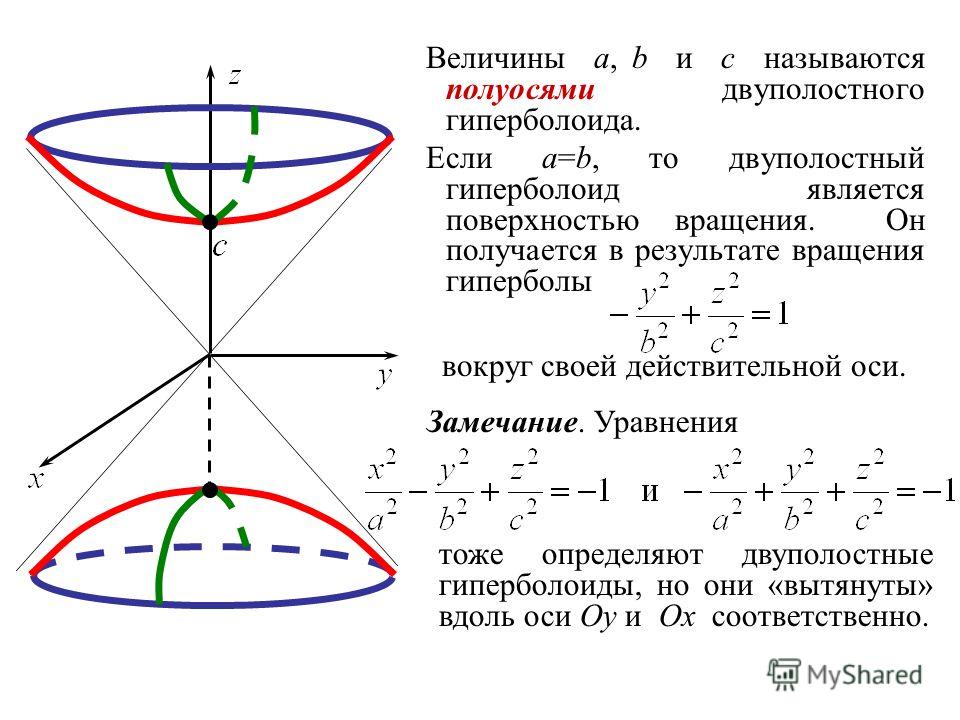
При этом, конечно же, никто вам не мешает использовать этот
оператор как обычную условную конструкцию, а возвращаемое значение
просто игнорировать. С другой стороны, оператор if можно
применять, например, для задания рекурсивных последовательностей:
Немного о самих условиях, которые могут проверяться
оператором if. Условия >, <, >=, <= записываются и расшифровываются традиционно, так же как и логические
операторы and, or, not. А вот о
равенствах-неравенствах нужно сказать пару слов. Равенство в Maxima
есть двух видов: синтаксическое и логическое. Знаком = обозначается как раз первое, а второе вычисляется с помощью
функции equal(). Чтобы не быть многословными, отличие
синтаксического равенства от логического продемонстрируем на примере;
здесь дополнительно используется предикат по имени is,
которые проверяет на истинность свой аргумент.
Ну и неравенств, соответственно, тоже существует два, с тем же
смыслом. Синтаксическое неравенство обозначается достаточно
непривычно — через #; видимо, этот символ разработчики
сочли наиболее визуально схожим со знаком ≠. Ну а логическое
неравенство обозначено через notequal().
Конечно, кроме упомянутых сравнений в условном операторе можно
использовать любые предикаты, то есть функции, возвращающие логические
значения true/false. Функций таких
достаточно много, но все они достаточно просты, поэтому не буду
тратить время на их описание: его можно почерпнуть в том же объеме из
документации.
Напоследок перейдем к циклам. Цикл в Maxima будто бы тоже один. Но он имеет столько различных вариантов, что назвать это все одним оператором цикла язык не поворачивается. Вот как выглядят основные разновидности:
for переменная:начало step шаг thru конец do выражениеfor переменная:начало step шаг while условие do выражениеfor переменная:начало step шаг unless условие do выражение
Первый прокручивает цикл, изменяя переменную с
заданным шагом от начала до конца; второй — от начала и пока
выполняется условие; третий — наоборот,
пока условие не выполняется.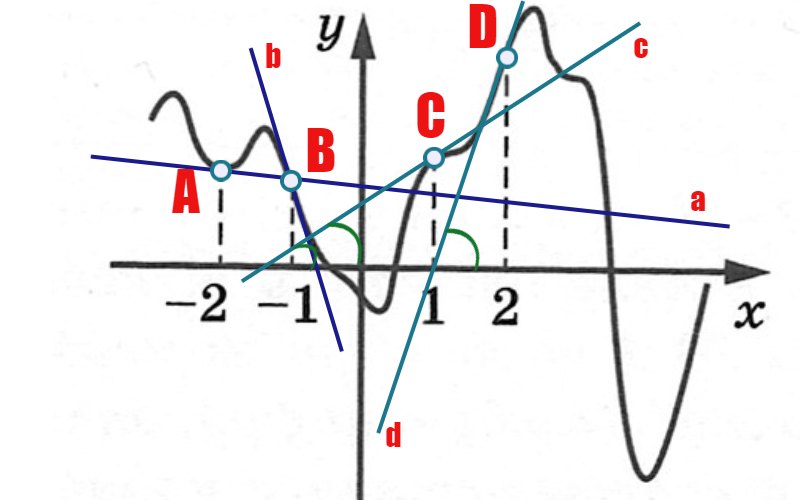 К примеру, мы можем получить
список из первых десяти членов последовательности из позапрошлого
примера:
К примеру, мы можем получить
список из первых десяти членов последовательности из позапрошлого
примера:
Как видите, в качестве оператора цикл в простейшем его виде, в
отличие от условия, использовать смысла нет, так как его возвращаемое
значение всегда равно done. В этом примере один из
элементов циклического оператора не указан; шаг, как видите, может
быть опущен и по умолчанию равен единице. Самое интересное в этом
операторе то, что опустить позволяется любую его часть,
кроме do; и в том числе в любых комбинациях. К примеру,
опустив кроме step еще и for, мы получаем из
этого же оператора традиционные циклы while и unless (второй и третий варианты). А проделав то же
самое с первым вариантом записи, получим цикл без счетчика
вида thru число do выражение, который просто
повторится заданное число раз. Можно, наоборот, опустить условие
окончания и получить цикл с индексной переменной, но бесконечный. А
оставив только
А
оставив только do, получим самый простой вариант
бесконечного цикла. Из таких бесконечных циклов можно выйти с помощью
оператора return(выражение) (точнее, конечно, конструкции
из двух операторов
вида if условие then return(выражение)), который прервет
выполнение цикла и вместо done вернет заданное выражение. Естественно,
оператор return() можно применять во всех видах циклов, а
не только в бесконечных.
Но и это еще не все. Кроме всех уже рассмотренных вариаций, цикл
может принимать еще две ипостаси. Во-первых, вместо step может использоваться конструкция next выражение, смысл
которой лучше тоже продемонстрировать на примере
После next может стоять любое вычислимое выражение
относительно индекса цикла, и применяться эта конструкция может во
всех трех вариантах цикла
(thru/while/unless).
А «во-вторых» — это еще один отдельный вариант
цикла: for переменная in список do выражение; либо
расширенная
форма: for переменная in список условие do выражение.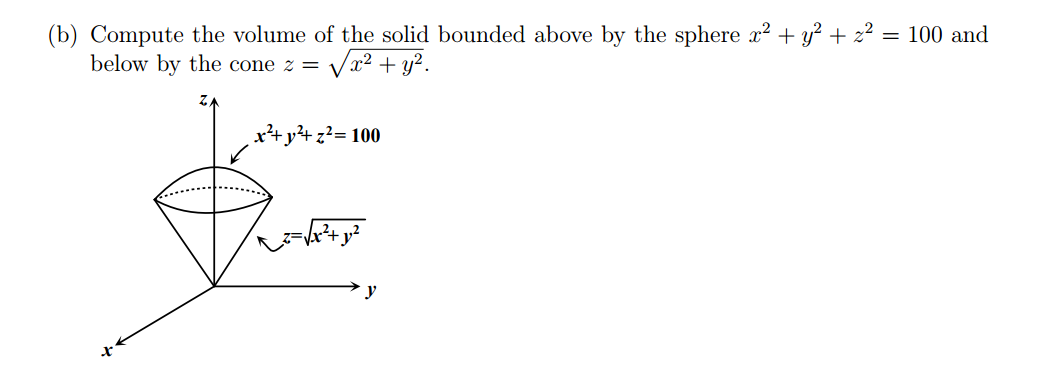 Здесь
цикл будет прокручен с
Здесь
цикл будет прокручен с переменной, изменяющейся по всем
элементам списка; плюс можно задать еще и
дополнительное условие на прерывание цикла. Вот теперь мы
с циклами действительно закончили. Как видите, все достаточно
разнообразно. Я, признаться, ничего, что здесь не реализовано, и
придумать не смог.
Но рассказ о циклах и условном операторе остается неполным, пока я
не рассказал о группировке выражений — ведь в обычном варианте
после then или do можно написать всего одно
из них. А группировка, или, как ее принято называть, составной
оператор, в Maxima — это опять-таки самый настоящий оператор, который
тоже, как и положено оператору, возвращает некоторое
значение. Обозначается он скобками, самыми что ни на есть круглыми и
обыкновенными; а разделяются сгруппированные операторы/выражения
внутри этих скобок не менее обыкновенными запятыми. Возвращаемым
значением составного оператора является последнее вычисленное
выражение.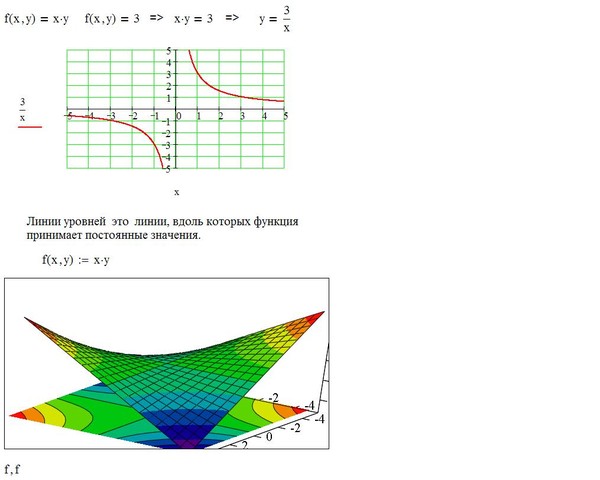
С условным оператором, столь разнообразными циклами и составным оператором мы уже можем, комбинируя их между собой и с любыми другими функциями и выражениями Maxima, писать полноценные программы с использованием богатого символьного математического аппарата. Естественно, теперь нам захочется сохранять эти программы в виде внешних файлов, чтобы не набирать их каждый раз вручную, а подгружать одной короткой командой. Об этом, а также о математических аналогах объявления переменных — в завершающей статье цикла.
Мы также поговорим о математических аналогах объявления переменных и рассмотрим практические примеры с применением уже достаточно богатого известного нам инструментария.
Представление данных в виде точечной диаграммы или графика
Точечные диаграммы и графики очень похожи друг на друга, особенно если точечная диаграмма отображается с соединительными линиями. Однако способ печати данных по горизонтальной оси (также известной как ось X) и вертикальной оси (ось Y) очень отличается.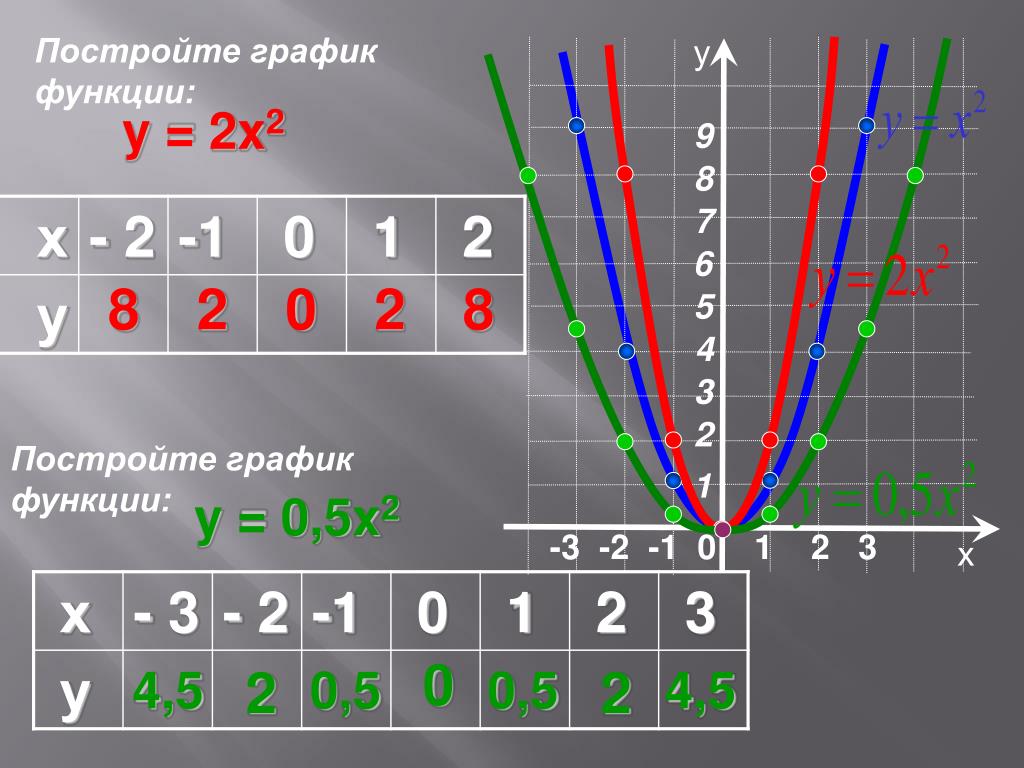
Примечание: Сведения о разных типах точек и графиков см. в таблице Типы диаграмм в Office.
Прежде чем выбрать один из этих типов диаграмм, вам может потребоваться узнать больше о различиях и узнать, когда лучше использовать точечная диаграмма вместо графика или наоборот.
Основное различие между точечная и графиками заключается в способе их отстройки на горизонтальной оси. Например, если использовать следующие данные листа для построения точечной диаграммы и графика, они будут представлены по-разному:
На точечной диаграмме значения суточного количества осадков из столбца A отображаются в виде значений X на горизонтальной оси (X), а показатели содержания твердых частиц из столбца B — в виде значений на вертикальной оси (Y). На точечной диаграмме категории никогда не отображаются на горизонтальной оси.
На точечной диаграмме всегда есть две оси значений, то есть один набор числовых данных представлен вдоль горизонтальной оси, а другой — вдоль вертикальной. На пересечении координат X и Y отображается точка данных, объединяющая эти два числовых значения. Такие точки данных могут быть распределены по горизонтальной оси равномерно или неравномерно, в зависимости от конкретных данных.
Первая точка данных на точечной диаграмме представляет значение Y (содержание частиц), равное 137, и значение X (суточная норма осадков), равное 1,9. Эти числа представляют значения в ячейках A9 и B9 на листе.
На графике те же значения суточного количества осадков и содержания частиц будут показаны как две разные точки данных, которые равномерно распределяются вдоль горизонтальной оси. Дело в том, что на графике есть только одна ось значений (вертикальная ось). Горизонтальная ось графика предназначена для отображения группировок (категорий) данных с равномерными интервалами.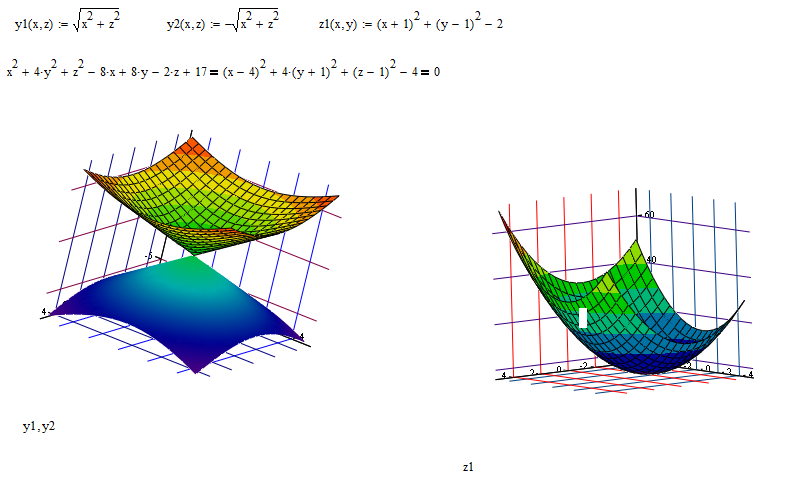 Так как категории не были заданы, они генерируются автоматически, например 1, 2, 3 и т. д.
Так как категории не были заданы, они генерируются автоматически, например 1, 2, 3 и т. д.
Это наглядный пример ситуации, когда график использовать не следует.
На графиках данные категории равномерно распределяются вдоль горизонтальной оси (оси категорий), а все числовые значения откладываются по вертикальной оси (оси значений).
Значение Y (содержание частиц), равное 137 (ячейка B9), и значение X (суточное количество осадков), равное 1,9 (ячейка A9), показаны на графике двумя разными точками данных. Ни одна из этих точек данных не является первой точкой данных, отображаемой на диаграмме. Вместо этого первая точка данных для каждого значения ряд данных ссылается на значения в первой строке данных на этом сайте (ячейки A2 и B2).
Различия между типами и шкалами осей
Так как горизонтальная ось точечной диаграммы всегда является осью значений, на ней можно показывать числа и даты (в том числе дни и часы), представляемые в виде числовых значений. Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, можно изменить параметры ее шкалы аналогично тому, как изменяется настройка шкалы вертикальной оси.
Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, можно изменить параметры ее шкалы аналогично тому, как изменяется настройка шкалы вертикальной оси.
Поскольку горизонтальная ось графика — это ось категорий, она может быть только осью текста или осью дат. На оси текста отображается только текст (нечисловые данные или числовые категории, не являющиеся значениями) с равномерными интервалами. На оси дат отображаются даты в хронологическом порядке через заданные интервалы (базовые единицы измерения), такие как число дней, месяцев или лет, даже если даты на листе расположены в ином порядке или выражены в других единицах.
Набор параметров шкалы оси категорий ограничен по сравнению с параметрами шкалы оси значений. Доступные параметры шкалы также зависят от типа используемой оси.
Точечные диаграммы обычно используются для отображения и сравнения числовых значений, например научных, статистических и инженерных данных. На таких диаграммах удобно демонстрировать связь между числовыми значениями, входящими в разные ряды данных; на диаграмме можно показать две группы чисел в виде одной последовательности точек.
На таких диаграммах удобно демонстрировать связь между числовыми значениями, входящими в разные ряды данных; на диаграмме можно показать две группы чисел в виде одной последовательности точек.
Графики позволяют представить непрерывный ряд информации в динамике по времени на стандартной шкале; они идеально подходят для отображения трендов данных с фиксированными равными интервалами или непрерывно с течением времени. На графике данные категорий равномерно распределены по горизонтальной оси, а все данные значений также равномерно распределены вдоль вертикальной оси. График обычно используется, если данные включают нечисловые значения X, а в случае числовых значений X лучше использовать точечную диаграмму.
Точечную диаграмму целесообразно использовать, если необходимо сделать следующее:
-
Изменить шкалу горизонтальной оси. Так как горизонтальная ось точечной диаграммы является осью значений, для нее доступно больше параметров шкалы.

-
Использовать логарифмическую шкалу на горизонтальной оси. Горизонтальную ось можно перевести в логарифмическую шкалу.
-
Отобразить данные листа, состоящие из пар или группированных наборов значений. На точечной диаграмме можно регулировать независимые шкалы осей, чтобы показать больше информации о сгруппированных значениях.
-
Показать особенности распределения данных в крупных наборах. С помощью точечных диаграмм удобно иллюстрировать особенности распределения данных, например показывать линейные и нелинейные тренды, кластеры и отклонения.

-
Сравнить большое количество точек данных без учета времени. Чем больше данных включено в точечную диаграмму, тем точнее будет проводимое сравнение.
Используйте график вместо точечной диаграммы, если необходимо сделать следующее:
-
Использовать текстовые подписи на горизонтальной оси. Такими подписями можно помечать значения, разделенные равными интервалами, например месяцы, кварталы или финансовые годы.
-
Использовать несколько числовых подписей на горизонтальной оси.
 Если используется небольшое число расположенных с равными промежутками числовых подписей, обозначающих интервалы времени, например годы, можно выбрать график.
Если используется небольшое число расположенных с равными промежутками числовых подписей, обозначающих интервалы времени, например годы, можно выбрать график. -
Использовать временную шкалу на горизонтальной оси. Если требуется отобразить данные в хронологическом порядке с определенными интервалами или в базовых единицах измерения, таких как число дней, месяцев или лет, даже если даты на листе не упорядочены или выражены в других единицах, используйте график.
Примечание: Следующая процедура относится к Office 2013 и более новой версии. Действия для Office 2010?
Создание точечной диаграммы
Как же была создана эта точечная диаграмма? Создать похожую диаграмма поможет следующая процедура. Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
-
Скопируйте данные примера на пустой лист или откройте лист с данными, которые нужно отражать на точечная диаграмма.
1
2
3
4
5
6
7
8
9
10
11
A
B
Суточное количество осадков
Твердые частицы
4,1
122
4,3
117
5,7
112
5,4
114
5,9
110
5,0
114
3,6
128
1,9
137
7,3
104
org/ListItem»>
-
На вкладке Вставка нажмите кнопку Вставить точечная (X, Y) или Пузырьковая диаграмма.
-
Нажмите кнопку Точечная.
Совет: Чтобы увидеть название какого-либо типа диаграммы, наведите на него указатель.
-
Щелкните область диаграммы диаграммы, чтобы отобразить вкладки Конструктор и Формат.

-
На вкладке Конструктор выберите нужный стиль диаграммы.
-
Щелкните название диаграммы и введите нужный текст.
-
Чтобы изменить размер шрифта названия диаграммы, щелкните его правой кнопкой мыши, выберите шрифт ивведите нужный размер в поле Размер. Нажмите кнопку ОК.
org/ListItem»>
-
На вкладке Конструктор нажмите кнопку Добавить элемент диаграммы > названия осейи сделайте следующее:
-
Чтобы добавить название горизонтальной оси, щелкните Основной горизонтальный.
-
Чтобы добавить название вертикальной оси, щелкните Основная вертикальная.

-
Щелкните каждое название, введите нужный текст и нажмите ввод.
-
Чтобы отформатировать дополнительные параметры, на вкладке Формат в поле Элементы диаграммы выберите название из списка и нажмите кнопку Формат выделения. Появится области Формат названия. Щелкните Размер & свойства , а затем выберите Вертикальное выравнивание, Направлениетекста или Настраиваемый угол.
-
-
Щелкните область построения диаграммы или на вкладке Формат в поле Элементы диаграммы выберите Область диаграммы в списке элементов диаграммы.

-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
-
Щелкните область диаграммы или на вкладке Формат в поле Элементы диаграммы выберите Область диаграммы в списке элементов диаграммы.
-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
org/ListItem»>
-
На вкладке Разметка страницы в группе Темы нажмите кнопку Темы.
-
В области Officeвыберите тему, которую вы хотите использовать.
Выберите данные, которые нужно отобрать на точечная диаграмма.
Щелкните в области диаграммы.
Если вы не хотите использовать цвета темы, которая по умолчанию применяется к книге, сделайте следующее:
Создание графика
Как же был создан этот график? Создать похожий график поможет следующая процедура. Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
-
Скопируйте данные листа-примера в пустой лист или откройте лист, содержащий данные, которые нужно отобразить на графике.
1
2
3
4
5
6
7
8
9
10
11
A
B
C
Дата
Суточное количество осадков
Твердые частицы
01.
 01.07
01.074,1
122
02.01.07
4,3
117
03.01.07
5,7
112
04.
 01.07
01.075,4
114
05.01.07
5,9
110
06.01.07
5,0
114
07.
 01.07
01.073,6
128
08.01.07
1,9
137
09.01.07
7,3
104
org/ListItem»>
-
На вкладке Вставка нажмите кнопку Вставить график или Диаграмма с областью.
-
Выберите тип График с маркерами.
-
Щелкните область диаграммы диаграммы, чтобы отобразить вкладки Конструктор и Формат.
org/ListItem»>
-
Щелкните название диаграммы и введите нужный текст.
-
Чтобы изменить размер шрифта названия диаграммы, щелкните его правой кнопкой мыши, выберите шрифт ивведите нужный размер в поле Размер. Нажмите кнопку ОК.
-
Щелкните в области диаграммы.
org/ListItem»>
-
Чтобы отобразить один из рядов данных по вторичной вертикальной оси, щелкните ряд данных или выберите его в списке элементов диаграммы (на вкладке Формат в группе Текущий выделение нажмите кнопку Элементы диаграммы).
-
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
 Появится области задач Формат ряда данных.
Появится области задач Формат ряда данных. -
В группе Параметры ряда выберите вариант По вспомогательной оси и нажмите кнопку Закрыть.
-
На вкладке Конструктор в группе Макеты диаграмм нажмите кнопку Добавитьэлемент диаграммы и сделайте следующее:
-
Чтобы добавить название основной вертикальной оси, щелкните Название оси >основной вертикальной. а затем в области Формат названия оси щелкните Размер & свойства , чтобы настроить нужный тип названия вертикальной оси.

-
Чтобы добавить название вторичной вертикальной оси, щелкните Название оси > По вторичной вертикальной оси, а затем в области Формат названия оси щелкните Размер & Свойства , чтобы настроить тип названия вертикальной оси.
-
Щелкните каждое название, введите нужный текст и нажмите ввод.
-
-
Щелкните область построения диаграммы или выберите ее в списке элементовдиаграммы (вкладка Формат, группа Текущий выделение, поле Элементы диаграммы).

-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
-
Щелкните в области диаграммы.
-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
-
Если вы не хотите использовать цвета темы, которая по умолчанию применяется к книге, сделайте следующее:
-
На вкладке Разметка страницы в группе Темы нажмите кнопку Темы.
-
В области Officeвыберите тему, которую вы хотите использовать.
Выделите данные, которые вы хотите отобразить на графике.
На вкладке Конструктор выберите нужный стиль диаграммы.
На диаграмме щелкните легенду или добавьте ее из списка элементов диаграммы (на вкладке Конструктор нажмите кнопку Добавить элемент диаграммы > Легендаи выберите место для легенды).
Создание точечная диаграммы или графика в Office 2010
Как же была создана эта точечная диаграмма? Создать похожую диаграмма поможет следующая процедура. Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
Вы можете скопировать эти данные на свой лист или использовать собственные данные.
-
Скопируйте данные листа-примера на пустой лист или откройте лист, содержащий данные, которые вы хотите показать на точечной диаграмме.
1
2
3
4
5
6
7
8
9
10
11
A
B
Суточное количество осадков
Твердые частицы
4,1
122
4,3
117
5,7
112
5,4
114
5,9
110
5,0
114
3,6
128
1,9
137
7,3
104
org/ListItem»>
-
На вкладке Вставка в группе Диаграммы щелкните Точечная.
-
Выберите тип Точечная с маркерами.
Совет: Чтобы увидеть название какого-либо типа диаграммы, наведите на него указатель.
-
Щелкните область диаграммы.

Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Конструктор в группе Стили диаграмм выберите стиль, который требуется использовать.
Для данной точечной диаграммы использовался стиль 26.
-
На вкладке Макет нажмите кнопку Название диаграммы и выберите расположение для заголовка в списке.
Мы выбрали над диаграммой.

-
Щелкните название диаграммы и введите нужный текст.
Для данной точечной диаграммы мы ввели название Уровни содержания твердых частиц в осадках.
-
Чтобы уменьшить размер названия диаграммы, щелкните его правой кнопкой мыши и введите нужное значение в контекстном меню в поле Размер шрифта.
Для данной точечной диаграммы использовался размер 14.
-
Щелкните в области диаграммы.

-
На вкладке Макет в группе Подписи нажмите кнопку Названия осей и выполните следующие действия:
-
Чтобы добавить название горизонтальной оси, щелкните Название основной горизонтальной оси и Название под осью.
-
Чтобы добавить название вертикальной оси, щелкните Название основной вертикальной оси и выберите нужный тип названия.
Для данной точечной диаграммы мы выбрали Повернутое название.

-
Щелкните каждое название, введите нужный текст и нажмите ввод.
Для данной точечной диаграммы мы ввели Суточное количество осадков в качестве названия горизонтальной оси и Содержание твердых частиц в качестве названия вертикальной оси.
-
-
Щелкните область построения диаграммы или выберите пункт Область построения в списке элементов диаграммы (вкладка Макет, группа Текущий фрагмент, поле Элементы диаграммы).

-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
Для данной точечной диаграммы был выбрано значение Слабый эффект — Акцент 3.
-
Щелкните в области диаграммы.
-
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.

Для данной точечной диаграммы был выбрано значение Слабый эффект — Акцент 1.
-
Если вы не хотите использовать цвета темы, которая по умолчанию применяется к книге, сделайте следующее:
-
На вкладке Разметка страницы в группе Темы нажмите кнопку Темы.
-
В группе Встроенные выберите тему, которую вы хотите использовать.

Для графика использовалась тема Office.
-
Выберите данные, которые нужно показать на точечной диаграмме.
Как же был создан этот график? Создать похожий график поможет следующая процедура. Для этой диаграммы были использованы данные листа-примера. Вы можете скопировать эти данные на свой лист или использовать собственные данные.
-
Скопируйте данные листа-примера в пустой лист или откройте лист, содержащий данные, которые нужно отобразить на графике.
1
2
3
4
5
6
7
8
9
10
11
A
B
C
Дата
Суточное количество осадков
Твердые частицы
01.
 01.07
01.074,1
122
02.01.07
4,3
117
03.
 01.07
01.075,7
112
04.01.07
5,4
114
05.
 01.07
01.075,9
110
06.01.07
5,0
114
07.
 01.07
01.073,6
128
08.01.07
1,9
137
09.
 01.07
01.077,3
104
-
Выделите данные, которые вы хотите отобразить на графике.
-
На вкладке Вставка в группе Диаграммы щелкните График.

-
Выберите тип График с маркерами.
-
Щелкните область диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
-
На вкладке Конструктор в группе Стили диаграмм выберите стиль, который требуется использовать.
Для данного графика использовался стиль 2.

-
На вкладке Макет в группе Подписи нажмите кнопку Название диаграммы и выберите пункт Над диаграммой.
-
Щелкните название диаграммы и введите нужный текст.
Для данного графика мы ввели название Уровни содержания твердых частиц в осадках.
-
Чтобы уменьшить размер названия диаграммы, щелкните его правой кнопкой мыши и введите нужное значение в контекстном меню в поле Размер.

Для данного графика использовался размер 14.
-
На диаграмме щелкните легенду или выберите ее в списке элементов (вкладка Макет, группа Текущий фрагмент, поле Элементы диаграммы).
-
На вкладке Макет в группе Подписи нажмите кнопку Легенда и выберите нужное расположение.
Для данного графика был выбран вариант Добавить легенду сверху.
-
Чтобы нанести один из рядов данных вдоль вспомогательной вертикальной оси, выделите ряд данных для количества осадков или выберите его в списке элементов диаграммы (вкладка Макет, группа Текущий фрагмент, поле Элементы диаграммы).

-
На вкладке Макет в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
-
В группе Параметры ряда выберите вариант По вспомогательной оси и нажмите кнопку Закрыть.
-
На вкладке Макет в группе Подписи нажмите кнопку Названия осей и выполните следующие действия:
-
Чтобы добавить название основной вертикальной оси, щелкните Название основной вертикальной оси и выберите нужный тип названия.
Для данного графика мы выбрали Повернутое название.
-
Чтобы добавить название вспомогательной вертикальной оси, щелкните Название вспомогательной вертикальной оси и выберите нужный тип названия.
Для данного графика мы выбрали Повернутое название.
-
Щелкните каждое название, введите нужный текст и нажмите клавишу ВВОД.

Для данной точечной диаграммы мы ввели Содержание твердых частиц в качестве названия основной вертикальной оси и Суточное количество осадков в качестве названия вспомогательной вертикальной оси.
Щелкните область построения диаграммы или выберите ее в списке элементов (вкладка Макет, группа Текущий фрагмент, поле Элементы диаграммы).
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
Для данного графика было выбрано значение Слабый эффект — Темный 1.
Щелкните в области диаграммы.
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительные и выберите нужный эффект.
Для данного графика был выбрано значение Слабый эффект — Акцент 3.
Если вы не хотите использовать цвета темы, которая по умолчанию применяется к книге, сделайте следующее:
На вкладке Разметка страницы в группе Темы нажмите кнопку Темы.
В группе Встроенные выберите тему, которую вы хотите использовать.
Для графика использовалась тема Office.
Создание точечной диаграммы
- org/ListItem»>
-
На вкладке Вставка нажмите кнопку Точечная диаграмма X Yи в области Точечная выберитедиаграмму.
-
Выбрав диаграмму, перейдите на вкладку Конструктор диаграмм, чтобы сделать следующее:
-
Нажмите кнопку Добавить элемент диаграммы, чтобы изменить такие сведения, как название, метки и легенда.
org/ListItem»>
Нажмите кнопку Быстрый макет, чтобы выбрать один из предопределельных наборов элементов диаграммы.
-
-
Чтобы изменить макет или стиль, щелкните одно из изображений для предварительного просмотра в коллекции стилей.
-
Нажмите кнопку Строка/столбецили Выберите данные, чтобы изменить представление данных.
-
Выбрав диаграмму, щелкните вкладку Конструктор, чтобы при желании изменить заливку фигуры, контур или эффекты элементов диаграммы.

Выберите данные, которые нужно отобрать на диаграмме.
Создание графика
-
Выберите данные, которые нужно отобрать на диаграмме.
-
На вкладке Вставка нажмите кнопку Линияи выберите один из доступных стилей графиков.
-
Выбрав диаграмму, перейдите на вкладку Конструктор диаграмм, чтобы сделать следующее:
- org/ListItem»>
Нажмите кнопку Добавить элемент диаграммы, чтобы изменить такие сведения, как название, метки и легенда.
-
Нажмите кнопку Быстрый макет, чтобы выбрать один из предопределельных наборов элементов диаграммы.
-
Чтобы изменить макет или стиль, щелкните одно из изображений для предварительного просмотра в коллекции стилей.
-
Нажмите кнопку Строка/столбецили Выберите данные, чтобы изменить представление данных.

-
Выбрав диаграмму, щелкните вкладку Конструктор, чтобы при желании изменить заливку фигуры, контур или эффекты элементов диаграммы.
См. также
Сохранение диаграммы как шаблона
3-8Поверхности, часть 2
Поверхности, часть 2Поверхности и контурные графики
г.
Часть 2: квадратные поверхности
Квадратные поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе. Подобно графикам квадратичных уравнений на плоскости, их формы зависят от знаки различных коэффициентов в их квадратных уравнениях.
Сферы и эллипсоиды
Сфера — это граф уравнение вида x 2 + y 2 + z 2 = p 2 для некоторого действительного числа p . Радиус сферы равен p (см. рисунок ниже). Эллипсоиды представляют собой графики уравнений вида x 2 + by 2 + c z 2 = 2 p где a , b и c все положительные. Особенно, сфера — это особый эллипсоид, для которого a , b и c все равны.
- Постройте график x 2 + y 2 + z 2 = 4
на вашем листе в декартовых координатах.
 Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид.
Затем выберите другие коэффициенты
в уравнении и постройте несферический эллипсоид. - Какие изгибы вы находите, когда пересекают сферу плоскостью, перпендикулярной одной из осей координат? Что вы нашли для эллипсоида?
Параболоиды
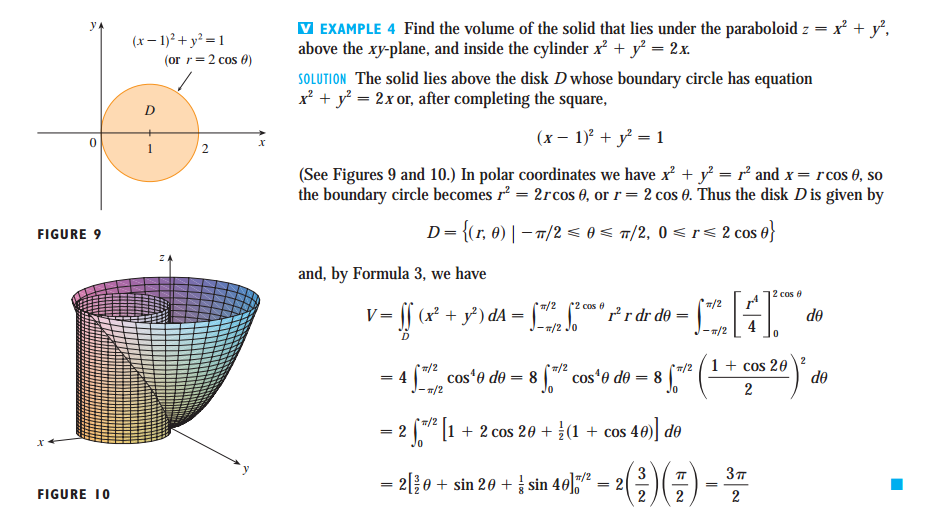
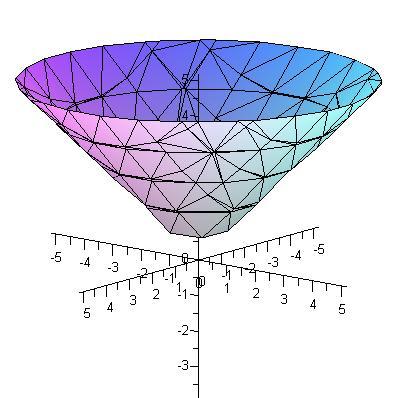
Поверхности, пересечения которых с плоскости, перпендикулярные любым двум координатным осям, являются параболами в тех самолеты называются параболоидами . Пример показан на рисунке ниже — это график z = x 2 + у 2 .
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения
эта поверхность с плоскостями, перпендикулярными х- и у- оси
являются параболами.
 [Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .]
[Подсказка: установите либо y = c , либо x = c .
для некоторой константы c .] - Измените уравнение на z = 3 x 2 + y 2 , и снова сюжет. Как изменится поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.
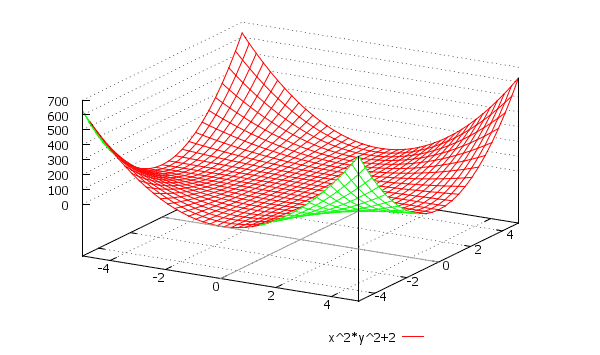
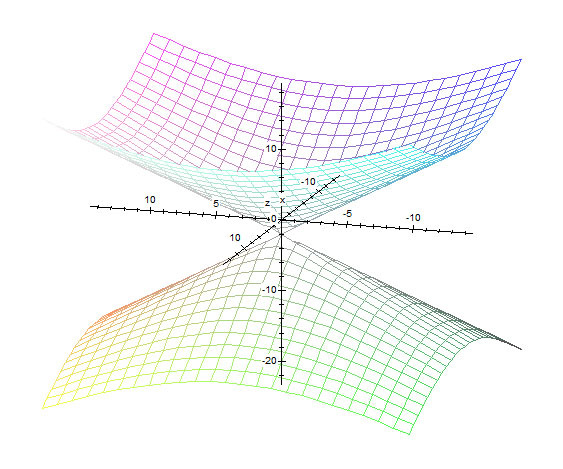
поверхность на следующем рисунке представляет собой график z = х 2 — у 2 . В этом случае пересечения с плоскостями, перпендикулярными x и и оси по-прежнему являются параболами, но два набора парабол различаются по форме. направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его также называют «седловидная поверхность».
- Сделайте свой собственный сюжет этого гиперболического
параболоида на листе и поворачивайте график, чтобы увидеть его с разных точек зрения.
 Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Гиперболоиды
Гиперболоиды — это поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определение характерно то, что их пересечения с плоскостями, перпендикулярными какому-либо две оси координат являются гиперболами. Есть два типа гиперболоидов — первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1, что показано на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на форму, обычно используемую для атомных электростанций градирни. (Источник: Агентство по охране окружающей среды Ответ на инцидент в Три-Майл-Айленде.)
Эта поверхность называется гиперболоидом .
из одного листа , потому что это все «связано» в одно целое. (Мы будем
перейти к другому делу в настоящее время.)
(Мы будем
перейти к другому делу в настоящее время.)
- Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в рабочем листе. Какие бывают пересечения ул. поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами. [Подсказка: установите либо г = c 91 844 или 91 843 x = c 91 844 для некоторой константы c .]
Другой тип — гиперболоид . из двух листов , и это проиллюстрировано графиком x 2 — y 2 — z 2 = 1, показано ниже.
- Сделайте свой собственный участок этой поверхности
на листе и поверните график, чтобы увидеть его с разных точек зрения.
 Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями формы z = c , для некоторой константы с ?
Следуйте предложениям в рабочем листе. Какие бывают пересечения ул.
поверхность с плоскостями формы z = c , для некоторой константы с ? - Покажите, что пересечения эти две поверхности с соответствующими координатными плоскостями являются гиперболами.
В каждом из этих примеров пересечения поверхности с семейством плоскостей многое говорит нам о структуре поверхности. Мы вернемся к этой теме в части 6. когда мы смотрим на контурные линии.
| КПК Главная | Материалы | Многовариантный Исчисление | Содержание модуля | Назад | Вперед |
модулей на math. duke.edu duke.edu | Авторское право КПК и автор(ы), 2001-2002 гг. |
Исчисление III. Квадратичные поверхности
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-4: квадратные поверхности
92}}} = 1\]Вот эскиз типичного эллипсоида.
Если \(a = b = c\), то у нас будет сфера.
Обратите внимание, что мы дали уравнение только для эллипсоида с центром в начале координат. Ясно, что эллипсоиды не обязательно должны быть центрированы в начале координат. Однако, чтобы немного упростить обсуждение в этом разделе, мы решили сосредоточиться на поверхностях, которые так или иначе «центрированы» в начале координат.
Конус
Вот общее уравнение конуса. 92}}}\]
Вот эскиз типичного конуса.
Обратите внимание, хотя мы и назвали это конусом, он больше похож на форму песочных часов, чем на то, что большинство назвало бы конусом. Конечно, верхняя и нижняя части песочных часов на самом деле представляют собой конусы, как мы обычно их себе представляем.
Возникает вопрос: а что, если нам действительно нужна только верхняя или нижняя часть (, т. е. , конус в традиционном смысле)? На это достаточно легко ответить. Все, что нам нужно сделать, это решить данное уравнение для \(z\) следующим образом, 92}} \) всегда будет отрицательным и поэтому будет уравнением только нижней части «конуса» выше.
Все, что нам нужно сделать, это решить данное уравнение для \(z\) следующим образом, 92}} \) всегда будет отрицательным и поэтому будет уравнением только нижней части «конуса» выше.
Также обратите внимание, что это уравнение конуса, который раскрывается вдоль оси \(z\). Чтобы получить уравнение конуса, раскрывающегося по одной из других осей, все, что нам нужно сделать, это немного изменить уравнение. Это относится и к остальным поверхностям, которые мы рассмотрим в этом разделе.
В случае конуса переменная, стоящая сама по себе по одну сторону от знака равенства, будет определять ось, вдоль которой раскрывается конус. Например, конус, который раскрывается вдоль оси \(x\), будет иметь уравнение 92}\]
Вот эскиз типичного цилиндра с эллипсным поперечным сечением.
Цилиндр будет центрирован на оси, соответствующей переменной, которая не фигурирует в уравнении.
Будьте осторожны, не перепутайте это с кругом. В двух измерениях это круг, а в трех измерениях — цилиндр. 2}}} = 1\]
92}}} = 1\]
2}}} = 1\]
92}}} = 1\]
Вот эскиз типичного гиперболоида из двух листов.
Переменная с положительным значением перед ней задает ось, вдоль которой центрируется график.
Обратите внимание, что единственная разница между гиперболоидом одного листа и гиперболоидом двух листов заключается в знаках перед переменными. Это прямо противоположные знаки.
Также обратите внимание, что так же, как мы могли бы сделать с конусами, если мы решим уравнение для \(z\), положительная часть даст уравнение для верхней части этого, а отрицательная часть даст уравнение для нижней части это. 92}}} = \frac{z}{c}\]
Как и в случае с цилиндрами, он имеет поперечное сечение в виде эллипса, а если \(a = b\), то он будет иметь поперечное сечение в виде круга. Когда мы будем иметь дело с ними, мы, как правило, будем иметь дело с теми, у которых круг вместо поперечного сечения.
Вот эскиз типичного эллиптического параболоида.
В этом случае переменная, не возведенная в квадрат, определяет ось, на которой раскрывается параболоид. Кроме того, знак \(с\) будет определять направление открытия параболоида. Если \(с\) положительное, то оно открывается вверх, а если \(с\) отрицательное, то открывается вниз. 92}}} = \frac{z}{c}\]
Кроме того, знак \(с\) будет определять направление открытия параболоида. Если \(с\) положительное, то оно открывается вверх, а если \(с\) отрицательное, то открывается вниз. 92}}} = \frac{z}{c}\]
Вот эскиз типичного гиперболического параболоида.
Эти графики имеют неопределенную седловидную форму, и, как и в случае с эллиптическим параболоидом, знак \(c\) будет определять направление, в котором поверхность «раскрывается». График выше показан для положительного \(c\).
При использовании обоих типов параболоидов, описанных выше, обратите внимание, что поверхность можно легко перемещать вверх или вниз, добавляя/вычитая константу с левой стороны.
92} + 6\]— это эллиптический параболоид, который открывается вниз (будьте осторожны, «-» стоит на \(x\) и \(y\) вместо \(z\)) и начинается в \(z = 6\) вместо \(z = 0\).
Вот несколько быстрых набросков этой поверхности.
Обратите внимание, что здесь мы дали две формы эскиза. Эскиз слева имеет стандартный набор осей, но цифры на оси плохо видны. Эскиз справа был «в рамке», и это облегчает просмотр цифр, чтобы придать эскизу ощущение перспективы. В большинстве эскизов, которые фактически включают числа в системе координат, мы даем оба эскиза, чтобы помочь понять, как выглядит эскиз.
Эскиз слева имеет стандартный набор осей, но цифры на оси плохо видны. Эскиз справа был «в рамке», и это облегчает просмотр цифр, чтобы придать эскизу ощущение перспективы. В большинстве эскизов, которые фактически включают числа в системе координат, мы даем оба эскиза, чтобы помочь понять, как выглядит эскиз.
Научное предложение
Научное предложение| Научный Приговор | Научный Калькуляторы | Решения за Уравнения |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Научное предложение | Интернет |
93,х,у). # И так далее…
установить параметрический
установить скрытый3d
установить изообразцы 21
установить автомасштабирование
установить вид 60,30
установить диапазон [-3:3]
установить vrange [-3:3]
установить заголовок «Действительная часть функции комплексного квадратного корня»
участок u**2-v**2,2*u*v,u # И так далее…
установить параметрический
установить скрытый3d
установить изообразцы 21
установить автомасштабирование
установить вид 60,30
установить диапазон [-3:3]
установить vrange [-3:3]
установить заголовок «Действительная часть функции комплексного квадратного корня»
участок u**2-v**2,2*u*v,uЩелкните здесь, чтобы получить минимальный сценарий для создания этого графика |
установить вид 60 210 установить заголовок «Действительная часть функции комплексного квадратного корня (другой вид)» переделывать |
установить вид 60 120 установить диапазон [-3:3] установить vrange [-3:3] установить заголовок "Мнимая часть функции комплексного квадратного корня" участок u**2-v**2,2*u*v,v |
установить просмотр 60 300 установить заголовок «Мнимая часть функции комплексного квадратного корня (другой вид)» переделывать |
установить вид 60,30 установить диапазон [-3:3] установить vrange [-3:3] установить заголовок "Действительная часть функции сложного кубического корня" участок u**3-3*u*v**2,3*u**2*v-v**3,u |
установить вид 60 210 установить заголовок «Вещественная часть функции сложного кубического корня (другой вид)» переделывать |
установить вид 60,30 установить диапазон [-3:3] установить vrange [-3:3] установить заголовок "Мнимая часть функции сложного кубического корня" участок u**3-3*u*v**2,3*u**2*v-v**3,v |
установить вид 60 210 установить заголовок «Мнимая часть функции сложного кубического корня (другой вид)» переделывать |
установить вид 60,30 установить изообразцы 31 установить диапазон [-1:1] установить vrange [-1:1] установить заголовок "Действительная часть сложной 4-й корневой функции" участок u**4-6*u**2*v**2+v**4,4*u**3*v-4*u*v**3,u |
установить вид 60 210 установить заголовок «Действительная часть сложной 4-й корневой функции (другой вид)» переделывать |
установить вид 60 120 установить диапазон [-1:1] установить vrange [-1:1] установить заголовок "Мнимая часть комплексной 4-й корневой функции" участок u**4-6*u**2*v**2+v**4,4*u**3*v-4*u*v**3,v |
установить просмотр 60 300 установить заголовок «Мнимая часть комплексной 4-й корневой функции (другой вид)» переделывать |
установить изообразцы 21 установить вид 60,20 установить диапазон [-3:3] установить vrange [-3:3] задать заголовок "Поверхность Эннепера" участок u-u**3/3+u*v**2,v-v**3/3+v*u**2,u**2-v**2 |
установить вид 60 110 установить заголовок "Поверхность Эннепера (другой вид)" переделывать |
установить изообразцы 31,11 установить вид 60,30 установить заголовок "Лента Мебиуса" установить диапазон [0:2*pi] установить vrange [-0,25:0,25] splot (2-v*sin(u/2))*sin(u),(2-v*sin(u/2))*cos(u),v*cos(u/2) |
установить вид 60 210 установить заголовок "Лента Мебиуса (вид с противоположной стороны)" переделывать |
ключ сброса установить xrange [-10:10] установить yrange [-10:10] установить zrange [-3:3] установить диапазон [0:2*pi] установить vrange [0:2*pi] установить изообразцы 39,60 установить вид 60 120 установить название "Бутылка Кляйна" splot (2*sin(u)*cos(v/2)-sin(2*u)*sin(v/2)+8)*cos(v), \ (2*sin(u)*cos(v/2)-sin(2*u)*sin(v/2)+8)*sin(v), \ 2*sin(u)*sin(v/2)+sin(2*u)*cos(v/2) |

 Если используется небольшое число расположенных с равными промежутками числовых подписей, обозначающих интервалы времени, например годы, можно выбрать график.
Если используется небольшое число расположенных с равными промежутками числовых подписей, обозначающих интервалы времени, например годы, можно выбрать график.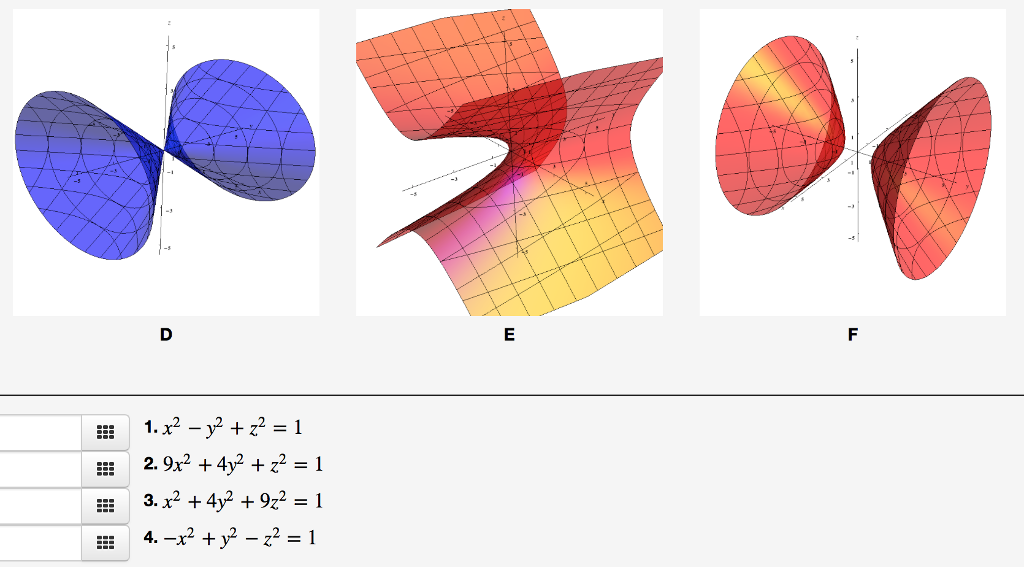
 01.07
01.07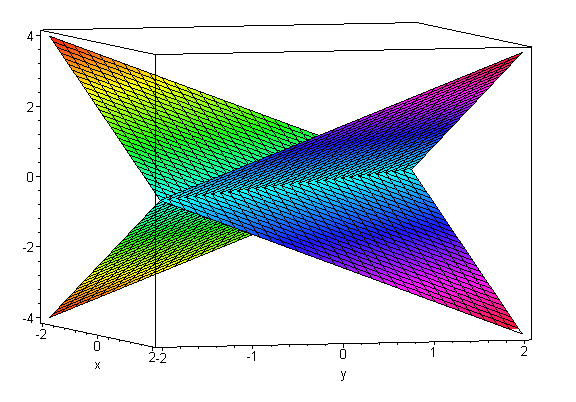 01.07
01.07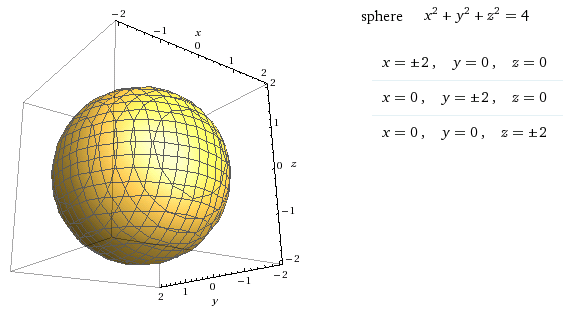 01.07
01.07