Таблица умножения от 11 до 20. Описание работы онлайн тренажера
С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Смотрите ниже шпаргалки в полной форме.
Умножение прямо на сайте (онлайн)
*
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 | |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Ни для кого не секрет, как важно знание таблицы умножения и деления, в частности при выполнении арифметических расчётов и решении примеров по математике .
Однако, что если ребёнка пугает этот огромный набор цифр, именующийся «Таблицей умножения и деления », а уж знать его наизусть, представляется совсем непосильной задачей?
Тогда спешим успокоить – Выучить всю таблицу умножения очень просто! Для этого необходимо запомнить всего лишь 36 комбинаций чисел (связки трех чисел) . Здесь мы не учитываем умножение на 1 и 10, так как это является элементарным действием не требующим особых усилий в запоминании.
Описание работы онлайн тренажера
Таким образом, запоминать таблицу умножения придётся небольшими порциями, что существенно снизит нагрузку, так как дети будут направлять своё внимание всего лишь на несколько примеров, забыв про весь «большой» объём.
В Тренажере есть меню настроек для выбора режима изучения таблицы. Имеется возможность выбора дейстия — «Умножение» или «Деление», диапазона примеров «Вся таблица» или «На какое-то число». Все это является рассширенным функционалом сайта и доступно после оплаты .
Каждый новый пример сопровождается справочной подсказкой , так ребёнку будет легче начать своё изучение и запоминать новые неизвестные ему комбинации.
Если же по ходу обучения, какой либо пример вызывает трудность, можно быстро напомнить себе его результат, воспользовавшись дополнительной подсказкой , это поможет эффективнее справляться с запоминанием трудных примеров.
Процентная шкала быстро даст вам понять каким уровнем знания таблицы умножения Вы обладаете.
Пример считается полностью выученным, если правильный ответ был дан 4 раза подряд . Однако при достижении 100% , призываем не бросать изучение, а вернуться на следующий день и освежить свои знания, повторно пройдя все примеры. Ведь именно регулярные занятия развивают память и закрепляют навыки!
Ведь именно регулярные занятия развивают память и закрепляют навыки!
Описание интерфейса онлайн тренажера
Во-первых, в тренажере присутствует «панель быстрого доступа», включающая в себя 4 кнопки. Они позволяют: перейти на главную страницу сайта, включить или отключить звуковые сигналы, сбросить результаты обучения (начать изучение сначала), а также попать на страницу отзывов и комментариев.
Во-вторых, это основная структура программы.
Выше всех находится процентная шкала , отобржающая примерный уровень знания таблицы умножения.
Ниже идет поле с примером , на который необходимо дать ответ. Во время ответа оно будет изменять свой цвет: станет красным — если был дан неверный ответ, зеленым — в случае правильного, голубым — после использования подсказки, и желтоватым — во время показа нового примера.
Следом располагается строка сообщений . В ней выводятся текстовая информация об ошибках, правильных ответах, а также справочной и дополнительной подсказками.
В конце находится экранная клавиатура , содержащая только необходимые для работы кнопки: все цифры, «забой» — если нужно исправить ответ, кнопки «Проверить» и «Дополнительная подсказка».
Мы уверены, что данный тренажер «Таблица умножения за 20 минут», поможет .
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.
сайт даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.
Таблица Пифагора
Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия.
Выделяем цветом одинаковые значения
Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.
Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.
Таблица для закрепления результата
Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами.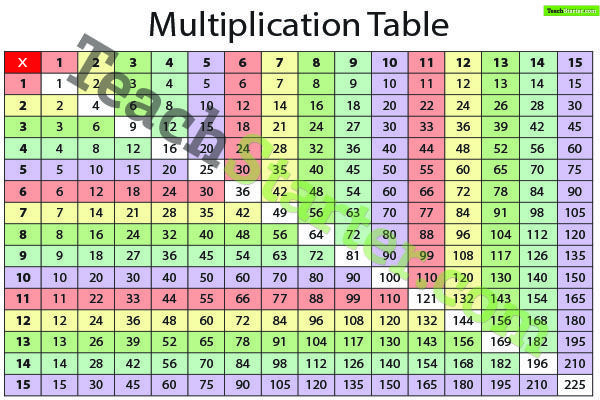 Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.
Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.
Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.
Таблица умножения или таблица пифагора — это известная математическая структура, помогающая школьникам выучить умножение, а также просто решить конкретные примеры.
Ниже Вы можете видеть ее в классическом виде. Обратите внимание на числа от 1 до 20, которыми озаглавлены строчки слева и столбцы сверху. Это множители.
Как пользоваться таблицей Пифагора?
1. Итак, в первой колонке находим число, которое необходимо умножить. Затем в верхней строчке ищем число, на которое будем умножать первое. Теперь смотрим, где пересекаются нужная нам строчка и столбец. Число, находящееся на этом пересечении, является произведением данных множителей. Иными словами, это результат их умножения.
Теперь смотрим, где пересекаются нужная нам строчка и столбец. Число, находящееся на этом пересечении, является произведением данных множителей. Иными словами, это результат их умножения.
Как видите, все довольно просто. Вы можете посмотреть данную таблицу на нашем сайте в любое время, а также при необходимости можно сохранить ее себе на компьютер в виде картинки, чтобы иметь к ней доступ без подключения к интернету.
2. И снова обратите внимание, ниже имеется та же таблица, но уже в более привычной форме – в виде математических примеров . Многим такая форма покажется проще и комфортнее для использования. Она также доступна для скачивания на любой носитель в виде удобной картинки.
И наконец, Вы можете воспользоваться нашим калькулятором, который присутствует на данной странице, в самом низу. Просто введите в пустые ячейки нужные Вам числа для умножения, кликните на кнопку Вычислить, и тут же в окошке Результат появится новое число, которое и будет их произведением.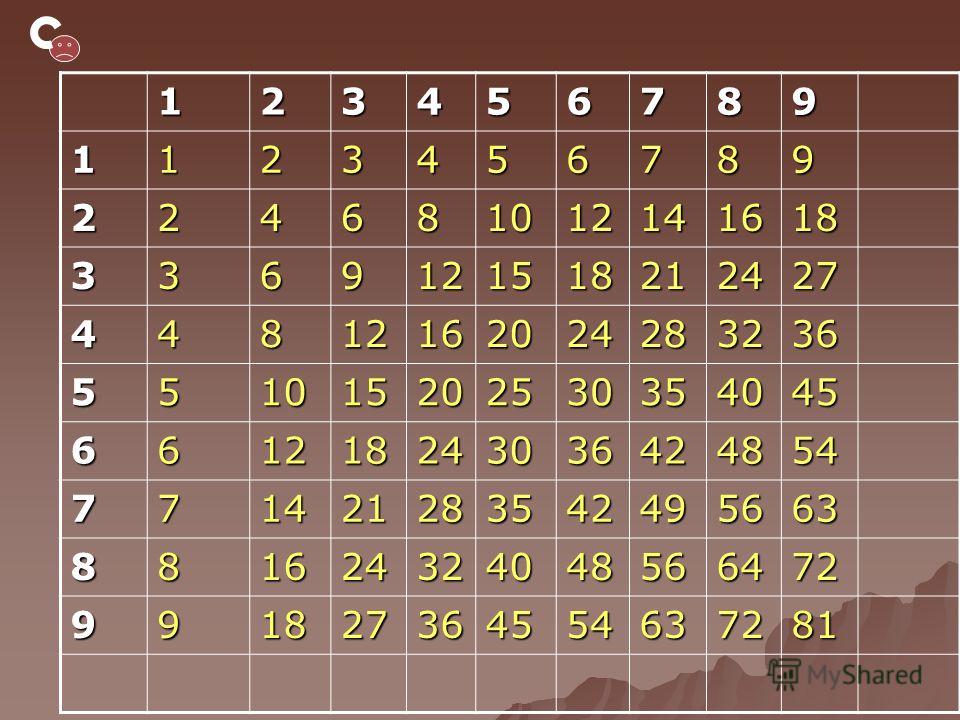
Надеемся, данный раздел будет Вам полезен, и наша таблица Пифагора в том или ином ее виде не раз поможет Вам в решении примеров с умножением и просто для заучивания данной темы.
Таблица пифагора от 1 до 20
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Таблица умножения в стандартном виде от 1 до 10
| 1 х 1 = 1 1 х 2 = 2 1 х 3 = 3 1 х 4 = 4 1 х 5 = 5 1 х 6 = 6 1 х 7 = 7 1 х 8 = 8 1 х 9 = 9 1 х 10 = 10 | 2 х 1 = 2 2 х 2 = 4 2 х 3 = 6 2 х 4 = 8 2 х 5 = 10 2 х 6 = 12 2 х 7 = 14 2 х 8 = 16 2 х 9 = 18 2 х 10 = 20 | 3 х 1 = 3 3 х 2 = 6 3 х 3 = 9 3 х 4 = 12 3 х 5 = 15 3 х 6 = 18 3 х 7 = 21 3 х 8 = 24 3 х 9 = 27 3 х 10 = 30 | 4 х 1 = 4 4 х 2 = 8 4 х 3 = 12 4 х 4 = 16 4 х 5 = 20 4 х 6 = 24 4 х 7 = 28 4 х 8 = 32 4 х 9 = 36 4 х 10 = 40 | 5 х 1 = 5 5 х 2 = 10 5 х 3 = 15 5 х 4 = 20 5 х 5 = 25 5 х 6 = 30 5 х 7 = 35 5 х 8 = 40 5 х 9 = 45 5 х 10 = 50 |
| 6 х 1 = 6 6 х 2 = 12 6 х 3 = 18 6 х 4 = 24 6 х 5 = 30 6 х 6 = 36 6 х 7 = 42 6 х 8 = 48 6 х 9 = 54 6 х 10 = 60 | 7 х 1 = 7 7 х 2 = 14 7 х 3 = 21 7 х 4 = 28 7 х 5 = 35 7 х 6 = 42 7 х 7 = 49 7 х 8 = 56 7 х 9 = 63 7 х 10 = 70 | 8 х 1 = 8 8 х 2 = 16 8 х 3 = 24 8 х 4 = 32 8 х 5 = 40 8 х 6 = 48 8 х 7 = 56 8 х 8 = 64 8 х 9 = 72 8 х 10 = 80 | 9 х 1 = 9 9 х 2 = 18 9 х 3 = 27 9 х 4 = 36 9 х 5 = 45 9 х 6 = 54 9 х 7 = 63 9 х 8 = 72 9 х 9 = 81 9 х 10 = 90 | 10 х 1 = 10 10 х 2 = 20 10 х 3 = 30 10 х 4 = 40 10 х 5 = 50 10 х 6 = 60 10 х 7 = 70 10 х 8 = 80 10 х 9 = 90 10 х 10 = 100 |
Таблица умножения в стандартном виде от 10 до 20
| 11 х 1 = 11 11 х 2 = 22 11 х 3 = 33 11 х 4 = 44 11 х 5 = 55 11 х 6 = 66 11 х 7 = 77 11 х 8 = 88 11 х 9 = 99 11 х 10 = 110 | 12 х 1 = 12 12 х 2 = 24 12 х 3 = 36 12 х 4 = 48 12 х 5 = 60 12 х 6 = 72 12 х 7 = 84 12 х 8 = 96 12 х 9 = 108 12 х 10 = 120 | 13 х 1 = 13 13 х 2 = 26 13 х 3 = 39 13 х 4 = 52 13 х 5 = 65 13 х 6 = 78 13 х 7 = 91 13 х 8 = 104 13 х 9 = 117 13 х 10 = 130 | 14 х 1 = 14 14 х 2 = 28 14 х 3 = 42 14 х 4 = 56 14 х 5 = 70 14 х 6 = 84 14 х 7 = 98 14 х 8 = 112 14 х 9 = 126 14 х 10 = 140 | 15 х 1 = 15 15 х 2 = 30 15 х 3 = 45 15 х 4 = 60 15 х 5 = 70 15 х 6 = 90 15 х 7 = 105 15 х 8 = 120 15 х 9 = 135 15 х 10 = 150 |
| 16 х 1 = 16 16 х 2 = 32 16 х 3 = 48 16 х 4 = 64 16 х 5 = 80 16 х 6 = 96 16 х 7 = 112 16 х 8 = 128 16 х 9 = 144 16 х 10 = 160 | 17 х 1 = 17 17 х 2 = 34 17 х 3 = 51 17 х 4 = 68 17 х 5 = 85 17 х 6 = 102 17 х 7 = 119 17 х 8 = 136 17 х 9 = 153 17 х 10 = 170 | 18 х 1 = 18 18 х 2 = 36 18 х 3 = 54 18 х 4 = 72 18 х 5 = 90 18 х 6 = 108 18 х 7 = 126 18 х 8 = 144 18 х 9 = 162 18 х 10 = 180 | 19 х 1 = 19 19 х 2 = 38 19 х 3 = 57 19 х 4 = 76 19 х 5 = 95 19 х 6 = 114 19 х 7 = 133 19 х 8 = 152 19 х 9 = 171 19 х 10 = 190 | 20 х 1 = 20 20 х 2 = 40 20 х 3 = 60 20 х 4 = 80 20 х 5 = 100 20 х 6 = 120 20 х 7 = 140 20 х 8 = 160 20 х 9 = 180 20 х 10 = 200 |
Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с .
понедельник, 7 января 2019 г.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Я вам уже рассказывал, что , при помощи которой шаманы пытаются сортировать » » реальности. Как же они это делают? Как фактически происходит формирование множества?
Давайте внимательно разберемся с определением множества: «совокупность различных элементов, мыслимая как единое целое».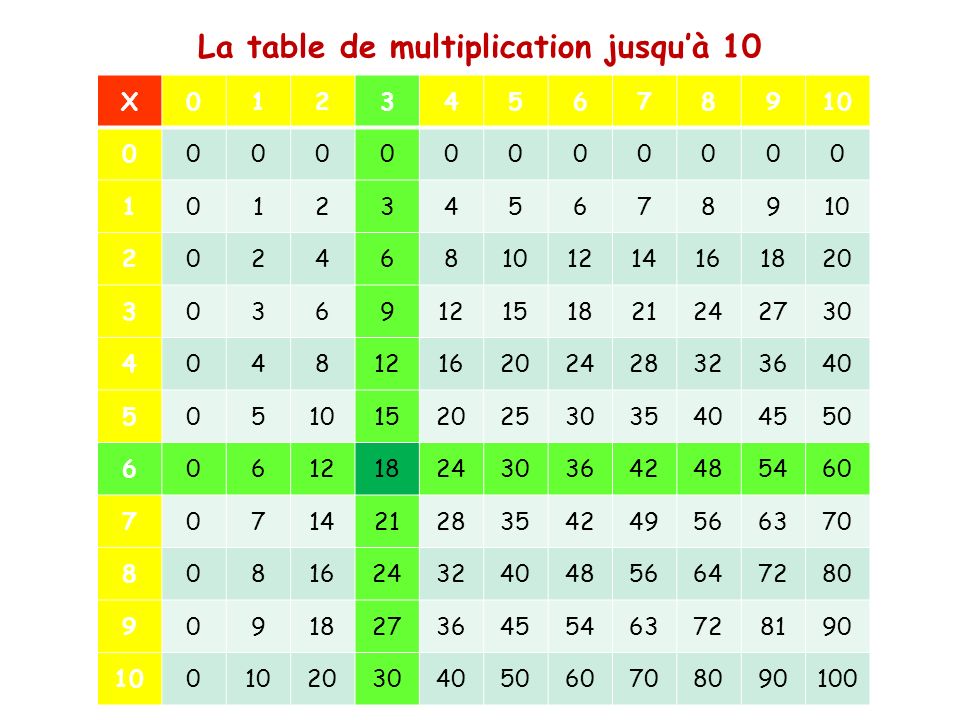 А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.
А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.
суббота, 30 июня 2018 г.
Если математики не могут свести понятие к другим понятиям, значит они ничего не понимают в математике. Отвечаю на : чем элементы одного множества отличаются от элементов другого множества? Ответ очень простой: числами и единицами измерения.
Это сегодня всё, что мы не возьмем, принадлежит какому-либо множеству (как нас уверяют математики). Кстати, вы в зеркале видели у себя на лбу список тех множеств, к которым принадлежите именно вы? И я такого списка не видел. Скажу больше — ни одна вещь в реальности не имеет бирочки со списком множеств, к которым эта вещь принадлежит. Множества — это всё выдумки шаманов. Как они это делают? Давайте заглянем немного в глубь истории и посмотрим, как выглядели
элементы множества до того, как математики-шаманы растащили их по своим
множествам.
Скажу больше — ни одна вещь в реальности не имеет бирочки со списком множеств, к которым эта вещь принадлежит. Множества — это всё выдумки шаманов. Как они это делают? Давайте заглянем немного в глубь истории и посмотрим, как выглядели
элементы множества до того, как математики-шаманы растащили их по своим
множествам.
Давним-давно, когда о математике ещё никто и не слышал, а кольца были только у деревьев и у Сатурна, огромные стада диких элементов множеств бродили по физическим полям (ведь математических полей шаманы ещё не придумали). Выглядели они приблизительно так.
Да, не удивляйтесь, с точки зрения математики все элементы множеств больше всего похожи на морских ежей — из одной точки, как иголки, во все стороны торчат единицы измерений. Для тех, кто , напоминаю, что любую единицу измерения геометрически можно представить как отрезок произвольной длины, а число — как точку. Геометрически любую величину можно представить как пучок отрезков, торчащих в разные стороны из одной точки. Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.
Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.
Какие же единицы измерения образуют элемент множества? Всякие, описывающие данный элемент с разных точек зрения. Это и древние единицы измерения, которыми пользовались наши предки и о которых все давно забыли. Это и современные единицы измерения, которыми мы пользуемся сейчас. Это и неизвестные нам единицы измерения, которые придумают наши потомки и которыми будут пользоваться они для описания реальности.
С геометрией мы разобрались — предлагаемая модель элементов множества имеет четкое геометрическое представление. А как с физикой? Единицы измерения — это и есть прямая связь математики с физикой. Если шаманы не признают единицы измерения как полноправный элемент математических теорий — это их проблемы. Настоящую науку математику без единиц измерения лично я уже не представляю. Вот почему в самом начале рассказа о теории множеств я говорил о ней как о каменном веке.
Но перейдем к самому интересному — к алгебре элементов множеств. Алгебраически любой элемент множества представляет из себя произведение (результат умножения) разных величин.Выглядит это так.
Я умышленно не применял условные обозначения, принятые в теории множеств, поскольку мы рассматриваем элемент множества в естественной среде обитания до возникновения теории множеств. Каждая пара буковок в скобках обозначает отдельную величину, состоящую из числа, обозначенного буквой «n » и единицы измерения, обозначенной буквой «a «. Индексы возле буковок указывают на то, что числа и единицы измерения — разные. Один элемент множества может состоять из бесконечного числа величин (на сколько у нас и наших потомков хватит фантазии). Каждая скобка геометрически изображается отдельным отрезком. В примере с морским ежом одна скобка — это одна иголка.
Как шаманы формируют множества из разных элементов? Фактически, по единицам измерения или по числам. Ничего не понимая в математике, они берут разных морских ежей и внимательно их рассматривают в поисках той единственной иголки, по которой они формируют множество.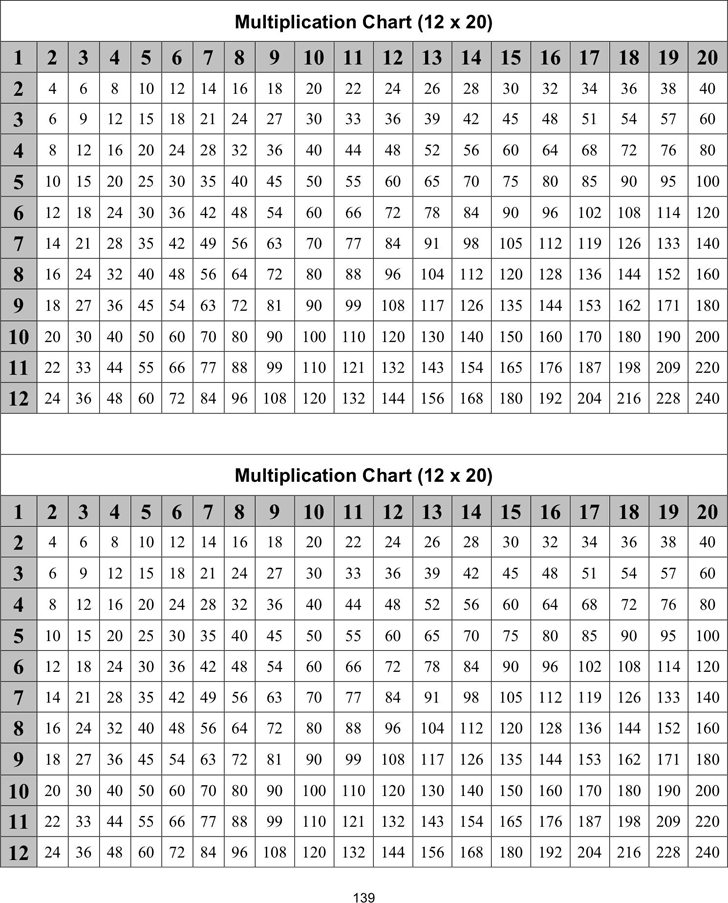 Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.
Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.
Как вы уже догадались, один и тот же элемент может принадлежать к самым разным множествам. Дальше я вам покажу, как формируются множества, подмножества и прочая шаманская галиматья. Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
Тематические материалы:
Поиск и удаление вирусов вручную Kaspersky Free — новый бесплатный антивирус от «Лаборатории Касперского Handy recovery 5.5 серийный. Плюсы и минусы Iobit malware fighter 4.4 expired код лицензии. Инструкция по активации IObit Malware Fighter Pro Лицензионный ключ для hitman pro 3 Iobit uninstaller 5.2 лицензионный ключ Hetman partition recovery 2 Driver Updater ключ активацииОбновлено: 28. 07.2021
07.2021
103583
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Таблица умножения
Таблица умноженияТаблица умножения — таблица, где строки и столбцы озаглавлены множителями, а ячейки таблицы содержат их произведение. Таблица применяется для обучения умножению.
Навигация по странице: Таблица умножения чисел от 1 до 10 Таблица умножения чисел от 1 до 20
Упражнения для проверки знания таблицы умножения!
Скачать таблицу умножения
Таблица умножения чисел от 1 до 10
| × 1 | × 2 | × 3 | × 4 | × 5 |
1 × 1 = 1 1 × 2 = 2 1 × 3 = 3 1 × 4 = 4 1 × 5 = 5 1 × 6 = 6 1 × 7 = 7 1 × 8 = 8 1 × 9 = 9 1 × 10 = 10 |
2 × 1 = 2 2 × 2 = 4 2 × 3 = 6 2 × 4 = 8 2 × 5 = 10 2 × 6 = 12 2 × 7 = 14 2 × 8 = 16 2 × 9 = 18 2 × 10 = 20 |
3 × 1 = 3 3 × 2 = 6 3 × 3 = 9 3 × 4 = 12 3 × 5 = 15 3 × 6 = 18 3 × 7 = 21 3 × 8 = 24 3 × 9 = 27 3 × 10 = 30 |
4 × 1 = 4 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 4 × 6 = 24 4 × 7 = 28 4 × 8 = 32 4 × 9 = 36 4 × 10 = 40 |
5 × 1 = 5 5 × 2 = 10 5 × 3 = 15 5 × 4 = 20 5 × 5 = 25 5 × 6 = 30 5 × 7 = 35 5 × 8 = 40 5 × 9 = 45 5 × 10 = 50 |
| × 6 | × 7 | × 8 | × 9 | × 10 |
6 × 1 = 6 6 × 2 = 12 6 × 3 = 18 6 × 4 = 24 6 × 5 = 30 6 × 6 = 36 6 × 7 = 42 6 × 8 = 48 6 × 9 = 54 6 × 10 = 60 | 7 × 1 = 7 7 × 2 = 14 7 × 3 = 21 7 × 4 = 28 7 × 5 = 35 7 × 6 = 42 7 × 7 = 49 7 × 8 = 56 7 × 9 = 63 7 × 10 = 70 | 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 8 × 6 = 48 8 × 7 = 56 8 × 8 = 64 8 × 9 = 72 8 × 10 = 80 | 9 × 1 = 9 9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 8 = 72 9 × 9 = 81 9 × 10 = 90 | 10 × 1 = 10 10 × 2 = 20 10 × 3 = 30 10 × 4 = 40 10 × 5 = 50 10 × 6 = 60 10 × 7 = 70 10 × 8 = 80 10 × 9 = 90 10 × 10 = 100 |
Не забудьте проверить знания таблицы умножения решая упражнения! 🙂
Таблица умножения чисел от 1 до 20
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Таблица умножения a × b Таблица квадратов a2 Таблица кубов a3 Таблица степеней an Таблица факториалов a!
Все таблицы и формулы
Таблица умножения по математике, бесплатно
Содержание:
- Таблица умножения 1 — 10
- Таблица умножения 11 — 20
- Таблица умножения 21 — 30
Таблица умножения — это первое, что дети учат в школе по математике.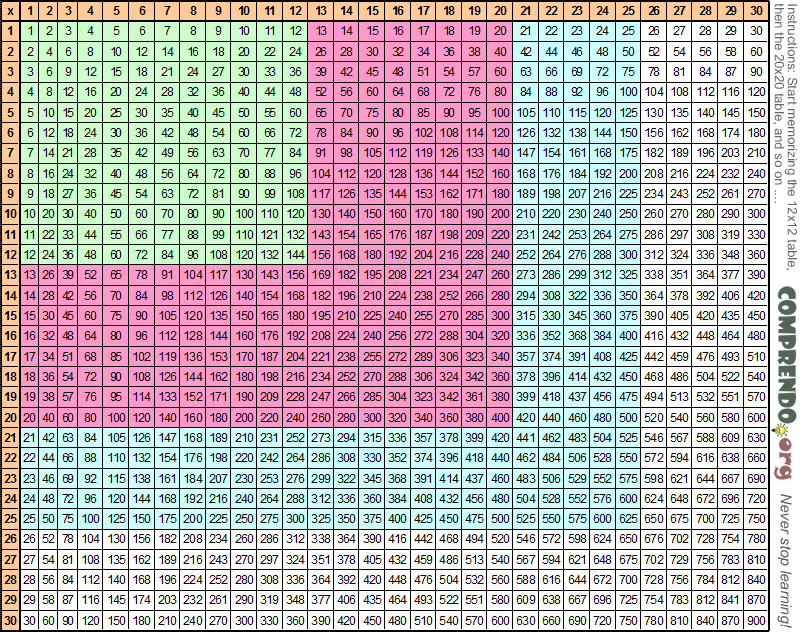 Советуем, как минимум, выучить таблицу умножения с 0 — 10, учить остальное можно по желанию, но
обязательно нужно понимать как считается. Формулы и свойства —
это краткий теоретический материал, выучив которые вы легко сможет выполнить задания в школе.
Советуем, как минимум, выучить таблицу умножения с 0 — 10, учить остальное можно по желанию, но
обязательно нужно понимать как считается. Формулы и свойства —
это краткий теоретический материал, выучив которые вы легко сможет выполнить задания в школе.
В нашем справочнике представлены 3 таблицы умножения ( 0 — 10, 11 — 20, 21 — 30), изучайте.
Таблица умножения 1 — 10
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Таблица умножения 11 — 20
| × | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 11 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Таблица умножения 21 — 30
| × | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 21 | 441 | 462 | 483 | 504 | 525 | 546 | 567 | 588 | 609 | 630 |
| 22 | 462 | 484 | 506 | 528 | 550 | 572 | 594 | 616 | 638 | 660 |
| 23 | 483 | 506 | 529 | 552 | 575 | 598 | 621 | 644 | 667 | 690 |
| 24 | 504 | 528 | 552 | 576 | 600 | 624 | 648 | 672 | 696 | 720 |
| 25 | 525 | 550 | 575 | 600 | 625 | 650 | 675 | 700 | 725 | 750 |
| 26 | 546 | 572 | 598 | 624 | 650 | 676 | 702 | 728 | 754 | 780 |
| 27 | 567 | 594 | 621 | 648 | 675 | 702 | 729 | 756 | 783 | 810 |
| 28 | 588 | 616 | 644 | 672 | 700 | 728 | 756 | 784 | 812 | 840 |
| 29 | 609 | 638 | 667 | 696 | 725 | 754 | 783 | 812 | 841 | 870 |
| 30 | 630 | 660 | 690 | 720 | 750 | 780 | 810 | 840 | 870 | 900 |
В этой статье описана таблица умножения на 3, 4, 5, 6, 7, 8, 9 и до 30! Также на сайте представлено много
онлайн калькуляторов для автоматического решения задач по математике, пользуйтесь на здоровье.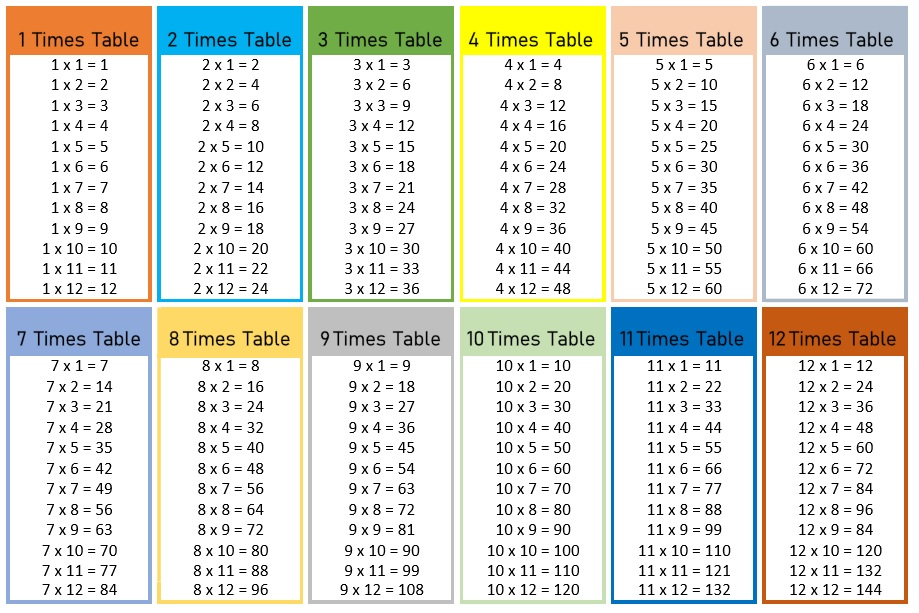
Если после изучения теоретического материала на нашем сайте у Вас останутся проблемы в решении задач или появятся вопросы образовательного характера, то вы всегда можете задать их на нашем форуме.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица умножения — традиционная 10×10, 12х12 и 20х20
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
App Store: Таблица умножения учить
Описание
В приложении: таблица умножения (от 1 до 10; от 1 до 12; от 11 до 20), умножение многозначных чисел; деление многозначных чисел.
Подробное описание:
Выучить таблицу умножения очень просто с помощью приложения! Вы научитесь умножать и делить цифры.
Приложение интуитивно понятно для изучения. Учите таблицу постепенно, начиная с самых простых примеров и переходите к более сложным.
Выберете одну или несколько цифр по вашему усмотрению. Уделяйте достаточно времени повторению. Нажмите «i» или «h» для подсказок, но попробуйте без них 🙂 Вы можете пройти тест и сохранить количество правильных ответов.
Постоянно повторяя таблицу умножения, вы запомните её совсем быстро, и сложные примеры станут для вас совсем простыми!
Умножение многозначных чисел, как в тетрадке, пошагово.
Выберите верхнюю двузначную или трехзначную цифру, затем нижнюю однозначную, двузначную или трехзначную цифру. Цифра будет выбрана случайным образом. Последовательно заменяйте правильные ответы, как вы делали в тетрадке.
Если вам нужно подготовиться к тесту по математике, обязательно пройдите его! Примеры в произвольном порядке без подсказок и без калькулятора. Если хотя бы один ответ неверен, неверен весь пример. После того, как вы решите все примеры, тест завершится, и количество правильных ответов будет автоматически сохранено.
Если хотя бы один ответ неверен, неверен весь пример. После того, как вы решите все примеры, тест завершится, и количество правильных ответов будет автоматически сохранено.
Калькулятор может помочь вам сделать домашнее задание или проверить себя. Вы можете использовать его при обучении. Если вы делаете тест, вы не можете использовать калькулятор — это все еще тест, поэтому без подсказок — используйте свою голову.
Деление многозначных чисел — это сложное сочетание различных математических операций. Вы должны быть хорошо знакомы с таблицей умножения и, конечно же, с сложением и вычитанием.
Вы можете тренировать свои математические навыки, которые приобрели ранее. Рабочие листы — это проверенный временем математический предмет. Теперь вы можете решать проблемы в приложении.
Выберите трехзначные, четырехзначные числа, которые вы научитесь делить в столбце на одно-, двух- или трехзначные числа. Тратьте время особенно на задачи с нулями. В приложении вы найдете бесконечное количество задач и научитесь делить без остатка.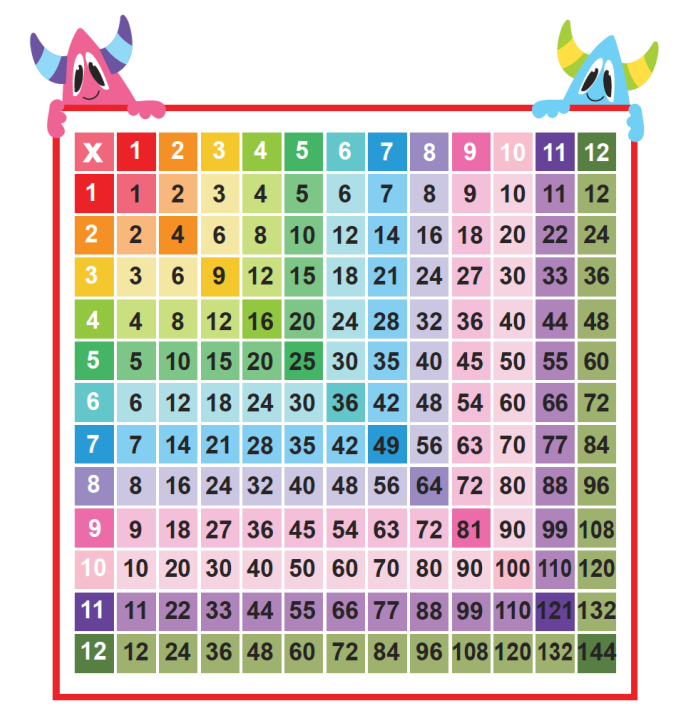
Интернет не нужен.
Бесконечное количество задач в случайном порядке.
УДАЧИ!
Версия 2.8
Performance improvement
Оценки и отзывы
Оценок: 14
Только платная версия
Качайте только в том случае если готовы купить это приложения (цена поднялась до 1290).
Любой клик переводит на покупку, даже кнопка Информация(i).
Почему нельзя сразу в шопе написать что приложение платное. Дешевый развод!
Конкурентам-разработчикам: я предлагаю такой функционал, которого у других нет.
Чтобы ребёнок мог легко и быстро всё выучить и усвоить. Вы бы занялись улучшением функционала своих приложений.
Как вы заботливо предупреждаете людей о встроенных покупках, а может каждый будет сам решать что ему делать без ваших советов?
Также заботливо следите за динамикой стоимости моего приложения.
Не используйте гопнические выражения: это вас не красит.
А любой комментарий, даже негативный, повышает рейтинг, поэтому я ваши комментарии не блокирую.
Без пробной версии.
Только платная версия за 849₽
Информативно…. Есть полностью бесплатные приложения. Приложения со встроенными покупками содержат пометочку такую: «Встроенные покупки».
Невозможно использовать
Чтобы не нажал выходит предложение купить.
В приложении все предельно ясно объяснено. Возможно использовать после покупки.
Разработчик Nikita Liubimov указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Сбор данных не ведется
Разработчик не ведет сбор данных в этом приложении.
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Информация
- Провайдер
- Nikita Liubimov
- Размер
- 10,5 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © Nick Limo
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Поддерживается
Другие приложения этого разработчика
Вам может понравиться
Урок 6.
 Изучение таблицы умножения
Изучение таблицы умноженияЦифры изучены, основные математические понятия усвоены, ребенок свободно считает до сотни, складывает и вычитает – все это говорит о том, что пора приступать к изучению таблицы умножения.
Таблица умножения может даваться будущему школьнику сложнее, чем основы математики, и как родитель, заинтересованный в развитии своего чада, вы обязаны оказать ему в этом деле поддержку. Как и раньше, вам потребуется солидная доля терпения и настойчивости.
Далее мы рассмотрим следующие вопросы:
- Как учить таблицу умножения
- Как запоминать ответы
- Как отслеживать прогресс
- Как поощрять ребенка
- Дополнительные рекомендации
1
Как учить таблицу умножения
Чтобы ваш ребенок выучил таблицу умножения быстро и эффективно, придерживайтесь такого алгоритма:
- Для начала определите время, в которое вы каждый день будете проводить занятия. Не занимайтесь, если не готовы уделить ребенку максимум внимания или если ребенок уставший.
 Одно занятие должно продолжаться примерно 30 минут. Превышение этого порога может снизить эффективность занятий. Старайтесь создать такую обстановку, чтобы вас ничего не отвлекало.
Одно занятие должно продолжаться примерно 30 минут. Превышение этого порога может снизить эффективность занятий. Старайтесь создать такую обстановку, чтобы вас ничего не отвлекало. - Начните изучать таблицу умножения с задач на «0», «1», «2» и «3». Информацию преподносите небольшими объемами, не стремясь запомнить сразу всю таблицу. Имейте в виду, что пока что ваш ребенок просто запоминает, а не считает.
- Если ребенок не понимает, как умножаются друг на друга числа, покажите ему принцип умножения на бумаге. Например, «3 х 3» можно представить, как «3 + 3 + 3» и т.д.
- Возьмите лист бумаги и изобразите на нем таблицу умножения, а рядом нарисуйте числовую ось с цифрами от «0» до «100». Объясните, что при помощи таблицы очень легко находить ответы, которые соответствуют конкретным колонкам и строкам. По мере возрастания чисел на числовой оси будут возрастать и числа в таблице умножения.
- Донесите до ребенка, что от перемены мест перемножаемых чисел их сумма не меняется, как и при сложении.
 Расскажете, что это свойство называется свойством коммутативности, и что, зная о нем, выучить таблицу значительно проще. Объясните, что, по сути, нужно выучить всего половину таблицы умножения, т.к. «3 х 6» будет то же самое, что «6 х 3» и т.п.
Расскажете, что это свойство называется свойством коммутативности, и что, зная о нем, выучить таблицу значительно проще. Объясните, что, по сути, нужно выучить всего половину таблицы умножения, т.к. «3 х 6» будет то же самое, что «6 х 3» и т.п. - После того как ваше чадо освоит таблицу умножения от «0» до «3», переходите к числам от «4» до «7». На следующем этапе изучайте таблицу от «8» до «10». Если ребенок усваивает материал хорошо, можете усложнить ему работу, предложив разобраться в том, как числа умножаются на «11», «12», «13» и т.д.
- Обязательно познакомьте будущего школьника с шаблонами таблицы. Не допускайте механического запоминания. Ребенок должен четко понимать, как «работает» таблица. Например, все задания с умножением на «10» заканчиваются на «0», все задания с умножением на «5» заканчиваются либо на «0», либо на «5» (также их результат ровно на половину меньше результата всех заданий с умножением на «10»), все задания с умножением на «0» равны «0».

В дополнение к вышеназванному алгоритму возьмите на заметку и несколько хитростей:
- Умея удваивать числа, можно совершенно просто умножать на «4». Для этого нужно дважды удваивать умножаемое число. Например, нужно посчитать, сколько будет «5 х 4». Пусть ребенок удвоит «5», тем самым получив «10». Теперь пусть удвоит «10», получив искомое решение – «20». Такой прием поможет решать некоторые задания автоматически.
- Для умножения любого числа на «11» его просто-напросто требуется продублировать. К примеру, «2 х 11»– это «22», «3 х 11»– «33» и т.д.
- При проявлении ребенком хороших математических способностей обучите его интересному приему умножения «11» на любое двузначное число. Чтобы выполнить действие быстро, необходимо разделить это двузначное число на цифры. Например, «11 х 18» – это «1…8», а чтобы заполнить пробел, нужно сложить эти цифры («1+8» «9») и вставить результат в середину. Получаем «198».
Но кроме усвоения системы, на которой построена таблица умножения, можно и нужно использовать методы, помогающие быстро запоминать ответы.
2
Как запоминать ответы
Помочь вашему ребенку быстро запоминать ответы помогут следующие приемы:
- По мере изучения таблицы умножения тренируйте свое чадо. Делайте это как можно чаще: 5 минут после приема пищи, 3 минуты во время рекламной паузы при просмотре кино, 10 минут во время прогулки по улице и обязательно 5 минут перед сном. Систематически повышайте темп тренировок, чтобы навык оттачивался и закреплялся.
- Изначально давайте задания по порядку, а когда в ответах ребенка уже не будет ошибок, перемешивайте задания, чтобы сделать память и мышление более гибкими.
- Старайтесь делать так, чтобы изучать таблицу умножения ребенку было весело и интересно. Привносите в занятия игровые элементы, и тогда результаты будут намного лучше.
- Пусть ваш ребенок сделает комплект карточек. К примеру, «6 х 6» напишет на одной стороне, а на обратной – «36». Данную процедуру следует повторить со всеми парами таблицы умножения. Когда карточки будут готовы, показывайте их ребенку, а он пускай дает ответы на время.
 Каждый раз засекайте минуту, и смотрите, как продвигается ваш подопечный. Кстати, при переписывании таблицы на карточки у ребенка будет тренироваться двигательная память, а материал будет усваиваться вдвойне лучше.
Каждый раз засекайте минуту, и смотрите, как продвигается ваш подопечный. Кстати, при переписывании таблицы на карточки у ребенка будет тренироваться двигательная память, а материал будет усваиваться вдвойне лучше. - Чтобы определить слабые места, просите своего ребенка время от времени по памяти записывать таблицу умножения на листке бумаги.
- Играйте в игру «Захват карточной колоды». Правила очень просты: отделите карты с цифрами от карт с картинками (последние отложите в сторону). Разделите оставшиеся карты поровну между собой и ребенком. Одновременно с ним выкладывайте карты цифрами вверх и на опережение умножайте имеющиеся на двух картах цифры (к примеру, если выпали «шестерка» и «восьмерка», нужно быстро умножить «6» на «8» и назвать «48»). Кто быстрее выполнит задание, тот забирает обе карты. Побеждает тот, кто соберет больше карт. Игру можно немного видоизменить: не убирайте карты с картинками, а присвойте каждой свое число: валету – «11», даме – «12», королю – «13», а тузу – «0».

- Тренируйте таблицу умножения способом «от обратного». Называйте ребенку число, к примеру, «40», а он пусть предлагает вам все варианты перемножения чисел для получения этой суммы.
- Играйте в «Бинго». Пусть ребенок нарисует на листе квадрат шесть на шесть клеток и заполнит его любыми двузначными числами. Ваша задача – давать задание, например, «7 х 7», и если в одной из клеток есть число «49», он должен его зачеркнуть. Продолжать игру следует до тех пор, пока не будут зачеркнуты все числа в квадрате. В качестве поощрения используйте какой-нибудь приятный для ребенка приз.
Используя эти простейшие методы, вы поможете своему ребенку в разы быстрее запоминать ответы примеров из таблицы умножения. Но учение – это одно, а насколько хорошо усвоен материал, нужно систематически проверять. Помимо обычного контроля выполнения заданий и правильности ответов можно использовать еще пару неплохих способов проверки.
3
Как отслеживать прогресс
Возможно, кто-то сочтет нижеследующие способы излишними, однако мы и не призываем к их обязательному применению. Но все же, если ими не пренебрегать, можно получить намного больше информации о том, есть ли в знаниях вашего чада пробелы.
Но все же, если ими не пренебрегать, можно получить намного больше информации о том, есть ли в знаниях вашего чада пробелы.
Вот два отличных способа отслеживания прогресса:
- Использование интерактивных онлайн-приложений. В интернете в настоящее время можно найти огромное количество всяческих игр, викторин, тестов и других приложений на проверку знаний. Существенный плюс этого способа в том, что он воспринимается детьми не как проверка, а скорее как игра. Благодаря этому минимизируется стрессовое воздействие на психику ребенка, что позволит ему во всей полноте применить свой потенциал.
- Если ребенок ходит в садик или даже уже начал посещать школу, каждый день спрашивайте его о том, чем он там занимался, были ли какие-то задания, каких успехов он достиг, какие оценки получил. Также спрашивайте о затруднениях – если таковые были, ищите способы их устранения: повторяйте пройденный материал и занимайтесь дополнительно. Помимо прочего, периодически звоните или навещайте воспитателя или школьного учителя, чтобы справиться об успехах своего ребенка.
 Таким образом вы сможете узнать о чем-то, о чем, вполне вероятно, он по каким-то причинам не хочет вам рассказывать. Собственно, это касается не только таблицы умножения или математики в целом, но и любого предмета и успеваемости вообще.
Таким образом вы сможете узнать о чем-то, о чем, вполне вероятно, он по каким-то причинам не хочет вам рассказывать. Собственно, это касается не только таблицы умножения или математики в целом, но и любого предмета и успеваемости вообще.
Несмотря на то, что по теме урока было сказано уже достаточно много, есть еще одна тема, которую мы хотели бы рассмотреть отдельно. Это тема поощрения ребенка.
4
Как поощрять ребенка
Всего мы предлагаем вам прибегать к трем основным методам поощрения:
- Похвала. Похвала и искренняя радость – это, пожалуй, самые эффективные способы дать ребенку понять, что у него все отлично получается, тем самым замотивировав его на последующие занятия. Как можно чаще выражайте свои эмоции по поводу успехов юного математика. Старайтесь воздерживаться от любых негативных оценок в его адрес, в противном случае он станет заниматься с меньшей охотой, а материал будет усваивать намного медленнее.
- Стимулирование.
- Отдых.
 Перерывы на отдых и расслабление должны стать неотъемлемой составляющей вашей практики обучения ребенка. Любые занятия, от элементарных до самых сложных, нужно сопровождать паузами, чтобы ребенок имел возможность восстановить силы. Взрослые люди не могут работать часами без передышки, что уж говорить о детях. Поэтому, как только увидели, что ваше чадо подает признаки усталости, прекратите занятия и возьмите время на отдых. Намного продуктивнее будет позаниматься через несколько часов или вообще на следующий день.
Перерывы на отдых и расслабление должны стать неотъемлемой составляющей вашей практики обучения ребенка. Любые занятия, от элементарных до самых сложных, нужно сопровождать паузами, чтобы ребенок имел возможность восстановить силы. Взрослые люди не могут работать часами без передышки, что уж говорить о детях. Поэтому, как только увидели, что ваше чадо подает признаки усталости, прекратите занятия и возьмите время на отдых. Намного продуктивнее будет позаниматься через несколько часов или вообще на следующий день.
И в заключение урока не будет лишним дать еще несколько рекомендаций, которые помогут вам в вашей работе со своим ребенком.
5
Дополнительные рекомендации
Кроме того, что нужно всегда проявлять к ребенку доброту и доброжелательность, требуется овладеть и несколькими простейшими педагогическими приемами:
- Если ребенок чего-то не понимает, никогда не переходите к следующему материалу. Работайте над изучением одной и той же темы, пока она не будет полностью усвоена.

- Изучайте материал небольшими «порциями», иначе ребенок не будет понимать того, что узнает, и, как следствие, у него возникнет неуверенность в своих силах.
- Чтобы таблица умножения давалась легче, работайте над двумя-тремя числами в одно время. Затем повторяйте изученное, убеждайтесь, что ребенку все понятно, и лишь после этого переходите к другим числам.
- Ребенок – это не калькулятор и не машинка для счета, поэтому быстрые ответы будут достигаться после многократного повторения, так что делайте это регулярно.
- Для облегчения решения поставленных задач при изучении таблицы умножения разрешайте ребенку пользоваться устным счетом, но когда таблица будет усвоена, следите, чтобы устный счет не применялся.
Не исключено, что в познании математической науки у вашего сына или дочери возникнут какие-то проблемы (что-то не дается, занятия вызывают отторжение, ребенок не проявляет совершенно никаких математических способностей и т. д.). И, естественно, эти проблемы нужно уметь решать. И как раз о том, как это делается, вы узнаете из восьмого урока нашего курса.
д.). И, естественно, эти проблемы нужно уметь решать. И как раз о том, как это делается, вы узнаете из восьмого урока нашего курса.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Cтатистика На весь экран
Кирилл
← 5 Принципы обучения счету7 Устранение проблем →
11 to 20 Times Tables
The range should be anywhere between 1 to 100
| 11 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 11 | = | 11 |
| 2 | x | 11 | = | 22 |
| 3 | x | 11 | = | 33 |
| 4 | x | 11 | = | 44 |
| 5 | x | 11 | = | 55 |
| 6 | x | 11 | = | 66 |
| 7 | x | 11 | = | 77 |
| 8 | x | 11 | = | 88 |
| 9 | x | 11 | = | 99 |
| 10 | x | 11 | = | 110 |
| 11 | x | 11 | = | 121 |
| 12 | x | 11 | = | 132 |
| 13 | x | 11 | = | 143 |
| 14 | x | 11 | = | 154 |
| 15 | x | 11 | = | 165 |
| 16 | x | 11 | = | 176 |
| 17 | x | 11 | = | 187 |
| 18 | x | 11 | = | 198 |
| 19 | x | 11 | = | 209 |
| 20 | x | 11 | = | 220 |
| 12 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 12 | = | 12 |
| 2 | x | 12 | = | 24 |
| 3 | x | 12 | = | 36 |
| 4 | x | 12 | = | 48 |
| 5 | x | 12 | = | 60 |
| 6 | x | 12 | = | 72 |
| 7 | x | 12 | = | 84 |
| 8 | x | 12 | = | 96 |
| 9 | x | 12 | = | 108 |
| 10 | x | 12 | = | 120 |
| 11 | x | 12 | = | 132 |
| 12 | x | 12 | = | 144 |
| 13 | x | 12 | = | 156 |
| 14 | x | 12 | = | 168 |
| 15 | x | 12 | = | 180 |
| 16 | x | 12 | = | 192 |
| 17 | x | 12 | = | 204 |
| 18 | x | 12 | = | 216 |
| 19 | x | 12 | = | 228 |
| 20 | x | 12 | = | 240 |
| 13 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 13 | = | 13 |
| 2 | x | 13 | = | 26 |
| 3 | x | 13 | = | 39 |
| 4 | x | 13 | = | 52 |
| 5 | x | 13 | = | 65 |
| 6 | x | 13 | = | 78 |
| 7 | x | 13 | = | 91 |
| 8 | x | 13 | = | 104 |
| 9 | x | 13 | = | 117 |
| 10 | x | 13 | = | 130 |
| 11 | x | 13 | = | 143 |
| 12 | x | 13 | = | 156 |
| 13 | x | 13 | = | 169 |
| 14 | x | 13 | = | 182 |
| 15 | x | 13 | = | 195 |
| 16 | x | 13 | = | 208 |
| 17 | x | 13 | = | 221 |
| 18 | x | 13 | = | 234 |
| 19 | x | 13 | = | 247 |
| 20 | x | 13 | = | 260 |
| 14 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 14 | = | 14 |
| 2 | x | 14 | = | 28 |
| 3 | x | 14 | = | 42 |
| 4 | x | 14 | = | 56 |
| 5 | x | 14 | = | 70 |
| 6 | x | 14 | = | 84 |
| 7 | x | 14 | = | 98 |
| 8 | x | 14 | = | 112 |
| 9 | x | 14 | = | 126 |
| 10 | x | 14 | = | 140 |
| 11 | x | 14 | = | 154 |
| 12 | x | 14 | = | 168 |
| 13 | x | 14 | = | 182 |
| 14 | x | 14 | = | 196 |
| 15 | x | 14 | = | 210 |
| 16 | x | 14 | = | 224 |
| 17 | x | 14 | = | 238 |
| 18 | x | 14 | = | 252 |
| 19 | x | 14 | = | 266 |
| 20 | x | 14 | = | 280 |
| 15 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 15 | = | 15 |
| 2 | x | 15 | = | 30 |
| 3 | x | 15 | = | 45 |
| 4 | x | 15 | = | 60 |
| 5 | x | 15 | = | 75 |
| 6 | x | 15 | = | 90 |
| 7 | x | 15 | = | 105 |
| 8 | x | 15 | = | 120 |
| 9 | x | 15 | = | 135 |
| 10 | x | 15 | = | 150 |
| 11 | x | 15 | = | 165 |
| 12 | x | 15 | = | 180 |
| 13 | x | 15 | = | 195 |
| 14 | x | 15 | = | 210 |
| 15 | x | 15 | = | 225 |
| 16 | x | 15 | = | 240 |
| 17 | x | 15 | = | 255 |
| 18 | 255 | |||
| 18 | 255 | |||
| 18 | 255 | |||
. 0017 0017 | ||||
| 19 | x | 15 | = | 285 |
| 20 | x | 15 | = | 300 |
| 16 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 16 | = | 16 |
| 2 | x | 16 | = | 32 |
| 3 | x | 16 | = | 48 |
| 4 | x | 16 | = | 64 |
| 5 | x | 16 | = | 80 |
| 6 | x | 16 | = | 96 |
| 7 | x | 16 | = | 112 |
| 8 | x | 16 | = | 128 |
| 9 | x | 16 | = | 144 |
| 10 | x | 16 | = | 160 |
| 11 | x | 16 | = | 176 |
| 12 | x | 16 | = | 192 |
| 13 | x | 16 | = | 208 |
| 14 | x | 16 | = | 224 |
| 15 | x | 16 | = | 240 |
| 16 | x | 16 | = | 256 |
| 17 | x | 16 | = | 272 |
| 18 | x | 16 | = | 288 |
| 19 | x | 16 | = | 304 |
| 20 | x | 16 | = | 320 |
| 17 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 17 | = | 17 |
| 2 | x | 17 | = | 34 |
| 3 | x | 17 | = | 51 |
| 4 | x | 17 | = | 68 |
| 5 | x | 17 | = | 85 |
| 6 | x | 17 | = | 102 |
| 7 | x | 17 | = | 119 |
| 8 | x | 17 | = | 136 |
| 9 | x | 17 | = | 153 |
| 10 | x | 17 | = | 170 |
| 11 | x | 17 | = | 187 |
| 12 | x | 17 | = | 204 |
| 13 | x | 17 | = | 221 |
| 14 | x | 17 | = | 238 |
| 15 | x | 17 | = | 255 |
| 16 | x | 17 | = | 272 |
| 17 | x | 17 | = | 289 |
| 18 | x | 17 | = | 306 |
| 19 | x | 17 | = | 323 |
| 20 | x | 17 | = | 340 |
| 18 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 18 | = | 18 |
| 2 | x | 18 | = | 36 |
| 3 | x | 18 | = | 54 |
| 4 | x | |||
| 4 | X | |||
| 4 | x | |||
| 4 | .||||
| 5 | x | 18 | = | 90 |
| 6 | x | 18 | = | 108 |
| 7 | x | 18 | = | 126 |
| 8 | x | 18 | = | 144 |
| 9 | x | 18 | = | 162 |
| 10 | x | 18 | = | 180 |
| 11 | x | 18 | = | 198 |
| 12 | x | 18 | = | 216 |
| 13 | x | 18 | = | 234 |
| 14 | x | 18 | = | 252 |
| 15 | x | 18 | = | 270 |
| 16 | x | 18 | = | 288 |
| 17 | x | 18 | = | 306 |
| 18 | x | 18 | = | 324 |
| 19 | x | 18 | = | 342 |
| 20 | x | 18 | = | 360 |
| 19 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 19 | = | 19 |
| 2 | x | 19 | = | 38 |
| 3 | x | 19 | = | 57 |
| 4 | x | 19 | = | 76 |
| 5 | x | 19 | = | 95 |
| 6 | x | 19 | = | 114 |
| 7 | x | 19 | = | 133 |
| 8 | x | 19 | = | 152 |
| 9 | x | 19 | = | 171 |
| 10 | x | 19 | = | 190 |
| 11 | x | 19 | = | 209 |
| 12 | x | 19 | = | 228 |
| 13 | x | 19 | = | 247 |
| 14 | x | 19 | = | 266 |
| 15 | x | 19 | = | 285 |
| 16 | x | 19 | = | 304 |
| 17 | x | 19 | = | 323 |
| 18 | x | 19 | = | 342 |
| 19 | x | 19 | = | 361 |
| 20 | x | 19 | = | 380 |
| 20 Times Table | ||||
|---|---|---|---|---|
| 1 | x | 20 | = | 20 |
| 2 | x | 20 | = | 40 |
| 3 | x | 20 | = | 60 |
| 4 | x | 20 | = | 80 |
| 5 | x | 20 | = | 100 |
| 6 | x | 20 | = | 120 |
| 7 | x | 20 | = | 140 |
| 8 | x | 20 | = | 160 |
| 9 | x | 20 | = | 180 |
| 10 | x | 20 | = | 200 |
| 11 | x | 20 | = | 220 |
| 12 | x | 20 | = | 240 |
| 13 | x | 20 | = | 260 |
| 14 | x | 20 | = | 280 |
| 15 | x | 20 | = | 300 |
| 16 | x | 20 | = | 320 |
| 17 | x | 20 | = | 340 |
| 18 | x | 20 | = | 360 |
| 19 | x | 20 | = | 380 |
| 20 | x | 20 | = | 400 |
Таблицы умножения от 11 до 20 доступны в формате pdf, удобном для печати и загрузки. Каждая таблица умножения в таблицах умножения от 11 до 20 содержит 20 строк с соответствующей операцией умножения, что будет очень полезно для учащихся начальной школы, чтобы изучить основы умножения. Нажмите кнопку загрузки, чтобы получить PDF-копию этих таблиц умножения с 11 по 20. Нажмите 9.2529 Ctrl + P , если вы используете компьютер с Windows, или нажмите команду + P , если вы используете компьютер MAC, чтобы распечатать эти 11-20 таблиц.
Каждая таблица умножения в таблицах умножения от 11 до 20 содержит 20 строк с соответствующей операцией умножения, что будет очень полезно для учащихся начальной школы, чтобы изучить основы умножения. Нажмите кнопку загрузки, чтобы получить PDF-копию этих таблиц умножения с 11 по 20. Нажмите 9.2529 Ctrl + P , если вы используете компьютер с Windows, или нажмите команду + P , если вы используете компьютер MAC, чтобы распечатать эти 11-20 таблиц.
Простые приемы для изучения таблицы умножения [от 11 до 20]
Изучение таблицы умножения чрезвычайно важно. В конце концов, они являются строительными блоками математики, и, овладев искусством умножения, вы сможете делать все что угодно! Прежде всего, изучая и запоминая таблицу умножения, вашим детям становится легко и просто решать сложные математические задачи. Освоив таблица умножения , дети начинают использовать свои творческие способности и навыки визуального мышления, чтобы отвечать на вопросы. Сегодня вы также можете рассмотреть возможность записать своих детей в онлайн-класс по ведической математике для общего роста и развития. Кроме того, это поможет им решать вопросы, связанные с умножением, сложением, вычитанием и делением. Прежде чем мы углубимся в понимание основных приемов и приемов изучения таблицы умножения, давайте попробуем понять, что такое таблица умножения?
Сегодня вы также можете рассмотреть возможность записать своих детей в онлайн-класс по ведической математике для общего роста и развития. Кроме того, это поможет им решать вопросы, связанные с умножением, сложением, вычитанием и делением. Прежде чем мы углубимся в понимание основных приемов и приемов изучения таблицы умножения, давайте попробуем понять, что такое таблица умножения?
Что такое таблица умножения?
Таблицу умножения можно определить как исчерпывающий список операций умножения, в котором показаны результаты умножения одного числа на набор других чисел. На самом деле, согласно некоторым исследованиям, проведенным математиками, они заявили, что тщательное заучивание таблиц умножения не помогает детям учиться и устанавливать связи между числами или понимать основные правила умножения. Математика, основанная на практическом подходе или использующая различные способы помощи детям в выполнении математических действий в реальной жизни, считается более эффективной, чем просто обучение фактам.
Волшебные приемы изучения таблицы умножения
Прежде чем мы рассмотрим некоторые из популярных и простых фокусов, с помощью которых ваш ребенок может в увлекательной игровой форме выучить таблицу умножения от 11 до 20, важно заинтересовать его. что они не напряжены и не перегружены. Во-первых, вам нужно объяснить ребенку, «почему» обучение умножению важно. Если вы сможете убедить своего ребенка, вы сможете мотивировать его друзей и одноклассников учиться, потому что это жизненно важно для учебного процесса.
Статья по теме: 7 основных преимуществ занятий ведической математикой для детей
Как освоить таблицу умножения?
Возможно, одним из самых простых способов выучить таблицу умножения от 11 до 20 является вовлечение детей в различные виды деятельности, которые помогут им активно запоминать ответы на вопросы умножения с помощью простой техники повторения. Вот как.
1. Взлом для Таблицы 11
В таблице умножения 11 вы получите произведение умножения 11 на целые числа. Выучить таблицу 11 сравнительно легко по сравнению с другими таблицами умножения. Кратные всегда представляют собой повторение одной и той же цифры, например 11 х 1 = 11, 11 х 2 = 22, 11 х 5 = 55, 11 х 9.= 99 и т. д. Овладение таблицей умножения 11 важно при решении математических задач, в основе которых лежат важные операции умножения и деления.
Выучить таблицу 11 сравнительно легко по сравнению с другими таблицами умножения. Кратные всегда представляют собой повторение одной и той же цифры, например 11 х 1 = 11, 11 х 2 = 22, 11 х 5 = 55, 11 х 9.= 99 и т. д. Овладение таблицей умножения 11 важно при решении математических задач, в основе которых лежат важные операции умножения и деления.
a) Советы по таблице 11
• Первые 9 кратных 11 очень легко запомнить.
• Чтобы рассчитать таблицу умножения на 11 для двузначных чисел, используется магический трюк. При умножении двузначного числа на 11 сумма цифр числа должна быть помещена между двумя цифрами исходного двузначного числа. Например, когда 11 умножается на 16, возьмите сумму 1 и 6, то есть 7. Теперь поместите сумму, которая равна 7, между 1 и 6. В результате получится 176. Следовательно, конечный продукт 11 и 16 — это 176, то есть 11 х 16 = 176,
2. Взлом для Таблицы 12
Знаете ли вы, что на сегодняшний день 12 человек побывали на Луне? Большинство из нас придерживаются 12-часовой системы времени.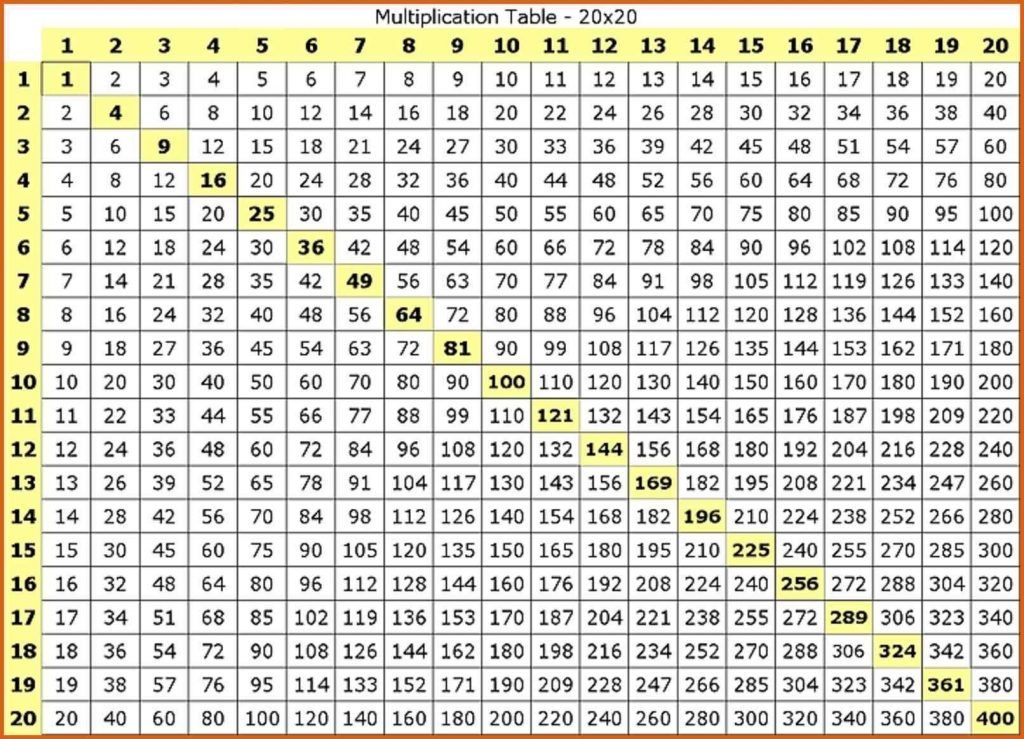 Эти факты наглядно подчеркивают важность числа 12 в нашей жизни. Изучение и освоение таблицы умножения 12 дает нам преимущество при решении задач, связанных с числом 12.
Эти факты наглядно подчеркивают важность числа 12 в нашей жизни. Изучение и освоение таблицы умножения 12 дает нам преимущество при решении задач, связанных с числом 12.
b) Советы по таблице 12
• В таблице умножения 12 нет никаких правил или рекомендаций. что облегчит запоминание его умножения, но если вы внимательно посмотрите, то поймете, что существует фиксированная последовательность для каждых пяти кратных 12, то есть 12, 24, 36, 48, 60, 72, 84, 96, 108, 120 и так далее.
• При внимательном наблюдении вы увидите, что эти множители всегда повторяются, а это означает, что учащиеся могут легко запомнить эти цифры, чтобы составить таблицу умножения числа 12. 13 состоит из умножения 13 на целые числа. Понимание и знание таблицы умножения на 13 делает обучение чрезвычайно легким в средней школе и даже за ее пределами. Наряду с таблицей 13, дети также должны изучить факты ее деления. Например, факты деления для таблицы 13 равны 39.÷ 13= 3, 52÷ 13= 4, 65÷ 13= 5.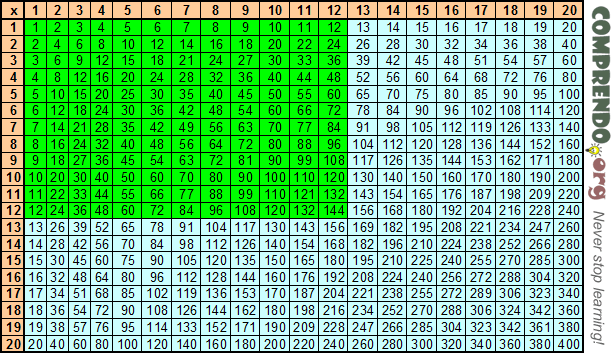 Это также поможет создать прочную основу для деления больших чисел.
Это также поможет создать прочную основу для деления больших чисел.
c) Советы по таблице 13
• Чтобы освоить таблицу умножения на 13, сначала нужно выучить таблицу умножения на 3. Кратность числа 3 следующая: 3, 6, 9, 12, 15, 18, 21 и так далее.
• Теперь, чтобы получить числа, кратные 13, прибавьте натуральные числа к разряду десятков. Следовательно, таблица 13 может быть получена по следующей формуле: (1+0)3, (2+0)6, (3+0)9, (4+1)2, (5+1)5, (6+1)8, (7+2)1, (8+2)4, (9+2)7, (10+3)0= 13, 26, 39, 52, 65, 78, 91, 104, 117 и 130.
4. Подсказка для таблицы 14
Запоминание и изучение таблицы умножения 14 может быть утомительной задачей для младших школьников. Знание таблицы 14 является обязательным условием при изучении математики. Итак, давайте рассмотрим несколько простых приемов, которые помогут вашим детям выучить таблицу 14.
d) Советы по таблице 14
• Чтобы освоить таблицу умножения 14, во-первых, вам нужно запомнить 4 раза стол.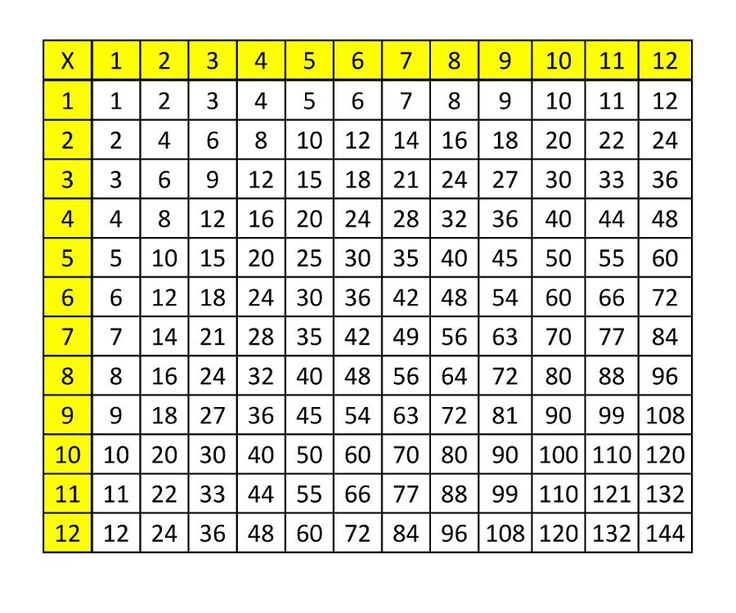 Следовательно, числа, кратные 4, следующие: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 и так далее.
Следовательно, числа, кратные 4, следующие: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 и так далее.
• Теперь, чтобы получить числа, кратные 14, прибавьте натуральные числа к разряду десятков. Следовательно, таблица 14 может быть получена как: (1+0)4, (2+0)8, (3+1)2, (4+1)6, (5+2)0, (6+2) )4, (7 + 2) 8, (8 + 3) 2, (9 + 3) 6, (10 + 4) 0, следовательно, итоговые кратные будут давать в сумме следующие цифры, указанные ниже:
14, 28, 42, 56, 70, 84, 98, 112, 126, 140 и так далее.
5. Хак для Таблицы 15
Таблицу 15 очень легко выучить и запомнить. Таблица создается путем умножения числа 15 на все натуральные числа, такие как 15 x 1 = 15 или 15 x 2 = 30. Здесь 15 и 30 кратны 15.
e) Советы по Таблице 15
• Чтобы быстро выучить таблицу умножения на 15, есть скрытый трюк. Чтобы справиться с этим трюком, вы должны иметь базовые знания о разрядах единиц, разрядах десятков, нечетных и четных числах. Хитрость в том, что в результате место единицы всегда будет следовать схеме 5-0.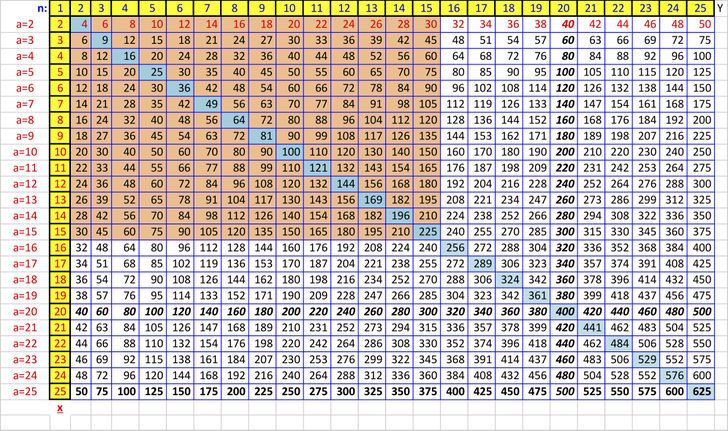 Например, 15 x 1 = 15 или 15 x 2 = 30.
Например, 15 x 1 = 15 или 15 x 2 = 30.
• Аналогично, для разряда десятков цифра s всегда будет следовать образцу 2 последовательных четных чисел и следующих 2 последовательных нечетных чисел. Например, 15 х 1 = 15 (нечетное число в десятках), 15 х 2 = 30 (нечетное число в десятках), 15 х 3 = 45 (четное число в десятках) и 15 х 4 = 60 (четное число). число в десятом разряде).
6. Взлом таблицы 16
Таблица умножения 16 получается путем умножения числа 16 на разные целые числа. Общий переход от счета на пальцах к ментальной арифметике осуществляется с помощью изучения и освоения таблицы умножения.
f) Краткие советы по изучению таблицы 16
• 16 не содержит каких-либо специальных правил или указаний, облегчающих понимание таблицы умножения, но существует определенная закономерность для каждых 5 кратных 16, то есть: 16 , 32, 48, 64, 80, 96, 112, 128, 144, 160 и так далее.
• Последняя цифра этих кратных всегда повторяется.
7. Взлом для Таблицы 17
Знаете ли вы, что таблица умножения 17 может улучшить математические способности детей? Таблица умножения 17 может быть важным инструментом, который дети могут использовать даже для решения длинных вопросов, связанных с умножением и делением. Следовательно, запоминание таблицы умножения 17 облегчает учащимся решение сложных математических задач.
g) Советы по изучению таблицы 17
• Чтобы понять и выучить таблицу умножения 17, ваши дети должны иметь базовое представление о таблице умножения 16. Давайте посмотрим на нее:
• 16 х 1 = 16
• 16 х 2 = 32
• 16 х 3 = 48
• 16 х 4 = 64
• 16 х 5 = 80
Теперь вам нужно превратить кратные 16 в кратные 17, добавляя натуральные числа от 1 до 10 к числам, кратным 16. Таким образом, ваши дети смогут быстро выучить обе таблицы умножения. Например:
• 16 x 1 = 16, Теперь прибавьте 16+1 = 17
• 16 x 2 = 32, Теперь прибавьте 32 +2 = 34
• 16 x 3 = 48, Теперь прибавьте 48 +3 = 51 и так далее.
8. Подсказка для таблицы 18
Вы будете удивлены, узнав, что таблица умножения 18 состоит из двойных множителей, которые мы можем получить из таблицы 9.
Чтобы запомнить таблицу 18, есть несколько специальных приемов, которым могут следовать ваши дети: • Вы можете выучить таблицу 18 с помощью таблицы 19, просто вычитая 1-10 натуральных чисел. • Все, что вам нужно сделать, это вычесть это же число из кратных, на которые вы умножаете 19. Например: 19 x 11 = 209, теперь вычтите 209-11 = 198. Аналогично, 19 x 12 = 228, Теперь вычтите 228-12 = 216 • Попросите ребенка тщательно выучить таблицу 8. Следовательно, первые 10 кратных 8 равны 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, и так далее. Наконец, попросите вашего ребенка получить числа, кратные 18, добавить натуральные числа к цифре десятков, то есть (1 + 0) 8, (2 + 1) 6, (3 + 1) 4, (4 + 3) 2, ( 5+4)0, (6+4)8, (7+5)6, (8+6)4, (9+7)2, (10+8)0 = 18, 36, 54, 72, 90, 108 и так далее. 9. Совет для таблицы 19 Знаете ли вы, что 19 — это восьмое простое число, которое делится только на единицу и само на себя? Давайте взглянем на некоторые из быстрых приемов, чтобы запомнить таблицу умножения 19. i) Быстрые приемы для изучения таблицы 19 Чтобы запомнить таблицу 19, есть несколько специальных приемов, которым могут следовать ваши дети: • Таблица 19 следует шаблону для каждых 10 кратных. Следовательно, все, что вам нужно сделать, это написать первые 10 нечетных чисел в правильной последовательности на месте десятков. • Теперь попросите детей начать писать с обратной стороны, то есть с 0-9 на разряде единиц. Например, • 19 х 1 = 19 • Еще один способ запомнить таблицу умножения 19 – это записать всю таблицу 19.. • Ниже указаны числа, кратные 9: 9,18,27,36,45,54,63,72,81,90 и т. 10. Взлом для таблицы 20 20 — наименьшее примитивное число. Изучение и запоминание таблицы умножения на 20 очень важно для начального образования ребенка. Давайте рассмотрим несколько лайфхаков для быстрого запоминания таблицы умножения 20. j) Быстрые приемы для изучения таблицы 20 • Чтобы освоить таблицу умножения на 20, сначала ваш ребенок должен выучить таблицу умножения на 2. Первые 10 кратных 2 были упомянуты ниже: 2,4,6,8,10,12,14,16,18 и 20. • (20 х 1 = 20) Основные выводы Вот несколько эффективных советов и лайфхаков, которые помогут вам уверенно и легко освоить таблицу умножения от 11 до 20. Кроме того, вы также можете записать своих детей на онлайн-семинары по математике. В PiggyRide мы предлагаем широкий спектр занятий и семинаров, которые помогут вашим детям овладеть искусством изучения таблицы умножения. От онлайн-уроков ведической математики для детей до уроков и мастер-классов по счетам — вы можете записать своих детей на захватывающее обучение. И знаете, что самое интересное? Дети обучаются под руководством опытных и высококвалифицированных педагогов. Пусть обучение ваших детей начнется сегодня. Исследуйте классы ведической математики АВТОР: Привет друзья! Я Ридхи Догра. Таблицы всегда помогают детям с более быстрыми и точными вычислениями, что делает математику интересным предметом. Запоминание таблиц позволяет детям быстро решать математические задачи, а это необходимо на всю жизнь. В начальной школе детей учат таблицам от 1 до 10. Как только это будет сделано, начинаются математические таблицы от 11 до 20. Таблицы от 11 до 20 помогают детям решать арифметические задачи на скорость. Ниже приведены таблицы умножения от 11 до 20 в одном месте, чтобы облегчить обучение ваших детей. Таблицы с таблицами от 11 до 20 – это учебное пособие, позволяющее детям лучше понимать и запоминать таблицы. Изучение таблиц от 11 до 20 может оказаться сложной задачей. Вот несколько советов и приемов, которые помогут детям легко выучить и запомнить таблицу умножения: 1. Абхишек купил 12 упаковок ручек, каждая упаковка стоит 5 рупий. Какова общая стоимость 12 пакетов? Решение: Стоимость каждой упаковки ручек: 5 рупий 2. Джон постоянно покупает мороженое в магазине в течение 10 дней. Решение: Стоимость каждого мороженого: 10 рупий 3. Майк зарабатывает 15 рупий в час. Сколько он зарабатывает, если работает по 8 часов в день? Решение: Майк зарабатывает в час: 15 рупий 4. Джонатан делает 13 стульев в день. Сколько стульев он сделал за 9 дней? Решение: Количество стульев, которые он изготавливает в день: 13 5. Клиент покупает 17 яблок в день. Сколько яблок он купил за 9дней? Решение: Количество яблок, купленных за день: 17 Изучение одиннадцати-двадцати таблиц помогает детям быстро считать. Это помогает им быстро решать математические задачи с точными результатами. Учащиеся могут запомнить таблицу умножения от 11 до 20, чтобы улучшить свои арифметические навыки. Наслаждайтесь изучением математики с быстрыми таблицами и получайте удовольствие от мира чисел! Читайте также: Таблицы умножения от 1 до 10 для детей Таблицы с 11 по 20: Учащиеся изучают школьные таблицы умножения от 1 до 10. Изучение таблиц умножения от 11 до 20 сокращает время решения задач во время школьных экзаменов и конкурсных экзаменов. В этой статье мы предоставили таблицы умножения от 11 до 20 онлайн. Студенты также могут загружать таблицы в формате PDF, а также в формате изображения и обращаться к ним в автономном режиме. Учащиеся могут обращаться к этим таблицам во время вычислений, пока они не смогут запомнить таблицу умножения наизусть. Продолжайте читать, чтобы узнать больше! Математическая таблица от 11 до 20 поможет учащимся в начальных и средних классах. Более того, они полезны в старших классах школы и даже в колледже, когда математические задачи становятся все более сложными и требуют много времени. Учащиеся могут загрузить PDF-файлы для таблиц по математике с 11 по 20, нажав на соответствующую ссылку, указанную ниже. Эти PDF-файлы можно даже распечатать, чтобы студенты могли легко обращаться к ним. Прочтите всю статью, чтобы скачать и выучить таблицу умножения от 11 до 20. Таблицы умножения используются для очень быстрого решения всех видов математических задач. Если у вас под рукой есть список таблиц от 11 до 20, это облегчит расчеты и сэкономит много времени. Для удобства ниже приведены полные таблицы умножения от 11 до 20. За исключением таблиц 17 и 19, остальные сравнительно легко выучить и запомнить. Если вы хотите свободно пользоваться таблицами умножения, ознакомьтесь с приведенной ниже таблицей таблиц, она поможет вам запомнить математические таблицы с 11 по 20. For all other tables, you can take предыдущее число в качестве основы и добавить числа в следующем порядке. На основе приведенного выше примера попробуйте 13, 17, 19 и укажите результат в разделе комментариев. Вот некоторые из часто задаваемых вопросов по таблицам с 11 по 20 pdf: Q.1: Что такое таблица 11? Q.2: Почему важно запоминать таблицу умножения? Q. Q.4: Как выучить математические таблицы устно? Q.5: Что такое трюк с таблицей умножения на 11? Q.6: Есть ли какой-то трюк, чтобы написать таблицу умножения 12? Практика от 11 до 20 таблиц Вопросы с советами и решениями Используйте эту таблицу умножения, чтобы выучить таблицу умножения в секундах. Наведите курсор на таблицу и посмотрите результат. Например, если вы ищете 14 в какой таблице, найдите 14 в этой таблице, и вы получите ответ ниже. Заучивание таблиц — задача, которая не нравится большинству детей. Мы упростили учащимся изучение таблицы умножения с помощью схемы умножения. Приведенную выше таблицу можно распечатать и загрузить одним щелчком мыши. Таблица умножения — это та таблица, которая отображает умножение двух чисел. Как правило, таблица умножения записывается путем набора чисел от 1 до 15 в самой верхней строке и в первом левом столбце. Таблица умножения позволяет сэкономить время при вычислениях. Таблица умножения от 1 до 15 содержит цифры от 1 до 15 в первой строке и первом столбце. Все остальные строки и столбцы таблицы умножения показывают произведение двух чисел, одно из первого столбца, а другое из первой строки. Например, произведение 8 и 6 равно 48. Таблица умножения от 2 до 20 — это строительный блок многозначных чисел, используемый для решения задач на умножение длинных чисел, дробей, процентов, и факторизация чисел. Таблицы умножения очень помогают детям решать арифметические задачи в уме. Изучив таблицу умножения от 2 до 20, дети могут стать экспертами в решении сложных математических задач. Таблицы умножения от 2 до 20 приведены ниже.
Статья по теме: Почему изучение счетов важно для вашего ребенка
• 19 х 2 = 38
• 19 х 3 = 57
• 19 х 4 = 76 и так далее. д.
д.
• Чтобы найти числа, кратные 19, попросите детей сложить натуральные числа. до цифры десятков для кратных 9. Следовательно, таблица 19 выглядит следующим образом: (1 + 0) 9, (2 + 1) 8, (3 + 2) 7, (4 + 3) 6, (5+ 4)5, (6+5)4, (7+6)3, (8+7)2, (9+8)1, (10+9)0, кратные указаны ниже:
19, 38 , 57, 76, 95, 114 и так далее.
• Теперь, чтобы получить кратные 20, добавьте 0 к разряду единиц в кратные 2. Например:
• Аналогично (20 х 2 = 40) и (20 х 3 = 60) и так далее.
Риди Догра
Я работаю писателем контента в PiggyRide. Я закончил Делийский университет со степенью бакалавра в области домоводства, а также получил степень бакалавра в области журналистики и массовых коммуникаций в Университете Амити. Я заядлый читатель, страстный путешественник и любитель кино.
Я заядлый читатель, страстный путешественник и любитель кино. Математические таблицы от 11 до 20
 Изучение таблиц в целом обеспечивает лучшее понимание практического мира чисел и операций. Используйте печатные формы или рабочие листы, чтобы научить вашего ребенка от 11 таблиц до 20. Обучение таблице умножения сложно, но несколько советов и приемов сделают написание таблиц от 11 до 20 увлекательным занятием.
Изучение таблиц в целом обеспечивает лучшее понимание практического мира чисел и операций. Используйте печатные формы или рабочие листы, чтобы научить вашего ребенка от 11 таблиц до 20. Обучение таблице умножения сложно, но несколько советов и приемов сделают написание таблиц от 11 до 20 увлекательным занятием. Зачем вашему ребенку учить таблицы от 11 до 20?
Таблицы умножения от 11 до 20
Таблица из 11 Таблица из 12 Таблица из 13 Таблица из 14 Таблица из 15 11 × 1 = 11 12 × 1 = 12 13 × 1 = 13 14 × 1 = 14 15 × 1 = 15 11 × 2 = 22 12 × 2 = 24 13 × 2 = 26 14 × 2 = 28 15 × 2 = 30 11 × 3 = 33 12 × 3 = 36 13 × 3 = 39 14 × 3 = 42 15 × 3 = 45 11 × 4 = 44 12 × 4 = 48 13 × 4 = 52 14 × 4 = 56 15 × 4 = 60 11 × 5 = 55 12 × 5 = 60 13 × 5 = 65 14 × 5 = 70 15 × 5 = 75 11 × 6 = 66 12 × 6 = 72 13 × 6 = 78 14 × 6 = 84 15 × 6 = 90 11 × 7 = 77 12 × 7 = 84 13 × 7 = 91 14 × 7 = 98 15 × 7 = 105 11 × 8 = 88 12 × 8 = 96 13 × 8 = 104 14 × 8 = 112 15 × 8 = 120 11 × 9 = 99 12 × 9 = 108 13 × 9 = 117 14 × 9 = 126 15 × 9 = 135 11 × 10 = 110 12 × 10 = 120 13 × 10 = 130 14 × 10 = 140 15 × 10 = 150 Таблица из 16 Таблица 17 Таблица из 18 Таблица из 19 Таблица из 20 16 × 1 = 16 17 × 1 = 17 18 × 1 = 18 19 × 1 = 19 20 × 1 = 20 16 × 2 = 32 17 × 2 = 34 18 × 2 = 36 19 × 2 = 38 20 × 2 = 40 16 × 3 = 48 17 × 3 = 51 18 × 3 = 54 19 × 3 = 57 20 × 3 = 60 16 × 4 = 64 17 × 4 = 68 18 × 4 = 72 19 × 4 = 76 20 × 4 = 80 16 × 5 = 80 17 × 5 = 85 18 × 5 = 90 19 × 5 = 95 20 × 5 = 100 16 × 6 = 96 17 × 6 = 102 18 × 6 = 108 19 × 6 = 114 20 × 6 = 120 16 × 7 = 112 17 × 7 = 119 18 × 7 = 126 19 × 7 = 133 20 × 7 = 140 16 × 8 = 128 17 × 8 = 136 18 × 8 = 144 19 × 8 = 152 20 × 8 = 160 16 × 9 = 144 17 × 9 = 153 18 × 9 = 162 19 × 9 = 171 20 × 9 = 180 16 × 10 = 160 17 × 10 = 170 18 × 10 = 180 19 × 10 = 190 20 × 10 = 200 Таблицы с умножением от 11 до 20 для детей
 Визуальные инструменты ускоряют процесс обучения, чем декламация.
Визуальные инструменты ускоряют процесс обучения, чем декламация. Советы по изучению и запоминанию таблиц умножения от 11 до 20 для детей
Например – 12, 24, 36, 48, 60, 72, 84 и так далее.
Например – 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168.
Например: 15 x 1 = 15, а 15 x 4 = 60. Обратите внимание, что 1 — нечетное число, оканчивающееся на 5, а 4 — четное число с нулем в конце. .
Например – 16, 32, 48, 64, 80, 96, 112, 128, 144, 160.
Например – 20 х 1 = 20, 20 х 2 = 40, 20 х 3 = 60 и так далее. Решенные примеры задач на основе таблиц с 11 по 20 Для детей
Общая стоимость 12 упаковок ручек: 12 x 5 = 60
Таким образом, общая стоимость 12 упаковок ручек составляет 60 рупий.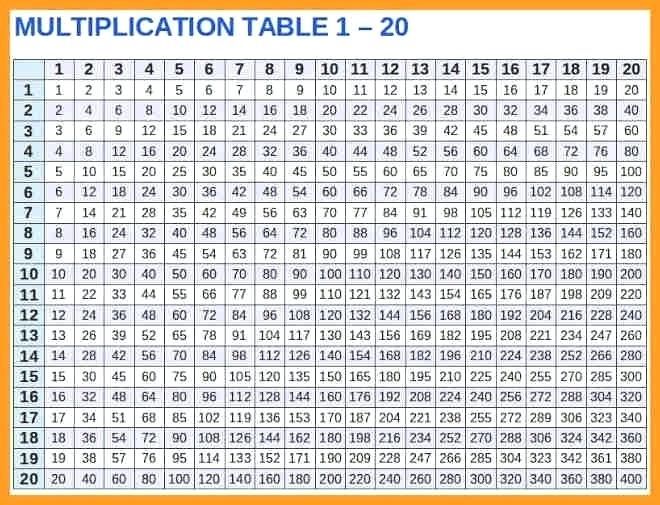 Каждое мороженое стоит 10 рупий. Сколько всего он потратил на мороженое?
Каждое мороженое стоит 10 рупий. Сколько всего он потратил на мороженое?
Количество дней, в течение которых он покупал мороженое: 10 дней
Таким образом, общие расходы на мороженое составляют 10 x 10 = 100 рупий.
Количество рабочих часов в день: 8 часов
Таким образом, общая заработная плата Майка составляет 15 x 8 = 120 рупий.
Следовательно, общее количество стульев, которое он изготавливает за 9 дней, равно 13 x 9 = 117.
Следовательно, общее количество яблок, купленных покупателем за 9 дней, равно 17 x 9 = 153 яблока.
Часто задаваемые вопросы
1. Каковы преимущества изучения таблиц с 11 по 20?
Таблицы умножения от 1 до 20 для детей Таблицы от 11 до 20: Изучите таблицы умножения от 11 до 20
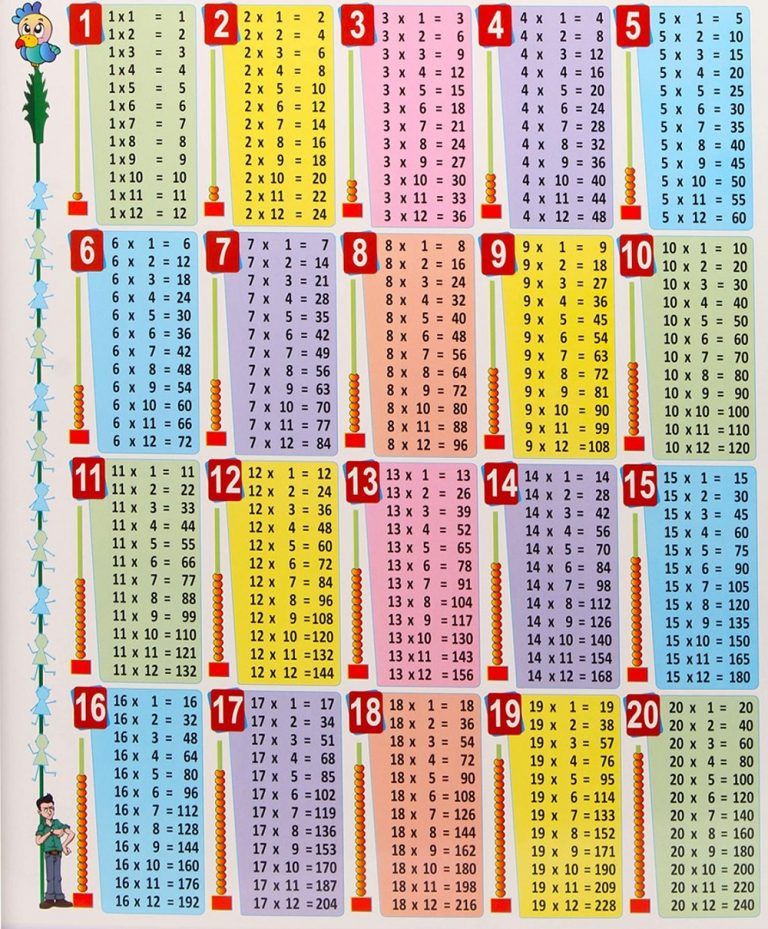 Важно, чтобы учащиеся имели под рукой таблицу умножения от 11 до 20.
Важно, чтобы учащиеся имели под рукой таблицу умножения от 11 до 20. Таблица умножения 11 Таблица Умножения 12 Таблица умножения 13 Умножение 9 Multiplication TABLE 140004 . 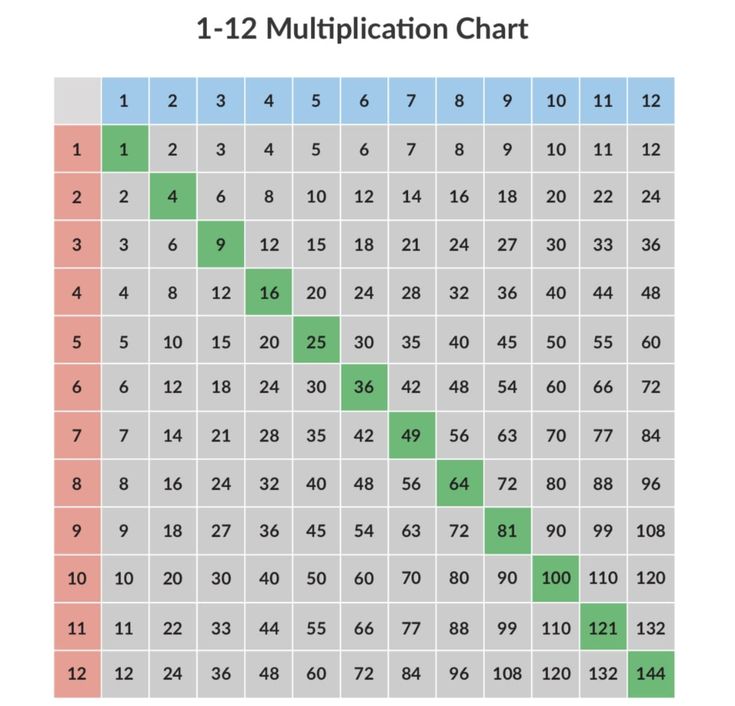 Таблица 16
Таблица 16 Таблица умножения 17 Таблица умножения 18 Таблица умножения чисел 19 Таблица умножения чисел 20 Таблица от 11 до 20 столов
Как легко выучить таблицу умножения от 11 до 20
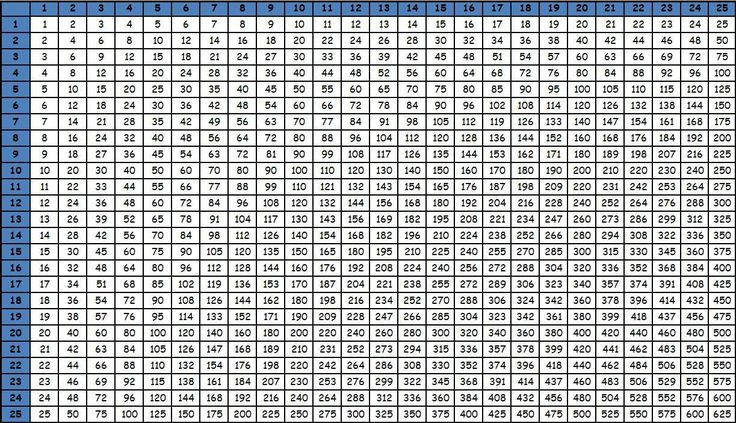
x 11 12 13 14 14 0003 15 16 17 18 19 20 1 11 12 13 14 15 16 17 18 19 20 2 22 24 26 28 30 32 34 36 38 40 3 33 36 39 42 45 48 51 54 57 60 4 44 48 52 56 60 64 68 72 76 80 5 55 60 65 70 75 80 85 90 95 100 6 66 72 78 84 90 96 102 108 114 120 7 77 84 91 98 105 112 119 126 133 140 8 88 96 104 112 120 128 136 144 152 160 9 99 108 117 126 135 144 153 162 171 180 10 110 120 130 140 150 160 170 180 190 200 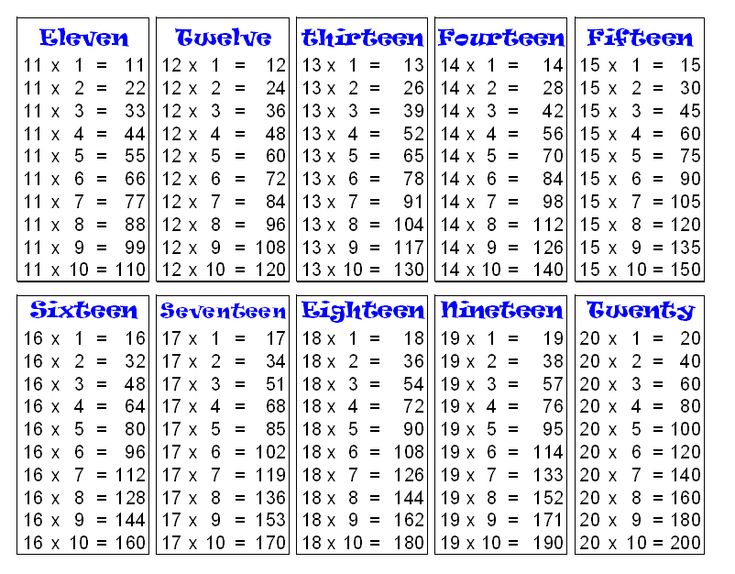
11 + 1 = 12
22 + 2 = 24
33 + 3 = 36
44 + 4 = 48
55 + 5 = 60
66 + 6 = 72
74 +
88 + 8 = 96
99 + 9 = 108 Часто задаваемые вопросы по таблицам с 11 по 20
Ответ : Таблица 11 записывается как:
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110.
Ответ : Запоминание от 11 до 20 таблиц позволяет учащимся решать математические задачи легче и быстрее.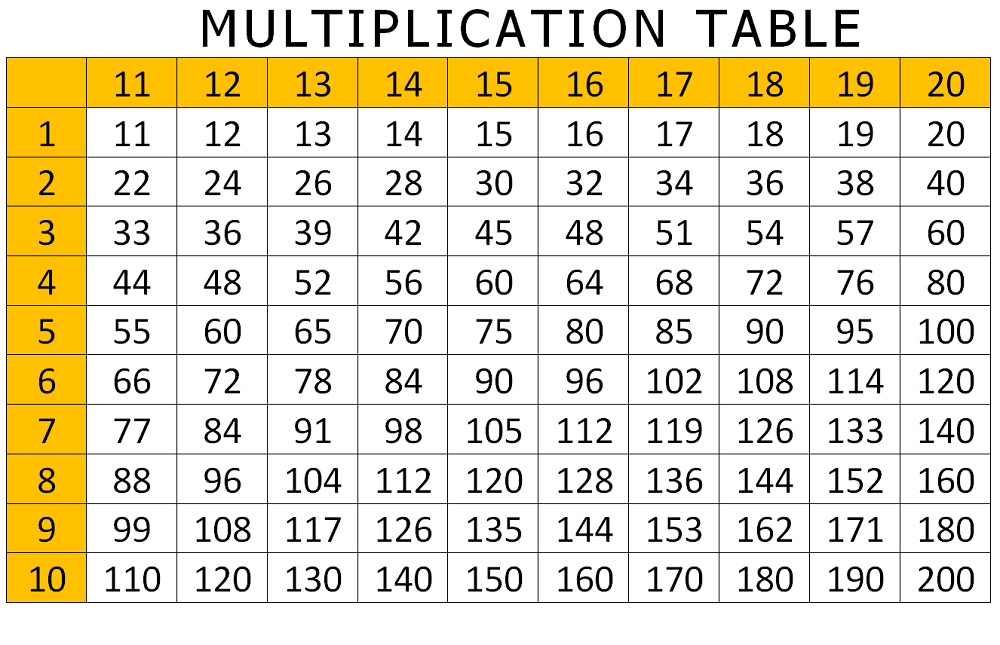 3: Что такое таблица 20?
3: Что такое таблица 20?
Ответ : Таблица 20 выглядит следующим образом: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200.
Ответ : Лучший способ выучить математические таблицы в устной форме — это громко повторять их. Вы можете воспользоваться помощью своих друзей или семьи. Также решение задач на умножение, где используются таблицы, полезно при изучении таблиц умножения.
Ответ. Хитрость при написании 11 таблиц заключается в том, чтобы записать числа от 1 до 9 в порядке возрастания, а затем начать снизу и записать числа от 9.до 1 в порядке убывания рядом с числами, которые были записаны ранее.
Ответ. Что вы можете сделать, так это написать 6 таблиц и умножить каждое число на 2, и вы получите 12 таблиц. Пример:
Что вы можете сделать, так это написать 6 таблиц и умножить каждое число на 2, и вы получите 12 таблиц. Пример:
6 х 1 = 6 х 2 = 12.
6 х 5 = 30 х 2 = 60. Таблица умножения — Таблица умножения
Что такое таблица таблицы умножения?
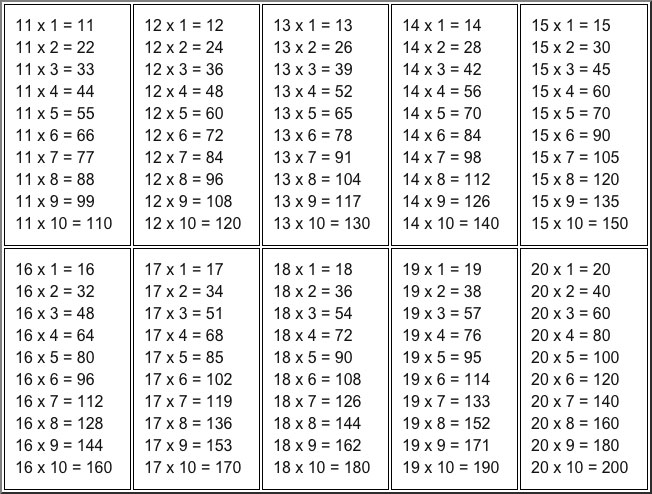
Таблицы умножения от 2 до 20
Times tables 6 to 9 Times Table of 2 Times Table of 3 Times Table of 4 Times Table of 5 2 x 1 = 2 3 х 1 = 3 4 х 1 = 4 5 x 1 = 5 2 x 2 = 4 3 x 2 = 6 4 x 2 = 8 5 x 2 = 10 2 x 3 = 6 3 x 3 = 4 x 3 = 12 5 x 3 = 15 2 x 4 = 8 3 x 4 = 12 4 x 4 = 16 5 x 4 = 200017 2 x 5 = 10 3 x 5 = 15 4 x 5 = 20 5 x 5 = 25 2 x 6 = 12 3 x 6 = 18 4 x 6 = 24 5 x 6 = 30 2 x 7 = 14 3 x 7 = 21 4 x 7 = 28 5 x 7 = 35 2 x 8 = 16 3 x 8 = 24 4 x 8 = 32 5 x 8 = 40 2 x 9 = 18 3 x 9 = 27 4 4 4 = 18 3 x 9 = 27 4 4 4. 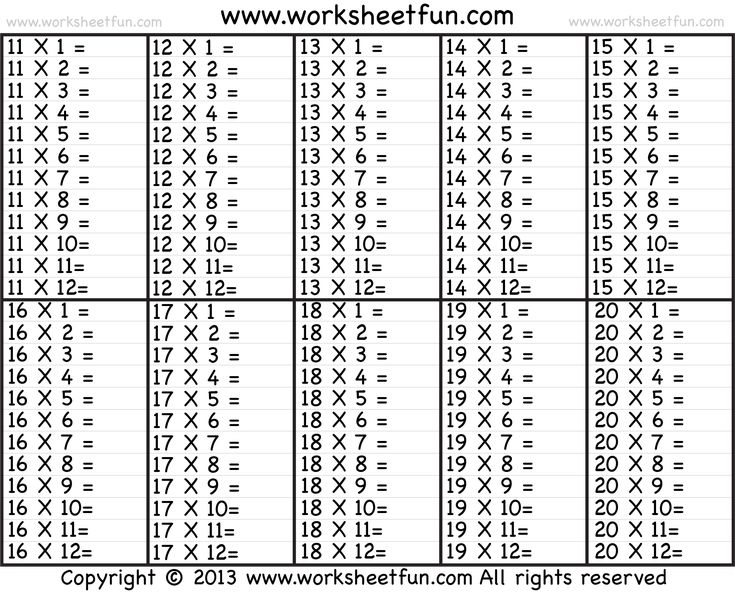 х 9 = 36
х 9 = 36 5 х 9 = 45 2 х 10 = 20 3 х 10 = 30 4 х 10 = 40 5 x 10 = 50 2 x 11 = 22 3 x 11 = 33 4 x 11 = 44 5 x 11 = 55 2 x 12 = 24 3 x 12 = 36 4 x 12 = 48 5 x 12 = 60
Таблицы умножения от 10 до 13 Times Table of 6 Times Table of 7 Таблица умножения на 8 раза таблица 9 6 x 1 = 6 7 x 1 = 7 8 x 1 = 8 9 x 1 = 6 x 2 = 12 7 x 2 = 14 8 x 2 = 16 9 x 2 = 18 6 x 3 = 18 7 x 3 = 21 8 x 3 = 24 9 x 3 = 27 6 x 4 = 24 7 x 4 = 28 8 x 4 = 32 9 x 4 = 36 6 x 5 = 30 7 x 5 = 35 8 x 5 = 40 9 x 5 = 45 6 x 6 = 36 7 x 6 = 42 8 x 6 = 48 9 x 6 = 54 6 x 7 = 42 7 x 7 = 49 8 x 7 = 56 9 x 7 = 63 6 x 8 = 48 7.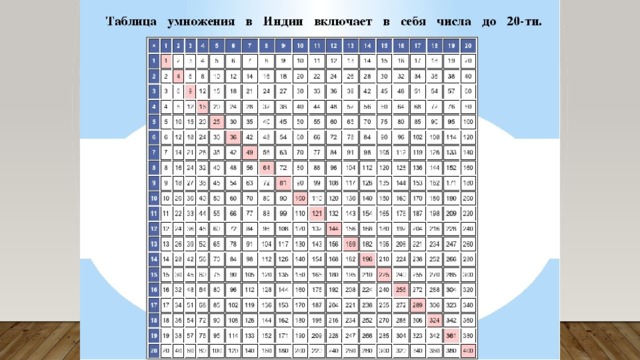
6 x 8 = 48 7. 6 x 8 = 48 70012 6 x. 8 = 56 8 x 8 = 64 9 x 8 = 72 6 x 9 = 54 7 x 9 = 63 8 x 9 = 72 9 x 9 = 81 6 x 10 = 60 7 x 10 = 70 8 x 10 = 80 9 x 10 = 9017 6 6. 11 = 66 7 x 11 = 77 8 x 11 = 88 9 x 11 = 99 6 x 12 = 72 7 x 12 = 84 8 x 12 = 96 99 8 x 12 = 96 9009 8 x x 12 = 108
Times tables 14 to 17 раза таблица 10 Таблица Таблицы 11 Таблица 12 Таблица 13 10 x 1 = 10 11 x 10017 10 x 1 = 100017 11 x 10017 12 12 12 12 1216 12 12 12 12 10 x 1 = 100017 11 x 10017 12 10 x 1 = 100017 11 x 10017 9009 10 x 1 = 100017 11 x 10017 9009 12 12 12.  x 1 = 12
x 1 = 12 13 x 1 = 13 10 x 2 = 20 11 x 2 = 22 12 x 2 = 24 13 x 2 = 26 10 x 3 = 30 11 х 3 = 33 12 х 3 = 36 13 x 3 = 39 10 x 4 = 40 11 x 4 = 44 12 x 4 = 48 13 x 4 = 52 10 x 5 = 50 11. 10 x 5 = 500017 5 = 55 12 x 5 = 60 13 x 5 = 65 10 x 6 = 60 11 x 6 = 66 12 x 6 = 72 13 x 6 = 78 9 10 x 7 = 70 11 x 7 = 77 12 x 7 = 84 13 x 7 = 91 10 x 8 = 80 11 x 8 = 88 12 x 8 = 96 13 x 8 = 104 10 x 90 11 x 999917 12 x 9017 11 x 99 12 x = 108 13 x 9 = 117 10 x 10 = 100 11 x 10 = 110 12 x 10 = 120 13 x 10 = 130 10 x 11010 10 x 1101017 10 x 11017 10 x 110017 10 x 110017 10 x 110016 10 x 110016 10 x 110016 11 х 11 = 121 12 х 11 = 132 13 х 11 = 143 10 x 12 = 120 11 x 12 = 132 12 x 12 = 144 13 x 12 = 156
Таблицы с 18 по 20 Times Table of 14 Таблица раз 15 Таблица TINE 16 Таблица 17 14 x 1 = 140017 15 x 1 = 15 16 x 1 = 16 15 x 1 = 15 16 x 1 = 160017 17 17 17 17 17 17 17 17 16 x 1 = 160017 17 17 17 . 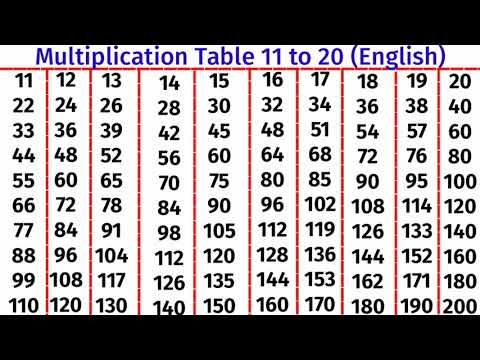 х 1 = 17
х 1 = 17 14 x 2 = 28 15 x 2 = 30 16 x 2 = 32 17 x 2 = 34 14 x 3 = 42 15 x 3 = 45 16 x 3. = 48 17 x 3 = 51 14 x 4 = 56 15 x 4 = 60 16 x 4 = 64 17 x 4 = 68 14 x 5 = 70017 14 x 5 = 70017 9 9 14 x 5 = 70017 14 x 5 = 70017 14 x 5 = 70017 14 x. 15 х 5 = 75 16 х 5 = 80 17 х 5 = 85 14 х 6 = 84 15 x 6 = 90 16 x 6 = 96 17 x 6 = 102 14 x 7 = 98 15 x 7 = 105 16 x 7 = 112 17 x 7 =. 119 14 x 8 = 112 15 x 8 = 120 16 x 8 = 128 17 x 8 = 136 14 x 9 = 126 15 x 1616 1616 1616 1616. 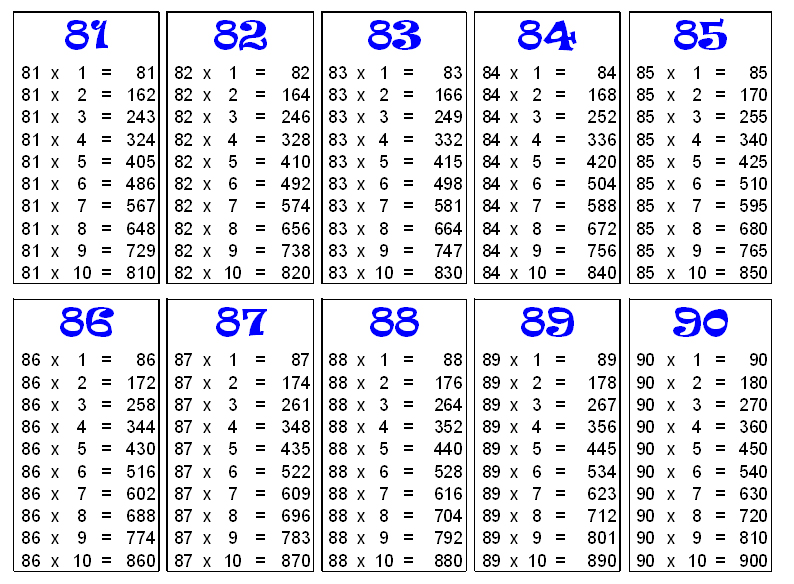 х 9 = 144
х 9 = 144 17 х 9 = 153 14 х 10 = 140 15 х 10 = 150 16 x 10 = 160 17 x 10 = 170 14 x 11 = 154 15 x 11 = 165 16 x 11 = 176 17 x 11 = 187 14 17 x 11 = 187 9009 14 140016 17 x 11 = 187 14 140016 140016 17 x 12 = 168 15 x 12 = 180 16 x 12 = 192 17 x 12 = 204 Times 7 00100100169003 9000. 0 9000. 001001001001009 9000.001001009 9000.001001009 9000.001001009 9000. 0 9000 0 0 .  Таблица умножения 19
Таблица умножения 19 раза таблица 20 18 x 1 = 18 19 x 1 = 19 20 x 1 = 20 18 x 2 = 36 19 x 2 = 38 20 x 2 = 40 18 x 3 = 54 19 x 3 = 57 20 x 3 = 60 18 x 4 = 72 19 x 4 = 76 20 x 4 = 80 19 = 76 20 x 40 18 х 5 = 90 19 х 5 = 95 20 х 5 = 100 18 x 6 = 108 19 x 6 = 114 20 x 6 = 120 18 x 7 = 126 19 x 7 = 133 20 x 7 = 14017 18 18. 8 = 144 19 x 8 = 152 20 x 8 = 160 18 x 9 = 162 19 x 9 = 171 20 x 9 = 180 18 x 10 = 180017 7017 18 x 100017 19 х 10 = 190 20 х 10 = 200 18 х 11 = 198 19 x 11 = 209 20 x 11 = 220 18 x 12 = 216 19 x 12 = 228 20 x 12 = 240 .
 Чтобы выучить и загрузить таблицу умножения 1-100, используйте приведенную выше таблицу умножения и напишите любое число для создания таблицы в поле и нажмите кнопку создания. Таблица умножения отобразится за доли секунды.
Чтобы выучить и загрузить таблицу умножения 1-100, используйте приведенную выше таблицу умножения и напишите любое число для создания таблицы в поле и нажмите кнопку создания. Таблица умножения отобразится за доли секунды.
Вы даже можете создать таблицу умножения от 1 до 1000 или больше.
Советы и рекомендации по изучению и запоминанию таблицы умножения
Дети на начальном этапе обучения обычно с трудом изучают и запоминают таблицу умножения. Ниже приведены несколько советов и приемов для детей, чтобы выучить и запомнить таблицу умножения.
- Добавление числа
Чтобы написать и изучить любую таблицу умножения, начните с натурального числа и продолжайте добавлять аналогичное число в каждом выводе. Например, если вы хотите выучить и написать таблицу умножения на 6, продолжайте прибавлять 6 в каждом счете. например
- 6 x 1 = 6
- 6 x 2 = 6 + 6 = 12
- 6 x 3 = 12 + 6 = 18 = 30
- 6 x 6 = 30 + 6 = 36
- 6 x 7 = 36 + 6 = 42
- 6 x 8 = 42 + 6 = 48
- Повторяя таблицу в порядке 51 .
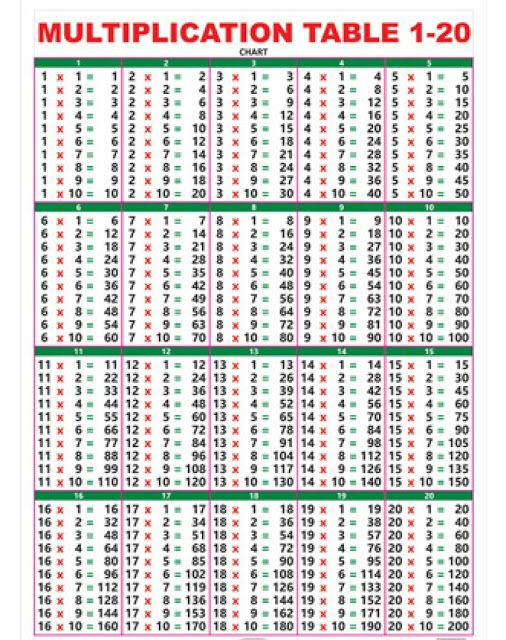
Чтобы выучить и запомнить любую таблицу, продолжайте повторять таблицу по порядку, например, начните учить как
- 4 раза 1 равно 4
- 4 раза по 2 равно 8
- 4 раза по 3 равно 12
- 4 раза по 4 равно 16
- 4 раза по 5 равно 20
И так далее. Продолжайте изучать таблицу снова и снова, пока не освоите ее.
- Продолжайте повторять таблицу в обратном порядке
Чтобы выучить таблицу умножения на кончике пальца, продолжайте изучать и повторять таблицы от начала до конца и наоборот. Посоревнуйтесь в подсчете таблиц, чтобы выучить таблицу умножения. Например,
- 8 раз 12 равно 96
- 8 раз 11 равно 88
- 8 раз 10 равно 80
- 8 раз 9 равно 72
- 8 раз 8 равно 64
- И так далее
- Изучение и запись таблицы умножения
Дети могут ежедневно писать таблицу умножения и повторять ее ежедневно, чтобы быстро запоминать таблицу умножения. Трюк с обучением и письмом используется, когда дети испытывают трудности с запоминанием таблицы умножения.
Трюк с обучением и письмом используется, когда дети испытывают трудности с запоминанием таблицы умножения.
- Использование умножения в повседневной жизни
Чтобы лучше изучить и понять таблицу умножения, попробуйте применить умножение в повседневной жизни. Например, покупать различные предметы, такие как чипсы, ириски и другие подобные термины. Затем умножьте цену одного предмета на количество предметов, увеличивая каждый предмет по одному.
- Определите шаблон
Каждая таблица умножения имеет шаблон. Попробуйте определить и изучить закономерность каждой таблицы умножения. Это будет очень полезно для быстрого запоминания таблицы умножения.
Какие таблицы следует выучить в первую очередь?
Сначала вы должны выучить 1, 2, 5, и 10 таблицу умножения. Эти таблицы просты по сравнению с остальными.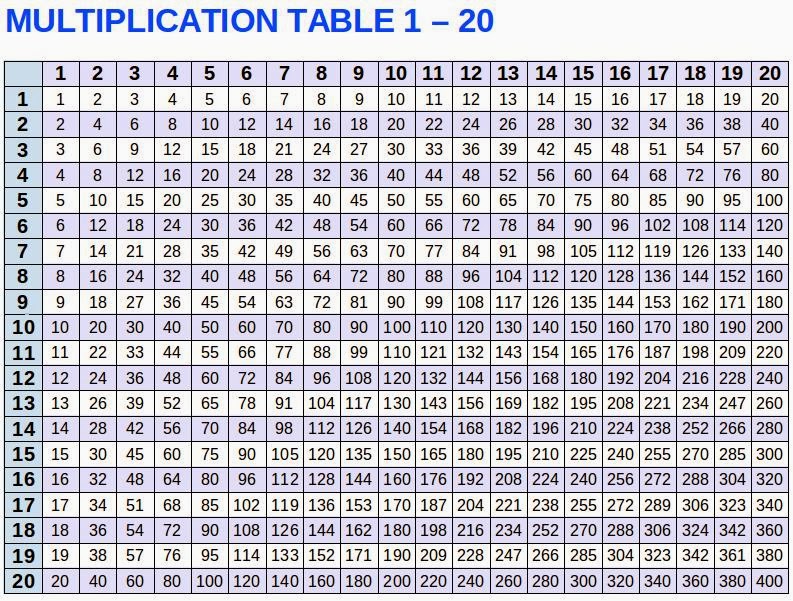 После заучивания этих таблиц следует запомнить 3, 4, 6, 7, 8, и 9 таблицу умножения.
После заучивания этих таблиц следует запомнить 3, 4, 6, 7, 8, и 9 таблицу умножения.
Самые любимые таблицы детей: 10 и 11 таблицы умножения, потому что запоминать их обе весело.
Как быстро выучить таблицу умножения?
1 Таблица умножения 2 Таблица умножения 3 Таблица умножения 4 Таблица умножения 5 Таблица умножения 6 Таблица умножения 7 Таблица умножения 8 Таблица умножения 9 Таблица умножения 10 Таблица умножения 11 Таблица умножения 12 Таблица умножения 13 Таблица умножения 14 Таблица умножения 15 Таблица умножения
Здесь несколько советов для быстрого запоминания таблиц.
5em;text-align:center;font:48px/1.5 sans-serif;color:white;text-shadow:0 0 0.5em black}</style><a cke-saved-href=https://www.youtube.com/embed/v1Ih4-mDPUk?autoplay=1 data-cke-saved-href=https://www.youtube.com/embed/v1Ih4-mDPUk?autoplay=1 href=https://www.youtube.com/embed/v1Ih4-mDPUk?autoplay=1><img cke-saved-src=https://img.youtube.com/vi/v1Ih4-mDPUk/hqdefault.jpg data-cke-saved-src=https://img.youtube.com/vi/v1Ih4-mDPUk/hqdefault.jpg src=https://img.youtube.com/vi/v1Ih4-mDPUk/hqdefault.jpg alt=’How to quickly learn times tables?’><span>▶</span></a>» title=»How to quickly learn times tables?»>
- Последовательно используйте диаграмму таблицы умножения.
- Начинайте учиться с самых простых.
- Прежде чем заучивать таблицу умножения, изучите сложение и вычитание.
- Ежедневно тренируйтесь в умножении фактов (таблиц).
- Потренируйтесь запоминать числа, например, в какой таблице находится 78 или в какой таблице находится 45.

Часто задаваемые вопросы
Как вы учите умножению учащихся, испытывающих затруднения?
Учащиеся могут выучить и запомнить умножение с помощью таблицы умножения, карточек и других математических головоломок.
Почему мы используем таблицу умножения?
Таблица умножения используется для нахождения произведения любых двух чисел и множителей любых чисел. Например, произведение 2 и 3, 143 в какой таблице, 117 в какой таблице, 182 в какой таблице, 156 в какой таблице и т.д.
Как посмотреть множители в таблице умножения?
Используйте диаграмму таблицы умножения для просмотра множителей чисел. Если вы хотите просмотреть множители числа в таблице умножения, прежде всего, найдите число в таблице таблицы умножения, а затем просмотрите соответствующий столбец и строку числа, которые будут множителями этого числа.
Например, в какой таблице встречается 169?
Следовательно, в таблице умножения 13
Как посмотреть произведение в таблице умножения?
Используйте диаграмму таблицы умножения для просмотра произведения двух чисел.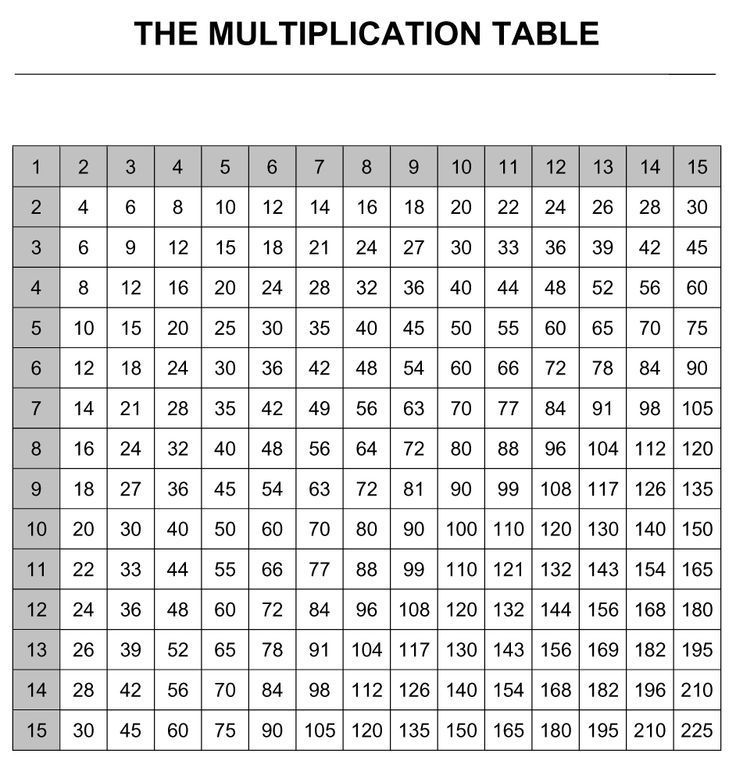 Если вы хотите просмотреть два числа в таблице умножения, сначала найдите первое число в первой строке таблицы таблицы умножения и второе число в первом столбце, а затем просмотрите пересекающееся число, которое будет произведением двух. числа.
Если вы хотите просмотреть два числа в таблице умножения, сначала найдите первое число в первой строке таблицы таблицы умножения и второе число в первом столбце, а затем просмотрите пересекающееся число, которое будет произведением двух. числа.
Например, чему равно произведение 12 и 14?
Следовательно, произведение 12 и 14 равно 168
Чем может быть полезно изучение таблиц 2–30?
Изучение таблиц умножения от 2 до 30 очень полезно для решения и отработки различных фактов умножения. Обычно это полезно при вычислении математических задач при выполнении умножения, деления, разложения на простые множители и математических выражений.
Вы можете легко выучить таблицу умножения со 2 по 30, используя приведенную выше таблицу таблицы умножения. Таблицы со 2 по 20 присутствуют в содержании. Вот таблицы с 21 по 30
Таблицы умножения 11-20
- Главная
- Таблицы
- Умножение
- 11 — 20
В математике таблица умножения — это математическая таблица, используемая для определения операции умножения в алгебраической системе.

 Таблица умножения в традиционном русском варианте (10х10).
Таблица умножения в традиционном русском варианте (10х10).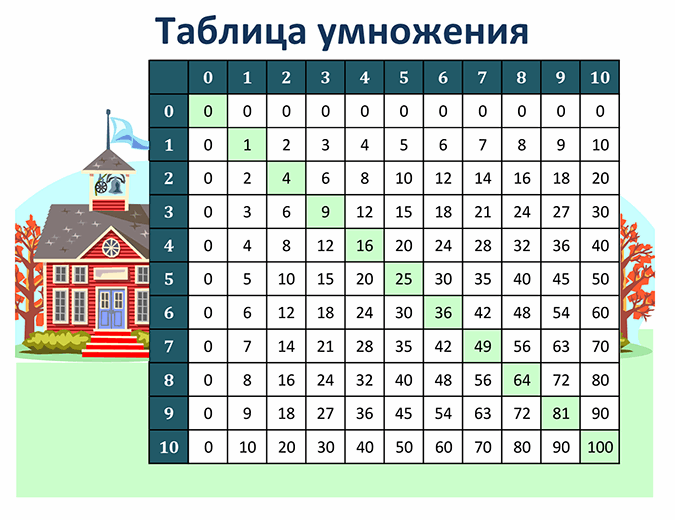 Таблица умножения в традиционном англо-саксонском варианте (12х12).
Таблица умножения в традиционном англо-саксонском варианте (12х12).  Таблица умножения Пифагора (20х20).
Таблица умножения Пифагора (20х20). 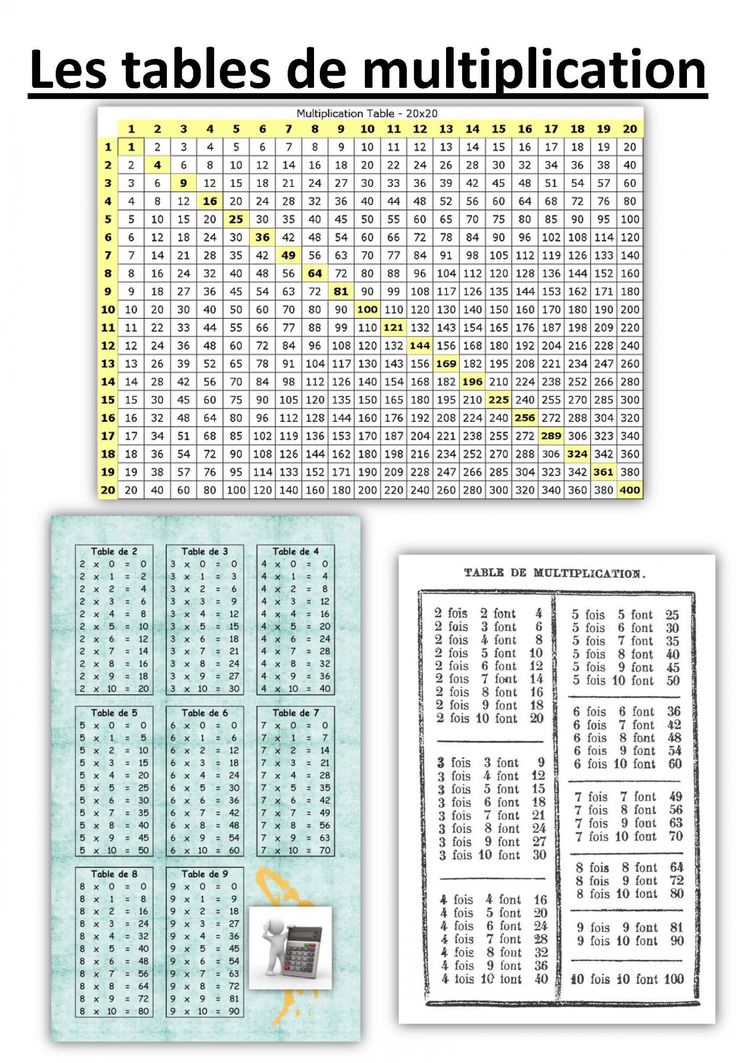 ru:
ru: Чтобы ребёнок мог легко и быстро всё выучить и усвоить. Вы бы занялись улучшением функционала своих приложений.
Чтобы ребёнок мог легко и быстро всё выучить и усвоить. Вы бы занялись улучшением функционала своих приложений.
 Одно занятие должно продолжаться примерно 30 минут. Превышение этого порога может снизить эффективность занятий. Старайтесь создать такую обстановку, чтобы вас ничего не отвлекало.
Одно занятие должно продолжаться примерно 30 минут. Превышение этого порога может снизить эффективность занятий. Старайтесь создать такую обстановку, чтобы вас ничего не отвлекало. Расскажете, что это свойство называется свойством коммутативности, и что, зная о нем, выучить таблицу значительно проще. Объясните, что, по сути, нужно выучить всего половину таблицы умножения, т.к. «3 х 6» будет то же самое, что «6 х 3» и т.п.
Расскажете, что это свойство называется свойством коммутативности, и что, зная о нем, выучить таблицу значительно проще. Объясните, что, по сути, нужно выучить всего половину таблицы умножения, т.к. «3 х 6» будет то же самое, что «6 х 3» и т.п.
 Каждый раз засекайте минуту, и смотрите, как продвигается ваш подопечный. Кстати, при переписывании таблицы на карточки у ребенка будет тренироваться двигательная память, а материал будет усваиваться вдвойне лучше.
Каждый раз засекайте минуту, и смотрите, как продвигается ваш подопечный. Кстати, при переписывании таблицы на карточки у ребенка будет тренироваться двигательная память, а материал будет усваиваться вдвойне лучше.
 Таким образом вы сможете узнать о чем-то, о чем, вполне вероятно, он по каким-то причинам не хочет вам рассказывать. Собственно, это касается не только таблицы умножения или математики в целом, но и любого предмета и успеваемости вообще.
Таким образом вы сможете узнать о чем-то, о чем, вполне вероятно, он по каким-то причинам не хочет вам рассказывать. Собственно, это касается не только таблицы умножения или математики в целом, но и любого предмета и успеваемости вообще. Перерывы на отдых и расслабление должны стать неотъемлемой составляющей вашей практики обучения ребенка. Любые занятия, от элементарных до самых сложных, нужно сопровождать паузами, чтобы ребенок имел возможность восстановить силы. Взрослые люди не могут работать часами без передышки, что уж говорить о детях. Поэтому, как только увидели, что ваше чадо подает признаки усталости, прекратите занятия и возьмите время на отдых. Намного продуктивнее будет позаниматься через несколько часов или вообще на следующий день.
Перерывы на отдых и расслабление должны стать неотъемлемой составляющей вашей практики обучения ребенка. Любые занятия, от элементарных до самых сложных, нужно сопровождать паузами, чтобы ребенок имел возможность восстановить силы. Взрослые люди не могут работать часами без передышки, что уж говорить о детях. Поэтому, как только увидели, что ваше чадо подает признаки усталости, прекратите занятия и возьмите время на отдых. Намного продуктивнее будет позаниматься через несколько часов или вообще на следующий день.
 0016 72
0016 72