Таблица значений функции: Таблица значений функции

Таблица значений функций для школьников и студентов

Готовые табличные значения функций для построения графика (с шагом 0,5 и 1) на системе координат. Все значения координат точек, принадлежащих функциям, округлены до 0,1.

y=x y=x+1 y=x+4 y=x-1 y=x-4

y=|x|; y=x2 y=-|x|; y=-x2 y=x2 y=x2+1 y=x3 y=x3+1

y=x y=-2x2 y=-13×2 y=0.5x2 y=32×2

Линейные функции

Линейная функция — функция вида y=kx+b (для функций одной переменной).

Графиком линейной функции является прямая.

y=x

x	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
y	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10

y=x+1

x	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9
y	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10

y=x+4

x	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9
y	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10	11	12	13

y=x-1

x	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9
y	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8

y=x-4

x	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8
y	-12	-11	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4

Нелинейные функции

y=|x|; y=x2

x	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
y	10	9	8	7	6	5	4	3	2	1	0	1	2	3	4	5	6	7	8	9	10

y=-|x|; y=-x2

x	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9
y	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	-1	-2	-3	-4	-5	-6	-7	-8	-9

y=x

²

x	-3	-2. 5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2	2.5	3
y	9	6.3	4	2.3	1	0.3	0	0.3	1	2.3	4	6.3	9

y=x

²+1

x	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2	2.5	3
y	10	7.3	5	3.3	2	1.3	1	1.3	2	3.3	5	7.3	10

y=x

³

x	-3	-2.5	-2	-1.5	-1	-0. 5	0	0.5	1	1.5	2	2.5	3
y	-27	-15.6	-8	-3.4	-1	-0.1	0	0.1	1	3.4	8	15.6	27

y=x

³+1

x	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2	2.5	3
y	10	7.3	5	3.3	2	1.3	1	1.3	2	3.3	5	7.3	10

y=x

x	0	1	2	3	4	5	6	7	8	9
y	0	1	1. 4	1.7	2	2.2	2.5	2.7	2.8	3

y=-2x

²

x	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2	2.5
y	-12.5	-8	-4.5	-2	-0.5	-0	-0.5	-2	-4.5	-8	-12.5

y=-13×2

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
y	-8.3	-5.3	-3	-1.3	-0.3	-0	-0.3	-1.3	-3	-5.3	-8.3

y=0.

5x²

x	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
y	18	12.5	8	4.5	2	0.5	0	0.5	2	4.5	8	12.5	18

y=32×2

x	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2	2.5
y	-2.1	-1.3	-0.8	-0.3	-0.1	-0	-0.1	-0.3	-0.8	-1.3	-2.1

• Коротко о важном
• Таблицы
• Формулы
• Формулы по геометрии
• Теория по математике

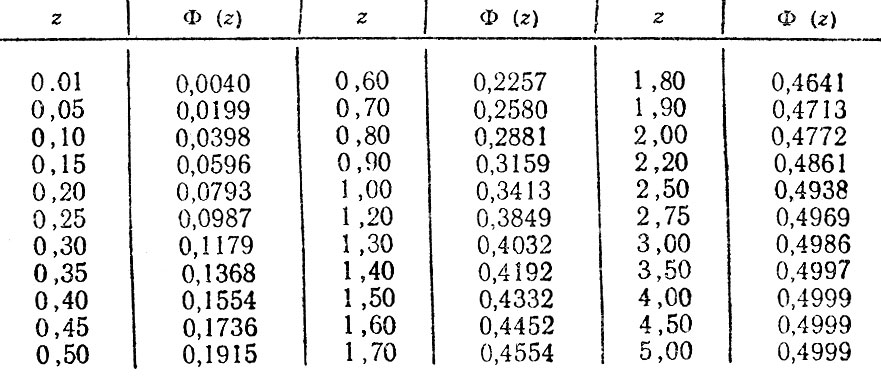
Таблица значений функции Лапласа

Оценить работу

Таблица значений функции Лапласа используется в теории вероятности довольно часто.

В данном разделе описываюся случаи, в которых необходимо использовать значения таблицы. Разбираются примеры и прикладывается сама таблица значений. 

 

Таблица значений:

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0	0	0,5	0,19146	1	0,34134	1,5	0,43319	2	0,47725	3	0,49865
0,01	0,00399	0,51	0,19497	1,01	0,34375	1,51	0,43448	2,02	0,47831	3,05	0,49886
0,02	0,00798	0,52	0,19847	1,02	0,34614	1,52	0,43574	2,04	0,47932	3,1	0,49903
0,03	0,01197	0,53	0,20194	1,03	0,34849	1,53	0,43699	2,06	0,4803	3,15	0,49918
0,04	0,01595	0,54	0,2054	1,04	0,35083	1,54	0,43822	2,08	0,48124	3,2	0,49931
0,05	0,01994	0,55	0,20884	1,05	0,35314	1,55	0,43943	2,1	0,48214	3,25	0,49942
0,06	0,02392	0,56	0,21226	1,06	0,35543	1,56	0,44062	2,12	0,483	3,3	0,49952
0,07	0,0279	0,57	0,21566	1,07	0,35769	1,57	0,44179	2,14	0,48382	3,35	0,4996
0,08	0,03188	0,58	0,21904	1,08	0,35993	1,58	0,44295	2,16	0,48461	3,4	0,49966
0,09	0,03586	0,59	0,2224	1,09	0,36214	1,59	0,44408	2,18	0,48537	3,45	0,49972
0,1	0,03983	0,6	0,22575	1,1	0,36433	1,6	0,4452	2,2	0,4861	3,5	0,49977
0,11	0,0438	0,61	0,22907	1,11	0,3665	1,61	0,4463	2,22	0,48679	3,55	0,49981
0,12	0,04776	0,62	0,23237	1,12	0,36864	1,62	0,44738	2,24	0,48745	3,6	0,49984
0,13	0,05172	0,63	0,23565	1,13	0,37076	1,63	0,44845	2,26	0,48809	3,65	0,49987
0,14	0,05567	0,64	0,23891	1,14	0,37286	1,64	0,4495	2,28	0,4887	3,7	0,49989
0,15	0,05962	0,65	0,24215	1,15	0,37493	1,65	0,45053	2,3	0,48928	3,75	0,49991
0,16	0,06356	0,66	0,24537	1,16	0,37698	1,66	0,45154	2,32	0,48983	3,8	0,49993
0,17	0,06749	0,67	0,24857	1,17	0,379	1,67	0,45254	2,34	0,49036	3,85	0,49994
0,18	0,07142	0,68	0,25175	1,18	0,381	1,68	0,45352	2,36	0,49086	3,9	0,49995
0,19	0,07535	0,69	0,2549	1,19	0,38298	1,69	0,45449	2,38	0,49134	3,95	0,49996
0,2	0,07926	0,7	0,25804	1,2	0,38493	1,7	0,45543	2,4	0,4918	4	0,49997
0,21	0,08317	0,71	0,26115	1,21	0,38686	1,71	0,45637	2,42	0,49224	4,05	0,49997
0,22	0,08706	0,72	0,26424	1,22	0,38877	1,72	0,45728	2,44	0,49266	4,1	0,49998
0,23	0,09095	0,73	0,2673	1,23	0,39065	1,73	0,45818	2,46	0,49305	4,15	0,49998
0,24	0,09483	0,74	0,27035	1,24	0,39251	1,74	0,45907	2,48	0,49343	4,2	0,49999
0,25	0,09871	0,75	0,27337	1,25	0,39435	1,75	0,45994	2,5	0,49379	4,25	0,49999
0,26	0,10257	0,76	0,27637	1,26	0,39617	1,76	0,4608	2,52	0,49413	4,3	0,49999
0,27	0,10642	0,77	0,27935	1,27	0,39796	1,77	0,46164	2,54	0,49446	4,35	0,49999
0,28	0,11026	0,78	0,2823	1,28	0,39973	1,78	0,46246	2,56	0,49477	4,4	0,49999
0,29	0,11409	0,79	0,28524	1,29	0,40147	1,79	0,46327	2,58	0,49506	4,45	0,5
0,3	0,11791	0,8	0,28814	1,3	0,4032	1,8	0,46407	2,6	0,49534	4,5	0,5
0,31	0,12172	0,81	0,29103	1,31	0,4049	1,81	0,46485	2,62	0,4956	4,55	0,5
0,32	0,12552	0,82	0,29389	1,32	0,40658	1,82	0,46562	2,64	0,49585	4,6	0,5
0,33	0,1293	0,83	0,29673	1,33	0,40824	1,83	0,46638	2,66	0,49609	4,65	0,5
0,34	0,13307	0,84	0,29955	1,34	0,40988	1,84	0,46712	2,68	0,49632	4,7	0,5
0,35	0,13683	0,85	0,30234	1,35	0,41149	1,85	0,46784	2,7	0,49653	4,75	0,5
0,36	0,14058	0,86	0,30511	1,36	0,41309	1,86	0,46856	2,72	0,49674	4,8	0,5
0,37	0,14431	0,87	0,30785	1,37	0,41466	1,87	0,46926	2,74	0,49693	4,85	0,5
0,38	0,14803	0,88	0,31057	1,38	0,41621	1,88	0,46995	2,76	0,49711	4,9	0,5
0,39	0,15173	0,89	0,31327	1,39	0,41774	1,89	0,47062	2,78	0,49728	4,95	0,5
0,4	0,15542	0,9	0,31594	1,4	0,41924	1,9	0,47128	2,8	0,49744	5	0,5
0,41	0,1591	0,91	0,31859	1,41	0,42073	1,91	0,47193	2,82	0,4976
0,42	0,16276	0,92	0,32121	1,42	0,4222	1,92	0,47257	2,84	0,49774
0,43	0,1664	0,93	0,32381	1,43	0,42364	1,93	0,4732	2,86	0,49788
0,44	0,17003	0,94	0,32639	1,44	0,42507	1,94	0,47381	2,88	0,49801
0,45	0,17364	0,95	0,32894	1,45	0,42647	1,95	0,47441	2,9	0,49813
0,46	0,17724	0,96	0,33147	1,46	0,42785	1,96	0,475	2,92	0,49825
0,47	0,18082	0,97	0,33398	1,47	0,42922	1,97	0,47558	2,94	0,49836
0,48	0,18439	0,98	0,33646	1,48	0,43056	1,98	0,47615	2,96	0,49846
0,49	0,18793	0,99	0,33891	1,49	0,43189	1,99	0,4767	2,98	0,49856

 

Рассмотрим примеры применения данной таблицы на конкретных примерах:

 

 

Таблицы функций (3 общих вопроса и примера) – JDM Educational

Иногда мы получаем таблицу значений из эксперимента или набора данных, а не изображение информации. Часто мы можем изучить информацию из таблицы функций, чтобы узнать больше о том, как моделировать данные.

Итак, что такое таблица функций? В таблице функций есть строки и столбцы, которые показывают входные и выходные значения для функции. Мы можем использовать таблицу функций, чтобы найти упорядоченные пары и нанести эти точки на график функции. Мы также можем вычислить разности, чтобы выяснить, какой тип функции указан в таблице.

Конечно, существуют всевозможные функции, которые мы можем представить с помощью таблицы функций, включая постоянные, линейные, квадратичные и экспоненциальные функции.

В этой статье мы поговорим о таблицах функций и рассмотрим несколько примеров. Мы также рассмотрим, как выяснить, какой тип функции у нас есть, на основе графика или просмотра данных в таблице функций.

Начнем.

Что такое таблица функций?

Таблица функций показывает нам значения (упорядоченные пары) для данной функции.

*Примечание: у нас также может быть таблица функций с упорядоченными тройками, упорядоченными четверками и т. д. для функции от 2, 3 и более переменных!

В таблице функций есть строки и столбцы, которые содержат входные и выходные значения функции рядом друг с другом.

Что не может быть многочленом?

Включите JavaScript

Что не может быть многочленом?

Вы можете увидеть пример таблицы функций ниже.

х	y
0	2
1	5
3	11
7	23
10	32

We может читать таблицу функций, чтобы найти упорядоченные пары. Например, мы получаем следующий набор упорядоченных пар из приведенной выше таблицы функций:

• (0, 2)
• (1, 5)
• (3, 11)
• (7, 23)
• (10, 32)

Теперь мы можем нанести эти точки на график, чтобы получить представление о том, как выглядит функция: 5 упорядоченных пар (точек) из таблицы выше. График выглядит линейным.

Если у нас достаточно данных (или мы знаем, какой у нас тип функции), мы можем нарисовать график функции.

Это набросок линейной функции из графика рассеяния выше.

Мы также можем вычислить разность (как для x, так и для y), чтобы помочь нам узнать, какой тип функции дан в таблице (подробнее об этом позже).

Что такое правило таблицы функций?

Правило таблицы функций просто говорит вам, как две переменные (входная и выходная) из таблицы связаны друг с другом.

. 2 4 3 6 4 8

Мы видим, что в каждой строке значение y в два раза превышает значение x. Другими словами, мы удваиваем x (вход), чтобы найти y (выход).

Как найти функцию в таблице?

Есть два метода, которые могут помочь нам найти функцию в таблице:

• График (построить все упорядоченные пары из таблицы функций, нарисовать график и сопоставить форму с типом функции, который мы знакомы).
• Разности (найдите первые разности x в таблице, а затем найдите первые разности y и вторые разности y и возьмите отношения, чтобы увидеть, как изменяются значения функции и наклоны).

Давайте рассмотрим несколько примеров того, как найти функцию в таблице (используя оба метода).

Пример 1. Таблица, не являющаяся функцией

Рассмотрим следующую таблицу:

x	y
0	-1
1	2
1	5
2	8
3	9

We can see right away that эта таблица не из функции, так как вход x = 1 имеет два возможных выхода: y = 2 и y = 5.

Эта неоднозначность выходов означает, что таблица дает нам отношение, которое не является функцией. Мы можем проверить это с помощью графика упорядоченных пар в таблице.

Вертикальная линия x = 1 пересекает этот график дважды, что означает, что он не прошел тест на вертикальную линию (это отношение, которое не является функцией).

Вертикальная линия x = 1 пересекала бы график более одного раза, поэтому график отношения не проходит тест вертикальной линии (это означает, что он не является функцией).

(Подробнее о проверке вертикальной линии и о том, что не может быть функцией, можно узнать здесь).

Пример 2: Таблица функций констант

См. таблицу ниже:

x	y
1	6
3	6
4	6
6	6
9	6

Независимо от значения x (вход), мы получаем то же значение y = 6, что и наш вывод. Это говорит о том, что у нас есть постоянная функция из таблицы.

График представляет собой горизонтальную линию при y = 6, изображенную ниже.

Горизонтальная линия y = 6 является постоянной функцией (один и тот же результат y = 6 получается при любом входе x).

Обратите внимание, что любые различия, которые мы принимаем для y, дадут нам ноль, что также предполагает постоянную функцию.

Example 3: Linear Function Table

Consider the table below:

x	y
1	5
4	11
6	15
7	17
9	21

Похоже, у нас есть функция, но она не постоянная (поскольку в таблице разные значения y).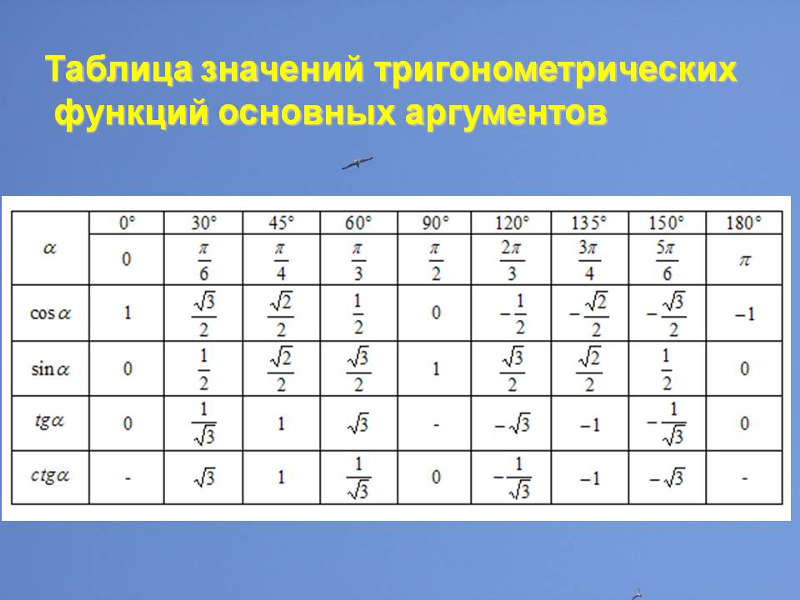 Итак, мы добавляем столбцы, чтобы посмотреть на различия для x и y в таблице.

Чтобы получить первые разности для x, мы просто вычитаем «следующее» значение x из «текущего» значения x. Мы делаем то же самое для значений y, чтобы получить первые различия для y.

Вы можете увидеть обновленную таблицу ниже, которая включает первые разности для x и первые разности для y, а также частные (первые разности y, разделенные на первые разности для x):

x	y	First Diff x	First Diff y	Quotient (Diff y / Diff x)
1	5
4	11	3	6	2
6	15	2	4	2
7	17	1	2	2
	21	2	4	2

ПРИМЕЧАНИЕ, что приведенные в таблице приведены все то же значение. Это говорит о том, что у нас есть линейная функция в таблице.

Мы можем убедиться в этом, нарисовав упорядоченные пары в таблице – вы можете увидеть график ниже:

На этом графике показаны 5 упорядоченных пар (точек) из таблицы выше. График выглядит линейным.

Судя по графику, мы получаем линейную функцию от y = 2x + 3. Мы можем проверить это уравнение, выбрав две точки (упорядоченные пары) из таблицы и выполнив вычисления:

Глядя на точки (4, 11) и (6, 15), получаем:

• Уклон = Подъем / Пробег
• м = (y ₂ – y ₁ ) / (x ₂ -x ₁ )
• M = (15-11) / (6-4)
• M = 4 /2
• M = 2

M = 2

Форма уравнения для линии: y = mx + b. Мы знаем, что m = 2, и мы можем использовать точку (4, 11), чтобы найти b:

• y = mx + b
• y = 2x + b   [мы нашли наклон m = 2 выше]
• 11 = 2(4) + b   [мы использовали точку (4, 11) ), поэтому x = 4 и y = 11]
• 11 = 8 + b
• 3 = b

Таким образом, точка пересечения этой прямой с осью y равна b = 3.

Это дает нам линейное уравнение y = 2x + 3. Все упорядоченные пары в таблице соответствуют этому уравнению.

Пример 4: Таблица квадратичных функций

Consider the table below:

x	y
1	6
3	14
4	21
6	41
9	86

Вроде функция у нас есть, но она не постоянная (поскольку в таблице разные значения y). Итак, мы добавляем столбцы, чтобы посмотреть на различия для x и y в таблице.

Мы используем ту же процедуру, что и в последнем примере, чтобы найти первые разности для x и y.

Вы можете увидеть обновленную таблицу ниже, которая включает первые разности для x и первые разности для y, а также частные (первые разности y, разделенные на первые разности для x): Разность
x Первая
Разность
у Частное
(Разность у /
Разность х) 1 6 3 14 2 8 4 4 21 1 7 7 6 41 2 20 10 86 3 45 15

. Это говорит о том, что у нас нет линейной функции в таблице.

Мы можем попытаться увидеть, какой у нас тип функции, нарисовав упорядоченные пары в таблице — вы можете увидеть график ниже:

На этом графике показаны 5 упорядоченных пар (точек) из таблицы выше. График выглядит квадратичным.

Оказывается, уравнение имеет вид y = x ² + 5. Все значения в таблице соответствуют этому уравнению.

*Примечание: чтобы найти это уравнение, все, что нам нужно сделать, это выбрать 3 точки (упорядоченные пары) из таблицы. Затем подставьте каждый набор точек в уравнение

• y = ax ² + bx + c (квадратичное число в стандартной форме)

Это даст нам набор из 3 уравнений с 3 неизвестными (a, b и c), которые мы можем решить используя алгебру.

Example 5: Exponential Function Table

Consider the table below:

x	y
0	3
1	6
3	24
4	48
6	192

. Итак, мы добавляем столбцы, чтобы посмотреть на различия для x и y в таблице.

Мы используем ту же процедуру, что и в последнем примере, чтобы найти первые разности для x и y.

Вы можете увидеть обновленную таблицу ниже, которая включает первые разности для x и первые разности для y, а также частные (первые разности y, разделенные на первые разности для x):

x	y	1st Diff x	1st Diff y	Quotient (Diff y / Diff x)
0	3
1	6	1	3	3
3	24	2	18	9
4	48	1	24	24
6	192	2	144	72

ПРИМЕЧАНИЕ, что цитаты в таблице выше не имеют той же значения. Это говорит о том, что у нас нет линейной функции в таблице.

Итак, мы изобразим точки из таблицы, чтобы получить представление о том, как выглядит функция – вы можете увидеть график ниже:

На этом графике показаны 5 упорядоченных пар (точек) из таблицы выше. График выглядит экспоненциальным.

Оказывается, что функция может быть экспоненциальной, которая имеет вид

• y = ab ^x

с ненулевым a и b не равным 0 или 1.

Мы можем использовать 2 точки из таблицу, чтобы получить 2 уравнения, а затем решить систему, чтобы найти a и b.

Первая точка, (3, 24), дает нам уравнение:

• Y = AB ^x
• 24 = AB ³

Вторая точка (4, 48) , дает нам уравнение:

• y = ab ^x
• 48 = ab ⁴

Разделим два уравнения, чтобы сократить a и найти b.

В левой части получаем 48 / 24 = 2.

В правой части получаем ab ⁴ / ab ³ = b.

Итак, b = 2.

Тогда наше уравнение выглядит так:

• y = a*2 ^x

Теперь нам просто нужно найти значение a. Мы можем использовать любую из точек выше, но давайте выберем (3, 24), которая имеет меньшие числа.

Подключение x = 3, y = 24 дает нам:

• y = a*2 ^x
• 24 = A*2 ³
• 24 = A*8
• 24 = A*8
• 24 = A*8
• 24 = A*8
9007
• 24 = A 3 = a

Теперь, когда мы знаем a = 3 и b = 2, мы можем записать экспоненциальную функцию: форма y = ab ^x + c, то первые различия в таблице дали бы нам другую экспоненциальную функцию, и мы могли бы использовать три точки и вместо этого решить систему трех уравнений (для решения для a, b и c) . Вы можете узнать больше здесь.

Заключение

Теперь вы знаете, что такое таблица функций и как определить, какая функция у вас есть в данной таблице.

Здесь вы можете найти ответы на распространенные вопросы о функциях.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на наш канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

---

Просмотр таблицы для функции

Просмотр таблицы для функции

---

Использование автоматического стола Функция

Функция должна быть введена в , чтобы получить ее график и таблицу. Для просмотра графика и таблицы значений функции , введите уравнение в . Чтобы просмотреть график функции, нажмите GRAPH . Результаты показано ниже на графике в стандарте окно . Для получения более подробной информации о графических функциях щелкните Graphing. функция.

 

Диапазон значений должен быть установлен для просмотра таблицы значений для , так же, как просмотр Для графика необходимо задать прямоугольник . Нажмите 2nd WINDOW [TBLSET] , чтобы установите начальное значение и приращение для X. На графике ниже TBLStart установлен на 0, а установлен на 1. Оба Авто следует выделить. Нажмите 2nd GRAPH [TABLE] для просмотра таблицы. Примечание что значения X начинаются с 0 и увеличиваются на 1. Клавиши со стрелками вниз и вверх позволяют прокручивать таблицу.

Чтобы изменить приращение для X на одну десятую, нажмите 2nd ОКНО [ТАБЛ.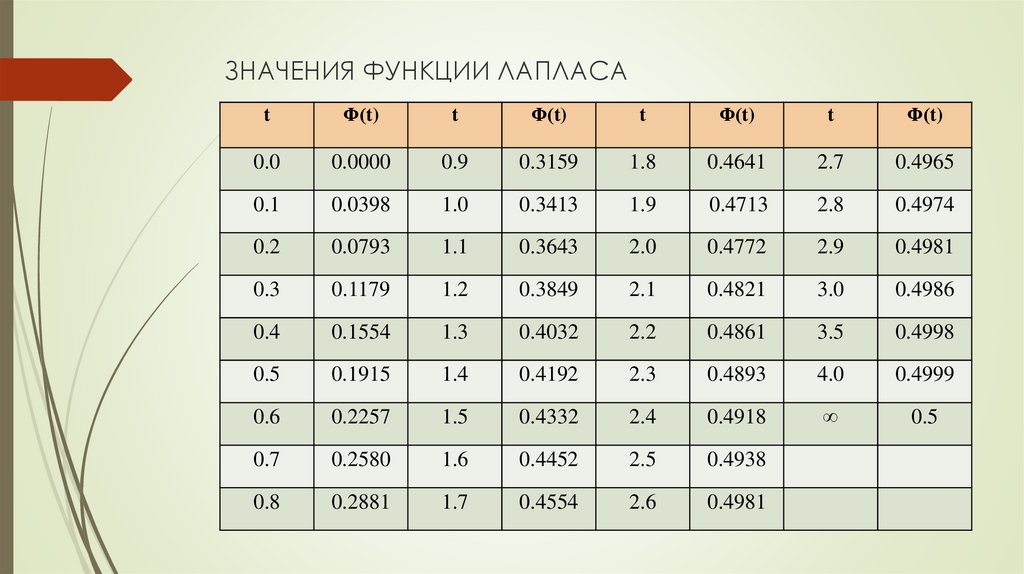 ] . Переместите курсор с помощью клавиши со стрелкой вниз к 1, который появляется рядом с. Введите .1 вместо 1. Нажмите 2nd ГРАФИК [ТАБЛИЦА] . Результаты показаны ниже. Х значения начинаются с 0, а приращение теперь составляет одну десятую. Оба начальных значения X и приращение может быть изменено для создания любой таблицы, необходимой для функции. Значения Y для каждого X вычисляются калькулятором и отображаются в стол.

 

Использование функции таблицы запросов

Иногда требуется только одно или несколько конкретных табличных значений. для функции. Например, найдите значения Y, связанные с X = 3 и X = 10 для функции. Поскольку функция уже введена на экране Y, нажмите 2nd ОКНО [НАБОР ТБЛ] . Дважды нажмите СТРЕЛКУ ВНИЗ , пока не появится цифра 9.

No related posts.