Тангенс угла онлайн: Тангенс угла tg(α) | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Тесты по теме «Тангенс» онлайн

1. Онлайн тесты
2. Тангенс

• Синус, косинус, тангенс

  16.12.2020 8663

  Тест для проверки знаний по темам «Синус, косинус, тангенс» и «Соотношение сторон и углов в прямоугольном треугольнике»

• Основное тригонометрическое тождество. Геометрия 7-9 классы.

  09.03.2022 359 0

  Онлайн задания на проверку усвоения основного тригонометрического тождества.

• Синус, косинус и тангенс острого угла прямоугольного треугольника.

  Самостоятельная работа с аудиоответом.

  28.02.2022 113 0

  Онлайн задания по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника.Значения синуса, косинуса и тангенса для углов 30о, 45о и 60о.»

• Синус, косинус и тангенс острого угла прямоугольного треугольника (с аудиоответом).

  03.03.2022 162 0

  Онлай тест, проверяющий усвоение понятий синус, косинус и тангенс острого угла прямоугольного треугольника.

• Тригонометрические преобразования

  06.12.2017 35 0

  Тест поможет проверить умения преобразовывать тригонометрические выражения. Все задания из реальных вариантов ЕГЭ.

• Простейшее тригонометрическое уравнение tg t = a

  03.02.2020 602 0

  Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Простейшее тригонометрическое уравнение tg t= a». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 10-15 минут.

• Соотношения между сторонами и углами в прямоугольном треугольнике

  24. 12.2020 870 0

  Тест предназначен для учащихся средней школы  для проверки уровня знаний по  теме «Соотношения между сторонами и углами в прямоугольном треугольнике».

• Преобразование тригонометрических выражений.

  22.01.2021

  635 0

  Данный тест предназначен для проверки усвоения знаний по теме: «Преобразование тригонометрических выражений».

• Тригонометрические соотношения в прямоугольном треугольнике.

  27.01.2022 26 0

  Тест предназначен для учащихся  8 и 9  классов средней школы  для проверки уровня знаний по  теме «Тригонометрические соотношения в прямоугольном треугольнике. «

• тест по теме:»Углы, прямоугольный треугольник»

  24.01.2020 59 0

  Тест состоит из 5 вопросов базового уровня по теме: «Прямоугольный треугольник», учебник Атанасян, геометрия 7-9

• Тригонометрические функции.

  05.12.2020 503 0

  Тест по теме: «Синус, косинус, тангенс и котангенс. Тригонометрические функции числового аргумента».

• Тригонометрические величины и их свойства

  27. 12.2020

  83 0

  Тест предназначен для проверки знания определения тригонометрических величин и их свойств

• Соотношения между сторонами и углами прямоугольного треугольника.

  20.01.2022 1298 0

  Тест предназначен для учащихся  8  класса средней школы  для проверки уровня знаний по  теме «Тригонометрические соотношения в прямоугольном треугольнике.»

• Викторина о тригонометрии

  21.02.2022 532 0

  Викторина о разделе математики, изучающем функции угла: синус, косинус и т.

  п. В рамках школьной программы.

• тригонометрические функции числового аргумента

  09.03.2022 5 0

  тест предназначен для учащихся 10 класса. темы: тригнометрические  уравнения и неравенства и тригонометрические функции числового аргумента.

• Тригонометрия в прямоугольном треугольнике

  05.06.2022 10 0

  Проверьте свои знания понятий синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике

• Равнобедренный и равносторонний треугольник

  07. 06.2022 4 0

  Тренажер по решению задач на вычисление элементов равнобедренного и равностороннего треугольника

• Таблица тригонометрических значений

  26.01.2023 13 0

  Основы тригонометрии. Синус, косинус, тангенс. Основное тригонометрическое тождество. Формулы приведения

• Соотношения между сторонами и углами прямоугольного треугольника

  07.02.2023 24 0

  Тест создан для проверки знаний по теме «Соотношения между сторонами и углами прямоугольного треугольника»

• Косинус, синус и тангенс

  27. 03.2023 41 0

  Тест на проверку ваших знаний и умений по теме «Знаки синуса, косинуса и тангенса»

Найти тангенс угла между прямыми онлайн калькулятор. Простейшие задачи с прямой на плоскости

Углом

между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Угол между прямой и плоскостью

Пусть прямая d — не перпендикулярна плоскости θ;
d ′− проекция прямой d на плоскость θ;
Наименьший из углов между прямыми d и d ′ мы назовем углом между прямой и плоскостью .
Обозначим его как φ=(d ,θ)
Если d ⊥θ , то (d ,θ)=π/2

Oi →j →k →− прямоугольная система координат.
Уравнение плоскости:

θ:Ax +By +Cz +D =0

Считаем, что прямая задана точкой и направляющим вектором: d [M 0,p →]
Вектор n →(A ,B ,C )⊥θ
Тогда остается выяснить угол между векторами n → и p →, обозначим его как γ=(n →,p →).

Если угол γ

Если угол γ>π/2 , то искомый угол φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Тогда, угол между прямой и плоскостью можно считать по формуле:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Вопрос29. Понятие квадратичной формы. Знакоопределенность квадратичных форм.

Квадратичной формой j (х 1 , х 2 , …, x n) n действительных переменных х 1 , х 2 , …, x n называется сумма вида , (1)

где a ij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a ij = a ji .

Квадратичная форма называется действительной, если a ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица Т. е. А Т = А . Следовательно, квадратичная форма (1) может быть записана в матричном виде j (х ) = х Т Ах , где х Т = (х 1 х 2 … x n ). (2)

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А . (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

положительно определенной (или строго положительной), если

j (х ) > 0 , для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы j (х ) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если

j (х ) х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Аналогично как и выше, матрица отрицательно определенной квад-ратичной формы также называется отрицательно определенной.

Следовательно, положительно (отрицательно) определенная квадра-тичная форма j (х ) достигает минимального (максимального) значения j (х* ) = 0 при х* = (0, 0, …, 0).

Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.

Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

то есть это миноры порядка 1, 2, …, n матрицы А , расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А .

Критерий положительной определенности (критерий Сильвестра)

х ) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть: М 1 > 0, M 2 > 0, …, M n > 0. Критерий отрицательной определенности Для того чтобы квадратичная форма j (х ) = х Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, т. е.: М 1 M 2 > 0, М 3 n

Определение. Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны, если k 1 = -1/ k 2 .

Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты А 1 = λА, В 1 = λВ. Если еще и С 1 = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку

Перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b представляется уравнением:

Расстояние от точки до прямой

Теорема. Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С =0 определяется как

.

Доказательство. Пусть точка М 1 (х 1 , у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М 1:

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Пример . Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k 1 = -3; k 2 = 2; tgφ = ; φ= p /4.

Пример . Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Решение . Находим: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример . Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение . Находим уравнение стороны АВ: ; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b . k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3 x + 2 y – 34 = 0.

Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых

1. Уравнение прямой, проходящей через данную точку A (x 1 , y 1) в данном направлении, определяемом угловым коэффициентом k ,

y — y 1 = k (x — x 1). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x 1 , y 1), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A (x 1 , y 1) и B (x 2 , y 2), записывается так:

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B . Если две прямые заданы уравнениями с угловым коэффициентом

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

то угол между ними определяется по формуле

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

угол между ними определяется по формуле

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k 1 = k 2 . (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Это условие может быть записано также в виде

k 1 k 2 = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A 1 A 2 + B 1 B 2 = 0. (12)

6. Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда

1. Напишите уравнения прямых, проходящих через точку M, одна из которых параллельна, а другая – перпендикулярна заданной прямой l.

а. Пусть даны две прямые Эти прямые как было указано в главе 1, образуют различные положительные и отрицательные углы, которые при этом могут быть как острыми, так и тупыми. Зная один из этих углов мы легко найдем какой-либо другой.

Между прочим, у всех этих углов численная величина тангенса одна и та же, различие может быть только в знаке

Уравнения прямых. Числа суть проекции направляющих векторов первой и второй прямой Угол между этими векторами равен одному из углов, образуемых прямыми линиями. Поэтому задача сводится к определению угла между векторами, Мы получим

Для простоты можно условиться под углом между двумя прямыми понимать острый положительный угол (как, например, на рис. 53).

Тогда тангенс этого угла будет всегда положительным. Таким образом, если в правой части формулы (1) получится знак минус, то мы его должны отбросить, т. е. сохранить только абсолютную величину.

Пример. Определить угол между прямыми

По формуле (1) имеем

с. Если будет указано, какая из сторон угла является его началом и какая концом, то, отсчитывая всегда направление угла против часовой стрелки, мы можем формулы (1) извлечь нечто большее. Как нетрудно убедиться из рис. 53 знак получающийся в правой части формулы (1), будет указывать, какой именно — острый или тупой — угол образует вторая прямая с первой.

(Действительно, из рис, 53 мы усматриваем, что угол между первым и вторым направляющими векторами или равен искомому углу между прямыми, или отличается от него на ±180°.)

d. Если прямые параллельны, то параллельны и их направляющие векторы, Применяя условие параллельности двух векторов получим!

Это есть условием необходимое и достаточное для параллельности двух прямых.

Пример. Прямые

параллельны, так как

e. Если прямые перпендикулярны то их направляющие векторы тоже перпендикулярны. Применяя условие перпендикулярности двух векторов мы получим условие перпендикулярности двух прямых а именно

Пример. Прямые

перпендикулярны ввиду того, что

В связи с условиями параллельности и перпендикулярности решим следующие две задачи.

f. Через точку провести прямую параллельно данной прямой

Решение проводится так. Так как искомая прямая параллельна данной, то за ее направляющий вектор можно взять тот же самый, что и у данной прямой, т. е. вектор с проекциями А и В. А тогда уравнение искомой прямой напишется в форме (§ 1)

Пример. Уравнение прямой, проходящей через точку (1; 3) параллельно прямой

будет следующее!

g. Через точку провести прямую перпендикулярно данной прямой

Здесь за направляющий вектор уже не годится брать вектор с проекциями А и , а надо веять вектор, ему перпендикулярный. Проекции этого вектора должны быть выбраны следовательно, согласно условию перпендикулярности обоих векторов, т. е. согласно условию

Выполнить же это условие можно бесчисленным множеством способов, так как здесь одно уравнение с двумя неизвестными Но проще всего взять иди же Тогда уравнение искомой прямой напишется в форме

Пример. Уравнение прямой, проходящей через точку (-7; 2) в перпендикулярной прямой

будет следующее (по второй формуле)!

h. В том случаем когда прямые заданы уравнениями вида

переписывая эти уравнения иначе, имеем

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите элементы уравнения в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.

×

Предупреждение

Очистить все ячейки?

Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т. д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L 1 и L

Таким образом, из формулы (1.4) можно найти угол между прямыми L 1 и L 2 . Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ 1 . Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L 1 и L 2: φ 1 =180-φ .

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Упростим и решим:

1.2. Условие параллельности прямых

Пусть φ =0. Тогда cosφ =1. При этом выражение (1.4) примет следующий вид:

Пример 2. Определить, параллельны ли прямые

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ =90°. Тогда cosφ =0. При этом выражение (1.4) примет следующий вид:

Пример 3. Определить, перпендикулярны ли прямые

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L 1 и L 2 заданы общими уравнениями

Из определения скалярного произведения двух векторов, имеем:

Пример 4. Найти угол между прямыми

Подставляя значения A 1 , B 1 , A 2 , B 2 в (1.23), получим:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

С другой стороны условие параллельности прямых L 1 и L 2 эквивалентно условию коллинеарности векторов n 1 и n 2 и можно представить так:

Удовлетворяется равенство (1. 24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L 1 и L 2 можно извлекать из формулы (1.20), подставляя cos (φ )=0. Тогда скалярное произведение (n 1 ,n 2)=0. Откуда

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L 1 и L 2 заданы каноническими уравнениями

где |q 1 | и |q 2 | модули направляющих векторов q 1 и q 2 соответственно, φ -угол между векторами q 1 и q 2 .

Из выражения (2.3) получим:

.

Упростим и решим:

.

Найдем угол φ

Задача 1

Найти косинус угла между прямыми $\frac{x+3}{5} =\frac{y-2}{-3} =\frac{z-1}{4} $ и $\left\{\begin{array}{c} {x=2\cdot t-3} \\ {y=-t+1} \\ {z=3\cdot t+5} \end{array}\right.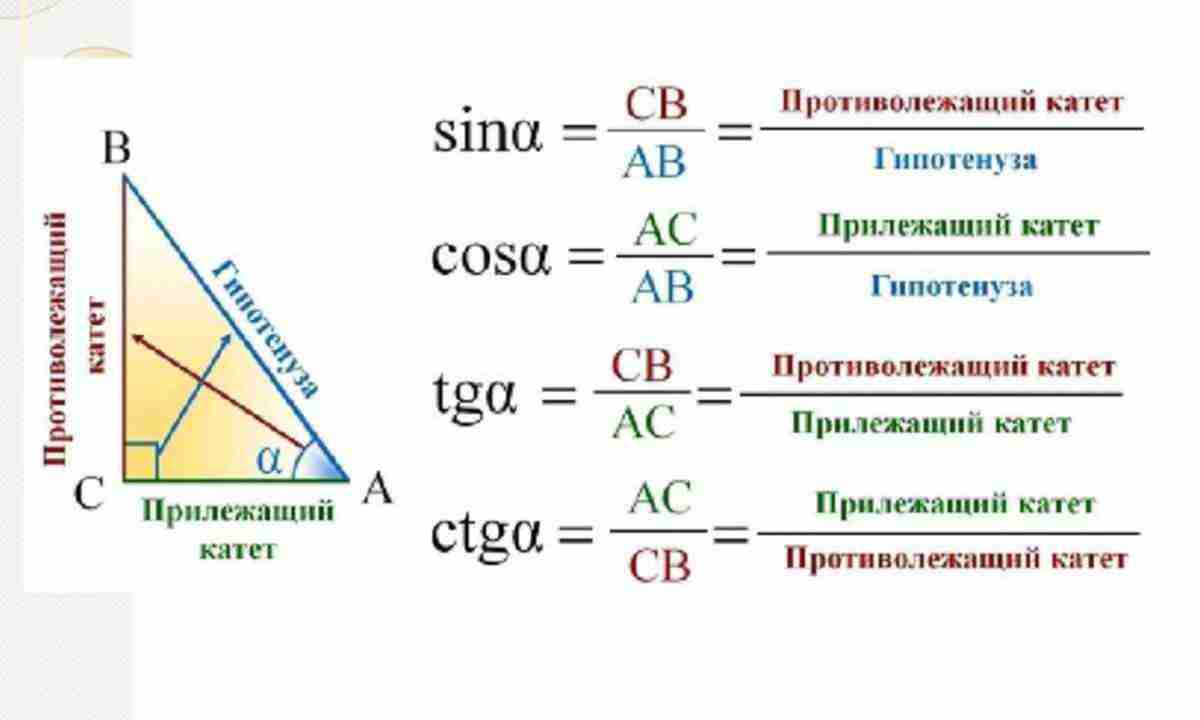 {2} } } =\frac{25}{\sqrt{50} \cdot \sqrt{14} } \approx 0,9449.\]

Задача 2

Первая прямая проходит через заданные точки $A\left(2,-4,-1\right)$ и $B\left(-3,5,6\right)$, вторая прямая — через заданные точки $C\left(1,-2,8\right)$ и $D\left(6,7,-2\right)$. Найти расстояние между этими прямыми.

Пусть некоторая прямая перпендикулярна к прямым $AB$ и $CD$ и пересекает их в точках $M$ и $N$ соответственно. При таких условиях длина отрезка $MN$ равна расстоянию между прямыми $AB$ и $CD$.

Строим вектор $\overline{AB}$:

\[\overline{AB}=\left(-3-2\right)\cdot \bar{i}+\left(5-\left(-4\right)\right)\cdot \bar{j}+\left(6-\left(-1\right)\right)\cdot \bar{k}=-5\cdot \bar{i}+9\cdot \bar{j}+7\cdot \bar{k}.\]

Пусть отрезок, изображающий расстояние между прямыми, проходит через точку $M\left(x_{M} ,y_{M} ,z_{M} \right)$ на прямой $AB$.

Строим вектор $\overline{AM}$:

\[\overline{AM}=\left(x_{M} -2\right)\cdot \bar{i}+\left(y_{M} -\left(-4\right)\right)\cdot \bar{j}+\left(z_{M} -\left(-1\right)\right)\cdot \bar{k}=\] \[=\left(x_{M} -2\right)\cdot \bar{i}+\left(y_{M} +4\right)\cdot \bar{j}+\left(z_{M} +1\right)\cdot \bar{k}. \]

Векторы $\overline{AB}$ и $\overline{AM}$ совпадают, следовательно, они коллинеарны.

Известно, что если векторы $\overline{a}=x_{1} \cdot \overline{i}+y_{1} \cdot \overline{j}+z_{1} \cdot \overline{k}$ и $\overline{b}=x_{2} \cdot \overline{i}+y_{2} \cdot \overline{j}+z_{2} \cdot \overline{k}$ коллинеарны, то их координаты пропорциональны, то есть $\frac{x_{{\it 2}} }{{\it x}_{{\it 1}} } =\frac{y_{{\it 2}} }{{\it y}_{{\it 1}} } =\frac{z_{{\it 2}} }{{\it z}_{{\it 1}} } $.

$\frac{x_{M} -2}{-5} =\frac{y_{M} +4}{9} =\frac{z_{M} +1}{7} =m$, где $m$ — результат деления.

Отсюда получаем: $x_{M} -2=-5\cdot m$; $y_{M} +4=9\cdot m$; $z_{M} +1=7\cdot m$.

Окончательно получаем выражения для координат точки $M$:

Строим вектор $\overline{CD}$:

\[\overline{CD}=\left(6-1\right)\cdot \bar{i}+\left(7-\left(-2\right)\right)\cdot \bar{j}+\left(-2-8\right)\cdot \bar{k}=5\cdot \bar{i}+9\cdot \bar{j}-10\cdot \bar{k}.\]

Пусть отрезок, изображающий расстояние между прямыми, проходит через точку $N\left(x_{N} ,y_{N} ,z_{N} \right)$ на прямой $CD$.

Строим вектор $\overline{CN}$:

\[\overline{CN}=\left(x_{N} -1\right)\cdot \bar{i}+\left(y_{N} -\left(-2\right)\right)\cdot \bar{j}+\left(z_{N} -8\right)\cdot \bar{k}=\] \[=\left(x_{N} -1\right)\cdot \bar{i}+\left(y_{N} +2\right)\cdot \bar{j}+\left(z_{N} -8\right)\cdot \bar{k}.\]

Векторы $\overline{CD}$ и $\overline{CN}$ совпадають, следовательно, они коллинеарны. Применяем условие коллинеарности векторов :

$\frac{x_{N} -1}{5} =\frac{y_{N} +2}{9} =\frac{z_{N} -8}{-10} =n$, где $n$ — результат деления.

Отсюда получаем: $x_{N} -1=5\cdot n$; $y_{N} +2=9\cdot n$; $z_{N} -8=-10\cdot n$.

Окончательно получаем выражения для координат точки $N$:

Строим вектор $\overline{MN}$:

\[\overline{MN}=\left(x_{N} -x_{M} \right)\cdot \bar{i}+\left(y_{N} -y_{M} \right)\cdot \bar{j}+\left(z_{N} -z_{M} \right)\cdot \bar{k}.\]

Подставляем выражения для координат точек $M$ и $N$:

\[\overline{MN}=\left(1+5\cdot n-\left(2-5\cdot m\right)\right)\cdot \bar{i}+\] \[+\left(-2+9\cdot n-\left(-4+9\cdot m\right)\right)\cdot \bar{j}+\left(8-10\cdot n-\left(-1+7\cdot m\right)\right)\cdot \bar{k}. \]

Выполнив действия, получаем:

\[\overline{MN}=\left(-1+5\cdot n+5\cdot m\right)\cdot \bar{i}+\left(2+9\cdot n-9\cdot m\right)\cdot \bar{j}+\left(9-10\cdot n-7\cdot m\right)\cdot \bar{k}.\]

Поскольку прямые $AB$ и $MN$ перпендикулярны, то скалярное произведение соответствующих векторов равно нулю, то есть $\overline{AB}\cdot \overline{MN}=0$:

\[-5\cdot \left(-1+5\cdot n+5\cdot m\right)+9\cdot \left(2+9\cdot n-9\cdot m\right)+7\cdot \left(9-10\cdot n-7\cdot m\right)=0;\] \

Выполнив действия, получаем первое уравнение для определения $m$ и $n$: $155\cdot m+14\cdot n=86$.

Поскольку прямые $CD$ и $MN$ перпендикулярны, то скалярное произведение соответствующих векторов равно нулю, то есть $\overline{CD}\cdot \overline{MN}=0$:

\ \[-5+25\cdot n+25\cdot m+18+81\cdot n-81\cdot m-90+100\cdot n+70\cdot m=0.\]

Выполнив действия, получаем второе уравнение для определения $m$ и $n$: $14\cdot m+206\cdot n=77$.

Находим $m$ и $n$, решив систему уравнений $\left\{\begin{array}{c} {155\cdot m+14\cdot n=86} \\ {14\cdot m+206\cdot n=77} \end{array}\right. {2} } \approx 3,8565$ лин. ед.

Тангенс угла задан Калькулятор противоположной и смежной сторон

✖Противоположная сторона угла A — это длина негипотенузного ребра прямоугольного треугольника, противоположного заданному непрямому углу A.ⓘ Противоположная сторона Сторона угла A [S напротив ]		AlnAngstromArpentАстрономическая единица АттометрAU длиныЯчменьМиллиард световых летBohr RadiusCable (International)Cable (UK)Cable (US)CalibreCentimeterChainCubit (Green)Cubit (L) ong)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance от SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeter МикродюймМикрометрМикронМилМиляМиля (Римская)Миля (Обзор США)МиллиметрМиллион Светового ГодаГвоздь (Ткань)НанометрМорская Лига (int)Морская Лига ВеликобританииМорская Миля (Международная) )Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Смежная сторона угла А — это длина негипотенузного ребра прямоугольного треугольника, примыкающего к данному непрямому углу А. ⓘ Смежная сторона угла A [S Смежный ]		AlnAngstromArpentАстрономическая единица АттометрAU длиныЯчменьМиллиард световых летБоровский радиусКабель (международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (греческий)Cu bit (Long)Cubit (UK)DecameterDecimeterEarth Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиЭлектронный радиус (классический)EllExameterFamnFathomFemtometerFermiFinger (ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMe terMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (ткань)NanometerNautical League (int)Nautical League UKМорская миля ( Международный)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Tan A — это значение тригонометрической функции тангенса заданного непрямого угла A в прямоугольном треугольнике. ⓘ Tan угла, заданного противоположной стороной и смежной стороной

⎘ Копировать

👎

Формула

Перезагрузить

👍

Tan of Angle задано решение противоположной стороны и смежной стороны

ШАГ 0: Итоги предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Противоположная сторона угла A: 2 метра —> 2 метра Преобразование не требуется
Прилегающая сторона угла A: 5 метров — -> 5 Meter Преобразование не требуется

ШАГ 2: Вычисление формулы

ШАГ 3: Преобразование результата в единицу измерения

0,4 —> Преобразование не требуется

< Калькуляторы 5 тригонометрических формул

Тангенс угла, заданный формулой противоположной стороны и смежной стороны

Tan A = противоположная сторона угла A/прилегающая сторона угла A
tan A = S _{Напротив} /S _Смежно

Что такое тригонометрия?

Тригонометрия — это раздел математики, который занимается отношениями между углами и сторонами треугольников, особенно прямоугольных треугольников. Он используется для изучения и описания таких свойств, как длины, углы и площади треугольников, а также отношений между этими свойствами и свойствами кругов и других геометрических фигур. Тригонометрия используется во многих областях, включая физику, инженерию и навигацию.

Как рассчитать тангенс угла, учитывая противоположную сторону и смежную сторону?

Тангенс угла с учетом противоположной и смежной сторон Калькулятор использует Tan A = противоположная сторона угла A/прилегающая сторона угла A для расчета Tan A, Tan угла с учетом противоположной и смежной сторон. Формула определяется как значение тригонометрическая функция тангенса заданного непрямого угла A в прямоугольном треугольнике. Тан А обозначается желто-коричневый Символ .

Как рассчитать тангенс угла при заданной противоположной стороне и смежной стороне с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для Тангенса угла с учетом противоположной стороны и смежной стороны, введите противоположную сторону угла A (S _{противоположную} ) и смежную сторону угла A (S _{смежную} ) и нажмите кнопку расчета.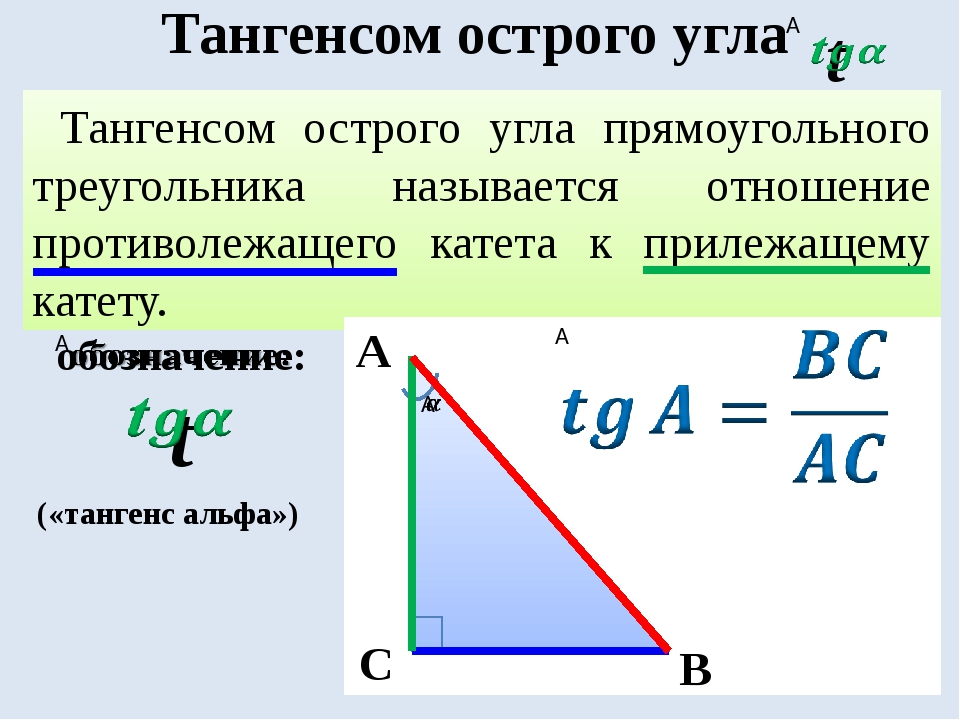 Вот как можно объяснить тангенс угла, заданный расчетом противоположной стороны и смежной стороны, с заданными входными значениями -> 0,4 = 0,02/0,05 .

Часто задаваемые вопросы

Чему равен тангенс угла, учитывая противоположную сторону и смежную сторону?

Тангенс угла с заданной противоположной стороной и формулой смежной стороны определяется как значение тригонометрической функции тангенса заданного непрямого угла A в прямоугольном треугольнике и представляется как tan A = S _{Противоположный} /S _{Смежный} или Tan A = противоположная сторона угла A/прилегающая сторона угла A . Противоположная сторона угла А — это длина негипотенузного ребра прямоугольного треугольника, противоположного данному непрямому углу А, а смежная сторона угла А — это длина негипотенузного ребра прямоугольного треугольника, смежный с заданным непрямым углом A.

Как вычислить Тангенс угла, учитывая противоположную сторону и смежную сторону?

Тангенс угла с учетом противолежащей и смежной сторон Формула определяется как значение тригонометрической функции тангенса заданного непрямого угла A в прямоугольном треугольнике, вычисляемое с использованием Tan A = Противоположная сторона угла A/Смежная сторона угла A . Чтобы рассчитать тангенс угла с учетом противоположной стороны и смежной стороны, вам потребуется противоположная сторона угла A (S _{противоположная} ) и смежная сторона угла A (S _{смежная} ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для противоположной стороны угла A и смежной стороны угла A и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Поделиться

Скопировано!

Калькулятор — tan(1000) — Solumaths

Тан, расчет онлайн

Резюме:

Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

тан онлайн

---

Описание:

Калькулятор позволяет использовать большинство тригонометрических функций , есть возможность вычислить желтовато-коричневый , синус и косинус угла через одноименные функции.

Тангенс тригонометрической функции отметил тангенс , позволяет рассчитать тангенс угла онлайн , можно использовать разные угловые единицы:

• радиан, что является угловой единицей по умолчанию,
• градусов или
• град.

1. Расчет касательной

Расчет тангенса угла в радианах

Калькулятор тангенса позволяет с помощью функции тангенса вычислить онлайн тангенс угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

Чтобы рассчитать тангенс онлайн от `pi/6`, введите tan(`pi/6`), после вычисления результат `sqrt(3)/3` возвращается.

Обратите внимание, что функция касательной может распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

Вычислить тангенс угла в градусах

Чтобы вычислить тангенс угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить тангенс 60, введите tan(60), после вычисления Возвращается результат `sqrt(3)`.

Вычисление тангенса угла в градусах

Чтобы вычислить тангенс угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить тангенс 50, введите tan(50), после вычисления, возвращается результат `1`.

Обратите внимание, что функция касательной может распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

2. Специальные значения тангенса

Тангенс допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения тангенса :

900 04

tan(`2*pi`)	`0`
tan(`pi`)	`0`
tan(`pi/4` )	`1`
tan(`pi/3`)	`sqrt(3)`
tan(`pi/6`)	`sqrt(3)/3`
tan(`2*pi/3`)	`-sqrt(3)`
желтовато-коричневый( `3*pi/4`)	`-1`
tan(`5*pi/6`)	`-sqrt(3)/3`
tan(`-2*pi `)	`0`
tan(`-pi`)	`0`
tan(`-pi/4`)	`-1` 900 10
желтовато-коричневый(`- пи/3`)	`-sqrt(3)`
tan(`-pi/6`)	`sqrt(3)/3`
tan(`-2*pi/3`)	`sqrt(3)`
tan( ` -3*pi/4`)	`1`
tan(`-5*pi/6`)	`sqrt(3)/3`

3. Основные свойства

`AA x в RR, k в ZZ`,

• `tan(-x)= -tan(x)`
• `tan(x+k*pi)=tan(x)`
• `tan(pi-x)=-tan(x)`
• `tan(pi+x)=tan(x)`
• `tan(pi/2-x)=1/tan(x)` 92`.

• Первообразная касательной

Первообразная касательной равна `-ln(cos(x))`.

• Свойства функции касательной

Функция тангенса является нечетной функцией, для каждого действительного x `tan(-x)=-tan(x)`. Следствием для кривой, представляющей функцию тангенса, является то, что она допускает начало отсчета как точку симметрии.

Синтаксис:

tan(x), где x — мера угла в градусах, радианах или градах. 92`

---

Тангенс первообразной :

Калькулятор начальных производных позволяет вычислить первообразную функции тангенса.

Первопроизводная tan(x) есть первопроизводная(`tan(x)`)=`-ln(cos(x))`

---

Предельный тангенс :

касательная функция.

Предел tan(x) is limit(`tan(x)`)

---

Тангенс обратной функции:

обратная функция тангенса — это функция арктангенса, отмеченная как arctan.

---

---

Графический тангенс :

Графический калькулятор может отображать функцию тангенса в заданном интервале.

---

---

Свойство тангенса функции:

Касательная функция является нечетной функцией.

---

Расчет онлайн с tan (тангенсом)

См. также

Список связанных калькуляторов:
• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo.

  No related posts.