Соотношение между сторонами и углами треугольника
Соотношение между сторонами и углами треугольника
План урока
- Теорема о площади треугольника
- Теорема синусов
- Теорема косинусов
- Решение треугольников
- Измерительные работы
Цели урока
- Знать теорему о площади треугольника, теорему синусов, теорему косинусов
- Уметь применять теорему о площади треугольника, теорему синусов, теорему косинусов при решении задач
- Уметь решать треугольник по трём элементам
- Знать методы измерительных работ
Разминка
- Как найти площадь треугольника?
- Что такое синус, косинус, тангенс угла?
- Как найти координаты точки на координатной плоскости?
Теорема о площади треугольника
Теорема (о площади треугольника)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Рис. 1. Теорема о площади треугольника
Доказательство
Дан треугольник . Найдем его площадь.
Пусть сторона BC=a, AC=b, ∠C=α
Введем систему координат с началом в точке C (рис. 1). Тогда координаты точки B равны: x=a·cosα, y=a·sinα.
Высота треугольника ABC, проведенная к стороне AC равна BH. Но, с другой стороны, BH — это ордината точки B т.е. BH= a·sinα.
Известно, что площадь треугольника равна половине произведения его основания на высоту. Тогда
SΔABC=12AC·BH=12b·(a·sinα)=12a·b·sinα.
Таким образом, S∆=12absinα, где стороны треугольника, α — угол между ними.
Теорема доказана
Пример 1
Найдите площадь треугольника ABC, если AB=38см, AC=2 см, ∠A=45°.
Рис. 2. Пример 1
Решение
Рассмотрим ∆ ABC, где AB=38 см,
AC=2 см, ∠A=45°(рис.
2).
SΔABC=12AB·AC·sinA=
=12·38·2·sin45°=38·22=
=6см2
Ответ: 6 cм2.
Теорема синусов
Теорема (синусов)
Стороны треугольника пропорциональны синусам противолежащих углов.
Рис. 3. Теорема синусов
Доказательство
Рассмотрим треугольник ABC. Пусть AB=c, AC=b, BC=a, (рис. 3). Используя теорему о площади, найдем площадь треугольника ABC разными способами:
S=12 a·b·sinC, S=12 b·c·sinA, S=12a·c·sinB
Приравняв первые два равенства, получим: 12a·b·sinC=12b·c·sinA , откуда asinA=csinC .Таким же образом, приравняв второе и третье равенство, получим asinA=bsinB .
Таким образом, asinA=bsinB=csinC.
Теорема доказана
Пример 2
В треугольнике OMK sinO=14, OK=8, MK=6.
Найти синус угла M.
Рис. 4. Пример 2
Решение
Рассмотрим треугольник OMK, где OK=8, MK=6, sinO=14(рис. 4).
Применим к этому треугольнику теорему синусов: MKsinO=OKsinM, отсюда 614=8sinM, sinM=13
Ответ: 13
Можно доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Таким образом, будет справедливо равенство:
asinA=bsinB=csinC=2R,
где a=BC, b=AC, c=AB – стороны треугольника ABC, R — радиус окружности, описанной около треугольника ABC.
Теорема косинусов
Теорема (косинусов)
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.
Рис. 5. Теорема косинусов
Доказательство
Пусть в треугольнике AB=c, AC=b, CB=a.
Поместим треугольник ABC в прямоугольную систему координат так, чтобы точка A совпадала с началом координат, точка B лежала на положительной полуоси
0x, а точка C располагалась в первой координатной четверти (рис. 5).
AH=AC cosA=b cosA
CH — это ордината точки C, а AH — абсцисса точки C, поэтому точка C имеет координаты (bcosA; bsinA).
По формуле расстояния между двумя точками имеем:
BC2=a2=(bcosA-c)2+b2sin2A=b2cos2A+b2sin2A-2bccosA+c2=
=b2(cos2A+sin2A)-2bccosA+c2=b2+c2-2bccosA
Теорема доказана
Пример 3
В треугольнике ABC cosB=-15, AB=5, BC=4. Найдите сторону AC
Решение
Применим к треугольнику ABC теорему косинусов: AC2=AB2+BC2-2·AB·BC·cos·B=52+42-2·5·4·(-15)=49.
Тогда AC=49=7.
Ответ: 7.
Теорема косинусов — обобщенная теорема Пифагора. В самом деле, если угол A прямой, то его косинус равен 0 и тогда a2=b2+c2.
Решение треугольников
Решить треугольник – это значит найти все его стороны и углы по каким-нибудь трём данным элементам. Рассмотрим три задачи на решение треугольника.
Пусть дан треугольник ABC, в котором AB=c, BC=a, CA=b.
Задача 1 (решение треугольника по двум сторонам и углу между ними)
Дано: a, b, ∠C.
Найти: c, ∠A, ∠B.
Решение
- Найдем сторону по теореме косинусов:
c=a2+b2-2ab cosC
2. По теореме косинусов найдем угол
cosA=b2+c2-a22bc
Зная косинус угла, можно найти сам угол с помощью таблицы или микрокалькулятора.
3. Теперь можем найти угол В.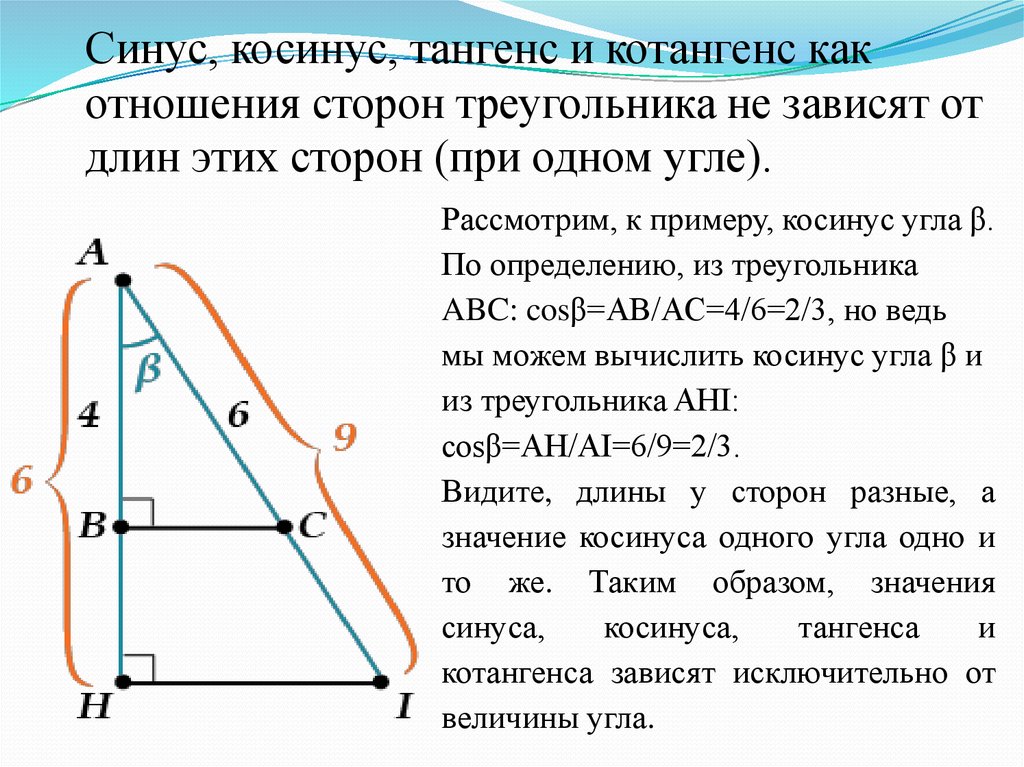
Сумма всех углов треугольника равна 180°, поэтому
∠B=180°-∠A-∠C
Таким образом, мы решили треугольник по двум сторонам и углу между ними.
Задача 2 (решение треугольника по стороне и прилежащим к ней углам)
Дано: a, ∠B, ∠C.
Найти: ∠A, b, c.
Решение
1. Так как сумма углов треугольника равна 180°, то ∠A=180°-∠B-∠C
2. Теперь по теореме синусов найдем стороны b и c:
b=a sinBsinA, c=a sinCsinA
Таким образом, мы решили треугольник по стороне и прилежащим к ней углам.
Задача 3 (решение треугольника по трём сторонам)
Дано: a, b, c
Найти: ∠A, ∠B, ∠C.
Решение
- Воспользуемся теоремой косинусов:
cosA=b2+c2-a22bc
Далее угол можно найти с помощью таблицы или микрокалькулятора.
2. Аналогичным образом найдем угол B:
cosB=a2+c2-b22ac
3.
Найдем угол C:
∠C=180°-∠A-∠B
Таким образом, мы решили треугольник по трём сторонам.
Пример 4
Решите треугольник ABC, если AB=4, BC=6, ∠B=60°.
Решение
Нужно решить треугольник по двум сторонам и углу между ними.
- Найдем сторону по теореме косинусов:
AC=AB2+BC2-2·AB·BC cosB
AC=42+62-2·4·6·cos60°=28=27
2. По теореме косинусов найдем угол A.
cosA=AC2+AB2-BC22·AC·AB
cosA=(27)2+42-622·2√7·4=127≈0,189
Значит, ∠A=79°.
3. Теперь можем найти угол C. Сумма всех углов треугольника равна 180°, поэтому
∠C=180°-∠A-∠C,
∠C=180°-79°-60°=41°.
Ответ: AC=27,∠A=79°, ∠C=41°
Тригонометрические формулы используются при проведении различных измерительных работ на местности. Например, при измерении высоты предмета или измерении расстояния до недоступной точки.
Рис. 6 Измерение высоты предмета
Пример 5 (Измерение высоты предмета)
Найти высоту дерева (рис. 6).
Решение
Отметим точку B на расстоянии a от основания H дерева. Измерим угол α. Тогда высоту предмета легко найти: AH=a·tgα.
В случае, если основание дерева a недоступно для измерения, нужно отметить две точки B и C на определенном расстоянии a друг от друга. Измерим углы a и β. Тогда ∠ABH — внешний угол треугольника и ∠A=α-β. По теореме синусов находим AB:
AB=a sinβsin (α-β).
Треугольник прямоугольный. Найдем высоту AH:
AH=AB·sinα
Таким образом, AH=a sinα sinβsin(α-β).
Пример 6 (Измерение расстояния до недоступной точки)
Нужно измерить расстояние d от пункта A до недоступного пункта C.
Рис. 7. Измерение расстояния до недоступной точки
Решение
На местности выберем точку B, измерим длину c отрезка AB и углы A и B: ∠A=α, ∠B=β
Теперь найдем угол C: ∠С=180°-α-β
sinC=sin(180°-α-β)=
=sin(α+β).
Далее воспользуемся теоремой синусов: ACsinB=ABsinC, AC=d, AB=c, ∠B=β, то d=c sinβsin(α+β)
Пример 7
Найдите синус угла треугольника, если биссектриса, проведенная из вершины этого угла, делит противолежащую сторону на отрезки 21 и 35, а разность двух сторон, прилежащих к этому углу равна 16.
Решение
Рис. 8. К решению примера 7
Пусть AK — биссектриса угла A треугольника ABC, BK=21, CK=35. Пусть AB=x, тогда
AC=16+x.
По свойству биссектрисы угла:
ABBK=ACCK,
x21=16+x35,
35x=2116+x,
x=24.
Тогда AB=24, AC=40, BC=56.
Используем в треугольнике ABC теорему косинусов, и выразим косинус угла A:
cosA=AB2+AC2-BC22·AB·AC,
cosA=576+1600-31362·24·40=-12.
Применив основное тригонометрическое тождество, получим sinA=32.
Ответ: 32.
Упражнение 1
1. Найдите площадь треугольника ABC, если AB=4 см, AC=7 см, ∠A=135°.
2. В треугольнике MPK sinM=16, MK=12, PK=4.
Найти синус угла P.
3. В треугольнике ABD cosD=-115, AD=5, BD=3. Найдите сторону AB.
4. Решите треугольник ABC, если BC=53 см, AB=10 см, ∠B=30°.
Контрольные вопросы
- По какой формуле можно вычислить площадь треугольника?
- Сформулируйте теорему синусов
- Сформулируйте теорему косинусов
- Как найти радиус описанной окружности, используя теорему синусов?
- Как решить треугольник, если известны сторона и два угла?
- Как измерить расстояние до недоступной точки?
Ответы
Упражнение 1
1. 72 см2.
2. 0,5.
3. 6.
4. AC=5 см, ∠A=60°, ∠C=90°.
Теорема синусов / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
- Теорема синусов
Теорема
| Стороны треугольника пропорциональны синусам противолежащих углов. |
Доказательство
Дано: АВС, АВ = , ВС = , АС = .
Доказать: .
Доказательство:
По теореме о площади треугольника:
, (1) , (2) . (3)
Из равенств (1) и (2) получим:
, откуда или .
(4)
Из равенств (2) и (3) получим:
, откуда или . (5)
Из равенств (4) и (5) следует:
.
Теорема доказана.
Замечание
| Отношение стороны треугольника к синусу противолежащего угла равно диаметру (двум радиусам) описанной окружности. |
Доказательство
Дано: окр(О, R) описана около АВС.
Доказать: .
Доказательство:
Проведем диаметр ВА1 и рассмотрим треугольник А1ВС.
Угол С АВС опирается на диаметр ВА1, поэтому С — прямой, тогда (6) (смотри формулы для вычисления координат точки).
Но . Действительно, если точка А1 лежит на дуге ВАС (см. рисунок выше), то А1 = А, а если на дуге ВDС (см. рисунок ниже), то
А1= 1800 — А. В обеих случаях .
Следовательно, учитывая (6), получим:
, при этом диаметр ВА1 = 2R, значит, , откуда . Что и требовалось доказать.
Из доказанного выше замечания получаем, что для любого АВС со сторонами АВ = , ВС = , АС = справедливы равенства
,
где R — радиус описанной окружности.
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество.
Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Теорема косинусов
Решение треугольников
Измерительные работы
Угол между векторами
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1027, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1028, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1029, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1032, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1058, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1060, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Тождества кофункций — формула, доказательство, применение, примеры
Тождества кофункций в тригонометрии дают взаимосвязь между различными тригонометрическими функциями и их дополнительными углами.
Напомним значение дополнительных углов. Два угла называются дополнительными, если их сумма равна π/2 радианам или 90°. Кофункциональные тождества — это тригонометрические тождества, которые показывают связь между тригонометрическими отношениями попарно (синус и косинус, тангенс и котангенс, секанс и косеканс). Мы используем свойство суммы углов треугольника, чтобы вывести тождества шести кофункций.
В этой статье мы выведем тождества кофункций и проверим их, используя формулы суммы и разности тригонометрических функций. Мы также решим различные примеры, чтобы понять использование этих тождеств кофункций для решения различных математических задач, связанных с тригонометрическими функциями.
| 1. | Что такое кофункция идентичности? |
| 2. | Формула идентичности кофункций |
| 3. | Подтверждение идентичности кофункций |
| 4. | Проверка идентичности кофункций |
5. | Использование идентификаторов кофункций |
| 6. | Часто задаваемые вопросы о кофункциональных идентификаторах |
Что такое Кофункция Идентичности?
Тождества кофункций — это тригонометрические тождества, которые показывают взаимосвязь между дополнительными углами и тригонометрическими функциями. У нас есть шесть таких тождеств, которые можно вывести, используя прямоугольный треугольник, свойство суммы углов треугольника и формулы тригонометрических отношений. Тождества кофункций дают связь между тригонометрическими функциями синуса и косинуса, тангенса и котангенса, а также секанса и косеканса. Эти функции называются кофункциями друг друга. Мы также можем вывести эти тождества, используя формулы суммы и разности, если они также являются тригонометрическими. В качестве альтернативы мы можем использовать формулы суммы и разности, чтобы проверить тождества кофункций.
Формула идентичности кофункций
Тождества кофункций дают взаимосвязь между попарными тригонометрическими функциями и их дополнительными углами, как показано ниже:
- Функция синуса и функция косинуса
- Функция тангенса и функция котангенса
- Функция секанса и функция косеканса
Два угла называются дополнительными, если их сумма равна 90 градусов.
Мы можем записать тождества кофункций в радианах и градусах, поскольку это две единицы измерения угла. Шесть тождеств кофункций даны в таблице ниже в радианах и градусах:
| Идентичности кофункций в радианах | Идентичности кофункций в градусах |
|---|---|
| sin (π/2 — θ) = cos θ | sin (90° — θ) = cos θ |
| cos (π/2 — θ) = sin θ | cos (90° — θ) = sin θ |
| тан (π/2 — θ) = детская кроватка θ | загар (90° — θ) = детская кроватка θ |
| раскладушка (π/2 — θ) = тангенс θ | раскладушка (90° — θ) = загар θ |
| сек (π/2 — θ) = cosec θ | сек (90° — θ) = cosec θ |
| csc (π/2 — θ) = сек θ | csc (90° — θ) = сек θ |
Давайте выведем эти тождества кофункций в следующем разделе.
Доказательство идентичности кофункций
Теперь, когда мы обсудили тождества кофункций в предыдущем разделе, давайте теперь выведем их, используя прямоугольный треугольник.
Рассмотрим прямоугольный треугольник ABC с прямым углом в B. Предположим, что угол C = θ, тогда, используя свойство суммы углов треугольника, мы имеем
∠A + ∠B + ∠C = 180°
⇒ ∠A + 90° + ∠C = 180° — [Поскольку угол B прямой]
⇒ ∠A + ∠C = 180° — 90°
⇒ ∠A + θ = 90°
⇒ ∠A = 90° — θ
Следовательно, мы имеем три угла треугольника ABC как ∠A = 90° — θ, ∠B = 90° и ∠C = θ. А теперь вспомним формулы тригонометрических формул ниже:
- sin x = Противоположная сторона / Гипотенуза
- cos x = смежная сторона / гипотенуза
- tan x = Противоположная сторона / Смежная сторона
- детская кроватка x = соседняя сторона/противоположная сторона
- сек х = гипотенуза / противоположная сторона
- csc x = гипотенуза/прилежащая сторона
Теперь, используя приведенные выше формулы, мы можем определить тождества кофункций для треугольника ABC.
- cos θ = BC / AC = sin (90° — θ)
- sin θ = AB / AC = cos (90° — θ)
- tan θ = AB / BC = cot (90° — θ)
- кроватка θ = BC / AB = tan (90° — θ)
- с θ = AC / BC = csc (90° — θ)
- csc θ = AC / AB = сек (90° — θ)
Таким образом, мы получили тождества кофункций.
Чтобы получить эти тождества в радианах, мы можем просто заменить 90° на π/2 и получить тождества как:
- cos θ = BC / AC = sin (π/2 — θ)
- sin θ = AB / AC = cos (π/2 — θ)
- тангенс θ = AB / BC = кроватка (π/2 — θ)
- раскладушка θ = BC / AB = загар (π/2 — θ)
- сек θ = AC / BC = csc (π/2 — θ)
- csc θ = AC / AB = сек (π/2 — θ)
Проверка идентичности кофункций
Теперь, когда мы доказали тождества кофункций, давайте проверим их, используя формулы суммы и разности тригонометрии. Мы будем использовать следующие формулы для проверки тождеств:
- sin(A — B) = sinA cosB — cosA sinB
- cos(A — B) = cosA cosB + sinA sinB
- тангенс A = sin A / cos A
Расширьте sin (π/2 — θ), cos (π/2 — θ) и tan (π/2 — θ), используя приведенные выше формулы.
- sin (π/2 — θ) = sin(π/2) cosθ — cos(π/2) sinθ
= 1 × cos θ — 0 × sin θ — [Поскольку sin (π/2) = 1 и cos (π/2) = 0]
= cos θ - cos (π/2 — θ) = cos(π/2) cosθ + sin(π/2) sinθ
= 0 × cos θ + 1 × sin θ — [Поскольку sin (π/2) = 1 и cos (π/2) = 0]
= грех θ - тангенс (π/2 — θ) = [sin (π/2 — θ)] / [cos (π/2 — θ)]
= cos θ / sin θ
= детская кроватка θ
Теперь проверим тождества кофункций для sec, csc и cot, используя взаимные тождества
- cot (π/2 — θ) = 1 / tan (π/2 — θ)
= 1 / кроватка θ
= тангенс θ - сек (π/2 — θ) = 1 / cos (π/2 — θ)
= 1 / sin θ
= csc θ - csc (π/2 — θ) = 1 / sin (π/2 — θ)
= 1 / потому что θ
= сек θ
Таким образом, мы проверили все шесть тождеств кофункций с помощью тригонометрических формул.
Использование идентификаторов кофункций
Теперь, когда мы вывели формулы для тождеств кофункций, давайте решим несколько задач, чтобы понять их применение.
Пример 1: Найдите значение острого угла x, если sin x = cos 20°.
Решение: Используя тождество кофункции, cos (90° — θ) = sin θ, мы можем записать sin x = cos 20° как
sin x = cos 20°
⇒ cos (90° — x) = cos 20°
⇒ 90° — x = 20°
Ответ: Значение x равно 70°, если sin x = cos 20°.
Пример 2: Оцените значение x, если sec (5x) = csc (x + 18°), где 5x — острый угол.
Решение: Чтобы найти значение x, воспользуемся тождеством кофункции csc (90° — θ) = sec θ. Мы можем написать
сек (5x) = csc (x + 18°)
⇒ csc (90° — 5x) = csc (x + 18°)
⇒ 90° — 5x = x + 18° — [Поскольку дается 5x острота]
⇒ 5x + x = 90 ° — 18°
⇒ 6x = 72°
⇒ x = 72° / 6
⇒ x = 12°
Ответ: Значение x равно 12°, если sec (5x) = csc (x + 18 °), где 5х — острый угол.
Важные замечания по тождествам кофункций
- Тождества кофункций показывают связь между тригонометрическими функциями и дополнительными углами.
- У нас есть шесть основных тождеств кофункций:
- cos θ = sin (90° — θ)
- sin θ = cos (90° — θ)
- tan θ = кроватка (90° — θ)
- кроватка θ = загар (90° — θ)
- с θ = csc (90° — θ)
- csc θ = сек (90° — θ)
- Эти тождества можно получить, используя свойство суммы углов прямоугольного треугольника и формулы суммы и разности.
☛ Похожие темы:
- Суммирование формул произведения
- Гиперболические функции
- Производная гиперболических функций
Часто задаваемые вопросы по идентификаторам кофункций
Что такое тождества кофункций в тригонометрии?
Кофункции тождества в тригонометрии — это формулы, которые показывают связь между тригонометрическими функциями и их дополнительными попарно углами — (синус и косинус, тангенс и котангенс, секанс и косеканс).
У нас есть в основном шесть тождеств кофункций, которые используются для решения различных задач тригонометрии.
Каковы основные шесть кофункций?
Шесть основных тождеств кофункций:
- cos θ = sin (90° — θ)
- sin θ = cos (90° — θ)
- tan θ = кроватка (90° — θ)
- кроватка θ = загар (90° — θ)
- с θ = csc (90° — θ)
- csc θ = сек (90° — θ)
Мы можем записать эти тождества, используя меру радианов, как указано ниже:
- cos θ = sin (π/2 — θ)
- sin θ = cos (π/2 — θ)
- тангенс θ = раскладушка (π/2 — θ)
- раскладушка θ = загар (π/2 — θ)
- сек θ = csc (π/2 — θ)
- csc θ = сек (π/2 — θ)
Как найти тождества кофункций?
Мы можем вывести формулы для тождеств шести кофункций, используя прямоугольный треугольник и свойство суммы углов треугольника. Мы также можем доказать эти тождества, используя формулы суммы и разности и обратные тождества в тригонометрии.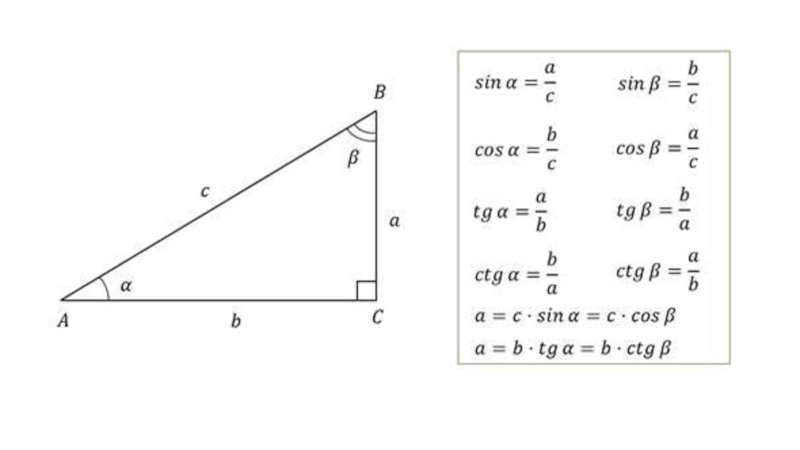
Что такое тождества кофункций для тангенса и котангенса?
Тождества кофункций для тангенса и котангенса приведены ниже:
- tan θ = cot (π/2 — θ)
- раскладушка θ = загар (π/2 — θ)
Мы также можем записать эти формулы в градусах также как:
- tan θ = cot (90° — θ)
- кроватка θ = загар (90° — θ)
Почему тождества кофункций верны для всех прямоугольных треугольников?
Мы говорим, что две функции являются кофункциями друг друга, если их углы дополняют друг друга, то есть сумма их углов равна π/2 рад. В произвольном прямоугольном треугольнике, поскольку один угол равен π/2 рад, сумма двух других углов всегда равна π/2, используя свойство суммы нагле. Таким образом, тождества кофункций верны для всех прямоугольных треугольников, и их можно легко вывести, используя прямоугольный треугольник и применяя к нему формулы тригонометрических отношений.
Когда использовать тождества кофункций?
Мы можем использовать тождества кофункций для упрощения различных сложных тригонометрических задач.
Они используются, когда вовлеченные углы дополняют друг друга, то есть их сумма равна 90 градусов. Тождества кофункций можно использовать для нахождения значений тригонометрических отношений с углами более 90 градусов для их упрощения.
Кофункции
Нет, вы не споткнетесь о кофункции, если окажетесь в Узле Дисфункций. Они глубоко встроены в тригонометрические функции. Вы заметили «со» в косинусе, косекансе и котангенсе?
«Co» — сокращение от «дополнительный».
Co + функция = co дополнительные функции.
Вам знакомо слово «дополнительный»? Из геометрии мы узнали, что дополнительные углы складываются в угол 90°.
Мы также знаем, что сумма углов треугольника должна быть 180°. Таким образом, если угол C является прямым углом (90°), сумма двух других углов должна составлять остальные 90°.
Поскольку A + B = 90°, A и B являются дополнительными углами.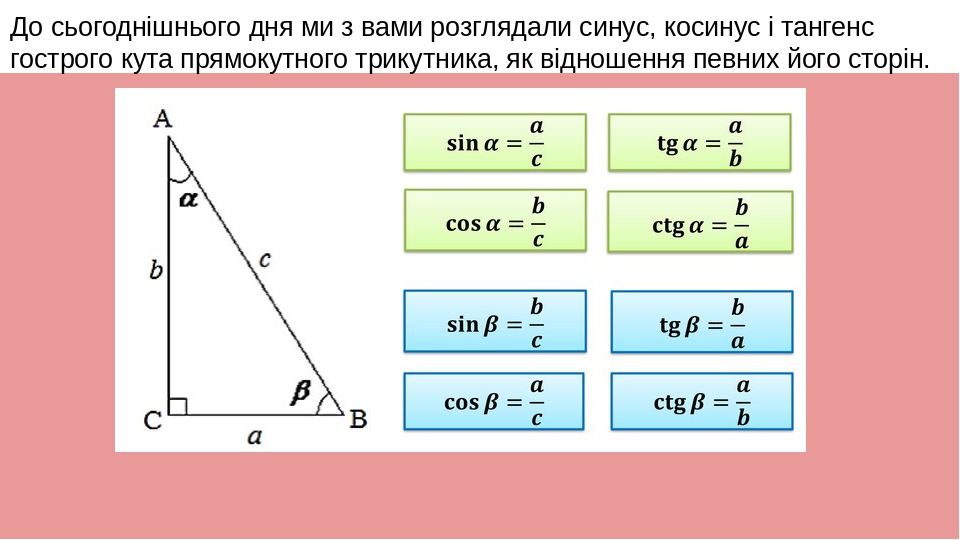
Немного поменяв местами, мы увидим, что:
B = 90° – A
и
A = 90° – B
Теперь применим наше «со» к триггерным функциям.
Косинус является co дополнительной функцией синуса.
Косеканс является co дополнительной функцией секанса.
Котангенс является co дополнительной функцией тангенса.
О чем все это? Вот сделка. Взгляните еще раз на наш треугольник:
В этом треугольнике косинус угла A равен синусу угла B .
cos A = sin B
Давай, пусть это впитается на секунду. Косинус — это сторона, прилежащая к гипотенузе (CAH), а синус — сторона, противоположная гипотенузе (SOH). Но сторона, примыкающая к углу А , есть то же самое , что и сторона, противолежащая углу В . Вот почему cos A = грех В . Они дают нам точно такое же соотношение.
Вот тут-то и вступают в игру кофункции. Подстановка в B = 90° – A дает нам:
cos A = sin(90° – A )
Смотри, что мы сделали ? Косинус A равен синусу дополнительного угла A .
Аналогично:
csc A = сек B
csc A = сек(90° – a )
и:
COT A = TAN B
COT A = TAN (90 ° — A )
Это работает по другим образом:
99A )
Это также работает. = cos B = cos(90° – A )
сек A = csc B = csc(90° – A )
tan A = ctg A = cot – A )
Пример задачи
Запишите sin(30°) через его кофункцию.
Это намного холоднее, чем может показаться. Кофункция синуса — это просто косинус. Используя sin A = cos(90° – A ), получаем:
sin(30°) = cos(90° – 30°)
sin(30°) = cos(60°)
Да, это оно.