Тесты с ответами по методам оптимальных решений: Математическое Бюро. Страница 404

Содержание

Тест по дисциплине Методы оптимальных решений

1.Модель – это
А) аналог (образ) оригинала, но построенный средствами и методами, отличными от оригинала;
Б) подобие оригинала;
В) копия оригинала

2.Экономико-математическая модель – это …
А) математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.)
Б) качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
В) эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)

3.Найти экстремум функции f(x) при выполнении ограничений Ri(x) = ai, φ (x) ≤ bj, наложенных на параметры функции – это задача
А) условной оптимизации
Б) линейного программирования
В) безусловной оптимизации
Г) нелинейного программирования
4. Задача, включающая целевую функцию f и функции g, входящие в ограничения, является задачей линейного программирования, если
А) все g и f являются линейными функциями относительно своих аргументов

Б) все g являются линейными функциями относительно своих аргументов, а функция f – нелинейна
В) функция f является линейной относительно своих аргументов, а функции g – нелинейны
Г) только часть функций g и функция f являются линейными относительно своих аргументов

5. Множество всех допустимых решений системы задачи линейного программирования
А) является
Б) выпуклым
В) вогнутым
Г) одновременно выпуклым и вогнутым

6.Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из …
А) вершин многоугольника (многогранника) допустимых решений
Б) внутренних точек многоугольника (многогранника) допустимых решений
В) во всех точках области допустимых решений

7.Задача линейного программирования не имеет конечного оптимума, если

А) в точке А области допустимых значений достигается максимум целевой функции F
Б) в точке А области допустимых значений достигается минимум целевой функции F
В) коэффициенты в целевой функции отрицательны
Г) целевая функция не ограничена сверху на множестве допустимых решений

8.Метод Жордана-Гаусса заключается в …

А) последовательном исключении переменных

Б) последовательном исключении свободных членов

В) вычислении вспомогательных определителей системы

Г) нахождении обратной матрицы

9. Программирование называется линейным, если:

А) целевая функция является линейной

Б) целевая функция является линейной, ограничения являются линейными функциями

В) целевая функция является нелинейной, ограничения являются линейными функциями

Г) целевая функция является линейной, ограничения являются нелинейными функциями

10. Какой вид имеет целевая функция задачи линейного программирования?

А) f(X) = c1x1 + c2x2 + … + cnxn Б) AX £ (=,³) B

В) X£ 0 Г) X³ 0

1. Какой вид имеют функциональные условия в матричном виде задачи линейного программирования?

А) f(X) = c1x1 + c2x2 + … + cnxn

Б) AX £ (=,³) B

В) X£ 0

Г) X³ 0

2. Какой порядок записи математической модели задачи линейного программирования является правильным?

А) Формулирование критерия оптимальности — ввод переменных — формулирование ограничений

Б) Ввод переменных — формулирование критерия оптимальности — формулирование ограничений

В) Формулирование ограничений — ввод переменных — формулирование критерия оптимальности

Г) Ввод переменных — формулирование ограничений — формулирование критерия оптимальности

Задача линейного программирования называется канонической, если система ограничений включает в себя:

А)только неравенства;

Б) равенства и неравенства;

В) только равенства.

4.Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то:

А) допустимое множество не ограничено;

Б) оптимальное решение не существует;

В) существует хотя бы одно оптимальное решение.

5.Задача может быть отнесена к классу задач нелинейного программирования, если в ней:

А) Все ограничения и целевая функция – линейны

Б) По меньшей мере, одно из ограничений является не линейным

В) Не задана целевая функция

Г) Все ограничения линейны, а целевая функция не линейна.

6. Целью транспортной задачи является:

А) минимизировать транспортные расходы

Б) удовлетворить потребности потребителей

В) запасы поставщиков исчерпать полностью

Г) среди ответов нет верного

Д) верными являются варианты а, б и в.

7. Транспортная задача называется открытой, если …

А) запасы поставщиков меньше запросов потребителей

Б) запасы поставщиков больше запросов потребителей

В) запасы поставщиков равны запросам потребителей

Г) среди ответов нет верного

Д) верные варианты а и б.

8. Транспортная задача называется закрытой, если …

А) запасы поставщиков меньше запросов потребителей

Б) запасы поставщиков больше запросов потребителей

В) запасы поставщиков равны запросам потребителей

Г) среди ответов нет верного

Д) верные варианты а и б.

9. Если транспортная задача открытая, то …

А) она не имеет решения вообще

Б) она имеет решение в открытом виде

В) она решается сведением к закрытому виду, введя дополнительного поставщика или потребителя

Г) среди ответов нет верного

10. Метод минимальной стоимости заключается в том, чтобы…

А) из всей таблицы транспортной задачи найти наибольшую стоимость перевозки единицы груза, и заполнить именно эту ячейку

Б) во всей таблице начинать заполнение ячеек с наименьшей стоимостью перевозок

В) в каждой строке и в каждом столбце найти ячейку с наименьшими затратами и начать заполнение с этих ячеек

Г) среди ответов нет верного

1. Из всех методов нахождения первоначального опорного плана транспортной задачи предпочтительнее тот метод, при котором …

А) суммарные затраты на перевозку груза максимальны

Б) суммарные затраты на перевозку груза минимальны

В) нет верного ответа

2. Для составления математической модели необходимо …

А) задать целевую функцию, выбрать переменные задачи и составить систему ограничений задачи

Б) выбрать переменные задачи и составить систему ограничений задачи

В) выбрать переменные задачи и составить систему ограничений задачи, задать целевую функцию

Г) нет верного ответа

3. Целевой функцией задачи называют …

А) совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов

Б) функцию, которая характеризует качество выполнения задачи и экстремум которой следует найти

В) нет верного ответа

4. Каноническая задача линейного программирования – это задача, в которой …

А) система ограничений состоит только из неравенств

Б) система ограничений состоит только из равенств

В) система ограничений состоит из равенств и неравенств

Г) нет верного ответа

Симметричная задача линейного программирования – это задача, в которой …

А) система ограничений состоит только из неравенств

Б) система ограничений состоит только из равенств

В) система ограничений состоит из равенств и неравенств

Г) нет верного ответа

6. Графический метод решения ЗЛП заключается …

А) на возможности графического изображения ОДР задачи и нахождении среди них оптимального решения

Б) на графическом изображении целевой функции задачи

В) на построении прямой, на которой целевая функция задачи принимает постоянное значение

Г) нет верного ответа

7. Выберите верное утверждение:

А) ЗЛП не имеет решения, если ОДР является непустым множеством

Б) линию уровня нужно перемещать в задаче на максимум в направлении вектора-нормали

В) если при перемещении линии уровня по ОДР линия уровня уходит в бесконечность, то задача не имеет решения

Г) среди утверждений нет верного

Д) б и в верные утверждения

8. Среди утверждений выберите верное:

А) ЗЛП можно решить исключительно графическим способом

Б) нелинейное программирование используется при решении задач только в том случае, когда целевая функция нелинейная, а ограничительные условия выражены линейными зависимостями

В) а и б верные утверждения

Г) верно только б

Д) нет верного утверждения

9. Для решения задачи нелинейного программирования условной оптимизации методом Лагранжа необходимо…

А) линейность ограничений

Б) наличие ограничений в виде равенств, отсутствие условия не отрицательности переменных

В) нелинейность целевой функции

Г) нелинейность ограничений

10. Какое число множителей Лагранжа может быть использовано при решении задачи нелинейного программирования условной оптимизации с количеством переменных, равным 8:

А) 8

Б) более 8

В) столько же, сколько ограничений в задаче

Г) нет верного ответа

1. Метод оптимизации, в котором осуществляется переход задачи с ограничениями к задаче без ограничений, называется методом …

А) классического анализа

Б) множителей Лагранжа

В) линейного программирования

Г) нелинейного программирования

2. Вид ограничений общей задачи линейного программирования — …

А) уравнений и неравенства

Б) только уравнения

В) только неравенства

Г) только условия неотрицательности

3. Если в ЗЛП допустимое множество не пусто и целевая функция ограничена, то

А) допустимое множество не ограничено

Б) решения не существует

В) существует хотя бы одно оптимальное решение

Г) среди ответов нет верного

4. Моделирование — это:

А) процесс замены реального объекта (процесса, явления) моделью, отражающей его существенные признаки с точки зрения достижения конкретной цели;

Б) процесс демонстрации моделей одежды в салоне мод;

В) процесс неформальной постановки конкретной задачи;

Г) процесс замены реального объекта (процесса, явления) другим материальным или идеальным объектом;

Д) процесс выявления существенных признаков рассматриваемого объекта.

5.Математическая модель объекта — это:

а) созданная из какого-либо материала модель, точно отражающая внешние признаки объекта-оригинала;

б) описание в виде схемы внутренней структуры изучаемого объекта;

в) совокупность данных, содержащих информацию о количественных характеристиках объекта и его поведения в виде таблицы;

г) совокупность записанных на языке математики формул, отражающих те или иные свойства объекта-оригинала или его поведение;

д) последовательность электрических сигналов.

6.Решение, минимизирующее или максимизирующее целевую функцию в задачах линейного программирования, называется

А) целевым

Б) оптимальным

В) ограничивающим

Г) нет верного ответа

7.Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то:

А) допустимое множество не ограничено;

Б) оптимальное решение не существует;

В) существует хотя бы одно оптимальное решение.

8.Метод минимальной стоимости заключается в том, чтобы…

Б) во всей таблице начинать заполнение ячеек с наименьшей стоимостью перевозок

В) в каждой строке и в каждом столбце найти ячейку с наименьшими затратами и начать заполнение с этих ячеек

Г) среди ответов нет верного

9.Задача линейного программирования не имеет конечного оптимума, если
А) в точке А области допустимых значений достигается максимум целевой функции F
Б) в точке А области допустимых значений достигается минимум целевой функции F
В) коэффициенты в целевой функции отрицательны
Г) целевая функция не ограничена сверху на множестве допустимых решений

10.Метод Жордана-Гаусса заключается в …

А) последовательном исключении переменных

Б) последовательном исключении свободных членов

В) вычислении вспомогательных определителей системы

Г) нахождении обратной матрицы

Ответы к тесту методы оптимальных решений

Базисным решением системы m линейных уравнений с n переменными называется решение, в котором.

1) все m неосновных переменных равны нулю
2) все n-m неосновных переменных равны нулю
3) все m неосновных переменных не равны нулю
4) все n-m неосновных переменных не равны нулю

При решении задачи линейного программирования геометрическим методом оптимальным решением может быть.

1) одна точка
2) две точки
3) отрезок
4) интервал

Общая задача линейного программирования может включать в себя.

1) систему ограничений в виде неравенств
2) систему ограничений в виде равенств
3) требования оптимизации нелинейной целевой функции
4) требования оптимизации линейной целевой функции

Критерий оптимальности решения задачи линейного программирования при отыскании максимума линейной функции с выражением линейной функции через неосновные переменные …, то решение задачи оптимально.

1) отсутствуют отрицательные коэффициенты при неосновных переменных
2) отсутствуют положительные коэффициенты при неосновных переменных
3) отсутствуют положительные коэффициенты при основных переменных
4) присутствуют положительные коэффициенты при основных переменных

Оценочные ограничения строки i разрешающего столбца s для симплекс — таблицы задача линейного программирования в следующие правила.

1) ¥, если b_i_{=0 и a_is<0}
2) ¥, если b_i_{=0 и a_is>0}
3) 0, если b_i_{=0 и a_is>0}
4) 0, если b_i_{=0 и a_is<0}

Для взаимно-двойственных задач линейного программирования.

1) в общих задачах ищется максимум или в обоих — минимум
2) в одной задаче ищется максимум в другой — минимум
3) матрицы коэффициентов при переменных в системах ограничений обеих задач совпадают
4) матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг другу

Метод северо-западного угла: «поставщик» — «потребитель» так, чтобы:

1) переменной x₁₁ дается минимально возможное значение
2) переменной x₁₁ дается максимально возможное значение
3) после вычеркивания первого столбца северо-западным элементом будет является элемент x₁₂
4) после вычеркивания первого столбца северо-западным элементом будет является элемент x₁₁
5) после вычеркивания первого столбца северо-западным элементом будет является элемент x₂₁

Согласно первой теореме двойственности:

1) если одна задача имеет оптимальное решение, то двойственная задача оптимального решения не имеет
2) если одна задача имеет оптимальное решение, то двойственная задача тоже имеет оптимальное решение
3) если линейная функция одной из задач не ограничена, то условия двойственной задачи противоречивы
4) если линейная функция одной из задач не ограничена, то линейная функция двойственной задачи тоже не ограничена

Распределенный метод решения транспортной задачи

1) поставка, передаваемая по циклу определяется как минимум среди поставок в клетках цикла со знаком «+»
2) поставка, передаваемая по циклу определяется как минимум среди поставок в клетках цикла со знаком «-«
3) поставка, передаваемая по циклу не может быть ни меньше, ни больше минимума поставок клеток цикла со знаком «-«
4) поставка, передаваемая по циклу не может быть ни меньше, ни больше минимума поставок клеток цикла со знаком «+»

Задачи конечномерной оптимизации делятся на . ..

1) точные
2) приближенные
3) аналитические
4) эвристические

Пусть решается задача определенного экстремума. Составим функцию Лагранжа: L(x₁,…,x_n)=f(x₁,…,x_n)+Sl_ij_i(x₁,…,x_n). Для определения стационарных точек необходимо.

1) приравнять к нулю производные L по переменным x₁,…,x_n
2) приравнять к нулю производные L по переменным l₁,…,l_m
3) приравнять к нулю производные L по переменным x₁,…,x_n и производные L по переменным l₁,…,l_m
4) приравнять к нулю производные L по переменным x₁,…,x_n и приравнять к нулю функции j₁,. ..,j_m

Математическая постановка задачи оптимального уравнения включает следующие элементы

1) математическое описание объекта управления
2) описание состояния внешней среды
3) предмодельный анализ экономической сущности
4) описание управляющего воздействия
5) математическое описание критерия качества управления
6) описание изменения (движения) объекта управления

Транспортная задача. Найти объемы перевозок для каждой пары «поставщик» — «потребитель» так, чтобы:

1) мощности всех поставщиков были реализованы
2) мощности всех поставщиков были минимальны
3) спросы всех потребителей были минимальны
4) спросы всех потребителей были удовлетворены
5) суммарные затраты на перевозку были минимальны
6) суммарные затраты на перевозку были бы удовлетворены

Методы отсечения:

1) мощности всех поставщиков были реализованы
2) сначала задача решается без условия целочисленности
3) сначала задается в задаче условие целочисленности
4) вводится дополнительное ограничение правильности отсечения
5) дополнительное ограничение правильности отсечения выполняются автоматически

В задаче многокритериальной оптимизации для оценки качества найденных решений используют эталонные точки:

1) идеальная точка
2) утопическая точка
3) оптимальная точка
4) надир

Задачи теории массового обслуживания:

1) определения максимальной длинны очереди
2) определение необходимой скорости обслуживания
3) рациональное построение очереди
4) определение количества приборов обслуживания, которые работают параллельно

Для Марковского процесса в физической системе характерно:

1) для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент
2) для каждого момента времени вероятность любого состояния системы в будущем зависит от состояния системы в прошлые моменты времени
3) для каждого момента времени вероятность любого состояния системы в будущем не зависит от того, каким образом система пришла в это состояние
4) для каждого момента времени вероятность любого состояния системы в будущем не зависит от того, каким образом система пришла в это состояние

Общая задача целочисленного программирования: Найти такое решение X=(x₁,. ..,x_n), при котором линейная функция Z=Sc_jx_j принимает минимальное или максимальное значение при ограничениях:

1) Z=Sc_jx_j , c_j и x_j — целые
2) Z=Sa_ijx_j=b_i , a_ij, x_j и b_i — целые
3) Z=Sa_ijx_j=b_i , a_ij и b_i — целые
4) x_j ³ 0, x_j — целые

Особенности модели динамического моделирования:

1) задача оптимизации интерпретируется как многошаговый процесс управления
2) целевая функция равна сумме целевых функций каждого шага
3) количество управляющих переменных может быть бесконечно
4) количество управляющих переменных — конечно

Методы оптимальных решений Тесты с ответами ИММиФ Тема 4-5

Главная » База вопросов » ИММиФ

Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)

Тема 4

Если число ресурсов, которые распределяются по работам равно числу работ и один ресурс назначаются только на одну работу, то задача линейного программирования, к которой сводится задача имеет основные ограничения…

+Все ограничения равенства

Все ограничения неравенства вида ≤

Все ограничения неравенства вида ≥

Ограничения могут быть как равенства, так и неравенства

Матрица эффективности задачи о назначениях при максимизации критерия имеет вид:

Какую матрицу нужно взять за исходную при решении задачи Венгерским методом?

Задача о назначениях с минимизацией критерия имеет матрицу затрат вида:

D E F

А 6 3 4

В 2 8 5

С 1 7 9

Ее решение будет:

+A-E, B-F, C-D

A-D, B-F, C-E

A-F, B-D, C-E

A-F, B-E, C-D

Суммарные затраты для предыдущей задачи равны…

Выберите один ответ.

Какие компьютерные программы предназначены для помощи ЛПР в решении многокритериальных задач о назначении?

Системы управления базами данных

+Интеллектуальные информационные системы

Коммуникационные системы

Системы программирования

Тема 5

В выборах участвуют 3 кандидата: А, В и С. Предпочтения 30 избирателей распределились следующим образом:

Помощь с обучением

Получи бесплатный расчет за 15 минут

Предпочтения Число голосов Предпочтение Число голосов

А→В→С 6 В→С→А 4

А→С→В 5 С→А→В 4

В→А→С 6 С→В→А 5

Кто победил по методу голосования Кондорсе?

Победил А

Победил В

Победил С

+Однозначно выявить победителя нельзя

Исходные данные о выборах приведены в задании 1. Кто победил по методу голосования Борда?

+Победил А

Победил В

Победил С

Однозначно выявить победителя нельзя

Исходные данные о выборах приведены в задании 1. Кто победил по методу большинства первых мест в одном туре?

+Победил А

Победил В

Победил С

Однозначно выявить победителя нельзя

Как называется принцип голосования «коллективный выбор в системе голосования должен повторять в точности единогласное мнение всех голосующих»?

Аксиома универсальности

+Аксиома единогласия

Аксиома полноты

Аксиома транзитивности

Из двух кандидатов каждый избиратель выбирает лучшего. Побеждает тот, который будет большее число раз выбран лучшим. Какая аксиома Эрроу не может быть проверена в данной системе голосования?

Аксиома универсальности

Аксиома единогласия

Аксиома полноты

Аксиома транзитивности

Несколько конкурентов, выпускающих аналогичный товар, пытаются договориться о объемах выпускаемого товара. Каждый производитель хочет увеличить свой объем выпуска за счет уменьшения выпуска у конкурентов. Какую математическую модель принятия решений целесообразно здесь использовать.

Организацию работы ГПР с помощью посредника

+Теорию игр

Принятие решений в условиях определенности

Метод голосования

Какой этап организации работы ГПР нужно выполнить в первую очередь?

Сбор информации

Разработка шкал оценки по критериям

+Определение списка критериев

Анализ информации

Помощь с обучением

Получи бесплатный расчет за 15 минут

Методы оптимальных решений (Ответы к тесту Синергия) — Тест Синергия — Ответы на тесты Синергия

Методы оптимальных решений (Ответы к тесту Синергия)

Тип: Тест Синергия Предмет: Методы оптимальных решений Год сдачи: 2018-2022 Итоговая оценка: 93 баллов 48 вопросов. Правильные ответы выделены маркером в документе Word. Тест сдан на «отлично» (93 баллов), скриншот с результатом прилагается к работе.

Аппарат динамического программирования позволяет решать задачи только
только финансового характера
только по управлению ресурсами
в динамике

Метод Дельфи относится к … методам
Количественным
Эвристическим
Формализованным

Модель принятия решения Врума-Йеттона …
Помогает руководителю обосновать принятое решение
Помогает руководителю найти альтернативы решения возникшей проблемы
помогает выбрать метод разработки решения
Дает возможность определить роль подчиненных в процессе принятия решения

Уровень риска характеризуется
Произведением вероятности возникновения ущерба и размера возможного ущерба
Вероятностью возникновения ущерба
размером возможного ущерба

Полнота набора критериев означает, что …
критерии должны быть определены так, чтобы не дублировался учет одних и тех же аспектов решаемой проблемы
критерии должны быть такими, чтобы их можно было объяснять другим, особенно в тех случаях, когда важнейшей целью работы является выработка и защита определенной позиции
критерий должен охватывать все важные аспекты проблемы

Процессы принятия управленческих решений в организациях, как правило, …
носят индивидуальный характер
протекают в паритетных группах
протекают в иерархических группах

Критерий – это …
вероятностный показатель оценки альтернатив
способ выражения различий в оценке альтернативных вариантов с точки зрения участников процесса выбора
один из возможных способов достижения цели или один из конечных вариантов решений

Понятие «чистый риск» означает …
вероятность получения убытка или нулевого результата
возможными величинами прибыли и убытков
все издержки, связанные с решением, минус вероятная прибыль количественную оценку
вероятности получения запланированной прибыли разность между максимально

Риск при принятии управленческих решений заключается …
в невозможности прогнозировать результаты решения
в вероятности потери ресурсов или неполучения дохода
в отсутствии необходимой информации для анализа ситуации
в опасности принятия неудачного решения

… представляет собой набор прогнозов по каждому рассматриваемому решению, его реализации, а также по возможным положительным и отрицательным последствиям
Активизирующий метод
Эвристический метод
Метод сценариев

Критерий Вальда – это критерий …
средневзвешенного выигрыша
недостаточного основания
максимального гарантированного результата
пессимизма-оптимизма
наименьших возможных потерь

Критерий Гурвица – это критерий …
пессимизма-оптимизма
наименьших возможных потерь
максимального гарантированного результата
средневзвешенного выигрыша
недостаточного основания

Критерий Сэвиджа – это критерий …
средневзвешенного выигрыша
наименьших возможных потерь
недостаточного основания
пессимизма-оптимизма
максимального гарантированного результата

Максиминные и минимаксные критерии относятся к принятию решений в условиях …
риска
определенности
неопределенности

Основу принятия всех решений на всех этапах процесса выработки решений составляют …
предпочтения ЛПР (лица, принимающего решения)
как предпочтения ЛПР, так и предпочтения эксперта
предпочтения эксперта

Для более эффективной реализации управленческого решения …
необходимо сформулировать имеющиеся ограничения
необходима система контроля
необходима оперативная система управления

Под владельцем проблемы понимается …
человек, решающий проблему и ответственный за принятые решения
субъект, который всерьез намерен устранить стоящую перед ним проблему, выделить на ее разрешение и реально задействовать имеющиеся у него активные ресурсы
человек, фактически осуществляющий выбор наилучшего варианта действия

Метод равномерной оптимизации применяется, если …
глобальное качество альтернативы представляет собой сумму локальных (частных) качеств
отсутствуют исходные данные
необходимо провести анализ критериев
необходимо провести детализированный анализ проблемы

Метод математического программирования …
применяется для расчета лучшего варианта решения по критерию оптимальности принятия управленческих решений
не применяется для проведения расчетов управленческих решений
применяется для подсчета вариантов принятия управленческих решений

Метод справедливого компромисса применяется, потому что …
глобальное качество альтернативы представляет собой сумму локальных (частных) качеств
имеется тесная связь с решением в некооперативных играх
необходимо провести анализ критериев
необходимо провести детализированный анализ проблемы

Методы психологической активизации и методы подключения новых интеллектуальных источников относятся …
к активизирующим методам
к методам сценариев
к эвристическим методам

Управление проектом – это …
декомпозиция проблемы на составляющие элементы
формализованное представление экономической задачи
профессиональная деятельность по руководству ресурсами

Альтернатива – это …
один из возможных способов достижения цели или один из конечных вариантов решений
вариант действий ЛПР (лица, принимающего решения)
способ выражения различий в оценке альтернативных вариантов с точки зрения участников процесса выбора

В условиях, когда значения параметра достоверности прогноза меньше единицы, для определения наиболее выгодных стратегий используется критерий …
Гурвица
Лапласа
Ходжа–Лемана

Величину общего эффекта от использования информации, содержащейся в прогнозе для ЛПР Vd , можно определить как …
Vx=uB(Vf–Vr)
Vy=Vf(uB–uA)
Vd=VxVy

Величина дополнительного выигрыша, получаемого вследствие повышения достоверности прогноза Vy, может быть определена по формуле …
Vx=uB(Vf–Vr)
Vy=Vf(uB–uA)
Vd=VxVy

Величина дополнительного выигрыша, получаемого вследствие изменения принимаемого решения Vх, может быть определена по формуле …
Vx=uB(Vf–Vr)
Vy=Vf(uB–uA)
Vd=VxVy

Метод мозгового штурма относится к … методам
количественным
формализованным
эвристическим

Параметрический метод относится к … методам
формализованным
количественным
эвристическим

Метод синектики относится к … методам
формализованным
количественным
эвристическим

Метод фокальных объектов относится к … методам
количественным
формализованным
эвристическим

Морфологический метод относится к … методам
количественным
формализованным
эвристическим

Транспортная задача относится к классу …
управленческих задач
экономических задач
задач линейного программирования (ЗЛП)

Применение ММ-критерия оправдано, если …
имеется тесная связь с решением в некооперативных играх
необходимо провести детализированный анализ проблемы
необходимо исключить какой бы то ни было риск

Основные достоинства системы «ринги» заключаются в том, что …
тщательно и всесторонне исследуется решаемая проблема
принимаемые решения более обоснованы
решения принимаются весьма оперативно
реализация решений проходит быстро и эффективно
менеджер несет персональную ответственность за результаты принятого решения

К группе методов исследования операций относится …
метод Дельфи
метод управления запасами
метод линейного программирования
метод теории игр
метод разработки сценария

Под нормализацией векторного критерия при многокритериальной оптимизации понимается …
анализ критериев
поиск оптимального решения
декомпозиция задачи на составляющие части
приведение всех критериев к единой шкале измерения

ЛПР (лицо, принимающее решения) – это …
человек, который лично работает в рассматриваемой области деятельности, является признанным специалистом по решаемой проблеме, может и имеет возможность высказать суждения по ней
группа людей, имеющая общие интересы и старающаяся оказать влияние на процесс выбора и его результат
субъект, который всерьез намерен устранить стоящую перед ним проблему, выделить на ее разрешение и реально задействовать имеющиеся у него активные ресурсы, суверенно воспользоваться положительными результатами от решения проблемы или взять на себя всю ответственность за неуспех, неудачу, за напрасные расходы

Активная группа – это …
группа лиц, принимающих решение
группа людей, имеющая общие интересы и старающаяся оказать влияние на процесс выбора и его результат
группа людей, владеющих проблемой

Решение, принятое по заранее определенному алгоритму, называется …
детерминированным
стандартным
хорошо структурированным
формализованным

Под эффективностью управленческого решения понимается …
результат, полученный от реализации решения
разность между полученным эффектом и затратами на реализацию решения
отношение эффекта от реализации решения к затратам на его разработку и осуществление
достижение поставленной цели

На основании матрицы потерь строится критерий …
Лапласа
Гурвица
Вальда
Сэвиджа

Метод анализа иерархий предполагает …
декомпозицию проблемы на простые составляющие части
иерархическое представление задачи
разработку оптимальной структуры управления

Набор критериев должен удовлетворять таким требованиям, как …
полнота, действительность, разложимость, неизбыточность и минимальность
полнота, действительность, неизбыточность и минимальность
полнота, действительность, разложимость, и минимальность

Эксперт – это …
группа людей, имеющая общие интересы и старающаяся оказать влияние на процесс выбора и его результат
человек, который лично работает в рассматриваемой области деятельности, является признанным специалистом по решаемой проблеме, может и имеет возможность высказать суждения по ней
субъект, который всерьез намерен устранить стоящую перед ним проблему, выделить на ее разрешение и реально задействовать имеющиеся у него активные ресурсы, суверенно воспользоваться положительными результатами от решения проблемы или взять на себя всю ответственность за неуспех, неудачу, за напрасные расходы

Дерево решений – это …
философское видение процесса управления
суть процесса принятия решений
графическое представление процесса принятия решений

Метод букета проблем относится к … методам
формализованным
эвристическим
количественным

Просмотры: 3067

Принятие управленческого решения — тест с ответами

Маркетинговая наука в общем смысле рассказывает как эффективнее всего осуществлять продажу товаров. С этой наукой впервые знакомятся студенты в университете. Не редко в конце пройденного курса, преподаватели решают устроить провести проверку усвоенных знаний проведя специальное тестирование. Мы подготовили тест с частыми вопросами, которые встречаются на экзаменах. Правильные ответы в нем выделены символом [+].

Вероятность будет определена объективно, в том случае если:

[+] а) поступит достаточно информации для того, чтобы прогноз оказался статистически достоверным

[-] б) при определении вероятности будут использованы научные методы

[-] в) будут произведены дополнительные исследования

Как правило, одного лишь суждения будет недостаточно для принятия решения:

[-] а) когда ситуация не дает достаточно информации

[+] б) когда ситуация уникальна или очень сложна

[-] в) когда ситуация довольно проста

Вероятность неуплаты заемщиком основного долга и процентов, причитающихся кредитору, представляет собой такой риск:

[-] а) процентный

[-] б) банкротства

[+] в) кредитный

Как называется отношение числа появлений случайного события к общему числу наблюдений:

[+] а) частота

[-] б) дисперсия

[-] в) вероятность

Результат реализации определенной последовательности шагов или действий, подобных тем, что предпринимаются при решении математического уравнения:

[-] а) жесткое решение

[-] б) незапрограммированное решение

[+] в) запрограммированное решение

Необходимость соблюдения четкой причинно-следственной связи общественного развития, преемственность, непротиворечивость развития:

[-] а) всесторонняя обоснованность решения

[+] б) согласованность решения с принятыми ранее решениями

[-] в) необходимая полнота содержания решения

Как называется противоречивость, неточность, неполноценность исходной информации; неоднозначность целей, способов их достижения и последствий принимаемых решений:

[-] а) вероятность

[-] б) случайность

[+] в) неопределенность

Как называют совокупность элементов организации, необходимых для решения и обеспечения выполнения управленческих задач:

[+] а) системой управления

[-] б) органом управления

[-] в) аппаратом управления

Работодатели, как правило, придают большое значение опыту при найме на работу, потому что:

[-] а) опыт позволяет принимать решения рационально

[-] б) опыт позволяет принимать решения с минимальными затратами

[+] в) суждение на основе опыта является основой множества повседневных управленческих решений

Как называются риски, связанные с убытком по причине задержки платежей, отказа от платежа в период транспортировки товара, непоставки товара:

[-] а) процентными

[+] б) транспортными

[-] в) имущественными

Теорема Неймана говорит:

[+] а) о существовании решений в смешанных стратегиях

[-] б) о свойствах оптимальных чистых стратегий

[-] в) о поиске оптимальных чистых стратегий

Оптимальные решения, полученные с учетом и без учета дисконтирования:

[-] а) несопоставимы

[+] б) могут различаться

[-] в) всегда совпадают

В качестве обобщенного критерия часто используется:

[+] а) сумма отдельных показателей

[-] б) частное от деления отдельных показателей

[-] в) произведение отдельных показателей

В задаче о продуктовом наборе критерием оптимальности являются требования:

[-] а) минимального объема

[-] б) минимального веса

[+] в) минимальной цены

В задаче о продуктовом наборе критерием оптимальности являются требования:

[+] а) максимальной калорийности

[-] б) минимального объема

[-] в) минимального веса

Транспортная задача сводится к такой задаче:

[-] а) в условиях неопределенности

[+] б) линейного программирования

[-] в) многокритериальной оптимизации

Поведение марковского процесса на долгосрочном горизонте планирования характеризует его … от начального состояния системы:

[-] а) линейную зависимость

[-] б) случайную зависимость

[+] в) независимость

Графическое решение игры – это нахождение решения игры посредством:

[-] а) проведения интерполирующей кривой через точки платежной матрицы

[-] б) построения огибающей значений платежной матрицы на координатной плоскости

[+] в) представления данных в виде линий на координатной плоскости

Метод компромиссов используется в задачах:

[-] а) статистического анализа

[-] б) линейного программирования

[+] в) многокритериальной оптимизации

Это является численным выражением предпочтения:

[-] а) вероятность

[+] б) полезность

[-] в) математическое ожидание

Преемственность, непротиворечивость развития, необходимость соблюдения четкой причинно-следственной связи общественного развития:

[+] а) согласованность решения с принятыми ранее решениями

[-] б) необходимая полнота содержания решения

[-] в) всесторонняя обоснованность решения

Интуитивные решения в организациях принимаются обычно:

[-] а) менеджерами низшего звена

[+] б) представителями высшего эшелона власти

[-] в) руководителями всех уровней власти в равной степени

То, что принятое решение не должно ни отставать, ни опережать потребности и задачи социально-экономической системы, означает:

[-] а) всестороннюю обоснованность решения

[-] б) согласованность решения с принятыми ранее решениями

[+] в) своевременность решения

Прогнозирование, организация, регулирование, координация, стимулирование, контроль риска в риск-менеджменте, относится к функциям:

[-] а) организации риск-менеджмента

[+] б) субъекта управления

[-] в) объекта управления

Учет фактора времени в некоторых случаях заставляет руководителей опираться на:

[-] а) консультации у специалистов

[-] б) научные методы принятия решений

[+] в) суждение или даже интуицию

Строгое соблюдение субъектом управления тех прав и полномочий, которые ему предоставлены высшим уровнем управления:

[-] а) необходимая полнота содержания решения

[+] б) полномочность решения

[-] в) всесторонняя обоснованность решения

Состоянию, когда в результате деятельности фирма рискует частью или всей величиной чистой прибыли, соответствует область:

[+] а) минимального риска

[-] б) приемлемого риска

[-] в) повышенного риска

Проблемы, в которых не всегда просматриваются условия, факторы, причинно-следственные связи:

[-] а) хорошо структурированные проблемы

[-] б) неструктурированные проблемы

[+] в) слабо структурированные проблемы

Все виды рисков, связанные с конкурентной инвестицией, относятся к таким рискам:

[+] а) несистематическим

[-] б) систематическим

[-] в) спекулятивным

Изначально определяет действия человека и влияет на принимаемые им решения его:

[-] а) интересы

[+] б) система ценностей

[-] в) свобода воли

Тест с ответами по теме Оптимизация

1. Оптимизация – это…

а) Получение оптимальных результатов в определенных пределов;

+ б) Целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях;

в) Ответы а и б – правильные;

г) Правильного ответа нет.

2. На основании выбранного критерия оптимальности составляют…

а) Оптимальную функцию;

б) Функцию критерия оптимальности;

+ в) Целевую функцию;

г) Правильного ответа нет.

3. В САПР основными методами оптимизации являются –…

а) Программные методы.

б) Векторные методы.

+ в) Поисковые методы.

г) Правильного ответа нет.

4. Необходимость оптимизации в проектировании уже появляется на этапе…

а) Эскизного проектировании;

б) Структурного синтеза;

в) Инженерного моделирования;

+ г) Ответы а и в – правильные.

5. Для решения задачи оптимизации первым необходимо сделать…

а) Выбрать критерий оптимальности;

+ б) Составить математическую модель;

в) Выбрать метод оптимизации;

г) Правильного ответа нет.

6. При записи математических задач оптимизации в общем виде обычно используют символы?

+ а) f(x), U;

б) l(x), U;

в) j(x), U;

г) Правильного ответа нет.

7. Область, в пределах которой выполняются все условия реализуемости называется …

а) Областью САПР;

б) Областью Парето;

+ в) Областью работоспособности;

г) Все ответы правильные.

8. Первый этап построения математической модели – …

а) Формализация;

+ б) Исследование объекта;

в) Исследование рынка;

г) Правильного ответа нет.

9. В задачах оптимизации различают критерии оптимизации…

а) Простые;

б) Сложные;

+ в) Ответы а и б – правильные;

г) Правильного ответа нет.

10. Анализ полученного решения бывает …

а) Формальным;

б) Содержательным;

в) Примитивным;

+ г) Ответы а и б – правильные.

11. В математическом программировании отделяют виды решения?

а) Программное;

б) Допустимое;

в) Собственное;

+ г) Ответы б и в – правильные.

12. Синтез проектных решений – это …

а) Сущность проектирования;

б) Необходимая составная часть проектирования;

+ в) Основа проектирования;

г) Правильного ответа нет.

13. Анализ – это…

а) Сущность проектирования;

+ б) Необходимая составная часть проектирования;

в) Основа проектирования;

г) Правильного ответа нет.

14. Синтез подразделяется на:

а) Анализирующий;

б) Параметрический;

в) Структурный;

+ г) Ответы б и в – правильные.

15. В САПР процедуры процедуры параметрического синтеза выполняются в:

а) Интерактивном режиме;

б) Автоматический режиме;

в) Ручном режиме;

+ г) Ответы а и б – правильные.

16. Каким этапом в общем процессе проектирования имеет место инженерное моделирование?

а) 1;

+ б) 2;

в) 3;

г) Правильного ответа нет.

17. Множество точек пространства выходных параметров, из которых невозможно перемещения, приводит к улучшению всех выходных параметров называют …

а) Областью САПР;

б) Областью работоспособности;

+ в) Областью Парето;

г) Другое.

18. Сепарабельное программирования…

а) Представляет собой Сепарабельное функцию;

б) Представляет собой нелинейную функцию;

+ в) Представляет собой сумму функций;

г) Правильного ответа нет.

19. Задача оптимизации сводится к нахождению?

а) Рост целевой функции;

+ б) Экстремума целевой функции;

в) Спада целевой функции;

г) Правильного ответа нет.

20. Любой критерий оптимальности имеет…

+ а) Экономическую природу;

б) Природу управления параметров;

в) Торговую природу;

г) Правильного ответа нет.

21. Каково назначение редактора Р-CAD Symbol Editor?

а) создание схемы Э3;

б) создание схемы Э2;

+ в) создание УГО элементов схемы Э3;

г) автотрасировщик.

22. С помощью которого редактора возможно создание посадочных мест элементов на печатную плату?

а) Р-CAD Symbol Editor;

+ б) Р-CAD Pattern Editor;

в) Р-CAD Schematic;

г) Р-CAD PCB.

23. С помощью какой команды, в программе Р-CAD Schematic, возможно генерирования списка электрических связей схемы для их дальнейшей обработки в Р-CAD PCB?

а) ERC;

+ б) Generate Netlist;

в) Load Netlist;

г) Правильного ответа нет.

24. Создание схем Э3 возможно с помощью программы?

а) Р-CAD Symbol Editor;

б) Р-CAD Pattern Editor;

+ в) Р-CAD Schematic;

г) Р-CAD PCB.

25. В каком слое вводится контур ПП?

а) Top;

б) Bottom;

+ в) Board;

г) Top Silk.

26. В чем заключается суть ручного проведения трасс?

+ а) Прокладка трасс проводиться полностью ручным способом в строгом соответствии с замыслом разработчика;

б) Разработчик только указывает направление фрагмента трассы, а система формирует ее сама с учетом принятых правил трассировки;

в) Ответы а и б – правильные;

г) Правильного ответа нет.

27. При котором алгоритме построения трасс ПП каждое соединение проводится по кратчайшему пути, обходя препятствия,которые встречаются?

а) Ортогональный;

б) Волновой;

+ в) Эврестический;

г) Правильного ответа нет.

28. Который с автотрассировщиков основан на безсеточной технологии и реализует принципы оптимизации нейронных сетей?

а) Quick-Route;

+ б) Shape—Based Router;

в) Ответы а и б – правильные;

г) Правильного ответа нет.

29. В чем заключается суть интерактивного проведения трасс?

а) Прокладка трасс проводиться полностью ручным способом в строгом соответствии с замыслом разработчика;

+ б) Разработчик только указывает направление фрагмента трассы, а система формирует ее сама с учетом принятых правил трассировки;

в) Ответы а и б – правильные;

г) Правильного ответа нет.

30. Имеет ли возможность P-CAD проверять схемы Э3 на работоспособность?

а) Да;

б) Нет;

+ в) Да, но с помощью специальных утилит.

Поделиться с друзьями:

Adblock
detector

Оптимизация

— Симплексный метод — несколько оптимальных решений?

спросил 6 лет, 10 месяцев назад

Изменено 6 месяцев назад

Просмотрено 11 тысяч раз

$\begingroup$

Мне нужно решить эту задачу оптимизации:

$$\begin{array}{ll}\text{свернуть} & z= x_1 — x_2 + 3x_3\\\\ \text{при условии} &x_1-x_2+x_3 -x_4=2\\ & 2x_1-2x_2-x_3+x_5=0\\ & x_1, x_2, x_3, x_4, x_5 \geq 0\end{массив}$$

Я использовал двухфазный симплексный метод, и вот окончательная таблица:

Текущее решение $(x_1,x_2,x_3,x_4,x_5) = (2/3,0,4/3,0,0)$ оптимально. * + \lambda(-y_2,e_2)$, где $(-y_2,e_2)$ — крайнее направление, поэтому множественные решения:

$\left(\frac 23,0,\frac43\right)’ + \lambda(1,1,0)’ = \left(\frac23+\lambda, \lambda, \frac43\right)’$ для $ \лямбда\ge 0$.

Итак, в качестве примера вы можете заметить, что при $\lambda=1$ вы получаете решение $\left(\frac 53,1,\frac 43\right)$, которое допустимо и также является оптимальным.

$\endgroup$

$\begingroup$

Неверный ответ , так как не учитывает неограниченные множества, которые помимо крайних точек могут иметь еще и крайние направления. Я не могу удалить его, так как он был принят, поэтому он останется для истории.

Приведенной стоимости для неосновной переменной недостаточно, чтобы заключить, что у нас есть несколько оптимальных решений. Для этого необходимо также, чтобы эта небазисная переменная могла входить в базис, другими словами, она должна иметь соответствующий опорный элемент в выбираемом столбце. Переменная $x_2$ не имеет кандидата на опорную точку (вообще нет положительных элементов), поэтому ее нельзя сделать базовой. Вывод: оптимальное решение единственно.

$\endgroup$

$\begingroup$

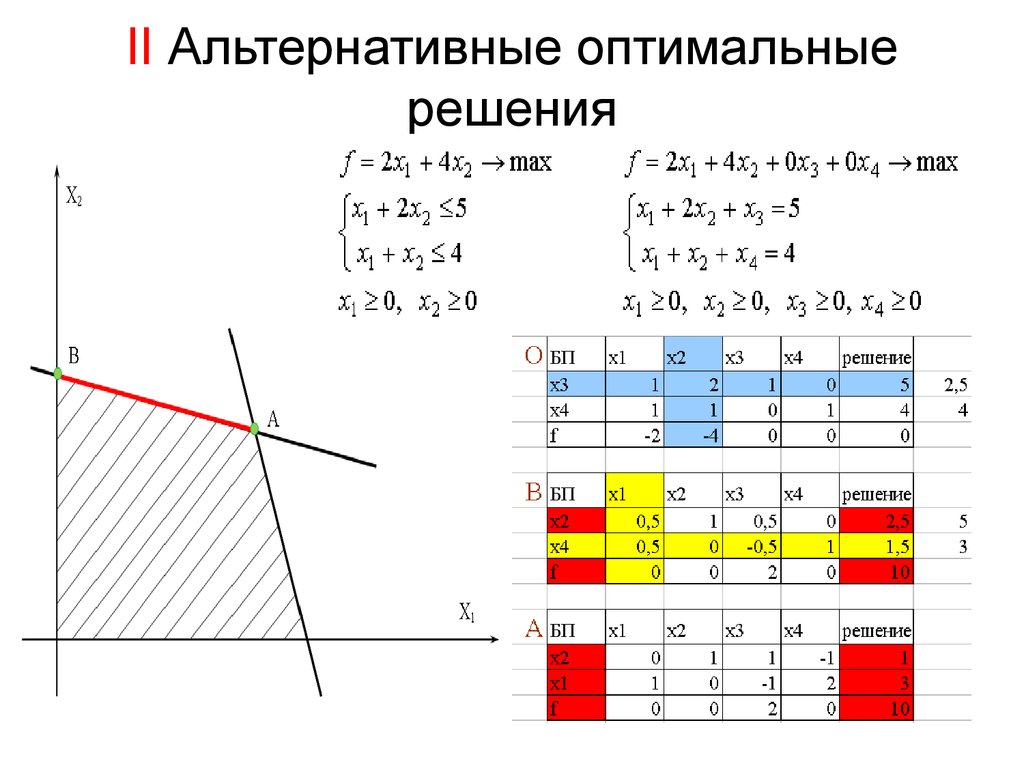
Ответ @mathematician правильный. Рассмотрим это изображение с неограниченной допустимой областью. При рассмотрении целевой функции, аналогичной $f(x)$ и $g(x)$ на изображении, черная точка является оптимальным решением. Теперь здесь у нас есть несколько оптимальных решений, и красная линия — это крайнее направление, и решения на нем также оптимальны.

Симплексная таблица в вопросе похожа на этот случай. Если есть небазисная переменная и все значения в ее столбце неположительны, допустимая область не ограничена в этом направлении (что опять же имеет место в симплексной таблице этого вопроса)

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Линейная оптимизация

Дальнейшие чтения:
Акофф Р., Лучшее Акоффа: его классические труды по менеджменту , Wiley, 1999.
Бендер Е., Введение в математическое моделирование , Dover Pubns, 2000.
Fdida S. и G. Pujolle, Методы моделирования и оценка производительности , Elsevier Science, 1987.
Гершенфельд Н., Природа математического моделирования , Кембриджский ун-т. Пр., 1998.

Задачи оптимизации широко распространены в математическом моделировании систем реального мира и охватывают очень широкий спектр приложений. Эти приложения возникают во всех областях экономики, финансов, химии, материаловедения, астрономии, физики, структурной и молекулярной биологии, инженерии, компьютерных наук и медицины.

Оптимизационное моделирование требует соответствующего времени. Общая процедура, которую можно использовать в технологическом цикле моделирования, заключается в следующем: (1) описать проблему, (2) предписать решение и (3) контролировать проблему путем непрерывной оценки/обновления оптимального решения при изменении параметров. и структуру проблемы. Ясно, что среди этих общих шагов всегда есть петли обратной связи.

Математическая формулировка проблемы: как только вы обнаружите проблему, подумать и понять ее, чтобы адекватно описать проблему в письменной форме. Разработайте математическую модель или структуру для представления реальности, чтобы разработать/использовать алгоритм решения оптимизации. Формулировка проблемы должна быть проверена до того, как будет предложено решение. Хорошая математическая формулировка оптимизации должна быть как инклюзивной (т. е. включать в себя то, что относится к задаче), так и исключающей (т. е. исключать то, что не относится к задаче).

Найдите оптимальное решение: это идентификация алгоритма решения и этапа его реализации. Единственный хороший план — это реализованный план, который остается реализованным!

Управленческая интерпретация оптимального решения: как только вы распознаете алгоритм и определите подходящий модуль программного обеспечения для применения, используйте программное обеспечение для получения оптимальной стратегии. Затем решение будет представлено лицу, принимающему решение, в том же стиле и на том же языке, что и лицо, принимающее решение. Это означает предоставление управленческой интерпретации стратегического решения с точки зрения непрофессионала, а не просто предоставление лицу, принимающему решение, компьютерной распечатки.

Анализ после решения: эти действия включают в себя обновление оптимального решения, чтобы контролировать проблему. В этом постоянно меняющемся мире крайне важно периодически обновлять оптимальное решение любой задачи оптимизации. Модель, которая была валидной, может потерять валидность из-за изменяющихся условий, становясь, таким образом, неточным представлением реальности и отрицательно влияя на способность лица, принимающего решения, принимать правильные решения. Создаваемая вами оптимизационная модель должна быть в состоянии справиться с изменениями.

Важность обратной связи и контроля. Необходимо уделить особое внимание важности размышлений об аспектах обратной связи и контроля в задаче оптимизации. Было бы ошибкой обсуждать контекст процесса оптимизационного моделирования и игнорировать тот факт, что никогда нельзя рассчитывать найти неизменное, неизменное решение проблемы принятия решений. Сама природа среды оптимальной стратегии меняется, и поэтому обратная связь и контроль являются важной частью процесса оптимизации-моделирования.

Вышеупомянутый процесс изображен как этапы системного анализа, проектирования и контроля на следующей блок-схеме, включая действия по проверке и проверке:

Дальнейшие чтения:
Бероджи Г., Моделирование решений в управлении политикой: введение в аналитические концепции , Бостон, Kluwer Academic Publishers, 1999.
Кэмм Дж. и Дж. Эванс, Наука управления: моделирование, анализ и интерпретация , Паб Юго-Западного колледжа, 1999.

Компоненты задач оптимизации и их классификация

Суть всех деловых решений, принимаемых для фирмы или отдельного лица, заключается в том, чтобы найти образ действий, который принесет вам наибольшую прибыль.

Человечество давно искало или заявляло, что ищет лучшие способы выполнения повседневных жизненных задач. На протяжении всей истории человечества человек сначала искал более эффективные источники пищи, а затем искал материалы, энергию и овладение физической средой. Однако относительно поздно в истории человечества общие вопросы стали количественно формулироваться сначала в словах, а затем перерастали в символические обозначения. Одним из широко распространенных аспектов этих общих вопросов был поиск «лучшего» или «оптимального». Большую часть времени менеджеры стремятся просто добиться некоторого повышения уровня производительности или решить проблему, связанную с достижением цели. Следует подчеркнуть, что эти слова обычно не имеют точного значения.

Были предприняты попытки описать сложные человеческие и социальные ситуации. Чтобы иметь смысл, задача должна быть записана в математическом выражении, содержащем одну или несколько переменных, в которых должны быть определены значения переменных. Затем задается вопрос: какие значения должны иметь эти переменные, чтобы математическое выражение имело максимально возможное числовое значение (максимизация) или наименьшее возможное числовое значение (минимизация). Этот процесс максимизации или минимизации называется оптимизацией.

Оптимизация, также называемая математическим программированием, помогает найти ответ, дающий наилучший результат — тот, который обеспечивает наибольшую прибыль, выпуск или счастье, или тот, который обеспечивает наименьшие затраты, потери или неудобства. Часто эти проблемы связаны с наиболее эффективным использованием ресурсов, включая деньги, время, оборудование, персонал, инвентарь и многое другое. Задачи оптимизации часто классифицируют как линейные или нелинейные, в зависимости от того, являются ли отношения в задаче линейными по отношению к переменным. Существует множество программных пакетов для решения задач оптимизации. Например, LINDO или ваш WinQSB решают линейные программные модели, а LINGO и What’sBest! решать нелинейные и линейные задачи.

Математическое программирование решает проблему определения оптимального распределения ограниченных ресурсов, необходимых для достижения поставленной цели. Цель должна представлять цель лица, принимающего решение. Например, ресурсы могут соответствовать людям, материалам, деньгам или земле. Из всех допустимых распределений ресурсов желательно найти одно или те, которые максимизируют или минимизируют некоторую числовую величину, такую как прибыль или стоимость. Модели оптимизации также называют предписывающими или нормативными моделями, поскольку они стремятся найти наилучшую возможную стратегию для лица, принимающего решения.

Существует множество доступных алгоритмов оптимизации. Однако некоторые методы подходят только для определенных типов проблем. Важно уметь распознавать характеристики проблемы и определять подходящий метод решения. В каждом классе задач существуют разные методы минимизации, которые различаются по вычислительным требованиям, свойствам сходимости и так далее. Задачи оптимизации классифицируются по математическим характеристикам целевой функции, ограничениям и контролируемым переменным решения.

Проблемы оптимизации состоят из трех основных компонентов:

Целевая функция, которую мы хотим минимизировать или максимизировать. То есть величина, которую вы хотите максимизировать или минимизировать, называется целевой функцией. Большинство задач оптимизации имеют единственную целевую функцию, в противном случае их часто можно переформулировать так, чтобы они выполнялись. Два интересных исключения из этого правила:
Проблема поиска цели: В большинстве бизнес-приложений менеджер хочет достичь определенной цели, удовлетворяя ограничениям модели. Пользователь особо не хочет ничего оптимизировать, поэтому нет смысла определять целевую функцию. Этот тип проблемы обычно называют проблемой осуществимости.
Множественные целевые функции: Часто пользователь хотел бы оптимизировать множество разных целей одновременно. Обычно разные цели несовместимы. Переменные, оптимизирующие одну цель, могут быть далеки от оптимальных для других. На практике задачи с несколькими целями переформулируются как задачи с одной целью либо путем формирования взвешенной комбинации различных целей, либо путем помещения некоторых целей в качестве «желательных» ограничений.
Управляемые входные данные представляют собой набор переменных решения, которые влияют на значение целевой функции. В производственной задаче переменные могут включать в себя распределение различных доступных ресурсов или трудозатраты на каждое действие. Переменные решения имеют важное значение. Если переменных нет, мы не можем определить целевую функцию и ограничения задачи.
Неуправляемые входы называются параметрами. Входные значения могут быть фиксированными числами, связанными с конкретной проблемой. Мы называем эти значения параметрами модели. Часто у вас будет несколько «кейсов» или вариантов одной и той же задачи для решения, и значения параметров будут меняться в каждом варианте задачи.
Ограничения — это отношения между переменными решения и параметрами. Набор ограничений позволяет некоторым переменным решения принимать определенные значения и исключать другие. Для производственной задачи нет смысла тратить отрицательное количество времени на какую-либо деятельность, поэтому мы ограничиваем все переменные «времени», чтобы они были неотрицательными. Ограничения не всегда необходимы. На самом деле область неограниченной оптимизации является большой и важной, для которой доступно множество алгоритмов и программного обеспечения. На практике ответы, которые имеют смысл относительно лежащей в основе физической или экономической проблемы, часто не могут быть получены без наложения ограничений на переменные решения.

Возможные и оптимальные решения: Значение решения для переменных решения, когда все ограничения выполняются, называется допустимым решением. Большинство алгоритмов решения сначала находят допустимое решение, затем пытаются его улучшить и, наконец, изменяют переменные решения, чтобы перейти от одного допустимого решения к другому допустимому решению. Этот процесс повторяется до тех пор, пока целевая функция не достигнет своего максимума или минимума. Этот результат называется оптимальным решением.

Основная цель процесса оптимизации состоит в том, чтобы найти значения переменных, которые минимизируют или максимизируют целевую функцию при соблюдении ограничений. Этот результат называется оптимальным решением.

Существует более 4000 алгоритмов решения различных задач оптимизации. Широко используемые алгоритмы решения разработаны для следующих математических программ: выпуклых программ, сепарабельных программ, квадратичных программ и геометрических программ.

Линейная программа

Линейное программирование имеет дело с классом задач оптимизации, в которых как оптимизируемая целевая функция, так и все ограничения являются линейными с точки зрения переменных решения.

Краткая история линейного программирования:

В 1762 году Лагранж решил решаемые задачи оптимизации с простыми ограничениями равенства.
В 1820 году Гаусс решил линейную систему уравнений с помощью того, что сейчас называется исключением Каусса. В 1866 году Вильгельм Джордан усовершенствовал метод, найдя метод наименьших квадратов ошибок как меру согласия. Сейчас он называется методом Гаусса-Джордана.
В 1945 году появился цифровой компьютер.
В 1947 году Данциг изобрел симплексные методы.
В 1968 году Фиакко и Маккормик представили метод внутренних точек.
В 1984 году Кармаркар применил внутренний метод для решения линейных программ, добавив свой новаторский анализ.

Линейное программирование оказалось чрезвычайно мощным инструментом как при моделировании реальных проблем, так и в качестве широко применимой математической теории. Однако многие интересные проблемы оптимизации являются нелинейными. Изучение таких задач включает разнообразную смесь линейной алгебры, многомерных исчисление, численный анализ и вычислительные методы. Важными областями являются проектирование вычислительные алгоритмы (включая методы внутренних точек для линейного программирования), геометрия и анализ выпуклых множеств и функций, а также изучение специально структурированных проблем, таких как квадратичное программирование. Нелинейная оптимизация обеспечивает фундаментальное понимание математических анализа и широко используется в различных областях, таких как инженерное проектирование, регрессионный анализ, управление запасами, геофизические исследования и экономика.

Квадратичная программа

Квадратичная программа (QP) включает в себя область оптимизации, чья широкая область применимости уступает только линейным программам. Широкий спектр приложений естественным образом подпадает под форму QP. Кинетическая энергия снаряда является квадратичной функцией его скорости. Регрессия методом наименьших квадратов с боковыми ограничениями была смоделирована как QP. Некоторые проблемы в планировании производства, анализе местоположения, эконометрике, анализе активации в проблеме химических смесей, а также в управлении и выборе финансового портфеля часто рассматриваются как QP. Существует множество алгоритмов решения для случая при ограниченном дополнительном условии, когда целевая функция выпукла.

Удовлетворение ограничений

Многие промышленные проблемы принятия решений, связанные с непрерывными ограничениями, могут быть смоделированы как непрерывные задачи удовлетворения ограничений и оптимизации. Проблемы удовлетворения ограничений имеют большой размер и в большинстве случаев связаны с трансцендентными функциями. Они широко используются в химических процессах и моделировании и оптимизации ограничений по стоимости.

Выпуклая программа

Выпуклая программа (КП) охватывает широкий класс задач оптимизации. Когда целевая функция выпукла, а допустимая область представляет собой выпуклое множество, обоих этих допущений достаточно, чтобы гарантировать, что локальный минимум является глобальным минимумом.

Анализ оболочки данных

Анализ охвата данных (DEA) — это показатель производительности, основанный на методах пограничного анализа из литературы по экономике и финансам. Методы анализа предельной эффективности (выход/вход) определяют передовую границу эффективности, которая относится к максимальным результатам, которые могут быть получены из заданного набора входных данных по отношению к выборке единиц, принимающих решения, с использованием сопоставимого процесса для преобразования входных данных в выходные.

Сила DEA частично зависит от того факта, что это непараметрический подход, который не требует спецификации какой-либо функциональной формы отношений между входами и выходами. Выходные данные DEA сводят несколько показателей производительности к одному, чтобы использовать методы линейного программирования. Взвешивание показателей эффективности зависит от полезности лица, принимающего решения.

Динамическое программирование

Динамическое программирование (DP) — это, по сути, восходящая рекурсия, при которой вы сохраняете ответы в таблице, начиная с базового случая (вариантов) и постепенно увеличивая параметры, используя рекурсивное правило (правила). Вы бы использовали этот метод вместо рекурсии, когда вам нужно вычислить решения для всех подзадач, а рекурсивное решение будет решать некоторые из подзадач повторно. Хотя, как правило, DP способна решать множество разнообразных задач, в большинстве случаев она может потребовать огромного объема памяти компьютера.

Отдельная программа

Разделимая программа (SP) включает частный случай выпуклых программ, где целевая функция и ограничения являются разделимыми функциями, т.

Е. Каждый член включает только одну переменную.

Геометрическая программа

Геометрическая программа (ГП) относится к невыпуклому программированию и имеет множество приложений, в частности, в задачах инженерного проектирования.

Дробная программа

В этом классе задач целевая функция представлена в виде дроби (т. е. отношения двух функций). Дробная программа (FP) возникает, например, при максимизации отношения прибыли капитала к затраченному капиталу или как показатель эффективности коэффициента потерь.

Эвристическая оптимизация

Эвристика — это нечто, «оказывающее помощь в направлении решения проблемы, но в остальном неоправданное или не поддающееся обоснованию». Таким образом, эвристические аргументы используются, чтобы показать, что мы могли бы попытаться доказать позже или что мы могли бы ожидать найти при запуске компьютера. В лучшем случае это обоснованные догадки.

За последнее десятилетие появилось несколько эвристических инструментов, которые облегчают решение задач оптимизации. проблемы, которые раньше было трудно или невозможно решить. Эти инструменты включают в себя эволюционные вычисление, имитация отжига, поиск табу, рой частиц и т. д.

Общие подходы включают, но не ограничиваются:

сравнение качества решения с оптимальным на контрольных задачах с известные оптимумы, среднее отличие от оптимума, частота, с которой эвристика находит оптимум.
сравнение качества решения с наиболее известным для эталонных задач, оптимальные решения которых не могут быть найдены.
сравнение вашей эвристики с опубликованной эвристикой для одного и того же тип задачи, разница в качестве решения для данного времени выполнения и, если актуально, лимит памяти.
профилирование среднего качества решения в зависимости от времени выполнения, для например, построение среднего значения и либо минимума и максимума, либо 5-го и 95-го процентили значения решения как функция времени — это предполагает, что у одного есть несколько экземпляров эталонных задач, которые сопоставимы.

Глобальная оптимизация

Целью глобальной оптимизации (ГО) является поиск наилучшего решения моделей принятия решений при наличии множества локальных решений. Пока оптимизация с ограничениями имеет дело с поиском оптимума целевой функции с учетом ограничений на ее решающие переменные, в отличие от неограниченная оптимизация ищет глобальный максимум или минимум функции во всем ее доменном пространстве без каких-либо ограничений на переменные решения .

Невыпуклая программа

Невыпуклая программа (NC) охватывает все задачи нелинейного программирования, которые не удовлетворяют предположениям о выпуклости. Однако, даже если вам удастся найти локальный минимум, нет никакой гарантии, что он также будет глобальным минимумом. Поэтому не существует алгоритма, гарантирующего нахождение оптимального решения для всех подобных задач.

Негладкая программа

Негладкие программы (NSP) содержат функции, для которых первая производная не существует. NSP возникают в нескольких важных приложениях науки и техники, включая контактные явления в статике и динамике или эффекты расслоения в композитах. Эти приложения требуют учета негладкости и невыпуклости.

Метаэвристика

Большинство метаэвристик было создано для решения задач дискретной комбинаторной оптимизации. Однако практические приложения в инженерии обычно требуют методов, которые обрабатывают непрерывные переменные или различные непрерывные и дискретные переменные. Как следствие, большие исследовательские усилия были сосредоточены на применении нескольких хорошо известных метаэвристик, таких как имитация отжига (SA), поиск табу (TS), генетические алгоритмы (GA), оптимизация муравьиной колонии (ACO), к непрерывным случаям. Общая метаэвристика направлена на преобразование дискретных областей применения в непрерывные с помощью:

Методологические разработки, направленные на адаптацию некоторых метаэвристик, особенно SA, TS, GA, ACO, GRASP, поиска переменных окрестностей, управляемого локального поиска, поиска рассеяния, к задачам с непрерывными или дискретными/непрерывными переменными.
Теоретические и экспериментальные исследования по метаэвристике, адаптированной к непрерывной оптимизации, например, анализ сходимости, методология оценки производительности, генераторы тестовых случаев, обработка ограничений и т. д.
Программные реализации и алгоритмы метаэвристики, адаптированные к непрерывной оптимизации.
Реальные приложения дискретной метаэвристики, адаптированные к непрерывной оптимизации.
Сравнение производительности дискретной метаэвристики (адаптированной к непрерывной оптимизации) с эффективностью конкурентных подходов, например, оптимизации роя частиц (PSO), алгоритмов оценки распределения (EDA), эволюционных стратегий (ES), специально созданных для непрерывной оптимизации.

Многоуровневая оптимизация

Во многих процессах принятия решений существует иерархия лиц, принимающих решения, и решения принимаются на разных уровнях этой иерархии. Многоуровневая оптимизация фокусируется на всей иерархии структура. Область многоуровневой оптимизации стала хорошо известной и важной областью исследований. Иерархические структуры можно найти в таких научных дисциплинах, как окружающая среда, экология, биология, химическая технология, механика, теория классификации, базы данных, проектирование сетей, транспорт, цепочка поставок, теория игр и экономика. Более того, постоянно внедряются новые приложения.

Многоцелевая программа

Многоцелевая программа (МП), известная также как Целевая программа, заключается в том, что одна объективная характеристика задачи оптимизации заменяется несколькими целями. При решении МП можно представить некоторые цели как ограничения, которые должны быть удовлетворены, в то время как другие цели могут быть взвешены, чтобы составить составную единую целевую функцию.

Оптимизация с несколькими целями отличается от случая с одной целью несколькими способами:

Обычное значение оптимума не имеет смысла в случае множественных целей, потому что решение, оптимизирующее все цели одновременно, в общем случае непрактично; вместо этого запускается поиск возможного решения, обеспечивающего наилучший компромисс между целями в наборе так называемых эффективных решений;
Определение наилучшего компромиссного решения требует учета предпочтений, выраженных лицом, принимающим решение;
Многочисленные задачи, встречающиеся в реальных задачах, часто являются математическими функциями противоположных форм.
Ключевым элементом модели программирования целей является функция достижения; то есть функция, измеряющая степень минимизации нежелательных переменных отклонения целей, рассматриваемых в модели.

Бизнес-приложение: в управлении портфелем кредитных карт прогнозирование поведения держателя карты в отношении расходов является ключом к снижению риска банкротства. Учитывая набор атрибутов для основных аспектов держателей кредитных карт и предопределенные классы поведения при расходах, можно построить модель классификации, используя линейное программирование с несколькими критериями для обнаружения моделей поведения держателей кредитных карт.

Программа небинарных ограничений

На протяжении многих лет сообщество программистов с ограничениями уделяло значительное внимание моделированию и решению проблем с использованием бинарных ограничений. Только недавно небинарные ограничения привлекли внимание из-за растущего числа реальных приложений. Небинарное ограничение — это ограничение, определенное для k переменных, где k обычно больше двух. Небинарное ограничение можно рассматривать как более глобальное ограничение. Моделирование проблемы как небинарного ограничения имеет два основных преимущества: оно облегчает выражение проблемы; и это обеспечивает более мощное распространение ограничений по мере того, как становится доступной более глобальная информация.

Успехи в составлении расписаний, планировании и маршрутизации доказали, что использование небинарных ограничений является многообещающим направлением исследований. На самом деле, все большее число работников OR/MS/DS считают, что эта тема имеет решающее значение для превращения технологии ограничений в реалистичный способ моделирования и решения реальных проблем.

Двухуровневая оптимизация

Большинство моделей математического программирования имеют дело с принятием решений с одной целевой функцией. С другой стороны, двухуровневое программирование разработано для приложений в децентрализованных системах планирования, в которых первый уровень называется лидером, а второй уровень относится к цели ведомого.

В задаче двухуровневого программирования каждое лицо, принимающее решение, пытается оптимизировать свою целевую функцию, не принимая во внимание цель другой стороны, но решение каждой стороны влияет на объективную ценность другой стороны, а также на пространство решений.

Задачи двухуровневого программирования — это задачи иерархической оптимизации, в которых ограничения одной задачи частично определяются второй задачей параметрической оптимизации. Если вторая задача имеет единственное оптимальное решение для всех значений параметров, то эта задача эквивалентна обычной задаче оптимизации с неявно заданной целевой функцией. Однако когда задача имеет неединственные оптимальные решения, применяются оптимистический (или слабый) и пессимистический (или сильный) подходы.

Комбинаторная оптимизация

Комбинаторный обычно означает, что пространство состояний является дискретным (например, символы, не обязательно числа). Это пространство может быть конечным или счетным множеством.

Например, дискретная задача является комбинаторной. Задачи, в которых пространство состояний полностью упорядочено, часто можно решить, сопоставив их с целыми числами и применив «численные» методы. Если пространство состояний неупорядочено или упорядочено только частично, эти методы не работают. Это означает, что методы эвристики становятся необходимыми, например, имитация отжига.

Комбинаторная оптимизация — это изучение упаковки, покрытия и разбиения, которые являются приложениями целочисленных программ. Это основные математические темы на стыке комбинаторики и оптимизации. Эти проблемы связаны с классификацией задач целочисленного программирования в соответствии со сложностью известных алгоритмов и разработкой хороших алгоритмов для решения специальных подклассов. В частности, изучаются проблемы сетевых потоков, паросочетания и их матроидные обобщения. Этот предмет является одним из объединяющих элементов комбинаторики, оптимизации, исследования операций и информатики.

Эволюционные методы

Природа — надежный оптимизатор. Анализируя природный механизм оптимизации, мы можем найти приемлемые методы решения неразрешимых проблем. Двумя наиболее многообещающими концепциями являются моделируемый отжиг и генетические методы. Планирование и составление расписания являются одними из наиболее успешных применений эволюционных методов.

Генетические алгоритмы (ГА) стали высокоэффективным инструментом для решения сложных задач оптимизации. Однако его теоретическая основа все еще довольно фрагментарна.

Оптимизация роя частиц

Particle Swarm Optimization (PSO) — это стохастический алгоритм оптимизации на основе популяции. Вместо конкуренции/отбора, как, например, в Evolutionary Computation, PSO использует сотрудничество в соответствии с парадигмой, которую иногда называют «роевым интеллектом». Такие системы обычно состоят из популяции простых взаимодействующих агентов без какого-либо централизованного контроля и вдохновлены случаями, которые можно найти в природе, такими как колонии муравьев, стаи птиц, стада животных, плесневение бактерий, стайка рыб и т.

д.

Существует множество вариантов PSO, включая ограниченные, многокритериальные, дискретные или комбинаторные версии, и во многих областях были разработаны приложения с использованием PSO.

Интеллект роя

Биологи давно изучают поведение общественных насекомых. После миллионов лет эволюции все эти виды выработали невероятные решения для широкого круга проблем. Разумные решения проблем естественным образом возникают в результате самоорганизации и непрямого общения этих людей. Косвенные взаимодействия происходят между двумя людьми, когда один из них изменяет среду, а другой реагирует на новую среду позже.

Swarm Intelligence — это инновационная распределенная интеллектуальная парадигма для решения задач оптимизации, которая изначально черпала вдохновение из биологических примеров явлений роения, стаи и стадности у позвоночных. Интеллектуальный анализ данных — это аналитический процесс, предназначенный для исследования больших объемов данных в поисках устойчивых шаблонов и/или систематических взаимосвязей между переменными, а затем для проверки результатов путем применения обнаруженных шаблонов к новым подмножествам данных.

Онлайн-оптимизация

Независимо от того, нужно ли сократить затраты, максимизировать прибыль или разумно использовать скудные ресурсы, методы оптимизации доступны для принятия решений. В онлайн-оптимизации основной проблемой являются неполные данные и научная проблема: насколько хорошо может работать онлайн-алгоритм? Можно ли гарантировать качество решения, даже не зная заранее всех данных? При оптимизации в реальном времени есть дополнительное требование: решения должны быть вычислены очень быстро по отношению к рассматриваемому нами периоду времени.

Дальнейшие чтения:
Абрахам А., К. Гросан и В. Рамос, Swarm Intelligence , Springer Verlag, 2006. В нем рассматривается применение роевого интеллекта в интеллектуальном анализе данных с использованием различных интеллектуальных подходов.
Чарнс А., Купер В., Левин А. и Л. Сейфорд, Анализ оболочки данных: теория, методология и приложения , Kluwer Academic Publications, 1994.
Демпе С. , Основы двухуровневого программирования , Клувер, 2002.
Diwekar U., Introduction to Applied Optimization , Kluwer Academic Publishers, 2003. Охватывает почти все вышеуказанные методы.
Лю Б. и А. Эсогбю, Критерии принятия решений и оптимальные процессы инвентаризации , Kluwer, 1999.
Люенбергер Д., Линейное и нелинейное программирование , Kluwer Academic Publishers, 2003.
Миллер Р., Оптимизация: основы и приложения , Wiley, 1999.
Мигдалас А., Пардалос П. и П. Варбранд, Многоуровневая оптимизация: алгоритмы и приложения , Kluwer, 1998.
Ривз С. и Дж. Роу, Генетические алгоритмы: принципы и перспективы , Kluwer, 2002.
Родин Р., Оптимизация в исследовании операций , Прентис Холл, Нью-Джерси, 2000.

Для получения дополнительных книг и журнальных статей по оптимизации посетите веб-сайт Ресурсы для принятия решений.

Линейное программирование

Линейное программирование часто является любимой темой как преподавателей, так и студентов.

Возможность введения ЛП с помощью графического подхода, относительная простота метода решения, широкая доступность программных пакетов ЛП и широкий спектр приложений делают ЛП доступным даже для студентов с относительно слабой математической подготовкой. Кроме того, LP предоставляет прекрасную возможность представить идею анализа «что, если» благодаря мощным инструментам постоптимального анализа, разработанным для модели LP.

Линейное программирование (ЛП) — это математическая процедура определения оптимального распределения дефицитных ресурсов. LP — это процедура, которая нашла практическое применение практически во всех сферах бизнеса, от рекламы до планирования производства. Проблемы планирования транспортировки, распределения и совокупного производства являются наиболее типичными объектами анализа LP. В нефтяной промышленности, например, менеджер по обработке данных в крупной нефтяной компании недавно подсчитал, что от 5 до 10 процентов компьютерного времени фирмы было посвящено обработке моделей LP и LP-подобных моделей.

Линейное программирование имеет дело с классом задач программирования, в которых как оптимизируемая целевая функция является линейной, так и все отношения между переменными, соответствующими ресурсам, являются линейными. Впервые эта проблема была поставлена и решена в конце 40-х гг. Редко какая новая математическая техника нашла такое широкое практическое применение в бизнесе, торговле и промышленности и одновременно получила столь полное теоретическое развитие за такой короткий период времени. Сегодня эта теория успешно применяется к проблемам планирования капиталовложений, разработки диет, сохранения ресурсов, стратегических игр, прогнозирования экономического роста и транспортных систем. В последнее время теория линейного программирования также помогла решить и унифицировать многие выдающиеся приложения.

Читателю важно с самого начала понять, что «программирование» в линейном программировании отличается от «программирования» в компьютерном программировании. В первом случае это означает планировать и организовывать, как в «Получить программу!», Она программирует вас своим решением. В то время как в последнем случае имеется в виду написание кодов для выполнения вычислений. Обучение одному виду программирования имеет очень мало прямого отношения к другому. На самом деле термин «линейное программирование» был придуман до того, как слово «программирование» стало тесно ассоциироваться с компьютерным программным обеспечением. Этой путаницы иногда можно избежать, используя термин линейная оптимизация как синоним линейного программирования.

Любая задача ЛП состоит из целевой функции и набора ограничений. В большинстве случаев ограничения исходят из среды, в которой вы работаете для достижения своей цели. Когда вы захотите достичь желаемой цели, вы поймете, что окружающая среда налагает некоторые ограничения (то есть трудности, ограничения) на выполнение вашего желания или цели. Вот почему такие религии, как буддизм, предписывают вести воздержанный образ жизни. Нет желания, нет боли. Можете ли вы принять этот совет в отношении вашей бизнес-цели?

Что такое функция: Функция — это вещь, которая что-то делает. Например, кофемолка — это функция, которая превращает кофейные зерна в порошок. (Цельная) функция отображает и переводит входную область (называемую допустимой областью) в выходной диапазон с двумя конечными значениями, называемыми максимальным и минимальным значениями.

Когда вы формулируете задачу принятия решений в виде линейной программы, вы должны проверить следующие условия:

Целевая функция должна быть линейной. То есть проверить, все ли переменные имеют степень 1, и они складываются или вычитаются (не делятся и не умножаются)
Целью должна быть максимизация или минимизация линейной функции. Цель должна представлять цель лица, принимающего решение.
Ограничения также должны быть линейными. При этом ограничение должно иметь следующий вид ( £, ³ или =, т. е. ЛП-ограничения всегда замкнуты ).

Например, следующая задача не является LP: Max X при условии, что X < 1. Эта очень простая задача не имеет решения.

Как всегда, нужно быть осторожным при классификации проблемы оптимизации как проблемы LP. Вот вопрос к вам. Является ли следующая проблема проблемой LP?

Макс Х2
предмет:
Х1 + Х2 £ 0
X1 ² — 4 £ 0

Хотя второе ограничение выглядит так, как если бы оно было нелинейным ограничением, это ограничение можно эквивалентно записать как:
X1 ³ -2, а X2 £ 2,
Следовательно, приведенная выше задача действительно является задачей ЛП.

Для большинства задач LP можно рассматривать два важных класса объектов: первый — это ограниченные ресурсы, такие как земля, производственная мощность или численность торгового персонала; во-вторых, это такие виды деятельности, как «производство низкоуглеродистой стали», «производство нержавеющей стали» и «производство высокоуглеродистой стали». Каждое действие потребляет или, возможно, вносит дополнительные объемы ресурсов. Должна быть целевая функция, то есть способ отличить плохое от хорошего, от даже лучшего решения. Проблема состоит в том, чтобы определить наилучшую комбинацию уровней активности, при которой не используется больше ресурсов, чем доступно на самом деле. Многие менеджеры сталкиваются с этой задачей каждый день. К счастью, когда вводится хорошо сформулированная модель, программное обеспечение для линейного программирования помогает определить наилучшую комбинацию.

Симплекс-метод является широко используемым алгоритмом решения для решения линейных программ. Алгоритм — это последовательность шагов, которые позволяют выполнить определенную задачу.

Процесс постановки задачи LP и его применение

Чтобы сформулировать задачу LP, я рекомендую использовать следующие рекомендации после внимательного прочтения постановки задачи несколько раз.

Любая линейная программа состоит из четырех частей: набора переменных решения, параметров, целевой функции и набора ограничений. Формулируя данную проблему принятия решения в математической форме, вы должны практиковаться в понимании проблемы (т. е. формулировании мысленной модели), внимательно читая и перечитывая формулировку задачи. Пытаясь понять проблему, задайте себе следующие общие вопросы:

Каковы переменные решения? То есть, что такое управляемые входы? Точно определите переменные решения, используя описательные имена. Помните, что контролируемые входные данные также известны как контролируемые действия, переменные решения и действия по принятию решений.
Какие параметры? То есть, что такое неконтролируемые входы? Обычно это заданные постоянные числовые значения. Точно определите параметры, используя описательные имена.
Какова цель? Что такое целевая функция? Кроме того, что хочет владелец проблемы? Как цель связана с его переменными решения? Это проблема максимизации или минимизации? Цель представляет собой цель лица, принимающего решение.
Какие ограничения? То есть какие требования должны быть соблюдены? Должен ли я использовать тип ограничения неравенства или равенства? Каковы связи между переменными? Запишите их словами, прежде чем придать им математическую форму.

Узнайте, что допустимая область не имеет ничего общего или имеет мало общего с целевой функцией (минимум или максимум). Эти две части в любой формуле LP происходят в основном из двух разных и разных источников. Целевая функция предназначена для выполнения желания (цели) лица, принимающего решения, тогда как ограничения, формирующие достижимую область, обычно исходят из среды, в которой лицо, принимающее решение, налагает некоторые ограничения/условия на достижение его/ее цели.

Ниже приведена очень простая иллюстративная задача. Однако способ, которым мы подходим к проблеме, одинаков для самых разных проблем принятия решений, а размер и сложность могут различаться. Первый пример — проблема ассортимента товаров.

Проблема плотника:

Распределение скудных ресурсов среди конкурентных средств Во время пары мозговых штурмов со столяром (нашим клиентом) он рассказал нам, что он, исключительно, делает столы и стулья, продает все изготовленные им столы и стулья на базаре, однако не имеет стабильного дохода, и желает сделать все возможное.

Цель состоит в том, чтобы узнать, сколько столов и стульев он должен сделать, чтобы максимизировать чистую прибыль. Мы начинаем с того, что сосредотачиваемся на временных рамках, т. е. на планировании временного горизонта, чтобы при необходимости еженедельно пересматривать наше решение. Чтобы узнать больше о его проблеме, мы должны пойти в его магазин и понаблюдать за тем, что происходит, и измерить то, что нам нужно, чтобы сформулировать (т. е. придать форму, создать модель) его проблемы. Мы должны подтвердить, что его целью является максимизация чистой прибыли. Мы должны общаться с клиентом.

Задача плотника состоит в том, чтобы выяснить, сколько столов и стульев нужно сделать в неделю; но сначала должна быть установлена целевая функция:

Поскольку общие затраты представляют собой сумму постоянных затрат (F) и переменных затрат на единицу продукции, умноженных на количество произведенных единиц. Следовательно, проблема решения состоит в том, чтобы найти X1 и X2 такие, что:

Максимизируйте 9X1 + 6X2 [(1,5X1 + X2) + (2,5X1 + 2X2) + F1 + F2],

где X1 и X2 — количество столов и стульев; в скобках указаны затраты на сырье и рабочую силу соответственно. F1 и F2 — постоянные затраты на два продукта соответственно. Не ограничивая общности и не влияя на оптимальное решение, положим F1 = 0 и F2 = 0. Целевая функция сводится к следующей функции чистой прибыли:

Максимум 5X1 + 3X2

То есть чистый доход (скажем, в долларах или десятках долларов) от продажи столов Х1 и стульев Х2.

Сдерживающими факторами, которые обычно исходят извне , являются ограничения на рабочую силу (это ограничение исходит от его семьи) и сырьевые ресурсы (это ограничение исходит от запланированной поставки). Время изготовления стола и стула измеряется в разное время суток и оценивается в 2 часа и 1 час соответственно. Общее количество рабочих часов в неделю составляет всего 40 часов. Сырье, необходимое для стола и стула, составляет 1 и 2 единицы соответственно. Общий запас сырья составляет 50 единиц в неделю. Таким образом, формулировка LP такова:

Максимум 5 X1 + 3 X2

Тема:
2 X1 + X2 £ 40 ограничение труда
X1 + 2 X2 £ 50 ограничение материала
и оба X1, X2 неотрицательны.

Это математическая модель задачи плотника. Переменные решения, т. е. управляемые входы, — это X1 и X2. Выходом для этой модели является общий чистый доход 5 X1 + 3 X2. Все функции, используемые в этой модели, являются линейными (переменная решения имеет степень, равную 1). Коэффициенты этих ограничений называются технологическими факторами (матрицей). Период обзора составляет одну неделю, подходящий период, в течение которого неконтролируемые входные данные (все параметры, такие как 5, 50, 2,..) с меньшей вероятностью изменятся (колеблются). Даже для такого короткого временного горизонта планирования мы должны выполнить анализ «что, если», чтобы реагировать на любые изменения в этих входных данных, чтобы контролировать проблему, то есть обновлять предписанное решение.

Обратите внимание: поскольку плотник не уходит с работы в конце горизонта планирования, мы добавили условия, согласно которым оба X1 и X2 должны быть неотрицательными, вместо требований, чтобы X1 и X2 были положительными целыми числами. Условия неотрицательности также известны как «подразумеваемые ограничения». Опять же, линейная программа подойдет для этой задачи, если плотник собирается продолжать производить эти продукты. Частичные элементы будут просто учитываться как незавершенное производство и в конечном итоге станут готовой продукцией, скажем, на следующей неделе.

Мы можем попытаться решить для X1 и X2, перечислив возможные решения для каждого и выбрав пару (X1, X2), которая максимизирует 5X1 + 3X2 (чистый доход). Однако перечисление всех возможных альтернатив занимает слишком много времени, и если альтернативы не перечислены исчерпывающе, мы не можем быть уверены, что выбранная нами пара (в качестве решения) является лучшей из всех альтернатив. Этот способ решения проблемы известен как «последовательное мышление» по сравнению с «одновременным мышлением». Более эффективные и действенные методологии, известные как методы линейного программирования, основанные на одновременном мышлении, коммерчески доступны в более чем 400 различных программных пакетах со всего мира.

Оптимальное решение, т. е. оптимальная стратегия, состоит в том, чтобы сделать X1 = 10 столов, а X2 = 20 стульев. Мы можем запрограммировать еженедельную деятельность плотника на изготовление 10 столов и 20 стульев. При этой (оптимальной) стратегии чистая прибыль составляет 110 долларов. Это предписанное решение стало неожиданностью для плотника, поскольку из-за большего чистого дохода от продажи стола (5 долларов) он делал больше столов, чем стульев!

Нанимать или нет? Предположим, что плотник может нанять кого-нибудь в помощь по цене 2 доллара в час. Кроме того, это почасовая заработная плата, которую он/она в настоящее время платит; в противном случае 2 доллара намного ниже текущей минимальной заработной платы в США. Следует ли нанимать плотника, и если да, то на сколько часов?

Пусть X3 будет количеством дополнительных часов, тогда модифицированная задача:

Максимум 5 X1 + 3 X2 — 2 X3

Тема:
2 X1 + X2 £ 40 + X3 трудозатраты с неизвестными дополнительными часами
X1 + 2 X2 £ 50 материальное ограничение

При этом новом условии мы увидим, что оптимальное решение — это X1 = 50, X2 = 0, X3 = 60 с оптимальным чистым доходом в 130 долларов. Следовательно, плотника следует нанять на 60 часов. Как насчет найма всего на 40 часов? Ответы на этот и другие типы вопросов «что, если» рассматриваются в рамках анализа чувствительности на этом веб-сайте.

В качестве упражнения используйте свое программное обеспечение LP, чтобы найти наибольший диапазон значений X, удовлетворяющих следующему неравенству с двумя членами абсолютного значения:

| 3X 4 | — | 2X 1 | 2 фунта стерлингов

Проблема замены продукта

Фирма, принимающая цены, продает S единиц своего продукта по рыночной цене p. Политика руководства заключается в том, чтобы заменять неисправные устройства без дополнительной оплаты в порядке поступления заявок, пока имеются запасные устройства. Поскольку руководство не хочет рисковать и совершать одну и ту же ошибку дважды, оно производит единицы, которые продает на рынке, на одной машине. Кроме того, он производит запасные части, обозначенные X, на втором, более качественном станке.

Фиксированные затраты, связанные с эксплуатацией обеих машин, переменные затраты и стоимость замещения даны в виде функции краткосрочных затрат C(X) = 100 + 20S + 30X.

Точная вероятность того, что единица окажется бракованной, равна r. Однако, действуя из осторожности, руководство всегда недооценивает надежность своего продукта. Тем не менее, он накладывает условие, что X ³ r.S. Спрос на продукцию фирмы определяется выражением S(r) = 10000e ^-0,2r . Следовательно, проблема принятия решения состоит в том, чтобы максимизировать функцию чистой прибыли P(X):

Максимизировать P(X) = 100000p e ^{— 0,2r} — 100 — 20S — 30X,
при условии: X ³ р.С.

Как мы узнаем, решения задач ЛП находятся в вершинах допустимой области. Следовательно, чистая прибыль P(X) будет максимальной, если руководство установит X = r.S.

Проблема диеты

Предположим, что в вашем местном магазине продаются только картофель и стейк. Решение о том, сколько каждого продукта покупать, должно приниматься исключительно из диетических и экономических соображений.

У нас есть информация о питании и стоимости в следующей таблице:

	Пер блок картофеля	Пер блок стейка	Минимум требования
Единицы углеводов	3	1	8
Единицы витаминов	4	3	19
Единицы белков	1	3	7
Блок стоимость	25	50

Задача состоит в том, чтобы найти диету (выбор количества единиц двух продуктов), удовлетворяющую всем минимальным требованиям к питанию при минимальных затратах.

Сформулируйте задачу в терминах линейных неравенств и целевой функции.
Решите задачу геометрически.
Объясните, как соотношение стоимости 2:1 (стейк к картофелю) диктует, что решение должно быть там, где вы сказали.
Найдите соотношение затрат, при котором оптимальное решение переместится к другому выбору количества единиц еды, но при этом потребуется покупать и стейк, и картофель.
Найдите соотношение затрат, при котором нужно будет покупать только один из двух продуктов, чтобы минимизировать затраты.

а) Начнем с установления ограничений для задачи. Первое ограничение представляет собой минимальную потребность в углеводах, которая составляет 8 единиц за некоторый неизвестный промежуток времени. 3 единицы можно потреблять на единицу картофеля и 1 единицу можно потреблять на единицу стейка. Второе ограничение представляет собой минимальную потребность в витаминах, которая составляет 19. единицы. 4 единицы можно потреблять на единицу картофеля и 3 единицы можно потреблять на единицу стейка. Третье ограничение представляет собой минимальную потребность в белках, которая составляет 7 единиц. 1 единица может быть употреблена на единицу картофеля и 3 единицы на единицу стейка. Четвертое и пятое ограничения представляют тот факт, что все допустимые решения должны быть неотрицательными, потому что мы не можем покупать отрицательные количества.

ограничения:

{3X1 + X2 ³ 8, 4X1+ 3X2 ³ 19, Х1+ 3Х2 ³ 7, Х1³ 0, Х2 ³ 0};

Затем мы строим набор решений неравенств, чтобы получить допустимую область возможностей.

c) Соотношение стоимости стейка и картофеля 2:1 диктует, что решение должно быть здесь, поскольку в целом мы видим, что одна единица стейка немного менее питательна, чем одна единица картофеля. Кроме того, в той категории, где стейк превосходит картофель по полезности (белки), необходимо всего 7 единиц. Таким образом, легче выполнить эти единицы, не покупая значительное количество бифштекса. Поскольку стейк дороже, покупка большего количества картофеля для удовлетворения этих потребностей в питании более логична.

г) Теперь мы выбираем новое соотношение затрат, которое переместит оптимальное решение к другому выбору количества пищевых единиц. И бифштекс, и картошка все равно будут куплены, но будет найдено другое решение. Давайте попробуем соотношение затрат 5:2.

Таким образом, оптимальным решением для данного соотношения затрат является покупка 8 стейков и отсутствие картошки в единицу времени для удовлетворения минимальных потребностей в питательных веществах.

Проблема смешивания

Bryant’s Pizza, Inc. — производитель замороженной пиццы. Компания получает чистую прибыль в размере 1,00 доллара США за каждую обычную пиццу и 1,50 доллара США за каждую произведенную пиццу класса люкс. В настоящее время фирма имеет 150 фунтов смеси для теста и 50 фунтов смеси для начинки. Для каждой обычной пиццы используется 1 фунт смеси для теста и 4 унции (16 унций = 1 фунт) смеси для начинки. На каждую роскошную пиццу уходит 1 фунт теста и 8 унций смеси для начинки. Основываясь на прошлом спросе в неделю, Брайант может продать не менее 50 обычных пицц и не менее 25 элитных пицц. Задача состоит в том, чтобы определить количество обычных и элитных пицц, которые компания должна производить, чтобы максимизировать чистую прибыль. Сформулируйте эту задачу как задачу ЛП.

Пусть X1 и X2 — количество обычной и элитной пиццы, тогда формулировка ЛП:

Развернуть X1 + 1,5 X2

Тема:
Х1 + Х2 150 фунтов стерлингов
0,25 X1 + 0,5 X2 50 фунтов стерлингов
Х1 ³ 50
Х2 ³ 25
Х1 ³ 0, Х2 ³ 0

Другие распространенные области применения LP

Линейное программирование является мощным инструментом для выбора альтернатив в задаче принятия решений и, следовательно, применяется в самых разных ситуациях.

Мы укажем несколько приложений, охватывающих основные функциональные области организации бизнеса.

Финансы: проблема инвестора может быть проблемой выбора портфеля. В общем, количество различных портфелей может быть намного больше, чем показано в примере, могут быть добавлены дополнительные и различные виды ограничений. Другая проблема принятия решений связана с определением сочетания финансирования для ряда продуктов, когда доступно более одного метода финансирования. Целью может быть максимизация общей прибыли, когда прибыль для данного продукта зависит от метода финансирования. Например, финансирование может осуществляться за счет внутренних средств, краткосрочной задолженности или промежуточного финансирования (амортизируемых кредитов). Могут быть ограничения на доступность каждого из вариантов финансирования, а также финансовые ограничения, требующие определенных отношений между вариантами финансирования, чтобы удовлетворить условия банковских кредитов или промежуточного финансирования. Также могут быть ограничения на производственные мощности для продуктов. Переменными решения будут количество единиц каждого продукта, которые будут финансироваться по каждому варианту финансирования.

Управление производством и операциями: довольно часто в перерабатывающих отраслях одно и то же сырье может быть превращено в широкий спектр продуктов. Например, в нефтяной промышленности сырая нефть перерабатывается в бензин, керосин, печное топливо и различные сорта моторного масла. Учитывая текущую норму прибыли по каждому продукту, проблема состоит в том, чтобы определить количество каждого продукта, которое должно быть произведено. Решение связано с многочисленными ограничениями, такими как ограничения на мощности различных операций по переработке, доступность сырья, требования к каждому продукту и любые навязанные государством политики в отношении выпуска определенных продуктов. Аналогичные проблемы существуют и в химической и пищевой промышленности.

Человеческие ресурсы: проблемы кадрового планирования также можно анализировать с помощью линейного программирования. Например, в телефонной отрасли спрос на услуги монтажников-ремонтников носит сезонный характер. Проблема состоит в том, чтобы определить количество монтажников-ремонтников и линейных ремонтников, которое должно иметься в рабочей силе каждый месяц, при этом общие затраты на найм, увольнения, сверхурочные и заработную плату в обычном режиме будут сведены к минимуму. Набор ограничений включает в себя ограничения на требования к обслуживанию, которые должны быть удовлетворены, использование сверхурочных часов, профсоюзные соглашения и доступность квалифицированных специалистов для найма. Этот пример противоречит предположению о делимости; однако уровни рабочей силы для каждого месяца, как правило, достаточно велики, чтобы округление до ближайшего целого числа в каждом случае не было бы вредным, при условии, что ограничения не нарушаются.

Маркетинг: линейное программирование можно использовать для определения правильного сочетания средств массовой информации для использования в рекламной кампании. Предположим, что доступными СМИ являются радио, телевидение и газеты. Проблема состоит в том, чтобы определить, сколько рекламных объявлений нужно разместить на каждом носителе. Конечно, стоимость размещения рекламы зависит от выбранного носителя. Мы хотим минимизировать общую стоимость рекламной кампании с учетом ряда ограничений. Поскольку каждое средство может обеспечить различную степень воздействия на целевую группу населения, может быть нижняя граница общего воздействия кампании. Кроме того, каждая среда может иметь различный рейтинг эффективности для получения желаемых результатов; таким образом, может существовать нижняя граница эффективности. Кроме того, могут быть ограничения на доступность каждого носителя для рекламы.

Распределение. Еще одно применение линейного программирования — распределение. Рассмотрим случай, когда имеется m фабрик, которые должны отгружать товары на n складов. Данная фабрика может осуществлять поставки на любое количество складов. Учитывая стоимость доставки одной единицы продукции с каждой фабрики на каждый склад, проблема состоит в том, чтобы определить схему доставки (количество единиц продукции, отправляемых каждой фабрикой на каждый склад), которая минимизирует общие затраты. Это решение связано с ограничениями, согласно которым спрос на каждом заводе не может отгружать больше продукции, чем он может произвести.

Графический метод решения

Процедура графического метода решения задач ЛП:

Является ли проблема LP? Да, если и только если:
Все переменные имеют степень 1, и они складываются или вычитаются (не делятся и не умножаются). Ограничение должно иметь следующие формы (£, ³ или =, то есть ЛВ-ограничения всегда замкнуты), а целью должна быть либо максимизация, либо минимизация.
Например, следующая задача не является LP: Max X при условии, что X < 1. Эта очень простая задача не имеет решения.
Могу ли я использовать графический метод? Да, если количество переменных решения равно 1 или 2.
Используйте миллиметровую бумагу. Нарисуйте каждое ограничение одно за другим, представив, что они равны (представьте, что все £ и ³ равны = ), а затем начертите линию. Изобразите прямую линию в системе координат на миллиметровой бумаге. Система координат имеет две оси: горизонтальную ось, называемую осью x (абсцисса), и вертикальную ось, называемую осью y (ордината). Оси пронумерованы, обычно от нуля до наибольшего значения, ожидаемого для каждой переменной.
При создании каждой линии разделите область на 3 части относительно каждой линии. Чтобы определить допустимую область для этого конкретного ограничения, выберите точку по обе стороны от линии и подставьте ее координаты в ограничение. Если она удовлетворяет условию, эта сторона допустима; в противном случае возможна другая сторона. Для ограничений равенства допустимы только точки на прямой.
Отбросьте стороны, которые невозможны.
После того, как все ограничения нанесены на график, у вас должна быть непустая (выпуклая) допустимая область, если только проблема не является неразрешимой.

К сожалению, некоторые границы допустимых областей, описанные в вашем учебнике, неверны. См., например, рисунки на стр. 56. Почти все неравенства нужно заменить равенством. Верно?

Создайте (по крайней мере) две строки значений изометрии из целевой функции, задав целевую функцию любыми двумя различными числами. Изобразите получившиеся линии. Перемещая эти линии параллельно, вы найдете оптимальный угол (крайнюю точку), если он существует.
В общем, если допустимая область находится в пределах первого квадранта системы координат (т. е. если X1 и X2 ³ 0), то для задач максимизации вы перемещаете целевую функцию изозначения, параллельную самой себе, на далеко от исходная точка (0, 0), имея по крайней мере общую точку с допустимой областью. Однако для задач минимизации верно обратное, то есть вы перемещаете цель изо-значения параллельно самой себе на ближе к исходной точке , имея при этом хотя бы общую точку с допустимой областью. Общая точка обеспечивает оптимальное решение.

Классификация возможных точек: : Допустимые точки любой непустой допустимой области LP могут быть классифицированы как внутренние области, границы или вершины. Как показано на следующем рисунке:

Например, точка B на двухмерном рисунке выше — это граничная точка 9.0096 допустимого множества, потому что каждый маленький круг с центром в точке B, каким бы маленьким он ни был, содержит как некоторые точки в множестве, так и некоторые вне множества. Точка I — это внутренняя точка , потому что оранжевый круг и все меньшие круги, а также некоторые большие; содержит исключительно точки множества. Совокупность граничных точек, принадлежащих одному набору, называется граничной линией (сегментом), например. отрезок cd. Пересечения граничных линий (отрезков) называются вершины , если возможно, это называется угловой точкой . В трехмерном пространстве и выше круги становятся сферами и гиперсферами.
Знайте, что ограничения LP обеспечивают вершины и угловые точки. Вершина — это пересечение 2-прямых или, вообще говоря, n-гиперплоскостей в задачах ЛП с n-переменные решения. Угловая точка — это вершина, которая также допустима.
Численный пример: задача плотника
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 £ 40
Х1 + 2 Х2 £ 50
и оба X1, X2 неотрицательны.
Примечание: Существует альтернатива методу целевой функции значений Iso с задачами, которые имеют небольшое количество ограничений и ограниченную допустимую область. Сначала найдите все угловые точки, которые называются крайними точками. Затем оцените целевую функцию в крайних точках, чтобы найти оптимальное значение и оптимальное решение.
Ясно, что у плотника есть множество альтернативных наборов действий. Однако четыре «крайних» варианта таковы:
Значение целевой функции в каждой угловой (т. е. экстремальной) точке
Выбор лиц, принимающих решения Координаты угловой точки Функция чистого дохода
Количество столов или стульев Х1, Х2 5 х 1 + 3 х 2
Не делать ни стола, ни стула 0, 0 0
Сделай все столы, какие сможешь 20, 0 100
Сделай все стулья, какие сможешь 0, 25 75
Производство смешанных продуктов 10, 20 110
Поскольку цель состоит в том, чтобы максимизировать, из приведенной выше таблицы мы считываем оптимальное значение, равное 110, которое можно получить, если плотник следует оптимальной стратегии X1 = 10 и X2 = 20.
Обратите внимание, что в задаче плотника выпуклая допустимая область предоставляет угловые точки с координатами, показанными в таблице выше.
Основной недостаток графического метода заключается в том, что он ограничен решением задач ЛП только с 1 или 2 решающими переменными. Однако главный и полезный вывод, который мы легко наблюдаем из графических методов, заключается в следующем:
Если линейная программа имеет ограниченное оптимальное решение, то одна из угловых точек обеспечивает оптимальное решение.
Доказательство этого утверждения следует из результатов следующих двух фактов:
Факт № 1: допустимая область любой линейной программы всегда является выпуклым множеством.
Поскольку все ограничения являются линейными, допустимая область (FR) представляет собой многоугольник. Более того, этот многоугольник является выпуклым множеством. В любой задаче ЛП выше, чем двумерная, границы Ф.Р. являются частями гиперплоскостей, а Ф. Р. в этом случае называется многогранником, который также является выпуклым. Выпуклым называется такое множество, у которого, если выбрать из него две допустимые точки, то все точки на отрезке прямой, соединяющем эти две точки, также допустимы. Доказательство того, что Ф.Р. линейных программ всегда являются выпуклыми множествами, следует от противного. На следующих рисунках показаны примеры для двух типов множеств: невыпуклого и выпуклого множества.
Множество допустимой области в любой линейной программе называется многогранником , оно называется многогранником , если оно ограничено.
Факт № 2: Значение Iso линейной целевой функции программы всегда является линейной функцией.
Этот факт следует из характера целевой функции в любой задаче ЛП. На следующих рисунках показаны два типичных вида изозначных целевых функций.
Из сочетания двух приведенных выше фактов следует, что если линейная программа имеет непустую ограниченную допустимую область, то оптимальное решение всегда является одной из угловых точек.
Чтобы преодолеть недостаток графического метода, мы воспользуемся этим полезным и практичным выводом при разработке алгебраического метода, применимого к многомерным задачам ЛП.
Выпуклость допустимой области для линейных программ упрощает решение задач ЛП. Из-за этого свойства и линейности целевой функции решением всегда является одна из вершин. Более того, поскольку количество вершин ограничено, необходимо найти все допустимые вершины, а затем вычислить целевую функцию в этих вершинах, чтобы найти оптимальную точку.
Для нелинейных программ решить задачу намного сложнее, потому что решение может находиться где угодно внутри допустимой области на границе допустимой области или в вершине.
К счастью, большинство задач бизнес-оптимизации имеют линейные ограничения, поэтому LP так популярен. Сегодня на рынке существует более 400 компьютерных пакетов, решающих задачи LP. Большинство из них основано на поиске вершин, то есть перепрыгивании с одной вершины на соседнюю в поисках оптимальной точки.
Вы уже заметили, что граф системы неравенств и/или равенств называется допустимой областью. Эти два представления, графическое и алгебраическое, эквивалентны друг другу, что означает, что координата любой точки, удовлетворяющей ограничениям, находится в допустимой области, а координата любой точки в допустимой области удовлетворяет всем ограничениям.
Числовой пример: Найдите систему ограничений, представляющую следующую допустимую область.
На приведенном выше рисунке система координат показана серым цветом на заднем плане. Построив уравнения граничных линий допустимой области, мы можем убедиться, что следующая система неравенств действительно представляет указанную выше допустимую область:
Х1 ³ -1
Х2 1
фунтов стерлингов X1 — X2 £ 1
Связь между ЛП и системами уравнений: алгебраический метод
Как указал Джордж Данциг, линейное программирование — это строго «теория и решение систем линейных неравенств». Базовыми решениями линейной программы являются решения систем уравнений, состоящих из ограничений в положении привязки. Не все базовые решения удовлетворяют всем ограничениям задачи. Те из них, которые удовлетворяют всем ограничениям, называются базисными допустимыми решениями. Основные допустимые решения точно соответствуют крайним точкам допустимой области.
Например, для задачи Карпентера можно вычислить все основные решения, взяв любые два уравнения и решив их одновременно, а затем, используя ограничения других уравнений, проверить допустимость этого решения. Если возможно, то это решение является базовым допустимым решением, которое обеспечивает координаты угловой точки допустимой области. Чтобы проиллюстрировать процедуру, рассмотрим ограничения Карпентера в позиции привязки (т. е. все со знаком =):
2Х1 + Х2 = 40
Х1 + 2Х2 = 50
Х1 = 0
Х2 = 0
Здесь у нас есть 4 уравнения с 2 неизвестными. С точки зрения «биномиального коэффициента» не более C ⁴ ₂ = 4! / [2! (4-2)!] = 6 основных решений. Решая шесть полученных систем уравнений, имеем:
Шесть основных решений с четырьмя основными возможными решениями
Х1 Х2 5Х1 + 3Х2
10 20 110*
0 40 infeasible
20 0 100
0 25 75
50 0 невозможно
0 0 0
Четыре из приведенных выше базовых решений являются базовыми допустимых решений, удовлетворяющих всем ограничениям, принадлежащих координатам вершин ограниченной допустимой области. Подставляя базовое допустимое решение в целевую функцию, мы вычисляем оптимальное значение. Следовательно, из приведенной выше таблицы мы видим, что оптимальное решение X1 = 10, X2 = 20 с оптимальным значением 110 долларов. Описанный выше подход может применяться при решении задач ЛП более высокой размерности при условии, что оптимальное решение ограничено.
Вам может понравиться использовать JavaScript для решения систем уравнений, чтобы проверить свои вычисления.
Дальнейшие чтения:
Аршам Х., Связи между линейной системой уравнений, обращением матриц и подпрограммами решателя линейных программ, Journal of Mathematical Education in Science and Technology , 29(5), 764-769, 1998.
Данциг Г., Линейное программирование и расширения , стр. 21, The Rand-Princeton U. Press, 1963.
Расширение до более высоких измерений
Графический метод ограничен в решении задач LP, имеющих одну или две переменные решения. Тем не менее, он дает четкую иллюстрацию того, где находятся допустимые и недопустимые области, а также вершины. Визуальное понимание проблемы помогает более рационально мыслить. Например, мы узнали, что: Если программа LP имеет ограниченное оптимальное решение, то оптимальное решение всегда является одной из вершин допустимой области (угловой точкой). Что необходимо сделать, так это найти все точки пересечения (вершины), а затем проверить, какая из всех возможных вершин обеспечивает оптимальное решение. Используя концепции аналитической геометрии, мы преодолеем это ограничение человеческого зрения. Алгебраический метод предназначен для распространения результатов графического метода на многомерную задачу ЛП, как показано в следующем числовом примере.
Численный пример: транспортная задача
Транспортные модели играют важную роль в логистике и управлении цепочками поставок для снижения затрат и улучшения обслуживания. Поэтому цель состоит в том, чтобы найти наиболее экономичный способ перевозки грузов.
Рассмотрим модель с 2 пунктами отправления и 2 пунктами назначения. Спрос и предложение в каждой точке отправления (например, на складе) O1, O2 и в пункте назначения (например, на рынке) D1 и D2 вместе с удельной стоимостью транспортировки приведены в следующей таблице.
Матрица удельных транспортных затрат
Д1 Д2 Поставка
О1 20 30 200
О2 10 40 100
Спрос 150 150 300
Пусть Xij’s обозначает количество отгрузки из источника i в пункт назначения j. ЛП-формулировка задачи минимизации общих транспортных расходов:
Мин. 20×11 + 30×12 + 10×21 + 40×22
при условии:
Х11 + Х12 = 200
Х21 + Х22 = 100
Х11 + Х21 = 150
Х12 + Х22 = 150
все Xij ³ 0
Обратите внимание, что допустимая область ограничена, поэтому можно использовать алгебраический метод. Поскольку эта транспортная задача является сбалансированной (общее предложение = общему спросу), все ограничения имеют форму равенства. При этом любое из ограничений является избыточным (добавляя любые два ограничения и вычитая еще одно, мы получаем оставшееся). Удалим последнее ограничение. Таким образом, задача сводится к:
Мин. 20×11 + 30×12 + 10×21 + 40×22
при условии:
Х11 + Х12 = 200
Х21 + Х22 = 100
Х11 + Х21 = 150
все Xij ³ 0
Эта задача ЛП не может быть решена графическим методом. Однако алгебраический метод не имеет ограничения на размерность LP. Ограничения уже находятся в положении привязки (равенства).
Обратите внимание, что у нас есть m = 3 ограничения равенства с (четырьмя подразумеваемыми неотрицательными) переменными решения. Следовательно, из этих четырех переменных не более m=3 переменных с положительным значением, а остальные должны быть на нулевом уровне. Например, установив поочередно любую из переменных в ноль, мы получим:
X11 X12 X21 X22 Total Transportation Cost
0 200 150 -50
невозможно
200 0 -50 150 невозможно
150 50
2 100 8500
50 150 100 0 6592*
*
*
Теперь, установив любую одну (или несколько) переменных в ноль, легко увидеть, проверив ограничения, что все другие решения недопустимы. Таким образом, из приведенной выше таблицы мы получаем оптимальную стратегию: X11 = 50, X12 = 150, X21 = 100 и X22 = 0, с наименьшими общими затратами на транспортировку в размере 6500 долларов.
Вы можете запустить эту проблему, используя модуль Net.Exe в вашем пакете WinQSB, чтобы проверить эти результаты самостоятельно.
Обратите внимание, что в приведенном выше примере имеется m = 3 ограничения (исключая условия неотрицательности) и n = 4 переменных решения. Оптимальная отгрузка означает, что менеджер не должен отправлять отгрузку из одного источника в один пункт назначения. Оптимальное решение состоит не более чем из 3 положительных переменных решения, что равно числу ограничений. Если менеджер отправляет товары из каждого источника в каждый пункт назначения, результат не является оптимальным.
Приведенные выше результаты, найденные в приведенном выше примере, с помощью алгебраического метода можно обобщить в следующем основном экономическом результате :
Для данной ЛП, имеющей ограниченную допустимую область, с m ограничениями (исключая любые знаковые ограничения, такие как условия неотрицательности) и n решающими переменными, если n > m, то не более m решающих переменных имеют положительное значение в оптимальном решении, а остальные (т. е. n-m) переменные решения должны быть установлены на нулевом уровне. Этот результат верен, если задача имеет ограниченное единственное оптимальное решение.
Приведенный выше результат следует из того факта, что использование теневых цен указывает на то, что альтернативные издержки для переменной решения на нулевом уровне превышают ее вклад.
Числовой пример: Найдите оптимальное решение для следующей производственной задачи с n=3 продуктами и m=1 (ресурсным) ограничением:
Максимум 3X1 + 2X2 + X3
При условии: 4X1 + 2X2 + 3X3 £ 12
все переменные Си ³ 0
Поскольку допустимая область ограничена, следуя алгебраическому методу, устанавливая все ограничения в позиции привязки, мы имеем следующую систему уравнений:
4X1 + 2X2 + 3X3 = 12
Х1 = 0
Х2 = 0
Х3 = 0
(Основные) решения, полученные из этой системы уравнений, приведены в следующей таблице.
Х1 Х2 X3 Total Net Profit
0 0 4 4
0 6 0 12*
3 0 0 9
0 0 0 0
Таким образом, оптимальная стратегия X1 = 0, X2 = 6, X3 = 0 с максимальной чистой прибылью 12 долларов.
Результат в приведенной выше таблице согласуется с применением указанного выше основного экономического результата. Другими словами, оптимальное решение можно найти, приравняв к нулю как минимум n — m = 3 — 1 = 2 переменные решения:
Для крупномасштабных задач LP со многими ограничениями алгебраический метод включает решение множества линейных систем уравнений. Когда в задаче ЛП много переменных и ограничений, решение многих систем уравнений вручную может стать очень утомительным. Даже для очень масштабных задач это невыполнимая задача. Следовательно, нам нужен компьютер, который сделает вычисления за нас. Одним из алгоритмических и компьютеризированных подходов является симплексный метод, который является эффективной и действенной реализацией алгебраического метода. Существует более 400 LP-решателей, все из которых используют симплекс-метод, включая ваше программное обеспечение. При решении задачи ЛП компьютерными пакетами оптимальное решение дает ценную информацию, такую как диапазоны анализа чувствительности.
Вам может понравиться использовать Solving Systems of Equations JavaScript для задач LP с тремя переменными решения, чтобы проверить свои вычисления алгебраическим методом.
Для получения подробной информации и других числовых примеров посетите веб-сайт Веб-сайт алгоритмов решения для моделей LP.
Как решить линейную систему уравнений с помощью LP Solvers?
В алгебраическом методе решения задач ЛП нам приходится решать некоторые системы уравнений. Существует связь между LP-решателями и системами решателей уравнений. Предположим, у нас есть очень большая система уравнений, которую мы хотели бы решить, и пакет LP-решателя, но у нас все еще нет доступного компьютерного пакета решателя для системы уравнений. Возникает вопрос: «Как использовать LP-решатель для поиска решения системы уравнений?» Следующие шаги описывают процесс решения любой линейной системы уравнений с помощью доступного решателя LP.
1- Поскольку некоторые решатели LP требуют, чтобы все переменные были неотрицательными, замените каждую переменную Xi = Yi — T везде.
2- Создайте фиктивную цель, например, свести к минимуму T.
3- Ограничениями задачи LP являются уравнения в системе после замен, описанных на шаге 1.
Численный пример. Решите следующую систему уравнений.
2Х1 + Х2 = 3
Х1-Х2 = 3
Так как пакет WinQSB принимает LP в различных форматах (в отличие от Lindo), решить эту проблему с помощью WinQSB несложно:
Во-первых, создайте LP с фиктивной целевой функцией, такой как Max X1, при условии, что 2X1 + X2 = 3, X1 — X2 = 3, а X1 и X2 не ограничены по знаку. Затем введите этот LP в модуль LP/ILP, чтобы получить решение. Сгенерированное решение имеет вид X1= 2, X2= -1, что легко проверить подстановкой.
Однако, если вы используете какой-либо LP-решатель, который требует по умолчанию (например, Lindo), чтобы все переменные были неотрицательными, вам необходимо сделать некоторые приготовления, чтобы выполнить это требование: Сначала подставьте X1 = Y1 — T и X2 = Y2 — T в обоих уравнениях. Нам также понадобится целевая функция. Пусть у нас есть фиктивная целевая функция, такая как минимизация T. В результате получается следующий LP:
Мин Т
Тема:
2Y1 + Y2 — 3T = 3,
Y1 — Y2 = 3.
Используя любой решатель ЛП, такой как Lindo, мы находим оптимальное решение Y1 = 3, Y2 = 0, T = 1. Теперь подставим это решение ЛП в оба преобразования X1 = Y1 — T и X2 = Y2 — T. Это дает числовые значения для наших исходных переменных. Следовательно, решением системы уравнений является X1 = 3 — 1 = 2, X2 = 0 — 1 = -1, что легко проверяется подстановкой.
Двойная задача: конструкция и ее значение
С каждой (основной) проблемой ЛП связана дополнительная проблема, называемая двойственной. Следующая классификация ограничений переменной решения полезна и проста для запоминания при построении двойственности. ————————————————— ————————— Конструкция двойной задачи
Цель: макс. (например, прибыль)
Типы ограничений:
£ Разумное ограничение
= ограниченное ограничение
³ Необычная константа.
Цель: Мин. (например, стоимость)
Типы ограничений:
³ Разумное ограничение
= ограниченная константа.
£ Необычная константа.
Типы переменных:
³ 0 a Явное состояние
… без ограничений по знаку
£ 0 Необычное состояние
————————————————————— —————————- Однозначное соответствие между типом ограничения и тип переменной существует с использованием этой классификации ограничений и переменные как для основной, так и для двойственной задач.
Конструкция двойной задачи:
— Если первичная задача является задачей максимизации, то двойственная к ней задача минимизации (и наоборот).
— Используйте тип переменной одной проблемы, чтобы найти тип ограничения другой проблемы.
— Используйте тип ограничения одной проблемы, чтобы найти тип переменной другой проблемы.
— Элементы RHS одной задачи становятся коэффициентами целевой функции другой задачи (и наоборот).
— Матричные коэффициенты ограничений одной задачи являются транспонированием матричных коэффициентов ограничений другой задачи. То есть строки матрицы становятся столбцами и наоборот.
Вы можете проверить свои правила двойных конструкций, используя ваш пакет WinQSB.
Числовые примеры:
Рассмотрим следующую основную задачу:
мин x1-2×2
подлежит:
х1+х2 ³ 2,
х1-х2£-1,
х2 ³ 3,
и х1, х2 ³ 0.
Следуя приведенному выше правилу построения, двойственная задача:
макс 2u1 — u2 + 3u3
при условии:
и1 + и2 £ 1,
и1 — и2 + и3 £ -2,
у1 ³ 0,
у2 £ 0,
и u3 ³ 0
Двойник задачи плотника:
Максимум 5X1 + 3X2
Тема:
2X1 + X2 40 фунтов стерлингов
Х1 + 2Х2 £ 50
Х1 ³ 0
Х2 ³ 0
Его двойственность:
Минимизируйте 40U1 + 50U2
Тема:
2У1 + У2 ³ 5
У1 + 2У2 ³ 3
У1 ³ 0
У2 ³ 0
Приложения: Двойственность можно использовать в самых разных приложениях, включая:
— Может быть более эффективно решить двойственное, чем простое.
— Двойное решение обеспечивает важную экономическую интерпретацию, такую как теневые цены, т. е. предельные значения элементов RHS. Исторически теневая цена определялась как улучшение значения целевой функции на единицу увеличения в правой части, потому что проблема часто ставилась в форме улучшения максимизации прибыли (имеется в виду увеличение). Скрытая цена может не совпадать с рыночной ценой. Скрытая цена — это, например, стоимость ресурса под «тенью» вашей деловой активности. Анализ чувствительности , т. е. анализ влияния небольших изменений параметров системы на выходные показатели можно изучить путем вычисления производных выходных показателей по параметру.
— Если ограничение в одной задаче не является обязывающим (т. е. значение левой стороны согласуется со значением правой стороны), то соответствующая переменная в другой задаче равна нулю. Если переменная решения в одной задаче не равна нулю, то связанное с ней ограничение в другой задаче является обязательным. Эти результаты известны как дополнительные условия слабости (CSC).
— Получить диапазон чувствительности RHS одной задачи из диапазона чувствительности стоимостного коэффициента в другой задаче, и наоборот.
Эти результаты подразумевают единственно возможные комбинации первичных и двойственных свойств, как показано в следующей таблице:
Возможные комбинации основных и двойных свойств
Основная задача Условие подразумевает Двойная задача
Выполнимо; ограниченный объектив « Выполнимо; ограниченная цель
Осуществимо; неограниченная цель ® Невозможно
Невозможно ¬ Выполнимо; неограниченная цель
Недостижимая « Невозможно
Множественные решения « Вырожденный раствор
Вырожденный раствор « Несколько решений
Обратите внимание, что почти все LP-решатели выдают диапазон чувствительности для последних двух случаев; однако эти диапазоны недействительны. По этой причине вы должны убедиться, что решение является уникальным и невырожденным при анализе и применении диапазонов чувствительности.
Дальнейшие чтения:
Аршам Х., Симплексный алгоритм без искусственных воздействий для общих моделей LP, Mathematical and Computer Modeling , Vol. 1997. Т. 25, № 1. С. 107-123.
Бенджамин А., Разумные правила для запоминания двойных _ Метод SOB, SIAM Review , Vol. 1995. Т. 37, № 1. С. 85-87.
Чемберс Р., Прикладной анализ производства: двойной подход , издательство Кембриджского университета, 1988.
Двойственная проблема задачи Плотника и ее интерпретация
В этом разделе мы построим двойственную задачу задачи Плотника и дадим ее экономическую интерпретацию.
В задаче Плотника неуправляемыми входными параметрами являются следующие:
Неконтролируемые входы
Стол Стул В наличии
Труд 2 1 40
Сырье 1 2 50
Чистая прибыль 5 3
и его формулировка LP как:
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 £ 40 ограничение труда
X1 + 2 X2 £ 50 ограничение материала
и оба X1, X2 неотрицательны.
Где X1 и X2 — количество столов и стульев, которые необходимо изготовить.
Предположим, Плотник желает купить страховку на свой чистый доход. Пусть U1 = сумма в долларах, подлежащая уплате Плотнику за каждый потерянный рабочий час (например, из-за болезни), а U2 = сумма в долларах, подлежащая уплате Плотнику за каждую потерянную единицу сырья (например, из-за пожара).
Сотрудник страховой компании пытается минимизировать общую сумму (40U1 + 50U2), подлежащую выплате Плотнику страховой компанией. Однако Плотник установит ограничения (то есть условия), настаивая на том, чтобы страховая компания покрыла все его/ее убытки, которые являются его чистым доходом, поскольку он/она не может производить продукцию. Таким образом, проблема страховой компании заключается в следующем:
Минимум 40 U1 + 50 U2
Тема:
2U1 + 1U2 ³ 5 Чистый доход со стола
1U1 + 2U2 ³ 3 Чистый доход от стула
и U1, U2 неотрицательны.
Реализация этой задачи на вашем компьютерном пакете показывает, что оптимальное решение U1 = $7/3 и U2 = $1/3 с оптимальным значением $110 (сумма, которую Плотник ожидает получить). Это гарантирует, что Плотник может управлять своей жизнью гладко. Единственная стоимость – это премия, которую взимает страховая компания.
Единица измерения теневой цены: Обратите внимание, что единицей измерения теневой цены RHS является единица измерения основной цели, деленная на единицу измерения RHS. Например, для задачи плотников U1 = [$/неделя] / часы/неделя] = $/час. Таким образом,
U1 = 7/3 $/час, а U2 = 1/3 $/единица сырья.
Как видите, проблема страховой компании тесно связана с исходной проблемой.
В терминологии моделирования OR/MS/DS исходная проблема называется основной проблемой, а связанная с ней проблема называется двойной проблемой.
В задаче Плотника и ее двойственной задаче оптимальное значение для обеих задач всегда одно и то же. Этот факт называется Равновесием (взятым из теории дополнительности, равновесия экономических систем и эффективности в смысле Парето) между Первичной и Двойственной проблемами. Следовательно, в линейном программировании нет разрыва двойственности.
Двойное решение обеспечивает важную экономическую интерпретацию, такую как предельные значения элементов RHS. Элементы двойственного решения известны как множители Лагранжа, потому что они обеспечивают (жесткую) границу оптимального значения простого числа, и наоборот. Например, при рассмотрении проблемы Карпентера двойственное решение можно использовать для нахождения нижней точной границы оптимального значения следующим образом. После преобразования ограничений неравенства в форму £, умножения каждого ограничения на соответствующее двойственное решение, а затем сложения их, мы получаем:
7/3 [ 2X1 + X2 £ 40]
1/3 [ X1 + 2X2 £ 50]
_____________________
5X1 + 3X2 110 фунтов стерлингов
Обратите внимание, что результирующая в левой части является целевой функцией основной задачи, и эта нижняя граница для нее является точной, поскольку оптимальное значение равно 110.
Управленческие ошибки округления
Вы должны быть осторожны всякий раз, когда округляете значение скрытых цен. Например, теневая цена ограничения ресурсов в приведенной выше задаче равна 8/3; поэтому, если вы хотите купить больше этого ресурса, вы не должны платить больше, чем 2,66 доллара США. Всякий раз, когда вы хотите продать какую-либо единицу этого ресурса, вы не должны продавать ее по цене ниже 2,67 доллара США.
Подобная ошибка может возникнуть всякий раз, когда вы округляете пределы диапазонов чувствительности. Нужно быть осторожным, потому что верхний предел и нижний предел должны быть округлены в большую и меньшую сторону соответственно.
Расчет скрытых цен
Вы уже знаете, что теневые цены являются решением двойственной проблемы . Вот числовой пример.
Вычислите теневую цену для обоих ресурсов в следующей задаче LP:
Макс -X1 + 2X2
С.Т. Х1 + Х2 £ 5
X1 + 2X2 £ 6
и оба X1, X2 неотрицательные
Решение этой первичной задачи (с использованием, например, графического метода) есть X1 = 0, X2 = 3, с остатком S1 = 2 первого ресурса, в то время как второй ресурс полностью используется, S2 = 0.
Скрытые цены являются решением двойной проблемы:
Мин. 5U1 + 6U2
С.Т. У1 + У2 ³ -1
У1 + 2У2 ³ 2
, а U1 и U2 неотрицательны.
Решением двойственной задачи (с использованием, например, графического метода) является U1 = 0, U2 = 1 — теневые цены на первый и второй ресурс соответственно. Обратите внимание, что всякий раз, когда резерв/излишек ограничения отличен от нуля, теневая цена, относящаяся к этой правой части этого ограничения, всегда равна нулю; однако обратный оператор может не содержать . В этом числовом примере S1 = 2 (т. е. резервное значение RHS1 первичного элемента), что не равно нулю; поэтому U1 равен нулю, как и ожидалось.
Рассмотрим следующую проблему:
Макс. X1 + X2
при условии:
X1 1 фунт стерлингов
X2 £ 1
X1 + X2 £ 2
все переменные решения ³ 0.
Используя свой компьютерный пакет, вы можете убедиться, что теневая цена для третьего ресурса равна нулю, в то время как при оптимальном решении X1 = 1, X2 = 1 этого ресурса не осталось.
Поведение изменений значений RHS оптимального значения
Для исследования направленных изменений оптимального значения по отношению к изменениям ПРЗ (при отсутствии избыточных ограничений и при всех ПРШ ³0) мы различаем следующие два случая:
Случай I: проблема максимизации
Для ограничения £: изменение происходит в том же направлении. То есть увеличение значения RHS не уменьшает оптимальное значение. Оно увеличивается или остается неизменным в зависимости от того, является ли ограничение обязательным или необязательным.
Для ограничения ³: изменение происходит в обратном направлении. То есть увеличение значения RHS не увеличивает оптимальное значение. Оно уменьшается или остается неизменным в зависимости от того, является ли ограничение обязательным или необязательным.
Ограничение For =: изменение может быть в любом направлении (см. раздел «Больше за меньшие деньги»).
Случай II: задача минимизации
Для ограничения типа £: изменение происходит в обратном направлении. То есть увеличение значения RHS не увеличивает оптимальное значение (скорее оно уменьшается или не меняется в зависимости от того, является ли ограничение обязательным или необязательным).
Для ограничения типа ³: изменение происходит в том же направлении. То есть увеличение значения RHS не уменьшает оптимальное значение (скорее, увеличивается или не изменяется в зависимости от того, является ли ограничение обязательным или необязательным).
Ограничение For =: изменение может быть в любом направлении (см. раздел «Больше за меньшие деньги»).
Бизнес-среда часто непредсказуема и неопределенна из-за таких факторов, как экономические изменения, правительственные постановления, зависимость от субподрядчиков и поставщиков и т. д. Менеджеры часто оказываются в динамичной, нестабильной среде, где даже краткосрочные планы необходимо постоянно пересматривать и постепенно корректировать. Все это требует менталитета, ориентированного на изменения, чтобы справиться с неопределенностью. Помните, что неожиданность не является элементом твердого решения.
Менеджеры используют математические и вычислительные конструкции (модели) для различных условий и целей, часто для того, чтобы получить представление о возможных результатах одного или нескольких вариантов действий. Это может касаться финансовых вложений, выбора (насколько и сколько) страховать, производственной практики и воздействия на окружающую среду. Недостатком использования моделей является неизбежное наличие неопределенностей, возникающих на разных этапах; в построении и подтверждении самой модели и в ее использовании. Его использование часто является виновником.
Каждое решение проблемы принятия решений основано на определенных параметрах, которые считаются фиксированными. Анализ чувствительности представляет собой набор действий после принятия решения для изучения и определения того, насколько решение чувствительно к изменениям в допущениях. Другими названиями таких действий являются анализ стабильности, анализ «что, если», моделирование сценариев, анализ диапазона, анализ специфичности, анализ неопределенности, вычислительная и численная нестабильность, функциональная нестабильность, анализ допустимости, анализ постоптимальности, допустимые увеличения и уменьшения и многие другие. подобные фразы, отражающие важность данного этапа моделирования.
Числовой пример. Рассмотрим следующую задачу:
Макс. 6X1 + 4,01X2
при условии:
X1 + 2X2 16 фунтов стерлингов
3X1 + 2X2 £ 24
все переменные решения ³ 0.
Оптимальное решение (X1 = 4, X2 = 6), но при незначительном изменении целевой функции можно получить совсем другое оптимальное решение. Например, если мы изменим его на 6X1 + 3,99X2, то оптимальное решение будет (X1 = 8, X2 = 0). То есть, уменьшая второй коэффициент на 0,5%, решение кардинально меняется! Следовательно, оптимальное решение не является устойчивым по отношению к этому входному параметру.
Анализ чувствительности не является типичным термином, используемым в эконометрике для метода исследования реакции решения на возмущения параметров. В эконометрике процесс изменения значения параметра в модели, чтобы увидеть его индивидуальное влияние на показатель эффективности, называется сравнительной статикой или сравнительной динамикой, в зависимости от типа рассматриваемой модели.
Неопределенность в модели может иметь различное происхождение в различных проблемах принятия решений. Это может быть связано либо с неполной информацией, либо с колебаниями, присущими проблеме, либо с непредсказуемыми изменениями в будущем. Текущие подходы к работе с неопределенностями включают:
Анализ сценариев: в этом подходе предполагаются сценарии (например, определенные комбинации возможных значений неопределенного параметра) и решается проблема для каждого из них. Решая задачу повторно для разных сценариев и изучая полученные решения, менеджер наблюдает за чувствительностью и эвристически принимает решение о приблизительном, что является субъективным.
Анализ наихудшего случая: этот метод пытается учесть запас прочности в проблеме на этапе планирования.
Подход Монте-Карло: стохастические модели предполагают, что неопределенность известна по ее статистическому распределению.
Анализ чувствительности и стохастическое программирование. Анализ чувствительности (SA) и стохастическое программирование (SP) являются двумя основными подходами, используемыми для работы с неопределенностью. SA — это постоптимальная процедура, не влияющая на решение. Он используется для исследования влияния неопределенности на рекомендации модели. Формулировка SP, с другой стороны, вводит вероятностную информацию о данных задачи, хотя и с первыми моментами (т.е. ожидаемыми значениями) распределения целевой функции по отношению к неопределенности. При этом игнорируются оценки риска лицами, принимающими решения, характеризуемые дисперсией или коэффициентом вариации.
С неопределенностью можно бороться более «детерминированным» способом. Этот подход имеет различные названия, такие как «моделирование сценариев», «детерминированное моделирование», «анализ чувствительности», «процедуры ранжирования» и «анализ стабильности». Идея состоит в том, чтобы субъективно составить ранжированный список неопределенностей более высокого уровня, которые предположительно могут оказать большее влияние на окончательный результат картирования. Это делается перед увеличением деталей любого конкретного «сценария» или модели.
Например, параметры задачи и неконтролируемые факторы, указанные на приведенном выше рисунке для задачи Плотника, требовали полного анализа чувствительности, чтобы плотник мог контролировать свой бизнес.
Управленческие ошибки округления: Вы должны быть очень осторожны, когда округляете значение пределов диапазонов чувствительности. Чтобы быть действительными, верхний предел и нижний предел должны быть округлены соответственно в меньшую и большую сторону.
Для построения области анализа чувствительности, которая позволяет анализировать любые типы изменений, включая зависимые, независимые и множественные изменения как значений RHS, так и стоимостных коэффициентов LP, посетите сайт Построение областей общей чувствительности.
Дальнейшие чтения:
Аршам Х., Алгоритмы получения информации о чувствительности при моделировании систем с дискретными событиями, Simulation Practice and Theory , 6(1), 1-22, 1998.
Аршам Х., Анализ возмущений общих моделей LP: унифицированный подход к анализу чувствительности, параметрического анализа, допуска и анализа «больше-за-меньше», Mathematical and Computer Modeling , 13(3), 79-102, 1990.
Kouvelis P., and G. Yu, Robust Discrete Optimization and its Applications , Kluwer Academic Publishers, 1997. Обеспечивает всестороннее обсуждение мотивов источников неопределенности в оптимизации.
Расчет диапазонов чувствительности для задач малого размера
Чтобы вычислить диапазоны чувствительности для задач LP с не более чем двумя переменными решения и/или не более чем двумя ограничениями, вы можете попробовать следующий простой в использовании подход.
Единственное ограничение состоит в том, что ограничение равенства не допускается. Наличие ограничения-равенства является случаем вырождения, потому что каждое ограничение-равенство, например, X1 + X2 = 1, означает два одновременных ограничения: X1 + X2 £ 1 и X1 + X2 ³ 1. Количество связывающих ограничений в таком случае будет больше, чем число переменных решения. Это известно как вырожденная ситуация, для которой обычный анализ чувствительности может оказаться недействительным.
Диапазон чувствительности к стоимости для задач LP с двумя переменными решения
Ссылаясь на проблему Карпентера, изменение прибыли на каждый продукт изменяет наклон целевой функции изоценности. Для «небольших» изменений оптимум остается в той же крайней точке. При больших изменениях оптимальное решение перемещается в другую точку. Затем мы должны изменить построение и решить новую задачу.
Задача состоит в том, чтобы найти диапазон для каждого коэффициента стоимости c(j) переменной Xj, такой, чтобы текущее оптимальное решение, т. е. текущая крайняя точка (угловая точка), оставалось оптимальным.
Для двумерной задачи ЛП вы можете попробовать следующий подход, чтобы узнать величину увеличения/уменьшения 90 095 любого из 90 096 коэффициентов целевой функции (также известных как коэффициенты стоимости). Исторически во время Второй мировой войны , первой задачей ЛП была задача минимизации затрат), чтобы сохранить справедливость текущего оптимального решения. Единственное условие, требуемое для этого подхода, состоит в том, что никакие ограничения равенства не допускаются, так как это приводит к случаю вырождения, для которого обычный анализ чувствительности может быть неприменим.
Шаг 1: Рассмотрим только два ограничения привязки в текущем оптимальном решении. Если имеется более двух связывающих ограничений, то это случай вырождения, для которого обычный анализ чувствительности может быть неприменим.
Шаг 2: Возмущаем коэффициент стоимости j ^th параметром cj (это неизвестное количество изменений).
Шаг 3: Постройте одно уравнение, соответствующее каждому ограничению привязки, следующим образом:
(Возмущенная стоимость Cj)/коэффициент Xj в ограничении = Коэффициент другой переменной в целевой функции/коэффициент этой переменной ограничения.
Шаг 4: Величина допустимого увеличения — это наименьшее положительное значение cj, а допустимое уменьшение — наибольшее отрицательное значение cj, полученное на шаге 3.
Заметим, что если нет положительного (отрицательного) cj, то величина увеличения (уменьшения) неограниченна.
Предупреждения:
Помните, что никогда нельзя делить на ноль. Практика деления на ноль является распространенной ошибкой, встречающейся в некоторых учебниках. Например, в
Introduction to Management Science ,
Taylor III, B., Prentice Hall,
автор, к сожалению, делит на ноль в Модуле A: Метод симплексного решения, стр. A26-A27, где вычисляет необходимое соотношение столбцов в симплексном методе.
Чтобы узнать больше об этом и других распространенных заблуждениях, посетите веб-сайт Сага о нулях и путаница с числами. Вот вопрос к вам: что из следующего верно и почему?
а) любое число, деленное на ноль, не определено;
б) ноль, деленный на любое число, равен нулю; или
в) любое число, деленное само на себя, равно 1.
Нахождение диапазона чувствительности к затратам графическим методом: Широко распространено мнение, что можно вычислить диапазон чувствительности к затратам, заключив в скобки (возмущенный) наклон целевой функции (изо-значения) по наклонам двух результирующих линий. от обязательных ограничений. Этот метод графического наклона для вычисления диапазонов чувствительности описан в популярных учебниках, таких как Anderson 9.0098 и др. (2007 г.), Лоуренс и Пастернак (2002 г.) и Тейлор (2010 г.).
К сожалению, это заблуждение. Следует предупредить, что их подход не является общим и работает тогда и только тогда, когда коэффициенты не меняют знак.
Предположим, что в LP с двумя переменными и ограничениями в виде неравенства у нас есть уникальный невырожденный оптимум на пересечении двух линий, как показано на следующем рисунке. Тогда диапазон цели коэффициенты, при которых это решение остается оптимальным, определяются наклоном двух линий.
Ниже приведен контрпример. Это указывает на то, что нужно быть осторожным, чтобы утверждать, что коэффициенты не меняют знак.
Контрпример : Maximixe 5X ₁ + 3X ₂
Х ₁ + Х ₂ £ 2,
Х ₁ — Х ₂ £ 0,
Х ₁ ³ 0, Х ₂ ³ 0.
Задача плотника:
Максимум 5X1 + 3X2
Тема:
2X1 + X2 40 фунтов стерлингов
Х1 + 2Х2 £ 50
Х1 ³ 0
Х2 ³ 0
Вычисление допустимого увеличения/уменьшения на C1 = 5: Связующими ограничениями являются первое и второе. Возмущая этот стоимостной коэффициент на c1, получаем 5 + c1. На шаге 3 имеем:
(5 + c1)/2 = 3/1 для первого ограничения и (5 + c1)/1 = 3/2 для второго ограничения. Решая эти два уравнения, имеем: c1 = 1 и c1 = -3,5. Допустимое увеличение равно 1, а допустимое уменьшение равно 1,5. Пока первый стоимостной коэффициент C1 остается в интервале [ 5 — 3,5, 5 + 1] = [1,5, 6], сохраняется текущее оптимальное решение.
Аналогично для второго коэффициента стоимости C2 = 3 мы имеем диапазон чувствительности [2,5, 10].
В качестве другого примера рассмотрим предыдущую задачу:
Максимум 5X1 + 3X2
Тема:
Х1 + Х2 £ 2
Х1 — Х2 £ 0
Х1 ³ 0
Х2 ³ 0
Вычисление допустимого увеличения/уменьшения на C1 = 5: Связующими ограничениями являются первое и второе. Возмущая этот стоимостной коэффициент на c1, получаем 5 + c1. На шаге 3 имеем:
(5 + c1)/1 = 3/1 для первого ограничения и (5 + c1)/1 = 3/(-1) для второго ограничения. Решая эти два уравнения, имеем: c1 = -2 и c1 = -8. Допустимое уменьшение равно 2, а допустимое увеличение не ограничено. Пока первый стоимостной коэффициент C1 остается в интервале [ 5 — 2, 5 + ¥] = [3, ¥], текущее оптимальное решение остается оптимальным.
Аналогично, для второго стоимостного коэффициента C2 = 3 мы имеем диапазон чувствительности
[3 — 8, 3 + 2] = [-5, 5].
Для построения области анализа чувствительности, которая позволяет анализировать любые типы изменений, включая зависимые, независимые и множественные изменения как значений RHS, так и стоимостных коэффициентов LP, посетите сайт Построение областей общей чувствительности.
Диапазон чувствительности RHS для задач LP с не более чем двумя ограничениями
Ссылаясь на проблему Карпентера, для небольших изменений в любом из ресурсов оптимальная стратегия (то есть создание смешанного продукта) остается в силе. Для больших изменений эта оптимальная стратегия перемещается, и Плотник должен сделать все столы или стулья, какие только сможет. Это радикальное изменение стратегии; поэтому приходится пересматривать формулировку и решать новую задачу.
Помимо приведенной выше необходимой информации, нас также интересует, сколько Плотник может продать (или купить) каждый ресурс по «разумной» цене (или стоимости). То есть, насколько мы можем увеличить или уменьшить RHS(i) для фиксированного i, сохраняя при этом действительность текущей теневой цены RHS(i)? То есть, насколько мы можем увеличить или уменьшить RHS(i) для фиксированного i, сохраняя текущее оптимальное решение двойственной задачи?
Исторически теневая цена определялась как улучшение значения целевой функции на единицу увеличения в правой части, потому что проблема часто ставилась в форме улучшения максимизации прибыли (имеется в виду увеличение).
Кроме того, знайте, что для любой RHS теневая цена (также известная также как ее предельная стоимость) представляет собой величину изменения оптимальной стоимости, пропорциональную изменению на единицу для этой конкретной RHS. Однако в некоторых случаях не разрешается так сильно изменять RHS. Диапазон чувствительности для RHS обеспечивает значения, для которых теневая цена имеет такое экономическое значение и остается неизменной.
Насколько мы можем увеличить или уменьшить каждый отдельный RHS, чтобы сохранить достоверность теневых цен? Этот вопрос эквивалентен вопросу о том, каков диапазон чувствительности коэффициента стоимости в двойственной задаче.
Двойственность задачи Плотника:
Минимизируйте 40U1 + 50U2
Тема:
2У1 + У2 ³ 5
У1 + 2У2 ³ 3
У1 ³ 0
У2 ³ 0
Оптимальное решение: U1 = 7/3 и U2 = 1/3 (теневые цены).
Задача плотника:
Максимум 5X1 + 3X2
Тема:
2X1 + X2 40 фунтов стерлингов
Х1 + 2Х2 £ 50
Х1 ³ 0
Х2 ³ 0
Вычисление диапазона для RHS1: Первые два ограничения являются обязательными, поэтому:
(40 + r1)/2 = 50/1 и (40 + r1)/1 = 50/2.
Решение этих двух уравнений дает: r1 = 60 и r1 = -15. Следовательно, диапазон чувствительности для первой правой части в задаче плотника составляет: [40-15, 40 + 60] = [25, 100].
Аналогично для второй РШ получаем: [50 — 30, 50 + 30] = [20, 80].
Для построения области анализа чувствительности, которая позволяет анализировать любые типы изменений, включая зависимые, независимые и множественные изменения как значений RHS, так и стоимостных коэффициентов LP, посетите сайт Построение областей общей чувствительности.
Дальнейшие чтения:
Лоуренс Дж., младший, и Б. Пастернак, Прикладная наука управления: моделирование, анализ электронных таблиц и коммуникация для принятия решений , Джон Уайли и сыновья, 2002.
Андерсон Д., Суини Д. и Уильямс Т., Введение в науку управления , West Publisher, 2007.
Тейлор III, Б., Введение в науку управления , Прентис Холл, 2006.
Предельный анализ и приоритизация факторов
Основными приложениями информации анализа чувствительности для лиц, принимающих решения, являются предельный анализ и приоритизация факторов:
Предельный анализ. Предельный анализ — это концепция, используемая в микроэкономике, где предельное изменение некоторого параметра может представлять интерес для лица, принимающего решения. Предельное изменение — это отношение очень небольшого добавления или вычитания к общему количеству некоторого параметра. Предельный анализ — это анализ взаимосвязей между такими изменениями по отношению к показателю производительности. Примеры предельного анализа: предельные издержки; предельный доход; предельный продукт; предельная норма замещения; предельная склонность к сбережению и др. В оптимизации предельный анализ используется в основном для объяснения различных изменений параметров и их влияния на оптимальное значение. Анализ чувствительности, т. Е. Анализ влияния небольших изменений параметров системы на выходные показатели, можно изучать путем вычисления производных выходных показателей по параметру.
Лица, принимающие решения, обдумывают, какие факторы являются важными и оказывают наибольшее влияние на результат решения. Предельный анализ направлен на выявление важных факторов (т. е. параметров) и ранжирование их в соответствии с их влиянием на оптимальное значение. Можно получить предельные значения, оценив первые производные показателя эффективности по параметру с конкретным значением.
Приоритизация факторов на основе диапазонов чувствительности: рассмотрим задачу Карпентера:
Максимум 5X1 + 3X2
Тема:
2X1 + X2 40 фунтов стерлингов
Х1 + 2Х2 £ 50
Х1 ³ 0
Хотя рассчитанные диапазоны чувствительности действительны для одного изменения за раз и не обязательно для одновременных изменений, они предоставляют полезную информацию для приоритизации неконтролируемых факторов. На следующем рисунке представлена сравнительная диаграмма для целей приоритезации стоимостных коэффициентов:
На следующем рисунке теневая цена представлена как наклон (т. е. предельное значение) линейной функции, измеряющей величину изменения оптимального значения в результате любого изменения RHS1, при условии, что изменение находится в пределах диапазона чувствительности RHS1. . Эту функцию также можно использовать для решения обратной задачи, то есть, каким должно быть значение RHS1 для достижения конкретного оптимального значения.
Что такое правило 100% (область чувствительности)
Диапазон чувствительности, представленный в предыдущем разделе, представляет собой тип анализа «что, если — одно изменение за раз». Рассмотрим задачу Плотника; предположим, мы хотим найти одновременные допустимые увеличения RHS ( r ₁ , r ₂ ³ 0). Здесь можно применить простой метод, известный как «правило 100%», согласно которому теневые цены остаются неизменными, если выполняется следующее достаточное условие: r ₁ /60 + r ₂ /30 £ 1, 0 £ r ₁ 60 фунтов стерлингов, 0 r ₂ 30 фунтов стерлингов.
В приведенном выше примере 60 и 30 являются допустимыми увеличениями для RHS, основанными на применении обычного анализа чувствительности. То есть всякий раз, когда первая и вторая правая шкала увеличиваются на r ₁ и r ₂ соответственно, пока сохраняется это неравенство, теневые цены для значений правой шкалы остаются неизменными. Обратите внимание, что это достаточное условие, так как при нарушении вышеприведенного условия теневые цены могут измениться или остаться прежними. Термин «правило 100%» становится очевидным, когда вы замечаете, что в левой части приведенного выше условия каждый член представляет собой неотрицательное число, меньшее единицы, которое можно представить в виде процентного допустимого изменения. Общая сумма таких изменений не должна превышать 100%.
Применяя правило 100 % к трем другим возможным изменениям правой стороны, мы имеем:
r ₁ /(-15) + r ₂ /(-30) £ 1, -15 £ r ₁ £ 0, -30 £ r ₂ £ 0. r ₁ /(60) + r ₂ /(-30) £ 1, 0 £ r ₁ £ 60, -30 £ r ₂ £ 0. r ₁ /(-15) + r ₂ /(30) £ 1, -15 £ r ₁ £ 0, 0 £ r ₂ 30 фунтов стерлингов.
На следующем рисунке показана область чувствительности для обоих значений RHS как результат применения правила 100% для задачи Карпентера.
С геометрической точки зрения обратите внимание, что многогранник с вершинами (60, 0), (0, 30), (-15, 0) и (0,-30) на приведенном выше рисунке представляет собой только подмножество большая область чувствительности для изменений обоих значений RHS. Поэтому оставаться в пределах этой области чувствительности является лишь достаточным условием (а не необходимым) для сохранения актуальности текущих теневых цен.
Аналогичные результаты можно получить и при одновременном изменении стоимостных коэффициентов. Например, предположим, что мы хотим найти одновременное допустимое уменьшение C ₁ и увеличение C ₂ . То есть сумма изменения обоих стоимостных коэффициентов на c ₁ £ 0 и c ₂ ³ 0.
Правило 100% гласит, что текущая база остается оптимальной при условии, что:
c ₁ /(-3,5) + c ₂ /7 £ 1, -3,5 £ c ₁ £ 0, 0 £ c ₂ £ 7.
Где 3,5 и 7 – допустимое уменьшение и увеличение стоимостного коэффициента С ₁ и С ₂ соответственно, которые мы нашли ранее путем применения обычного анализа чувствительности.
На приведенном выше рисунке также показаны все другие возможности увеличения и уменьшения обоих значений стоимостных коэффициентов в результате применения правила 100% при сохранении текущего оптимального решения задачи Карпентера.
В качестве другого числового примера рассмотрим следующую задачу:
Максимум 5X1 + 3X2
Тема:
Х1 + Х2 £ 2
Х1 — Х2 £ 0
Х1 ³ 0
Х2 ³ 0
Возможно, вы помните, что мы уже рассчитали диапазоны чувствительности с однократным изменением для этой задачи в разделе «Вычисление диапазонов чувствительности». Диапазон чувствительности для первого коэффициента стоимости [ 5 — 2, 5 + ¥] = [3, ¥], а для второго коэффициента стоимости [3 — 8, 3 + 2] = [-5, 5] . Вы должны быть в состоянии воспроизвести рисунок, аналогичный приведенному выше, изображающий все другие возможности увеличения/уменьшения обоих значений стоимостных коэффициентов как результаты применения правила 100%, сохраняя при этом текущее оптимальное решение этой проблемы.
Применение правила 100%, представленное здесь, является общим и может быть распространено на любую задачу LP большого размера. По мере того, как размер проблемы становится больше, этот тип области чувствительности становится меньше и, следовательно, менее полезным для менеджеров. Существуют более мощные (обеспечивающие как необходимые, так и достаточные условия) и полезные для менеджеров приемы зависимого (или независимого) одновременного изменения параметров.
Для построения области анализа чувствительности, позволяющей анализировать любые типы изменений, включая зависимые, независимые и множественные изменения как значений RHS, так и стоимости. коэффициенты визита ЛП на площадку «Строительство ООП».
Добавление нового ограничения
Процесс: Вставьте текущее оптимальное решение во вновь добавленное ограничение. Если ограничение не нарушается, новое ограничение НЕ влияет на оптимальное решение. В противном случае необходимо решить новую задачу, чтобы получить новое оптимальное решение.
Удаление ограничения
Процесс: Определите, является ли ограничение связывающим (т. е. активным, важным) ограничением, установив, равно ли его резервное/избыточное значение нулю. В случае привязки удаление, скорее всего, изменит текущее оптимальное решение. Удалите ограничение и повторно решите проблему. В противном случае (если это не обязательное ограничение) удаление не повлияет на оптимальное решение.
Замена ограничения
Предположим, мы заменяем ограничение новым ограничением. На что влияет этот обмен?
Процесс: определить, является ли старое ограничение связывающим (т. е. активным, важным) ограничением, выяснив, равно ли его резервное/избыточное значение нулю. В случае привязки замена, скорее всего, повлияет на текущее оптимальное решение. Замените ограничение и устраните проблему. В противном случае (если это не обязательное ограничение) определите, удовлетворяет ли текущее решение новому ограничению. Если да, то этот обмен не повлияет на оптимальное решение. В противном случае (если текущее решение не удовлетворяет новому ограничению) замените старое ограничение новым и решите проблему.
Изменения коэффициентов ограничений
Любые изменения коэффициентов ограничений могут привести к существенным изменениям номинальной (исходной) задачи. Любые такие изменения логически подпадают под анализ чувствительности; однако это не те изменения, которые можно проанализировать, используя информацию, полученную в результате оптимального решения. С такими изменениями лучше всего бороться, решая модифицированную задачу заново.
Добавление переменной (например, введение нового продукта)
Коэффициент новой переменной в целевой функции и теневые цены ресурсов предоставляют информацию о предельной стоимости ресурсов, и, зная потребности в ресурсах, соответствующие новой переменной, можно принять решение, например, является ли новый продукт прибыльным. или нет.
Процесс: подсчитайте, каковы будут ваши потери, если вы произведете новый продукт, используя значения теневой цены (т. е. то, что пойдет на производство нового продукта). Затем сравните его с чистой прибылью. Если прибыль меньше или равна сумме убытка, НЕ ПРОИЗВОДИТЕ новый продукт. В противном случае выгодно производить новый продукт. Чтобы узнать уровень производства нового продукта решает новую проблему.
Удаление переменной (например, удаление продукта)
Процесс: если для текущего оптимального решения значение удаленной переменной равно нулю, то текущее оптимальное решение остается оптимальным без включения этой переменной. В противном случае удалите переменную из целевой функции и ограничений, а затем решите новую проблему.
Проблема оптимального распределения ресурсов
Поскольку ресурсов всегда не хватает, менеджеры озабочены проблемой их оптимального распределения. Вы помните, что в формулировке задачи плотника мы рассматривали оба ресурса как параметры, то есть как заданные фиксированные числовые значения:
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 £ 40 ограничение труда
X1 + 2 X2 £ 50 ограничение материала
и оба X1, X2 неотрицательны.
Обычно мы классифицируем ограничения как ограничения типа ресурсов или производства. Это факт, что в большинстве задач максимизации ограничения ресурсов являются естественной частью проблемы, в то время как в задаче минимизации производственные ограничения являются наиболее важной частью проблемы.
Предположим, мы хотим найти наилучшее распределение трудовых ресурсов для Плотника. Другими словами, какое количество часов плотник лучше всего должен уделять своему делу?
Пусть выделенное количество часов равно R, которое мы хотим использовать при определении его оптимального значения. Следовательно, математическая модель состоит в том, чтобы найти R1 такое, что:
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 £ R1 трудовое ограничение
X1 + 2 X2 £ 50 ограничение материала
и все переменные X1, X2 и R1 неотрицательны.
Теперь мы рассматриваем R1 не как параметр, а как переменную решения. То есть максимизация осуществляется по всем трем переменным; Х1, Х2 и R1:
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 — R1 £ 0 трудовое ограничение
X1 + 2 X2 £ 50 ограничение материала
и все переменные X1, X2 и R1 неотрицательны.
Используя ваше программное обеспечение LP, оптимальное решение X1 = 50, X2 = 0 с оптимальным распределением рабочей силы R1 = 100 часов. Это приносит оптимальное значение в 250 долларов.
Обратите внимание, что оптимальное значение распределения ресурсов всегда совпадает с верхней границей диапазона чувствительности RHS1, сгенерированного вашим программным обеспечением.
Допустимое увеличение количества часов составляет 100 — 40 = 60 часов, что дает дополнительные 250 — 110 = 140.
Используя эту информацию, мы можем даже получить теневую цену на этот ресурс. Скрытая цена – это скорость изменения оптимального значения по отношению к изменению RHS. Следовательно, (250 — 110)/(100 — 40) = 140/60 = 7/3, что является теневой ценой RHS1, как мы нашли другими методами в предыдущих разделах.
Определение наименьшей чистой прибыли продукта
В большинстве бизнес-систем, ориентированных на получение цены, чистая прибыль является неконтролируемым фактором. Менеджер заинтересован в том, чтобы узнать наименьшую чистую прибыль для продукта, производство которого вообще делает его прибыльным.
Вы можете вспомнить, что в «Задаче плотника» мы рассматривали обе чистые прибыли (5 и 3 доллара) как неконтролируемые ресурсы, то есть значения, определяемые рынком:
Максимум 5 X1 + 3 X2
Тема:
2 X1 + X2 £ 40 ограничение труда
X1 + 2 X2 £ 50 ограничение материала
И оба X1, X2 неотрицательны.
Это имеет оптимальную стратегию X1 = 10, X2 = 20 с оптимальным значением 110 долларов.
Предположим, что Плотник хочет узнать наименьшее значение первого коэффициента целевой функции, которое в настоящее время составляет 5 долларов, чтобы производство первого продукта (т. е. столов) по-прежнему было прибыльным.
Предположим, что наименьшая чистая прибыль составляет c1 долларов; следовательно, задача состоит в том, чтобы найти c1 такое, что:
Максимизируйте c1 X1 + 3 X2
Тема:
2 X1 + X2 £ 40 ограничение труда
X1 + 2 X2 £ 50 ограничение материала
И все переменные X1, X2, c1 неотрицательны.
Двойственная задача задачи Плотника теперь выглядит так:
Минимум 40 U1 + 50 U2
Тема:
2U1 + 1U1 ³ c1 Чистая прибыль из таблицы
1U1 + 2U2 ³ 3 Чистая прибыль от стула
А U1, U2, c1 неотрицательны.
Теперь мы рассматриваем чистую прибыль c1 как переменную решения. Минимизация осуществляется по всем трем переменным; Х1, Х2 и с1:
Минимум 40 U1 + 50 U2
Тема:
2У1 + 1У1 — с1 ³ 0
1У1 + 2У2 ³ 3
А U1, U2, c1 неотрицательны.
Реализация этой задачи на вашем компьютере показывает, что оптимальное решение U1 = 7/3 доллара, U2 = 1/3 доллара и c1 = 1,5 доллара.
Существуют альтернативные решения для этого граничного значения диапазона чувствительности стоимостного коэффициента. Решение соответствует нижней границе диапазона анализа чувствительности коэффициента стоимости, вычисленного ранее для задачи Карпентера. Наименьшая чистая прибыль всегда совпадает с нижней границей диапазона чувствительности стоимостного коэффициента, генерируемого вашим программным обеспечением.
Расчет мин. макс. и макс. мин. в однократном выполнении
Предположим, мы хотим найти наихудшее из нескольких значений целевых функций, определенных на общем наборе ограничений в однопроходной компьютерной реализации.
В качестве приложения предположим, что в задаче Плотника без ограничения общности у нас есть три рынка с целевыми функциями 5X1 + 3X2, 7X1 + 2X2 и 4X1 + 4X2 соответственно. Плотник заинтересован в том, чтобы узнать худший рынок. То есть решение следующей задачи:
Проблема минимум-максимум:
Мин. Макс. {5X1 + 3X2, 7X1 + 2X2, 4X1 + 4X2}
Тема:
2 X1 + X2 £ 40
Х1 + 2 Х2 £ 50
и оба X1, X2 неотрицательны.
Задача «Минимум-максимум» эквивалентна:
Макс у
Тема:
у £ 5×1 + 3X2
у £ 7Х1 + 2Х2
у £ 4X1 + 4X2
2X1 + X2 40 фунтов стерлингов
Х1 + 2Х2 £ 50
И все переменные X1, X2, y неотрицательны.
Если вы возьмете все переменные в левой части ограничений и реализуете эту задачу на своем компьютерном пакете, оптимальное решение будет X1 = 10, X2 = 20, y = 110 долларов. Это означает, что первый и второй рынки являются худшими (поскольку ограничения первого и второго являются обязательными) и приносят только 110 долларов чистой прибыли.
Точно так же можно решить максимум min нескольких целевых функций за один прогон.
Проблема осуществимости: индикаторы достижения цели
В большинстве бизнес-приложений менеджер хочет достичь определенной цели, соблюдая при этом ограничения модели. Пользователь особо не хочет ничего оптимизировать, поэтому нет смысла определять целевую функцию. Этот тип проблемы обычно называют проблемой осуществимости.
Хотя некоторые лица, принимающие решения, предпочли бы оптимальное. Однако в большинстве практических ситуаций лицо, принимающее решение, стремится удовлетворить требования или внести постепенные изменения, а не оптимизировать. Это так, потому что человеческий разум имеет ограниченную рациональность и, следовательно, не может постичь все альтернативы. В поэтапном подходе к принятию решений. менеджер делает лишь небольшие шаги или постепенно уходит от существующей системы. Обычно это достигается с помощью «локального поиска», чтобы найти «достаточно хорошее» решение. Эта проблема называется «проблемой удовлетворения», «проблемой осуществимости» или «проблемой поиска цели». Таким образом, цель состоит в том, чтобы добиться глобального улучшения до уровня, который является достаточно хорошим, учитывая текущую информацию и ресурсы.
Одна из причин, по которой бизнес-менеджер переоценивает важность оптимальной стратегии, заключается в том, что организации часто используют индикаторы в качестве «прокси» для удовлетворения своих непосредственных потребностей. Большинство менеджеров обращают внимание на показатели, такие как прибыль, денежный поток, цена акций и т. д., чтобы показать выживание, а не как цель для оптимизации.
Чтобы решить задачу поиска цели, нужно сначала добавить цель в набор ограничений. Чтобы преобразовать задачу поиска цели в задачу оптимизации, необходимо создать фиктивную целевую функцию. Это может быть линейная комбинация подмножества переменных решения. Если вы максимизируете эту целевую функцию, вы получите допустимое решение (если оно существует). Если вы минимизируете его, вы можете получить еще один (обычно на другой «стороне» допустимой области). Вы можете оптимизировать с различными целевыми функциями.
Другой подход заключается в использовании моделей «целевого программирования», которые имеют дело именно с проблемами удовлетворения ограничений, не обязательно имея единственную цель. По сути, они рассматривают меры нарушения ограничений и пытаются минимизировать их. Вы можете формулировать и решать модели целевого программирования в обычном ЛП, используя обычные коды решения ЛП.
В алгоритме свободного решения с искусственными переменными можно использовать нулевую фиктивную целевую функцию, но не в некоторых программных пакетах, таких как Lindo. При использовании программных пакетов можно максимизировать или минимизировать любую переменную как целевую функцию.
Числовой пример
Рассмотрим пример 1 в разделе «Инициализация симплексного метода» на сайте-компаньоне этого сайта. Вместо максимизации мы теперь хотим достичь цели 4. То есть,
Цель: -X1 + 2X2 = 4
при условии:
Х1 + Х2 ³ 2,
-Х1+Х2 ³ 1,
Х2 3 фунта стерлингов,
и Х1, Х2 ³ 0.
Добавляя эту цель к набору ограничений и преобразовывая ограничения в форму равенства, мы имеем:
X1 + X2 — S1 = 2, -X1 + X2 — S2 = 1, X2 + S3 = 3 и
Х1, Х2, S1, S2, S3 ³ 0.
Решение: X1 = 2, X2 = 3, S1 = 3, S2 = 0 и S3 = 0.
Дополнительные сведения об алгоритмах решения см. на веб-сайте «Алгоритмы свободного решения с искусственными переменными».
Дальнейшие чтения:
Borden T., and W. Banta, (Ed.), Использование показателей эффективности для принятия стратегических решений , Jossey-Bass Pub., 1994.
Эйлон С., Искусство расчета: анализ критериев эффективности , Academic Press, 1984.
Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Этот сайт может быть зеркально отражен без изменений (включая эти уведомления) на любом сервере с публичным доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.
Пожалуйста, пришлите мне по электронной почте ваши комментарии, предложения и проблемы. Спасибо.
Профессор Хоссейн Аршам
5.6 — Линейное программирование
5.6 — Линейное программирование
В бизнесе часто желательно найти такие уровни производства, которые приносят максимальную прибыль или минимальные затраты. Производственный процесс может часто описываются набором линейных неравенств, называемых ограничениями. Функция прибыли или затрат, которую необходимо максимизировать или минимизировать, называется целью функция. Процесс нахождения оптимальных уровней с помощью системы линейных неравенства называется линейным программированием (в отличие от нелинейного программирования).
Определения
Целевая функция
Линейная функция (знак равенства), представляющая стоимость, прибыль или какую-либо другую количество, которое должно быть максимизировано или минимизировано с учетом ограничений.
Ограничения
Система линейных неравенств.
Ограничения задачи
Линейные неравенства, полученные из приложения. Например, машина может использоваться только 40 часов в неделю, поэтому общее время его использования должно быть <= 40. Ограничения проблемы обычно указано в задаче рассказа.
Ограничения неотрицательности
Линейные неравенства x>=0 и y>=0. Они включены, потому что x и y обычно представляют собой количество произведенных изделий, и вы не можете произвести отрицательное количество предметов, наименьшее количество предметов, которое вы можете произвести равен нулю. Они (обычно) не оговариваются, они подразумеваются.
Возможная область
Решение системы линейных неравенств. То есть множество все точки, удовлетворяющие всем ограничениям. Только точки в допустимых регион можно использовать.
Угловая точка
Вершина допустимой области. Не каждое пересечение линий является углом точка. Угловые точки встречаются только в вершинах допустимой области. Если будет найдено оптимальное решение задачи линейного программирования, это произойдет в одной или нескольких угловых точках или на отрезке между две угловые точки.
Ограниченная область
Возможная область, которую можно заключить в круг. Ограниченная область будет имеют максимальное и минимальное значения.
Неограниченная область
Допустимая область, которую нельзя заключить в круг.
Основная теорема линейного программирования
Вспомним, что почти в каждой области математики есть своя фундаментальная теорема.
Вот некоторые из фундаментальных теорем или принципов, которые встречаются в вашей текст.
Основная теорема арифметики (стр. 8)
Каждое целое число больше единицы либо простое, либо может быть выражено как уникальное произведение простых чисел.
Основная теорема алгебры (стр. 264)
Каждый многочлен от одной переменной степени n > 0 имеет хотя бы один действительный или комплексный ноль.
Основной принцип счета (стр. 543)
Если есть m способов сделать одно и n способов сделать другое, то есть m*n способов сделать и то, и другое.
Основная теорема линейного программирования
Если есть решение задачи линейного программирования, то оно произойдет в угловой точке или на отрезке между двумя угловыми точками.
Фундаментальная теорема линейного программирования очень поможет. Вместо тестируя все бесконечное количество точек в допустимой области, вы только нужно проверить угловые точки. Какая угловая точка дает наибольшее значение поскольку целевая функция является максимальной, и любая угловая точка дает наименьшее значение целевой функции является минимальным.
Решение задачи линейного программирования
Если проблема не в истории, перейдите к шагу 3.
Определите переменные. Обычно хорошим выбором для определения является количество, которое они просили вас найти в задаче.
Напишите задачу, определив целевую функцию и систему линейные неравенства. Не забывайте об ограничениях неотрицательности, где необходимый.
Нарисуйте систему линейных неравенств, чтобы получить допустимую область.
Определите каждую угловую точку допустимой области. Вы можете найти угол точек, составив систему линейных уравнений 2×2 из двух линий, которые пересекаются в этой точке и решают эту систему.
Оцените целевую функцию в каждой угловой точке.
Выберите точку, дающую наибольшее значение или наименьшее значение в зависимости от от того, является ли задача задачей максимизации или минимизации.
Будьте осторожны при ответе. Ответ должен давать не только максимальный или минимальное значение (значение целевой функции), но также должно указать место, где находится этот экстремум. Пример: максимальное значение 9, когда х=2 и у=3. Если это сюжетная задача, то дайте ответ в терминах исходных определений x и y.
Геометрический Подход
Если наклон целевой функции отрицательный и вы берете линию с этот наклон, проходящий через начало координат, и переместите его вправо через возможной области, последняя угловая точка, затронутая этой движущейся линией, будет максимальное значение.
В показанном примере последняя линия с наклоном m=-4/3, которая касается область касается в угловой точке (6,3).
Поскольку z=4(6)+3(3)=24+9=33, максимальное значение равно 33, когда x=6 и y=3.
Алгебраический подход
Теперь проверим решение негеометрически. Поскольку мы знаем оптимальное решение должно произойти в одной или нескольких угловых точках, мы составляем таблицу со списком всех угловых точек и оценить целевую функцию в этих точках.
Угловая точка х и г = 4х + 3у
А 0 0 0
Б 0 4 12
С 4 5 31
Д 6 3 33
Е 5 0 20
Как видите, угловая точка с максимальным значением находится в точке (6,3).
Мы также можем определить минимальное значение из этой таблицы. Подходящий ответ, предполагая, что проблема запросила как максимум, так и минимум …
Минимальное значение равно 0, если x=0 и y=0.
Максимальное значение равно 33, если x=6 и y=3.
оптимизировать Транспортная проблема | Towards Data Science
Транспортная задача (TP) с примером (правило N-W Corner, метод наименьших затрат, VAM, сбалансированный TP, несбалансированный TP)
Фото Зейна Ли на Unsplash
В этом быстро меняющемся мире потребность в товар растет день ото дня. Соответственно, важность транспорта играет большую роль в жизни общества. Прибыль и состояние компаний, перемещающих товары из одного уголка страны в другой, определяются транспортом. Это особенно верно, когда транспортные расходы и время транспортировки превышают производственные затраты и время производства. Что, если транспортировка во всех областях осуществляется профессионально и если соответствующие затраты сделаны оптимальными, производительность страны повысится, даже если не будет затронут ни один другой фактор!
Изучение оптимальной транспортировки и распределения ресурсов; Теория транспорта или теория транспорта. Французский математик Гаспар Монж формализовал эту проблему в 1781 году. Значительные успехи в этой области были достигнуты во время Второй мировой войны советским математиком и экономистом Леонидом Канторовичем, поэтому известная как транспортная задача Монжа-Канторовича .
Важный тип транспортной проблемы, который решается линейным программированием (ЛП), находится в области физического распределения товаров и услуг из нескольких центров снабжения в центры спроса. Другими словами, транспортные проблемы связаны с перемещением товаров из разных источников в разные пункты назначения с общей целью минимизации транспортных расходов. Такая формулировка транспортной задачи с помощью линейного программирования также известна как транспортная задача Хичкока – Купманса.
Применения транспортной модели используются в авиационной отрасли, исследованиях и разработках, коммивояжерах, перевалочных перевозках и т. д. количество источников.
n= количество адресатов.
Общее количество, доступное в каждом источнике.
Общее количество, необходимое для каждого пункта назначения.
Стоимость перевозки одной единицы товара от каждого источника до каждого пункта назначения.
ПРЕДПОЛОЖЕНИЯ
Перед использованием любого метода транспортировки делаются следующие основные предположения:
Общее количество, доступное во всех источниках, равно общему количеству, необходимому в пунктах назначения. Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные адресаты.
Удельная стоимость перевозки из одного пункта отправления в пункт назначения известна и определена.
Стоимость единицы товара не зависит от количества перевозимых товаров.
Цель состоит в том, чтобы минимизировать общую стоимость транспортировки.
Хотя транспортные задачи могут быть сформулированы как LPP, для их решения разработаны другие более простые алгоритмы.
В основном существует 3 основных шага
1. Формулировка транспортной модели в LPP
2. Поиск базового допустимого решения (BFS)
3. Проверка оптимальности ТРАНСПОРТИРОВОЧНОЙ МОДЕЛИ в LPP
При решении задачи исследования операций ключевой момент заключался в формулировании модели путем расшифровки задачи. Для транспортной задачи обычно задача задается в табличной форме или в матричной форме, называемой транспортной таблицей или матрицей эффективности затрат.
Давайте проверим пример ниже.
Пример транспортной задачи с источником = {A, B, C} с общим предложением = 70 и пунктами назначения = {1,2,3} с общим спросом = 70 [изображение автора]
Здесь,
Источник = {A, B, C}
Они представляют источники с мощностью предложения 10,35,25 единиц товаров соответственно (выделены оранжевым цветом)
Следовательно, общее предложение=10+35+25=70
Направления= {1,2,3}
Представляют направления, требующие 20,25,25 единиц товаров соответственно (обозначены зеленым цветом).
Следовательно, общий спрос = 20+25+25=70
Элементы, представленные в матрице (выделены белым цветом), называются затратами. т. е. стоимость единицы товара, связанная с перемещением единицы товара из одного пункта отправления в другой пункт назначения.
Например,
Затраты на перемещение 1 единицы товара из источника A в пункт назначения 1= 2 ₹/-
Затраты на перемещение 1 единицы товара из источника A в пункт назначения 1= 2 ₹/- (здесь мы смотрим на сечение источника A и места назначения 1 ) [изображение автора]
Аналогично,
Затраты на перемещение одной единицы товара из источника B в место назначения 2 = ₹ 4/-
и так далее. [Здесь мы рассматриваем пересечение источника и назначения]
ВИДЫ ТРАНСПОРТНЫХ ЗАДАЧ
Прежде чем двигаться дальше, давайте проверим различные типы транспортных задач.
Существуют в основном 2 типа транспортных задач:
1. Сбалансированная транспортная задача
2. Несбалансированная транспортная задача
Классификация транспортных задач на сбалансированные и несбалансированные на основе имеющегося предложения и требуемого спроса. [изображение автора]
Давайте заглянем внутрь.
1. Сбалансированная транспортная задача
общее доступное количество = общее требуемое количество
т. е. общее предложение = общий спрос
Давайте проверим пример ниже.
Пример сбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 75 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]
Здесь,
Общее предложение =75
Общий спрос=75
Следовательно, общий объем предложения= общий спрос
2. Несбалансированная транспортная задача
общее доступное количество ≠ общее требуемое количество
т. е. общее предложение ≠ общий спрос
Общее количество, доступное во всех источниках, равно общему количеству, необходимому в пунктах назначения. Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные пункты назначения, чтобы сделать это стандартной транспортной задачей.
Есть 2 ситуации, приводящие к этому несбалансированному состоянию
(и). Общее предложение> Общий спрос
(ii). Общий объем предложения< Общий спрос
(i). Общее предложение> Общий спрос
То есть общее доступное количество > общее необходимое количество
Давайте проверим приведенный ниже пример.
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 60 [изображение автора]
Здесь,
Общее предложение = 65
Общий спрос = 60
Следовательно, общее предложение> Общий спрос
В таких случаях мы добавляем фиктивный пункт назначения, давая фиктивный спрос с каждой стоимостью, равной нулю (0) но фиктивный спрос для фиктивного пункта назначения как общий спрос-предложение.
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с фиктивным спросом = 5, создающим общий спрос = 65 [изображение автора]
В этом примере фиктивный спрос = 65–60 = 5
Таким образом, общий объем предложения = общий спрос
(ii). Общее предложение < Общее потребление
То есть общее доступное количество <общее необходимое количество
Давайте проверим пример ниже.
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]
Здесь,
Общее предложение =65
Общий спрос = 75
Следовательно, общий запас < общий спрос
В таких случаях мы добавляем фиктивный источник, дающий фиктивный источник с каждой стоимостью, равной нулю (0), но фиктивный запас для фиктивного пункта назначения как общий спрос-общий объем поставок .
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с фиктивным предложением = 10, что дает общее предложение = 75 [изображение автора]
In в этом примере фиктивное предложение = 75–65 = 10.
Таким образом, общее предложение = общий спрос
Решение, которое ищет любая транспортная проблема, заключается в том, чтобы количество товара из каждого источника направлялось в какой пункт назначения, чтобы все потребности и в то же время затраты были сведены к минимуму.
Для этого мы должны преобразовать каждую задачу в стандартную задачу, чтобы идти дальше.
2. ОСНОВНОЕ ДОПУСТИМОЕ РЕШЕНИЕ (BFS)
Существуют различные методы получения начального основного допустимого решения. Их:
(1). Северо-Западный (СЗ) Угловой Правило
(2). Метод наименьших затрат (или метод матричного минимума)
(3). Метод приближения Фогеля [VAM] (или метод штрафа)
Давайте углубимся в каждый метод.
Для этого рассмотрим пример задачи для лучшего понимания.
Вопрос приведен ниже.
[изображение автора]
Первый шаг — сделать это стандартной транспортной задачей.
Для этого проверьте, является ли это сбалансированной или несбалансированной транспортной задачей.
[изображение автора]
Данная задача является сбалансированной транспортной задачей. Итак, продолжим.
Теперь нам нужно найти базовое допустимое решение. Для того же у нас есть 3 разных метода. Давайте проверим один за другим с помощью этой задачи.
(1). Правило северо-западного угла (N-W)
Северо-западное направление [изображение автора]
Выберите ячейку северо-западного угла. т. е. стоимость пересечения 1-й строки и 1-го столбца. [Здесь 5 (выделено синим цветом)]
Сравните спрос и предложение этой ячейки. [Здесь 65 и 70 (выделено красным)]
[изображение автора]
Выделить ячейку с наименьшим значением [Здесь 65 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 70–65=5]
[изображение автора]
Удалите столбец или строку соответственно, вычеркнув их. [Здесь столбец с пунктом назначения 1 (отмечен красной линией)]
Всегда общий спрос и предложение будут оставаться одинаковыми. (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 42+43+65=150 (общая потребность) и 5+30+50+65=150 (общая поставка)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите ячейку North-West(N-W) и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]
Здесь и спрос, и предложение будут одинаковыми, которые будут в дальнейшем распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один способ проверить, были ли все вышеперечисленные шаги правильными или нет.)
Методы проверки правильности процесса:
Суммарный спрос и предложение останутся неизменными на всех этапах.
На последнем этапе одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Решение о том, какой из них выбрать, остается исключительно за пользователем. 👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает начальное допустимое решение методом N-W Corner.
[изображение автора]
Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(65×5) +(5×7) +(30×4) +(7×7) +(43×7)
=325+35+120+49+301
=830
Теперь давайте разберемся, что мы выяснили.
₹830 — это общие затраты, связанные с перемещением товаров.
Пройденный путь представлен красными стрелками, как мы нашли с помощью метода N-W Corner.
[изображение автора]
Представим то же самое в виде таблицы
таблица окончательного решения [изображение автора]
Это может представлять или не представлять оптимальное решение этой задачи, т.е. могут существовать другие способы распределение, которое может дать лучшее решение с более низкой общей стоимостью.
Необходимо провести тест на оптимальность, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
(2). Метод наименьшей стоимости (или метод минимума матрицы)
Давайте обсудим на том же примере.
[изображение автора] [изображение автора]
Выберите наименьшее значение среди всех затрат (выделены белым цветом). то есть минимальная стоимость. [Здесь, 4 (выделены синим цветом)]
Здесь есть две ячейки с наименьшей стоимостью. Это исключительно выбор пользователя, чтобы решить, какой из них выбрать.
Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, среди них можно выбрать любой. (Это исключительно выбор пользователя, чтобы решить, какой из них выбрать.👍)
[изображение автора]
Сравните спрос и предложение этой ячейки. [Здесь 30 и 65 (выделено красным)] Выделить ячейку с наименьшим значением [Здесь 30 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 65–30=35]
Исключите столбец или строку, соответственно, вычеркнув их. [Здесь строка с источником B (отмечена красной линией)]
Всегда общий спрос и предложение остаются неизменными. (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 35+42+43+30=150 (общая потребность) и 70+50+30=150 (общая поставка)]
Теперь продолжим процесс с оставшимися ячейками.
Снова найдите ячейку с наименьшей стоимостью и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]
Здесь и спрос, и предложение будут одинаковыми, которые будут в дальнейшем распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
Методы проверки правильности процесса:
Общий спрос и предложение останутся неизменными через шаги.
На последнем этапе одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Это чисто выбор пользователя, чтобы решить, какой из них выбрать.👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает изначально допустимое решение методом наименьших затрат.
[изображение автора]
Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(35х5) +(30х4) +(35х7) +(7х7) +(43х7)
=175+120+245+49+301
=890
Теперь разберемся, что мы обнаружили
₹890 — представляет собой общую стоимость, связанную с перемещением товаров.
Путь, по которому мы шли, перепечатывается красными стрелками, как мы нашли методом наименьших затрат.
[изображение автора]
Представим то же самое в виде таблицы.
таблица окончательного решения [изображение автора]
Это может представлять или не представлять оптимальное решение этой проблемы, т. е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью
Тест на оптимальность необходимо провести, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
( 3). Метод приближения Фогеля [VAM] (или метод штрафа)
Давайте обсудим на том же примере.
[изображение автора]
Выбор ячейки затрат для распределения не так прост в VAM, как если бы мы обсуждали метод N-W Corner и метод ячейки наименьшей стоимости. (Остынь, чувак,😎 это не так сложно. 😇Но процесс немного дольше, чем раньше.😅)
В VAM мы должны сначала определить разницу между двумя самыми низкими затратами в каждой строке и столбце. Они известны как Штрафы/дополнительные расходы.
Учитывается разница между двумя наименьшими значениями.
[изображение автора]
[Здесь штрафы = {2,0,1,1,3,1}]
Теперь найдите максимальное значение среди штрафов независимо от строки или столбца.
[Здесь макс. (Пенальти)=3 (выделены розовым цветом)]
Если ничья, выберите любого. (Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)
[изображение автора]
Теперь просмотрите соответствующую строку или столбец соответственно.
[Здесь столбец (выделен розовым цветом)]
Выберите наименьшее значение среди всех затрат (выделено розовым цветом). то есть минимальная стоимость. [Здесь, 4 (выделены синим цветом на рисунке ниже)]
Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, среди них можно выбрать любой. (Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)
[изображение автора]
Сравните спрос и предложение этой ячейки [Здесь, 30 и 42 (выделено красным)]
[изображение автора]
Выделить ячейку с наименьшим значением [Здесь 30 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 42–30=12]
Удалите столбец или строку, соответственно, вычеркнув их. [Здесь столбец с источником B (отмечен красной линией)]
Всегда общий спрос и предложение будут оставаться одинаковыми. (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 65+12+43+30=150 (общая потребность) и 70+50+30=150 (общая поставка)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите штраф и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]
Здесь и спрос, и предложение будут одинаковыми, которые будут в дальнейшем распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один способ проверить, были ли все вышеперечисленные шаги правильными или нет.)
Методы проверки правильности процесса:
Суммарный спрос и предложение останутся неизменными на всех этапах.
На последнем шаге одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Решение о том, какой из них выбрать, остается исключительно за пользователем. 👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает начальное допустимое решение с помощью VAM.
[изображение автора]
Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(65×5) +(5×7) +(30×4) +(7×7) +(43×7)
=325+35+120+49+301
= 830
Теперь давайте разберемся, что мы выяснили.
₹830 — это общие затраты на перемещение товаров.
Путь обозначен красными стрелками, как мы нашли VAM.
[изображение автора]
Представим то же самое в виде таблицы.
таблица окончательного решения [изображение автора]
Это может представлять или не представлять оптимальное решение этой проблемы, т.е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью.
Необходимо провести тест на оптимальность, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
3. Тест на ОПТИМАЛЬНОСТЬ
Хотя базовое допустимое решение может учитывать все ограничения по источникам и местоположению, оно не обязательно должно давать решение с наименьшими затратами. Может быть несколько основных возможных решений, но оптимальным считается то, которое минимизирует общие транспортные расходы. После того, как базовое допустимое решение было определено любым из перечисленных выше методов, решение должно быть дополнительно проверено на предмет оптимальности. Тесты на оптимальность проверят, является ли данное решение лучшим, а если нет, то оно приведет нас к лучшему или оптимальному решению (I предпочел бы плохой вариант худшему.😉)
(Подробно об этом поговорим в другой статье, так как она сама мне кажется длинной😂)
[1]Dr. K. P. Phaneesh, Operations Research (2009), Sudha Publications
До сих пор мы обсуждали поиск простого возможного решения. Мы можем сделать вывод о выборе правильного пути только после теста на оптимальность, о котором будет рассказано в другой статье.
Оптимизационное моделирование в Python: несколько целей | Игорь Шваб | Аналитика Видья
В двух предыдущих статьях я описал точные и приблизительные решения задач оптимизации с одной целью. В то время как большинство проблем, с которыми можно столкнуться на практике, действительно являются одноцелевыми, многокритериальная оптимизация ( MOO ) имеет свою область применения в обрабатывающей и автомобильной промышленности.
В этой статье я покажу разницу между задачами однокритериальной и многокритериальной оптимизации и дам краткое описание двух самых популярных методов решения последних — алгоритмы ε-ограничения и NSGA-II .
x1, x2, xj … x_n — координатное пространство поиска задачи оптимизации.
x (x1, x2, xj … x_n) — вариант решения. Точка в пространстве поиска.
Fi — значение целевой функции при разрешении x .
В задаче однокритериальной оптимизации превосходство решения над другими решениями легко определяется путем сравнения значений их целевых функций. В многоцелевом случае нельзя напрямую сравнивать значения одной целевой функции с другой целевой функцией. В этом случае качество решения определяется доминирование .
Решение x1 Доминирует x2 IF:
Решение x1 не хуже, чем x2 во всех целях
и раствор x1 — строго лучше, чем x2 , x1 , строго лучше, чем x2 , x1 , строго лучше, чем x2 , x1 .
Согласно этому определению любое множество решений можно разделить на доминируемое и недоминируемое подмножества. Недоминируемое множество всего допустимого пространства решений называется Парето-оптимальный набор или Парето-эффективный набор . Эффективность по Парето — это ситуация, когда нельзя улучшить решение x относительно Fi , не ухудшив его для Fj , и наоборот. В этом наборе нет одного «лучшего решения», поэтому пользователь может выбрать любое решение в зависимости от потребностей бизнеса. Часто оптимальные по Парето решения можно соединить линией или поверхностью. Такая граница называется Парето-оптимальным фронтом .
Оба решения B и C не доминируют друг над другом и оптимальны по Парето.
Цель многокритериальной оптимизации состоит в том, чтобы найти множество решений, максимально близких к фронту Парето. В оставшейся части этой статьи я покажу две практические реализации решения задач MOO.
ε-ограничение — классический прием, относящийся к методам скаляризации задачи МОО. По существу методы скаляризации пытаются каким-то образом переформулировать МОО как однокритериальную задачу. Например, в простейшем подходе несколько целей линейно объединяются в одну общую целевую функцию с произвольными весами. Недостаток этого подхода заключается в том, что для выбора соответствующих весов необходимо заранее знать каждую целевую функцию. В ε-ограничение мы оптимизируем только одну целевую функцию, ограничивая другие в пределах пользовательских значений, в основном рассматривая их как ограничения. Рассмотрим рассмотрение Super Simple Linear Пример:
Maximize F1 = x1
Maxize F2 = 3×1 + 4×2
Ограничения : x1 <= 20
x2 <= 40
5×1 + 4×2 <= 200005
x2 <= 400005
5×1 + 4×2 <= 200005
x2 <= 400005
5×1 + 4x 4.
Мы собираемся решить эту проблему, используя открытый исходный код Pyomo 9Модуль оптимизации 0049. Фрагмент кода ниже.
Вкратце:
Сначала мы оптимизируем F1 и F2 отдельно, просто чтобы знать диапазон значений F2 во время оптимизации F1 .
Затем мы переписываем F2 функцию как ограничение: F2 — slack_variable == ε . Где ε — значение, определяемое пользователем, а необязательная переменная резерва просто помогает оптимизатору лучше исследовать всю область принятия решений. На данный момент вся задача имеет только одну целевую функцию F1 и одно дополнительное ограничение.
Наконец, переберите все возможные значения ε из диапазона значений F2 и оптимизируйте вновь сформулированную задачу на каждом шаге.
Фронт Парето для этой простой линейной задачи MOO показан на рисунке выше. Стоит отметить, что решения в большинстве случаев распределяются очень неравномерно. Например, для этой конкретной проблемы многие решения сгруппированы в правом нижнем углу. В следующем примере я покажу, как отбирать оптимальные по Парето решения, чтобы получить разнообразный набор решений.
В реальных приложениях, когда целевые функции нелинейны или имеют разрывное пространство переменных, классические методы, описанные выше, могут работать неэффективно. Эвристические методы, такие как генетический алгоритм (ГА), оказались отличной альтернативой классическим методам. В этом разделе мы применим один из самых популярных эвристических методов — NSGA-II (генетический алгоритм недоминируемой сортировки) к нелинейной задаче МОО. В частности, мы будем тестировать NSGA-II на тестовой функции Kursawe 9.0049 .
Прежде чем углубляться в код, стоит отметить, что традиционно ГА имеет дело с бинарными векторами, т.е. векторами, состоящими из 0 и 1. В данном примере векторы решений состоят из десятичных знаков x (x1, x2, x3). Хотя всегда можно преобразовать десятичные числа в двоичную форму, мы все же можем применить ту же логику ГА к обычным векторам.
В терминологии эволюционных алгоритмов векторы решения называются хромосомами , их координаты называются генами , а значение целевой функции называется приспособленностью . Подробно прокомментированный код Python приведен внизу страницы. Вот краткое описание алгоритма и график значений целевой функции.
35 приемов и методов решения сложных проблем
Блог
Джеймс Смарт on on 20 мая 2022 г. 24 мин. чтения 2 комментария
Все команды и организации сталкиваются с проблемами по мере своего роста. Есть проблемы, которые могут возникнуть у команд, когда дело доходит до недопонимание или решение важных для бизнеса проблем . Вы можете столкнуться с проблемами, связанными с ростом , дизайном , вовлеченностью пользователей, и даже командной культурой и счастьем. Короче говоря, методы решения проблем должны быть частью набора навыков каждой команды.
Методы решения проблем в первую очередь предназначены для того, чтобы помочь группе или команде в процессе первоначального выявления проблем и задач , обдумывания возможных решений , а затем с оценкой наиболее подходящего .
Найти эффективные решения сложных проблем непросто, но, используя правильный процесс и методы, вы можете помочь своей команде стать более эффективной в этом процессе.
Так как же разработать увлекательные стратегии и дать возможность вашей команде эффективно решать проблемы?
В этом сообщении блога мы делимся рядом инструментов для решения проблем, которые вы можете использовать на своем следующем семинаре или совещании команды. Вы также найдете несколько советов по облегчению процесса и тому, как помочь другим решать сложные проблемы.
Начнем!
Как вы определяете проблемы?
Как определить правильное решение?
Советы по более эффективному решению проблем
Комплексные методы решения проблем
Методы решения проблем для выявления и анализа проблем
Методы решения проблем для выработки решений процесс решения проблем
Как вы определяете проблемы?
Прежде чем вы сможете перейти к поиску правильного решения для данной проблемы, вам сначала нужно определить и определить проблему, которую вы хотите решить.
Здесь вы хотите четко сформулировать, в чем проблема , и позволить вашей группе сделать то же самое. Помните, что у всех в группе могут быть разные точки зрения, и необходимо согласование, чтобы помочь группе двигаться вперед.
Точное выявление проблемы также требует, чтобы все члены группы могли делиться своими взглядами открыто и безопасно. Людям может быть страшно вставать и вносить свой вклад, особенно если проблемы или проблемы носят эмоциональный или личный характер. Обязательно постарайтесь создать психологически безопасное пространство для подобных дискуссий.
Помните, что проблема анализ и дальнейшее обсуждение также важны. Недостаток времени для полного анализа и обсуждения проблемы может привести к разработке решений, которые не соответствуют цели или не решают основную проблему.
Успешное выявление и последующий анализ проблемы означает помощь группе посредством действий, призванных помочь им ясно и честно сформулировать свои мысли и получить полезную информацию.
Используя эти данные, вы можете затем составить описание проблемы , в котором четко описывается проблема, которую вы хотите решить, а также указывается цель любого процесса, который вы предпринимаете для решения этой проблемы.
Как определить правильное решение?
Поиск решений — конечная цель любого процесса. Сложные организационные проблемы можно решить только с помощью соответствующего решения, но для их обнаружения необходимо использовать правильный инструмент решения проблем.
После изучения проблемы и обсуждения идей вам необходимо помочь команде обсудить и выбрать правильное решение. Инструменты и методы достижения консенсуса, подобные приведенным ниже, помогают группе изучить возможные решения, прежде чем голосовать за лучшее. Это отличный способ задействовать коллективный разум группы для достижения отличных результатов!
Помните, что процесс часто повторяется. Хорошие решатели проблем часто взвешенно тестируют жизнеспособное решение, чтобы увидеть, что работает. Хотя вы можете не получить правильное решение с первой попытки, приведенные ниже методы помогают командам найти решение, которое с наибольшей вероятностью принесет успех, а также оставят пространство для улучшений.
Советы по более эффективному решению проблем
Действия по решению проблем — это только часть головоломки. Хотя отличный метод может помочь раскрыть способность вашей команды решать проблемы, без вдумчивого подхода и сильного содействия решения могут оказаться нецелесообразными.
Давайте рассмотрим несколько советов по решению проблем, которые вы можете применить к любому процессу, чтобы добиться успеха!
Четко определите проблему
Прямые переходы к решениям могут быть заманчивыми, хотя без четкой формулировки проблемы решение может оказаться неправильным. Многие из приведенных ниже действий по решению проблем включают разделы, в которых проблема исследуется и четко определяется, прежде чем двигаться дальше.
Это жизненно важная часть процесса решения проблемы, и если вы потратите время на полное определение проблемы, это поможет сэкономить время и силы в дальнейшем. Четкое определение помогает выявить ненужную информацию, а также гарантирует, что ваша команда пойдет по правильному пути.
Не делайте поспешных выводов
Группам легко проявлять когнитивную предвзятость или иметь предвзятые представления как о проблемах, так и о возможных решениях. Обязательно подкрепляйте любые заявления о проблемах или потенциальные решения фактами, исследованиями и достаточной предусмотрительностью.
Лучшие методы требуют от участников быть методичными и бросать вызов предвзятым представлениям. Убедитесь, что вы предоставили группе достаточно времени и пространства для сбора соответствующей информации и рассмотрения проблемы по-новому. Подходя к процессу с ясным и рациональным мышлением, вы часто обнаружите, что лучшие решения появляются быстрее.
Попробуйте разные подходы
Проблемы бывают разных форм и размеров, как и методы, которые вы используете для их решения. Если вы обнаружите, что один подход не дает результатов, а ваша команда не находит разных решений, попробуйте их смешать. Вы будете удивлены тем, как использование нового творческого занятия может раскрепостить вашу команду и генерировать отличные решения.
Не принимайте это близко к сердцу
В зависимости от характера вашей команды или организационных проблем разговоры могут легко накаляться. Хотя участникам полезно участвовать в дискуссиях, следите за тем, чтобы эмоции не были слишком сильными и чтобы при поиске решений не возникало обвинений.
Вы все вместе, и даже если ваша команда или отдел сталкиваются с проблемами, это не обязательно является унижением вас лично. Использование навыков фасилитации для управления групповой динамикой — один из эффективных способов сделать беседу более конструктивной.
Пригласите нужных людей в комнату
Ваш метод решения проблем часто настолько эффективен, насколько эффективна группа, использующая его. Привлечение к работе нужных людей и управление количеством присутствующих также важно!
Если группа слишком мала, вам может не хватить разных точек зрения для эффективного решения проблемы. Если группа слишком большая, вы можете ходить по кругу на этапах формирования идей.
Создание правильного состава группы также важно для обеспечения наличия у вас необходимого опыта и навыков как для выявления потенциальных решений, так и для их реализации. Тщательно продумайте, кого включить на каждом этапе, чтобы обеспечить соблюдение вашего метода решения проблем и обеспечить его успех.
Документируйте все
Лучшие решения требуют доработки, итераций и размышлений. Выработайте привычку документировать свой процесс, чтобы сохранить все выводы из сессии и позволить идеям созреть и развиться. Многие из описанных ниже методов включают создание документов или общих ресурсов. Обязательно сохраните и поделитесь ими, чтобы каждый мог извлечь выгоду из проделанной работы!
Пригласите ведущего
Координатор призван упростить групповые процессы. С таким потенциально эмоциональным и важным предметом, как решение проблем, наличие беспристрастной третьей стороны в виде фасилитатора может иметь решающее значение для поиска отличных решений и поддержания процесса. Рассмотрите возможность привлечения фасилитатора на сеанс решения проблем, чтобы получить лучшие результаты и найти значимые решения!
Развивайте свои навыки решения проблем
Чтобы эффективно решать проблемы, требуется время и практика. В то время как некоторые роли или участники могут более естественно тяготеть к решению проблем, может потребоваться разработка и планирование, чтобы помочь всем найти лучшие решения.
Вы можете разработать программу обучения, провести семинар по решению проблем или просто попросить свою команду попрактиковаться в использовании приведенных ниже методов. Прочтите наш пост о навыках решения проблем, чтобы узнать, как вы и ваша группа можете развить правильный мыслительный процесс и стать более устойчивыми к проблемам!
Разработайте правильную повестку дня
Семинары — отличный формат для решения проблем. При правильном подходе вы можете сфокусировать внимание группы и помочь им найти решения их собственных проблем. Но разработка процесса может занять много времени, а поиск правильных действий может быть затруднен.
SessionLab упрощает планирование процесса решения важных задач. Вы можете найти методы, подходящие для вашей цели, в библиотеке и добавить их в свою повестку дня. Вы даже найдете шаблоны, разработанные опытными фасилитаторами, которые помогут вам начать работу над дизайном мастерской.
Полные методы решения проблем
В этом разделе мы рассмотрим подробные методы решения проблем, которые обеспечивают полный сквозной процесс разработки эффективных решений. Они помогут вашей команде пройти путь от обнаружения и определения проблемы до предоставления правильного решения.
Если вы ищете всеобъемлющий метод или модель решения проблем, эти процессы — отличное место для начала. Они попросят вашу команду бросить вызов предвзятым идеям и принять образ мышления для более эффективного решения проблем.
Шесть шляп мышления
Решение о молнии.
Индивидуальные подходы к решению проблемы могут сильно различаться в зависимости от того, какую команду или роль занимает человек. Существующие предубеждения или точки зрения могут легко найти свое место в смеси, а внутренняя политика может направить разговор.
«Шесть шляп мышления» — это классический метод выявления проблем, которые необходимо решить, и позволяющий вашей команде рассмотреть их с разных точек зрения, будь то путем сосредоточения внимания на фактах и данных, творческих решениях или анализе причин конкретного решения. может не работать.
Как и все системы решения проблем, Six Thinking Hats эффективно помогает командам устранять препятствия из разговора или обсуждения и согласовать все аспекты, необходимые для решения сложных проблем.
https://www.sessionlab.com/methods/6-thinking-hats
2. Lightning Decision Jam
Рекомендовано Джонатаном Кортни из AJ&Smart Berlin, Lightning Decision Jam — одна из тех стратегий, которые должны в каждом наборе инструментов для фасилитации. Изучение проблем и поиск решений часто носит творческий характер, хотя, как и в любом творческом процессе, существует вероятность того, что вы потеряете фокус и потеряетесь.
Неструктурированные обсуждения могут в конце концов привести вас к цели, но гораздо эффективнее использовать метод, который создает четкий процесс и групповую направленность.
В Lightning Decision Jam участникам предлагается начать с написания проблем, опасений или ошибок на стикерах, не обсуждая их, прежде чем модератор пригласит их представить их группе.
Оттуда команда голосует за проблемы, которые нужно решить, и руководствуется шагами, которые позволят им переформулировать эти проблемы, создать решения, а затем решить, над чем работать.
Путем решения проблем, которые необходимо решить в команде, прежде чем двигаться дальше, этот групповой процесс отлично подходит для обеспечения согласованности всей команды и ее возможности взять на себя ответственность за следующие этапы.
https://www. sessionlab.com/methods/lightning-decision-jam-ldj
3. Процесс определения проблемы
Хотя проблемы могут быть сложными, методы их решения проблемы часто могут быть простыми по дизайну.
Потратив время на то, чтобы по-настоящему определить и определить проблему, прежде чем просить группу переосмыслить проблему как возможность, этот метод является отличным способом добиться изменений.
Начните с определения основного вопроса и изучения способов его проявления, прежде чем разделиться на пять команд, каждая из которых будет рассматривать проблему, используя разные методы: бегство, обращение, преувеличение, искажение или принятие желаемого за действительное. Команды разрабатывают цель проблемы и создают идеи в соответствии со своим методом, а затем возвращают их группе.
Этот метод отлично подходит для углубленного обсуждения, а также создает пространство для поиска творческих решений!
Problem Definition #problem solving #idea generation #creativity #online #remote-friendly
A problem solving technique to define a problem, challenge or opportunity and to generate ideas .
4. 5 «почему»
Иногда группе нужно пойти дальше в своих стратегиях и проанализировать первопричину, лежащую в основе организационных проблем. RCA или анализ основных причин — это процесс определения того, что лежит в основе бизнес-проблем или повторяющихся проблем.
«5 почему» — это простой и эффективный метод, помогающий группе найти первопричину любой проблемы или проблемы и провести анализ, который даст результаты.
Начав с создания формулировки проблемы и пройдя пять этапов для ее уточнения, программа «5 почему» предоставляет все необходимое, чтобы действительно обнаружить причину проблемы.
5 Почему #hyperisland #innovation
Этот простой и действенный метод полезен для понимания сути проблемы или задачи. Как следует из названия, группа определяет проблему, затем пять раз задает вопрос «почему», часто используя полученное объяснение в качестве отправной точки для творческого решения проблемы.
5. World Cafe
World Cafe — это простая, но мощная техника фасилитации, помогающая большим группам сосредоточить свою энергию и внимание на решении сложных проблем.
World Cafe позволяет использовать этот подход, создавая непринужденную атмосферу, в которой участники могут самоорганизоваться и исследовать актуальные и важные для них темы, связанные с центральной целью решения проблем. Создайте правильную атмосферу, смоделировав свое пространство по образцу кафе, и после того, как группа проведет метод, позвольте им взять на себя инициативу!
Сделать решение проблем частью культуры вашей организации в долгосрочной перспективе может оказаться сложной задачей. Более доступные форматы, такие как World Cafe, могут быть особенно эффективными для привлечения людей, не знакомых с семинарами.
World Cafe #hyperisland #innovation #issue analysis
World Café – это простой, но эффективный метод, созданный Хуанитой Браун, для создания актуальных и содержательных бесед, полностью управляемых участниками. и важно для них. Фасилитаторы создают пространство в стиле кафе и дают простые рекомендации. Затем участники самоорганизуются и изучают набор соответствующих тем или вопросов для разговора.
6. Диалог «Открытие и действие» (DAD)
Один из лучших подходов — создать безопасное пространство для группы, где можно делиться и узнавать о практиках и поведении, которые могут помочь им найти собственные решения.
С помощью DAD вы можете помочь группе выбрать, какие проблемы они хотят решить и какие подходы они будут использовать для этого. Это здорово помогает устранить сопротивление изменениям, а также может помочь заручиться поддержкой на каждом уровне!
Этот процесс обеспечения непосредственного участия отлично подходит для обеспечения последующей деятельности и является одним из методов, которые вы должны иметь в своем наборе инструментов в качестве фасилитатора.
Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly
DADs make it easy for a group or community обнаружить практики и модели поведения, которые позволяют некоторым людям (не имеющим доступа к специальным ресурсам и сталкивающимся с теми же ограничениями) находить лучшие решения общих проблем, чем их сверстники. Это называется позитивным девиантным (PD) поведением и практиками. DAD позволяют людям в группе, подразделении или сообществе самостоятельно обнаруживать эти методы ПД.

DAD также создают благоприятные условия для стимулирования творчества участников в местах, где они могут чувствовать себя в безопасности, чтобы изобретать новые и более эффективные практики. Сопротивление изменениям исчезает, поскольку участники получают возможность свободно выбирать, какие методы они будут применять или пробовать и какие проблемы они будут решать. DAD позволяют получить непосредственное владение решениями.
7. Design Sprint 2.0
Хотите увидеть, как команда может решить большие проблемы и продвинуться вперед с созданием прототипов и тестированием решений за несколько дней? Шаблон Design Sprint 2.0 от Джейка Кнаппа, автора книги Sprint, представляет собой комплексную повестку дня с проверенными результатами.
Разработка правильной программы может потребовать сложного, но необходимого планирования. Обеспечение выполнения всех правильных шагов также может быть напряженным или трудоемким в зависимости от вашего уровня опыта.
Используйте этот полный шаблон 4-дневного семинара, если вы обнаружите, что нет очевидного решения вашей проблемы, и хотите сосредоточить свою команду на конкретной проблеме, которая может потребовать быстрого запуска минимально жизнеспособного продукта или ожидания организации- широкое внедрение решения.
8. Технология открытого пространства
Технология открытого пространства, разработанная Харрисоном Оуэном, создает пространство, в котором большие группы могут взять на себя ответственность за решение своих проблем и провести индивидуальные занятия. Технология открытого пространства — отличный формат, когда у вас есть большой опыт и понимание в комнате, и вы хотите использовать разные взгляды и подходы к определенной теме или проблеме, которую вам нужно решить.
Начните с того, что соберите участников, чтобы они объединились вокруг центральной темы и сосредоточили свои усилия. Объясните основные правила, которые помогут направить процесс решения проблем, а затем предложите участникам определить любую проблему, связанную с центральной темой, в которой они заинтересованы и готовы взять на себя ответственность.
После того, как участники определились со своим подходом к основной теме, они пишут свою проблему на листе бумаги, сообщают о ней группе, выбирают время и место сеанса и прикрепляют лист бумаги к стене. По мере того, как стена заполняется сессиями, группа приглашается присоединиться к тем сессиям, которые их интересуют больше всего и в которых они могут внести свой вклад, после чего вы готовы начать!
Все присоединяются к группе решения проблем, на которую они подписаны, записывают обсуждение и, если это уместно, результаты могут быть впоследствии переданы остальной группе.
Технология открытого пространства #Action План #IDEA Generation #Problem Решение #ISSUE Analysis #GRAY GROUP 9083 #SONLINE #LUNGE GROUP 9083 #ONLINE . для больших групп, чтобы создать свою повестку дня, выделяя важные темы для обсуждения, подходящие для конференций, собраний сообщества и фасилитации всей системы
Методы выявления и анализа проблем
Использование метода решения проблем для помощи команде в выявлении и анализе проблемы может быть быстрым и эффективным дополнением к любому семинару или совещанию.
Хотя дальнейшие действия всегда необходимы, вы можете легко создать импульс и согласование, и эти действия — отличное место для начала.
Мы составили этот список методов, чтобы помочь вам и вашей команде в выявлении проблем, их анализе и обсуждении, которые закладывают основу для разработки эффективных решений.
Посмотрим!
Flip It
The Creativity Dice
Fishbone Analysis
Problem Tree
SWOT Analysis
Agreement-Certainty Matrix
SQUID
Speed Boat
The Journalistic Six
LEGO Challenge
What, So Что, что теперь?
Журналисты
9.
Flip It
Индивидуальные и групповые точки зрения невероятно важны, но что происходит, если люди твердо настроены и нуждаются в изменении точки зрения, чтобы более эффективно подойти к проблеме?
Flip Этот метод нам нравится, потому что он прост для понимания и применения, а также позволяет группам понять, как формируются их взгляды и предубеждения.
Участникам Flip It сначала предлагается рассмотреть опасения, вопросы или проблемы с точки зрения страха и записать их на флип-чарте. Затем группу просят рассмотреть те же вопросы с точки зрения надежды и поменять свое понимание.
Ни одна проблема и решение не свободны от существующих предубеждений, и, изменив точки зрения с помощью Flip It, вы сможете быстро и эффективно разработать модель решения проблем.
Переверни! #gamestorming #решение проблем #action
Часто изменение проблемы или ситуации происходит просто из-за изменения нашей точки зрения. Переверните его! это быстрая игра, предназначенная для того, чтобы показать игрокам, что перспективы создаются, а не рождаются.
10. Кости творчества
Один из самых полезных навыков решения проблем, которому вы можете научить свою команду, — подходить к задачам творчески, гибко и открыто. Такие игры, как The Creativity Dice, позволяют командам преодолевать потенциальное препятствие, связанное со слишком линейным мышлением, и подходить к процессу весело и быстро.
В игре «Кости творчества» участники распределяются по определенной теме и бросают кубик, чтобы определить, над чем они будут работать в течение 3 минут. Они могут выбросить 3 и работать над изучением фактической информации по выбранной теме. Они могут выбросить 1 и работать над определением конкретных целей, стандартов или критериев для сессии.
Поощрение быстрой работы и итерации, а также просьба к участникам быть гибкими — отличные навыки, которые нужно развивать. Наличие сцены для инкубации идей в этой игре также важно. Моменты паузы могут помочь убедиться, что выдвигаемые идеи являются наиболее подходящими.
Кости творчества #творчество #решение проблем #thiagi #анализ проблемы
Слишком много творческого мышления опасно для решения проблем. Чтобы быть креативным, вы должны подойти к проблеме (или возможности) с разных точек зрения. Вы должны оставить одну мысль висеть в воздухе и перейти к другой. Этот пропуск предотвращает преждевременное закрытие и позволяет вашему мозгу инкубировать одну линию мысли, в то время как вы сознательно преследуете другую.
11. Анализ «рыбьей кости»
Организационные или командные проблемы редко бывают простыми, и важно помнить, что одна проблема может быть признаком чего-то более глубокого и может потребовать дальнейшего рассмотрения для решения.
Анализ «рыбьей кости» помогает группам копнуть глубже и понять истоки проблемы. Это отличный пример метода анализа первопричин, с которым легко разобраться всем в команде.
Участников этого упражнения просят аннотировать диаграмму рыбы, сначала добавив проблему или проблему, над которой нужно работать, на голове рыбы, а затем провести мозговой штурм основных причин проблемы и добавить их в виде костей на рыбу.
Использование абстракций, таких как диаграмма рыбы, действительно может помочь команде вырваться из привычного мышления и развить творческий подход.
Анализ рыбьей кости ##решение проблем ##анализ основных причин #принятие решений #онлайн-фасилитация
12. Дерево проблем
Поощрение визуального мышления может быть неотъемлемой частью многих стратегий. Просто переформулируя и проясняя проблемы, группа может перейти к разработке модели решения проблем, которая им подходит.
В «Дереве проблем» группам предлагается сначала провести мозговой штурм по списку проблем — это могут быть проблемы дизайна, командные проблемы или более крупные бизнес-задачи — а затем организовать их в иерархию. Иерархия может быть от наиболее важной к наименее важной или от абстрактной к практической, хотя ключевой момент в играх по решению проблем, которые включают этот аспект, заключается в том, что ваша группа каким-то образом управляет и сортирует все возникающие проблемы.
После того, как вы составили список проблем, которые необходимо решить, и организовали их соответствующим образом, вы готовы к следующим шагам решения проблем.
Дерево проблем #определить намерения #создать #дизайн #анализ проблем
Дерево проблем в рамках проектного проекта — это инструмент для прояснения иерархии проблем, решаемых командой; он представляет проблемы высокого уровня или связанные с ними проблемы подуровня.
13. SWOT-анализ
Скорее всего, вы уже слышали о SWOT-анализе. Этот метод решения проблем фокусируется на выявлении сильных и слабых сторон, возможностей и угроз и является испытанным методом как для отдельных лиц, так и для команд.
Начните с создания желаемого конечного состояния или результата и помните об этом — любая модель решения процессов становится более эффективной, если вы знаете, к чему вы движетесь. Создайте квадрант, состоящий из четырех категорий SWOT-анализа, и попросите участников генерировать идеи на основе каждого из этих квадрантов.
После того, как вы соберете эти идеи в свои квадранты, сгруппируйте их вместе на основе их сходства с другими идеями. Затем эти кластеры используются для облегчения групповых бесед и продвижения вперед.
SWOT-анализ #gamestorming #решение проблем #action #содействие
, а также то, что мы могли бы улучшить. Это дает нам возможность оценить приближающиеся возможности и опасности, а также оценить серьезность условий, влияющих на наше будущее. Когда мы поймем эти условия, мы сможем повлиять на то, что будет дальше.
14. Матрица согласия-уверенности
Не каждый подход к решению проблем подходит для каждой задачи, и выбор правильного метода для решения поставленной задачи является ключевой частью эффективной команды.
Матрица уверенности в соглашении помогает командам согласовать характер стоящих перед ними задач. Сортируя проблемы от простых до хаотичных, ваша команда может понять, какие методы подходят для каждой проблемы и что они могут сделать, чтобы обеспечить эффективные результаты.
Если вы уже используете методы Освобождения структур как часть своей стратегии решения проблем, Матрица согласия-уверенности может стать бесценным дополнением к вашему процессу. Мы обнаружили, что это особенно важно, если у вас возникают проблемы с повторяющимися проблемами в вашей организации и вы хотите глубже понять основную причину.
Матрица согласия-определенности #анализ проблемы #освобождение структур #решение проблем
Вы можете помочь отдельным лицам или группам избежать частой ошибки, когда они пытаются решить проблему методами, которые не соответствуют характеру их проблемы. Сочетание двух вопросов позволяет легко сортировать задачи по четырем категориям: простые, сложные, сложные и хаотичные .
Проблема проста , когда ее можно надежно решить с помощью методов, которые легко воспроизвести.
сложно , когда от экспертов требуется разработать сложное решение, которое предсказуемо даст желаемые результаты.
Проблема представляет собой сложный случай, когда есть несколько допустимых способов действий, но результаты невозможно предсказать в деталях.
Хаотичный — когда контекст слишком неспокойный, чтобы определить путь вперед.
Для описания этих различий можно использовать свободную аналогию: простое похоже на следование рецепту, сложное похоже на запуск ракеты на Луну, сложное похоже на воспитание ребенка, а хаотичное похоже на игру «Приколите хвост ослу».
Матрица соответствия освобождающих структур в главе 5 может быть использована в качестве первого шага, чтобы прояснить природу проблемы и избежать несоответствий между проблемами и решениями, которые часто лежат в основе хронических, повторяющихся проблем.
15. SQUID
Организация и составление графиков прогресса команды могут иметь важное значение для обеспечения ее успеха. SQUID (Sequential Question and Insight Diagram) — отличная модель, которая позволяет команде эффективно переключаться между вопросами и ответами и развивать навыки, необходимые им, чтобы не сбиться с пути на протяжении всего процесса.
Начните с двух стикеров разного цвета — одного для вопросов и одного для ответов — и с вашей центральной темы (голова кальмара) на доске. Попросите группу сначала придумать серию вопросов, связанных с их лучшим предположением о том, как подойти к теме. Попросите группу придумать ответы на эти вопросы, прикрепить их к доске и соединить линией. После некоторого обсуждения вернитесь в режим вопросов, отвечая на сгенерированные ответы или другие пункты на доске.
Приятно видеть, как диаграмма растет на протяжении всего упражнения, а завершенный SQUID может предоставить визуальный ресурс для будущих усилий и в качестве примера для других команд.
SQUID #gamestorming #планирование проекта #анализ проблемы #решение проблем
При изучении информационного пространства им важно знать, где в любое время им дано знать информационное пространство. Используя SQUID, группа намечает территорию по мере продвижения и может ориентироваться в соответствии с ней. SQUID расшифровывается как Sequential Question and Insight Diagram.
16. Скоростной катер
В продолжение нашей морской темы, Скоростной катер — это короткое и приятное задание, которое может помочь команде быстро определить, с чем у сотрудников, клиентов или пользователей услуг могут возникнуть проблемы, и проанализировать, что может быть не так. на пути достижения решения.
Методы, которые позволяют группе проводить наблюдения, делать выводы и быстро достигать моментов озарения, бесценны при попытке решить сложные проблемы.
В Speed Boat подход заключается в том, чтобы сначала рассмотреть, какие якоря и проблемы могут сдерживать организацию (или лодку). Бонусные баллы, если вы сможете определить акул в воде и разработать идеи, которые также могут бороться с конкурентами!
Скоростной катер #gamestorming #решение проблем #action
Скоростной катер — это короткий и удобный способ определить, что вашим сотрудникам или клиентам не нравится в вашем продукте или услуге путь к желанной цели.
17. The Journalistic Six
Одним из наиболее эффективных способов решения проблем является поощрение команд к более инклюзивному и разнообразному мышлению.
Основываясь на шести ключевых вопросах, на которые студентов-журналистов учат отвечать в статьях и новостях, «Журналистская шестерка» помогает создавать команды, чтобы увидеть картину в целом. Используя кто, что, когда, где, почему и как облегчить обсуждение и поощрить творческое мышление, ваша команда может убедиться, что этапы выявления и анализа проблем охвачены исчерпывающе и вдумчиво. Блокнот репортера и диктофон по желанию.
Журналистская шестерка – Кто Что Когда Где Почему Как #генерация идей #анализ проблем #решение проблем #онлайн #креативное мышление #удобный дистанционный метод , исследование вопросов, объяснение для генерирования идей
900
18.
LEGO Challenge
Теперь немного необычного занятия. LEGO Serious Play — это методология фасилитации, которую можно использовать для улучшения творческого мышления и навыков решения проблем.
LEGO Challenge включает в себя предоставление каждому члену команды задания, скрытого от остальной группы, пока они создают структуру, не говоря ни слова.
Задача LEGO представляет собой забавный рабочий пример работы с заинтересованными сторонами, которые могут быть не согласны с решением проблем. Кроме того, это LEGO! Кто не любит LEGO!
LEGO Challenge #hyperisland #team
Командная деятельность, в которой группы должны работать вместе, чтобы построить структуру из LEGO, но у каждого человека есть секретное «задание», которое делает совместный процесс более сложной. Он подчеркивает групповое общение, динамику лидерства, конфликты, сотрудничество, терпение и стратегию решения проблем.
19. Что, и что, что теперь?
При отсутствии тщательного управления этапы выявления и анализа проблем в процессе решения проблем могут фактически создать больше проблем и недоразумений.
Что, ну и что, что теперь? деятельность по решению проблем предназначена для того, чтобы помочь собрать информацию и двигаться вперед, а также устранить возможность разногласий, когда речь идет о выявлении, прояснении и анализе организационных или рабочих проблем.
Фасилитация заключается в том, чтобы объединить группы, чтобы они могли работать над достижением общей цели, а лучшие стратегии решения проблем гарантируют, что команды будут согласованы в целях, если изначально не во мнениях или понимании.
На протяжении трех этапов этой игры вы даете каждому члену команды возможность подумать о проблеме, задав вопросы, что произошло, почему это важно и какие действия следует предпринять.
Это может быть отличным упражнением для выражения нашего индивидуального восприятия проблемы или задачи и контекстуализации их в условиях более крупной группы. Это один из самых важных навыков решения проблем, который вы можете привнести в свою организацию.
W³ – Что, ну и что, что теперь? #анализ проблем #инновация #освобождение структур
Вы можете помочь группам осмыслить общий опыт таким образом, чтобы добиться понимания и стимулировать скоординированные действия, избегая при этом непродуктивного конфликта.
Каждый голос может быть услышан при одновременном поиске идей и формировании нового направления. Пошаговое продвижение делает это практичным — от сбора фактов о What Happened к осмыслению этих фактов с Итак, что и, наконец, к тому, какие действия логически следуют с Теперь что . Общая прогрессия устраняет большинство недоразумений, которые в противном случае разжигали бы разногласия по поводу того, что делать. Вуаля!
20. Журналисты
Анализ проблемы может быть одним из самых важных и решающих этапов всех инструментов решения проблем. Иногда команда может увязнуть в деталях и не в состоянии двигаться вперед.
Журналисты — это деятельность, которая может помочь группе избежать застревания на этапах выявления проблемы или анализа проблемы в процессе.
В задании «Журналисты» группе предлагается нарисовать первую полосу вымышленной газеты и выяснить, какие истории заслуживают того, чтобы быть на обложке, и какие заголовки будут у этих историй. Переформулировав подход к своим проблемам и задачам, вы можете помочь команде продуктивно продвигаться по процессу и лучше подготовиться к последующим шагам.
Журналисты #видение #общая картина #анализ проблемы #remote-friendly
Это упражнение нужно использовать, чтобы увидеть общую картину в деталях и с трудом. Также хорошо для определения видения.
Методы решения проблем для выработки решений
Успех любого процесса решения проблем можно измерить решениями, которые он дает. После того, как вы определили проблему, изучили существующие идеи и придумали, пришло время сузиться до правильного решения.
Используйте эти методы решения проблем, если вы хотите помочь своей команде найти консенсус, сравнить возможные решения и перейти к действиям по конкретной проблеме.
Mindspin
Improved Solutions
Four-Step Sketch
15% Solutions
How-Now-Wow matrix
Impact Effort Matrix
Dotmocracy
21. Mindspin
Brainstorming is part of the bread и масло процесса решения проблем, и все стратегии решения проблем выигрывают от выдвижения идей и стимулирования команды к быстрому поиску решений.
С помощью Mindspin участников поощряют не только генерировать идеи, но и делать это в условиях ограниченного времени, бросая карточки и передавая их дальше. Проведя несколько раундов, ваша команда может начать с свободного создания возможных решений, прежде чем перейти к разработке этих решений и поощрению дальнейших идей.
Это одно из наших любимых занятий по решению проблем, которое отлично подходит для поддержания энергии на протяжении всего семинара. Помните о важности вовлечения людей в процесс — энергичные методы решения проблем, такие как Mindspin, могут помочь вашей команде оставаться вовлеченной и счастливой, даже когда проблемы, которые они собираются решать вместе, сложны.
MindSpin #teampedia #генерация идей #решение проблем #действие
Быстрый и громкий метод мозгового штурма для улучшения команды. Поскольку в этой деятельности есть более чем круглые повторяющиеся идеи, ее можно исключить, оставив более творческие и новаторские ответы на вызов.
22. Улучшенные решения
После того, как команда успешно определила проблему и предложила несколько решений, может возникнуть соблазн назвать работу по решению проблемы завершенной. Тем не менее, первое решение не обязательно является лучшим, и, включив в свою модель решения проблемы дальнейший обзор и размышление, вы можете гарантировать, что ваша группа достигнет наилучшего возможного результата.
Улучшенные решения, одна из нескольких игр от Thiagi Group, посвященных решению проблем, помогут вам сделать все возможное и разработать предлагаемые решения с тщательным рассмотрением и экспертной оценкой. Поддерживая обсуждение нескольких проблем одновременно и меняя роли в команде, этот метод решения проблем является динамичным способом поиска наилучшего решения.
Улучшенные решения #креативность #thiagi #решение проблем #action #team
Вы можете улучшить любое решение, объективно изучив его сильные и слабые стороны и внеся соответствующие корректировки. В этой творческой рамочной игре вы улучшаете решения нескольких проблем. Чтобы сохранить объективную непривязанность, вы имеете дело с отдельной проблемой в течение каждого из шести раундов и берете на себя разные роли (владелец проблемы, консультант, критик, сторонник, усилитель и оценщик) в каждом раунде. В конце задания каждый игрок получает два решения своей проблемы.
23. Эскиз из четырех шагов
Творческое мышление и визуальное представление не обязательно ограничивать начальными этапами ваших стратегий решения проблем. Упражнения, включающие наброски и прототипирование на бумаге, могут быть эффективны на этапе поиска решения и разработки процесса, а также отлично подходят для вовлечения команды.
Перейдя от простых заметок к сумасшедшему раунду из 8 секунд, который включает в себя быстрое набрасывание 8 вариантов своих идей, а затем создание окончательного наброска решения, группа может быстро и визуально повторять итерации. Методы решения проблем, такие как «Четырехшаговый набросок», отлично подходят, если у вас есть группа разных мыслителей и вы хотите изменить ситуацию, отказавшись от более текстового или дискуссионного подхода.
Четырехэтапный набросок #дизайн-спринт #инновация #генерация идей #удобный для удаленного доступа структурированный процесс, включающий:
Обзор ключевую информацию
Начало проектирования работу на бумаге,
Рассмотрение нескольких вариантов ,
Создание подробного решения .
Этому упражнению предшествует ряд других действий, позволяющих группе уточнить задачу, которую они хотят решить. Посмотрите, как упражнение «Набросок из четырех шагов» вписывается в дизайн-спринт
24. 15% Решения
Некоторые проблемы проще других, и с помощью правильных действий по решению проблем вы можете дать людям возможность предпринять немедленные действия, которые могут помочь создать организационные изменения.
Часть инструментария освобождения структур, 15% решений — это метод решения проблем, который фокусируется на быстром поиске и реализации решений. Процесс итерации и быстрого внесения небольших изменений может помочь создать импульс и желание решать сложные проблемы.
Стратегии решения проблем могут жить и умирать в зависимости от того, есть ли на борту люди. Получение нескольких быстрых побед — отличный способ привлечь людей к участию в процессе.
Команде может быть очень полезно осознать, что методы решения проблем можно быстро и легко применять, а также провести разграничение между вещами, на которые они могут оказать положительное влияние, и теми вещами, которые они не могут изменить.
15% Решения #действие #освобождение структур #remote-friendly
Вы можете показать действия, пусть даже небольшие, которые каждый может выполнить немедленно. Как минимум, это создаст импульс, и это может иметь БОЛЬШОЕ значение.
15% Решения показывают, что нет причин ждать, чувствовать себя бессильным или бояться. Они помогают людям поднять уровень. Они заставляют отдельных лиц и группу сосредоточиться на том, что находится в их компетенции, а не на том, что они не могут изменить.
С помощью очень простого вопроса вы можете перевести разговор на то, что можно сделать и найти решения больших проблем, которые часто широко распространены в неизвестных заранее местах. Перемещение нескольких песчинок может вызвать оползень и изменить весь ландшафт.
25. Матрица How-Now-Wow
Процесс решения проблем часто бывает творческим, так как сложные проблемы обычно требуют изменения мышления и творческого подхода, чтобы найти наилучшие решения. Хотя на первых этапах обычно поощряется творческое мышление, группы часто могут тяготеть к знакомым решениям, когда дело доходит до конца процесса.
Выбирая решения, вы не хотите терять свою творческую энергию! Матрица How-Now-Wow от Gamestorming — это отличное упражнение по решению проблем, которое позволяет группе сохранять творческий подход и мыслить нестандартно, когда дело доходит до выбора правильного решения для данной проблемы.
Методы решения проблем, стимулирующие творческое мышление, а также создание и выбор новых решений, могут быть наиболее эффективными при организационных изменениях. Попробуйте Матрицу «Как-Сейчас-Вау», и не только из-за того, как приятно это произносить вслух.
Матрица How-Now-Wow #gamestorming #генерация идей #remote-friendly
. Однако когда дело доходит до конвергенции, люди часто выбирают идеи, которые им наиболее знакомы. Это называется «творческий парадокс» или «креадокс».
Матрица How-Now-Wow — это инструмент выбора идей, который ломает предрассудки, заставляя людей взвешивать каждую идею по 2 параметрам.
26. Матрица воздействия и усилий
Все методы решения проблем надеются не только найти решения данной проблемы или задачи, но и найти наилучшее решение. Когда дело доходит до поиска решения, группам предлагается надеть свои шляпы для принятия решений и по-настоящему подумать о том, как предложенная идея будет работать на практике.
Матрица воздействия и усилий — это один из методов решения проблем, относящихся к этому лагерю. Он позволяет участникам сначала генерировать идеи, а затем классифицировать их в матрице 2×2 на основе воздействия и усилий.
Действия, которые побуждают к критическому мышлению, оставаясь при этом простыми, бесценны. Используйте матрицу воздействия и усилий, чтобы перейти от идей к оценке потенциальных решений, прежде чем принимать их.
Матрица воздействия и усилия #gamestorming #принятие решений #action #remote-friendly
В этом упражнении по принятию решений возможные действия сопоставляются на основе двух факторов: усилий, необходимых для реализации, и потенциального воздействия. Категоризация идей по этим направлениям — полезная техника при принятии решений, поскольку она обязывает участников взвешивать и оценивать предлагаемые действия, прежде чем совершать их.
27. Дотмократия
Если вы успешно выполнили все этапы решения проблем в своей группе, вы должны двигаться к концу своего процесса с кучей возможных решений, разработанных с учетом конкретной проблемы. Но как помочь группе перейти от идеи к воплощению решения в жизнь?
Дотмократия, или точечное голосование, — это испытанный метод, помогающий команде в процессе решения проблем принимать решения и осуществлять действия с определенной степенью надзора и консенсуса.
Один из методов решения проблем, который должен быть в наборе инструментов каждого фасилитатора. Точечное голосование является быстрым и эффективным и может помочь определить наиболее популярные и лучшие решения и помочь группе эффективно принять решение.
Дотмократия #action #принятие решений #групповая расстановка приоритетов #гиперостров #удаленно-дружественный
Точкамократия – это простой метод групповой расстановки приоритетов или принятия решений. Это не деятельность сама по себе, а метод, который можно использовать в процессах, целью которых является расстановка приоритетов или принятие решений. Метод поддерживает группу, чтобы быстро увидеть, какие варианты наиболее популярны или актуальны. Варианты или идеи пишутся на стикерах и прикрепляются к стене, чтобы их могла видеть вся группа. Каждый человек голосует за варианты, которые, по его мнению, являются самыми сильными, и эта информация используется для обоснования решения.
Разминка для решения проблем
Все фасилитаторы знают, что разминка и разминка полезны для любого семинара или группового процесса. Семинары по решению проблем ничем не отличаются.
Используйте эти методы решения проблем, чтобы разогреть группу и подготовить ее к остальной части процесса. Активация вашей группы путем использования некоторых из лучших навыков решения проблем может быть одним из лучших способов увидеть отличные результаты вашего сеанса.
Регистрация заезда/отъезда
Совместное рисование
Покажи и расскажи
Созвездия
Нарисуй дерево
28.
Заезд/выезд
Твердые процессы планируются от начала до конца, и лучшие фасилитаторы знают, что задают тон и создание безопасной, открытой среды может быть неотъемлемой частью успешного процесса решения проблем.
Регистрация заезда/отъезда — это отличный способ начать и/или завершить семинар по решению проблем. Регистрация на сеансе подчеркивает, что каждый будет увиден, услышан и, как ожидается, внесет свой вклад.
Если вы проводите серию совещаний, установление последовательного шаблона регистрации и завершения может действительно помочь вашей команде войти в ритм. Мы рекомендуем это занятие по открытию-закрытию для малых и средних групп, хотя оно может работать и в больших группах, если они дисциплинированы!
регистрация / выезд . команда, которая открывает или закрывает процесс символически и совместно. Регистрация заезда/отъезда предлагает каждому члену группы присутствовать, быть увиденным и услышанным, а также выразить свое мнение или чувство. Регистрация подчеркивает присутствие, сосредоточенность и групповую приверженность; выезд подчеркивает размышления и символическое закрытие.
29. Совместное рисование
Творческое мышление и умение не бояться вносить предложения являются важными навыками решения проблем для любой группы или команды, и разминка путем поощрения такого поведения – отличный способ начать.
«Рисуем вместе» — одна из наших любимых творческих игр-ледоколов. Она быстрая, эффективная и увлекательная, а также может упростить все последующие шаги по решению проблем, поощряя группу к совместной работе визуально. Передавая карточки и добавляя дополнительные элементы по мере их прохождения, группа семинара попадает в полосу совместного творчества и развития идей, что имеет решающее значение для поиска решений проблем.
Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #ice breaker #remote-friendly
Создавайте дикие, странные и часто забавные открытки вместе и укрепляйте творческую уверенность группы.
30. «Покажи и расскажи»
Возможно, вы помните какую-то версию «Покажи и расскажите», когда учились в школе, и это отличное занятие по решению проблем для начала занятия.
Попросите участников подготовить что-нибудь перед семинаром, принеся предмет для показа и рассказа, это поможет им разогреться еще до начала сеанса! Игры, включающие физический объект, также могут стимулировать раннее вовлечение, прежде чем переходить к более масштабному мышлению.
Попросив участников рассказать истории о том, почему они решили принести тот или иной предмет в группу, вы поможете командам взглянуть на вещи с новой точки зрения и увидеть как различия, так и сходства в их подходе к теме. Отличная основа для подхода к процессу решения проблем в команде!
Show and Tell #GAMESTORMING #Action #Opening #meeting Feartitation
Показать и рассказать Taps at Methors. Цель игры — получить более глубокое понимание взглядов заинтересованных сторон на что-либо — новый проект, организационную реструктуризацию, изменение видения компании или динамику команды.
31. Созвездия
Кто не любит звезды? Созвездия — отличная разминка для любого семинара, поскольку они поднимают людей с ног, заряжают энергией и готовы по-новому заняться уже известными темами. Это также отлично подходит для демонстрации существующих убеждений, предубеждений и шаблонов, которые могут стать частью вашего сеанса.
Использование игр для разогрева, которые помогают укрепить доверие и связь, а также позволяют невербальные ответы, может помочь людям облегчить процесс решения проблем и поощрить участие всех в группе. Созвездия отлично подходят для больших пространств, которые позволяют двигаться, и, безусловно, являются практическим упражнением, позволяющим группе увидеть узоры, которые в противном случае невидимы.
Созвездия #TRUST #Connection #Opening #coaching #patterns #sysstem
9000 3. . Используется с командами для выявления системы, скрытых закономерностей, перспектив.
32. Нарисуй дерево
Игры на решение проблем, которые помогают повысить осведомленность группы с помощью центральной объединяющей метафоры, могут быть эффективными способами разогреть группу в любой модели решения проблем.
«Нарисуй дерево» — это простая разминка, которую можно использовать в любой группе и которая может дать быстрый заряд энергии. Начните с того, что попросите участников нарисовать дерево всего за 45 секунд — они могут выбрать, будет ли оно абстрактным или реалистичным.
Когда таймер истечет, спросите группу, сколько людей включили корни дерева, и используйте это как средство для обсуждения того, как мы можем игнорировать важные части любой системы просто потому, что они не видны.
Все стратегии решения проблем становятся более эффективными благодаря критическому осмыслению проблем и выявлению вещей, которые обычно остаются незамеченными. Разминочные игры, такие как «Нарисуй дерево», хороши тем, что они быстро демонстрируют некоторые ключевые навыки решения проблем в доступной и эффективной форме.
Нарисуйте дерево #THIAGI #Opening #Perspectives #Удаленные брюшные
с этой игрой, которую вы можете поднять, и известно, что мы сможем, что мы сможем, что мы смогут быть более важными, и известны.
Завершение процесса решения проблем
Каждый этап семинара по решению проблем выигрывает от разумного развертывания действий, игр и методов. Эффективное завершение сеанса помогает обеспечить выполнение решений и отметить достигнутое.
Вот некоторые действия по решению проблем, которые вы можете использовать, чтобы эффективно завершить семинар или собрание и гарантировать, что проделанная вами большая работа может быть продолжена после этого.
One Breath Feedback
Who What When Matrix
Response Cards
Как завершить процесс решения проблемы?
Все хорошее когда-нибудь заканчивается. Когда большая часть работы уже сделана, может возникнуть соблазн быстро завершить семинар, не тратя время на подведение итогов и согласование. Это может быть проблематично, поскольку не позволяет вашей команде полностью обработать результаты или обдумать процесс.
В конце эффективной сессии ваша команда пройдет через процесс, который хоть и продуктивный, но может быть утомительным. Важно дать вашей группе время перевести дух, убедиться, что у них есть четкое представление о будущих действиях, и предоставить краткую обратную связь, прежде чем покинуть место.
Основной целью любого метода решения проблем является создание решений, а затем их реализация. Не забудьте воспользоваться возможностью, чтобы убедиться, что все согласованы и готовы эффективно реализовать решения, которые вы разработали на семинаре.
Помните, что каждый процесс можно улучшить, и, уделив короткое время сбору отзывов во время сеанса, вы сможете еще больше усовершенствовать свои методы решения проблем и добиться дальнейших успехов в будущем.
33. Обратная связь на одном дыхании
Сохранение внимания и сосредоточенности на заключительных этапах семинара по решению проблем может оказаться непростой задачей, поэтому краткая обратная связь может иметь большое значение. Легко навлечь на себя «смерть из-за обратной связи», если некоторые члены команды будут слишком долго делиться своими взглядами в ходе быстрого раунда обратной связи.
One Breath Feedback — отличное завершающее занятие для семинаров. Вы даете всем возможность оставить отзыв о том, что они сделали, но только на одном дыхании. Это делает обратную связь короткой и по существу, а также означает, что каждому предлагается предоставить наиболее важную часть обратной связи.
Обратная связь на одном дыхании #закрытие #обратная связь #действие
Это раунд обратной связи всего на одном дыхании, который превосходен в сохранении максимального внимания: каждый участник может говорить всего за один вдох … для люди, это около 20-25 секунд . .. если, конечно, вы не были глубоководным ныряльщиком, и в этом случае вы сможете делать это дольше.
34. Кто Что Когда Матрица
Матрицы являются частью многих эффективных стратегий решения проблем, и на то есть веские причины. Они легко узнаваемы, просты в использовании и дают результаты.
Матрица «Кто, что, когда» — отличный инструмент, который можно использовать при завершении сеанса решения проблем, приписывая кто, что и когда действиям и решениям, которые вы выбрали. Полученная матрица — это простой и удобный способ обеспечить продвижение вашей команды вперед.
Великие решения не могут быть реализованы без действий и сопричастности. Ваш процесс решения проблем должен включать в себя этап распределения задач между отдельными лицами или группами и создание реалистичных сроков реализации или проверки этих решений. Используйте этот метод, чтобы сделать процесс реализации решения ясным и простым для всех участников.
Кто/Что/Когда Матрица #gamestorming #action #planning проекта
С помощью матрицы «Кто/Что/Когда» вы можете связать людей с четкими действиями, которые они определили и которые они взяли на себя.
35. Карточки ответов
Групповое обсуждение может включать в себя большую часть действий по решению проблем, и к концу процесса вы можете обнаружить, что ваша команда выговорилась!
Предоставление вашей команде средств для обратной связи с помощью коротких письменных заметок может гарантировать, что каждый будет руководить и сможет внести свой вклад без необходимости вставать и говорить. В зависимости от потребностей группы предоставление альтернативы может помочь гарантировать, что каждый сможет внести свой вклад в вашу модель решения проблем так, как это наиболее удобно для них.
Карточки с ответами — отличный способ закрыть семинар, если вы ищете мягкую разминку и хотите получить быстрое обсуждение некоторых полученных отзывов.
Ответные карты #Debrifing #Close #Structured Sharing #questions и ответы #ThiAgi 9083 # #ThiAgi 9083 # #ThiAgi 9083 # #ThiAgi .
No related posts.