Обьясните, пожалуйста, как решать тождества
Ответ оставил Гость
Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят.
Доказать(решить) тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части. В алгебре существует несколько различных способов доказательства тождеств.
Способы:
1. Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным.
2. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным.
3. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным.
4. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Например, x*(a+b) + a*(b-x) = b*(a+x)
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства: x*(a+b) + a*(b-x) = x*a+x*b+a*b – a*x.
Приведем подобные слагаемые и вынесем общий множитель за скобку:
x*a+x*b+a*b – a*x = x*b+a*b = b*(a+x).
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством. Всё!!!
Примеры тождеств:
a + b = b + a;
a + (b + c) = (a + b) + c;
a*b = b*a;
a*(b*c) = (a*b)*c;
a*(b + c) = a*b + a*c;
a + 0 = a;
a*0 = 0;
a*1 = a;
a*(-1) = -a.
Оцени ответ
reshebka.comТождество. Тождественные выражения, преобразования
Тождество – это равенство, обе части которого являются тождественно равными выражениями. Тождества делятся на буквенные и числовые.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными), если при любых численных значениях букв они имеют одинаковую численную величину. Таковы, например, выражения:
x(5 + x) и 5x + x2
Оба представленных выражения, при любом значении x будут равны друг другу, поэтому их можно назвать тождественными или тождественно равными.
Так же тождественными можно назвать и числовые выражения, равные между собой. Например:
20 — 8 и 10 + 2
Буквенные и числовые тождества
Буквенное тождество
(a + b)m = am + bm
(a + b)2 = a2 + 2ab + b2
Числовое тождество – это равенство, содержащее только числа, выраженные цифрами, у которого обе части имеют одинаковую численную величину. Например:
4 + 5 + 2 = 3 + 8
5 · (4 + 6) = 50
Тождественные преобразования выражений
Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, тождественное первому.
При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения или просто преобразованием выражения. Все преобразования выражений выполняются на основе свойств действий над числами.
Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:
10x — 7x + 3x = (10 — 7 + 3)x = 6x
Выполнение данного преобразования основано на распределительном законе умножения.
naobumium.info
Тождество, тождественные преобразования | Формулы с примерами
Что такое тождество?
Определение
Выражение 1 = Выражение 2 — тождество, если это равенство выполняется при любых значениях переменных (букв), входящих в выражения.
Правило При этом говорят, что «Выражение 1» тождественно равно
«Выражению 2». Примеры x + 5x + 6 = 6x + 6
верно при любых x — тождество;
3 (xy — 16 ) + 23 — yx = 2xy — 25
верно при любых a и b — тождество;
3x + y = 6 -x — 1,3z
верно при любых x, y и z — не тождество.
Тождественные преобразования выражений
Определение
Тождественным преобразованием называется замена выражения тождественно равным ему выражением.

Правило
Раскрытие скобок, вынесение общего множителя, приведение подобных,
перемена мест слагаемых — примеры тождественных преобразований
выражений.
Тождественные преобразования уравнений
Правило 11. Перенос слагаемых из одной части уравнения в другую с изменением
их знаков на противоположные.
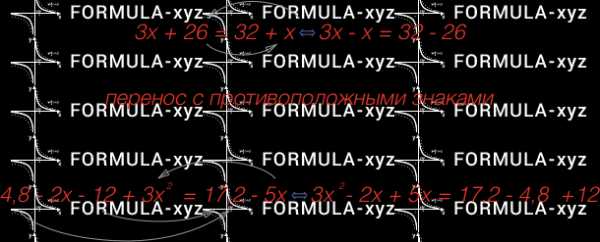
2. Умножение или деление обеих частей уравнения на одно и то же
не нулевое число.

Помни
! В правой и левой частях уравнения можно выполнять любые
тождественные преобразования выражений, т.е. раскрывать скобки, приводить
подобные и т.д.
formula-xyz.ru
Как доказать тождество?
Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
В простых случаях, когда тождество не содержит переменных и иррациональности, можно просто вычислить правую и левую части.
Пример. Доказать тождество \((2,5+5\cdot\) \(\frac{6}{15}\)\()^2=22-1,75\).
Решение:
\((2,5+5\cdot\) \(\frac{6}{15}\)\()^2=22-1,75\)
\( (2,5+\) \(\frac{6}{3}\)\()^2=20,25\)
\((2,5+2)^2=20,25\)
\((4,5)^2=20,25\)
\(20,25=20,25\)
Тождество доказано.
В более сложных случаях, доказывая тождество, приходится прибегать к преобразованиям, потому что просто посчитать «в лоб» уже нельзя. При этом можно:
- Преобразовывать обе части одновременно (как в примере выше).
- Преобразовывать только левую или только правую часть.
- Переносить слагаемые через равно, меняя знак.
- Умножать левую и правую часть на одно и то же число.
- Использовать все математические правила и формулы (формулы сокращенного умножения, свойства степени, правила работы с дробями и разложения на множители и так далее и тому подобное). Именно пятый пункт при доказательстве тождеств используется чаще всего, поэтому все эти свойства и правила нужно знать, помнить и уметь использовать.
Пример.
Доказать тождество \((a+b)^2+(a-b)^2=2(a^2+b^2)\).
Решение:
|
\((a+b)^2+(a-b)^2=2(a^2+b^2)\) |
Работаем с левой частью, не трогая правую. |
|
\(a^2+2ab+b^2+a^2-2ab+b^2=2(a^2+b^2)\) |
…затем приводим подобные слагаемые,… |
|
\(2a^2+2b^2=2(a^2+b^2)\) |
…после чего вынесем за скобку двойку. |
|
\(2(a^2+b^2 )=2(a^2+b^2)\) |
Обе части равны — тождество доказано |
Пример.
Доказать тождество \(x^2+\frac{1}{x^2} =(x+\frac{1}{x})^2-2\).
Решение:
|
\(x^2+\frac{1}{x^2} =(x+\frac{1}{x})^2-2\) |
Преобразуем правую часть, не трогая левую. |
|
\(x^2+\frac{1}{x^2} =x^2+2x\cdot\frac{1}{x}+\frac{1}{x^2} -2\) |
…упростим одно из слагаемых, сократив \(x\) и \(\frac{1}{x}\), … |
|
\(x^2+\frac{1}{x^2} =x^2+2+\frac{1}{x^2} -2\) |
… и приводим подобные слагаемые (\(2\) и \(-2\)). |
|
\(x^2+\frac{1}{x^2} =x^2+\frac{1}{x^2}\) |
Слева и справа одинаковые выражения, значит тождество доказано. |
Смотрите также:
Тождество
Как доказать тригонометрическое тождество?
Скачать статью
cos-cos.ru
Доказательство тождеств
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (76,3 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- Повторить определения тождества и тождественно равных выражений.
- Ввести понятие тождественного преобразования выражений.
- Развивать у учащихся навыки доказательства тождеств методом тождественного преобразования выражений.
- Воспитывать коммуникативную культуру учащихся.
Ход урока
Перед началом урока учащиеся класса разбиваются на шесть учебных групп смешанного состава.
I
Учитель: Здравствуйте, ребята, я предлагаю учебный кабинет превратить на время в научно-исследовательскую лабораторию, а нам с вами в ученых-магистров математических наук.
Но каждый, уважающий себя ученый, постоянно решает какую-нибудь очень важную проблему, вот и нам, прежде всего, предстоит узнать: над какой проблемой мы будем сегодня работать?
Для этого нам нужно решить две задачи: (Слайд 1)
- Разложите на множители выражение 4х – 8ху. (После выполнения задания на слайде появляется слово «Доказательство»)
- Представьте выражение -5у(у – 2) в виде многочлена. (После выполнения задания на слайде появляется слово «Тождеств»)
Учитель: Работать сегодня мы будем над «Доказательством тождеств», а девизом нашей работы я предлагаю взять вот эти замечательные слова: (Слайд 2)
Пусть каждый день и каждый час
Нам новое добудет,
Пусть добрым будет ум у нас,
А сердце умным будет!
II
Учитель: Господа ученые, прежде чем решать поставленную задачу, нам необходимо укрепить свою теоретическую базу, ведь понятие тождества вам уже знакомо. И поэтому в рубрике (Слайд 3) «Повторение – мать учения» я предлагаю вам провести следующую работу:
В каждой научной группе находятся формулировки трех понятий на карточке 1, вы должны среди них найти два определения: 1) Определение тождества, 2) Определение тождественно равных выражений.
(Учащиеся в течение 2-3 минут изучают эти определения, спрашиваются представители тех групп, которые быстрее всех справились с заданием, остальные участники других групп показывают согласие или несогласие с помощью сигнальных карточек зеленого и красного цветов)
Карточка 1
| … – это равенство, верное при любых допустимых значениях, входящих в его состав переменных. |
| Два выражения, соответственные значения которых равны при любых значениях переменных, называются … равными. |
| Замену одного выражения другим, тождественно равным ему, называют … преобразованием выражения. |
После того как учащиеся дают верное определение, оно высвечивается на экране.
Учитель: Хорошо, а сейчас проверим себя. На экране будут появляться равенства, если это равенство будет являться тождеством, то я предлагаю вам встать, если же – нет, то вы продолжаете сидеть: (Слайд 4)
- — (а – в) = — а + в
- а (в + с) = ав — ас
- а – (в + с) = а – в + с
- (а + в) – с = а – с + в
- — (а + в) = — в — а
III
Учитель: Хорошо, а сейчас пришла пора из теоретиков нам превращаться в ученых- практиков, но для этого нам нужно узнать, что нужно использовать, чтобы доказать тождество, и здесь нам не обойтись без научной литературы, ответ на этот вопрос мы найдем на странице … вашего учебника. Учащиеся находят в учебнике ответ: «Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений». Согласие или несогласие участники остальных групп показывают специальными сигналами, о которых говорилось выше. (Слайд 5)
Учитель: Молодцы, но теперь возникает следующий вопрос, а что такое тождественное преобразование выражений? Ответ можно найти на карточке 1, это оставшееся третье определение.
«Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения» (учитель предлагает ответить на этот вопрос одного из участников любой группы) (Слайд 6)
Вот сейчас мы уже «созрели» для практической работы, и я попрошу вас обратить свое внимание на карточку 2. Задание: «Докажите тождество», каждая группа ученых получила пример, который она должна решить самостоятельно, если будут возникать затруднения на помощь придут карточки- консультанты.
Карточка 2
| Докажите тождество | |
| 1. 10х–(5х+4)=5х–4 | Карточка-консультант |
| Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 2. 5х – 7 = 28х – 3 – х – 4 – 22х | Карточка-консультант |
| Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 3. (х – 5)(х + 2) = (х + 4)(х – 7) + 18 | Карточка-консультант |
| Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 4. –(2х – 3) + (х2 + 2х – 3) = х2 | Карточка-консультант |
| Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 5. 11х – 3 = 2х + 12 + 9х – 15 | Карточка-консультант |
Карточка 2
| Докажите тождество | |
| 6. –4(3у – 1) + 1 = –6(2у – 1) – 1 | Карточка-консультант |
| Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод. | |
Теперь нам необходимо защитить свои работы. (Презентация выполненных работ у доски, выступают желающие участники групп)
Учитель
: Замечательно, а теперь уважаемые коллеги пора подводить итоги, что же нам необходимо сделать, чтобы доказать, что равенство является тождеством? Предполагаемые ответы учащихся: (Слайд 7)- Выписать левую часть равенства, ее преобразовать и убедиться, что она равна правой.
или - Выписать правую часть равенства, ее преобразовать и убедиться, что она равна левой.
или - Преобразовать и левую и правую часть равенства и убедиться в том, что они равны одному и тому же выражению.
Учитель: Какой вывод можно сделать в том случае, когда все то, о чем мы только что сказали, не будет выполняться? Предполагаемый ответ учащихся: Равенство не будет являться тождеством.
IV
Учитель: Чтобы полученные знания были прочными, эту работу мы продолжим дома:
Домашнее задание: п. 30, 773, * Составить равенство, которое будет являться тождеством.
V
Учитель: А сейчас настал час для творчества: В стихотворении, которое вы видите, вставьте пропущенные слова: (Слайды 8-9)
Равенства всякие, братцы, бывают,
И каждый об этом, конечно же, знает.
Есть – с переменными, есть – (числовые),
Сложные очень и очень (простые),
Но есть среди равенств особенный класс,
О нем поведем свой рассказ мы сейчас.
(Тождеством) равенство это зовется.
Но это еще доказать нам придется.
Для этого нужно нам только лишь взять
И равенство это (преобразовать)
Несложно, конечно, нам будет узнать
Какую придется нам часть изменять,
А, может, придется нам обе менять,
По равенства виду нетрудно (понять)
Ура! Удалось применить наши знания,
Окончено равенства преобразование.
И смело уже говорим мы ответ:
Так (тождество) это, или все-таки нет!
VI
Учитель: Спасибо за урок!
5.03.2011
urok.1sept.ru
Тождественные преобразования
Доказать тождество ${(a+b+c)}^2- 2(ab+ac+bc)=a^2+b^2+c^2$
Решение: Для доказательства данного тождества мы используем первый из приведенных выше приемов, а именно будем преобразовывать левую часть тождества до ее равенства с правой.
Рассмотрим левую часть тождества:$\ {(a+b+c)}^2- 2(ab+ac+bc)$- она представляет собой разность двух многочленов. При этом первый многочлен является квадратом суммы трех слагаемых.Для возведения в квадрат суммы нескольких слагаемых используем формулу:
\[{(a+b+c)}^2=a^2+b^2+c^2+2ab+2ac+2bc\]Далее для преобразования раскроем скобку $2(ab+ac+bc).$
Для этого нам необходимо выполнить умножение числа на многочлен.Вспомним, что для этого надо умножить общий множитель,стоящий за скобками на каждое слагаемое многочлена,стоящего в скобках.Тогда получим:
$2(ab+ac+bc)=2ab+2ac+2bc$
Теперь вернемся к исходному многочлену,он примет вид:
${(a+b+c)}^2- 2(ab+ac+bc)=\ a^2+b^2+c^2+2ab+2ac+2bc-(2ab+2ac+2bc)$
Обратим внимание, что перед скобкой стоит знак «-» значит при раскрытии скобок все знаки, которые были в скобках меняются на противоположные.
${(a+b+c)}^2- 2(ab+ac+bc)=\ a^2+b^2+c^2+2ab+2ac+2bc-(2ab+2ac+2bc)= a^2+b^2+c^2+2ab+2ac+2bc-2ab-2ac-2bc$
Приведем подобные слагаемые,тогда получим, что одночлены $2ab$, $2ac$,$\ 2bc$ и $-2ab$,$-2ac$, $-2bc$ взаимно уничтожатся, т.е. их сумма равна $0$.
${(a+b+c)}^2- 2(ab+ac+bc)=\ a^2+b^2+c^2+2ab+2ac+2bc-(2ab+2ac+2bc)= a^2+b^2+c^2+2ab+2ac+2bc-2ab-2ac-2bc=a^2+b^2+c^2$
Значит путем тождественных преобразований мы получили тождественное выражение в левой части исходного тождества
${(a+b+c)}^2- 2(ab+ac+bc)=\ a^2+b^2+c^2$
Заметим, что полученное выражение показывает, что исходное тождество —верно.
Обратим внимание, что в исходном тождестве допустимы все значения переменной, значит мы доказали тождество используя тождественные преобразования, и оно верно при всех допустимых значениях переменной.
spravochnick.ru
Тождества. Рабочие материалы
Дополнительные сочиненияНа данном уроке мы сформируем понятие и дадим определение тождества, сформулируем его отличия от уравнения. Кроме того, мы научимся определять допустимые значения переменных. Мы решим много различных примеров, связанных с тождествами и тождественными преобразованиями.
Тема: Разложение многочленов на множители
Урок: Тождества
1. Формулировка понятия тождества
Рассмотрим примеры.
Пример 1:
;
Данное уравнение мы решали методом выделения полного квадрата и получили корни или
Пример 2:
;
Данное уравнение мы также решали методом выделения полного квадрата и получили ответ или .
Это означает, что в случае примера 1 только при или уравнение превращалось в верное числовое равенство, для второго примера только при или уравнение превращалось в верное числовое равенство.
Повторим ход решения примера 1. После преобразований мы получили уравнение , из которого явно видно, что и являются решениями данного уравнения.
Уравнение из примера 2 раскладывалось так: и отсюда тоже явно следует ответ.
Для нас важно то, что приведенные выше выражения справедливы каждое только для своей пары значений переменной и эти значения имеют название корни уравнения.
Но существуют такие выражения, которые справедливы при любых значениях переменных, которые в них входят. Рассмотрим примеры:
Пример 3:
;
Подставив в выражение любые значения , мы получим верное числовое равенство.
Пример 4:
;
Формула квадрата разности утверждает, что данное выражение справедливо при любых значениях
Выражения из примеров 3 и 4 мы будем называть тождествами. Подобных примеров можно привести очень много:
Пример 5:
;
Данное выражение также справедливо при любых значениях переменных
В этом и заключается принципиальное отличие уравнения от тождества. Тождество – это такое равенство, которое верно при любых значениях переменных, которые в него входят, уравнение же справедливо только при некоторых значениях переменных.
Уточним, что значит любые значения переменных. Рассмотрим элементарное равенство:
;
какое бы значение не принимал, равенство будет справедливым.
Разделим обе стороны на
Данное выражение будет справедливо при любых , кроме , потому что в знаменателе обеих дробей стоит двучлен , и эти дроби определены, то есть их можно вычислить, только если знаменатель не равен нулю: , то есть .
Пример 6:
Данное выражение является тождеством, так как оно справедливо во всех случаях кроме тех, когда знаменатель равен нулю. То есть, оно справедливо при всех , кроме , так как в этом случае дробь не имеет смысла.
2. Решение простых примеров
Итак, появились значения переменных, при которых даже само выражение не имеет смысла, в связи с этим скорректируем определение тождества: тождество это выражение, обращающееся в верное равенство при всех допустимых значениях переменных, которые в него входят.
Рассмотрим задачи.
Пример 7 – доказать тождество:
;
Мы уже встречались с подобными примерами, говорили, что .
Теперь докажем, что выражение под квадратом можно умножить на минус единицу и получится верное равенство. Для этого в заданном выражении раскроем скобки:
;
Мы знаем, что от перемены мест слагаемых сумма не меняется, таким образом, тождество доказано.
Но его можно доказать и другим способом:
;
Пример 8:
;
Преобразуем левую часть:
;
После преобразований получаем:
;
Тождество доказано.
Заметим, что тождественные преобразования – это те преобразования, при которых одно выражение заменяется другим, тождественно ему равным.
Пример 9:
;
Есть два способа решения данной задачи. Первый – это напрямую в левой части раскрыть квадрат, выполнить умножение одночлена на двучлен, привести подобные члены и посмотреть, окажется ли выражение тождеством или нет.
Второй способ – преобразовать левую часть при помощи метода вынесения общего множителя:
;
Теперь мы видим, что левая часть – это разность квадратов. Преобразует ее:
;
Получаем выражение:
;
Тождество доказано.
Пример 10 – доказать, что если , , , то выражения и тождественно равны при любых значениях :
Рассмотри два заданных выражения. В первом стоят с плюсом, а с минусом, во втором наоборот стоит с плюсом, а стоят с минусом, значит первое выражение равно второму, взятому с противоположным знаком. То есть имеем некоторое выражение :
, , ,
подставим значения A, B и С в заданное выражение:
;
Упростим выражение:
;
Приведем подобные члены:
;
;
Тождество доказано.
3. Решение примеров с определением допустимых значений переменных
Пример 11 – установите, является ли данное равенство тождеством и если да, то укажите допустимые значения переменных:
Начнем с определения допустимых значений :
, , и ;
Получили, что все значения , кроме и являются допустимыми, так как в этих двух точках знаменатель обращается в ноль и дробь не имеет смысла.
Теперь нужно упростить выражение в левой части. Это алгебраическая дробь и мы знаем, что нужно разложить на множители входящие в нее многочлены и сократить. В числителе применим формулу разности квадратов, а знаменатель оставим:
Получаем:
;
Данное выражение является тождеством при всех значениях , кроме и .
Пример 12 — установите, является ли данное равенство тождеством и если да, то укажите допустимые значения переменных:
Левая часть является алгебраической дробью, многочлены в числителе и знаменателе нужно разложить на множители:
Мы видим в числителе и знаменателе одинаковые выражения, которые можно сократить, но обязательно при этом нужно указывать допустимые значения:
Получаем:
Выражение является тождеством для всех значений, кроме:
4. Доказательство более сложных тождеств
Пример 13 – доказать тождество:
Пример 14 – доказать тождество:
Сначала упростим дробь:
Приведем подобные в левой части:
Свернем полный квадрат по формуле:
5. Выводы по уроку
Вывод: в данном уроке мы ознакомились с понятием тождества, дали его определение, научились определять допустимые значения переменных. Мы решили много примеров различной сложности и научились доказывать тождества, преобразуя только одну часть выражения или сразу обе.
Список рекомендованной литературы
1. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю. М., Ткачёва М. В., Фёдорова Н. Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет:
1. школьный помощник .
2. Задачи и тесты по геометрии, алгебре, физике и математике .
3. Портал для всей семьи .
Рекомендованное домашнее задание:
Задание 1 – доказать тождество: а) ; б) ; в) ; г)
Задание 2 – доказать тождество: а) ; б) ; в) ; г) ;
Задание 3 – доказать тождество и указать допустимые значения переменных:
а) ; б)
dp-adilet.kz
