Симплекс метод. Транспортная задача
Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары [2]. В табл.2 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий).
Таблица 2.
Производственные мощности (в шт.)
|
|
Кухни |
Кофеварки |
Самовары |
|
Штамповка |
20000 |
30000 |
12000 |
|
Отделка |
30000 |
10000 |
10000 |
|
Сборка |
20000 |
12000 |
8000 |
|
Объем выпуска |
Х1 |
Х2 |
Х3 |
|
Удельная прибыль (на одно изделие) |
15 |
12 |
14 |
При этом штамповка
и отделка проводятся на одном и том же
оборудовании. Оно позволяет штамповать
за заданное время или 20000 кухонь, либо
30000 кофеварок, либо и то, и другое, не в
меньшем количестве. А вот сборка
проводится на отдельных участках.
Задача линейного программирования имеет вид:
Х1 ≥ 0 , Х2 ≥ 0 , Х3 ≥ 0 , (0)
Х1 / 200 + Х2 / 300 + Х3 / 120 ≤ 100 , (1)
Х1 / 300 + Х2 / 100 + Х3 / 100 ≤ 100 , (2)
Х1 / 200 ≤ 100 , (3)
Х2 / 120 ≤ 100 , (4)
Х3 / 80 ≤ 100 , (5)
F = 15 Х1 + 12 Х2 + 14 Х3 → max .
Заметим, что
неравенство (3) вытекает из неравенства
(1), а неравенство (4) — из (2). Поэтому
неравенства (3) и (4) можно из формулировки
задачи линейного программирования
исключить.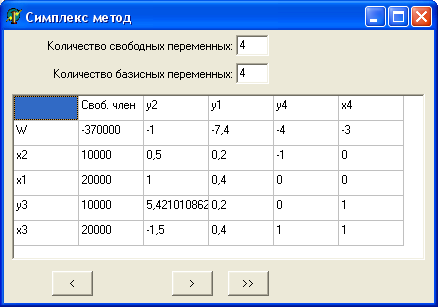
Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане Х3 = 0, т.е. самовары выпускать невыгодно.
Симплекс-метод. Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Симплекс-метод был предложен американцем Г. Данцигом в 1951 г. Основная его идея состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум. Разберем пример на основе данных табл.2.
Рассмотрим задачу линейного программирования, сформулированную выше при рассмотрении оптимизации номенклатуры и объемов выпуска:
F = 15 Х1 + 12 Х2 + 14 Х3 → max .Х1 / 200 + Х2 / 300 + Х3 / 120 ≤ 100 ,
Х1 / 300 + Х2 / 100 + Х3 / 100 ≤ 100 ,
Х3
/ 80 ≤ 100 .
При этом все переменные не отрицательны.
В соответствии с симплекс-методом введем т.н. «свободные переменные» Х4, Х5, Х6, соответствующие недоиспользованным мощностям, т.е. от системы неравенств перейдем к системе уравнений:
Х1 / 200 + Х2 / 300 + Х3 / 120 + Х4 = 100 ,
Х3 / 80 + Х6 = 100 ,
15 Х1 + 12 Х2 + 14 Х3 = F .
У этой системы имеется очевидное решение, соответствующее одной из вершин многогранника допустимых значений переменных:
Х1
= Х2
= Х3
= 0, Х4
= Х5 =
Х6
= 100,
F
= 0.
В терминах исходной задачи это означает, что ничего не надо выпускать. Такое решение приемлемо только на период летних отпусков.
В соответствии с симплекс-методом выбираем переменную, которая входит в целевую функцию F с самым большим положительным коэффициентом. Это Х1.
Сравниваем частные от деления свободных членов в первых трех уравнениях на коэффициенты при только что выбранной переменной Х1:
100 / (1/200) = 20000, 100 / (1/300) =30000, 100/0 = + ∞ .
Выбираем строку из системы уравнений, которой соответствует минимальное из всех положительных отношений. В рассматриваемом примере — это первая строка, которой соответствует отношение 20000.
Умножим первую строку на 200, чтобы получить Х1 с единичным коэффициентом:
Х1 + 2/3 Х2 + 2/1,2 Х3 + 200 Х4 = 20000 .
Затем умножим вновь полученную строку на (-1/300) и сложим со второй строкой, чтобы исключить член с Х1, получим
7/900 Х2 +
4/900 Х3
— 2/3 Х4
+ Х
Ту же преобразованную первую строку умножим на (-15) и сложим со строкой, в правой части которой стоит F, получим:
2 Х2 — 11 Х3 — 3000 Х4 = F — 300000.
В результате система уравнений преобразуется к виду, в котором переменная Х1 входит только в первое уравнение:
Х1 + 2/3 Х2 + 2/1,2 Х3 + 200 Х4 = 20000 ,
7/900 Х2 + 4/900 Х3 — 2/3 Х4 + Х5 = 100/3,
Х3 / 80 + Х6 = 100 ,
2 Х2 — 11 Х3 — 3000 Х4 = F — 300000.
Очевидно, у новой системы имеется улучшенное по сравнению с исходным решение, соответствующее другой вершине выпуклого многогранника в шестимерном пространстве:
Х1
= 20000,
Х2
= Х3
= Х4
= 0, Х5 =
100/3, Х6
= 100, F
= 300000.
В терминах исходной задачи это решение означает, что надо выпускать только кухни. Такое решение приемлемо, если допустимо выпускать только один вид продукции.
Повторим описанную выше операцию. В строке с F имеется еще один положительный коэффициент — при Х2 (если бы положительных коэффициентов было несколько — мы взяли бы максимальный из них). На основе коэффициентов при Х2 (а не при Х1, как в первый раз) образуемчастные от деления соответствующих свободных членов на эти коэффициенты:
20000 / (2/3) = 30000, (100/3) / (7/900) = 30000/7, 100/0 = + ∞.
Таким образом,
нужно выбрать вторую строку, для которой
имеем наименьшее положительное отношение
30000/7. Вторую строку умножим на 900/7 (чтобы
коэффициент при Х2
равнялся
1). Затем добавим обновленную строку ко
всем строкам, содержащим Х2,
предварительно умножив их на подходящие
числа, т.е.
такие, чтобы все коэффициенты
при Х2 стали
бы после сложения равны 0, за исключением
коэффициента второй строки, который
уже стал равняться 1. Получим систему
уравнений:
Х1 + 9/7 Х3 + 1800/7 Х4 — 600/7 Х5 = 120000/7 ,
Х2 + 4/7 Х3
— 600/7 Х4 + 900/7 Х5 = 30000/7,Х3 / 80 + Х6 = 100 ,
— 85/7 Х3 — 19800/7 Х4 — 1800/7 Х5 = F — 308571.
Поскольку все
переменные неотрицательны, то из
последнего уравнения следует, что
прибыль F
достигает своего максимального значения,
равного 308571, при Х3
= Х4
= Х5
= 0. Из
остальных уравнений следует, что при
этом Х1
= 120000/7
= 17143, Х2
= 30000/7 =
4286, Х6
= 100.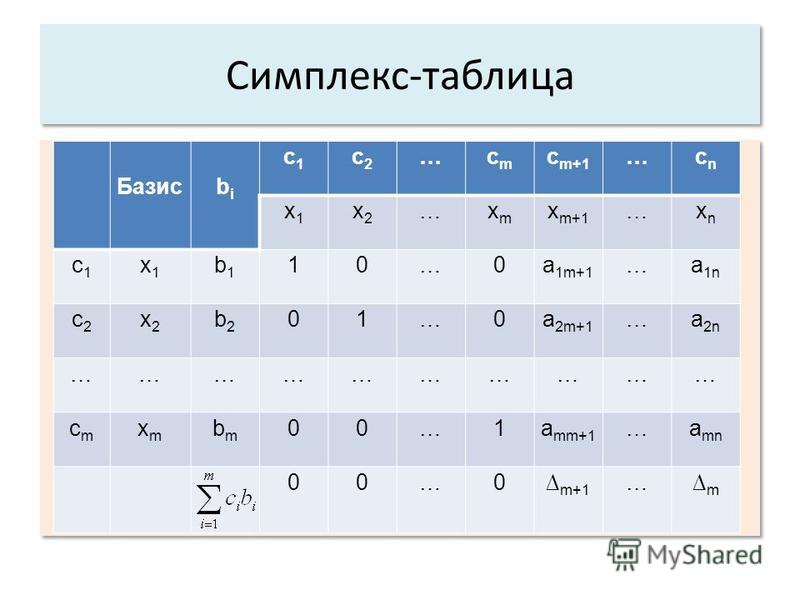
Поскольку в строке с F
не осталось ни одного положительного коэффициента
при переменных, то алгоритм симплекс-метода
закончил свою работу, оптимальное
решение найдено.
Практические рекомендации таковы: надо выпустить 17143 кухни, вчетверо меньше, т.е. 4286, кофемолок, самоваров не выпускать вообще. При этом прибыль будет максимальной и равной 308571. Все производственное оборудование будет полностью загружено, за исключением линии по сборке самоваров.
Транспортная
задача. Различные
технико-экономические и экономические
задачи менеджмента, от оптимальной
загрузки станка и раскройки стального
листа или полотна ткани до анализа
межотраслевого баланса и оценки темпов
роста экономики страны в целом, приводят
к необходимости решения тех или иных
задач линейного программирования. В
книге [1] приведен обширный перечень
публикаций, посвященный многочисленным
применениям линейного программирования
в металлургии, угольной, химической,
нефтяной, бумажной и прочих отраслях
промышленности, в проблемах транспорта
и связи, планирования производства,
конструирования и хранения продукции,
сельском хозяйстве, в научных исследованиях,
в том числе экономических, и даже при
регулировании уличного движения.
В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать «прикрепление» потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке.
Например, может
идти речь о перевозке песка — сырья для
производства кирпичей. В Москву песок
обычно доставляется самым дешевым
транспортом — водным. Поэтому в качестве
складов можно рассматривать порты, а в
качестве запасов — их суточную пропускную
способность. Потребителями являются
кирпичные заводы, а их потребности
определяются суточным производством
(в соответствии с имеющимися заказами).
Для доставки необходимо загрузить
автотранспорт, проехать по определенному
маршруту и разгрузить его.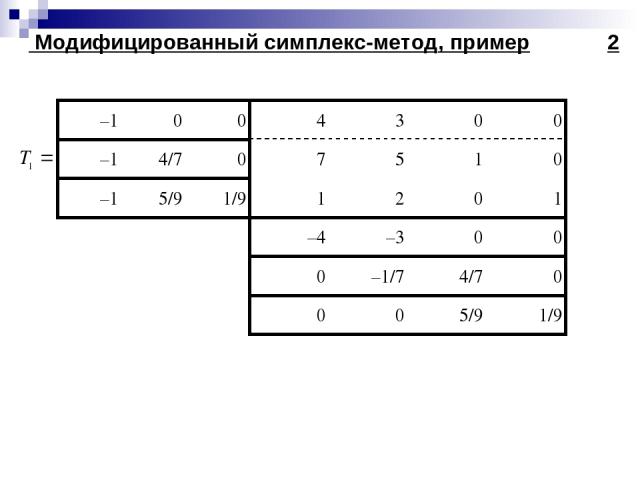
Стоимость
этих операций рассчитывается по известным
правилам, на которых не имеет смысла
останавливаться. Поэтому затраты на
доставку товара с определенного склада
тому или иному потребителю можно считать
известными.
Рассмотрим
пример транспортной задачи, исходные
данные к которой представлены в табл.
3. В ней, кроме объемов потребностей и
величин запасов, приведены стоимости
доставки единицы товара со склада i,
i =
1,2,3, потребителю j,
j =
1,2,3,4. Например, самая дешевая доставка
— со склада 2 потребителям 1 и 3, а также
со склада 3 потребителю 2. Однако на
складе 2 имеется 80 единиц товара, а
потребителям 1 и 3 требуется 50+70 =120 единиц,
поэтому к ним придется вести товар и с
других складов. Обратите внимание, что
в табл.3 запасы на складах равны суммарным
потребностям. Для примера с доставкой
песка кирпичным заводам это вполне
естественное ограничение — при невыполнении
такого ограничения либо порты будут
засыпаны горами песка, либо кирпичные
заводы не выполнят заказы.
Таблица 3.
Исходные данные к транспортной задаче.
|
|
Потреби-тель 1 |
Потреби-тель 2 |
Потреби-тель 3 |
Потреби-тель 4 |
Запасы на складах |
|
Склад 1 |
2 |
5 |
5 |
5 |
60 |
|
Склад 2 |
1 |
2 |
1 |
4 |
80 |
|
Склад 3 |
3 |
1 |
5 |
2 |
60 |
|
Потреб-ности |
50 |
40 |
70 |
40 |
200 |
Надо спланировать
перевозки, т.
е. выбрать объемы
Хij поставок товара
со склада i
потребителю j
, где i
= 1,2,3; j
= 1,2,3,4. Таким образом, всего в задаче
имеется 12 переменных. Они удовлетворяют
двум группам ограничений. Во-первых,
заданы запасы на складах:
X11 + Х12 + Х13 + Х14 = 60 ,
X21 + Х22 + Х23 + Х24 = 80 ,
X31 + Х32 + Х33 + Х34 = 60 .
Во-вторых, известны потребности клиентов:
X11 + Х21 + Х31 = 50 ,
X12 + Х22 + Х32 = 40 ,
X13 + Х23 + Х33 = 70 ,
X14
+
Х24
+ Х34
=
40
.
Итак, всего 7 ограничений типа равенств. Кроме того, все переменные неотрицательны — еще 12 ограничений.
Целевая функция — издержки по перевозке, которые необходимо минимизировать:
F = 2 X11 + 5 Х12 + 4 Х13 + 5 Х14 + X21 + 2 Х22 + Х23 + 4 Х24 +
+ +3 X31 + Х32 + 5 Х33 + 2 Х34 → min .
Кроме обсуждаемой, рассматриваются также различные иные варианты транспортной задачи. Например, если доставка производится вагонами, то объемы поставок должны быть кратны вместимости вагона.
Количество переменных и ограничений в транспортной задаче таково, что для ее решения не обойтись без компьютера и соответствующего программного продукта.
Задача — Транспортная задача
Контрольная работа
- формат docx
- размер 105.
44 КБ - добавлен 20 октября 2010 г.
Составление экономико-математической модели по условию. Нахождение
опорного плана методом наименьших стоимостей и методом
северо-западного угла. Ввод фиктивного потребителя. Метод
потенциалов проверки на опттимальность.
7 стр. (Методичка неизвестна, на белорусском языке, Задание III,
Вариант 8)
Смотрите также
- формат djvu
- размер 7.38 МБ
- добавлен 09 декабря 2009 г.
Пер. с англ. — М.: Радио и связь, 1989. — 176 с: ил. ISBN 5-256-00186-8. В книге английского автора освещены основные положения и методы линейного программирования. Рассмотрены симплекс-метод и его реализация на ЭВМ, проблема вырожденности, анализ чувствительности и двойственный симплекс-метод, транспортная задача, задача о назначении, двойственность в линейном программировании и др.
Алгоритмы решения различных задач линейного программирования ре…
- формат doc
- размер 1.28 МБ
- добавлен 29 июня 2009 г.
По каждой теме приведены все типовые примеры с подробным описанием решения задач. Содержание. Общая задача линейного программирования. Преобразование исходной модели. Графическое решение. Симплекс-метод. Двойственный симплекс-метод. Составление двойственных задач. Транспортная задача линейного программирования. а) Нахождение опорного плана. б) Правило «Минимального элемента». в) Метод потенциалов. Алгоритм решения транспортной задачи методом поте…
- формат djvu
- размер 8.56 МБ
- добавлен 01 ноября 2010 г.
Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа М.
: Наука, ФИЗМАТЛИТ, 1969. — 384 с. В практике применения линейного программирования часто приходится иметь дело с так называемыми специальными линейными задачами, системы ограничений которых обладают теми или иными особенностями. Учет этих особенностей в ряде случаев позволяет разработать для анализа специальных задач методы, значительно более экономные по сравнен…
- формат pdf
- размер 7.55 МБ
- добавлен 04 декабря 2011 г.
Москва: Изд-во «Знание», 1968. СОДЕРЖАНИЕ: Оценки оптимального плана. Общая задача линейного программирования. Транспортная задача. Динамическое программирование. Нелинейное программирование. Целочисленное программирование. Стохастическое программирование.
Лабораторная
- формат doc
- размер 145.
02 КБ - добавлен 06 ноября 2009 г.
НГТУ, 3 курс 2 семестр. Транспортная задача Метод потенциалов реешния ТЗ Модули: fminimax.m — решение задачи минимакса, fminicon.m — поиск минимума нелинейной задачи с ограничениями
Лабораторная
- формат doc
- размер 387.57 КБ
- добавлен 07 февраля 2011 г.
Тема: Оптимизация. Ход решения: найти методами наименьшего элемента и диагональным опорный план и построить его на оптимальность. Задача динамического программирования. Функциональное уравнение Беллмана. Условная оптимизация. Оптимальное распределение капитала
Статья
- формат doc
- размер 50.
8 КБ - добавлен 21 февраля 2005 г.
Транспортная задача как частный случай общей. распределительной задачи. Составление опорного плана. Распределительный метод достижения оптимального плана. Решение транспортной задачи методом потенциалов. Транспортная задача с правильным балансом. Транспортная задача с неправильным балансом. Решение транспортной задачи с помощью ЭВМ.
program
- формат exe
- размер 3.68 МБ
- добавлен 26 марта 2009 г.
ЗЛП: графический метод, симплекс-метод с различн. вариациями (М-метод, двухэтапный метод, двойственный с. м. ), транспортная задача (методом потенциалов), ЗЦЛП (метод ветвей и границ).
rn
- формат doc
- размер 1.48 МБ
- добавлен 14 октября 2008 г.
Задача максимизации целевой функции. Задача минимизации целевой функции.
Статья
- формат pdf
- размер 1.3 МБ
- добавлен 13 января 2011 г.
Воткинский филиал Ижевского государственного технического университета. . Тематика лекций: Постановка задачи линейного программирования. Основная задача линейного программирования. Геометрическая интерпретация задачи линейного программирования. Симплекс-метод. Теория двойственности. Двойственный симплекс-метод. Транспортная задача. Примеры задач: симплекс-метод, двойственный симплекс-метод, транспортная задача.
Транспортная задача: транспортный симплекс-метод | by Radzion Chachura
Это часть курса «Оптимизация для программистов».
Репозиторий GitHub с исходным кодомСимплексный метод транспортировки можно описать в четыре шага.
- Сбалансируйте проблему.
- Найдите начальное базовое допустимое решение одним из методов, например, с помощью правила северо-западного угла.
- Для всех основных переменных используйте u₁ = 0 и uᵢ + vⱼ = cᵢⱼ для расчета uᵢ и vⱼ . Для всех неосновных переменных вычислите wᵢⱼ = uᵢ + vⱼ -ciⱼ . Если wᵢⱼ ≤ 0 , текущее базовое допустимое решение является оптимальным. В противном случае выберите переменную с наиболее положительным значением wᵢⱼ в качестве входной переменной.
- Получите новое базовое допустимое решение, используя поворот цикла, и перейдите к шагу 3 .
Первый и второй шаги мы уже рассмотрели в предыдущих статьях, а теперь рассмотрим, как реализовать шаги 3 и 4.
После того, как мы получили начальное базовое допустимое решение, мы можем вычислить каждые uᵢ и vⱼ , перебирая каждую ячейку, содержащую базовую переменную.
u₁ = 0 и uᵢ + vⱼ = cᵢⱼДалее мы вычисляем wᵢⱼ для всех неосновных переменных. Поскольку есть некоторые wᵢⱼ , которые больше нуля, это означает, что мы не достигли оптимального решения. Поэтому мы выбираем переменную, которая войдет в следующее базовое допустимое решение.
выберите переменную с самым положительным значением wᵢⱼ в качестве входной переменной. Поняв, как выбрать переменную, которая будет входить в базовое допустимое решение, мы можем написать код для этого. Во-первых, давайте создадим функцию, которая будет вычислять uᵢ и vⱼ для каждой ячейки с базовой переменной. Он получает два параметра — базовое допустимое решение и затраты, просматривает каждую базовую переменную и заполняет списки, содержащие uᵢ и vⱼ .
Затем мы пишем функцию, которая получает основные переменные, затраты, нас, vs и возвращает список с wᵢⱼ . Он вычисляет wᵢⱼ для каждой неосновной переменной, используя простую формулу ( wᵢⱼ = uᵢ + vⱼ -ciⱼ), wᵢⱼ , представленную в виде кортежа, содержащего его позицию и значение.
Если это какое-то wᵢⱼ больше нуля, значит, решение можно улучшить.
Если решение можно улучшить, мы выбираем переменную для ввода, находя wᵢⱼ с наибольшим значением и вернуть его позицию.
Больше никаких прокрастинаций. У вас есть время для целей! Увеличитель поможет вам.
Реализуй свои амбиции!Цикл — это упорядоченная последовательность не менее четырех различных ячеек, удовлетворяющих всем трем условиям:
- Любые две последовательные ячейки лежат либо в одной строке, либо в одном столбце.
- Никакие три или более последовательных ячеек не лежат в одной строке или столбце.
- Последняя ячейка находится в той же строке или столбце, что и первая ячейка.
Мы используем цикл, поворачивающий , чтобы улучшить базовое возможное решение, и его процесс можно описать в четыре шага.
- Найдите единственный цикл, включающий входящую переменную и некоторые из основных допустимых переменных.
- Подсчитайте ячейки в цикле (начиная с 0), пометьте их как нечетные или четные ячейки.
- Найдите нечетную ячейку с наименьшим значением. Назовите это значение θ. Эта ячейка соответствует уходящей переменной.
- Уменьшить каждую нечетную ячейку в петле на θ и увеличить каждую четную ячейку в петле на θ.
Мы уже знаем положение входящей переменной и можем найти единственный возможный цикл. В начале мы движемся вверх от входной переменной (здесь мы выбираем направление случайным образом), затем мы идем прямо к последней базовой переменной в строке, поскольку мы не можем иметь три последовательных ячейки в строке, а затем одну ячейку вниз.
Затем мы помечаем ячейки цикла как четные и нечетные.
После этого находим нечетную ячейку с наименьшим значением.
Затем мы просматриваем каждую ячейку в цикле и добавляем θ к значению, если ячейка четная, и вычитаем, если нечетная.
В конце операции поворота у нас есть новое базовое допустимое решение.
Теперь давайте закодируем поворотную часть. Во-первых, мы пишем функцию, которая возвращает возможные следующие узлы для данного цикла. Это довольно просто.
Затем нам нужна функция, которая возвращает цикл для заданного списка с позициями основных переменных и позицией входящей переменной. Мы используем рекурсию в этой функции. Если цикл можно закрыть, мы переходим к позиции get_possible_next_nodes только входной переменной. Если цикл не может быть закрыт, мы рекурсивно проходим каждый возможный следующий узел.
Функция, выполняющая поворотную операцию, получает предыдущее базовое допустимое решение и цикл. Сначала мы собираем четные и нечетные ячейки, затем берем оставшуюся переменную и возвращаем новые базовые переменные.
Теперь мы можем собрать все воедино.
Чтобы рассчитать общую сумму, нам нужно пройтись по каждой стоимости, взять количество единиц из решения, умножить стоимость перевозки и количество единиц, которые будут отправлены, и добавить к общей стоимости.
Выйдите на новый уровень концентрации внимания и производительности с помощью увеличить.org.
УвеличениеТранспортировка Simplex Method с Python
Home
Сообщения
Программирование
Оптимизация и эксплуатационные исследования с Python
7.
6362 •5 MIN.
Транспортный симплексный метод можно описать четырьмя этапами.
-
Сбалансируйте проблему.
-
Найдите начальное базовое допустимое решение одним из методов, например, с помощью правила северо-западного угла.
-
Для всех основных переменных используйте u₁ = 0 и uᵢ + vⱼ = cᵢⱼ для расчета uᵢ и vⱼ .
Для всех неосновных переменных вычислите wᵢⱼ = uᵢ + vⱼ -ciⱼ . Если wᵢⱼ ≤ 0 , текущее базовое допустимое решение является оптимальным. В противном случае выберите переменную с наиболее положительным значением wᵢⱼ в качестве входной переменной. -
Получите новое базовое допустимое решение, используя поворот цикла, и перейдите к шагу 9.0012 3 .
Мы уже рассмотрели первый и второй шаги в предыдущих статьях, а теперь рассмотрим, как реализовать шаги 3 и 4.
Выбор входящей переменной
uᵢ и vⱼ , просматривая каждую ячейку, содержащую базовую переменную.
u₁ = 0 и uᵢ + vⱼ = cᵢⱼ
Затем мы вычисляем wᵢⱼ для всех неосновных переменных. Так как есть какие-то wᵢⱼ больше нуля, значит мы не достигли оптимального решения. Поэтому мы выбираем переменную, которая войдет в следующее базовое допустимое решение.
выберите переменную с самым положительным wᵢⱼ в качестве входной переменной.
Поняв, как выбрать переменную, которая будет входить в базовое допустимое решение, мы можем написать код для этого. Во-первых, давайте создадим функцию, которая будет вычислять uᵢ и *vⱼ * для каждой ячейки с базовой переменной. Он получает два параметра — базовое допустимое решение и затраты, перебирает каждую базовую переменную и заполняет списки, содержащие uᵢ и vⱼ .
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде get_us_and_vs.ipynb размещено с ❤ на GitHub
Затем мы пишем функцию, которая получает основные переменные, затраты, нас, vs и возвращает список с wᵢⱼ . Он вычисляет wᵢⱼ для каждой неосновной переменной, используя простую формулу ( wᵢⱼ = uᵢ + vⱼ -ciⱼ), *wᵢⱼ * представлено в виде кортежа, содержащего его позицию и значение.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде get_ws.ipynb размещено с ❤ на GitHub
Если это какое-то wᵢⱼ , что больше нуля, это означает, что решение можно улучшить.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде can_be_improved.ipynb размещено с помощью ❤ на GitHub
Если решение можно улучшить, мы выбираем переменную для ввода, находя *wᵢⱼ * с наибольшим значением и возвращая ее позицию.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть необработанный get_entering_variable_position.ipynb размещено с помощью ❤ by GitHub
Сводка цикла
Цикл представляет собой упорядоченную последовательность не менее четырех различных ячеек, которые удовлетворяют всем трем условиям:
-
Любые две последовательные ячейки лежат либо в одной строке, либо в одном столбце.
-
Никакие три или более последовательных ячеек не лежат в одной строке или столбце.
-
Последняя ячейка находится в той же строке или столбце, что и первая ячейка.
последние два примера не удовлетворяют всем условиям и не могут рассматриваться как цикл.
Мы используем цикл, поворачивающий , чтобы улучшить базовое допустимое решение, и его процесс можно описать в четыре шага.
-
Найдите единственный цикл, включающий входящую переменную и некоторые из основных допустимых переменных.
-
Подсчитайте ячейки в цикле (начиная с 0), пометьте их как нечетные или четные ячейки.
-
Найдите нечетную ячейку с наименьшим значением. Назовите это значение θ. Эта ячейка соответствует уходящей переменной.
-
Уменьшить каждую нечетную ячейку в петле на θ и увеличить каждую четную ячейку в петле на θ.
Мы уже знаем позицию входящей переменной и можем найти единственный возможный цикл. В начале мы движемся вверх от входной переменной (здесь мы выбираем направление случайным образом), затем мы идем прямо к последней базовой переменной в строке, поскольку мы не можем иметь три последовательных ячейки в строке, а затем одну ячейку вниз.
Затем мы помечаем ячейки цикла как четные и нечетные.
После этого находим нечетную ячейку с наименьшим значением.
Затем мы просматриваем каждую ячейку в цикле и добавляем θ к значению, если ячейка четная, и вычитаем, если нечетная.
В конце операции поворота у нас есть новое базовое допустимое решение.
Теперь давайте закодируем поворотную часть. Во-первых, мы пишем функцию, которая возвращает возможные следующие узлы для данного цикла. Это довольно просто.
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| по определению get_possible_next_nodes (цикл, не_посещено): | |
| последний_узел = цикл[-1] | |
| nodes_in_row = [n для n в not_visited, если n[0] == last_node[0]] | |
| nodes_in_column = [n для n в not_visited, если n[1] == last_node[1]] | |
| , если длина (цикл) < 2: | |
| вернуть nodes_in_row + nodes_in_column | |
| иначе: | |
| пред_узел = цикл[-2] | |
| row_move = предыдущий_узел[0] == последний_узел[0] | |
| , если row_move: вернуть nodes_in_column | |
| вернуть nodes_in_row |
просмотр необработанных данных
get_possible_next_nodes.
py
размещено с ❤ на GitHub
Затем нам нужна функция, которая возвращает цикл для данного списка с позициями основных переменных и позицией ввода переменной. Мы используем рекурсию в этой функции. Если цикл можно закрыть, мы переходим к позиции get_possible_next_nodes только входной переменной. Если цикл не может быть закрыт, мы рекурсивно проходим каждый возможный следующий узел.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде get_loop.ipynb размещено с помощью ❤ от GitHub
Функция, выполняющая поворотную операцию, получает предыдущее базовое допустимое решение и цикл. Сначала мы собираем четные и нечетные ячейки, затем берем оставшуюся переменную и возвращаем новые базовые переменные.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде loop_pivoting.ipynb размещено с помощью ❤ от GitHub
Окончательный алгоритм
Теперь мы можем собрать все воедино.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.
просмотреть в исходном виде transport_simplex_method.ipynb размещено на ❤ на GitHub
Чтобы рассчитать общую сумму, нам нужно пройтись по каждой стоимости, взять количество единиц из решения, умножить стоимость перевозки на количество единиц, которые будут отправлены, и добавить к общей стоимости.
Извините, что-то пошло не так. Перезагрузить?
К сожалению, мы не можем отобразить этот файл.
К сожалению, этот файл недействителен, поэтому его нельзя отобразить.