Вычислить сторону треугольника онлайн
Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными, тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны треугольника.
- Сторона треугольника равностороннего через радиус описанной окружности
- Сторона треугольника равностороннего через радиус вписанной окружности
- Сторона треугольника равностороннего через высоту
- Сторона треугольника равностороннего через площадь треугольника
- Основание равнобедренного треугольника через боковые стороны и угол между ними
- Основание равнобедренного треугольника через боковые стороны и угол при основании
- Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
- Боковая сторона равнобедренного треугольника через основание и угол при основании
- Катет прямоугольного треугольника через гипотенузу и острый угол
- Катет прямоугольного треугольника через гипотенузу и другой известный катет
- Гипотенуза прямоугольного треугольника через катет и острый угол
- Гипотенуза прямоугольного треугольника через катеты
- Сторона треугольника через две известные стороны и угол между ними
- Сторона треугольника через известную сторону и два угла
Сторона равностороннего треугольника через радиус описанной окружности
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:
Таким образом, формула будет выглядеть
следующим образом:
a = R * √3
где а — сторона треугольника, R — радиус описанной окружности.
Радиус (R):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.
Сторона равностороннего треугольника через радиус вписанной окружности
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6 / √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на квадратный корень из трех):
a = 2r * √3
где а — сторона треугольника, R — радиус вписанной окружности.
Радиус (R):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.
Сторона равностороннего треугольника через высоту
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4 =h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести формулу для нахождения стороны через высоту:
a = 2h / √3
где а — сторона, h — высота равностороннего треугольника.
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 * 45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.
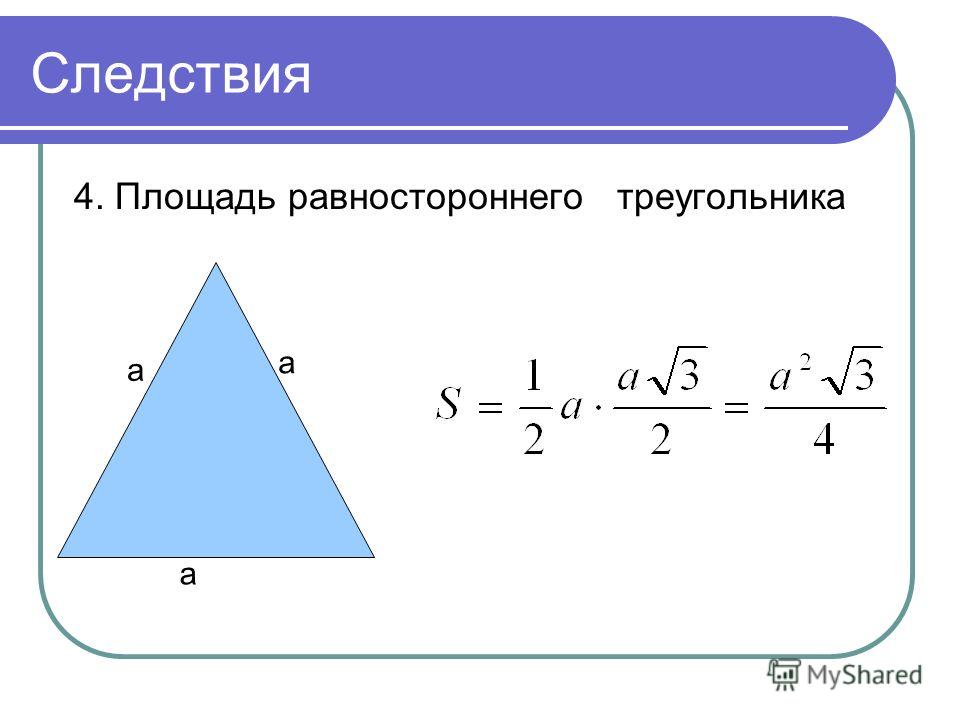
Сторона равностороннего треугольника через площадь
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую формулу
a = √(4S / √3)
где а — сторона, S — площадь равностороннего треугольника.
Площадь (S):
мм²см²дм²м²
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.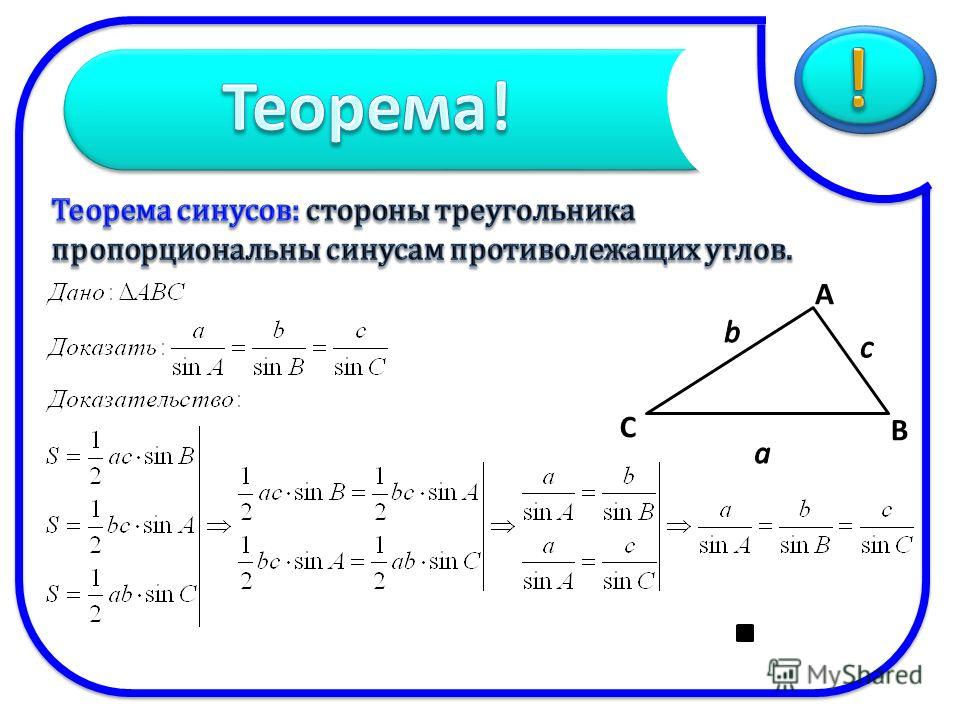
Основание равнобедренного треугольника через боковые стороны и угол между ними
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:
a = 2b * sin (α/2)
где a — длина основания треугольника, b — длина стороны треугольника; α — это угол, который противоположен основанию.
Сторона (b):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.
Основание равнобедренного треугольника через боковые стороны и угол при основании
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше.
a = 2b + cos β
где b — боковая сторона, β — угол при основании.
Сторона (b):
ммсмдмм
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.
Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.
Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми сторонами:
b = a / (2 * sin(α/2))
где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.
Основание (a):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11 см.
Боковая сторона равнобедренного треугольника через основание и угол при основании
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет выглядеть следующим образом:
b = a / 2 * cos β
где a — это основание, β — угол при основании равнобедренного треугольника.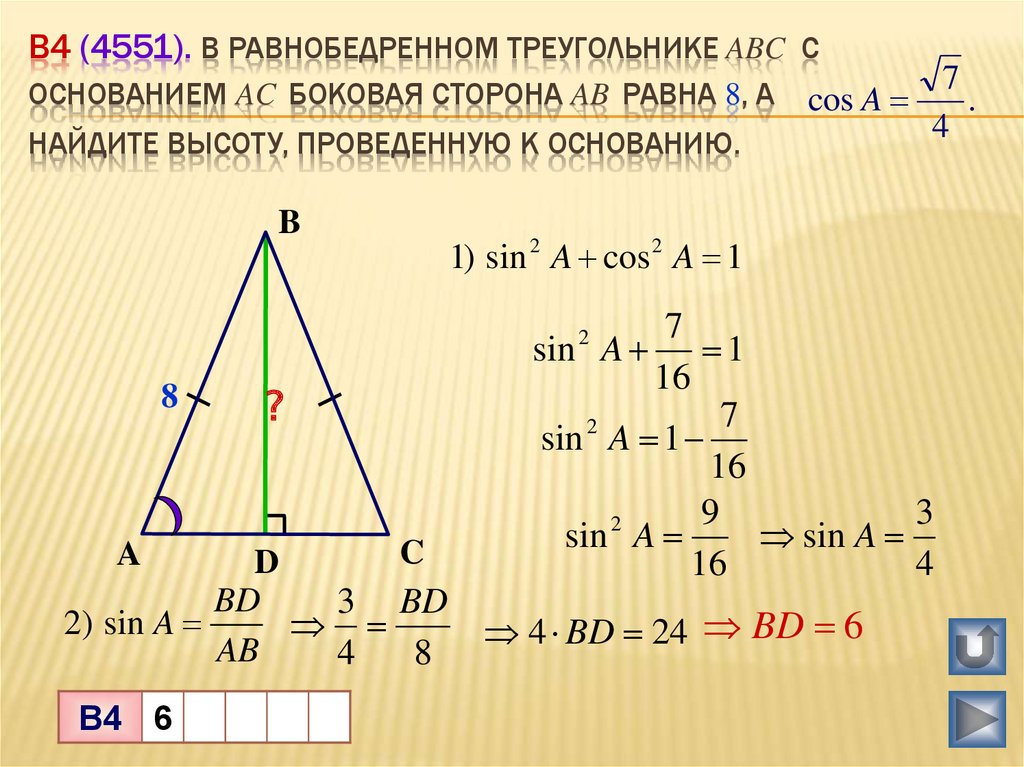
Основание (a):
ммсмдмм
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.
Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b = 35 / 2 * 0,5=35 мм.
Катет прямоугольного треугольника через гипотенузу и острый угол
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет, противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть следующим образом:
a = c * sin α
где c — гипотенуза, α — острый угол прямоугольного треугольника.
Гипотенуза (c):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим следующее: a = 77 * 0,98 = 75,8см.
Катет прямоугольного треугольника через гипотенузу и другой известный катет
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо воспользоваться формулой:
a = √(c² — b²)
где c — гипотенуза, b — катет который известен прямоугольного треугольника.
Гипотенуза (c):
ммсмдмм
Катет (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см
Гипотенуза прямоугольного треугольника через катет и острый угол
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол можно узнать по формуле:
c = a / sin(β)
где a — катет, β — острый угол прямоугольного треугольника.
Катет (a):
ммсмдмм
Угол (β):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.
Гипотенуза прямоугольного треугольника через катеты
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов: c² = a² + b² следовательно:
c = √(a² + b²)
где c — гипотенуза, a и b — катеты.
Катет (a):
ммсмдмм
Катет (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см
Сторона треугольника через две известные стороны и угол между ними
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны треугольника:
a = b² + c² — 2bc * cos α
где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.
Сторона (b):
ммсмдмм
Сторона (c):
ммсмдмм
Угол (α):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение.
Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.
Сторона треугольника через известную сторону и два угла
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться теоремой синусов и формула будут следующая:
a = (b * sin α) / sin β
где b — сторона треугольника; β, α — углы треугольника.
Сторона (b):
ммсмдмм
Угол (α):
градусырадианыsin
Угол (β):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Пусть сторона треугольника b равна 10, угол β = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30 = 8.71723 мм.
Пусть сторона треугольника b равна 10, угол β = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30 = 8.71723 мм.
Как найти сторону треугольника — в помощь школьнику :: SYL.ru
Золотой маникюр станет хитом 2023 года: тенденции и свежие новинки дизайна
Капуста понравится даже детям. Готовим ее в духовке
Крышка будет чистой. Как отмыть кухонную утварь без труда
Чтобы после стирки вещи выглядели аккуратными, положите кубики льда в барабан
Ракушки, цветы, браслеты и манжеты: ключевые ювелирные тренды 2023 года
И на этом этапе можно выглядеть грациозно: тренды осени-зимы для будущих мам
Модная обувь зимы 2022-2023: актуальные тренды, которые согреют в любые морозы
Превращение греха в стиль жизни: 5 ситуаций, в которых не стоит обвинять Дьявола
Появляются — и начинается скандал: люди, которых надо убрать из своей жизни
Пышно и вкусно.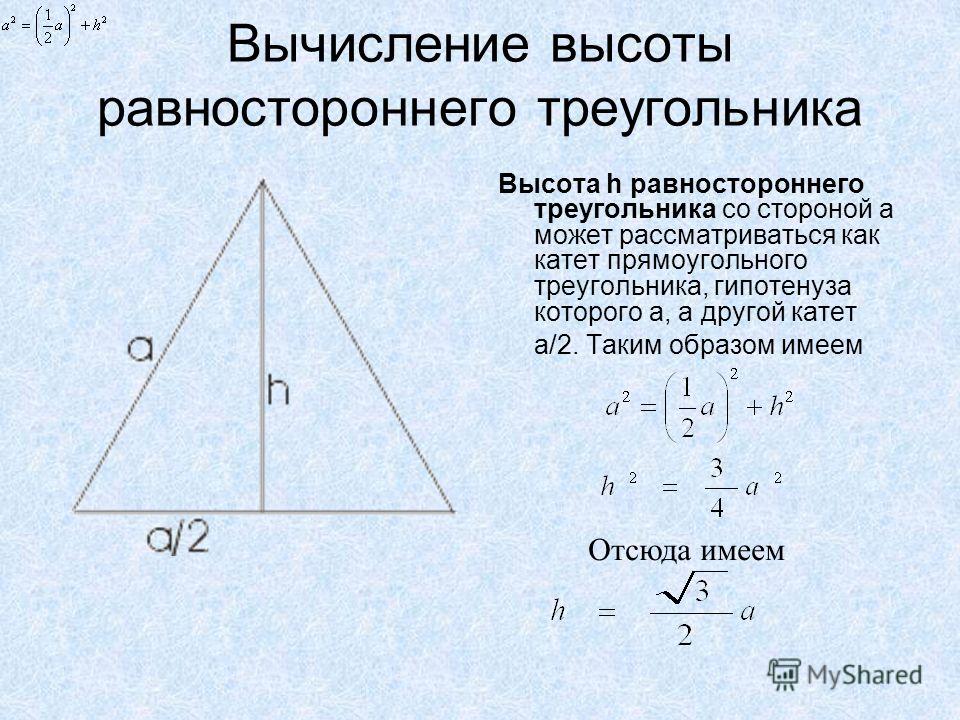 Готовим ароматные пряники на молоке
Готовим ароматные пряники на молоке
Автор Оксана Кисленкова
Есть несколько способов решения этой геометрической задачи. Они описаны в статье.
При помощи сторон и углов
Итак, первый способ нахождения сторон треугольника — это по нескольким сторонам и углу между ними (и аналогично с углами и одной прилежащей стороной). Данный способ подойдет для старшей школы, так как здесь используются такие понятия, как синус, косинус, квадрат числа и корень. Итак, как найти сторону треугольника, который является произвольным? Для начала нарисуем эту самую фигуру. Теперь давайте обзовем элементы нашей фигуры. Стороны будут a, b и c. Угол, находящийся напротив стороны a, у нас будет «альфа», напротив b -«бета», напротив c — «гамма».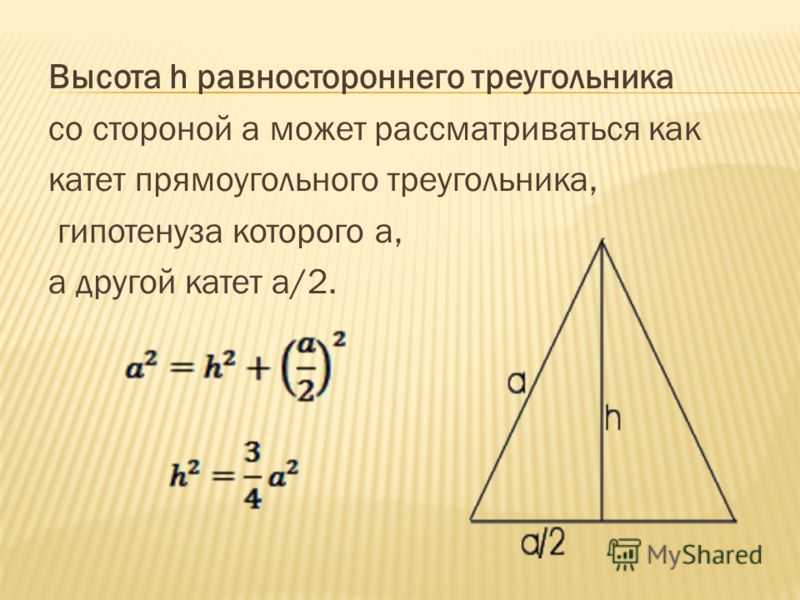 (1/2). Будьте внимательны, ведь если угол, расположенный напротив искомой стороны, будет тупым, то косинус примет отрицательное значение. Еще одна формула нахождения сторон треугольника — по двум углам и сторонам. Сразу приведем формулу-равенство, так как для понимания наглядный вид проще, чем длинная роспись. По-прежнему нам нужно найти сторону a. Тогда, опираясь на обозначения, получим следующее: a=(b*sin»альфа»)/sin»бета»=(b*sin»альфа»)/sin(«альфа»+»гамма»)=(b*sin(«бета»+»гамма»))/sin»бета». Вот таким мудреным способом можно найти неизвестную сторону произвольного треугольника.
(1/2). Будьте внимательны, ведь если угол, расположенный напротив искомой стороны, будет тупым, то косинус примет отрицательное значение. Еще одна формула нахождения сторон треугольника — по двум углам и сторонам. Сразу приведем формулу-равенство, так как для понимания наглядный вид проще, чем длинная роспись. По-прежнему нам нужно найти сторону a. Тогда, опираясь на обозначения, получим следующее: a=(b*sin»альфа»)/sin»бета»=(b*sin»альфа»)/sin(«альфа»+»гамма»)=(b*sin(«бета»+»гамма»))/sin»бета». Вот таким мудреным способом можно найти неизвестную сторону произвольного треугольника.
Равнобедренный треугольник
Что такое равнобедренный треугольник? Сам по себе он имеет две одинаковые стороны и так называемое основание. Стороны-близнецы обозначим буквой a, основание — b. Стало быть, раз у треугольника есть два «бедра» одной величины, то и углы на «фундаменте» тоже будут одинаковыми. Их назовем «альфа». Для того чтобы ответить, как найти сторону равнобедренного треугольника, необходимо ввести еще одну величину — угол, образованный между равными «бедрами». (1/2) или же a=b/(2/cos»альфа»). Какую именно запись нужно использовать? Все зависит от поставленной задачи и условий. Конечно же, можно произвести проверку вычислений по всем формулам, если у вас есть абсолютно все данные. Теперь можем двигаться дальше.
(1/2) или же a=b/(2/cos»альфа»). Какую именно запись нужно использовать? Все зависит от поставленной задачи и условий. Конечно же, можно произвести проверку вычислений по всем формулам, если у вас есть абсолютно все данные. Теперь можем двигаться дальше.
Прямоугольный треугольник
Наверное, каждый школьник, который только начал изучение геометрии, знает, что такое прямоугольный треугольник. С первого взгляда в данной фигуре нет ничего особенного, сложного и непонятного. Но вот когда «теряются» данные о той или иной стороне сего геометрического объекта, начинаются проблемы. Дело все в том, что вопрос: «Как найти сторону прямоугольного треугольника?» — затрагивает не только понятия синуса и косинуса, а еще и тангенсов углов. Таким образом, вычисления становятся намного сложнее и больше. Итак, сначала обозначим два катета нарисованного прямоугольного треугольника через a и b. Углы, лежащие напротив этих сторон, как и принято было прежде, назовем «альфа» и «бета» соответственно. (1/2). Вот простой и незамысловатый ответ на вопрос, как найти сторону треугольника. Не пугайтесь огромных вычислений.
(1/2). Вот простой и незамысловатый ответ на вопрос, как найти сторону треугольника. Не пугайтесь огромных вычислений.
Итоги
Итак, сегодня мы разобрались, как найти сторону треугольника, и выучили много новых формул. Для того чтобы лучше их запомнить, запишите их на какую-нибудь бумажку, по которой потом будет проще учить все наизусть. Не стоит пугаться «страшных» цифр и больших вычислений. Все проще, чем кажется.
Похожие статьи
- Находим периметр треугольника различными способами
- Что такое синус и косинус в тригонометрии?
- Как находить синус угла
- Как узнать площадь равностороннего треугольника: основные формулы
- Как вычислить площадь треугольника
- Прямоугольная трапеция: все формулы и примеры задач
- Прямоугольный треугольник и его свойства
Также читайте
Решение треугольников SSS
«SSS» означает «Бок, Бок, Бок»
« SSS » — это когда мы знаем три стороны треугольника и хотим найти недостающих углов . |
Чтобы решить треугольник SSS:
|
Мы используем «угловую» версию закона косинусов:
соз(С) = а 2 + б 2 − в 2 2аб
соз(А) = б 2 + в 2 − а 2 2bc
соз(В) = в 2 + а 2 − б 2 2ка
(у всех одинаковая формула, просто разные этикетки)
Пример 1
В этом треугольнике мы знаем три стороны:
- a = 8,
- б = 6 и
- с = 7,
Сначала используйте закон косинусов, чтобы найти один из углов.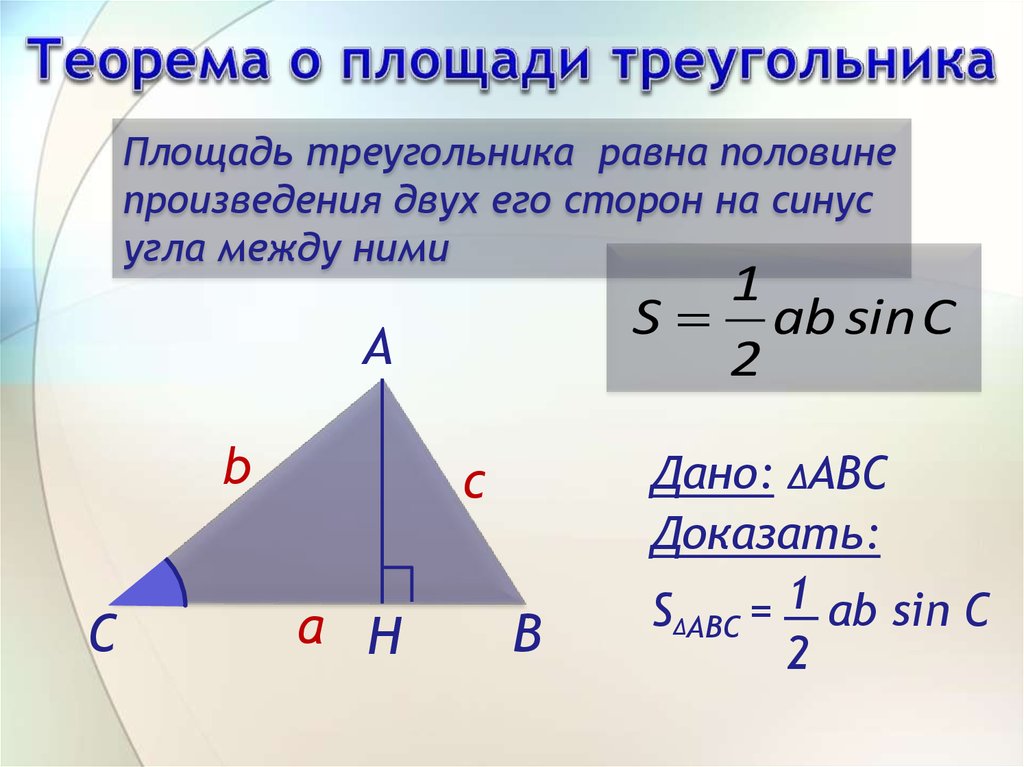 Неважно, какой. Сначала найдем угол A :
Неважно, какой. Сначала найдем угол A :
cos(A) = (b 2 + c 2 − a 2 ) / 2bc
cos(A) = (6 2 2 − 8 2 ) / (2×6×7)
cos(A) = (36 + 49 − 64) / 84
cos(A) = 0,25
A = cos -1 (0,25)
А = 75,5224…°
А = 75,5° с точностью до одного десятичного знака.
Далее находим другую сторону. Снова используем закон косинусов, на этот раз для угла B:
cos(B) = (c 2 + a 2 − b 2 )/2ca
cos(B) = (7 2 + 8 2 − 6 2 )/(2×7×8)
cos(B) = (49 + 64 − 36) / 112
cos(B) = 0,6875
B4 = cos 7 -1 (0,6875)
B = 46,5674…°
B = 46,6° с точностью до одного знака после запятой
Наконец, мы можем найти угол C, используя выражение «углы треугольника прибавить к 180°»:
C = 180° − 75,5224…° − 46,5674. ..°
..°
C = 57,9° с точностью до одной десятой
Теперь мы полностью решили треугольник, т.е. нашли все его углы.
В треугольнике могут быть буквы, отличные от ABC:
Пример 2
Это также треугольник SSS.
В этом треугольнике нам известны три стороны: x = 5,1, y = 7,9 и z = 3,5. Используйте закон косинусов, чтобы сначала найти угол X:
cos(X) = (y 2 + z 2 − x 2 )/2yz
cos(X) = ((7,9) 2 + (3,5) 2 − (5,1) 2 90 ×3,5)
cos(X) = (62,41 + 12,25 − 26,01)/55,3
cos(X) = 48,65/55,3 = 0,8797…
X = cos -1 (0,87005…)
X = 28,3881…°
X = 28,4° с точностью до одной десятой
Далее мы снова воспользуемся законом косинусов, чтобы найти угол Y:
cos(Y) = (z 2 + x 2 − y 2 )/2zx
cos(Y) = −24,15/35,7 = −0,6764…
cos(Y) = (12,25 + 26,01 − 62,41)/35,7
5 cos(Y) 90(Y) = -24,15/35,7 = -0,6764. ..
..
Y = cos -1 (-0,6764…)
Y = 132,5684…°
Y = 132,6° с точностью до одного десятичного знака.
Наконец, мы можем найти угол Z, используя «углы треугольника прибавляют к 180°»:
Z = 180° − 28,3881…° − 132,5684…°
Z = 19,0° к единице десятичный разряд
Вот еще один (немного более быстрый) способ решения треугольника SSS:
|
Наибольший угол?
Почему мы пытаемся сначала найти наибольший угол? Таким образом, два других угла должны быть острыми (меньше 90°), и закон синусов даст правильные ответы.
Закон синусов трудно использовать с углами выше 90° . Может быть два ответа по обе стороны от 90° (пример: 95° и 85°), но калькулятор даст вам только меньший.
Таким образом, если сначала вычислить наибольший угол с помощью закона косинусов, остальные углы будут меньше 90°, и закон синусов можно без труда применить к любому из них.
Пример 3
B — наибольший угол, поэтому сначала найдите B, используя закон косинусов: cos(B) = (11,6 2 + 7,4 2 − 15,2 2 ) / (2×11,6×7,4)
cos(B) = (134,56 + 54,76 − 231,04) / 1701,6 cos ) = −41,72 / 171,68
cos(B) = −0,2430…
B = 104,1° с точностью до одного десятичного знака
Используйте закон синусов, sinC/c = sinB/b, чтобы найти угол A:
sin(C) / 7,4 = sin(104,1°) / 15,2
sin(C) = 7,4 × sin(104,1°) / 15,2
sin(C) = 0,4722…
C = 28,2° с точностью до десятой до 180″:
A = 180° − (104,1° + 28,2°)
A = 180° − 132,3°
A = 47,7° с точностью до одного знака после запятой 9{2},}a2+b2=c2,
используется для нахождения длины любой стороны прямоугольного треугольника.
ccc
, а длины других сторон помечены какaaa
иbbb
, теорема Пифагора утверждает, что 9\circ90∘). Прямоугольный треугольник – это треугольник, в котором один угол прямой. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии.
Сторона, противолежащая прямому углу, называется гипотенузой (на рисунке сторона
ссс
). Стороны, примыкающие к прямому углу, называются катетами (стороны
aaa
и
bbb
). Сторона
aaa
может быть идентифицирована как сторона, прилегающая к углу
BBB
и напротив (или напротив) угла
AAA
. Сторона
Сторона
bbb
— это сторона, примыкающая к углу
AAA
и противолежащая углу
BBB
.
Прямоугольный треугольник: Теорему Пифагора можно использовать, чтобы найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, такой треугольник называется пифагорейским треугольником, а длины его сторон в совокупности называются пифагорейской тройкой.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии. Он определяет отношение между тремя сторонами прямоугольного треугольника. В нем говорится, что квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон. Теорему можно записать в виде уравнения, связывающего длины сторон
Теорему можно записать в виде уравнения, связывающего длины сторон
aaa
,
bbb
9{2}}a2+b2=c2В этом уравнении
ccc
представляет собой длину гипотенузы, а
aaa
и
bbb
— длины других сторон треугольника.
Хотя часто говорят, что знание теоремы предшествовало ему, [2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 – ок. 495 до н.э.). Ему приписывают первое зарегистрированное доказательство.
Теорема Пифагора: 92a2+b2=c2
.
Поиск недостающей длины стороны
Пример 1. Прямоугольный треугольник имеет длину стороны
101010
футов и длину гипотенузы
202020
футов.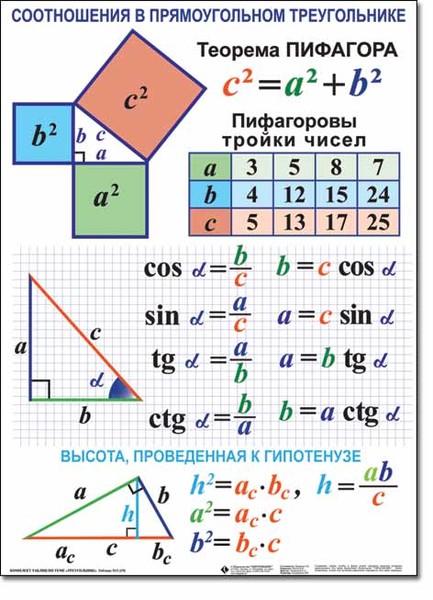 Найдите длину другой стороны. (округлить до десятых долей фута)
Найдите длину другой стороны. (округлить до десятых долей фута)
Подставить
a=10a=10a=10
и
c=20c=20c=20
в теорему Пифагора и найти 5 7
b bb2.
92} &=\sqrt{300} \\ б &=17,3 ~\mathrm{футов} \end{выравнивание} }a2+b2(10)2+b2100+b2b2b2b=c2=(20)2=400=300=300
=17,3 фута
Пример 2. Длина сторон прямоугольного треугольника равна
333
см и
444
см. Найдите длину гипотенузы.
Подставьте
a=3a=3a=3
и
b=4b=4b=4
в теорему Пифагора и найдите
ccc
. 92} &=\sqrt{25} \\ с &=5~\mathrm{см} \end{выравнивание} }a2+b232+429+1625c2c2
c=c2=c2=c2=c2=25=25
=5 см
Как работают тригонометрические функции
Тригонометрические функции можно использовать для нахождения отсутствующих длин сторон в прямоугольных треугольниках.
Цели обучения
Узнайте, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определите их входы и выходы
Основные выводы
Ключевые моменты 9{\ circ} 90 ∘
) Три тригонометрические функции, наиболее часто используемые для определения недостающей стороны прямоугольного треугольника: }sint=hypotenuseopposite ,cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
, иtant=oppositeadjacent\displaystyle{\tan{ t} = \frac {противоположный} {смежный}} tant=соседний напротив
Тригонометрические функции
Мы можем определить тригонометрические функции через угол
ttt
и длины сторон треугольника. Прилегающая сторона – это сторона, ближайшая к углу. (Смежный означает «рядом с».) Противоположная сторона – это сторона, расположенная напротив угла.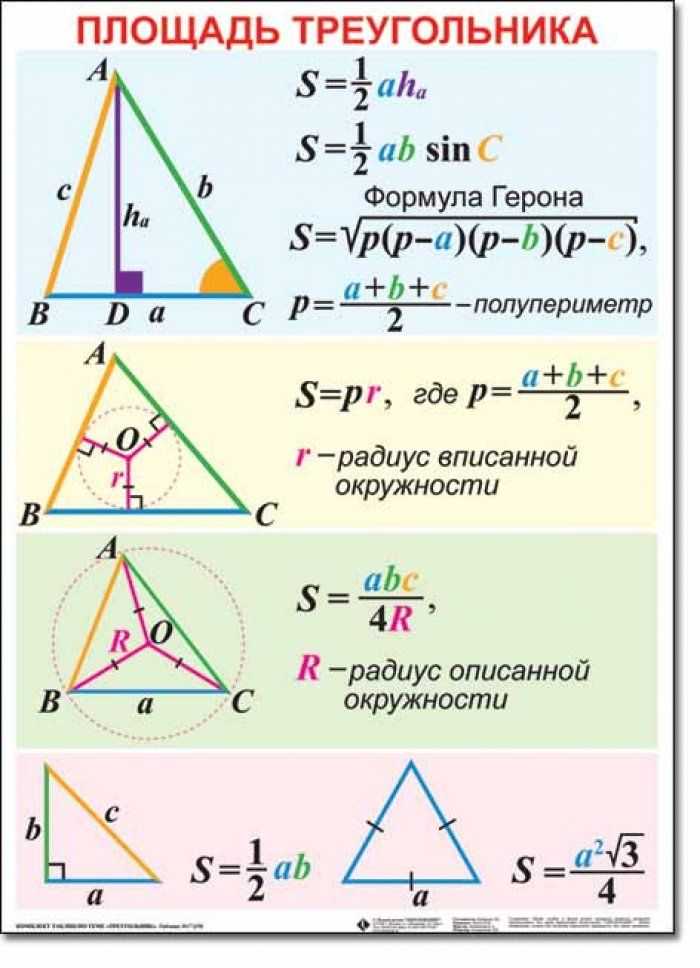 Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Прямоугольный треугольник: Стороны прямоугольного треугольника относительно угла
ttt
.
При поиске отсутствующей стороны прямоугольного треугольника, но единственной полученной информацией является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже: {t} = \frac {напротив} {гипотенуза}}sint=гипотенузанапротив
cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
tant=противоположныйсмежный\displaystyle{\tan{t} = \frac {напротив}{смежный}}tant=adjacentopposite
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника. При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.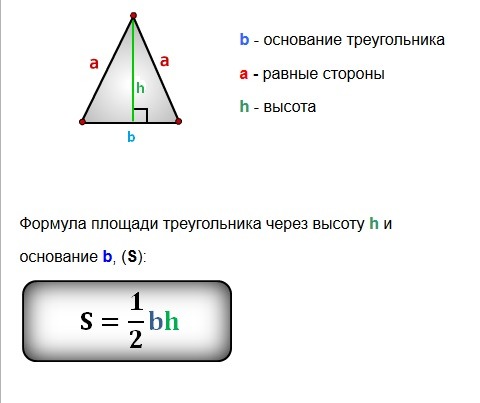
Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угла, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ( 9{\circ}34∘
и длины гипотенузы
252525
футов, найдите длину стороны, противоположной острому углу (округлите до десятых):
Прямоугольный треугольник: Дан прямоугольный треугольник с острого угла
343434
градусов и длины гипотенузы
252525
футов, найдите длину противоположной стороны.
Глядя на рисунок, найдите сторону, противоположную острому углу
343434 9{\circ}83∘
и длину гипотенузы
300300300
футов, найдите длину гипотенузы (округлив до десятых):
Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом
838383
градусов и длину гипотенузы
300300300
футов, найдите длину гипотенузы.
Глядя на рисунок, найдите гипотенузу острого угла
838383
градусов. Отношение сторон равно 9{\circ}\right)}} \\ x &= \frac{300}{\left(0,1218\dots\right)} \\ х &=2461,7~\mathrm{футы} \end{выравнивание} }costcos(83∘)x⋅cos(83∘)xxx=hypotenuseadjacent=x300=300=cos(83∘)300=(0,1218…)300=2461,7 футов
Синус, косинус и Тангенс
Мнемонику
SohCahToa можно использовать для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников
Key Takeaways
Key Points
- Общая мнемоника для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- Sohcahtoa сформирована из первых букв « S INE O PPOSITE Более H Ypotenus ), Тангенс противоположен соседнему ( Тоа ).

Определения тригонометрических функций
Для прямоугольного треугольника с острым углом
ttt
первые три тригонометрические функции: sint=hypotenuseopposite
cost=adjacenthypotenuse\displaystyle{ \cos{t} = \frac {adjacent}{hypotenuse} }cost=hypotenuseadjacent
tant=противоположный\displaystyle{ \tan{t} = \frac {противоположный}{прилегающий} }tant=adjacentopposite
Обычная мнемоника для запоминания этих отношений — SOHCAHTOA , образованный из первых букв « S INE O PPOSIT более ч ypotenuse ( Cah ), Тангенс противоположен соседнему ( 9{\ circ} 62 ∘
и смежная сторона
454545
футов, найдите длину противоположной стороны. (округлите до десятых)
Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом
626262
градусов и смежной стороной
454545
футов. Найдите длину противоположной стороны.
Найдите длину противоположной стороны.
Сначала определите, какую тригонометрическую функцию использовать, если дана смежная сторона, и вам нужно решить для противоположной стороны. Всегда определяйте, какая сторона дана, а какая неизвестна по острому углу ( 9\circ32∘
, гипотенуза равна 30 футам, а недостающая длина стороны равна противоположному катету,
xxx
футов.
Определите, какую тригонометрическую функцию использовать, если задана гипотенуза, и вам нужно решить для противоположной стороны. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противоположные стороны или «h» и «o», которые будут использовать «S» или тригонометрическую функцию синуса.
sint=противоположная гипотенуза in(32∘)=x3030⋅sin(32∘)=xx=30⋅sin(32∘)x=30⋅(0,529{\ круг} \ справа)} \\ x &= 30\cdot\left( 0.5299\dots\right) \\ х &= 15,9 ~\mathrm{футов} \end{выравнивание} }sintsin(32∘)30⋅sin(32∘)xxx=hypotenuseopposite=30x=x=30⋅sin(32∘)=30⋅(0,5299…)=15,9 футов
Нахождение углов из отношений : Обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для нахождения измерения острого угла прямоугольного треугольника.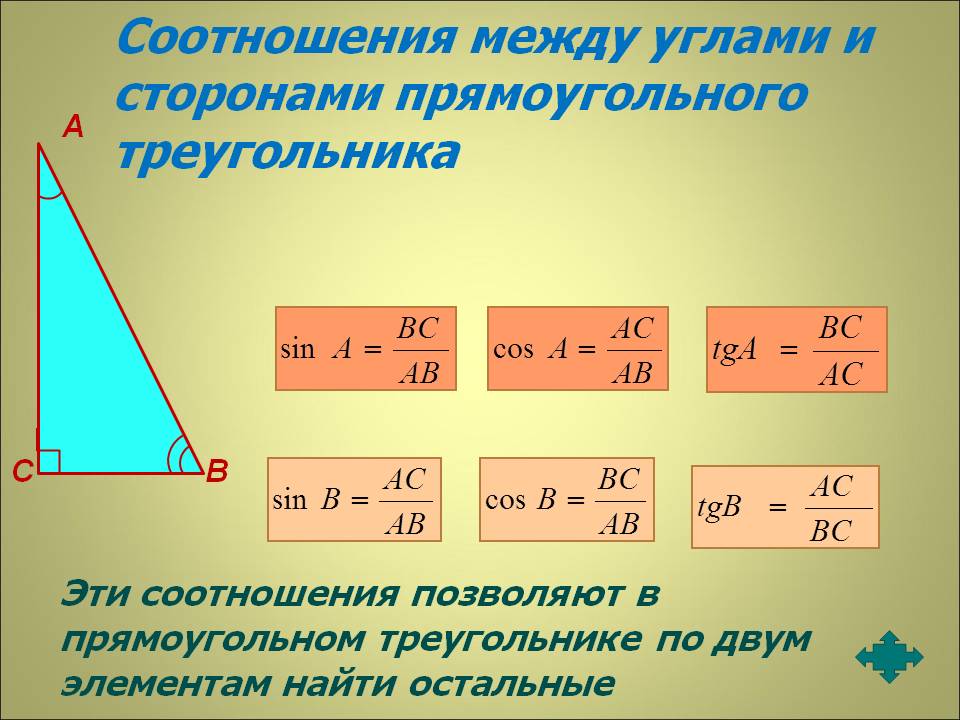
Цели обучения
Использование обратных тригонометрических функций при решении задач на прямоугольные треугольники 9{-1}tan−1
.Использование тригонометрических функций для определения отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, составление уравнения и решение. Найти недостающий острый угол по двум сторонам прямоугольного треугольника так же просто.
Обратные тригонометрические функции
Чтобы найти недостающий острый угол, используйте те же три тригонометрические функции, но используйте обратный ключ ( 9\circA∘
с противоположной стороной
12 футов12~\mathrm{feet}12 футов
, найдите острый угол с точностью до ближайшего градуса:
Прямоугольный треугольник: Найдите величину угла
AAA , если даны противолежащий катет и гипотенуза.
Из угла
AAA
даны стороны напротив и гипотенуза . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса. 9{\ круг} \end{выравнивание} }sinA∘sinA∘A∘A∘A=hypotenuseopposite=2512=sin-1(2512)=sin-1(0.48)=29∘
Лицензии и атрибуты
Лицензионное содержимое CC, ранее опубликованное
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Прямоугольный треугольник. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теорема Пифагора. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.
 svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах.
 Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike - Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Trigonometric_functions. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.
 org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike - 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигурка Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : openstax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигурка Джанет Хаймбах.


 svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike 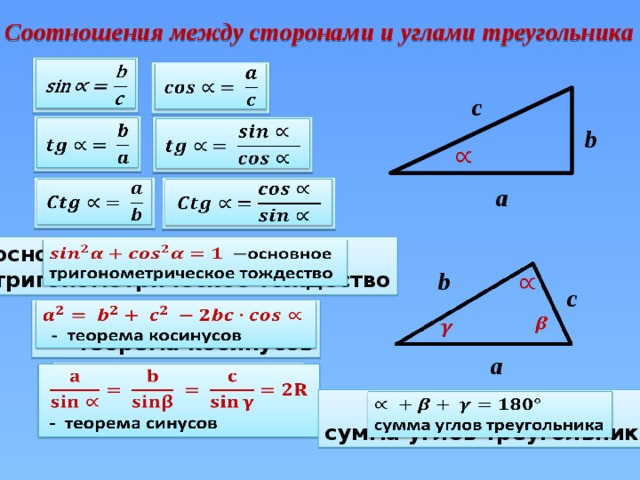 Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike 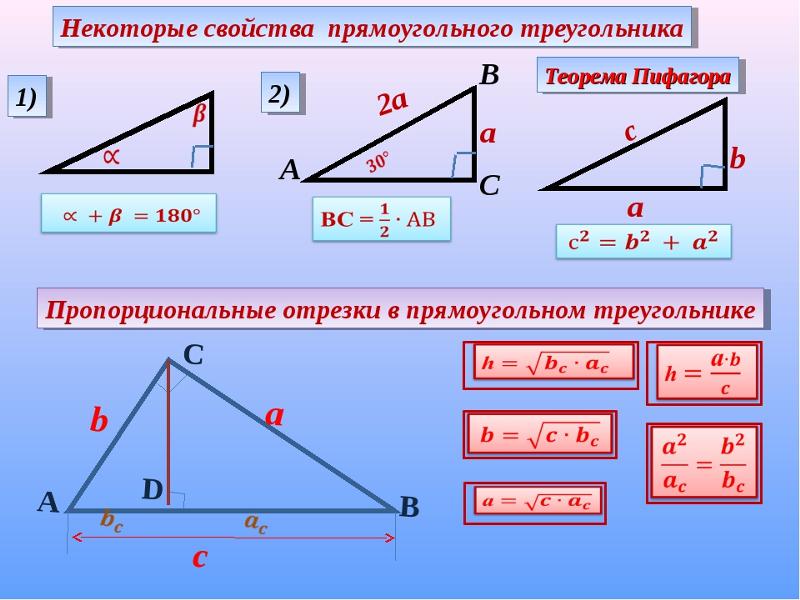 org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 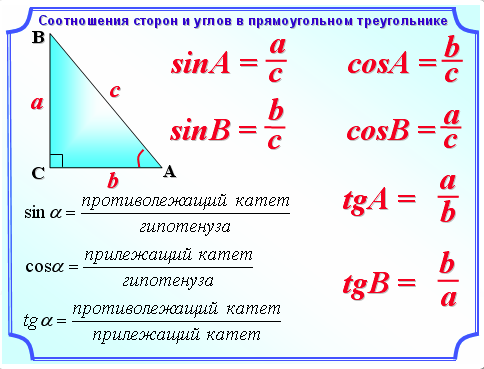 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 