Треугольник вписанный в окружность — формулы, свойства, примеры
Главная » геометрия
Обновлено
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:\[ r = \frac{S}{(a+b+c)/2} \]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:\[ r = \frac{S}{\frac{1}{2}P} \]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:\[ r = \sqrt{\frac{(p-a)(p-b)(p-c)}{p}} \]
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:\[ R = \frac{AC}{2 \sin \angle B} \]
- Радиус описанной окружности около треугольника,
если известны все стороны и площадь:\[ R = \frac{abc}{4S} \]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:\[ R = \frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}} \]
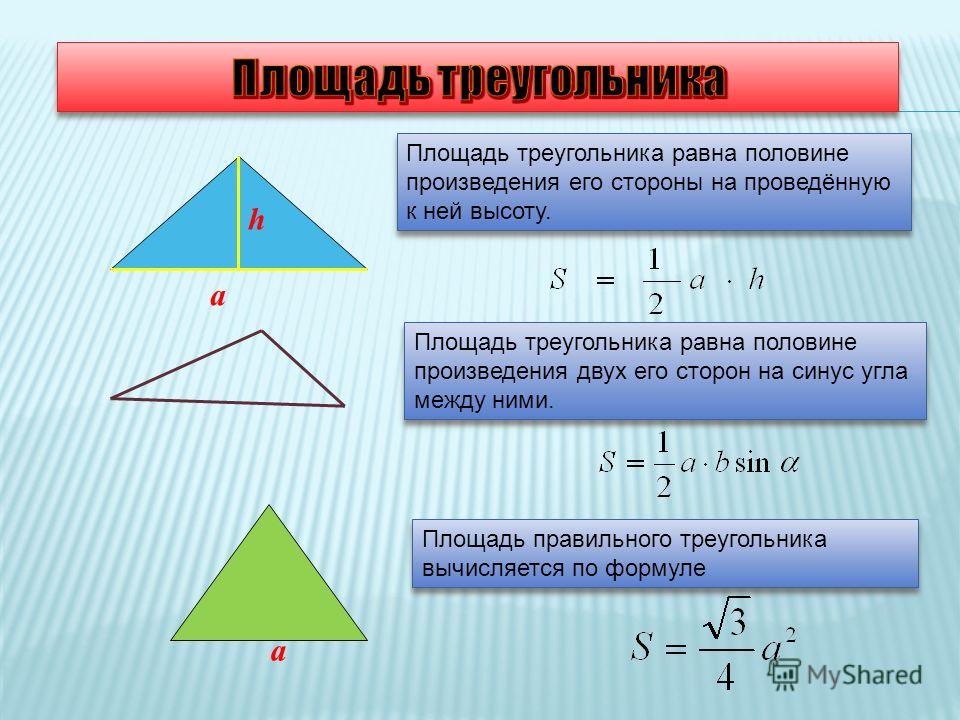
Площадь треугольника
S — площадь треугольника.
2}{2\cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} \]Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:\[ S = \frac{1}{2}ab \cdot \sin \angle C \]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:\[ P = a + b + c \]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:\[ P = \frac{2S}{r} \]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:\[ P = \sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) \]
Сторона треугольника
a — сторона треугольника.
2-2bc \cdot \cos \alpha}}{2} \]
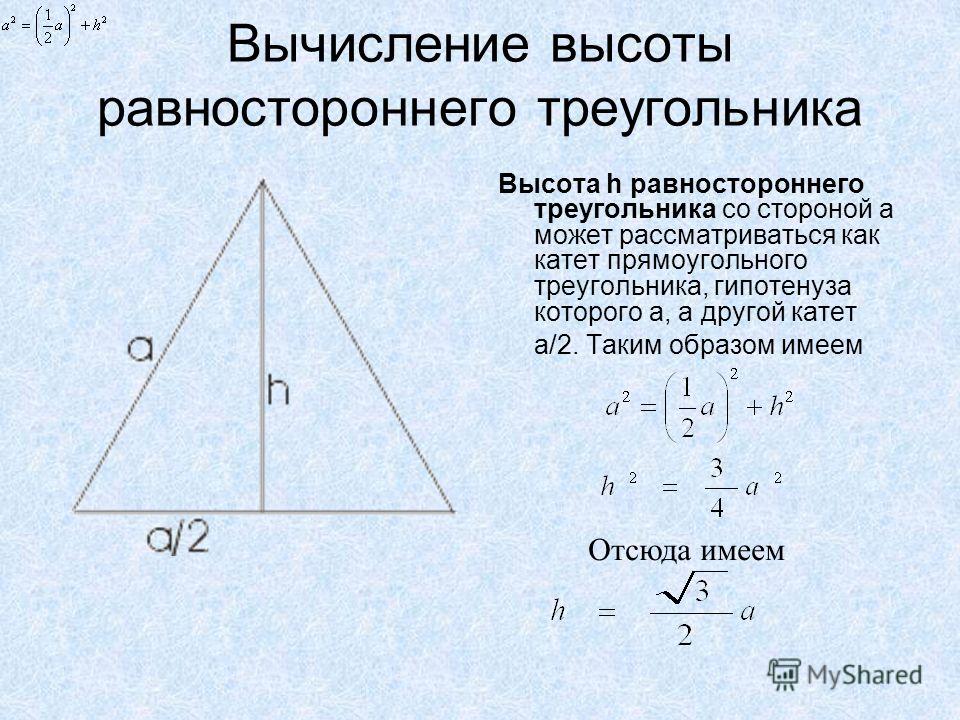
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:\[ h = \frac{2S}{a} \]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:\[ h = b \cdot \sin \alpha \]
- Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:\[ h = \frac{bc}{2R} \]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис.- В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.- Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.- Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.- Все вершины треугольника, вписанного
в окружность, лежат на окружности.- Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
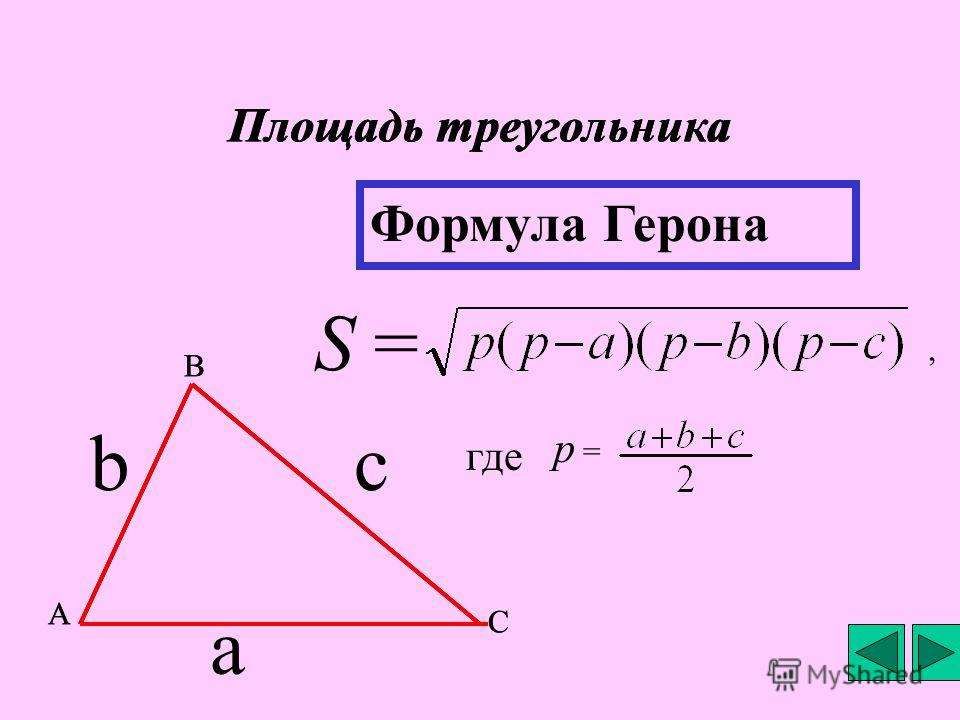
формуле Герона.Доказательство
Около любого треугольника, можно
описать окружность притом только одну.Дано: окружность и треугольник
,
которые изображены на рисунке 2.Доказать: окружность описана
около треугольника.Доказательство:
- Проведем серединные
перпендикуляры — HO, FO, EO.- O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.- Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.Следовательно: окружность описана около треугольника,
что и требовалось доказать.Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.Треугольник | ЕГЭ по математике (профильной)
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
На рисунке:
$А,В,С$ — вершины треугольника.
$АВ,ВС$ и $АС$ – стороны треугольника.
Виды треугольников по величине углов:
1. Остроугольный треугольник — такой треугольник, в котором все углы меньше $90°$, т.е. острые.
2. Прямоугольный треугольник — треугольник, имеющий прямой угол.
3. Тупоугольный треугольник — треугольник, содержащий тупой угол, т.е. угол от $90°$ до $180°$.
Виды треугольников по соотношению сторон:
1. Равносторонний (правильный) треугольник – это такой треугольник, у которого все стороны и углы равны.
2. Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
3. Разносторонний треугольник – это такой треугольник, у которого длины всех сторон разные.
Медиана, биссектриса, высота
Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке $O$, эта точка делит каждую медиану в отношении $2:1$, считая от вершины.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника.
Основные свойства треугольников:
- Сумма всех углов в треугольнике равна $180°$.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
- В равностороннем треугольнике все углы по $60°$.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
- Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN‖AC, MN={AC}/{2}$
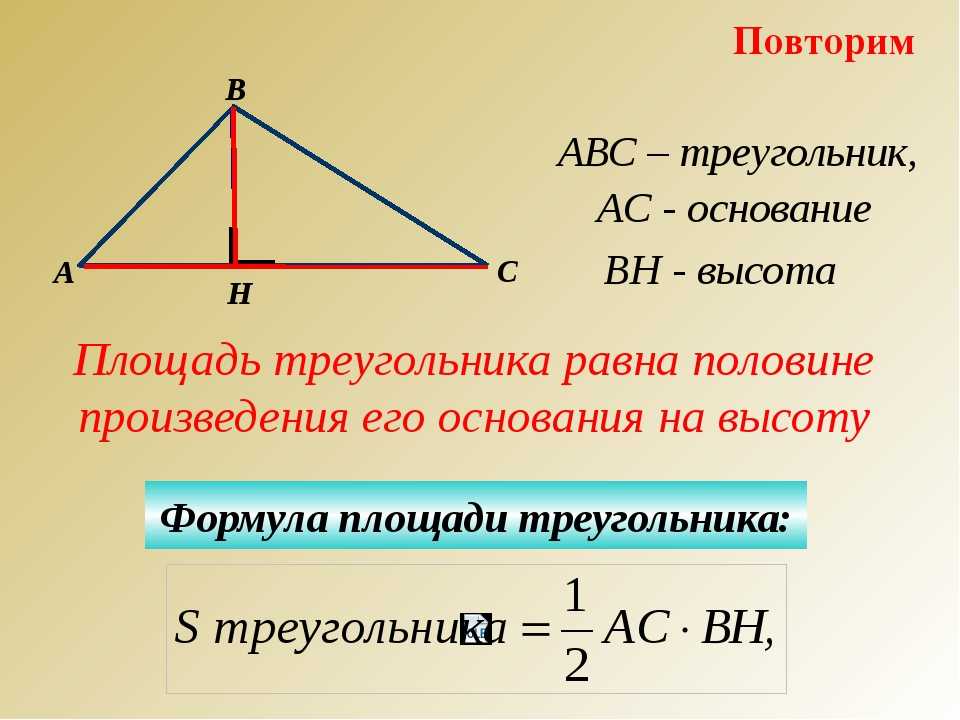
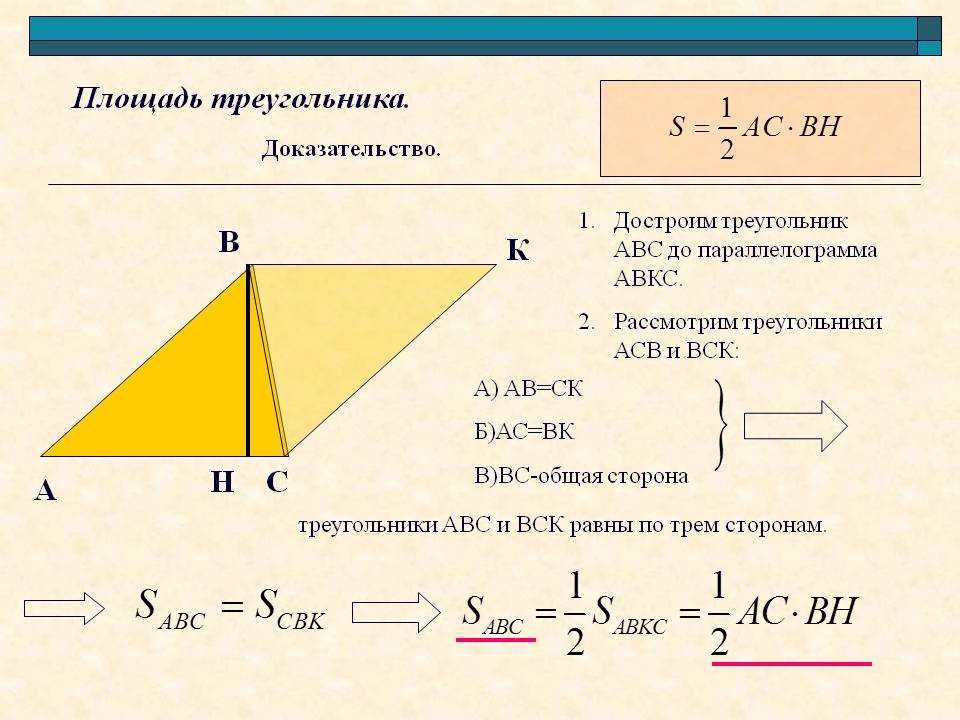
Площадь треугольника:
- $S={a∙h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
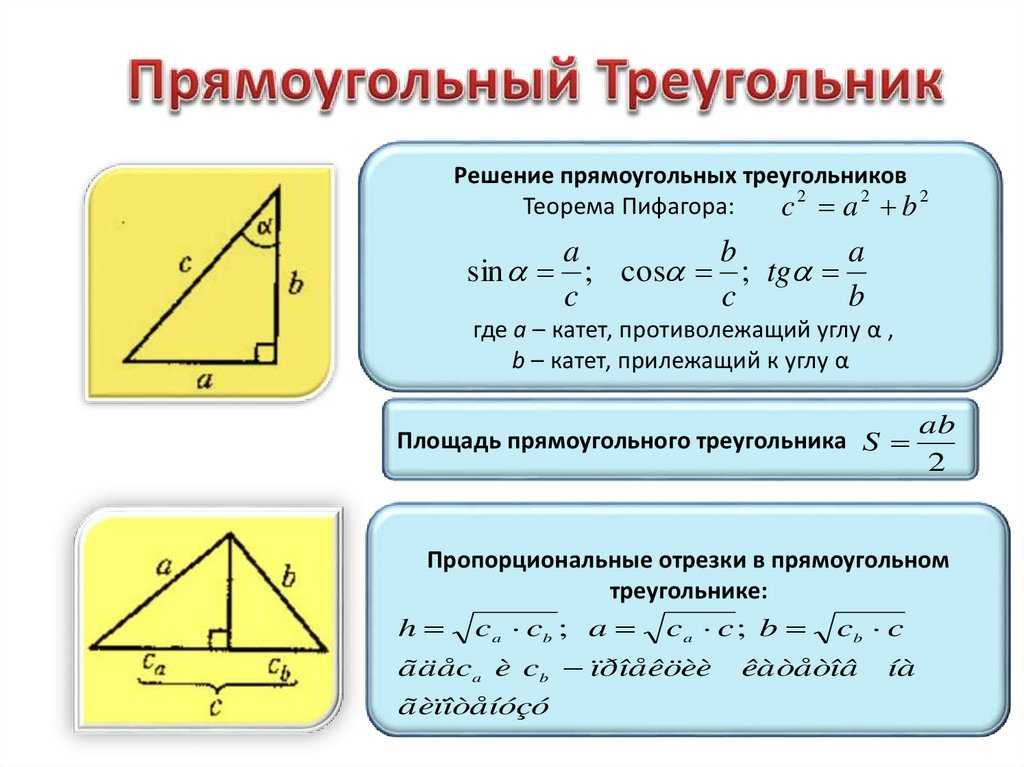
{2}√3}/{4}$, где $а$ — длина стороны. - В прямоугольном треугольнике $S={a∙b}/{2}$, где $а,b$ — катеты.
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
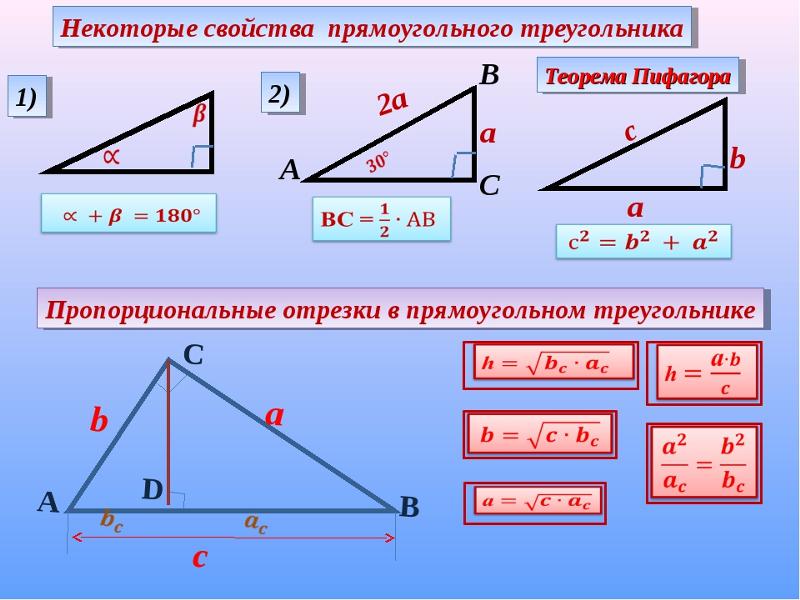
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
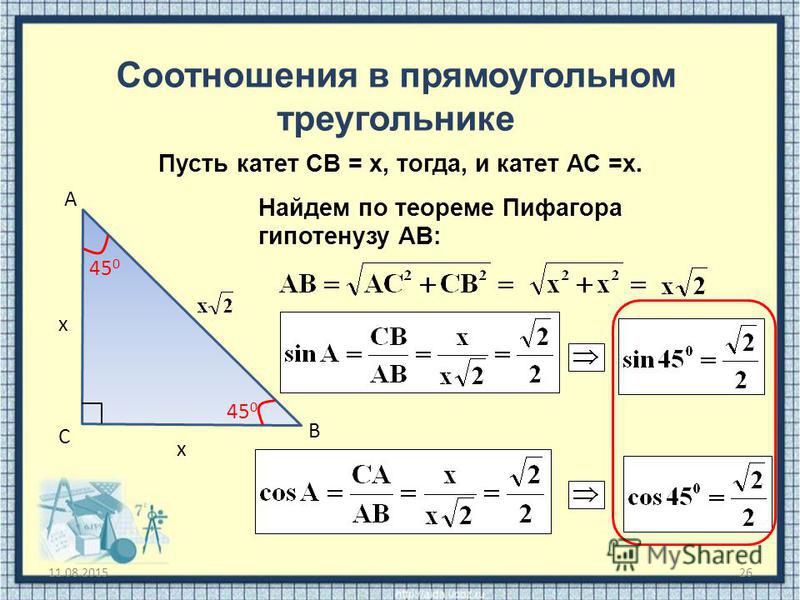
- Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
- Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
- Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
- Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.
2x=1$
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
$α$ $30$ $45$ $60$ $sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$ $cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$ $tgα$ ${√3}/{3}$ $1$ $√3$ $ctgα$ $√3$ $1$ ${√3}/{3}$ В треугольнике $АВС$ угол $С$ прямой, гипотенуза равна $39, cosB={5}/{13}$.
Найдите $АС$.
Решение:
Так как нам известен cos угла $В$, то распишем его по определению: косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
2=(39-15)(39+15)=24∙54=1296$
$АС=36$
Ответ: $36$
Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)
Треугольник
Треугольник – это фигура, состоящая из трех точек и трех отрезков, при этом три точки не лежат на одной прямой, а три отрезка попарно эти точки соединяют. Если быть точнее, то точки треугольника называются его вершинами, а отрезки – сторонами. Обозначается треугольник его вершинами, а вместо длинного слова треугольник рисуют символ Δ.
Давайте теперь подробнее рассмотрим разновидности треугольников.
- Равнобедренный треугольник – это такой треугольник, который имеет две одинаковые стороны, которые еще называют боковыми, третья сторона, отличная от тех двух, называется основанием.
- Равносторонний треугольник – треугольник с одинаковыми сторонами, также его иногда называют правильным треугольников.
- Прямоугольный треугольник – треугольник, который имеет прямой угол (90 градусов).
- Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90 градусов).
- Тупоугольный треугольник – треугольник, у которого один из углов тупой (то есть больше 90 градусов).
В принципе запомнить особенности каждого из вида треугольников легко, так каких названия говорят сами за себя.
Возьмем, к примеру, треугольник АВС. А, В, С являются его вершинами, а АВ, ВС и АС -соответственно его стороны.
Теперь рассмотрим строение данного треугольника более подробно. Угол треугольника АВС при вершине А – это угол, который образовался полупрямыми АВ и АС. Аналогично мы можем определить углы, которые лежат при вершине В и при вершине С.
Высота треугольника – это перпендикуляр, который опускается из заданной вершины к прямой, которая противоположна вершине.
Биссектриса треугольника – это отрезок биссектрисы угла данного треугольника, который соединяет вершину с точкой на противолежащей стороне.
Медиана треугольника, которая проводится из заданной вершины, является отрезок, соединяющий данную вершину с серединой противоположной стороны треугольника.
Средняя линия треугольника – это отрезок, который соединяет середины двух сторон данного треугольника. К этому обозначению также есть определенная теорема, которая говорит о том, что средняя линия треугольника всегда параллельна третьей стороне, а также равна ее половине.
Все эти обозначения (медиана, биссектриса, высота, средняя линия треугольника) обязательно понадобятся в решении практических задач. Скажем более того, без знания свойств этих вершин вы вряд ли сможете решить хоть какую-либо задачу, связанную с треугольниками.
Обозначения
A, B, C — вершины; α, β, γ — углы; a, b, c — стороны, противолежащие углам α, β, γ (вершинам А, В, С) соответственно;
h
a, h
b, h
c— высоты, опущенные на стороны a, b, c соответственно;
m
a, m
b, m
c— медианы;
l
a, l
b, l
c— биссектрисы; R — радиус описанной окружности; r — радиус вписанной окружности.
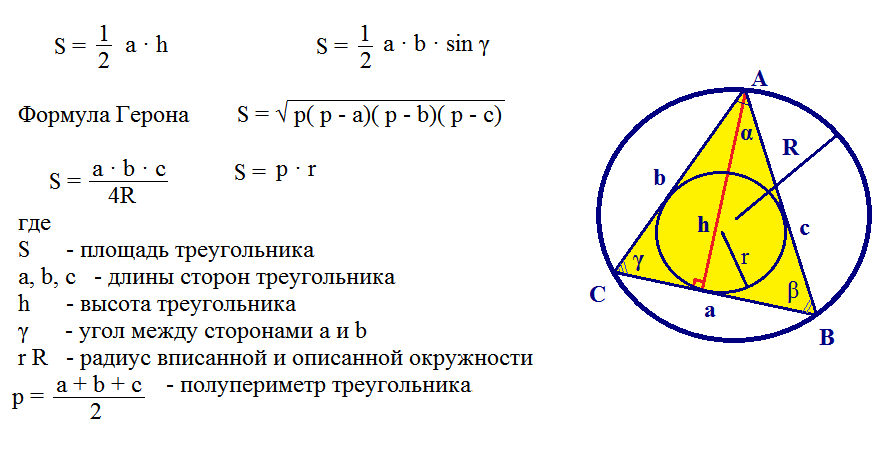
Формулы вычисления площади треугольника
S = 1
2ah
a= 1
2bh
b= 1
2ch
c
S = 1
2absinγ = 1
2acsinβ = 1
2bcsinα
S = √ p(p — a)(p — b)(p — c) (периметр p = 1
2(a + b + c) )
S = rp; S = abc
4R
Формулы вычисления медианы, биссектрисы, высоты через стороны треугольника
m 2
a= 2b 2
+ 2c 2
— a 2
4
l 2
a= bc((b + c) 2
— a 2
) (b + c) 2
h 2
a= 4p(p — a)(p — b)(p — c) a 2
Отношения высот и сторон треугольника
h
a: h
b: h
c= 1
a: 1
b: 1
c
Теорема косинусов
a 2
= b 2
+ c 2
— 2bccosα
b 2
= a 2
+ c 2
— 2accosβ
c 2
= a 2
+ b 2
— 2abcosγ
Теорема синусов
a
sinα= b
sinβ= c
sinγ= 2R
Теорема тангенсов (формулы Региомонтана)
a + b
a — b= tg α + β
2= ctg γ
2tg α — β
2tg α — β
2
a + c
a — c= tg α + γ;
2= ctg β
2tg α — γ
2tg α — γ
2
b + c
b — c= tg β + γ
2= ctg α
2tg β — γ
2tg β — γ
2
Теорема Пифагора
c 2
= a 2
+ b 2
(∠C = 90°)
R = c
2= m
c
a
c= a a c
b
c= b b c
b
c= h h a
c
Площадь прямоугольного треугольника
S = 1
2ab = 1
2hc (∠C = 90°)
Равносторонний треугольник
S = a 2
√ 3 4
h = a √ 3 2 R = 2r
R = a √ 3 r = a √ 3 3 6
Решение треугольников
Прямоугольный треугольникa = c * sinα b = c*cosα a = b * tgα b = a*ctgα
c = a
sinαc = b
cosα
Произвольный треугольник
a = b sinα
sinβb = c sinβ
sinγ
a = c sinα
sinγc = a sinγ
sinα
b = a sinβ
sinαc = b sinγ
sinβa = b*cosγ + c*cosβ b = c*cosα + a*cosγ c = a*cosβ + b*cosα
tgα = asinγ
b — acosγ
sin α
2= √ (p — b)(p — c)
bc
cos α
2= √ p(p — a)
bc
tg α
2= √ (p — b)(p — c)
p(p — a)Формула треугольника Паскаля — GeeksforGeeks
Вероятность является основой математики.
Он говорит о том, как событие может произойти. Он имеет дело с числовым обоснованием принятия более вероятных решений. Чем выше вероятность, тем больше вероятность того, что событие произойдет, и наоборот. Треугольник Паскаля — это красивая концепция вероятности, разработанная известным математиком Блезом Паскалем, которая используется для нахождения коэффициентов в разложении любого биномиального выражения.
Треугольник Паскаля
Треугольник Паскаля — это метод определения биномиальных коэффициентов членов биномиального выражения (x + y) n , где n может быть любым положительным целым числом, а x,y — действительными числами. Треугольник Паскаля представлен в виде треугольника, это своего рода числовой узор в виде треугольного расположения. Он начинается с 1 на вершине и с 1 на двух сторонах треугольника. В треугольнике Паскаля каждое новое число между двумя числами и ниже затем и его значение является суммой двух чисел выше. Этот треугольник используется в различных типах вероятностных условий.
Здесь каждая строка представляет коэффициент расширения (x + y) п .
Нулевая строка n = 0, (x + y) 0
Первая строка n = 1 , (x + y) 1
Вторая строка n = 2, (x + y) 2
3
3 Третья строка n = 3, (x + y) 3
Четвертая строка n = 4, (x + y) 4
Здесь степень y в любом разложении (x + y) n представляет собой столбец треугольника Паскаля. n представляет строку треугольника Паскаля. Строка и столбец имеют индекс 0 в треугольнике Паскаля.
Построение треугольника Паскаля
Треугольник Паскаля построить очень просто. Начните с верхней строки (0-й строки), написав только число 1. В соответствующих строках новый квадрат в треугольнике Паскаля будет суммой квадратов непосредственно над этим квадратом и касаясь его. Например, нахождение суммы квадратов строки 4 и столбца 2 равно сумме квадратов столбца 1 строки 3 и столбца 2 строки 3.
Таким образом, квадрат строки 4 столбца 2 имеет значение 1 + 2 = 3,
Свойства треугольника Паскаля
- Каждое число в треугольнике Паскаля является суммой двух чисел над ним.
- Числа в ряду симметричны по своей природе.
- Каждое число представляет биномиальный коэффициент.
- Числа слева и справа от треугольника всегда равны 1.
- n-я строка содержит (n+1) чисел.
Формула треугольника Паскаля
Формула треугольника Паскаля для нахождения элементов в n-й строке и k-м столбце треугольника равна
= {p-1} \выберите {q-1} {p-1} \выберите {q-1} +
Здесь 0 ≤ q ≤ p, p — неотрицательное число
Или формула чтобы найти число в n-й строке и r-м столбце, задается как p C q = p!/(p – q)!q!
p C q = p C q-1 + p-1 C q-1
Pascal’s Triangle Binomial Expansion
As we already know that pascal’s triangle defines биномиальные коэффициенты членов биномиального выражения (x + y) n , Таким образом, разложение (x + y) n равно:
(x + y) n = a 0 x n + a 900-n + x 1
1 ……a n-1 xy n-1 + a n y n
Примеры вопросов
+ у) 3 .

Решение:
Метод 1:
Мы смотрим на 3-ю строку треугольника Паскаля, потому что n равно 3, и на 1-й столбец треугольника Паскаля, потому что степень y равна 1 в члене x 2y . Таким образом, коэффициент равен 3.
Метод 2:
Мы просто применяем n C r , где n = 3, r = 1.
Таким образом, коэффициент x 2y 900 (x + y) 3 равно 3 C 1 = 3
Вопрос 2: Найдите коэффициент при члене x 2 y 2 в расширении (4x + 3y) 4 .
Решение:
Метод 1:
Мы смотрим на 4-ю строку треугольника Паскаля, потому что n равно 4, и на 2-й столбец треугольника Паскаля, потому что степень y 9 x 2 равна 20 в члене 00 г 2 . Таким образом, число в треугольнике Паскаля равно 6.
Но мы видим, что коэффициент x равен 4, а y равен 3, поскольку степень x равна 2, а y равно 2 в члене x 2 y 2 поэтому паскаль Число треугольника будет умножено на 4 2 и 3 2 , чтобы найти коэффициент.
Коэффициент = 6 x 4 2 x 3 2 = 864
Метод 2:
Мы просто применяем N C R , где N = 4, R = 2.
SO PASCAL Triangle Triangle число членов x 2 y 2 в расширении (4x +3y) 4 равно 4 C 2 = 6.
Но мы видим, что коэффициент при x равен 4, а y теперь равен 3, поскольку степень x равна 2, а y равна 2 в термине x 2 y 2 , поэтому паскаль Число треугольника будет умножено на 4 2 и 3 2 чтобы найти коэффициент.
Коэффициент = 6 x 4 2 x 3 2 = 864
Вопрос 3: Напишите 6 -й ряд треугольника Паскаля
Решение:
6 -й ряд можно.
6С1 6С2 6С3 6С4 6С5 6С6
1, 6, 15, 20, 15, 6, 1
Вопрос 4: Найдите коэффициент термина X 4 в расширении (2x + y) 4 .
Решение:
Метод 1:
Мы смотрим на 4-ю строку треугольника Паскаля, поскольку n равно 4, и на 0-й столбец треугольника Паскаля, поскольку степень y равна 9 x 40 в члене 00 . Итак, число в треугольнике Паскаля равно 1,9.0003
Но мы видим, что коэффициент x равен 2, а y теперь равен 0, поскольку степень x равна 4, а y равна 0 в термине x 4 , поэтому число треугольника Паскаля будет умножено на 2 4 и 1 0 найти коэффициент.
Коэффициент = 1 x 2 4 x 1 0 = 16
Метод 2:
Мы просто применяем N C R , где n = 4, r = 0.
SO Pascal Triangle Triangle количество терминов x 4 в расширении (2x + y) 4 равно 4 C 0 = 1.
Но мы видим, что коэффициент x равен 2, а y равен 0, так как степень x равна 4, а y равно 0 в члене x 4 , поэтому треугольник Паскаля число будет умножено на 2 4 и 1 0 , чтобы найти коэффициент.
Коэффициент = 1
Вопрос 5: Найдите коэффициент члена xy 2 в разложении (2x + y) 3 .
Решение:
Метод 1:
Мы смотрим на строку 3-й строки треугольника Паскаля, потому что n равно 3, и на 2-й столбец треугольника Паскаля, потому что степень y равна 2 в члене xy 2 . Таким образом, число в треугольнике Паскаля равно 3.
Но мы видим, что коэффициент x равен 2, а y равен 1, поскольку степень x равна 2, а y равна 1 в термине xy 2 , поэтому число треугольника Паскаля будет умножено на 2 1 и 1 2 , чтобы найти коэффициент.
92, поэтому число треугольника Паскаля будет умножено на 2 1 и 1 2 , чтобы найти коэффициент.Коэффициент = 3 x 2 1 x 1 2 = 6
3.3: Формула площади треугольника
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 39639
- Иллюстративная математика
- OpenUp Resources
Lesson
Давайте напишем и воспользуемся формулой для нахождения площади треугольника.
Упражнение \(\PageIndex{1}\): основания и высоты треугольника
Изучите примеры и не примеры оснований и высот в треугольнике.
Рисунок \(\PageIndex{1}\)
- Примеры: Эти пунктирные сегменты представляют высоты треугольника.
Рисунок \(\PageIndex{2}\)
- Непримеры: эти пунктирные сегменты , а не представляют высоты треугольника.
Выберите все верных утверждений о основаниях и высотах в треугольнике.
- Любая сторона треугольника может быть основанием.
- Возможна только одна высота.
- Высота всегда является одной из сторон треугольника.
- Высота, соответствующая основанию, должна быть проведена под острым углом к основанию.
- Высота, соответствующая основанию, должна быть проведена под прямым углом к основанию.
- Как только мы выбираем основание, остается только один сегмент, представляющий соответствующую высоту.
- Отрезок, представляющий высоту, должен проходить через вершину.
Упражнение \(\PageIndex{2}\): нахождение формулы площади треугольника
За каждый треугольник:
Рисунок \(\PageIndex{3}\)
- Определите основание и соответствующую высоту и запишите их длины в таблицу.
- Найдите площадь треугольника и запишите ее в последний столбец таблицы.
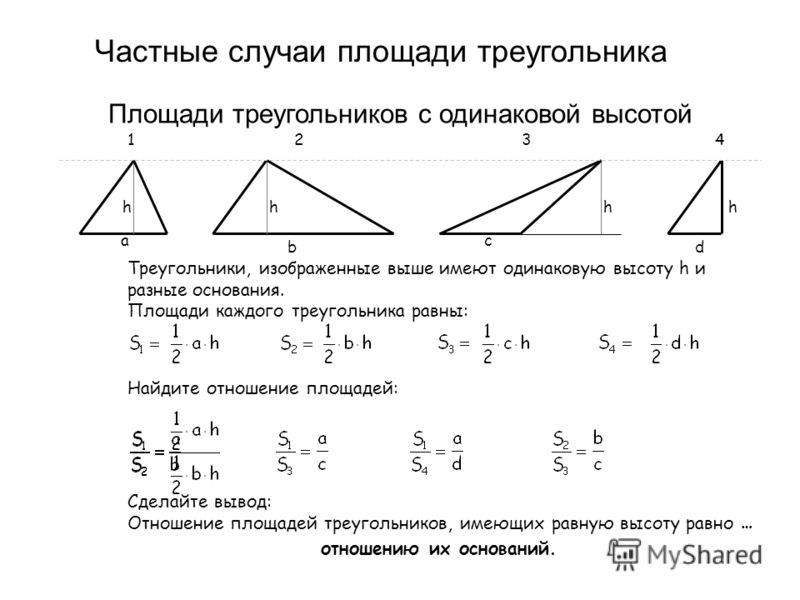
треугольник база (шт.) высота (шт.) площадь (кв. ед.) А Б С Д любой треугольник \(б\) \(ч\) Таблица \(\PageIndex{1}\) В последней строке напишите выражение для площади любого треугольника, используя \(b\) и \(h\).
Упражнение \(\PageIndex{3}\): Применение формулы площади треугольников
Для каждого треугольника обведите базовое измерение, которое можно использовать для нахождения площади треугольника. Затем найдите площади любых трех треугольников. Покажите свои рассуждения.
Рисунок \(\PageIndex{4}\)Резюме
- Мы можем выбрать любую из трех сторон треугольника, чтобы назвать основанием . Термин «база» относится как к стороне, так и к ее длине (размеру).
- Соответствующая высота есть длина перпендикулярного отрезка от основания до противоположной ему вершины. Вершина , противоположная , — это вершина, которая является , а не конечной точкой основания.
Вот три пары оснований и высот одного и того же треугольника. Штриховые сегменты на диаграммах обозначают высоты.
Рисунок \(\PageIndex{5}\)Сегмент, показывающий высоту, должен быть нарисован под прямым углом к основанию, но он может быть нарисован более чем в одном месте.
Рисунок \(\PageIndex{6}\)Он не должен проходить через противоположную вершину, если он соединяет основание и линию, параллельную основанию и проходящую через противоположную вершину, как показано здесь.
Пары «основание-высота» в треугольнике тесно связаны с параллелограммом. Напомним, что две копии треугольника можно составить в один или несколько параллелограммов. Каждый параллелограмм имеет по крайней мере одно общее основание с треугольником.
Рисунок \(\PageIndex{7}\): Два одинаковых треугольника, каждый из которых имеет копию, составляющую треугольник в два разных параллелограмма. В каждом параллелограмме нижняя сторона обозначена основанием, а пунктирные линии, расположенные под прямым углом к основанию, обозначают высоту параллелограмма.Для любой базы, которую они разделяют, соответствующая высота также является общей, как показано пунктирными сегментами.
Мы можем использовать измерения высоты основания и наши знания о параллелограммах, чтобы найти площадь любого треугольника.
Рисунок \(\PageIndex{8}\)
- Формула площади параллелограмма с основанием \(b\) и высотой \(h\): \(b\cdot h\).
- Треугольник занимает половину площади параллелограмма с тем же основанием и высотой. Таким образом, мы можем выразить площадь \(A\) треугольника как: \(A=\frac{1}{2}\cdot b\cdot h\)
- Площадь треугольника A составляет 15 квадратных единиц, потому что \(\frac{1}{2}\cdot 5\cdot 6=15\).
- Площадь треугольника B равна 4,5 квадратных единиц, потому что \(\frac{1}{2}\cdot 3\cdot 3=4,5\).
- Площадь треугольника C составляет 24 квадратных единицы, потому что \(\frac{1}{2}\cdot 12\cdot 4=24\).
В каждом случае одна сторона треугольника является основанием, но ни одна из других сторон не является высотой. Это потому, что угол между ними не является прямым углом.
Однако в прямоугольных треугольниках две перпендикулярные стороны могут быть основанием и высотой.
Площадь этого треугольника составляет 18 квадратных единиц, используем ли мы 4 единицы или 9 единиц для основания.
Рисунок \(\PageIndex{9}\)Словарь терминов
Определение: Противоположная вершина
Для каждой стороны треугольника есть одна вершина, которая не лежит на этой стороне. Это противоположная вершина.
Например, точка \(A\) является вершиной, противоположной стороне \(BC\).
Рисунок \(\PageIndex{10}\)Практика
Упражнение \(\PageIndex{4}\)
Выберите все чертежей, на которых правильно определена соответствующая высота \(h\) для данного основания \(b\).
Рисунок \(\PageIndex{11}\): Шесть изображений одного и того же треугольника, помеченных A, B, C, D, E и F. Треугольник A, верхняя сторона помечена как b, а пунктирная линия помечена как h, идет прямо вниз от правой вершины. Треугольник B, верхняя сторона которого обозначена буквой b, а пунктирная линия, обозначенная буквой h, проходит от центра верхней стороны к противоположной вершине. Треугольник C, правая сторона которого обозначена буквой b, и пунктирная линия проходит от левой верхней вершины прямо вниз до уровня нижней вершины, обозначенной буквой h.Левая сторона треугольника D обозначена буквой b, а перпендикулярная линия, обозначенная буквой h, продолжается до противоположной вершины. Треугольник E, левая сторона которого обозначена буквой b, а пунктирная линия, обозначенная буквой h, проходит от нижней вершины под прямым углом к правой стороне. Треугольник F, правая сторона которого обозначена буквой b, а перпендикулярная пунктирная линия, обозначенная буквой h, проходит от стороны, обозначенной буквой b, к противоположной вершине.
- А
- Б
- С
- Д
- Е
- Ф
Упражнение \(\PageIndex{5}\)
Для каждого треугольника помечены основание и соответствующая ему высота.
Рисунок \(\PageIndex{12}\): 3 треугольника на сетке с пометками A, B, C. A, основание = 4, высота = 6. B, основание = 8, высота = 4. C, основание = 6, высота = 4.
- Найдите площадь каждого треугольника.
- Как площадь связана с основанием и соответствующей ему высотой?
Упражнение \(\PageIndex{6}\)
Вот прямоугольный треугольник.
Рисунок \(\PageIndex{13}\)Назовите соответствующую высоту для каждого основания.
- Сторона \(d\)
- Сторона \(е\)
- Боковой \(f\)
Упражнение \(\PageIndex{7}\)
Найдите площадь заштрихованного треугольника. Покажите свои рассуждения.
Рисунок \(\PageIndex{14}\): квадрат с заштрихованным треугольником внутри него. Левая и нижняя стороны квадрата отмечены цифрой 6, а правая сторона обозначена цифрой 2 выше точки, где вершина заштрихованного треугольника встречается со стороной, и цифрой 4 ниже точки, где вершина встречается со стороной.(из модуля 1.3.2)
Упражнение \(\PageIndex{8}\)
Андре провел линию, соединяющую два противоположных угла параллелограмма. Выберите всех верных утверждений о треугольниках, образованных линией, которую провел Андре.
Рисунок \(\PageIndex{15}\)
- Каждый треугольник имеет две стороны по 3 единицы длины.
- Сторона каждого треугольника равна длине диагонали.
- Каждый треугольник имеет одну сторону длиной 3 единицы.
- Если один треугольник поместить поверх другого и их стороны выровняются, мы увидим, что один треугольник больше другого.
- Два треугольника имеют одинаковую площадь.
(из модуля 1.3.1)
Упражнение \(\PageIndex{9}\)
Вот восьмиугольник. (Примечание: диагональные стороны восьмиугольника составляют , а не 4 дюйма в длину.)
Рисунок \(\PageIndex{16}\)
- Оценивая площадь восьмиугольника, Лин пришел к выводу, что она должна быть меньше 100 квадратных дюймов. Вы согласны? Объясните свои рассуждения.
- Найдите точную площадь восьмиугольника. Покажите свои рассуждения.
(из блока 1.1.3)
Эта страница под названием 3.3: Формула площади треугольника распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Illustrative Mathematics посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts.
; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Иллюстративная математика
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Метки
- источник!@https://access.openupresources.org/curricula/our6-8math/en/grade-6/index.html
- источник@https://access.
openupresources.org/curricula/our6-8math/en/grade-6/index.html
Как рассчитать скорость, расстояние и время с помощью треугольника
Расчет скорости, расстояния и времени является важной частью многих ролей, в том числе в вооруженных силах или на транспорте.
Если вы претендуете на должность в этих отраслях, вы можете пройти тестирование в рамках процесса найма. Вопросы позволят вашему работодателю проверить ваши прикладные математические способности.
Как рассчитать скорость, расстояние и время: формула треугольника вам понадобится?
Чтобы вычислить скорость, разделите расстояние пути на время, затраченное на путешествие, таким образом, скорость = расстояние, деленное на время. Чтобы рассчитать время, разделите расстояние на скорость. Чтобы получить расстояние, умножьте скорость на время.
Вы можете увидеть эти уравнения в упрощенном виде: s=d/t, , где s — скорость, d — расстояние, а t — время.
Эту формулу можно представить в виде треугольника выше. В треугольнике скорость и время образуют основу, так как они перемножаются, чтобы вычислить расстояние.
Треугольник позволяет легко запомнить формулу и сэкономить время при работе над экзаменационными вопросами. Треугольник поможет вам запомнить три формулы:
- Формула скорости: Скорость = Расстояние ÷ Время
- Формула времени: Время = Расстояние ÷ Скорость
- Формула расстояния: Расстояние = Скорость x Время
Треугольник показывает, какой расчет следует использовать. Поскольку расстояние находится в верхней части треугольника, чтобы вычислить его, вам нужно умножить скорость на время.
Поскольку скорость и время находятся в нижней части треугольника, вам нужно разделить это число на цифру расстояния, чтобы получить правильный ответ.
Приступая к подготовке к пробному тесту, обязательно напишите треугольник на бумаге.
Это поможет вам запомнить его.
Как рассчитать скорость
Чтобы рассчитать скорость, нужно расстояние разделить на время. Вы можете решить это, используя треугольник. Если вы скроете скорость, со временем у вас останется дистанция.
Вот пример:
Если водитель проехал 180 миль, и ему понадобилось 3 часа, чтобы преодолеть это расстояние, то для определения его скорости нужно:
180 миль / 3 часа -> 180 / 3 = 60
Таким образом, скорость водителя будет 60 миль в час.
Как рассчитать расстояние
Чтобы вычислить пройденное расстояние, вам нужно будет умножить скорость и время.
Вот пример:
Если водитель ехал со скоростью 100 миль в час в течение 4 часов, то для расчета расстояния вам нужно будет умножить скорость на время.
100 миль в час x 4 часа -> 100 x 4 = 400
Расстояние 400 миль.
Как рассчитать время
Чтобы рассчитать время, которое заняло путешествие, вам нужно знать скорость движения и пройденное расстояние.
Вот пример:
Если водитель проехал 50 миль со скоростью 5 миль в час, то для определения затраченного времени нужно разделить:
50 миль / 5 миль в час -> 50 / 5 = 10
Затраченное время пройти это расстояние составляет 10 миль в час.
Три примера вопросов о скорости/расстоянии/времени
- Энди проезжает на своем грузовике 400 миль, что занимает у него 8 часов. Гарри проезжает 200 миль, что занимает у него 4,5 часа. Кто едет быстрее?
Ответ: Энди едет со скоростью 50 миль в час, а Гарри едет со скоростью 44,44 мили в час. Итак, Энди едет быстрее.
- Каждую субботу Тесса участвует в забеге на 5 км со своим беговым клубом. Она проходит это за 40 минут. Если она будет поддерживать ту же скорость, за какое время она пробежит 8 км?
Ответ: Ее скорость 7,5 км/ч. Если она пробежит 10 км со скоростью 7,5 км/ч, чтобы вычислить время, нужно разделить 8 на 7,5, что равно 1,066. Если мы переведем это в часы и минуты, ей потребуется 1 час и 4 минуты, чтобы пробежать 8 км.

- Ханна отправляется в велосипедную прогулку. В первой половине пути она ехала со скоростью 10 миль в час в течение 2 часов. Во второй половине она едет со скоростью 20 миль в час в течение 90 минут. Сколько всего она проедет?
Ответ: В первой половине своего пути она проходит 20 миль (10 х 2 = 20). Во второй половине она проходит 30 миль (20 х 1,5 = 30). 20+30=50, значит, всего она проехала 50 миль.
Методы улучшения ответов на эти вопросы
Чтобы улучшить свои навыки ответов на вопросы о скорости, расстоянии, времени, вы можете сделать две основные вещи.
Во-первых, убедитесь, что вы знакомы с формулой треугольника. Ключом к ответу на эти вопросы является знание формулы наизнанку, чтобы вы всегда знали, какое уравнение использовать, независимо от того, просит ли вас экзаменационный вопрос вычислить скорость или расстояние.
Убедившись, что вы запомнили формулу во всех ее вариантах, вы сэкономите время при ответах на вопросы.


 2-2bc \cdot \cos \alpha}}{2} \]
2-2bc \cdot \cos \alpha}}{2} \]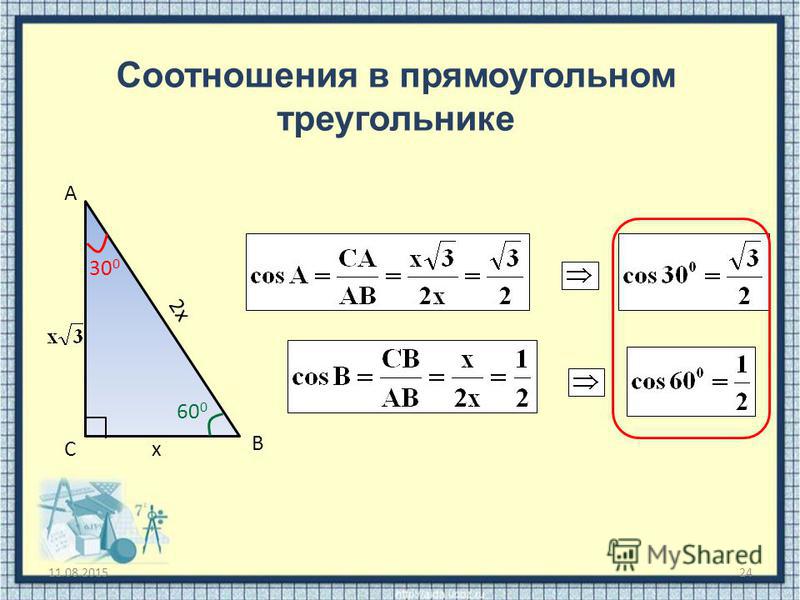


 2x=1$
2x=1$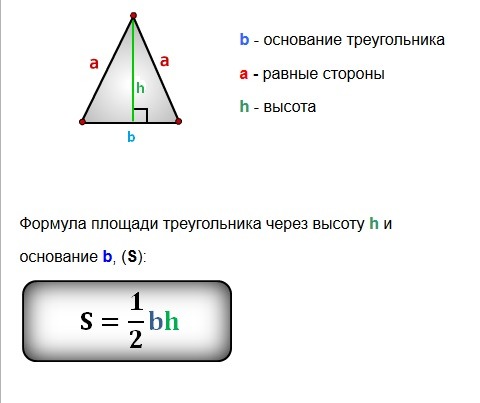 2=(39-15)(39+15)=24∙54=1296$
2=(39-15)(39+15)=24∙54=1296$


 Он говорит о том, как событие может произойти. Он имеет дело с числовым обоснованием принятия более вероятных решений. Чем выше вероятность, тем больше вероятность того, что событие произойдет, и наоборот. Треугольник Паскаля — это красивая концепция вероятности, разработанная известным математиком Блезом Паскалем, которая используется для нахождения коэффициентов в разложении любого биномиального выражения.
Он говорит о том, как событие может произойти. Он имеет дело с числовым обоснованием принятия более вероятных решений. Чем выше вероятность, тем больше вероятность того, что событие произойдет, и наоборот. Треугольник Паскаля — это красивая концепция вероятности, разработанная известным математиком Блезом Паскалем, которая используется для нахождения коэффициентов в разложении любого биномиального выражения.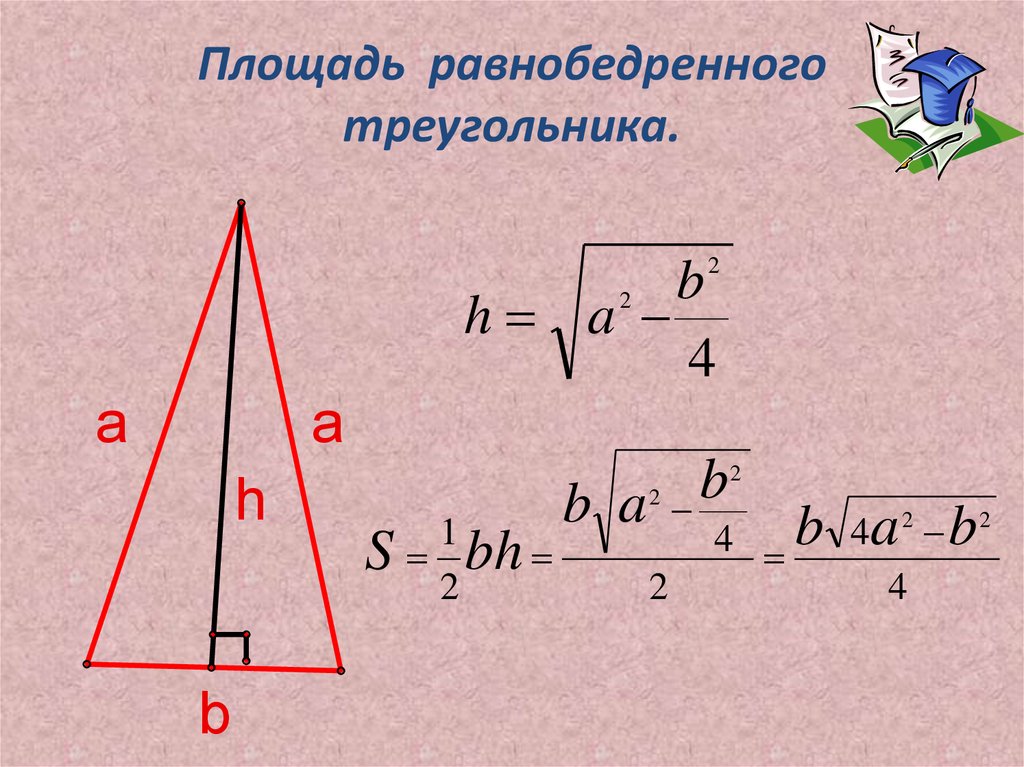 Здесь каждая строка представляет коэффициент расширения (x + y) п .
Здесь каждая строка представляет коэффициент расширения (x + y) п . Таким образом, квадрат строки 4 столбца 2 имеет значение 1 + 2 = 3,
Таким образом, квадрат строки 4 столбца 2 имеет значение 1 + 2 = 3,

 6С1 6С2 6С3 6С4 6С5 6С6
6С1 6С2 6С3 6С4 6С5 6С6



 Он не должен проходить через противоположную вершину, если он соединяет основание и линию, параллельную основанию и проходящую через противоположную вершину, как показано здесь.
Он не должен проходить через противоположную вершину, если он соединяет основание и линию, параллельную основанию и проходящую через противоположную вершину, как показано здесь.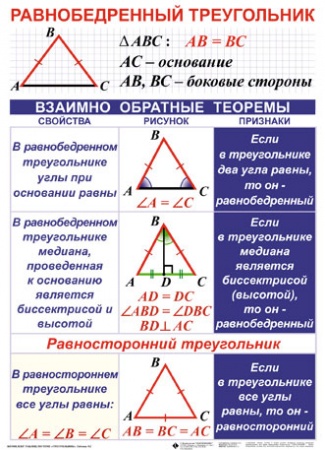
 Левая сторона треугольника D обозначена буквой b, а перпендикулярная линия, обозначенная буквой h, продолжается до противоположной вершины. Треугольник E, левая сторона которого обозначена буквой b, а пунктирная линия, обозначенная буквой h, проходит от нижней вершины под прямым углом к правой стороне. Треугольник F, правая сторона которого обозначена буквой b, а перпендикулярная пунктирная линия, обозначенная буквой h, проходит от стороны, обозначенной буквой b, к противоположной вершине.
Левая сторона треугольника D обозначена буквой b, а перпендикулярная линия, обозначенная буквой h, продолжается до противоположной вершины. Треугольник E, левая сторона которого обозначена буквой b, а пунктирная линия, обозначенная буквой h, проходит от нижней вершины под прямым углом к правой стороне. Треугольник F, правая сторона которого обозначена буквой b, а перпендикулярная пунктирная линия, обозначенная буквой h, проходит от стороны, обозначенной буквой b, к противоположной вершине. Назовите соответствующую высоту для каждого основания.
Назовите соответствующую высоту для каждого основания.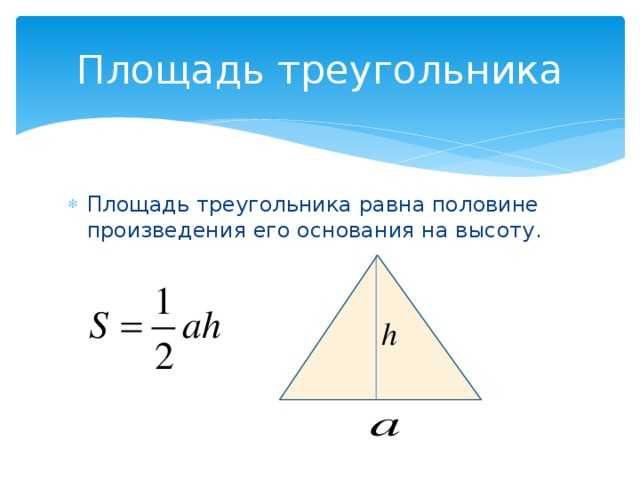
 ; подробная история редактирования доступна по запросу.
; подробная история редактирования доступна по запросу.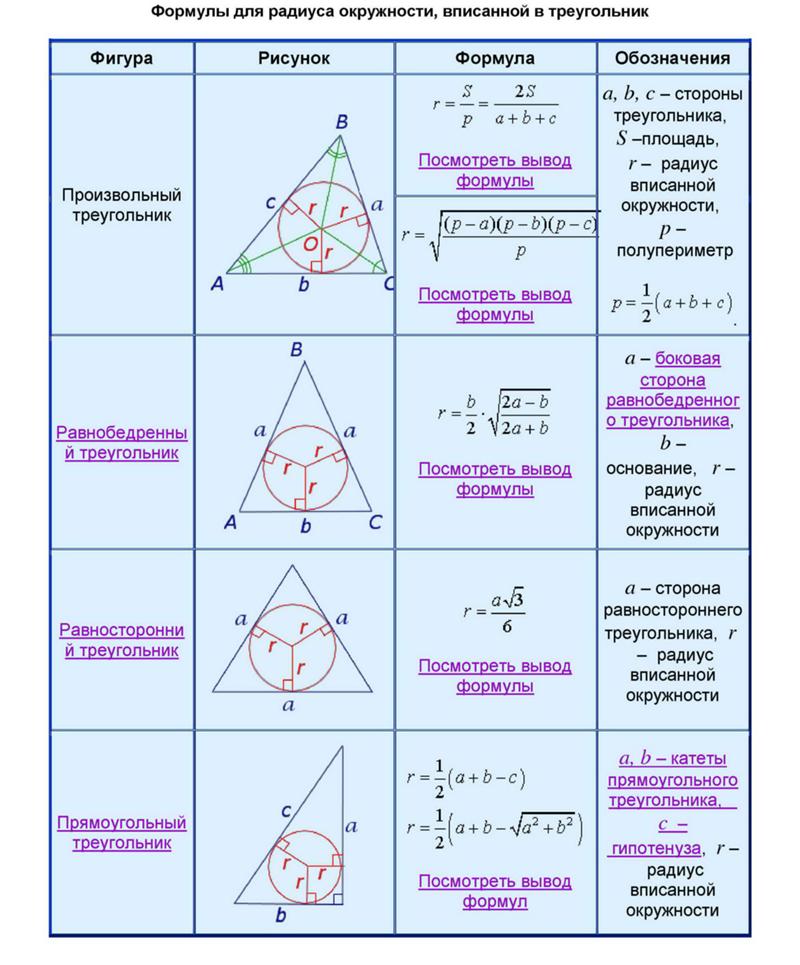 Это поможет вам запомнить его.
Это поможет вам запомнить его.