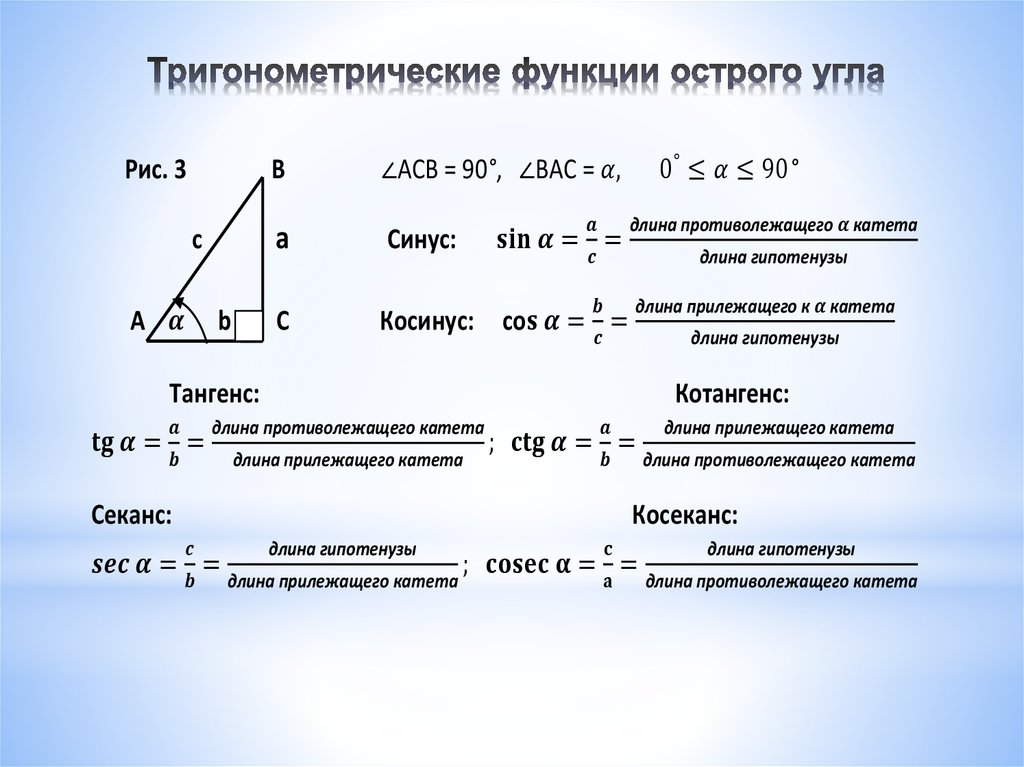
Тригонометрические соотношения в прямоугольном треугольнике
Соотношения сторон треугольника является основой тригонометрии и геометрии. Большинство задач сводится к использованию свойств треугольников и окружностей, а также прямых. Рассмотрим, что такое тригонометрические соотношения простым языком.
Тригонометрическими соотношениями в прямоугольном треугольнике называются соотношения длин его сторон. При этом такое соотношение всегда одно и то же по отношению к углу, который лежит между сторонами, соотношение между которыми должно быть вычислено.
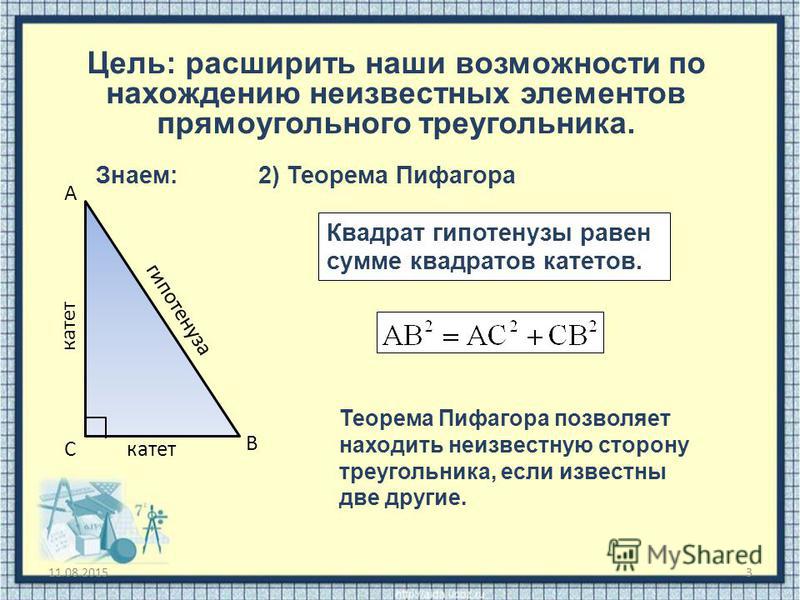
На рисунке обозначен прямоугольный треугольник ABC.
Рассмотрим тригонометрические соотношения его сторон относительно угла A (на рисунке он также обозначен греческой буквой α).
Примем во внимание, что сторона AB треугольника является его гипотенузой. Сторона AC является катетом, прилежащим к углу α, а сторона BC является катетом, противолежащим углу α.
Относительно угла α в прямоугольном треугольнике существуют следующие соотношения:
Косинусом угла называется отношение прилежащего к нему катета к гипотенузе данного прямоугольного треугольника. (см. что такое косинус и его свойства).
(см. что такое косинус и его свойства).
На рисунке косинусом угла α является соотношение cos α = AC/AB (прилежащий катет делить на гипотенузу).
Обратите внимание, что для угла β прилежащим катетом является уже сторона BC, поэтому cos β = BC / AB. То есть тригонометрические соотношения вычисляются в соответствии с положением сторон прямоугольного треугольника относительно угла.
При этом буквенные обозначения могут быть любыми. Важно лишь взаимное расположение угла и сторон прямоугольного треугольника.
Синусом угла называется соотношение противолежащего к нему катета к гипотенузе прямоугольного треугольника (см. что такое синус и его свойства).
На рисунке синусом угла α является соотношение sin α = BC / AB (противолежащий катет делить на гипотенузу).
Тангенсом угла называется соотношение противолежащего данному углу катета к прилежащему катету прямоугольного треугольника (см. что такое тангенс и его свойства ).
На рисунке тангенс угла α будет равен соотношению tg α = BC / AC. (противолежащий углу катет делить на прилежащий катет)
Для угла β, руководствуясь принципов взаимного расположения сторон, тангенс угла можно будет вычислить как tg β = AC / BC.
Котангенсом угла называется соотношение прилежащего данному углу катета на противолежащий катет прямоугольного треугольника. Как видно из определения, котангенс — эта функция, связанная с тангенсом соотношением 1/tg α . То есть они взаимно обратные.
Решение.
Поскольку cos α = 4/5, то AC / AB = 4 / 5. То есть стороны соотносятся как 4:5.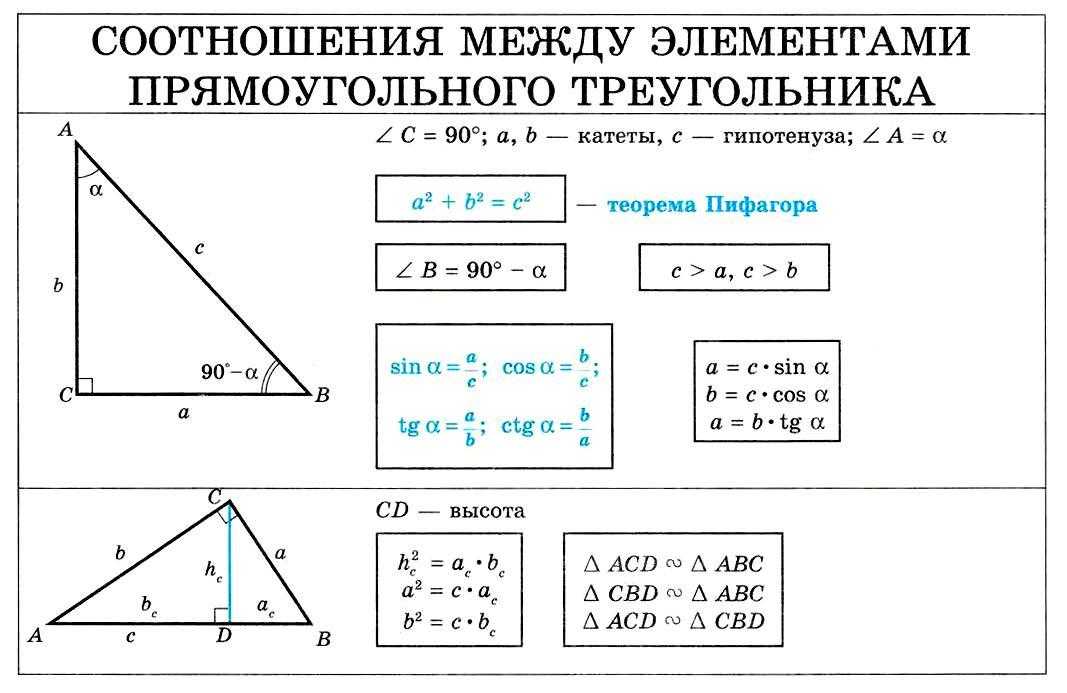 Обозначим длину AC как 4x, тогда AB = 5x.
Обозначим длину AC как 4x, тогда AB = 5x.
По теореме Пифагора:
BC2 + AC2 = AB2
Тогда
BC2 + ( 4х )2 = ( 5х )2
BC2 + 16х2 = 25х2
BC2 = 9х2
BC = 3x
sin α = BC / AB = 3x / 5x = 3/5
sin β = AC / AB, а его значение и так известно по условию, то есть 4/5
Ответ: 3/5, 4/5
0
Тангенс и его свойства | Описание курса | Тригонометрический круг
Соотношения между сторонами и углами прямоугольного треугольника 8 класс онлайн-подготовка на Ростелеком Лицей |
Соотношения между сторонами и углами прямоугольного треугольника.
В прямоугольном треугольнике тригонометрические функции используются для вычисления сторон и острых углов треугольника.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.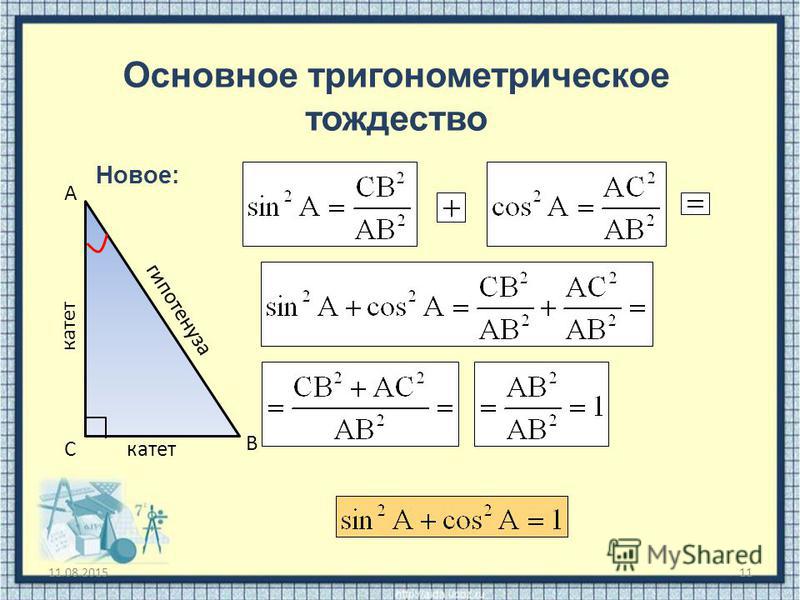
sinα = противолежащий катет : гипотенуза
sinα = a:c
Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
cosα = прилежащий катет : гипотенуза
cosα = b:c
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tgα = противолежащий катет : прилежащий катет
tgα = a:b
Тангенс угла равен отношению синуса угла к косинусу угла.
Доказательство: sinα:cosα=ac:bc=ab=tgα.
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны, тангенсы этих углов равны.
Докажем справедливость равенства sin2α+cos2α=1.
sin2α+cos2α=ac2+bc2=a2c2+b2c2=a2+b2c2
По теореме Пифагора c2=a2+b2, значит, у полученной дроби равны числитель и знаменатель – такая дробь равна 1.
Равенство sin2α+cos2α=1 называется основным тригонометрическим тождеством.
Как выбрать правильную функцию при решении задачи?
Если используются только катеты, применяется tg.
Если используется гипотенуза (дана или надо вычислить), то применяются sin или cos.
Если используется противолежащий катет (дан или надо вычислить), то применяется sin.
Если используется прилежащий катет, то применяется cos.
Если в треугольнике даны оба острых угла, лучше на рисунке отметить только один угол, чтобы однозначно понять, где прилежащий и где противолежащий катеты.
Значения тригонометрических функций (которые нужно знать наизусть):
|
30° |
45° |
60° |
|
|
sinα |
12 |
22 |
32 |
|
cosα |
32 |
22 |
12 |
|
tgα |
33 |
1 |
3 |
Величины остальных углов можно найти в таблице или приблизительно вычислить с помощью калькулятора.
Пример. В прямоугольном треугольнике с прямым углом B известно, что АВ = 6 см, ∠А = 60°. Найти АС.
Искомый отрезок — гипотенуза; дан угол и прилежащий катет, поэтому будем использовать cos.
cosA=ABAC=cos60°=12=6AC, следовательно, АС = 12 см.
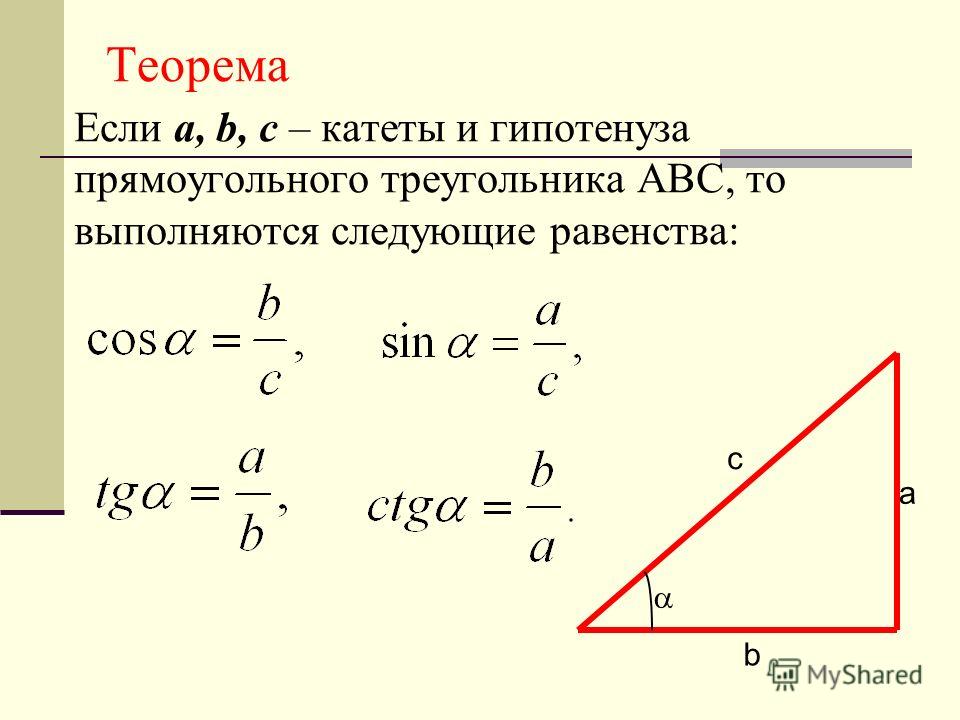
Тригонометрические функции в прямоугольном треугольнике
В этом разделе мы вводим тригонометрические функции, используя прямоугольный треугольник. Существует 6 основных тригонометрических функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для острых углов эти функции можно определить как отношения между сторонами прямоугольного треугольника.
Рассмотрим прямоугольный треугольник ABC с острым углом A = α. Сторона b между углом α и прямой угол C называется катетом, примыкающим к углу α . Соответственно другой катет a называется противоположным углу α .
Рис. 1.Синус \(\alpha,\) сокращенно \(\sin \alpha,\) есть отношение длины противолежащего катета к длине гипотенузы:
\[\sin \alpha = \frac{a}{c} = \frac{\text{противоположный катет}}{\text{гипотенуза}}\]
Косинус \(\alpha,\) сокращенно \(\cos \alpha,\) представляет собой отношение длины прилежащего катета к длине гипотенузы:
\[\cos \alpha = \frac{b}{c} = \frac{\text{прилегающий отрезок}}{\text{гипотенуза}}\]
Тангенс \(\alpha,\), сокращенно \(\tan \alpha,\), представляет собой отношение длины противоположного катета к длине соседнего катета:
\[\tan \alpha = \frac{a}{b} = \frac{\text{противоположный отрезок}}{\text{соседний отрезок}}\]
Функция тангенса может быть выражена через синус и косинус:
\[\tan \ alpha = \ frac {a} {b} = \ frac {a} {c} \ cdot \ frac {c} {b} = \ frac {{\ frac {a} {c}}} {{\ frac {b} {c}}} = \ frac {{\ sin \ alpha}} {\ cos \ alpha}}.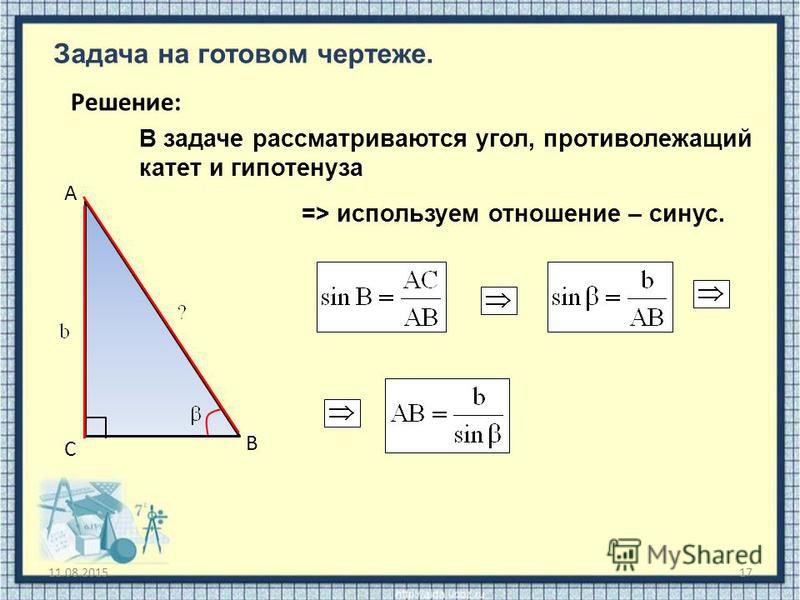
Если мы возьмем обратные функции синуса, косинуса и тангенса, мы получим выражения для других тригонометрических функций \(3\).
Функция, обратная синусу, называется косекансом. Косеканс \(\alpha,\), обозначаемый \(\csc \alpha,\), представляет собой отношение длины гипотенузы к длине противоположного катета:
\[\csc \alpha = \frac{1}{\sin\alpha} = \frac{c}{a} = \frac{\text{гипотенуза}}{\text{противоположный катет}}\]
Функция, обратная косинусу, называется секансом. Секанс \(\alpha,\), обозначаемый \(\sec \alpha,\), представляет собой отношение длины гипотенузы к длине прилежащего катета:
\[\sec \alpha = \frac{1}{\cos\alpha} = \frac{c}{b} = \frac{\text{гипотенуза}}{\text{прилегающий отрезок}}\]
Обратная величина тангенса называется котангенсом. Котангенс \(\alpha,\), обозначаемый \(\cot \alpha,\), представляет собой отношение длины соседнего катета к длине противоположного катета:
\[\cot \alpha = \frac{1}{\tan\alpha} = \frac{b}{a} = \frac{\text{смежный отрезок}}{\text{противоположный отрезок}}\]
Пример
Вершина Эйфелевой башни видна с расстояния \(d=500\,м\) под углом \(\alpha = 31^\окр.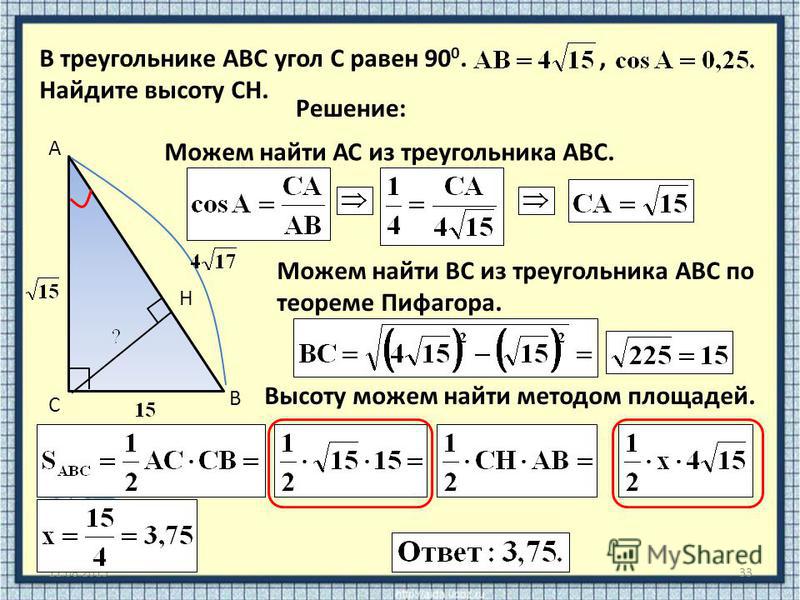 \) Найдите высоту башни. 9\circ} = 500 \times 0,6 = 300\,m.\]
\) Найдите высоту башни. 9\circ} = 500 \times 0,6 = 300\,m.\]
См. решенные проблемы на стр. 2.
2.3: Тригонометрия прямоугольного треугольника — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 32548
- OpenStax
- OpenStax
Цели обучения
- Использование прямоугольных треугольников для вычисления тригонометрических функций.
- Найдите значения функции для 30°(\(\dfrac{\pi}{6}\)), 45°(\(\dfrac{\pi}{4}\)) и 60°(\(\dfrac{ \pi}{3}\)).
- Используйте равные кофункции дополнительных углов.
- Используйте определения тригонометрических функций любого угла.

- Используйте тригонометрию прямоугольного треугольника для решения прикладных задач.
Эверест, расположенный на границе Китая и Непала, является самой высокой горой в мире. Измерение его высоты — непростая задача, и на самом деле фактическое измерение было источником споров на протяжении сотен лет. Процесс измерения включает использование треугольников и раздел математики, известный как тригонометрия. В этом разделе мы определим новую группу функций, известную как тригонометрические функции, и выясним, как их можно использовать для измерения высоты, например высоты самых высоких гор.
Ранее мы определили синус и косинус угла через координаты точки на единичной окружности, пересекаемой конечной стороной угла:
\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]
В этом разделе мы увидим другой способ определения тригонометрических функций с использованием свойств прямоугольных треугольников .
Использование прямоугольных треугольников для вычисления тригонометрических функций
В предыдущих разделах мы использовали единичный круг для определения тригонометрические функции . В этом разделе мы расширим эти определения, чтобы их можно было применять к прямоугольным треугольникам. Значением функции синуса или косинуса \(t\) является ее значение в \(t\) радианах. Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке \(\PageIndex{1}\) показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок из точки \((x,y)\) на ось x , мы получим прямоугольный треугольник, у которого вертикальная сторона имеет длину \(y\), а горизонтальная сторона имеет длину \(x\). Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
В этом разделе мы расширим эти определения, чтобы их можно было применять к прямоугольным треугольникам. Значением функции синуса или косинуса \(t\) является ее значение в \(t\) радианах. Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке \(\PageIndex{1}\) показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок из точки \((x,y)\) на ось x , мы получим прямоугольный треугольник, у которого вертикальная сторона имеет длину \(y\), а горизонтальная сторона имеет длину \(x\). Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
Мы знаем
\[ \cos t= \frac{x}{1}=x \]
Аналогично, мы знаем
\[ \sin t= \frac {y}{1}=y \]
Эти отношения по-прежнему применяются к сторонам прямоугольного треугольника, когда не используется единичная окружность и когда треугольник не находится в стандартном положении и не отображается на графике с использованием \((x,y )\) координаты. Чтобы иметь возможность свободно использовать эти отношения, мы дадим сторонам более общие имена: вместо \(x\) мы будем называть сторону между данным углом и прямым углом примыкающая сторона к углу \(t\). (Adjacent означает «рядом с».) Вместо \(y\) мы будем называть сторону, наиболее удаленную от данного угла, стороной, противоположной от угла \(t\). И вместо \(1\) мы будем называть сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой . Эти стороны обозначены на рисунке \(\PageIndex{2}\).
Чтобы иметь возможность свободно использовать эти отношения, мы дадим сторонам более общие имена: вместо \(x\) мы будем называть сторону между данным углом и прямым углом примыкающая сторона к углу \(t\). (Adjacent означает «рядом с».) Вместо \(y\) мы будем называть сторону, наиболее удаленную от данного угла, стороной, противоположной от угла \(t\). И вместо \(1\) мы будем называть сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой . Эти стороны обозначены на рисунке \(\PageIndex{2}\).
Понимание отношений прямоугольного треугольника
Дан прямоугольный треугольник с острым углом \(t\),
\[\begin{align} \sin (t) &= \dfrac{\text{напротив}}{\text{гипотенуза}} \ label{sindef}\\ \cos (t) &= \dfrac{\text{смежный}}{\text{гипотенуза}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{напротив }}{\text{adjacent}} \label{tandef}\end{align}\]
Обычной мнемоникой для запоминания этих взаимосвязей является SohCahToa, образованная из первых букв « S ine is o pposite over ч ypotenuse, C osine это a djacent над h ypotenuse, T angent это o pposite над a djacent. ”
”
как: Зная длины сторон прямоугольного треугольника и один из острых углов, найти синус, косинус и тангенс этого угла
- Найти синус как отношение противолежащего катета к гипотенузе.
- Найдите косинус как отношение прилежащего катета к гипотенузе.
- Найдите тангенс отношения противолежащего катета к прилежащему.
Пример \(\PageIndex{1}\): вычисление тригонометрической функции прямоугольного треугольника
Учитывая треугольник, показанный на рисунке \(\PageIndex{3}\), найдите значение \(\cos α\) .
Рисунок \(\PageIndex{3}\)Решение
Сторона, прилегающая к углу, равна 15, а гипотенуза треугольника равна 17, поэтому по уравнению \ref{cosdef}:
\[\begin {align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{гипотенуза}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]
Упражнение \(\PageIndex{1}\)
Учитывая треугольник, показанный на рисунке \(\PageIndex{4}\), найдите значение \(\sin t\).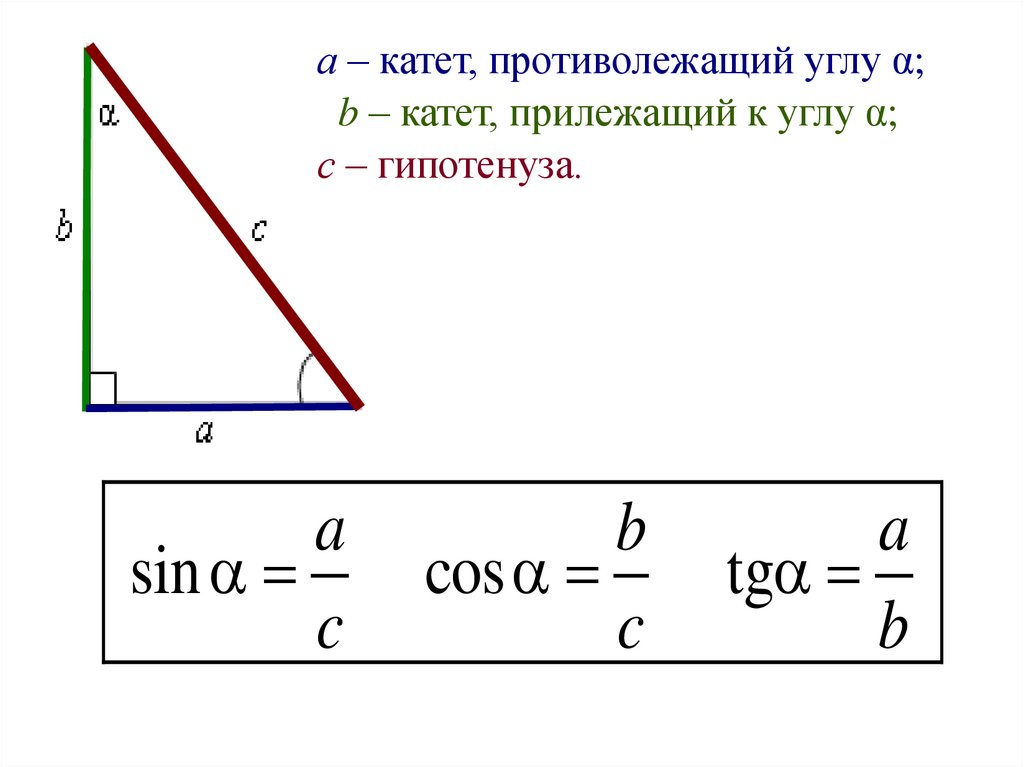
- Ответ
\(\frac{7}{25}\)
Взаимосвязь углов и их функции
При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника. На самом деле, мы можем вычислить шесть тригонометрических функций любого из двух острых углов треугольника на рисунке \(\PageIndex{5}\). Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.
Рисунок \(\PageIndex{5}\): Сторона, примыкающая к одному углу, противоположна другому. Нас попросят найти все шесть тригонометрических функций для данного угла в треугольнике. Наша стратегия состоит в том, чтобы сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что обратная величина синуса является косекансом, обратная величина косинуса является секансом, а обратная величина тангенса является котангенсом.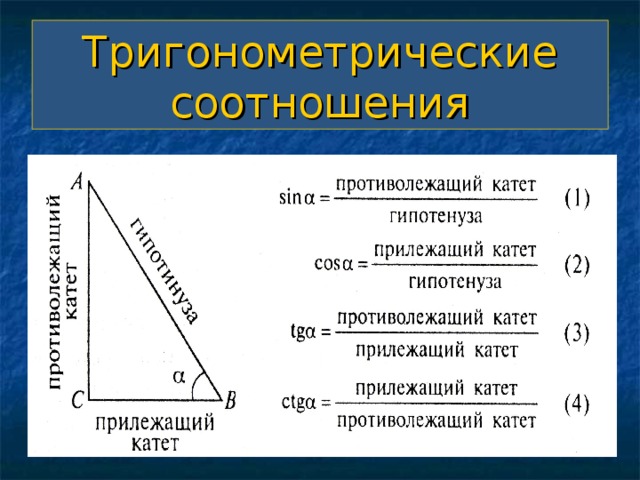
как: Зная длины сторон прямоугольного треугольника, вычислить шесть тригонометрических функций одного из острых углов
- При необходимости нарисуйте прямоугольный треугольник и обозначьте его угол.
- Определите угол, прилежащую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.
- Найдите нужную функцию:
- синус как отношение противолежащего катета к гипотенузе
- косинус как отношение прилежащего катета к гипотенузе
- тангенс как отношение противоположной стороны к прилежащей стороне
- секанс как отношение гипотенузы к прилежащему катету
- косеканс как отношение гипотенузы к противолежащему катету
- котангенс как отношение прилежащей стороны к противолежащей стороне
Пример \(\PageIndex{2}\): оценка тригонометрических функций углов, не находящихся в стандартном положении
Используя треугольник, показанный на рисунке \(\PageIndex{6}\), оцените \( \sin α, \cos α , \tan α, \sec α, \csc α,\) и \( \cot α\).
Решение
\[ \begin{align*} \sin α &= \dfrac{\text{напротив} α}{\text{гипотенуза}} = \dfrac {4}{5} \\ \cos α &= \dfrac{\text{рядом с}α}{\text{гипотенуза}}=\dfrac{3}{5} \\ \tan α &= \dfrac{ \text{напротив}α}{\text{рядом с}α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{гипотенуза}}{\text{рядом с}α} = \dfrac{5}{3} \\ \csc α &= \dfrac{\text{гипотенуза}}{\text{напротив}α}=\dfrac{5}{4} \\ \cot α &= \ dfrac{\text{рядом с}α}{\text{напротив}α}=\dfrac{3}{4} \end{align*}\]
Упражнение \(\PageIndex{2}\)
Используя треугольник, показанный на рисунке \(\PageIndex{7}\), оцените \( \sin t, \cos t,\tan t, \sec t, \ csc t,\) и \(\cot t\).
Рисунок \(\PageIndex{7}\)- Ответ
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \ \ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]
Нахождение тригонометрических функций специальных углов с использованием длин сторон
Мы уже обсуждали тригонометрические функции, связанные с особыми углами на единичной окружности. Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы. Мы делаем это потому, что когда мы оцениваем специальные углы в тригонометрических функциях, они имеют относительно удобные значения, значения, которые либо не содержат, либо содержат только один квадратный корень из отношения. Поэтому эти углы часто используются в математических и научных задачах. Мы будем использовать числа, кратные \(30°, 60°,\) и \(45°\), однако помните, что при работе с прямоугольными треугольниками мы ограничены углами между \(0° \text{ и } 90°\).
Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы. Мы делаем это потому, что когда мы оцениваем специальные углы в тригонометрических функциях, они имеют относительно удобные значения, значения, которые либо не содержат, либо содержат только один квадратный корень из отношения. Поэтому эти углы часто используются в математических и научных задачах. Мы будем использовать числа, кратные \(30°, 60°,\) и \(45°\), однако помните, что при работе с прямоугольными треугольниками мы ограничены углами между \(0° \text{ и } 90°\).
Предположим, у нас есть треугольник \(30°,60°,90°\), который также можно описать как \(\frac{π}{6}, \frac{π}{3},\frac{ π}{2}\) треугольник. Стороны имеют длины в соотношении \(s,\sqrt{3}s,2s.\) Стороны треугольника \(45°,45°,90°\), который также может быть описан как \(\ frac{π}{4},\frac{π}{4},\frac{π}{2}\) треугольника, имеют длины в соотношении \(s,s,\sqrt{2}s.\) Эти отношения показаны на рисунке \(\PageIndex{8}\).
Затем мы можем использовать отношения длин сторон для вычисления тригонометрических функций особых углов.
Даны тригонометрические функции специального угла, оцените, используя длины сторон.
- Используйте длины сторон, показанные на рисунке \(\PageIndex{8}\), для специального угла, который вы хотите оценить.
- Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.
Пример \(\PageIndex{3}\): вычисление тригонометрических функций специальных углов с использованием длин сторон
Найдите точное значение тригонометрических функций \(\frac{π}{3}\) с использованием длин сторон.
Решение
\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\ sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text {hyp}} = \ dfrac {s} {2s} = \ dfrac {1} {2} \\ \ tan (\ dfrac {π} {3}) & = \ dfrac {\ text {opp}} {\ text {adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{ \text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} = \dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π} {3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}= \dfrac{\sqrt{3}}{3} \end{align*}\]
Упражнение \(\PageIndex{3}\)
Найдите точное значение тригонометрических функций \(\frac{π}{4}\), используя длины сторон.
- Ответить
\( \ sin (\ frac {π} {4}) = \ frac {\ sqrt {2}} {2}, \ cos (\ frac {π} {4}) = \ frac {\ sqrt {2} {2}, \tan (\frac{π}{4})=1,\)
\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{ 4}) =1 \)
Использование равной кофункции дополнений
Если мы более внимательно посмотрим на соотношение между синусом и косинусом специальных углов относительно единичного круга, мы заметим закономерность. В прямоугольном треугольнике с углами \(\frac{π}{6}\) и \(\frac{π}{3}\) синус \(\frac{π}{3}\ ), а именно \(\frac{\sqrt{3}}{2}\), также является косинусом \(\frac{π}{6}\), а синус \(\frac{π}{ 6}\), а именно \(\frac{1}{2},\) также является косинусом \(\frac{π}{3}\) (рис. \(\PageIndex{9}\)).
\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{ \sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2 } \end{выравнивание*}\]
Рисунок \(\PageIndex{9}\): синус \(\frac{π}{3}\) равен косинусу \(\frac{π}{6}\) и наоборот.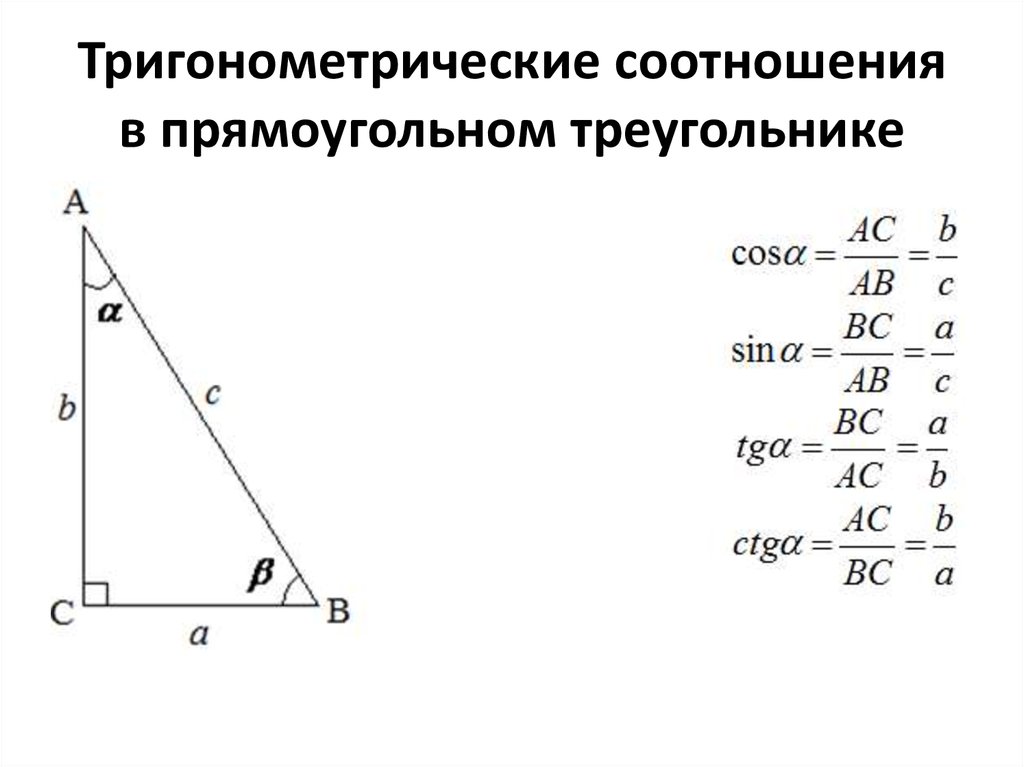
Этот результат не должен удивлять, поскольку, как видно из рисунка \(\PageIndex{9}\), сторона, противоположная углу \(\frac{π}{3}\), также является стороной, примыкающей к \( \frac{π}{6}\), так что \(\sin (\frac{π}{3})\) и \(\cos (\frac{π}{6})\) имеют точно такое же отношение из тех же двух сторон, \(\sqrt{3} s\) и \(2s.\) Аналогично, \( \cos (\frac{π}{3})\) и \( \sin (\frac{ π}{6})\) также являются одним и тем же отношением, используя те же две стороны, \(s\) и \(2s\).
Взаимосвязь между синусом и косинусом фигур \(\frac{π}{6}\) и \(\frac{π}{3}\) также имеет место для двух острых углов любого прямоугольного треугольника, поскольку в каждом В этом случае отношение тех же двух сторон составит синус одного угла и косинус другого. Поскольку сумма трех углов треугольника равна π, а прямой угол равен \(\frac{π}{2}\), оставшиеся два угла также должны составлять \(\frac{π}{2}\) . Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с \(\frac{π}{2}\) — другими словами, любыми двумя дополнительными углами. Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это удостоверение показано на рисунке \(\PageIndex{10}\).
Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это удостоверение показано на рисунке \(\PageIndex{10}\).
ИДЕНТИЧНОСТИ КОФУНКЦИЙ
тождества кофункций в радианах перечислены в таблице \(\PageIndex{1}\).
| \( \cos t= \sin (\frac{π}{2}−t)\) | \( \sin t= \cos (\dfrac{π}{2}−t)\) |
| \( \tan t= \cot (\dfrac{π}{2}−t) \) | \( \cot t= \tan (\dfrac{π}{2}−t)\) |
| \( \sec t= \csc (\dfrac{π}{2}−t) \) | \( \csc t= \sec (\dfrac{π}{2}−t)\) |
как: Зная синус и косинус угла, найти синус или косинус его дополнения.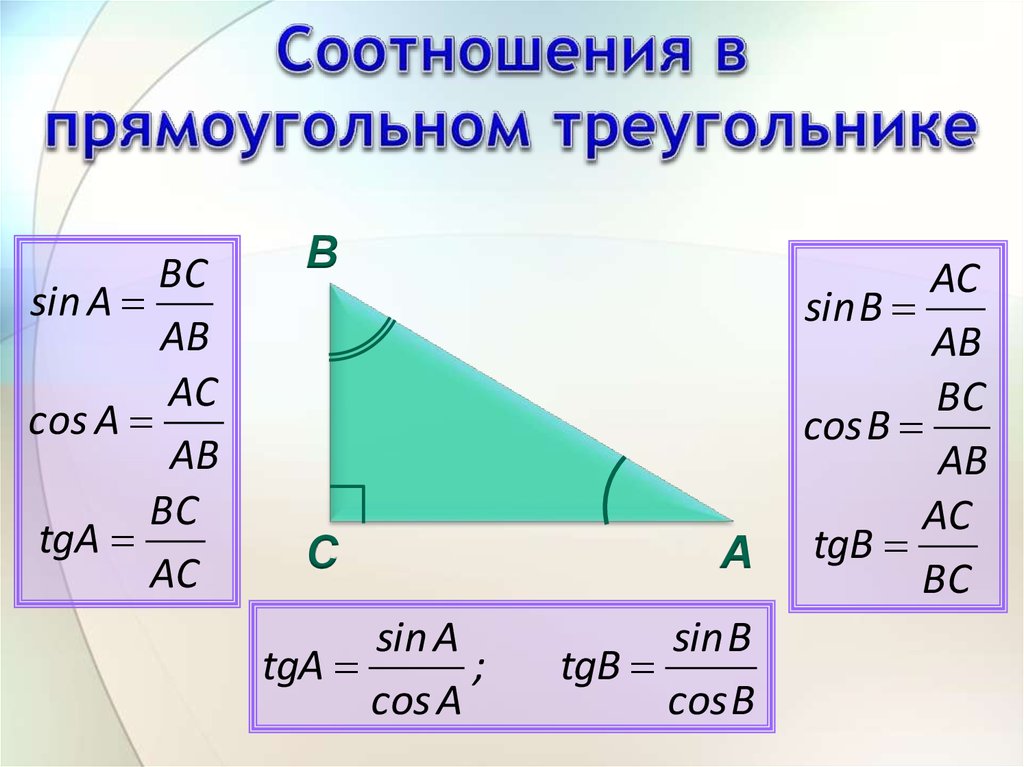
- Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
- Чтобы найти косинус дополнительного угла, найдите синус исходного угла.
Пример \(\PageIndex{4}\): использование тождеств кофункций
Если \( \sin t = \frac{5}{12},\) найти \(( \cos \frac{π}{2} −t)\).
Решение
Согласно тождествам кофункций для синуса и косинуса,
\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]
Итак,
\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]
Упражнение \(\PageIndex{4}\)
Если \(\csc (\frac{π}{6})=2,\) найти \( \sec (\frac{π} {3}).\)
Решение
2
Использование тригонометрических функций
В предыдущих примерах мы вычисляли синус и косинус в треугольниках, для которых были известны все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.
как: Имея прямоугольный треугольник, длину одной стороны и величину одного острого угла, найти остальные стороны знаменатель. Известная сторона, в свою очередь, будет знаменателем или числителем.
Пример \(\PageIndex{5}\): нахождение недостающих длин сторон с помощью тригонометрических соотношений
Найдите неизвестные стороны треугольника на рисунке \(\PageIndex{11}\).
Рисунок \(\PageIndex{11}\)Решение
Нам известны угол и противоположная сторона, поэтому мы можем использовать касательную, чтобы найти прилежащую сторону.
\[ \tan (30°)= \dfrac{7}{a} \nonumber\]
Перегруппируем, чтобы найти \(a\).
\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]
Мы можем использовать синус, чтобы найти гипотенузу.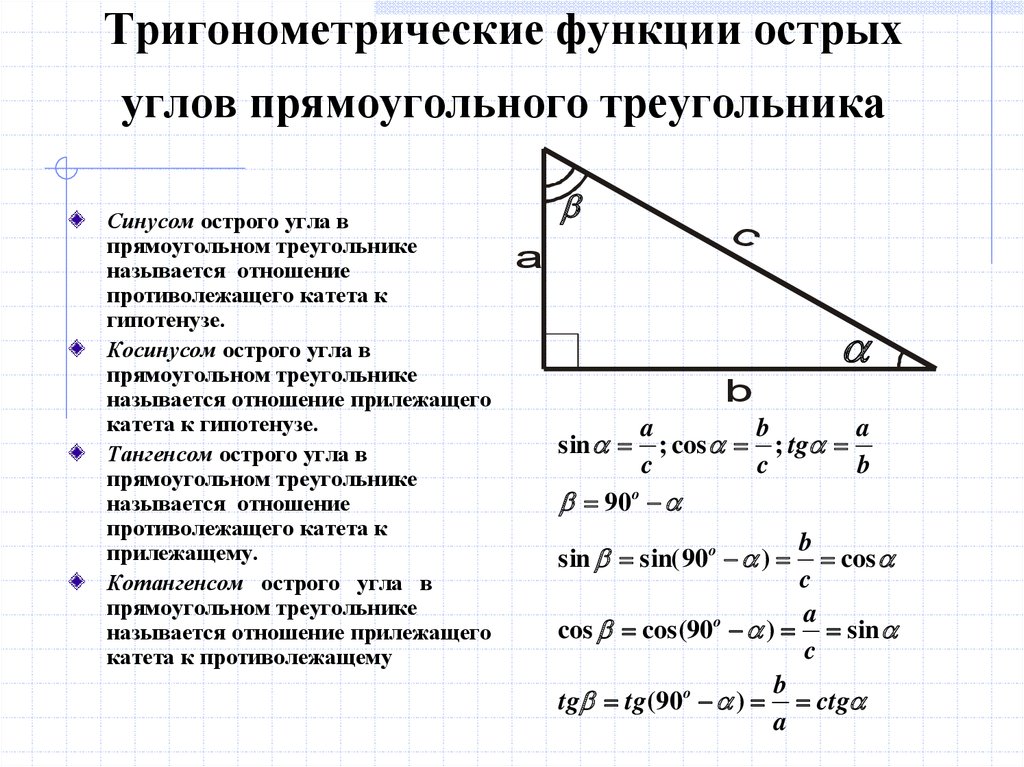
\[ \sin (30°)= \dfrac{7}{c} \nonumber\]
Снова переставляем, чтобы найти \(c\).
\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]
Упражнение \(\PageIndex{5}\):
Прямоугольный треугольник имеет один угол \(\frac{π}{3}\) и гипотенузу 20. Найдите неизвестные стороны и угол треугольника.
- Ответить
\(\mathrm{adjacent=10; напротив=10 \sqrt{3}; }\) недостающий угол равен \(\frac{π}{6}\)
Использование тригонометрии прямоугольного треугольника для решения прикладных задач
Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, возможность вычислить длины сторон треугольника позволяет найти высоту высокого предмета, не взбираясь на его вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. угол наклона объекта ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от объекта к глазу наблюдателя. См. рисунок \(\PageIndex{12}\).
угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. угол наклона объекта ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от объекта к глазу наблюдателя. См. рисунок \(\PageIndex{12}\).
как: Имея высокий объект, косвенно измерьте его высоту
- Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.

- Отметьте измеренное расстояние от основания объекта до точки, где хорошо виден верх объекта.
- На другом конце измеренного расстояния посмотрите на верхнюю часть объекта. Измерьте угол, который линия взгляда образует с горизонтом.
- Напишите уравнение, связывающее неизвестную высоту, измеренное расстояние и тангенс угла луча зрения.
- Решите уравнение для неизвестной высоты.
Пример \(\PageIndex{6}\): Косвенное измерение расстояния
Чтобы найти высоту дерева, человек идет к точке в 30 футах от основания дерева. Она измеряет угол 57° 57° между линией обзора верхушки дерева и землей, как показано на рисунке \(\PageIndex{13}\). Найдите высоту дерева.
Рисунок \(\PageIndex{13}\)Решение
Мы знаем, что угол возвышения равен \(57°\) и длина прилегающей стороны 30 футов. Противоположная сторона — неизвестная высота.
Тригонометрическая функция, связывающая сторону, противоположную углу, и сторону, примыкающую к углу, называется тангенсом. Таким образом, мы сформулируем нашу информацию в терминах тангенса \(57°\), пусть \(h\) будет неизвестной высотой.
Таким образом, мы сформулируем нашу информацию в терминах тангенса \(57°\), пусть \(h\) будет неизвестной высотой.
\[\begin{array}{cl} \tan θ = \dfrac{\text{напротив}}{\text{смежный}} & \text{} \\ \tan (57°) = \dfrac{h }{30} & \text{Найти }h. \\ h=30 \tan (57°) & \text{Умножить.} \\ h≈46,2 & \text{Использовать калькулятор.} \end{массив} \]
Высота дерева примерно 46 футов.
Упражнение \(\PageIndex{6}\):
Какова длина лестницы, чтобы добраться до подоконника на высоте 50 футов над землей, если лестница упирается в здание под углом \(\frac{5π}{12 }\) с землей? Округлить до ближайшего фута.
- Ответить
Около 52 футов
носитель:
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики по тригонометрии прямоугольного треугольника.
- Поиск триггерных функций на калькуляторе
- Нахождение триггерных функций с помощью прямоугольного треугольника
- Связь триггерных функций со сторонами прямоугольного треугольника
- Определение функций шести триггеров по треугольнику
- Определить длину стороны прямоугольного треугольника
Посетите этот веб-сайт, чтобы получить дополнительные практические вопросы от Learningpod.
Ключевые уравнения
Тождества кофункций
\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{ π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}-t) \\ \csc t &= \sec (\frac{π}{2}-t) \end{align*}\]
Ключевые понятия
- Мы можем определить тригонометрические функции как отношения длин сторон прямоугольного треугольника. См. Пример.
- Одинаковую длину сторон можно использовать для вычисления тригонометрических функций любого острого угла прямоугольного треугольника. См. Пример.
- Мы можем вычислить тригонометрические функции специальных углов, зная длины сторон треугольников, в которых они встречаются. См. Пример.
- Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
- Если два угла дополняют друг друга, тождества кофункций утверждают, что синус одного равен косинусу другого и наоборот.
 См. Пример.
См. Пример. - Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
- Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне. См. Пример.
- Тригонометрия прямоугольного треугольника позволяет измерять недоступные высоты и расстояния.
- Неизвестную высоту или расстояние можно найти, составив прямоугольный треугольник, в котором неизвестная высота или расстояние является одной из сторон, а другая сторона и угол известны. См. Пример.
Глоссарий
- смежная сторона
- в прямоугольном треугольнике, сторона между данным углом и прямым углом
- угол наклона
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен ниже, чем наблюдатель
- угол возвышения
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен выше наблюдателя
- противоположная сторона
- в прямоугольном треугольнике, сторона, наиболее удаленная от данного угла
- гипотенуза
- сторона прямоугольного треугольника, противоположная прямому углу
Эта страница под названием 2.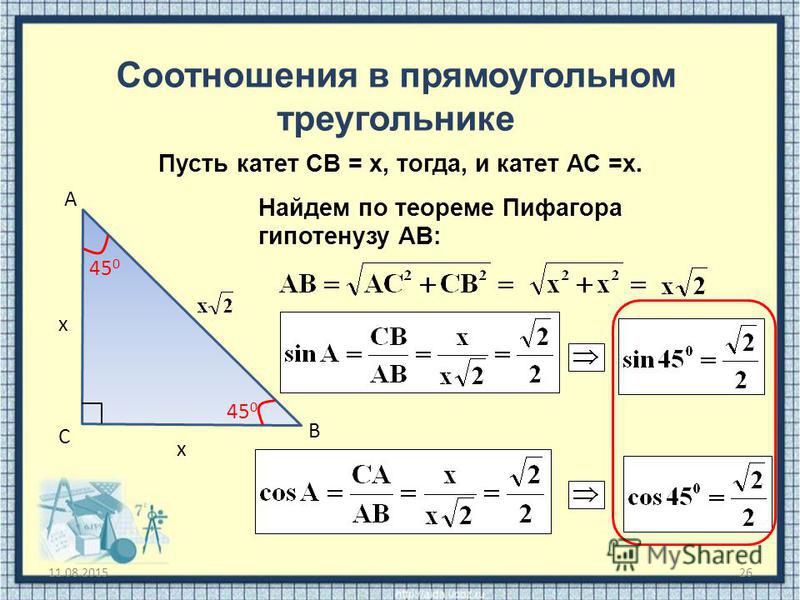


 См. Пример.
См. Пример.