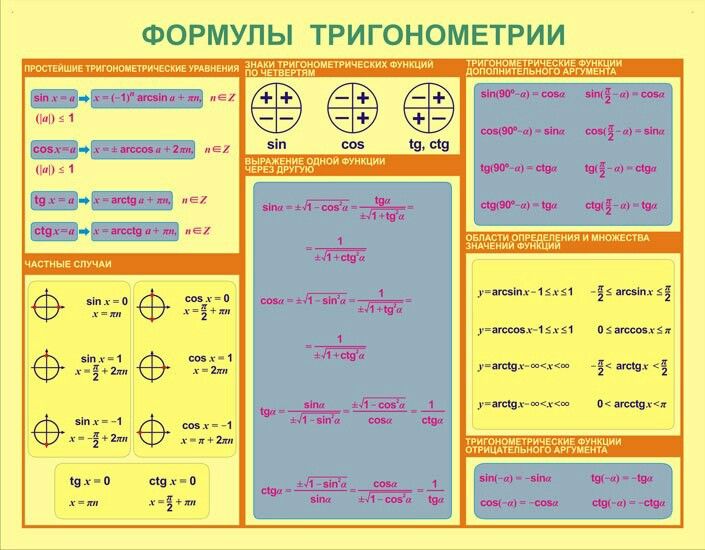
Эти тождества используются для преобразования тригонометрических выражений; позволяют по значению одной из тригонометрических функций находить значения всех остальных.
ПРИМЕР
Найти \(\ \operatorname{tg} \alpha \) , если известно, что
\(\ \sin \alpha=\frac{1}{3} \), \(\ \cos \alpha=-\frac{2 \sqrt{2}}{3} \)
Используя тригонометрическую формулу \(\ \operatorname{tg} \alpha=\frac{\sin \alpha}{\cos \alpha} \) , получим, что искомое значение
\(\ \operatorname{tg} \alpha=\frac{\frac{1}{3}}{-\frac{2 \sqrt{2}}{3}}=-\frac{1}{2 \sqrt{2}}=-\frac{\sqrt{2}}{4} \)
\(\ \operatorname{tg} \alpha=-\frac{\sqrt{2}}{4} \)
Признаки тригонометрических функций
ОПРЕДЕЛЕНИЕ
Синус угла \(\ \alpha \) является ординатой (т. е. Координатой у) точки на единичной тригонометрической окружности, которая возникает, когда радиус поворачивается на указанный угол \(\ a \):
\(\ \sin \alpha=y \)
Отсюда можно заключить, что значения синусов углов в первом и втором четверти положительны (поскольку ординаты точек в этих четвертях больше нуля), а значения в третьем и четвертом кварталах отрицательны.
ОПРЕДЕЛЕНИЕ
Косинус угла \(\ \alpha \) является абсциссой — координата x является точкой на единичной окружности, которая возникает, когда радиус поворачивается на угол \(\ \alpha \):
\(\ \cos \alpha=x \)
ОПРЕДЕЛЕНИЕ
Тангенсом угла \(\ \alpha \) является отношение синуса к косинусу:
\(\ \operatorname{tg} \alpha=\frac{\sin \alpha}{\cos \alpha}=\frac{y}{x} \)
ОПРЕДЕЛЕНИЕ
Котангенсом угла \(\ \alpha \) является отношение косинуса к синусоидальному:
\(\ \operatorname{ctg} \alpha=\frac{\cos \alpha}{\sin \alpha}=\frac{x}{y} \)
Знак тригонометрической функции зависит только от координатного квартала, в котором находится числовой аргумент.
ПРИМЕР
В каком квартале находится угол \(\ \alpha \) , если известно, что его синус положителен, а косинус отрицателен?
Синус некоторого угла положительно, если угол находится в первом или втором координатах, а косинус отрицателен во втором и третьем кварталах.
{2}-\sin 2 \alpha=1+\sin 2 \alpha-\sin 2 \alpha=1
\)
\(\ \mathrm{A}=1 \)
Формулы половинного аргумента
Названные формулы выражают функции половинного аргумента \(\ \frac{\alpha}{2} \) через тригонометрические функции аргумента \(\ \alpha \) . При меняются в тригонометрических преобразованиях.
\(\ \sin \frac{\alpha}{2}=\mp \sqrt{\frac{1-\cos \alpha}{2}} \)
\(\ \cos \frac{\alpha}{2}=\mp \sqrt{\frac{1+\cos \alpha}{2}} \)
\(\ \operatorname{tg} \frac{\alpha}{2}=\mp \sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}}=\frac{1-\cos \alpha}{\sin \alpha}=\frac{\sin \alpha}{1+\cos \alpha} \)
\(\ \operatorname{ctg} \frac{\alpha}{2}=\mp \sqrt{\frac{1+\cos \alpha}{1-\cos \alpha}}=\frac{1+\cos \alpha}{\sin \alpha}=\frac{\sin \alpha}{1-\cos \alpha} \)
ПРИМЕР
Найти \(\ _{1} \operatorname{tg} \frac{\alpha}{2} \) , если известно, что \(\ \sin \alpha=\frac{1}{2} \) и \(\ \alpha \)– угол первой четверти.
Для нахождения нужного значения воспользуемся формулой
\(\ \operatorname{tg} \frac{\alpha}{2}=\frac{\sin \alpha}{1+\cos \alpha} \)
Найдем косинус угла.
{2}}=\frac{\sqrt{3}}{2}
\)
А отсюда имеем, что
\(\ \operatorname{tg} \frac{\alpha}{2}=\frac{\frac{1}{2}}{1+\frac{\sqrt{3}}{2}}=\frac{1}{2+\sqrt{3}} \)
\(\ \operatorname{tg} \frac{\alpha}{2}=\frac{1}{2+\sqrt{3}} \)
Формулы сложения и вычитания аргументов
Тригонометрические формулы сложения и вычитания углов представляют собой тригонометрические уравнения, в которых в качестве аргумента тригонометрической функции выступает сумма или разность двух \(\ \alpha \) и \(\ \beta \) . Данные формулы позволяют по известным тригонометрическим функциям аргументов \(\ \alpha \) и \(\ \beta \) определять значения этих функций для сумм или разностей указанных аргументов.
\(\ \sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \)
\(\ \sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta \)
\(\ \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \)
\(\ \cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta \)
\(\ \operatorname{tg}(\alpha+\beta)=\frac{\operatorname{tg} \alpha+\operatorname{tg} \beta}{1-\operatorname{tg} \alpha \operatorname{tg} \beta} \)
\(\ \operatorname{tg}(\alpha-\beta)=\frac{\operatorname{tg} \alpha-\operatorname{tg} \beta}{1+\operatorname{tg} \alpha \operatorname{tg} \beta} \)
\(\ \operatorname{ctg}(\alpha+\beta)=\frac{\operatorname{ctg} \alpha \operatorname{ctg} \beta-1}{\operatorname{ctg} \alpha+\operatorname{ctg} \beta} \)
\(\ \operatorname{ctg}(\alpha-\beta)=\frac{\operatorname{ctg} \alpha \operatorname{ctg} \beta+1}{\operatorname{ctg} \alpha-\operatorname{ctg} \beta} \)
ПРИМЕР
Найти значение выражения \(\ \sin 37^{\circ} \cos 23^{\circ}+\cos 37^{\circ} \sin 23^{\circ} \)
Применим формулу «синус суммы» справа налево, то есть в виде
\(\ \sin \alpha \cos \beta+\cos \alpha \sin \beta=\sin (\alpha+\beta) \)
Тогда будем иметь, что
\(\ \sin 37^{\circ} \cos 23^{\circ}+\cos 37^{\circ} \sin 23^{\circ}=\sin \left(37^{\circ}+23^{\circ}\right)=\sin 60^{\circ}=\frac{\sqrt{3}}{2} \)
\(\ \sin 37^{\circ} \cos 23^{\circ}+\cos 37^{\circ} \sin 23^{\circ}=\frac{\sqrt{3}}{2} \)
Формулы преобразования суммы тригонометрических функций в произведение
Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса:
\(\ \sin \alpha+\sin \beta=2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \)
\(\ \sin \alpha-\sin \beta=2 \sin \frac{\alpha-\beta}{2} \cos \frac{\alpha+\beta}{2} \)
\(\ \cos \alpha+\cos \beta=2 \cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \)
\(\ \cos \alpha-\cos \beta=-2 \sin \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2} \)
\(\ \operatorname{tg} \alpha+\operatorname{tg} \beta=\frac{\sin (\alpha+\beta)}{\cos \alpha \cos \beta} \)
\(\ \operatorname{tg} \alpha-\operatorname{tg} \beta=\frac{\sin (\alpha-\beta)}{\cos \alpha \cos \beta} \)
\(\ \operatorname{ctg} \alpha+\operatorname{ctg} \beta=\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta} \)
\(\ \operatorname{ctg} \alpha-\operatorname{ctg} \beta=-\frac{\sin (\alpha-\beta)}{\sin \alpha \sin \beta}=\frac{\sin (\beta-\alpha)}{\sin \alpha \sin \beta} \)
\(\ \operatorname{tg} \alpha+\operatorname{ctg} \alpha=\frac{2}{\sin 2 \alpha} \)
\(\ \operatorname{tg} \alpha+\operatorname{ctg} \alpha=-2 \operatorname{ctg} 2 \alpha \)
\(\ \operatorname{tg} \alpha+\operatorname{ctg} \beta=\frac{\cos (\alpha-\beta)}{\cos \alpha \sin \beta} \)
\(\ \operatorname{tg} \alpha-\operatorname{ctg} \beta=-\frac{\cos (\alpha+\beta)}{\cos \alpha \sin \beta} \)
\(\ \sin \alpha+\sin 3 \alpha+\ldots+\sin (2 n-1) \alpha=\sin n \alpha, n \in Z \)
\(\ \cos \alpha+\cos 3 \alpha+\ldots+\cos (2 n-1) \alpha=\cos n \alpha, n \in Z \)
Формулы для разложения тригонометрических выражений на множители.
ПРИМЕР
Разложить на множители \(\ \sin 2 \alpha+\sin \alpha \)
Применим формулу «сумма синусов»:
\(\ \sin \alpha+\sin \beta=2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \)
Тогда
\(\ \sin 2 \alpha+\sin \alpha=2 \sin \frac{2 \alpha+\alpha}{2} \cos \frac{2 \alpha-\alpha}{2}=2 \sin \frac{3 \alpha}{2} \cos \frac{\alpha}{2} \)
\(\ \sin 2 \alpha+\sin \alpha=2 \sin \frac{3 \alpha}{2} \cos \frac{\alpha}{2} \)
Формулы преобразования произведения тригонометрических функций в сумму
Эти формулы получаются из сложения/вычитания соответствующих формул сложения и вычитания аргументов и дальнейшего упрощения:
\(\ \sin \alpha \sin \beta=\frac{\cos (\alpha-\beta)-\cos (\alpha+\beta)}{2} \)
\(\ \sin \alpha \cos \beta=\frac{\sin (\alpha+\beta)+\sin (\alpha-\beta)}{2} \)
\(\ \cos \alpha \cos \beta=\frac{\cos (\alpha-\beta)+\cos (\alpha+\beta)}{2} \)
Используются при тригонометрических преобразованиях.
{2} \beta}&\\ \hline
\end{array}
\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Разность кубов Сумма кубов Куб разности Куб суммы
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
Тригонометричні перетворення | Математика, логіка, інтелект
Тригонометричні формули (або тригонометричні тотожності) — математичні вирази для тригонометричних функцій,
які виконуються при всіх значеннях аргумента.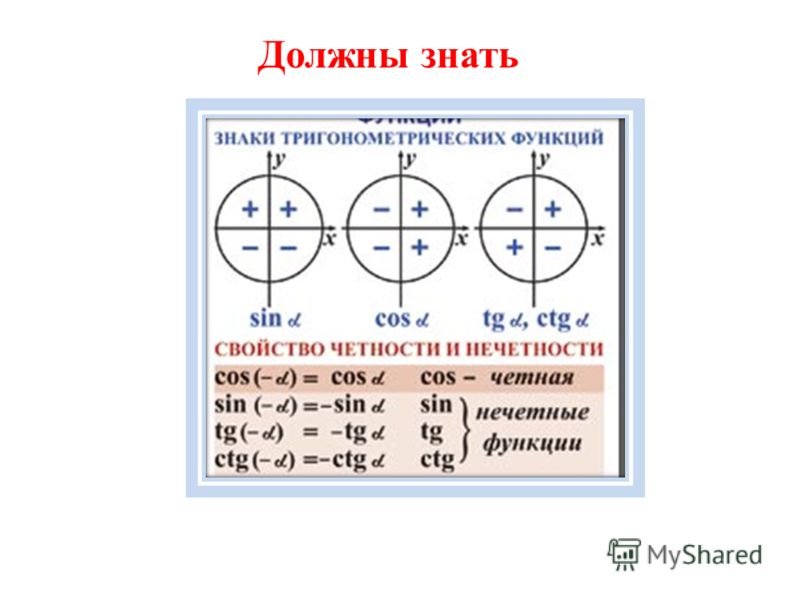
{2} \alpha}, ~\alpha \ne \pi k\]
Формули додавання
\[\sin(\alpha + \beta) = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta\]
\[\sin(\alpha — \beta) = \sin \alpha \cdot \cos \beta — \cos \alpha \cdot \sin \beta\]
\[\cos(\alpha + \beta) = \cos \alpha \cdot \cos \beta — sin \alpha \cdot \sin \beta\]
\[\cos(\alpha — \beta) = \cos \alpha \cdot \cos \beta + sin \alpha \cdot \sin \beta\]
\[\operatorname{tg}(\alpha + \beta) = \frac{\operatorname{tg} \alpha + \operatorname{tg} \beta} {1 — \operatorname{tg} \alpha \cdot \operatorname{tg} \beta}\]
\[\operatorname{tg}(\alpha — \beta) = \frac{\operatorname{tg} \alpha — \operatorname{tg} \beta}{1 + \operatorname{tg} \alpha \cdot \operatorname{tg} \beta}, ~\alpha, ~\beta, ~\alpha — \beta \ne \frac{\pi}{2} + \pi k, k\in \mathbb{Z}\]
Формули подвійного аргументу
\[\sin 2\alpha = 2\sin\alpha \cdot \cos \alpha\]
\[\cos 2\alpha = \cos^{2} \alpha — sin^{2} \alpha = 2\cos^{2} \alpha — 1 = 1 — 2\sin^{2} \alpha\]
\[\operatorname{tg} 2\alpha = \frac{2\operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha }\]
Формули половинного аргументу
\[\sin^{2} \frac{\alpha}{2} = \frac{1-\cos \alpha}{2}\]
\[\cos^{2} \frac{\alpha}{2} = \frac{1+\cos \alpha}{2}\]
\[\operatorname{tg} \frac{\alpha}{2} = \frac{\sin \alpha}{1+\cos \alpha} = \frac{1-\cos \alpha}{\sin \alpha}, ~\alpha \ne \pi + 2 \pi k, k\in \mathbb{Z}\]
Формули перетворення суми в добуток
\[\sin \alpha + \sin \beta = 2\sin\Big(\frac{\alpha + \beta}{2}\Big) \cdot \cos\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\sin \alpha — \sin \beta = 2\cos\Big(\frac{\alpha + \beta}{2}\Big) \cdot \sin\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\cos \alpha + \cos \beta = 2\cos\Big(\frac{\alpha + \beta}{2}\Big) \cdot \cos\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\cos \alpha — \cos \beta = — 2\sin\Big(\frac{\alpha + \beta}{2}\Big) \cdot \sin\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\operatorname{tg} \alpha + \operatorname{tg} \beta = \frac{\sin( \alpha + \beta )}{\cos \alpha \cdot \cos \beta}\]
\[\operatorname{tg} \alpha — \operatorname{tg} \beta = \frac{\sin(\alpha — \beta)}{\cos \alpha \cdot \cos \beta}, ~\alpha, \beta \ne \frac{\pi}{2} + \pi k, k\in \mathbb{Z}\]
Формули перетворення добутку в суму
\[\sin \alpha \cdot \sin \beta = \frac{\cos(\alpha — \beta) — \cos(\alpha + \beta )}{2}\]
\[\cos \alpha \cdot \cos \beta = \frac{\cos(\alpha — \beta) + \cos(\alpha + \beta )}{2}\]
\[\sin \alpha \cdot \cos \beta = \frac{\sin(\alpha — \beta) + \sin(\alpha + \beta )}{2}\]
Співвідношення між \(\sin\alpha\), \(\cos\alpha\) і \(\operatorname{tg}\frac{\alpha}{2}\)
\[\sin \alpha = \frac{ 2\operatorname{tg}\large\frac{\alpha}{2} }{ 1+\operatorname{tg}^{2}\large\frac{\alpha}{2} }, ~\alpha \ne (2k+1) \pi\]
\[\cos \alpha = \frac{ 1-\operatorname{tg}^{2}\large\frac{\alpha}{2} }{ 1+\operatorname{tg}^{2}\large\frac{\alpha}{2} }, ~\alpha \ne (2k+1) \pi\]
Додаткові формули
\[\sin 3\alpha = 3\sin \alpha — 4\sin^{3}\alpha\]
\[\cos 3\alpha = 4\cos^{3}\alpha — 3\cos \alpha\]
Формули зведення
| \(x\) | \(\frac{\pi}{2} + \alpha\) | \(\pi + \alpha\) | \(\frac{3\pi}{2} + \alpha\) | \(-\alpha\) | \(\frac{\pi}{2} — \alpha\) | \(\pi — \alpha\) | \(\frac{3\pi}{2} — \alpha\) |
| \(\sin x\) | \(\cos \alpha\) | \(-\sin \alpha\) | \(-\cos \alpha\) | \(-\sin \alpha\) | \(\cos \alpha\) | \(\sin \alpha\) | \(-\cos \alpha\) |
| \(\cos x\) | \(-\sin \alpha\) | \(-\cos \alpha\) | \(\sin \alpha\) | \(\cos \alpha\) | \(\sin \alpha\) | \(-\cos \alpha\) | \(-\sin \alpha\) |
| \(\operatorname{tg}x\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) |
| \(\operatorname{ctg}x\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) |
Значення тригонометричних функцій деяких кутів
| \(\alpha\) | \(0 (0^{\circ})\) | \(\frac{\pi}{6} (30^{\circ})\) | \(\frac{\pi}{4} (45^{\circ})\) | \(\frac{\pi}{3} (60^{\circ})\) | \(\frac{\pi}{2} (90^{\circ})\) |
| \(\sin \alpha\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
| \(\cos \alpha\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) |
| \(\operatorname{tg} \alpha\) | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | Не існує |
| \(\operatorname{ctg} \alpha\) | Не існує | \(\sqrt{3}\) | \(1\) | \(\frac{\sqrt{3}}{3}\) | \(0\) |
| \(\alpha\) | \(\pi (180^{\circ})\) | \(\frac{3\pi}{2} (270^{\circ})\) | \(2 \pi (360^{\circ})\) |
| \(\sin \alpha\) | \(0\) | \(-1\) | \(0\) |
| \(\cos \alpha\) | \(-1\) | \(0\) | \(1\) |
| \(\operatorname{tg} \alpha\) | \(0\) | Не існує | \(0\) |
| \(\operatorname{ctg} \alpha\) | Не існує | \(0\) | Не існує |
Значення тригонометричної функції
| sincostgctg | \(\Big(\) | градусирадіани | \(\Big)\) |
Значення тригонометричної функції будь-якого гострого кута
| sincostgctg | \(\Big(\) | ° ′ | \(\Big)\) |
Обчислення кута за тригонометричною функцією
Основные формулы тригонометрии для ЕГЭ — Видеоуроки по математике и физике для ЕГЭ и ОГЭ
Содержание
- Прагматическая тригонометрия — Введение
- Основные формулы тригонометрии для ЕГЭ
- Первая группа выводимых формул
- Вторая группа выводимых формул
- Третья группа выводимых формул
- Формула дополнительного аргумента: частные случаи
- Формула дополнительного аргумента: общий случай
- Список формул.
Что дальше? - Решение неравенств
Что дальше?
В этой статье и видео мы рассматриваем основные формулы тригонометрии, которые нужны нам для решения задач ЕГЭ, включая 13, 15(редко) и 18.
0 Тригонометрическая окружность и табличные значения тригонометрических функций
Тригонометрическая окружность — окружность радиуса единица, с центром в начале координат прямоугольной (декартовой) системы координат. То есть, тригонометрическая окружность представляет из себя два объекта — саму окружность и сопутствующие ей оси координат. На оси абсцисс, откладываются значения $sin \alpha$, а на оси ординат откладываются значения $cos \alpha$.
Подробное видео-объяснение тригонометрической окружности:
Угол $ \alpha $ отмеряется по окружности, как угол меджду неподвижным горизонтальным радиусом, и подвижным радиусом, который может свободно вращаться по всей окружности.
Направление вращения против часовой стрелки — положительное, по часовой стрелке — отрицательное. То есть, любой поворот подвижного радиуса против часовой стрелки даст вам положительный угол, а против — отрицательный.
Для быстрого и безошибочного решения задач, связанных с тригонометрией, и, в частности, тригонометрических задач ЕГЭ, нужно уметь отмечать на окружности стандартные углы. Я назвал стандартными углы, которые чаще называют табличными — такие углы, значения синуса, косинуса и тангенса которых нужно помнить. Они перечислены в следующей минимальной таблице:
| Угол $$ (\alpha) $$ | $$ sin \alpha $$ | $$ cos \alpha $$ | $$ tg \alpha $$ |
| 0 | 0 | 1 | 0 |
| $$ \frac {\pi} {6} $$ | $$ \frac {1} {2} $$ | $$ \frac {\sqrt{3}} {2} $$ | $$ \frac {1} {\sqrt{3}} $$ |
| $$ \frac {\pi} {4} $$ | $$ \frac {\sqrt{2}} {2} $$ | $$ \frac {\sqrt{2}} {2} $$ | 1 |
| $$ \frac {\pi} {3} $$ | $$ \frac {\sqrt{3}} {2} $$ | $$ \frac {1} {2} $$ | $$ {\sqrt{3}} $$ |
| $$ \frac {\pi} {2} $$ | 1 | 0 | не существует |
Эта таблица минимальна в том смысле, что это самый необходимый для запоминания минимум.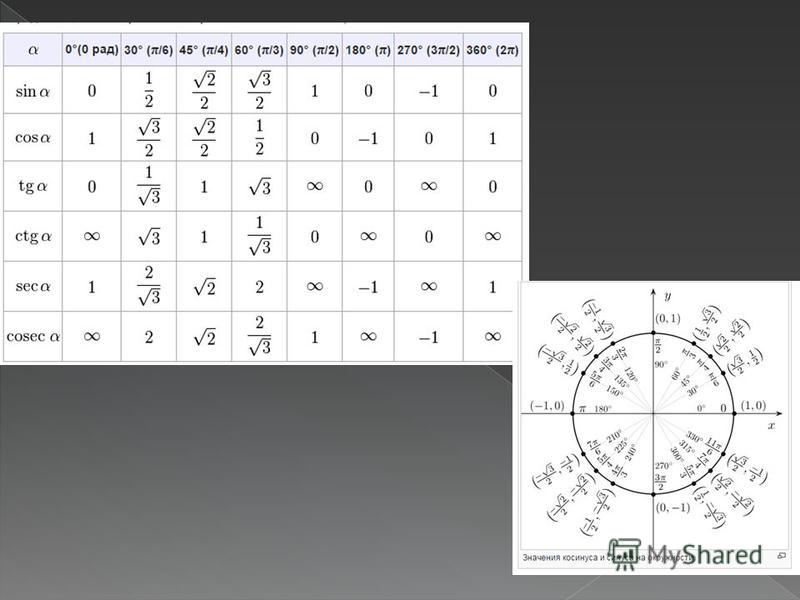
Как видите, перечисленные в первом столбце углы расположены в первой координатной четверти. Остальные углы, соответствующие табличным значениям функций и расположенные в других четвертях координатной плоскости, легко увидеть на тригонометрической окружности.
Вот неплохая интерактивная тригонометрическая окружность. С ее помощью можно потренировать табличные углы и значения тригонометрических функций. Можно поставить себе на смартфон специальное приложение, они есть под любую операционную систему.
Для того, чтобы выучить и закрепить табличные значения тригонометрических функций, на моем сайте дистанционного обучения для вас открыты тесты по основам тригонометрии. Вы можете войти, как гость, и проделать все тесты. Если вы хотите, чтобы система запомнила ваши результаты, и вам в личном кабинете была доступна статистика — зарегистрируйтесь, это не потребует больших усилий.
1 Теорема Пифагора и основное тригонометрическое тождество.
Я еще не встречал школьника, не знающего теорему Пифагора.
2 \alpha = 1 $$
2 Синус и косинус суммы и разности
Это — основные формулы. Для любознательных в приложении приведен простой геометрический вывод этих формул. Формул не четыре, а фактически две, потому что формула с минусом получается из формулы с плюсом, если учесть свойства нечетности синуса и четности косинуса. Но можно и запомнить четыре формулы.
$$ sin ( \alpha +\beta)=sin\, \alpha \cdot cos\, \beta + cos\, \alpha \cdot sin\, \beta $$
$$ sin ( \alpha — \beta)=sin\, \alpha \cdot cos\, \beta — cos \,\alpha\cdot sin\, \beta $$
$$ cos ( \alpha +\beta)=cos \,\alpha \cdot cos \,\beta — sin\, \alpha\cdot sin\, \beta $$
$$ cos ( \alpha — \beta)=cos\, \alpha \cdot cos\, \beta + sin\, \alpha \cdot sin\, \beta $$
Вторые формулы каждой пары получаются из первых с учетом
$$ sin ( — \alpha )= -sin \, \alpha $$
$$ cos ( — \alpha )= cos \, \alpha $$
То есть, синус — нечетная функция ( $f(-x)=-f(x)$), а косинус — четная ($f(-x)=f(x)$
В Приложении приведено простое геометрическое доказательство формул сложения.
2 \alpha} $$
4 Это весь необходимый минимум
Запомните формулы из пункта 2 и научитесь выводить формулы из остальных пунктов данной статьи.
В дальнейшем мы выведем из этого набора формул все остальные.
Удачи на экзаменах!
ДВИ МГУ по математике, ЕГЭ по математике, математика, тригонометрия
1,420 total views, 1 views today
Поделиться ссылкой:
Тригонометрические формулы — Примеры | Список тригонометрических формул
Тригонометрические формулы представляют собой наборы различных формул, включающих тригонометрические тождества, используемые для решения задач, основанных на сторонах и углах прямоугольного треугольника. Эти формулы тригонометрии включают тригонометрические функции, такие как синус, косинус, тангенс, косеканс, секанс, котангенс для заданных углов. Давайте подробно изучим эти формулы, включающие тождества Пифагора, тождества произведения, тождества кофункций (углы сдвига), тождества суммы и разности, тождества двойного угла, тождества половинного угла и т.
д., в следующих разделах.
| 1. | Список формул тригонометрии |
| 2. | Основные формулы тригонометрии |
| 3. | Тригонометрические формулы, включающие взаимные тождества |
| 4. | Таблица тригонометрических соотношений |
| 5. | Тригонометрические формулы, включающие периодические тождества (в радианах) |
| 6. | Тригонометрические формулы, включающие тождества кофункций (в градусах) |
| 7. | Тригонометрические формулы, включающие тождества суммы и разности |
| 8. | Множественные и субмножественные углы |
| 9. | Сумма и произведение тождеств |
| 10. | Формулы обратной тригонометрии |
| 11. | Тригонометрические формулы, использующие законы синусов и косинусов |
12. | Часто задаваемые вопросы по формулам тригонометрии |
Список формул тригонометрии
Тригонометрические формулы можно разделить на различные категории в зависимости от задействованных тригонометрических тождеств. Давайте посмотрим на приведенные ниже наборы различных формул тригонометрии.
- Формулы основных тригонометрических соотношений: это формулы тригонометрии, относящиеся к основным тригонометрическим соотношениям sin, cos, tan и т. д.
- Взаимные тождества: сюда входят формулы тригонометрии, имеющие дело с обратными отношениями между отношениями триггеров.
- Таблица тригонометрических соотношений: Значения тригонометрии представлены для стандартных углов в таблице тригонометрии.
- Периодические тождества: они включают формулы тригонометрии, которые помогают найти значения тригонометрических функций для сдвига углов на π/2, π, 2π и т. д.
- Тождества кофункций: Тригонометрические формулы для тождеств кофункций изображают взаимосвязи между тригонометрическими функциями.
- Тождества суммы и разности: Эти тригонометрические формулы используются для нахождения значения тригонометрической функции для суммы или разности углов.
- Половинные, двойные и тройные тождества: Эти тригонометрические формулы включают значения тригонометрических функций для половинных, двойных или тройных углов.
- Идентичности суммы произведений: эти тригонометрические формулы используются для представления произведения тригонометрических функций в виде их суммы или наоборот.
- Формулы обратной тригонометрии: формулы обратной тригонометрии включают формулы, связанные с обратными тригонометрическими функциями, такими как обратный синус, обратный косинус и т. д.
- Закон синусов и закон косинусов
Некоторые основные формулы тригонометрии можно увидеть на изображении ниже. Рассмотрим их подробно в следующих разделах.
Основные формулы тригонометрии
Основные формулы тригонометрии используются для нахождения соотношения тригонометрических соотношений и отношения соответствующих сторон прямоугольного треугольника.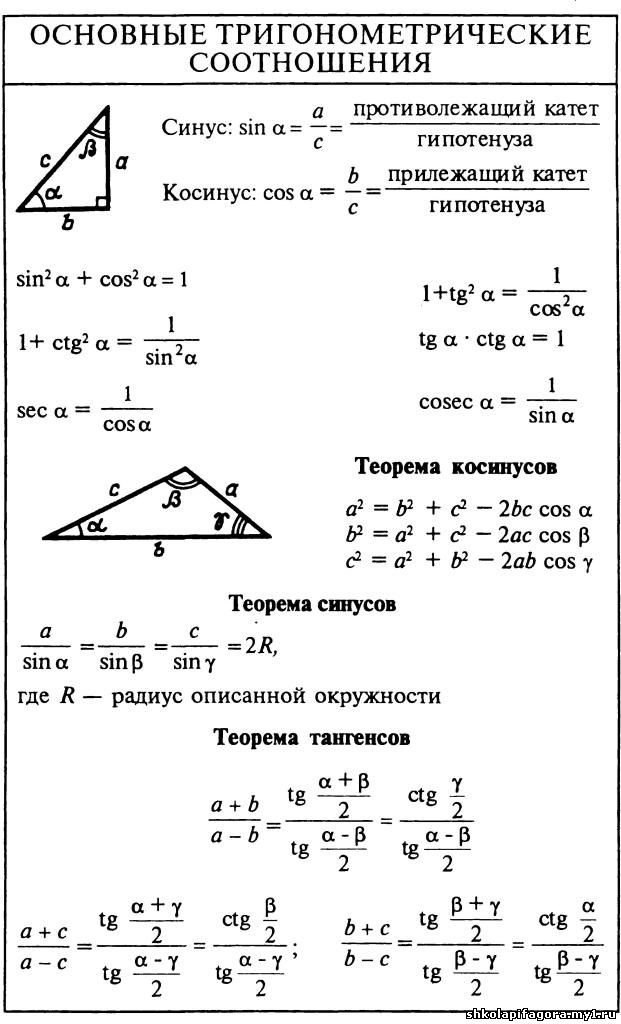
В тригонометрии используются шесть основных тригонометрических отношений, также называемых тригонометрическими функциями: синус, косинус, секанс, косеканс, тангенс и котангенс, которые записываются как sin, cos, sec, csc, tan, cot. Тригонометрические функции и тождества выводятся с использованием прямоугольного треугольника в качестве эталона. Мы можем узнать значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, учитывая размеры прямоугольного треугольника, используя формулы тригонометрии, как,
Формулы тригонометрических соотношений
- sin θ = Перпендикуляр/Гипотенуза
- cos θ = Основание/Гипотенуза
- тангенс θ = Перпендикуляр/Основание
- с θ = гипотенуза/основание
- cosec θ = гипотенуза/перпендикуляр
- кроватка θ = основание/перпендикуляр
Тригонометрические формулы, включающие взаимные тождества
Косеканс, секанс и котангенс являются обратными величинами основных тригонометрических отношений синуса, косинуса и тангенса.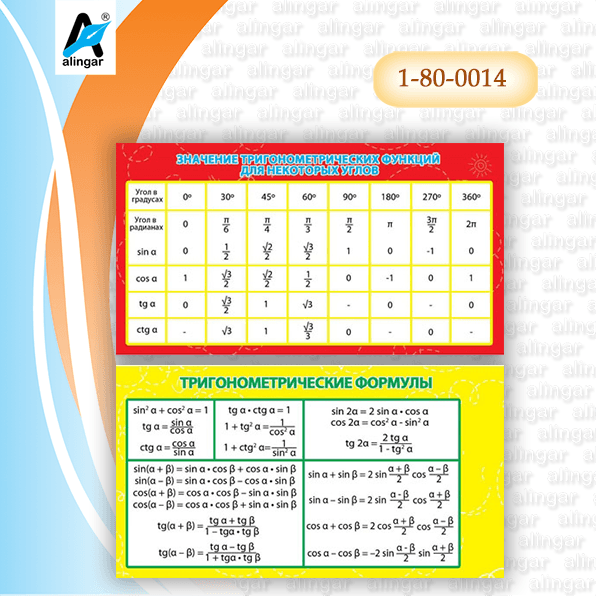
Все взаимные тождества также получены с использованием прямоугольного треугольника в качестве эталона. Эти взаимные тригонометрические тождества выводятся с использованием тригонометрических функций. Формулы тригонометрии на взаимных тождествах, приведенные ниже, часто используются для упрощения тригонометрических задач.
- cosec θ = 1/sin θ
- сек θ = 1/cos θ
- раскладушка θ = 1/загар θ
- sin θ = 1/косек θ
- потому что θ = 1/сек θ
- загар θ = 1/кот θ
Таблица тригонометрических соотношений
Вот таблица тригонометрических формул для углов, которые обычно используются для решения тригонометрических задач. Таблица тригонометрических соотношений помогает найти значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 9°.0°.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Углы (в радианах) | 0° | №/6 | №/4 | №/3 | №/2 | № | 3π/2 | 2π |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| желто-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Тригонометрические формулы, включающие периодические тождества (в радианах)
Тригонометрические формулы, включающие периодические тождества, используются для сдвига углов на π/2, π, 2π и т.
д. Все тригонометрические тождества цикличны по своей природе, что означает, что они повторяются через точку. Этот период различен для разных формул тригонометрии периодических тождеств. Например, tan 30° = tan 210°, но это неверно для cos 30° и cos 210°. Вы можете обратиться к формулам тригонометрии, приведенным ниже, чтобы проверить периодичность функций синуса и косинуса.
Первый квадрант:
- sin (π/2 – θ) = cos θ
- cos (π/2 – θ) = sin θ
- sin (π/2 + θ) = cos θ
- cos (π/2 + θ) = – sin θ
Второй квадрант:
- sin (3π/2 – θ) = – cos θ
- cos (3π/2 – θ) = – sin θ
- sin (3π/2 + θ) = – cos θ
- потому что (3π/2 + θ) = грех θ
Третий квадрант:
- sin (π – θ) = sin θ
- потому что (π – θ) = – потому что θ
- грех (π + θ) = – грех θ
- , потому что (π + θ) = – потому что θ
Четвертый квадрант:
- sin (2π – θ) = – sin θ
- потому что (2π — θ) = потому что θ
- грех (2π + θ) = грех θ
- , потому что (2π + θ) = потому что θ
Тригонометрические формулы, включающие тождества кофункций (в градусах)
Тригонометрические формулы тождеств кофункций обеспечивают взаимосвязь между различными тригонометрическими функциями.
Формулы тригонометрии кофункций представлены в градусах ниже:
- sin(90° − x) = cos x
- потому что (90 ° — х) = грех х
- загар (90° — x) = кроватка x
- кроватка(90° — х) = загар х
- сек(90° — х) = косек х
- косек(90° — х) = сек х
Тригонометрические формулы, включающие тождества суммы и разности
Тождества суммы и разности включают тригонометрические формулы sin(x + y), cos(x — y), cot(x + y) и т. д.
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) — sin(x)sin(y)
- tan(x + y) = (tan x + tan y)/(1 — tan x • tan y)
- sin(x – y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- тангенс (х — у) = (тангенс х — тангенс у) / (1 + тангенс х • тангенс у)
Тригонометрические формулы для кратных и дольных углов
Тригонометрические формулы для кратных и дольных углов могут быть использованы для расчета значения тригонометрических функций для половинного угла, двойного угла, тройного угла и т.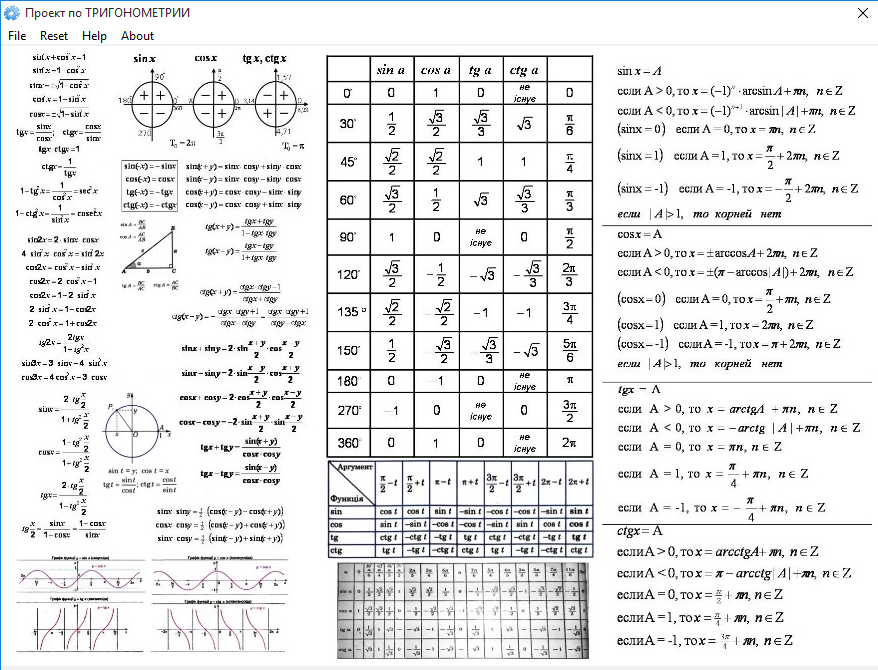
д.
Тригонометрические формулы, включающие тождества половин угла
Половина угла x представлена в нескольких приведенных ниже тригонометрических формулах.
sin (x/2) = ±√[(1 — cos x)/2]
cos (x/2) = ± √[(1 + cos x)/2]
tan (x/2) = ±√[(1 — cos x)/(1 + cos x)]
или, tan (x/2) = ±√[(1 — cos x)(1 — cos x)/(1 + cos x) )(1 — cos x)]
tan (x/2) = ±√[(1 — cos x) 2 /(1 — cos 2 x)]
⇒ tan (x/2) = (1 — cos x)/sin x
Тригонометрические формулы, включающие тождества двойного угла
Двойной угол x представлен несколькими приведенными ниже тригонометрическими формулами.
- sin (2x) = 2sin(x) • cos(x) = [2tan x/(1 + tan 2 x)]
- cos (2x) = cos 2 (x) — sin 2 (x) = [(1 — tan 2 x)/(1 + tan 2 x)]
- cos (2x) = 2cos 2 (x) — 1 = 1 — 2sin 2 (x)
- тангенс (2x) = [2tan(x)]/ [1 — тангенс 2 (х)]
- сек (2x) = сек 2 х/(2 — сек 2 х)
- косек (2x) = (сек х • косек х)/2
Тригонометрические формулы, включающие тождества тройного угла
Тройка угла x представлена с помощью нескольких приведенных ниже тригонометрических формул.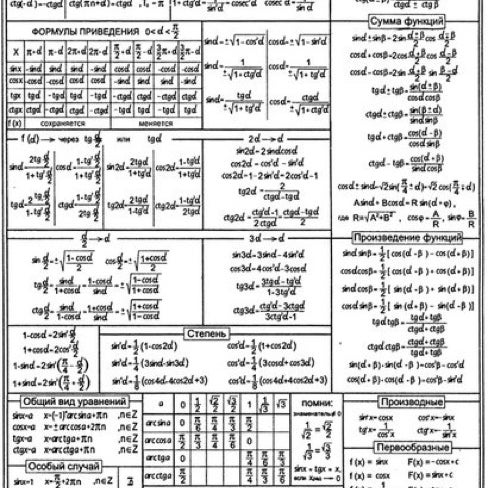
- sin 3x = 3sin x — 4sin 3 x
- cos 3x = 4 cos 3 x — 3cos x
- tan 3x = [3tanx — tan 3 x]/[1 — 3tan 2 х]
Формулы тригонометрии. Тождества суммы и произведения
Тригонометрические формулы для суммы или произведения тождеств используются для представления суммы любых двух тригонометрических функций в форме их произведения или наоборот.
Тригонометрические формулы, включающие тождества продуктов
- sinx⋅cosy = [sin(x + y) + sin(x − y)]/2
- cosx⋅cosy = [cos(x + y) + cos(x − y)]/2
- sinx⋅siny = [cos(x − y) − cos(x + y)]/2
Тригонометрические формулы, включающие тождества суммы и произведения
Комбинация двух острых углов A и B может быть представлена через тригонометрические отношения в приведенных ниже тригонометрических формулах.
- sinx + siny = 2[sin((x + y)/2)cos((x − y)/2)]
- sinx − siny = 2[cos((x + y)/2) sin((x − y)/2)]
- cosx + cosy = 2[cos((x + y)/2)cos((x − y)/2)]
- cosx − уютный = −2[sin((x + y)/2)sin((x − y)/2)]
Формулы обратной тригонометрии
Используя формулы обратной тригонометрии, тригонометрические отношения инвертируются для создания обратных тригонометрических функций, таких как sin θ = x и θ = sin −1 x.
Здесь x может иметь значения в целых числах, десятичных дробях, дробях и показателях степени.
- sin -1 (-x) = -sin -1 x
- , потому что -1 (-x) = π — потому что -1 x
- желтовато-коричневый -1 (-x) = -tan -1 x
- cosec -1 (-x) = -cosec -1 x
- сек -1 (-x) = π — сек -1 x
- детская кроватка -1 (-x) = π — детская кроватка -1 x
Тригонометрические формулы, использующие законы синусов и косинусов
Закон синуса: Закон синуса и закон косинуса определяют отношение между сторонами и углами треугольника. Закон синусов дает отношение сторон и угла, противолежащего стороне. В качестве примера берется отношение стороны «а» и противолежащего ей угла «А».
(sin A)/a = (sin B)/b = (sin C)/c
Закон косинуса: Закон косинуса помогает найти длину стороны для заданных длин двух других сторон и включенный угол.
Например, длину «а» можно найти с помощью двух других сторон «b» и «с» и прилежащего к ним угла «А».
- a 2 = b 2 + c 2 — 2bc cosA
- b 2 = a 2 + c 2 — 2ac cosB
- с 2 = а 2 + b 2 — 2ab cosC
где, a, b, c — длины сторон треугольника, а A, B, C — углы треугольника.
Связанные темы
- Грех Кос Тан
- Тригонометрические тождества
- Функции косеканса, секанса и котангенса
- Тригонометрические соотношения
- Тригонометрические формулы для класса 10
- Тригонометрический калькулятор
Примеры использования формул тригонометрии
Пример 1: Рэйчел дано тригонометрическое соотношение тангенса θ = 5/12. Помогите Рэйчел найти тригонометрическое отношение cosec θ, используя формулы тригонометрии.
Решение:
TAN θ = перпендикуляр/ основа = 5/12
Перпендикуляр = 5 и основание = 12
Гипотеназа 2 = перпендикулярно 2 + база 2 2 + базовый0002 гипотенуза 2 = 5 2 + 12 2
Гипотенуза 2 = 25 + 144
Hypotenus
cosec θ = гипотенуза/перпендикуляр = 13/5
Ответ: Используя формулы тригонометрии, cosec θ = 13/5
Пример 2: В рамках задания Сэмюэль должен найти значение Sin 15º, используя формулы тригонометрии. Как мы можем помочь Самуэлю найти ценность?
Решение:sin 15°
= sin (45° — 30°)
= sin 45°cos 30° — cos 45°sin 30° √2) × (1/2)] = (√3 — 1)/2√2
Ответ: sin 15° = (√3 — 1)/2√2
Пример 3: Если sin θcos θ = 5, найдите значение (sin θ + cos θ) 2 , используя формулы тригонометрии.
Решение:
(sin θ + cos θ) 2
= sin 2 θ + cos 2 θ + 2sinθcosθ
= (1) + 2 (5) = 1 + 10 = 11
Ответ: (sin θ + cos θ) 2 6666 ( (sin θ + cos θ) = 11
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по тригонометрической формуле
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по тригонометрическим формулам
Что такое тригонометрические формулы?
Тригонометрические формулы используются для решения задач, основанных на сторонах и углах прямоугольного треугольника, с использованием различных тригонометрических тождеств.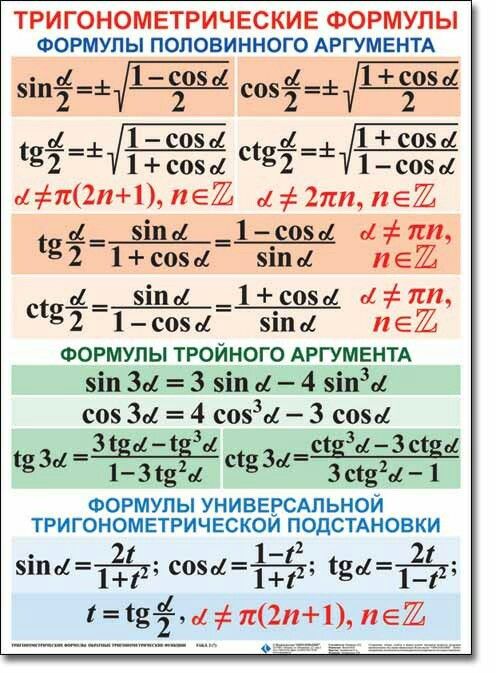
Эти формулы можно использовать для вычисления тригонометрических отношений (также называемых тригонометрическими функциями), sin, cos, tan, csc, sec и cot.
Что такое Основная формула тригонометрии?
Основные формулы тригонометрии включают представление основных тригонометрических соотношений в терминах отношения соответствующих сторон прямоугольного треугольника. Они задаются следующим образом: sin θ = Противоположная сторона/Гипотенуза, cos θ = Прилегающая сторона/Гипотенуза, tan θ = Противоположная сторона/Прилегающая сторона.
Что такое формулы тригонометрических соотношений?
В тригонометрии используются три основные функции: синус, косинус и тангенс. Формулы тригонометрических соотношений имеют следующий вид:
- Функция синуса: sin(θ) = противоположность / гипотенуза
- Функция косинуса: cos(θ) = смежная / гипотенуза
- Функция касания: tan(θ) = Противоположный / Смежный
Что такое тригонометрические формулы для четных и нечетных тождеств?
Тригонометрические формулы, включающие четные и нечетные тождества, задаются следующим образом:
- sin(–x) = –sin x
- cos(-x) = cosx
- тангенс(–х) = –тангенс х
- csc (–x) = –csc x
- сек (-x) = сек х
- детская кроватка (-x) = -кроватка x
Какие формулы тригонометрии включают пифагорейские тождества?
Три фундаментальные формулы тригонометрии, включающие пифагорейские тождества, задаются как
- sin 2 A + cos 2 A = 1
- 1 + тангенс 2 А = сек 2 А
- 1 + детская кроватка 2 А = косек 2 А
К какому треугольнику применимы тригонометрические формулы?
Тригонометрические формулы применимы к прямоугольным треугольникам.
Эти тригонометрические формулы представляют собой тригонометрические отношения с точки зрения отношения соответствующих сторон прямоугольного треугольника.
Что такое формулы тригонометрии сложения?
Тригонометрические формулы для тригонометрических соотношений, когда углы складываются, даются следующим образом:
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) — sin(x)sin(y)
- tan(x + y) = (tan x + tan y)/(1 — tan x • tan y)
Как легко запомнить формулы тригонометрии?
Уловка для изучения основных формул тригонометрии заключается в использовании мнемоники «SOHCAHTOA», которую можно использовать для запоминания тригонометрических соотношений, например,
.
SOH: синус = противоположность / гипотенуза
CAH: косинус = смежный / гипотенуза
TOA: Касательная = Противоположная / Смежная
Что такое тригонометрическая формула sin 3x?
Тригонометрическая формула, sin 3x — это синус трех углов прямоугольного треугольника, он выражается как: sin 3x = 3sin x — 4sin 3 x.
Тригонометрические формулы и тождества — полный список
Последнее обновление Teachoo: 8 октября 2021 г.
В формулах тригонометрии мы узнаем
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, потому что, загар в разных квадрантах
радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется после 2π
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Закон синуса
Закон косинуса
Что такое обратные тригонометрические функции?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
- Подстановки обратной тригонометрии
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Чтобы узнать знак греха, потому что, загар в разных квадрантах,
мы помним
А дд → С угар → Т о → С кофе
Представление в виде таблицы
Квадрант я | Квадрант II | Квадрант III | Квадрант IV | |
грех | + | + | – | – |
потому что | + | – | – | – |
загар | + | – | + | – |
радианы
Радианная мера = π/180 × градусная мера
Также,
1 градус = 60 минут
то есть 1° = 60’
1 минута = 60 секунд
то есть 1’ = 60’’
Отрицательные углы (четно-нечетные тождества)
грех (–х) = – грех х
соз (–х) = соз х
тангенс (–x) = – тангенс х
сек (–x) = сек х
cosec (–x) = – cosec x
детская кроватка (–x) = – детская кроватка x
Значение sin, cos, tan повторяется после 2π
грех (2π + х) = грех х
потому что (2π + х) = потому что х
загар (2π + х) = загар х
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
sin (π/2 – x) = cos x | потому что (π / 2 — х) = грех х |
грех (π/2 + х) = потому что х | cos (π/2 + x) = – sin x |
sin (3π/2 – x) = – cos x | cos (3π/2 – x) = – sin x |
sin (3π/2 + x) = – cos x | потому что (3π/2 + х) = грех х |
грех (π — х) = грех х | cos (π – x) = – cos x |
грех (π + х) = – грех х | cos (π + x) = – cos x |
грех (2π – х) = – грех х | потому что (2π — х) = потому что х |
грех (2π + х) = грех х | потому что (2π + х) = потому что х |
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Продукт для суммирования тождеств
2 cosx cosy = cos (x + y) + cos(x — y)
-2 sinx siny = cos (x + y) — cos(x — y)
2 sinx cosy = sin (x + y) + sin(x — y)
2 cosx siny = sin (x + y) — sin(x — y)
Закон синуса
Здесь
- A, B, C — вершины Δ ABC
- a — сторона, противоположная A, т. е. BC
- b — сторона, противоположная B, т.е. AC
- c — сторона, противоположная C, т.е. AB
е. BCЗакон косинуса
Так же, как закон синуса, у нас есть закон косинуса
Что такое обратные тригонометрические функции
Если грех θ = х
Затем положить грех на правую сторону
θ = грех -1 Икс
грех -1 х = θ
Таким образом, обратным греху является угол.
Точно так же обратная ко всем функциям тригонометрии угол.
Примечание : Здесь угол измеряется в радианах, а не в градусах.
Итак, у нас есть
грех -1 Икс
потому что -1 Икс
загар -1 Икс
cosec -1 Икс
сек -1 Икс
загар -1 Икс
Область определения и область значений обратных тригонометрических функций
Домен | Диапазон | |
грех -1 | [–1, 1] | [-π/2,π/2] |
потому что -1 | [–1, 1] | [0,π] |
загар -1 | р | (-π/2,π/2) |
cosec -1 | р – (–1, 1) | [π/2,π/2] — {0} |
сек -1 | р – (–1, 1) | [0,π]-{π/2} |
детская кроватка -1 | р | (0, π) |
Формулы обратной тригонометрии
Некоторые формулы обратной тригонометрии:
грех –1 (–x) = – грех -1 Икс
потому что –1 (–x) = π – грех -1 Икс
загар –1 (–x) = – загар -1 Икс
cosec –1 (–x) = – cosec -1 Икс
сек –1 (–x) = – сек -1 Икс
детская кроватка –1 (–x) = π – детская кроватка -1 Икс
Замена обратной тригонометрии
Разрешите все свои сомнения с Teachoo Black (уже доступен новый ежемесячный пакет!)
Присоединяйтесь к Teachoo Black
Тригонометрические формулы для 12-го класса
Тригонометрические формулы для 12-го класса, предоставляемые Vedantu, представляют собой наборы различных формул, использующих тригонометрические тождества, которые используются для решения математических задач на основе сторон и углов прямоугольного треугольника.
Эти формулы тригонометрии для класса 12 включают тригонометрические функции, такие как синус, косинус, тангенс, косеканс, секанс, котангенс для заданных углов. Эти формулы тригонометрии очень полезны для учащихся 12-го класса, которые подробно охватывают тождества Пифагора, тождества произведения, тождества кофункций (углы сдвига), тождества суммы и разности, тождества двойного угла, тождества половинного угла и т. д., чтобы получить хорошие оценки по математике. Экзамен в 12 классе.
Что такое тригонометрия?
Тригонометрия – это изучение взаимосвязей между углами, высотами и длинами треугольников, а также взаимосвязей между различными частями круга и другими геометрическими фигурами. В 12 классе тригонометрии мы изучаем тригонометрию, которая находит свое применение в области астрономии, инженерии, архитектурного проектирования и физики. Тригонометрические формулы для класса 12 содержат все основные тригонометрические тождества, которые могут вызвать некоторые прямые вопросы на конкурсных экзаменах на основе формул.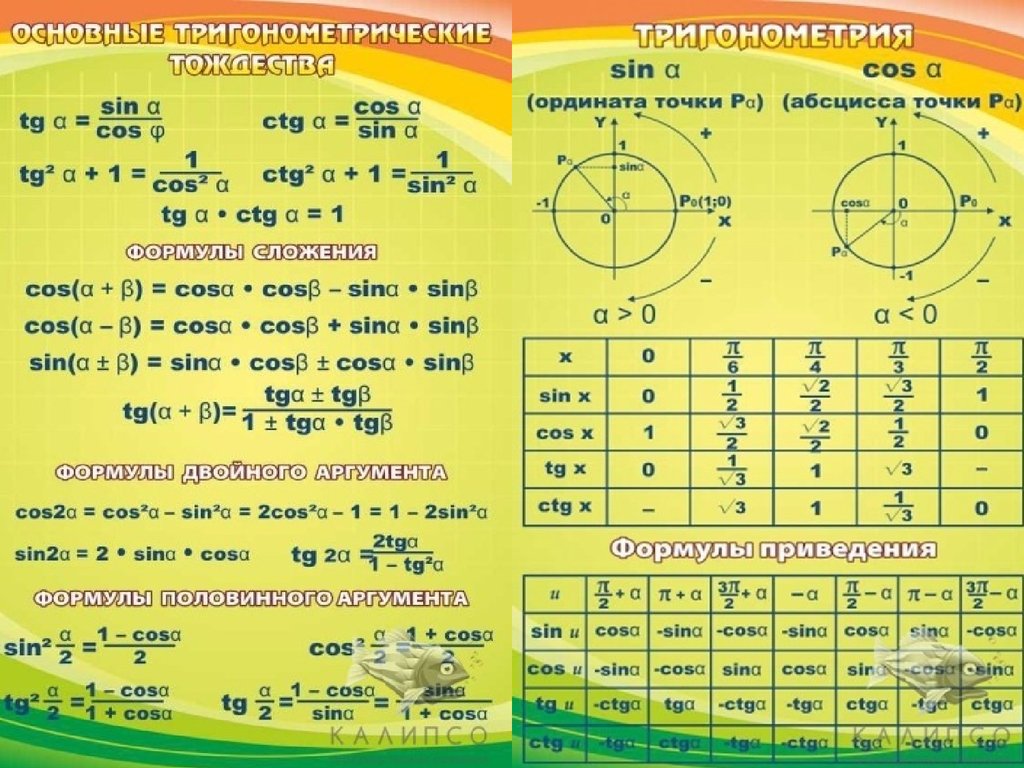
Тригонометрические тождества, приведенные в 12-й формуле тригонометрии, очень полезны и помогают лучше решать задачи. Существует огромное количество областей, в которых используются эти тригонометрические тождества и тригонометрические уравнения.
Разница между тригонометрическими тождествами и тригонометрическими отношениями:
Тригонометрические тождества. Равенства в тригонометрических функциях известны как тригонометрические тождества.
92 \theta — 1} \] \[sinA sinB = \frac{1}{2} \begin{bmatrix} cos(A-B) — cos( A+B) \end{bmatrix}\]
\[cosA cosB = \frac{1}{2} \begin{bmatrix} cos(A-B) + cos(A+B) \end{bmatrix}\ ]
\[sinA cosB = \frac{1}{2} \begin{bmatrix} sin(A+B) + sin(A-B) \end{bmatrix}\]
\[cosA sinB = \frac{1}{2} \begin{bmatrix} cos(A+B) + sin(A-B) \end{bmatrix}\]
\[Sin(\frac{x}{2}) = \pm \sqrt{( \frac{1 — cos(x)} {2} )}\ ]
\[Cos(\frac{x}{2}) = \pm \sqrt{( \frac{ 1+ cos(x)} {2} )}\]
\[Tan( \ frac {x} {2}) = \ pm \ sqrt {\ frac {1 — cos (x)} {1+ cos (x)}} = \ frac {1 — cos (x)} {sin (x) } = \frac{sin(x)}{1 + cos(x)} \]
Слово «Тригонометрия» взято из слова «Мера треугольника».
Преобразование произведений в суммы и разности:
Тождества половинного угла:
Возводя в квадрат приведенные выше тождества, мы можем переформулировать приведенные выше уравнения следующим образом:
9{-1}(x) = arctan(x)\]
Domain and Range:
Function | Domain | Range |
θ = sin — 1 (x) | −1 ≤ x ≤ 1 | — π /2 ≤ θ ≤ π /2 |
θ = cos -1 (x) | ||
θ = cos -1 (x) | −1 ≤ x ≤ 1 | 0 ≤ θ ≤ π |
θ = tan — 1 (x) | −∞ ≤ x ≤ ∞ | — π/ 2 <θ <π/ 2 |
9
211616161616161616161616161616.
Name | Usual Notation | Definition | Domain of x for real number | Range of usual principal values (Radians) | . | − π /2 ≤ y ≤ π/2 | −90⁰ ≤ y ≤ 90⁰ | ||||||||||||||||||||||||||||||||||
arccosine | y=arcos(x) | x=cos(y) | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0⁰ ≤ y ≤ 180⁰ | ||||||||||||||||||||||||||||||||||||
Arctangent | y = Arctan (x) | x = tan (Y) | x = tan (Y) | 9000 | 9000 | 9000 9000 9000 | . | −90⁰ ≤ y ≤ 90⁰ | |||||||||||||||||||||||||||||||||
arccotangent | y=arccot(x) | x=cot(y) | All real числа | 0 ≤ y ≤ π | 0⁰ ≤ y ≤ 180⁰ | ||||||||||||||||||||||||||||||||||||
arcsecant | y=arcsec(x) | x=sec(y) | x ≤ -1 or 1 ≤ x | 0 ≤ y <π/2 или π/2 | 0 ≤ y <90⁰ или 90⁰ | ||||||||||||||||||||||||||||||||||||
ARCCOSECANT | yrcosec. | x=cosec(x) | x ≤ -1 или 1 ≤ x 9{-1}(1) = \frac{\pi}{4} \] Забавные факты |
2 ≤ y ≤ π/2