Виды уравнений и способы их решения
Цели урока:
Обучающие:
- Обобщить знания по всем видам уравнений, подчеркнуть значимость всех способов, применяемых при решении уравнений.
- Активизирование работы учащихся за счет, разнообразных приемов на уроке.
- Проверить теоретические и практические навыки при решении уравнений.
- Заострить внимание на том, что, одно уравнение можно решить несколькими способами
Развивающие:
- Повысить интерес учащихся к предмету, через использование ИКТ.
- Ознакомление учащихся с историческим материалом по теме.
- Развитие мыслительной деятельности при определении вида уравнения и способов его решения.
Воспитательные:
- Воспитать дисциплину на уроке.
- Развитие способности к восприятию прекрасного,
в себе самом, в другом человеке и в окружающем
мире.

Тип урока:
- Урок обобщения и систематизации знаний.
Вид урока:
- Комбинированный.
Материально-техническое оснащение:
- Компьютер
- Экран
- Проектор
- Диск с презентацией темы
Методы и приемы:
- Использование презентации
- Фронтальная беседа
- Устная работа
- Игровые моменты
- Работа в парах
- Работа у доски
- Работа в тетрадях
План урока:
- Организационный момент (1минуты)
- Расшифровка темы урока (3минуты)
- Сообщение темы и цели урока (1минута)
- Теоретическая разминка (3минут)
- Исторический экскурс (3минуты)
- Игра “Убери лишнее” (2минуты)
- Творческая работа (2минуты)
- Задание “Найди ошибку” (2минуты)
- Решение одного уравнения несколькими способами (на слайде) (3минуты)
- Решение одного уравнения несколькими способами (у доски) (24 минут)
- Самостоятельная работа в парах с последующим объяснением (5минут)
- Индивидуальное домашнее задание(1минуты)
- Итог урока рефлексия (1минута)
Эпиграф урока:
“Учиться можно только весело, чтобы переваривать знания, нужно поглощать их с аппетитом”.

А.Франс
Конспект урока
Организационная часть
Проверяю готовность учащихся к уроку, отмечаю отсутствующих на уроке. Ребята, Французский писатель 19 века А.Франс однажды заметил “ Учиться можно только весело, чтобы переваривать знания, нужно поглощать их с аппетитом”. Так давайте на нашем уроке следовать совету, писателя и переваривать знания с большим аппетитом, ведь они пригодятся в нашей жизни.
Расшифровка темы урока
Для того, чтобы перейти к более сложном заданием, давайте разомнем свои мозги простыми заданиями. Тема нашего урока зашифрована, решив устные задания и найдя к ним ответ, зная, что каждый ответ имеет свою букву, мы раскроем тему урока. Презентация слайд 3
Сообщение темы и цели урока
Вы, сегодня сами назвали тему урока
“Виды уравнений и способы их решения”. Презентация
слайд 4
Презентация
слайд 4
Цель: Вспомнить и обобщить все виды уравнений и способы их решения. Решить одно уравнение всеми способами. Презентация слайд 5 Прочитать высказывание Эйнштейна Презентация слайд 5
Теоретическая разминка
Вопросы Презентация слайд 7
Ответы
- Равенство, содержащее переменную величину, обозначенную какой-то буквой.
- Это значит найти все его корни, или доказать, что корней нет.
- Значение переменной, при котором уравнение обращается в верное равенство.
- После этого определения прочесть стихотворение об уравнении Презентация слайд 12,13,14
Ответы на 2 последних вопроса Презентация слайд 9,10,11
Исторический экскурс
Историческая справка, о том “Кто и когда придумал уравнение” Презентация слайд 15
Представим себе, что первобытная мама по
имени.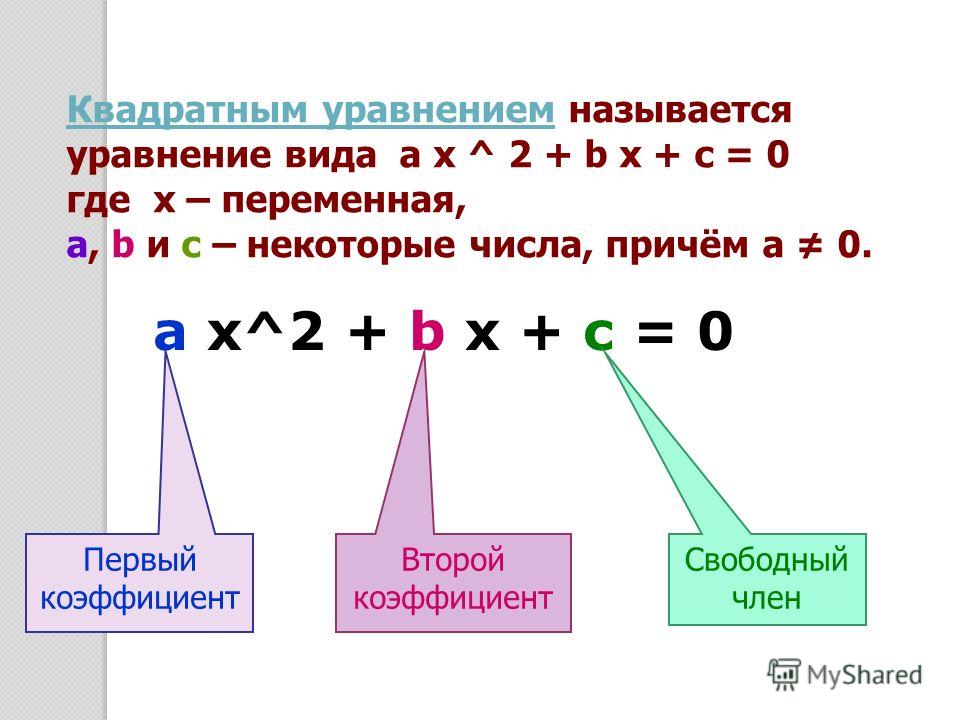
 Наибольших успехов в развитие учения об
уравнениях достиг греческий учёный Диофант(III
век), о котором писали:
Наибольших успехов в развитие учения об
уравнениях достиг греческий учёный Диофант(III
век), о котором писали:Он уйму всяких разрешил проблем.
И запахи предсказывал, и ливни.
Поистине, его познанья дивны.
Большой вклад в решение уравнений внёс
среднеазиатский математик Мухаммед ал Хорезми
(IХ век). Его знаменитая книга ал-Хорезми
посвящена решению уравнений. Она называется
“Китаб ал-джебр вал-мукабала”, т. е. “Книга о
восполнении и противопоставлении”. Эта книга
стала известна европейцам, а от слова “ал-джебр”
из ее заглавия произошло слово “алгебра” –
название одной из главных частей математики. В
дальнейшем многие математики занимались
проблемами уравнений. Общее правило решений
квадратных уравнений приведённых к виду х2+вх=0
было сформулировано немецким математиком
Штифелем, проживавшим в ХV веке. После трудов
нидерландского математика Жирара (ХVI век), а
также Декарта и Ньютона, способ решения принял
современный вид.
Напрасно французы пытались найти ключ к шифру,
и тогда король обратился к Виету. Рассказывают,
что Виет нашёл за две недели непрерывной работы
ключ к шифру, после чего, неожиданно для Испании,
Франция стала выигрывать одно сражение за
другим. Будучи уверенным, что шифр разгадать не
возможно, испанцы обвинили Виета в связи с
дьяволом и приговорили к сожжению на костре. К
счастью, он не был выдан инквизиции и вошёл в
историю как великий математик.
К
счастью, он не был выдан инквизиции и вошёл в
историю как великий математик.
Игра “Убери лишнее”
Цель игры ориентирование в видах уравнений.
У нас даны три столбика уравнений ,в каждом из них, уравнения определены по какому-то признаку ,но одно из них лишнее ваша задача его найти и охарактеризовать. Презентация слайд 16
Творческая работа
Цель этого задания: Восприятие на слух математической речи ориентировании детей в видах уравнений .
На экране вы видите 9 уравнений. Каждое уравнение имеет свой номер, я буду называть вид этого уравнения, а вы должны найти уравнение этого вида, и поставить только номер, под которым оно стоит, в результате вы получите 9-значное число Презентация слайд 17
- Приведенное квадратное уравнение.
- Дробно-рациональное уравнение
- Кубическое уравнение
- Логарифмическое уравнение
- Линейное уравнение
- Неполное квадратное уравнение
- Показательное уравнение
- Иррациональное уравнение
- Тригонометрическое уравнение
Задание “Найди ошибку”
Один ученик решал уравнения, но весь класс
смеялся, в каждом уравнении он допустил ошибку,
ваша задача найти ее и исправить.
Решение одного уравнения несколькими способами
А теперь решим одно уравнение всеми возможными способами, для экономии времени на уроке одно уравнение на экране. Сейчас вы назовете вид этого уравнения, и объясните какой способ используется , при решении этого уравнения Презентация слайды 19-27
Решение одного уравнения несколькими способами (у доски)
Мы посмотрели пример, а теперь давайте решим уравнение у доски всевозможными способами.
=x-2 - иррациональное уравнение
Возведем в квадрат обе части уравнения.
2x-1=(x-2)2
2x-1=x2-4x+4
-x2+2x+4x-1-4=0
x2-6x+5=0
Решаем это уравнение у доски 9 способами.
Самостоятельная работа в парах с последующим объяснением у доски
А сейчас вы поработаете в парах, на парту я даю
уравнение, ваша задача определить вид уравнения,
перечислить все способы решения этого уравнения,
решить 1-2 наиболее рациональными для вас
способами.
Задания для работы в парах
Решите уравнение
- =x-2
- =6
- 36-x=33x-2
- 9x-83x-9=0
- 23x+1-3x=15
- = 4
После самостоятельной работы в парах один представитель выходит к доске представляет свое уравнение, решает одним способом
Индивидуальное домашнее задание (дифференцируемо)
Решите уравнение
- =x-2
- =6
- 36-x=33x-2
- 9x-83x-9=0
- 23x+1-3x=15
- =4
- 3x5=96
- |x+2|=
(определить вид уравнения, решить всеми способами на отдельном листе)
Итог урока рефлексия.
Подвожу итог урока, заостряю внимание на том, что одно уравнение можно решить многими способами, выставляю оценки, делаю вывод, кто был активным кому надо быть поактивнее. Зачитываю высказывание Калинина Презентация слайд 28
Посмотрите внимательно на те цели которые мы с вами поставили для сегодняшнего урока:
- Что на ваш взгляд нам удалось сделать?
- Что получилось не очень хорошо?
- Что вам особенно понравилось и запомнилось?
- Сегодня я узнал новое…
- На уроке мне пригодились знания…
- Для меня было сложно…
- На уроке мне понравилось…
Литература.
- Дорофеев Г.В. “Сборник заданий для проведения письменного экзамена по математике за курс средней школы” — М.: Дрофа, 2006.
- Гарнер Мартин. Математические головоломки и развлечения.
- Ивлев Б.
 М., Саакян С.М. Дидактические материалы
по алгебре и началам анализа для 10 кл., 11 кл. М.:
Просвещение. 2002.
М., Саакян С.М. Дидактические материалы
по алгебре и началам анализа для 10 кл., 11 кл. М.:
Просвещение. 2002.
УРОК — ПРАКТИКУМ «Виды уравнений. Методы решения уравнений»
Цели:
повторить различные виды уравнений; повторить методы решения уравнений; закрепить навыки решения уравнений различными методами;
Задачи:
- Подготовка к экзамену по математике
- Закрепить способы решения различных видов уравнений;
- Учить составлять алгоритм решения задания по образцу;
- Развивать познавательную активность обучающихся на основе поисковой деятельности;
- Продолжить работу по развитию творческого мышления;
- Развивать умения работать с книгой, самостоятельно добывать знания;
- Содействовать развитию у обучающихся способностей к логическим операциям: анализу, сравнению, умению классифицировать, обобщать;
- Развивать трудолюбие, умение общаться со своими сверстниками в процессе работы в парах.
 Прививать чувство сопереживания и участия при ответах своих одногруппников.
Прививать чувство сопереживания и участия при ответах своих одногруппников. - Создание комфортного темпа работы для каждого студента.
Тип урока: урок повторения и обобщения знаний, закрепления умений
Обеспечение урока: Компьютер, мультимедийный проектор, экран,
инструкционные карта по различным видам уравнения; опорный конспект; карточки – задания; учебная литература
Формы работы: фронтальный опрос, работа в группах, взаимопроверка, индивидуальная-дифференцированная работа.
ХОД УРОКА
1. Организационный момент:
Здравствуйте, ребята и уважаемые гости. Ребята, нам предстоит поработать над очень важной темой для подготовки к экзамену. Вы уже достаточно знаете и умеете по этой теме, поэтому наша с вами задача: обобщить и сложить в систему все те знания и умения, которыми вы владеете.
Эпиграфом к нашему уроку станут слова С. Коваля: «Уравнения – это золотой ключик, открывающий все математические сезамы».
2. Самоопределение к деятельности.
- Ребята, как вы думаете, о чем пойдет речь на нашем уроке? — об уравнениях.
- А как вы понимаете это высказывание? (То есть другими словами можно сказать, что если вы будете уметь решать уравнения, то экзамена по математике вам не стоит бояться.)
Тема «Уравнения» — одна из важнейших тем курса алгебры. Тема для вас как таковая не новая. В школе и уже на 1 курсе вы изучили большую часть видов уравнений, а также методы их решения. На сегодняшнем уроке нам ещё раз необходимо повторить эти виды и закрепить навыки решения уравнений различными методами.
В тетради запишите дату и тему урока «Виды уравнений. Методы решения уравнений»
3. Актуализация знаний. Систематизация знаний, умений и навыков по теме «Уравнения».
- Что называется уравнением? — это равенство, содержащее переменную.
- Что называется корнем уравнения? – значение переменной, которое приводит уравнение в верное равенство.

- Что значит решить уравнение? – значит найти корни уравнения.
- Какие «неприятности» могут быть при решении уравнений? (При решении уравнений могут появиться посторонние корни; произойти потеря корней.)
- Как избежать этих неприятностей? (1. Выполнять равносильные переходы. Выполнять проверку корней по ОДЗ или подстановкой в исходное уравнение)
Как я уже сказала на сегодняшнем уроке нам необходимо вспомнить все известные вам виды уравнений.
Какие вы помните виды уравнений? (ответы учащихся)
Теперь давайте классифицируем все виды.
- Линейные
- Квадратные
- Дробно-рациональные
- Иррациональные
- Показательные
- Логарифмические
- Тригонометрические
Решение всех сложных уравнений всегда сводится к решению простейших уравнений. Сейчас мы проверим ваши знания и умения по решению простейших уравнений. А простейшими в данном случае являются линейные уравнения.
4х = 60 15y = 90; 12t = 0; 6z = — 5,4
2х-3=17 3,2+х=8,4 6х+21=22 14-6х=-2х+18
Теперь давайте проверим, насколько хорошо вы умеете определять виды уравнений. Вашему вниманию предлагается слайд, в котором записано задание на соотнесение объектов слева к объектам справа. (самопроверка по слайду)
Вашему вниманию предлагается слайд, в котором записано задание на соотнесение объектов слева к объектам справа. (самопроверка по слайду)
4. Закрепление. (работа в группах)
Сейчас мы перейдём к решению различных видов уравнений. Вы будете работать в группах, используя инструкционную карту. В начале урока я вам раздала ключи различного цвета, так вот вам необходимо сформировать 4 группы по цвету ключа.
1 группа работает по теме «Квадратные уравнения»
2 групп – «Иррациональные уравнения»
3 группа – «Показательные уравнения»
4 группа – «Логарифмические уравнения»
Тригонометрические уравнения мы оставим на следующий урок, так как эта тема потребует от нас много времени на повторение.
Вам необходимо за 10 минут ответить на вопросы инструкционной карты и решить уравнения различными методами.
Затем каждая группа должна представить свой вид уравнений, рассказав о методах решения представит решение на доске (время для представления 3 мин. )
)
5. Самостоятельная работа
6. Рефлексия:
Давайте вернемся к эпиграфу нашего урока (на доске — эпиграф): «Уравнения – это золотой ключик, открывающий все математические сезамы».
Возьмите ваши ключики и напишите, что вам понравилось на уроке, а что нет. И приклейте к замочной скважине, изображенной у меня на плакате. Чем ближе ключ, тем легче вам было работать на уроке и вы все поняли
Мне хотелось бы вам пожелать, чтобы каждый из вас нашел в жизни свой «золотой ключик», с помощью которого перед вами открывались бы любые двери. Всем вам ребята спасибо за работу! Удачи вам на экзаменах!
Уравнения, виды уравнений и способы их решений
Тема. Решение дробных рациональных уравнений. Обобщение и систематизация темы: «Уравнения, виды уравнений и способы их решения»
Цели обучения Образовательная:
— систематизировать и обобщить знания обучающихся об уравнениях;
— расширить и обобщить знания обучающихся по теме – решение дробных рациональных уравнений, используя при этом различные приемы и методы.
— повторить различные способы решения дробных рациональных уравнений.
— продолжить обучение решению дробных рациональных уравнений по алгоритму решения дробных рациональных уравнений. — провести проверку уровня усвоения темы путем проведения самостоятельной работы.
Развивающая:
— развитие коммуникативных навыков общения и умения слушать и слышать;
— развитие умения правильно оперировать полученными знаниями, логически мыслить;
— развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
— развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
Воспитательная:
— воспитание познавательного интереса к предмету;
— стимулировать самостоятельную деятельность, способствовать формированию коммуникативных навыков. — воспитание воли и упорства для достижения конечных результатов. Цель урока: — обеспечить осознанное усвоение обучающимися алгоритма решения дробно-рациональных уравнений;
— активизировать мыслительную деятельность школьников через активное участие каждого в процессе работы.
Тип урока: Урок систематизации и обобщения знаний и умений.. Методы и технологии, используемые на уроке: проблемно-поисковые, словесные практические, ИКТ, групповые, технология развития критического мышления, технология коллективной мыслительной деятельности (КМД)
Технология креативного мышления «Шесть думающих шляп». Оборудование и наглядность: базовый учебник Макарычев Ю.Н. Алгебра. 9 класс: учеб. Для обучающихся общеобразовательных учреждений. «Просвещение», 2014г; ноутбук, дополнительный раздаточный материал. Ресурсы: презентация «Решение дробных рациональных уравнений», наборы шляпок, кластеры уравнений, раздаточный материал для рефлексии.
Планируемые результаты | Личностные | Метапредметные | Предметные |
умение понимать смысл поставленной задачи, критичность мышления | Познавательные: понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом Регулятивные: целеполагание, планирование, контроль, коррекция, оценка Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли | Формирование навыка решения рациональных уравнений, умения работать с текстом задачи; грамотно использовать математическую терминологию и символику. | |
Основные понятия | Линейное уравнение, квадратное уравнение, полное, неполное, алгоритм решения линейного и квадратного уравнения, рациональное уравнение, решение дробных рациональных уравнений и алгоритм решения дробно- рациональных уравнений. | ||
Ход урока
І.Организационный момент.
Добрый день, ребята! Запишите дату в тетрадях и тему урока: « Решение дробных рациональных уравнений»
Девиз урока
Покоряет вершины тот,
кто к ним стремится
.Установка на успех
1.Определи для себя значение данного материала. 2.Наметь цель и не отступай от неё. 3. Радуйся, когда тебе удастся достичь хотя бы маленького успеха. 4. Не огорчайся, если с первого раза не удастся. Попробуй ещё раз. 5. Не бойся попросить помощи. 6. Спрашивай, если в чём-то сомневаешься. 7. Я верю, что каждый из вас справится.
6. Спрашивай, если в чём-то сомневаешься. 7. Я верю, что каждый из вас справится.
Успехов вам!
II.Проверка домашнего задания, воспроизведение и коррекция опорных знаний обучающихся. Актуализация знаний
Двое учащихся работают у доски (решение упражнений аналогичных домашним)
При каких значениях a равно нулю значение дроби:
а) ; Ответ :0 б) . Ответ: 0 (Работа в диалоге)
2. Остальные учащиеся проверяют выполнение домашнего задания, применяя «Инсерт»
3. Проверь себя ( Слайд )
Пример 1.
Общий знаменатель 2(x+1)(х -1) =2( х2 -1)
x1 =6, x2= — 2,2. Ответ: -2,2 ;6.
Пример 2.
нет решений
Общий знаменатель х(1-х)
Ответ: нет решений
.
П ример 3.
x = -8 ОДЗ: х
Ответ: -8.
4. Решите устно:
а) ; б) ; в) .
Ответ: а) 5; б) корней нет; в) – 6.
5. Проверка кластеров «Уравнения, виды и способы их решений»
III. Постановка цели и задач урока. Мотивация учебной деятельности обучающихся.
Сегодня на уроке мне хотелось бы вас пригласить поглубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.
Слово учителя о преемственности при изучении темы «Уравнения, виды и способы их решений»
Уравнения в школьном курсе математике занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
IV.Обобщение и систематизация знаний по теме «Уравнения, виды и способы их решений»
1.Начальная школа
В период обучения в начальной школе формируются базовые знания, умения и навыки, на основе которых будет строиться дальнейшее изучение математики. Начальная школа занимает решающее место: проблема преемственности может не возникнуть только в случае, когда правильно организованно начальное обучение. Другими словами, на начальную школу возлагается высочайшая ответственность за все дальнейшее обучение математики. Вот почему так важно дать учащимся наиболее полную информацию о сущности уравнения и показать им пути его решения.
2 класс «Знакомство с уравнениями. Решение уравнений методом подбора»
— Ребята, посмотрите, пожалуйста, на доску. Вам знакома такая запись?
+ 4 = 12 (Да, это пример с «окошком»)
— А такая: а + 4? (Да, это буквенное выражение)
— Что вы делали в первом случае? (подбирали число, чтобы запись была верной)
— Что делали во втором случае? (Вместо буквы подставляли числа и вычисляли).
— А сейчас внимательно посмотрите на запись, которую принёс нам Знайка Математик.
х + 4 = 12
— На что она похожа? (И на пример с «окошечком» и на буквенное выражение).
— Что нам говорит знак «=»? (Это равенство)
— Какое равенство? Все числа в нём известны? (нет).
— Что неизвестно? (первое число)
— Как оно обозначено? (латинской буквой)
— Если оно неизвестно, перед нами какая встаёт задача? (Найти, узнать какое это число)
— Найдите это число, чтобы равенство было верным. (Это число 8, потому что 8 + 4 = 12)
— А знаете, что вы сейчас сделали? Вы решили уравнение х+4=12
— Попробуем сделать вывод из всего сказанного и сделанного. Уравнение это (учитель показывает знак «=») (Равенство)
— Которое содержит что (показываю на х)? (Неизвестное число)
— Что надо сделать с неизвестным числом? (Его надо найти)
— Как обозначается неизвестное число? (Латинской буквой)
— Кто может сказать, что такое уравнение? (Уравнение – это равенство, которое содержит неизвестное число)
— Что значит «решить уравнение»? Найти такое число, чтобы равенство было верным)
— Давайте решим уравнения (3 человека у доски)
8 + х = 14 13 — х = 7 a – 5 = 9
— Как нашли неизвестное число? ( Дети рассказывают алгоритм: 1) Чтобы найти неизвестное слагаемое, надо из суммы вычесть другое слагаемое.
2) Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. 3) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое).
. Итог урока.
— Ребята, вот и близится к концу наш урок. С каким математическим понятием мы познакомились? (Мы познакомились с понятием «уравнение»)
— Тогда скажите, что же такое уравнение?
(Равенство, которое содержит неизвестное число).
— А что значит решить уравнение?
(Решить уравнение – значит найти неизвестное число, чтобы равенство было верным).
3 класс
– Что такое уравнение? (Равенство, содержащее неизвестное число, которое надо найти).
Самоопределение к деятельности
– Среди записей найдите уравнение.
38 + х 74 – 18 = 56 х + 6 3
46 + 12 = 58 х – 8 = 63 х – 22
– Как вы догадались? (Ответы детей)
– Давайте вспомним, как называются компоненты при вычитании? Что нам нужно найти? Какое правило поможет нам найти уменьшаемое? (Чтобы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое). Решите уравнение.
Решите уравнение.
х – 8 = 63
х = 63 + 8
х = 71
71 – 8 = 63
63 = 63
– Как вы думаете, чем мы будем заниматься сегодня на уроке?
– Совершенно верно. Мы продолжим учиться решать уравнения.
Или:
1. Повторение связи между суммой и слагаемыми.
5+7=12
-Давай вспомним компоненты при сложении( Слагаемое, слагаемое, сумма)
-Что такое 5? (Первое слагаемое)
-Что такое 7? (Второе слагаемое)
-Что такое 12? (Сумма).
-Что необходимо сделать, чтобы найти неизвестное первое слагаемое? (Нужно из суммы вычесть второе слагаемое). 12-7=5
-Что необходимо сделать, чтобы найти второе слагаемое? (Надо из суммы вычесть первое слагаемое). 12—5=7
4 класс
алгоритм действий по решению простых уравнений
· Прочитать уравнение.
· Определить, что неизвестно в уравнении.
· Применить правило нахождения неизвестного слагаемого.
· Произвести вычисления.
· Сделать проверку.
Алгоритм решения сложного уравнения.
1)Прочитать уравнение.
2) Упростить правую часть уравнения.
3)Определить, что неизвестно.
4)Применить правило нахождение неизвестного слагаемого.
5)Произвести вычисления.
6)Сделать проверку.
24 + Х = 79 – 30
24+x=49
X=25
24+25=79-30
49=49
— Понятие об уравнении
Способы решения уравнений:
а) способ подбора;
б) решение уравнений на основе зависимости между компонентами действий.
в) решение уравнений на основе соотношения между частью и целым.
г) решение уравнений на основе знаний конкретного смысла умножения.
2. 5-6 классы
3. 7-8 классы
7 класс
1.Уравнения с одной переменной или с одним неизвестным
а).Что такое уравнение? (Равенство, содержащее неизвестное).
б).Что такое корень уравнения? (Значение переменной, при котором уравнение обращается в верное равенство).
в).Что значит решить уравнение? (Значит найти все его корни или доказать, что их нет).
2. Линейное уравнение
Уравнение вида ах =в , где х – переменная , а и в — некоторые числа , называется линейным уравнением с одной переменной .
Уравнение вида ах =в при а имеет один корень,
при а=0, в не имеет корней,
при а =0 , в= 0 имеет бесконечно много корней ( любое число является его корнем)
класс
1.Квадратные уравнения
Квадратным уравнением называется уравнение вида где x — переменная, а , в и с – некоторые числа, причём а 0.
а , в и с – коэффициенты КУ, число а – называется первым коэффициентом, число в – вторым коэффициентом и число с – свободным членом.
Степень уравнения вида ( наибольшая степень переменной х – квадрат), поэтому – квадратное уравнение.
Квадратное уравнение, в котором коэффициент при равен 1, называется приведенным квадратным уравнением.
Квадратное уравнение, в котором хотя бы один из коэффициентов b или с равен нулю, называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
, где с ;
, где в
.
Выражение — 4ac называют дискриминантом квадратного уравнения и его обозначают буквой D = — 4ac
Если D , уравнение имеет два корня,
Если D , то уравнение не имеет корней,
Если D , то уравнение имеет один корень.
Формулы корней КУ:
1. , где D = — 4ac,
2. , где D = — ac для квадратного уравнения ,
3.Теорема Виета — сумма корней квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, т.е. х1 + х2 = — ,
а произведение корней равно свободному члену, т.е. х1 х2 = ..
2.Дробные рациональные уравнения
Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля, называют целыми выражениями.
Выражения, помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменной, называются дробными выражениями
Целые и дробные выражения называют рациональными выражениями.
Что является допустимым значением рациональной дроби (допустимым значением рациональной дроби являются те значения переменных, при которых не обращается в нуль знаменатель дроби)
Уравнения, в которых левая и правая части являются рациональными выражениями, называются рациональными уравнениями.
Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным.
Рациональное уравнение, в котором левая или правая часть является целым выражением, называют целым.
Способы решения дробно- рациональных уравнений:
1.Исползование свойство дроби равной нулю,
2.Использование свойства дроби, равной 1,
3. Использование свойства пропорции,
4. Введение новой переменной.
Введение новой переменной.
4 . 9 класс
Какое уравнение с одной переменной называется целым (целым уравнением с одной переменной называется уравнение, левая и правая части которого — целые выражения)
Дайте определение биквадратного уравнения (уравнение вида + c = 0, где являющемся квадратным относительно , называется биквадратным уравнением).
Какое уравнение называется дробным рациональным (дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них – дробным выражением).
Какие существует способов решения дробных рациональных уравнений:
1.Приведение дробей к общему знаменателю;
2.Умножение дробей на общий знаменатель всех дробей.
3. Графический способ;
4. Введение новой переменной;
5.Выделение из дробей целой части)
Когда дробь равна нулю (дробь равна нулю когда числитель равен нулю, а знаменатель не равен нулю)
Первый алгоритм решения дробных рациональных уравнений:
1. Находят общий знаменатель дробей, входящих в уравнение.
Находят общий знаменатель дробей, входящих в уравнение.
2. Умножают обе части уравнения на этот знаменатель.
3.Решают получившееся целое уравнение.
4.Исключают из его коней те, которые обращают в нуль общий знаменатель дроби.
5. Записываем ответ.
Второй алгоритм решения дробных рациональных уравнений:
Найти допустимые значения дробей, входящих в уравнение.
Найти общий знаменатель дробей, входящих в уравнение.
Умножить обе части уравнения на общий знаменатель.
Решить получившееся уравнение.
Исключить корни, не входящие в допустимые значения дробей уравнения.
Обобщая весь теоретический материал, хочу вас спросить:
Какие виды уравнений вы знаете? Определение. (линейные, квадратные и приводимые к квадратным, дробные, целые, рациональные , дробно- рациональные)
Когда в уравнении появляются посторонние корни?
V.Применение знаний и умений в новой ситуации
VI. Контроль усвоения, обсуждение допущенных ошибок и их коррекция
Контроль усвоения, обсуждение допущенных ошибок и их коррекция
3.71. Тракторист должен был вспахать за некоторое время поле площадью 180 га. Но ежедневно он вспахивал на 2 га больше, чем планировал, поэтому закончил работу на 1 день раньше срока. За сколько дней тракторист вспахал поле?
Во время объяснения задачи применяем технологию «Шесть думающих шляпок»
1.Надеваем белую шляпу – и собираем информацию, которая у нас имеется.
А имеется …… проговариваем условие задачи……
Необходимо определить ……. За сколько дней тракторист вспахал поле?
А как это сделать? …… Площадь поля разделить на количество гектар, которые он вспахивал каждый день
2. Надеваем черную шляпу – ребята, рассмотрим, какие имеются недостатки, проблемы в решении задачи. Но мы не знаем его ежедневной нормы по плану
3.Надеваем красную шляпу – ребята выскажите свои эмоции предположения по данному вопросу, есть ли у вас предложения, как решить задачу, что необходимо сделать.
4.Надеваем желтую шляпу – мы видим, что у …. Давайте посчитаем, …. Каким правилом можно воспользоваться, чтобы узнать ….?
5. Надеваем зеленую шляпу – мы определили, что ……
6.Надеваем синюю шляпу – решим полученное уравнение
Решение
Пусть тракторист по плану в день должен вспахать х га.,- дневная норма
но по факту он вспахивал по (х+2) га . Тогда
— дней по плану для выполнение задания;
— дней по факту для выполнение задания.
По условию задачи составляем и решаем уравнение:
— = 1
ОДЗ: х 0, х -2
Общий знаменатель .
Умножим обе части уравнения на
получим ,
180х +360 – 180х =
D = 4+ 1440 =1444 , 2 корня
х= (-2 , — удовлетворяет условию задачи
– не удовлетворяет условию задачи так, как количество гектаров не может быть отрицателным числом.
180 18 =10 ( дней) по плану, а по факту – (10-1) = 9 ( дней).
Ответ: 9 дней.
VII. Информация о домашнем задании, инструктаж по его выполнению
3.10. Решите уравнение
3.11. Решите уравнение
3.12. Решите уравнение
3.13. Решите уравнение
VIII.Рефлексия
Применение метода на этапе РЕФЛЕКСИИ:
Белая: На мой взгляд, больше всего удалось….. (факты, информация).
Красная: Меня удивило….. (эмоции, интуиция).
Чёрная: Я думаю, что ……. (критика, оценка).
Жёлтая: Для меня было открытием то, что………….. (логический позитив, оптимизм).
Зелёная: На будущее я учту…………. (креатив, новая идея).
Синяя: Я могу похвалить за….. (обобщение).
С помощью светофора ученики оценивают свою работу.
Урок прошел удачно: я участвовал в работе класса, с заданиями справился успешно. Я очень доволен собой.
Сегодня на уроке не все задания оказались легкими. Мне было трудно, но я справился. Я доволен собой!
Я доволен собой!
Задания на уроке оказались трудными. Мне нужна помощь!
Список использованной литературы: (слайд 13)
1. Макарычев Ю.Н. Алгебра.8 класс.- М.:«Просвещение»,2016
2. Жохов В.И., Карташева Г.Д. Уроки алгебры в 8 классе.-М.:«Просвещение»,2014
3. Ященко И.В. ОГЭ (ГИА-9): 3000 задач с ответами по математике. Все задания части 1.-М.: Издательство «Экзамен», 2015
4. Лаппо Л.Д. ЕГЭ. Математика. Тематические тренировочные задания. -М.: Издательство «Экзамен», 2015
26 различных типов уравнений — Nayturr
Хотя это и не очевидно, изучение уравнений важно в нашей повседневной жизни. Без него у нас не было бы компьютеров, GPS, спутникового телевидения и других изобретений, которые делают современное общество таким, какое оно есть.
Некоторые из уравнений, изменивших наш образ жизни, – это Теорема Пифагора, Фундаментальная теорема исчисления и Универсальный закон всемирного тяготения Ньютона, и это лишь некоторые из них.
Уравнение необходимо для медицины, экономики, информатики, инженерии и многих других областей. Читайте дальше, если хотите узнать больше об этой динамической концепции.
Типы уравнений – алгебраические Кубическое уравнениеКубическое уравнение представляет собой полиномиальное уравнение, в котором наибольшая сумма показателей степени переменных в любом члене равна трем. Другими словами, это уравнение, включающее кубический многочлен; т. е. одна из форм. Он имеет следующий вид:
ax 3 + bx 2 + cx + d = 0, где a ≠ 0
Примечание. Этот пост может содержать партнерские ссылки, которые приведут вас к интернет-магазинам, продающим товары и услуги. . Если вы нажмете на один и купите что-нибудь, я могу заработать на соответствующих покупках. Подробнее см. в разделе «Раскрытие информации о партнерских программах».
Экспоненциальное уравнение Экспоненциальные уравнения имеют переменные вместо показателей и могут быть решены с использованием этого свойства: axax = ayay => x = y. Примеры включают следующее:
Примеры включают следующее:
- 4 x = 0
- 8 x = 32
- a b = 0 (где «a» — основание, а «b» — показатель степени)
- 8 90 Полиномиальное уравнение
Иррациональные полиномиальные уравнения — это уравнения, в которых хотя бы один полином стоит под знаком радикала.
Линейное уравнениеЛинейные уравнения — это уравнения, в которых каждый член является константой или произведением одной переменной на константу. Если есть две переменные, график линейного уравнения всегда будет прямой линией. Как правило, линейное уравнение выглядит следующим образом:
y = mx + c, m ≠≠ 0
В этом примере m называется наклоном, а c представляет точку, в которой он пересекает ось y.
В линейных уравнениях с разными переменными:
Уравнение только с одной переменной: уравнение только с одной переменной. Примеры включают следующее:
- 8a – 8 = 0
- 9a = 72
Уравнение имеет две переменные: уравнение, которое имеет только два типа переменных.
 Примеры включают следующее:
Примеры включают следующее:- 9a + 6b – 82 = 0
- 7x + 7y = 12
- 8a – 8d = 74
Уравнение с тремя переменными: это уравнение только с тремя типами переменных в уравнение. Примеры включают следующее:
- 13a — 8b + 31c = 74
- 5x + 7y — 6z = 12
- 6p + 14q — 74 + 82 = 0
Полиномиальные уравнения содержат либо переменные, либо неопределенные числа и коэффициенты. Они участвуют в таких операциях, как сложение, вычитание, умножение и неотрицательные целые степени. Примеры включают следующее:
- ax + by + c = 0ax + by + c = 0 со степенью = 1 и двумя переменными
- ax 2 + bx + c = 0ax 2 + bx = c = 0 со степенью = 2 и одной переменная
- ax + b = 0 со степенью = 1 и одной переменной
- axy + c = 0axy + c = 0 со степенью = 2 и двумя переменными
Квадратное уравнение является уравнением второй степени уравнение, в котором одна переменная содержит переменную с показателем степени, равным двум.
 Пример и общая форма показаны ниже.
Пример и общая форма показаны ниже.AX 2 + BX + C = 0, A in пункта 0
Другие примеры включают:- 5A 2 — 5A = 35
- 8x 2 + 7x — 75 = 0.
- 4y 2 + 14y – 8 = 0
Радикальные уравнения — это те, у которых максимальный показатель степени переменной равен 12 и которые содержат более одного члена. Можно также сказать, что радикальным уравнением является уравнение, в котором переменная лежит внутри радикального символа, обычно в форме квадратного корня. Примеры включают следующее:
- + 10 = 26
- + x – 1
Рациональное уравнение включает рациональные выражения.
Трансцендентные уравнения Трансцендентные уравнения — это уравнения, включающие трансцендентные функции. Экспоненциальные уравнения являются примерами трансцендентных уравнений.
Экспоненциальные уравнения являются примерами трансцендентных уравнений.
Проще говоря, тригонометрические уравнения — это те уравнения, которые включают тригонометрические функции, обычно с неизвестными углами, такими как cos B = ½.
Пример тригонометрического уравнения находится здесь:
x =
Другие примеры тригонометрических уравнений можно найти здесь.
Другие примеры алгебраических уравнений можно найти здесь.
Типы уравнений – геометрические Рисунки – формулы для объема (V) и площади поверхности (SA)Общая призма
- V = Bh = площадь основания x высота
- SA = сумма площади граней
Прямоугольная призма
- V = lwh = длина x ширина x высота
- SA = 2lw + 2hw + 2lh
- = 2(длина x ширина) + 2(высота x ширина) + 2(длина х высота)
Правый круговой конус
- V = Bh = x площадь основания x высота
- SA = B + C
- = площадь основания + (x длина окружности основания x наклонная высота)
Правый круговой цилиндр
9 V = Bh = площадь основания x высота SA = 2B + Ch = (2 x площадь основания) + (окружность x высота) Сфера
- V = 3 = x x куб радиуса
- SA = 4 2 = 4 x квадрат радиуса
Квадратная пирамида
- V = Bh = x площадь основания x высота
- SA = B + P
- = площадь основания + (x периметр основания x наклонная высота)
Формы – формулы для площади (A) и окружность (C) Окружность
A = 2 = x квадрат радиуса
C = 2 r = 2 x x радиус
C = = x диаметр
2 Параллелограмм = основание x высота
Прямоугольник
A = lw = длина x ширина
Трапеция
A = (b 1 + b 2 )h = x сумма оснований x высота Уравнения прямой
Стандартная форма
Ax + By = 0, где A и B не равны нулю наклон, (x 1 , y 1 ) = точка на линии
Форма пересечения наклона 9
Геометрические формулы Площадь круга: 2 ( = 3,14 приблизительно)
Площадь прямоугольника: длина x высота
Площадь квадрата: длина 2 (l x l)
Площадь треугольника: ½ x длина x высота
Окружность круга: 2 ( x диаметр)
Объем конуса: 1/3 x площадь основания х высота; 1/3 х (г/2) 2 х в
Объем цилиндра: площадь основания x высота; (d/2) 2 x h
Объем прямоугольной призмы: длина x высота x глубина
Ознакомьтесь с нашей статьей «7 различных типов треугольников». (Или вам может понравиться «7 различных типов фракций»)
(Или вам может понравиться «7 различных типов фракций»)
Типы химических реакций Комбинированные химические реакции В этой реакции один продукт образуется двумя или более реагентами.
Кроме того, в комбинированной химической реакции может образовываться более одного продукта, в зависимости от условий или относительных количеств реагентов.
Химические реакции горения Химические реакции горения происходят, когда соединение, обычно содержащее углерод, соединяется с газообразным кислородом, находящимся в воздухе. Этот процесс называется горением, так как теплота является наиболее важным продуктом большинства химических реакций горения.
Пропан входит в состав соединений, называемых углеводородами, состоящих только из углерода и водорода. Результатом этой реакции является тепло. Кроме того, химические реакции горения также являются разновидностью окислительно-восстановительных химических реакций.
Химические реакции разложения На самом деле химические реакции разложения являются полной противоположностью реакциям соединения. При реакциях разложения одно соединение распадается на два или более более простых по своей природе вещества, обычно на соединения и/или элементы.
Химические реакции с двойным замещением В реакциях с одним замещением замещается только один химический компонент; однако в реакциях двойного замещения, также называемых реакциями метатезиса, замещаются два вещества, обычно ионы.
Чаще всего эти типы химических реакций происходят в растворе, в результате чего образуется либо вода (реакции нейтрализации), либо нерастворимое твердое вещество (реакции осаждения).
Химические реакции нейтрализации Это еще один тип химической реакции двойного замещения, которая происходит между основанием и кислотой. Эта химическая реакция с двойным замещением, называемая реакцией нейтрализации, образует воду. Примеры включают следующее:
Примеры включают следующее:
Смешение гидроксида натрия (щелока) и серной кислоты (автоаккумуляторная кислота) представляет собой реакцию, которая представлена как:
Химические реакции полимеризации Полимеризация представляет собой процесс, при котором молекулы мономера вступают в химическую реакцию, которая приводит к образованию полимерных цепей, также называемых трехмерными сетями. Существует множество форм полимеризации в дополнение к различным системам, которые классифицируют каждую из них. Примеры включают следующее:
nH 2 C=CH 2 → [-CH 2 CH 2 -] n
Это уравнение представляет собой объединение тысяч молекул этилена, в результате которого получается полиэтилен.
Как в целлюлозе, так и в крахмале молекулы глюкозы соединяются вместе с одновременным отщеплением молекулы воды для каждой образующейся связи. Пример этого демонстрируется как:
nC 6 H 12 O 6 → -[-C 6 H 10 O 5 -]-n + nH 2 O
Осаждение Химические реакции Смешивание раствора нитрата серебра с раствором хлорида калия приводит к образованию белого нерастворимого вещества. Каждый раз, когда вы образуете нерастворимое твердое вещество в растворе, это называется осаждением, а образующееся белое нерастворимое твердое вещество называется хлоридом серебра.
Каждый раз, когда вы образуете нерастворимое твердое вещество в растворе, это называется осаждением, а образующееся белое нерастворимое твердое вещество называется хлоридом серебра.
Окислительно-восстановительные химические реакции Эти реакции, также называемые химическими реакциями восстановления-окисления, включают обмен электронами.
Это также примеры других типов реакций, включая реакции сочетания, реакции простого замещения и реакции горения, но все они являются окислительно-восстановительными реакциями. Все они связаны с переносом электронов от одного химического вида к другому.
Окислительно-восстановительные химические реакции также участвуют в процессах ржавчины, фотосинтеза, горения, батарей, дыхания и многих других процессах.
Химические реакции с одним замещением Реакции с одним замещением происходят, когда более активный элемент вытесняет или выталкивает из соединения другой менее активный элемент. Например, если вы поместите немного металлического цинка в раствор сульфата меди, цинк фактически вытеснит медь.
Например, если вы поместите немного металлического цинка в раствор сульфата меди, цинк фактически вытеснит медь.
В этом уравнении обозначение (водн.) означает, что соединение растворено в воде, которая представляет собой водный раствор. Поскольку в данном случае цинк заменяет медь, он считается более активным. Если вы поместите кусок меди в раствор сульфата цинка, ничего не произойдет.
Дополнительную информацию о химических реакциях можно посмотреть здесь.
Глоссарий алгебраических терминов Абсолютное значение: Относится к расстоянию от 0,
Алгебра: Тип математики, использующий математические символы и правила, используемые для работы с этими символами.
Связанный закон сложения: Утверждается, что для любых трех чисел a, b и c всегда верно следующее: (a+b)+c=a+(b+c)
Основание: Число увеличено к власти.
Потолок Функция: Потолок(x) — ближайшее целое число, большее или равное x.
Коэффициент: Это константа, умноженная на выражение или переменную.
Состав: Композиция двух функций, f и g, представляет собой функцию f∘g, которая преобразует x в f(g(x)).
Координаты: Точка на двумерной плоскости всегда описывается парой: (x, y). В этом примере координата x задается метками под сеткой, а координата y задается метками, найденными слева от сетки.
Кубический корень : Кубический корень из а, который записывается как 3 а, представляет собой число, кубом которого является а; другими словами, ( 3 а) 3 =а.
Данные : Набор связанных измерений.
Домен: Набор входных данных (координат x) функции или отношения.
Уравнение: Математическое предложение со знаком равенства; например, 3x+5=11.
Показатель степени: В степени представляет собой количество раз, когда основание умножается само на себя.
Выражение: Комбинация чисел и переменных с использованием арифметики; например, 6-х.
Фактор: Выражение, умноженное на другое выражение, или выражение, которое можно умножить на другое выражение для получения определенного результата.
Функция: Отношение, при котором координата x не встречается более чем в одной упорядоченной паре (x, y). Другими словами, подумайте о функции как о преобразовании, переводящем каждую координату x в соответствующую ей единственную координату y.
Неравенство: Это математическая последовательность, использующая один из следующих символов: <, >, ≤ или ≥.
Целое число: Целое число или отрицательное значение целого числа; например, 37, 0 и -5 — целые числа, а 2,7 — нет.
Изолировать: Чтобы переменная появлялась одна на одной стороне неравенства или уравнения и не появлялась на другой стороне неравенства или уравнения.
Совместная частота: Это относится к количеству событий, которые удовлетворяют обеим частям двух указанных критериев.
Совместная относительная частота: Это общая частота, разделенная на общее количество событий.
Моник: Многочлен, первый или старший коэффициент которого равен 1.
Моном: Произведение чисел и переменных; например, 3x или 5x 2 . Его также иногда называют термином.
Корень энной степени: Корнем энной степени из а является число b, имеющее энную степень числа а. Другими словами, b n =a.
Начало: Это точка на координатной плоскости, где оси x и оси y пересекаются друг с другом. Он всегда представлен координатами (0,0).
Кусочно-определяемая функция: Это функция, определяемая разными формулами для разных входных данных.
Точка: Точка – это точка на координатной плоскости. Он имеет координаты (x, y), где x задается метками под координатной сеткой, а y задается метками слева от координатной сетки.
Он имеет координаты (x, y), где x задается метками под координатной сеткой, а y задается метками слева от координатной сетки.
Диапазон: Набор выходных данных, т. е. координат y, функции или отношения.
Отношение: Этот термин относится к набору упорядоченных пар, т. е. (x, y).
Относительная частота: Частота, деленная на общее количество событий. Обычно выражается в процентах.
Последовательность: Список чисел, которые могут быть сгенерированы по некоторому правилу.
Набор: Неупорядоченный набор чисел или других объектов математического характера без повторений.
Аналогично: Две геометрические фигуры считаются подобными, если они имеют одинаковую форму, но потенциально разные размеры, а также соответствующие длины, отличающиеся одним общим масштабным коэффициентом.
Упрощение: Это относится к переписыванию выражения, при котором оно означает то же самое, но короче или проще. Например, вы можете просто 3x-x+6 превратить в 2x+6.
Например, вы можете просто 3x-x+6 превратить в 2x+6.
Наклон: Это число показывает, насколько крута линия. Он показывает величину изменения высоты линии при перемещении на одну единицу вправо. Например, наклон линии y=mx+b соответствует букве m.
Форма пересечения наклона: Для линейного уравнения используется форма y=mx+b, где b и m являются константами. Числа b и m задают наклон и точку пересечения по оси y линии, которая представляет собой график в этом конкретном разделе.
Решение: В любом неравенстве или уравнении числа могут быть заменены на переменную, чтобы это уравнение или неравенство стало верным. Если в неравенстве уравнения более одной переменной, решение относится к списку чисел, которые при замене списка переменных делают неравенство или уравнение верным. Для систем с более чем одним неравенством или уравнением решение должно сделать все неравенства или уравнения верными. Кроме того, в химии под раствором понимается жидкая смесь.
Набор решений: Это относится ко всем решениям неравенства, уравнения или системы.
Решить: Решить — значит найти решение неравенства, уравнения или системы.
Квадратный корень: Квадратный корень из a — это число b, квадрат которого равен a. Другими словами, b2=a. Если b — квадратный корень из a, то и -b тоже.
Стандартное отклонение: Этот термин относится к квадратному корню из дисперсии.
Стандартная форма: В линейном уравнении форма Ax+By=C, где A, B и C являются константами. Для квадратных уравнений используется либо форма ax2+bx+c=0, либо форма y=ax2+bx+c, где a, b и c — константы.
Статистика: Статистика – это число, которое описывает или обобщает данные.
Статистика: Статистика — это изучение данных; это также относится к методам, используемым для обобщения или описания данных.
Ступенчатая функция: Это относится к кусочно-определяемой функции, при которой формула каждой части постоянна; то есть он не меняется с x. На самом деле график функции выглядит как ступени лестницы.
На самом деле график функции выглядит как ступени лестницы.
Замена: Это исключение переменной в уравнении или выражении; это делается путем замены его другим выражением, которому оно равно.
Система: Для неравенств или уравнений достаточно, чтобы два или более из них были истинными.
Таблица: Математический термин, включающий прямоугольное расположение столбцов и строк.
Термин: Термин – это элемент разности, суммы или последовательности.
Трансляция: Трансляция – это жесткое движение на постоянное расстояние в одном направлении; то есть без отражения или вращения.
Единица измерения: Относится к стандартным измерениям; например, час или метр.
Значение: Это число, которому может быть равно либо выражение, либо переменная.
Переменная: Буква (например, x), которая используется для обозначения разных чисел в разное время.
Дисперсия: Среднеквадратичное расстояние значений данных от их среднего значения m. его можно вычислить, добавив (x-m)2 для каждого значения данных x, а затем разделив на количество значений данных n. Если вы измеряете выборки из совокупности (например, рост людей), дисперсия выборки обычно отличается от дисперсии всей совокупности.
Вершина: Это точка, в которой парабола пересекает свою ось симметрии, или конец стороны многоугольника, или даже угловая точка угла.
Математические уравнения: изучите различные типы уравнений
В математике уравнение — это утверждение, что два выражения равны. Он состоит из двух выражений слева и справа от символа «равно». Существуют различные математические уравнения. Ниже приведен пример математического уравнения:
7+8=15
Уравнение утверждает, что 7 + 8 равно 15. Наиболее распространенные математические уравнения включают одну или несколько переменных (символы, обозначающие неизвестные). Например,
Например,
x=15+25
Поскольку обе части уравнений должны быть равны, x=37. Есть только одно значение x, которое делает уравнение верным. Это означает, что 37 удовлетворяет уравнению. Способ нахождения значения (значений) переменной, удовлетворяющей уравнению, называется «решением уравнения».
Распространенная ошибка думать, что выражение представляет собой уравнение вида 92-7.
Выражения не утверждают равенства. Помните, уравнение должно иметь знак равенства и быть истинным.
Существует множество типов математических уравнений. Алгебраические, трансцендентные, параметрические, дифференциальные, интегральные — вот лишь некоторые из различных типов уравнений. В этой статье речь пойдет о решении наиболее распространенных алгебраических уравнений.
1. Линейные математические уравнения
Линейные уравнения — это любые математические уравнения, которые можно записать в форме
ax+b=0
, где a и b — действительные числа, а x — переменная. Это иногда называют стандартной формой линейного уравнения.
Это иногда называют стандартной формой линейного уравнения.
Существует множество способов решения линейных уравнений, в зависимости от уровня сложности линейного уравнения, которое вы пытаетесь решить. Эмпирическое правило решения любого уравнения заключается в уравновешивании . Что бы вы ни делали с одной частью уравнения, то же самое следует делать и с другой его частью. Это приведет нас к свойствам равенства, которые будут активно использоваться при решении математических уравнений. Например, решить
9(x+4)+2x=64-3x
Сначала упростим обе части уравнения. Удалите любые группировки по дистрибутивному закону. Затем объедините подобные термины.
\begin{alignedat}{2}9x+36+2x=64−3x\\ 11x+36=64-3x\end{alignedat}
Следующим шагом является прибавление 3x к обеим сторонам и вычитание 36 из обеих сторон стороны уравнения.
11x+3x+36-36=64-36-3x+3x\\14x=28
Затем разделите обе части на 14.
\frac { 14x }{ 14 } =\frac { 28 }{ 24 } \\x=2
В отдельной статье мы будем иметь дело с другими линейными уравнениями, например, с дробными коэффициентами и уравнениями пропорций. 9{ 2 }+bx+c=0 , где a≠0
9{ 2 }+bx+c=0 , где a≠0
Существует несколько способов решения квадратных уравнений, таких как разложение на множители, свойство квадратного корня, квадратичная формула путем завершения квадрата, а также недавно разработанный в 2019 году метод профессора Ло. В этой статье мы обсудим три основных способа: разложение на множители, свойство квадратного корня и квадратичную формулу. Квадратичная формула и свойство квадратного корня будут работать всегда. Хотя метод факторинга не всегда будет работать. Последнему требуется немного больше работы, чтобы его можно было использовать в некоторых квадратичных вычислениях.
Решение с помощью разложения на множители
Некоторые квадратичные уравнения можно решить с помощью простого разложения на множители. В этом методе нам нужно будет запомнить свойство нулевого продукта, в котором указано
. Если ab=0, то a=0 или b=0 (или оба).
Это означает, что если \left( x-2 \right) \left( x+3 \right) =0 , то
x-2=0 или x+3=0
Следовательно, x=2 или x =3 . Свойство нулевого продукта не будет работать, как
Свойство нулевого продукта не будет работать, как
ab=10 , тогда a=2 или b=5.
Уравнение всегда должно быть равно нулю, чтобы оно работало. 9{ 2 }-4\left( 1 \right) \left( -7 \right) } }{ 2\left( 1 \right) }\\x&=\frac { 5\pm \sqrt { 25+28 } } { 2 }\\x&=\frac { 5\pm \sqrt { 53 } }{ 2 } \end{alignedat}
Вы должны знать как минимум два способа решения квадратных уравнений, поэтому можете использовать один из них, чтобы перепроверить свой ответ .
3. Полиномиальные уравнения
Полиномиальные уравнения забирают предел степени, которую вы можете иметь в уравнении. Это означает, что линейные, квадратные и кубические уравнения являются полиномиальными уравнениями. Полиномиальные уравнения более высокой степени иногда можно решить с помощью факторизации. 9{ 2 }+16x+64 и 361 — оба идеальные квадраты. Разложите все выражение, используя то, что мы знаем о разнице квадратов.
x\left( { x+8-19 } \right) \left( x+8+19 \right) =0
Упростите левую часть, затем решите forx. { 2 }\quad &= \квадратный { 9{ 2 }\\x+3&=81\\x+3-3&=81-3\\x&=78\end{выровнено по}.
{ 2 }\quad &= \квадратный { 9{ 2 }\\x+3&=81\\x+3-3&=81-3\\x&=78\end{выровнено по}.
Как и в любом уравнении, мы всегда хотим подставить полученное значение переменной обратно в уравнение, чтобы проверить, верно ли наше решение. Мы делаем это специально для радикальных математических уравнений, потому что иногда у нас может быть лишнее решение — ошибочное значение переменной, которое не удовлетворяет уравнению.
\begin{alignedat}{2}\sqrt { 78+3 } -9& ≟0\\\sqrt { 81 } -9& ≟0\\9-9&≟0\\0&=0\quad True\end{ выровнено} 92+3x-4&=0\\\left( x+4 \right) \left( x-1 \right) &=0 \end{alignedat}
\begin{alignedat}{2}x&=-4\end {alignedat} или \begin{alignedat}{2}x&=1\end{alignedat}
Проверить наличие посторонних решений.
\begin{alignedat}{2}\sqrt { 5-\left(-4 \right)} -1+1&≟-4+1\\\sqrt {9} -1+1&≟-3\\3 -1+1 &≟ -3\\3&\neq -3\quad False\end{alignedat}
\begin{alignedat}{2}\sqrt { 5-1 } -1+1 &≟ 1+1\ \\sqrt { 4-1 } +1&≟2\\2-1+1&≟ 2\\2&=2\quad True\end{alignedat}
Следовательно, единственным решением уравнения является x=1.
Имейте в виду, что при решении уравнений с квадратным корнем всегда нужно проверять наличие посторонних решений. Уравнение с квадратным корнем может иметь только одно решение или вообще не иметь его.
5. Экспоненциальные уравнения
Экспоненциальные уравнения – это уравнения, в которых переменные встречаются в качестве показателя степени. Есть два способа решения показательных уравнений. Но мы ограничимся решением показательных уравнений, сделав основания в обеих частях уравнений одинаковыми (первое, что мы хотим проверить в первую очередь, если это возможно). Мы обсудим решение показательных уравнений с использованием журналов в другой статье. 9{ \frac { 1 }{ 2 } }\end{alignedat}
Приравняйте уравнения с обеих сторон и найдите x.
\begin{alignedat}{2}7x-\frac { 39 }{ 2 } &=\frac { 1 }{ 2 }\\2\left( 7x-\frac { 39 }{ 2 } \right)& =\frac { 1 }{ 2 } \left( 2 \right)\\14x-39&=1\\14x-39+39&=1+39\\\frac { 14x }{ 14 } &=\frac { 40 }{ 14 }\\x&=\frac { 20 }{ 7 }\end{alignedat}
Заключение
Помните, что при решении уравнения всегда следует применять правило «что бы вы ни делали с одной стороной, делайте это с другой стороны». другой.» В следующих статьях мы рассмотрим больше алгебраических уравнений и дадим простые способы их решения. А пока просматривайте нашу страницу блога, чтобы найти разные забавные образовательные блоги по математике.
другой.» В следующих статьях мы рассмотрим больше алгебраических уравнений и дадим простые способы их решения. А пока просматривайте нашу страницу блога, чтобы найти разные забавные образовательные блоги по математике.
Резюме
Типы уравнений | Superprof
Если вы здесь, значит, вы знаете, что такое уравнение. В этом мире бесконечные уравнения. Нам потребовалось бы много времени, чтобы понять их, если бы мы не классифицировали их. Вот почему математики классифицировали уравнения по разным типам, чтобы их было легче понять. Самым большим преимуществом категоризации уравнений является то, что мы можем легко с ними справиться. Как только мы найдем тип уравнения, мы можем легко решить его, чтобы найти корни или решения. Например, если вы видите такое уравнение, первое, что вы сделаете, это поймете его. Вы знаете, что это квадратное уравнение, и следующее, о чем вы будете думать, это как решить это квадратное уравнение? С помощью разбиения среднего члена или квадратичной формулы. Ну, это история для другого блога, но мы знаем, что вам должно быть интересно, что такое квадратное уравнение? Продолжайте читать, чтобы узнать.
Ну, это история для другого блога, но мы знаем, что вам должно быть интересно, что такое квадратное уравнение? Продолжайте читать, чтобы узнать.
Проверьте, нет ли поблизости выдающихся репетиторов по математике.
1. Полиномиальные уравнения
Полиномиальные уравнения имеют вид P(x) = 0, где P(x) — полином. Эти типы уравнений также известны как эквивалентные уравнения, потому что обе части уравнения имеют одно и то же решение. Кроме того, в уравнении может быть более одного неизвестного. Слово «поли» означает «более одного», а «номинальный» означает количество терминов. Существует три типа полиномиальных уравнений.
Типы полиномиальных уравнений
1.1 Линейные уравнения
Линейные уравнения – это уравнения типа , с , или любые другие уравнения, в которых члены могут быть обработаны и упрощены до уравнения той же формы. Например:
Введение с обеих сторон уравнения:
Граф линейного уравнения всегда будет прямой линейкой. Степень линейного уравнения всегда будет .
Степень линейного уравнения всегда будет .
1.2 Квадратные уравнения
Квадратные уравнения – это уравнения типа , где . Квадратное уравнение всегда будет иметь 2 корня. Вы даже можете преобразовать другие уравнения в квадратные уравнения, мы называем их «биквадратными уравнениями» . Если вы нарисуете график квадратного уравнения, вы обнаружите, что график имеет U-образную форму. График всегда будет иметь точку максимума или минимума, и эта же точка также известна как точка симметрии. Это означает, что в этот момент, если вы объедините обе стороны, они будут перекрывать друг друга. Степень квадратного уравнения всегда будет .
Получите информацию о стоимости обучения математике в Великобритании.
1.3 Полиномиальное уравнение
В этот момент вы, должно быть, задаетесь вопросом, что мы изучаем полиномиальное и почему полиномиальный тип имеет то же имя, что и «полиномиальный»? Если уравнение не является ни линейным, ни квадратичным, мы называем это уравнение полиномиальным. Например, этот тип уравнения является полиномиальным уравнением. Степень этих типов уравнений всегда будет больше . Кубическое уравнение, как и уравнение четвертой степени, является типом полиномиального уравнения.
Например, этот тип уравнения является полиномиальным уравнением. Степень этих типов уравнений всегда будет больше . Кубическое уравнение, как и уравнение четвертой степени, является типом полиномиального уравнения.
Лучшие репетиторы по математике
Поехали
Неполные квадратные уравнения
Неполные уравнения — это разновидность квадратных уравнений. Если значение b или c (в некоторых случаях даже оба) равны нулю, полученное уравнение будет неполным уравнением. Ниже приведены некоторые примеры неполных уравнений:
Решение неполных уравнений очень просто и не требует сложной математики (или других формул).
1.3 Кубические уравнения
Кубические уравнения – это уравнения типа , с . Степень кубического уравнения всегда будет .
1.4 Уравнения четвертой степени
Уравнения четвертой степени – это уравнения типа , . Кроме того, полиномиальная степень уравнения четвертой степени всегда будет .
Биквадратные уравнения
Биквадратные уравнения — это уравнения четвертой степени, в которых нет членов с нечетной степенью. По сути, это уравнение высокой полиномиальной степени, но оно преобразуется в квадратное уравнение, что упрощает его решение.
По сути, это уравнение высокой полиномиальной степени, но оно преобразуется в квадратное уравнение, что упрощает его решение.
, с.
2. Рациональные полиномиальные уравнения
Рациональные полиномиальные уравнения имеют вид , где и – полиномы. Слово «рациональное» означает отношение, что означает, что рациональные полиномиальные уравнения всегда будут дробными. Кроме того, и не будет равно нулю.
3. Иррациональные полиномиальные уравнения
Иррациональные уравнения – это те, в которых есть по крайней мере полином под знаком радикала.
4. Трансцендентные уравнения
Трансцендентные уравнения — это уравнения, включающие трансцендентные функции.
4.1 Показательные уравнения
Показательные уравнения — это уравнения, в которых неизвестное входит в показатель степени.
4.2 Логарифмические уравнения
Логарифмические уравнения – это уравнения, в которых на неизвестное влияет логарифм.
 (Или вам может понравиться «7 различных типов фракций»)
(Или вам может понравиться «7 различных типов фракций»)
 Примеры включают следующее:
Примеры включают следующее: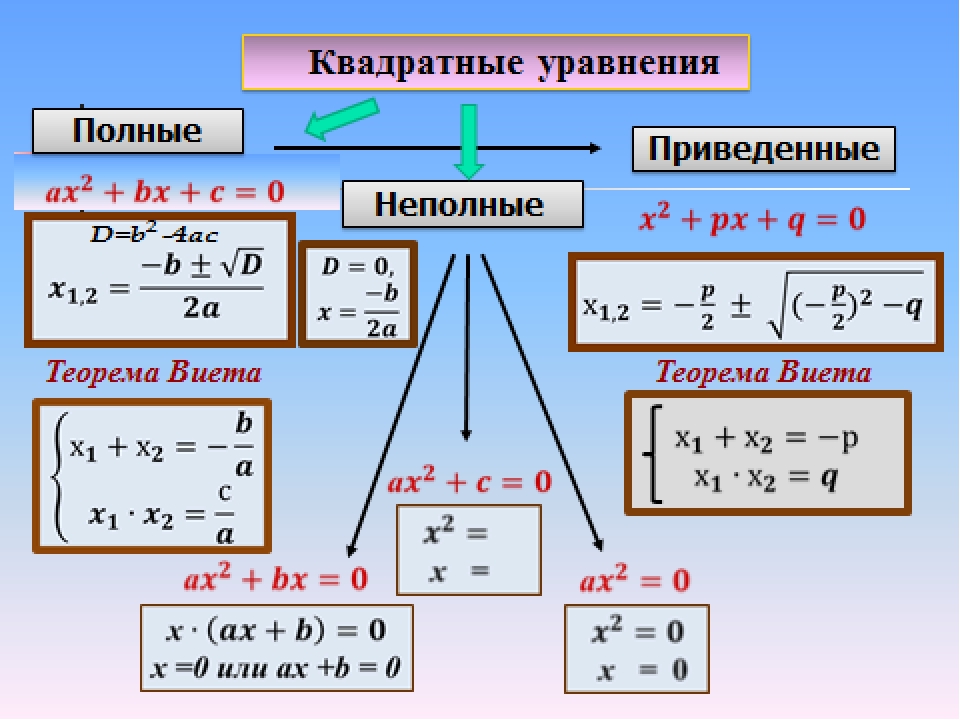 Каждый раз, когда вы образуете нерастворимое твердое вещество в растворе, это называется осаждением, а образующееся белое нерастворимое твердое вещество называется хлоридом серебра.
Каждый раз, когда вы образуете нерастворимое твердое вещество в растворе, это называется осаждением, а образующееся белое нерастворимое твердое вещество называется хлоридом серебра. Например, если вы поместите немного металлического цинка в раствор сульфата меди, цинк фактически вытеснит медь.
Например, если вы поместите немного металлического цинка в раствор сульфата меди, цинк фактически вытеснит медь.Алгебра: Тип математики, использующий математические символы и правила, используемые для работы с этими символами.
Связанный закон сложения: Утверждается, что для любых трех чисел a, b и c всегда верно следующее: (a+b)+c=a+(b+c)
Основание: Число увеличено к власти.
Потолок Функция: Потолок(x) — ближайшее целое число, большее или равное x.

Коэффициент: Это константа, умноженная на выражение или переменную.
Состав: Композиция двух функций, f и g, представляет собой функцию f∘g, которая преобразует x в f(g(x)).
Координаты: Точка на двумерной плоскости всегда описывается парой: (x, y). В этом примере координата x задается метками под сеткой, а координата y задается метками, найденными слева от сетки.
Кубический корень : Кубический корень из а, который записывается как 3 а, представляет собой число, кубом которого является а; другими словами, ( 3 а) 3 =а.
Данные : Набор связанных измерений.
Домен: Набор входных данных (координат x) функции или отношения.
Уравнение: Математическое предложение со знаком равенства; например, 3x+5=11.
Показатель степени: В степени представляет собой количество раз, когда основание умножается само на себя.

Выражение: Комбинация чисел и переменных с использованием арифметики; например, 6-х.
Фактор: Выражение, умноженное на другое выражение, или выражение, которое можно умножить на другое выражение для получения определенного результата.
Функция: Отношение, при котором координата x не встречается более чем в одной упорядоченной паре (x, y). Другими словами, подумайте о функции как о преобразовании, переводящем каждую координату x в соответствующую ей единственную координату y.
Неравенство: Это математическая последовательность, использующая один из следующих символов: <, >, ≤ или ≥.
Целое число: Целое число или отрицательное значение целого числа; например, 37, 0 и -5 — целые числа, а 2,7 — нет.
Изолировать: Чтобы переменная появлялась одна на одной стороне неравенства или уравнения и не появлялась на другой стороне неравенства или уравнения.

Совместная частота: Это относится к количеству событий, которые удовлетворяют обеим частям двух указанных критериев.
Совместная относительная частота: Это общая частота, разделенная на общее количество событий.
Моник: Многочлен, первый или старший коэффициент которого равен 1.
Моном: Произведение чисел и переменных; например, 3x или 5x 2 . Его также иногда называют термином.
Корень энной степени: Корнем энной степени из а является число b, имеющее энную степень числа а. Другими словами, b n =a.
Начало: Это точка на координатной плоскости, где оси x и оси y пересекаются друг с другом. Он всегда представлен координатами (0,0).
Кусочно-определяемая функция: Это функция, определяемая разными формулами для разных входных данных.
Точка: Точка – это точка на координатной плоскости.
 Он имеет координаты (x, y), где x задается метками под координатной сеткой, а y задается метками слева от координатной сетки.
Он имеет координаты (x, y), где x задается метками под координатной сеткой, а y задается метками слева от координатной сетки. Диапазон: Набор выходных данных, т. е. координат y, функции или отношения.
Отношение: Этот термин относится к набору упорядоченных пар, т. е. (x, y).
Относительная частота: Частота, деленная на общее количество событий. Обычно выражается в процентах.
Последовательность: Список чисел, которые могут быть сгенерированы по некоторому правилу.
Набор: Неупорядоченный набор чисел или других объектов математического характера без повторений.
Аналогично: Две геометрические фигуры считаются подобными, если они имеют одинаковую форму, но потенциально разные размеры, а также соответствующие длины, отличающиеся одним общим масштабным коэффициентом.
Упрощение: Это относится к переписыванию выражения, при котором оно означает то же самое, но короче или проще.
 Например, вы можете просто 3x-x+6 превратить в 2x+6.
Например, вы можете просто 3x-x+6 превратить в 2x+6. Наклон: Это число показывает, насколько крута линия. Он показывает величину изменения высоты линии при перемещении на одну единицу вправо. Например, наклон линии y=mx+b соответствует букве m.
Форма пересечения наклона: Для линейного уравнения используется форма y=mx+b, где b и m являются константами. Числа b и m задают наклон и точку пересечения по оси y линии, которая представляет собой график в этом конкретном разделе.
Решение: В любом неравенстве или уравнении числа могут быть заменены на переменную, чтобы это уравнение или неравенство стало верным. Если в неравенстве уравнения более одной переменной, решение относится к списку чисел, которые при замене списка переменных делают неравенство или уравнение верным. Для систем с более чем одним неравенством или уравнением решение должно сделать все неравенства или уравнения верными. Кроме того, в химии под раствором понимается жидкая смесь.

Набор решений: Это относится ко всем решениям неравенства, уравнения или системы.
Решить: Решить — значит найти решение неравенства, уравнения или системы.
Квадратный корень: Квадратный корень из a — это число b, квадрат которого равен a. Другими словами, b2=a. Если b — квадратный корень из a, то и -b тоже.
Стандартное отклонение: Этот термин относится к квадратному корню из дисперсии.
Стандартная форма: В линейном уравнении форма Ax+By=C, где A, B и C являются константами. Для квадратных уравнений используется либо форма ax2+bx+c=0, либо форма y=ax2+bx+c, где a, b и c — константы.
Статистика: Статистика – это число, которое описывает или обобщает данные.
Статистика: Статистика — это изучение данных; это также относится к методам, используемым для обобщения или описания данных.
Ступенчатая функция: Это относится к кусочно-определяемой функции, при которой формула каждой части постоянна; то есть он не меняется с x.
 На самом деле график функции выглядит как ступени лестницы.
На самом деле график функции выглядит как ступени лестницы. Замена: Это исключение переменной в уравнении или выражении; это делается путем замены его другим выражением, которому оно равно.
Система: Для неравенств или уравнений достаточно, чтобы два или более из них были истинными.
Таблица: Математический термин, включающий прямоугольное расположение столбцов и строк.
Термин: Термин – это элемент разности, суммы или последовательности.
Трансляция: Трансляция – это жесткое движение на постоянное расстояние в одном направлении; то есть без отражения или вращения.
Единица измерения: Относится к стандартным измерениям; например, час или метр.
Значение: Это число, которому может быть равно либо выражение, либо переменная.
Переменная: Буква (например, x), которая используется для обозначения разных чисел в разное время.

Дисперсия: Среднеквадратичное расстояние значений данных от их среднего значения m. его можно вычислить, добавив (x-m)2 для каждого значения данных x, а затем разделив на количество значений данных n. Если вы измеряете выборки из совокупности (например, рост людей), дисперсия выборки обычно отличается от дисперсии всей совокупности.
Вершина: Это точка, в которой парабола пересекает свою ось симметрии, или конец стороны многоугольника, или даже угловая точка угла.
 Например,
Например, Это иногда называют стандартной формой линейного уравнения.
Это иногда называют стандартной формой линейного уравнения. 9{ 2 }+bx+c=0 , где a≠0
9{ 2 }+bx+c=0 , где a≠0 Свойство нулевого продукта не будет работать, как
Свойство нулевого продукта не будет работать, как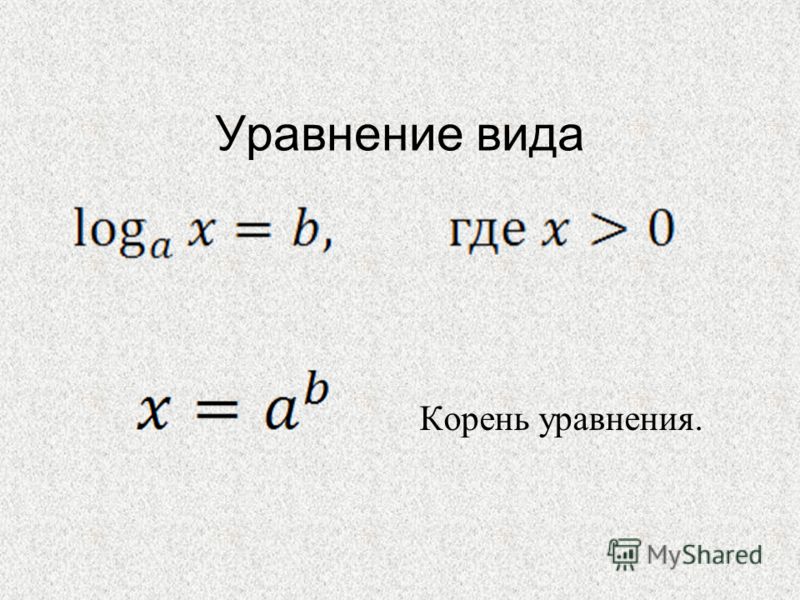 { 2 }\quad &= \квадратный { 9{ 2 }\\x+3&=81\\x+3-3&=81-3\\x&=78\end{выровнено по}.
{ 2 }\quad &= \квадратный { 9{ 2 }\\x+3&=81\\x+3-3&=81-3\\x&=78\end{выровнено по}.\begin{alignedat}{2}x&=-4\end {alignedat} или \begin{alignedat}{2}x&=1\end{alignedat}

 другой.» В следующих статьях мы рассмотрим больше алгебраических уравнений и дадим простые способы их решения. А пока просматривайте нашу страницу блога, чтобы найти разные забавные образовательные блоги по математике.
другой.» В следующих статьях мы рассмотрим больше алгебраических уравнений и дадим простые способы их решения. А пока просматривайте нашу страницу блога, чтобы найти разные забавные образовательные блоги по математике.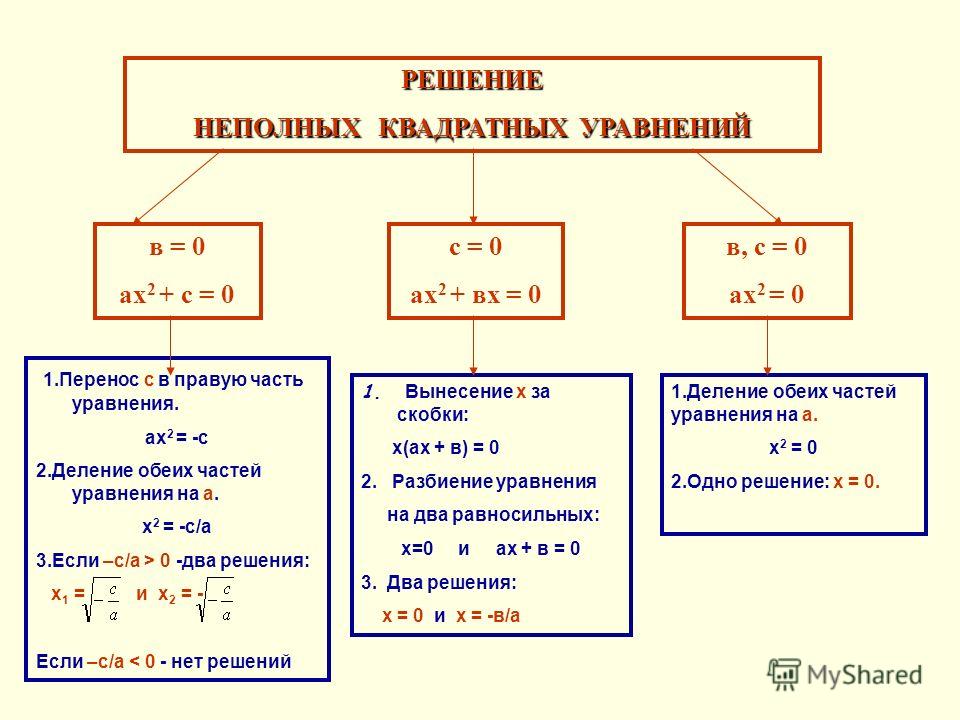 Ну, это история для другого блога, но мы знаем, что вам должно быть интересно, что такое квадратное уравнение? Продолжайте читать, чтобы узнать.
Ну, это история для другого блога, но мы знаем, что вам должно быть интересно, что такое квадратное уравнение? Продолжайте читать, чтобы узнать. Степень линейного уравнения всегда будет .
Степень линейного уравнения всегда будет . Например, этот тип уравнения является полиномиальным уравнением. Степень этих типов уравнений всегда будет больше . Кубическое уравнение, как и уравнение четвертой степени, является типом полиномиального уравнения.
Например, этот тип уравнения является полиномиальным уравнением. Степень этих типов уравнений всегда будет больше . Кубическое уравнение, как и уравнение четвертой степени, является типом полиномиального уравнения. По сути, это уравнение высокой полиномиальной степени, но оно преобразуется в квадратное уравнение, что упрощает его решение.
По сути, это уравнение высокой полиномиальной степени, но оно преобразуется в квадратное уравнение, что упрощает его решение.



 М., Саакян С.М. Дидактические материалы
по алгебре и началам анализа для 10 кл., 11 кл. М.:
Просвещение. 2002.
М., Саакян С.М. Дидактические материалы
по алгебре и началам анализа для 10 кл., 11 кл. М.:
Просвещение. 2002. Прививать чувство сопереживания и участия при ответах своих одногруппников.
Прививать чувство сопереживания и участия при ответах своих одногруппников.

 Примеры включают следующее:
Примеры включают следующее: Пример и общая форма показаны ниже.
Пример и общая форма показаны ниже.