VCE Математические методы — Разделы 1 и 2 — 6A
Цели обучения:
В этом разделе мы рассмотрим:
- Граф квадратного корня и его преобразования (расширения, отражения и переводы).
- Как построить график функции квадратного корня из заданного уравнения.
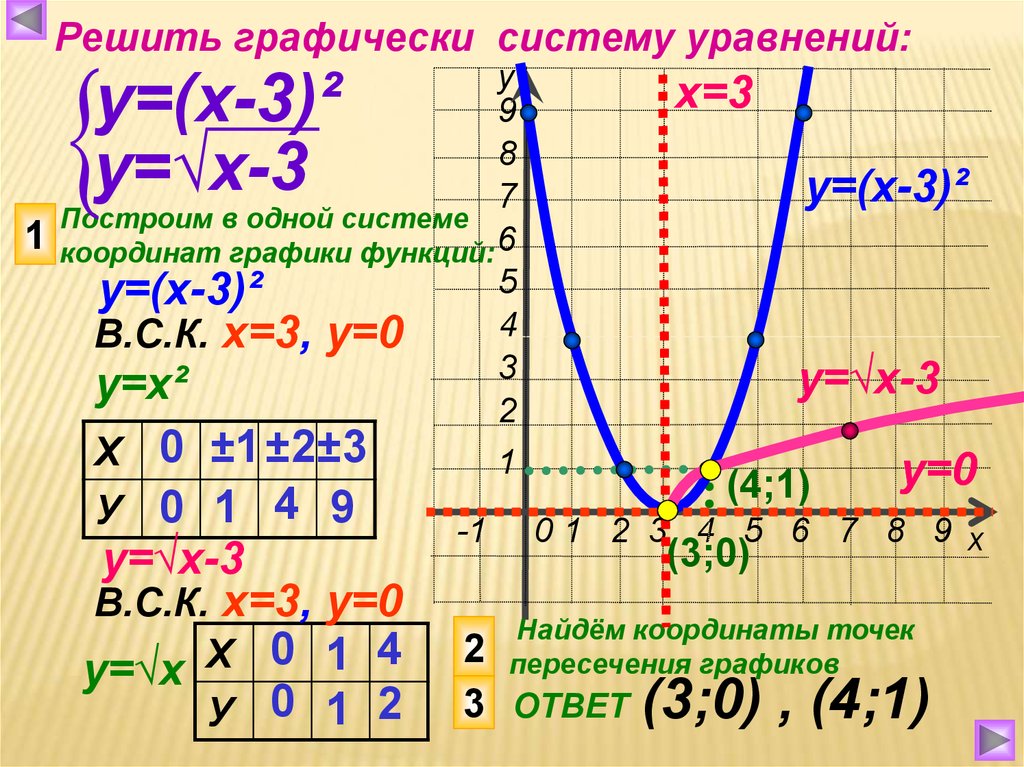
График квадратного корня
Функция квадратного корня имеет общий вид: параметры а, н, з и к .
Введение в граф квадратного корня
Рассмотрим следующие числа и их квадратные корни:
Таблица 1 см. форму графика квадратного корня:
Рисунок 1 — График квадратного корня.
Отражение по оси x 9Рисунок 2
Отражение по оси y
Отражение по оси x происходит при наличии отрицательного члена n :
Рисунок 3 — График квадратного корня и -ось.
Заглядывая вперед: область определения функции
В ближайшем будущем мы рассмотрим область определения функции. Домен — это набор всех координат x (или первых элементов пары порядка). Когда мы рассматриваем области определения функций, они могут быть максимальными/подразумеваемыми или ограниченными.
- Для функции квадратного корня максимальная область определения ограничена выражением под квадратным корнем, которое больше или равно нулю. Это потому, что вы не можете получить квадратный корень из отрицательного числа — он не определен.
Преобразования графика квадратного корня
При рассмотрении преобразования графика квадратного корня проще всего иметь уравнение в следующей форме:
Мы можем учитывать влияние каждого параметра ( a, n , h и k ) на графе квадратного корня.
- и вызовут вертикальное расширение в и раз относительно оси x .

- n приведет к горизонтальному расширению — если n < 0 (отрицательный) график отражается по оси y .
- h приведет к горизонтальному перемещению h единиц.
- k приведет к вертикальному перемещению k единиц.
Изучение индивидуальных эффектов A , H и K
Эффекты параметра A
0025 a на графике квадратного корня
- Пожалуйста нажмите кнопку воспроизведения в нижнем левом углу, чтобы оживить !
Из приведенного выше графика видно, что:
- Когда a > 1, график круче.
- Когда 0 < a < 1, график становится более мелким.
- когда a < 0 (отрицательный) график отражает по оси x .
a вызывает расширение в a раз от оси x .
Влияние параметра n
Динамический рабочий лист GeoGebra иллюстрирует влияние n на график квадратного корня оживить !
Из графика выше видно, что:
- когда n < 0 (отрицательный) график отражает по оси y .
Влияние параметра h
Динамический рабочий лист GeoGebra иллюстрирует влияние параметра h на график квадратного корня.
- Пожалуйста, нажмите кнопку воспроизведения в левом нижнем углу, чтобы оживить !
Из графика выше видно, что:
- Когда ч > 0 (положительное) график переводится ч единиц в отрицательном x -направлении.
- Когда h < 0 (отрицательное) график смещается на h единиц в положительном x -направлении.

Влияние параметра k
Динамический рабочий лист GeoGebra иллюстрирует влияние k на графике квадратного корня.
- Пожалуйста, нажмите кнопку воспроизведения в левом нижнем углу, чтобы оживить !
На приведенном выше графике мы видим, что:
- Когда K> 0 (положительный) График переводится H .
- Когда k < 0 (отрицательный) график переводится ч единиц в отрицательном у -направлении.
Изучение комбинированных эффектов A , H и K
Рабочий лист динамической геогебры иллюстрирует комбинированный эффект A , H и K . , H и K .
- Пожалуйста, используйте ползунки для настройки параметров и наблюдения за преобразованиями.

Скоро!
График функции квадратного корня
При построении графика функции квадратного корня необходимо обозначить (с координатами):
- Любые точки пересечения осей (если они существуют).
- Конечные точки функции.
Прежде чем строить график функции квадратного корня, убедитесь, что он имеет следующую форму:
Чтобы найти x -перехват пусть y = 0 и найдите x .
Чтобы найти y -перехват , пусть x = 0 и найдите y .
Конечная точка графа квадратного корня будет находиться в точке ( h, k ), если не указано иное.
6A — ВИДЕО ПРИМЕР 1 :
Постройте следующую функцию квадратного корня:
youtube.com/embed/uFR5z8Uzy9Y» allowfullscreen=»»/> 6A — ВИДЕО ПРИМЕР 20005 6A — Видео Пример 3 : График. Следующая квадратная функция корня: 6A — Видео Пример 4 : График. Следующая квадратная функция: УСПЕКЦИЯ. Вы добьетесь успеха, если сможете: В этой статье показано, как нарисовать график функции квадратного корня, используя только три разных значения для «x», затем нахождение точек, через которые рисуется график уравнений / функций, также покажет, как графики перемещаются по вертикали (движется вверх или вниз), перемещаются по горизонтали (двигаются влево или вправо) и как график одновременно делает Оба перевода. Уравнение функции квадратного корня имеет форму… y = f(x) = A√x, где (A) не должно быть равно нулю (0). Если (A) больше нуля ( 0 ), то есть ( A ) является положительным числом, то форма графика функции квадратного корня аналогична верхней половине буквы «C». Чтобы нарисовать график уравнения… y = f(x) = A√x, мы выбираем три значения для ‘x’, x = (-1), x = (0) и x = (1 ). Мы подставляем каждое значение ‘x’ в уравнение,… y = f(x) = A√x и получаем соответствующее значение для каждого ‘y’. Учитывая y = f(x) = A√x, где (A) — действительное число и (A) не равно нулю (0), и подставляя x = (-1) в уравнение, мы получаем y = f(-1) = A√(-1) = i (это мнимое число). Итак, Первая точка не имеет реальных координат, следовательно, через эту точку нельзя провести график. Теперь подставив x = ( 0 ), мы получим y = f (0) = A√ (0) = A (0) = 0. Таким образом, вторая точка имеет координаты (0,0). И Подставляя x = ( 1 ), мы получаем y = f (1) = A√ (1) = A (1) = A. Таким образом, третья точка имеет координаты (1, A). Поскольку координаты первой Точки не были реальными, теперь мы ищем четвертую Точку и выбираем x = (2). Как нарисовать график функции квадратного корня, ( f(x)=√ x )
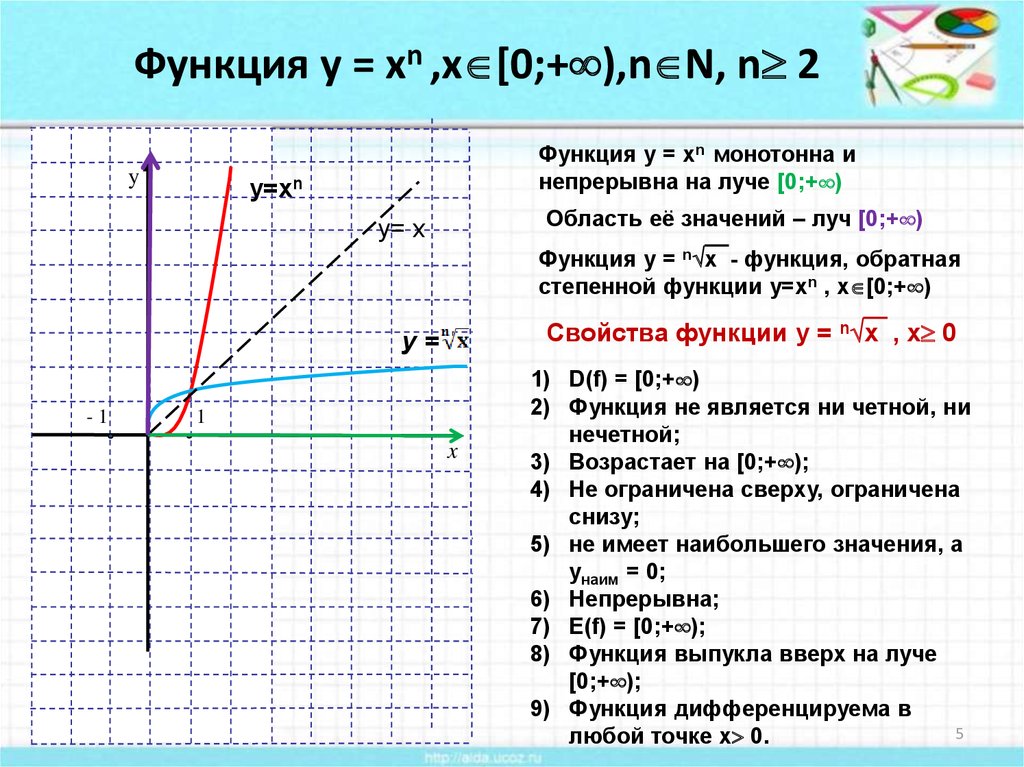 Если ( A ) меньше нуля ( 0 ), то есть ( A ) является отрицательным числом, форма графика аналогична форме нижней половины буквы «C». Пожалуйста, нажмите на изображение для лучшего просмотра.
Если ( A ) меньше нуля ( 0 ), то есть ( A ) является отрицательным числом, форма графика аналогична форме нижней половины буквы «C». Пожалуйста, нажмите на изображение для лучшего просмотра.
Учитывая уравнение y = f(x) = A√x + B, где B — любое действительное число, график этого уравнения будет сдвигаться по вертикали ( B ) единиц. Если ( B ) является положительным числом, график будет двигаться вверх ( B ) единиц, а если ( B ) является отрицательным числом, график будет двигаться вниз ( B ) единиц. Чтобы нарисовать графики этого уравнения, мы следуем инструкциям и используем те же значения «x», что и в шаге № 3. Пожалуйста, нажмите на изображение, чтобы получить лучшее представление.
Учитывая уравнение y = f(x) = A√(x — B), где A и B — любые действительные числа, а ( A ) не равно нулю ( 0 ) и x ≥ B. График этого уравнения переведет по горизонтали ( B ) единиц. Если ( B ) является положительным числом, график будет двигаться вправо ( B ) единиц, а если ( B ) является отрицательным числом, график будет двигаться влево ( B ) единиц.
Теперь мы будем использовать следующие три значения для ‘x’, x = (B), x = (B + 1) и x = (B + 2). Мы подставляем каждое значение ‘x’ в уравнение,… y = f(x) = A√(x — B) и получаем соответствующее значение для каждого ‘y’.
Учитывая y = f(x) = A√(x — B), где A и B — действительные числа, и ( A ) не равно нулю ( o ), где x ≥ B. Подставляя x = (B) в Уравнение мы получаем y = f(B) = A√(B-B) = A√(0) = A(0) = 0. Итак, первая точка имеет координаты (B,0). Теперь подставив x = ( B + 1 ), мы получим y = f (B + 1) = A√(B + 1 — B) = A√1 = A(1) = A. Таким образом, вторая точка имеет координаты ( B+1,A), и подставляя x = ( B + 2 ), получаем y = f(B+2) = A√(B+2-B) = A√(2) =A(1.41) = 1,41A . Итак, третья точка имеет координаты (B+2,1.41A). Теперь мы нарисуем кривую через эти три точки. Пожалуйста, нажмите на изображение для лучшего просмотра.