Алгебра 7-9 класс. Рациональные неравенства — math200.ru
Skip to contentАлгебра 7-9 класс. Рациональные неравенстваadmin2022-10-07T14:28:47+03:00
Скачать файл в формате pdf.
Алгебра 7-9 класс. Рациональные неравенства
| Задача 1. Укажите решение неравенства: \(\left( {x + 3} \right)\left( {x — 8} \right) \geqslant 0\) 1) \(\left[ { — 3;8} \right]\) 2) \(\left( { — \infty ; — 3} \right] \cup \left[ {8; + \infty } \right)\) 3) \(\left[ {8; + \infty } \right)\) 4) \(\left[ { — 3; + \infty } \right)\) Ответ ОТВЕТ: 2. |
| Задача 2. Укажите решение неравенства: \(\left( {x + 2} \right)\left( {x — 7} \right) \leqslant 0\) 1) \(\left[ { — 2;7} \right]\) 2) \(\left( { — \infty ; — 2} \right] \cup \left[ {7; + \infty } \right)\) 3) \(\left( { — \infty ;7} \right]\) 4) \(\left( { — \infty ; — 2} \right]\) Ответ ОТВЕТ: 1. |
| Задача 3. Укажите решение неравенства: \(\left( {x + 5} \right)\left( {x — 9} \right) > 0\) 1) \(\left( { — 5; + \infty } \right)\) 2) \(\left( { — 5;9} \right)\) 3) \(\left( {9; + \infty } \right)\) 4) \(\left( { — \infty ; — 5} \right) \cup \left( {9; + \infty } \right)\) Ответ ОТВЕТ: 4. |
| Задача 4. Укажите решение неравенства: \(\left( {x + 6} \right)\left( {x — 1} \right) < 0\) 1) \(\left( { — \infty ;1} \right)\) 2) \(\left( { — 6;1} \right)\) 3) \(\left( { — \infty ; — 6} \right)\) 4) \(\left( { — \infty ; — 6} \right) \cup \left( {1; + \infty } \right)\) Ответ ОТВЕТ: 2. |
| Задача 5. Укажите решение неравенства: \(\left( {x + 4} \right)\left( {x — 9} \right) \geqslant 0\) Ответ ОТВЕТ: 3. |
| Задача 6. Укажите решение неравенства: \(\left( {x + 1} \right)\left( {x — 6} \right) \leqslant 0\) Ответ ОТВЕТ: 1. |
| Задача 7. Решите неравенство \(\left( {x — 3} \right)\left( {x — 7} \right) < 0.\) В ответ запишите количество целых решений неравенства. Ответ ОТВЕТ: 3. |
| Задача 8. Решите неравенство \(\left( {2x — 5} \right)\left( {x + 3} \right) < 0.\) В ответ запишите количество целых решений неравенства. Ответ ОТВЕТ: 5. |
| Задача 9. Решите неравенство \(\left( {3 — x} \right)\left( {2x + 2} \right) \geqslant 0.\) В ответ запишите сумму целых решений неравенства. Ответ ОТВЕТ: 5. |
| Задача 10. Решите неравенство \(\left( { — 3 — x} \right)\left( {3x — 9} \right) \geqslant 0.\) В ответ запишите сумму целых решений неравенства. ОТВЕТ: 0. |
Задача 11. Решите неравенство \(\left( {x — 3} \right)\left( {x — 5} \right)\left( {x + 2} \right) \geqslant 0.\) В ответ запишите наименьшее целое положительное решение неравенства. 2} — 10x + 25} \right)\left( {x + 6} \right) \geqslant 0\) 2} — 10x + 25} \right)\left( {x + 6} \right) \geqslant 0\)Ответ ОТВЕТ: \(\left[ { — 6;\;\infty } \right).\) |
| Задача 28. Решите неравенство \(\frac{{x — 2}}{{x — 3}} > 0\) Ответ ОТВЕТ: \(\left( { — \infty ;\;2} \right) \cup \left( {3;\;\infty } \right).\) |
| Задача 29. Решите неравенство \(\frac{{2x + 3}}{{7 — 4x}} > 0\) Ответ ОТВЕТ: \(\left( { — \frac{3}{2};\;\frac{7}{4}} \right).\) |
| Задача 30. Решите неравенство \(\frac{{\left( {x — 2} \right)\left( {x — 3} \right)\left( {x — 4} \right)}}{{x + 2}} \geqslant 0\) Ответ ОТВЕТ: \(\left( { — \infty ;\; — 2} \right) \cup \left[ {2;\;3} \right] \cup \left[ {4;\;\infty } \right).\) |
| Задача 31. Решите неравенство \(\frac{{2 — x}}{{x\left( {x + 3} \right)\left( {x — 4} \right)}} \geqslant 0\) Ответ ОТВЕТ: \(\left( { — 3;\;0} \right) \cup \left[ {2;\;4} \right). Ответ ОТВЕТ: \(\left( { — \frac{1}{2};\;0} \right) \cup \left( {0;\;5} \right].\) |
| Задача 40. Решите неравенство \(1 — \frac{1}{x} \geqslant 0\) Ответ ОТВЕТ: \(\left( { — \infty ;\;0} \right) \cup \left[ {1;\;\infty } \right).\) |
| Задача 41. Решите неравенство \(\frac{{2x — 1}}{{x + 1}} \leqslant 1\) ОТВЕТ: \(\left( { — 1;\;2} \right].\) |
| Задача 42. Решите неравенство \(\frac{{2x + 3}}{{x — 1}} \geqslant 2\) Ответ ОТВЕТ: \(\left( {1;\;\infty } \right).\) |
| Задача 43. Решите неравенство \(\frac{1}{{x — 1}} \geqslant — \frac{2}{{x + 2}}\) Ответ ОТВЕТ: \(\left( { — 2;\;0} \right] \cup \left( {1;\;\infty } \right).\) |
| Задача 44. Решите неравенство \(\frac{3}{x} \leqslant \frac{{x + 3}}{6}\) Ответ ОТВЕТ: \(\left[ { — 6;\;0} \right) \cup \left[ {3;\;\infty } \right). |
| Задача 45. Решите неравенство \(\frac{{x + 1}}{{x — 1}} > x + 1\) Ответ ОТВЕТ: \(\left( { — \infty ;\; — 1} \right) \cup \left( {1;\;2} \right).\) |
| Задача 46. Решите неравенство \(\frac{{x + 2}}{{x — 3}} \geqslant \frac{{x + 2}}{{x — 4}}\) Ответ ОТВЕТ: \(\left( { — \infty ;\; — 2} \right] \cup \left( {3;\;4} \right).\) |
| Задача 47. Решите неравенство \(\frac{1}{{x — 1}} + \frac{4}{{x + 2}} \geqslant 2\) Ответ ОТВЕТ: \(\left( { — 2;\; — \frac{1}{2}} \right] \cup \left( {1;\;2} \right].\) |
| Задача 48. Решите неравенство \(\frac{2}{{x — 2}} — \frac{4}{{x + 1}} \leqslant 1\) Ответ ОТВЕТ: \(\left( { — \infty ;\; — 4} \right] \cup \left( { — 1;\;2} \right) \cup \left[ {3;\;\infty } \right).\) |
| Задача 49. Решите неравенство \(\frac{1}{{2 — x}} + \frac{5}{{2 + x}} < 1\) Ответ ОТВЕТ: \(\left( { — \infty ;\; — 2} \right) \cup \left( {2;\;\infty } \right). Ответ ОТВЕТ: \(\left( { — 2;\; — 1} \right) \cup \left[ {0;\;1} \right] \cup \left[ {2;\;\infty } \right).\) |
| Задача 52. Решите неравенство \(x \leqslant 3 — \frac{1}{{x — 1}}\) Ответ ОТВЕТ: \(\left( { — \infty ;\;1} \right) \cup \left\{ 2 \right\}.\) |
Реклама
Поддержать нас
Алгебра для 8 класса
Необходимо решить уравнение: х*(143)=2х-30:
1
-2
2
Необходимо решить уравнение: 2*(х2х3х4х)=600:
30
20
4
Необходимо решить уравнение: 3*(5х7х)2=576:
7
9
8
Какие из представленных значений С и М соответствует уравнению С(ХМ)=0, если Х=-7. С и М – больше нуля:
М=3
С=0
М=0
С=0
М=7
С=2
Укажите квадратный корень из 16:
-4
8
4
Укажите квадратный корень из 25:
10
5
2,5
Укажите квадратный корень из 64:
16
18
8
При каких значениях x график функции y=2x-7 расположен выше оси x:
при x>3,5
при x< -3,5
при x< 3,5
Необходимо найти наименьшее целочисленное решение неравенства 2x-5< 4×7:
6
1
-5
Необходимо решить уравнение х2 – 2х = 0. В ответе укажите сумму корней:
В ответе укажите сумму корней:
1
2
4
Если дискриминант квадратного уравнения отрицательный, то уравнение:
не имеет корней
имеет 1 корень
имеет 2 корня
Книга стоила 320 р., цена была увеличена на 20%. Сколько стоит эта книга теперь:
364
384
380
Понятие этих чисел вызвано потребностью счёта предметов. Какое они название носят:
Натуральные
простые
целые
Какие цифры мы используем в школе:
Римские
Индийские
Арабские и Римские
Какое из чисел является решением неравенства 3х > х 3:
0
-2
3
Неравенству х < 5 соответствует промежуток:
[5; ∞)
( – ∞; 5)
(5; ∞)
Необходимо решить неравенство: 3х < 18:
[6; ∞)
(6; ∞)
( – ∞; 6)
Какое из чисел является решением неравенства 4х – 3 > х:
0
2
1
Неравенству х > 4 соответствует промежуток:
(-∞; 4]
(-∞; 4)
(4; ∞)
Необходимо решить неравенство: 6х ≤ 30:
(5; ∞)
( – ∞; 5]
[5; ∞)
Какое из чисел не является решением неравенства 4,5 3у >0:
-1,5
3
4,5
Необходимо решить неравенство: 6 -7х > 3х – 7:
(0,1; ∞)
(-∞; 1,3)
(-∞; 0,1)
Сколько целых решений неравенства 2с < -1,3 принадлежит промежутку (-6; 3]:
4
3
5
Какое из предложенных неравенств является верным при любых значениях х и у, удовлетворяющих условию х > у:
у – х < -1
х – у > -2
х – у > 3
Какое из чисел не является решением неравенства 2,6 2у < 0
4,5
-3
-1,3
Необходимо решить уравнение: 3х-4*(82х)-710х=2х3*(6х7):
-2
-4
2
Выберите число, заключенное между числами 3,128 и 3,131:
3,12(8)
3,127
3,1(3)
Необходимо сравнить числа 0,791(6) и 37/48:
0,791(6) < 37/48
0,791(6) = 37/48
0,791(6) > 37/48
Порядок числа 20331,22 равен:
6
4
2
Наибольшее из предложенных цифр:
2,5
√7
√5
функций — Каково решение этого неравенства: $| 2х-3| > — | х+3|?$
спросил
Изменено 4 года, 7 месяцев назад
Просмотрено 360 раз
$\begingroup$
Используя графический метод, я получаю все действительные числа. Где я не прав в графическом методе? Как решить это с помощью расчета?
Где я не прав в графическом методе? Как решить это с помощью расчета?
- функции
- неравенство
$\endgroup$
$\begingroup$
Поскольку абсолютное значение числа всегда неотрицательно, единственный способ нарушить это неравенство — обе стороны равны нулю одновременно, что явно невозможно, поскольку
Ваша картинка хороша, но обычно картинка не является доказательством, она только намекает.
$\endgroup$
2
$\begingroup$
Поскольку абсолютные значения всегда положительны, мы имеем
$$
\lvert 2x — 3 \rvert \geq 0 \geq -\lvert x + 3 \rvert
$$
для всех значений $x$. Следовательно, единственный случай, когда $\lvert 2x — 3 \rvert > -\lvert x + 3 \rvert$ потенциально может иметь значение , а не , это когда обе стороны равны $0$.
$\endgroup$
$\begingroup$
Переставить: $$|2x-3|>-|x+3| \iff|2x-3|+|x+3|>0 \iff \\ |2x-3|\ne 0 \ \text{and} \ |x+3|\ne 0 \iff x\ne \frac32 \ \text{and} \ x\ne -3 \iff x\in(-\ infty,+\infty).$$
$\endgroup$
8
$\begingroup$
1) Пусть $x\not = -3. $
Правая часть неравенства $<0$ для $x \in \mathbb{R}$ \ {$-3$}.
Левая часть $\ge 0$ для $x \in \mathbb{R}$ \ {$-3$}.
2) Пусть $x=-3:$
Правая часть = $0$, левая часть $>0$, хорошо.
Следовательно, неравенство верно для всех $x \in \mathbb{R}.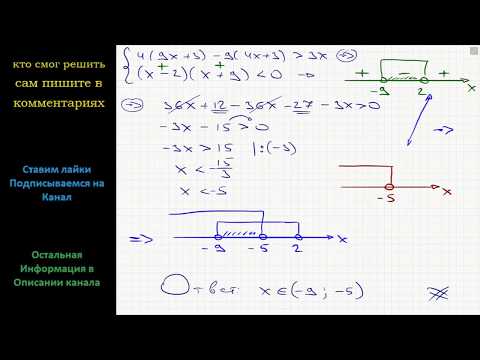 $
$
$\endgroup$
$\begingroup$
Обозначим $$f(x)=|2x-3|+|x+3|.$$ Нам нужно решение для $f(x)>0$.
На самом деле, $$f(х)= \begin{случаи} -3x,x<-3;\\ -x+6,-3 \leq x<\dfrac{3}{2};\\ 3x,x \geq \dfrac{3}{2} \end{case}$$
Таким образом, все $x \in \mathbb{R}$ являются решением для $f(x)>0$.
$\endgroup$
какое число не является решением неравенства 2x + 3 > 7?
- Главная
- какое число не является решением неравенства.
 ..
..
варианты ответа
10 5 4 3 или 0
- решение неравенства
Ваш ответ
| Ваше имя для отображения (необязательно): |
| Напишите мне на этот адрес, если мой ответ выбран или прокомментирован: Напишите мне, если мой ответ выбран или прокомментирован |
Конфиденциальность: Ваш адрес электронной почты будет использоваться только для отправки этих уведомлений. |
| Проверка на спам: |
Во избежание этой проверки в будущем, пожалуйста, войдите или зарегистрируйтесь. |
1 Ответ
3+3×3-3+3 =
2x+3> 7
Решайте для X
2x> 7 — 3
2x> 4
x> 2. 2x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x>
2x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x> 2 x>
2x> 7 — 3
0 не является решением неравенства.
ответил к Уолтджхолл Пользователь 10 уровня (55,7 тыс. баллов)Похожие вопросы
1 ответ
Какая точка НЕ является частью решения неравенства y < |3x| + 1?
спросил 30 апреля 2013 г. по алгебре 2 Ответы к анонимный | 3.2k просмотров
- решение неравенств
1 ответ
4 приводит к решению неравенства, которого не нашел Нили. (Подсказка: что важно в значении 4-N?) 7. Теперь напишите полное решение неравенства N/(4 — N) Покажите, как предположение N>4 приводит к решению неравенства, которое сделал Нили не найти. (Подсказка: что важно в значении 4-N?)
спросил
28 ноября 2022 г. в Word ответы на задачи
к
анонимный
| 116 просмотров
в Word ответы на задачи
к
анонимный
| 116 просмотров
- решение неравенств
- словесных задач
- рациональное неравенство
1 ответ
Напишите неравенство и укажите значение, которое может или не может быть решением неравенства.
спросил 12 апреля 2012 г. по алгебре 1 ответы к анонимный | 585 просмотров
- решение неравенств
1 ответ
Какое значение переменной является решением неравенства? t>-5
спросил 30 октября 2013 г. по алгебре 1 ответы к Айрис Малфой Пользователь 1-го уровня (560 баллов) | 715 просмотров
- решение неравенств
- задач по алгебре
2 ответа
15″>найти решение неравенства -5(2x+7)>15
спросил 30 мая 2013 г. по алгебре 1 ответы к анонимный | 726 просмотров
- решение неравенства
1 ответ
Нарисуйте решение неравенства на числовой прямой. |x+4|<4
|x+4|<4
вопрос 16 ноября 2011 г. по алгебре 1 ответы к анонимный | 842 просмотра
- задачи по алгебре
- абсолютное значение
- решение неравенств
1 ответ
9 и как изобразить набор решений на графике. 2 февраля 2014 г. по алгебре 1 ответы к принцессатира Пользователь 1-го уровня (140 баллов) | 2.7k просмотров
- решение неравенств
1 ответ
-5″>Как решить следующее неравенство 3x + 7 > -5?
спросил 23 февраля 2019 г. по алгебре 1 ответы к анонимный | 1.7k просмотров
- решение неравенств
1 ответ
какое значение не является целым числом -5 0 4 113
спросил 22 августа 2012 г. наименьшее общее кратное к анонимный | 762 просмотров
- задачи по алгебре
- решение неравенств
1 ответ
Решить составное неравенство 4v+4 меньше или равно 12 или 3v-3 меньше -12. Запишите решение в интервальной записи, если решения нет, запишите решение без решения.
Запишите решение в интервальной записи, если решения нет, запишите решение без решения.
спросил 4 марта 2017 г. по алгебре 1 ответы к анонимный | 1.9k просмотров
- решение неравенств
- больше или меньше
- обозначение интервалов
- решение уравнений
1 ответ
-3m-18″> его решение. -8м)>-3м-8
спросил 14 сентября 2014 г. по алгебре 1 ответы к Сабина | 1.5k просмотров
- решение неравенств
1 ответ
какое решение имеет линейное неравенство -0,8x +5,2 < 0?
спросил 7 сентября 2014 г. в ответы по геометрии к анонимный | 407 просмотров
- задачи по алгебре
- набор решений
- построение графиков линейных уравнений
- решение неравенств
1 ответ
какое решение неравенства 12-x0 0 5 спросил 6 августа 2014 г. по алгебре 1 ответы к анонимный | 492 просмотра
- решение неравенств 92-10<-18x с ответом в наборе решений
вопрос 30 июня 2014 г.
 по алгебре 2 Ответы
к
Элиз
| 552 просмотра
по алгебре 2 Ответы
к
Элиз
| 552 просмотра- решение неравенств
- задач по алгебре
- решение уравнений
- математика
1 ответ 6 марта 2014 г. по алгебре 1 ответы к анонимный | 575 просмотров
- задачи по алгебре
- решение неравенств
1 ответ
решить абсолютное неравенство |2a|<6 и построить график набора решений
вопрос 27 августа 2013 г. по алгебре 1 ответы к анонимный | 2.0k просмотров
- решение неравенств
1 ответ
1?»>Каково решение неравенства x/3 > 1?
спросил 25 июня 2013 г. по алгебре 2 Ответы к анонимный | 1.0k просмотров
- решение неравенств
- задач по алгебре
- решение уравнений
1 ответ
0 какое множество решений?»>какое множество решений полиномиального неравенства?
задан вопрос 10 мая 2013 г.




 2} + 5x}}{{x\left( {2x + 1} \right)\left( {x + 1} \right)}} \geqslant 0\)
2} + 5x}}{{x\left( {2x + 1} \right)\left( {x + 1} \right)}} \geqslant 0\) \)
\)
 ..
.. по алгебре 2 Ответы
к
Элиз
| 552 просмотра
по алгебре 2 Ответы
к
Элиз
| 552 просмотра