Умножение вектора на вектор: Умножение вектора на число — урок. Геометрия, 9 класс.

Скалярное умножение

Скалярное умножение

В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников

Суперобложка / Обложка / Содержание

От автора Введение Векторы .Геометрическое определение вектора .Алгебраические операции над направленными отрезками ..Сложение направленных отрезков ..Умножение направленных отрезков на число .Проекции вектора ..Параллельное проектирование вектора в пространстве ..Параллельное проектирование вектора в пространстве …Проекция точки на плоскость …Проекция вектора на плоскость . .Ортогональная проекция вектора в пространстве …Ортогональная проекция вектора на плоскость …Ортогональная проекция вектора на прямую и направленную ось .Метод координат ..Коллинеарные векторы ..Компланарные векторы ..Векторы в трехмерном геометрическом пространстве ..Линейная зависимость векторов и размерность пространства .Декартова система координат ..Различные формы записи векторов ..Линейные операции над векторами в координатной форме ..Скалярное умножение векторов …Свойства скалярного умножения …Скалярное умножение в декартовых координатах ..Некоторые примеры использования скалярного умножения .Измерение площадей и объемов ..Площадь параллелограмма, построенного на векторах . .Свойства определителя второго порядка ..Задачи на применение определителей ..Объем параллелепипеда, построенного на векторах ..Определитель третьего порядка и его свойства ..Векторное произведение векторов ..Векторное умножение векторов базиса декартовой системы координат На подступах к тензорам .Преобразования координат .Скалярное умножение векторов в произвольных косоугольных координатах .Метрический тензор .Взаимный координатный базис .Ковариантные и контравариантные координаты вектора .Площадь и объем в косоугольных координатах ..Индексная форма записи для выражений с определителями ..Символы Веблена ..Свойства символов Веблена ..Тензор Леви-Чивиты ..Операция векторного умножения в произвольных косоугольных координатах . Линейные преобразования или операторы .Линейный оператор и его матрица ..Примеры линейных операторов .Доказательство теоремы об определителе Тензоры .Определение тензора .Общие определения алгебраических операций с тензорами .Примеры на применение тензоров в физике ..Тензор инерции ..Тензор напряжений .Задачи ..Задачи на тождественные преобразования Методические комментарии Литература

 

 

Впервые слово «скаляр» ввел в математику Виет, но современное значение ему придал Гамильтон (1843 г. ), назвав скалярной величину отличную от векторной. Скалярная величина – это величина, которая может, в отличие от векторной, быть задана одним числовым значением. Проще говоря, скаляр – это число. По смыслу названия, при скалярном умножении векторов должно получаться число.

Определение скалярного произведения векторов (22)

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное умножение обычно обозначается точкой: .

 

Введение такой странной, на первый взгляд, операции находит как физическое, так и геометрическое оправдание.

Если – постоянная сила, которая действует на точку, а – вектор перемещения этой точки, то работа A, которая совершается силой на этом перемещении, может быть вычислена как скалярное произведение силы на перемещение: .

С геометрическими приложениями скалярного умножения мы познакомимся в дальнейшем.

Вспомнив, что и , мы можем записать: .

Свойства скалярного умножения

1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда векторы взаимно ортогональны.

Пусть векторы и не равны нулю. Тогда из равенства нулю скалярного произведения следует, что , а это и означает, что .

Если же хотя бы один из векторов нулевой, то . С другой стороны, для нулевого вектора понятие направления не имеет смысла. Но раз смысла нет, то любое соглашение не погрешит против правды. Мы можем принять, что нулевой вектор параллелен любому другому, если захотим, или, что он ортогонален к любому направлению, что мы и сделаем. Но если нулевой вектор ортогонален к любому другому, в том числе и нулевому же, то и этот случай не является исключением.

2. Скалярное умножение векторов коммутативно (перестановочно).

– это сразу следует из определения.

3. Скалярное умножение ассоциативно по отношению к числовому множителю.

так же непосредственно следует из определения.

4. Скалярное умножение дистрибутивно (распределительно) относительно сложения векторов.

.

Данное свойство, несмотря на привычный вид, не является очевидным.

Рис. 17

В самом деле (рис. 17), ,

а . Глядя на рис. 17, трудно предположить, что эти два выражения равны, однако это так.

Доказательство

Для доказательства мы используем свойства проекций.

.

Можно это свойство доказать и непосредственно вычисляя соответствующие длины и углы, но этот путь значительно дольше.

Скалярное умножение в декартовых координатах

Общее выражение для скалярного произведения в произвольных координатах значительно сложнее, и мы займемся им позже.

Для начала найдем результат скалярного умножения базисных векторов декартовой системы координат.

и аналогично .

и аналогично .

i j k i 1 0 0 j 0 1 0 k 0 0 1

Полученные результаты можно свести в таблицу скалярного умножения базисных векторов.

Теперь мы можем доказать следующее утверждение:

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат: .

Доказательство

В самом деле,

. Воспользовавшись свойствами скалярного умножения и таблицей умножения для векторов базиса, мы получаем: .

..Некоторые примеры использования скалярного умножения

Длина или модуль вектора в координатной форме

Пусть произвольный вектор. Скалярное произведение этого вектора самого на себя равно:

С другой стороны, , следовательно,

и .

Расстояние между двумя точками

Рис. 18

Пусть нам даны две точки и , и требуется определить расстояние l между ними. Проведем из начала координат в эти точки радиусы-векторы и , тогда . Модуль или длина вектора как раз и будет равна этому расстоянию. Следовательно,

.

Если расстояние между двумя точками мы обозначим , полученное выражение перепишется в виде:

.

В качестве следующих примеров рассмотрим доказательство двух теорем элементарной геометрии. Этим мы убьем двух зайцев: во-первых, вспомним элементарную геометрию, во-вторых, получим удовольствие от эффективности метода.

Теорема

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Рис. 19

Совместим векторы и со сторонами параллелограмма (рис. 19), тогда сумма и разность этих векторов совпадут с его диагоналями.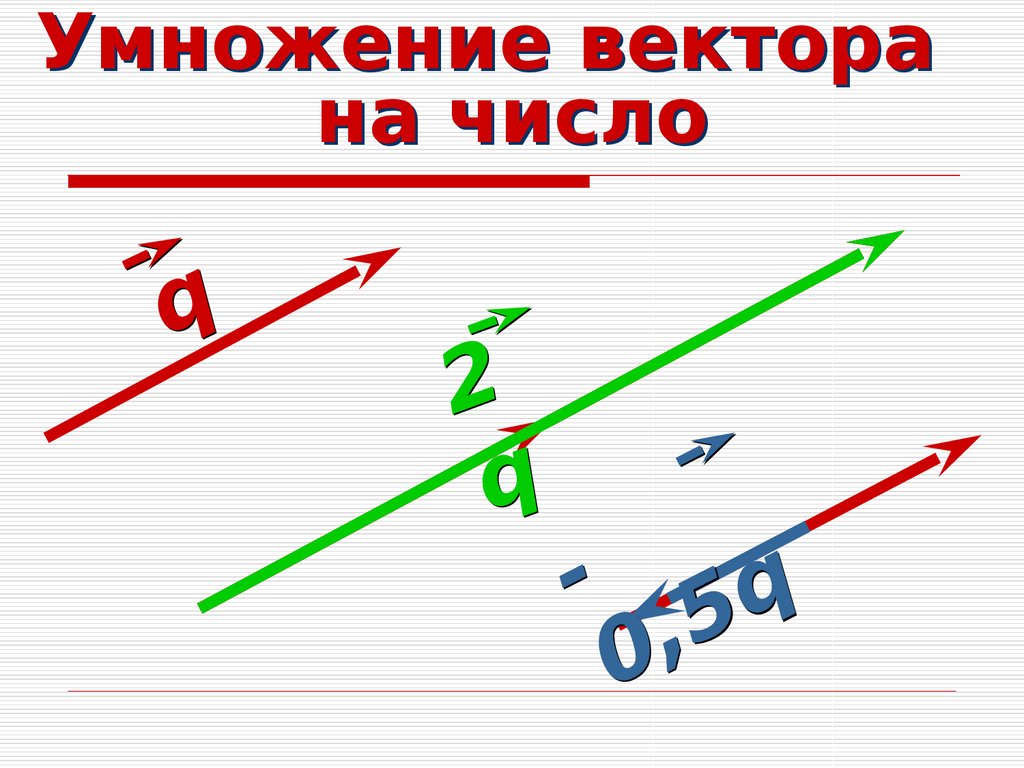

и соответственно

.

Сложив эти выражения, мы получим:

.

Мы видим, что левая часть равенства – это сумма квадратов диагоналей. Правая же часть, как и следовало ожидать – сумма квадратов сторон.

Теорема

Квадрат стороны треугольника равен сумме квадратов двух других его сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.

Рис. 20

Совместим векторы и со сторонами треугольника (рис. 20), тогда вектор совпадет с третьей его стороной.

И окончательно: .

Напомним, что a и b означают модули соответствующих векторов.

 

 

К оглавлению

04.

06. Умножение вектора на скаляр

Умножение вектора на скаляр

Действие умножения вектора на скаляр является естественным обобщением знаний, полученных при решении прикладных задач. ПРОИЗВЕДЕНИЕМ (или ) ВЕКТОРА НА СКАЛЯР L является вектор, имеющий модуль, равный произведению модуля данного вектора на абсолютную величину скаляра, и ориентацию, совпадающую с ориентацией данного вектора, если скаляр положителен, или же противоположную, если скаляр меньше нуля.

Очевидно, что произведение вектора на скаляр обратится в нуль, если один из сомножителей равен нулю.

Пусть дан вектор и скаляр . Введенное действие подчиняется следующим законам:

1. , где  – также скалярный множитель. Это равенство определяет сочетательный закон относительно скалярных множителей. Действительно, как следует из определения, последовательность выполнения операций в левой и правой частях этого равенства не влияет на результат.

2.  – распределительный закон скалярного сомножителя относительно суммы векторов;

 – распределительный закон векторного сомножителя относительно суммы скаляров;

3.  – сочетательный закон относительно скалярных сомножителей.

Равенства 2 выражают закон двоякой распределительности и позволяют, как в алгебре числовых величин, выполнять почленно действия умножения суммы векторов на скаляр и суммы скаляров на вектор. Например, если даны векторы и , приведенные к общему началу 0 (рис. 3.14, а), скаляр и , то вектор , изображенный на рис. 3.14, б, окажется равным вектору построенному на рис. 3.14, в. Это и подтверждает первое из равенств закона двоякой распределительности.

А) Б) В)

 

Рис. 3.14. Распределительный закон относительно
Скалярного множителя.

Операция деления вектора на скаляр определяется через уже введенную операцию умножения:

Где

Операция деления вектора на вектор не имеет особого смысла при решении реальных прикладных задач, поэтому в векторной алгебре она обычно не вводится.

Итак, мы определили линейные операции над векторами. Эти операции очень важны для формулировки многих законов физики. Так, например, второй закон Ньютона записывается в виде:

Где m – масса,  – ускорение точки.

Какой физический смысл имеет величина, равная произведению углового ускорения на момент инерции I?

Возможно, гениальность Ньютона как раз и состояла в том, что во времена, когда векторная алгебра только зарождалась, он сумел понять связь между векторными величинами, характеризующими различные силовые воздействия на тело, и одной единственной векторной величиной, определяющей его динамику и имеющей даже совсем другую размерность, – вектором ускорения. Эта связь осуществляется через скалярный множитель m –массу точки, которая, по его первому закону, является мерой инерции тела.

Развитие математических идей подталкивает, стимулирует прикладные исследования. Именно так произошло с одним из фундаментальных понятий математики, основанным на выполнении линейных операций над векторами – понятием линейной зависимости. Возникнув в математике, оно углубило представление о различных физических процессах и способствовало рождению многих открытий.

 

< Предыдущая		Следующая >

Умножение

векторов. Умножение векторов ФУНДАМЕНТАЛЬНО… | Соломон Се | Основы линейной алгебры

Умножение векторов — ФУНДАМЕНТАЛЬНЫЙ навык решения Умножение матриц .

. Самое первое, что нужно сделать с ВЕКТОРНОЕ Умножение или Матрикс Умножение — это все около , чтобы забыть о 9. . 0015 АРИФМЕТИЧЕСКОЕ УМНОЖЕНИЕ !!
ИНАЧЕ ВЫ ПОПАДЕТЕ В БЕСКОНЕЧНУЮ ЗАМУТИЦУ!

Просто чтобы знать, умножение векторов или матриц, НЕ на самом деле умножение, но просто выглядите так. Вы можете видеть их как операций, чтобы получить ЧТО-ТО .

Есть две операции, называемые умножением для векторов:

• Скалярное произведение : выразить как V₁ · V₂ , названное по символу точки. Он предназначен для получения Произведение двух величин .
• Перекрестное произведение : выразить как V₁ × V₂ , названное в честь символа креста. Он предназначен для получения нового вектора .

Перекрестное произведение очень-очень-очень ограничено в использовании и НЕ так часто используется, как скалярное произведение . Так что не тратьте на это время, если только вы не пользуетесь им.

ЭТО САМЫЙ ОСНОВНОЙ СМЫСЛ УМНОЖЕНИЯ ВЕКТОРОВ ИЛИ МАТРИЦ.

Умножение НЕ просто Повторить счет в арифметике больше.
Больше не 4×3 = 4+4+4 !

Это скорее вроде Рост , или расширение возможностей, или усиление .
Мы бы сказали мы утроили 4 , или скажем число 4 растет со скоростью 3 , или скажем число 4 растет со скоростью 3 .
Что бы вы ни говорили, вы поняли.
Процесс умножения числа в два, три, четыре раза... .

ПРОСТО ПОМНИТЕ: ЗАБУДЬТЕ ОБ АРИФМЕТИЧЕСКОМ УМНОЖЕНИИ, ВСЕГДА СЧИТАЙТЕ УМНОЖЕНИЕ КАК ПОВЫШЕНИЕ.

ПОМНИТЕ: РАСЧЕТНОЕ ПРОИЗВЕДЕНИЕ НЕ ДАЕТ ВАМ ВЕКТОР, А ТОЛЬКО ЧИСЛО, СКАЛЯР, ПРОИЗВЕДЕНИЕ ДВУХ ВЕЛИЧИН.

Цель:
Это Не , чтобы получить новый вектор и Не до Уменьшение , 0035 его единственная цель IS получить количество , величину, число!

Интуитивно понятное видео см. в физике Академии Хана: скалярное произведение.
Более подробно объясняет: Векторное исчисление: понимание скалярного произведения
Математика — это весело: скалярное произведение.
3Blue1Brown: скалярные произведения и двойственность | Сущность линейной алгебры

См. «Введение в линейную алгебру» Гилберта Стрэнга: 1.2_.

Гораздо разумнее думать скалярным произведением в физике , чем математике алгебраически.

Просто для того, чтобы подумать Две силы "A & B" . сколько на направление б ?

Давайте упростим задачу, прежде чем углубляться:
предположим, что угла нет, Две силы "a и b" тянут в одном и том же направлении,
так какая сила будет притянута?

Итак, сила a & b работает вместе, это процесс Повышение энергии!
Это больше не СЛОЖЕНИЕ вместе , это УСИЛЕНИЕ !
Допустим, сила а имеет 3 единицы мощность, b имеет 6 единиц мощности .
Итак, каждые 1 единица мощности a тянет, b будет тянуть 2 единицы мощности.
Тогда это имеет смысл:
Суммарная сила, тянущая предмет, будет 3 · 6 = 18 единиц

Итак, Две силы НЕ тянут коробку больше в одном направлении, сколько силы она тянула? направление , или сколько на направлении b ?

Давайте подумаем, сколько энергии он потребляет в направлении b .
Так как тянет немного неправильно , поэтому сила НЕ работает на 100% на b 's .
Сколько энергии там осталось?
Зависит от угла.
Таким образом, чтобы вычислить, сколько осталось, мы используем |a| × cos(θ) ,
и мы получили ПРОЕКЦИЮ или отражение или тень из a на b !
Потом снова стало как на картинке:

Как это здорово!
И теперь мы можем Увеличить питание на b: |b| × |a|×cosθ

Существует два способа вычисления скалярного произведения (названия я придумал):

• Shadow Boost:

• Axes Boost:

Результат двух способов SAME .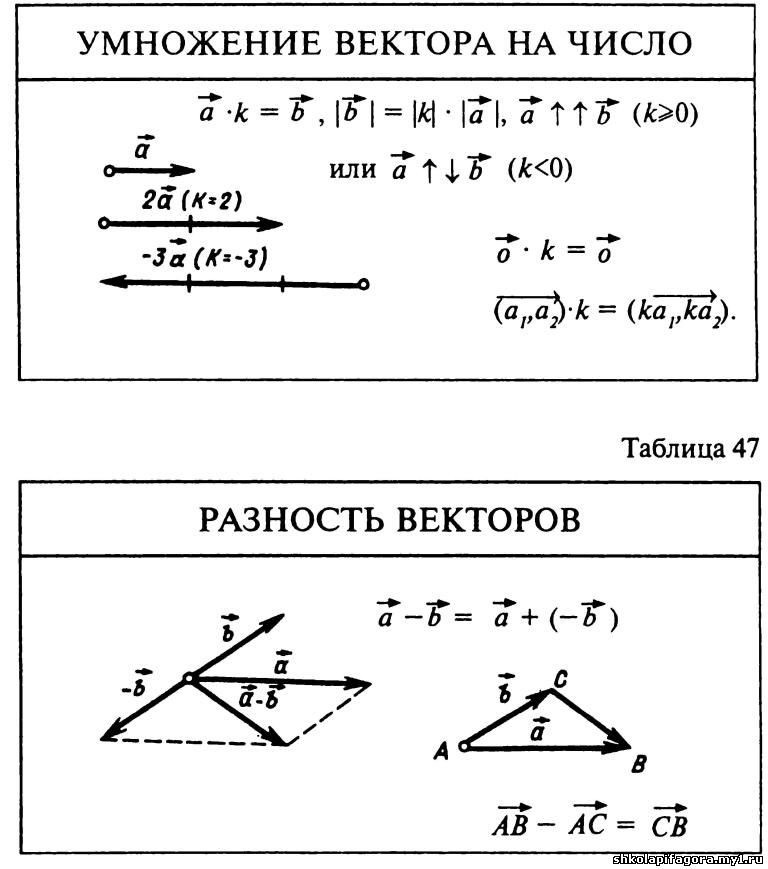

Помните: бустинг не работает, когда два вектора равны Перпендикуляр , какой продукт 0 .

Отражаем один вектор на другой, затем Буст энергию.

Интуиция:

Разбиваем два вектора на X-ось и Y-оси 5

95

5 каждый.

Легче запомнить формулу:

Интуиция:

Скалярный продукт связан с симметрией.

См. лекцию в Имперском колледже Лондона: Соглашение Эйнштейна о суммировании и симметрия скалярного произведения

-

1.2: Умножение векторов - Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

16287

• Том Вайдеман
• Калифорнийский университет в Дэвисе

Теперь мы знаем, как выполнять некоторые математические операции с векторами, и возникает вопрос: «Если мы можем складывать и вычитать векторы, можем ли мы также их умножать?» Ответ да, и нет. Оказывается, существует не один единственный способ определить произведение двух векторов, а два…

Скалярное произведение

Вскоре мы рассмотрим, как можно описать влияние силы, действующей на объект, на его скорость при перемещении из одного положения в другое. Сила является вектором, потому что у нее есть величина (величина толчка) и направление (направление толчка). И движение объекта тоже является вектором (хвост в начальной точке объекта, а голова в его конечной точке). Выяснится, что этот эффект математически описывается как произведение количества силы и количества движения. Это просто вычислить, если толчок направлен вдоль направления движения, но что, если это не так? Получается, что только количество толчка, которое действует в направлении движения влияет на скорость объекта.

Поэтому мы хотели бы ввести понятие проекции одного вектора на другой. Лучшее описание этого — «количество данного вектора, которое указывает вдоль другого вектора». Это можно представить как «тень», которую один вектор отбрасывает на другой вектор:

0003 Итак, если мы хотим умножить длину вектора на количество второго вектора, спроецированного на него, мы получим:

\[ ( \text{проекция } \overrightarrow A \text{ на } \overrightarrow B )( \text{величина } \overrightarrow B ) = (A \cos \theta) (B) = AB \cos \theta\]

Это первый из двух типов векторного умножения, и он называется скалярное произведение , потому что результатом произведения является скаляр. Обычно мы пишем продукт через точку (указывая его альтернативное имя 9).0004 скалярный продукт ):

\[\overrightarrow A \cdot \overrightarrow B \equiv AB\cos \theta ,\;\;\;\;\;\theta = угол\;между\;\overrightarrow A \; и\;\overrightarrow B \]

Пример \(\PageIndex{1}\)

Вектор \(\overrightarrow A\) имеет величину 120 единиц, и при проецировании на \(\overrightarrow B\) , прогнозируемая часть имеет значение 105 единиц. Предположим, что \(\overrightarrow B\) теперь проецируется на \(\overrightarrow A\), а длина проекции равна 49единицы. Найдите величину \(\overrightarrow B\).

Решение

Коэффициент, определяющий длину проекции, равен \(\cos \theta\). Угол между двумя векторами одинаков независимо от того, какой вектор проецируется, поэтому коэффициент одинаков в обоих направлениях. Проекция \(\overrightarrow A\) на \(\overrightarrow B\) составляет 7/8 величины \(\overrightarrow A\), поэтому величина \(\overrightarrow B\) должна быть 8/7 его проекции, что составляет 56 ед. Обратите внимание, что когда проекция одного вектора умножается на величину другого, получается одно и то же произведение независимо от того, каким образом происходит проекция. То есть скалярное произведение одинаково в любом порядке (то есть оно коммутативно). 92\]

Сразу должно быть ясно, каковы скалярные произведения единичных векторов. Они имеют единичную длину, поэтому скалярное произведение единичного вектора на самого себя равно 1.

\[\widehat i \cdot \widehat i = \widehat j \cdot \widehat j = \widehat k \cdot \widehat k = 1\]

Они также взаимно ортогональны , поэтому скалярные произведения друг на друга равны нулю:

\[\widehat i \cdot \widehat j = \widehat j \cdot \widehat k = \widehat k \cdot \широкая шляпа я = 0\]

Это дает нам альтернативный способ взглянуть на компоненты, которые являются проекциями вектора на оси координат. Поскольку единичные векторы указывают вдоль направлений \(x\), \(y\) и \(z\), компоненты вектора могут быть выражены как скалярное произведение. Например:

\[ \begin{align} \overrightarrow A \cdot \widehat i &= (A_x \widehat i + A_y \widehat j + A_z \widehat k) \cdot \widehat i \nonumber\\[5pt] &= A_x \cancelto{1}{\widehat i \cdot \widehat i} + A_y \cancelto{0} {\widehat j \cdot \widehat i} +A_z \cancelto{0}{\widehat k \cdot \widehat i} \end{выравнивание}\]

Единичные векторы также показывают нам простой способ получить скалярное произведение двух векторов, компоненты которых нам известны. Начните с двух векторов, записанных в компонентной форме:

\[\overrightarrow A = A_x\widehat i + A_y \widehat j\nonumber\]

\[\overrightarrow B = B_x\widehat i + B_y \widehat j\nonumber\ ]

затем просто выполните «нормальную алгебру», распределяя скалярное произведение, как при обычном умножении:

\[ \begin{align} \overrightarrow A \cdot \overrightarrow B &= (A_x \widehat i + A_y \widehat j) \cdot (B_x \widehat i + B_y \widehat j) \nonumber\\[5pt] &= (A_x B_x) \cancelto{1}{\widehat i \cdot \widehat i} + (A_y B_x) \cancelto {0} {\widehat j \cdot \widehat i} + (A_x B_y) \cancelto{0}{\widehat i \cdot \widehat j} + (A_y B_y) \cancelto{1}{\widehat j \cdot \ широкоугольный j} \nonumber\\[5pt] &= A_x B_x + A_yB_y \end{align} \]

Если бы у нас не было этого простого результата, подумайте о том, что нам пришлось бы делать: нам нужно было бы вычислить углы, которые каждый вектор образует, скажем, с осью \(x\). Затем из этих двух углов нам нужно вычислить углы между двумя векторами. Затем нам нужно будет вычислить величины двух векторов. Наконец, с величинами векторов и углом между векторами мы наконец-то можем подключиться к нашему уравнению скалярного произведения.

Предупреждение

При наличии двух разных способов вычисления скалярного произведения должно быть ясно, что самый простой метод будет зависеть от предоставленной информации. Если вам известны (или вы можете легко установить) величины векторов и угол между ними, используйте уравнение 1.2.2, но если вам известны (или вы можете легко установить) компоненты векторов, используйте уравнение 1.2.7. .

Пример \(\PageIndex{2}\)

Два приведенных ниже вектора перпендикулярны друг другу. Найдите неизвестную \(z\)-компоненту.

\[\overrightarrow A = +5 \widehat i - 4 \widehat j - \widehat k \;\;\;\;\;\; \overrightarrow B = +2 \widehat i + 3 \widehat j + B_z \widehat k \nonumber\]

Решение

Скалярное произведение двух векторов пропорционально косинусу угла между ними. Это означает, что если они ортогональны, скалярное произведение равно нулю. Скалярный продукт легко вычислить, если известны компоненты, поэтому мы делаем это и находим \(B_z\):

\[0 = \overrightarrow A \cdot \overrightarrow B = \left( +5 \right) \left( +2 \right) + \left(-4 \right) \left( +3 \right) \ + \влево( -1 \вправо) \влево( B_z \вправо) \;\;\; \Правая стрелка \;\;\; B_z = -2 \номер\]

Скалярное произведение двух векторов с точки зрения векторов-столбцов работает именно так, как вы ожидаете — просто перемножьте похожие компоненты и просуммируйте все произведения.

Произведение векторов

Как упоминалось ранее, существует два способа определения произведения векторов. Если скалярное произведение включает количество одного вектора, равное 9Если 0004 параллелен другому вектору, то неудивительно, что наше другое произведение включает в себя количество вектора, которое перпендикулярно другому вектору.

Рисунок 1.2.2 – Часть одного вектора, перпендикулярная другому

то, что мы получили для скалярного произведения, на этот раз с функцией синуса, а не косинуса. По причинам, которые вскоре станут ясны, этот тип продукта упоминается как 9.0004 векторный продукт . Поскольку это отличается от скалярного произведения, мы также используем другое математическое обозначение — крест, а не точку (что дало ему альтернативное название перекрестного произведения ). Это имеет простую (хотя и не совсем полезную, по крайней мере, не в физике) геометрическую интерпретацию в терминах параллелограмма, заданного двумя векторами:

\[величина\; из\; \overrightarrow A \times \overrightarrow B = \left| \overrightarrow A \times \overrightarrow B \right| = \ влево | \overrightarrow А\право| \влево| \overrightarrow В \право| \sin\theta = AB\sin\theta \]

Но есть еще одно, еще большее различие между векторным и скалярным произведениями. Хотя проекция всегда располагается параллельно второму вектору, перпендикулярная часть подразумевает ориентацию, поскольку перпендикулярная часть может указывать в нескольких направлениях. Любая величина, имеющая ориентацию, потенциально может быть вектором, и на самом деле мы определим вектор, являющийся результатом этого типа продукта, следующим образом: если мы проследим периметр параллелограмма выше в направлении, заданном двумя векторами, мы получаем ориентацию по часовой стрелке [ Получили бы мы ту же ориентацию, если бы произведение было в обратном порядке: \(\overrightarrow B\) \(\times\) \(\overrightarrow A\)? ]. Мы превращаем это направление циркуляции в векторное направление (указывающее в определенном направлении в пространстве), используя соглашение, называемое правилом правой руки :

. Соглашение: правило правой руки

. руку в направлении первого вектора в продукте, затем поверните руку так, чтобы эти пальцы естественным образом сгибались в направлении второго вектора в продукте. Когда ваши пальцы сгибаются, вытянутый большой палец указывает в направлении, перпендикулярном обоим векторам в произведении. Это направление вектора, полученного в результате перекрестного произведения.

Если мы выполняем векторное произведение с векторами в обратном порядке, наши пальцы сгибаются в противоположном направлении, что заставляет наш большой палец указывать в противоположном направлении в пространстве. Это означает, что векторное произведение обладает антикоммутативным свойством: так как часть первого вектора, перпендикулярная второму вектору, равна нулю: 92 \sin 0 = 0\]

Как и скалярное произведение, векторное произведение можно легко выразить с помощью компонентов и единичных векторов. Векторные произведения единичных векторов сами на себя равны нулю. Каждый из единичных векторов находится под прямым углом к ​​двум другим единичным векторам, поэтому величина векторного произведения двух единичных векторов также является единичным вектором (поскольку синус угла между ними равен 1).

Условные обозначения: Правосторонние системы координат

Мы всегда будем выбирать правостороннюю систему координат, что означает, что использование правила правой руки на оси от +\(x\) до +\(y\) дает ось +\(z\).

Таким образом, с точки зрения единичных векторов имеем:

\[ \widehat i \times \widehat i = \widehat j \times \widehat j = \widehat k \times \widehat k = 0\]

и

\[\widehat i \times \widehat j =-\widehat j \times \widehat i = \widehat k ,\;\;\;\;\;\; \widehat j \times \widehat k =-\widehat k \times \widehat j =\widehat i ,\;\;\;\;\;\; \widehat k \times \widehat i =-\widehat i \times \widehat k =\widehat j \]

Это позволяет нам делать перекрестные произведения чисто математически (не прибегая к правилу правой руки), когда мы знаем компоненты, как мы сделали для скалярного произведения. Снова начнем с двух векторов в компонентной форме:

\[\overrightarrow A = A_x\widehat i + A_y \widehat j\nonumber\]

\[\overrightarrow B = B_x\widehat i + B_y \widehat j\nonumber\]

тогда, как в случае скалярного произведения, просто выполните «нормальную алгебру», распределив перекрестное произведение и применив приведенное выше перекрестное произведение единичных векторов:

\[ \begin{align} \overrightarrow A \times \overrightarrow B &= (A_x \widehat i + A_y \widehat j) \times (B_x \widehat i + B_y \widehat j) \\[5pt] &= (A_x B_x) \cancelto{0}{\widehat i \times \widehat i} + (A_yB_x) \ Cancelto{- \widehat k} {\widehat j \times \widehat i} + (A_x B_y) \cancelto{+\widehat k}{\widehat i \times \widehat j} + (A_y B_y) \cancelto{0} {\widehat j \times \widehat j} \\[5pt] &= (A_x B_y - A_yB_x) \widehat k \end{align}\]

Сейчас неясно, как мы будем использовать скалярное произведение и векторное произведение в физике, но оно уже на подходе, так что неплохо бы уже сейчас усвоить эти важные инструменты.

No related posts.