Умножения вектора на число определение: Умножение вектора на число — урок. Геометрия, 9 класс.

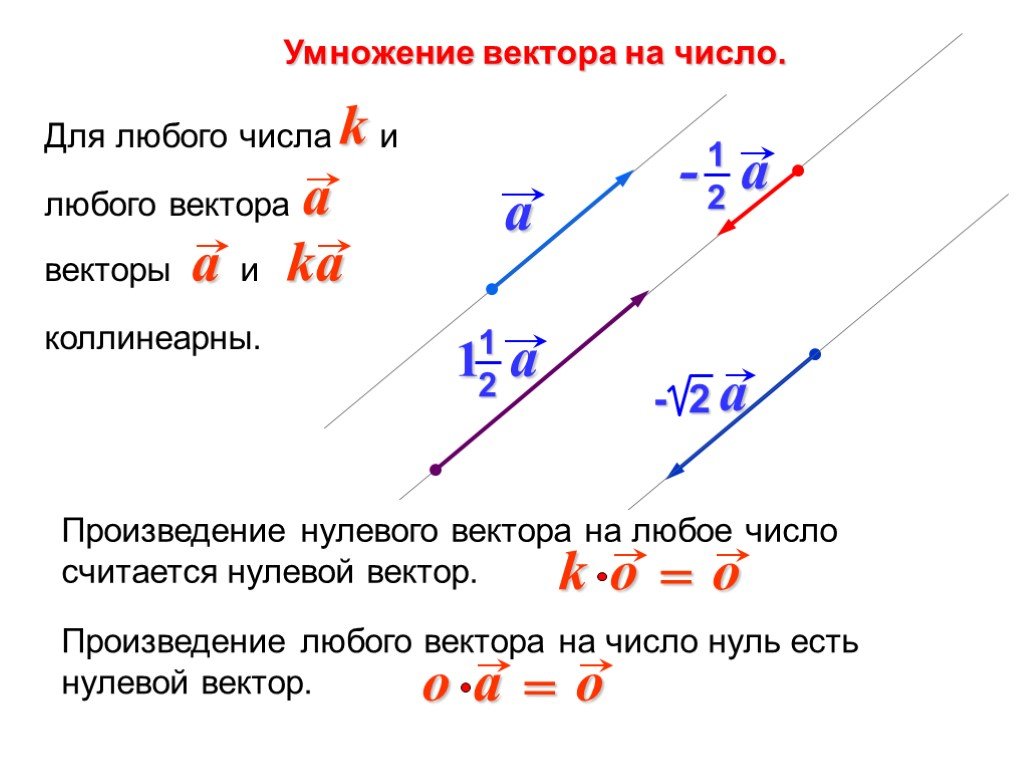
32. Операция умножения вектора на число и ее свойства

Определение 13. Произведением вектора A на число L Называется такой вектор B, что

1) | B | = | L || A |

2) если l > 0, то A­­B, если l < 0, то A­¯B, если l = 0 или A = 0, то B = 0.

Произведение вектора A на число l обозначается символом L A. Числа называют также Скалярными величинами или Скалярами.

Теорема 8. Вектора A ≠ 0 Коллинеарен вектору B тогда и только тогда, когда найдется такое число, что B = L A.

Доказательство. Если, то по определения 13 следует, что векторы коллинеарны. Обратно, пусть вектора коллинеарны. Тогда, полагая

L = ±|B|/|A|, где стоит знак «+», если A­­B, стоит знак «-«, если A­¯B, по определению 13 получим B = L A.

Теорема 9. Для любых векторов A, B и для любых чисел l, m Справедливы свойства:

1) l(m A) = (lm) A — Смешенный ассоциативный закон;

2) (l + m) A = l A+ m A — Дистрибутивный закон;

3) l (A + B) = l A + l B — Дистрибутивный закон;

4) 1 A = A — Свойство умножения на единицу.

Доказательство. 1. Если векторы A или B равны 0 Или числа m равны нулю, то равенства 1-3 теоремы почти очевидны (проверте их). Также по определению равенства векторов проверяется равенство 4.

Поэтому дальше будем считать, что A ≠ 0, B ≠ 0, lm ≠ 0.

1. Длины векторов l(m A), (lm) A равны |l||m| |A|, и поэтому равны между собой. Далее оба эти вектора коллинеарны вектору A. Если числа l и m одного знака, то направление векторов l(m A), (lm) A совпадает с направлением вектора A. Если числа l и m противоположных знаков, то эти векторы противоположны вектору A. Отсюда по определению векторы l(m A), (lm) A равны.

2. Если числа l и m одного знака, то векторы (l + m) A, l A, m A сонаправлены и |l A+m A| = |l A|+|m A|= |l ||A| + | m||

A| = (| l | + | m | )| A|.

Так как в этом случае |l + m | = | l | + | m |, то |(l + m) A| = || l A + m A|.

Отсюда, по определению равенства векторов (l + m) A = l A + m A.

Случай, когда числа l и m противоположного знака рассмотрите самостоятельно.

3. Если векторы A и B коллинеарны, то по теореме 8 его можно представить в виде B = m A. Тогда по свойствам 1, 2 и 4 имеем

L (A + B) = l (1A + m A) = l (1A) + l (m A) =l A + l (m A) = l A + l B.

Если векторы A и B неколлинеарны, то построим сумму A +

B = = +.

Построим вектор l A =, l (A + B) = (см. рис. 15 при l > 0 и рис. 16 при l < 0). Получим, что треугольники ОAB и OCD подобны. Из подобия треугольников и определения 13 получаем, что = l A. Отсюда находим, что l (A + B) = = =+=lA + l B.

Пространство геометрических векторов. Множество V3 всех геометрических векторов пространства является векторным пространством на полем действительных чисел относительно операций сложения векторов и умножения вектора на число (см. теоремы 6 и 9 § 1).. Также векторным пространством является множество V2 (V1) всех векторов плоскости (прямой).

Множество всех геометрических векторов, коллинеарных данному вектору

A образует подпространство пространства V3 всех геометрических векторов.

< Предыдущая		Следующая >

Умножение вектора на число

• Главная
• Справочник
• Геометрия
• Вектора
• Умножение вектора на число

• Произведением вектора на число

Векторы: , ,

Нулевой вектор:

Координаты векторов: , ,

Действительные числа: ,

Произведением вектора на число называется вектор , модуль которого равен , направление которого совпадает с вектором при и противоположно ему при

Произведение вектора на число при и/или равно нулевому вектору .

Операция умножения вектора на число обладает следующими линейными свойствами :

Коммутативность умножения вектора на число  

Дистрибутивность умножения относительно сложения чисел  

Дистрибутивность умножения относительно сложения векторов  

Ассоциативность умножения вектора на число  

Умножение вектора на единицу  

Умножение вектора на число в координатной форме  

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Вектора Формулы Геометрия Алгебра Теория Обозначения 2865

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

• Вектор. Определение и основные понятия

  Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Координаты вектора

  Координатами вектора называются проекции вектора на оси координат

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Сложение и вычитание векторов

  Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Декартовы координаты и векторы в пространстве

  Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Скалярное произведение векторов

  Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Векторное произведение векторов

  Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Смешанное произведение векторов

  Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Калькулятор для ЕГЭ. Как отличить непрограммируемый калькулятор от программируемого?

  ЕГЭ Экзамены

• Калькулятор калорий для похудения онлайн

  Калькуляторы веса и калорий Калькулятор Расчёт

• Сколько битов в байте, Кб, Мб, Гб и Тб

  Разное Единицы измерения Справочник

• Расчет расхода калорий

  Калькуляторы веса и калорий Калькулятор Расчёт

• Размеры форматов листов А5, А4, А3, А2, А1, А0 в миллиметрах и мегабайтах

  Разное Размеры

• Что такое Ватт

  1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.

  Электротехника Формулы Физика Теория Электричество

• Как перевести число из двоичной системы в восьмеричную и шестнадцатеричную

  Основы Расчёт Справочник Информатика Программирование

• 1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?

  Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.

  Разное Единицы измерения Деньги Справочник

Скаляр, Вектор, Матрица

(… и матрицы)

Что такое скаляры и векторы?

Скаляр

имеет только величину  (размер):

3,044, −7 и 2½ являются скалярами

Расстояние, скорость, время, температура, масса, длина, площадь, объем, плотность, заряд, давление, энергия, работа и мощность — все это скаляры.

Вектор

имеет величину и направление :

Перемещение, скорость, ускорение, сила и импульс являются векторами.

И обратите внимание на эти специальные слова:

Расстояние против смещения

• Расстояние является скаляром («3 км»)
• Смещение — это вектор («3 км к юго-востоку»)

Вы можете пройти большое расстояние, но ваше перемещение может быть небольшим (или нулевым, если вы вернетесь к началу).

Скорость против скорости

• Скорость — это скорость движения объекта.
• Скорость — это скорость в направлении .

Если сказать, что собака Ариэль бежит со скоростью 9 км/ч, то (километров в час) — это скорость.

Но если сказать, что он бежит 9 км/ч на запад , то это скорость.

См. Скорость и Скорость, чтобы узнать больше.

Обозначение

Вектор часто записывается жирным шрифтом , например a или b , поэтому мы знаем, что это не скаляр:

• , поэтому c — это вектор, он имеет величину и направление
• , но c — это скаляр, например 3 или 12,4
.

Пример: k b на самом деле скаляр, умноженный на вектор b .

Вектор также можно записать в виде букв его головы и хвоста со стрелкой над ними, например:

Использование скаляров

Скаляры просты в использовании. Просто относитесь к ним как к обычным числам.

Пример: 3 кг + 4 кг = 7 кг

Использование векторов

На странице о векторах есть более подробная информация, но вот краткий обзор:

Мы можем добавить два вектора, соединив их лоб в лоб:

Мы можем вычесть один вектор из другого:

• Сначала мы меняем направление вектора, который хотим вычесть,
• , затем добавьте их как обычно:

а − б

Мы можем умножить вектор на скаляр (это называется «масштабированием» вектора):

Пример: умножить вектор

м = (7,3) на скаляр 3

a = 3 м = (3×7,3×3) = (21,9)

Он по-прежнему указывает в том же направлении, но в 3 раза длиннее

(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз. )

Полярный или декартовый

Вектор может находиться в:

• величина и направление (полярная) форма,
• или в x и y (декартово) форма

Вот так:

	<=>
Вектор a в полярных координатах		Вектор a в декартовом Координаты

(Прочитайте, как преобразовать их в полярные и декартовы координаты.)

Пример: вектор

13 при 22,6°

В полярной форме (величина и направление):

) форма:

Вектор (12,5)

Попробуйте векторный калькулятор, чтобы понять, как он работает.

Умножение вектора на вектор (скалярное произведение и векторное произведение)

Как нам умножить два вектора вместе? Существует более чем один способ! Скаляр или скалярное произведение (результатом является скаляр). Вектор или векторное произведение (результатом является вектор). (Дополнительную информацию см. на этих страницах.)

Больше двух измерений

Векторы также прекрасно работают в 3-х и более измерениях:

Вектор (1,4,5)

Список номеров

Таким образом, вектор можно рассматривать как список из чисел :

.

• 2 числа для двумерного пространства, например (4,7)
• 3 числа для трехмерного пространства, например (1,4,5)
• и т. д.

 

Скаляры, векторы и матрицы

И когда мы включаем матрицы, мы получаем эту интересную закономерность:

• Скаляр — это число, например 3, -5, 0,368 и т. д. ,
• Вектор представляет собой список чисел (может быть в строке или столбце),
• Матрица — это массив чисел (одна или несколько строк, один или несколько столбцов).

Фактически вектор также является матрицей ! Потому что матрица может иметь только одну строку или один столбец.

Таким образом, правила, которые работают для матриц, также работают и для векторов.

 

11913, 11914, 11915, 11916, 11917, 11918, 11919, 11920, 11921, 11922

Логический класс | Главная

УМНОЖЕНИЕ ВЕКТОРОВ НА ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

УМНОЖЕНИЕ ВЕКТОРОВ НА ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

Умножение вектора A на положительное число \(\lambda\) дает вектор, величина которого изменяется на коэффициент \(\lambda\), но направление такое же, как у A.

\(% MathType!MTEF!2!1!+- % feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqWaaeaacq % aH7oaBcaWGbbaacaGLhWUaayjcSdGaeyypa0Jaeq4UdW2aaqWaaeaa % caWGbbaacaGLhWUaayjcSdGaamyAaiaadAgacqaH7oaBcqGH+aGpca % айВааааа!4783! \влево| {\ лямбда А} \ справа | = \лямбда\влево| А \право|если\лямбда > 0\)

Например, если A умножить на 2, результирующий вектор 2A имеет то же направление, что и A , и его величина вдвое больше |A| как показано на рис. 4.3 (а). Умножение вектора A на отрицательное число -\(\lambda\) дает другой вектор, направление которого противоположно направлению A и величина которого равна \(\lambda\), умноженной на |A|.

Умножение заданного вектора A на отрицательные числа, например –1 и –1,5, дает векторы, как показано на рис. 4.3(b).

                                    

                      рис. 4.3. (a) Вектор A и результирующий вектор после умножения A на положительное число 2. ​​​​​​

                               (b)Вектор A и результирующие векторы после его умножения на отрицательное число – 1 и –1.

Фактор\(\лямбда\), с помощью которого вектор A умножается может быть скаляром, имеющим собственное физическое измерение. Тогда размерность \(\lambda\) A является произведением размерностей \(\lambda\) и A. Например, если мы умножим вектор постоянной скорости на продолжительность (времени), мы получим вектор смещения.

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ — ГРАФИЧЕСКИЙ МЕТОД

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ-ГРАФИЧЕСКИЙ МЕТОД

Как упоминалось в разделе 4.2, векторы по определению подчиняются закону треугольника или, что то же самое, закону сложения параллелограмма. Опишем теперь этот закон сложения графическим методом. Рассмотрим два вектора A и B, лежащие в плоскости, как показано на рис. 4.4(a). Длины отрезков, представляющих эти векторы, пропорциональны величине векторов. Чтобы найти сумму A + B, мы помещаем вектор B так, чтобы его хвост находился в начале вектора A, как на рис. 4.4(b). Затем мы присоединяем хвост A к началу B. Эта линия OQ представляет собой вектор R , то есть сумма векторов A и B. Поскольку в этой процедуре сложения векторов

векторов

 

         

   

           

       

    рис  4.4 (a) Векторы А и В . (b) Векторы A и B добавлены графически.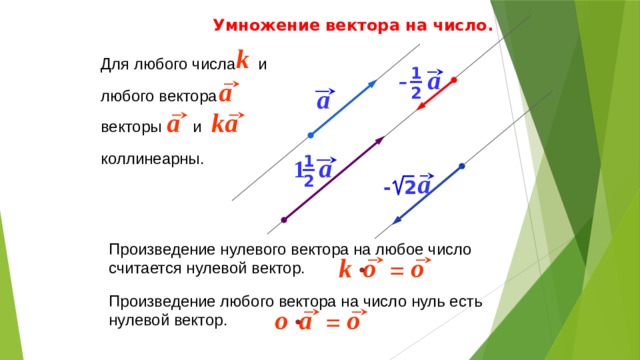

    (c) Векторы B и A добавлены графически.

        (d) Иллюстрация ассоциативного закона сложения векторов.

 

, расположенные «голова к хвосту», этот графический метод называется методом «голова к хвосту». Два вектора и их результат образуют три стороны треугольника, поэтому этот метод также известен как треугольный метод сложения векторов. Если мы найдем равнодействующую B + A, как на рис. 4.4(c), получится тот же вектор R. Таким образом, сложение векторов коммутативно:

                A + B = B + A(4.1)

 

Сложение векторов также подчиняется ассоциативному закону, как показано на рис. 4.4(d). Результат сложения сначала векторов A и B, а затем добавления вектора C такой же, как результат сложения сначала B и C, а затем добавления вектора A:

               (A + B) + C = A + (B + C)

 

 

Что получится, если сложить два равных и противоположных вектора? Рассмотрим два вектора A и –A, показанные на рис. 4.3(b). Их сумма равна A + (–A). Поскольку величины двух векторов одинаковы, но направления противоположны, результирующий вектор имеет нулевую величину и представлен 0, называемым нулевым вектором или нулевым вектором:

 

А – А = 0        |0|= 0

Поскольку модуль нулевого вектора равен нулю, его направление указать нельзя.

Нулевой вектор также получается, когда мы умножаем вектор A на ноль. Основные свойства 0:

А + 0 = А

\(\лямбда\) 0 = 0

0 А = 0

 

Каков физический смысл нулевого вектора? Рассмотрим векторы положения и смещения на плоскости, как показано на рис. 4.1 (а). Теперь предположим, что объект, находящийся в точке P в момент времени t , перемещается в \(% MathType!MTEF!2!1!+- % feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmiuayaafa % аааа!36D7! P’\), а затем возвращается к P. Каково же тогда его смещение? Поскольку начальное и конечное положения совпадают, перемещение является «нулевым вектором».

 

Вычитание векторов может быть определено как сложение векторов. Определим разность двух векторов A и B как сумму двух векторов A и –B:

                        A – B = A + (–B)       

Это показано на рис. 4.5. Вектор –B добавляется к вектору A, чтобы получить R ₂  = (A – B). Вектор R ₁  = A + B также показан на том же рисунке для сравнения. Мы также можем использовать метод параллелограмма, чтобы найти сумму двух векторов. Предположим, у нас есть два вектора A и B. Чтобы сложить эти векторы, мы приводим их хвосты к общему началу O, как показано на рис. 4.6(a). Затем мы проводим линию от головы A параллельно B и другую линию от головы B параллельно A, чтобы завершить параллелограмм OQSP. Теперь присоединяем точку пересечения этих двух линий к началу координат

O. Результирующий вектор R направлен из общего начала O по диагонали (OS) параллелограмма [рис. 4.6(б)]. На рис. 4.6(c) закон треугольника используется для получения равнодействующей A и B, и мы видим, что оба метода дают один и тот же результат. Таким образом, эти два метода эквивалентны.

            

                  

 

                   рис.4.5. (a) Два вектора A и B, – также показан B .

                 (b) Вычитание вектора B из вектора A – дает результат R ₂ .

                   Для сравнения также показано сложение векторов A и B, т.е. R ₁ .

 

ПРИМЕР 1

 

Дождь падает вертикально со скоростью 35 м с ^–1 . Через какое-то время начинает дуть ветер со скоростью 12 м с ^–1 в направлении с востока на запад. В каком направлении должен держать зонтик мальчик, ожидающий на автобусной остановке?

 

ОТВЕТ

 

           

       

                    рис.