Упражнения со степенями математика: Задачи со степенями

alexxlab / / Разное

Разработка урока «Действия со степенями»

Разделы: Математика

Цели урока:

  • Отработка приемов вычислений со степенями;
  • Выработка умений решения задач на нахождение значения выражения;
  • Развитие элементов творческой деятельности учащихся и умение контролировать свои действия;
  • Систематизировать знания учащихся, полученные ранее;
  • Расширить их знания при решении более сложных упражнений.

Оборудование: кодоскоп, печатные бланки.

Тип урока: Урок комплексного применения знаний, умений и навыков.

План урока:

  1. Организационный момент;
  2. Проверка домашнего задания;
  3. Устная работа;
  4. Работа с тестами;
  5. Самостоятельная работа;
  6. Задание на дом;
  7. Подведение итогов.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания.

К доске вызывается один ученик, который выполняет № 457, дети не сделавшие номер дома, работают с учителем, кто справился с заданием, выполняют упражнения:

а)

б)

3. Устная работа: учащиеся отвечают на вопросы, поставленные учителем.

— Какие действия со степенями вы знаете?

— Когда появляется степень?

— Из чего состоит степень?

— О чем говорит основание степени?

— О чем говорит показатель степени?

— Сформулируйте правила умножения, деления степеней с одинаковыми основаниями, правило возведения степени в степень; правило возведения в степень произведения, дроби.

4. Работа с тестами.

На каждую парту раздается тест с напечатанными заданиями. Учащиеся по очереди выходят к доске и выполняют задания данного теста:

Представьте в виде степени:

I.
II.
III.
IV.
V. Поставьте вместо звездочки нужное выражение.
VI. Сравните с нулем выражения.

VII. Что можно сказать о квадратах противоположных чисел?

VIII. Что можно сказать о кубах противоположных чисел?

IX. Сторону квадрата увеличили в два раза. Во сколько раз изменилась его площадь?

X. Объем куба увеличился в 27 раз. Что произошло с ребром куба?

5. Самостоятельная работа.

С помощью кодоскопа на экран проецируется текст самостоятельной работы. Учащиеся выполняют ее по вариантам (в двух экземплярах с помощью копировальной бумаги). Проверка осуществляется с помощью кодоскопа.

I вариант   II вариант
 
 
 
 
 
 
 
 
 
 

6.

Домашнее задание: №№ 451, 456, 457, 458.

7. Подведение итогов урока.

Литература

  1. Алгебра:Учеб. Для 7 кл.общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков,С.Б. Сурова; Под ред. С. А. Теляковского.- 5-е изд.-М. :Просвещение, 1997.- 240 с..

Алгоритм работы по теме «СТЕПЕНЬ» | Тренажёр по алгебре (7 класс) на тему:

№

          Действия со СТЕПЕНЯМИ

                        АЛГОРИТМ    РАБОТЫ    ( ПРАВИЛА )

1.

Найти значение выражения:

1 – 4х2 ; при х = — 3

1 — 4·(-3)2 = 1 — 4 ·(-3)·(-3) = 1 – 36 = — 35

Подставить  вместо Х его значение -3, получится запись       1 — 4(-3)2 =

Заменить  запись степени (-3)2 подробной записью по определению степени- если показатель 2 то повторяем 2 раза умножение (-3)(-3), т. е. какой показатель столько раз и повторяем умножение числа. Получаем пример и решаем его по действиям:

1 — 4(-3)2 = 1 — 4 (-3)(-3) = 1 – 36 = — 35

2.

Выполните действие  умножения степеней:

а4а7 = а4+7 = а11

При умножении степеней основание степени оставляют тем же, а показатели (маленькие числа вверху ) складывают.

3.

Выполнить действие деления степеней:

х9: х5 = х9 – 5 = х4

При делении степеней основание степени оставляют тем же, а показатели (маленькие числа вверху)  вычитают.

4.

Выполните действие возведение степени в другую стерень:         (у2)7 = у2·7 = у14

При возведении степени в другую степень  основание степени оставляют тем же ,а показатели (маленькие числа вверху)  перемножают.

5.

Выполните возведение в степень произведения двух множителей:

    (2в) 4 = 24·в4 =2·2·2·2·в4 = 16·в4

При  возведении в степень произведения двух множителей, к каждому из этих множителей по очереди приписывают этот показатель степени и считают число в степени (перемножают его столько раз, какой показатель степени), а буквенную степень оставляют без изменения.

6.

Вычислите: ( 363·65) : 67= (( 62)3·65): 67 =

= (62·3+5) : 67 = ( 611) : 67 = 611-7 = 64 =

 =6·6·6·6 = 36 ·36 = 1296

а) Надо сначала все степени сделать с одинаковыми основаниями, т.е.заменить 36 = 62 

б) Потом воспользоваться правилами  возведения степени в другую степень  и умножения степеней, чтобы посчитать действие в скобках

в) Воспользоваться правилом для деления степеней

г)Довести до конца ответ, умножив основание 6 столько раз, каков показатель степени

7.

Упростите выражение: -2а·в4  3 а2в3=

=-2·3·а·а2в4в3 = -6а1+2в4+3 = -6а3в7

а) Примените  сначала перестановку одинаковых множителей

б) Потом числа умножьте, а у одинаковых оснований а и в сложите показатели.

8.

Упростите выражение: (-2а5в3) 3 =

= (-2)3 ·а5·3в3·3 = (-2)·(-2)·(-2)·а15·в9 = — 8а15в9

При  возведении в степень произведения нескольких множителей, к каждому из этих множителей по очереди приписывают этот показатель степени, основание степени оставляют тем же, а показатели (маленькие числа вверху)  перемножают.

Считают число в степени (перемножают его столько раз, какой показатель степени), а буквенную степень оставляют без изменения.

Карточка составлена учителем математики Головлянициной Лидией Вадимовной

Пользуясь данной таблицей алгоритма работы со степенями, выполните упражнения для закрепления знаний:

1. Найти значение выражения:    2 – 3х2 ; при х =  — 4

2. Выполните действия: а) у5·у12       б) у24: у14    в)( у2)7     г) ( 2у)3

3.Вычислите:    ( 253·54):57

4.Упростите выражение:  а) -2ав54а3в2     б) ( -3а4в2)4

практических задач | Математический институт

  1. Дом
  2. Учись здесь
  3. Бакалавриат
  4. Добро пожаловать в Математический институт!

На этой странице содержатся листы вопросов, которые многие колледжи рассылают новым студентам до того, как они прибудут для получения степени бакалавра. Эти вопросы являются подходящим промежуточным материалом для студентов, изучающих математику с одним уровнем A, когда они поступают в университет — материал является частично пересмотренным, частично новым материалом.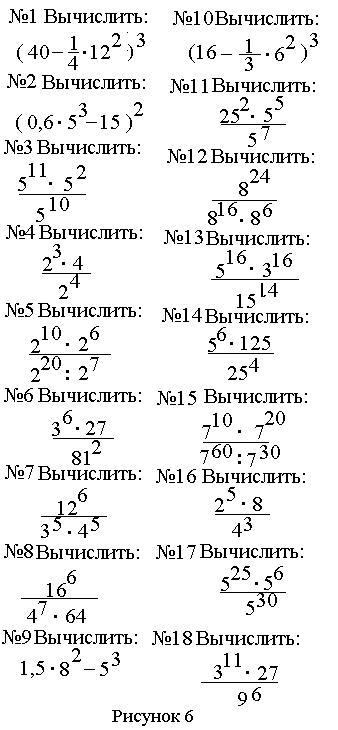

Все 11 листов охватывают материалы, относящиеся к курсам математики, математики и статистики и математики и философии; листы 8, 9и 10 не имеют отношения к степени математики и компьютерных наук.

На каждом листе кратко описывается тематика, а также есть рекомендуемые материалы для чтения; номера глав относятся к четвертому изданию книги Д. У. Джордана и П. Смита Mathematical Techniques, , опубликованной Oxford University Press в 2008 г.

  • Вопросы:
    • Лист 1: Стандартные функции и методы, PDF
      Материалы для чтения: §§ 1.3, 1.6–1.8, 1.10–1.16
    • Лист 2: Дифференциация, PDF
      Чтение: Глава 2
    • Лист 3: Дальнейшие различия, PDF
      Чтение: §§ 3.1–3.5, 3.9–3.10
    • Лист 4: Приложения дифференциации, PDF
      Чтение: §§ 4.1-4.4
    • Лист 5: Серия Тейлора, PDF
      Чтение: §§ 5.1-5.4
    • Лист 6: Комплексные числа, PDF
      Чтение: Глава 6
    • Лист 7: Матрицы, PDF
      Чтение: Глава 7
    • Лист 8: Векторы, PDF
      Чтение: §§ 9. 1-9.4, 9,6
    • Лист 9: Скалярное «точечное» произведение, PDF
      Чтение: §§ 10.1-10.3, 10.9
    • Лист 10: Векторное «перекрестное» произведение, PDF
      Чтение: §§ 11.1-11.2
    • Лист 11: Интеграция, PDF
      Чтение: §§ 14.1-15.4, 15.8
    • Все вышеперечисленные 11 листов одним файлом: PDF
  • Более сложные вопросы:
    • Введение 1: PDF
      Чтение: R.B.J.T. Алленби
      Числа и доказательства       , Глава 7
    • Введение 2: PDF
      Чтение: R.B.J.T. Алленби Числа и доказательства , Глава 7
    • Алгебра 1: PDF
      Чтение: нет требований
    • Алгебра 2: PDF
      Чтение: главы 7 и 8
    • Исчисление 1 — Зарисовка кривой: PDF
      Чтение: §§ 4.1-4.4
    • Исчисление 2 — Численные методы и оценка: PDF
      Чтение: §4.6, §5.2
    • Исчисление 3 — Методы интеграции: PDF
      Чтение: §§17.5-17.7
    • Исчисление 4 — Дифференциальные уравнения: PDF
      Чтение: §§ 22.3-22. 4, Глава 18
    • Исчисление 5 — Дополнительные дифференциальные уравнения: PDF
      Чтение: глава 19, §22.5
    • Комплексные числа: PDF
      Чтение: Глава 6
    • Геометрия: PDF
      Чтение: §10.1, §10.9, §11.1, §16.1
    • Вторые 11 листов одним файлом: PDF
  • Дополнительные листы по прикладной математике (для студентов, изучающих математику, математику и статистику)
    • Динамика 1 — Основные определения. Второй закон Ньютона PDF
    • Динамика 2 — Колебания и другие примеры. ПДФ

комбинаторика — Упражнения на степени и длины графов

спросил

Изменено 5 лет, 5 месяцев назад

Просмотрено 206 раз

$\begingroup$

Мультиграфы не допускаются, а $\delta$ представляет наименьшую степень.

Пусть $P$ — самый длинный простой путь в графе $G$, а $\lambda$ представляет длина $P$. ($P$ содержит ребра $\lambda$ и вершины $\lambda + 1$.)

(a) Покажите, что каждый конец $P$ имеет степень, меньшую или равную $\lambda$.

(b) Докажите, что в любом графе минимальной степени $\delta$ существует простой путь длины $\ge \delta$.

Решение:

(a) Единственные вершины, с которыми могут соединяться концы $P$, — это вершины на $P.$ В противном случае $P$ больше не будет самым длинным простым путем. Поскольку мультиграфы не разрешены, каждая конечная точка может соединяться с вершинами $\lambda$. Таким образом, степень концов не превосходит $\lambda.$

(b) В графе не может быть меньше ребер, чем $\delta.$ Таким образом, $\lambda \ge \delta.$

Выглядит правильно? Спасибо.

  • комбинаторика
  • дискретная математика
  • доказательство-верификация
  • теория графов

$\endgroup$

$\begingroup$

Ваше доказательство части (а) в основном правильное.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *