Аналитическая геометрия
Аналитическая геометрия
Задача 1. Дан треугольник АВС: А(2,1), В(-1,3), С(-4,1). Найти:
уравнение и длину высоты АD; уравнение и длину медианы СЕ; внутренний угол В; систему линейных неравенств, определяющую треугольник. Сделать чертеж.
Решение. Сделаем чертеж.
Y
D
B
3
E
C 1 A
-4 -1 0 2 X
1. Составим
уравнения
всех сторон
треугольника,
используя
уравнение
прямой,
проходящей
через две
данные точки.
Составим
уравнения
всех сторон
треугольника,
используя
уравнение
прямой,
проходящей
через две
данные точки.
.
Так как точки А и С имеют одинаковую ординату, используем данное уравнение в преобразованном виде:
.
2. Найдем длину высоты АD. Используем формулу расстояния от точки до прямой:
.
Приведем уравнение ВС к общему уравнению прямой.
.
3. Составим уравнение высоты АD. Она проходит через точку А(2,1) и перпендикулярна прямой ВС, kBC=2/3. Из условия перпендикулярности kAD=-1/kBC=-3/2. Воспользуемся уравнением прямой, проходящей через данную точку в данном направлении:

4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки Е как середины отрезка АВ.
Точка Е (1/2,2).
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. kBC=2/3, kAB=-2/3.
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде
AB: 2x+3y=7,
BC: 2x-3y=-11,
AC: y=1.
Подставим точку с координатами (-1, 2), лежащую внутри треугольника, в левые части равенств.
2x+3y=-2+6=4<7,
2x-3y=-2-6=-8>-11,
y=2>1.
Следовательно, система неравенств, описывающая треугольник, имеет вид
Задача
2. Составить
каноническое
уравнение гиперболы,
если
известно, что
ее эксцентриситет
равен 1,25 и
гипербола
проходит
через точку .
Составить
каноническое
уравнение гиперболы,
если
известно, что
ее эксцентриситет
равен 1,25 и
гипербола
проходит
через точку .
Решение. Каноническое уравнение гиперболы имеет вид . Так как гипербола проходит через точку А (8; ), то ее координаты удовлетворяют уравнению гиперболы, т.е. . Так, как = 1,25, то = 1,25, но , тогда = 1,5625или .
Итак, получаем систему двух уравнений с двумя неизвестными
Решая эту систему, находим = 16 и = 9, следовательно, каноническое уравнение гиперболы имеет вид .
Задача
3. Составить
уравнение
прямой,
проходящей через
вершину параболы
и
центр окружности
.
Составить
уравнение
прямой,
проходящей через
вершину параболы
и
центр окружности
.
Решение. Найдем координаты вершины параболы и координаты центра окружности. Для этого выделим полные квадраты по каждой переменной.
Уравнение параболы: ;
уравнение окружности: .
Следовательно, вершина параболы имеет координаты В (2;3), а центр окружности имеет координаты С (-2; 1).
Тогда уравнение искомой прямой составим по формуле
.
Получим , или .
1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром.
 3 Задача 20 Найти пределы указанных функций. 5 Задача 40 … — Контрольная работа #1400418 — Высшая математика Задача 10. 3
3 Задача 20 Найти пределы указанных функций. 5 Задача 40 … — Контрольная работа #1400418 — Высшая математика Задача 10. 3Задача 20. 5
Задача 40. 6
Задача 50. 7
Задача 60. 10
Задача 70. 11
Список использованной литературы 13
Решить задачи (6 задач) Вариант 16
Задача 10 Даны координаты вершин треугольника АВС. Найти: 1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром. 3
Задача 20 Найти пределы указанных функций. 5
Задача 40 …
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1. Учеб. Пособие для вузов.: Изд-во «ОНИКС 21 век»: Мир и образование, 2002. – 416 с.
3. Справочник по высшей математике / под ред. Выгодского М.Я. М.:. «Большая медведица».
 – 2001. 864 с.
– 2001. 864 с.| Тема: | Решить задачи (6 задач) Вариант 16 Задача 10 Даны координаты вершин треугольника АВС. Найти: 1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром. 3 Задача 20 Найти пределы указанных функций. 5 Задача 40 … |
| Артикул: | 1400418 |
| Дата написания: | 25.09.2008 |
| Тип работы: | Контрольная работа |
| Предмет: | Высшая математика |
| Оригинальность: | Антиплагиат.ВУЗ — 90% |
| Количество страниц: | 13 |
Составить уравнение сторон треугольника с вершинами
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | |||
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
Даны вершины треугольника… Расчет треугольника на плоскости
Косинус угла между двумя векторами:
Угловой коэффициент прямой, перпендикулярной данной:
Координаты середины отрезка:
Уравнение прямой, проходящей через две точки:
Уравнение прямой, проходящей через заданную точку в заданном направлении:
Задача
Даны вершины треугольника.
Найти:
1) внутренний угол
в радианах с точностью до 0,0001; 2) уравнение
высоты, проведенной через вершину
; 3) уравнение медианы проведенной через
вершину
; 4) систему линейных неравенств, определяющих
внутреннюю область треугольника
. Сделать чертеж.
Сделать чертеж.
Решение
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
1) Внутренний угол найдем как угол между векторами и :
Косинус угла :
Искомый угол:
2) Высота, проведенная через вершину будет перпендикулярна стороне :
Уравнение :
Угловой коэффициент:
Угловой коэффициент высоты:
Высота, опущенная из вершины :
Искомое уравнение высоты:
3) Медиана проходит через точку -середину стороны :
Уравнение медианы :
-уравнение медианы
4) Найдем уравнение стороны :
Найдем уравнение стороны :
Уравнения сторон треугольника:
Система неравенств, определяющих треугольник :
Сделаем чертеж:
Даны три вершины треугольника найти уравнение медианы
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны.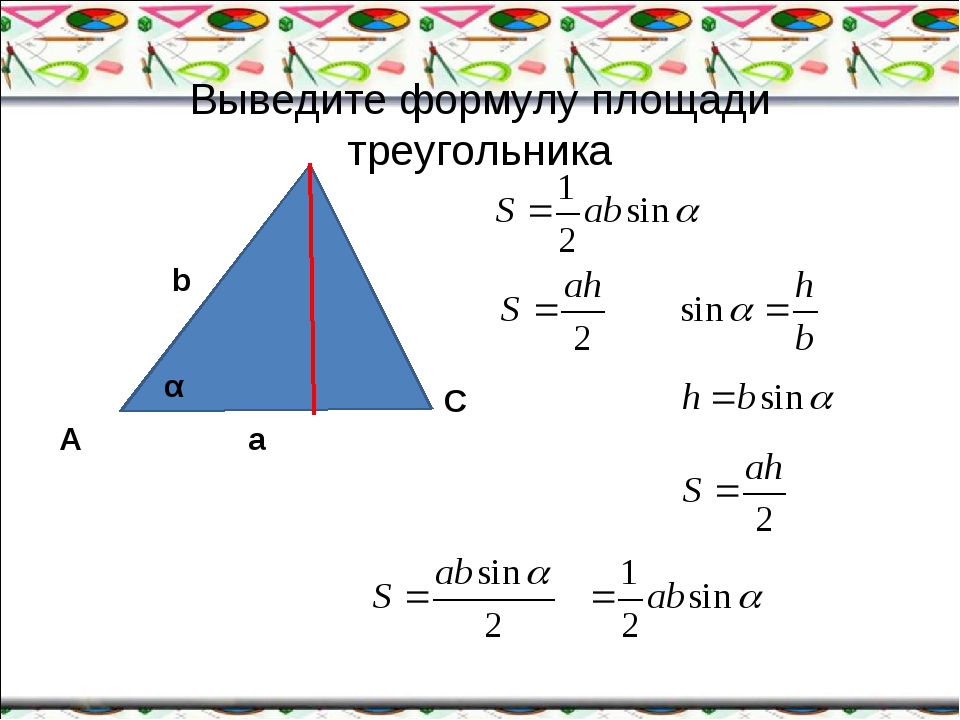 Следовательно, при решении задачи составления уравнения медианы нужно:
Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.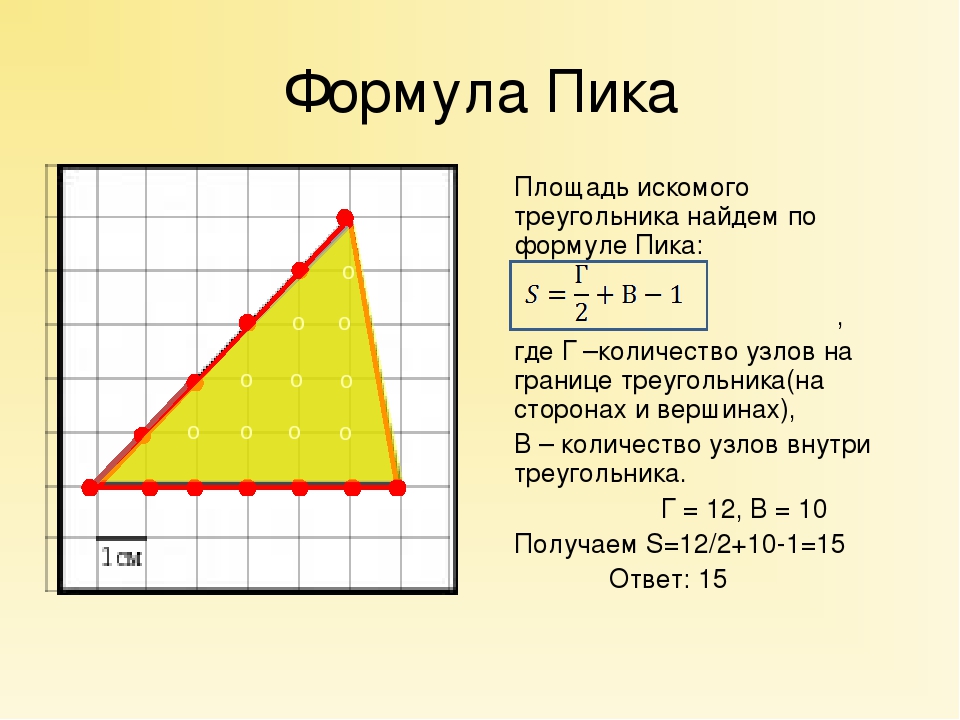
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @
Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)
Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:
Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0
Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна.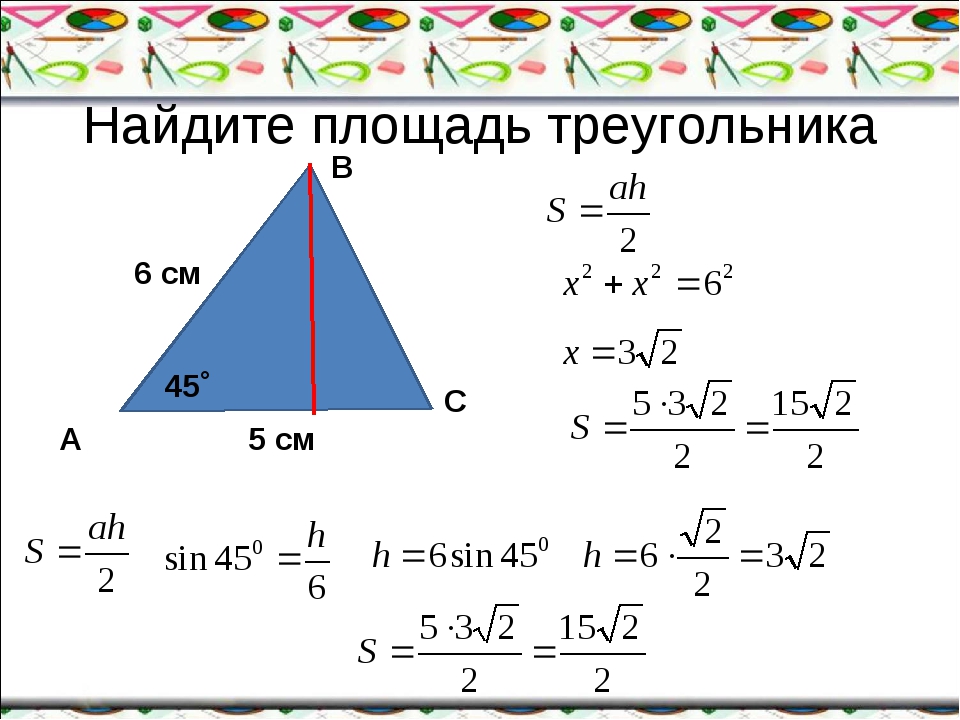 Это прямая AB (уравнение у нас есть). Выразим y через x явно:
Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9
Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:
y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.
10 = (32/3) + d,
d = -2/3
Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0
Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: XE = 6, YE = -1
Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.
(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0
Это уравнение медианы AE.
Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:
S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв.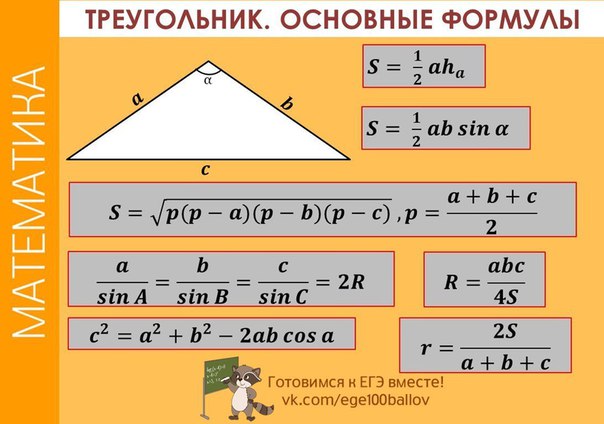 ед.)
ед.)
Задача 1. Даны вершины треугольника АВС. Найти:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ НАЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к решению задач по дисциплине Высшая математика и варианты контрольных заданий практические
Подробнее3 (3, 2, -7) A A (3, 4, -7) Задачи для контрольной работы 1 1(3, 4, 2) A 2 (1, 2, 1) A 3 (-2, -3, 4) A 4 (3, -6, -3) 1(1, 3, 1) A 2 (-1, 4, 6) A
Задачи для контрольной работы Задание. Дана система линейных уравнений a a a a a a a a a b b b Решить систему: а) методом Гаусса; по правилу Крамера; средствами матричного исчисления (зад.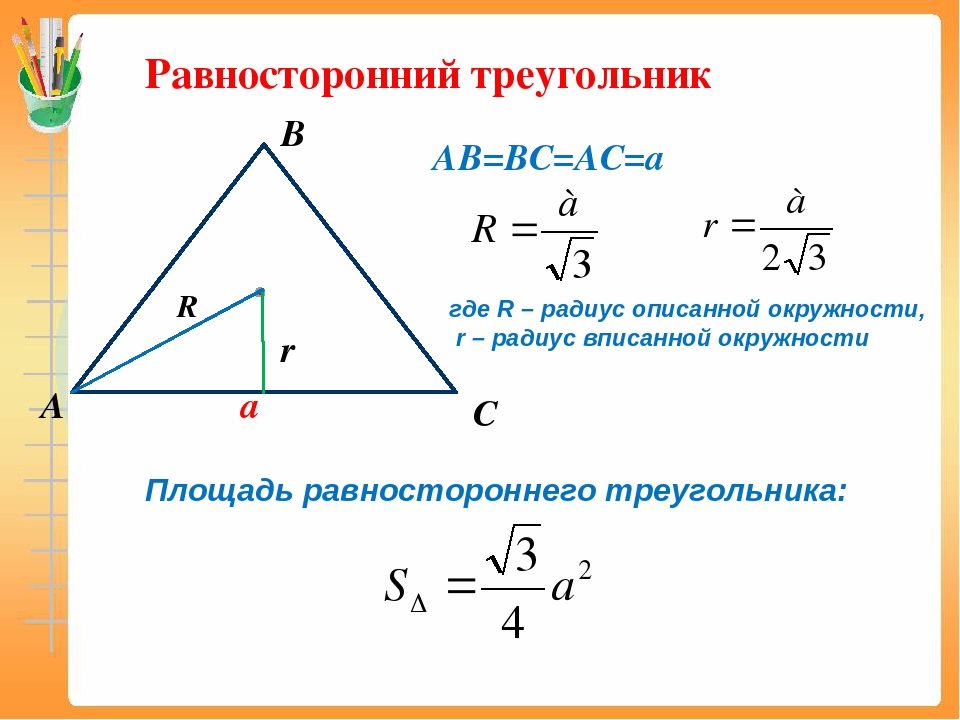 )… 5. 7. 9.
)… 5. 7. 9.
Примеры решений контрольных работ
Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 3. Аналитическая геометрия на плоскости 1. Составить уравнения прямых, проходящих через точку A(4; 1) a) параллельно прямой
Подробнееx ydy x y dx, где дуга линии 2 x y dxdy 2 r drd B ; y dx xydy, где дуга эллипса x 2cost y t, x t, t ; y zdxdy xzdydz x ydxdz 2cos t, 2sin t,
cos, sin,,, J dd dd d d 5 Вычислить zdd zddz ddz, где внешняя сторона поверхности z, отсекаемая плоскостью z Р е ш е н и е Поверхность представляет собой параболоид, заданный явно уравнением z Поэтому
ПодробнееИНСТРУКЦИЯ К ДОМАШНЕМУ ЗАДАНИЮ 3
ИНСТРУКЦИЯ К ДОМАШНЕМУ ЗАДАНИЮ Для выполнения домашнего задания необходимо пользуясь табл. заполнить первую строку табл. затем выписать соответствующие вашему номеру варианта данные из табл.. Например
заполнить первую строку табл. затем выписать соответствующие вашему номеру варианта данные из табл.. Например
БАНК ЗАДАЧ для вступительных испытаний в магистратуру (базовая часть)
БАНК ЗАДАЧ для вступительных испытаний в магистратуру (базовая часть) Задания билета,, 4 5 Разделы, 4, 5, 6, 7, 0,,,, 8, 9,, 6, 7, 8, 0 4, 5, 9 Количество баллов 5 б 0 б 5 б Содержание Раздел Производная,
ПодробнееНеопределенный и определенный интегралы
~ ~ Неопределенный и определенный интегралы Понятие первообразной и неопределѐнного интеграла. Определение: Функция F называется первообразной по отношению к функции f, если эти функции связаны следующим
Подробнееcos xdx ВХОДНОЙ КОНТРОЛЬ Вариант Найти dy, если: а) y =, в) y = tg, 2.Построить область, ограниченную линиями:
ВХОДНОЙ КОНТРОЛЬ Вариант Найти d, если: а) =, в) = tg, б) = cos7, г) = Построить область, ограниченную линиями: а) = +, =, б) =, = Привести уравнение окружности + 6 = к каноническому виду, построить и
ПодробнееБАНК ЗАДАЧ для вступительных испытаний в магистратуру (базовая часть)
БАНК ЗАДАЧ для вступительных испытаний в магистратуру (базовая часть) Задания билета,, 4 5 Разделы, 4, 5, 6, 7,,,,, 8, 9,, 6, 7, 8, 4, 5, 9 Количество баллов 5 б б 5 б Содержание Раздел Производная, частная
Подробнее10.
 АЛГЕБРАИЧЕСКИЕ ЛИНИИ НА ПЛОСКОСТИ
АЛГЕБРАИЧЕСКИЕ ЛИНИИ НА ПЛОСКОСТИ. АЛГЕБРАИЧЕСКИЕ ЛИНИИ НА ПЛОСКОСТИ.. ЛИНИИ ПЕРВОГО ПОРЯДКА (ПРЯМЫЕ НА ПЛОСКОСТИ… ОСНОВНЫЕ ТИПЫ УРАВНЕНИЙ ПРЯМЫХ НА ПЛОСКОСТИ Ненулевой вектор n перпендикулярный заданной прямой называется нормальным
ПодробнееНайти х из уравнений:
Методические указания для обучающихся по освоению дисциплины (модуля) Планы практических занятий Матрицы и определители, системы линейных уравнений Матрицы Операции над матрицами Обратная матрица Элементарные
ПодробнееГлава 7 Плоскость в пространстве
Глава 7 Плоскость в пространстве Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:, где А, В, С координаты вектора i j k -вектор нормали к плоскости. Возможны
ПодробнееR может быть задана с помощью
5. .. Уравнения плоскости. Плоскость в пространстве 5.. ПЛОСКОСТЬ. R может быть задана с помощью n, B, C, вектора перпендикулярного плоскости, и точки M,, этой плоскости. Вектор n, B, C,, лежащей на E перпендикулярный
.. Уравнения плоскости. Плоскость в пространстве 5.. ПЛОСКОСТЬ. R может быть задана с помощью n, B, C, вектора перпендикулярного плоскости, и точки M,, этой плоскости. Вектор n, B, C,, лежащей на E перпендикулярный
система { (x + 1) 2 + ( y 1 1) 2 = 4, март 2013 г.
Московский государственный университет Вариант VII Московский государственный университет Вариант VII arctg ( + ) + arcctg ( ) 7 arctg ( + ) + arcctg ( ) 5 7. Найдите все значения a, при каждом из которых
ПодробнееЭкзаменационный билет 1.
Экзаменационный билет 1. 1. Векторы в пространстве. Основные определения и операции над векторами: сумма векторов, произведение вектора на число. Свойства. Теорема о коллинеарных векторах. 2. Расстояние
ПодробнееУчебный план дисциплины.
3 Учебный план дисциплины. Студенты дневного отделения изучают математику на I и II курсах. Общий объем учебных часов на дисциплину 600 часов. В первом семестре изучаются следующие разделы: линейная алгебра,
Студенты дневного отделения изучают математику на I и II курсах. Общий объем учебных часов на дисциплину 600 часов. В первом семестре изучаются следующие разделы: линейная алгебра,
БАНК ЗАДАЧ ПО ТЕМЕ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ» y 2. * Найти площадь плоской области, ограниченной линиями. (D область, заданная неравенствами ( D)
БАНК ЗАДАЧ ПО ТЕМЕ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ» * Изменить порядок интегрирования + d d * Найти площадь плоской области, ограниченной линиями =, =, = * Вычислить ( D) + acctg d, где ) +, + 9,, = (D область,
Подробнее3. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ЗАНЯТИЕ ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ Написать векторное уравнение плоскости и объяснить смысл величин, входящих в это уравнение Написать общее уравнение плоскости
Подробнее«Линейная алгебра» B Решить
Контрольные работы по дисциплине «Высшая математика» для студентов направления 876 () «Техносферная безопасность» Тематических перечень Линейная алгебра Векторная алгебра Аналитическая геометрия на плоскости
ПодробнееЧасть I(Вариант 609) 3) 2 3) 3 4)
Часть I(Вариант 609) A Внесите множитель под знак корня 8 q A ) q 8 ) q 8 ) q 8 ) q 8 8 8 q q Верный ответ ) Найдите значение выражения ),5 ) Верный ответ ) 9 при a = a a ) ) 8 A log 8 Найдите значение
Подробнее7 класс 1.
 Виды углов.
Виды углов.7 класс 1. Виды углов. Угол называется прямым, если он равен 90 0. Угол называется острым, если он меньше 90 0. Угол называется тупым, если он больше 90 0, но меньше 180 0. Прямой угол Острый угол Тупой
ПодробнееКривые второго порядка.
Кривые второго порядка. Определение : Линией кривой) второго порядка называется множество {М} точек плоскости, декартовы координаты X, Y) которых удовлетворяют алгебраическому уравнению второй степени:,
Подробнее2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.1. Координатные системы и векторная алгебра.1.1. Теоретические сведения Понятия координаты точки являются базовыми понятиями аналитической геометрии. Наиболее употребительными
Подробнее8. Кривые второго порядка Окружность
8 Кривые второго порядка 81 Окружность Множество точек плоскости, равноудаленных от одной точки, называемой центром, на расстояние, называемое радиусом, называется окружностью Пусть центр окружности находится
ПодробнееИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Министерство образования и науки Российской Федерации Южно-Уральский государственный университет Кафедра общей математики 57(7) Б7 ЕА Богонос, ВИ Осмоловский, АА Эбель ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Руководство
ПодробнееВведение в линейную алгебру
Введение в линейную алгебру Матрицы. Определение. Таблица m n чисел вида m m n n mn состоящая из m строк и n столбцов называется матрицей. Элементы матрицы нумеруются аналогично элементам определителя
Определение. Таблица m n чисел вида m m n n mn состоящая из m строк и n столбцов называется матрицей. Элементы матрицы нумеруются аналогично элементам определителя
«Функции нескольких переменных»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет
ПодробнееРешить квадратное уравнение / Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника / Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет. · GitHub
Решить квадратное уравнение / Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника / Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет.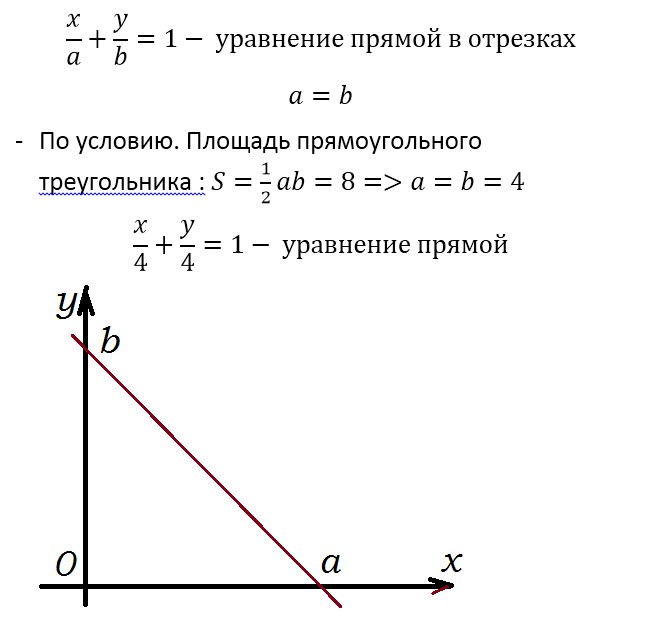 · GitHub
· GitHubInstantly share code, notes, and snippets.
Решить квадратное уравнение / Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника / Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет.
| import UIKit | |
| // 1. Решить квадратное уравнение | |
| let a:Float = 1 | |
| let b:Float = 2 | |
| let c:Float = 3 | |
| var x1:Float | |
| var x2:Float | |
| var d:Float | |
| var discriminant:Float | |
| d = b * b — (4 * a * c) | |
| if(d >= 0){ | |
| discriminant = sqrt(d) | |
| x1 = (-b + discriminant) / (2 * a) | |
| x2 = (-b — (discriminant)) / (2 * a) | |
| print(x1, x2) | |
| }else if(d < 0){ | |
| d = ((4 * a * c) — pow(b,2)) / (2 * a) | |
| print(d) | |
| } | |
// 2. Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника. Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника. | |
| var v:Double = 6 | |
| var n:Double = 8 | |
| var m:Double = 10 | |
| var p:Double | |
| p = v + n + m | |
| m = sqrt(pow(v,2) + pow(n,2)) | |
| print(«Периметр треугольника равен \(p)») | |
| print(«гипотенуза треугольника равна \(m)») | |
// 3. Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет. Найти сумму вклада через 5 лет. | |
| var deposit:Float = 1000 | |
| var percent:Float = 15 | |
| percent = percent / 100 | |
| var result1 = deposit + (deposit * percent) | |
| var result2 = result1 + (result1 * percent) | |
| var result3 = result2 + (result2 * percent) | |
| var result4 = result3 + (result3 * percent) | |
| var result5 = result4 + (result4 * percent) | |
| var counter = 1 | |
| var time = [result1, result2,result3, result4, result5] | |
| for i in time{ | |
| print(«Чрезе \(counter) год/лет сумма вклада будет равна \(i)») | |
| counter += 1 | |
| } |
 You signed in with another tab or window. Reload to refresh your session.
You signed out in another tab or window. Reload to refresh your session.
You signed in with another tab or window. Reload to refresh your session.
You signed out in another tab or window. Reload to refresh your session.графических функций — есть ли какое-нибудь уравнение для треугольника?
Хорошо, у меня есть ответ.
Это очень дерзкий ответ , который опирается на множество технических деталей, но, короче говоря, мы собираемся склеить кучу функций в трехстороннюю форму.
Прежде чем мы перейдем к тому, как это будет выглядеть, я думаю, вы должны увидеть клей. Он полагается на несколько свойств нуля. А именно:
- Никакие два положительных вещественных ненулевых числа не могут быть сложены для получения нуля.
- Ноль, умноженный на любое значение, дает ноль.
- Никакие два ненулевых действительных числа нельзя умножить вместе, чтобы получить ноль.
Это дает нам пару формул, которые, в свою очередь, можно вычислить почти как операторы логической логики: $$ a * b = 0 $$
В нашу формулу вставляется логическое ИЛИ; вы получите ноль только в том случае, если $ a $ равно нулю или $ b $ равно нулю. Если оба они являются действительными числами с ненулевыми значениями, полученный результат также будет отличным от нуля.
$$ | a | + | b | = 0 $$
Если оба они являются действительными числами с ненулевыми значениями, полученный результат также будет отличным от нуля.
$$ | a | + | b | = 0 $$
Запекает логическое И; вы получите ноль только в том случае, если оба значения $ a $ и $ b $ равны нулю.Обратите внимание на использование абсолютных значений; это гарантирует, что и $ a $, и $ b $ должны быть оценены как положительные числа, и эта формула не будет работать без них, поскольку вполне возможно иметь $ a = -b $.
Наконец, обратите внимание на тот факт, что стандартные формулы либо определены в терминах нуля, либо их легко преобразовать в ноль, что дает нам хорошие возможности plug-and-play.
В целом наша формула будет такой: $$ AB * AC * BC = 0 $$
Или, проще говоря: «Точка $ (x, y) $ — это решение для треугольника $ ABC $, если это решение для линейного сегмента $ AB $, линейного сегмента $ AC $ или линейного сегмента $ BC $.«
Проблема в том, что у нас нет стандартного уравнения для отрезка линии. Мы могли бы создать один, если бы направили два луча друг на друга (так, чтобы все коллинеарные точки между их двумя исходными точками были включены в набор решений), но у нас также нет стандартного уравнения для лучей.
Мы могли бы создать один, если бы направили два луча друг на друга (так, чтобы все коллинеарные точки между их двумя исходными точками были включены в набор решений), но у нас также нет стандартного уравнения для лучей.
То, что у нас , есть у , есть некоторая черная магия:
$$ мой (| x-2x_0 | + x) / 2 — mx (y + y_0 — x_0) = 0 $$ $$ mx (| y-2y_0 | + x) / 2 — мой (x + x_0 — y_0) = 0 $$
Каждое из этих уравнений дает набор решений, который включает в себя как луч, исходящий из точки $ (x_0, y_0) $ и движущийся в направлении $ (mx, my) $, так и второй луч, исходящий из той же точки и перемещающийся. параллельно одной из осей (ось x для первой формулы, ось y для второй).Если вы И эти две формулы вместе, вы получите луч. Однако, если вы И их вместе, идущие с противоположных направлений, вместо этого вы получите отрезок линии, что означает, что, хотя мы могли направить два луча друг на друга, определяя их по отдельности, мы можем вдвое уменьшить размер нашей окончательной формулы, определив сегменты линии напрямую.
Итак, для каждого сегмента мы получаем следующие формулы: $$ AB: | ((y_b — y_a) (| x-2x_a | + x) / 2 — (x_b — x_a) (y + y_a — x_a)) | + | ((x_a — x_b) (| y-2y_b | + x) / 2 — (y_a — y_b) (x + x_b — y_b)) | = 0 $$ $$ AC: | ((y_c — y_a) (| x-2x_a | + x) / 2 — (x_c — x_a) (y + y_a — x_a)) | + | ((x_a — x_c) (| y-2y_c | + x) / 2 — (y_a — y_c) (x + x_c — y_c)) | = 0 $$ $$ BC: | ((y_b — y_c) (| x-2x_c | + x) / 2 — (x_b — x_a) (y + y_c — x_c)) | + | ((x_c — x_b) (| y-2y_b | + x) / 2 — (y_c — y_b) (x + x_b — y_b)) | = 0 $$
Что дает окончательное уравнение (* вдыхает *):
$$ (| ((y_b — y_a) (| x-2x_a | + x) / 2 — (x_b — x_a) (y + y_a — x_a)) | + | ((x_a — x_b) (| y-2y_b | + x) / 2 — (y_a — y_b) (x + x_b — y_b)) |) * (| ((y_c — y_a) (| x-2x_a | + x) / 2 — (x_c — x_a) (y + y_a — x_a)) | + | ((x_a — x_c) (| y-2y_c | + x) / 2 — (y_a — y_c) (x + x_c — y_c)) |) * (| ((y_b — y_c ) (| x-2x_c | + x) / 2 — (x_b — x_a) (y + y_c — x_c)) | + | ((x_c — x_b) (| y-2y_b | + x) / 2 — (y_c — y_b) (x + x_b — y_b)) |) = 0 $$
Теперь у вас есть не только средство сжатия любого треугольника в сингулярное уравнение, но и метод объединения любого многоугольника в такое уравнение, а также любой случайный набор отрезков прямых, лучей или любых других элементов, для которых у вас есть стандартное уравнение, так что, надеюсь, это был полезный ответ, несмотря на всю вуду, происходящую с числами.
Однако, как вы, вероятно, можете понять, просто взглянув, это уравнение ужасно непрактично для большинства приложений, особенно по сравнению с большинством других методов. Самая большая польза, которую вы получите от этого, — это напугать своих одноклассников, когда вы копируете / вставляете гигантское уравнение в Desmos, и оно выплевывает пентаграмму с надписью «HAIL SATAN» под ней.
Калькулятор треугольников
Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать».Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники обычно описывают на основе длины их сторон, а также их внутренних углов.Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Кроме того, треугольники обычно описывают на основе длины их сторон, а также их внутренних углов.Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различным количеством концентрических дуг, расположенных в вершинах треугольника.Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника. После ввода фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
После ввода фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
Факты, теоремы и законы о треугольнике
- Учитывая длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.

Площадь треугольника
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h .«Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:
Другой метод вычисления площади треугольника основан на формуле Герона.В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и окружной радиус
Медиана
Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны.Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника. См. Рисунок ниже для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
Inradius
Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вращения и одной из сторон треугольника.Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вращения и одной из сторон треугольника.Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:
где a, b и c — стороны треугольника
Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
Площади треугольников
Наиболее распространенная формула для определения площади треугольника: K = ½ bh , где K — площадь треугольника, b — основание треугольника и h высота. (Буква K используется для обозначения площади треугольника, чтобы избежать путаницы при использовании буквы A для обозначения угла треугольника.) Полезны три дополнительные категории формул площади.
Две стороны и включенный угол (SAS): Учитывая Δ ABC (рисунок), высота определяется как h = c sinA.Следовательно,
Рисунок 1
Справочные треугольники для формул площади.
Два угла и сторона (AAS) или (ASA): Использование закона синусов и замена в предыдущих трех формулах приводит к следующим формулам:
Аналогично
Три стороны (SSS): Известный греческий философ и математик Герон (или Герой) разработал формулу, которая вычисляет площадь треугольников, учитывая только длины трех сторон.Это известно как формула Герона . Если a, b и c — это длины трех сторон треугольника, а s — это полупериметр , то
и
Одно из многих доказательств формулы Герона начинается с Закона косинусов:
Пример 1: (SAS) Как показано на Рисунке 2, две стороны треугольника имеют размеры 25 и 12. Измерение включенного угла составляет 51 °. Найдите площадь треугольника.
Измерение включенного угла составляет 51 °. Найдите площадь треугольника.
Рисунок 2
Чертеж для примера 1.
Используйте формулу SAS:
Пример 2: (AAS и ASA) Найдите площадь треугольника, показанного на рисунке 3.
Рисунок 3
Рисунок для примера 2.
Сначала найдите размер третьего угла треугольника, так как все три угла используются в формуле площади.
Пример 3: (AAS или ASA) Найдите площадь равностороннего треугольника с периметром 78.
Если периметр равностороннего треугольника равен 78, то размер каждой стороны равен 26. Нетригонометрическое решение этой задачи дает ответ
Тригонометрическое решение дает тот же ответ.
Пример 4: (SSS) Найдите площадь треугольника, если его стороны равны 31, 44 и 60. {2}} [/ latex].
{2}} [/ latex].
Ключевые термины
- ножки : стороны, прилегающие к прямому углу в прямоугольном треугольнике.
- прямоугольный треугольник : [латекс] 3 [/ латекс] -сторонняя форма, где один угол имеет значение [латекс] 90 [/ латекс] градусов
- гипотенуза : сторона, противоположная прямому углу треугольника, и самая длинная сторона прямоугольного треугольника.
- Теорема Пифагора : Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ([ латекс] с [/ латекс]).\ circ [/ latex]). Прямоугольный треугольник — это треугольник, в котором один угол является прямым. Соотношение сторон и углов прямоугольного треугольника является основой тригонометрии.
Сторона, противоположная прямому углу, называется гипотенузой (на рисунке сторона [латекс] c [/ латекс]). Боковые стороны, прилегающие к прямому углу, называются ножками (стороны [латекс] a [/ латекс] и [латекс] b [/ латекс]).
 Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].Прямой треугольник: С помощью теоремы Пифагора можно найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, треугольник называется треугольником Пифагора, а длины его сторон в совокупности известны как тройка Пифагора.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии.{2}} [/ латекс]
В этом уравнении [латекс] c [/ латекс] представляет длину гипотенузы, а [латекс] a [/ латекс] и [латекс] b [/ латекс] — длины двух других сторон треугольника.

Хотя часто говорят, что знание теоремы предшествовало ему, [2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 — ок. 495 до н. Э.). Ему приписывают первое записанное доказательство.
Теорема Пифагора: Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ( [латекс] c [/ латекс]).2} & = \ sqrt {25} \\ c & = 5 ~ \ mathrm {cm} \ end {align}} [/ latex]
Как работают тригонометрические функции
Тригонометрические функции могут использоваться для поиска недостающих длин сторон в прямоугольных треугольниках.
Цели обучения
Узнавать, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определять их входные и выходные данные
Основные выводы
Ключевые моменты
- Прямоугольный треугольник имеет один угол со значением 90 градусов ([latex] 90 ^ {\ circ} [/ latex]) Три тригонометрические функции, которые наиболее часто используются для определения недостающей стороны прямоугольного треугольника: [латекс ] \ Displaystyle {\ грех {т} = \ гидроразрыва {противоположный} {гипотенуза}} [/ латекс], [латекс] \ Displaystyle {\ соз {т} = \ гидроразрыва {прилегающий} {гипотенуза}} [/ латекс], и [латекс] \ displaystyle {\ tan {t} = \ frac {противоположный} {смежный}} [/ latex]
Тригонометрические функции
Мы можем определить тригонометрические функции через угол [латекс] t [/ латекс] и длины сторон треугольника.
 Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.Прямой треугольник: Стороны прямоугольного треугольника относительно угла [латекс] t [/ латекс].
При нахождении недостающей стороны прямоугольного треугольника, но единственной информацией, являющейся измерением острого угла и длиной стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника.
 При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угол, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ([latex] \ sin {} [/ latex], [latex] \ cos {} [/ latex], [latex] \ tan {} [/ latex]), определите стороны и заданный угол , составьте уравнение и воспользуйтесь калькулятором и алгеброй, чтобы найти недостающую длину стороны.{\ circ} [/ latex] и длина гипотенузы [latex] 25 [/ latex] футов, найдите длину стороны, противоположной острому углу (округлите до ближайшей десятой):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 34 [/ латекс] градуса и длиной гипотенузы [латекс] 25 [/ латекс] футов найдите длину противоположной стороны.

Глядя на рисунок, решите для стороны, противоположной острому углу [латекса] 34 [/ латекса] градуса. Отношение сторон будет равняться противоположной стороне и гипотенузе .{\ circ} [/ latex] и длина гипотенузы [latex] 300 [/ latex] футов, найдите длину гипотенузы (округлите до десятых):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 83 [/ латекс] градуса и длиной гипотенузы [латекс] 300 [/ латекс] футов найдите длину гипотенузы.
Глядя на рисунок, решите гипотенузу острого угла [латекс] 83 [/ латекс] градуса. Соотношение сторон будет равняться смежной стороне и гипотенузе .{\ circ} \ right)}} \\ x & = \ frac {300} {\ left (0,1218 \ dots \ right)} \\ x & = 2461,7 ~ \ mathrm {feet} \ end {align}} [/ латекс]
Синус, косинус и тангенс
Мнемоника
SohCahToa может использоваться для определения длины стороны прямоугольного треугольника.Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников.

Основные выводы
Ключевые моменты
- Общая мнемоника для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образуется из первых букв « S » — это o pposite за часов ypotenuse ( Soh ), C osine — a djacent over h ypotenuse ), Касательная противоположна соседней ( Тоа ) ».
Определения тригонометрических функций
Для прямоугольного треугольника с острым углом [латекс] t [/ латекс] первые три тригонометрические функции:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Распространенным мнемоником для запоминания этих отношений является SohCahToa , образованный из первых букв « S , равный o pposite в течение часов.
 более ч ypotenuse ( Cah ), касательная противоположна соседней ( Toa ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
более ч ypotenuse ( Cah ), касательная противоположна соседней ( Toa ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)Прямой треугольник: Дан прямоугольный треугольник с острым углом [латекс] 62 [/ латекс] градуса и прилегающей стороной [латекс] 45 [/ латекс] ступней, решите для длины противоположной стороны.
Сначала определите, какую тригонометрическую функцию использовать при заданной соседней стороне, и вам нужно найти противоположную сторону. Всегда определяйте, какая сторона дана, а какая неизвестна под острым углом ([латекс] 62 [/ латекс] градуса).\ circ [/ latex], гипотенуза составляет 30 футов, а длина отсутствующей стороны — это противоположная ножка, [latex] x [/ latex] футов.
Определите, какую тригонометрическую функцию использовать при заданной гипотенузе, и вам нужно найти противоположную сторону. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противоположные «h» и «o», что означает использование «S» или тригонометрической функции синуса.
 {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
{\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]Определение углов по отношениям: обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для определения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач с прямоугольными треугольниками
Основные выводы
Ключевые моменты
- Отсутствующее значение острого угла прямоугольного треугольника может быть найдено, если заданы две длины стороны.{-1} [/ латекс].
Использование тригонометрических функций для поиска отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, создание уравнения и решение. Так же просто найти недостающий острый угол при наличии двух сторон прямоугольного треугольника.
 {- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной стороной [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
{- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной стороной [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:Прямой треугольник: Найдите угол [латекс] A [/ латекс], если задана противоположная сторона и гипотенуза.
От угла [латекс] A [/ латекс] даны стороны напротив и гипотенузы . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.{\ circ} \ end {align}} [/ латекс]
Уравнение медиан треугольника
Чтобы найти уравнение медианы треугольника, рассмотрим следующий пример: Рассмотрим треугольник с вершинами $$ A \ left ({- 3,2} \ right) $$, $$ B \ left ({5,4 } \ right) $$ и $$ C \ left ({3, — 8} \ right) $$.
Если $$ G $$ является серединой стороны $$ AB $$ данного треугольника, то его координаты задаются как $$ \ left ({\ frac {{- 3 + 5}} {2}, \ frac {{2 + 4}} {2}} \ right) = \ left ({\ frac {2} {2}, \ frac {6} {2}} \ right) = \ left ({1,3} \ справа) $$.

Поскольку медиана $$ CG $$ проходит через точки $$ C $$ и $$ G $$, используя двухточечную форму уравнения прямой, можно найти уравнение медианы $$ CG $$ как
\ [\ begin {gather} \ frac {{y — 3}} {{- 8 — 3}} = \ frac {{x — 1}} {{3 — 1}} \\ \ Rightarrow \ frac { {y — 3}} {{- 11}} = \ frac {{x — 1}} {2} \\ \ Rightarrow 2 \ left ({y — 3} \ right) = — 11 \ left ({x — 1} \ right) \\ \ Rightarrow 11x + 2y — 17 = 0 \\ \ end {собрано} \]Если $$ H $$ является серединой стороны $$ BC $$ данного треугольника, то его координаты задаются как $$ \ left ({\ frac {{3 + 5}} {2}, \ frac { {- 8 + 4}} {2}} \ right) = \ left ({\ frac {8} {2}, \ frac {{- 4}} {2}} \ right) = \ left ({4, — 2} \ right) $$.
Поскольку медиана $$ AH $$ проходит через точки $$ A $$ и $$ H $$, используя двухточечную форму уравнения прямой, можно найти уравнение медианы $$ AH $$ как
\ [\ begin {gather} \ frac {{y — \ left ({- 2} \ right)}} {{2 — \ left ({- 2} \ right)}} = \ frac {{x — 4}} {{- 3 — 4}} \\ \ Rightarrow \ frac {{y + 2}} {4} = \ frac {{x — 4}} {{- 7}} \\ \ Rightarrow — 7 \ left ({y + 2} \ right) = 4 \ left ({x — 4} \ right) \\ \ Rightarrow 5x + 7y — 2 = 0 \\ \ end {собрано} \]Если $$ I $$ является серединой стороны $$ AC $$ данного треугольника, то его координаты задаются как $$ \ left ({\ frac {{- 3 + 3}} {2}, \ frac {{2 — 8}} {2}} \ right) = \ left ({0, \ frac {- 6}} {2}} \ right) = \ left ({0, — 3} \ right) $ $.
Поскольку медиана $$ BI $$ проходит через точки $$ B $$ и $$ I $$, используя двухточечную форму уравнения прямой, можно найти уравнение медианы $$ BI $$ как
Формула треугольника
\ [\ begin {gather} \ frac {{y — \ left ({- 3} \ right)}} {{4 — \ left ({- 3} \ right)}} = \ frac {{x — 0}} {{5 — 0}} \\ \ Rightarrow \ frac {{y + 3}} {7} = \ frac {x} {5} \\ \ Rightarrow 5 \ left ({y + 3} \ right ) = 7x \\ \ Rightarrow 7x — 5y — 15 = 0 \\ \ end {собрано} \]— Типы треугольников
Примечание: Два оставшихся угла прямоугольного треугольника всегда являются острыми углами.Важное свойство прямоугольных треугольников — это теорема Пифагора . В нем указано, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника.
На рисунке выше DABC представляет собой прямоугольный треугольник, поэтому (AB) 2 + (AC) 2 = (BC) 2 . Здесь AB = 6 и AC = 8, поэтому BC = 10, так как 6 2 + 8 2 = 36 + 64 = 100 = (BC) 2 и BC = & redic; 100.
Обязательно читать статьи о треугольниках
Любой треугольник, в котором длины сторон находятся в соотношении 3: 4, всегда является прямоугольным треугольником.
В общем случае, если x, by и z — длины сторон треугольника, в котором x 2 + y 2 = z 2 , то треугольник называется прямоугольным.
Есть несколько пифагоровых троек, которые часто используются в вопросах. Эти тройни лучше запомнить.
- 3, 4 и 5
- 5, 12 и 13
- 7, 24 и 25
- 8, 15 и 17
- 9, 40 и 41
- 11, 60 и 61
- 12, 35 и 37
- 16, 63 и 65
- 20, 21 и 29
- 28, 45 и 53.
Любое кратное этих пифагоровых троек также будет пифагоровым триплетом, т.е. когда мы говорим, что это тройка 5,12,13, если мы умножим все эти числа на 3, это также будет тройка i.е. 15, 36, 39 также будут триплетом Пифагора.
(iv) 45 ° — 45 ° -90 ° Треугольник : специальные треугольники: если три угла треугольника составляют 45 °, 45 ° и 90 °, тогда перпендикулярная сторона этого прямоугольного треугольника в 1/2 раза больше гипотенузы треугольника. В треугольнике 45 ° — 45 ° — 90 ° длины трех сторон этого треугольника находятся в соотношении 1: 1: & redic; 2.
Например, в ∆PQR, если PR = 2 см, то PQ = & redic; 2 см, а QR = & redic; 2 см.
(v) 30 ° — 60 ° — 90 ° Треугольник : В треугольнике 30 ° — 60 ° — 90 °, длины трех сторон этого треугольника находятся в соотношении 1: & redic; 3: 2. Например, в ∆ABC, если AC = 3, то AB = 3 & redic; 3 и BC = 6. Подводя итог, приведенные ниже формулы могут применяться для расчета две другие стороны треугольника 30 ° — 60 ° -90 °, если задана одна из трех сторон.
Сторона, противоположная 30 ° = ½ гипотенузы.
Сторона, противоположная 60 ° = & redic; 3/2 гипотенузы.
Некоторые важные свойства треугольников
(i) Сумма трех внутренних углов треугольника равна 180 °.
In ∆ABC, ABC + ∠BAC + ∠ACB = 180 °
(ii) Сумма внутреннего угла и прилегающего внешнего угла составляет 180 °.
На рисунке на предыдущей странице ABC + ∠ABH = 180 °
ABC + ∠CBI = 180 °
(iii) Два внешних угла с одинаковой вершиной конгруэнтны.
(iv) Размер внешнего угла равен сумме измерений двух внутренних углов (называемых удаленными внутренними углами) треугольника, не прилегающего к нему.
(vi) Сумма любых двух сторон треугольника всегда больше третьей стороны.
В ∆ABC AB + BC> AC, также AB + AC> BC и AC + BC> AB.
(vii) Разница любых двух сторон всегда меньше, чем у третьей стороны.
Высота: Высота треугольника — это отрезок, проведенный из вершины, перпендикулярной стороне, противоположной этой вершине. Относительно этой вершины и высоты противоположная сторона называется основанием.
Площадь треугольника равна: (длина высоты) × (длина основания) / 2.
BD = 5
В ∆ABC, BD — это высота до основания AC, а AE — высота до основания BC.
Формула треугольника : Площадь треугольника ∆ABC равна ½ × BD × AC = ½ × 5 × 8 = 20.
Площадь треугольника также равна (AE × BC) / 2. Если DABC выше равнобедренный и AB = BC, то высота BD делит основание пополам; то есть AD = DC = 4. Аналогично, любая высота равностороннего треугольника делит пополам сторону, к которой он обращается.
Конгруэнтность треугольников : Если стороны и углы одного треугольника равны соответствующим сторонам и углам другого треугольника, то два треугольника называются конгруэнтными.
Два треугольника равны, если
- Две стороны и включенный угол треугольника соответственно равны двум сторонам и включенному углу другого треугольника (SAS).
- 2 угла и 1 сторона треугольника равны соответственно двум углам и соответствующей стороне другого треугольника (AAS).
- Три стороны треугольника равны трем сторонам другого треугольника (SSS).
- 1 сторона и гипотенуза прямоугольного треугольника соответственно конгруэнтны 1 стороне и гипотенузе другой правой стороны.треугольник (RHS).
Подобие треугольников:
Два треугольника называются подобными друг другу, если они похожи только по форме. Соответствующие углы этих треугольников равны, но соответствующие стороны только пропорциональны. Все конгруэнтные треугольники подобны, но все похожие треугольники не обязательно конгруэнтны.
Два треугольника похожи, если
- Три стороны треугольника пропорциональны трем сторонам другого треугольника (SSS).
- Два угла треугольника равны двум углам другого треугольника (AA) соответственно.
- Две стороны треугольника пропорциональны двум сторонам другого треугольника, а входящие углы равны (SAS).
Свойства треугольников :
- Если два треугольника похожи, отношения сторон = отношение высот = отношение медиан = отношение биссектрис угла = отношение внутренних радиусов = отношение радиусов окружности.
- Соотношение площадей = b 1 h 1 / b 2 h 2 = (s 1 ) 2 / (s 2 ) 2 , где b 1 & h 1 — это основание и высота первого треугольника, а b 2 и h 2 — основание и высота второго треугольника. s 1 & s 2 — соответствующие стороны первого и второго треугольника соответственно.
- Два треугольника на каждой стороне перпендикуляра, проведенного от вершины прямого угла к наибольшей стороне i.е. Гипотенузы похожи друг на друга и также похожи на больший треугольник.
∆ DBA аналогичен ∆ DCB, который аналогичен ∆ BCA.
- Высота от вершины прямого угла до гипотенузы — это среднее геометрическое значение отрезков, на которые делится гипотенуза.
то есть (DB) 2 = AD * DC
Центр окружности : Центр окружности — это центр окружности окружности треугольника.Его можно найти по пересечению серединных перпендикуляров.
Incenter : Incenter — это точка, представляющая центр вписанной окружности многоугольника. Соответствующий радиус вписанной окружности называется внутренним радиусом вписанной окружности.
Сводка тригонометрических формул
Сводка тригонометрических формулЭти формулы относятся к длине и площади определенных кругов или треугольников. На следующей странице вы найдете личности.Идентичности не относятся к конкретным геометрическим фигурам, но верны для всех углов.
Формулы дуг и секторов окружностей
Вы можете легко найти как длину дуги, так и площадь сектора для угла θ в окружности радиуса r .
Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.Чтобы преобразовать градусы в радианы, умножьте количество градусов на π /180. Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах. Формулы для прямоугольных треугольников
Наиболее важные формулы для тригонометрии — формулы для прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус тета — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а тангенс — это отношение сторона, противоположная соседней стороне.
Эти три формулы известны мнемоническим языком SohCahToa. Помимо этого, существует очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.
Зная, что два острых угла дополняют друг друга, то есть они складываются в 90 °, вы можете решить любой прямоугольный треугольник:
- Если вы знаете две из трех сторон, вы можете найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Формулы наклонных треугольников
Эти формулы работают для любого треугольника, будь то острый, тупой или прямой. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначаются прописными буквами A , B и C , а три противоположные им стороны соответственно обозначаются строчными буквами a , . b и c .
Есть две важные формулы для наклонных треугольников. Их называют законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники. В нем говорится, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумме квадратов двух других сторон минус 2. ab cos & nbsp C , удвоить их произведение, умноженное на косинус противоположного угла.Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне является одинаковым соотношением для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Если вы знаете два угла и сторону, вы можете найти третий угол и две другие стороны.
- Если вы знаете две стороны и включенный угол, вы можете найти третью сторону и оба других угла.
- Если вам известны две стороны и угол, противоположный одной из них, есть две возможности для угла, противоположного другой (острый и тупой), и для обеих возможностей вы можете определить оставшийся угол и оставшуюся сторону.
Формулы площади для треугольников
Есть три разные полезные формулы для вычисления площади треугольника, и какая из них вы используете, зависит от того, какая информация у вас есть.
Половина основания, умноженная на высоту. Это обычный вариант, так как он самый простой и обычно у вас есть такая информация. Выбирайте любую сторону для вызова базы b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh . Формула Герона. Это полезно, если вы знаете три стороны треугольника: , , b, и c, , и все, что вам нужно знать, — это площадь.Пусть s будет половиной их суммы, называемой полупериметром .

 Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
 Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная. При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.

 более ч ypotenuse ( Cah ), касательная противоположна соседней ( Toa ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
более ч ypotenuse ( Cah ), касательная противоположна соседней ( Toa ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых) {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
{\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex] {- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной стороной [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
{- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной стороной [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса: