Уравнение перпендикулярной прямой | Треугольники
Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?
Пусть y=k1x+b1 — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид
Если эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b.
Примеры.
1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.
Решение:
Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то
Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид
Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:
откуда b=1.
Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)
Ответ: y= -0,2x+1.
2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).
Решение:
Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.
Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.
Ответ: y=9.
3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).
Решение:
Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.
Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.
Ответ: x=7.
Условие перпендикулярности прямых | Треугольники
I. Выясним условие перпендикулярности двух прямых y=k
1x+b1 и y=k2x+b2.Пусть прямые y=k1x+b1 и y=k2x+b2 образуют с положительным направлением оси Ox углы α1 и α2 соответственно.
Обозначим точки пересечения прямых с осью абсцисс через A и B, точку пересечения прямых — C.
Так как α2 — внешний угол при вершине B треугольника ABC, то
Отсюда угловой коэффициент второй прямой
Итак,
условие перпендикулярности прямых:
прямые, заданные уравнениями y=k1x+b1 и y=k2x+b2 перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку:
II. Для общего уравнения прямой
угловые коэффициенты
Отсюда
и условие перпендикулярности прямых в этом случае имеет вид:
Уравнение прямой
Прямые, заданные
общими уравнениями: 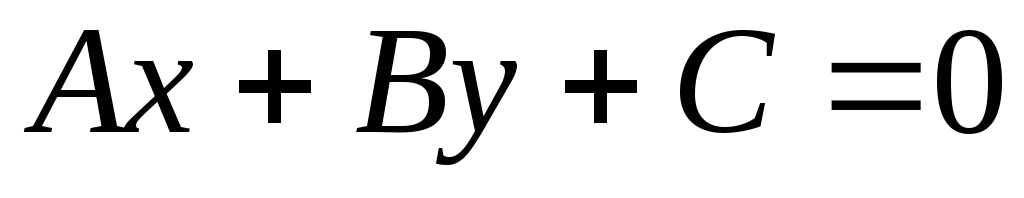 и
и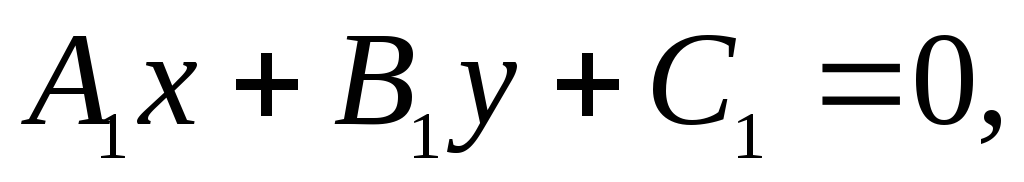 взаимно перпендикулярны тогда и только
тогда, когда
взаимно перпендикулярны тогда и только
тогда, когда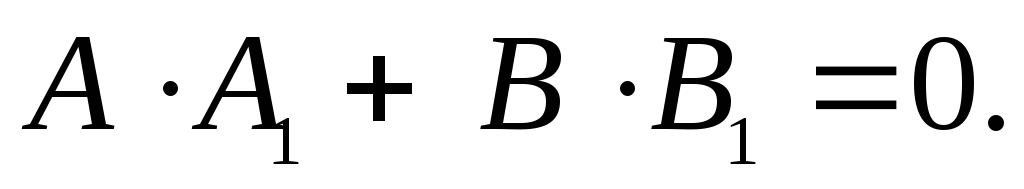 Данные прямые параллельны тогда и только
тогда, когда
Данные прямые параллельны тогда и только
тогда, когда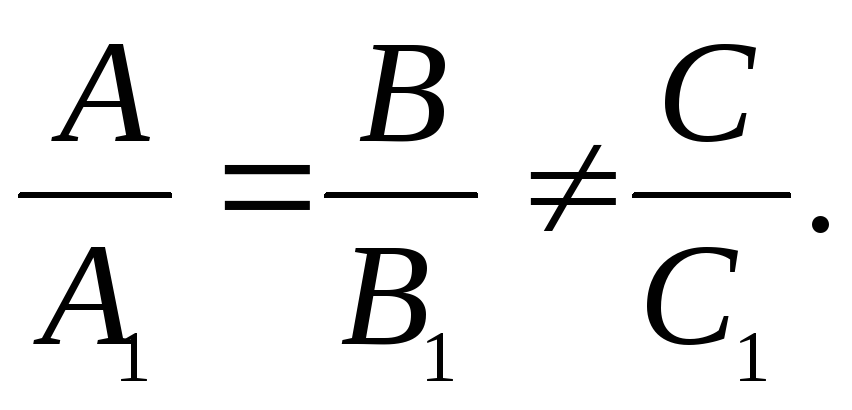
Прямые на плоскости,
заданные в виде: 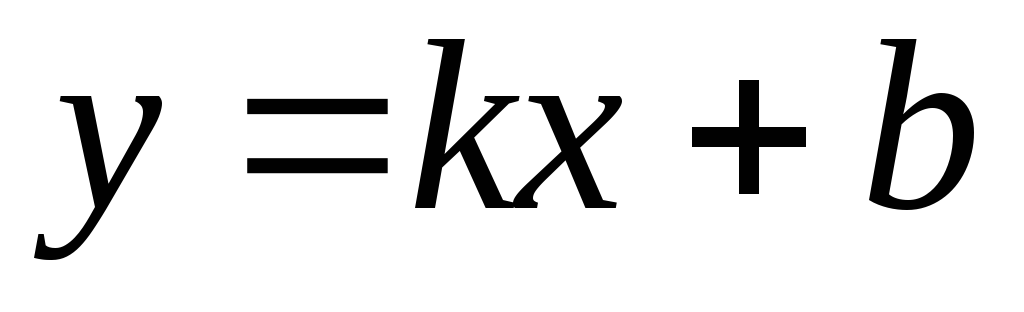
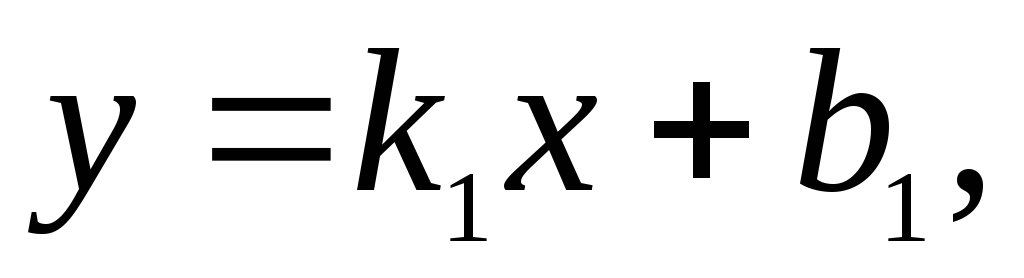 перпендикулярны только том случае,
когда
перпендикулярны только том случае,
когда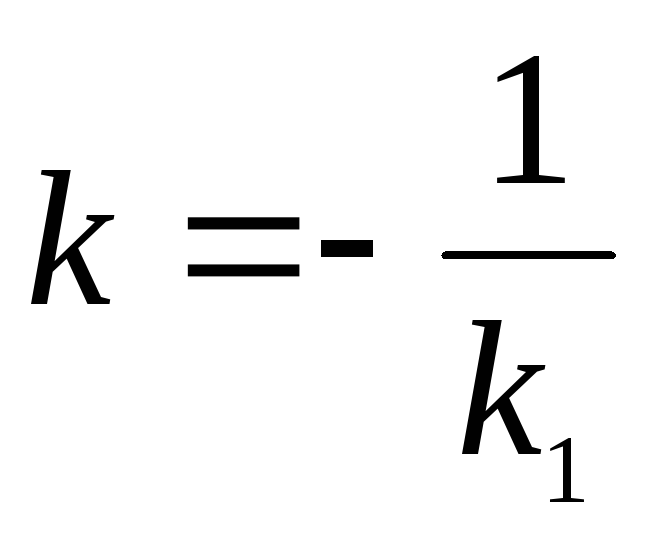 (при
(при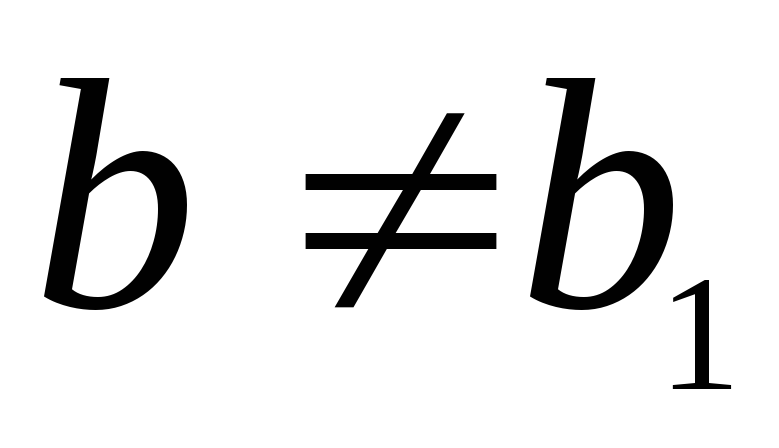 ).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.
).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.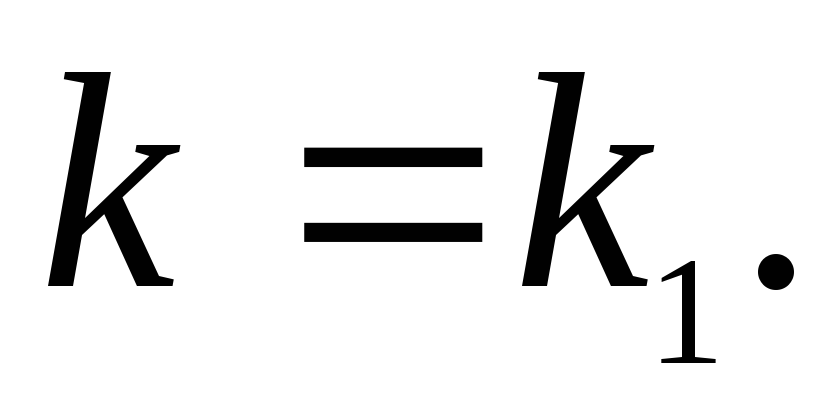
Прямые, заданные
своими каноническими уравнениями: 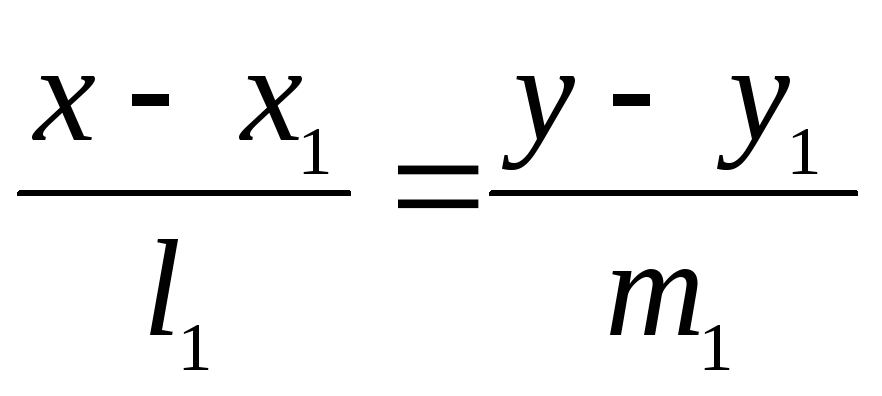 и
и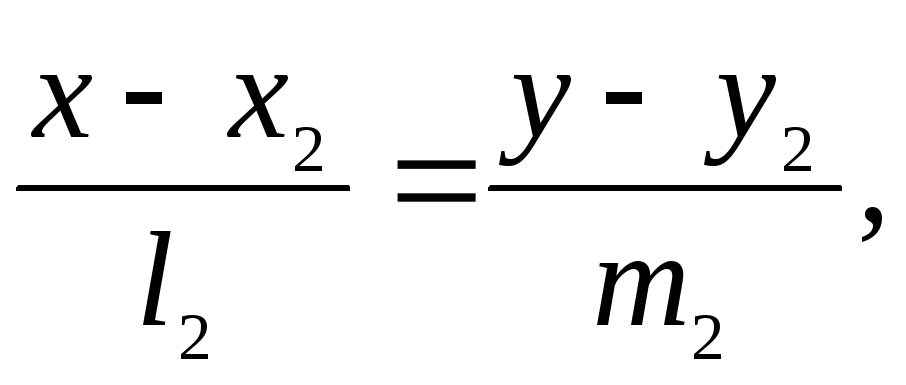 взаимно перпендикулярны тогда и только
тогда, когда
взаимно перпендикулярны тогда и только
тогда, когда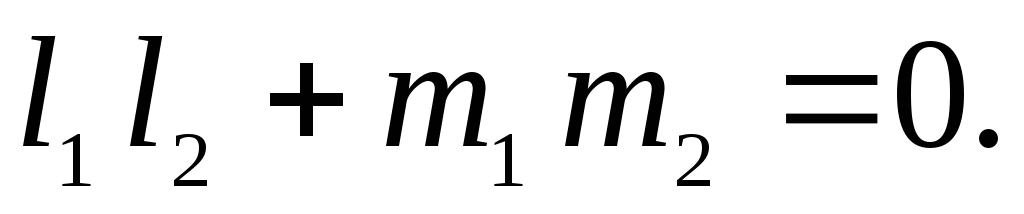 Данные прямые параллельны, если только
выполнено условие:
Данные прямые параллельны, если только
выполнено условие: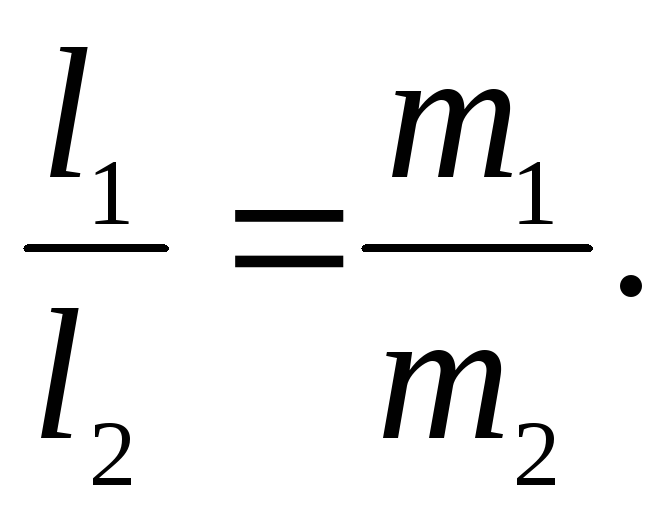
2.7. Точка пересечения непараллельных прямых
Если на плоскости
заданы две прямые: 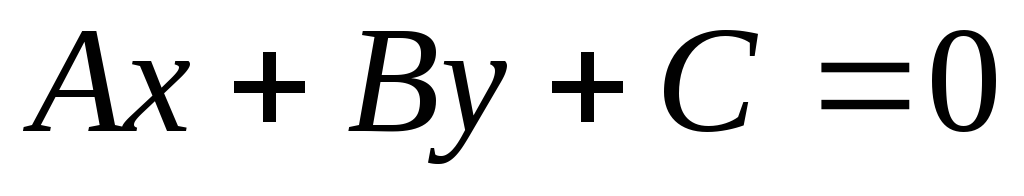 и
и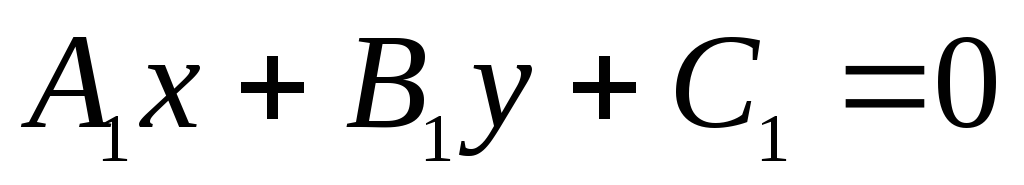 ,
то согласно утверждению 2 координаты
,
то согласно утверждению 2 координаты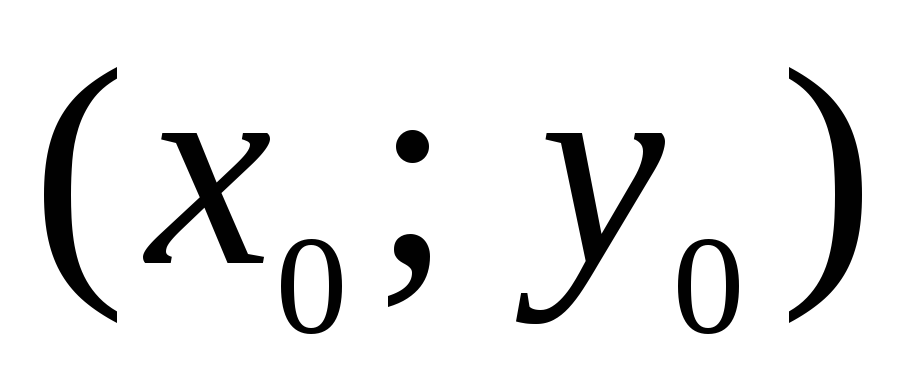 точки пересечения этих прямых можно
вычислить по формулам:
точки пересечения этих прямых можно
вычислить по формулам:
| (21) |
| (22) |
Лекция 10. Прямая в пространстве
Общее уравнение прямой
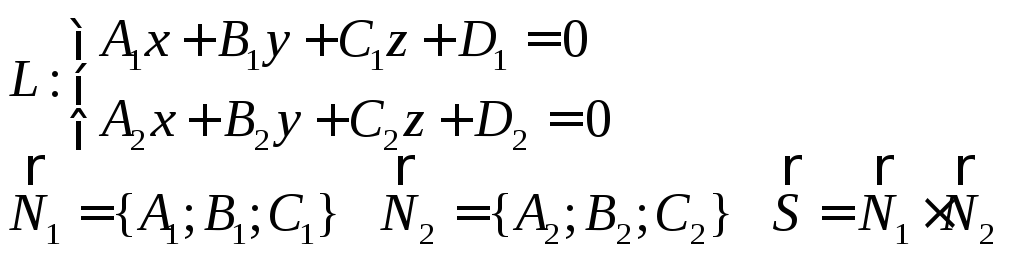
 направляющий вектор прямой
направляющий вектор прямой
Каноническое уравнение прямой
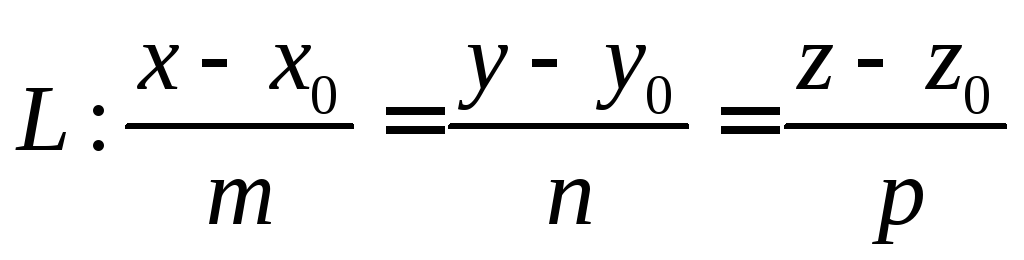
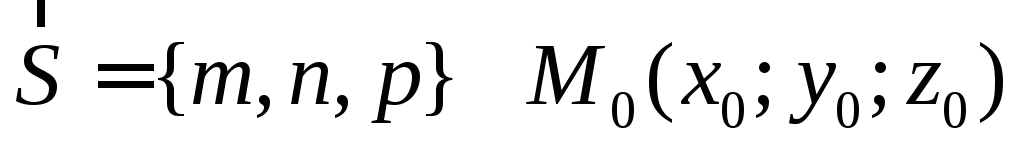
Параметрические уравнения прямой

Уравнение прямой проходящей через 2 данные точки
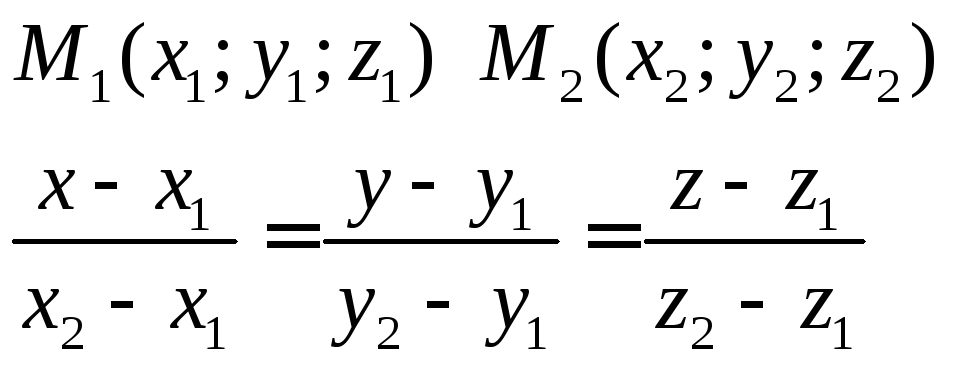
Угол между прямыми
 и
и
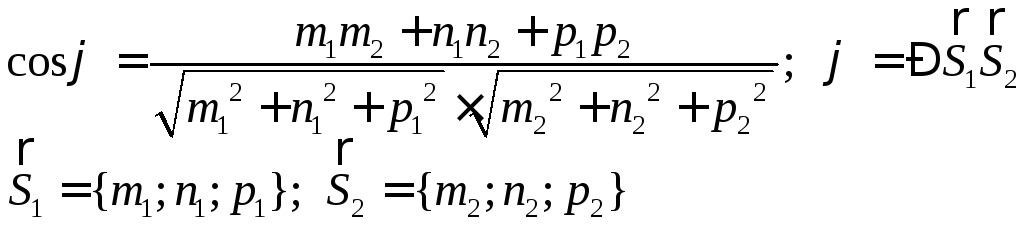
6.
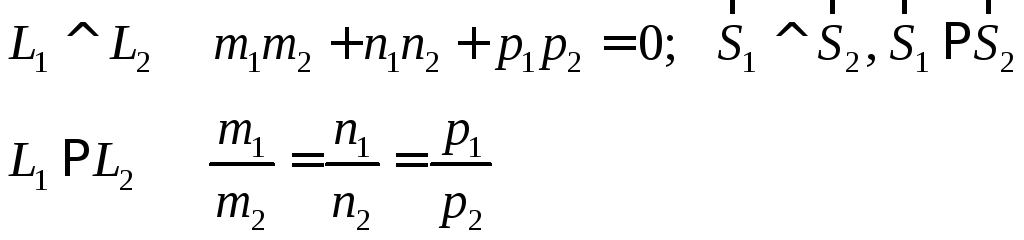
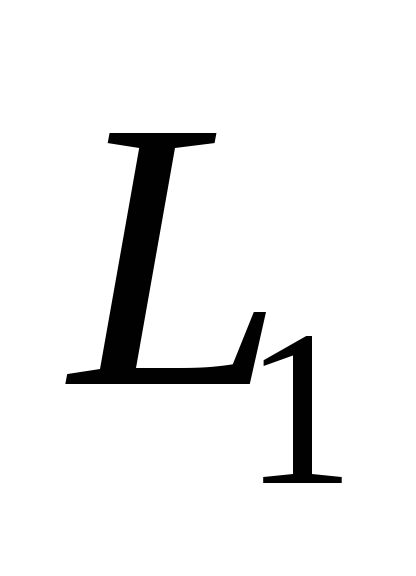 и
и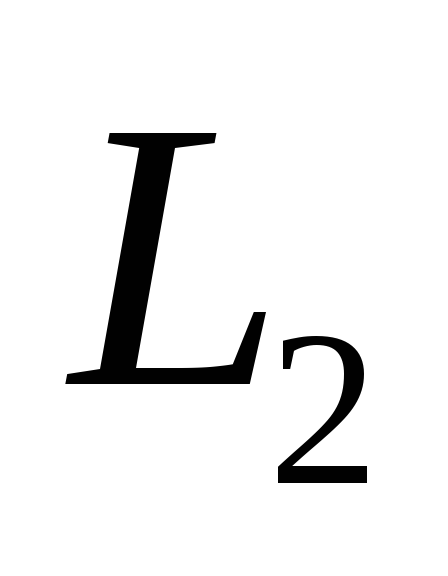 лежат в одной плоскости
лежат в одной плоскости
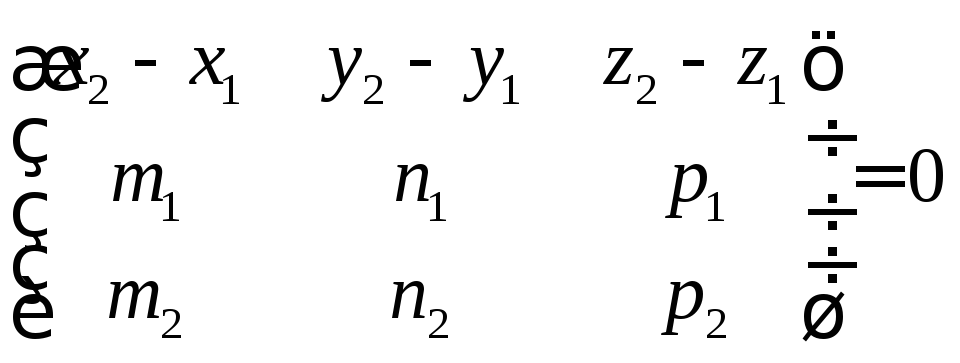
Прямая и плоскость в пространстве
Угол между прямой L и плоскостью

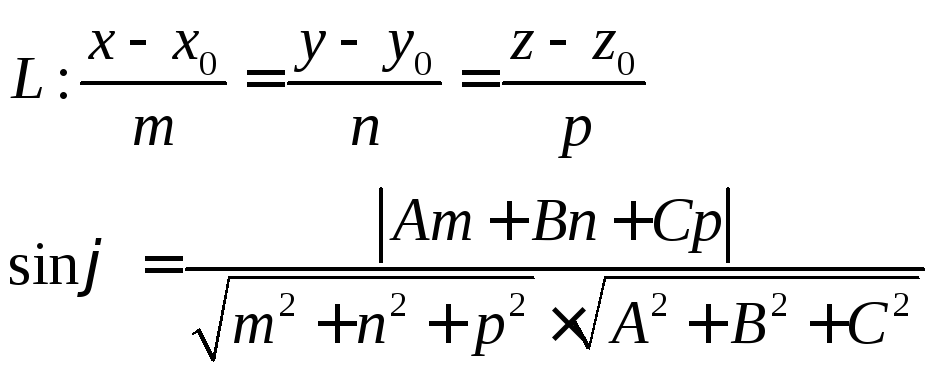
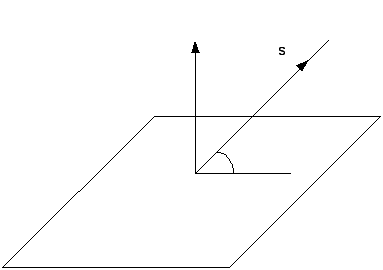
2. 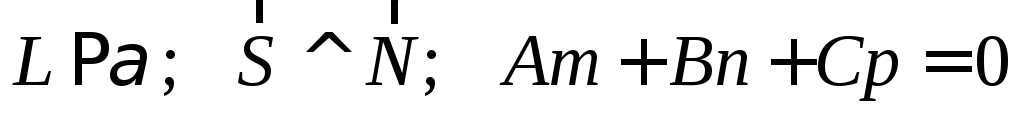
L-
лежит в
плоскости 
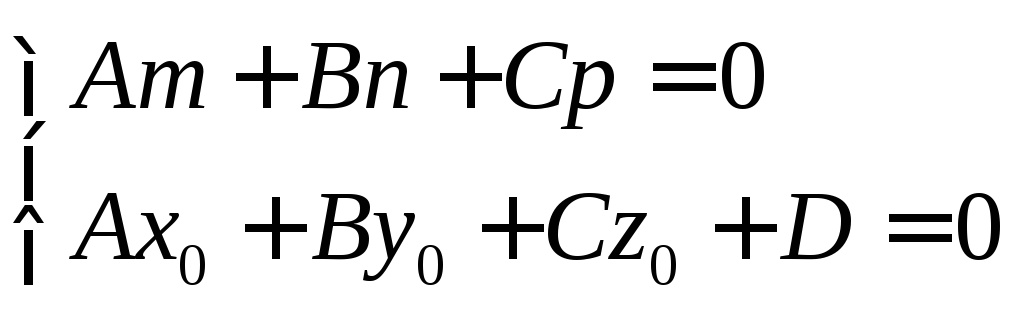
3. 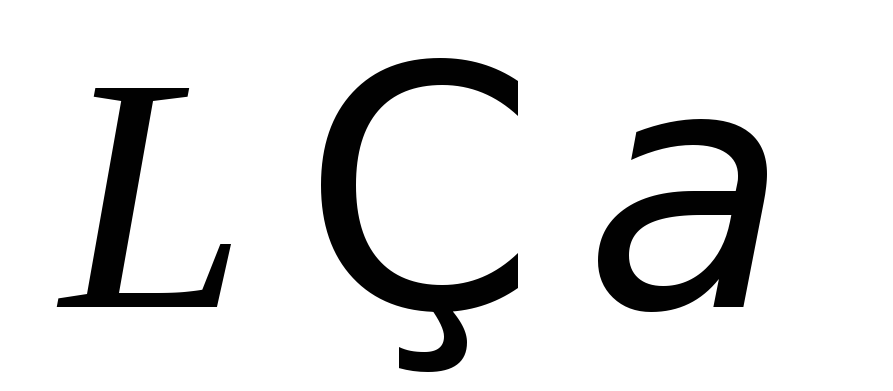 если
если 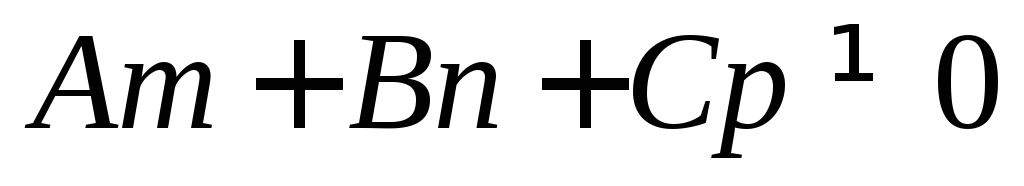
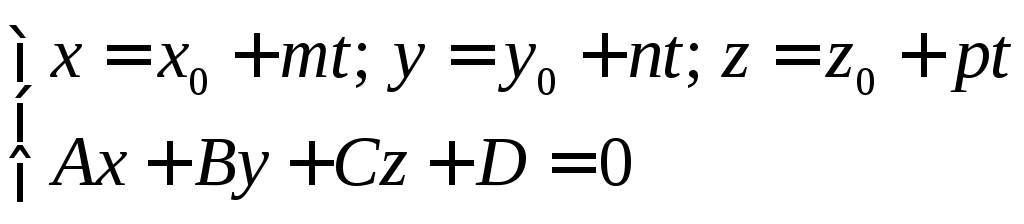
4. 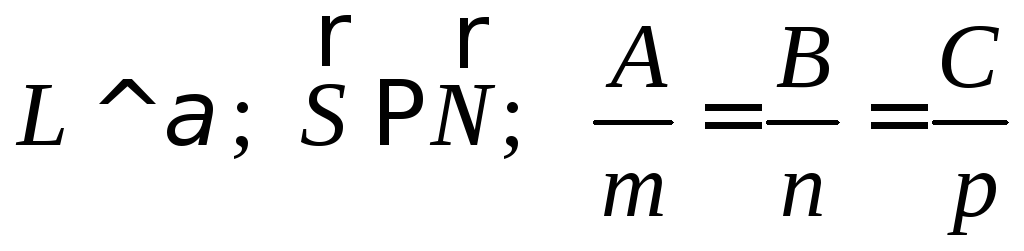
Лекция 11. Кривые второго порядка
Кривой второго
порядка называется геометрическое
место точек, задаваемых уравнением: 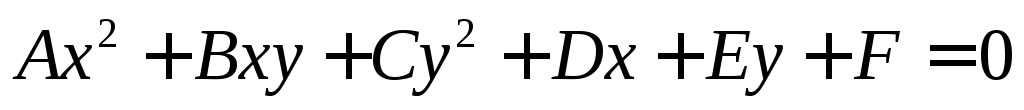
Классификация кривых второго порядка







Эллипс | Гипербола | Парабола | Точка (0;0) | Пара пересекающихся прямых | Пара совпадающих прямых | Пара параллельных прямых |
Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение
| Каноническое
уравнение |
Признак вырожденности кривой: уравнение можно представить в виде произведения двух сомножителей.
Эллипс
Кривая второго
порядка, заданная каноническим уравнением 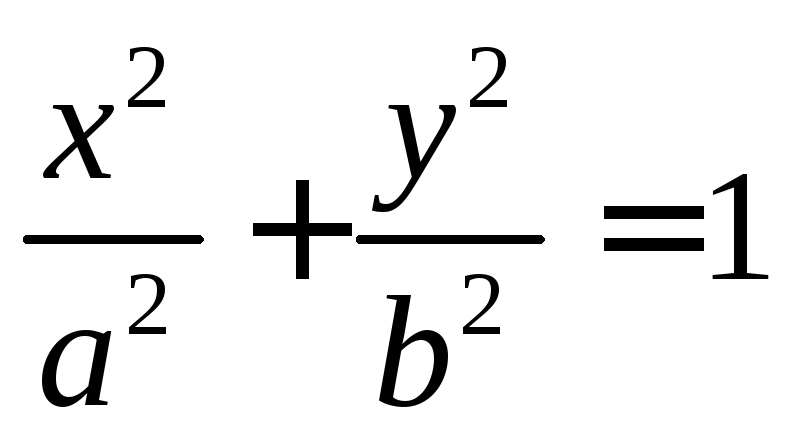 ,
называется эллипсом.a,b – полуоси
эллипса. Если
,
называется эллипсом.a,b – полуоси
эллипса. Если 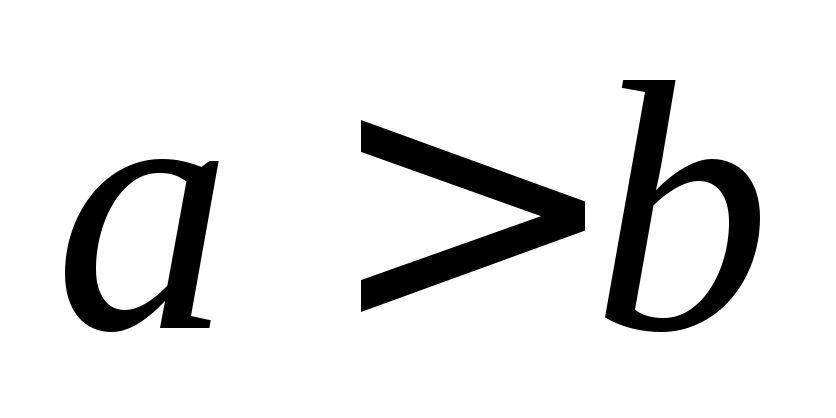 ,
то a—
большая полуось, b—
малая полуось.
,
то a—
большая полуось, b—
малая полуось.
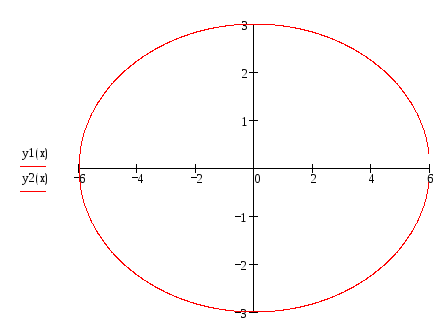
Построение эллипса,
заданного каноническим уравнением 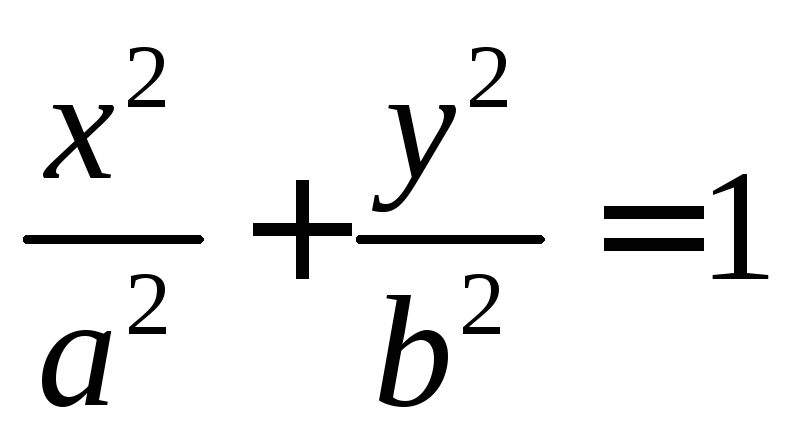 .
Пусть уравнение эллипса имеет вид
.
Пусть уравнение эллипса имеет вид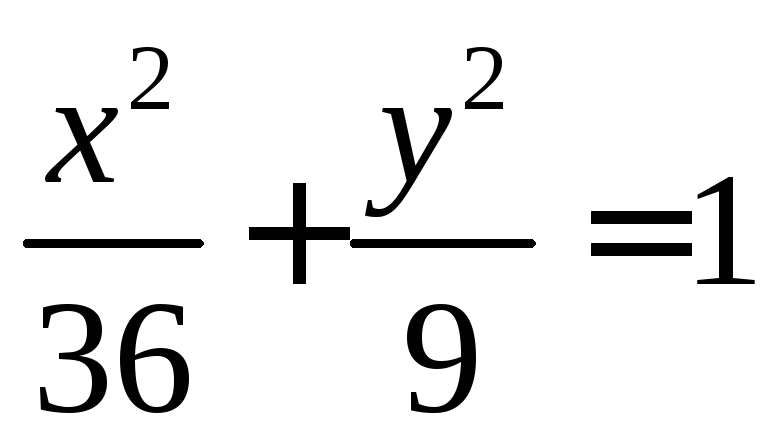 .
Построим прямыеx=6 и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам
.
Построим прямыеx=6 и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам 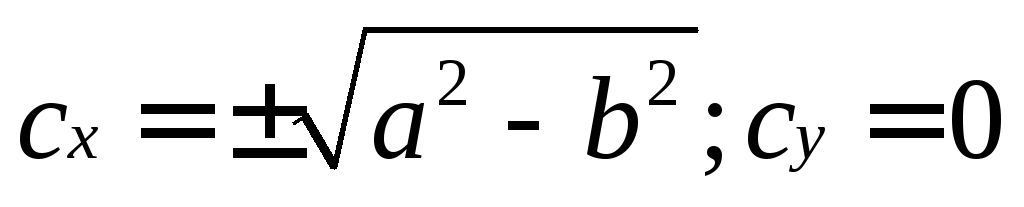 если в уравнении
если в уравнении 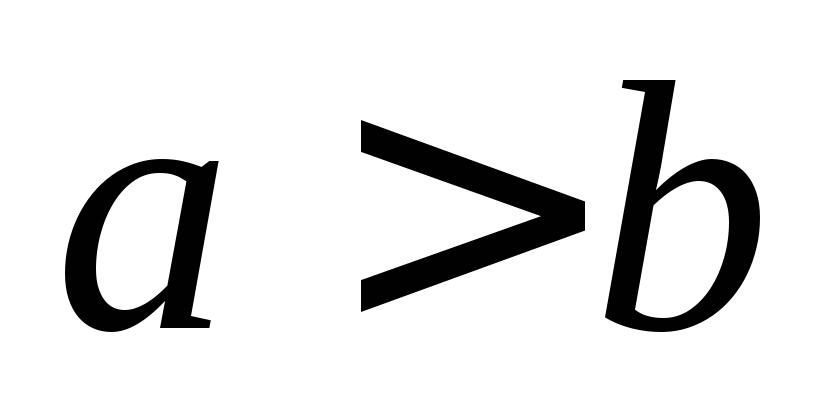 .
Если
.
Если 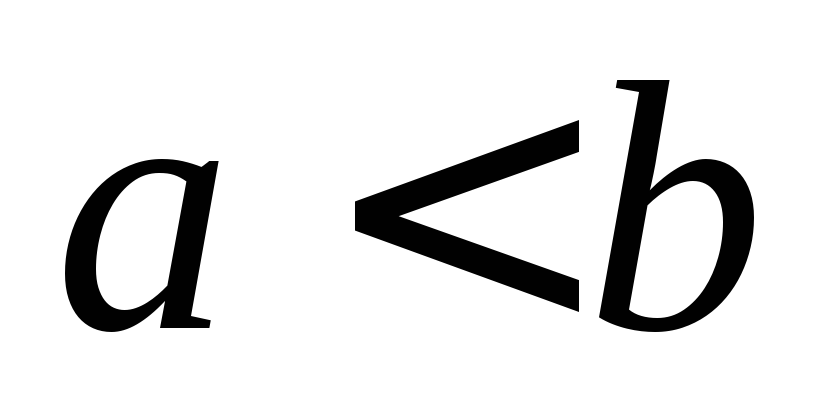 ,
то фокусы имеют координаты
,
то фокусы имеют координаты 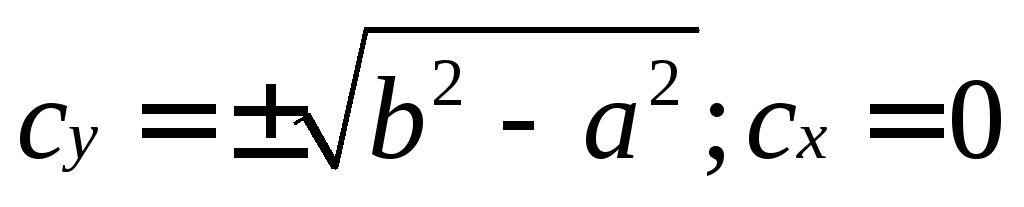 (эллипс ориентирован вертикально).
(эллипс ориентирован вертикально).
Оптическое свойство эллипса состоит в том, что если точечный источник света поместить в один фокус эллипса, то в другом фокусе появится его изображение.
Эксцентриситет
эллипса – степень его вытянутости
— отношение расстояния от центра эллипса
до фокуса к его большой полуоси,
вычисляется по формуле 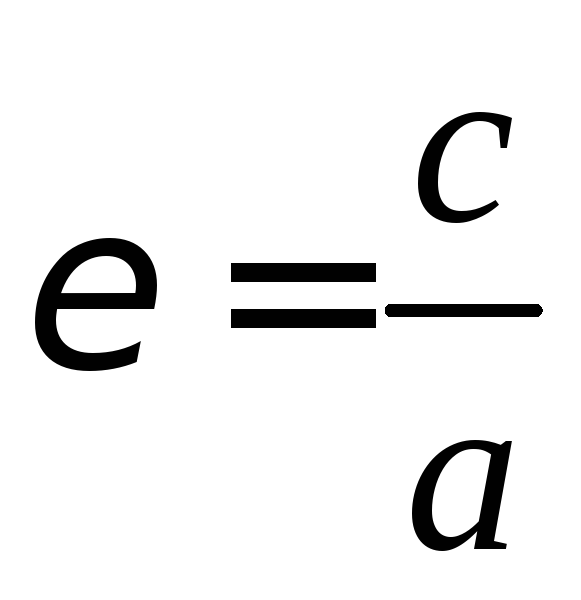 .
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением
.
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением 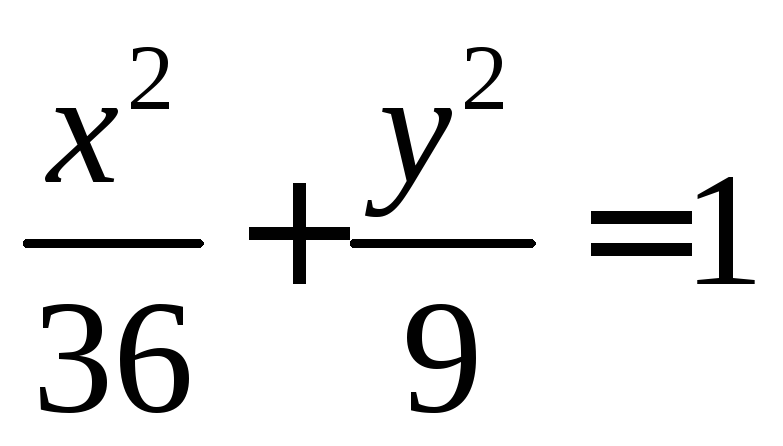 эксцентриситет
эксцентриситет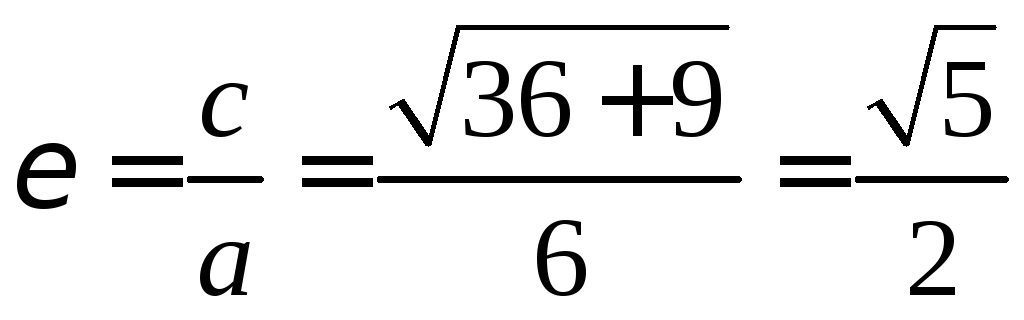 ,
а фокусы находятся в точках
,
а фокусы находятся в точках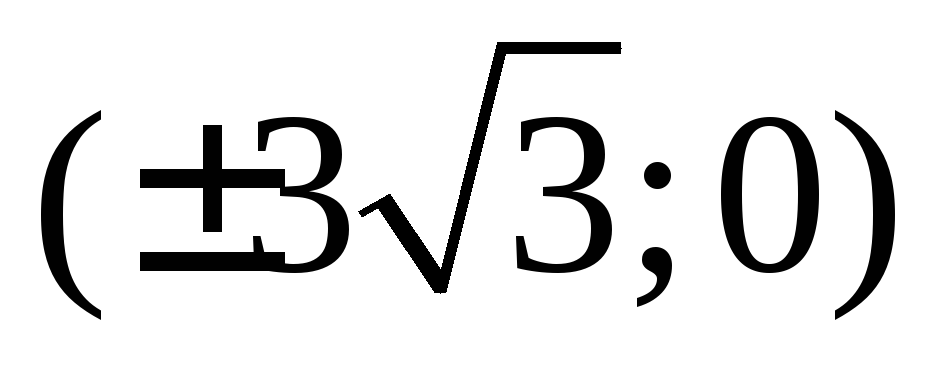 .
.
Окружность
– частный случай эллипса, задается
уравнением 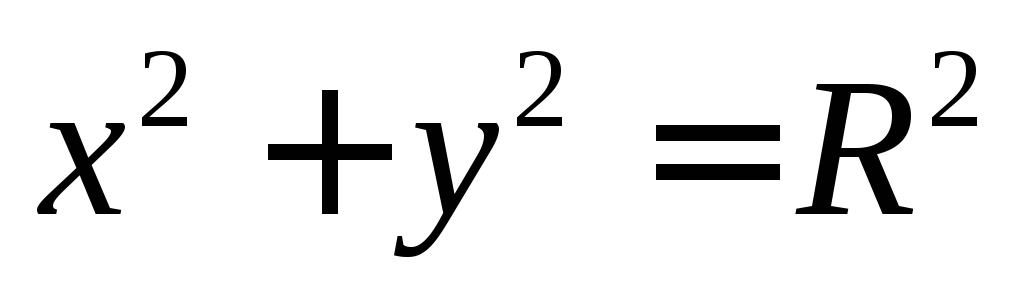 ,
гдеR – радиус окружности. У окружности 0,
а фокусы совпадают с центром ( началом
координат).
,
гдеR – радиус окружности. У окружности 0,
а фокусы совпадают с центром ( началом
координат).
Гипербола
Гипербола
– кривая, задаваемая каноническим
уравнением 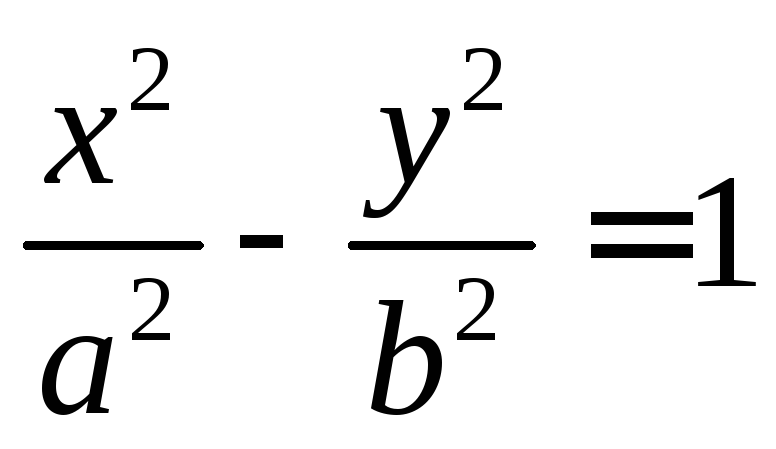 или
или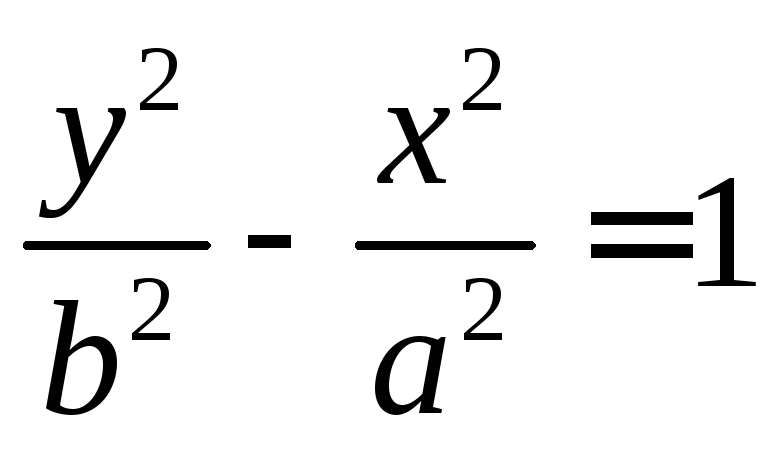 .a,b – полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые
.a,b – полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые 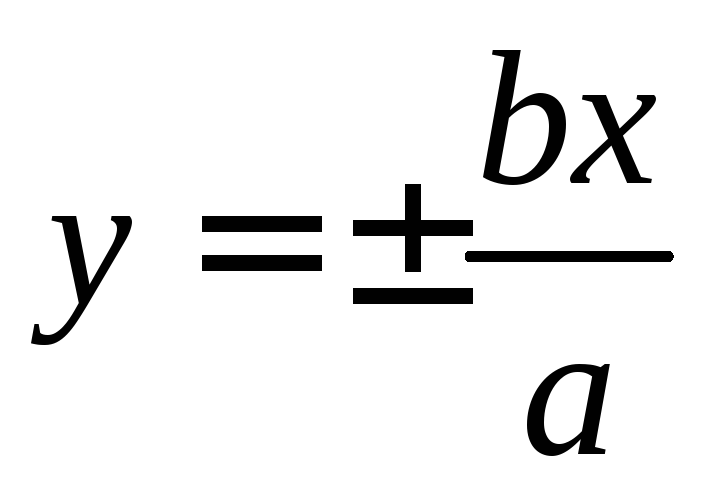 — асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
— асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
Построение гиперболы
Построение
гиперболы, заданной уравнением начинаем
с отложения по оси Ox
отрезка длиной a единиц, а по
оси Oy
– длиной b единиц.
Строим прямые 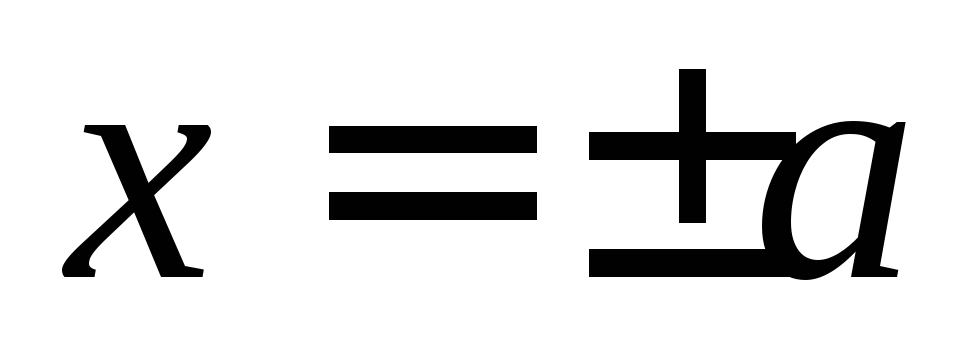 и
и 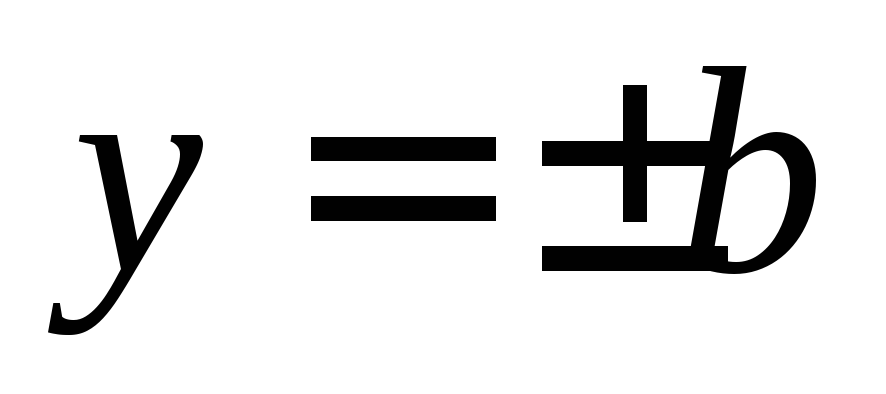 .
Гипербола будет касаться полученного
прямоугольника в двух точках
.
Гипербола будет касаться полученного
прямоугольника в двух точках 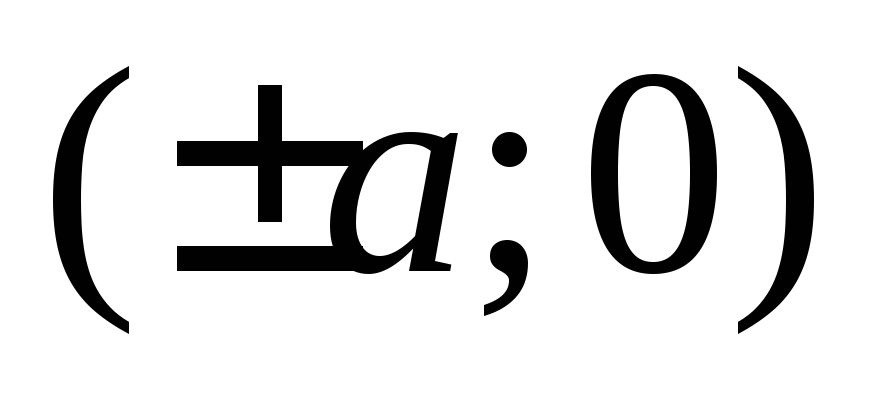 .
Проведем прямые
.
Проведем прямые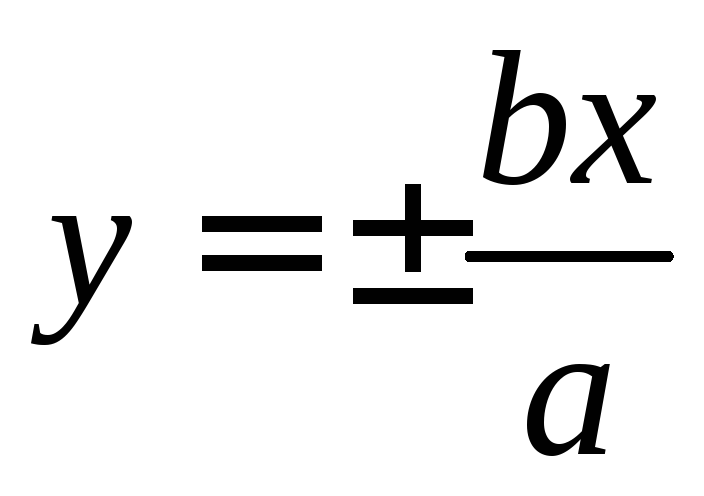 — асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением
— асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением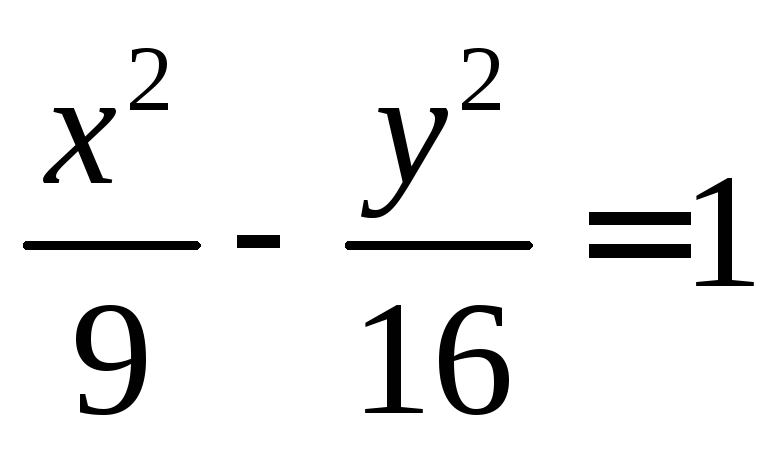 )
представлен на рисунке. Если в уравнении
гиперболы
)
представлен на рисунке. Если в уравнении
гиперболы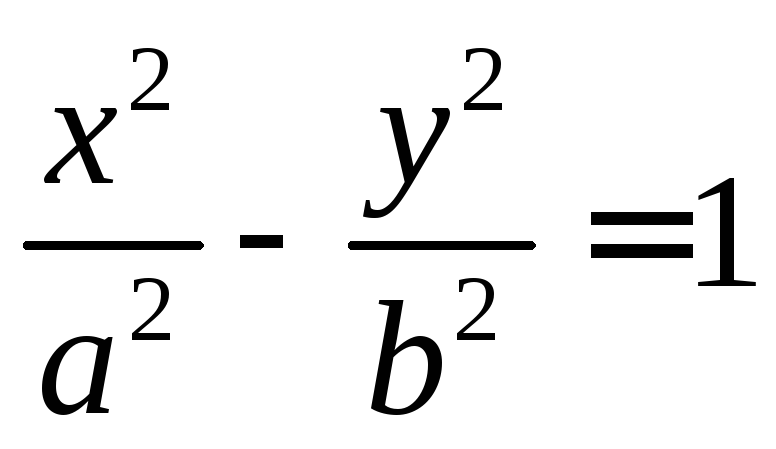 поменять знаки передx
и y,
то получим сопряженную ей гиперболу
поменять знаки передx
и y,
то получим сопряженную ей гиперболу 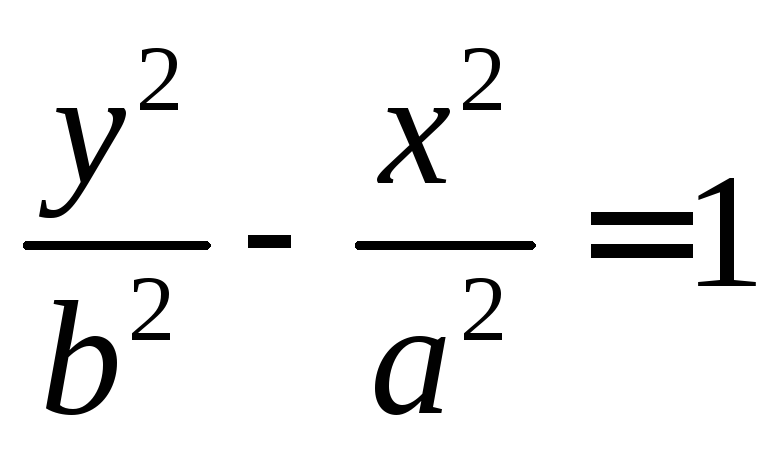 ,
которая имеет те же асимптоты.
,
которая имеет те же асимптоты.
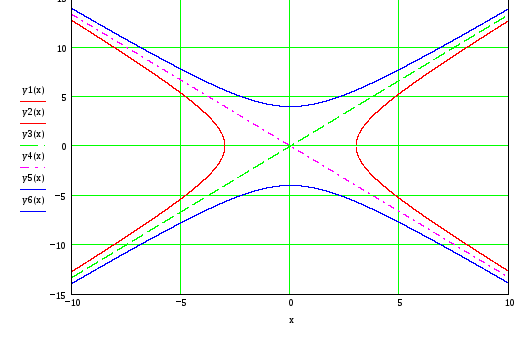
Так же как и эллипс,
гиперболу можно определить как
геометрическое
место точек, разность расстояний которых
от фокусов постоянна.
Фокусы гиперболы имеют координаты 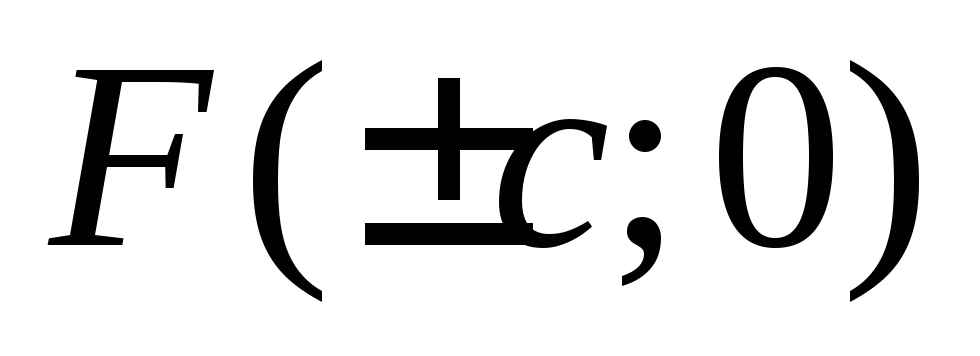 ,
где
,
где 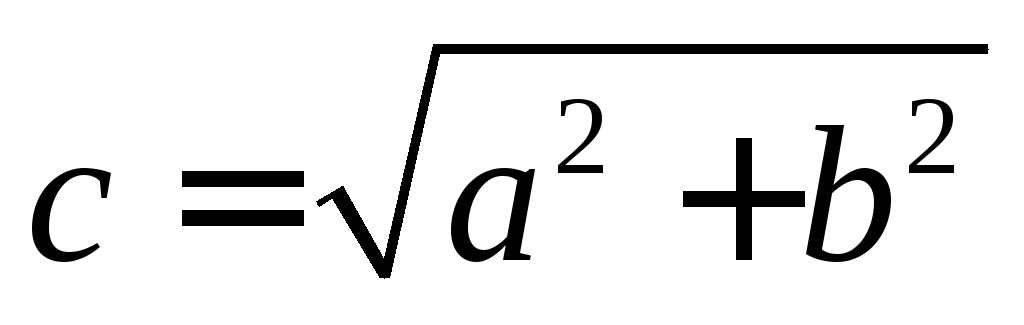 (значенияa,b берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках
(значенияa,b берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках 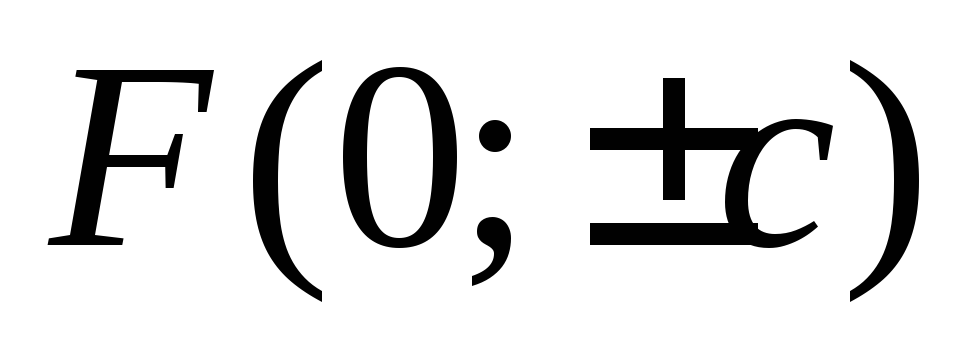 .
.
Оптическое свойство гиперболы состоит в том, что если источник света поместить в один фокус гиперболы, то из бесконечно удаленной точки он будет виден так, как будто он находится во втором фокусе.
Эксцентриситет
гиперболы – степень ее вытянутости.
Для гиперболы
(в общем случае >1)
, задаваемой
уравнением 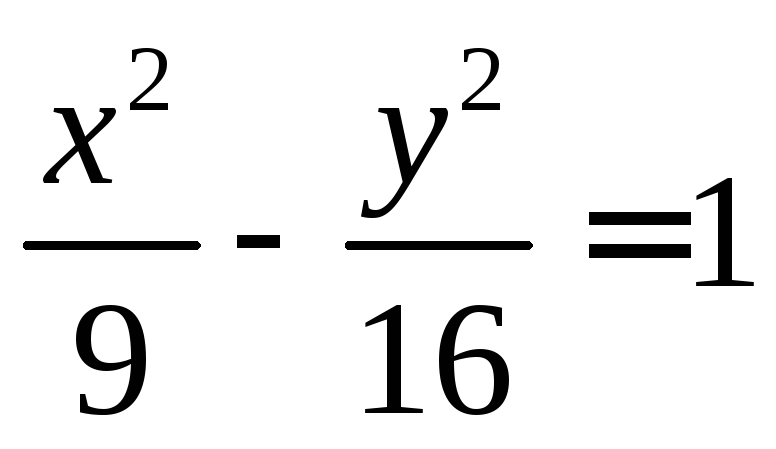 эксцентриситет
эксцентриситет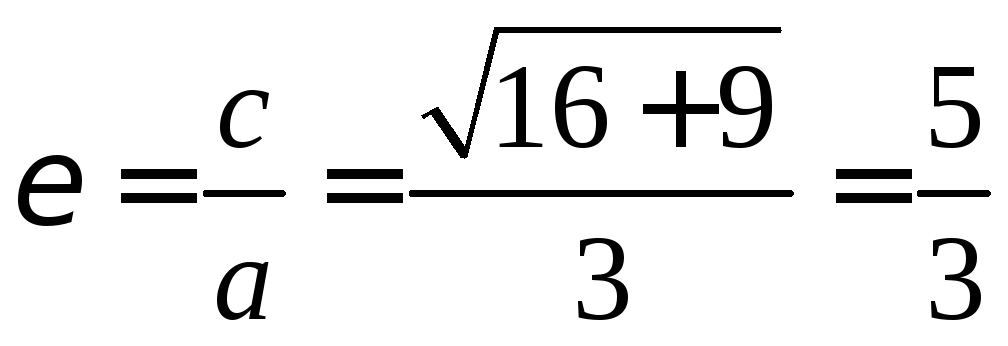 ,
а фокусы находятся в точках
,
а фокусы находятся в точках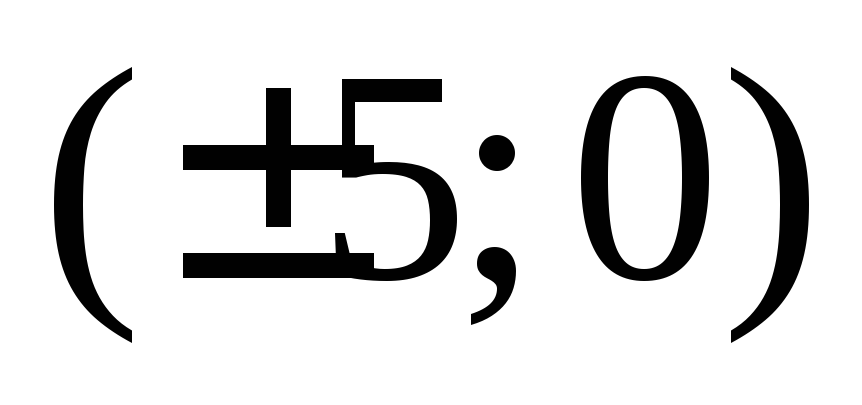 .
.
Парабола
Параболой
называется
кривая второго порядка, задаваемая
каноническим уравнением вида 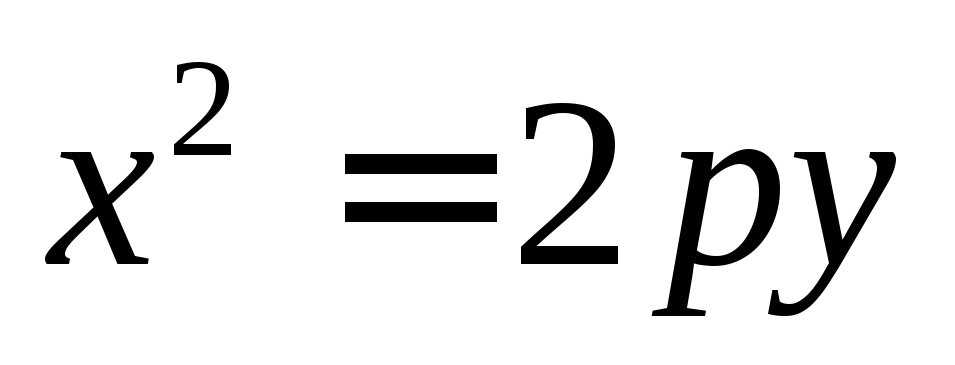 или
или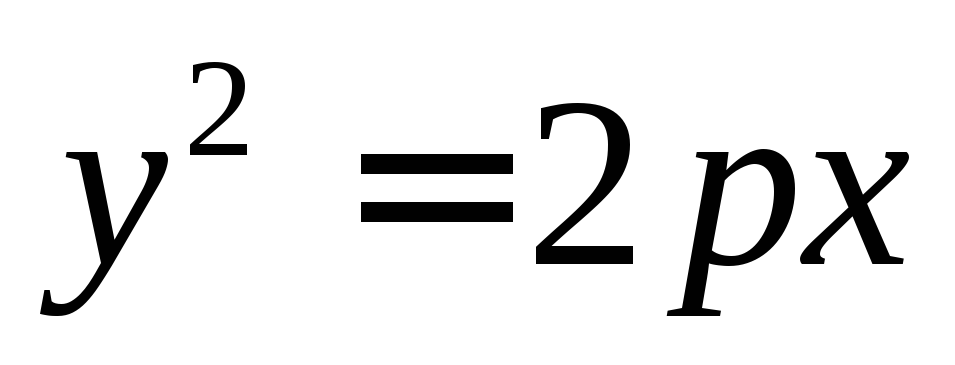 ,
гдеp – параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
,
гдеp – параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
Вверх, в случае если уравнение имеет вид
 приp>0.
приp>0.Вниз, в случае если уравнение имеет вид
 приp<0.
приp<0.Вправо, в случае если уравнение имеет вид
 приp>0.
приp>0.Влево, в случае если уравнение имеет вид
 приp<0.
приp<0.
Параболу можно
определить как геометрическое место
точек, равноудаленных от точки 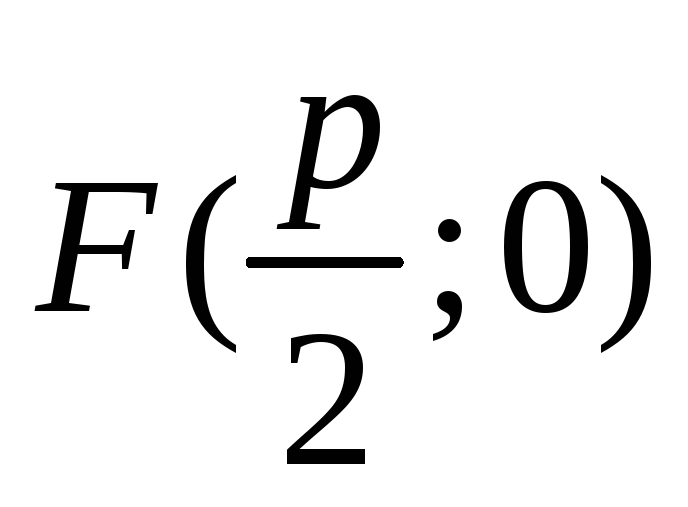 — фокуса — и прямой
— фокуса — и прямой 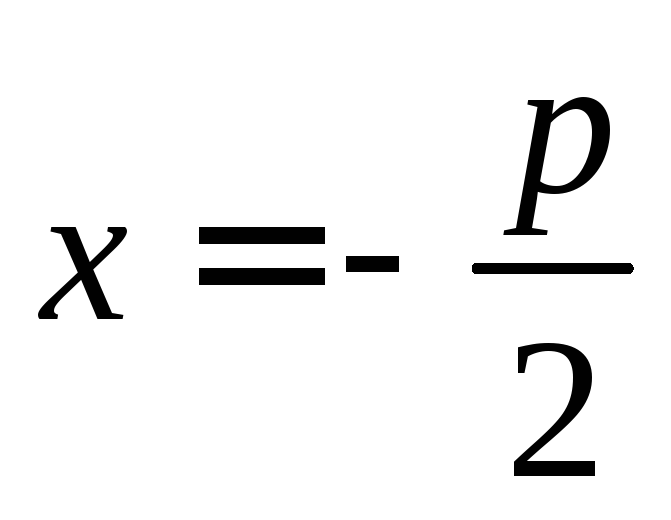 — директрисы.
— директрисы.
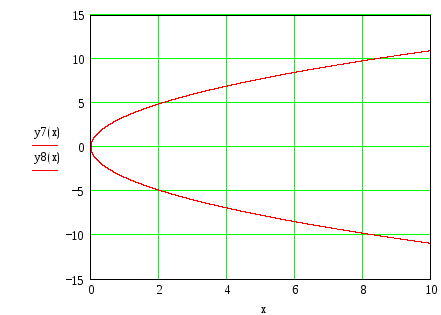
Оптическое свойство параболы состоит в том, что если в фокус параболы поместить точечный источник света, то из нее будет выходить параллельный пучок лучей.
Приведение уравнений кривых второго порядка к каноническому виду.
Общее
уравнение кривой 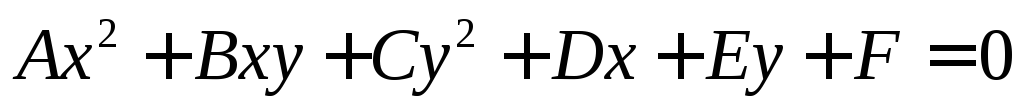 ,
причем примем ( для упрощения расчетов)B=0.
Существуют два метода преобразования
уравнения общего вида к каноническому:
,
причем примем ( для упрощения расчетов)B=0.
Существуют два метода преобразования
уравнения общего вида к каноническому:
Выделение полного квадрата
Замена переменной
Для данного уравнения замену удобно ввести замену в виде:
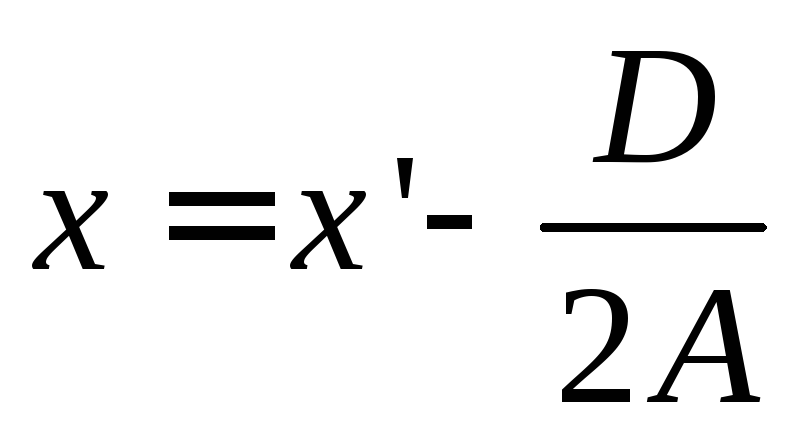
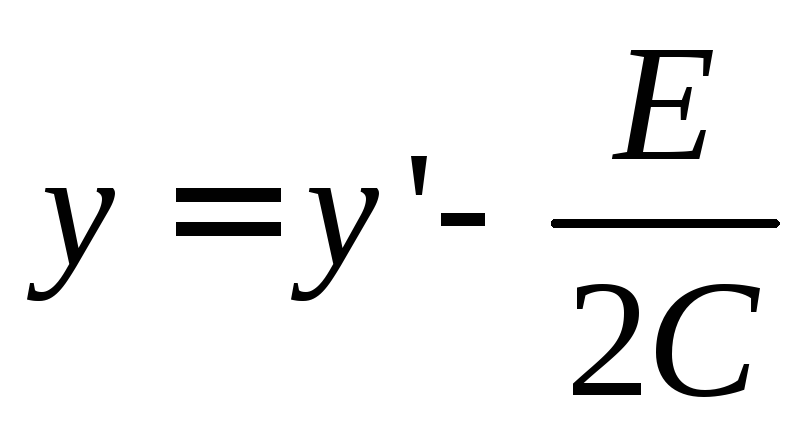 ,
где x’ и y’ – новые переменные.
,
где x’ и y’ – новые переменные.
Если
A
и C
не равны 0, то 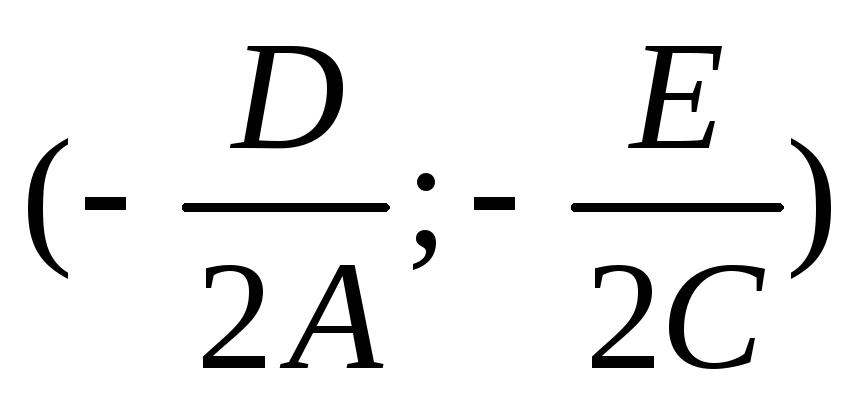 — новый центр кривой второго порядка, аx’ и y’ — новые оси.
— новый центр кривой второго порядка, аx’ и y’ — новые оси.
Пример:
1.
Кривая второго порядка задана уравнением 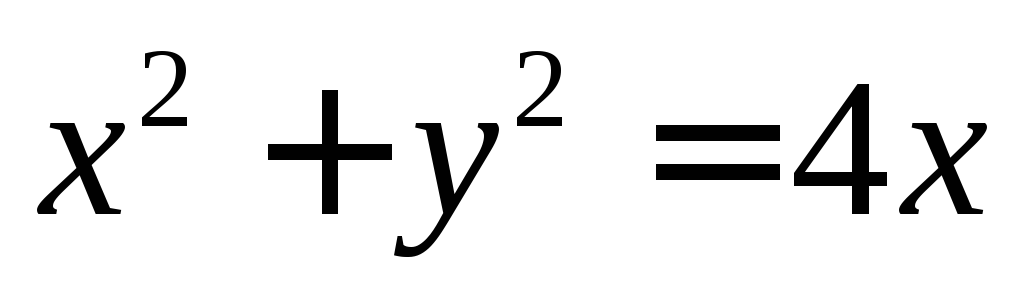 .
Выяснить, чему оно соответствует.
.
Выяснить, чему оно соответствует.
Данному
уравнению соответствует окружность со
смещенным центром, имеющая каноническое
уравнение 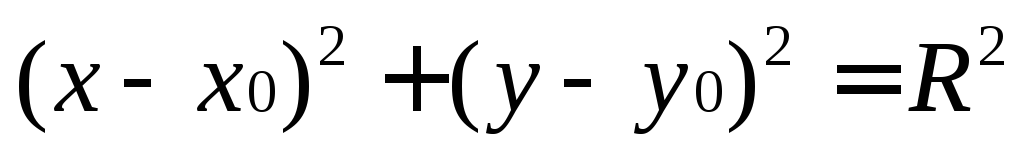 ,
где (x0;y0)
– координаты центра окружности, а R
– ее радиус. Воспользуемся
методом выделения полного квадрата для
нахождения канонического вида уравнения.
,
где (x0;y0)
– координаты центра окружности, а R
– ее радиус. Воспользуемся
методом выделения полного квадрата для
нахождения канонического вида уравнения.
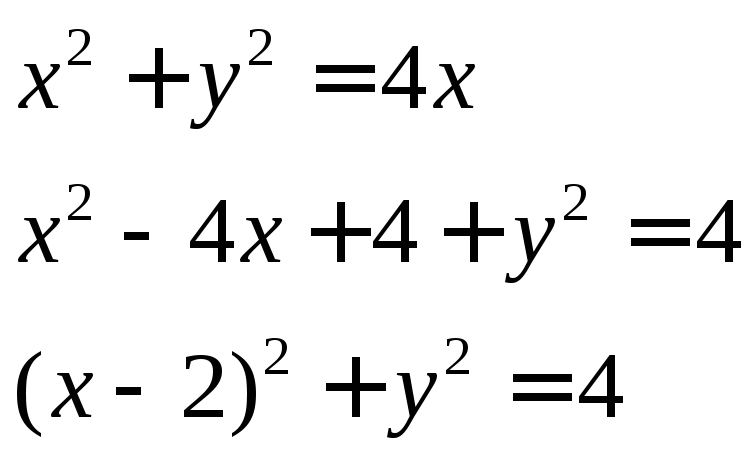
Итак, данное уравнение соответствует окружности радиуса 2 ед. с центром в точке (2;0).
Привести уравнение к каноническому виду и построить кривую:
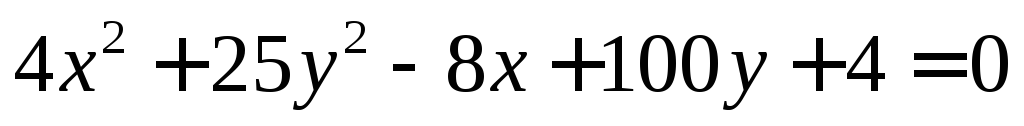
Воспользуемся методом замены переменных. Имеем:
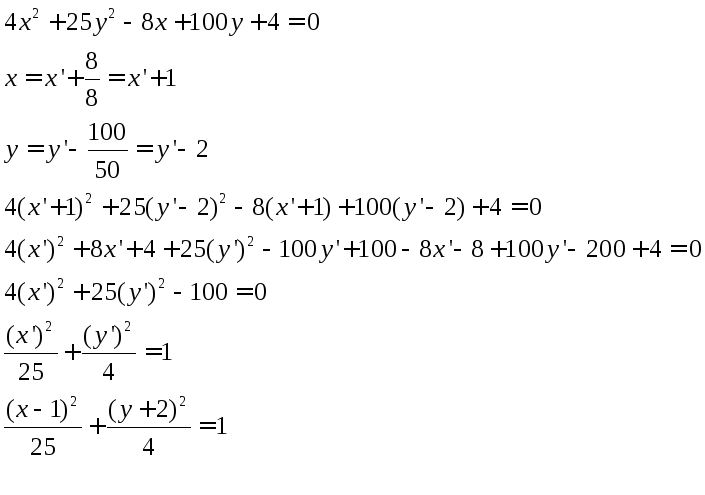
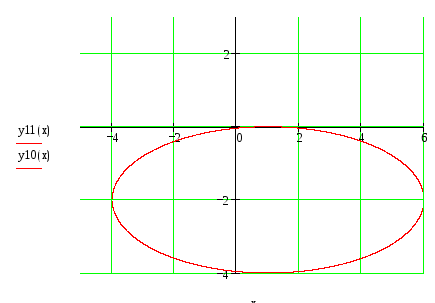
Получилось каноническое уравнение эллипса с центром в точке (1;-2). Строим его по вышеописанному алгоритму.
Привести к каноническому виду уравнение
 .
Построить кривую, заданную вышеописанным
уравнением.
.
Построить кривую, заданную вышеописанным
уравнением.
Используем метод выделения полного квадрата и замены переменной.
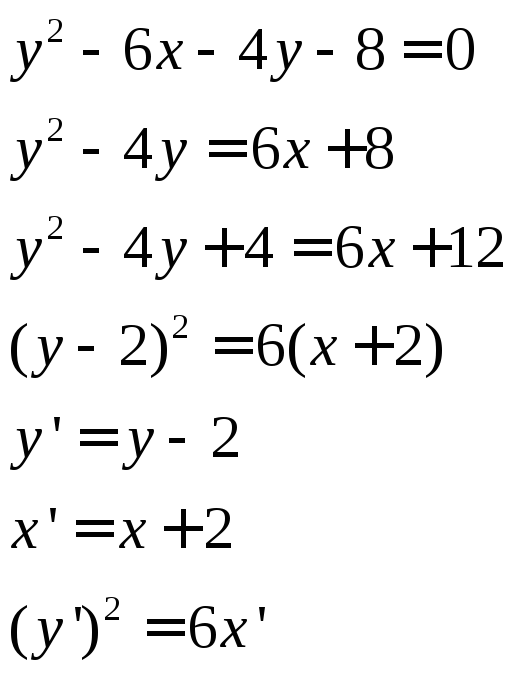
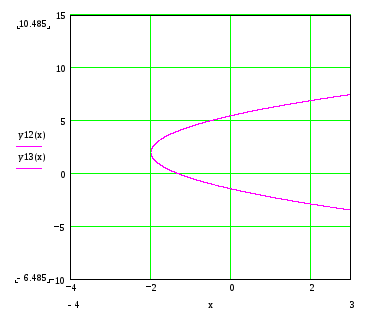
Получилось уравнение параболы с центром в точке (-2;2)
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости
Наша цель построить уравнение прямой, проходящей через данную точку M0 и перпендикулярной к данной плоскости Ax+By+Cz+D=0.
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональный плоскости (1) имеет следующий вид:
Пример 1. Построить прямую, проходящую через точку M0(5, -4, 4) и перпендикулярной плоскости
Решение.
Общее уравнение плоскости имеет вид (1), где :
Подставляя координаты точки M0(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:
Ответ:
Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияДля функционирования Mathway необходим javascript и современный браузер.
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияДля функционирования Mathway необходим javascript и современный браузер.
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияДля функционирования Mathway необходим javascript и современный браузер.
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
Поиск параллельных и перпендикулярных линий
Как использовать алгебру, чтобы найти параллельные и перпендикулярные линии.
параллельных линий
Как мы узнаем, что две линии параллельны ?
Их склоны одинаковы!
Пример:
Найти уравнение линии, которая:
- параллельно у = 2х + 1
- и проходит через точку (5,4)
Наклон y = 2x + 1 : 2
Параллельная линия должна иметь одинаковый наклон 2.
Мы можем решить это, используя уравнение «точка-наклон» линии:
г — у 1 = 2 (х — х 1 )
И затем положить в точку (5,4):
у — 4 = 2 (х — 5)
И этот ответ в порядке, но давайте также поместим его в виде y = mx + b:
г. — 4 = 2x — 10
г. = 2x — 6
Вертикальные Линии
Но это не работает для вертикальных линий… Я объясняю, почему в конце.
Не та же линия
Будь осторожен! Они могут быть той же линией (но с другим уравнением), и поэтому не параллельны .
Как мы узнаем, действительно ли они одной линии? Проверьте их точки пересечения Y (где они пересекают ось Y), а также их наклон:
Пример: y = 3x + 2 параллельно y — 2 = 3x?
Для y = 3x + 2 : уклон равен 3, а y-перехват равен 2
Для y — 2 = 3x : наклон равен 3, а y-перехват равен 2
На самом деле это одна и та же линия, и поэтому они не параллельны
перпендикулярных линий
Две линии перпендикулярны, когда они встречаются под прямым углом (90 °).
Чтобы найти перпендикулярный уклон:
Когда одна линия имеет наклон m, перпендикулярная линия имеет наклон -1 м
Другими словами отрицательный ответ
Пример:
Найти уравнение линии, которая
- перпендикулярно y = −4x + 10
- и проходит через точку (7,2)
Наклон y = −4x + 10 : −4
отрицательных обратных этого наклона:
m = -1 −4 = 1 4
Таким образом, перпендикулярная линия будет иметь наклон 1/4:
г — г 1 = (1/4) (х — х 1 )
А теперь поставьте в точке (7,2):
у — 2 = (1/4) (х — 7)
И этот ответ в порядке, но давайте также поместим его в форме «y = mx + b»:
г. — 2 = х / 4 — 7/4
г. = х / 4 + 1/4
Быстрая проверка перпендикуляра
Когда мы умножаем наклон m на его перпендикулярный наклон -1 m , мы получаем просто -1.
Итак, чтобы быстро проверить, перпендикулярны ли две линии:
Когда мы умножаем их наклоны, мы получаем -1
Понравилось:
Перпендикулярны ли эти две линии?
| Линия | Склон |
| у = 2х + 1 | 2 |
| у = −0,5х + 4 | −0,5 |
Когда мы умножаем два уклона, мы получаем:
2 × (−0.5) = −1
Да, мы получили -1, поэтому они перпендикулярны.
Вертикальные линии
Предыдущие методы работают хорошо, за исключением вертикальной линии :
В этом случае градиент неопределен (поскольку мы не можем разделить на 0):
m = y A — y B x A — x B = 4 — 1 2 — 2 = 3 0 = не определено
Так что просто полагайтесь на то, что:
- вертикальная линия параллельна другой вертикальной линии.
- вертикальная линия перпендикулярна горизонтальной линии (и наоборот).
Резюме
- параллельных линий: с тем же уклоном
- перпендикулярных линий: отрицательный обратный наклон (-1 / м)
Purplemath
Существует еще одно соображение для линейных уравнений: поиск параллельных и перпендикулярных линий. Вот общий формат упражнений на эту тему:
Учитывая линию 2 x — 3 y = 9 и точку (4, –1), найдите линии в форме пересечения наклона через заданную точку так, чтобы две линии были соответственно:
(а) параллельно данной линии, и
(б) перпендикулярно к нему.
Они дали мне контрольную линию, а именно 2 x — 3 y = 9; это линия, на склон которой я буду ссылаться позже в своей работе.
MathHelp.com

Эта линия имеет некоторое значение наклона (хотя, конечно, не имеет значения «2», потому что это уравнение линии не решается для « y =»).
я сначала нужно найти наклон опорной линии. Я мог бы использовать метод двойного подключения значений x к базовой линии, нахождения соответствующих значений y , а затем подключения двух точек, которые я нашел в формуле наклона, но я бы просто решил для « y =». (Это только мое личное предпочтение. Если ваши предпочтения отличаются, используйте любой метод, который вам больше нравится). Итак:
Первое, что я сделаю, это решу «2 x — 3 y = 9» для « y =», чтобы я мог найти свой опорный наклон:
2 x — 3 y = 9
–3 y = –2 x + 9
y = ( 2 / 3 ) x — 3
Таким образом, опорный склон от опорной линии м = 2 / 3 .
Теперь мне нужно найти два новых склона и использовать их с той точкой, которую они мне дали; а именно с точкой (4, –1). Они хотят, чтобы я нашел линию через (4, –1), параллельную 2 x — 3 y = 9; то есть через заданную точку они хотят, чтобы я нашел линию, которая имеет тот же наклон, что и контрольная линия. И тогда они хотят, чтобы я нашел линию через (4, –1), которая перпендикулярна 2 x — 3 y = 9; то есть, через данную точку, они хотят, чтобы найти строку, которая имеет наклон, который является отрицательным взаимным наклоном опорной линии.
Поскольку параллельная линия имеет одинаковый наклон, то параллельная линия через (4, –1) будет иметь наклон м = 2 / 3 . Эй, теперь у меня есть точка и уклон! Поэтому я буду использовать форму точки наклона, чтобы найти линию:
y — (–1) = ( 2 / 3 ) ( x — 4)
y + 1 = ( 2 / 3 ) x — 8 / 3
y = ( 2 / 3 ) x — 8 / 3 — 3 / 3
y = ( 2 / 3 ) x — 11 / 3
Это параллельная линия, о которой они просили, и она указана в форме перехвата наклона.
Для перпендикулярной линии я должен найти перпендикулярный наклон. Опорный наклон составляет м = 2 / 3 . Для перпендикулярного уклона я переверну опорный уклон и поменяю знак. Тогда перпендикулярный уклон составляет м. = — 3 / 2 .
Опять же, у меня есть точка и наклон, поэтому я могу использовать форму наклона точки, чтобы найти свое уравнение. Обратите внимание, что единственное изменение в последующих вычислениях, которые я только что сделал (для параллельной линии), заключается в том, что наклон отличается, теперь он является наклоном перпендикулярной линии.
y — (–1) = (- 3 / 2 ) ( x — 4)
y + 1 = (- 3 / 2 ) x + 6
y = (- — 3 / 2 ) x + 5
Тогда полное решение этого упражнения:
параллельно: y = ( 2 / 3 ) x — 11 / 3
перпендикулярно: y = (- — 3 / 2 ) x + 5
Предупреждение: Если в вопросе вас спрашивают, являются ли две данные линии «параллельными, перпендикулярными или ни одной из них», вы должны ответить на этот вопрос, найдя их наклоны, а не , не нарисовав картинку! Картинки могут только дать вам приблизительное представление о том, что происходит.
Например, вы просто не сможете сказать, просто «посмотрев» на картинку, что нарисованные линии с уклонами, скажем, м 1 = 1,00 и м 2 = 0,99 НЕ являются параллель — и они точно так же, как и , будут смотреть параллельно на картинке. Но так как 1,00 не равен 0,99, линии не могут быть параллельными.
Другими словами, чтобы ответить на это упражнение, всегда находите числовые наклоны; не пытайтесь сойти с рук, просто нарисовав красивые картинки.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении параллельной линии через заданную точку. Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с Mathway. (Следующий виджет предназначен для поиска перпендикулярных линий.) Или перейдите к двум сложным примерам, которые следуют.
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы попадете на сайт Mathway для платного обновления.)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении перпендикулярной линии через заданную точку. Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с Mathway.
(При нажатии «Нажмите, чтобы просмотреть шаги» на экране ответов виджета вы попадете на сайт Mathway для платного обновления.)
Практически все упражнения для нахождения уравнений параллельных и перпендикулярных линий будут аналогичны или точно так же, как приведенные выше.Вот два примера более сложных типов упражнений:
Для какого значения a это линия y = ax , перпендикулярная линии ( 2 / 3 ) y — 6 x = 3?
Поскольку наклон — это значение, которое умножается на « x », когда уравнение решается для « y =», то значение « a » будет значением наклона для перпендикулярной линии.Другими словами, они спрашивают меня о перпендикулярном склоне, но они немного замаскировали свое предназначение. Я должен заметить связь.
Первое, что нужно сделать, это найти наклон опорной линии. Я решу для « y =»:
(2/3) y — 6 x = 3
2 y — 18 x = 9
y — 9 x = 9/2
y = 9 x + 9/2
Тогда эталонный уклон составляет м. = 9.Перпендикулярный наклон (являющийся значением « a », о котором они меня спрашивали) будет отрицательным обратным значением эталонного наклона.
Я начинаю с преобразования «9» в дробную форму, помещая его над «1». Затем я переворачиваю и меняю знак. Результат:
Каково расстояние между линиями, определяемое уравнениями 3 x + 2 y = 15 и 4 y + 6 x = 3?
Единственный способ, которым эти две линии могут иметь расстояние между ними, если они параллельны.(В противном случае они должны встретиться в некоторой точке, в которой расстояние между линиями, очевидно, будет равно нулю.) Являются ли эти линии параллельными? Я буду решать каждый за « y =», чтобы быть уверенным:
3 x + 2 y = 15
2 y = –3 x + 15
y 1 = (–3/2) x + 15/2
..и:
4 y + 6 x = 3
4 y = –6 x + 3
y = (–6/4) x + 3/4
y 2 = (–3/2) x + 3/4
Линии имеют одинаковый наклон, поэтому они действительно параллельны. И у них разные и -приятия, поэтому они не совпадают.Следовательно, между этими двумя линиями действительно есть некоторое расстояние. Но как мне найти это расстояние? Это будет перпендикулярное расстояние между двумя линиями, но как мне это найти?
Я знаю, что могу найти расстояние между двумя точками; Я включаю две точки в формулу расстояния. Но у меня нет двух пунктов. Ах; но я могу выбрать любую точку на одной из линий, а затем найти перпендикулярную линию через эту точку.Поскольку исходные линии параллельны, эта перпендикулярная линия также перпендикулярна второй из исходных линий. Тогда я могу найти, где пересекаются перпендикулярная линия и вторая линия . Эта точка пересечения будет второй точкой, которая мне понадобится для формулы расстояния.
Я знаю, что опорный наклон составляет м. = –3/2. Тогда мой перпендикулярный уклон будет м. = 2/3. Теперь мне нужна точка, через которую можно поставить мою перпендикулярную линию.Я выберу x = 1 и вставлю это в уравнение первой строки, чтобы найти соответствующее значение y :
y = (–3/2) (1) + 15/2
= –3/2 + 15/2
= 12/2 = 6
Итак, моя точка зрения (в первой строке, которую они мне дали) — (1, 6). С этой точкой и моим перпендикулярным уклоном я могу найти уравнение перпендикулярной линии, которое даст мне расстояние между двумя исходными линиями:
y — 6 = (2/3) ( x — 1)
y — 6 = (2/3) x — 2/3
y = (2/3) x — 2/3 + 18/3
y = (2/3) x + 16/3
Хорошо; Теперь у меня есть уравнение перпендикуляра.Расстояние будет длиной отрезка вдоль этой линии, которая пересекает каждую из исходных линий.
Где эта линия пересекает вторую из указанных линий? Она будет пересекать, где уравнения двух линий равны, поэтому я установлю равные не и сторон экватона второй исходной линии и уравнения перпендикулярной линии и решу:
(–3/2) x + 3/4 = (2/3) x + 16/3
–9 x + 9/2 = 4 x + 32
9/2 — 32 = 13 x
(–55/2) / 13 = x
x = –55/26
Вышеуказанное более чем завершает часть упражнения с линейным уравнением.Я оставлю остальные упражнения для вас, если вам интересно.
(Чтобы закончить, вам нужно вставить это последнее значение x в уравнение перпендикулярной линии, чтобы найти соответствующее значение y . Это даст вам вашу вторую точку. [Оказывается, (–55/26, 51/13) , если вы делаете математику.] Затем вам нужно будет включить эту точку вместе с первой (1, 6) в формулу расстояния, чтобы найти расстояние между линиями.[Расстояние оказывается (27/26) * SQRT [13] или около 3.7442, если вы пашете вычисления.])
Обратите внимание, что расстояние между линиями равно , а не , как расстояние по вертикали или горизонтали между линиями, поэтому вы можете , а не , использовать перехватчики x или y в качестве прокси для расстояния.
Что еще важнее, обратите внимание, что в этом упражнении нигде не сказано ничего о параллельных или перпендикулярных линиях и не дано указаний найти какое-либо уравнение линии.Студент должен был решить, какие инструменты могут быть полезны. Не бойтесь таких упражнений. Да, они могут быть длинными и грязными. Но даже всего лишь , которые пробуют , вместо того, чтобы сразу бросить руки в поражении, укрепят ваши навыки, а также принесут вам несколько «коричневых очков» с вашим инструктором.
URL: https://www.purplemath.com/modules/strtlneq3.HTM
,склон: параллельные и перпендикулярные линии
Purplemath
Параллельные линии и их наклоны просты. Поскольку наклон — это мера угла линии от горизонтали, а параллельные линии должны иметь одинаковый угол, то параллельные линии имеют одинаковый наклон — и линии с одинаковым наклоном параллельны.
Перпендикулярные линии немного сложнее.
Если вы визуализируете линию с положительным наклоном (то есть это возрастающая линия), то перпендикулярная линия должна иметь отрицательный наклон (потому что это должна быть убывающая линия). Так что перпендикулярные линии имеют склоны, которые имеют противоположные знаки.
MathHelp.com

Другая «противоположная» вещь с перпендикулярными уклонами состоит в том, что их значения являются взаимными; то есть вы берете одно значение наклона и переворачиваете его вверх дном.(Это , а не — очевидная вещь о наклонах перпендикулярных линий.) Соедините это с изменением знака, и вы получите, что наклон перпендикулярной линии является «отрицательным обратным» наклону исходной линии — и две линии с наклонами, которые являются отрицательными взаимными ответами друг друга, перпендикулярны друг другу.
Чтобы привести числовой пример «отрицательных обратных величин», если наклон одной линии составляет м = 4 / 5 , то наклон перпендикулярной линии будет равен м = –5 / 4 .Или, если уклон одной линии равен м, = –2, то уклон перпендикулярной линии будет равен м = 1 / 2 . (Помните, что любое целое число можно превратить в дробь, поставив его над 1.)
В своей домашней работе вам, вероятно, дадут несколько пар точек, и вас попросят указать, являются ли линии, проходящие через пары точек, «параллельными, перпендикулярными или ни одной из них».Чтобы ответить на вопрос, вам придется рассчитать уклоны и сравнить их. Вот как это работает:
Одна линия проходит через точки (–1, –2) и (1, 2); другая линия проходит через точки (–2, 0) и (0, 4). Эти линии параллельны, перпендикулярны или нет?
Чтобы ответить на этот вопрос, я найду два склона.Так что я могу держать вещи прямо и сказать разницу между двумя склонами, я буду использовать подписки.
Поскольку эти две линии имеют одинаковые наклоны, то:
эти линии параллельны.
Одна линия проходит через точки (0, –4) и (–1, –7); другая линия проходит через точки (3, 0) и (–3, 2).Эти линии параллельны, перпендикулярны или нет?
Я найду значения уклонов.
Если бы я преобразовал «3» в дробную форму, поместив ее над «1», затем перевернул и изменил ее знак, я бы получил « –1 / 3 » ,Эта отрицательная обратная величина первого наклона соответствует значению второго наклона. Другими словами, эти наклоны являются отрицательными взаимными, поэтому:
линии перпендикулярны.
Одна линия проходит через точки (–4, 2) и (0, 3); другая линия проходит через точки (–3, –2) и (3, 2).Эти линии параллельны, перпендикулярны или нет?
Я найду склоны.
Эти значения наклона не совпадают, поэтому линии не параллельны. Значения наклона также не являются отрицательными обратными величинами, поэтому линии не перпендикулярны.Тогда ответ:
Найти наклон линии, перпендикулярной линии y = –4 x + 9.
Они дали мне исходное уравнение линии, и оно в форме « y =», поэтому легко найти наклон. Я могу просто прочитать значение из уравнения: м = –4.
Этот уклон можно превратить в дробь, поставив его более 1, поэтому этот уклон можно переформулировать как:
Чтобы получить отрицательный ответ, мне нужно перевернуть эту дробь и изменить знак. Тогда наклон любой линии, перпендикулярной данной линии:
Предупреждение. Когда задают вопрос такого типа («эти линии параллельны или перпендикулярны?»), , а не , начинают рисовать картинки.Если линии близки к параллельности или близки к перпендикулярному (или если вы рисуете линии беспорядочно), вы очень легко можете получить неправильный ответ на своей картинке.
Кроме того, они не спрашивают, выглядят ли линии параллельными или перпендикулярными ; они спрашивают, действительно ли линии параллельны или перпендикулярны. Единственный способ убедиться в своем ответе — это сделать алгебру.
URL: https: // www.purplemath.com/modules/slope3.htm
,Если уклон одной линии равен м, то уклон другой

Попробуй это Перетащите точки C или D. Отметьте уклоны, когда линии расположены под прямым углом друг к другу.
Когда две линии перпендикулярны друг другу (под прямым углом или 90 °), их наклоны имеют определенное отношение друг к другу.Если наклон одной линии равен м, то , то наклон другой линии является отрицательной обратной величиной m или

Так, например, на рисунке выше, линия AB имеет наклон 0,5, что означает, что она увеличивается на половину для каждого поперечного сечения. Линия CD, если она перпендикулярна AB, имеет наклон -1 / 0,5 или -2. Отрегулируйте точки C или D, чтобы сделать CD перпендикулярным AB и проверьте этот результат.

Рис. 1. Линии еще перпендикулярны
Помните, что уравнение работает в обоих направлениях, поэтому не имеет значения, с какой строки вы начинаете.На рисунке выше наклон CD-2. Таким образом, наклон AB, когда перпендикулярно

Также обратите внимание, что линии, которые не должны пересекаться, должны быть перпендикулярными. На фиг.1 две линии перпендикулярны друг другу, даже если они не соприкасаются. Отклонение отношения все еще сохраняется.
Пример 1. Перпендикулярны ли две линии?

Рис. 1. Эти линии перпендикулярны?
На фиг.1 линия AB и отрезок CD, по-видимому, расположены под прямым углом друг к другу.Определите, правда ли это.
Чтобы сделать это, мы находим наклон каждой линии и затем проверяем, является ли один наклон отрицательным обратным по отношению к другому.


Если линии перпендикулярны, каждая будет отрицательной обратной величиной другой. Не имеет значения, с какой строки мы начнем, поэтому мы выберем AB:

Таким образом, наклон CD равен -2,22, а отрицательный обратный угол наклона AB составляет -2,79. Это не одно и то же, поэтому линии , а не перпендикулярно, даже если они выглядят так.Если вы внимательно посмотрите на диаграмму, то увидите, что точка C находится слишком далеко влево, чтобы линии были перпендикулярны.
Пример 2. Определите линию через точку, перпендикулярную линии
На рис. 1 найдите линию, проходящую через точку E, перпендикулярную CD.
Точка E находится на оси y, а также является точкой y пересечения желаемой линии. Как только мы узнаем наклон линии, мы можем выразить ее, используя ее уравнение в форме пересечения наклона y = mx + b, где m — наклон, а b — пересечение по y.
Сначала найдите наклон линии CD:
 Линия, которую мы ищем, будет иметь наклон, который является отрицательной обратной величиной этого:
Линия, которую мы ищем, будет иметь наклон, который является отрицательной обратной величиной этого: 
Перехват равен 10, точка, где линия пересечет ось Y. Подставляя эти значения в уравнение, нужная нам линия описывается уравнением
у = 0,45х + 10
Это один из способов определения линии, поэтому мы решили проблему. Если бы мы хотели построить линию, мы нашли бы другую точку на линии, используя уравнение, а затем проведем линию через эту точку и точку пересечения.Подробнее об этом см. Уравнение линии (наклон — форма пересечения)
Что попробовать
- На диаграмме вверху страницы нажмите «сброс».
- Обратите внимание, что поскольку наклон одной линии отрицателен по отношению к другой, линии перпендикулярны.
- Отрегулируйте одну из точек C, D. Линии больше не перпендикулярны.
- Нажмите на «Скрыть детали». Определите наклон обеих линий и докажите, что они не перпендикулярны. Нажмите «показать координаты» если вы хотите знать их точно.Нажмите «показать детали» для подтверждения.
Ограничения
В целях ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к тому, что расчеты будут немного отклонены.
Для более см. Учебные заметки
Другие темы координатной геометрии
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

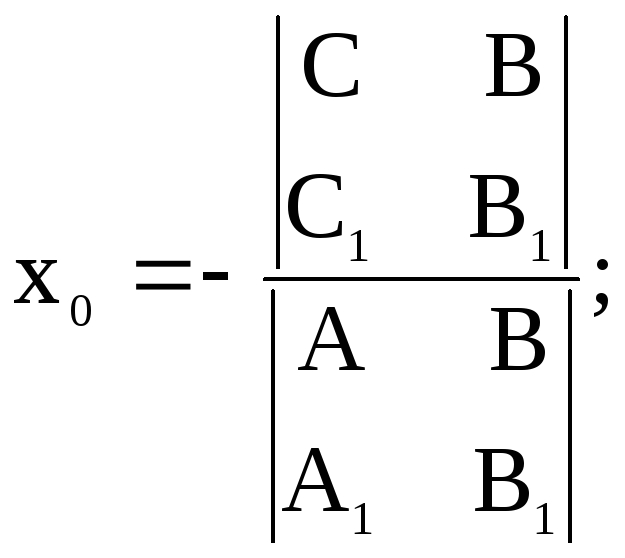
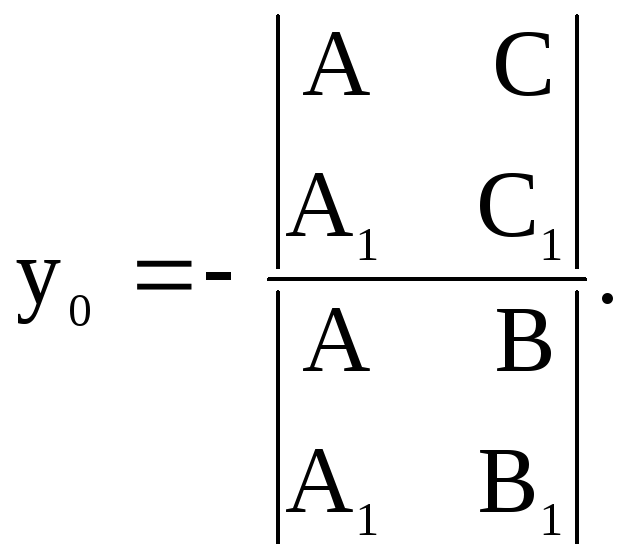
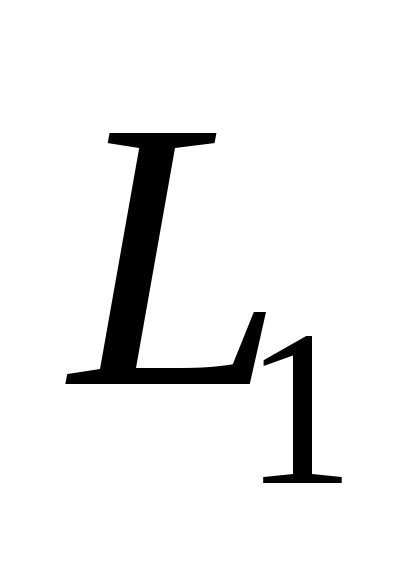
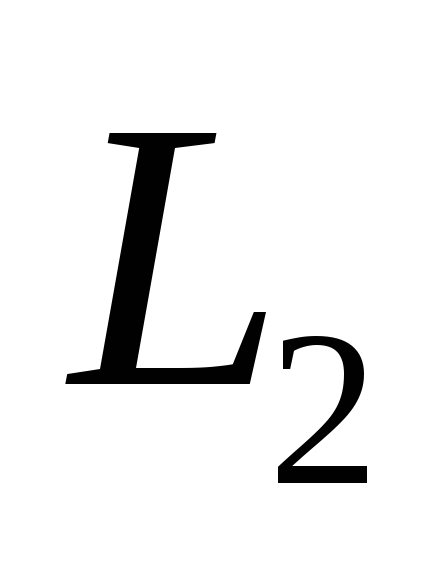

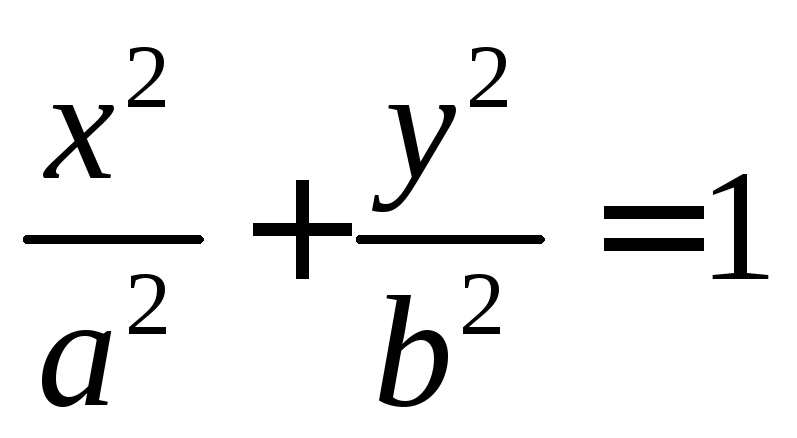
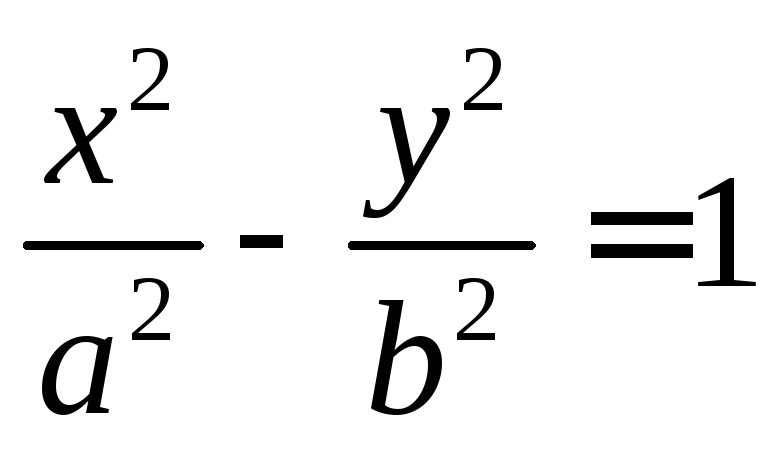
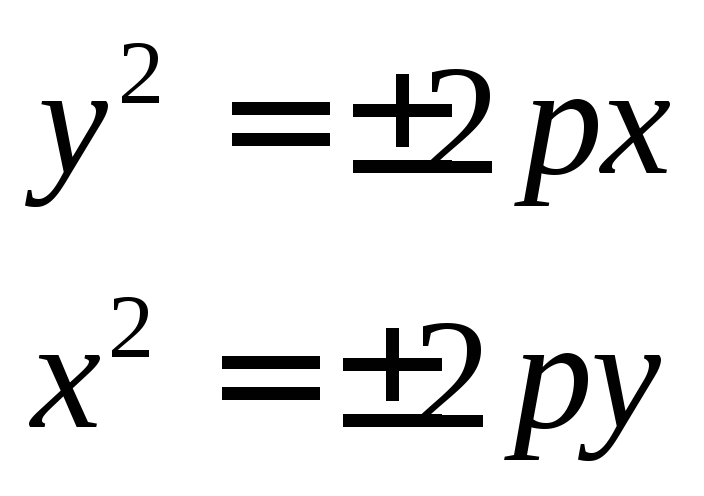
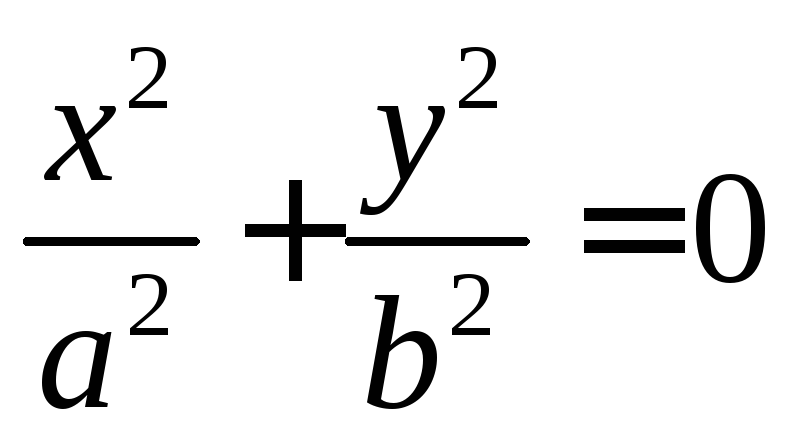
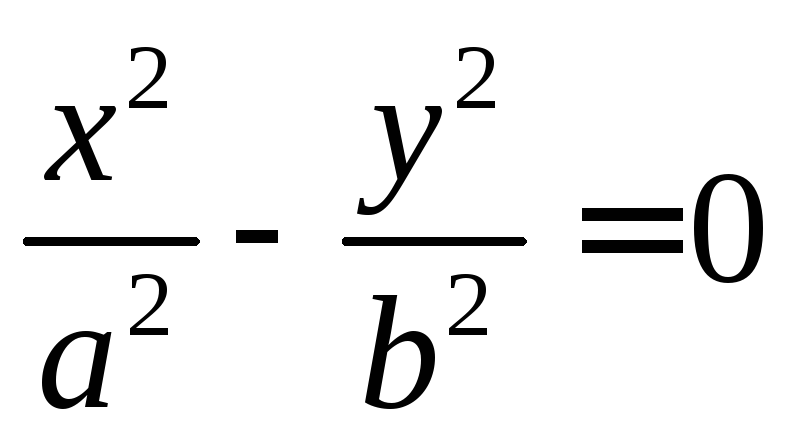
 или
или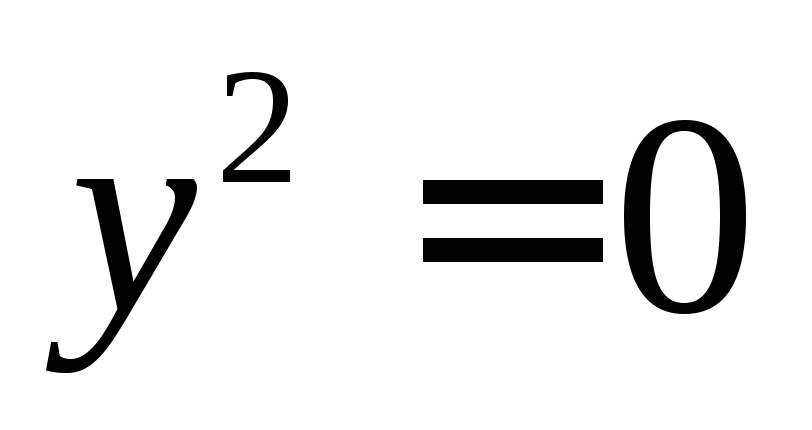
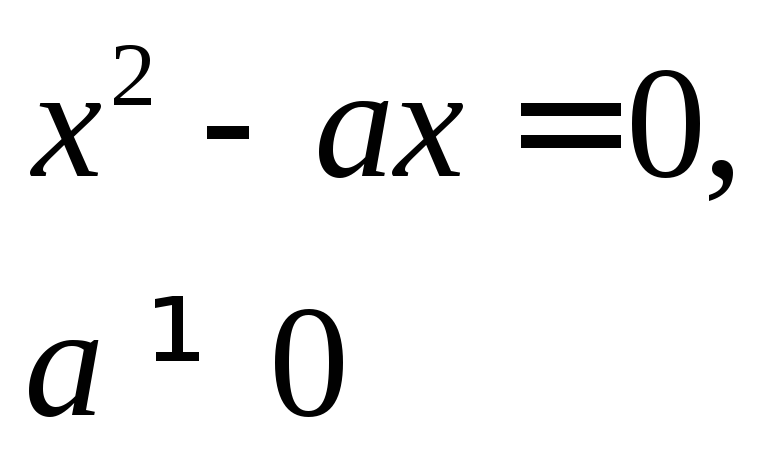
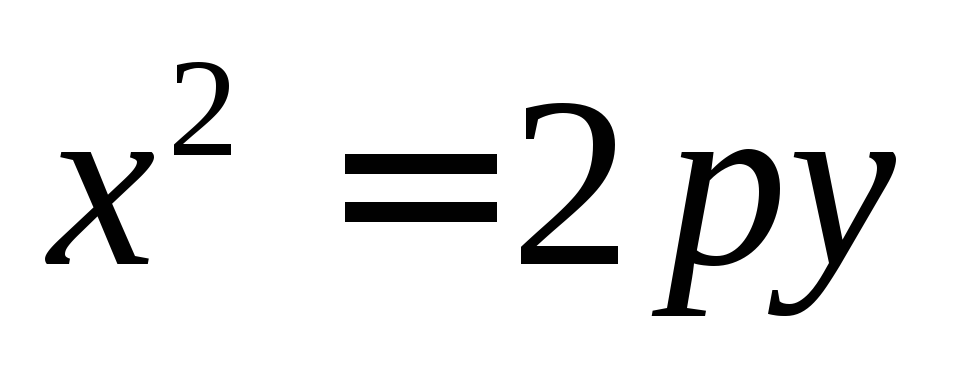 приp>0.
приp>0.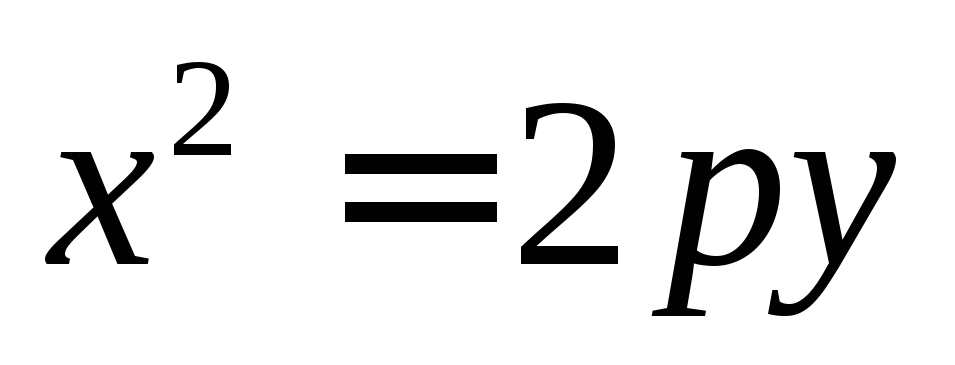 приp<0.
приp<0.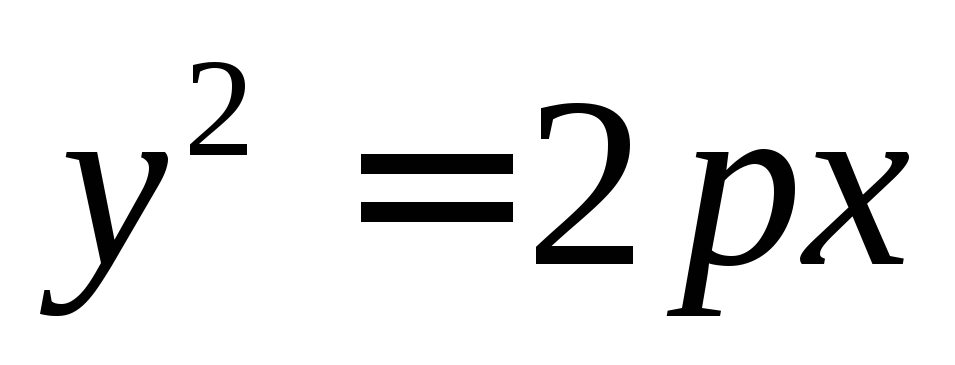 приp>0.
приp>0.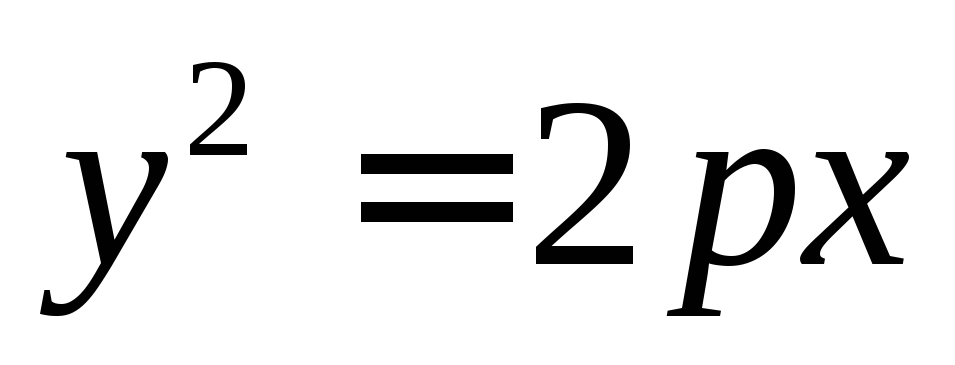 приp<0.
приp<0.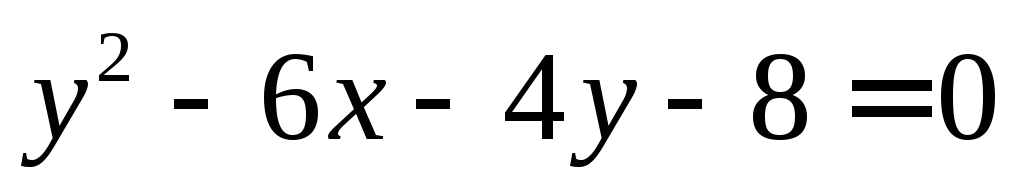 .
Построить кривую, заданную вышеописанным
уравнением.
.
Построить кривую, заданную вышеописанным
уравнением.