Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Решение уравнений sinx=a. Понятие арксинуса числа
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6.
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение уравнений sinx=a. Понятие арксинуса числа.
2. Вопросы по домашнему заданию
Решить уравнения:3
1) cos 3t =
;
2
2
x
2) cos
= 2 ;
8
7
3)cos t =
9
4. Решить уравнения:
• №286 (б,г)2
cos x
4
2
5. Самостоятельная работа
6. АРКСИНУС ЧИСЛА
Определение. Арксинусом числатакое число ;
2 2 ,
а 1;1
синус которого равен
sin arcsin a a,
называется
arcsin a
2
1 a 1
2
,
а
7. АРКСИНУС ЧИСЛА
• Например2
arcsin
;
2
4
arcsin 0 0;
3
arcsin
;
3
2
т.к.
т.к.
т.к.
2
; sin
.
2 4 2
4
2
2
0
2
; sin 0 0.
3
; sin
.
2 3 2
3 2
8. АРКСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ
y 1а
arcsin a
0
1
x
-а
arcsin a arcsin a
arcsin a
9. АРКСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ
• Например2
2
1
1
2 arcsin 3 arcsin
2 arcsin
2
2
2
2
3
13
3 2
4
6
4
3
12
1
3
2.
2 arcsin 1 5 arcsin 0
arcsin
2
2
1. 3 arcsin
1
3
arcsin
2 5 0
2
2
2
1
7
2 3
6
6
АРКСИНУС ЧИСЛА
ОСНОВНЫЕ ФОРМУЛЫ
sin arcsin a a, arcsin a ; , a 1;1
2 2
arcsin a arcsin a
arcsin sin , ;
2 2
11. АРКСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ
• Например7. tg 5 arcsin 2 tg tg tg 1
4
4
4
2
1
1
cos arcsin
1
1
3
9
8. ctg arcsin
1
1
3
sin arcsin
3
3
5
8
3 2 2
9
12. Уравнение sinx=a
sin x a, a 1y1
arcsin a
arcsin a
a
0
1
x
x arcsin a 2 k
x arcsin a 2 k , k Z
x 1 arcsin a n, n Z
n
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
sin x 1
x
2
2 k , k Z
13.
Уравнение sinx=ax 1 arcsin a n, n Zn
Пусть n-чётное число, n=2k, тогда
x 1 arcsin a 2 k arcsin a 2 k , k Z
2k
Пусть n-нечётное число, n=2k+1, тогда
x 1
2 k 1
Итак
arcsin a 2k 1 arcsin a 2 k , k Z
x arcsin a 2 k
x arcsin a 2 k , k Z
14. Уравнение sinx=a
• Пример1.
1
2 x arcsin 2 2 k
2 x arcsin 1 2 k
2
x 12 k
, k Z.
x 5 k
12
1
sin 2 x
2
2 x 6 2 k
;
;
2 x 2 k
6
2
x
2 k
6
2 x 5 2 k ;
6
или
1
2 x 1 n arcsin n;
2
2 x 1 n
x 1
n
6
12
n
n
2
;
, n Z.
15. Уравнение sinx=a
Пример 2.2
sin x
4
2
2
2 k
x arcsin
4
2
;
x arcsin 2 2 k
2
4
x 4 4 2 k
;
x 2 k
4
4
2
x
arcsin
2 k
4
2
;
2
x
arcsin
2 k
4
2
x 2 k
3
x 2 k , k Z .
2
16. Уравнение sinx=a
• Пример 3.
3sin x 1 2 sin x 1 0
3sin x 1 0;
2 sin x 1 0;
1
sin x ;
3
1
sin x ;
2
1
x 1 arcsin n, n Z .
3
n
1
x arcsin 2 2 k
;
x arcsin 1 2 k
2
x
2 k
6
, k Z.
x 7 2 k
6
English Русский Правила
ОСНОВНЫЕ УРАВНЕНИЯ – ТРИГОНОМЕТРИЯ
Уравнение, включающее тригонометрические функции неизвестного угла, называется тригонометрическим уравнением.
Основные тригонометрические уравнения имеют вид sin x =a, cos x = a, tan x = a, cot x = a, , где x — неизвестное число, а a — любое действительное число.
sin x = a Учитывая уравнение sin x = a , как мы можем найти x ?
Посмотрите на рисунок. Для любого числа на оси синуса есть два соответствующих значения на единичной окружности. Одно значение равно x 1 = ARCSIN A , а другой — x 2 = π — ARCSIN A .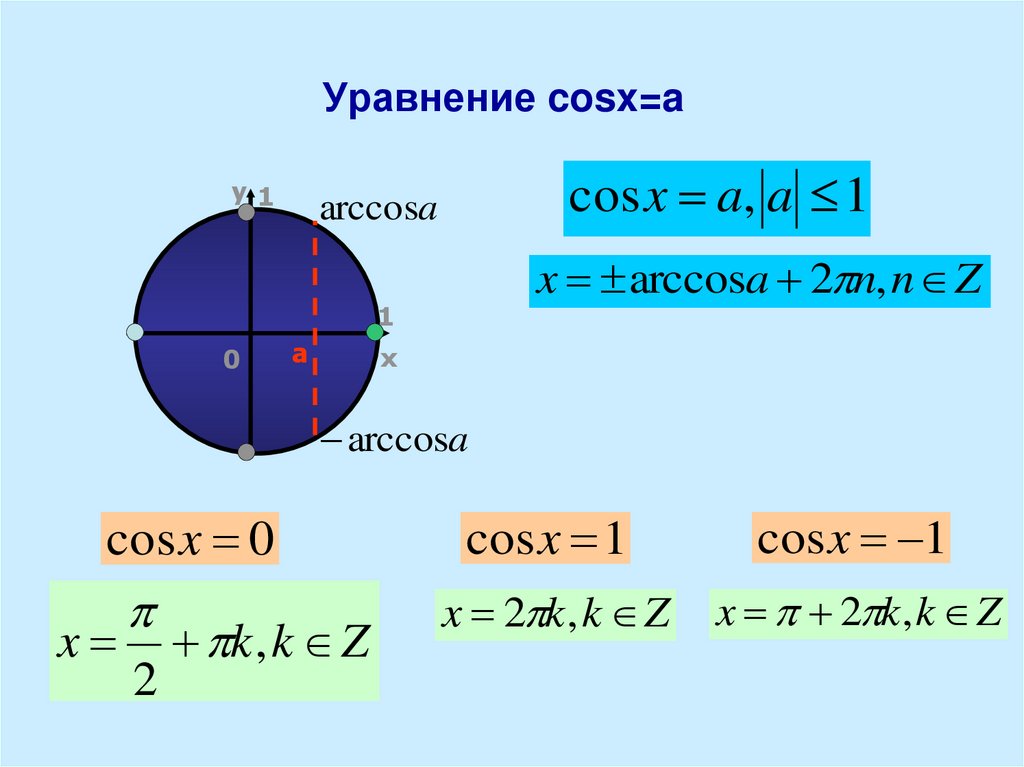
Мы также должны рассмотреть сотерминальные углы x₁ и x 2 , например arcsin a + 2π, arcsin a + 4π, arcsin a + 6π, … .
Итак, мы можем написать:
sin x = a ⇔ { x = arcsin a + 2kπ, k∈ Z } 9k Arcsin a + kπ, k ∈ Z для -1 ≤ A ≤ 1.
Специальные результаты:
, когда x = 0 , x = 1 или x = -1 4. можно написать ответ короче, не используя формулу:
sin x = 0 ⇔ x = kπ, k ∈ Z k ∈ Z
sin x = -1 ⇔ x = -π/2 + 2kπ, k ∈ Z
Если cos x = a, , чему равно x?
Посмотрите на рисунок. Для любого числа на оси косинуса есть два соответствующих значения на единичной окружности. Одно значение — x 1 = Arccos A , а другой — x 2 = -ARCCOS A .
Мы также должны учитывать котерминальные углы x 1 и x 2 например, arccos a + 2π, arccos a + 4π, … .
Итак, мы можем написать:
COS x = a ⇔ x = ± arccos a + 2Kπ, K ∈ Z
, где -1 ≤ A ≤ 1.
Специальные результаты:
cos x = 0 ⇔ x = π/2 + kπ, k ∈ Z
cos x = 1 ⇔ x = 2kπ, k ∈ 9 Z 0025 cos x = -1⇔ x = π + 2kπ, k ∈ Z
потому что х. Тогда мы получаем
cos x = √3/2, и знаем arccos √3/2 = 30° = π/6. Итак, x = ± π/6 + 2kπ, k∈ Z.
Если tan x = a, , чему равно x?
Посмотрите на рисунок. Для любого числа на касательной оси есть два соответствующих значения на единичной окружности. Одно значение равно x 1 = Arctan A , а другой — симметрия x 1 относительно происхождения, что означает x 2 = πs +.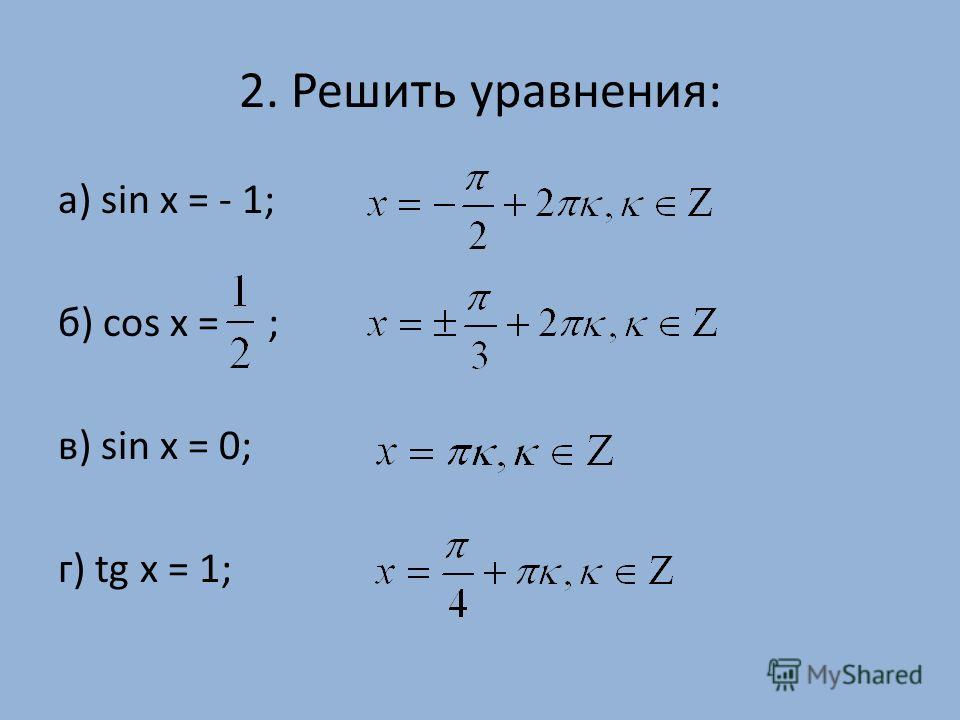
+. +. . . . . +. . . .
Учитывая также котерминальные углы, мы можем написать:
tan x = a ⇔ x = arctan a + kπ, k ∈ Z для a ∈ R 90 в красной линии 90 фигура — касательная ось.
Пример: Решить 4tan (5x + π/3) + 4 = 0
Решение: Преобразование уравнения дает нам tan(5x + π/3) = -1.
arctan(-1) = -45° = -π/4, поэтому по формуле имеем 5x + π/3 = -π/4 + kπ
5x = -π/4 – π/3 + kπ =
Если cot x = a, , чему равно x?
Посмотрите на рисунок. Для любого числа на оси котангенса есть два соответствующих значения на единичной окружности. Одно значение равно x 1 = ARCCOT A , а остальная — симметрия x 1 С уважением к происхождению, что означает x 2 .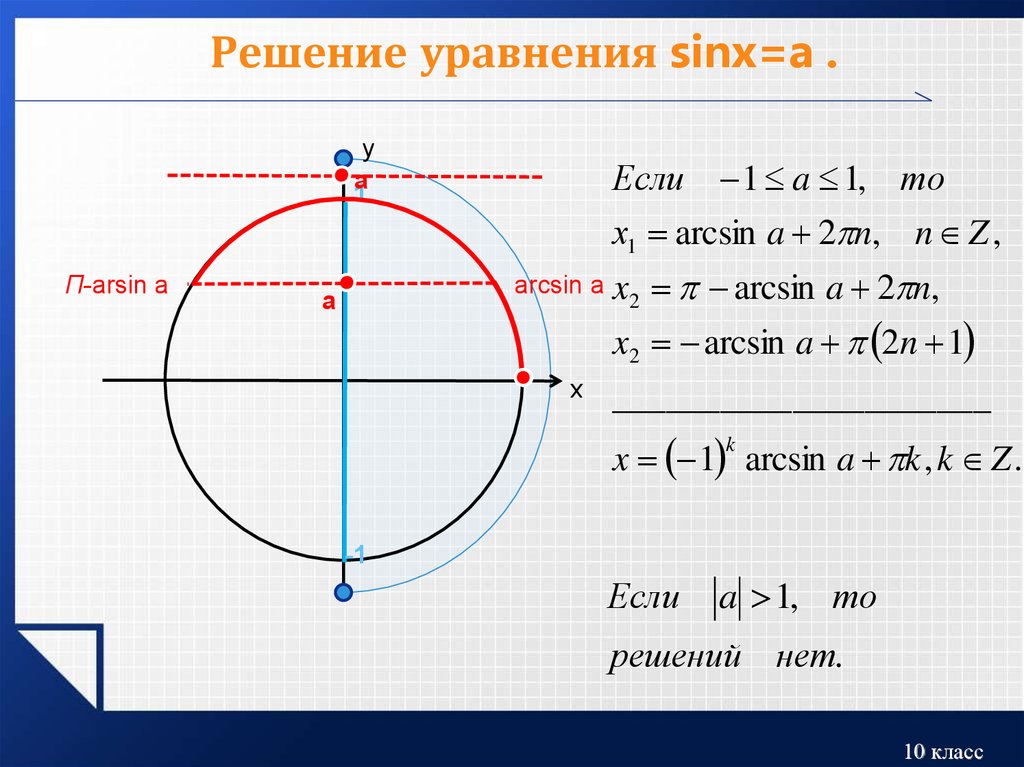
+ аркот а.
. Также учитывая угла, мы можем написать:
COT x = a ⇔ x = Arccot A + Kπ, K ∈ Z для A ∈ R.
7 0002 Красная линия на рисунке — ось котангенса.
Пример: Решите cot (-x/2) = -1
Решение: arccot (-1) = 135° = 3π/4, , -3 по формуле /2 = 3π/4 + kπ и x = – 3π/2 – 2kπ, k ∈ Z. Обратите внимание, что, поскольку k – любое целое число, оно может быть отрицательным или положительным, поэтому мы также можем записать
x = -3π /2 – 2kπ = -3π/2 + 2kπ, k ∈ Z.
Видео ниже посвящено решению основных тригонометрических уравнений:
Нравится:
Нравится Загрузка.
..
тригонометрия — Решение тригонометрических уравнений вида $a\sin x + b\cos x = c$
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 24к раз
$\begingroup$
Предположим, что существует тригонометрическое уравнение вида $a\sin x + b\cos x = c$, где $a,b,c$ вещественны и $0 < x < 2\pi$. Пример уравнения будет выглядеть следующим образом: $\sqrt{3}\sin x + \cos x = 2$, где $0 Как решить это уравнение без использования метода, который сдвигает $b\cos x$ вправо и возводит в квадрат левую и правую части уравнения? И почему решение $\sqrt{3}\sin x + \cos x = 2$ равно решению $\sin (x+ \frac{\pi}{6}) = 1$ $\endgroup$ 3 $\begingroup$ Идея состоит в том, чтобы использовать тождество $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$. $$a\sin x+b\cos x=\cos\beta\sin x+\sin\beta\cos x=\sin(x+\beta)\;.$$ 92}}\right)=\ln(1)$$ обращается в нуль, как и ожидалось, и аргумент равен $$\theta=\pm\arctan\left(\frac dc\right)+\arctan\left(\frac ab\right).$$ Последняя формула может быть переписана с одним $\arctan$, используя $$\theta=\arctan\left(\tan(\theta)\right)=\arctan\ влево (\ frac {\ pm \ dfrac dc + \ dfrac ab} {1 \ mp \ dfrac dc \ dfrac ab} \ right) = \ arctan \ left (\ frac {\ pm bd + ac} {bc \ mp ad} \ справа).$$ $\endgroup$ $\begingroup$
92$ при $d \geq 0$, и мы видим, что
$$\theta = \operatorname{atan}\frac{a}{b} + \operatorname{atan}\frac{d}{c} \tag{1}$$
(Если бы треугольник «$a$» был выше, чем треугольник «$b$», то «$+$» стал бы «$-$». По сути, мы можем взять $d$ отрицательным, чтобы получить «другое». Если $b+c=0$, то $$\iff \tan\frac{x}{2}=\frac{c-b}{2a}\iff x=2\left(\arctan\frac{ c-b}{2a}+n\pi\right),\, n\in\Bbb Z$$ $\endgroup$ $\begingroup$ https://en.wikibooks.org/wiki/Trigonometry/Simplifying_a_sin(x)_%2B_b_cos(x) Хотя приведенные выше ответы идеально отвечают на ваш вопрос, вам может быть полезно взглянуть на приведенную выше ссылку.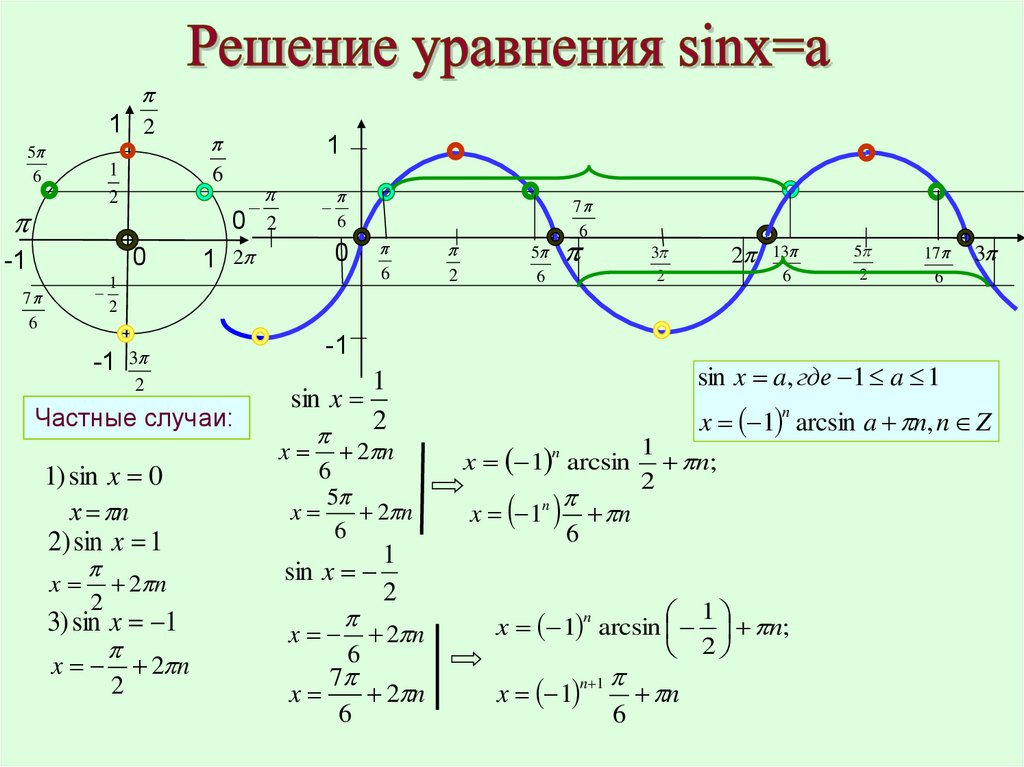
У вас есть $a\sin x+b\cos x$, поэтому вы хотите найти угол $\beta$ такой, что $\cos\beta=a$ и $\sin\beta=b$, так как тогда вы можно написать
2}
\end{align}\quad\right\rbrace\quad\to\quad \tan\theta = \frac{ac+bd}{bc-ad} \tag{2}$$
Мы можем прийти к $(2)$ немного более геометрическим способом, заметив
$$c d = (a\sin\theta + b \cos\theta)d = c( b\sin\theta — a \cos\theta ) \;\to\; ( b c — a d)\sin\theta = \left( a c + b d \right)\cos\theta \;\to\; (2) $$
где каждый член в расширенной форме первого уравнения можно рассматривать как площадь прямоугольной области на тригонографе. (Например, $b c \sin\theta$ — это площадь всей фигуры.) 92$.