Тема 1. Масштабы карт. Измерение длин и площадей объектов по топографическим картам — Мегаобучалка
Цель работы: сформировать представление о масштабных свойствах топографических карт.
Масштабом карты называется отношение длины линии на карте к горизонтальной проекции соответствующей линии на местности. Масштаб— это величина, показывающая во сколько раз длина на местности (земной поверхности) уменьшена при переносе ее на карту.
Масштаб указывают под южной рамкой карты и выражают отношениями чисел (численный масштаб), словесно (именованный масштаб) и графически (линейный масштаб).
а) Численный масштаб записывается в виде дроби, в числителе которой единица, а в знаменателе — число, выражающее степень уменьшения горизонтальных проекций – линий местности при изображении их на карте. Всегда дается в сантиметрах (см).
Например: 1 : 1 000 000 — 1 см на карте соответствует 1000 000 см на местности (степень уменьшения в 1 000 000 раз).
1 : 200 000 — 1 см на карте соответствует 200000 см на местности
1 : 50 000 — 1 см на карте соответствует 50000 см на местности
1 : 100 — 1 см на карте соответствует 100 см на местности
1 : 5 — 1 см на карте соответствует 5 см на местности
Запомнить1 : 1 000 000 см см на карте на местности расстояние на местности соответствует 1 см на карте.
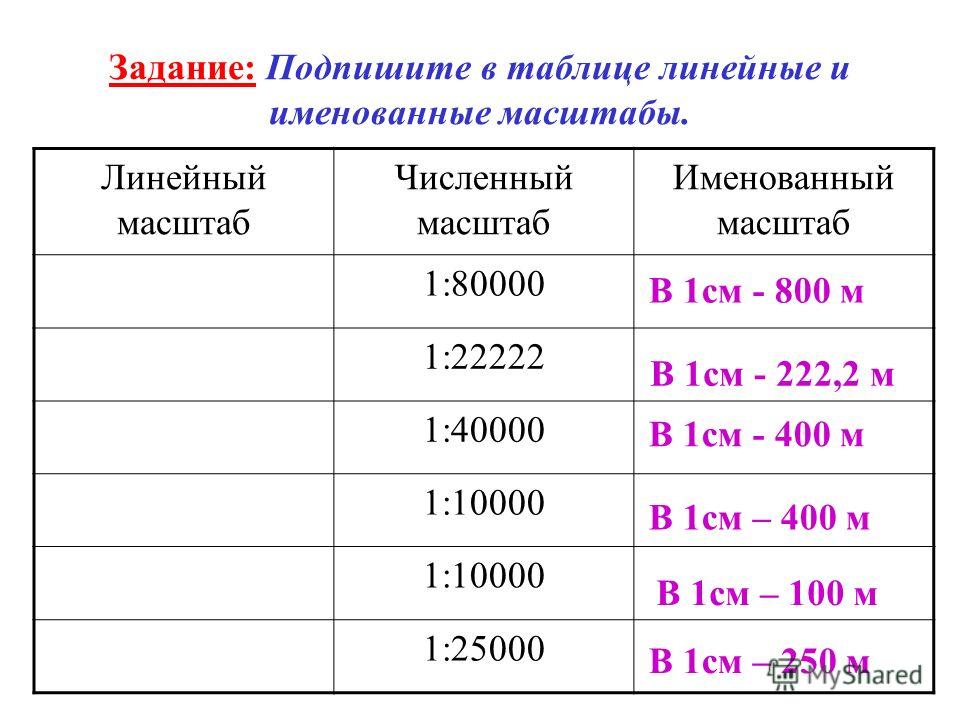
б) Именованный масштаб указывается в виде подписи, какое расстояние на местности соответствует 1 см на карте.
Например:
в 1 см 1 км или 1 : 1 000 00
в 1 см 10 км или 1 : 10 000 00
в 1 см 500 м или 1 : 500 00
в 1 см 10 м или 1 : 10 00
в 1 см 30 см или 1 : 30
в) Линейный масштаб дается в виде линейки, разделенной на равные отрезки (соответствующие 1 см) с подписями, означающими расстояние на местности. Линейный масштаб строят и используют для удобства пользования картами и планами, он позволяет избежать расчетов при переводе длин линий местности в масштаб карты или плана и наоборот. На топографических картах и планах линейный масштаб вычерчивается под южной рамкой карты или плана.
На топографических картах и планах линейный масштаб вычерчивается под южной рамкой карты или плана.
Равные отрезки на линейном масштабе (соответствующие 1 см на карте) называются основанием масштаба (а) а = 1 см = 100 м (соответствующие 1 мм на карте) для измерения расстояний с большей точностью — это точность масштаба (в) 1 в = 1 мм = а = 10 м
Линейное расстояние на местности, выражающееся 0,1 мм на карте данного масштаба называется предельной точностью масштаба (в1) (величина, приближенно соответствующая разрешающей способности глаза) в1 = 0, 1 мм = в = 1 м
Для построения линейного масштаба, на прямой несколько раз откладывается отрезок одинаковой длины, который называется основанием масштаба. Чаще всего основание линейного масштаба принимается равным 2 см.
Для повышения точности построения или измерения отрезков на картах или планах, крайний левый отрезок линейного масштаба делят на 10 или 20 равных частей, которые называются делениями основного масштаба.
Линейный масштаб используют следующим образом:
1). в раствор циркуля-измерителя с карты или плана берут отрезок, длину которого необходимо определить;
2). прикладывают циркуль к линейному масштабу таким образом, чтобы одна иголка находилась на нулевом или другом находящимся справа от нуля штрихе линейного масштаба;
3). по второй иголке отсчитывают части левого основания масштаба.
На рисунке ниже, длины измеренных отрезков по плану масштаба 1:5000 равны 220 метров и 60 метров.
Например: 1 : 1 000 000
а = 1 см = 1 000 000 см = 1 000 0 м = 10 км
в = 1 мм = 1 000 00 см = 1 000 м = 1 км
в1 = 0,1 мм = 1 000 0 см = 1 00 м = 0, 1 км
1 : 1 000 000, 1 см на карте соответствует 1 000 000 см на местности.
Второе число необходимо перевести в более крупные единицы длины, используемые для измерений на местности, т.е. в метры или километры. Получится, что в 1 см на карте содержится 10 км на местности.
Вспомнить: 1 см — 10 мм, 1 м = 100 см, 1 км = 1000 м
1 : 500 000
а = 1 см = 500 000 см = 500 0 м = 5 км
в = 1 мм = 500 00 см = 500 м
в1 = 0,1 мм = 500 0 см = 50 м
Рис. 1. Обозначение численного и линейного масштабов на карте.
К сведению: в старых русских картах использовались следующие меры длины:
1 верста = 1,067 км, 1 сажень = 2,134 м, 1 дюйм = 2,54 см. Английская система мер — 1 миля = 1,609 км.
Поперечный масштаб, в отличие от линейного масштаба, позволяет измерять и переносить линии на карту или план с большей точностью.
Начало построения поперечного масштаба аналогично построению линейного масштаба.
Рис.2. Длины измеренных отрезков по плану поперечного масштаба 1:5000 равны 252 метра и 477 метров
Задание 1.Дать словесное выражение численным масштабам.
1: 50 000; 1: 20 000; 1: 1 000; 1: 500; 1: 300; 1:50; 1:25; 1: 100 000; 1: 200 000; 1: 5 000; 1: 10 000; 1: 1 250; 1: 25 000; 1: 500 000.
Например: 1 : 25 — в 1 см 25 см
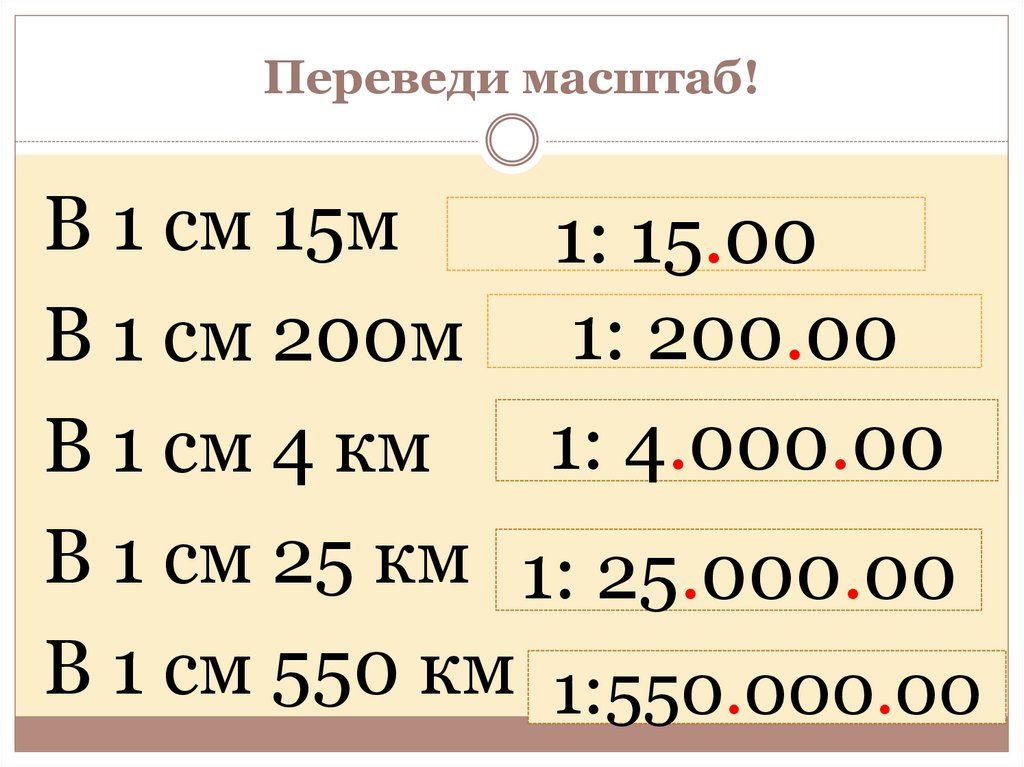
Задание 2.Именованный масштаб заменить численным.
в 1 см 5 см; в 1 см 50 м; в 1 см 250 м; в 1 см 3 км; в 1 см 500 км;
в 3 см 600 м; в 2 см 10 км; в 4 см 1 км, 1 см — 50м; 1 см – 200 м; 2 см – 1 км; 1 см – 500 м; 1 см – 100 м; 1 м – 1000 м; 2 см – 2 км; 2 см – 10 м; 4 см – 1 км; 10 см – 1 км; 1 см – 2 м; 1 см – 2 км; 1 см – 10 км; 1 см – 5 км.
Например: в 1 см 5 см — 1: 5
в 3 см 600 м — 3см : 600 00 см — 1: 200 00
Задание 3.С помощью циркуля измерителя и поперечного масштаба отложить отрезки следующей длины: 0,78 см; 1,84 см; 27,4мм; 41,3 мм; 5,5 мм; 11,2 м; 33,8 мм; 13,0 мм; 20,5 мм; 6,7 мм; 1,3 мм; 0,8 мм; 10,2 мм; 12,0 мм; 15,4 мм; 19,9 мм; 2,2 мм; 5,7 мм; 9,8 мм; 12,6 мм; 4,8 мм; 25,8 мм; 30,9 мм; 45,8 мм.
Задание 4.Построить удобные линейные метрические масштабы для карт заданных масштабов:
1: 42 000; 1: 840 000; 1: 62 500; 1: 21 000;
1 дюйм – 250 саж. ; 1 дюйм – 500 саж.; 1: 126 000.
; 1 дюйм – 500 саж.; 1: 126 000.
Задание 5. Определить масштабы карт по длине линий на карте и местности
| № В-та | Длина линии на местности | Длина линии на карте | Масштаб карты |
| А Б В Г Д Е Ж З И К Л М | 1250 м 19,2 км 550 м 840 м 570 м 2,87 км 5280 м 1285 м 150 м 420 м 9710 м 374 м | 1,25 см 192 мм 11 мм 84 мм 22,8 мм 57,4 мм 26,4 мм 128,5 мм 30 мм 16,8 мм 194,2 мм 3,7 мм |
Задание 6.Найти расстояние между городами (используя атласы по географии) на карте и на местности.
1) Санкт-Петербург — Москва
2) Москва — Самара
3) Самара — Новосибирск
4) Новосибирск — Братск
5) Братск – Комсомольск – на – Амуре
6) Комсомольск – на – Амуре – Владивосток
Проверь свои знания
Тесты по теме: «Масштабы карт. Измерение длин и площадей объектов по топографическим картам».
Измерение длин и площадей объектов по топографическим картам».
1. Расстояния на местности, равные 1 см на карте называют…
1. точностью масштаба
2. основанием масштаба
3. предельной точностью масштаба
2. Дробь, в числителе которого единица, а в знаменателе число, показывающее степень уменьшения называется…
1. именованным масштабом
2. линейным масштабом
3. численным масштабом
4. поперечным масштабом
3. Графическое построение в виде линейки, разделенной на равные отрезки с подписями, означающими соответствующее расстояние на местности называется …
1.численным масштабом
2.именованным масштабом
3.линейным масштабом
5. Дополните таблицу
| Виды масштаба | Как изображается | Что показывает | Для чего используется |
| Именованный | Словами и числами | ||
| Численный | Величину масштаба | ||
| Линейный | Для измерений расстояний циркулем |
6. Закончите фразу:
Закончите фразу:
Если длина отрезка СК на карте в 20 000 раз меньше, чем на местности, то масштаб этой карты …
Если отрезок АВ=1см изображен на карте с масштабом 1: 10 000, то на местности его длина равна…
7.Отрезком какой длины обозначается на ней расстояние в 500; 50 км, если масштаб карты 1: 10 000 000?
8.Каково расстояние между двумя пунктами, если на карте оно изображено отрезком в 2; 4 км.
Масштаб карты
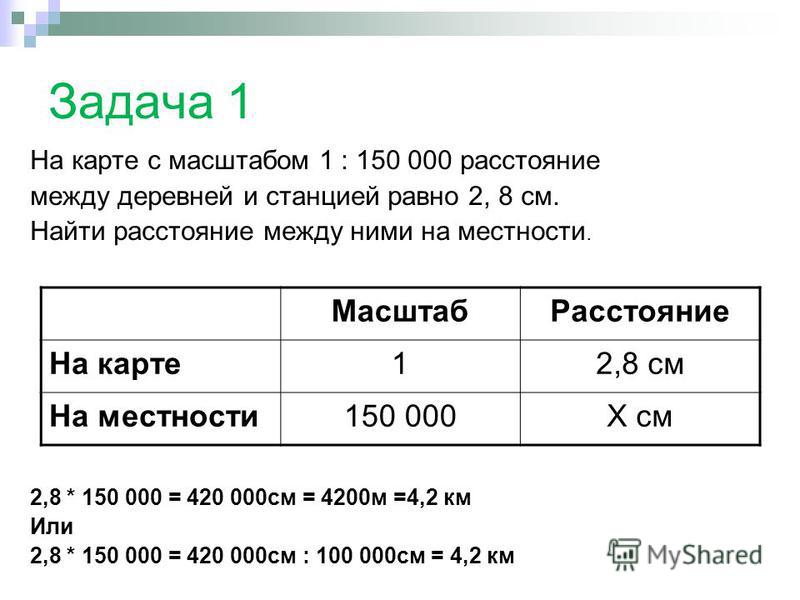
Задачи из экзаменов по географииЗадача 1.
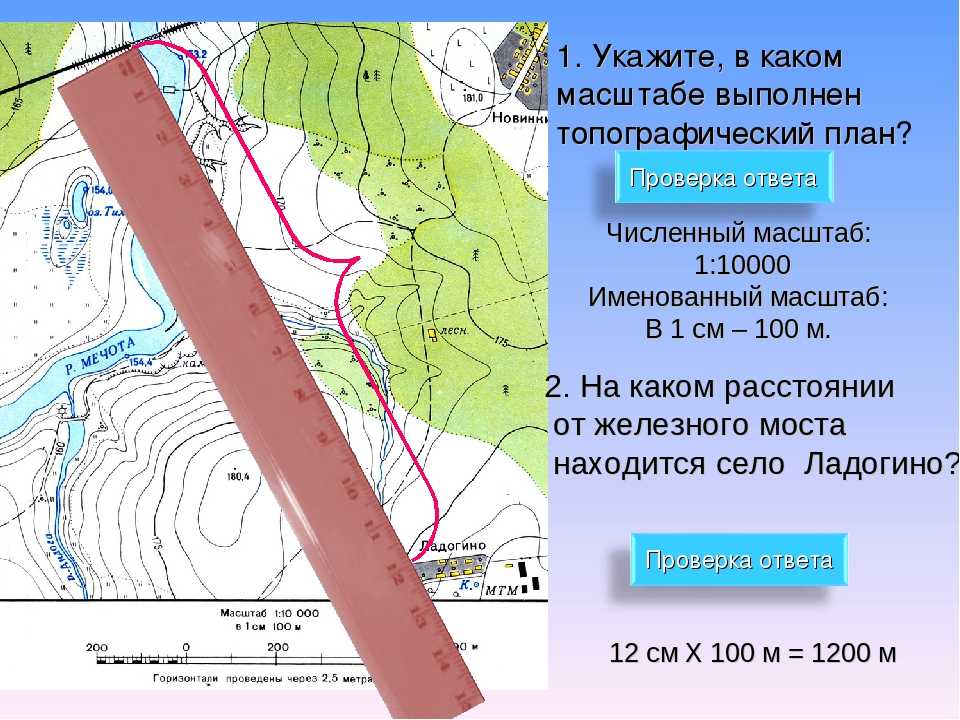
Определите по карте расстояние на местности по прямой от родника до дома лесника. Полученный результат
округлите до десятков метров. Ответ запишите в виде числа.
(демоверсия ФИПИ ЕГЭ по географии;
в демоверсии ОГЭ задание аналогично)
Решение:
Найдем указанные объекты и измерим расстояние между ними (красный пунктир). На распечатке в оригинальном размере при измерении линейкой это расстояние 27 мм (2 см 7 мм).
На распечатке в оригинальном размере при измерении линейкой это расстояние 27 мм (2 см 7 мм).
Через пропорцию найдем соответствующее расстояние на местности:
2,7 см = х м
х = (2,7 см * 100 м) / 1 см = 270 м.
(округлять не пришлось, но если бы получили 273м или 267 м, то округляем, согласно условию задачи до десятков метров — 270 м).
Ответ согласно условию задачи записываем без размерных единиц.
Ответ: 270
Задача 2.
С корабля, находящегося в точке с координатами 13° с.ш. 73° з.д., поступило радиосообщение о неисправности двигателя. Какое расстояние (в км) до неисправного судна пройдёт ремонтный корабль из порта Риоача (11° с.ш. 73° з.д.), если известно, что корабль будет идти строго по меридиану, а неисправное судно останется в той же точке, откуда было передано сообщение? Запишите решение задачи.Ответ округлите до целого числа
. Задача 3.
(демоверсия ФИПИ ЕГЭ по географии)
Решение:
Согласно условию задачи корабль будет двигаться строго по меридиану 73° з. д., и пройдет путь с 11° с.ш. до 13° с.ш., т.е. расстояние, соответствующее 2° длины меридиана.
д., и пройдет путь с 11° с.ш. до 13° с.ш., т.е. расстояние, соответствующее 2° длины меридиана.
Длина 1° любого меридиана примерно 111 км
(критерии оценки ФИПИ позволяют использовать длину дуги 1° меридиана от 111,0 до 111,7 км, рекомендуется брать значение 111 км)
Необходимо записать в решение подсчёт:
(13 — 11) * 111 км = 222 км
(округлять не пришлось, но если бы получили 222,2 км (взяв за длину 1° 111,1 км), то согласно условию задачи нужно округлить до целого — 222 км)
Ответ: 222 км
Постройте профиль рельефа местности по линии А – В. Для этого перенесите основу для построения профиля на бланк ответов, используя горизонтальный масштаб в 1 см 50 м и вертикальный масштаб в 1 см 5 м.
Укажите на профиле знаком «Х» положение родника.
(демоверсия ФИПИ ЕГЭ по географии, в демоверсии ОГЭ задача проще — вместо построения предложено выбрать правильный профиль из вариантов ответов)
Решение:
1) Сделаем построения на рисунке из условия
1) Соединим т. А и т. B и измерим длину отрезка.
А и т. B и измерим длину отрезка.
В распечатке длина составляет 40 мм.
Промерим расстояния относительно точки А в мм, где отрезок пересекает горизонтали, в этих точках нам известны точные высоты — значения этих горизонталей.
2) Построим в бланке ответов заготовку для профиля с высотными положениями т. А и т. B и вертикальной шкалой по образцу, приведенному в задании, соблюдая масштаб вертикальной оси в 1 см 5 м. Т.к. горизонтальный масштаб профиля по условию — в 1 см 50 м (в 2 раза крупнее, чем карты), то длина построенного профиля 40 мм * 2 = 80 мм, все значения, где линия AB пересекает горизонтали и родник также удваиваем и наносим на горизонтальную шкалу и проводим асимптоты до соответствующих высот, по которым строится профиль.
Крестиком отмечаем родник.
Задачи из экзаменов и школьной программы по математике
Задача 1.
Масштаб карты 1:200 000. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 2,5 см?
Чему равно расстояние между городами A и B (в км), если на карте оно составляет 2,5 см?
Решение:
Масштаб 1:200 000,
т.е. в 1 см 200 000 см
или в 1 см 2 км
Составим пропорцию:
1 см = 2 км
2,5 см = x км
x = (2,5 см * 2 км) / 1 см
x = 5 (км)
Ответ: 5 км.
Задача 2.
Отрезку на карте, длина которого 2,4 см, соответствует расстояние на местности в 96 км. Каково расстояние между городами, если на этой карте между ними 15 см?
Решение:
Составим пропорцию:
2,4 см = 96 км
15 см = x км
x = (15 см * 96 км) / 2,4 см
x = 600 (км)
Ответ: 600 км.
Задача 3.
Расстояние на местности в 75 км изображено на карте отрезком 1,5 см. Определите масштаб карты (именованный и численный).
Решение:
Составим пропорцию:
1,5 см = 75 км
1 см = x км
x = (1 см * 75 км) / 1,5 см
x = 50 (км)
следовательно в 1 см 50 км
или в 1 см 5 000 000 см,
т. е. 1:5000000
е. 1:5000000
Ответ: в 1 см 50 км или 1:5000000.
Задача 4.
Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1:50000?
Решение:
4,5 км = 4500 м = 450 000 см
Составим пропорцию:
1 см = 50000 см
x см = 450000 см
x = (450000 см * 1 см) / 50000 см
x = 9 (см)
Ответ: 9 см.
Задача 5.
Длина железной дороги Москва — Петербург приближенно равна 650 км. Сколько сантиметров займет изображающий ее отрезок в масштабе 1:10 000 000?
Решение:
Масштаб 1:10000000
т.е. 1 см 10000000 см,
или в 1 см 100 км
Составим пропорцию:
1 см = 100 км
x см = 650 км
x = (650 км * 1 см) / 100 км
x = 6,5 (см)
Ответ: 6,5 см.
Задача 6.
Длина реки на карте в масштабе 1:50000, равна 7,2 см. Чему будет равна длина этой реки на другой карте в масштабе 1:200000?
Решение:
1) Найдем длину реки на местности по карте масштаба 1:50000:
1 см = 50000 см
7,2 см = x см
из пропорции x = 360000 (см) — длина реки на местности
2) Найдем длину реки на карте 1:200000:
1 см = 200000 см
x см = 360000 см
из пропорции x = 1,8 (см) — длина реки на второй карте
Решение коротким способом:
Карта 1:200000 (в 1 см 2 км) мельче карты 1:50000 (в 1 см 500м) в 4 раза (200000/50000 = 4).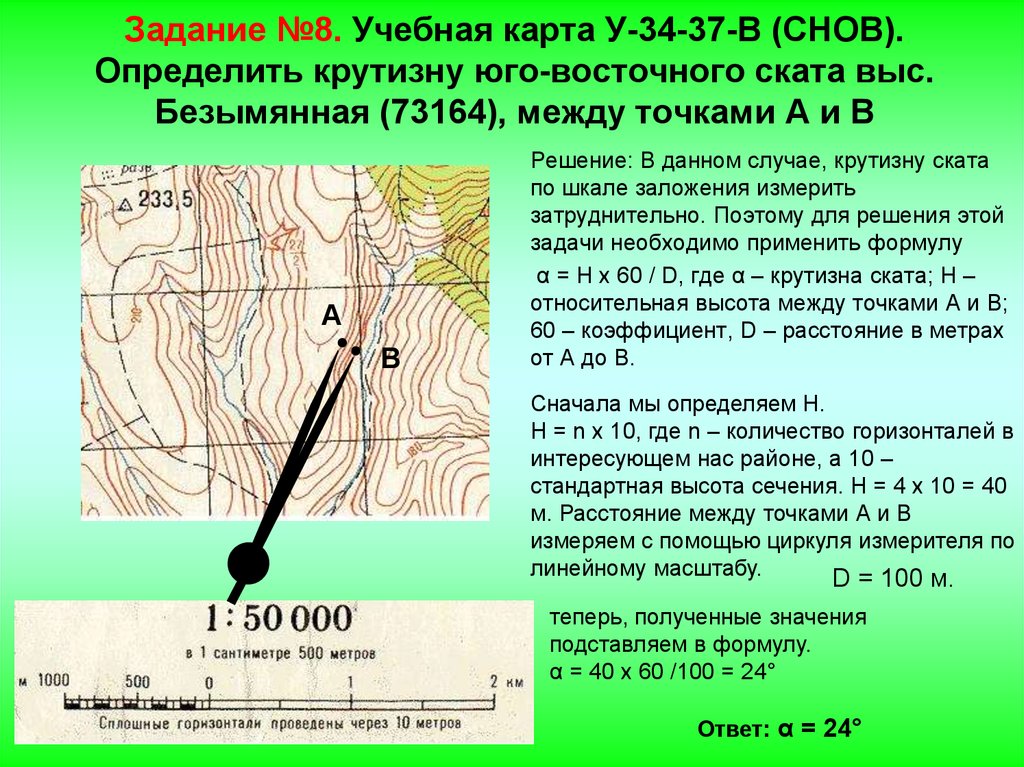 Следовательно длина реки на второй карте в 4 раза короче: 7,2 см / 4 = 1,8 см.
Следовательно длина реки на второй карте в 4 раза короче: 7,2 см / 4 = 1,8 см.
Ответ: 1,8 см.
Масштаб карты
Репетиторы ❯ Математика ❯ Масштаб карты
Автор: Владимир Л., онлайн репетитор по математике
●
21.12.2011
●
Раздел: Математика
Каждая карта имеет масштаб – число, которое показывает, сколько сантиметров на местности соответствует одному сантиметру на карте.
Масштаб карты обычно указан на ней. Запись 1 : 100 000 000 означает, что если расстояние между двумя точками на карте равно 1 см, то расстояние между соответствующими точками её местности равно 100 000 000 см.
Масштаб может быть указан в численной форме в виде дроби – численный масштаб (например, 1 : 200 000). А может быть обозначен в линейной форме: в виде простой линии или полосы, разделенной на единицы длины (обычно на километры или мили).
Чем крупнее масштаб карты, тем с более детально могут быть изображены на ней элементы ее содержания, и наоборот, чем мельче масштаб, тем более обширное пространство может быть показано на листе карты, но местность на ней изображается с меньшими подробностями.
Масштаб представляет собой дробь, в числителе которой единица. Чтобы определить, какой из масштабов крупнее и во сколько раз, вспомним правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель.
Отношение расстояния на карте (в сантиметрах) к соответствующему расстоянию на местности (в сантиметрах) равно масштабу карты.
Как же эти знания помогут нам при решении задач по математике?
Пример 1.
Рассмотрим две карты. Расстоянию в 900 км между пунктами А и В соответствует на одной карте расстояние в 3 см. Расстоянию в 1 500 км между пунктами С и D соответствует на другой карте расстояние в 5 см. Докажем, что масштабы карт одинаковы.
Решение.
Найдём масштаб каждой карты.
900 км = 90 000 000 см;
масштаб первой карты равен: 3 : 90 000 000 = 1 : 30 000 000.
1500 км = 150 000 000 см;
масштаб второй карты равен: 5 : 150 000 000 = 1 : 30 000 000.
Ответ. Масштабы карт одинаковы, т.е. равны 1 : 30 000 000.
Пример 2.
Масштаб карты – 1 : 1 000 000. Найдём расстояние между точками А и В на местности, если на карте
АВ = 3,42 см?
Решение.
Составим уравнение: отношение АВ = 3,42 см на карте к неизвестному нам расстоянию х (в сантиметрах) равно отношению между теми же пунктами А и В на местности к масштабу карты:
3,42 : х = 1 : 1 000 000;
х · 1 = 3,42 · 1 000 000;
х = 3 420 000 см = 34,2 км.
Ответ: расстояние между пунктами А и В на местности равно 34,2 км.
Пример 3
Масштаб карты – 1 : 1 000 000. Расстояние между пунктами на местности 38,4 км. Каково расстояние между этими пунктами на карте?
Решение.
Отношение неизвестного нам расстояния х между пунктами А и В на карте к расстоянию в сантиметрах между теми же пунктами А и В на местности равно масштабу карты.
38,4 км = 3 840 000 см;
х : 3 840 000 = 1 : 1 000 000;
х = 3 840 000 · 1 : 1 000 000 = 3,84.
Ответ: расстояние между пунктами А и В на карте равно 3,84 см.
Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Физика
Курсы по физике 10 класс
«Масштаб».
 6-й класс
6-й классЦели урока:
- показать практическое применение понятия масштаб;
- формировать у учащихся практические умения и навыки, связанные с математическими вычислениями при решении текстовых задач;
- способствовать развитию умения делать выводы на основе собственных наблюдений, сравнения, обобщения, использования личного опыта; развивать логическое мышление и пространственные представления;
- закрепить навыки, связанные с преобразованием величин.
Оборудование: компьютер, мультимедийная разработка урока, проектор, модели машинок, копии планов квартир с БТИ, модели геометрических тел, географическая карта.
Ход урока
1. Орг. момент.
2. Устный счёт, устная работа. (слайд2)
1) выразите в километрах:
а)32000000см;
б)600000см;
в)32000см;
г)5000000см.
— Что нужно сделать, чтобы выразить данные величины в км? /так как 1км = 100000см, то нужно разделить на 100000./
2) выразите в метрах:
а)32000000см;
б) 600000см;
в)32000см;
г)5000000см.
— Что необходимо сделать?
Актуализация знаний.
— Скажите, а с чем вы сейчас работали, какие знания применили? / Меры длины/.
Без них нам сегодня на уроке никак не обойтись. Вспомним перевод одних единиц в другие (Слайд 3).
Молодцы. Тема, которую нам сегодня предстоит изучить, покажет практическое применение отношений.
3. Изучение нового материала
1)) Подготовительная работа. (слайд4)
— Составьте отношения:
а) 1см к 4000м;
б) 1см к 120 м;
в) 1см к 10000 км;
г) 1 см к 25 см.
— Что сначала необходимо сделать?/привести в одинаковые единицы измерения/
Работа с понятием “масштаб”.
— Хорошо. Запишем все величины в сантиметрах.
Решение:
а) 1: 400000;
б) 1 : 12000;
в) 1 : 1000000000;
г) 1 : 25.
— Мы с вами знаем, что участки земной поверхности, детали машин и многое другое изображают на бумаге в уменьшенном виде.
— Если на карте, плане или чертеже встретите такие отношения, то это масштаб карты, плана или чертежа.
— Что же мы будем сегодня изучать? /Масштаб/ Запишите тему урока в тетрадочку. (слайд 5)
Уточнение понятия с опорой на имеющиеся знания.
— Итак, “масштаб”. О чем вам говорит это слово?
Ответы детей можно дополнить демонстрацией реальных моделей предметов (глобус земли, географическая карта, показом моделей машинок)
— Мы увидели, что использование масштаба позволяет создавать модели реальных предметов.
— Само слово “масштаб” пришло к нам из
немецкого языка. Maс означает: “мера”, штаб
означает “размер”, что уже говорит о связи с
математикой. Слово “масштаб”, придя из
немецкого языка, хорошо прижилось в нашей речи.
Какие родственные слова к нему вы можете назвать?
(масштабный, крупномасштабный). Реже
используется слово “масштабировать”, что
означает – изменять все размеры в определенное
количество раз. Это слово сегодня нам
понадобится.
Maс означает: “мера”, штаб
означает “размер”, что уже говорит о связи с
математикой. Слово “масштаб”, придя из
немецкого языка, хорошо прижилось в нашей речи.
Какие родственные слова к нему вы можете назвать?
(масштабный, крупномасштабный). Реже
используется слово “масштабировать”, что
означает – изменять все размеры в определенное
количество раз. Это слово сегодня нам
понадобится.
(Слайд 6). Полное определение “масштаба” звучит так: Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом. Аналогично можно сказать о чертеже или плане.
Масштаб — жезл размеренный или мерило, мерник, размерник, мера линейная, принятая для чертежа или иной работы. (Из толкового словаря В.И. Даля.) (слайд7)
Вернёмся к уже написанным отношениям. Объясните, что означают данные масштабы (слайд 8-9)
/ответы учащихся: а) если масштаб карты 1 : 400000, то
на этой карте длина каждого отрезка уменьшена в
400000 раз. На такой карте расстояние, равное 4 км,
будет изображаться в 1см.
На такой карте расстояние, равное 4 км,
будет изображаться в 1см.
— Масштаб карты 1 : 400000 говорит, что карта сделана в масштабе одначетырёхсоттысячная и.т.д.
Хорошо. Молодцы. Выполните такую задачу. (слайд10)
Расстояние от школы до дома, в которой учится Коля, равно 200 м. Изобразите это расстояние отрезком в масштабе 1:4000.
Запись решения в тетради. Выразим 200 м в см. 200 м = 20000 см. Масштаб 1:4000 означает, что 1 см на плане будет в 4000 раз меньше расстояния на местности.
20000 : 4000 = 5 (см)
Ответ: длина отрезка равна 5 см.
Проверка (Слайд 11-12)
Задача. (слайд13) Длина отрезка на карте 15 см. Найдите длину соответствующего отрезка на местности, если масштаб карты 1 : 10000.
— Что означает масштаб 1 : 10000?
— Решим данную задачу, оформив краткую запись в виде таблицы.
Решение: Пусть х(м) – расстояние на местности.
| Расстояние | Масштаб | |
| На карте На местности |
15 см х |
1 10000 |
15 : х = 1 : 10000
Х = 150000(см) =1500 м= 1,5 км
1,5 км расстояние на местности
Ответ: 1,5 км
Физкультминутка.
Закрепление изученного материла, практическая работа по учебнику № 820 стр 134
— Прочитайте задание. Можем сразу найти расстояние?
— Что нужно знать? /Длину отрезка на карте/
— Как узнать длину отрезка на карте? /измерить линейкой/
— Измерьте расстояние на карте. Что означает масштаб 1 : 100000? /1см на карте равен 100000см на местности/
Запишем краткую запись в виде таблицы
| Расстояние | Масштаб | |
| На карте На местности |
3 см х |
1 100000 |
Составим пропорцию: 3 : х =1 : 100000; х =300000см = 3000 м =3 км – расстояние на местности
Ответ: 3 км.
№ 821 стр 134 (слайд16)
— Прочитайте задачу. Что известно? Что нужно найти? Что означает данный масштаб? /1см на карте равен 1000000см на местности/
Решение:
Пусть х(м) – расстояние на местности.
| Расстояние | Масштаб | |
| На карте На местности |
8,5 см х |
1 1000000 |
Составим пропорцию: 8,5 : х =1 : 1000000; х =8500000см = 85 км – расстояние на местности
Ответ: 85 км.
Задача. Длина отрезка на местности 300 км. Найдите длину соответствующего отрезка на карте, если масштаб карты 1:1000000.
— Чем интересна эта задача?
Для решения составим табличку – краткую
запись.
| Расстояние | Масштаб | |
| На карте На местности |
х 300 км = 30000000 см |
1 1000000 |
Составим пропорцию: х : 30000000 = 1 : 1000000; х =1*30000000 : 1000000 =30см – длина на карте
Ответ: 30 см.
№ 822 самостоятельно, с последующей проверкой.(слай 17)
| Расстояние | Масштаб | |
| На карте На местности |
х см 650км = 65000000см |
1 10000000 |
Составим пропорцию: х : 65000000= 1 : 10000000;х =1*65000000 : 10000000=6,5см
Ответ: 6,5см
Возможность масштабирования заложена и в
фотоаппаратах и видеокамерах: мы приближаем и
отдаляем объекты для съемки. При этом все их
размеры одинаково увеличиваются или отдаляются.
При этом все их
размеры одинаково увеличиваются или отдаляются.
Работа в группах — парах
Масштаб квартиры 1 : 100. Определить по плану, какие размеры имеют комнаты №1, №2, №3 и какова их площадь в действительности.
Решение: По плану размеры первой комнаты 27мм * 41мм; второй комнаты 38мм*43мм, третьей комнаты 30мм*28мм. Если масштаб 1:100, то размеры первой комнаты 2700мм*41мм = 2м 70см * 4м 10см; второй комнаты 3800мм*4300мм = 3м 80см * 4м 30см, третьей комнаты 3000мм*2800мм = 3м * 2м 80см.
Ответ: Площадь первой комнаты 11,07м2; площадь второй комнаты 16,34м2; а площадь третьей комнаты 8,4м2.
Домашнее задание: задача № 842, 844, № 846 (а).
Творческое задание: придумать и красиво оформить свою задачу по теме: “Масштаб”.
Подведение итогов. Рефлексия.
- Что нового вы узнали сегодня?
- На какие вопросы получили ответы?
- Какие новые вопросы появились?
- Какие виды заданий вызвали затруднения?
- Какие моменты урока вас обрадовали или огорчили?
Я надеюсь, сегодняшний урок помог вам открыть
неизвестное в известном ранее понятии
“масштаб”.
Масштаб. Презентация. 6 кл.
Масштаб
Подготовила: Задыляк Л.М.,
учитель МАОУ СОШ №26
г. Калининград
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
Виды масштаба
Численный . Масштаб можно обозначить в виде дроби 1:10 000 (одна десятитысячная), где цифра 1 – это отрезок длиной 1см на плане (карте), 10 000 – это соответствующее этому отрезку расстояние на местности в см. Оно показывает величину уменьшения расстояния.
Именованный . Ч.м. можно записать словами « в 1см -100 м ». Расстояние на местности, соответствующее 1 см на плане, называют величиной масштаба . С ее помощью удобно определять расстояния.
Линейный . Его изображают прямой линией, разделенной на равные отрезки ( см ). Первый слева от 0 отрезок поделен на мм . Соответствующие плану расстояния на местности указываются над линейкой.
Его изображают прямой линией, разделенной на равные отрезки ( см ). Первый слева от 0 отрезок поделен на мм . Соответствующие плану расстояния на местности указываются над линейкой.
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
Как называется число?
- Численный масштаб
1 : 2 000
Что показывает число?
Что показывает число?
2. Именованный масштаб
?
в 1 см – 200 м
Как называется число?
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
Как называется число?
- Численный масштаб
1 : 2 000
расстояние на плане (карте), в см
Что показывает число?
2. Именованный масштаб
Именованный масштаб
?
в 1 см – 200 м
Как называется число?
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
Как называется число?
- Численный масштаб
1 : 2 000
Расстояние на местности,
в см
расстояние на плане (карте),
в см
2. Именованный масштаб
?
в 1 см – 200 м
Как называется число?
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
величина уменьшения
- Численный масштаб
1 : 2 000
Расстояние на местности,
в см
расстояние на плане (карте),
в см
2. Именованный масштаб
Именованный масштаб
?
в 1 см – 200 м
Как называется число?
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
величина уменьшение
- Численный масштаб
1 : 2 000
расстояние на местности,
в см
расстояние на плане (карте),
в см
2. Именованный масштаб
в 1 см – 20 м
Как называется число
Масштаб – это отношение длины отрезка на плане (карте ) к длине соответствующего отрезка на местности
величина уменьшение
- Численный масштаб
1 : 2 000
расстояние на местности,
в см
расстояние на плане (карте),
в см
2. Именованный масштаб
в 1 см – 20 м
величина масштаба
При измерении длины кривых линий применяются специальные приборы – курвиметры . Они действуют как счетчики расстояний. По кривым линиям к. устанавливают колесиком на крайнюю точку измеряемого отрезка и катят его строго по измеряемой линии. Замеренное расстояние отсчитывается к. и показывается в см стрелкой на его шкале. Полученное в см расстояние можно перевести по масштабу в м или км.
Они действуют как счетчики расстояний. По кривым линиям к. устанавливают колесиком на крайнюю точку измеряемого отрезка и катят его строго по измеряемой линии. Замеренное расстояние отсчитывается к. и показывается в см стрелкой на его шкале. Полученное в см расстояние можно перевести по масштабу в м или км.
- Переведите линейный масштаб в именованный и численный
1)
2)
3)
4)
- Переведите линейный масштаб в именованный и численный
в 1 см — 100 м 1:10 000
1)
2)
3)
4)
- Переведите линейный масштаб в именованный и численный
в 1 см — 100 м 1:10 000
1)
2)
3)
4)
в 1 см – 250 м 1:25 000
- Переведите линейный масштаб в именованный и численный
в 1 см — 100 м 1:10 000
1)
2)
3)
4)
в 1 см – 250 м 1:25 000
в 1 см – 500 м 1:50 000
- Переведите линейный масштаб в именованный и численный
в 1 см — 100 м 1:10 000
1)
2)
3)
4)
в 1 см – 250 м 1:25 000
в 1 см – 500 м 1:50 000
в 1 см – 1 км 1:100 000
2. Переведите численный масштаб в именованный
Переведите численный масштаб в именованный
1:3 000 000
1)
2)
3)
4)
1:2 000
1:40 000 000
1:500
2. Переведите численный масштаб в именованный
1:3 000 000 в 1 см – 30 км
1)
2)
3)
4)
1:2 000
1:40 000 000
1:500
2. Переведите численный масштаб в именованный
1:3 000 000 в 1 см – 30 км
1)
2)
3)
4)
1:2 000 в 1 см – 20 м
1:40 000 000
1:500
2. Переведите численный масштаб в именованный
1:3 000 000 в 1 см – 30 км
1)
2)
3)
4)
1:2 000 в 1 см – 20 м
1:40 000 000 в 1 см – 400 км
1:500
2. Переведите численный масштаб в именованный
Переведите численный масштаб в именованный
1:3 000 000 в 1 см – 30 км
1)
2)
3)
4)
1:2 000 в 1 см – 20 м
1:40 000 000 в 1 см – 400 км
1:500 в 1 см – 5 м
3. Переведите именованный масштаб в численный
в 1 см – 10 м
1)
2)
3)
4)
в 1 см – 4 км
в 1 см – 70 км
в 1 см – 50 м
3. Переведите именованный масштаб в численный
в 1 см – 10 м 1:1 000
1)
2)
3)
4)
в 1 см – 4 км
в 1 см – 70 км
в 1 см – 50 м
3. Переведите именованный масштаб в численный
в 1 см – 10 м 1:1 000
1)
2)
3)
4)
в 1 см – 4 км 1:400 000
в 1 см – 70 км
в 1 см – 50 м
3. Переведите именованный масштаб в численный
Переведите именованный масштаб в численный
в 1 см – 10 м 1:1 000
1)
2)
3)
4)
в 1 см – 4 км 1:400 000
в 1 см – 70 км 1:7 000 000
в 1 см – 50 м
3. Переведите именованный масштаб в численный
в 1 см – 10 м 1:1 000
1)
2)
3)
4)
в 1 см – 4 км 1:400 000
в 1 см – 70 км 1:7 000 000
в 1 см – 50 м 1:5 000
4. Если численный масштаб карты 1:100 000, то это означает, что:
в 1 см – 100 000 км
1)
2)
3)
4)
в 1 см – 1 км
в 1 см – 1 000 км
в 1 см – 10 км
4. Если численный масштаб карты 1:100 000, то это означает, что:
в 1 см – 100 000 км
1)
2)
3)
4)
в 1 см – 1 км
в 1 см – 1 000 км
в 1 см – 10 км
5. Если именованный масштаб карты в 1 см – 500 к м, то численный масштаб:
Если именованный масштаб карты в 1 см – 500 к м, то численный масштаб:
1:500
1)
2)
3)
4)
1:50 000
1:500 000
1:50 000 000
5. Если именованный масштаб карты в 1 см – 500 к м, то численный масштаб:
1:500
1)
2)
3)
4)
1:50 000
1:500 000
1:50 000 000
6. Наиболее подробно территория изображена на карте масштаба:
1:2 500
1)
2)
3)
4)
1:25 000
1:250 000
1:25 000 000
6. Наиболее подробно территория изображена на карте масштаба:
1:2 500
1)
2)
3)
4)
1:25 000
1:250 000
1:25 000 000
7. Установите соответствие «масштаб – тип карты по масштабу»:
Установите соответствие «масштаб – тип карты по масштабу»:
А.
крупномасштабная
1:250 000
1)
Б.
2)
3)
В.
среднемасштабная
1:60 000
мелкомасштабная
1:7 200 000
7. Установите соответствие «масштаб – тип карты по масштабу»:
А.
крупномасштабная
1:250 000
1)
Б.
2)
3)
В.
среднемасштабная
1:60 000
мелкомасштабная
1:7 200 000
- Численный масштаб 1:10 000.
- Численный масштаб 1:10 000.
- Численный масштаб 1:10 000.
Как называется число 10 000 ?
9. Именованный масштаб «в 1 см – 50 м».
Как называется число 50?
З а д а н и я
1
Перевести именованный масштаб в численный:
2
в 1 см – 10 м
3
Перевести численный масштаб в именованный
в 1 см-50 км
4
1:10 000
Измерить расстояние на карте и вычислить действительное расстояние на местности (по топографической карте)
в 1 см-200 м
5
Учащиеся прошли на север 500 м. Начертите маршрут движения с помощью масштаба в 1 см – 1 км
Начертите маршрут движения с помощью масштаба в 1 см – 1 км
1:750 000
в 1 см-750 км
1:30 000
Чему равна действительная площадь квадрата, который на карте масштаба 1:35 000 000 изображен в виде квадрата стороной в 1 см?
6
1:100 000
Определите масштаб плана, если дорога длиной 5 км на нем имеет длину 20 см.
З а д а н и е
1.
Дробь, показывающая, сколько километров на местности содержится в 1 см на карте, называется:
2.
А) численным масштабом
Если изображение местности имеет масштаб
3.
4.
Если численный масштаб карты 1:25 000, то это значит, что:
А) план
Б) именованным
1:1 000 000, то это
В) линейным
5.
А) в 1 см – 25 000 км
Если именованный масштаб в 1 см – 100 км, это значит, что:
Б) карта
6.
Определите масштаб плана, если на них дорога длиной в 3 км имеет длину 10 см
А) 1:100
Б) в 1 см – 250 м
В) в 1 см -25 км
7.
Б) 1: 10 000 000
А) в 1 см – 5 000 м
В каком масштабе расстояние 30 км соответствует 3 см?
А) 1: 1 000 000
Отрезок длиной 3 см на карте масштаба 1:7 500 000 соответствует расстоянию в
В) 1:100 100
Б) в 1 см – 50 км
- 125 км
- 225 км
- 275 км
- 350 км
В) в 1 см – 500 м
Б) 1: 300 000
В) 1: 1 000 000
В) 1: 30 000 000
Г) 1: 300 000
Задание
8.
Какой масштаб мельче:
9.
Масштаб мелкомасштабной карты — это
10.
- 1: 85 000
- 1: 8 500
- 1: 850 000
- 1: 8 500 000
Масштаб крупномасштабной карты — это
- 1:10 000
- 1:500 000
- 1:250 000
- 1:10 000 000
11.
- 1:1 000 000
- 1:2 000 000
- 1:5 000 000
- 1:200 000
Топографическая карта имеет масштаб
- Крупнее 1:200 000
- 1:200 000-1:10 000 000 включительно
- Мельче 1:1 000 000
- 1:2 000 000 – 1:10 000 000 включительно
Деление карт по масштабу
- Крупномасштабные : в 1см˂2 км Среднемасштабные : в 1 см 2 до 10 км Мелкомасштабные : в 1 см˃10 км
- Крупномасштабные : в 1см˂2 км
- Среднемасштабные : в 1 см 2 до 10 км
- Мелкомасштабные : в 1 см˃10 км
Масштаб на карте в чем измеряется. Масштаб. Измерение расстояний по планам, картам и глобусу. Урок 3
Чтобы измерить расстояние по плану, карте или глобусу, нужно знать, что такое масштаб и уметь им пользоваться. Масштаб – одна из основных математических составляющих любой географической модели Земли, он показывает, во сколько раз уменьшены все расстояния на карте по сравнению с теми же расстояниями на местности.
Если масштабирование не произвести, то никакой бумаги не хватит, чтобы изобразить на ней даже небольшой участок поверхности. На старинных картах размеры и расстояния уменьшены в неодинаковое количество раз, поэтому по ним можно узнать очертания объектов, но не их величину.
Как обозначается масштаб?
Масштаб плана или карты всегда один, но указываться он может тремя разными способами. Способы обозначения масштаба следующие:
- численные;
- именованные;
- графические (линейные и поперечные).
Численный масштаб имеет вид дроби, например 1:1000, числитель которой показывает единицу измерения на карте, а знаменатель – во сколько раз она уменьшена по сравнению с действительным расстоянием, второе число называется величиной масштаба.
Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз.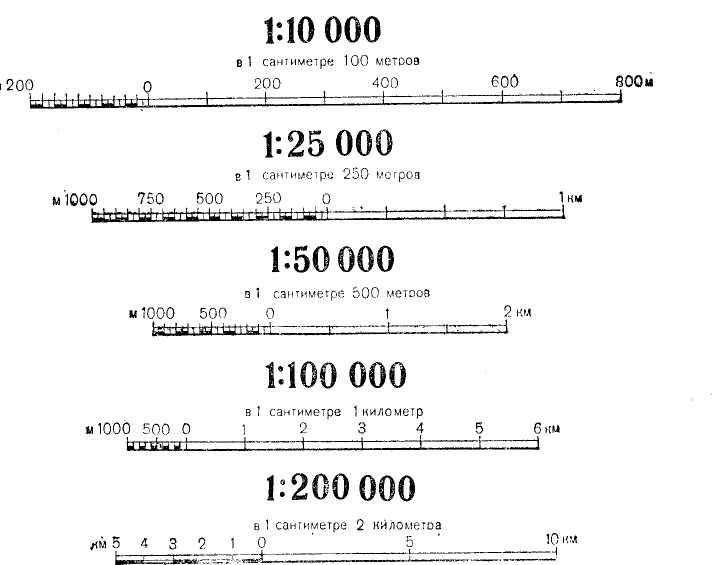 Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так.
Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так.
Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб топографическтй карты
Но, зная математику, мы легко можем перевести сантиметры в метры или километры. Чтобы делать это быстрее, переводя в метры, просто зачёркиваем 2 нуля, так как в 1м – 100 см, а в километры – убираем 5 нулей. Пример: 1:1000 – убираем 2 нуля и получаем 10 метров.
Если масштаб один к ста тысячам, например, тогда уже можно перевести знаменатель и в километры – 1:100 000, для этого уберём 5 нулей, потому что в 1 км 100 000 см.
Получим, что в 1 см на карте 10 км на местности, а это будет уже другой вид масштаба – именованный.
Именованный масштаб указывается на всех картах, он дополняется словами. В 1 см – 10 м, 10 м – это величина масштаба. Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
- 1:25 000 000 – 1см-250 км;
- 1:10 000 000 – 1см-100 км;
- 1:20 000 – 1см-200 м.
При необходимости обратного перевода добавляем те же нули, при переводе километров в сантиметры добавим 5 нулей, метров в сантиметры – 2 нуля. Например:
- 1 см-300 м – это 1:30 000;
- 1см-250 км – это 1:25 000 000.
Для непосредственного определения расстояния по картам и планам служит линейный масштаб. Это график, помещаемый внизу карты в виде линейки (масштабная линейка), в России она разделёна на сантиметры.
Справа от нуля у каждого деления линейки подписано истинное расстояние на местности, равное одному, двум или нескольким величинам масштаба.
Слева от нуля сантиметр линейки разбивают на меньшие деления, например на миллиметры, для получения более точных результатов.
Как измерять расстояние по карте, плану или глобусу?
Измерять расстояния можно при помощи масштаба или градусной сетки (на плане её нет). Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Измерения нужно производить очень точно, учитывая миллиметры. Затем полученные данные умножить на величину масштаба.
Например, если при измерении мы получили расстояние 1,4 см, а масштаб карты в 1см 10 000 км, нужно умножить 1,4 на 10 000, получится 14 000 км – это и есть расстояние на местности.
Нужно знать, что мы узнаём не действительное расстояние, а его проекцию. Линия на карте может иметь разные неточности в связи с углом наклона земной поверхности.
При помощи линейного масштаба измеряют расстояние линейкой или циркулем, переносят это расстояние на масштабную линейку и без дополнительных расчетов получают искомое расстояние. При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Глобус – объёмная модель Земли. Он показывает шарообразную форму нашей планеты. На нём все объекты изображены в неискажённом виде. В отличие от карты, они сохраняют свою форму, площадь, длину.
Направления на глобусе совпадают с направлениями на Земле. У глобуса всюду один и тот же масштаб, который обычно надписывается в южной части Тихого океана. Масштабы школьных глобусов очень мелкие: 1:50 000 000, т. е.
в 1 см – 500 км, истинное расстояние на нём уменьшается в 50 миллионов раз.
Для определения расстояний по глобусу надо ниткой или полоской бумаги измерить расстояние между заданными пунктами и, зная масштаб глобуса, вычислить истинное расстояние с помощью пропорции, как по обычной карте.
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
- мелкомасштабные (обзорные) — с масштабом менее 1: 1 000 000;
- среднемасштабные (обзорно-топографические) – в пределах 1: 200 000 до 1: 1 000 000;
- крупномасштабные (топографические) – от 1: 200 000 до 1: 10 000.
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.
Измерения по топографической карте
Местность на карте всегда изображается в уменьшенном виде. Степень уменьшения местности определяется масштабом карты.
Масштаб показывает во сколько раз длина линии на карте меньше соответствующей ей длины на местности. Масштаб указан – на каждом листе карты под южной (нижней) стороной рамки в числовом и графическом виде.
Масштаб указан – на каждом листе карты под южной (нижней) стороной рамки в числовом и графическом виде.
Численный масштаб обозначается на картах в виде отношения единицы к числу, показывающему, во сколько раз уменьшены длины линий на местности при изображении их на карте.
Пример: масштаб 1:50000 означает, что все линии местности изображены на карте с уменьшением в 50000 раз, т. е. 1 см на карте соответствует 50000 см на местности.
Количество метров (километров) на местности, соответствующее 1 см на карте, называется величиной масштаба. Она указывается на карте под численным масштабом.
Полезно запомнить правило: если в правой части отношения зачеркнуть два последних нуля 1:50000, то оставшееся число покажет, сколько метров на местности содержится в 1 см на карте, т. е. величину масштаба.
При сравнении нескольких масштабов более крупным будет тот , у которого число в правой части отношения меньше. Чем крупнее масштаб карты, тем подробнее и точнее на ней изображена местность.
Линейный масштаб – графическое изображение численного масштаба в виде прямой линии с делениями (в километрах, метрах) для непосредственного отчета расстояний, измеряемых на карте.
Способы измерения расстояний по карте
- Расстояние по карте измеряют, пользуясь численным или линейным масштабом.
- Расстояние на местности равно произведению длины отрезка, измеренного на карте в сантиметрах на величину масштаба.
- Расстояние между точками по прямым или ломаным линиям измеряют обычно при помощи линейки, умножая это значение на величину масштаба.
Пример 1: по карте 1:50000 (СНОВ) измерить длину дороги от мукомольного завода в свх.
Беличи (6511) до пересечения с железной дорогой.
- Длина дроги на карте – 4, 6 см
- Величина масштаба – 500 м
- Длина дороги на местности 4,6х500 = 2300 м
Пример 2: по карте 1:50000 (СНОВ) измерить длину полевой дороги от Воронихи (7419) до моста через реку Губановку (7622). Длина дороги по карте равна 2 см + 1 см + 2, 3 см + 1, 4 см + 0,4 см = 7, 1 см. длина полевой дороги на местности 7, 1 х 500 = 3550 м.
Длина дороги по карте равна 2 см + 1 см + 2, 3 см + 1, 4 см + 0,4 см = 7, 1 см. длина полевой дороги на местности 7, 1 х 500 = 3550 м.
Небольшие прямолинейные участки измеряют, пользуясь линейным масштабом без всяких вычислений. Для этого достаточно отложить циркулем расстояние между заданными точками на карте и, приложив циркуль к линейному масштабу, снять готовый отсчет в метрах или километрах.
- Пример 3: по карте 1:50000 (СНОВ) определить длину озера Камышовое (7412) при помощи линейного масштаба.
- Длина озера – 575 м.
- Пример 4: пользуясь линейным масштабом определить длину реки Воронка от плотины (6717) до впадения в реку Соть.
- Длина реки Воронка – 2175 м.
- Для измерения кривых и извилистых линий используют либо циркуль-измеритель, либо специальный прибор – курвиметр.
- При использовании циркуля – измерителя необходимо установить раствор циркуля, соответствующий целому числу метров (километров), а также соизмеримый с кривизной измеряемой линии.

- Пример 5: по карте 1:50000 (СНОВ) измерить длину участка реки Андога от железнодорожного моста до места впадения Андоги в реку Соть.
- Выбранный раствор циркуля – 0,5 см.
- Количество шагов – 6.
- Остаток – 0,2 см.
- Величина масштаба – 500 м.
- Длина участка реки Андоги на местности (0,5 х 6) х 500 + (0,2 х 500) = 1500 м + 100 м = 1600 м.
Для измерения кривых и извилистых линий используют также специальный прибор – курвиметр. Механизм этого прибора состоит из измерительного колесика, соединенного со стрелкой, которая движется по циферблату. При движении колесика вдоль измеряемой по карте линии стрелка передвигается по циферблату и указывает пройденное колесиком расстояние в сантиметрах.
Для измерения кривых линий курвиметром следует предварительно установить стрелку курвиметра на «0», а затем прокатить его по измеряемой линии, следя за тем, чтобы стрелка курвиметра двигалась по направлению движения часовой стрелки. Умножив показания курвиметра в см на величину масштаба, получают расстояние на местности.
Умножив показания курвиметра в см на величину масштаба, получают расстояние на местности.
- Пример 6: по карте 1:50000 (СНОВ) при помощи курвиметра измерить длину участка железной дороги Мирцевск – Бельцово ограниченного рамкой карты.
- Показания стрелки курвиметра – 33 см
- Величина масштаба – 500 м
- Длина участка железной дороги Мирцевск – Бельцово на местности составляет: 33х500 = 16500 м = 16, 5 км.
- Точность измерения расстояния по карте.
- Точность измерения расстояний по карте зависит от ее масштаба, погрешностей в составлении самой карты, помятости и деформации бумаги, рельефа местности, измерительных приборов, зрения и аккуратности человека.
- Предельная графическая точность в топографии принята 0,5 мм 5% от величины масштаба карты.
Измеренные по карте расстояния получаются всегда несколько короче действительных. Это происходит потому что, по карте измеряются горизонтальные проложения, в то время как соответствующие им линии на местности наклонные, т. е. длиннее своих горизонтальных проложений.
е. длиннее своих горизонтальных проложений.
- Поэтому при расчетов приходится вводить соответствующие поправки на наклон линий.
- Наклон линий — 10° поправка – 2% от длины линии
- Наклон линий — 20° поправка – 6% от длины линии
- Наклон линий — 30° поправка – 15% от длины линии
- Измерение площадей по карте.
Площади объектов чаще всего измеряют подсчетом квадратов координатной сетки. Каждому квадрату сетки карт 1:10000 – 1:50000 на местности соответствует 1 км, 1:100000 – 4 км, 1:200000 – 16 км.
- При измерении больших площадей по карте или аэрофотоснимку применяется геометрический способ, который заключается в измерении линейных элементов участка и последующем вычислении его по формулам.
- Если участок на карте имеет сложную конфигурацию, его делят прямыми линиями на прямоугольники ( (а+в) х 2), треугольника ((ахв) : 2) и вычисляют площади полученных фигур, которые затем суммируют.
- Площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы.

- Площадь радиоактивного заражения местности рассчитывают по формуле для определения площади трапеции:
- P = Ra:2,
- где R – радиус круга заражения, км
- а – хорда, км.
Понятие системы координат
Координатами называются линейные или угловые величины, определяющие положение точки на плоскости или в пространстве.
Системой координат называется совокупность линий и плоскостей, относительно которых определяют положение точек, объектов, целей и т.п.
Существует множество систем координат, которые находят применение в математике, физике, технике, военном деле.
В военной топографии для определения положения точек (объектов, целей) на земной поверхности и на карте применяются географические, плоские прямоугольные и полярные системы координат.
Географическая система координат
В этой системе положение любой точки на наземной поверхности определяется двумя углами – географической широтой и географической долготой, относительно экватора и начального (нулевого меридиана).
Географическая широта (В) – это угол, образованный плоскостью экватора и ответственной линией в данной точке земной поверхности.
Широты отсчитываются по дуге меридиана к северу и к югу от экватора от) 0° на экваторе до 90° у полюсов. В северном полушарии – южные широты.
Географическая долгота (L) – угол, образованный плоскость начального (нулевого) меридиана и плоскостью меридиана, проходящего через данную точку.
За начальный меридиан принят меридиан, проходящий через астрономическую обсерваторию в Гринвиче (около Лондона). Все точки на земном шаре, расположенные к востоку от начального меридиана имеют восточную долготу от 0° до 180° а к западу – западную долготу, также от 0° до 180°. Все точки, лежащие на одном меридиане имеют одинаковою долготу.
Разность долгот двух точек показывает не только их взаимное расположение, но и разницу во времени в этих точках. Каждые 15° по долготе соответствует 1 час, т. к. поворот Земли на 360° совершается на 24 часа.
Таким образом, зная долготу двух пунктов, легко определить разность местного времени в этих пунктах.
- Географическая сетка на топографических картах.
- Линии, соединяющие точки земной поверхности одинаковой широты, называется параллелями.
- Линии, соединяющие точки земной поверхности одинаковой долготы, называются меридианами.
- Параллели и меридианы являются рамками листов топографических карт.
- Нижняя и верхняя стороны рамки являются параллелями, а боковые стороны – меридианами.
Широты и долготы рамки подписываются на углах каждого листа кары (прочитать и показать на карте и плакате). На крупномасштабных и среднемасштабных топографических картах стороны рамок разделены на отрезки, равные одной минуте. Минутные отрезки оттенены через один черной краской и разделены точками на части по 10 секунд.
Кроме того, непосредственно на карте показывается пересечения средних параллелей и меридианов и дается их оцифровка в градусах и минутах, а по внутренней рамке показываются штрихами 2-3 мм выходы минутных делений.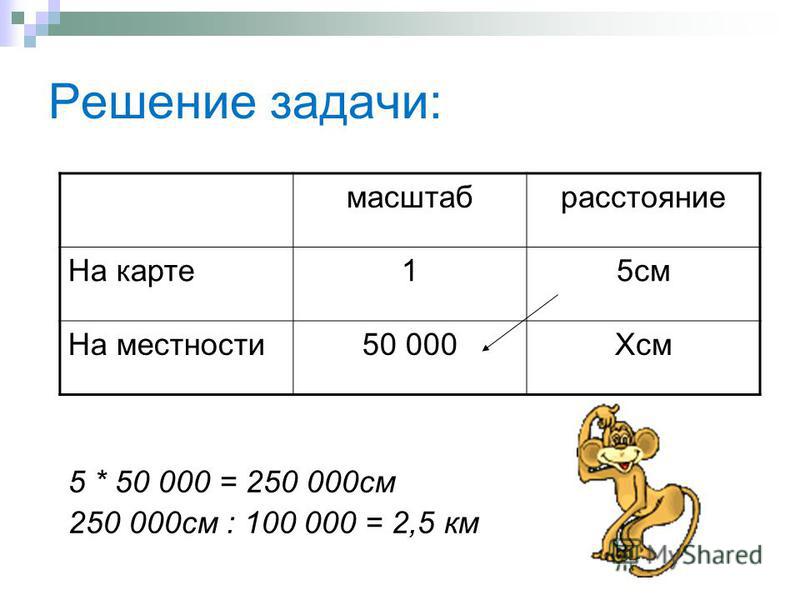
Это позволяет прочерчивать параллели и меридианы на карте, склеенной из нескольких листов.
Чтобы определить географические координаты, какой либо точки по топографической карте, нужно через эту точку провести линии параллели и меридиана. Для чего из этой точки опустить перпендикуляры на нижнюю (верхнюю) и боковую стороны рамки карты. После этого произвести расчеты градусов, минут и секунд по шкалам широт и долгот на сторонах рамки карты.
- Точность определения географических координат по крупномасштабным картам составляет около 2-х секунд.
- Пример: географические координаты условного знака аэродрома (7407) на карте СНОВ будут соответственно:
- B = 54 45’ 23” – северной широты;
- L = 18 00’ 20” – восточной долготы.
Система плоских прямоугольных координат
- Плоскими прямоугольными координатами в топографии называются линейные величины:
- Абсцисса Х,
- Ордината У.

Эти координаты несколько отличаются от принятых в математике декартовых координат на плоскости. За положительное направление осей координат принято для оси абсцисс (осевой меридиан зоны) направление на север, для оси ординат (экватора эллипсоида) на восток.
Оси координат делят шестиградусную зону на четыре четверти, счет которых ведется по ходу часовой стрелки от положительного направления оси абсцисс Х. Положение любой точки, например точки М, определяется кратчайшим расстоянием до осей координат, то есть по перпендикулярам.
Ширина любой координатной зоны составляет на экваторе примерно 670 км, на широте 40 – 510 км, на широте 50 – 430 км. В северном полушарии Земли (I и IV четверти зон) знаки абсцисс положительные. Знак ординаты в IV четверти отрицательный.
Чтобы не иметь отрицательных значений ординат при работе с топографическими картами, в точке начала координат каждой зоны величина ординаты принята равной 500 км, а ордината точки расположенной к западу от осевого меридиана зоны, будет всегда положительной и по абсолютному значению меньше 500 км, а ордината точки, расположенной к востоку от осевого меридиана, будет всегда больше 500 км.
Что такое масштаб карты в географии?
Масштабом называют соотношение настоящих размеров объекта к изображению, модели объекта. Географический масштаб помогает определить, во сколько раз на карте уменьшили все реальные размеры — площадь территории, отдельных объектов, длину рек, дорог и т.д.
В древности масштаба не знали, потому объекты располагали на карте на произвольном расстоянии друг от друга. Пользуясь такой картой, человек не мог определить, будет он добираться до нужного места 2 дня, 2 недели или 2 месяца.
Первым картографом, применившим в составлении карты масштаб, был Анаксимандр Милетский — древнегреческий учёный (VI – V вв. до н. э.), придумавший термин «закон» и предложивший первую формулировку закона сохранения материи.
- В зависимости от масштаба карты условно разделяют на:
- – мелкомасштабные (обзорные) — менее 1:1 000 000;
- – среднемасштабные (обзорно-топографические) — от 1:200 000 до 1:1 000 000;
- – крупномасштабные (топографические) — от 1:10 000 до 1:100 000.

- Масштабы до 1:5 000 используют преимущественно в составлении топографического плана.
- В легендах географических карт используют графический (он же — линейный) и численный масштаб, редко прибегают к именованному.
Масштаб численный
Для его записи применяют дроби, в которых числители — это 1 см (если не оговорено иного), а знаменатели — числа, показывающие, в какое количество раз уменьшен показатель. К примеру, масштаб 1:25 000 демонстрирует, что 1 см карты соответствует 25 000 см (250 м) местности.
Чем меньше знаменатель, тем крупнее масштаб: 1:1000 крупнее, чем 1:5 000, т.к. в первом случае в 1 см карты «умещается» 10 м, а во втором — 50 м. Карты с крупным масштабом подробнее, содержательнее, но использовать их можно для небольших участков местности.
Линейный (графический) масштаб
Линейный, или графический масштаб, особенно удобен и даёт возможность узнавать расстояния, размеры без расчётов и переводов длин из масштабных в реальные. Линейный масштаб выглядит как линейка с делениями — мелкими и крупными, каждое из которых подписано соответствующим метрическим значением.
Линейный масштаб выглядит как линейка с делениями — мелкими и крупными, каждое из которых подписано соответствующим метрическим значением.
Основное деление — это обычно отрезок в 2 см, для которого указан размер масштабирования, например — 100 м, 500 м и т.д. Чтобы воспользоваться графическим масштабом, раствор циркуля, равный измеряемому отрезку, прикладывают к линейке масштаба и тут же узнают расстояние между объектами, длину нужного участка и т.д.
Именованный масштаб
Именованный масштаб отличается от прочих тем, что в нём словами прописано, сколько в 1 см содержится метров или километров. Например: в 1 см — 250 м; в 1 см — 5 км.
Где искать масштаб на карте?
Чтобы узнать масштаб географической карты, нужно посмотреть углы карты или её легенду. Легендой называют список обозначений с их разъяснением.
Очень часто на картах приводятся все 3 вида масштабов, чтобы каждый человек смог разобраться, во сколько раз реальные расстояния уменьшены на карте.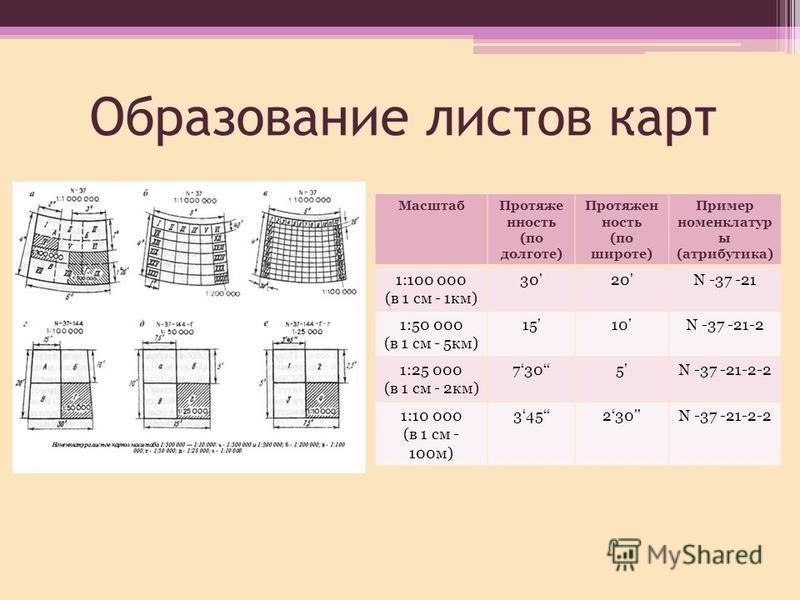
Стандарты численных масштабов
- В Российской Федерации приняты следующие стандарты численного масштаба:
- 1:10 000 1:25 000 1:50 000 1:100 000 1:200 000 1:300 000 1:500 000
- 1:1 000 000
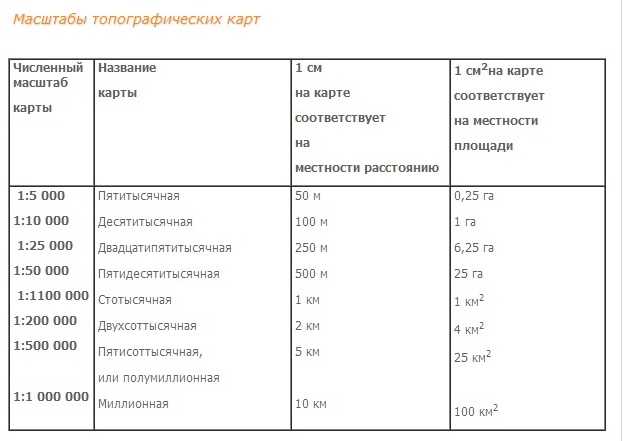
Масштабы топографических карт и планов
- Масштаб карты – это отношение длины отрезка на карте к его действительной длине на местности.
- Масштаб (от немецкого Stab – палка) – это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности.
- Рассмотрим виды масштабов.
Численный масштаб
Это масштаб, выраженный в виде дроби, где числитель – единица, а знаменатель – число, показывающее во сколько раз уменьшено изображение.
Численный масштаб – масштаб, выраженный дробью, в которой:
- числитель равен единице,
- знаменатель равен числу, показывающему во сколько раз уменьшены линейные размеры на карте.
Именованный (словесный) масштаб
- Это вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.

- Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.
- Например, в 1 сантиметре 5 километров (в 1 см 5 км).
Линейный масштаб
Это вспомогательная мерная линейка, наносимая на карты для облегчения измерения расстояний.
Масштаб плана и масштаб карты
Масштаб плана одинаков во всех его точках.
Масштаб карты в каждой точке имеет свое частное значение, зависящее от широты и долготы данной точки. Поэтому его строгой числовой характеристикой является численный масштаб – отношение длины бесконечно малого отрезка Д на карте к длине соответствующего бесконечно малого отрезка на поверхности эллипсоида земного шара.
Однако при практических измерениях на карте используют её главный масштаб.
Формы выражения масштаба
Обозначение масштаба на картах и планах имеет три формы – численный, именованный и линейный масштабы.
Численный масштаб выражают дробью, в которой:
- числитель — единица,
- знаменатель М – число, показывающее, во сколько раз уменьшены размеры на карте или плане (1:М)
В России для топографических карт приняты стандартные численные масштабы
- 1:1 000 000
- 1:500 000
- 1:300 000
- 1:200 000
- 1:100 000
- 1:50 000
- 1:25 000
- 1:10 000
- для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000
- 1:5000
- 1:2000
- 1:1000
- 1:500
- В землеустроительной практике планы землепользований чаще всего составляют в масштабах 1:10 000 и 1:25 000, а иногда — 1:50 000.

- При сравнении различных численных масштабов более мелким является тот, у которого больше знаменатель М, и, наоборот, чем меньше знаменатель М, тем крупнее масштаб плана или карты.
- Так, масштаб 1:10000 крупнее, чем масштаб 1:100000, а масштаб 1:50000 мельче масштаба 1:10000.
- Примечание
- Применяемые в топографических картах масштабы установлены Приказом Министерства экономического развития РФ «Об утверждении требований к государственным топографическим картам и государственным топографическим планам, включая требования к составу сведений, отображаемых на них, к условным обозначениям указанных сведений, требования к точности государственных топографических карт и государственных топографических планов, к формату их представления в электронной форме, требований к содержанию топографических карт, в том числе рельефных карт» (№ 271 от 6 июня 2017 года с изменениями на 11 декабря 2017 года).

Именованный масштаб
Так как длины линий на местности принято измерять в метрах, а на картах и планах в сантиметрах, то масштабы удобно выражать в словесной форме, например:
В одном сантиметре 50 м. Это соответствует численному масштабу 1:5000. Поскольку 1 метр равен 100 сантиметрам, то число метров местности, содержащееся в 1 см карты или плана, легко определяют путём деления знаменателя численного масштаба на 100.
Линейный масштаб
Представляет собой график в виде отрезка прямой, разделенного на равные части с подписанными значениями соразмерных им длин линий местности. Линейный масштаб позволяет без вычислений измерять или строить расстояния на картах и планах.
Точность масштаба
Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0.01 см. Соответствующее ей число метров местности в масштабе карты или плана представляет собой предельную графическую точность данного масштаба.
Поскольку точность масштаба выражает длину горизонтального проложения линии местности в метрах, то для ее определения следует знаменатель численного масштаба разделить на 10 000 (1 м содержит 10 000 отрезков по 0.01 см). Так, для карты масштаба 1:25 000 точность масштаба равна 2.5 м; для карты 1:100 000 — 10 м и т. п.
Масштабы топографических карт
| численный масштаб карты | название карты | 1 см на карте соответствует на местности расстоянию | 1 см2 на карте соответствует на местности площади |
| 1:5 000 | пятитысячная | 50 м | 0.25 га |
| 1:10 000 | десятитысячная | 100 м | 1 га |
| 1:25 000 | двадцатипятитысячная | 250 м | 6.25 га |
| 1:50 000 | пятидесятитысячная | 500 м | 25 га |
| 1:1100 000 | стотысячная | 1 км | 1 км2 |
| 1:200 000 | двухсоттысячная | 2 км | 4 км2 |
| 1:500 000 | пятисоттысячная, или полумиллионная | 5 км | 25 км2 |
| 1:1000000 | мииллионная | 10 км | 100 км2 |
Ниже приведены численные маштабы карт и соответствующие им именованые масштабы:
Масштаб 1:100 000
- 1 мм на карте – 100 м (0.
 1 км) на местности
1 км) на местности - 1 см на карте – 1000 м (1 км) на местности
- 10 см на карте – 10000 м (10 км) на местности
Масштаб 1:10000
- 1 мм на карте – 10 м (0.01 км) на местности
- 1 см на карте – 100 м (0.1 км) на местности
- 10 см на карте – 1000 м (1 км) на местности
Масштаб 1:5000
- 1 мм на карте – 5 м (0.005 км) на местности
- 1 см на карте – 50 м (0.05 км) на местности
- 10 см на карте – 500 м (0.5 км) на местности
Масштаб 1:2000
- 1 мм на карте – 2 м (0.002 км) на местности
- 1 см на карте – 20 м (0.02 км) на местности
- 10 см на карте – 200 м (0.2 км) на местности
Масштаб 1:1000
- 1 мм на карте – 100 см (1 м) на местности
- 1 см на карте – 1000 см (10 м) на местности
- 10 см на карте – 100 м на местности
Масштаб 1:500
- 1 мм на карте – 50 см (0.
 5 м) на местности
5 м) на местности - 1 см на карте – 5 м на местности
- 10 см на карте – 50 м на местности
Масштаб 1:200
- 1 мм на карте – 0,2 м (20 см) на местности
- 1 см на карте – 2 м (200 см) на местности
- 10 см на карте – 20 м (0.2 км) на местности
Масштаб 1:100
- 1 мм на карте – 0,1 м (10 см) на местности
- 1 см на карте – 1 м (100 см) на местности
- 10 см на карте – 10 м (0.01 км) на местности
Пример 1
Переведите численный масштаб карты в именованный:
- 1:200 000
- 1:10 000 000
- 1:25 000
- Решение:
- Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.
- Например, в масштабе 1:500 000 в знаменателе после цифры 5 находится пять нулей.
- Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.

- Пример для масштаба 1:500 000
В знаменателе после цифры – пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.
- Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.
- Если, например, в знаменателе масштаба 1:10 000 закроем два нуля, получим:
- в 1 см – 100 м.
- Ответы:
- в 1 см – 2 км
- в 1 см – 100 км
- в 1 см – 250 м
Используйте линейку, накладывайте на карты для облегчения измерения расстояний.
Пример 2
Переведите именованный масштаб в численный:
- в 1 см – 500 м
- в 1 см – 10 км
- в 1 см – 250 км
- Решение:
- Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.

- Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.
- Например, для именованного масштаба в 1 см – 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1:10 000.
- Для масштаба в 1 см – 5 км приписываем к пятерке пять нулей и получаем: 1:500 000.
- Ответы:
- 1:50 000
- 1:1 000 000
- 1:25 000 000
Типы карт в зависимости от масштабов
Карты в зависимости от масштабов условно подразделяют на следующие типы:
- топографические планы 1:400 – 1:5 000
- крупномасштабные топографические карты 1:10 000 – 1:100 000
- среднемасштабные топографические карты от 1:200 000 – 1:1 000 000
- мелкомасштабные топографические карты менее 1:1 000 000
Топографическая карта
- Топографическими называются такие карты, содержание которых позволяет решать по ним разнообразные технические задачи.

- Карты либо являются результатом непосредственной топографической cъемки местности, либо составляются по имеющимся картографическим материалам.
- Местность на карте изображается в определенном масштабе.
Чем меньше знаменатель численного масштаба, тем крупнее масштаб. Планы составляют в крупных масштабах, а карты – в мелких.
В картах учитывается «шарообразность» земли, а в планах – нет. Из-за этого планы не составляются для территорий площадью свыше 400 км² (то есть участков земли примерно 20 км х 20 км).
- Стандартные масштабы топографических карт
В нашей стране приняты следующие масштабы топографических карт:
- 1:1 000 000
- 1:500 000
- 1:200 000
- 1:100 000
- 1:50 000
- 1:25 000
- 1:10 000
Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.
- Крупномасштабные топографические карты
Карты масштабов:
- 1:10 000 (1см =100 м)
- 1:25 000 (1см = 100 м)
- 1:50 000 (1см = 500 м)
- 1:100 000 (1см =1000 м)
- называются крупномасштабными.

- Топографические карты территории России до масштаба 1:50 000 включительно являются секретными, топографические карты масштаба 1:100 000 — ДСП (для служебного пользования), а мельче – не секретными.
- В настоящее время существует методика создания топографических карт и планов любых масштабов, не имеющих грифа секретности и предназначенных для открытого пользования.
Сказка про карту в масштабе 1:1
Жил-был Капризный Король. Однажды он объехал своё королевство и увидел, как велика и прекрасна его земля. Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них.
И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.
Однако, Капризный Король остался недоволен. Он хотел видеть на карте не только очертания горных цепей, но и изображение каждой горной вершины. Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.
Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.
Картографы вновь принялись за работу, трудились много лет и нарисовали другую карту, размером в два раза больше предыдущей. Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.
Капризный Король умер, так и не дождавшись окончания работы. Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.
Наконец картографы нарисовали Невероятную карту! Она изображала всё королевство в мельчайших подробностях — и была точно такого же размера, как само королевство. Теперь уже никто не мог найти различия между картой и королевством.
Где же собирались хранить Капризные Короли свою замечательную карту? Ларца для такой карты не хватит. Понадобится огромное помещение вроде ангара, и в нем карта будет лежать во много слоев. Только нужна ли такая карта? Ведь карта в натуральную величину может быть с успехом заменена самой местностью ))))
Полезно ознакомиться и с этим
- Ознакомиться с используемыми в России единицами измерения площадей земельных участков можно здесь.
- Для тех, кого интересует возможность увеличения площади земельных участков для ИЖС, ЛПХ, садоводства, огродничества, находящихся в собственности, полезно ознакомиться с порядком оформления прирезок.
- С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 г.

- С 1 марта 2015 года вступил в силу новый Федеральный закон «О внесении изменений в Земельный кодекс РФ и отдельные законодательные акты РФ» (N 171-ФЗ от 23.06.2014 г.), в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов. Ознакомиться с основными положениями закона можно здесь.
- В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия.
Лекция 2
Лекция 2 Лекция 2Весы
Точная геометрическая связь между картой и регионом, который она изображает.— одна из важнейших характеристик современной карты.
— Большинство карт значительно уменьшены в размерах по сравнению с их предметами, поэтому масштаб является небольшой долей.
Определение: Отношение размера карты к ее тематике:
Масштаб = расстояние на карте / расстояние на местности
Пример:
— Две точки на земле находятся на расстоянии 1000 м друг от друга.
— Представлено на карте точками, отстоящими друг от друга только на 1 см
— Рассчитайте масштаб следующим образом:
— 1 см соответствует 1000 м
— 1000 м = 100 000 см
— таким образом, 1 см соответствует 100 000 см
— таким образом, масштаб = 1 см / 100 000 см = 1/100 000
— Шкала представляет собой дробь, выраженную тремя способами:
— Репрезентативная дробь (RF) , например. 1:100,000
— Вербальная шкала «Один см соответствует одному километру»
— Графическая шкала — линия, помеченная расстоянием, которое она представляет.
Графический масштаб остается точным при увеличении или уменьшении карты. Вербальные и RF весы не имеют.
В графическом масштабе интервалы должны быть удобными круглыми числами.
Примеры весов
пример: расстояние до земли = 5 км, расстояние до карты = 2 см.— ЭТАП 1: — 2 см соответствует 5 км — (запишите полностью)
— ЭТАП 2: — 1 см соответствует 2,5 км — (разделите так, чтобы левая часть = 1)
— ЭТАП 3: — 1 см соответствует 250 000 см — ( преобразовать в те же единицы)
— ШАГ 4: — масштаб 1 : 250 000 — (выразить в виде репрезентативной дроби)
пример: расстояние по карте = 3,5 см, масштаб карты = 1:15 000
— какое реальное расстояние?
— ШАГ 1: — 1 см соответствует 15 000 см — (укажите масштаб прописью, в тех же единицах, что и ваши измерения)
— ШАГ 2: — 3,5 см соответствует (3,5 x 15 000) см = 52 500 см — (умножьте обе стороны на расстояние по карте )
— ШАГ 3: — 3,5 см соответствует 525 м — (перевести в более удобные единицы измерения)
ответ: 525 м
Масштаб (2)
Большие и малые масштабы:— Масштаб представляет собой дробь.

— 1/2 больше, чем 1/4.
— 1/5000 больше, чем 1/100 000.
— масштаб 1:5000 больше, чем 1:100 000.
— «Крупный масштаб» зависит от контекста, но обычно относится к масштабам более 1:50 000.
(ПРИМЕЧАНИЕ — это не имеет ничего общего с выражением типа «большая стройка»)
Увеличение или уменьшение:
— Масштаб представляет собой расстояние по карте / расстояние по земле.
— При увеличении карты (на ксероксе и т.д.) расстояние карты увеличивается, соответственно меняется масштаб.
— Большая карта = больший масштаб, меньшая карта = меньший масштаб.
— Умножьте расстояние карты на процентное изменение и пересчитайте масштаб.
пример: Расстояние до карты = 1 см, Расстояние до земли = 1 км.
— Масштаб = 1:100 000
— Увеличить на 141% на копировальной машине.
— Расстояние до карты = 1,41 см Расстояние до земли = 1 км
— Масштаб = 1,41/100 000 = 1:70 921
Направления
Три основных способа выразить направление.
1. Стрелки компаса
— Пригодны для приблизительных указаний, а не для точной работы.
— Направления обычно лежат между точками компаса, однако часто вы их подразделяете.
2. Азимут (числовая версия № 1)
— ШАГ 1: Посмотрите строго на север, если интересующая вас точка находится совсем к северу от вас. Смотри строго на юг, если он южнее тебя.
— ШАГ 2: Повернитесь на восток или запад, пока не окажетесь лицом к точке.
— ШАГ 3: Измерьте угол этого поворота.
— ШАГ 4: Выразите пеленг, используя все три элемента информации из шагов 1, 2 и 3:
— Север 30 o Запад
— Север 45 o Восток
— Юг 12 o Запад
— Юг 87 o Восток
3. Азимут
— ШАГ 1: Посмотрите на север.
— ШАГ 2: Поверните по часовой стрелке, пока не окажетесь лицом к интересующей вас точке.
— Шаг 3: Измерьте угол поворота. Этот угол является СЕВЕРНЫМ АЗИМУТОМ, обычно просто называемым азимутом:
— 330 градусов
— 45 градусов
— 192 градуса
— 93 градуса
Уметь конвертировать пеленги и азимуты!
Добавление углов
Полезно при съемке и навигации.
— Помните: 60′ = 1 o 60″ = 1′
— 35 o 22′ 40″ + 5 o 15′ 30″ = 40 o 38′ 10″
0 Определение северной широты
0
Три общих подхода: 1. Истинный север (по координатной сетке широта — долгота).
— Указывает точно на северный географический полюс (ось вращения).
2. Магнитный Север (направление указывает стрелка компаса).
— Точки вдоль силовых линий магнитного поля, примерно в направлении северного магнитного полюса (в СЗТ).
— отличается от истинного севера в большинстве мест, потому что магнитный и географический полюсы не совпадают.
— Изменяется со временем по мере дрейфа магнитного полюса.
— Положение магнитного севера необходимо пересчитывать, если карте больше нескольких лет.
— Скорость изменения напечатана на краю карты.
пример:
— «Магнитный север находился на 7 o 30 футов к западу от истинного севера в 1985 году, ежегодно уменьшаясь на 12 футов».
— таким образом, в 1992 году, через семь лет:
— Магнитный север будет равен 7 o 30′ к западу от истинного севера, МИНУС 7 умножить на 12′ = 84′
— 84′ = 1 o 24′
— таким образом, в 1992 году магнитный север находится на 6 o 6′ к западу от истинного севера
3. Северная сетка (относится к сетке UTM).
— то же, что и истинный север в центре каждой шестиградусной зоны UTM.
— Изменения в каждую сторону, потому что квадратная сетка не соответствует схождению меридианов к полюсу.
— На большинстве топографических карт три севера показаны на полях.
— Некоторые карты показывают только один север. Если это не ИСТИННЫЙ север, он ДОЛЖЕН быть идентифицирован.
Лекция: Масштаб карт, доктор Родриг
Лекция: Масштаб карт, доктор Родриг
III. Масштаб карты — это понятие, относящееся к тому факту, что карты представляют собой
области, которые они представляют (ну, я полагаю, вы могли бы нанести на карту что-то под
микроскоп, и в этот момент карта будет расширением области, которую она
представляет собой). Они должны сказать вам, насколько они уменьшают землю, так что вы
может делать такие вещи, как измерение расстояния и интерпретация относительного размера. "Шкала"
это индекс редукции, который дает вам эту информацию. Есть
три основных способа сделать это.
A. Графическая шкала или линейчатая шкала. Это просто линия, отмеченная в
километров или миль, так что вы можете просто использовать линейку или любой другой
линейка для измерения реального расстояния между любыми двумя
места на карте.
1. Эти шкалы могут быть даны в километрах или милях или
комбинация двух, как вы видите здесь.
2. Приятной особенностью графических масштабов является то, что их можно уменьшать или уменьшать.
увеличены и по-прежнему сохраняют свое пропорциональное значение. Все остальные
Типы шкал должны быть переделаны, если вы планируете уменьшить или увеличить
карта.
3. Возможны два недостатка:
а.
Они должны сказать вам, насколько они уменьшают землю, так что вы
может делать такие вещи, как измерение расстояния и интерпретация относительного размера. "Шкала"
это индекс редукции, который дает вам эту информацию. Есть
три основных способа сделать это.
A. Графическая шкала или линейчатая шкала. Это просто линия, отмеченная в
километров или миль, так что вы можете просто использовать линейку или любой другой
линейка для измерения реального расстояния между любыми двумя
места на карте.
1. Эти шкалы могут быть даны в километрах или милях или
комбинация двух, как вы видите здесь.
2. Приятной особенностью графических масштабов является то, что их можно уменьшать или уменьшать.
увеличены и по-прежнему сохраняют свое пропорциональное значение. Все остальные
Типы шкал должны быть переделаны, если вы планируете уменьшить или увеличить
карта.
3. Возможны два недостатка:
а. Как и в случае с любой шкалой, вы должны доверять ее точности только в
центр карты и рассматривать его только как приближение вокруг
края, особенно на картах, на которых изображены большие территории.
б. Шкала может быть привязана к культуре в том смысле, что если вы только
укажите масштаб в милях, большая часть остального мира не будет
возможность использовать вашу карту без большого количества дополнительных вычислений.
Точно так же, если вы предоставляете только километры, большинство американцев
чем тем, кто занимается науками, будет трудно прочитать его без
много дополнительной работы. Будьте вежливы и предоставьте и то, и другое.
B. Вербальная шкала или заявленная шкала. Один дюйм равен одной миле или 1
сантиметр равен одному километру или что-то в этом роде. Опять же, вы бы использовали линейку
для оценки различий в реальном мире.
1.
Как и в случае с любой шкалой, вы должны доверять ее точности только в
центр карты и рассматривать его только как приближение вокруг
края, особенно на картах, на которых изображены большие территории.
б. Шкала может быть привязана к культуре в том смысле, что если вы только
укажите масштаб в милях, большая часть остального мира не будет
возможность использовать вашу карту без большого количества дополнительных вычислений.
Точно так же, если вы предоставляете только километры, большинство американцев
чем тем, кто занимается науками, будет трудно прочитать его без
много дополнительной работы. Будьте вежливы и предоставьте и то, и другое.
B. Вербальная шкала или заявленная шкала. Один дюйм равен одной миле или 1
сантиметр равен одному километру или что-то в этом роде. Опять же, вы бы использовали линейку
для оценки различий в реальном мире.
1. Преимущество этого в том, что большинству людей легко
ОПРЕДЕЛЕННАЯ культура его использования.
2. Одним из недостатков является то, что это действительно сложно перевести на
другая числовая культура (каким-то образом 2,5 см = 1,6 км не соответствует
сделайте это для меня, и 0,4" = 0,6 мили).
3. Еще один небольшой недостаток заключается в том, что для его использования вам понадобится настоящая линейка:
Вы не можете просто отметить лист бумаги на графической шкале
прямо тогда и там.
4. Один БОЛЬШОЙ недостаток заключается в том, что вам придется пересчитывать и переформулировать его, если
вы увеличиваете или уменьшаете карту.
C. Репрезентативная фракция или коэффициент карты показывает масштаб как фракцию или
соотношение, в котором числитель всегда равен единице. Примеры были бы
1:500 000, или 1/100 000, или 1/63 360, или 1:62 500. знаменатель
обозначает количество ОДИНАКОВЫХ ЕДИНИЦ (например, сантиметров или дюймов)
что карта показывает в реальном мире.
Преимущество этого в том, что большинству людей легко
ОПРЕДЕЛЕННАЯ культура его использования.
2. Одним из недостатков является то, что это действительно сложно перевести на
другая числовая культура (каким-то образом 2,5 см = 1,6 км не соответствует
сделайте это для меня, и 0,4" = 0,6 мили).
3. Еще один небольшой недостаток заключается в том, что для его использования вам понадобится настоящая линейка:
Вы не можете просто отметить лист бумаги на графической шкале
прямо тогда и там.
4. Один БОЛЬШОЙ недостаток заключается в том, что вам придется пересчитывать и переформулировать его, если
вы увеличиваете или уменьшаете карту.
C. Репрезентативная фракция или коэффициент карты показывает масштаб как фракцию или
соотношение, в котором числитель всегда равен единице. Примеры были бы
1:500 000, или 1/100 000, или 1/63 360, или 1:62 500. знаменатель
обозначает количество ОДИНАКОВЫХ ЕДИНИЦ (например, сантиметров или дюймов)
что карта показывает в реальном мире. Таким образом, 1:100 000 будет означать один
дюйм на карте равен 100 000 дюймов в реальном мире (около
1,6 мили). В равной степени это означало бы, что один сантиметр на карте равен
100 000 сантиметров в реальном мире (1 км).
1. Таким образом, каждый может прочитать вашу карту в любом измерении
система, с которой им комфортно. Все счастливы.
2. Как и вербальная шкала, репрезентативная дробь должна быть
пересчитывается каждый раз, когда вы увеличиваете или уменьшаете карту.
3. Самый большой недостаток в том, что трудно представить, о, 125 000
дюймов или 125 000 сантиметров. Мы должны преобразовать его из
изящные единицы сантиметров и дюймов в более крупные
единицы, которые мы используем в путешествии: километры и мили. Так что вы
нужно сделать небольшое разделение, чтобы сделать их разумными для вас
а. В метрической системе 100 000 см/км, так что просто разделите
знаменатель на 100 000.
Таким образом, 1:100 000 будет означать один
дюйм на карте равен 100 000 дюймов в реальном мире (около
1,6 мили). В равной степени это означало бы, что один сантиметр на карте равен
100 000 сантиметров в реальном мире (1 км).
1. Таким образом, каждый может прочитать вашу карту в любом измерении
система, с которой им комфортно. Все счастливы.
2. Как и вербальная шкала, репрезентативная дробь должна быть
пересчитывается каждый раз, когда вы увеличиваете или уменьшаете карту.
3. Самый большой недостаток в том, что трудно представить, о, 125 000
дюймов или 125 000 сантиметров. Мы должны преобразовать его из
изящные единицы сантиметров и дюймов в более крупные
единицы, которые мы используем в путешествии: километры и мили. Так что вы
нужно сделать небольшое разделение, чтобы сделать их разумными для вас
а. В метрической системе 100 000 см/км, так что просто разделите
знаменатель на 100 000. я. 1:500 000 это 1 см = 5 км
II. 1:250 000 это 1 см=2,5 км
III. 1:125 000 это 1 см = 1,25 км
IV. 1:100 000 это 1 см=1 км
v. 1:62 500 1 см = 0,625 км
ви. Здесь вы можете понять, почему ученым нравится эта метрика.
система -- простое деление (мы ленивые)!
б. Большинство американцев используют английскую систему, хотя английская
отказался от него ради удовольствия владеть нулевым меридианом и
хоть американцы и англичан в Революцию хлестали
что породили США и ото всех оторвались
виды других англицизмов (например, то, как они пишут такие вещи, как
«честь», «защита» и «среди»). В английской системе один
миля, уххххх, сколько футов? Хммммм. Это тяжело.
Кто-нибудь знает навскидку? Я никогда не помню этого сам, и я
на самом деле пришлось искать его для этой лекции
я. 1:500 000 это 1 см = 5 км
II. 1:250 000 это 1 см=2,5 км
III. 1:125 000 это 1 см = 1,25 км
IV. 1:100 000 это 1 см=1 км
v. 1:62 500 1 см = 0,625 км
ви. Здесь вы можете понять, почему ученым нравится эта метрика.
система -- простое деление (мы ленивые)!
б. Большинство американцев используют английскую систему, хотя английская
отказался от него ради удовольствия владеть нулевым меридианом и
хоть американцы и англичан в Революцию хлестали
что породили США и ото всех оторвались
виды других англицизмов (например, то, как они пишут такие вещи, как
«честь», «защита» и «среди»). В английской системе один
миля, уххххх, сколько футов? Хммммм. Это тяжело.
Кто-нибудь знает навскидку? Я никогда не помню этого сам, и я
на самом деле пришлось искать его для этой лекции . Одна миля составляет 5280 футов. Почему 5280? Нажмите здесь, чтобы
узнайте, если вы болезненно любопытны. Итак, сколько дюймов
там в ногу? Двенадцать. Итак, сколько дюймов в
миля? Двенадцать умножить на 5 280 (вы сидите?) 63 360. Ага,
одна миля составляет 63 360 дюймов. Итак, просто разделите знаменатель на
63 360. Кусок пирога!!! 1:500,000, тогда будет, посмотрим,
500 000/63 360 = 7,8914 миль. О, ЭТО хорошее круглое число
мы все можем ярко представить, верно? Нет. Итак, Соединенные Штаты,
чтобы сделать английскую систему немного более управляемой в Геологической службе США
карты, выдумки немного. В целях использования карт Геологической службы США вы
предположим, что одна миля равна 62 500 дюймам. Почему? Потому что
это как бы близко к реальному числу 63 360 и проще
разделить на эти знаменатели.
Одна миля составляет 5280 футов. Почему 5280? Нажмите здесь, чтобы
узнайте, если вы болезненно любопытны. Итак, сколько дюймов
там в ногу? Двенадцать. Итак, сколько дюймов в
миля? Двенадцать умножить на 5 280 (вы сидите?) 63 360. Ага,
одна миля составляет 63 360 дюймов. Итак, просто разделите знаменатель на
63 360. Кусок пирога!!! 1:500,000, тогда будет, посмотрим,
500 000/63 360 = 7,8914 миль. О, ЭТО хорошее круглое число
мы все можем ярко представить, верно? Нет. Итак, Соединенные Штаты,
чтобы сделать английскую систему немного более управляемой в Геологической службе США
карты, выдумки немного. В целях использования карт Геологической службы США вы
предположим, что одна миля равна 62 500 дюймам. Почему? Потому что
это как бы близко к реальному числу 63 360 и проще
разделить на эти знаменатели. Итак, 1:500,000 теперь включает
500 000/62 500. Итак, 1 дюйм «равняется» 8 милям.
я. 1:500,000 это 1 дюйм = 8 миль.
II. 1:250 000 — это 1 дюйм = 4 мили.
III. 1:125 000 — это 1 дюйм = 2 мили.
IV. 1:100 000 — это 1 дюйм = 1,6 мили.
v. 1:62 500 - это 1 дюйм = 1 миля.
ви. 1:63 360 также 1 дюйм = 1 миля.
vii. Теперь вы понимаете, почему американские ученые так возмущены тем, что
большинство американцев не хотят переходить на метрическую систему, несмотря на США
подписание Метрического договора еще в 1875 году, несмотря на то, что Томас
Джефферсон и Джон Куинси Адамс призывают новые США
учитывать достоинства французской системы, несмотря на американскую.
Конгресс разрешил США перейти на метрическую систему в 1866 году, несмотря на
Конгресс США (снова) принимает Закон о преобразовании метрических единиц
из 1975 о создании надзорного органа «для координации
добровольный переход на метрическую систему», и, несмотря на
экономические и торговые издержки нашего отказа от участия в
международная (и простая в использовании) система, которую страна
сам помог разработать!!! Эээээ!! Извините, я думаю, что
восстановил мое самообладание.
Итак, 1:500,000 теперь включает
500 000/62 500. Итак, 1 дюйм «равняется» 8 милям.
я. 1:500,000 это 1 дюйм = 8 миль.
II. 1:250 000 — это 1 дюйм = 4 мили.
III. 1:125 000 — это 1 дюйм = 2 мили.
IV. 1:100 000 — это 1 дюйм = 1,6 мили.
v. 1:62 500 - это 1 дюйм = 1 миля.
ви. 1:63 360 также 1 дюйм = 1 миля.
vii. Теперь вы понимаете, почему американские ученые так возмущены тем, что
большинство американцев не хотят переходить на метрическую систему, несмотря на США
подписание Метрического договора еще в 1875 году, несмотря на то, что Томас
Джефферсон и Джон Куинси Адамс призывают новые США
учитывать достоинства французской системы, несмотря на американскую.
Конгресс разрешил США перейти на метрическую систему в 1866 году, несмотря на
Конгресс США (снова) принимает Закон о преобразовании метрических единиц
из 1975 о создании надзорного органа «для координации
добровольный переход на метрическую систему», и, несмотря на
экономические и торговые издержки нашего отказа от участия в
международная (и простая в использовании) система, которую страна
сам помог разработать!!! Эээээ!! Извините, я думаю, что
восстановил мое самообладание. ... (конец разглагольствования на данный момент).
D. Очень запутанной концепцией является понятие крупного масштаба и малого масштаба.
карты. Здесь действительно нужно сосредоточиться.
1. Крупномасштабная карта — это карта, которая показывает большое количество деталей о
небольшая площадь. Другими словами, его репрезентативная фракция представляет собой большую
число (что означает, что оно имеет относительно небольшой знаменатель). Есть
все это? Просто помните: крупный масштаб означает большую ДЕТАЛИ.
2. Мелкомасштабная карта — это карта, которая показывает небольшое количество деталей о
большая площадь. Его репрезентативная часть представляет собой небольшое число
(что математически означает, что у него большой знаменатель). Запомнить:
Малый масштаб соответствует небольшому количеству деталей.
3. Итак, какая карта крупнее? 1:10 000 или 1:100 000? (первый
один)
4.
... (конец разглагольствования на данный момент).
D. Очень запутанной концепцией является понятие крупного масштаба и малого масштаба.
карты. Здесь действительно нужно сосредоточиться.
1. Крупномасштабная карта — это карта, которая показывает большое количество деталей о
небольшая площадь. Другими словами, его репрезентативная фракция представляет собой большую
число (что означает, что оно имеет относительно небольшой знаменатель). Есть
все это? Просто помните: крупный масштаб означает большую ДЕТАЛИ.
2. Мелкомасштабная карта — это карта, которая показывает небольшое количество деталей о
большая площадь. Его репрезентативная часть представляет собой небольшое число
(что математически означает, что у него большой знаменатель). Запомнить:
Малый масштаб соответствует небольшому количеству деталей.
3. Итак, какая карта крупнее? 1:10 000 или 1:100 000? (первый
один)
4. Какая карта меньшего масштаба? 1:250 000 или
1:1 000 000 000? (второй)
5. Какая карта будет крупнее? Тот, который показывает все
мир или тот, который показывает только Калифорнию? (Калифорния)
E. Если вы хотите узнать больше об этих вопросах, вы можете посетить:
Интерпретация карты
Конверсия: показатели
Следующая лекция будет посвящена символизации карт.
Какая карта меньшего масштаба? 1:250 000 или
1:1 000 000 000? (второй)
5. Какая карта будет крупнее? Тот, который показывает все
мир или тот, который показывает только Калифорнию? (Калифорния)
E. Если вы хотите узнать больше об этих вопросах, вы можете посетить:
Интерпретация карты
Конверсия: показатели
Следующая лекция будет посвящена символизации карт.
Документ и © поддерживаются Dr.
Родриг
Первое размещение в сети: 16.09.00
Последняя редакция: 08.06.07
сантиметров в километры конвертировать
Выберите тип преобразования:
сантиметры => километры-километры => сантиметры
Варианты округления:
1 знак после запятой2 знака после запятой3 знака после запятой4 знака после запятой5 знаков после запятой6 знаков после запятой7 знаков после запятой8 знаков после запятой9 знаков после запятой10 знаков после запятой
Перевести километры в сантиметры (км в см)
▶
Таблица преобразования
см
в километры см км 10000 0. 1
1 20000 0.2 30000 9 0.202 40000 0.4 50000 0.5 60000 0.6 70000 0.7 80000 0.8 0.9 100000 1 110000 1. 1
1 120000 1.2 40203 1.3 140000 1.4 150000 1.5 160000 1.6 170000 1.7 180000 1.8 1 1.9 200000 2
Как преобразовать
1 сантиметр (см) = 0,00001 километр (км). Сантиметр (см) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе. Сантиметры также можно обозначить как сантиметров .
Сантиметр (см) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе. Сантиметры также можно обозначить как сантиметров .
Километр
— Единица измерения расстояния/длины Обозначение/сокращение единицы измерения: км
Где единица измерения используется в мире:
Километр используется как единица измерения расстояний или длин.
Это стандартная мера пройденных расстояний, географических расстояний и карт в большинстве стран, за исключением США и Великобритании, где для этой цели до сих пор используется миля.
между географическими точками на суше, и в большинстве стран является официальной единицей для этой цели. Основными исключениями являются Соединенное Королевство, Либерия, Мьянма и Соединенные Штаты Америки, где миля остается стандартной частью имперской системы.
Определение единицы измерения:
Километр (километр в британском написании) — единица длины/расстояния в метрической системе (система единиц СИ), эквивалентная одной тысяче метров.
1 км эквивалентен 0,62137 мили.
История подразделения:
Хотя метр был определен в 1799 году во Франции, километр был впервые принят для повседневного использования голландцами в 1817 году под местным названием mijl. Мириаметры (10 000 метров) и «lieues de Poste» (почтовые лиги, 4 288 метров) предпочитались «километру» для повседневного использования во Франции в 1919 году.век. В середине 19 века километр уже использовался в повседневном использовании в Италии и Нидерландах, а мириаметр все еще использовался во Франции.
CIPM (Международный комитет мер и весов) официально отменил приставку «мириа-» и «мириаметр» в 1935 году, оставив километр в качестве признанной единицы длины вместо мириаметра.
Где используется:
Километр обычно используется на дорожных знаках для обозначения расстояния до определенного места, на картах для обозначения масштаба, для обозначения одометра в автомобильной промышленности. Это также самая популярная единица для описания расстояния между географическими точками и местами.
Эквиваленты в других единицах и масштабах:
- 1 км = 1000000 миллиметров (мм)
- 1 км = 100 000 сантиметров (см)
- 1 км = 10000 дециметров (дм)
- 1 км = 1000 метров (м)
- 1 км = 3280,84 фута (фута)
- 1 мегаметр = 1000 км
- 1 гигаметр = 1000000 км
- Единицы длины в метрической системе СИ основаны на кратных или долях метра.
- Существуют измерения длины/расстояния в метрической системе СИ, превышающие километр, которые могут быть выражены в километрах.
1 км эквивалентен 0,621371 мили.
Километр является единицей длины в метрической системе СИ и равен одной тысяче метров.
Испанский Русский французский
[PDF] Масштаб и расстояние на картах
1 Масштаб и расстояние на картах В этом разделе объясняется, как использовать и преобразовывать различные типы масштабов. Также обсуждается ч…
Также обсуждается ч…
Масштаб и расстояние на картах В этом разделе объясняется, как использовать и преобразовывать различные типы масштабов. Также обсуждается, как измерять расстояния на картах. К концу этого раздела вы должны уметь:
Измерять кривые и прямые расстояния
Использовать масштаб для преобразования расстояний на карте в реальные расстояния
Преобразовывать (изменять) один масштаб в другой.
Топографические карты показывают искусственные объекты, такие как дома, дороги, железные дороги, ветряные мельницы и т. д., а также природные объекты, такие как реки и горы.
Часть топографической карты района Огонго масштаба 1:50 000
Давайте навестим моего дядю в Сельскохозяйственном колледже.
Можем ли мы пройти пешком от Ошитутума до колледжа?
Не знаю, давайте посмотрим на нашу карту. Он имеет масштаб масштаба 1:50 000. На карте от Ошитутума до колледжа около 7 см. Формула: расстояние карты × масштаб, поэтому 7 см × 50 000 см равно 350 000 см. Теперь мы должны разделить 350 000 см на 100 000 см, чтобы перевести расстояние в километры. Таким образом, реальное расстояние составляет 350 000 ÷ 100 000 = 3,5 км. Да, мы сможем дойти до колледжа пешком.
Формула: расстояние карты × масштаб, поэтому 7 см × 50 000 см равно 350 000 см. Теперь мы должны разделить 350 000 см на 100 000 см, чтобы перевести расстояние в километры. Таким образом, реальное расстояние составляет 350 000 ÷ 100 000 = 3,5 км. Да, мы сможем дойти до колледжа пешком.
В словесной шкале могут использоваться разные единицы измерения, например, если 1 см равен 0,5 км, то 1 мм равен 0,05 км.
Рубен и Сельма используют топографическую карту, чтобы найти дорогу в колледж. Чтобы определить, каким будет реальное расстояние, они должны уметь пользоваться масштабом карты. Они также должны знать, как измерять расстояния на карте.
Масштаб карты Масштаб карты показывает соотношение между расстоянием на карте и соответствующим расстоянием на поверхности земли. Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы. 1
Масштабы слова
Если 1 см на карте соответствует 50 000 см в действительности, то 1 см также соответствует 0,5 км.
2
Шкалы пропорций
Если масштаб пропорций 1:50 000, то 1 см равен 50 000 см. Вот примеры других шкал отношений: 1:2 000 000 1:4 000
Чтобы преобразовать шкалу слов в шкалу отношений, вы должны следовать двум правилам: 1
Шкала отношений всегда должна начинаться с 1.
2
Размеры до и после двоеточия (:) должны быть в одних и тех же единицах измерения. Например, чтобы преобразовать масштаб слова 4 см в 2 км, необходимо применить оба правила. Поэтому вы должны сначала преобразовать 2 км в см (2 × 100 000 = 200 000), а затем разделить 4 на 4 (=1). Помните, что вы также должны разделить 200 000 на 4 (= 50 000). Таким образом, масштаб соотношения составляет 1:50 000.
3
Линейная шкала
Линейная шкала состоит из линии, разделенной на основные единицы, со второстепенными единицами слева от 0. Помните, что основные единицы слева от 0 должны быть точно такого же размера или длина в качестве основных единиц справа от 0.
Приведенный выше пример линейного масштаба означает, что 1 см на карте равен 1 км на местности. Изучите следующие два примера и попытайтесь преобразовать их в словесные шкалы. Не беспокойтесь, если вы не можете этого сделать. Мы объясним больше о преобразованиях масштаба позже. 2 см = 3 км или 1 см = 1,5 км
Следующие шаги помогут вам нарисовать линейную шкалу. Они используются в приведенном ниже примере, чтобы показать вам, как вы рисуете линейную шкалу. Пример: Нарисуйте линейную шкалу с основными и дополнительными единицами, где 2 см равняется 100 м. Шаг 1: Начертите линейную шкалу (линию)… __________________________________(начертите линию любой длины)
Шаг 2: где 2 см…(разделите линию на 2 см)
Шаг 3: равно 100 м
(каждые 2 см равняется 100 м) Шаг 4: Разделите единицы слева от 0 на более мелкие второстепенные единицы по вашему выбору.
Как преобразовать масштабы Один тип масштаба может быть преобразован в другой тип масштаба. Посмотрите на пример ниже, чтобы увидеть, как это сделать. Пример:
Пример:
Преобразовать в:
Словесный масштаб: 1 см соответствует 0,5 км
Коэффициентный масштаб:
Линейный:
Словесный масштаб: 1 см соответствует 1 км
Чтобы иметь возможность преобразовать один масштаб в другой масштаб или один единицы в другую, необходимо знать следующее:
Есть:
Для перевода из: 1 000 000 мм в 1 км
мм в км вас ÷ на 1 000 000
100 000 cm в 1 км
cm в км вас ÷ на 100 000
1 000 м в 1 км см в 1 м
см в м you ÷ на 100
1 000 мм в 1 м
мм в m you ÷ на 1 000
Измерение расстояния На карте расстояния можно измерять двумя способами: по прямой линии или по кривой линии. Вдоль прямой линии Чтобы измерить прямую линию, просто используйте линейку. Например, показанное здесь расстояние от А до В равно 5,6 см.
1
По кривой линии
Для измерения кривой вам понадобится лист бумаги с прямым краем. Шаг 1: Поместите полоску бумаги прямым краем на первую прямую часть дороги или изогнутую линию. Отметьте точку B на полосе в ее начале и сделайте еще одну отметку (b) там, где дорога начинает изгибаться от бумажной полосы.
Отметьте точку B на полосе в ее начале и сделайте еще одну отметку (b) там, где дорога начинает изгибаться от бумажной полосы.
Шаг 2: Удерживая отметку (b) прочно закрепленной, поверните прямой край бумажной полоски, пока он не пройдет по следующему прямому участку дороги. Теперь отметьте (c), где дорога снова изгибается (вверх или вниз) от бумажной полоски.
Шаг 3: Продолжайте вращать бумажную полоску и отмечать части на полоске, пока все изогнутое расстояние от B до Намутони не будет отмечено на полоске бумаги.
Шаг 4: Положите бумажную полоску на линейку и прочтите расстояние от B до Намутони, как показано ниже. Определите реальное расстояние, используя предоставленные масштабы карты. .
Вычисление расстояния с использованием различных масштабов Если вы умеете пользоваться масштабами карты, вы сможете легко вычислить реальное расстояние между местами.
Карта имеет соотношение и линейный масштаб. Чтобы использовать шкалу отношения, вы должны понимать следующую формулу: Масштаб отношения = Расстояние на карте × масштаб (если перевести из см в км) 100 000 Давайте измерим расстояние, пройденное самолетом между Могадишо в Сомали и Найроби в Кении, используя нашу формула. Расстояние карты = 1,5 см × масштаб карты = 1,5 см × 60 000 000 см = 90 000 000 см ÷ 100 000 (для преобразования в км) = 900 км
Расстояние карты = 1,5 см × масштаб карты = 1,5 см × 60 000 000 см = 90 000 000 см ÷ 100 000 (для преобразования в км) = 900 км
Чтобы использовать линейный масштаб, вы должны понимать, как читать расстояние на этот тип шкалы. Он позволяет измерять реальное расстояние между точками на карте. Воспользуйтесь линейкой и измерьте расстояние от Виндхука до Луанды на карте Африки (рис. 1.5). Расстояние 2,7 см. Теперь поместите линейку на линейную шкалу так, чтобы отметка 2,7 см на линейке находилась непосредственно под отметкой 1 200 км на линейной шкале (между 2 и 3 см). Теперь изучите рисунок 1.6. Пункт А — Виндхук, Б — Луанда. Точка А лежит где-то в второстепенных единицах слева от 0 (нуля). Возьмите показание от 0 на линейной шкале до точки B. Сделайте то же самое от 0 на линейной шкале до точки A и сложите два показания (расстояния). Ответ даст вам расстояние в км (километрах) между Виндхуком и Луандой. От нуля до В
= 1200 км
От нуля до А
= 450 км
Виндхук до Луанды = 1650 км
Итоги урока • Каждая карта имеет шкалу, показывающую соотношение между расстоянием на карте и таким же расстоянием в реальности. жизнь. • Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы, причем одна шкала может быть преобразована в другую. •Расстояние на карте можно измерять по прямой линии между двумя точками или по кривой линии, например, по дороге. Масштаб затем используется для преобразования расстояния на карте в реальное расстояние в метрах или километрах.
жизнь. • Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы, причем одна шкала может быть преобразована в другую. •Расстояние на карте можно измерять по прямой линии между двумя точками или по кривой линии, например, по дороге. Масштаб затем используется для преобразования расстояния на карте в реальное расстояние в метрах или километрах.
5.2 Масштаб карты | NWCG
5.2 Масштаб карты | СЗКГ Перейти к основному содержанию
View Navigation
Масштаб карты печатается в легенде карты. Он дается как отношение дюймов на карте к дюймам, футам или милям на земле. Например, масштаб карты, показывающий соотношение 1:24 000 (дюйм/дюйм), означает, что на каждый дюйм карты приходится 24 000 дюймов земли. Наземные расстояния на картах обычно указываются в футах или милях.
Map Scale Conversion Factors
Scale Representative Fraction Map in/mi Map in/ch map ft/in 1:253,440 253. 44
44 0.25 0.0031 21,120 1:126,720 126.72 0.50 0.0063 10,560 1:63,360 63.36 1.00 0.0125 5,280 1:62,500 62.50 1.01 0.0127 5,208 1:31,680 31.68 2 0.025 2,640 1:24,000 24.00 2.64 0.033 2,000 1:21,120 21.12 3 0.038 1,760 1:15,840 15.84 4 0.05 1,320 1:7,920 7.92 8 0.1 660
Table 5.1. Коэффициенты преобразования масштаба карты
Пример 1. Преобразование масштаба карты 1:24 000 (дюйм/дюйм) в (дюйм/фут).
Шаг 1. Настройте таблицу отмены, чтобы все единицы измерения отменялись, кроме нужной единицы, фут/дюйм.
На карте 1 дюйм равен 2000 футов на земле, 1:2000 (дюйм/фут).
Пример 2. Преобразование 1:2 000 (дюйм/фут) в (дюйм/миля).
Шаг 1. Настройте таблицу отмены так, чтобы все единицы измерения отменялись, кроме нужной единицы, мили/дюйм.
На карте 1 дюйм равен 0,4 мили.
Пример 3a. Расстояние на карте между двумя точками составляет 6 дюймов. Масштаб карты 1:24 000 (дюйм/дюйм). Какое расстояние до земли в футах?
Настройте таблицу отмены так, чтобы все единицы измерения отменялись, кроме нужной единицы, футов.
Расстояние до земли составляет 12 000 футов.
Использование модифицированной сетки площади (прозрачность)
для использования прозрачности сетки площади, следуйте этим шагам:
Масля Акров на квадратный дюйм Коэффициент преобразования, равный каждой точке 1:20,000 3. 168
168 63.769 1.736 Acres 1:24,000 2.640 91.827 2.500 Acres 1:62,500 1.014 622.449 16.946 Acres Таблица 5.2 Таблица 5.2 Таблица 5.2- Поместите прозрачную сетку площади в акрах на измеряемую площадь.
- Подсчитайте точки внутри нарисованной области. Подсчитайте каждую вторую точку, когда точки попадают на граничную линию.
- Умножьте общее количество точек на коэффициент преобразования в масштабе карты, чтобы определить общую площадь. (См. Таблицу 5.2.)
- Пример 3b – Используя информацию из примера 3a, найдите расстояние по земле в цепях, милях и дюймах.
Шаг 1. Настройте таблицу отмены, чтобы все единицы, кроме нужной единицы, отменяли цепочки.
12 000 футов = 182 цепи
Шаг 2. Настройте таблицу отмены так, чтобы все единицы измерения, кроме нужной единицы, миль, были отменены.
Шаг 3. Настройте таблицу отмены так, чтобы все единицы измерения исключались, кроме требуемой единицы измерения, дюймов.
12 000 футов = 182 цепи = 2,3 мили = 144 000 дюймов
Иногда на карте может не быть масштаба. Масштаб можно рассчитать, зная расстояние между двумя точками на карте и измерив расстояние на карте. Кроме того, если на карте есть линии сечения, расстояние между линиями сечения обычно составляет 1 милю.
Пример 4. Расстояние между точками A и B на карте составляет 6 дюймов. Известное расстояние до земли составляет 3600 футов. Какой масштаб в дюймах/футах?
Масштаб карты 1:600 дюймов/фут.
Пример 5. Используйте масштаб карты из примера 6. Известное наземное расстояние между точками B и C составляет 1/2 мили. Скольким дюймам соответствует это расстояние на карте?
масштаб карты = известное расстояние / измеренное расстояние
Переставьте члены, умножив каждую сторону на измеренное расстояние и разделив каждую сторону на карту 9Масштаб 0004.
измеренное расстояние = известное расстояние / масштаб карты
Шаг 1. Настройте таблицу отмены так, чтобы все единицы измерения отменялись, кроме нужной единицы, футов. Шаг 2. Используйте масштаб карты из примера 6, чтобы найти расстояние по карте.
измеренное расстояние = известное расстояние
масштаб карты
измеренное расстояние = 2640 футов 1 дюйм = 4,4 дюйма
600 футов
На земле половина мили соответствует 4,4 дюймам на карте.
0
1
2
3
4
5
6
7
8
9
Часть B: Роль соотношения (45 минут)
В этой части
- Соотношение и масштаб
- Постоянные отношения
- Использование теоремы Пифагора
Соотношение и масштаб
Измерение — это процесс количественной оценки свойств объекта путем сравнения их с некоторыми стандартными единицами измерения. Таким образом, мера есть отношение. Когда мы утверждаем, что объект имеет длину 8 дюймов, это сравнивается с единицей измерения 1 дюйм. Точно так же заявление о том, что мешок сахара весит 5 фунтов, подразумевает, что 5 фунтов сравниваются с единицей измерения 1 фунт. ., хотя мы и не указываем это явно.
Таким образом, мера есть отношение. Когда мы утверждаем, что объект имеет длину 8 дюймов, это сравнивается с единицей измерения 1 дюйм. Точно так же заявление о том, что мешок сахара весит 5 фунтов, подразумевает, что 5 фунтов сравниваются с единицей измерения 1 фунт. ., хотя мы и не указываем это явно.
Мы используем пропорциональные рассуждения другими способами в ситуациях измерения. Например, все мы знакомы с масштабами карт. Если 1 см на карте соответствует расстоянию в 250 км, каково приблизительное расстояние длины, представленной 2,7 см? Мы можем составить пропорцию, чтобы показать, что расстояние равно 675 км:
1 см = 2,7 см
250 км x км
Решая уравнение относительно x, получаем x = 250 • 2,7 = 675 км.
Одна единица измерения на чертеже в масштабе соответствует n единицам измерения в действительности. Единицы могут быть любыми — сантиметры, метры и т. д. На самом деле, это даже не обязательно должны быть одни и те же единицы; в приведенном выше примере использовались сантиметры и километры. В этой шкале могли использоваться те же единицы измерения (1 см на карте соответствует определенному количеству сантиметров в действительности), но преобразование сантиметров в километры упрощает задачу для пользователя.
В этой шкале могли использоваться те же единицы измерения (1 см на карте соответствует определенному количеству сантиметров в действительности), но преобразование сантиметров в километры упрощает задачу для пользователя.
Задача B1
Масштаб 1 см:250 км сравнивает сантиметры с километрами. Перепишите шкалу, чтобы показать такое же отношение при сравнении сантиметров к сантиметрам (1 см:х см или просто 1:х).
Помните, что 1 км = 1000 м, а 1 м = 100 см.
Чертежи и модели в масштабе — это еще один способ использования соотношения в измерениях. Обычно шкала сравнивает линейные меры. Изучите чертежи в масштабе ниже. Масштаб 1:1 подразумевает, что рисунок кузнечика такой же, как реальный объект. Масштаб 1:2 подразумевает, что рисунок меньше (половина размера), чем реальный объект (иными словами, размеры умножаются на коэффициент масштабирования 0,5). Масштаб 2:1 предполагает, что рисунок больше реального кузнечика — в два раза длиннее и в два раза выше (мы говорим, что размеры умножены на коэффициент масштабирования, равный 2). Если в шкале не указаны единицы, то можно считать, что чертеж и объект измеряются в одних и тех же единицах. Например, масштаб 1:2 может представлять 1 см:2 см или 1 дюйм:2 дюйма 9.0010
Если в шкале не указаны единицы, то можно считать, что чертеж и объект измеряются в одних и тех же единицах. Например, масштаб 1:2 может представлять 1 см:2 см или 1 дюйм:2 дюйма 9.0010
Задача B2
На стене нарисована собака. Увеличенная собака была 45 футов в высоту. Если средний рост этой породы собак составляет 3 фута, каков масштабный коэффициент этого увеличения? Можете ли вы выразить эту шкалу более чем одним способом?
Задача B3
Представьте, что вам нужно нарисовать себя (стоящим), чтобы полностью поместиться на 8,5 на 11 дюймов. лист бумаги. Определите масштабный коэффициент, допускающий не более дюйма границы вверху и внизу страницы. Как долго ваши руки будут на рисунке? Note 8
Попробуйте масштаб 1:10 (т. е. ваш рисунок будет в десять раз меньше вашего фактического размера) или 1:8. Измерьте различные части тела, такие как длина головы, рук, туловища и ног, а затем используйте соотношение, чтобы определить размер этой части тела на рисунке.
Чертежи в масштабе особенно полезны при сравнении относительных величин очень больших объектов. В музеях науки часто есть масштабная модель нашей Солнечной системы, чтобы помочь нам понять огромные расстояния между Солнцем и каждой планетой. Представьте, что вам нужно спроектировать модель солнечной системы для своей школы.
Ниже приведена таблица с некоторыми важными данными. Обратите внимание, что расстояние от Солнца указано в экспоненциальной записи:
.
Диаметр (в км)
Расстояние от Солнца в научных обозначениях (в км)
Вс 1 392 000 Меркурий 4 900 5,8 • 10 7 Венера 12 100 1,08 • 10 8 Земля 12 760 1,5 • 10 8 Марс 6 790 2,28 • 10 8 Юпитер 143 000 7,78 • 10 8 Сатурн 121 000 1,43 • 10 9 Уран 51 000 2,87 • 10 9 Нептун 50 000 4,5 • 10 9 Плутон 2 300 5,9 • 10 9
Продолжайте: Проблема B4
а.
Какой масштаб вы бы использовали, если бы хотели показать учащимся, насколько далеко планеты от Солнца? б. Какой масштаб вы бы использовали, если бы хотели помочь учащимся понять разницу в диаметре планет? Можно ли использовать одну и ту же шкалу для обеих целей? Примечание 9
Иди дальше Проблема B5
Научный парк в Вестерборке, Голландия, использует масштаб 1:3,7 • 10 9 для масштабной модели Солнечной системы. Как вы думаете, какие юниты решили использовать в парке?
Постоянные отношения
Отношение играет важную роль в измерениях и может использоваться для прогнозирования. Если отношение дюймов к сантиметрам составляет 1 к 2,54 (1:2,54), то мы можем считать, что длина 12 дюймов составляет примерно 30 см (30,48).
Однако не все соотношения в природе постоянны. По словам математика Эрнеста Зебровски-младшего, «большинство соотношений на самом деле непостоянны. Если, например, потребовалось 24 гребца, чтобы грести на галере со скоростью 15 миль/ч, это не означает, что 48 гребцов разогнали бы лодку до 30 миль/ч и что при 144 гребцах лодка достигла бы 90 миль/ч. (На самом деле, эта цепочка рассуждений предполагает, что древние могли преодолеть звуковой барьер, просто собрав достаточное количество гребцов.) …. Хотя для бухгалтера или математика несложно утверждать, что конкретное отношение является постоянным, законы природы являются окончательным арбитром. Очевидно, что прежде чем делать прогнозы на основе предполагаемого постоянного соотношения, нам нужно, чтобы кто-то проверил реальность ситуации».
По словам математика Эрнеста Зебровски-младшего, «большинство соотношений на самом деле непостоянны. Если, например, потребовалось 24 гребца, чтобы грести на галере со скоростью 15 миль/ч, это не означает, что 48 гребцов разогнали бы лодку до 30 миль/ч и что при 144 гребцах лодка достигла бы 90 миль/ч. (На самом деле, эта цепочка рассуждений предполагает, что древние могли преодолеть звуковой барьер, просто собрав достаточное количество гребцов.) …. Хотя для бухгалтера или математика несложно утверждать, что конкретное отношение является постоянным, законы природы являются окончательным арбитром. Очевидно, что прежде чем делать прогнозы на основе предполагаемого постоянного соотношения, нам нужно, чтобы кто-то проверил реальность ситуации».
В то время как Зебровски утверждает, что многие отношения непостоянны, в ситуациях измерения обнаруживаются некоторые постоянные отношения. Одно постоянное отношение, которое мы регулярно используем, — это π. Мы подробнее рассмотрим это соотношение на занятии 7, посвященном кругам.
Другая распространенная ситуация измерения связана с прямоугольными треугольниками. Теперь мы более внимательно рассмотрим прямоугольные треугольники, начав с нескольких прямоугольных треугольников разных размеров.
Задача B6
Распечатайте фигуры из файла PDF (обязательно распечатайте этот документ в полном масштабе). Сантиметровой линейкой измерьте гипотенузы этих треугольников. Мы исследуем, существует ли константа пропорциональности.
Заполните таблицу. (Обратите внимание, что это все равнобедренные прямоугольные треугольники.):
Длина гипотенузы (H) в см
Соотношение S:S
Соотношение В:Ш
1 2 3 4 5 6
Проблема B7
а.
Какие постоянные отношения вы нашли в равнобедренных прямоугольных треугольниках (45°-45°-90°)? б. Иногда вы не можете измерить что-то напрямую (например, с помощью линейки), но вы все равно можете определить его меру. Меры, найденные косвенно с помощью математики, часто называют «производными» мерами. Например, если мы знаем длины катетов равнобедренного прямоугольного треугольника, как мы можем определить меру его гипотенузы?
Использование теоремы Пифагора
Помните, что теорема Пифагора утверждает, что в прямоугольных треугольниках с длинами катетов a и b и длиной гипотенузы c выполняется следующее соотношение: a 2 + b 2 = c 2 . Примечание 10 Когда вы используете теорему Пифагора, ваш ответ может быть нелегко сократить от радикальной формы (как квадратный корень). Вместо того, чтобы использовать калькулятор для извлечения квадратного корня, вы можете вместо этого выразить ответ в сокращенной радикальной форме. Вот как: Выразите число как произведение множителей, где один из множителей (если возможно) является квадратным числом. Затем возьмите квадратный корень только из квадратного числа и оставьте ответ как произведение квадратного корня и радикала:
Вот как: Выразите число как произведение множителей, где один из множителей (если возможно) является квадратным числом. Затем возьмите квадратный корень только из квадратного числа и оставьте ответ как произведение квадратного корня и радикала:
Задача B8
- Используйте теорему Пифагора, чтобы найти длины гипотенуз для всех треугольников из задачи B6. Оставив длину в радикальной форме, заполните пустые столбцы в таблице ниже. Сделайте это на бумаге, распечатав эту страницу, если на вашем компьютере невозможно ввести символ квадратного корня. Обратите внимание на закономерности в соотношении H:S.
Длина сторон (S) в см
Длина гипотенузы (H) в см
Соотношение S:S
Отношение Пифагора H:S
1 1:1 2 2:2 3 3:3 4 4:4 5 5:5 6 6:6
- Какие измерения точнее — линейкой или по теореме Пифагора? Объяснять.

Задача B9
В большинстве прямоугольных треугольников одно или несколько значений длины стороны иррациональны. Примечание 11
С точки зрения измерения, каковы последствия того, что одно или несколько значений являются иррациональными?
Примечания
Примечание 8
Если вы работаете в группе, работайте в парах над Задачей B3. Попрактикуйтесь в настройке пропорций (два соотношения, которые равны друг другу), чтобы определить длину различных частей тела на вашем рисунке.
Примечание 9
Решение этой проблемы может занять некоторое время, особенно если вы пытаетесь использовать одну шкалу как для диаметра планет, так и для их расстояний от Солнца. Часто создаются модели, которые фокусируются на одном или другом (размер или расстояние). Если вы выберете масштаб, позволяющий расстоянию от Солнца поместиться в большую комнату, вы обнаружите, что модели некоторых планет очень и очень малы. Если вы выберете масштаб, позволяющий модели планет быть достаточно большими, чтобы вы могли их наблюдать, вы обнаружите, что расстояния между планетами в модели должны быть очень большими.
Если вы выберете масштаб, позволяющий модели планет быть достаточно большими, чтобы вы могли их наблюдать, вы обнаружите, что расстояния между планетами в модели должны быть очень большими.
ПРИМЕЧАНИЕ 10
, чтобы узнать больше о теореме Пифагора, перейдите к Обучение Математика: Геометрия, Сессия 6.
Примечание 11
Примечание
. потому что его нельзя выразить в виде дроби a/b, где a и b — целые числа, а b — 0. Другими словами, это значение нельзя записать в виде дроби или повторяющегося или завершающего десятичного числа. Если бы мы выразили его в виде десятичного числа, оно имело бы бесконечное количество цифр справа от десятичной точки в неповторяющемся шаблоне. Система действительных чисел состоит из бесконечного числа рациональных чисел (тех, которые соответствуют указанному выше свойству дроби) и бесконечного числа иррациональных чисел. Есть много ситуаций, когда длина на самом деле является иррациональным числом (например, гипотенузы равнобедренных прямоугольных треугольников), поэтому мы не можем точно измерить длину. Идея о том, что мера всегда является приблизительной величиной, трудно понять, поскольку в повседневной жизни мы обращаемся с мерами как с точными величинами.
Есть много ситуаций, когда длина на самом деле является иррациональным числом (например, гипотенузы равнобедренных прямоугольных треугольников), поэтому мы не можем точно измерить длину. Идея о том, что мера всегда является приблизительной величиной, трудно понять, поскольку в повседневной жизни мы обращаемся с мерами как с точными величинами.
Решения
Задача B1
Поскольку 1 км = 100 000 см, масштаб 1 см:250 км эквивалентен 1 см:250 • 100 000 см, или 1:25 000 000.
Задача B2
Масштабный коэффициент 45:3. Его можно упростить до 15:1 или выразить другими способами, например, 7,5:0,5 или 150:10.
Задача B3
Ответы будут разными. Вот один пример: предположим, что кто-то ростом ровно 6 футов, с руками 3 фута в длину. Масштабный коэффициент будет 9дюймов: 6 футов, чтобы оставить 1 дюйм границы сверху и снизу. Чтобы упростить это, помните, что 6 футов = 72 дюйма. Масштабный коэффициент может быть выражен как 9:72 или 1:8. Руки этого человека были бы на 1/8 длиннее на чертеже в масштабе; 1/8 от 3 футов (36 дюймов) равно 4,5 дюйма
Масштабный коэффициент может быть выражен как 9:72 или 1:8. Руки этого человека были бы на 1/8 длиннее на чертеже в масштабе; 1/8 от 3 футов (36 дюймов) равно 4,5 дюйма
Задача B4
- Самая дальняя планета от Солнца, Плутон, имеет среднее расстояние от Солнца около 5,9 млрд км. Для размещения на школьной территории (скажем, в пределах 100 м) потребуется масштабный коэффициент 100 м: 5,9.00 000 000 км. Поскольку 1 км = 1000 м, коэффициент масштаба может быть выражен как 100 м: 5 900 000 000 000 000 м, или 1 м: 59 млрд. М:
100 м 1 • 10 2 м 1 5,9 • 10 9 км = 5,9 • 10 • 10 12 км = 5,9 • 10 10 м - Этот масштаб был бы безнадежно большим для визуализации разницы в размерах диаметров между планетами, поскольку самый большой диаметр (Юпитера) составляет всего около 143 000 км. В масштабе 1 м: 59 миллиардов м диаметр Юпитера составляет примерно 2,4 мм, что очень мало.
 Лучший масштаб может быть 1 м: 590 миллионов м, что составляет диаметр Юпитера примерно 24 см. Самая маленькая планета, Плутон, будет иметь диаметр 3,8 мм в этом масштабе, что все еще мало, но, безусловно, заметно.
Лучший масштаб может быть 1 м: 590 миллионов м, что составляет диаметр Юпитера примерно 24 см. Самая маленькая планета, Плутон, будет иметь диаметр 3,8 мм в этом масштабе, что все еще мало, но, безусловно, заметно.
Проблема B5
Скорее всего, выбрали мили. Наибольшее расстояние от Солнца, 5,9 • 10 9 , становится равным 1,6 км. Это чуть меньше одной мили, поэтому масштаб, вероятно, был выбран таким, чтобы вся модель уместилась в пределах одной мили. Используя этот масштаб, наименьший фрагмент данных (диаметр Плутона) становится равным 0,62 мм, что очень мало, но все же заметно.
Задача B6
Ответы могут различаться в зависимости от измерений. Здесь ответы даны с точностью до десятых долей сантиметра:
Длина сторон (S) в см
Длина гипотенузы (H) в см
Соотношение S:S
Соотношение В:Ш
1 1,4
1:1
1,4:1
2 2,8
2:2
2,8:2
3 4,2
3:3
4,2:3
4 5,7
4:4
5,7:4
5 7. 1
1
5:5
7,1:5
6 8,5
6:6
8,5:6
Задача B7
- Неудивительно, что отношение сторон постоянно и равно 1:1, поскольку мы работали исключительно с равнобедренными прямоугольными треугольниками. Отношения между гипотенузой и катетом также кажутся примерно одинаковыми (это становится очевидным, если разделить отношения H:S и записать их в виде десятичных дробей). Так что здесь тоже может быть постоянное соотношение. Все наблюдения находятся между 1,4 и 1,425, поэтому постоянное отношение (если оно есть) может находиться между этими значениями.
- Мы могли бы умножить длину стороны на 1,41 (среднее отношение), чтобы получить приблизительный ответ. Мы также можем использовать теорему Пифагора (описанную в следующем разделе), чтобы вывести меру гипотенузы.

Проблема B8
Длина сторон (S) в см
Длина гипотенузы (H) в см
Соотношение S:S
Отношение Пифагора H:S
1 √2 1:1 √2:1 2 2√2 2:2 2√2:2 3 3√2 3:3 3√2:3 4 4√2 4:4 4√2:4 5 5√2 5:5 5√2:5 6 6√2 6:6 6√2:6
б.
— Указывает точно на северный географический полюс (ось вращения).
— Точки вдоль силовых линий магнитного поля, примерно в направлении северного магнитного полюса (в СЗТ).
— отличается от истинного севера в большинстве мест, потому что магнитный и географический полюсы не совпадают.
— Изменяется со временем по мере дрейфа магнитного полюса.
— Положение магнитного севера необходимо пересчитывать, если карте больше нескольких лет.
— Скорость изменения напечатана на краю карты.
— «Магнитный север находился на 7 o 30 футов к западу от истинного севера в 1985 году, ежегодно уменьшаясь на 12 футов».

— таким образом, в 1992 году, через семь лет:
— Магнитный север будет равен 7 o 30′ к западу от истинного севера, МИНУС 7 умножить на 12′ = 84′
— 84′ = 1 o 24′
— таким образом, в 1992 году магнитный север находится на 6 o 6′ к западу от истинного севера
— то же, что и истинный север в центре каждой шестиградусной зоны UTM.
— Изменения в каждую сторону, потому что квадратная сетка не соответствует схождению меридианов к полюсу.
— На большинстве топографических карт три севера показаны на полях.
— Некоторые карты показывают только один север. Если это не ИСТИННЫЙ север, он ДОЛЖЕН быть идентифицирован.
 Они должны сказать вам, насколько они уменьшают землю, так что вы
может делать такие вещи, как измерение расстояния и интерпретация относительного размера. "Шкала"
это индекс редукции, который дает вам эту информацию. Есть
три основных способа сделать это.
A. Графическая шкала или линейчатая шкала. Это просто линия, отмеченная в
километров или миль, так что вы можете просто использовать линейку или любой другой
линейка для измерения реального расстояния между любыми двумя
места на карте.
1. Эти шкалы могут быть даны в километрах или милях или
комбинация двух, как вы видите здесь.
2. Приятной особенностью графических масштабов является то, что их можно уменьшать или уменьшать.
увеличены и по-прежнему сохраняют свое пропорциональное значение. Все остальные
Типы шкал должны быть переделаны, если вы планируете уменьшить или увеличить
карта.
3. Возможны два недостатка:
а.
Они должны сказать вам, насколько они уменьшают землю, так что вы
может делать такие вещи, как измерение расстояния и интерпретация относительного размера. "Шкала"
это индекс редукции, который дает вам эту информацию. Есть
три основных способа сделать это.
A. Графическая шкала или линейчатая шкала. Это просто линия, отмеченная в
километров или миль, так что вы можете просто использовать линейку или любой другой
линейка для измерения реального расстояния между любыми двумя
места на карте.
1. Эти шкалы могут быть даны в километрах или милях или
комбинация двух, как вы видите здесь.
2. Приятной особенностью графических масштабов является то, что их можно уменьшать или уменьшать.
увеличены и по-прежнему сохраняют свое пропорциональное значение. Все остальные
Типы шкал должны быть переделаны, если вы планируете уменьшить или увеличить
карта.
3. Возможны два недостатка:
а. Как и в случае с любой шкалой, вы должны доверять ее точности только в
центр карты и рассматривать его только как приближение вокруг
края, особенно на картах, на которых изображены большие территории.
б. Шкала может быть привязана к культуре в том смысле, что если вы только
укажите масштаб в милях, большая часть остального мира не будет
возможность использовать вашу карту без большого количества дополнительных вычислений.
Точно так же, если вы предоставляете только километры, большинство американцев
чем тем, кто занимается науками, будет трудно прочитать его без
много дополнительной работы. Будьте вежливы и предоставьте и то, и другое.
B. Вербальная шкала или заявленная шкала. Один дюйм равен одной миле или 1
сантиметр равен одному километру или что-то в этом роде. Опять же, вы бы использовали линейку
для оценки различий в реальном мире.
1.
Как и в случае с любой шкалой, вы должны доверять ее точности только в
центр карты и рассматривать его только как приближение вокруг
края, особенно на картах, на которых изображены большие территории.
б. Шкала может быть привязана к культуре в том смысле, что если вы только
укажите масштаб в милях, большая часть остального мира не будет
возможность использовать вашу карту без большого количества дополнительных вычислений.
Точно так же, если вы предоставляете только километры, большинство американцев
чем тем, кто занимается науками, будет трудно прочитать его без
много дополнительной работы. Будьте вежливы и предоставьте и то, и другое.
B. Вербальная шкала или заявленная шкала. Один дюйм равен одной миле или 1
сантиметр равен одному километру или что-то в этом роде. Опять же, вы бы использовали линейку
для оценки различий в реальном мире.
1. Преимущество этого в том, что большинству людей легко
ОПРЕДЕЛЕННАЯ культура его использования.
2. Одним из недостатков является то, что это действительно сложно перевести на
другая числовая культура (каким-то образом 2,5 см = 1,6 км не соответствует
сделайте это для меня, и 0,4" = 0,6 мили).
3. Еще один небольшой недостаток заключается в том, что для его использования вам понадобится настоящая линейка:
Вы не можете просто отметить лист бумаги на графической шкале
прямо тогда и там.
4. Один БОЛЬШОЙ недостаток заключается в том, что вам придется пересчитывать и переформулировать его, если
вы увеличиваете или уменьшаете карту.
C. Репрезентативная фракция или коэффициент карты показывает масштаб как фракцию или
соотношение, в котором числитель всегда равен единице. Примеры были бы
1:500 000, или 1/100 000, или 1/63 360, или 1:62 500. знаменатель
обозначает количество ОДИНАКОВЫХ ЕДИНИЦ (например, сантиметров или дюймов)
что карта показывает в реальном мире.
Преимущество этого в том, что большинству людей легко
ОПРЕДЕЛЕННАЯ культура его использования.
2. Одним из недостатков является то, что это действительно сложно перевести на
другая числовая культура (каким-то образом 2,5 см = 1,6 км не соответствует
сделайте это для меня, и 0,4" = 0,6 мили).
3. Еще один небольшой недостаток заключается в том, что для его использования вам понадобится настоящая линейка:
Вы не можете просто отметить лист бумаги на графической шкале
прямо тогда и там.
4. Один БОЛЬШОЙ недостаток заключается в том, что вам придется пересчитывать и переформулировать его, если
вы увеличиваете или уменьшаете карту.
C. Репрезентативная фракция или коэффициент карты показывает масштаб как фракцию или
соотношение, в котором числитель всегда равен единице. Примеры были бы
1:500 000, или 1/100 000, или 1/63 360, или 1:62 500. знаменатель
обозначает количество ОДИНАКОВЫХ ЕДИНИЦ (например, сантиметров или дюймов)
что карта показывает в реальном мире. Таким образом, 1:100 000 будет означать один
дюйм на карте равен 100 000 дюймов в реальном мире (около
1,6 мили). В равной степени это означало бы, что один сантиметр на карте равен
100 000 сантиметров в реальном мире (1 км).
1. Таким образом, каждый может прочитать вашу карту в любом измерении
система, с которой им комфортно. Все счастливы.
2. Как и вербальная шкала, репрезентативная дробь должна быть
пересчитывается каждый раз, когда вы увеличиваете или уменьшаете карту.
3. Самый большой недостаток в том, что трудно представить, о, 125 000
дюймов или 125 000 сантиметров. Мы должны преобразовать его из
изящные единицы сантиметров и дюймов в более крупные
единицы, которые мы используем в путешествии: километры и мили. Так что вы
нужно сделать небольшое разделение, чтобы сделать их разумными для вас
а. В метрической системе 100 000 см/км, так что просто разделите
знаменатель на 100 000.
Таким образом, 1:100 000 будет означать один
дюйм на карте равен 100 000 дюймов в реальном мире (около
1,6 мили). В равной степени это означало бы, что один сантиметр на карте равен
100 000 сантиметров в реальном мире (1 км).
1. Таким образом, каждый может прочитать вашу карту в любом измерении
система, с которой им комфортно. Все счастливы.
2. Как и вербальная шкала, репрезентативная дробь должна быть
пересчитывается каждый раз, когда вы увеличиваете или уменьшаете карту.
3. Самый большой недостаток в том, что трудно представить, о, 125 000
дюймов или 125 000 сантиметров. Мы должны преобразовать его из
изящные единицы сантиметров и дюймов в более крупные
единицы, которые мы используем в путешествии: километры и мили. Так что вы
нужно сделать небольшое разделение, чтобы сделать их разумными для вас
а. В метрической системе 100 000 см/км, так что просто разделите
знаменатель на 100 000. я. 1:500 000 это 1 см = 5 км
II. 1:250 000 это 1 см=2,5 км
III. 1:125 000 это 1 см = 1,25 км
IV. 1:100 000 это 1 см=1 км
v. 1:62 500 1 см = 0,625 км
ви. Здесь вы можете понять, почему ученым нравится эта метрика.
система -- простое деление (мы ленивые)!
б. Большинство американцев используют английскую систему, хотя английская
отказался от него ради удовольствия владеть нулевым меридианом и
хоть американцы и англичан в Революцию хлестали
что породили США и ото всех оторвались
виды других англицизмов (например, то, как они пишут такие вещи, как
«честь», «защита» и «среди»). В английской системе один
миля, уххххх, сколько футов? Хммммм. Это тяжело.
Кто-нибудь знает навскидку? Я никогда не помню этого сам, и я
на самом деле пришлось искать его для этой лекции
я. 1:500 000 это 1 см = 5 км
II. 1:250 000 это 1 см=2,5 км
III. 1:125 000 это 1 см = 1,25 км
IV. 1:100 000 это 1 см=1 км
v. 1:62 500 1 см = 0,625 км
ви. Здесь вы можете понять, почему ученым нравится эта метрика.
система -- простое деление (мы ленивые)!
б. Большинство американцев используют английскую систему, хотя английская
отказался от него ради удовольствия владеть нулевым меридианом и
хоть американцы и англичан в Революцию хлестали
что породили США и ото всех оторвались
виды других англицизмов (например, то, как они пишут такие вещи, как
«честь», «защита» и «среди»). В английской системе один
миля, уххххх, сколько футов? Хммммм. Это тяжело.
Кто-нибудь знает навскидку? Я никогда не помню этого сам, и я
на самом деле пришлось искать его для этой лекции  Одна миля составляет 5280 футов. Почему 5280? Нажмите здесь, чтобы
узнайте, если вы болезненно любопытны. Итак, сколько дюймов
там в ногу? Двенадцать. Итак, сколько дюймов в
миля? Двенадцать умножить на 5 280 (вы сидите?) 63 360. Ага,
одна миля составляет 63 360 дюймов. Итак, просто разделите знаменатель на
63 360. Кусок пирога!!! 1:500,000, тогда будет, посмотрим,
500 000/63 360 = 7,8914 миль. О, ЭТО хорошее круглое число
мы все можем ярко представить, верно? Нет. Итак, Соединенные Штаты,
чтобы сделать английскую систему немного более управляемой в Геологической службе США
карты, выдумки немного. В целях использования карт Геологической службы США вы
предположим, что одна миля равна 62 500 дюймам. Почему? Потому что
это как бы близко к реальному числу 63 360 и проще
разделить на эти знаменатели.
Одна миля составляет 5280 футов. Почему 5280? Нажмите здесь, чтобы
узнайте, если вы болезненно любопытны. Итак, сколько дюймов
там в ногу? Двенадцать. Итак, сколько дюймов в
миля? Двенадцать умножить на 5 280 (вы сидите?) 63 360. Ага,
одна миля составляет 63 360 дюймов. Итак, просто разделите знаменатель на
63 360. Кусок пирога!!! 1:500,000, тогда будет, посмотрим,
500 000/63 360 = 7,8914 миль. О, ЭТО хорошее круглое число
мы все можем ярко представить, верно? Нет. Итак, Соединенные Штаты,
чтобы сделать английскую систему немного более управляемой в Геологической службе США
карты, выдумки немного. В целях использования карт Геологической службы США вы
предположим, что одна миля равна 62 500 дюймам. Почему? Потому что
это как бы близко к реальному числу 63 360 и проще
разделить на эти знаменатели. Итак, 1:500,000 теперь включает
500 000/62 500. Итак, 1 дюйм «равняется» 8 милям.
я. 1:500,000 это 1 дюйм = 8 миль.
II. 1:250 000 — это 1 дюйм = 4 мили.
III. 1:125 000 — это 1 дюйм = 2 мили.
IV. 1:100 000 — это 1 дюйм = 1,6 мили.
v. 1:62 500 - это 1 дюйм = 1 миля.
ви. 1:63 360 также 1 дюйм = 1 миля.
vii. Теперь вы понимаете, почему американские ученые так возмущены тем, что
большинство американцев не хотят переходить на метрическую систему, несмотря на США
подписание Метрического договора еще в 1875 году, несмотря на то, что Томас
Джефферсон и Джон Куинси Адамс призывают новые США
учитывать достоинства французской системы, несмотря на американскую.
Конгресс разрешил США перейти на метрическую систему в 1866 году, несмотря на
Конгресс США (снова) принимает Закон о преобразовании метрических единиц
из 1975 о создании надзорного органа «для координации
добровольный переход на метрическую систему», и, несмотря на
экономические и торговые издержки нашего отказа от участия в
международная (и простая в использовании) система, которую страна
сам помог разработать!!! Эээээ!! Извините, я думаю, что
восстановил мое самообладание.
Итак, 1:500,000 теперь включает
500 000/62 500. Итак, 1 дюйм «равняется» 8 милям.
я. 1:500,000 это 1 дюйм = 8 миль.
II. 1:250 000 — это 1 дюйм = 4 мили.
III. 1:125 000 — это 1 дюйм = 2 мили.
IV. 1:100 000 — это 1 дюйм = 1,6 мили.
v. 1:62 500 - это 1 дюйм = 1 миля.
ви. 1:63 360 также 1 дюйм = 1 миля.
vii. Теперь вы понимаете, почему американские ученые так возмущены тем, что
большинство американцев не хотят переходить на метрическую систему, несмотря на США
подписание Метрического договора еще в 1875 году, несмотря на то, что Томас
Джефферсон и Джон Куинси Адамс призывают новые США
учитывать достоинства французской системы, несмотря на американскую.
Конгресс разрешил США перейти на метрическую систему в 1866 году, несмотря на
Конгресс США (снова) принимает Закон о преобразовании метрических единиц
из 1975 о создании надзорного органа «для координации
добровольный переход на метрическую систему», и, несмотря на
экономические и торговые издержки нашего отказа от участия в
международная (и простая в использовании) система, которую страна
сам помог разработать!!! Эээээ!! Извините, я думаю, что
восстановил мое самообладание. ... (конец разглагольствования на данный момент).
D. Очень запутанной концепцией является понятие крупного масштаба и малого масштаба.
карты. Здесь действительно нужно сосредоточиться.
1. Крупномасштабная карта — это карта, которая показывает большое количество деталей о
небольшая площадь. Другими словами, его репрезентативная фракция представляет собой большую
число (что означает, что оно имеет относительно небольшой знаменатель). Есть
все это? Просто помните: крупный масштаб означает большую ДЕТАЛИ.
2. Мелкомасштабная карта — это карта, которая показывает небольшое количество деталей о
большая площадь. Его репрезентативная часть представляет собой небольшое число
(что математически означает, что у него большой знаменатель). Запомнить:
Малый масштаб соответствует небольшому количеству деталей.
3. Итак, какая карта крупнее? 1:10 000 или 1:100 000? (первый
один)
4.
... (конец разглагольствования на данный момент).
D. Очень запутанной концепцией является понятие крупного масштаба и малого масштаба.
карты. Здесь действительно нужно сосредоточиться.
1. Крупномасштабная карта — это карта, которая показывает большое количество деталей о
небольшая площадь. Другими словами, его репрезентативная фракция представляет собой большую
число (что означает, что оно имеет относительно небольшой знаменатель). Есть
все это? Просто помните: крупный масштаб означает большую ДЕТАЛИ.
2. Мелкомасштабная карта — это карта, которая показывает небольшое количество деталей о
большая площадь. Его репрезентативная часть представляет собой небольшое число
(что математически означает, что у него большой знаменатель). Запомнить:
Малый масштаб соответствует небольшому количеству деталей.
3. Итак, какая карта крупнее? 1:10 000 или 1:100 000? (первый
один)
4. Какая карта меньшего масштаба? 1:250 000 или
1:1 000 000 000? (второй)
5. Какая карта будет крупнее? Тот, который показывает все
мир или тот, который показывает только Калифорнию? (Калифорния)
E. Если вы хотите узнать больше об этих вопросах, вы можете посетить:
Интерпретация карты
Конверсия: показатели
Следующая лекция будет посвящена символизации карт.
Какая карта меньшего масштаба? 1:250 000 или
1:1 000 000 000? (второй)
5. Какая карта будет крупнее? Тот, который показывает все
мир или тот, который показывает только Калифорнию? (Калифорния)
E. Если вы хотите узнать больше об этих вопросах, вы можете посетить:
Интерпретация карты
Конверсия: показатели
Следующая лекция будет посвящена символизации карт.
Документ и © поддерживаются Dr.
Родриг
Первое размещение в сети: 16.09.00
Последняя редакция: 08.06.07
сантиметры => километры-километры => сантиметры
1 знак после запятой2 знака после запятой3 знака после запятой4 знака после запятой5 знаков после запятой6 знаков после запятой7 знаков после запятой8 знаков после запятой9 знаков после запятой10 знаков после запятой
 1
1 1
1| 1.3 | |
| 140000 | 1.4 |
| 150000 | 1.5 |
| 160000 | 1.6 |
| 170000 | 1.7 |
| 180000 | 1.8 |
| 1 | 1.9 |
| 200000 | 2 |
Как преобразовать
1 сантиметр (см) = 0,00001 километр (км). Сантиметр (см) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе. Сантиметры также можно обозначить как сантиметров .
Сантиметр (см) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе. Сантиметры также можно обозначить как сантиметров .
Километр
— Единица измерения расстояния/длиныОбозначение/сокращение единицы измерения: км
Где единица измерения используется в мире:
Километр используется как единица измерения расстояний или длин.
Это стандартная мера пройденных расстояний, географических расстояний и карт в большинстве стран, за исключением США и Великобритании, где для этой цели до сих пор используется миля.
между географическими точками на суше, и в большинстве стран является официальной единицей для этой цели. Основными исключениями являются Соединенное Королевство, Либерия, Мьянма и Соединенные Штаты Америки, где миля остается стандартной частью имперской системы.
Определение единицы измерения:
Километр (километр в британском написании) — единица длины/расстояния в метрической системе (система единиц СИ), эквивалентная одной тысяче метров.
1 км эквивалентен 0,62137 мили.
История подразделения:
Хотя метр был определен в 1799 году во Франции, километр был впервые принят для повседневного использования голландцами в 1817 году под местным названием mijl. Мириаметры (10 000 метров) и «lieues de Poste» (почтовые лиги, 4 288 метров) предпочитались «километру» для повседневного использования во Франции в 1919 году.век. В середине 19 века километр уже использовался в повседневном использовании в Италии и Нидерландах, а мириаметр все еще использовался во Франции. CIPM (Международный комитет мер и весов) официально отменил приставку «мириа-» и «мириаметр» в 1935 году, оставив километр в качестве признанной единицы длины вместо мириаметра.
Где используется:
Километр обычно используется на дорожных знаках для обозначения расстояния до определенного места, на картах для обозначения масштаба, для обозначения одометра в автомобильной промышленности. Это также самая популярная единица для описания расстояния между географическими точками и местами.
Эквиваленты в других единицах и масштабах:
- 1 км = 1000000 миллиметров (мм)
- 1 км = 100 000 сантиметров (см)
- 1 км = 10000 дециметров (дм)
- 1 км = 1000 метров (м)
- 1 км = 3280,84 фута (фута)
- 1 мегаметр = 1000 км
- 1 гигаметр = 1000000 км
- Единицы длины в метрической системе СИ основаны на кратных или долях метра.
- Существуют измерения длины/расстояния в метрической системе СИ, превышающие километр, которые могут быть выражены в километрах.
1 км эквивалентен 0,621371 мили.
Километр является единицей длины в метрической системе СИ и равен одной тысяче метров.
Испанский Русский французский
[PDF] Масштаб и расстояние на картах
1 Масштаб и расстояние на картах В этом разделе объясняется, как использовать и преобразовывать различные типы масштабов. Также обсуждается ч…
Также обсуждается ч…
Масштаб и расстояние на картах В этом разделе объясняется, как использовать и преобразовывать различные типы масштабов. Также обсуждается, как измерять расстояния на картах. К концу этого раздела вы должны уметь:
Измерять кривые и прямые расстояния
Использовать масштаб для преобразования расстояний на карте в реальные расстояния
Преобразовывать (изменять) один масштаб в другой.
Топографические карты показывают искусственные объекты, такие как дома, дороги, железные дороги, ветряные мельницы и т. д., а также природные объекты, такие как реки и горы.
Часть топографической карты района Огонго масштаба 1:50 000
Давайте навестим моего дядю в Сельскохозяйственном колледже.
Можем ли мы пройти пешком от Ошитутума до колледжа?
Не знаю, давайте посмотрим на нашу карту. Он имеет масштаб масштаба 1:50 000. На карте от Ошитутума до колледжа около 7 см. Формула: расстояние карты × масштаб, поэтому 7 см × 50 000 см равно 350 000 см. Теперь мы должны разделить 350 000 см на 100 000 см, чтобы перевести расстояние в километры. Таким образом, реальное расстояние составляет 350 000 ÷ 100 000 = 3,5 км. Да, мы сможем дойти до колледжа пешком.
Формула: расстояние карты × масштаб, поэтому 7 см × 50 000 см равно 350 000 см. Теперь мы должны разделить 350 000 см на 100 000 см, чтобы перевести расстояние в километры. Таким образом, реальное расстояние составляет 350 000 ÷ 100 000 = 3,5 км. Да, мы сможем дойти до колледжа пешком.
В словесной шкале могут использоваться разные единицы измерения, например, если 1 см равен 0,5 км, то 1 мм равен 0,05 км.
Рубен и Сельма используют топографическую карту, чтобы найти дорогу в колледж. Чтобы определить, каким будет реальное расстояние, они должны уметь пользоваться масштабом карты. Они также должны знать, как измерять расстояния на карте.
Масштаб карты Масштаб карты показывает соотношение между расстоянием на карте и соответствующим расстоянием на поверхности земли. Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы. 1
Масштабы слова
Если 1 см на карте соответствует 50 000 см в действительности, то 1 см также соответствует 0,5 км.
2
Шкалы пропорций
Если масштаб пропорций 1:50 000, то 1 см равен 50 000 см. Вот примеры других шкал отношений: 1:2 000 000 1:4 000
Чтобы преобразовать шкалу слов в шкалу отношений, вы должны следовать двум правилам: 1
Шкала отношений всегда должна начинаться с 1.
2
Размеры до и после двоеточия (:) должны быть в одних и тех же единицах измерения. Например, чтобы преобразовать масштаб слова 4 см в 2 км, необходимо применить оба правила. Поэтому вы должны сначала преобразовать 2 км в см (2 × 100 000 = 200 000), а затем разделить 4 на 4 (=1). Помните, что вы также должны разделить 200 000 на 4 (= 50 000). Таким образом, масштаб соотношения составляет 1:50 000.
3
Линейная шкала
Линейная шкала состоит из линии, разделенной на основные единицы, со второстепенными единицами слева от 0. Помните, что основные единицы слева от 0 должны быть точно такого же размера или длина в качестве основных единиц справа от 0.
Приведенный выше пример линейного масштаба означает, что 1 см на карте равен 1 км на местности. Изучите следующие два примера и попытайтесь преобразовать их в словесные шкалы. Не беспокойтесь, если вы не можете этого сделать. Мы объясним больше о преобразованиях масштаба позже. 2 см = 3 км или 1 см = 1,5 км
Следующие шаги помогут вам нарисовать линейную шкалу. Они используются в приведенном ниже примере, чтобы показать вам, как вы рисуете линейную шкалу. Пример: Нарисуйте линейную шкалу с основными и дополнительными единицами, где 2 см равняется 100 м. Шаг 1: Начертите линейную шкалу (линию)… __________________________________(начертите линию любой длины)
Шаг 2: где 2 см…(разделите линию на 2 см)
Шаг 3: равно 100 м
(каждые 2 см равняется 100 м) Шаг 4: Разделите единицы слева от 0 на более мелкие второстепенные единицы по вашему выбору.
Как преобразовать масштабы Один тип масштаба может быть преобразован в другой тип масштаба. Посмотрите на пример ниже, чтобы увидеть, как это сделать. Пример:
Пример:
Преобразовать в:
Словесный масштаб: 1 см соответствует 0,5 км
Коэффициентный масштаб:
Линейный:
Словесный масштаб: 1 см соответствует 1 км
Чтобы иметь возможность преобразовать один масштаб в другой масштаб или один единицы в другую, необходимо знать следующее:
Есть:
Для перевода из: 1 000 000 мм в 1 км
мм в км вас ÷ на 1 000 000
100 000 cm в 1 км
cm в км вас ÷ на 100 000
1 000 м в 1 км см в 1 м
см в м you ÷ на 100
1 000 мм в 1 м
мм в m you ÷ на 1 000
Измерение расстояния На карте расстояния можно измерять двумя способами: по прямой линии или по кривой линии. Вдоль прямой линии Чтобы измерить прямую линию, просто используйте линейку. Например, показанное здесь расстояние от А до В равно 5,6 см.
1
По кривой линии
Для измерения кривой вам понадобится лист бумаги с прямым краем. Шаг 1: Поместите полоску бумаги прямым краем на первую прямую часть дороги или изогнутую линию. Отметьте точку B на полосе в ее начале и сделайте еще одну отметку (b) там, где дорога начинает изгибаться от бумажной полосы.
Отметьте точку B на полосе в ее начале и сделайте еще одну отметку (b) там, где дорога начинает изгибаться от бумажной полосы.
Шаг 2: Удерживая отметку (b) прочно закрепленной, поверните прямой край бумажной полоски, пока он не пройдет по следующему прямому участку дороги. Теперь отметьте (c), где дорога снова изгибается (вверх или вниз) от бумажной полоски.
Шаг 3: Продолжайте вращать бумажную полоску и отмечать части на полоске, пока все изогнутое расстояние от B до Намутони не будет отмечено на полоске бумаги.
Шаг 4: Положите бумажную полоску на линейку и прочтите расстояние от B до Намутони, как показано ниже. Определите реальное расстояние, используя предоставленные масштабы карты. .
Вычисление расстояния с использованием различных масштабов Если вы умеете пользоваться масштабами карты, вы сможете легко вычислить реальное расстояние между местами.
Карта имеет соотношение и линейный масштаб. Чтобы использовать шкалу отношения, вы должны понимать следующую формулу: Масштаб отношения = Расстояние на карте × масштаб (если перевести из см в км) 100 000 Давайте измерим расстояние, пройденное самолетом между Могадишо в Сомали и Найроби в Кении, используя нашу формула. Расстояние карты = 1,5 см × масштаб карты = 1,5 см × 60 000 000 см = 90 000 000 см ÷ 100 000 (для преобразования в км) = 900 км
Расстояние карты = 1,5 см × масштаб карты = 1,5 см × 60 000 000 см = 90 000 000 см ÷ 100 000 (для преобразования в км) = 900 км
Чтобы использовать линейный масштаб, вы должны понимать, как читать расстояние на этот тип шкалы. Он позволяет измерять реальное расстояние между точками на карте. Воспользуйтесь линейкой и измерьте расстояние от Виндхука до Луанды на карте Африки (рис. 1.5). Расстояние 2,7 см. Теперь поместите линейку на линейную шкалу так, чтобы отметка 2,7 см на линейке находилась непосредственно под отметкой 1 200 км на линейной шкале (между 2 и 3 см). Теперь изучите рисунок 1.6. Пункт А — Виндхук, Б — Луанда. Точка А лежит где-то в второстепенных единицах слева от 0 (нуля). Возьмите показание от 0 на линейной шкале до точки B. Сделайте то же самое от 0 на линейной шкале до точки A и сложите два показания (расстояния). Ответ даст вам расстояние в км (километрах) между Виндхуком и Луандой. От нуля до В
= 1200 км
От нуля до А
= 450 км
Виндхук до Луанды = 1650 км
Итоги урока • Каждая карта имеет шкалу, показывающую соотношение между расстоянием на карте и таким же расстоянием в реальности. жизнь. • Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы, причем одна шкала может быть преобразована в другую. •Расстояние на карте можно измерять по прямой линии между двумя точками или по кривой линии, например, по дороге. Масштаб затем используется для преобразования расстояния на карте в реальное расстояние в метрах или километрах.
жизнь. • Существует три типа шкал: шкалы слов, шкалы отношений и линейные шкалы, причем одна шкала может быть преобразована в другую. •Расстояние на карте можно измерять по прямой линии между двумя точками или по кривой линии, например, по дороге. Масштаб затем используется для преобразования расстояния на карте в реальное расстояние в метрах или километрах.
5.2 Масштаб карты | NWCG
5.2 Масштаб карты | СЗКГПерейти к основному содержанию
View Navigation
Масштаб карты печатается в легенде карты. Он дается как отношение дюймов на карте к дюймам, футам или милям на земле. Например, масштаб карты, показывающий соотношение 1:24 000 (дюйм/дюйм), означает, что на каждый дюйм карты приходится 24 000 дюймов земли. Наземные расстояния на картах обычно указываются в футах или милях.
Map Scale Conversion Factors
| Scale | Representative Fraction | Map in/mi | Map in/ch | map ft/in |
|---|---|---|---|---|
| 1:253,440 | 253. 44 44 | 0.25 | 0.0031 | 21,120 |
| 1:126,720 | 126.72 | 0.50 | 0.0063 | 10,560 |
| 1:63,360 | 63.36 | 1.00 | 0.0125 | 5,280 |
| 1:62,500 | 62.50 | 1.01 | 0.0127 | 5,208 |
| 1:31,680 | 31.68 | 2 | 0.025 | 2,640 |
| 1:24,000 | 24.00 | 2.64 | 0.033 | 2,000 |
| 1:21,120 | 21.12 | 3 | 0.038 | 1,760 |
| 1:15,840 | 15.84 | 4 | 0.05 | 1,320 |
| 1:7,920 | 7.92 | 8 | 0.1 | 660 |
Table 5.1. Коэффициенты преобразования масштаба карты
Пример 1. Преобразование масштаба карты 1:24 000 (дюйм/дюйм) в (дюйм/фут).
Шаг 1. Настройте таблицу отмены, чтобы все единицы измерения отменялись, кроме нужной единицы, фут/дюйм.
На карте 1 дюйм равен 2000 футов на земле, 1:2000 (дюйм/фут).
Пример 2. Преобразование 1:2 000 (дюйм/фут) в (дюйм/миля).
Шаг 1. Настройте таблицу отмены так, чтобы все единицы измерения отменялись, кроме нужной единицы, мили/дюйм.
На карте 1 дюйм равен 0,4 мили.
Пример 3a. Расстояние на карте между двумя точками составляет 6 дюймов. Масштаб карты 1:24 000 (дюйм/дюйм). Какое расстояние до земли в футах?
Настройте таблицу отмены так, чтобы все единицы измерения отменялись, кроме нужной единицы, футов.
Расстояние до земли составляет 12 000 футов.
Использование модифицированной сетки площади (прозрачность)
для использования прозрачности сетки площади, следуйте этим шагам:
Масля Шаг 1. Настройте таблицу отмены, чтобы все единицы, кроме нужной единицы, отменяли цепочки. 12 000 футов = 182 цепи Шаг 2. Настройте таблицу отмены так, чтобы все единицы измерения, кроме нужной единицы, миль, были отменены. Шаг 3. Настройте таблицу отмены так, чтобы все единицы измерения исключались, кроме требуемой единицы измерения, дюймов. Иногда на карте может не быть масштаба. Масштаб можно рассчитать, зная расстояние между двумя точками на карте и измерив расстояние на карте. Кроме того, если на карте есть линии сечения, расстояние между линиями сечения обычно составляет 1 милю. Пример 4. Расстояние между точками A и B на карте составляет 6 дюймов. Известное расстояние до земли составляет 3600 футов. Какой масштаб в дюймах/футах? Пример 5. Используйте масштаб карты из примера 6. Известное наземное расстояние между точками B и C составляет 1/2 мили. Скольким дюймам соответствует это расстояние на карте? масштаб карты = известное расстояние / измеренное расстояние Переставьте члены, умножив каждую сторону на измеренное расстояние и разделив каждую сторону на карту 9Масштаб 0004. измеренное расстояние = известное расстояние / масштаб карты Шаг 2. Используйте масштаб карты из примера 6, чтобы найти расстояние по карте. измеренное расстояние = известное расстояние На земле половина мили соответствует 4,4 дюймам на карте. 0 1 2 3 4 5 6 7 8 9 Измерение — это процесс количественной оценки свойств объекта путем сравнения их с некоторыми стандартными единицами измерения. Мы используем пропорциональные рассуждения другими способами в ситуациях измерения. Например, все мы знакомы с масштабами карт. Если 1 см на карте соответствует расстоянию в 250 км, каково приблизительное расстояние длины, представленной 2,7 см? Мы можем составить пропорцию, чтобы показать, что расстояние равно 675 км: 1 см = 2,7 см Решая уравнение относительно x, получаем x = 250 • 2,7 = 675 км. Одна единица измерения на чертеже в масштабе соответствует n единицам измерения в действительности. Единицы могут быть любыми — сантиметры, метры и т. д. На самом деле, это даже не обязательно должны быть одни и те же единицы; в приведенном выше примере использовались сантиметры и километры. Задача B1 Масштаб 1 см:250 км сравнивает сантиметры с километрами. Перепишите шкалу, чтобы показать такое же отношение при сравнении сантиметров к сантиметрам (1 см:х см или просто 1:х). Помните, что 1 км = 1000 м, а 1 м = 100 см. Чертежи и модели в масштабе — это еще один способ использования соотношения в измерениях. Обычно шкала сравнивает линейные меры. Изучите чертежи в масштабе ниже. Масштаб 1:1 подразумевает, что рисунок кузнечика такой же, как реальный объект. Масштаб 1:2 подразумевает, что рисунок меньше (половина размера), чем реальный объект (иными словами, размеры умножаются на коэффициент масштабирования 0,5). Масштаб 2:1 предполагает, что рисунок больше реального кузнечика — в два раза длиннее и в два раза выше (мы говорим, что размеры умножены на коэффициент масштабирования, равный 2). Задача B2 На стене нарисована собака. Увеличенная собака была 45 футов в высоту. Если средний рост этой породы собак составляет 3 фута, каков масштабный коэффициент этого увеличения? Можете ли вы выразить эту шкалу более чем одним способом? Задача B3 Представьте, что вам нужно нарисовать себя (стоящим), чтобы полностью поместиться на 8,5 на 11 дюймов. лист бумаги. Определите масштабный коэффициент, допускающий не более дюйма границы вверху и внизу страницы. Как долго ваши руки будут на рисунке? Note 8 Попробуйте масштаб 1:10 (т. е. ваш рисунок будет в десять раз меньше вашего фактического размера) или 1:8. Измерьте различные части тела, такие как длина головы, рук, туловища и ног, а затем используйте соотношение, чтобы определить размер этой части тела на рисунке. Чертежи в масштабе особенно полезны при сравнении относительных величин очень больших объектов. В музеях науки часто есть масштабная модель нашей Солнечной системы, чтобы помочь нам понять огромные расстояния между Солнцем и каждой планетой. Представьте, что вам нужно спроектировать модель солнечной системы для своей школы. Ниже приведена таблица с некоторыми важными данными. Обратите внимание, что расстояние от Солнца указано в экспоненциальной записи: Диаметр (в км) Расстояние от Солнца в научных обозначениях (в км) Продолжайте: Проблема B4 Проблема B5 Научный парк в Вестерборке, Голландия, использует масштаб 1:3,7 • 10 9 для масштабной модели Солнечной системы. Как вы думаете, какие юниты решили использовать в парке? Отношение играет важную роль в измерениях и может использоваться для прогнозирования. Если отношение дюймов к сантиметрам составляет 1 к 2,54 (1:2,54), то мы можем считать, что длина 12 дюймов составляет примерно 30 см (30,48). Однако не все соотношения в природе постоянны. В то время как Зебровски утверждает, что многие отношения непостоянны, в ситуациях измерения обнаруживаются некоторые постоянные отношения. Одно постоянное отношение, которое мы регулярно используем, — это π. Мы подробнее рассмотрим это соотношение на занятии 7, посвященном кругам. Другая распространенная ситуация измерения связана с прямоугольными треугольниками. Теперь мы более внимательно рассмотрим прямоугольные треугольники, начав с нескольких прямоугольных треугольников разных размеров. Задача B6 Распечатайте фигуры из файла PDF (обязательно распечатайте этот документ в полном масштабе). Сантиметровой линейкой измерьте гипотенузы этих треугольников. Мы исследуем, существует ли константа пропорциональности. Заполните таблицу. (Обратите внимание, что это все равнобедренные прямоугольные треугольники.): Длина гипотенузы (H) в см Соотношение S:S Соотношение В:Ш Проблема B7 Помните, что теорема Пифагора утверждает, что в прямоугольных треугольниках с длинами катетов a и b и длиной гипотенузы c выполняется следующее соотношение: a 2 + b 2 = c 2 . Примечание 10 Когда вы используете теорему Пифагора, ваш ответ может быть нелегко сократить от радикальной формы (как квадратный корень). Вместо того, чтобы использовать калькулятор для извлечения квадратного корня, вы можете вместо этого выразить ответ в сокращенной радикальной форме. Задача B8 Длина сторон (S) в см Длина гипотенузы (H) в см Соотношение S:S Отношение Пифагора H:S Задача B9 В большинстве прямоугольных треугольников одно или несколько значений длины стороны иррациональны. Примечание 11 Примечание 8 Если вы работаете в группе, работайте в парах над Задачей B3. Попрактикуйтесь в настройке пропорций (два соотношения, которые равны друг другу), чтобы определить длину различных частей тела на вашем рисунке. Примечание 9 Решение этой проблемы может занять некоторое время, особенно если вы пытаетесь использовать одну шкалу как для диаметра планет, так и для их расстояний от Солнца. Часто создаются модели, которые фокусируются на одном или другом (размер или расстояние). Если вы выберете масштаб, позволяющий расстоянию от Солнца поместиться в большую комнату, вы обнаружите, что модели некоторых планет очень и очень малы. ПРИМЕЧАНИЕ 10 , чтобы узнать больше о теореме Пифагора, перейдите к Обучение Математика: Геометрия, Сессия 6. Примечание 11 Примечание . потому что его нельзя выразить в виде дроби a/b, где a и b — целые числа, а b — 0. Другими словами, это значение нельзя записать в виде дроби или повторяющегося или завершающего десятичного числа. Если бы мы выразили его в виде десятичного числа, оно имело бы бесконечное количество цифр справа от десятичной точки в неповторяющемся шаблоне. Система действительных чисел состоит из бесконечного числа рациональных чисел (тех, которые соответствуют указанному выше свойству дроби) и бесконечного числа иррациональных чисел. Задача B1 Поскольку 1 км = 100 000 см, масштаб 1 см:250 км эквивалентен 1 см:250 • 100 000 см, или 1:25 000 000. Задача B2 Масштабный коэффициент 45:3. Его можно упростить до 15:1 или выразить другими способами, например, 7,5:0,5 или 150:10. Задача B3 Ответы будут разными. Вот один пример: предположим, что кто-то ростом ровно 6 футов, с руками 3 фута в длину. Масштабный коэффициент будет 9дюймов: 6 футов, чтобы оставить 1 дюйм границы сверху и снизу. Чтобы упростить это, помните, что 6 футов = 72 дюйма. Задача B4 Проблема B5 Скорее всего, выбрали мили. Наибольшее расстояние от Солнца, 5,9 • 10 9 , становится равным 1,6 км. Это чуть меньше одной мили, поэтому масштаб, вероятно, был выбран таким, чтобы вся модель уместилась в пределах одной мили. Используя этот масштаб, наименьший фрагмент данных (диаметр Плутона) становится равным 0,62 мм, что очень мало, но все же заметно. Задача B6 Ответы могут различаться в зависимости от измерений. Здесь ответы даны с точностью до десятых долей сантиметра: Длина сторон (S) в см Длина гипотенузы (H) в см Соотношение S:S Соотношение В:Ш 1,4 1:1 1,4:1 2,8 2:2 2,8:2 4,2 3:3 4,2:3 5,7 4:4 5,7:4 7. 5:5 7,1:5 8,5 6:6 8,5:6 Задача B7 Проблема B8 Длина сторон (S) в см Длина гипотенузы (H) в см Соотношение S:S Отношение Пифагора H:S б. Акров на квадратный дюйм Коэффициент преобразования, равный каждой точке 1:20,000 3.  168
168 63.769 1.736 Acres 1:24,000 2.640 91.827 2.500 Acres 1:62,500 1.014 622.449 16.946 Acres Таблица 5.2 Таблица 5.2 Таблица 5.2

12 000 футов = 182 цепи = 2,3 мили = 144 000 дюймов
Масштаб карты 1:600 дюймов/фут.
масштаб карты
измеренное расстояние = 2640 футов 1 дюйм = 4,4 дюйма
600 футов Часть B: Роль соотношения (45 минут)
В этой части
Соотношение и масштаб
 Таким образом, мера есть отношение. Когда мы утверждаем, что объект имеет длину 8 дюймов, это сравнивается с единицей измерения 1 дюйм. Точно так же заявление о том, что мешок сахара весит 5 фунтов, подразумевает, что 5 фунтов сравниваются с единицей измерения 1 фунт. ., хотя мы и не указываем это явно.
Таким образом, мера есть отношение. Когда мы утверждаем, что объект имеет длину 8 дюймов, это сравнивается с единицей измерения 1 дюйм. Точно так же заявление о том, что мешок сахара весит 5 фунтов, подразумевает, что 5 фунтов сравниваются с единицей измерения 1 фунт. ., хотя мы и не указываем это явно.
250 км x км В этой шкале могли использоваться те же единицы измерения (1 см на карте соответствует определенному количеству сантиметров в действительности), но преобразование сантиметров в километры упрощает задачу для пользователя.
В этой шкале могли использоваться те же единицы измерения (1 см на карте соответствует определенному количеству сантиметров в действительности), но преобразование сантиметров в километры упрощает задачу для пользователя. Если в шкале не указаны единицы, то можно считать, что чертеж и объект измеряются в одних и тех же единицах. Например, масштаб 1:2 может представлять 1 см:2 см или 1 дюйм:2 дюйма 9.0010
Если в шкале не указаны единицы, то можно считать, что чертеж и объект измеряются в одних и тех же единицах. Например, масштаб 1:2 может представлять 1 см:2 см или 1 дюйм:2 дюйма 9.0010
Вс 1 392 000 Меркурий 4 900 5,8 • 10 7 Венера 12 100 1,08 • 10 8 Земля 12 760 1,5 • 10 8 Марс 6 790 2,28 • 10 8 Юпитер 143 000 7,78 • 10 8 Сатурн 121 000 1,43 • 10 9 Уран 51 000 2,87 • 10 9 Нептун 50 000 4,5 • 10 9 Плутон 2 300 5,9 • 10 9 а. 
Какой масштаб вы бы использовали, если бы хотели показать учащимся, насколько далеко планеты от Солнца? б. Какой масштаб вы бы использовали, если бы хотели помочь учащимся понять разницу в диаметре планет? Можно ли использовать одну и ту же шкалу для обеих целей? Примечание 9
Иди дальше Постоянные отношения
 По словам математика Эрнеста Зебровски-младшего, «большинство соотношений на самом деле непостоянны. Если, например, потребовалось 24 гребца, чтобы грести на галере со скоростью 15 миль/ч, это не означает, что 48 гребцов разогнали бы лодку до 30 миль/ч и что при 144 гребцах лодка достигла бы 90 миль/ч. (На самом деле, эта цепочка рассуждений предполагает, что древние могли преодолеть звуковой барьер, просто собрав достаточное количество гребцов.) …. Хотя для бухгалтера или математика несложно утверждать, что конкретное отношение является постоянным, законы природы являются окончательным арбитром. Очевидно, что прежде чем делать прогнозы на основе предполагаемого постоянного соотношения, нам нужно, чтобы кто-то проверил реальность ситуации».
По словам математика Эрнеста Зебровски-младшего, «большинство соотношений на самом деле непостоянны. Если, например, потребовалось 24 гребца, чтобы грести на галере со скоростью 15 миль/ч, это не означает, что 48 гребцов разогнали бы лодку до 30 миль/ч и что при 144 гребцах лодка достигла бы 90 миль/ч. (На самом деле, эта цепочка рассуждений предполагает, что древние могли преодолеть звуковой барьер, просто собрав достаточное количество гребцов.) …. Хотя для бухгалтера или математика несложно утверждать, что конкретное отношение является постоянным, законы природы являются окончательным арбитром. Очевидно, что прежде чем делать прогнозы на основе предполагаемого постоянного соотношения, нам нужно, чтобы кто-то проверил реальность ситуации».
1 2 3 4 5 6 а. 
Какие постоянные отношения вы нашли в равнобедренных прямоугольных треугольниках (45°-45°-90°)? б. Иногда вы не можете измерить что-то напрямую (например, с помощью линейки), но вы все равно можете определить его меру. Меры, найденные косвенно с помощью математики, часто называют «производными» мерами. Например, если мы знаем длины катетов равнобедренного прямоугольного треугольника, как мы можем определить меру его гипотенузы? Использование теоремы Пифагора
 Вот как: Выразите число как произведение множителей, где один из множителей (если возможно) является квадратным числом. Затем возьмите квадратный корень только из квадратного числа и оставьте ответ как произведение квадратного корня и радикала:
Вот как: Выразите число как произведение множителей, где один из множителей (если возможно) является квадратным числом. Затем возьмите квадратный корень только из квадратного числа и оставьте ответ как произведение квадратного корня и радикала: 1 1:1 2 2:2 3 3:3 4 4:4 5 5:5 6 6:6 
С точки зрения измерения, каковы последствия того, что одно или несколько значений являются иррациональными? Примечания
 Если вы выберете масштаб, позволяющий модели планет быть достаточно большими, чтобы вы могли их наблюдать, вы обнаружите, что расстояния между планетами в модели должны быть очень большими.
Если вы выберете масштаб, позволяющий модели планет быть достаточно большими, чтобы вы могли их наблюдать, вы обнаружите, что расстояния между планетами в модели должны быть очень большими. Есть много ситуаций, когда длина на самом деле является иррациональным числом (например, гипотенузы равнобедренных прямоугольных треугольников), поэтому мы не можем точно измерить длину. Идея о том, что мера всегда является приблизительной величиной, трудно понять, поскольку в повседневной жизни мы обращаемся с мерами как с точными величинами.
Есть много ситуаций, когда длина на самом деле является иррациональным числом (например, гипотенузы равнобедренных прямоугольных треугольников), поэтому мы не можем точно измерить длину. Идея о том, что мера всегда является приблизительной величиной, трудно понять, поскольку в повседневной жизни мы обращаемся с мерами как с точными величинами. Решения
 Масштабный коэффициент может быть выражен как 9:72 или 1:8. Руки этого человека были бы на 1/8 длиннее на чертеже в масштабе; 1/8 от 3 футов (36 дюймов) равно 4,5 дюйма
Масштабный коэффициент может быть выражен как 9:72 или 1:8. Руки этого человека были бы на 1/8 длиннее на чертеже в масштабе; 1/8 от 3 футов (36 дюймов) равно 4,5 дюйма
100 м 1 • 10 2 м 1 5,9 • 10 9 км = 5,9 • 10 • 10 12 км = 5,9 • 10 10 м Лучший масштаб может быть 1 м: 590 миллионов м, что составляет диаметр Юпитера примерно 24 см. Самая маленькая планета, Плутон, будет иметь диаметр 3,8 мм в этом масштабе, что все еще мало, но, безусловно, заметно.
Лучший масштаб может быть 1 м: 590 миллионов м, что составляет диаметр Юпитера примерно 24 см. Самая маленькая планета, Плутон, будет иметь диаметр 3,8 мм в этом масштабе, что все еще мало, но, безусловно, заметно. 1 2 3 4 5  1
1 6 
1 √2 1:1 √2:1 2 2√2 2:2 2√2:2 3 3√2 3:3 3√2:3 4 4√2 4:4 4√2:4 5 5√2 5:5 5√2:5 6 6√2 6:6 6√2:6