Масштабы
Горизонтальные проекции отрезков (см. рис. 1.3,б отрезкиab илиа’b’) при составлении карт и планов изображают на бумаге в уменьшенном виде. Степень такого уменьшения характеризуется масштабом.
Масштабкарты (плана) – отношение длины линии на карте (плане) к длине горизонтального проложения соответствующей линии местности:
.
Масштабы бывают численные и графические. Численный масштаб фиксируют двумя способами.
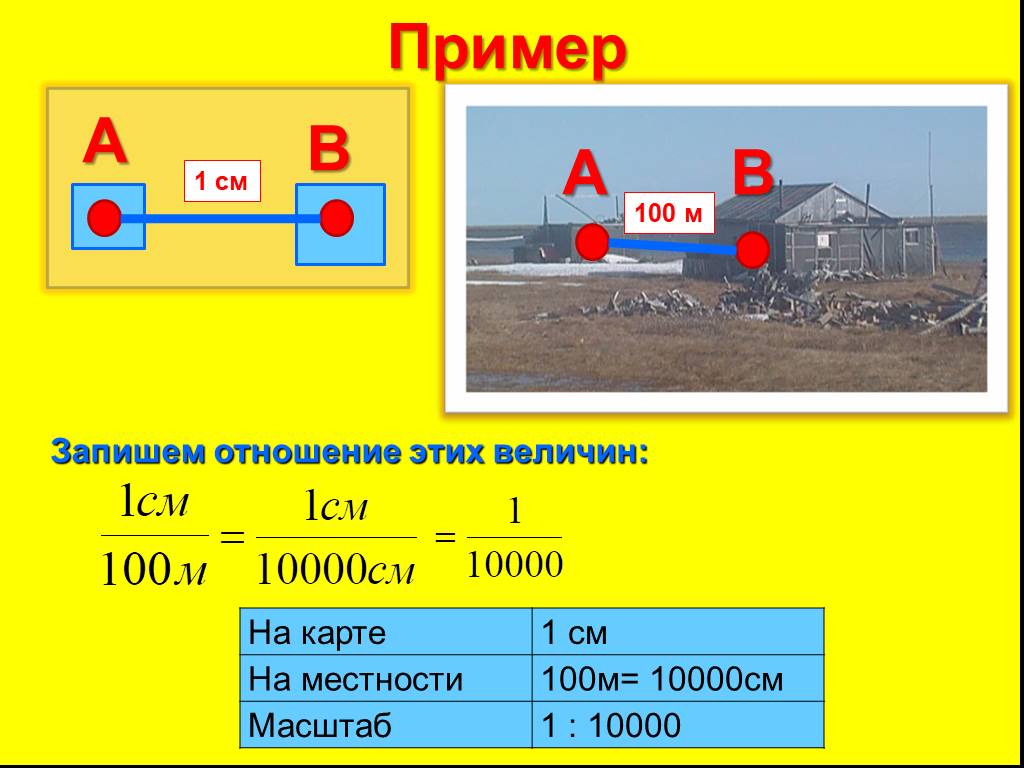
1. В виде простой дроби –в числителе единица, в знаменателе степень уменьшения m, например (или М = 1:2000).
2. В виде
именованного соотношения, например в
1 см 20 м. Целесообразность такого
соотношения определяется тем, что при
изучении местности по карте удобно и
привычно оценивать длину отрезков на
карте в сантиметрах, а длину горизонтальных
проложений на местности представлять
в метрах или километрах.
Пример 1. На плане(в 1 см 50 м) расстояние между точками составляет 1,5 см. Определить горизонтальное проложение между этими же точками на местности.
Решение: 1,5 5000 = 7500 см = 75 м (или 1,5 50 = 75 м).
Пример 2. Горизонтальное проложение между двумя точками на местности равно 40 м. Чему будет равно расстояние между этими же точками на плане М = 1:2000 (в 1 см 20 м)?
Решение: см.
Чтобы избежать вычислений и ускорить работу, пользуются графическими масштабами. Таких масштабов два: линейный и поперечный.
Для
построения линейного
масштаба выбирают
исходный отрезок, удобный для данного
масштаба (чаще длиной 2 см). Этот исходный
отрезок называется основанием масштаба
(рис. 1.5). Основание откладывают на прямой
линии необходимое число раз, крайнее
левое основание делят на части (обычно
на 10 частей).
Для обеспечения необходимой точности измерений угол между плоскостью карты и каждой ножкой циркуля-измерителя (рис. 1.5,б) не должен быть менее 60°, и измерение длины отрезка следует произвести не менее двух раз. Расхождение S, м между результатами измерений должно быть , гдеТ – число тысяч в знаменателе численного масштаба. Так, например, при измерении отрезков по карте Ми пользовании линейным масштабом, который помещен обычно за южной стороной рамки листа карты, расхождения при двойных измерениях не должны превышать 1,510 = 15 м.
Рис. 1.5. Линейный масштаб
Если
отрезок длиннее построенного линейного
масштаба, то его измеряют по частям.
В
этом случае расхождение между результатами
измерения в прямом и обратном направлениях
не должно превышать
,
гдеп – число установок измерителя при измерении
данного отрезка.
Для более точных измерений пользуются поперечным масштабом, имеющим на линейном масштабе дополнительное построение по вертикали (рис. 1.6).
После
того как необходимое количество оснований
масштаба отложено (также обычно длиной
2 см, тогда масштаб называется нормальным),
восстанавливают перпендикуляры к
исходной линии и делят их на равные
отрезки (на m частей). Если
основание разделено на п частей и точки
деления верхнего и нижнего основания
соединены наклонными линиями
(трансверсалями) так, как показано на
рис. 1.6, то отрезок
.
Соответственно отрезокef = 2cd; рq = 3сd и т. д. Если m
= п = 10, то cd
= 0,01 основания,
т.е. такой
поперечный масштаб позволяет определенным
образом оценить отрезок с точностью в
0,01 доли основания, дополнительную часть
этой доли – на глаз.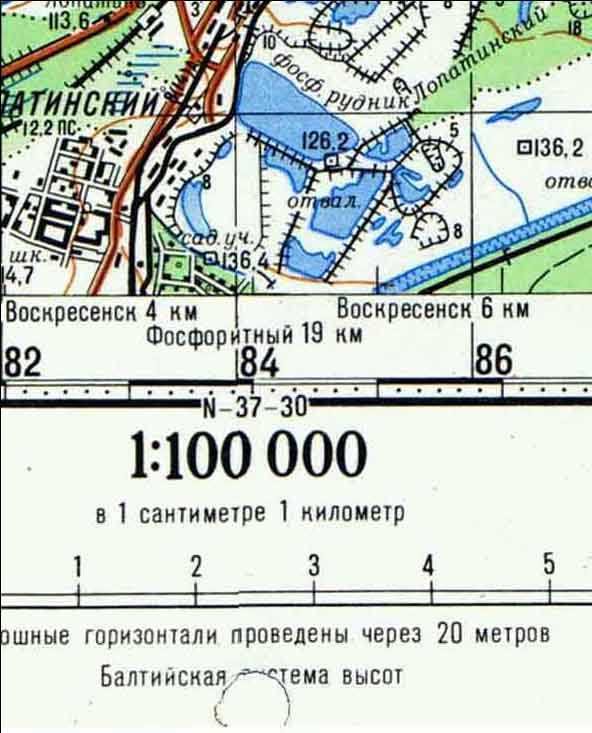
Поперечный масштаб,
у которого длина основания 2 см и m
= п = 10, называют
сотенным нормальным.
Рис. 1.6. Построение поперечного масштаба
Поперечный масштаб гравируют на металлических линейках, которые называются масштабными. Перед применением масштабной линейки следует оценить основание и его доли по следующей схеме.
Пусть численный масштаб 1:5000, именованное соотношение будет: в 1 см 50 м. Если поперечный масштаб нормальный (основание 2
рис. 1.7) так, чтобы линияАБ отсекала 0,35 промежутка между этими
линиями (отрезокДЕ). Обратная задача
(определение длины отрезка, взятого в
раствор измерителя) соответственно и
решается в обратном порядке. Добившись
совмещения игл измерителя с соответствующими
вертикальной и наклонной линиями так,
чтобы обе ножки измерителя находились
на одной горизонтальной линии, считываем
количество оснований и его долей ( dBГ = 235,3 м).Рис. 1.7. Поперечный масштаб
При
проведении съемок местности для получения
планов неизбежно возникает вопрос:
какие наименьшие размеры объектов
местности должны отобразиться на плане?
Очевидно, чем крупнее масштаб съемки,
тем меньше будет линейный размер таких
объектов. Для того чтобы применительно
к конкретному масштабу плана можно было
принять определенное решение,
вводится понятие о точности масштаба.
При этом исходят из следующего. Опытным
путем установлено, что измерить
расстояние, пользуясь циркулем и
масштабной линейкой, точнее, чем 0,1 мм,невозможно.
Соответственно под точностью
масштаба понимают длину отрезка на
местности, соответствующую 0,1 мм на
плане данного масштаба. Так, если
Следует иметь в виду, что при измерениях на плане взаимного положения контуров точность определяется не графической точностью, а точностью самого плана, где ошибки могут составлять в среднем 0,5 мм вследствие влияния других, кроме графических, погрешностей.
Интегрированный урок по географии и математике в 6-м классе по теме «Масштаб»
Цель урока: дать понятие «Масштаб».
Задачи урока:
- раскрыть виды масштаба;
- уметь перевести численный масштаб в именованный и обратно;
- уметь определять расстояние по масштабу.
Оборудование: набор топографических карт г. Снов разного масштаба, линейка, циркуль.
ХОД УРОКА
I. Географ проводит проверку домашнего задания в виде географического диктанта
– Чертеж, изображающий земную поверхность
сверху в уменьшенном виде…
– Аэрофотоснимки – это…
– Нарисуйте условные знаки: колодец, родник, река
с мостом, смешанный лес, кустарники, вырубленный
лес, луг, фруктовый сад.
II. Изучение нового материала
1. Вступительное слово учителя географии: Однажды
мальчик Вова, гуляя по городу, совершенно
случайно очутился на аллее, которую раньше
никогда не видел, Аллея была длинная-предлинная,
и по обеим ее сторонам росли старые липы. Они
давали густую тень в солнечные и жаркие дни.
Здесь было очень тихо. Не слышно было рокота
машин, только пешеходы изредка проходили по
аллее. На одной самой высокой и старой липе
собрались птицы.
Они расселись по веткам и стали
распевать свои веселые песенки. Мальчику так
понравилась аллея, и он решил сделать ее план,
чтобы рассказать об этом месте своим друзьям и
привести их сюда.
Но, к сожалению, у него ничего не получилось. Вова
знал все условные знаки, но не мог понять, как
уместить всю эту длинную аллею на листе бумаги.
О чем не знал Вова?
Он не знал о существовании масштаба.
2. Раскроем понятие масштаб.
Масштаб – это дробь, где в числителе
единица, а в знаменателе то число, которое
показывает во сколько раз уменьшено расстояние
на плане местности, чем на местности.
Например: 1:1000 (одна тысячная), значит все
расстояния на местности уменьшены в тысячу раз.
3. Работа с топографическими картами разного масштаба
Вывод: Чем больше число в знаменателе
дроби, тем больше уменьшение и тем больше охват
территории.
Масштаб бывает:
1. Численный, выражается в числах.
1 : 1000
2. Именованный, выражается словами, то есть см переводим в м
в 1см 10м 10м – это величина масштаба
3. Линейный
Зная величину масштаба, мы можем определить расстояния.
4. Работа по учебнику по рис. 8 на стр.15
Определим длину школы: 6 * 10 = 60 м
Ширина школы: 1,3 * 10 = 13 м
Длина школьного фруктового сада: 4 * 10 = 40 м
Ширина школьного фруктового сада: 2,3 * 10 = 23 м
5. Слово учителю математики:
Задание 1. Переведите численные масштабы в именованные:
Решение:
1 : 10000 в 1 см 100 м
1 : 25000 в 1 см 250 м
1 : 1000000 в 1 см 10 км
Задание 2.
Переведите именованные
масштабы в численные:
Решение:
в 1 см 10 м 1 : 1000
в 1 см 1 км 1 : 100000
в 1 см 20 м 1 : 2000
Географ: По величине масштаба можно построить линейный масштаб, для точного определения расстояний.
Берем прямую линию, делим на см. Отмечаем точку
0, а вправо и влево от нуля пишем величину
масштаба, т.е. 10. Деление, то, что влево делим на
пять равных частей и самое маленькое деление
будет равным 2мм. На правой стороне прибавляем по
10 см и будет 20 см, 30 см, 40 см и т. д. Чтобы
использовать линейный масштаб пользуются
циркулем.
Построим линейные масштабы для других масштабов.
Математик: Приступим к решению задач.
Задание 1. Ученик изобразил на чертеже расстояние 500 м в масштабе в 1 см 50 м. Чему равно это расстояние на чертеже?
Решение: 500 : 50 = 10 см
Задание 2. Ученик изобразил на чертеже расстояние 700 м в масштабе 1 : 70000. Чему равно расстояние на чертеже?
Решение: в 1см 700 м, значит расстояние равно 1 см.
Задание 3. Ученик изобразил на чертеже расстояние 500м отрезком длиной 5 см. Определите, какой численный масштаб он выбрал для выполнения задания.
Решение: Если 5 см соответствует 500 м, то 1 см равен 100 м. Именованный масштаб переводим в численный – 1 : 10000.
6. Работа с линейным масштабом
Чтобы пользоваться линейным масштабом, нужно
определить, чему равны большое и маленькое
деления.
Измеряемый отрезок нужно отложить на
линейном масштабе циркулем от нуля вправо.
Правая ножка циркуля оказывается при этом обычно
где-то в пределах большого отрезка, а не на его
конце. Сдвинем циркуль немного влево, чтобы
правая ножка пришлась на конец большого отрезка.
При этом мы сможем получить длину отрезка как
сумму больших отрезков вправо от нуля и
маленьких отрезков влево от него.
В заключение предлагаются два-три задания на
определение расстояний с помощью линейного
масштаба.
III. Итог урока
- Что называется масштабом?
- Перечислите виды масштаба.
- Что показывает знаменатель численного масштаба?
IV. Домашнее задание: параграф 4, задание 3 (письменно).
Направление вектора
Эта веб-страница предназначена для дополнительной практики использования масштабированных векторных диаграмм для представления величины и направления вектора.
Определите величину и направление следующих векторов в вопросах № 1– № 6 . Используйте правило против часовой стрелки (с востока), которое обсуждалось в классе, чтобы определить направление. Используйте указанный масштаб и преобразование масштаба, чтобы определить величину. Используйте выпадающее меню для просмотра ответов.
1. Учитывая МАСШТАБ : 1 см = 10 м/с
2. Учитывая МАСШТАБ: 1 см = 50 км/ч , определите величину и направление этого вектора.
3. Учитывая МАСШТАБ : 1 см = 10 м/с , определите величину и направление этого вектора.
4. Учитывая МАСШТАБ : 1 см = 50 км/ч , определите величину и направление этого вектора.
5. Учитывая МАСШТАБ : 1 см = 10 м/с , определите величину и направление этого вектора.
6. Учитывая МАСШТАБ: 1 см = 50 км/ч , определите величину и направление этого вектора.
Используйте точно нарисованную масштабированную векторную диаграмму, чтобы представить величину и направление следующих векторов в вопросах №7–№12. Используйте указанный масштаб и правило против часовой стрелки, обсуждавшееся в классе. Нажмите на горячую ссылку , чтобы проверить ответы.
ПРИМЕЧАНИЕ: Поскольку ваши ответы были определены с использованием масштабированной векторной диаграммы, небольшие ошибки в измерении направления и величины любого из векторов могут привести к небольшому расхождению между вашими ответами и правильными ответами, показанными здесь. Это не должно быть поводом для беспокойства.
7. Учитывая МАСШТАБ : 1 см = 10 м , представьте вектор 50 м, 30 градусов с помощью масштабированной векторной диаграммы.
8. Учитывая МАСШТАБ : 1 см = 10 м , представьте вектор 60 м, 150 градусов с помощью масштабированной векторной диаграммы.
9. Учитывая МАСШТАБ : 1 см = 20 м , представьте вектор 140 м/с, 200 градусов с помощью масштабированной векторной диаграммы.
10.
Учитывая МАСШТАБ : 1 см = 15 м/с , представьте вектор 120 м/с, 240 градусов с помощью масштабированной векторной диаграммы.
11. Учитывая МАСШТАБ : 1 см = 5 м/с , представьте вектор 35 м/с, 270 градусов с помощью масштабированной векторной диаграммы.
12. Учитывая МАСШТАБ : 1 см = 5 м/с , представьте вектор 31 м/с, 310 градусов, с помощью масштабированной векторной диаграммы.
Калькулятор масштаба карты | Преобразование масштабов карты онлайн
Поделись!
Содержание
- Как рассчитывается шкала?
- Большой против малого масштаба
- Масштаб для цифровых карт
- Топографические карты
Даже сейчас, в эпоху портативных систем GPS, многофункциональных часов и других технических устройств, старые добрые карты по-прежнему занимают важное место в альпийском мире.
Очевидная причина в том, что они никогда не иссякнут.
Важным числом, которое может вызвать первоначальное замешательство, является масштаб. Это дает отношение расстояния карты к расстоянию на земле . На первый взгляд это может показаться сложным, но это просто означает, что при масштабе 1:50 000 один сантиметр на карте соответствует 50 000 см на местности.
Как рассчитывается шкала?
Шкала обычно задается как 1:номер шкалы . Формула расчета стоимости, которая, конечно же, должна иметь ту же единицу измерения:
Масштаб = Расстояние по карте ÷ Расстояние по земле
Масштабный коэффициент = Расстояние на земле ÷ Расстояние на карте
Если мы возьмем приведенный выше пример, масштабный коэффициент составит 50 000, и, следовательно, масштаб будет 1:50 000. Если бы два сантиметра на карте соответствовали расстоянию на местности в 50 000 сантиметров, масштаб был бы 1:25 000.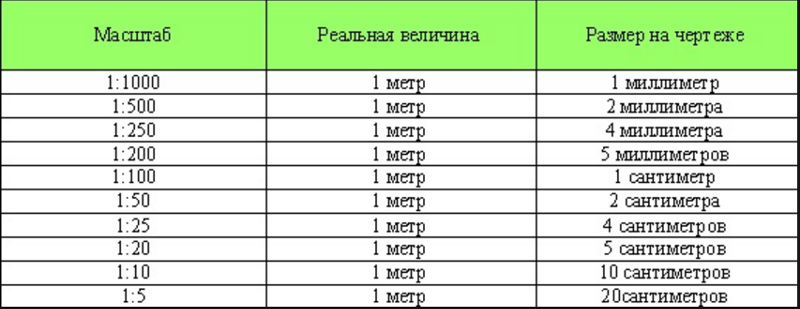
Как правило, шкала расположена на относительно видном месте – как на обложке карты, так и в углу самой развернутой карты, поэтому с помощью линейки на компасе относительно быстро и легко определить расстояние .
Большой или малый масштаб
Масштабы наружных картТермины «крупный» или «мелкий» масштаб поначалу могут сбивать с толку. Это не относится к коэффициенту масштабирования, это на самом деле означает уровень детализации на карте. Если объект изображен на карте большим, масштабный коэффициент будет меньше. Все еще звучит довольно сложно, не так ли? Но это всего лишь означает, что на карте масштаба 1:25 000 (крупная) можно показать больше деталей, чем на карте масштаба 1:100 000 (маленькая).
Масштаб, используемый на каждой карте, зависит от ее назначения. В общем, можно сказать, что чем быстрее вы движетесь, тем меньше будет масштаб. Карты пеших прогулок имеют соответственно крупный масштаб, обычно 1:25 000 или 1:50 000, в то время как карты велосипедных прогулок имеют тенденцию к масштабу 1:100 000, а карты в дорожных атласах начинаются с меньшего масштаба 1:200 000.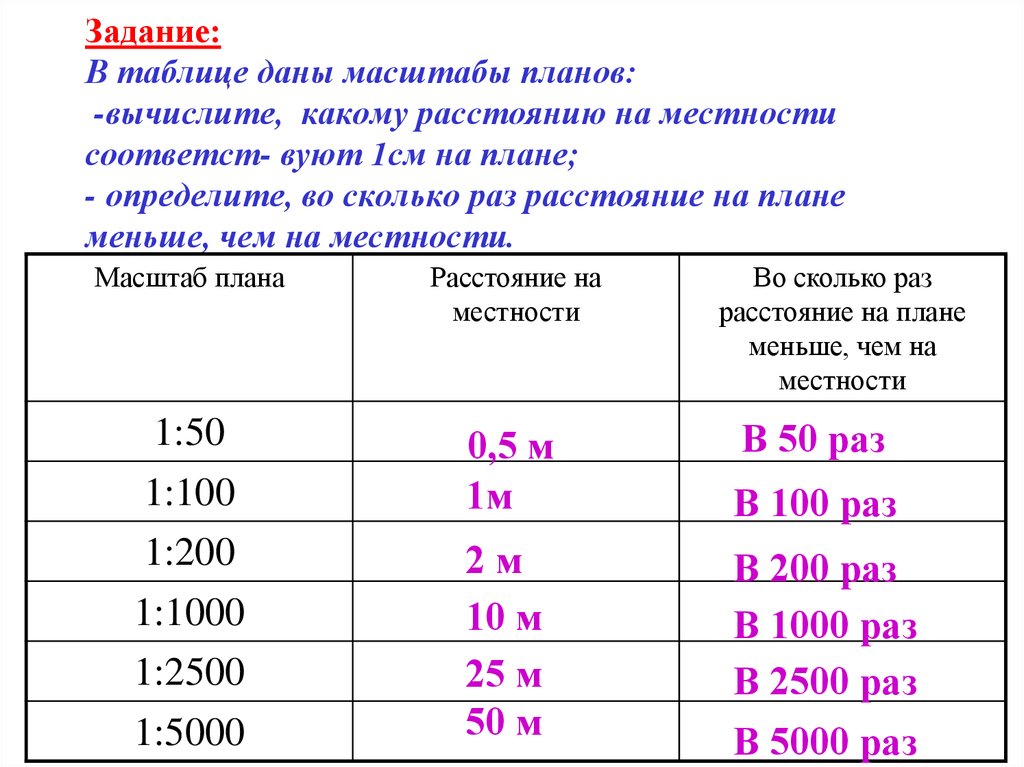
А цифровые карты?
Как вы понимаете, самым большим преимуществом цифровых карт является вариативность масштаба. Устройства GPS часто дают вам выбор из увеличение и уменьшение масштаба и изменение масштаба. Но это не единственное преимущество этих электронных помощников! Часто на этих устройствах можно сохранить более одной карты, а это означает, что вам не нужно таскать с собой множество аналоговых карт в длительные походы.
И у них нет складок, поэтому вы можете легко их достать даже в самых маленьких местах. Самое большое преимущество классических карт довольно очевидно: они никогда не иссякают! Но лучшая система для вас зависит, прежде всего, от того, для чего вам нужно ее использовать.
Топографические карты и расчет времени ходьбы
Наружные карты обычно всегда топографические. Это означает, что они имеют очерченные контурные линии и дают дополнительную информацию о местности. Отмечены отличительные особенности, такие как вершины и мосты, а также большие водоемы.