В каких пределах находятся значения sin a если 0 a 180: Разработка урока по геометрии «Синус, косинус и тангенс. Урок 2″(9 класс)

Урок геометрии по теме «Синус, косинус, тангенс и котангенс угла». 9-й класс

• Давыдова Наталья Валерьевна, учитель математики
• Скрипник Лилия Исмагиловна, учитель

Разделы: Математика

Класс: 9

---

Цели:

• cистематизировать знания по теме синус, косинус, тангенс и котангенс острого угла;
• eметь применять формулы приведения для решения алгебраических и тригонометрических задач;
• hазвивать тригонометрический аппарат для решения алгебраических и тригонометрических задач.

Оформление: чертежи единичной полуокружности, прямоугольного треугольника, таблица значений тригонометрических функций.

 Подготовка:

• готовые чертежи и таблицы;
• презентация “Своя игра”.

ХОД УРОКА

I.. Актуализация знаний учащихся.

1. Как выражается sinα, cosα, tgα и ctgα острого угла прямоугольного треугольника?

2. Выясните, принадлежат ли единичной окружности точки:

А(-;), В(-; 2), С(- ;), D(; - ).

3. Выясните, какие точки лежат в I и во II четвертях: М(; - ), N (; ), Р (; ), S (- ; ).

4. Найдите значения sinα, tgα и ctgα, если cosα=- .

II. Систематизация знаний учащихся.

На прямоугольной системе координат построим полуокружность радиуса, равного 1 – единичная полуокружность. Возьмем точку М(х; у), принадлежащую этой полуокружности.

Sinα – это ордината точки, т. е. sinα=у.

Cosα – это абсцисса точки, т. е. cosα=х.

Так как координаты (х; у) точек единичной полуокружности заключены в промежутках 0<у<1 и -1<х<1, то для любого α справедливы следующие неравенства: 0< sinα <1 и -1< cosα <1.

(Приложение 1)

Рассмотрим треугольник АВС – прямоугольный. <А=α. Тангенсом острого угла α называется отношение противолежащего катета к прилежащему катету, т.е. tgα==

Аналогично, выражаем котангенс острого угла α. Мы вводили определение, хотя в учебнике оно не рассматривалось. Котангенсом острого угла α называется отношение прилежащего катета к противолежащему катету, т.е. ctgα==

Основное тригонометрическое тождество:

sin²α+cos²α=1

tgα=

ctgα=.

Справедливы следующие тождества:

sin(90⁰-α)=сosα sin(90⁰+α)=сosα

cos(90⁰-α)= sinα cos(90⁰+α)=-sinα

sin(180⁰-α)=sinα cos(180⁰-α)= — cosα — это формулы приведения.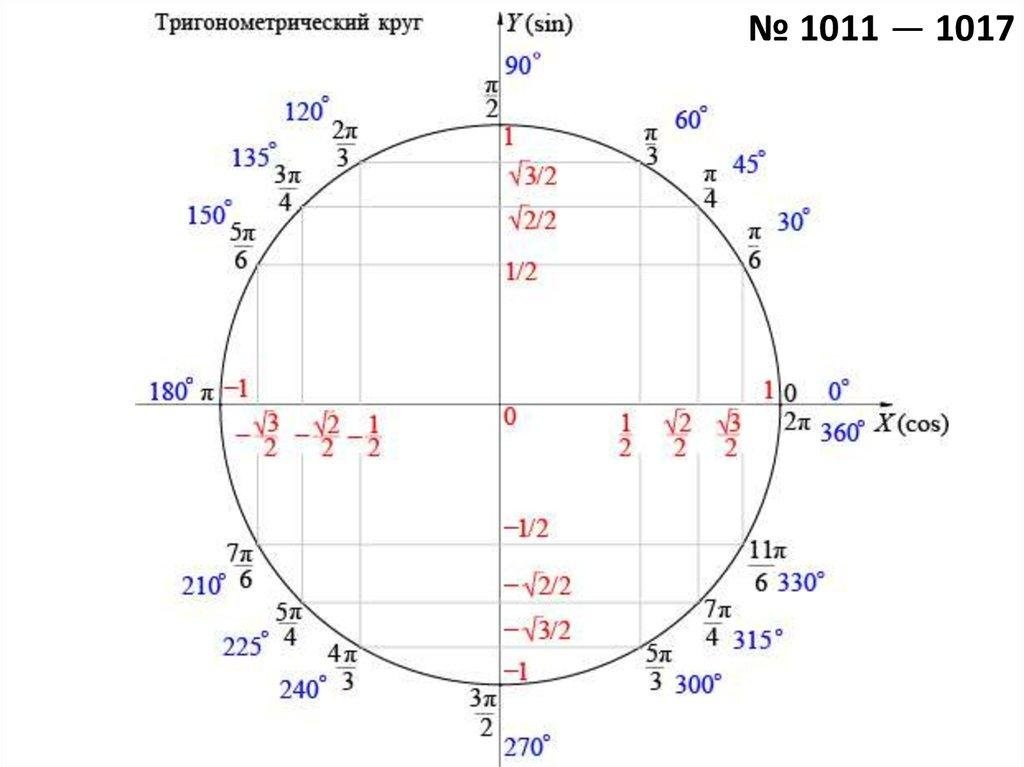

А теперь вспомним значения sinα, cosα, tgα и ctgα для табличных углов (Приложение 2).

III. Решение задач.

В приложении 3 дан чертеж: полуокружность с обозначениями дуг вида 15⁰n и точек 0, ±1, ±0,5, ± на оси абсцисс и полуоси ординат. По чертежу определите:

1. Может ли синус быть числом отрицательным?
2. Может ли косинус быть числом положительным?
3. В каких пределах может изменяться косинус?
4. В каких пределах может изменяться синус?
5. Чему равен синус 150⁰?
6. Каким может быть тангенс в I и во II четвертях?
7. Найдите sinα, tgα и ctgα, если cosα=-.
8. Найдите tgα и ctgα, если sinα= и 90⁰<α<180⁰.
9. Вычислите sinα, cosα, tgα и ctgα, если α=135⁰ и α=120⁰.

IV. Рефлексия.

Приложение 4 – “Своя игра”.

 V. Подведение итогов. Домашнее задание.

1. Вычислите sinα, cosα, tgα и ctgα, если α=150⁰.
2. Найдите cosα, tgα и ctgα, если sinα=

26.05.2014

Как определить значения синуса, косинуса, тангенса и котангенса

Определение значения синуса, косинуса, тангенса и котангенса

Определение

Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.

Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.

Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.  

Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:

1. Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
2. Весь пример, подвергать упрощению или преобразования постепенно;
3. Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:

\[ \sin x=\frac{a}{c} ; \cos x=\frac{b}{c} ; \operatorname{tg} x=\frac{\sin x}{\cos x} ; \operatorname{ctg}=\frac{1}{\operatorname{tg} x}=\frac{\sin x}{\cos x} \]

Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.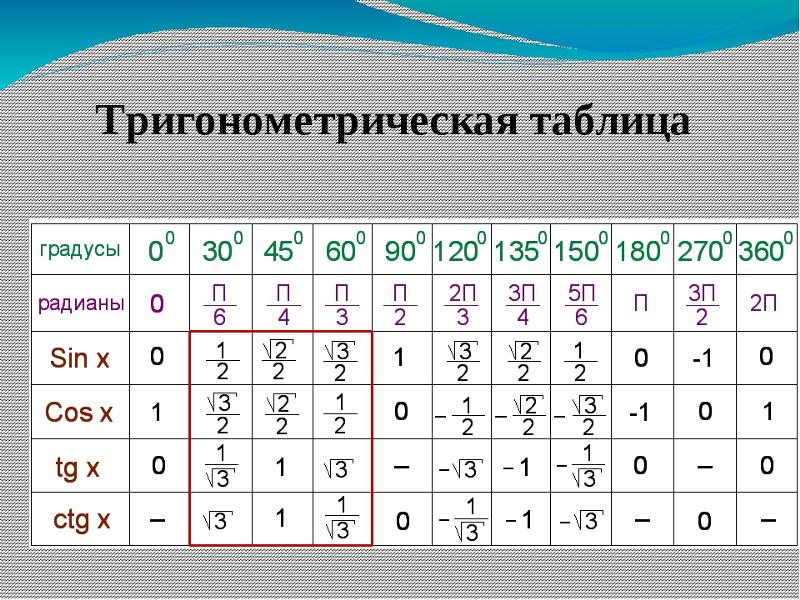 {\circ} \]

Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются

Мы произвели основные расчеты. Определили результаты угловых значений.

Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.

Таблица1.  Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан

Продолжение таблицы 1Продолжение таблицы 1

Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.

Например:

Значение заданной функции берется из таблицы. {\circ}.\]

Таблица Брадиса для решения основных задач по тригонометрии

Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух.  Произвести простых четыре перемножения.  Дважды разделить, умножить и отнять.

Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.  В таблице представлены следующие данные:

• число в квадратной и кубической степени;
• числа квадратных корней;
• логарифмические функции и значение;
• функции тригонометрии, представленный в градусах и радианах;
• обратные функции.

Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.

Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)

Примеры решения задач

Пример 1:

Необходимо определить синус угла 18 ° 44 ‘.

По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘   

Нужное значение равняется —  0,0006.

Узнав все необходимые значения, находим окончательное решение:

 sin   18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214

Пример 2:

Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.

Ответ: синус 76 ° 12 =0,2284.

Пример 3:

Нужно найти значение синус 16 градусов 32 минут.  Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть

 sin   16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214

Пример 4:

Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение  22 ° 12,  в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как  22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум  и видим, что нужный нам градус равный  22 ° имеет значение 0,0005. Далее записываем:

 sin   22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773

Пример 5:

Нужно найти значение косинус 50 градусов 33 минут.  Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0. 6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:

 косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454

Пример 6:

Нужно найти tg 35 градусов 6 минут.  В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.

Пример 7:

Нужно найти значение котангенс 13 градусов 42 минут.  Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2.  Находим искомое значение 4,102.

Пример 8:

Нужно найти значение косинус для 49° 33 минут.  

Для того чтобы вычислить  значение 49° 31.  В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка  равняется  трем. Значение  49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 .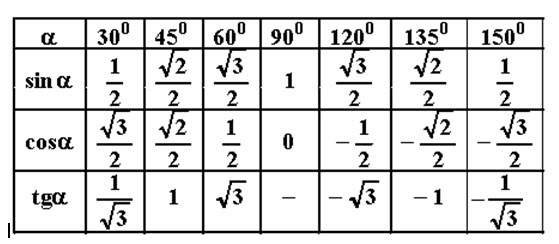 6361 +(- 0 . 0007) = 0,6454

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Основные способы, которые помогут заполнить таблицу функций

1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).

2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение \[\frac{\sqrt{x}}{2}\] и подставляем числовые значения, то есть величины углов.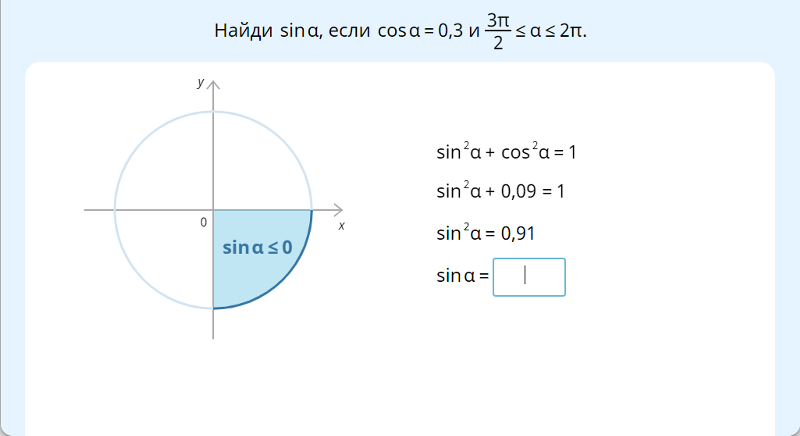 они записаны в первом столбике. Далее применяя   \[\frac{\sqrt{x}}{2}\] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.

Для наглядности все прописанные действия, можно разобрать на конкретном примере.

Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении \[\frac{\sqrt{x}}{2}\] записываем значение угла.

Получаем следующую запись: \[\frac{\sqrt{x}}{2}=\frac{0}{2}=0\]. Затем, проводим те же операции для заполнения оставшихся пустых строк.

\[ \frac{\sqrt{1}}{2}=\frac{1}{2} ; \frac{\sqrt{2}}{2}=\frac{(\sqrt{2 \cdot 2})}{(2 \cdot \sqrt{2})}=\frac{2}{2 \cdot \sqrt{2}}=\frac{1}{\sqrt{2}} ; \frac{\sqrt{3}}{2} \frac{\sqrt{4}}{2}=\frac{2}{2}=1 \]

Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.

3. Действие: Продолжаем считать таблицу. {\circ}=\frac{1}{\frac{1}{2}}=2\]

Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.

\[\text { Таким же методом заполняются оставшиеся строки таблицы. Так } \text { как } \operatorname{ctg}=\frac{1}{t g}, \text { в свою очередь } \operatorname{ctg}=\frac{\cos }{\sin }\]

Вычисление данных при помощи фигуры — прямоугольный треугольник

Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.  

Вычисление при помощи длин сторон треугольника происходит следующим образом:

• обозначается катет;
• сторона возле угла;
• сторона напротив угла с прямым значением. {\circ}=\frac{4}{6}=0,67\]

  Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.  

  В процессе решения задачи, это придется применять постоянно.

  Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.

  Косеканс находится \[\operatorname{cosec}=\frac{1}{\sin }\] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету \[\mathrm{sec}=\frac{1}{\cos }\].

  Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8.  Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.

  При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.

  Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.

  Вычисление значений углов по окружности

  Самый простой и понятный способ для вычисления углов и радиан.

  Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:

  Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.

  \[ \cos (\alpha+360 \cdot n)=\sin \alpha ;\] \[ \sin (\alpha+360 \cdot n)=\sin \alpha / \]

  Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.

  \[ \operatorname{tg} \alpha=\frac{\sin \alpha}{\cos \alpha} ; \operatorname{ctg} \alpha=\frac{\cos \alpha}{\sin \alpha} \]

  Расчет

  — Предел $\frac{\sin(\theta)}{\theta}$ в градусах

  спросил 8 лет, 3 месяца назад

  Изменено 2 года, 3 месяца назад

  Просмотрено 3к раз

  $\begingroup$

  Чему равно $\lim \limits_{\theta\to0}\dfrac{\sin(\theta)}{\theta}$, если $\theta$ выражено в градусах? 9\ circ} = \ lim _ {\ theta \ to0} \ frac {\ sin \ left ( \ dfrac {\ pi \ theta} {180} \ text { радианы} \ right)} {\ theta} = \ lim _ {\ eta \to0} \frac{\sin(\eta\text{радианы})}{\left(\dfrac{180\eta}{\pi} \right)} = \frac\pi{180}\lim_{\eta \to0} \frac{\sin\eta}{\eta}. $$

  Вот почему используются радианы: Когда используются радианы, то $\lim\limits_{\eta\to0} \dfrac{\sin \eta} \eta=1$.

  Постскриптум в ответ на комментарии ниже:

  Вопрос как найти \начать{выравнивать} & \lim_{\theta\to0} \frac{\text{синус $\theta$ градусов}}\theta = \lim_{\theta\to0}\frac{\text{функция синуса в радианах}\left(\ dfrac{\pi\theta}{180}\right)} \theta \\[12pt] = {} & \ frac \ pi {180} \ lim _ {\ theta \ to0} \ frac {\ text {функция синуса в радианах} \ left (\ dfrac {\ pi \ theta} {180} \ right)} {\ dfrac{\pi\theta}{180}} = \frac\pi{180}\lim_{\eta\to0} \frac{\text{функция синуса в радианах}(\eta)}\eta. \end{выравнивание} 9*(x) = \sin\left(\frac{2\pi x}{360}\right)$$

  (над этим стоит немного подумать)

  Во всяком случае, сейчас мы пытаемся вычислить

  $ $\lim_{x\rightarrow 0} \frac{\sin(\frac{2\pi x}{360})}{x}$$

  Применяя L’Hopital, это равно пределу

  $$ \lim_{x\стрелка вправо 0} \frac{2\pi}{360} \frac{\cos(\frac{2\pi x}{360})}{1} = \frac{2\pi}{360 } \sim 0. 01745.$$

  $\endgroup$

  2

  $\begingroup$

  Если известен предел в радианах $$\lim_{x \to 0} \frac{\sin x}{x}$$, то предел с $x$ в градусах равен $$\lim_{x \to 0} \frac{\sin \frac{\pi x}{180}}{x} = \frac{\pi}{180}\lim_{x \to 0} \frac{ \sin \frac{\pi x}{180}}{\frac{\pi x}{180}}$$

  $\endgroup$

  5

  $\begingroup$

  Когда говорят, что углы выражены в градусах, это на самом деле означает, что при применении тригонометрических функций они интерпретируются как градусы. Следовательно, в вопросе «$\sin(\theta)$» следует понимать как $$\sin\left(\frac{\pi\theta}{180}\right)$$, где $\sin$ — обычный синус функция (аргументы в радианах), и вы на самом деле вычисляете

  $$\lim_{\theta\to0}\frac{\sin\left(\dfrac{\pi\theta}{180}\right)}\theta. $$

  знаменатель, деление по-прежнему обычное деление. Только тригонометрическая функция является «особой».

  $\endgroup$

  $\begingroup$

  Вопрос поставлен неправильно.

  В любых единицах измерения угла результат один и тот же $(=1).$

  Для всех единиц (градусы, радианы) 9\circ}{n}$

  Я не готов касаться основной части вашего поста, но что касается цикличности рассуждений, которые вас больше всего беспокоят, я позволю себе не согласиться. Все остальное, что вы опубликовали, кажется, связано с примерами, для которых ваша озабоченность имеет последствия, а не как отдельные вопросы сами по себе.

  Градусы как единица измерения углов предшествуют радианам. Тригонометрические функции определяются в углах, а не в какой-либо конкретной единице измерения, поэтому их можно измерять в любых желаемых единицах измерения.

  Тригонометрические функции веками вычислялись в градусах. Нет, на самом деле, думая о тригонометрических функциях в терминах радианов, а не более абстрактно в терминах углов, на мой взгляд, ЕСТЬ , где имеет место цикличность рассуждений. Это связано с тем, что радиан ставится перед функцией, а не из-за необходимости специальной единицы при обработке тригонометрических функций в исчислении. Возможно, эта точка зрения слишком уважительна к истории, чтобы ее можно было придерживаться в математике, но мне нравится рассматривать математику в хронологическом порядке, в котором она была открыта; это, как правило, устраняет большую часть цикличности.

  В определении $\sin(x)$ нет цикличности, когда $x$ выражается в градусах. Единственный раз, когда возникает конфликт, это когда $x$ также существует за пределами аргумента функции — например, $x\sin(x)$, ясно, что единица меняет решение. Или когда путем какого-либо преобразования (например, дифференцирования) из аргумента выводится константа — если $x$ выражено в радианах, то $\frac{d}{dx}\sin(x)=\cos(x )$, но если $x$ в градусах, то $\frac{d}{dx}\sin(x) = \frac{\pi}{200}\cos(x)$. Также следует отметить полиномиальные представления тригонометрических функций, приближенные или иные, но это потому, что они построены на дифференцировании. Список можно продолжать, я уверен. Это не является исчерпывающим. Я только предполагаю, что если выражение каким-то образом получено из тригонометрической функции, особенно с использованием исчисления, то необходимо соблюдать осторожность.

  Я мог бы доказать, что $\frac{d}{dx}\sin(x) = \frac{\pi}{180}\cos(x)$, если бы хотел использовать только градусы. Математика совершенно верна и совершенно строга, но если бы вы просто слепо выполняли движения, вы могли бы не понять, почему. Если бы вы думали только с точки зрения радианов, вы, вероятно, назвали бы это неправильным. Но именно так выглядела бы идентичность, если бы мы никогда не создавали радиан. Таким образом, многие из тех выражений, которые вы написали, будут содержать константы, включающие отношения пи к 180, и это просто запутает. Это одна из причин, по которой радиан был изобретен и стандартизирован как единица измерения угла: он устраняет эти константы.

  No related posts.