Варианты комбинаций из 4 цифр: «Сколько можно составить различных пин-кодов из 4 цифр, если пин-коды из 4-х одинаковаых цифр запрещены?» — Яндекс Кью

Сколько вариантов комбинаций из 4 цифр? Ответ с примерами.

Очень интересный вопрос, а именно сколько вариантов комбинаций можно получить из четырёх цифр. Чтобы ответить на этот вопрос достаточно просто посчитать, но нужно знать как правильно это делать. Итак, сегодня мы разберём, как правильно считать комбинации цифр, и не только с четырьмя цифрами, но и с другими. Чтобы вы смогли посчитать любое количество вариантов. А также ответим на вопрос, сколько же вариантов можно получить.

Итак, у кодового замка четыре цифры, каждая из цифр имеет 10 вариантов, потому что каждая колёсико может быть от нуля до девяти, а значит это 10 вариантов в каждом колёсике. Конечно цифры могут повторяться.

Если в замке четыре цифры, то это всё можно найти количество комбинаций по формуле. берём n — это количество чисел, их 10. И возводим 10 в 4 степени, так как замок четырёх разрядный. 10 в четвёртой степени = 10 000 комбинаций.

Итак, со всеми другими замками точно также.

Если там три цифры, значит 10 в третьей степени, если необходимо пять цифр, значит 10 в пятой степени.

Можно посчитать и по другой формуле, если цифра ноль входит в те знаки, которые есть могут быть кодом замке, то количество чисел будет больше нуля или равно 0. Таким образом можно перебирать цифры начиная с 0000, потом 0001 итд. Конечно, в итоге вы придёте к числу 9999, а значит таких комбинаций как раз и получилось 9999, но так как у нас ещё есть число ноль мы прибавляем его, как число, и получаем, что всего комбинация 9999 + 1 = 10 000 комбинаций.

Также во внимание можно брать подсказки, например, если число 0 у вас не входит в цифры, то начинается с одного, то получается не 10 цифр, а девять. Соответственно, мы берём 9 в четвёртой степени, то получает 6561.

Или например, два крайних ролика разные. то возникают другие варианты, либо ролики у всех разные цифры, тогда мы вычитаем такие цифры, как 9999, либо 1111, потому что цифры не должны повторяться, либо цифры на правом ролике не должны совпадать с цифрами, на левом тогда максимальное количество комбинаций 25, а во втором случае для права ролика, получается только девять возможных комбинаций.

Также во внимание можно взять, что по статистике люди часто выбирают коды с четными цифрами, например, 2684 итд. Редко встречаются и нечетные комбинации, например, 1357. Также ещё чаще встречаются комбинации 1111 и 0000.

Если высчитывать по времени, то для подборки, если у вас 10000 комбинаций, то если вы будете тратить по 10 секунд, на каждый код уйдёт более 27 часов и подбором данном случае пользоватся будет очень тяжело.
Ну если нужно открыть замок, то можно почувствовать разболтанность колёсика, если этот замок открывали часто.

Поэтому подбирать 10000 комбинаций или не подбирать, выбор каждого. По такому же принципу можно высчитать количество комбинаций для 5-ти значных кодов , 6-ти значных и любых других кодов.

Поделиться с друзьями:

Сколько комбинаций можно составить из 4 цифр

Магазины › Фикс Прайс › Замок из Фикс Прайса кодовый как открыть

Можно сказать что это числа от 0 до 9999. Значит всего возможных комбинаций 10 000. Ответ: 10 000 комбинаций.

• Всего возможных комбинаций из 4 цифр — 10 000.
• Количество комбинаций из цифр 1, 2, 3, 4 — 24.
• Шанс угадать пароль из 4 цифр, если он выбирается случайным образом — 0,001.
• Наиболее распространенные пароли из 4 цифр — 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998.
• Количество комбинаций из 3 цифр 1, 2, 3, 4 без повторений — 6.
• Количество комбинаций из 3 цифр — 60.
• Количество комбинаций из 6 цифр с повторениями — 720.
• Количество возможных комбинаций пароля зависит от количества разрешенных символов и длины пароля.
• Формула для определения количества возможных комбинаций цифр — nCr = n! / р!.

1. Сколько комбинаций можно составить из цифр 1 2 3 4
2. Какой шанс угадать пароль из 4 цифр
3. Какой может быть пароль из 4 цифр
4. Сколько комбинаций из 3 цифр 1 2 3 4 без повторений
5. Какое количество комбинаций из 3 цифр
6. Сколько комбинаций из 6 цифр с повторений
7. Сколько возможных комбинаций пароля
8. Как посчитать количество комбинаций цифр
9. Как угадать пароль от карточки
10. Как поставить пароль на 4 цифры
11. Какой самый сложный пароль из цифр
12. Какие люди ставят пароли
13. Сколько комбинаций из 999 цифр
14. Сколько комбинаций из 10 цифр без повторений
15. Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6 цифры не могут повторяться
16. Сколько комбинаций из 5 цифр 12345
17. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5 6 без повторений
18. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5
19. Какой самый лучший пин код
20. Какой шанс угадать 6 цифр
21. Как должен выглядеть пароль
22. Что люди чаще всего ставят на пароль
23. Что не должен содержать пароль
24. Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются
25. Как посчитать количество комбинаций без повторений
26. Сколько четырехзначных чисел можно составить из цифр 1 3 5 7 9
27. Сколько комбинаций из 4 цифр от 1 до 2
28. Как рассчитать количество возможных комбинаций
29. Сколько комбинаций можно составить из 8 цифр

Сколько комбинаций можно составить из цифр 1 2 3 4

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.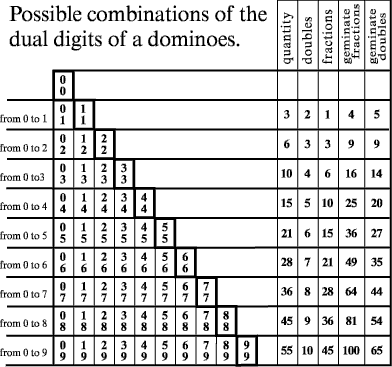

Какой шанс угадать пароль из 4 цифр

0000, 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999. Если считать, что pin-код выбирается случайным образом, то вероятность что он состоит из четырех одинаковых цифр: 10 / 10000 = 0,001. Ответ: 0,001.

Какой может быть пароль из 4 цифр

Наиболее распространенными четырехзначными PIN-кодами оказались 1234, 0000, 2580, 1111, 5555, 5683, 0852, 2222, 1212 и 1998, а шестизначными — 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789456 и 159753.

Сколько комбинаций из 3 цифр 1 2 3 4 без повторений

Рассмотрим комбинации из трёх цифр 1,2,3 без повторений. Таких комбинаций 6.

Какое количество комбинаций из 3 цифр

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, )

Сколько комбинаций из 6 цифр с повторений

Допустим, есть шесть цифр. То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов. k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля.

Как посчитать количество комбинаций цифр

Формула для определения количества возможных комбинаций выглядит следующим образом: nCr = n! / р!

Как угадать пароль от карточки

PIN-код (персональный идентификационный номер) — набор цифр платежной карты, известен только держателю карты для его идентификации при осуществлении операций. Он генерируется таким образом, что его не знает ни один сотрудник (даже тот, кто выдавал вам конверт с кодом), его нельзя посмотреть ни в одной системе банка.

Как поставить пароль на 4 цифры

Шаг 1: Откройте приложение «Настройки» и перейдите к «Touch ID и пароль». Вам нужно будет ввести шестизначный пароль для доступа к этому меню. Шаг 2: Прокрутите вниз и коснитесь параметра «сменить код-пароль. Шаг 3: Введите существующий шестизначный пароль для продолжения.

Какой самый сложный пароль из цифр

Очень сложным и самым лучшим считается пароль от 10-12 символов длиной, с использованием заглавных, прописных букв, цифр и спецсимволов: L2jh4d61e%Fh — пример сложного и стойкого пароля.

Какие люди ставят пароли

В частности, в десятку самых популярных паролей вошли: 123456, 123456789, qwerty, password, 12345, qwerty123, 1q2w3e, 12345678, 111111, 1234567890.

Сколько комбинаций из 999 цифр

999). Всего комбинаций из цифр и букв может быть: 676 × 9 999 999 = 6 759 999 324 (6 млрд. 759 млн.

Сколько комбинаций из 10 цифр без повторений

Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 3610 или 3,6561584×1015. Если символы не могут повторяться, то мы имеем дело с размещениями.

Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6 цифры не могут повторяться

Ответ: Можно составить 32 трехзначных четных числа.

Сколько комбинаций из 5 цифр 12345

Комбинаторика. Сколько всего возможных комбинаций из пяти чисел 12345, да 120, надо лишь эти числа между собой перемножить 12345=120, но есть одно «но» нужно подсчитать еще и такие варианты как например 11234, 11123, 11112, 12234, 12333, 12222, 12344 и т.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5 6 без повторений

Ответ: Можно составить 120 чисел.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5

ПРИМЕР 3. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? И сколько из них с неповторяющимися цифрами? = 5× 4×3 = 60.

Какой самый лучший пин код

Анализ позволил выявить несколько интересных фактов. Самым популярным PIN-кодом является 1234, его устанавливают почти 11% пользователей. На втором месте идёт 1111 (6%). Двадцатка самых популярных комбинаций покрывает 26,83% всех паролей, хотя при нормальном статистическом распределении она составляла бы всего 0,2%.

Какой шанс угадать 6 цифр

Совпадение 6 чисел — шанс 0,00000012 (в процентном выражении — 0,000012%). Совпадение 5 чисел — шанс 0,000029 (0,0029%).

Как должен выглядеть пароль

Что такое надежный пароль?:

• Не менее 12 символов. Чем длиннее ваш пароль — тем лучше.
• Содержит прописные и строчные буквы, цифры и специальные символы.
• Не содержит буквы или цифры, которые идут подряд в раскладке.
• Не основан на вашей личной информации.
• Пароль уникален для каждой вашей учетной записи.

Что люди чаще всего ставят на пароль

Топ-10 самых используемых паролей в России выглядит так:

• 123456789;
• 12345;
• password;
• qwerty123;
• 1q2w3e;
• 12345678;
• 1234567890;
• 1q2w3e4r5t.

Что не должен содержать пароль

Пароли НЕ ДОЛЖНЫ состоять из: Вашего имени, отчества или фамилии ни в каком виде (т. е. написаны в строчном, в прописном, в смешанном виде, задом наперед, два раза и т.

Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются

Ответ. Всего из этих цифр можно составить 120 чисел, без повтора цифр внутри них.

Как посчитать количество комбинаций без повторений

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n! (n−k)! ⋅k!.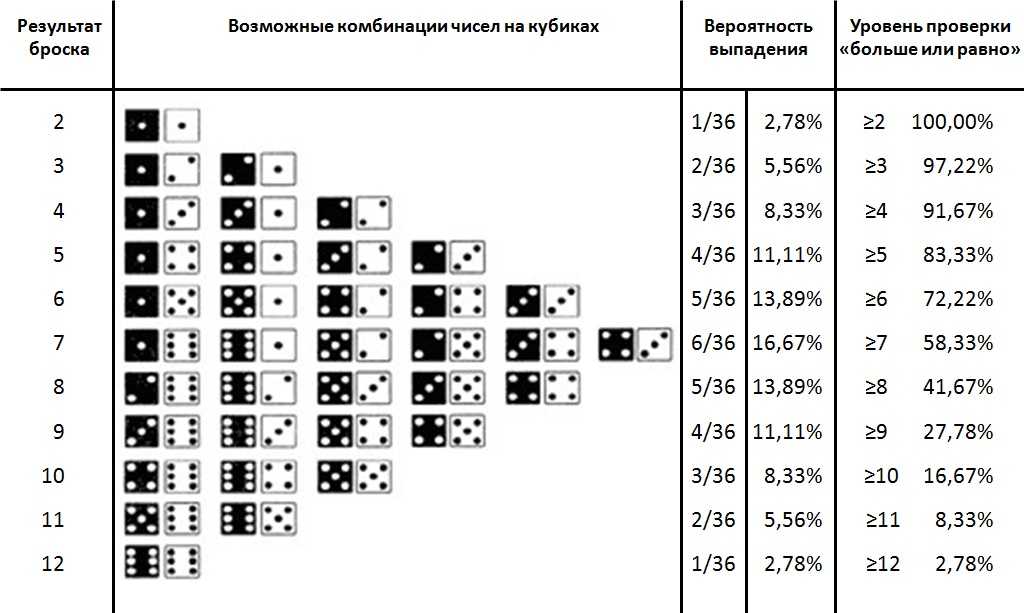 15.

• Как посчитать количество комбинаций цифр
• Как посчитать сколько всего комбинаций
• Как рассчитать все возможные комбинации
• Как узнать количество комбинаций цифр
• Как узнать сколько будет комбинаций
• Как узнать сколько комбинаций можно составить
• Какое количество комбинаций из 4 цифр
• Сколько вариантов комбинаций из 4 цифр
• Сколько вариантов комбинаций с 4 цифрами
• Сколько комбинаций из 10 цифр по 4
• Сколько комбинаций из 4 цифр от 0 до 1
• Сколько комбинаций с 3 цифр
• Сколько нужно комбинаций из 3 цифр
• Сколько различных кодовых комбинаций можно составить при использовании 4 разрядного двоичного кода
• Сколько существует комбинаций из 3 цифр

Сколько четырехзначных чисел можно составить из повторяющихся цифр 1, 2, 3, 4, 5?

В математике перестановка относится к функции упорядочивания всех членов группы в некоторый ряд или порядок. Другими словами, если группа уже направлена, то перенаправление ее компонентов называется процессом перестановки. Перестановки происходят более или менее важным образом почти в каждой области математики. Они часто появляются при соблюдении различных команд на определенных ограниченных местах.

Перестановка

Перестановка известна как процесс упорядочивания группы, тела или чисел по порядку, выбор или чисел из набора, известен как комбинации таким образом, что последовательность целых чисел не беспокоить.

Формула перестановки

При перестановке r элементов собираются из n элементов без какой-либо замены. В этой последовательности собираем материю.

^н П _р = (п!)/(п – г)!

Здесь

n = размеры набора, общее количество объектов в наборе

r = размеры подмножества, количество объектов на выбор из набора

Комбинация

Комбинация является способом выбора объектов из группы, так что (в отличие от перестановок) последовательность выбора не имеет значения. В меньших случаях можно представить, суммируя, количество комбинаций. Комбинация относится к комбинации n объектов, взятых k одновременно без повторения. Говоря о комбинациях, в которых допускается повторение, часто используются выражения k-выбор или k-комбинация с повторением.

Формула комбинации

В комбинации r объектов выбираются из группы n объектов, причем последовательность выбора не имеет значения.

ⁿ C _r = n!⁄((n – r)! r!)

Здесь

n = количество объектов, выбранных из группы

r = количество объектов, выбранных из группы

Сколько четырехзначных чисел можно составить из чисел 1, 2, 3, 4, 5 с повторяющимися цифрами?

Решение:

Допускается повторение цифры. Итак, для разряда единиц у нас есть 5 вариантов, т.е. 1,2,3,4,5, аналогично для разряда десятков у нас снова 5 вариантов, т.е. 1,2,3,4,5 для сотого места, у нас есть 5 вариантов, т. е. , 1,2,3,4,5 аналогично, для тысячного разряда имеем 5 вариантов т.е. 1,2,3,4,5.

Общее количество четырехзначного числа = 5 × 5 × 5 × 5

                                               = 625

Похожие вопросы

Вопрос 1: Сколько шестизначных чисел можно составить, используя цифры 0,1,2,3,4,5. Допускается ли повторение цифр?

Ответ:

Допускается повтор цифр. Итак, для первого места у нас есть 6 вариантов, т.е. 0,1,2,3,4,5, аналогично для второго места у нас снова 6 вариантов, т.е. 0,1,2,3,4,5 для третьего места мы имеем 6 вариантов, т.е. 0,1,2,3,4,5, для четвертого места имеем 6 вариантов, т.е. 0,1,2,3,4,5, а для пятого тысячного места имеем 6 вариантов, т.е. 0 ,1,2,3,4,5, а для шестого места у нас есть 5 вариантов, то есть 1,2,3,4,5, мы не можем взять 0 на последнем месте, потому что если 0 будет заполнен на последнем месте, он будет не станет 6-значным числом, оно будет принято как 5-значное число.

Общее количество шестизначного числа = 4 × 5 × 5 × 5 × 5 × 5

                                                             = 12500

1,0) если повтор цифр не допускается?

Ответ:

Для четного числа целое число должно быть 0. Теперь целые числа выдерживают 5, т.е. 3,5,7,9,1 теперь для тысячного разряда у нас есть 5 вариантов для сотого разряда мы есть 4 варианта, а для разряда десятков у нас есть 3 варианта

Общее количество из 4 цифр можно найти равномерное число = 5 × 4 × 3

= 60

Вопрос 3: Сколько 8 -значных чисел можно найти, используя цифры 1, 2, 3,4,5,6 и 7 ( разрешены повторения) таким образом, чтобы число читалось одинаково слева направо или справа налево?

Решение:

Восьмизначное число, которое читается одинаково слева направо и справа налево, означает, что последние четыре цифры совпадают с первыми четырьмя цифрами, но в противоположном направлении. Итак, это четырехзначное число.

Повторение цифры разрешено. Итак, для первого числа у нас есть 7 вариантов, аналогично для второго числа у нас снова 7 вариантов, для третьего числа у нас есть 7 вариантов, а для четвертого числа у нас есть 7 вариантов.

 Таким образом, возможные числа = 7 × 7 × 7 × 7

                                                         6 и 7, чтобы цифры не повторялись, а последние цифры были четными, это

Решение:

Так как последние цифры четные.

Таким образом, 1-е место можно проникнуть 3 способами, а последнее место можно проникнуть 2 способами, а остальные места можно проникнуть

⁵ P ₄ ​= 120 способами  

Следовательно, число шесть число цифр, так что последние цифры четные, равно 3 × 120 × 2 = 720.  

Сколько 4 числовых комбинаций с использованием 1 2 3 4 и что это такое?

5

5 ответов

Эйдан Маккартни ответил

Всего существует 24 комбинации цифр, которые можно составить, используя только цифры 1, 2, 3 и 4.

Эти 24 комбинации цифр перечислены ниже в порядке комбинаций цифр, начиная с цифры 1. и заканчивая комбинациями цифр, которые начинаются с цифры четыре.

1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 1431, 3124, 3142, 3214, 3241, 3412, 3421, 2, 41323, 4 4312, 4321.

В математике комбинация — это способ выбора нескольких элементов из большей группы, где, в отличие от перестановок, порядок не имеет значения. В меньших случаях можно подсчитать количество комбинаций. Например, учитывая три фрукта, скажем, яблоко, апельсин и грушу, из этого набора можно составить три комбинации: яблоко и груша; яблоко и апельсин; или груша и апельсин.

Более формально k-комбинация множества S — это подмножество k различных элементов S. Если множество состоит из n элементов, количество k-комбинаций равно биномиальному коэффициенту. Комбинациями можно считать комбинации из n вещей, взятых k за раз без повторений или с повторениями. Однако если бы можно было получить два фрукта любого вида, то было бы еще 3 комбинации: одна с двумя яблоками, одна с двумя апельсинами и одна с двумя грушами.

Зачем актерам и артистам нужны…

Пожалуйста, включите JavaScript

Зачем актерам и артистам нужны сценические имена? (Пример из практики)

При работе с большими наборами возникает необходимость использовать математику для определения количества комбинаций. Например, покерную комбинацию можно описать как комбинацию из 5 (k = 5) карт из колоды из 52 карт (n = 52). Все 5 карт в руке различны, и порядок карт в руке не имеет значения. Таких комбинаций 2 598 960, а вероятность случайного выпадения любой руки составляет 1/2,59.8960.

поблагодарил автора.

брякнул это.

Анонимный ответил

1234,1243,1324,1342,1423,1432
2134,2143,2314,2341,2413,1431
3124,3142,3218,41240,41241,41241. 123,4132,4213,4231,4312 ,4321

24 номера.

поблагодарил автора.

брякнул это.

Bernie Zuccarelli ответил

Приветствие:

Это основа всех лотерей Pick-Four по всей стране.

Существует 10 000 возможных комбинаций чисел от одного до четырех. Они варьируются от 0000 до 9999.

Как вы получаете ответ, довольно просто. 10000 это 10х10х10. Если вы начнете с 10, у вас будет 10 возможных комбинаций однозначных чисел от 0 до 9.  Умножьте на десять, и вы получите 100.  Существует 100 комбинаций двузначных чисел… от 00 до 9.9.  Умножьте 100 на 10, и вы получите 1000 комбинаций трехзначных чисел от 000 до 999.  Умножьте еще раз на 10, и вы получите 10 000 комбинаций.

Все просто.

Я надеялся, что это помогло.

Bernie520
Сиэтл, Вашингтон

поблагодарил автора.

брякнул это.

Анонимный ответил

Перечислите комбинации.

No related posts.