Векторы для чайников. Часть 1. Сложение, разность, умножение на число. — Блог
Векторы для чайников. Часть 1. Сложение, разность, умножение на число.
18 июня 2021 0 Marina Pashnina
Есть на баше одна уже старая шутка про черного кота, которая звучит как-то так:
— Если чёрный кот перешел дорогу туда и обратно, это значит, что он удвоил наказание или отменил своё решение?
— Кот скалярный или векторный? Если скалярный — то удвоил, если векторный — то отменил.
В общем, с этой ноты и начинается статья про то, что было бы, если бы уже знакомый нам кот по имени Котаненс был векторным или скалярным, или статья о векторах.
Вектор — это направленный отрезок и главное, что нужно знать о векторе — у него есть величина и направление. Тут пока все сходится с котом, переходящим дорогу: кот идет в определенном направлении и проходит при этом определенное расстояние.
В школьном курсе геометрии рассматриваются некоторые действия над векторами: сложение векторов, умножение вектора на число, разность векторов. В основном, эти действия интуитивно понятные, достаточно только представить или нарисовать вектор или пару векторов. Давайте коротко рассмотрим эти действия.
Отдельно оговорюсь о существовании нулевых векторов — таких векторов, у которых начало и конец находятся в одной точке. Для упрощения материала этот нулевой вектор будет местами игнорироваться ввиду малой практической значимости.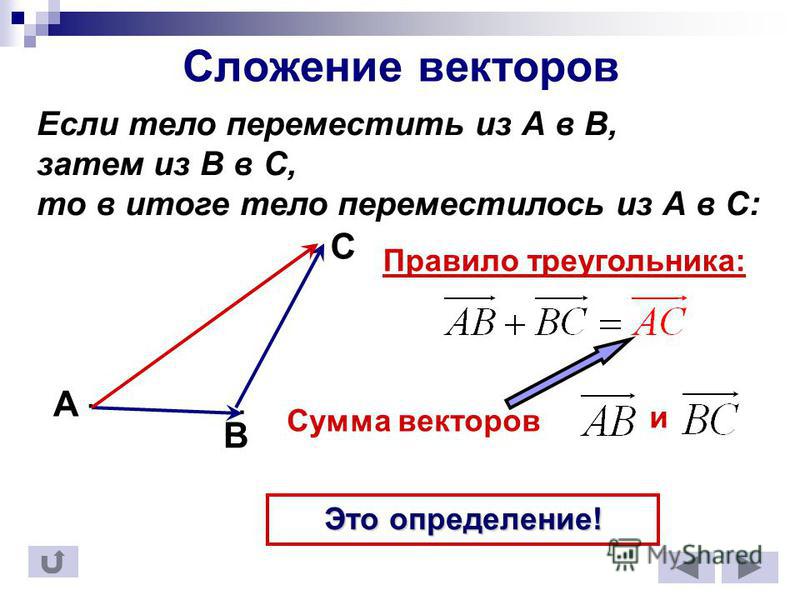
Что ж, начнем.
Сложение векторов
Есть несколько методов сложения векторов, которые руководствуются похожими принципами.
Для сложения двух векторов нам понадобятся вектора ā и b̅ (кто бы мог подумать?) .
Отложим вектор b̅ от вектора ā и проведем от конца вектора ā до начала вектора b̅ результирующий вектор. Этот прием называется правило треугольника.
Результатом сложения будет вектор ā + b̅. Всё также, как с котом: сначала кот прошел по вектору ā (определенное расстояние в определенном направлении), затем по вектору b̅. То, что он прошел в итоге — это и есть результирующий вектор ā + b̅.
Это же работает и для сложения нескольких векторов: кот может пробежать по зиг-загу, или же статно пройти по результирующему вектору.
Если же вектор b̅ отложить не от конца, а от начала вектора ā, то получится правило параллелограмма.
Тут можно вспомнить векторного кота из шутки — если векторный кот пройдет туда-обратно, результирующий вектор, по которому он пройдет — будет равняться 0, а значит — кот отменит свое проклятье.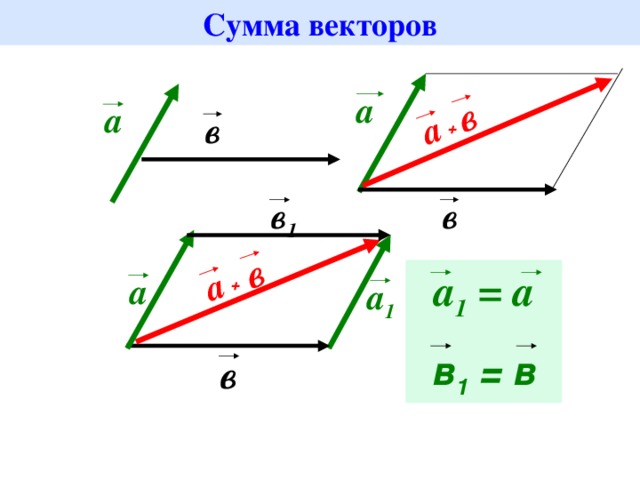
Скалярный же кот при проходе туда-обратно сложит длины векторов и получит число в 2 раза больше изначального, а значит и проклятье удвоится.
Разность векторов
Разность векторов ā и b̅ также можно рассчитать несколькими способами.
ā — b̅, как частный случай сложения — это сложение вектора ā с вектором, обратному b̅, т.е. ā + (-b̅).
Вектор -b̅, обратный к вектору b̅ сделать просто: кот просто должен пойти в обратную сторону.
А дальше просто складываем этот вектор с вектором ā.
Второй способ получить разность векторов чуть сложнее для осознания: разностью векторов ā и b̅ называется такой вектор, сумма которого с вектором b̅ дает вектор ā. Для понимания достаточно просто нарисовать на листочке и все станет ясно.
Умножение вектора на число
Умножение вектора a на число n создает такой вектор, длина которого равна |ā| * | n |, где |ā| — это длина вектора a, а направление сохраняется при n >= 0 и меняется при n < 0.
Эта статья оказалась достаточно объемной, поэтому я рещила разделить ее на 2 части: во второй части статьи будет рассказано про векторное и скалярное произведение векторов и об этом можно почитать в статье «Векторы для чайников. Часть 2.».
Скалярное и векторное произведения. Проекция вектора на вектор
В данной статье будут изложены основные инструкции, относительно векторов. С их помощью Вы будете знать что с ними можно делать, а что нет. Поэтому переходим к изучению операций над векторами.
І. Суммой двух -мерных векторов
и называют-мерный вектор , координаты которого равны сумме соответствующих координат векторов — слагаемых:
Например, если ,
то
Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов
ІІ. Произведением числа (скаляра) на -мерный вектор называется -мерный вектор , координаты которого равны произведению числа на соответствующие координаты вектора
Например
Операции сложения векторов и умножения числа на вектор ( — некоторые числа) обладают свойствами:
1)
2)
3)
4)
5)
6)
7) Для произвольного вектора существует противоположный вектор такой, что
ІІІ.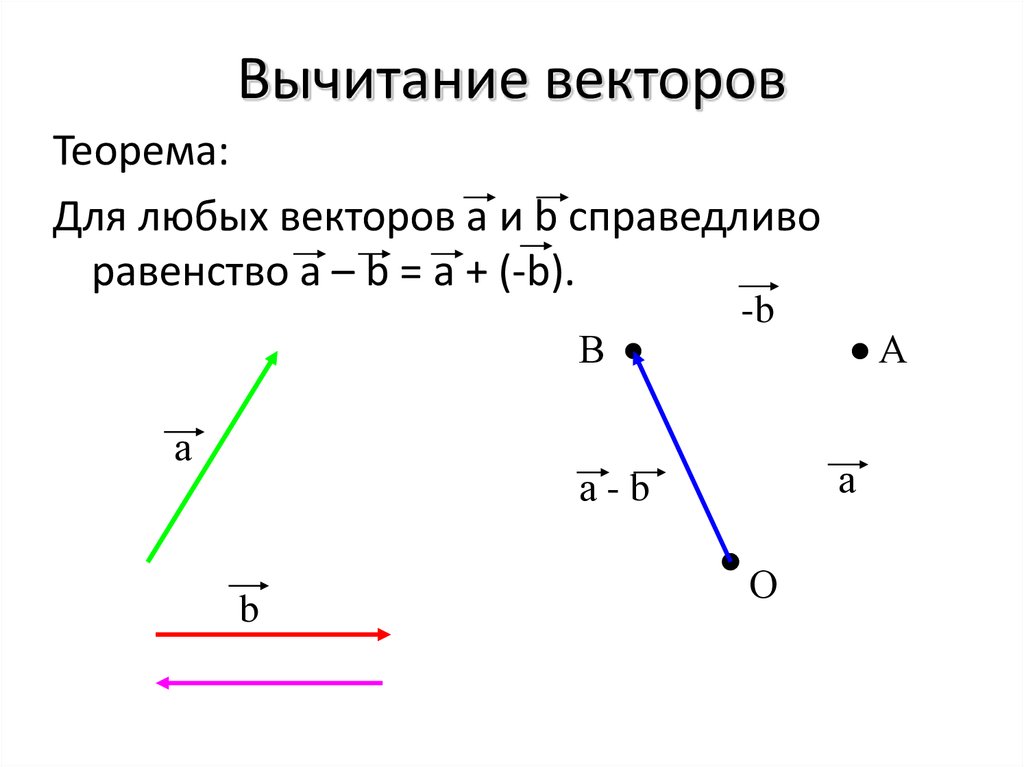
Скалярным произведением двух -мерных векторов и называют число, равное сумме произведений соответствующих координат векторов:
Например,
если, то
Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними
Из приведенного выше определения можно получить формулу для вычисления угла между векторами
или в координатной форме
Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого
Из последнего определения вытекают формулы для нахождения проекции вектора на вектор
или в координатной форме
Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.
Алгебраические свойства скалярного произведения векторов:
1)
2)
3)
4)Равенство имеет место при условии
Геометрические свойства скалярного произведения
1)векторы перпендикулярны между собой, если
2) угол между векторами острый в случаях, когда
3) угол между векторами тупой в случаях, когда
ІV.
Векторным произведением или двух векторов называется вектор , который отвечает следующим условиям:
1) модуль вектора равен произведению модулей векторов и на синус угла между ними
2) вектор нормальный к плоскости, построенной на векторах и ;
3) вектор направлен так, что с его конца кратчайший поворот от вектора к происходит против часовой стрелки. Иными словами, векторы образуют правую тройку.
Векторное произведение имеет следующие геометрические свойства:
Его модуль равен площади параллелограмма построенного на векторах и
Поэтому площадь треугольника построенного на векторах и равна модулю половины векторного произведения этих векторов
Алгебраические свойства векторного произведения
1) векторное произведение равно нулю в случае коллинеарности векторов или когда один из них нулевой;
2) от перестановки векторов векторное произведение меняет знак на противоположный
3)
4)
На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее
Рассмотрим конкретные примеры для усвоения пройденного материала.
———————————————
Задача 1.
Заданы векторы и
Найти следующие величины
1) сумму векторов
2) скалярное произведение векторов
3) ) векторное произведение площадь треугольника построенного на векторах
4) угол между векторами
5) проекцию каждого из векторов на другой
Решение
1) Проведем вычисления
2) Скалярное произведение будет равно
3) Векторное произведение вычисляем по формуле
Площадь треугольника будет равна
4) Найдем угол между векторами по формуле
В ней скалярное произведение уже найдено поэтому находим длины векторов
Подставляем нужные значения в формулу
Находим значение угла
5) Найдем проекции векторов
Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится
На этом урок окончен.
Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.
——————————————————
Посмотреть материалы:
- Длина вектора. Угол между векторами
- Скалярное произведение векторов
- Разложение вектора по базису
- Смешанное произведение векторов
- Деление отрезка в заданном отношении
- Треугольная пирамида
Почему вектор C равен вектору A — B?
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 475 раз
$\begingroup$
Я новичок в многомерном исчислении и не могу не спросить себя, почему вектор $\vec{C}$ равен $\vec{A} -\vec{B}$?
Изменить: + исправлено на —
- векторов
$\endgroup$
2
$\begingroup$
Это не исчисление, а просто векторная алгебра.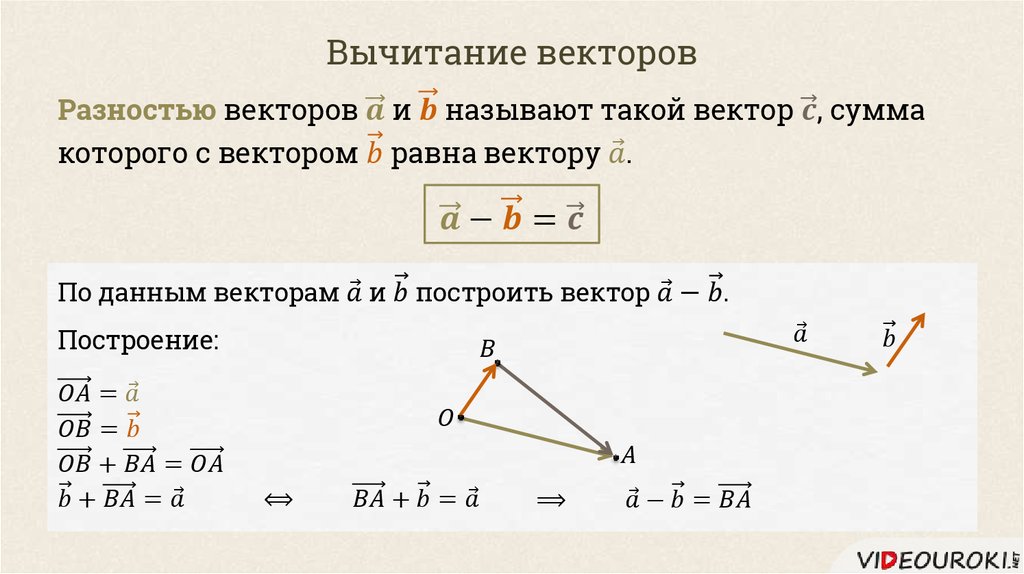
Имеем $a=b+c$ по определению векторной суммы (закон параллелограмма).
По определению вычитания , $c=a-b$ точно тогда, когда $a=b+c$.
$\endgroup$
$\begingroup$
Если вы стоите в точке A и идете по $\vec{B}$, вы окажетесь в точке C. Затем вы пройдете по $\vec{C}$ и окажетесь в B, в том же месте, где вы были бы, если бы вы ходили по $\vec{A}$ в начале. Итак, $$ \vec{B}+\vec{C}=\vec{A} \Leftrightarrow \vec{A}-\vec{B}=\vec{C} $$ Обратите внимание, что начальная точка не имеет значения. У вас есть (посмотрев на график) $$ \vec{A}=\begin{pmatrix}1\\2\end{pmatrix} $$ $$ \vec{B}=\begin{pmatrix}2\\-2\end{pmatrix} $$ $$ \vec{C}=\begin{pmatrix}-1\\4\end{pmatrix} $$ Теперь вы можете ясно видеть, что $$ \vec{A}-\vec{B}=\begin{pmatrix}1\\2\end{pmatrix} -\begin{pmatrix}2\\-2\end{pmatrix} =\begin{pmatrix}-1 \\4\конец{pmatrix} =\vec{C}\qquad $$
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
9\circ $Ответ
Проверено
208.8k+ просмотров
Подсказка: Сложение двух или более векторов происходит в одном и том же месте, а результат перекрестного произведения двух векторов лежит перпендикулярно плоскости этих двух векторы.
Полный пошаговый ответ
Из вопроса мы знаем, что отношение между векторами C, A и B равно $ {\rm{\vec C}} = {\rm{\vec A}} + {\ rm{\vec B}} $ и соотношение между векторами D, A и B равно $ {\rm{\vec D}} = {\rm{\vec A}} \times {\rm{\vec B}} $ .
Также мы знаем, что результат векторного произведения двух векторов лежит в перпендикулярной плоскости этих двух векторов. Итак, ${\rm{\vec D}}$ лежит перпендикулярно плоскости ${\rm{\vec A}}$ и ${\rm{\vec B}}$.
