5.3 Метод динамического программирования
Динамическое программирование – это метод оптимизации, приспособленный к поэтапным операциям нахождения решения. Задача разбивается на ряд последовательных шагов или этапов.
Условием
применимости метода является аддитивность целевой функции, т.е. возможность
представления функции от 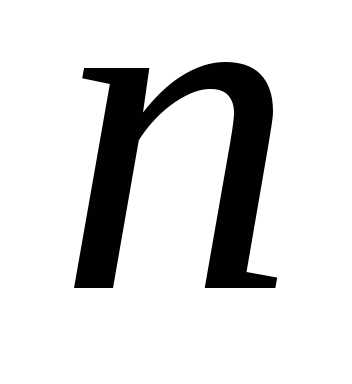 переменных в виде суммы функции, каждая
из которых зависит только от одной
переменной:
переменных в виде суммы функции, каждая
из которых зависит только от одной
переменной:
.
К числу задач динамического программирования относятся задачи: о замене и загрузке оборудования; оптимального распределения ресурсов по этапам планирования; оптимального управления запасами; оптимального распределения капиталовложений и многие другие.
Рассмотрим модель нелинейного программирования
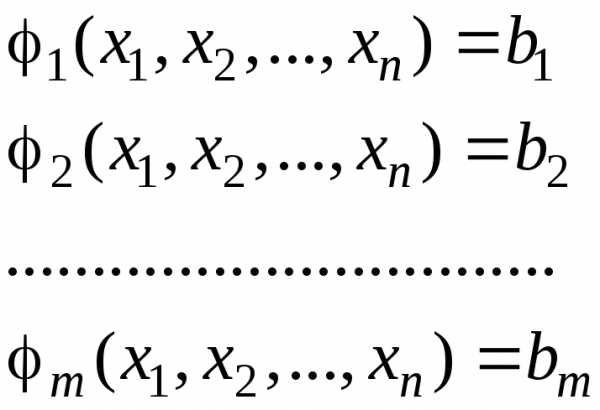
При использовании метода динамического программирования задача разбивается на количество шагов по числу неизвестных. На каждом шаге решается задача оптимизации только по одной переменной. Таким образом, процесс нахождения оптимального плана многомерной задачи распадается на ряд более простых одномерных задач оптимизации.
Принимая
решение 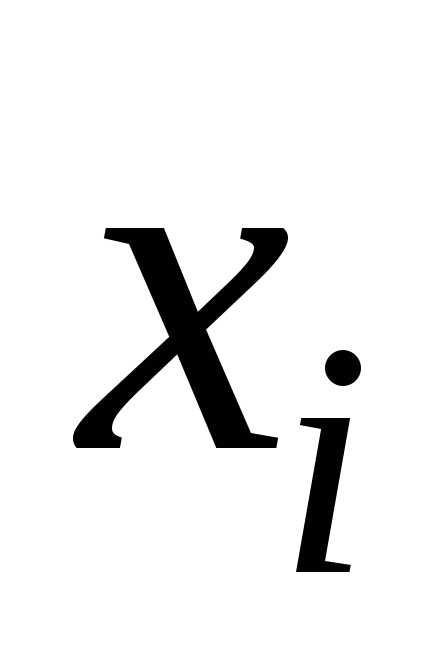 на
на шаге надо учитывать его влияние на
будущее, т.е. учитывать влияние принимаемого
решения на эффективность последующих
шагов. Имеется единственный шаг в решении
задачи в котором можно планировать без
учета влияния решения на последующие
шаги – это последний шаг. Его можно
планировать так, чтобы он изолированно
принес наибольшую выгоду. Поэтому
процесс поиска оптимального решения
начинается от конца к началу.
шаге надо учитывать его влияние на
будущее, т.е. учитывать влияние принимаемого
решения на эффективность последующих
шагов. Имеется единственный шаг в решении
задачи в котором можно планировать без
учета влияния решения на последующие
шаги – это последний шаг. Его можно
планировать так, чтобы он изолированно
принес наибольшую выгоду. Поэтому
процесс поиска оптимального решения
начинается от конца к началу.
Чтобы
планировать последний шаг, надо знать
чем окончился предыдущий, а это неизвестно.
В этом случае находят (предполагают) варианты условий
начала последнего 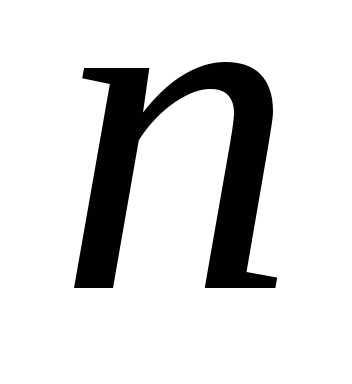 -го
шага, т.е. варианты окончания
-го
шага, т.е. варианты окончания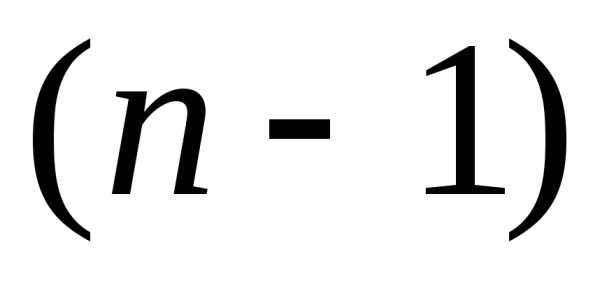 -го
шага. Для каждого варианта находят
такие решения, при которых выигрыш на
последнем шаге будет максимальным. Этот
выигрыш определяется по функциональному
уравнению Беллмана для последнего шага:
-го
шага. Для каждого варианта находят
такие решения, при которых выигрыш на
последнем шаге будет максимальным. Этот
выигрыш определяется по функциональному
уравнению Беллмана для последнего шага:
,
где 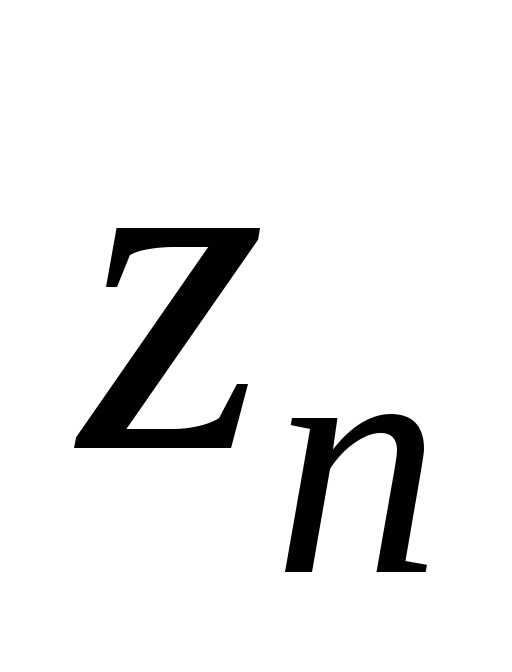 – варианты условий начала
– варианты условий начала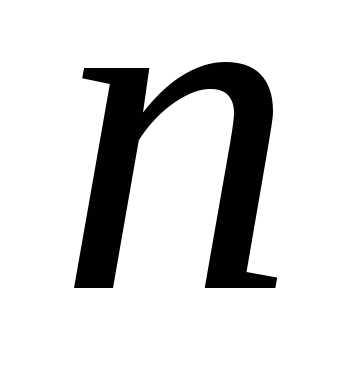 -го
шага.
-го
шага.
Аналогично
оптимизируется решение на предпоследнем 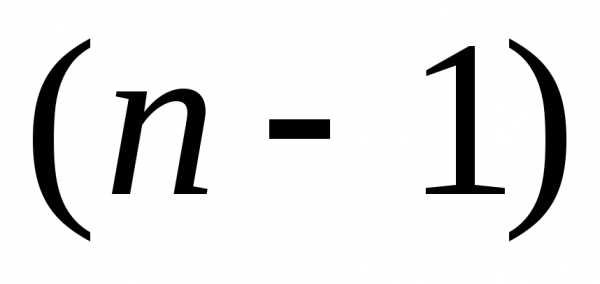 -м
шаге применительно к вариантам условий
начала этого шага, но с учетом решений,
найденных на
-м
шаге применительно к вариантам условий
начала этого шага, но с учетом решений,
найденных на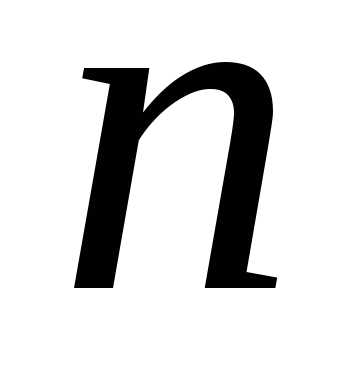
Уравнение Беллмана для шагов, начиная с предпоследнего до начала процесса, имеет вид:
,
где 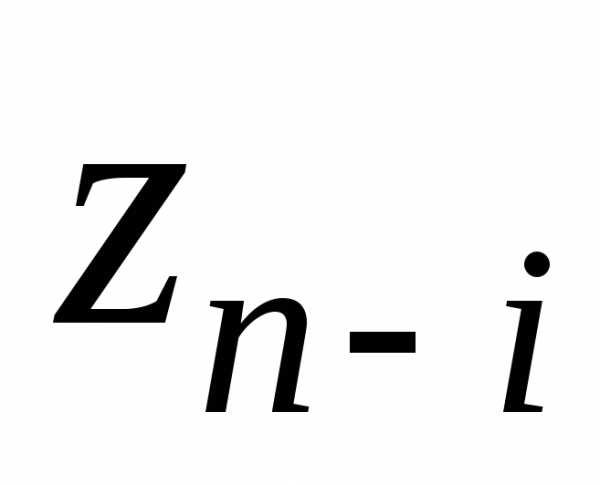 – варианты условий начала
– варианты условий начала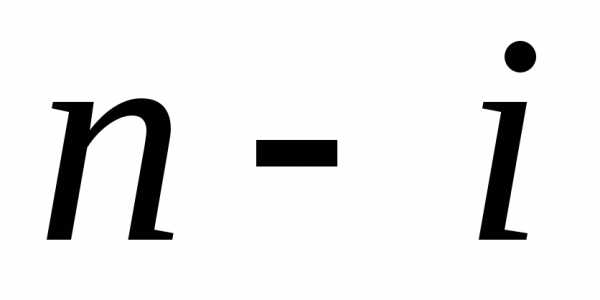 -го
шага;
-го
шага;
–функция Беллмана, найденная на предыдущем шаге.
При динамическом программировании многошаговый процесс проходят два раза:
1) от конца к началу – находят условные оптимальные решения на каждом шаге с учетом выигрыша на всех шагах, начиная с данного до конца;
2) от начала к концу – находят оптимальные шаговые решения на всех шагах.
5.4 Применение динамического программирования для решения задач о замене оборудования и эффективного использования
ресурсов
Задача
эффективного использования ресурсов. Имеется
некоторое количество ресурса 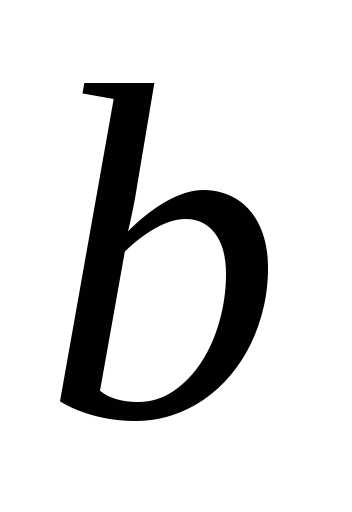
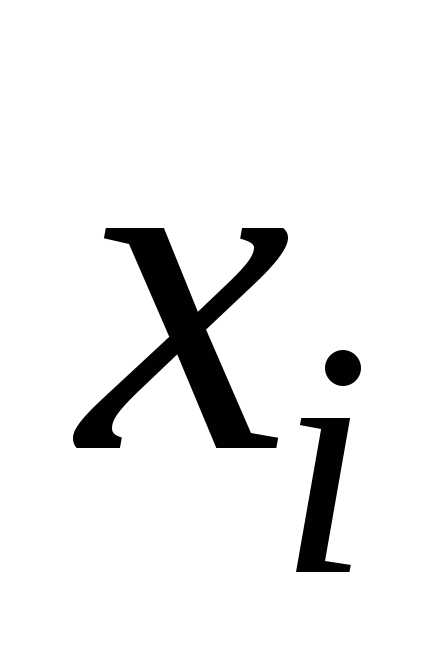 –количестворесурса,используемое
–количестворесурса,используемое 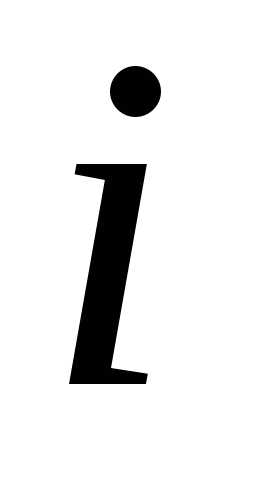 -м
способом,
-м
способом,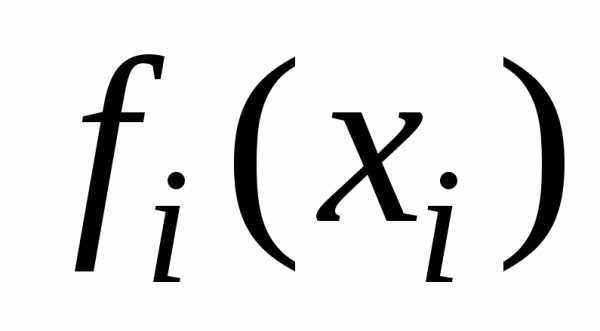 – доход от использования ресурса
– доход от использования ресурса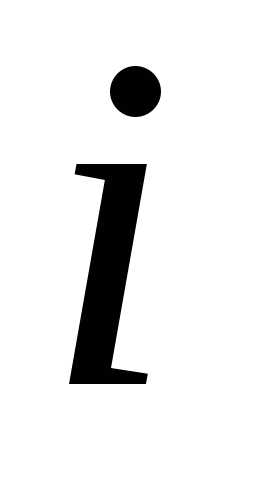 -м
способом ().
-м
способом (). Требуется
распределить общее количество ресурса 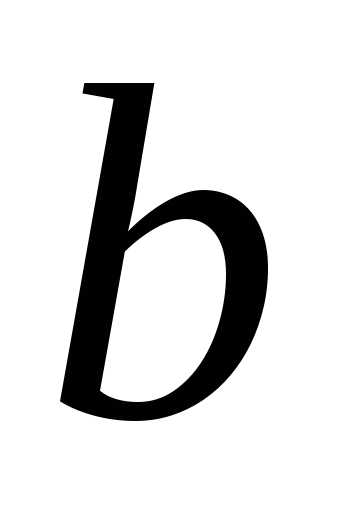 между различными способами, чтобы
суммарный доход был максимальным.
между различными способами, чтобы
суммарный доход был максимальным.
Модель оптимального использования ресурса имеет вид:
(5.13)
(5.14)
 . (5.15)
. (5.15)
Вместо
одной оптимизационной задачи (5.13)-(5.15),
с заданным количеством ресурса и
содержащей 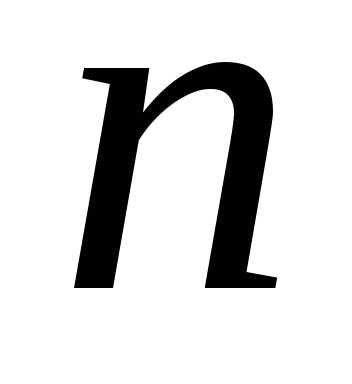
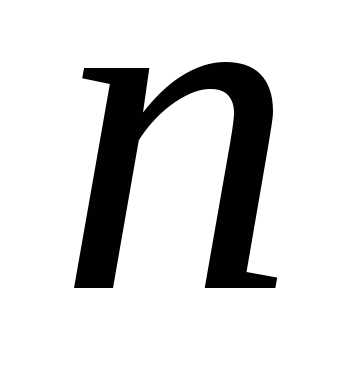 задач, в каждой из которых максимум
находится лишь по одной переменной.
Таким образом, процесс поиска решения
исходной задачи как бы разворачивается
во времени по шагам.
задач, в каждой из которых максимум
находится лишь по одной переменной.
Таким образом, процесс поиска решения
исходной задачи как бы разворачивается
во времени по шагам.На последнем шаге определяется функция
.
Для всех остальных шагов используется рекуррентное соотношение
, ,
здесь 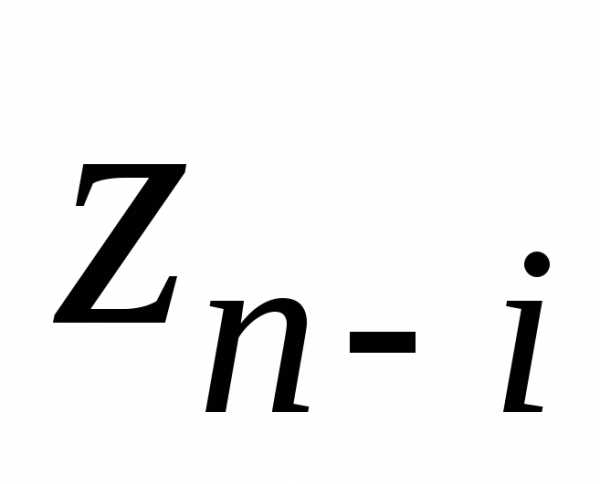 – количество ресурса, оставшееся для
распределения к началу
– количество ресурса, оставшееся для
распределения к началу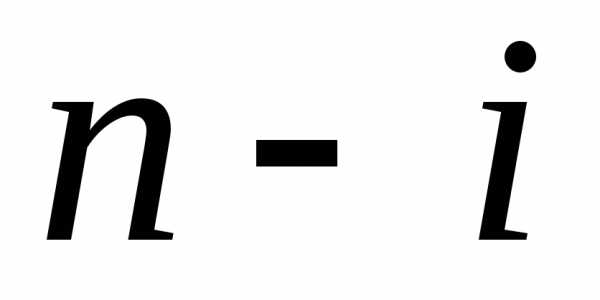 -го
шага.
-го
шага.
Очевидно,
.
Метод динамического программирования можно использовать и в случае распределения нескольких видов ресурсов, однако, с увеличением размерности решение становится все более сложным.
Задача 5.3 Необходимо составить план вложений денежных средств в три отделения предприятия, исходя из общей суммы средств, которая равна 250 денежным единицам.
Известны функции прибыли fi(xi) по каждому отделению, где xi — средства, вкладываемые в i-е отделение (таблица 5.1). Размеры вложений ограничены: для первого отделения суммой 250 ден. ед., для второго отделения – 100 ден. ед.; для третьего — 250 ден. ед.
Найти оптимальное распределение денежных средств по отделениям, соответствующее максимуму суммарной но трем отделениям прибыли.
Таблица 5.1 – Функции прибыли по трем отделениям
xi | ||||||
f | 0 | 50 | 100 | 150 | 200 | 250 |
f1 | 0 | 7 | 9 | 10 | 11 | 12 |
f2 | 0 | 5 | 8 | — | — | — |
f3 | 0 | 3 | 5 | 9 | 13 | 15 |
решение.
Введем обозначения:
x1 — количество вложенных денежных средств в первое отделение; x2 — количество вложенных денежных средств во второе отделение; x3 — количество вложенных денежных средств в третье отделение.
Целевая функция имеет смысл суммарной но трем отделениям прибыли.
Математическая модель задачи
 .
.
Процесс
решения начинаем с последнего шага,
т.е. оптимизируем вложение денежных
средств в третье отделение. При этом мы
не знаем: сколько осталось денег после
вложения в первые два отделения. Обозначим
величину оставшихся для вложения денег 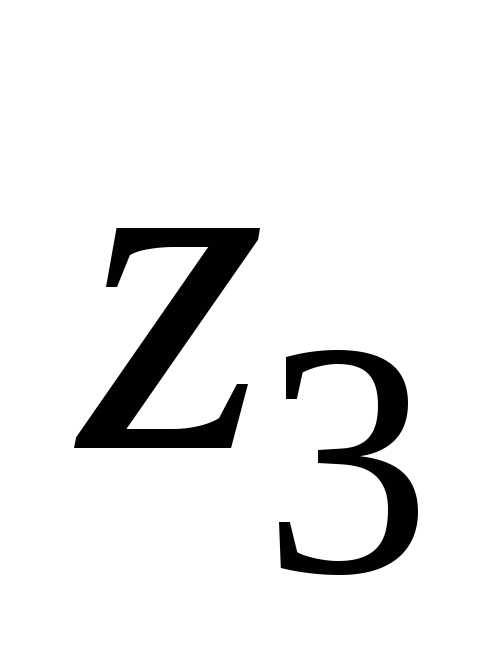 .
Таким образом, переменная
.
Таким образом, переменная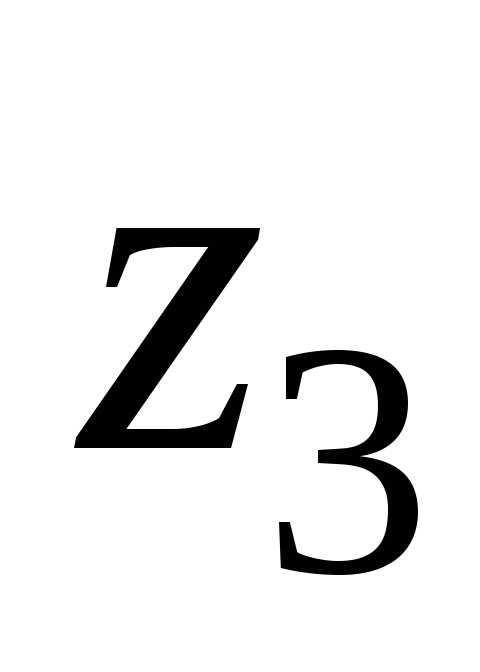 выражает всевозможные варианты условий
начала последнего шага. Уравнение
Беллмана для последнего шага имеет вид:
выражает всевозможные варианты условий
начала последнего шага. Уравнение
Беллмана для последнего шага имеет вид:
,
x3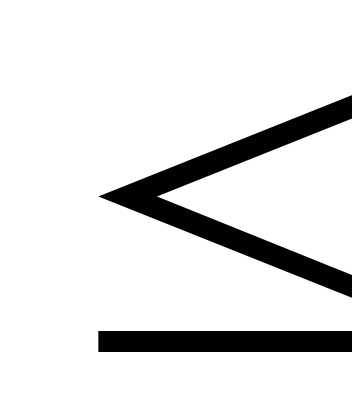 250.
250.
Поскольку функции прибыли fi(xi) заданы таблично, метод динамического программирования будем применять в табличном виде.
Так
как с ростом x3 функция f3(x3)
возрастает, то на последнем этапе все
оставшиеся средства нужно отдать
третьему отделению, таким образом, x3 = z3.
x3 = z3.
Таблица 5.2 – Условно-оптимальные планы для третьего отделения
z3 | 0 | 50 | 100 | 150 | 200 | 250 |
x3 | 0 | 50 | 100 | 150 | 200 | 250 |
F1(z3 ) | 0 | 3 | 5 | 9 | 13 | 15 |
Запишем уравнение Беллмана для второго шага распределения средств:
(5.16)
x2 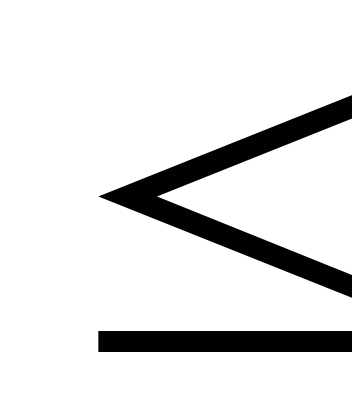 100
100
здесь – средства, оставшиеся для вложений во второе и третье отделение, следовательно,
. (5.17)
В
таблицу 5.3 внесем все элементы формулы
(5.16). В графы 2 и 4 записываем все возможные
сочетания значений 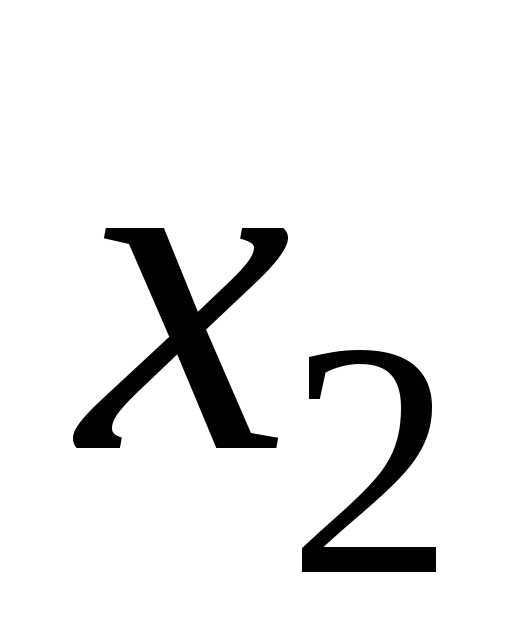 и
и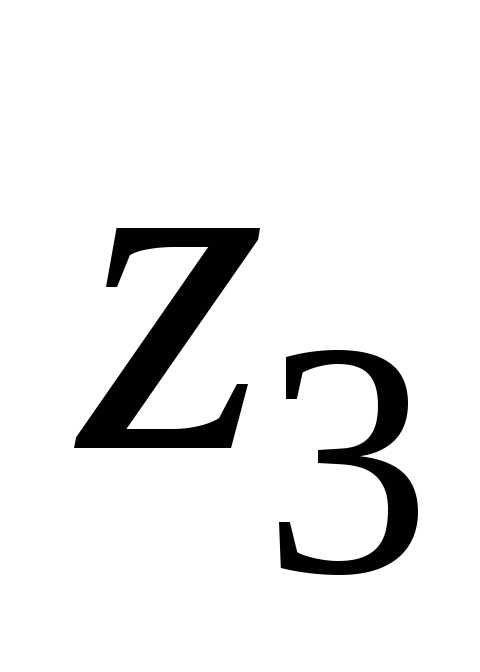 ,
которые в сумме составят величину
,
которые в сумме составят величину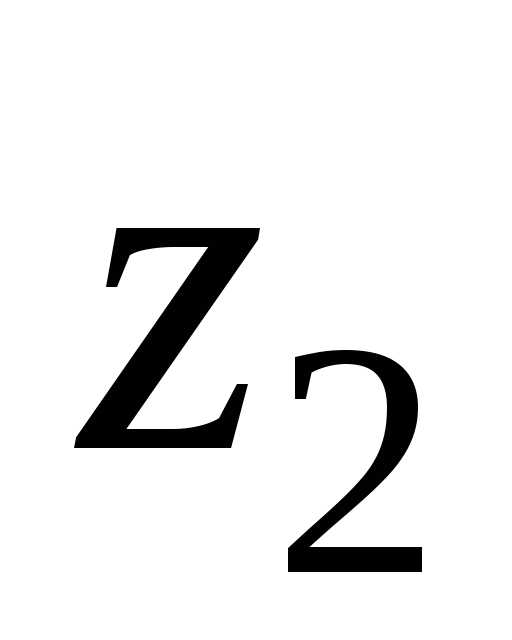 согласно выражению (5.17). При этом
учитываем, что
согласно выражению (5.17). При этом
учитываем, что
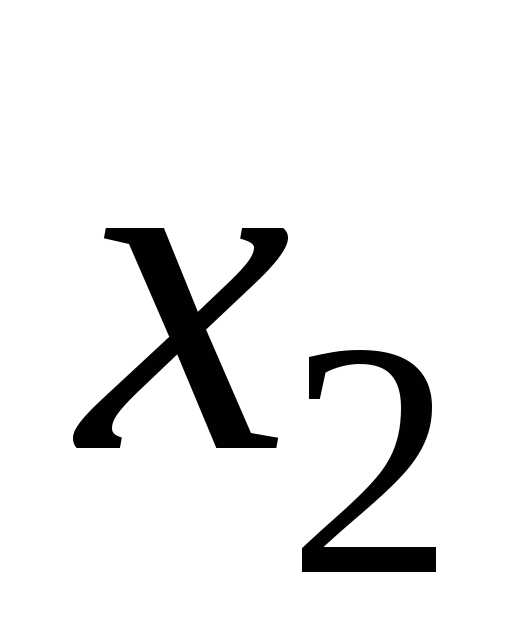 не
должен превышать 100.
не
должен превышать 100.
Таблица 5.3 – Условно-оптимальные планы для второго отделения
z2 | x2 | f2(x2) | z3 | F1(z3 ) | f2(x2)+F1(z3) | F2(z2) |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
250 | 0 | 0 | 250 | 15 | 15 | |
50 | 5 | 200 | 13 | 18 | 18 | |
100 | 8 | 150 | 9 | 17 | ||
200 | 0 | 0 | 200 | 13 | 13 | |
50 | 5 | 150 | 9 | 14 | 14 | |
100 | 8 | 100 | 5 | 13 | ||
150 | 0 | 0 | 150 | 9 | 9 | |
50 | 5 | 100 | 5 | 10 | ||
100 | 8 | 50 | 3 | 11 | 11 | |
100 | 0 | 0 | 100 | 5 | 5 | |
50 | 5 | 50 | 3 | 8 | 8 | |
100 | 8 | 0 | 0 | 8 | 8 | |
50 | 0 | 0 | 50 | 3 | 3 | |
50 | 5 | 0 | 0 | 5 | 5 |
Уравнение Беллмана для первого шага:
.
Переменная 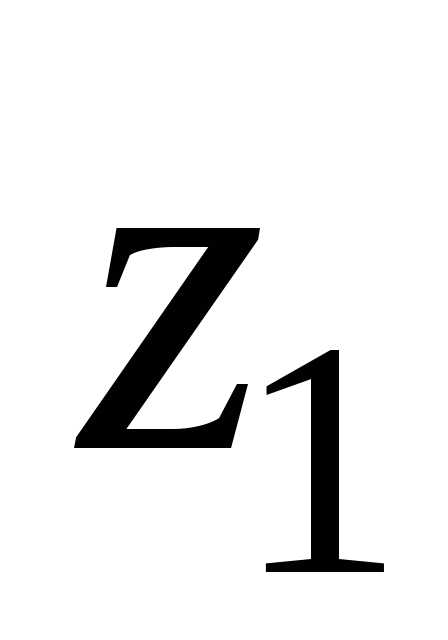 имеет смысл денежных средств для
вложений во все три отделения предприятия
и, следовательно, имеет единственное
значение, равное общей сумме вложений
250 ден. ед. Значения функцииF2(z2 ) будем
брать из последнего столбца таблицы
5.3.
имеет смысл денежных средств для
вложений во все три отделения предприятия
и, следовательно, имеет единственное
значение, равное общей сумме вложений
250 ден. ед. Значения функцииF2(z2 ) будем
брать из последнего столбца таблицы
5.3.
Таблица 5.4 – Условно-оптимальные планы для первого отделения.
z1 | x1 | f1(x1) | z2 | F2(z2 ) | f1(x1)+F1(z3) | F1(z1) |
250 | 0 | 0 | 250 | 18 | 18 | |
50 | 7 | 200 | 14 | 21 | 21 | |
100 | 9 | 150 | 11 | 20 | ||
150 | 10 | 100 | 8 | 18 | ||
200 | 11 | 50 | 5 | 16 | ||
250 | 12 | 0 | 0 | 12 |
Мы выполнили шаги динамического программирования конца к началу. В результате чего определили максимальную суммарную прибыль от вложений во все отделения предприятия
.
Теперь в ходе движения от первого шага к концу определим оптимальные величины вложений. Из таблицы 5.4 видим, что максимальная прибыль достигается при x1, равном 50, и z2, равном 200. Рассмотрим второй шаг (таблица 5.3). При z2,равном 200, функция Беллмана F2(z2) = 14. Это значение соответствует строке, в которой x2 равно 50, следовательно, на долю третьего отделения остается 150 денежных единиц.
Таким образом, максимум прибыли от вложения денежных средств составляет
.
Оптимальный план вложений:
– в первое отделение 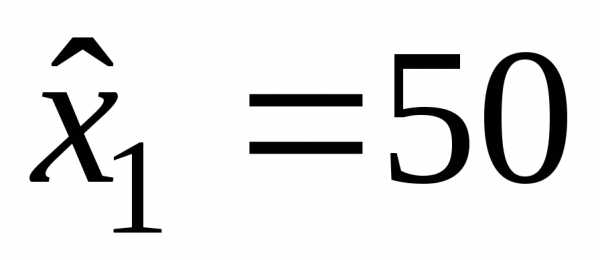 ден.
ед.;
ден.
ед.;
– во второе отделение 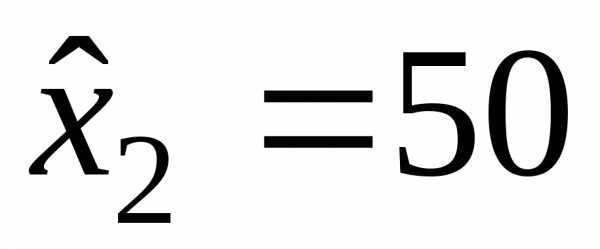 ден.
ед.;
ден.
ед.;
– в третье отделение 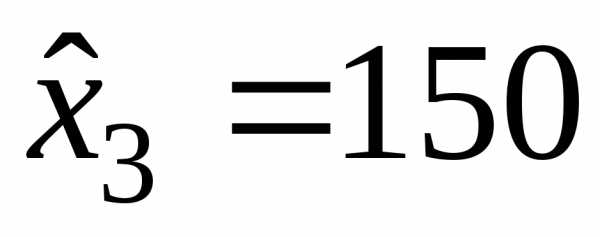 ден. ед..
ден. ед..
Задача о замене оборудования.
Задача 5.4 К началу пятилетнего периода на предприятии установлено новое оборудование. Зависимость производительности этого оборудования от времени его использования предприятием, а также зависимость затрат на содержание и ремонт оборудования при различном времени его использования приведены в таблице 5.5.
Таблица 5.5 – Зависимость выпуска и эксплуатационных затрат от времени использования оборудования
Показатель | Время | |||||
0 | 1 | 2 | 3 | 4 | 5 | |
Выпуск
продукции | 95 | 88 | 81 | 74 | 57 | 50 |
Эксплуатационные
затраты оборудования | 22 | 31 | 40 | 49 | 58 | 67 |
Зная, что затраты, связанные с приобретением и установкой нового оборудования, идентичного с установленным, составляют 35 ден. ед., а заменяемое оборудование списывается, составить такой план замены оборудования в течение пятилетки, при котором общая прибыль за данный период максимальна.
решение.
Обозначим:
 – время службы оборудования;
– время службы оборудования;
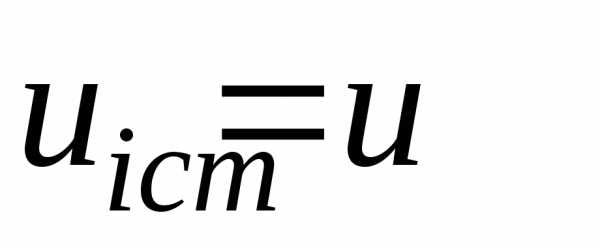 – принятие решения в начале
– принятие решения в начале 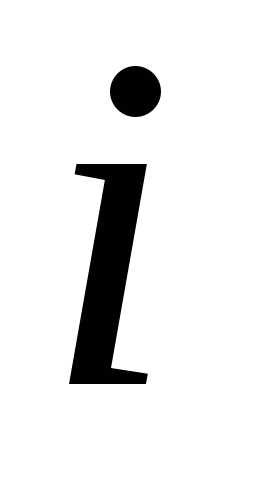 -го
года об использовании имеющегося
оборудования;
-го
года об использовании имеющегося
оборудования;
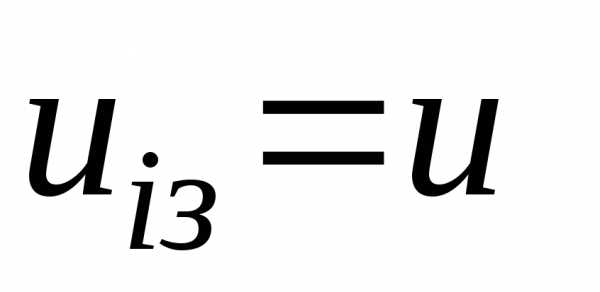 – принятие решения в начале
– принятие решения в начале 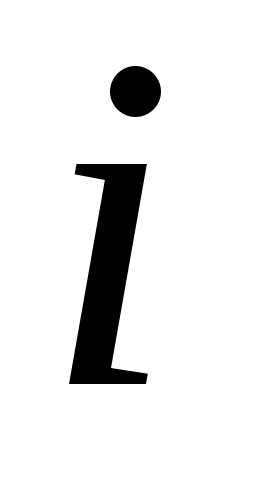 -го
года о замене оборудования;
-го
года о замене оборудования;
 – стоимость нового оборудования.
– стоимость нового оборудования.
Целевая функция имеет смысл суммарной за пятилетний период прибыли.
Математическая модель задачи
, (5.18)
где
– прибыль предприятия за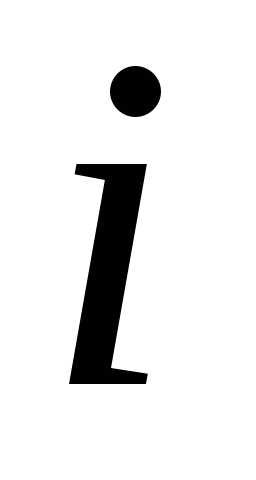 -й
год.
-й
год.
,
Модель (5.18) относится к классу нелинейного программирования c булевыми (логическими) переменными. Целевая функция аддитивна. Поскольку задача имеет пять неизвестных, динамическое программирование также будет иметь пять шагов.
Уравнения Беллмана для последнего шага имеет вид:
, (5.19)
здесь 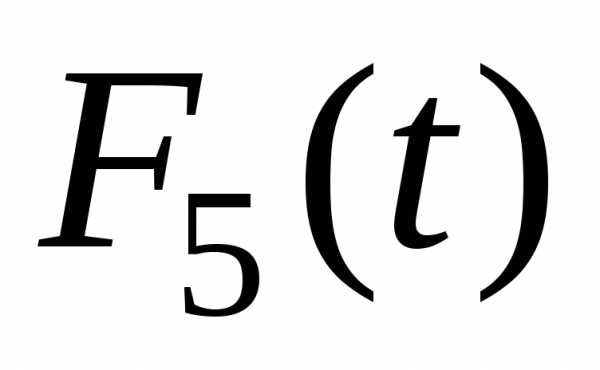 –функция
максимальной прибыли за последний год
в зависимости от возраста оборудования
в начале года
–функция
максимальной прибыли за последний год
в зависимости от возраста оборудования
в начале года  .
.
Уравнения
Беллмана для 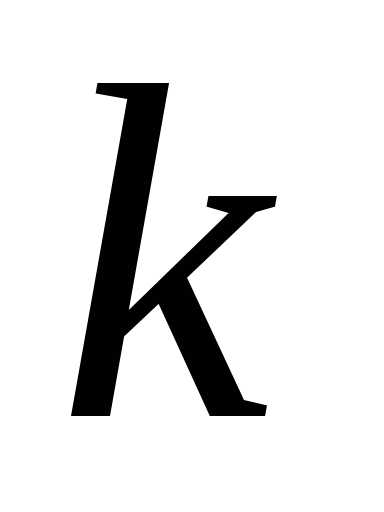 -го
шага
-го
шага
; (5.20)
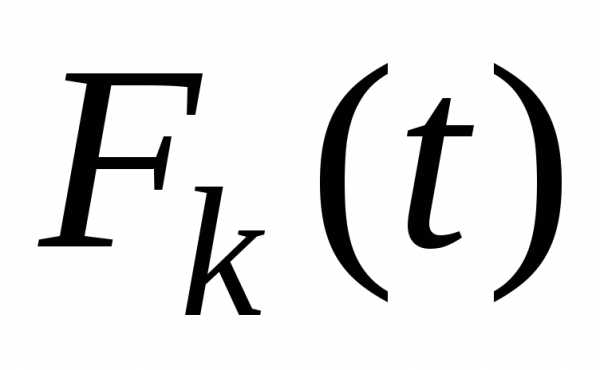 –максимальная
прибыль, начиная с
–максимальная
прибыль, начиная с 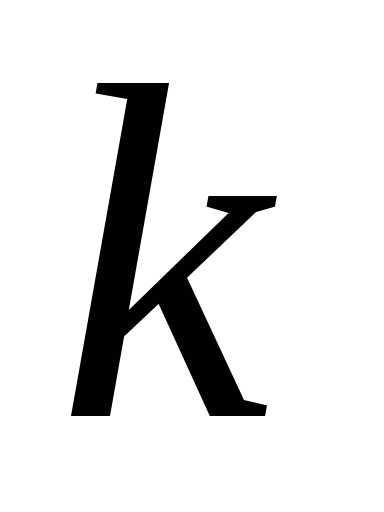 -го
года и до конца периода в зависимости
от возраста оборудования в начале
-го
года и до конца периода в зависимости
от возраста оборудования в начале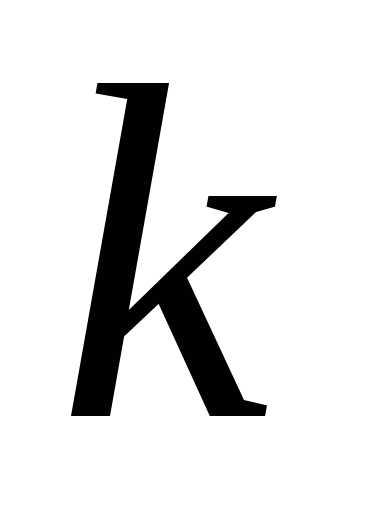 -го
года.
-го
года.
Планируем
замену оборудования в начале пятого
года. Предполагаем варианты условий
начала данного шага, т.е. последовательно
перебираем возможные значения возраста
оборудования к началу пятого года.
Расчеты проводим по уравнению (5.19).  принимает значения: 1, 2, 3, 4. В результате
получаем функцию максимальной прибыли
за последний год в зависимости от
возраста оборудования:
принимает значения: 1, 2, 3, 4. В результате
получаем функцию максимальной прибыли
за последний год в зависимости от
возраста оборудования:
(5.21)
Планируем
начало четвертого года. Расчеты проводим
по уравнению (5.20).  принимает значения: 1, 2, 3. Получаем
функцию максимальной прибыли за последние
два года в зависимости от возраста
оборудования:
принимает значения: 1, 2, 3. Получаем
функцию максимальной прибыли за последние
два года в зависимости от возраста
оборудования:
(5.22)
Планируем
начало третьего года. Расчеты проводим
по уравнению (5.20).  принимает значения: 1, 2. Получаем функцию
максимальной прибыли за последние три
года в зависимости от возраста
оборудования:
принимает значения: 1, 2. Получаем функцию
максимальной прибыли за последние три
года в зависимости от возраста
оборудования:
(5.23)
Планируем начало второго года. Расчеты проводим по уравнению (5.20). Получаем функцию максимальной прибыли за период со второго по пятый год:
(5.24)
Планируем начало первого года.
(5.25)
Значение
функции Беллмана 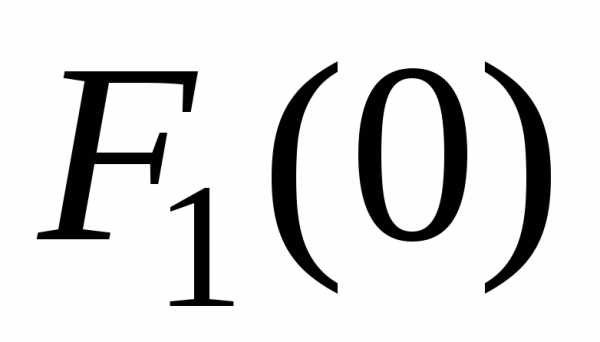 представляет собой максимальную прибыль
предприятия за пятилетний период.
представляет собой максимальную прибыль
предприятия за пятилетний период.
Мы выполнили расчет шагов динамического программирования от конца к началу периода. В результате определили
.
Теперь в направлении от начала периода до его конца найдем оптимальный план замены оборудования.
По
условию задачи в начале первого года
оборудование было обновлено, т.е. 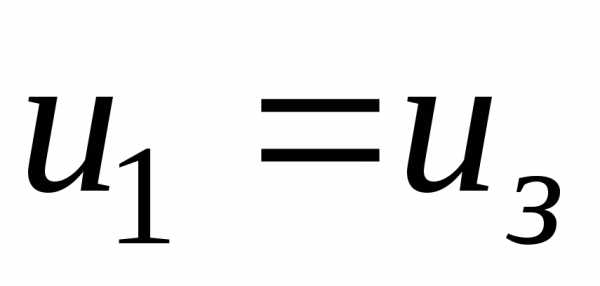 .
.
В
выражение (5.25) входит значение
.
Оно было вычислено по формуле (5.24) и
соответствует 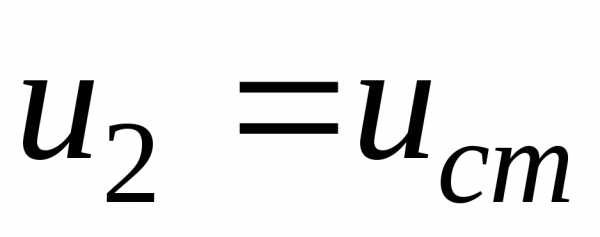 .
.
В
свою очередь это выражение содержит
значение
,
вычисленное по (5.23) при 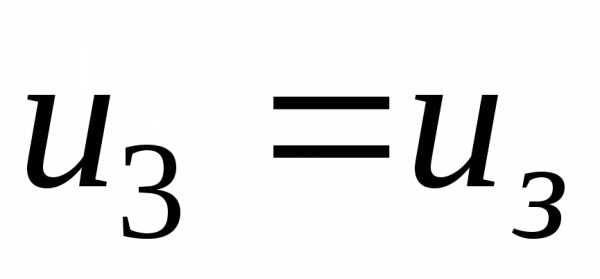 .
.
В
(5.23) входит
,
вычисленное по (5.22) при 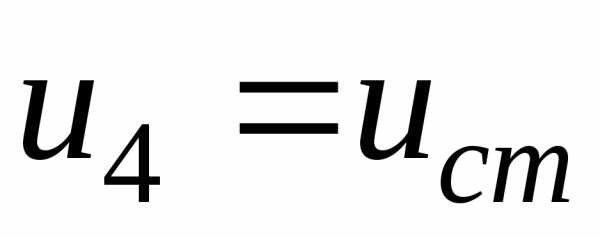 .
.
И,
наконец, из выражения (5.21) ясно, что 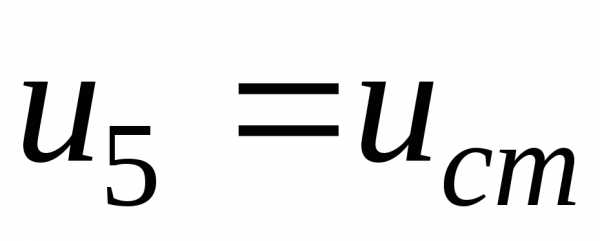 .
.
studfiles.net
Общая постановка задач динамического программирования.
Рассмотрим управляемый процесс. Например, распределение средств между предприятиями, использующими ресурсы в течение ряда лет.
В результате управления система (объект)
Sпереходит из состояния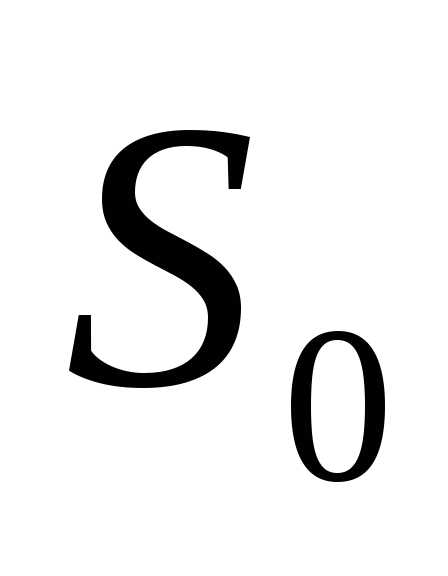 в состояние
в состояние .
.
Пусть управление можно разбить на nшагов, то есть решения принимаются
последовательно на каждом шаге, а
управление, переводящее системуSиз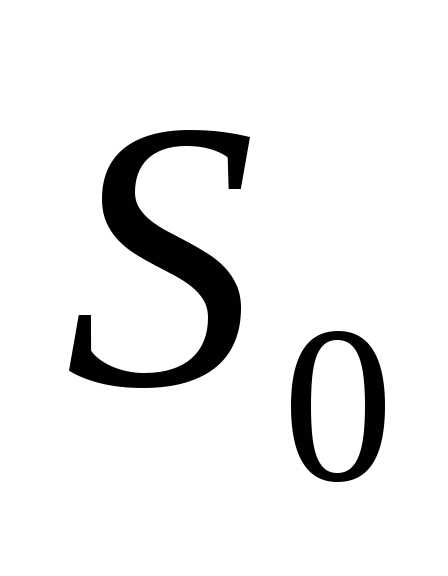 в
в (
(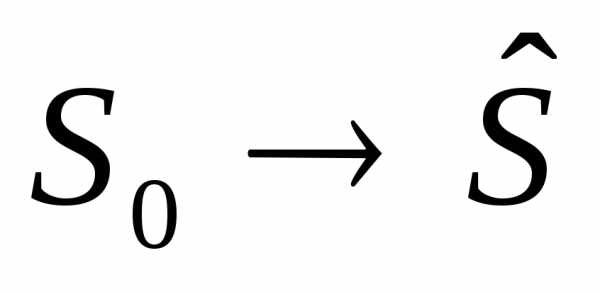 ),
представляет собой совокупностьnпошаговых управлений.
),
представляет собой совокупностьnпошаговых управлений.
Пусть 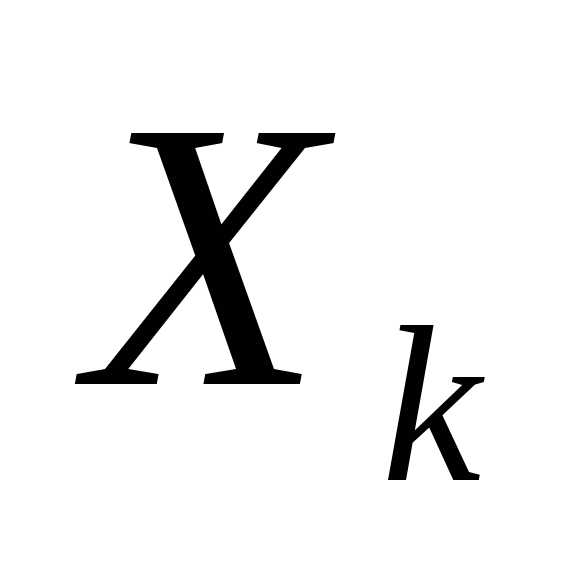 — управление на k-ом шаге и
— управление на k-ом шаге и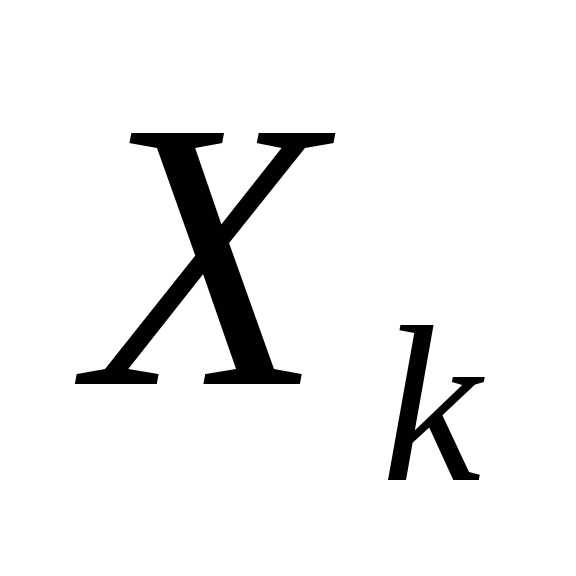 удовлетворяет некоторым ограничениям
и в этом смысле называется допустимым.
удовлетворяет некоторым ограничениям
и в этом смысле называется допустимым.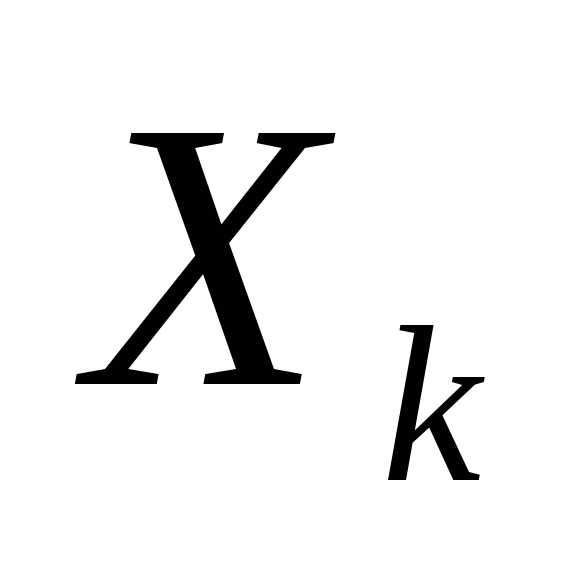 может быть числом, точкой, функцией,
качественным признаком.
может быть числом, точкой, функцией,
качественным признаком.
управление, переводящее системуSиз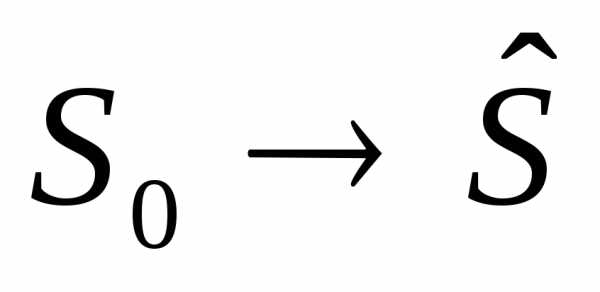 .
.
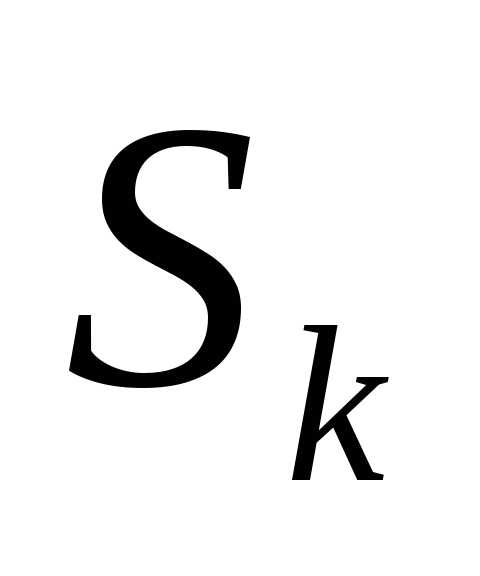 состояние
системы после к-ого шага управления.
состояние
системы после к-ого шага управления.
Рисунок 9
— целевая функция, показатель эффективности
рассматриваемой управляемой операции.
Целевая функция зависит от начального
состояния системы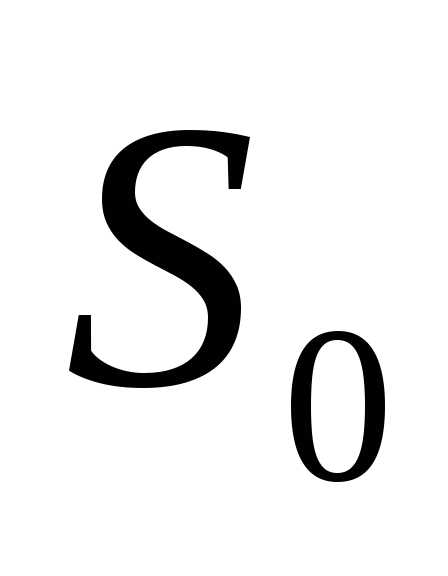 и управления Х.
и управления Х.
Предположим:
Состояние
 зависит только от предыдущего состояния
зависит только от предыдущего состояния и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.
и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.Целевая функция является аддитивной от показателей эффективности на каждом шаге. Обозначим показатель эффективности к-ого шаге через:
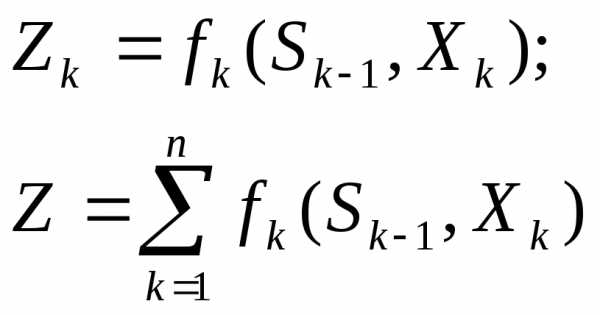
Тогда задача динамического программирования
(пошаговой оптимизации) формулируется
так: определить такое допустимое
управление Х, переводящее систему Sиз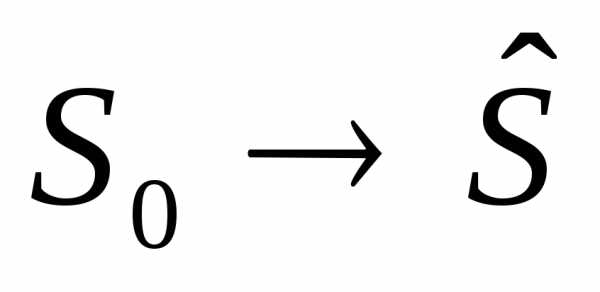 ,
при котором целевая функция принимает
наибольшее (наименьшее) значение.
,
при котором целевая функция принимает
наибольшее (наименьшее) значение.
Особенности динамического программирования:
Задача оптимизации интерпретируется как n-шаговый процесс управления.
Целевая функция равна сумме целевых функций на каждом шаге.
Выбор управления на k-ом шаге зависит от состояния системы к этому шагу, не влияет на предшествующие шаги (отсутствие обратной связи).
Состояние
 послеk-ого шага зависит
только от предшествующего состояния
послеk-ого шага зависит
только от предшествующего состояния и управления
и управления (нет последствий).
(нет последствий).На каждом шаге управление
 зависит от конечного числа управляющих
переменных, а состояние
зависит от конечного числа управляющих
переменных, а состояние от конечного числа параметров.
от конечного числа параметров.
Вычислительная схема задач динамического программирования безразлична к способам задания функции и ограничений, связана с принципом оптимальности и использует рекуррентные соотношения.
Принцип оптимальности.
Принцип оптимальности(был предложен Беллманом в 1953 г.): каково бы ни было состояние системыSв результате какого либо числа шагов, на ближайшем шаге надо выбирать управление так, чтобы оно в совокупности с оптимальными управлениями на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Основное требование принципа оптимальности состоит в том, что процесс управления должен быть без обратных связей, то есть управление на каждом шаге не должно оказывать влияние на предшествующие шаги.
При оптимальном управлении, утверждается, что любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого процесса по отношению к исходному состоянию этого процесса. Следовательно, решение на каждом шаге является наилучшим с точки зрения управления в целом.
studfiles.net
Задачи динамического программирования
Задачи динамического программирования. Её решение методом динамического программирования.
Определение. Задача динамического программирования (ДП) – это задача оптимального управления некоторым многошаговым процессом.
Подобных задач, ровно как и методов их решения, существует великое множество. Изобретаются они в каждом конкретном случае индивидуально, но все объединены общей идей решения – так называемого метода решения задачи через чайник: что бы вскипятить воду, нужно налить её в чайник, поставить его на плиту, включить плиту и т.д. Если же вода в чайнике уже налита, то нужно её вылить. А что делать дальше, мы уже знаем. Таким образом, в процессе решения мы сводим задачу к той, решать которую уже научились на предыдущем шаге.
Рассуждения при этом приводятся примерно следующие.
Нам необходимо найти оптимальное решение в конце маршрута. Если бы мы знали оптимальное решение для всех предыдущих этапов, то нашли бы решение для последнего. Чтобы найти решение для предпоследнего этапа, мы должны знать решение для второго с конца этапа, и т.д. То есть, разрабатывается метод динамического программирования с конца. Реализуется же он с начала: высчитываем оптимальные значение с самого начала и находим оптимальную стоимость. После этого необходимо найти собственно оптимальный маршрут. Его находим с конца.
Задача. Рассмотрим задачу оптимального управления многошаговым процессом. Над ребрами данного графа проставлены стоимости переходов из одной вершины в другую. Необходимо найти путь по которому с минимальными затратами можно попасть из S(0)в S(5) (см. рисунок 4.1).
Рисунок 4.1. – исходный граф.
Идея решения. В принципе мы умеем решать подобные задачи по алгоритму Дейкстры и Форда-Беллмана. Попробуем теперь решить эту задачу методом динамического программирования. Он изобретается с конца. Нам необходимо найти минимально возможную сумму, имея которую, мы можем добраться до S(5).
Рассуждаем так: если бы мы знали «стоимости» всех вершин. Из которых мы можем попасть в S(5) (то есть вершин ), то мы бы нашли стоимости всех вершинS(5) (для этого к стоимости вершин из S(4) прибавляем стоимости переездов и выбираем минимум из получившихся сумм). Чтобы найти стоимости S(4) мы должны знать стоимости S(3) и т.д. Так спускаемся до вершины S(0), стоимость которой равна нулю.
Итак,
Здесь – минимально возможная сумма денег, имея которую мы можем добрать отИмеем:
Рисунок 4.2. – Здесь – полученный стоимости вершин.
10
Реализация метода ДП происходим от начала к концу (то есть слева направо в нашем случае). Самый внешний цикл – по i; в нём в прямом порядке перебираем уровни вершин. Следующий по вложенности цикл – по j; в нём перебираем вершины одного уровня. Самый внутренний цикл – по k. Изменение направления прохода двух вложенных циклов не повлияет на конечный результат.
Последний этап – восстановление оптимального пути – реализуется из конца в начало. Для этого смотрим, из какой вершины предыдущего уровня была достигнута стоимость нашей вершины, постепенно продвигаясь справа налево.
Рисунок 4.3. – Восстановление оптимально пути.
studfiles.net
5. Динамическое программирование
В ряде реальных экономических и производственных задач необходимо учитывать изменение моделируемого процесса во времени и влияние времени на критерии оптимальности. Для решения указанных задач используется метод динамического планирования (динамическое программирование). Этот метод более сложен по сравнению с методами расчета статических оптимизационных задач, изложенных выше. Также не простым делом является процесс построения для реальной задачи математической модели динамического программирования.
5.1. Постановка задачи динамического программирования. Основные условия и область применения
Пусть
рассматривается задача, распадающаяся
на 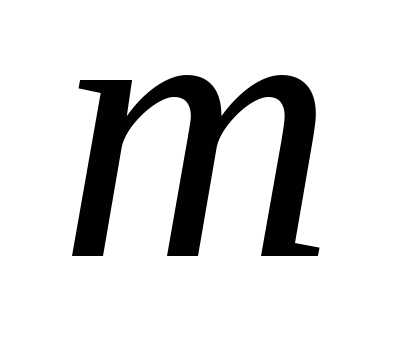 шагов
или этапов, например планирование
деятельности предприятия на несколько
лет, поэтапное планирование инвестиций,
управление производственными мощностями
в течение длительного срока. Показатель
эффективности задачи в целом обозначим
через W, а
показатели эффективности на отдельных
шагах – через
шагов
или этапов, например планирование
деятельности предприятия на несколько
лет, поэтапное планирование инвестиций,
управление производственными мощностями
в течение длительного срока. Показатель
эффективности задачи в целом обозначим
через W, а
показатели эффективности на отдельных
шагах – через  ,
, 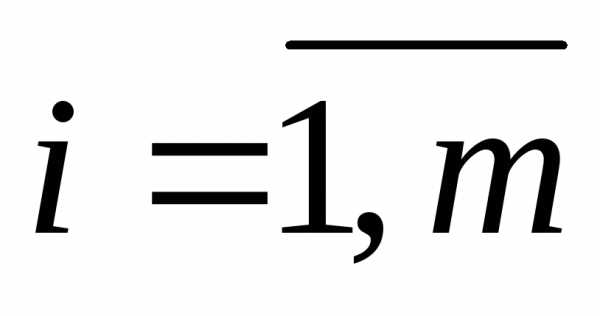 .
Если W обладает свойством аддитивности, т.е.
.
Если W обладает свойством аддитивности, т.е.
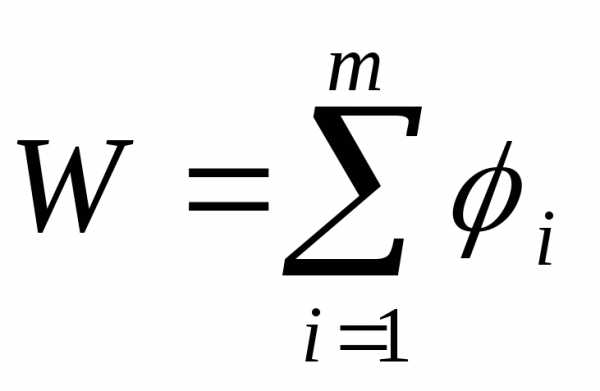 , (5.1.1)
, (5.1.1)
то можно найти оптимальное решение задачи методом динамического программирования.
Таким образом, динамическое программирование – это метод оптимизации многошаговых или многоэтапных процессов, критерий эффективности которых обладает свойством (5.1.1). В задачах динамического программирования критерий эффективности называется выигрышем. Данные процессы управляемые, и от правильного выбора управления зависит величина выигрыша.
Определение
5.1.1. Переменная 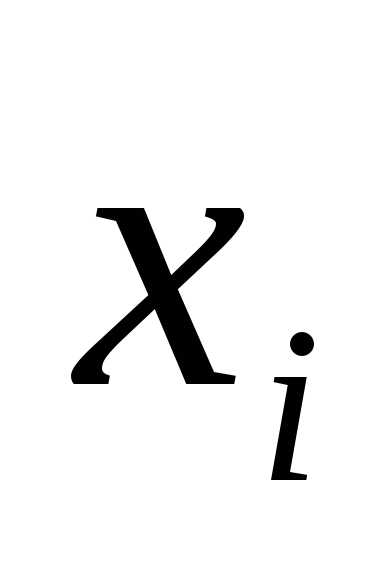 ,
от которой зависят выигрыш на
,
от которой зависят выигрыш на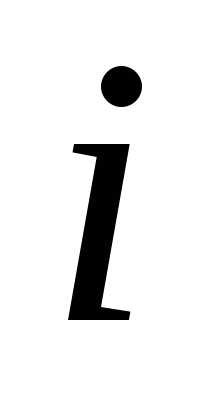 -м шаге
и, следовательно, выигрыш в целом,
называется шаговым управлением,
-м шаге
и, следовательно, выигрыш в целом,
называется шаговым управлением, 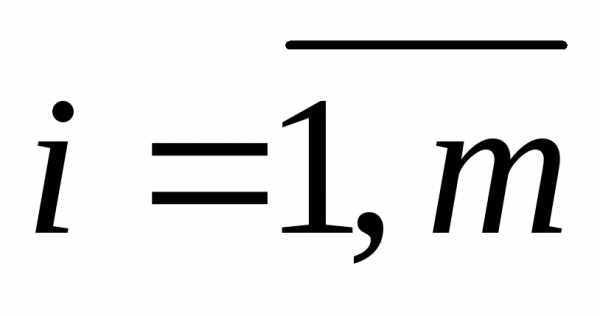 .
.
Определение 5.12. Управлением процесса в целом (х) называется последовательность шаговых управлений .
Определение 5.1.3. Оптимальное управление х* – это значение управления х, при котором значение W(x* ) является максимальным (или минимальным, если требуется уменьшить проигрыш)
, (5.1.2)
где Х — область допустимых управлений.
Оптимальное управление х* определяется последовательностью оптимальных шаговых управлений
В основе метода динамического программирования лежит принцип оптимальности Беллмана, формулирующийся следующим образом: управление на каждом шаге надо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.
Поясним это правило. При решении задачи динамического программирования на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Бели считать все шаги независимыми друг от друга, то оптимальным шаговым управлением будет то управление, которое приносит максимальный выигрыш именно на данном шаге. Но, например, при покупке новой техники взамен устаревшей на ее приобретение затрачиваются определенные средства. Поэтому прибыль от ее эксплуатации вначале может быть небольшой. Однако в следующие годы новая техника будет приносить большую прибыль. И наоборот, если руководитель примет решение оставить старую технику для получения прибыли в текущем году, то в дальнейшем это приведет к значительным убыткам. Данный пример демонстрирует следующий факт: в многошаговых процессах все шаги зависят друг от друга, и, следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс.
Другой
момент, который следует учитывать при
выборе управления на данном шаге, – это
возможные варианты окончания предыдущего
шага: Эти варианты определяют состояние
процесса. Например, при определении
количества средств, вкладываемых в
предприятие в 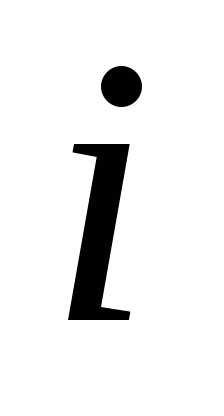 -м
году, необходимо знать, сколько средств
осталось в наличии к этому году и какая
прибыль получена в предыдущем(
-м
году, необходимо знать, сколько средств
осталось в наличии к этому году и какая
прибыль получена в предыдущем(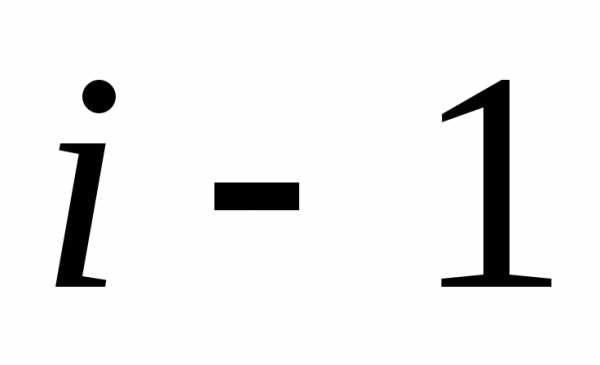 )-м году.
Таким образом, при выборе шагового
управления необходимо учитывать: 1)
возможные исходы предыдущего шага и 2)
влияние управления на все оставшиеся
до конца процесса шаги.
)-м году.
Таким образом, при выборе шагового
управления необходимо учитывать: 1)
возможные исходы предыдущего шага и 2)
влияние управления на все оставшиеся
до конца процесса шаги.
В
задачах динамического программирования
первый пункт учитывают, делая на каждом
шаге условные предположения о возможных
вариантах окончания предыдущего шага
и проводя для каждого из вариантов
условную оптимизацию. Выполнение второго
пункта обеспечивается тем, что в задачах
динамического программирования условная
оптимизация проводится от конца процесса
к началу. Сперва оптимизируется последний 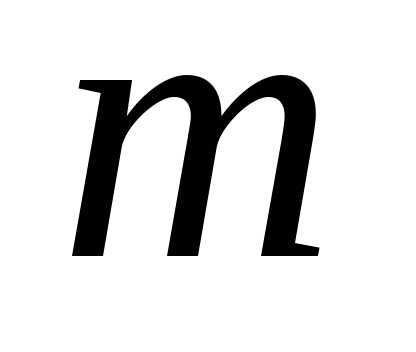 -й шаг,
на котором не надо учитывать возможные
воздействия выбранного управления
-й шаг,
на котором не надо учитывать возможные
воздействия выбранного управления 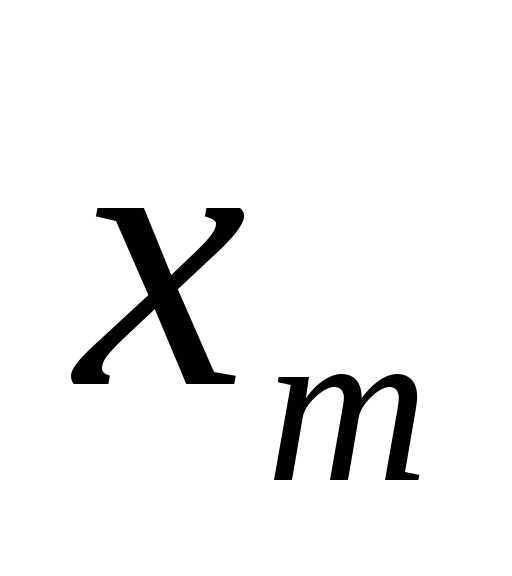 на
все последующие шага, так как эти шаги
просто отсутствуют. Делая предположения
об условиях окончания (
на
все последующие шага, так как эти шаги
просто отсутствуют. Делая предположения
об условиях окончания (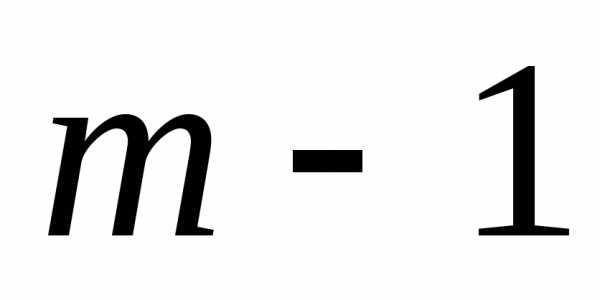 )-гo шага, для каждого из них проводят условную
оптимизацию
)-гo шага, для каждого из них проводят условную
оптимизацию 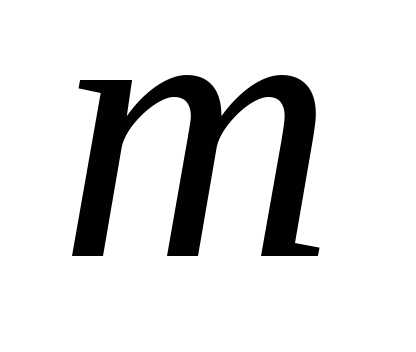 -го шага
и определяют условное оптимальное
управление
-го шага
и определяют условное оптимальное
управление 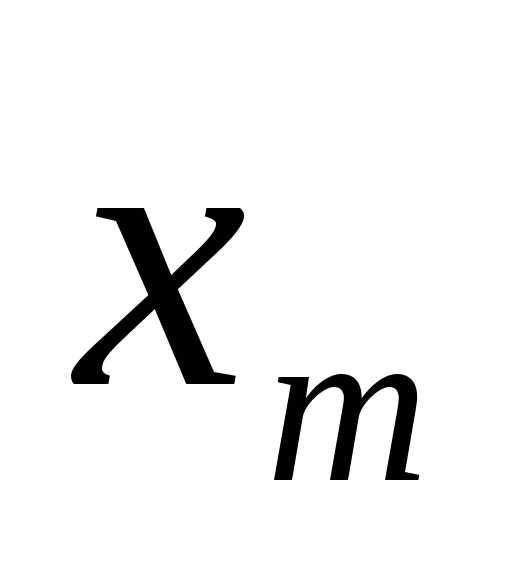 . Аналогично
поступают для (
. Аналогично
поступают для (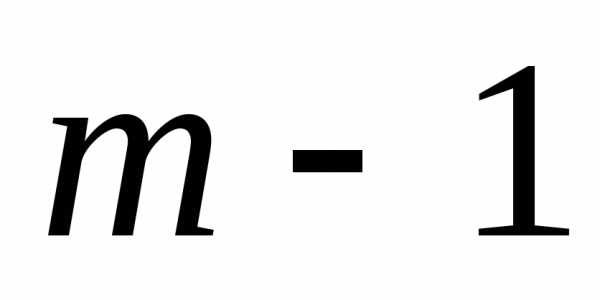 )-го шага, делая предположения об исходах
окончания (
)-го шага, делая предположения об исходах
окончания (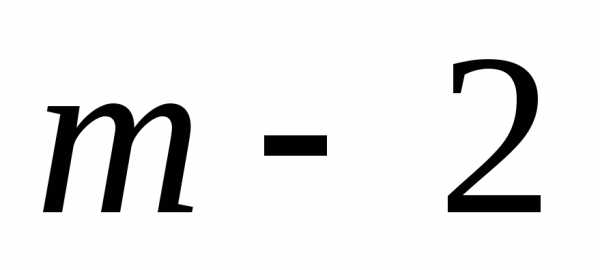 )-го шага и определяя условное оптимальное
управление на (
)-го шага и определяя условное оптимальное
управление на (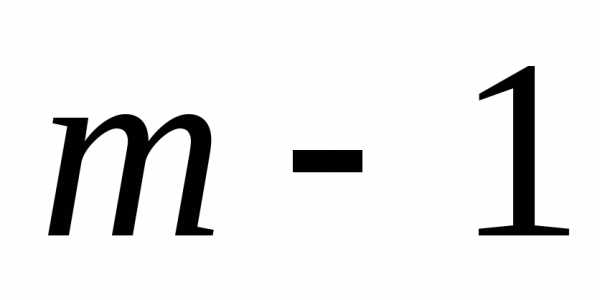 )-м шаге, приносящее оптимальный выигрыш
на двух последних шагах – (
)-м шаге, приносящее оптимальный выигрыш
на двух последних шагах – (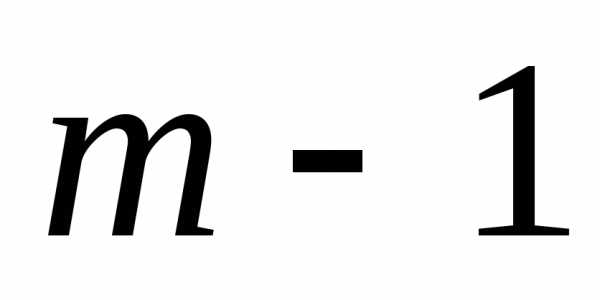 )-м и
)-м и 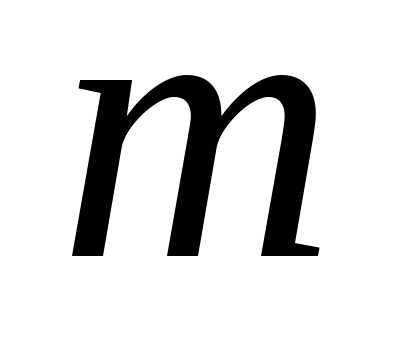 -м. Так
же действуют на всех остальных шагах
до первого. На первом шаге, как правило,
не надо делать условных предположений,
так как состояние системы перед первым
шагом обычно известно.
-м. Так
же действуют на всех остальных шагах
до первого. На первом шаге, как правило,
не надо делать условных предположений,
так как состояние системы перед первым
шагом обычно известно.
Для этого состояния выбирают оптимальное шаговое управление, обеспечивающее оптимальный выигрыш на первом и всех последующих шагах. Это управление является безусловным оптимальным управлением на первом шаге и, зная его, определяются оптимальное значение выигрыша и безусловные оптимальные управления на всех шагах. Ниже это будет пояснено на примерах.
studfiles.net
Понятие Динамического программирования. Классификация задач динамического программирования. Компьютерная технология решения задачи динамического программирования.
Динамическое программирование — это вычислительный метод для решения задач определенной структуры. Возникло и сформировалось в 1950-1953 гг. благодаря работам Р. Беллмана над динамическими задачами управления запасами. В упрощенной формулировке динамическое программирование представляет собой направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму.
Основные необходимые свойства задач, к которым возможно применить этот принцип:
Задача должна допускать интерпретацию как n-шаговый процесс принятия решений.
Задача должна быть определена для любого числа шагов и иметь структуру, не зависящую от их числа.
При рассмотрении k-шаговой задачи должно быть задано некоторое множество параметров, описывающих состояние системы, от которых зависят оптимальные значения переменных. Причем это множество не должно изменяться при увеличении числа шагов.
Выбор решения (управления) на k-м шаге не должен оказывать влияния на предыдущие решения, кроме необходимого пересчета переменных.
Задача о выборе траектории, задача последовательного принятия решения, задача об использовании рабочей силы, задача управления запасами — классические задачи динамического программирования.
Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи.
В основе решения всех задач динамического программирования лежит «принцип оптимальности» Беллмана, который выглядит следующим образом:
Каково бы ни было состояние системы S в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Этот принцип впервые был сформулирован Р. Беллманом в 1953 г. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование- процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Классификация:
Нисходящее: задача разбивается на подзадачи меньшего размера, они решаются, и затем комбинируются для решения исходной задачи.
Восходящее: все подзадачи, которые впоследствии понадобятся для решения исходной задачи, просчитываются заранее и затем используются для построения решения исходной задачи Восходящее ДП лучше нисходящего в смысле размера необходимого стека и количества вызовов функций.
Динамическое программирование.
Примеры задач:
· Наибольшая общая подпоследовательность
· Наибольшая увеличивающаяся подпоследовательность
· Задача о редакционном расстоянии
· Порядок перемножения матриц
· Задача о коммивояжере
· Наибольшее независимое множество вершин дерева
· Задача о кратчайших путях
Система Mathematica объединяет в себе запас мировых математических знаний, накопленных в справочной литературе, и использует свои собственные
революционные алгоритмы, чтобы развивать эти знания.
Умение проводить аналитические расчеты — одно из главных достоинств этой программы, автоматизирующей математические расчеты. Mathematica умеет преобразовывать и упрощать алгебраические выражения, дифференцировать и вычислять определенные и неопределенные интегралы, вычислять конечные и бесконечные суммы и произведения, решать алгебраические и дифференциальные уравнения и системы, а также разлагать функции в ряды и находить пределы
Mathematica позволяет строить двух и трехмерные графики различных типов в виде точек и линии на плоскости, поверхностей, а также контурные, градиентные (dencity plot), параметрические. Mathematica выполняет построение графика в три этапа. На первом создается множество графических примитивов, на втором они преобразуются в независимое от вычислительной платформы описание на языке PostScript, а на третьем это описание переводится в графический формат для той системы, на которой установлена Mathematica.
Система MatLab
Данная система ориентирована на матричные и векторные вычисления (её названием является сокращение словосочетания Matrix Laboratory) и предназначена в основном для численного моделирования технических систем. Её последние версии содержат элементы универсальных систем компьютерной алгебры: специальный модуль MatLab Notebook, позволяющий, в том числе, использовать возможности Microsoft Word для оформления документов, а также приобретённый у компании Maple Waterloo модуль основной символьной библиотеки системы Maple V 4.0 для выполнения некоторых аналитических расчётов. Входной язык в определённой мере напоминает BASIC (с элементами Фортрана и Паскаля). Интерфейс менее доступный и красочный, чем у системы MathCAD, однако скорость вычислений выше.
Использование в образовании нецелесообразно; система предназначена для профессиональной работы в области математики и смежных областях.
Система MatLab предназначена для выполнения инженерных и научных расчетов и высококачественной визуализации получаемых результатов. Эта система применяется в математике, вычислительном эксперименте, имитационном моделировании.
В пакет входит множество хорошо проверенных численных методов (решателей), операторы графического представления результатов, средства создания диалогов. Отличительной особенностью MatLab по сравнению с обычными языками программирования является матричное представление данных и большие возможности матричных операций над данными. Используя пакет MatLab можно, как из кубиков конструктора, построить довольно сложную математическую модель, или написать свою программу (весьма похожую на Фортран-программу). А можно используя SIMULINK и технологию визуального моделирования составить имитационную модель или систему автоматического регулирования.
Гибкий язык MatLab дает возможность инженерам и ученым легко реализовывать свои идеи. Мощные численные методы и графические возможности позволяют проверять предположения и новые возникающие идеи, а интегрированная среда дает возможность быстро получать практические результаты.
cyberpedia.su
Динамическое программирование, основные принципы
Для выбора оптимального решения при выполнении задач программирования иногда требуется перебирать большое количество комбинаций данных, что нагружает память персонального компьютера. К таким методам относится, например, метод программирования «разделяй и властвуй». В данном случае алгоритмом предусмотрено разделение задачи на отдельные мелкие подзадачи. Такой метод применяется только в тех случаях, когда мелкие подзадачи независимы между собой. Для того чтобы избежать выполнения лишней работы в том случае, если подзадачи взаимозависимы, используется метод динамического программирования, предложенный американцем Р.Беллманом в 50-х годах.
Суть метода
Динамическое программирование заключается в определении оптимального решения n-мерной задачи, разделяя ее n отдельных этапов. Каждый из них является подзадачей по отношению к одной переменной.
Основным преимуществом такого подхода можно считать то, что разработчики занимаются одномерными оптимизационными задачами подзадач вместо n-мерной задачи, а решение главной задачи собирается «снизу вверх».
Целесообразно применять динамическое программирование в тех случаях, когда подзадачи взаимосвязаны, т.е. имеют общие модули. Алгоритмом предусмотрено решение каждой из подзадач один раз, и сохранение ответов выполняется в специальной таблице. Это дает возможность не вычислять ответ заново при встрече с аналогичной подзадачей.
Задача динамического программирования решает вопрос оптимизации. Автором этого метода Р. Беллманом был сформулирован принцип оптимальности: каким бы ни являлось начальное состояние на каждом из шагов и решение, определенное на этом шаге, все следующие выбираются оптимальными по отношению к тому состоянию, которое принимает система в конце шага.
Метод усовершенствует выполнение задач, решаемых с помощью перебора вариантов или рекурсий.
Построение алгоритма задачи
Динамическое программирование предполагает построение такого алгоритма задач, при котором задача так разбивается на две или больше подзадач, чтобы ее решение складывалось из оптимального решения всех подзадач, входящих в нее. Далее возникает необходимость в написании рекуррентного соотношения и вычислении оптимального значения параметра для задачи в целом.
Иногда на 3-м шаге нужно дополнительно запоминать некоторую вспомогательную информацию о ходе выполнения каждой подзадачи. Это называется обратным ходом.
Применение метода
Динамическое программирование применяется при наличии двух характерных признаков:
- оптимальность для подзадач;
- наличие в задаче перекрывающихся подзадач.
Решая оптимизационную задачу методом динамического программирования, сначала необходимо описать структуру решения. Задача обладает оптимальностью, если решение задачи складывается из оптимальных решений ее подзадач. В этом случае целесообразно использовать динамическое программирование.
Второе свойство задачи, существенное при данном методе, — небольшое число подзадач. Рекурсивное решение задачи использует одни и те же перекрывающиеся подзадачи, количество которых зависит от размера исходной информации. Ответ хранится в специальной таблице, программа экономит время, пользуясь этими данными.
Особенно эффективно применение динамического программирования тогда, когда по существу задачи нужно принимать решения поэтапно. Например, рассмотрим простой пример задачи замены и ремонта оборудования. Допустим, на литейной машине завода по изготовлению шин делают одновременно шины в двух разных формах. В том случае, если одна из форм выходит из строя, приходится машину разбирать. Понятно, что иногда выгоднее заменить и вторую форму для того, чтобы не разбирать машину на случай, если и эта форма окажется неработоспособной на следующем этапе. Тем более, бывает проще заменить обе работающие формы до того, как они начнут выходить из строя. Метод динамического программирования определяет наилучшую стратегию в вопросе о замене таких форм, учитывая все факторы: выгоду от продолжения эксплуатации форм, потери от простоя машины, стоимость забракованных шин и другое.
fb.ru
Примеры задач динамического программирования
Задача о найме работников.Рассмотрим вопросы применения методов динамического программирования в конкретных экономико-математических моделях.
Отдельно отметим, что данные вычислительные схемы, вообще говоря, достаточно часто используются для решения конкретных задач: задача о ранце, задача о кратчайшем пути, задачи транспортного типа.
Одним из важнейших классов задач, для которых применение динамического программирования оказывается плодотворным, являются задачи последовательного принятия решений. Их особенностью является то, что искомые переменные должны определяться в строгой временной последовательности и не должны меняться местами. В качестве примера опишем так называемую задачу о найме работников (задачу об использовании рабочей силы).
В данной задаче рассматривается некоторый экономический объект (фирма, магазин, завод и т. п.), функционирующий в течение конечного числа периодов, обозначаемых номерами k . Каждый период k характеризуется нормативной потребностью в определенном количестве однотипных работников . Тот же объем работ может быть выполнен другим количеством сотрудников , что, однако, влечет дополнительные затраты либо за счет нерационального использования рабочей силы, либо ввиду повышения оплаты за интенсивный труд. Размеры этих дополнительных издержек описываются функциями ,где — отклонение фактической численности работающих от планово необходимой , причем .Управленческое решение на шаге k заключается в выборе величины изменения числа сотрудников , что однозначно определяет количество работающих в течение следующего периода: . Затраты по изменению количества работников (найму и увольнению) при переходе от периода k кпериоду задаются функцией , где также Тогда суммарные издержки, вызванные принятым на шаге k решением, характеризуются значением функции
,
План задачи (стратегия управления) заключается в выборе поэтапных изменений количества работников, а его суммарная эффективность описывается аддитивной функцией
15)
На основе сформулированной модели ставится задача минимизации целевой функции (издержек) (15). Причём постановка задачи не будет корректной, если не задать начальное условие на количество работников. Существуют две модификации данной задачи, определяемые типом начального условия: в первом случае задается исходное значение на первом этапе , а во втором — требуемое количество в n-м периоде .
Рассмотрим первый случай. Поскольку фиксированным является начальное количество работников и, напротив, ничего не известно о том, каким это количество должно быть на последнем этапе, то рассмотрение процесса принятия решений удобнее начать с конца. Оптимальное управление на последнем этапе п по условию равно ,поэтому минимальные издержки полностью определяются количеством работников в последнем периоде:
(16)
Для остальных предшествующих шагов основное рекуррентное соотношение примет вид
(17)
где — минимальные затраты с k-го по n-й периоды, в предположении, что количество работников в k-й период равно . Точки , в которых достигаются минимумы (17), определяют условное оптимальное управление на каждом шаге.
Последовательно определяя и дойдя до этапа 1, мы сможем найти безусловное оптимальное управление из того условия, что на начало первого периода численность работников должна составлять , аименно
Остальные компоненты оптимального плана и состояния , образующие оптимальную траекторию, последовательно находятся по рекуррентным формулам
, ,
после чего не составляет труда вычислить оптимальное значение целевой функции (15).
Остановимся теперь на втором случае, когда задано финальное состояние управляемого объекта, т. е. желаемое количество работников на последнем периоде . Очевидно, что в данной ситуации следует поступить с точностью «до наоборот» и рассмотреть процесс принятия решений от начала к концу. Наилучшее условное управление на первом шаге будет найдено в процессе вычисления функции
(18)
где состояние является возможным количеством работников на начальном шаге. Соответственно, основное рекуррентное соотношение выразит минимальные издержки вплоть до k-гопериода через таковые для предыдущих периодов (с первого по -й) при условии, что численность работников в k-й период будет равна :
(19)
Одновременно будут найдены функции , ,определяющие условные оптимальные управления. На последнем периоде, в силу начального условия, . Отсюда путем последовательного решения рекуррентных уравнений могут быть найдены оптимальные численности работников и безусловные оптимальные управления:
, ,
В заключение, как и в первом случае, подсчитывается минимальная величина издержек.
Обобщая изложенные схемы решения, приходим к выводу:
При использовании алгоритмов динамического программирования, если задано начальное состояние управляемой системы, то задача решается в обратном направлении,а если конечное, то — в прямом.Наконец, если заданы как начальное, так и конечное состояния, то задача существенно усложняется. (В качестве компромисса в этом случае можно отказаться от оптимизации на первом или последнем этапе.)
Продемонстрируем процесс решения задачи о найме работников на конкретном примере:
Для функционирования некоторого предприятия в течение четырех месяцев (нумеруемых от 1 до 4) по нормам требуются следующие количества работников одинаковой квалификации:
причем перед началом первого месяца (в нулевом месяце) фактически имеется сотрудников. Администрация планирует в конце каждого месяца k (кроме последнего) корректировать число работающих на величину На прием одного сотрудника необходимо затратить 9 у. е., а на увольнение — 6 у. е. Предполагается, что расходы на содержание избыточного работника составляют 8 у. е., а в случае нехватки персонала приходится нести затраты в размере 12 у. е. за каждое вакантное место.
Требуется найти оптимальные значения приращений численности работающих в конце каждого из первых трех месяцев, при которых суммарные издержки за весь рассматриваемый период будут минимальными.
В начале решения запишем в аналитической форме функции издержек на прием-увольнение сотрудников (и), а также на содержание ненормативного штата (g). С этой целью введем функции
(20)
(21)
Оценки эффективности управления на каждом шаге имеют вид:
; ,
Поскольку в поставленной задаче задано начальное условие , ее решение начинается с конца, и, следовательно, будут применяться рекуррентные соотношения (17). С технической точки зрения будет удобно на каждом шаге составлять две таблицы значений: функции издержек, получаемых начиная с текущего шага в зависимости от текущего состояния и управления,
(22)
и функции минимальных издержек в зависимости от текущего состояния
(23)
Для сокращения объема табулируемых значений можно воспользоваться свойством выпуклости функции , вытекающим из выпуклости f и g. Из выпуклости функции следует, что заполнять таблицу ее значений необходимо лишь до тех пор, пока они уменьшаются, т. е. можно остановиться, как только очередное значение оказывается больше предыдущего.
Итерация 1. Полагаем . На данном этапе функция состояния может быть найдена непосредственно, если учесть, что и :
Таблица значений данной функции и условные оптимальные управления имеют вид
Итерация 2. Полагаем . Предварительно заполним таблицу значений функции для достаточно большого множества аргументов согласно формуле:
Выбирая минимальные по значения , составим таблицу и соответствующие значения условных оптимальных управлений :
Итерация 3. Полагаем . Так же, как на предыдущей итерации, заполним таблицу значений функции согласно формуле:
Выбирая минимальные по значения , составим таблицу и соответствующие значения условных оптимальных управлений :
Итерация 4. Полагаем . Аналогично предыдущему, заполним таблицу значений функции согласно формуле:
Выбирая минимальные по , значения , составим таблицу и соответствующие значения условных оптимальных управлений :
Итерация 5. На последней итерации, в связи с наличием начального условия , достаточно вычислить
и найти как точку минимума . Простые вычисления показывают, что минимум
достигается при . Следовательно, ,после чего обратным ходом последовательно вычисляются оптимальные управления и оптимальные состояния (оптимальная траектория):
;
;
;
.
Таким образом, результаты расчета свидетельствуют, что при заданной системе расценок в третьем месяце выгоднее не брать 5-го работника, а компенсировать его отсутствие дополнительными выплатами за сверхурочную работу имеющимся сотрудникам.
Динамические задачи управления запасами.Одной из наиболее известных сфер приложения методов динамического программирования является такая область математической экономики, как теория управления запасами. Ее предметом является разработка и исследование математических моделей систем, занимающих промежуточное положение между источниками (производителями) тех или иных ресурсов и их потребителями. При математической формализации процессов управления запасами очень часто приходится использовать скачкообразные, недифференцируемые и кусочно-непрерывные функции. Как правило, это обусловливается необходимостью учета эффектов концентрации, фиксированных затрат и платы за заказ. В связи с этим получаемые задачи с трудом поддаются аналитическому решению классическими методами, однако могут быть успешно решены с помощью аппарата динамического программирования. Рассмотрим достаточно типичную задачу, возникающую в процессе планирования деятельности системы снабжения, — так называемую динамическую задачу управления запасами.
Пусть имеется некоторая система снабжения (склад, оптовая база и т. п.), планирующая свою работу на п периодов. Ее деятельность сводится к обеспечению спроса конечных потребителей на некоторый продукт, для чего она осуществляет заказы производителю данного продукта. Спрос клиентов (конечных потребителей) в данной модели рассматривается как некоторая интегрированная величина, принимающая заданные значения для каждого из периодов, и он должен всегда удовлетворяться (т. е. не допускаются задолженности и отказы). Также предполагается, что заказ, посылаемый производителю, удовлетворяется им полностью, и временем между заказом и его выполнением можно пренебречь (т. е. рассматривается система с мгновенным выполнением заказа). Введем обозначения:
— остаток запаса после -го периода;
— заранее известный суммарный спрос в k-м периоде;
— заказ (поставка от производителя) в k-мпериоде;
) — затраты на выполнение заказа объема в k-мпериоде;
— затраты на хранение запаса объема в k-мпериоде.
После получения поставки и удовлетворения спроса объем товара, подлежащего хранению в период k, составит . Учитывая смысл параметра , можно записать соотношение:
. (24)
Расходы на получение и хранение товара в период k описываются функцией
.
Планом задачи можно считать вектор компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (24) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все п периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции:
. 25)
Естественной в рамках сформулированной модели представляется задача нахождения последовательности оптимальных управлений (заказов) и связанных с ними оптимальных состояний (запасов) , которые обращают в минимум (25). В качестве начального условия используем требование о сохранении после завершения управления заданного количества товара уп+1 , именно
. (26)
При решении поставленной задачи методом динамического программирования в качестве функции состояния управляемой системы логично взять минимальный объем затрат, возникающих за первые k периодов при условии, что в k-йпериод имеется запас . Тогда можно записать основное рекуррентное соотношение
,(27)
так как и
. (28)
Система рекуррентных соотношений (27)-(28) позволяет найти последовательность функций состояния , ,…, и условных оптимальных управлений , ,…, . На n-м шаге с помощью начального условия (26) можно определить . Остальные значения оптимальных управлений определяются по формуле:
. (29)
Особый интерес представляет частный случай задачи (24)- (25), при котором предполагается, что функции затрат на пополнение запаса являются вогнутыми по , a функции затрат на хранение являются линейными относительно объема хранимого запаса, т. е. . Параллельно заметим, что обе предпосылки являются достаточно реалистичными. Обозначим функцию затрат в течение k-гопериода через
(30)
или, что то же самое,
. (31)
В силу сделанных предположений все функции затрат являются вогнутыми (как суммы вогнутой и линейной функций). Данное свойство значительно упрощает процесс решения, так как для поиска минимума вогнутых функций достаточно рассмотреть только две крайние точки множества, на котором отыскивается минимум. С учетом введенного обозначения задачу (24)-(25) можно записать в виде:
(32)
при условиях
. (33)
Рассмотрим процедуру решения (32)-(33). Так как ищется минимум суммы вогнутых функций , то решение будет достигаться на одной из крайних точек множества, определяемого условиями (33). Общее число переменных и в системе (33) равно . Однако, учитывая то, что в ней только п уравнений, в оптимальном плане будет не более п ненулевых компонент, причем для каждого периода k значения и не могут равняться нулю одновременно (в силу необходимости удовлетворения спроса либо за счет заказа, либо за счет запаса). Формально это утверждение можно представить в виде условия дополняющей нежесткости:
,(34)
где
(35)
С точки зрения содержательной интерпретации условия (34)-(35) означают, что при оптимальном управлении заказ поставщику на новую партию не должен поступать, если в начале периода имеется ненулевой запас, или размер заказа должен равняться величине спроса за целое число периодов. Отсюда следует, что запас на конец последнего периода должен равняться нулю: Последнее позволяет решать задачу в прямом направлении, применяя рекуррентное соотношение
, (36)
где .
Учитывая (34)-(35) и вогнутость заключаем, что минимум (36) достигается в одной из крайних точек или , поэтому
, (37)
тогда для предыдущего периода функция состояния может быть выражена в виде
(38)
Следовательно, в общем виде получаем модифицированную форму для рекуррентного соотношения
. (39)
При дальнейших конкретизирующих предположениях о виде функций можно получить еще более компактные формы для рекуррентных соотношений.
Похожие статьи:
poznayka.org

 ,
в течение которого используется
оборудование, год
,
в течение которого используется
оборудование, год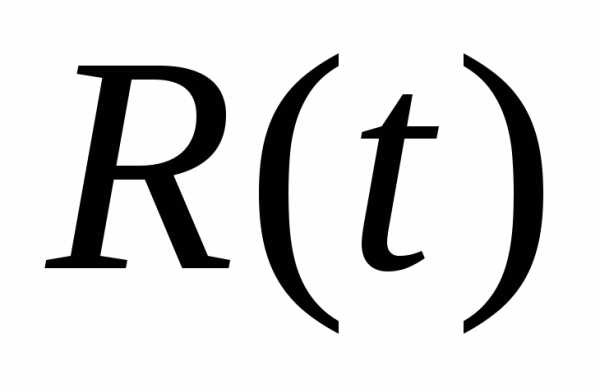 в стоимостном выражении, ден. ед.
в стоимостном выражении, ден. ед.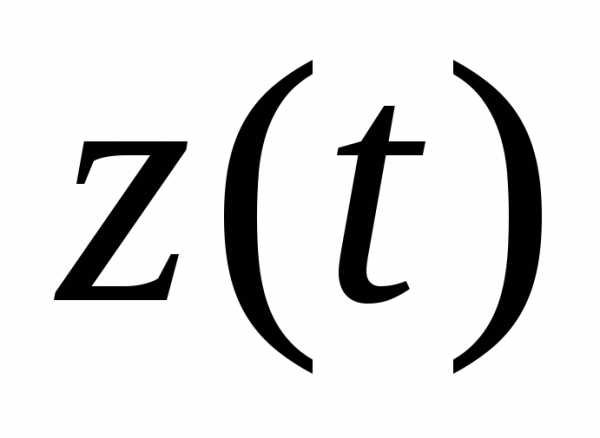 ,
ден. ед.
,
ден. ед.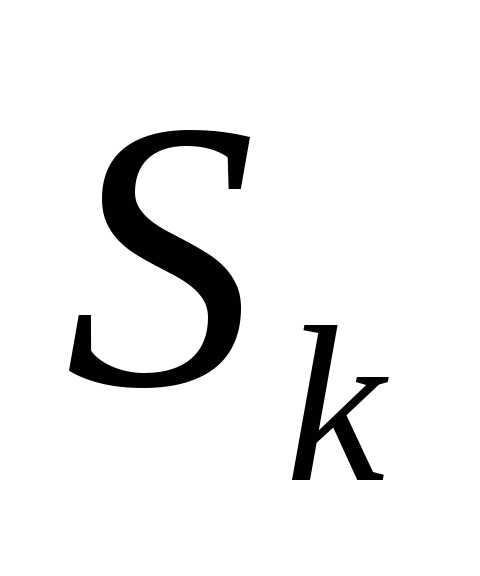 зависит только от предыдущего состояния
зависит только от предыдущего состояния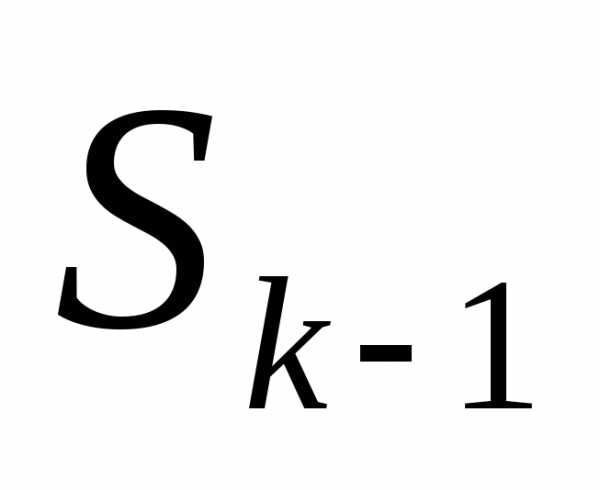 и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.
и управления на предыдущем шаге и не
зависит от предшествующих состояний
и управлений. Это требование называется
«отсутствие последствий».- уравнение состояний.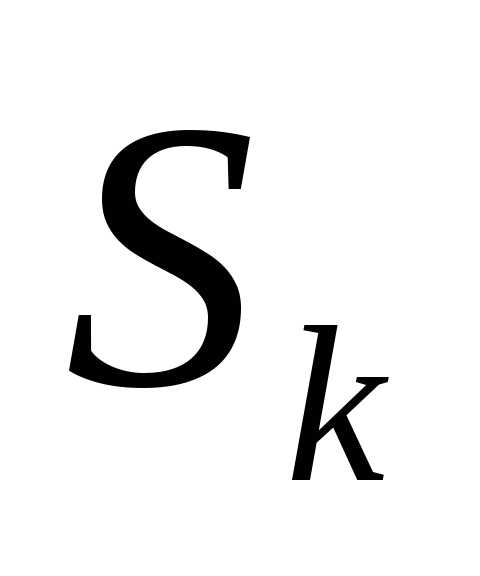 послеk-ого шага зависит
только от предшествующего состояния
послеk-ого шага зависит
только от предшествующего состояния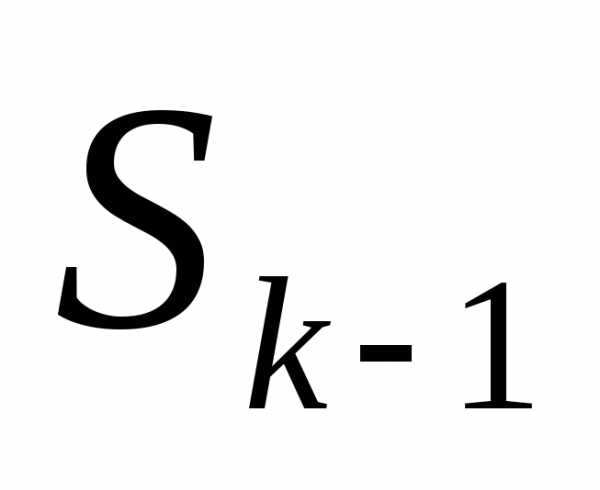 и управления
и управления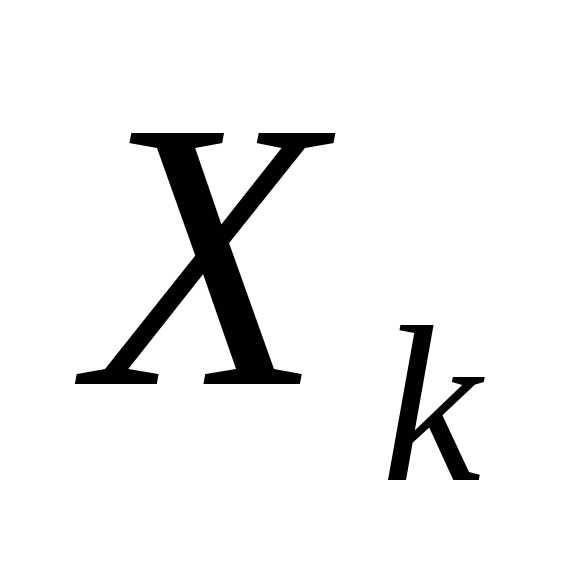 (нет последствий).
(нет последствий).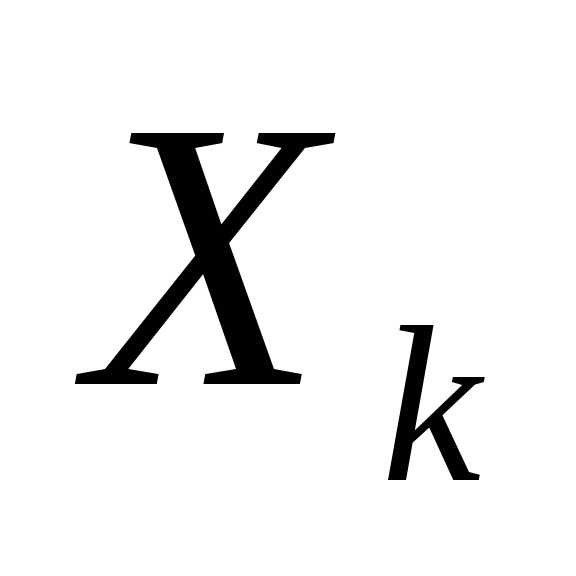 зависит от конечного числа управляющих
переменных, а состояние
зависит от конечного числа управляющих
переменных, а состояние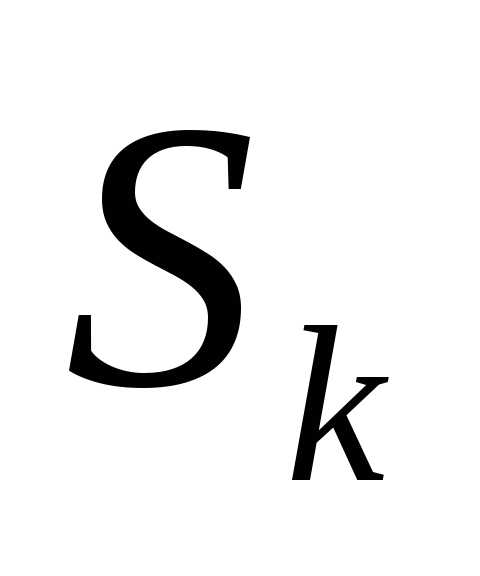 от конечного числа параметров.
от конечного числа параметров.