xy вектор бесплатно | AI, SVG и EPS
- Все
- AI
- CDR
- EPS
- SVG
- Все
- Белый
- Красный
- Оранжевый
- Зелёный
- Вода
- Синий
- Фиолетовый
- Розовый
- Чёрный
- Серый
xy dna
Gender — XY chromosome
XY & XX Genes Black and White Icon with Long Shadow
Sex X and Y chromosome.
 Determine male, female. Design element stock vector illustration
Determine male, female. Design element stock vector illustrationXY and XX Genes Icon on Black and White Vector Backgrounds
lady justice Themis 3
Sex chromome structure.
 Male and Female. Biological study
Male and Female. Biological studyXY & XX Genes Blue Triangle Node Vector Pattern
Sex chromosome structure. Male and Female. Biological study. Chromosome X and Y.
XY & XX Genes Icon on Black Button with White Rollover
New Year 2020
XY & XX Genes Icon on Checkerboard Transparent Background
1.
 4.3. X-Y график двух векторов MathCAD 12 руководство
4.3. X-Y график двух векторов MathCAD 12 руководствоRADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1354 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM / org/Breadcrumb»>MathCAD 12
- Основные сведения о Mathcad
- 1.1. Знакомство с Mathcad
- 1.1.1. Назначение Mathcad
- 1.1.2. Интерфейс пользователя
- 1.1.3. Панели инструментов
- 1.1.4. Справочная информация
- 1.2 Основы вычислений в Mathcad
- 1.2.1. Операторы численного и символьного вывода
- 1.2.2. Математические выражения и встроенные функции
- 1.2.3. Переменные и оператор присваивания
- 1.2.4. Функции пользователя
- 1.2.5. Типы чисел
- 1.2.6. Ранжированные переменные и матрицы
- 1.2.7. Размерные переменные
- 1.3. Ввод и редактирование формул
- 1.3.1. Элементы интерфейса редактора формул
- 1.3.2. Ввод формул
- 1.3.3. Перемещение линий ввода внутри формул
- 1.3.4. Изменение формул
- 1.3.5. Программирование
- 1.
 4. Графики
4. Графики
- 1.4.1. Типы графиков
- 1.4.2. Создание графика
- 1.4.3. X-Y график двух векторов
- 1.4.4. X-Y график функции
- 1.4.5. Построение нескольких рядов данных
- 1.4.6. Форматирование графиков
- 1.4.7. Трехмерные графики
Самый простой и наглядный способ получить декартов график — это сформировать два вектора данных, которые будут отложены вдоль осей х и Y. Последовательность построения графика двух векторов х и у показана на рис. 1.23.
Рис. 1.23. X-Y график двух векторов
В этом случае в местозаполнители возле осей вводятся просто имена векторов. Также допускается откладывать по осям элементы векторов, т. е. вводить в местозаполнители возле осей имена xi и yi соответственно. В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных, или кривой (trace).
ПРИМЕЧАНИЕ
Обратите внимание, что Mathcad автоматически определяет границы графика, исходя из диапазона значений элементов векторов.
Стоит отметить, что подобным образом легко создать и X-Y график столбцов или строк матрицы, применяя оператор выделения столбца и откладывая соответствующие выражения по осям графика (множество подобных примеров вы найдете на рисунках в последующих главах книги).
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
10019 0
Глава 10 Работа с информационными ресурсами Mathcad 11
7015 0
Глава 2 Работа с файлами Mathcad 11
12655 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.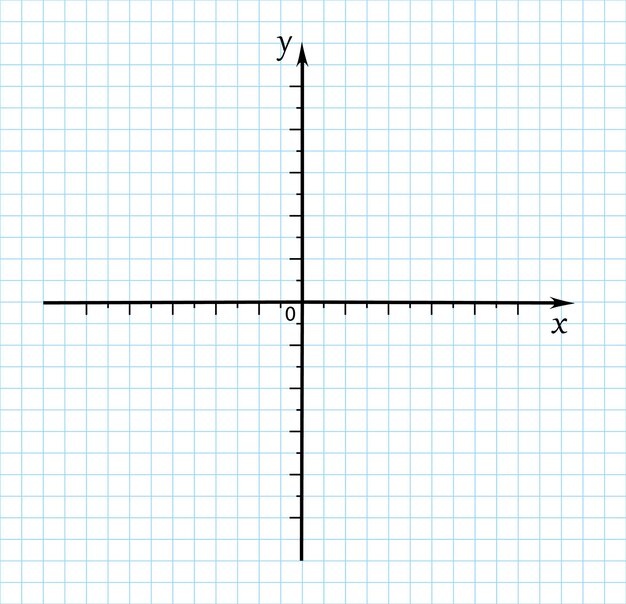 ru обязательна. 0.2373 s
ru обязательна. 0.2373 s
векторов и 2D-движение
Точка может быть расположена в системе координат x, y по ее координаты х и у.
Координата x описывает, как далеко по оси x находится точка расположен, в то время как координата y описывает, как далеко вдоль по оси Y расположена точка.
Координаты x и y могут быть как положительными, так и отрицательными в зависимости от видно в примерах выше.
Мы будем использовать жирный шрифт для обозначения вектора, такого как р . Записывая вектор от руки, мы будем указывать, что что-то является вектором, нарисовав над ним стрелку как . Некоторые такие отличительные обозначения важны. Не писать вектор без какой-либо отличительной характеристики или обозначение.
Мы можем описать точку (x,y) как точку, расположенную вектор r , который имеет компоненты x и y.
Мы можем назвать эту x-компоненту вектором вдоль x-направления длину x и указать, что это вектор размером x или . Точно так же мы можем назвать эту y-компоненту вектором вдоль y-направление длины y и указать, что это вектор и или . Тогда мы можем написать
или
= +
Обратите внимание, что это _ не _ правильно писать r = x + у.
r — длина вектора или величина вектора. Угол (тета) указывает направление вектора. Как r, x, y и связанный?
Обратите внимание, что r, x и y образуют стороны правой стороны . треугольник . Прямоугольные треугольники особенные из-за их Связь с тригонометрическими функциями.
Если мы знаем r, x и y, мы можем найти триггерные функции для
угол .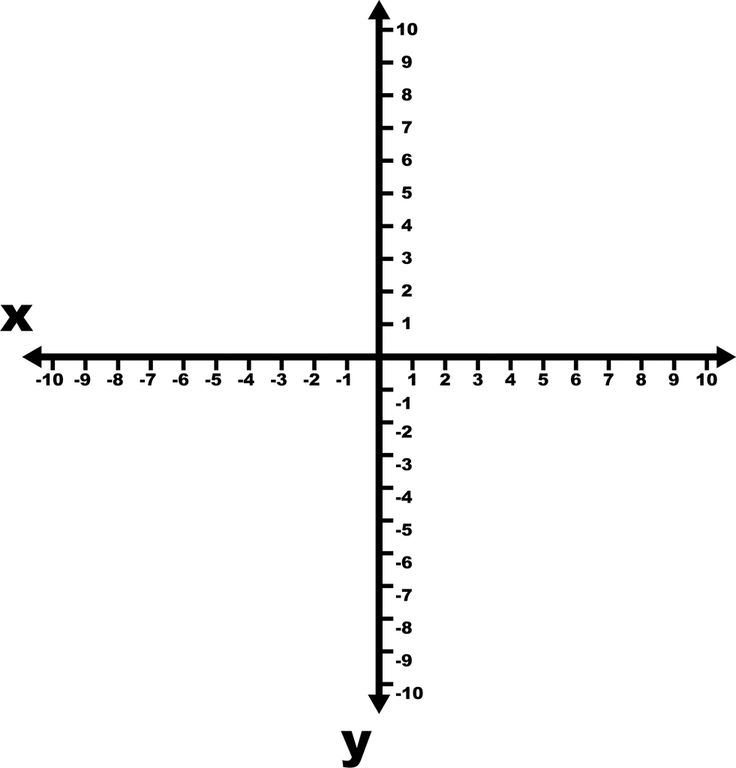 Хотя более вероятна ситуация, когда мы знаем x и y и хотим
найти р и .
Или мы можем знать г и и
хочу найти х и у. Все эти ситуации можно разрешить с помощью
триггерные функции.
Хотя более вероятна ситуация, когда мы знаем x и y и хотим
найти р и .
Или мы можем знать г и и
хочу найти х и у. Все эти ситуации можно разрешить с помощью
триггерные функции.
Обычно угол измеряют от положительную ось абсцисс и измерить ее положительных для против часовой стрелки направление. Показанный ниже пример может быть для угла = 53 или . Тогда, если r = 10, компонентов будет
у = г грех = (10) (0,8) = 8
Пожалуйста, , а не , запомните эти уравнения. Помните более основные определения триггерных функций,
соз = прил / гип
загар = опп/прил
Затем , для этого конкретного случая измерения угла от ось х, мы имеем
х = прил
г = опп
и , что означает, что
соз = х/р
загар = г / х
или
y = r sin
Конечно, угол
не обязательно ограничиваться первым квадрантом. Ниже может быть
схема для
= 150 o . Опять же, пусть r = 10 для этого числового примера.
Для этого случая
Ниже может быть
схема для
= 150 o . Опять же, пусть r = 10 для этого числового примера.
Для этого случая
у = г грех = (10) ( sin 150 o ) = (10) ( 0,500) = 5,00
Обратите внимание на знаки и сравните их со схемой. х = — 8,66 расположен слева от и y = + 5.00 расположен выше . Всегда составляйте схему! А потом сравните свои результаты — ваши ответы — с вашей схемой. Знаки жизненно важны, и это слишком легко отбросить их и просто использовать величины.
Диаграмма ниже может быть для r = 10 и = 210 или . Для этих значений мы можем найти компоненты к
у = г грех =
(10) ( sin 210 o ) = (10) ( — 0,500) = —
5. 00
00
Снова обратите внимание на знаки и сравните их со схемой. х = — 8.66 расположен слева от и у = — 5.00 расположен вниз . Всегда составляйте схему! А потом сравните свои результаты — ваши ответы — с вашей диаграммой. Знаки жизненно важны, и это слишком легко отказаться от них и просто использовать величины.
Мы можем описать этот вектор как r = 10, = 210 или , как указано выше. Или мы можем измерить угол по часовой стрелке как мы имеем ниже, и описываем этот вектор как r = 10, = — 150 или . Любое описание так же хорошо, как и другое. Это два способа описания одного и того же вектора или одного и того же точка.
В то время как является общим для измерения углов от оси X и
измерить их как положительных , если они против часовой стрелки , это _ не _ необходимо сделать так.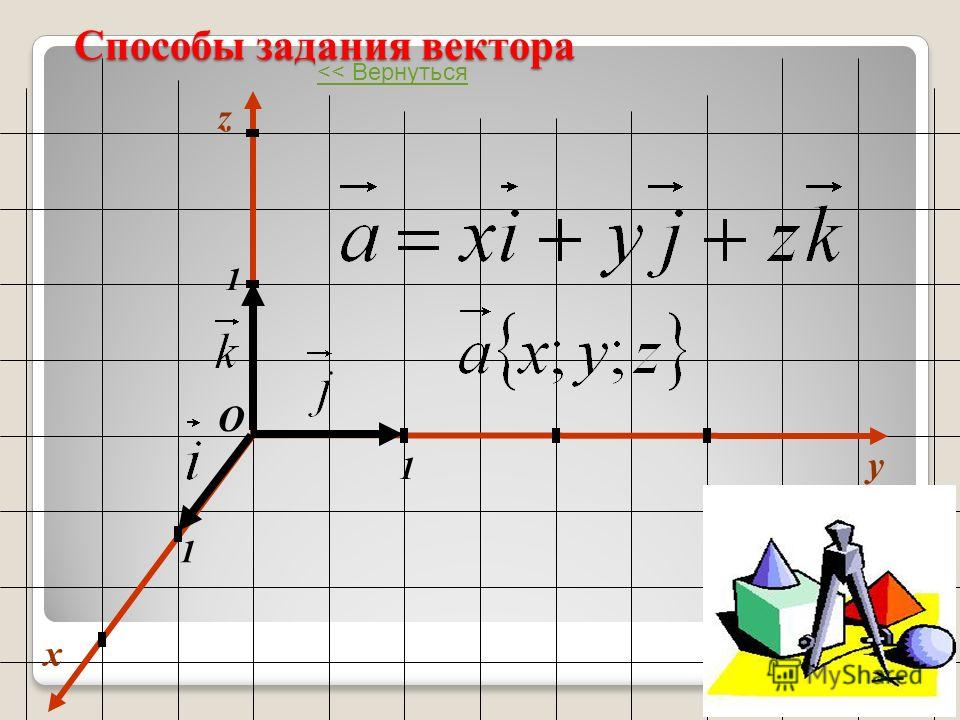 Пилоты самолетов обычно измеряют углы или направления от North (y) и измерьте их как положительный для по часовой стрелке углов. Ниже может быть местоположение или вектор
г = 10 км, =
53 или . В данном случае имеем
Пилоты самолетов обычно измеряют углы или направления от North (y) и измерьте их как положительный для по часовой стрелке углов. Ниже может быть местоположение или вектор
г = 10 км, =
53 или . В данном случае имеем
у = г соз = (10 км) (cos 53 o ) = (10 км) (0,6) = 6 км
Обратите внимание, что для этого расположения x теперь является противоположным . сторона (сторона прямоугольного треугольника, противоположная углу ) и y теперь является смежной стороной (сторона прямоугольного треугольника прилегает к углу ). Если вы всегда начните с основных определений синуса и косинус, проблем не будет.
Задание местоположения или вектора через координаты (x,
y) означает, что мы используем декартову систему координат (или
система отсчета).
Задание местоположения или вектора через координаты (r, ) означает, что мы используем полярную систему координат (или опорную рамка).
2.4: Системы координат и компоненты вектора (часть 1)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3973
- OpenStax
- OpenStax
Цели обучения
- Описать векторы в двух и трех измерениях с точки зрения их компонентов, используя единичные векторы вдоль осей.

- Различать векторные компоненты вектора и скалярные компоненты вектора.
- Объясните, как величина вектора определяется через компоненты вектора.
- Определить угол направления вектора на плоскости.
- Объясните связь между полярными координатами и декартовыми координатами на плоскости.
Векторы обычно описываются с точки зрения их компонентов в системе координат. Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь направление к определенному месту, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37° к северу от востока.
В прямоугольной (декартовой) системе координат xy на плоскости точка на плоскости описывается парой координат (x, y). Аналогичным образом вектор \(\vec{A}\) на плоскости описывается парой своих векторных координат. Координата x вектора \(\vec{A}\) называется его x-компонентой, а y-координата вектора \(\vec{A}\) называется его y-компонентой. Компонента x вектора — это вектор, обозначаемый \(\vec{A}_{x}\). Компонента вектора y — это вектор, обозначаемый \(\vec{A}_{y}\). В декартовой системе x и y компоненты вектора вектора являются ортогональными проекциями этого вектора на оси \(х\) и \(у\) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
Компонента x вектора — это вектор, обозначаемый \(\vec{A}_{x}\). Компонента вектора y — это вектор, обозначаемый \(\vec{A}_{y}\). В декартовой системе x и y компоненты вектора вектора являются ортогональными проекциями этого вектора на оси \(х\) и \(у\) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
\[ \vec{A} = \vec{A}_{x} + \vec{A}_{y} \ldotp \label{2.10}\]
Как показано на рисунке \(\PageIndex{1}\), вектор \(\vec{A}\) – это диагональ прямоугольника, где x-компонента \(\vec{A}_{x}\) равна сторона, параллельная оси x, и компонент y \(\vec{A}_{y}\) является стороной, параллельной оси y. Компонента вектора \(\vec{A}_{x}\) ортогональна компоненте вектора \(\vec{A}_{y}\).
Рисунок \(\PageIndex{1}\): Вектор \(\vec{A}\) на плоскости в декартовой системе координат представляет собой векторную сумму своих векторных x- и y-компонент.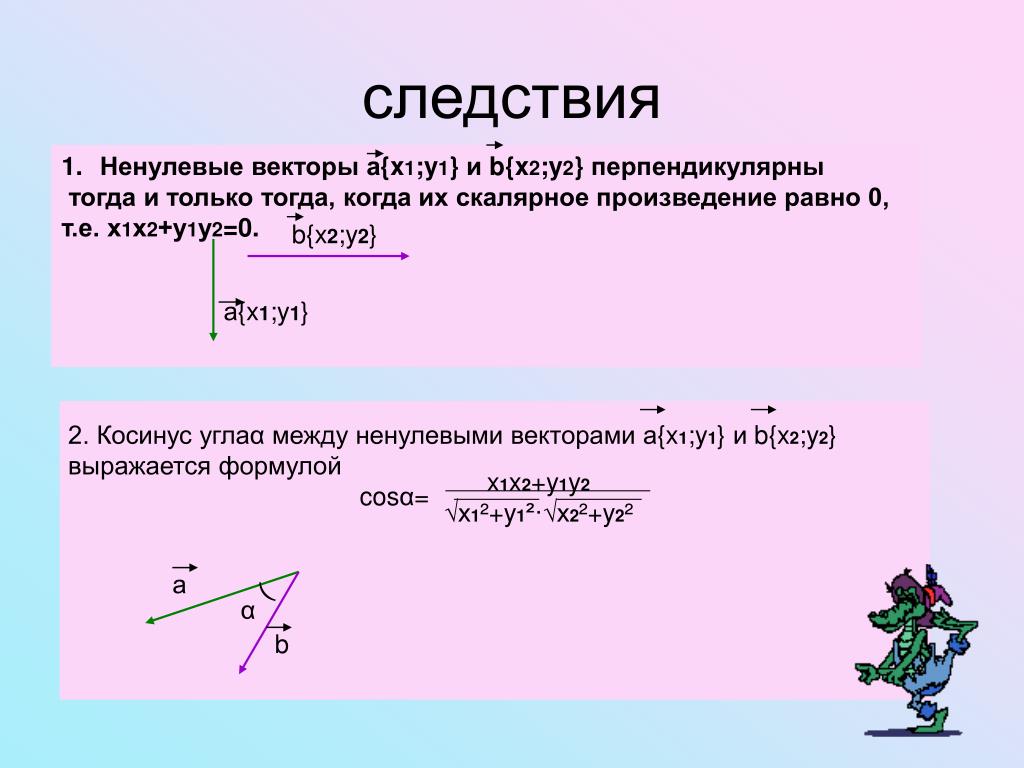 Компонента x-вектора \(\vec{A}_{x}\) является ортогональной проекцией вектора \(\vec{A}\) на ось x. Компонента вектора y \(\vec{A}_{y}\) является ортогональной проекцией вектора \(\vec{A}\) на ось y. Числа A x и A y , на которые умножаются единичные векторы, являются скалярными компонентами вектора.
Компонента x-вектора \(\vec{A}_{x}\) является ортогональной проекцией вектора \(\vec{A}\) на ось x. Компонента вектора y \(\vec{A}_{y}\) является ортогональной проекцией вектора \(\vec{A}\) на ось y. Числа A x и A y , на которые умножаются единичные векторы, являются скалярными компонентами вектора.Обычно положительное направление по оси x обозначается единичным вектором \(\hat{i}\), а положительное направление по оси y — единичным вектором \(\hat{j}\). Единичные векторы осей \(\hat{i}\) и \(\hat{j}\) определяют два ортогональных направления на плоскости. Как показано на рисунке \(\PageIndex{1}\), компоненты вектора x и y теперь могут быть записаны в терминах единичных векторов осей:
\[ \begin{cases} \vec{A}_{x} = A_{x} \hat{i} \\ \vec{A}_{y} = A_{y} \hat{j} \end {случаи} \метка{2.11}\]
Векторы \(\vec{A}_{x}\) и \(\vec{A}_{y}\), определяемые уравнением 2.11, являются векторными компонентами вектора \(\vec{A}\). Числа A x и A y , которые определяют компоненты вектора в уравнении \ref{2. 11}, являются скалярными компонентами вектора \(\vec{A}\). Комбинируя уравнение \ref{2.10} с уравнением \ref{2.11}, мы получаем компонентную форму вектора :
11}, являются скалярными компонентами вектора \(\vec{A}\). Комбинируя уравнение \ref{2.10} с уравнением \ref{2.11}, мы получаем компонентную форму вектора :
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} \ldotp \label{2.12}\]
Если мы знаем координаты \(b(x_b, y_b)\) исходной точки вектора (где b означает «начало») и координаты e(x e , y e ) конца точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:
\[ \begin{cases} A_{x} = x_{e} — x_{b} \\ A_{y} = y_{e} — y_{b} \ldotp \end{cases} \label{2.13} \]
Пример \(\PageIndex{1}\): смещение указателя мыши
Указатель мыши на мониторе компьютера в исходном положении находится в точке (6,0 см, 1,6 см) относительно левого нижнего угла боковой угол. Если вы переместите указатель на значок, расположенный в точке (2,0 см, 4,5 см), каков будет вектор смещения указателя?
Стратегия
Начало системы координат xy — нижний левый угол монитора компьютера. Таким образом, единичный вектор \(\hat{i}\) на оси x указывает горизонтально вправо, а единичный вектор \(\hat{j}\) на оси y указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2.0, 4.5). Подставьте координаты этих точек в уравнение \ref{2.13}, чтобы найти скалярные компоненты D x и D y вектора смещения \(\vec{D}\). Наконец, подставьте координаты в уравнение \ref{2.12}, чтобы записать вектор смещения в форме компонента вектора.
Таким образом, единичный вектор \(\hat{i}\) на оси x указывает горизонтально вправо, а единичный вектор \(\hat{j}\) на оси y указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2.0, 4.5). Подставьте координаты этих точек в уравнение \ref{2.13}, чтобы найти скалярные компоненты D x и D y вектора смещения \(\vec{D}\). Наконец, подставьте координаты в уравнение \ref{2.12}, чтобы записать вектор смещения в форме компонента вектора.
Решение
Отождествляем x b = 6,0, x e = 2,0, y b = 1,6 и y e = 4,5, где физическая единица равна 1 см. Скалярные x- и y-компоненты вектора смещения равны
\[D_{x} = x_{e} — x_{b} = (2,0 — 6,0)\; см = -4,0\; см,\]
\[D_{y} = y_{e} — y_{b} = (4.5 — 1.6)\; см = + 2,9\; см \ldotp\]
Форма векторной компоненты вектора смещения:
\[\vec{D} = D_{x}\; \шляпа{я} + D_{у}\; \шляпа{j} = (-4,0\; см)\; \шляпа{i} + (2,9\; см)\; \шляпа{j} = (-4. 0\; \шляпа{i} + 2.9\; \шляпа{j})\; cm \ldotp \label{2.14}\]
0\; \шляпа{i} + 2.9\; \шляпа{j})\; cm \ldotp \label{2.14}\]
Это решение показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): График вектора смещения. Вектор указывает от начальной точки \(b\) до конечной точки \(e\).Значение
Обратите внимание, что физическая единица — здесь 1 см — может быть помещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении \ref{2.14}. Часто последний способ удобнее, потому что он проще.
Компонента вектора x \(\vec{D}_{x}\) = −4,0 \(\hat{i}\) = 4,0(\(- \hat{i}\)) вектора смещения имеет величину |\(\vec{D}_{x}\)| = |− 4,0||\(\шляпа{i}\)| = 4,0, потому что модуль единичного вектора равен |\(\hat{i}\)| = 1. Обратите внимание также, что направление x-компоненты равно \(− \hat{i}\), что антипараллельно направлению +x-оси; следовательно, вектор x-компоненты \(\vec{D}_{x}\) указывает налево, как показано на рисунке \(\PageIndex{2}\).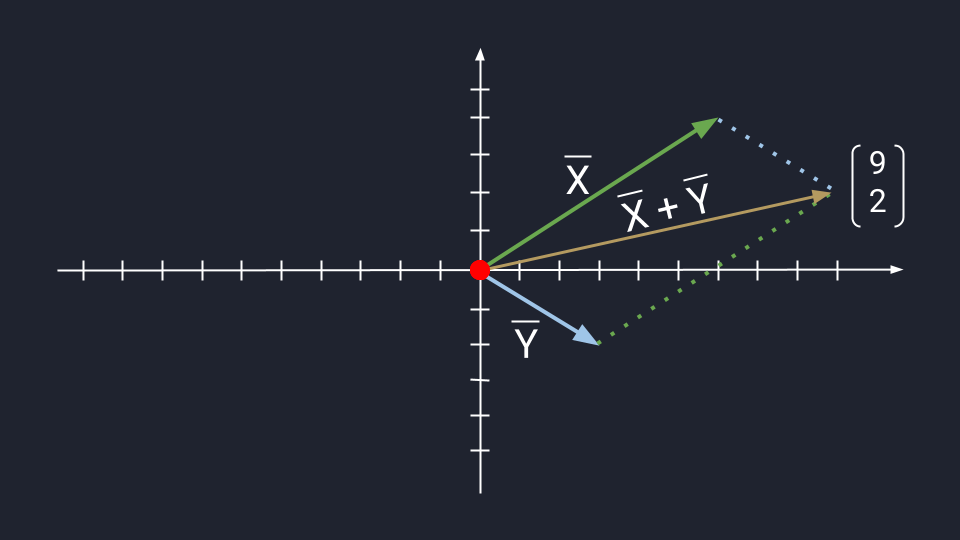 Скалярная x-компонента вектора \(\vec{D}\) равна D х = -4,0. Аналогично, векторная y-компонента \(\vec{D}_{y}\) = \(+ 2,9 \hat{j}\) вектора смещения имеет величину |\(\vec{D}_{y} \)| = |2.9||\(\шляпа{j}\)| = 2,9, потому что модуль единичного вектора равен |\(\hat{j}\)| = 1. Направление компонента y равно \(+ \hat{j}\), которое параллельно направлению оси +y. Следовательно, вектор y-компоненты \(\vec{D}_{y}\) направлен вверх, как показано на рисунке \(\PageIndex{2}\). Скалярная y-компонента вектора \(\vec{D}\) равна D y = + 2,9. Вектор смещения \(\vec{D}\) является равнодействующей двух его компонент вектора.
Скалярная x-компонента вектора \(\vec{D}\) равна D х = -4,0. Аналогично, векторная y-компонента \(\vec{D}_{y}\) = \(+ 2,9 \hat{j}\) вектора смещения имеет величину |\(\vec{D}_{y} \)| = |2.9||\(\шляпа{j}\)| = 2,9, потому что модуль единичного вектора равен |\(\hat{j}\)| = 1. Направление компонента y равно \(+ \hat{j}\), которое параллельно направлению оси +y. Следовательно, вектор y-компоненты \(\vec{D}_{y}\) направлен вверх, как показано на рисунке \(\PageIndex{2}\). Скалярная y-компонента вектора \(\vec{D}\) равна D y = + 2,9. Вектор смещения \(\vec{D}\) является равнодействующей двух его компонент вектора.
Форма векторной составляющей вектора смещения Уравнение \ref{2.14} говорит нам, что указатель мыши переместился на мониторе на 4,0 см влево и на 2,9 см вверх от своего начального положения.
Упражнение 2.4
Синяя муха приземляется на лист миллиметровой бумаги в точке, расположенной на 10,0 см правее его левого края и на 8,0 см выше его нижнего края, и медленно движется к точке, расположенной на расстоянии 5,0 см от левого края и 5,0 см от нижнего края. Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Зная скалярные компоненты A x и A y вектора \(\vec{A}\), мы можем найти его величину A и направляющий угол \(\theta_{A}\). Угол направления — или, для краткости, направление — это угол, который образует вектор с положительным направлением на оси x. Угол \(\theta_{A}\) измеряется против часовой стрелки от оси +x к вектору (рисунок \(\PageIndex{3}\)). Поскольку длины A, A x и A y образуют прямоугольный треугольник, они связаны по теореме Пифагора: 9{-1} \left(\dfrac{A_{y}}{A_{x}}\right) \ldotp \label{2.16}\]
Рисунок \(\PageIndex{3}\): Для вектора \(\vec{A}\) его величина A и его направляющий угол \(\theta_{A}\) связаны с величинами его скалярных компонентов, поскольку A , A x и A y образуют прямоугольный треугольник. Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент A x положителен (рисунок \(\PageIndex{4}\)), угол \(\theta\) в уравнении \ref{ 2. 16}) идентичен дирекционному углу \(\theta_{A}\). Для векторов в четвертом квадранте угол \(\theta\) отрицателен, что означает, что для этих векторов направляющий угол \(\theta_{A}\) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \(\theta\) отрицателен. Когда вектор лежит либо во втором, либо в третьем квадранте, где компонент A x отрицательно, угол направления равен \(\theta_{A}\) = \(\theta\) + 180° (рисунок \(\PageIndex{4}\)).
16}) идентичен дирекционному углу \(\theta_{A}\). Для векторов в четвертом квадранте угол \(\theta\) отрицателен, что означает, что для этих векторов направляющий угол \(\theta_{A}\) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \(\theta\) отрицателен. Когда вектор лежит либо во втором, либо в третьем квадранте, где компонент A x отрицательно, угол направления равен \(\theta_{A}\) = \(\theta\) + 180° (рисунок \(\PageIndex{4}\)).
Пример \(\PageIndex{2}\): величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см).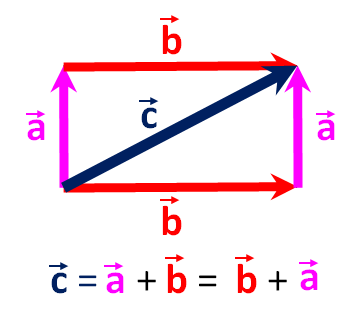 Каковы величина и направление вектора смещения указателя?
Каковы величина и направление вектора смещения указателя?
Стратегия
В примере \(\PageIndex{1}\) мы нашли вектор смещения \(\vec{D}\) указателя мыши (см. уравнение \ref{2.14}). Мы идентифицируем его скалярные компоненты D x = -4,0 см и D y = + 2,9 см и подставляем в уравнение \ref{2.15} и уравнение \ref{2.16}, чтобы найти величину D и направление \(\theta_{ Д}\) соответственно. 9{o} \ldotp\]
Упражнение 2.5
Если вектор смещения синей мухи, идущей по листу миллиметровой бумаги, равен \(\vec{D} = (−5,00\; \hat{i} − 3,00\ ; \hat{j})\) см, найти его величину и направление.
Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте, что 400 автомобилей движутся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина дает мосту разные толчки в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок. У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к прямоугольному треугольнику на рисунке \(\PageIndex{3}\). Отношение смежной стороны A x к гипотенузе A есть функция косинуса направляющего угла \(\theta_{A}\), A x /A = cos \(\theta_{A}\), и отношение противоположной стороны A y к гипотенузе A является синусоидальной функцией \(\theta_{A}\), A y /A = sin \(\theta_{A}\). Когда величина A и направление \(\theta_{A}\) известны, мы можем решить эти соотношения для скалярных компонент:
\[\begin{cases} A_{x} = A \cos \theta_{A} \\ A_{y} = A \sin \theta_{A} \ldotp \end{cases} \label{2. 17}\]
17}\]
При расчете компонентов вектора по уравнению \ref{2.17} следует соблюдать осторожность при выборе угла. Направленный угол \(\theta\) A вектора представляет собой угол, измеренный против часовой стрелки от положительного направления по оси x к вектору. Измерение по часовой стрелке дает отрицательный угол.
Пример \(\PageIndex{3}\): компоненты векторов смещения
Группа спасения пропавшего ребенка следует за поисковой собакой по кличке Солдат. Десантник много бродит и делает много пробных обнюхиваний по разным тропам. Солдат в конце концов находит ребенка, и у истории счастливый конец, но его перемещения на разных ногах кажутся действительно запутанными. На одной из ног он проходит 200,0 м на юго-восток, затем бежит на север около 300,0 м. На третьем этапе он внимательно исследует запахи на протяжении 50,0 м в направлении 30° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, улавливает свежий запах и поворачивает на 23° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
Стратегия
Давайте примем прямоугольную систему координат с положительной осью x в направлении географического востока с положительным направлением y, указывающим на географический север. В явном виде единичный вектор \(\hat{i}\) оси x указывает на восток, а единичный вектор \(\hat{j}\) оси y указывает на север. Десантник делает пять ног, поэтому есть пять векторов смещения. Начнем с определения их величин и углов направления, затем воспользуемся уравнением \ref{2.17}, чтобы найти скалярные компоненты перемещений, и уравнением \ref{2.12} для векторов смещения.
Решение
На первом участке величина смещения L 1 = 200,0 м, направление юго-восточное. В качестве дирекционного угла \(\theta_{1}\) мы можем взять либо 45°, измеренные по часовой стрелке с востока, либо 45° + 270°, измеренные против часовой стрелки с востока. {o} = 141,4\; м,\] 9{о} = -138,1\; m,\]
{o} = 141,4\; м,\] 9{о} = -138,1\; m,\]
\[\vec{L}_{5} = L_{5x}\; \шляпа{я} + L_{5у}\; \шляпа{j} = (-58,6\; \шляпа{i} — 138,1\; \шляпа{j})\; м \ldotp\]
Упражнение 2.6
Если десантник перед отдыхом пробежит 20 м на запад, каков вектор его перемещения?
Эта страница под названием 2.4: Системы координат и компоненты вектора (Часть 1) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Угол направления
- скалярные компоненты
- источник@https://openstax.


 Determine male, female. Design element stock vector illustration
Determine male, female. Design element stock vector illustration Male and Female. Biological study
Male and Female. Biological study 4. Графики
4. Графики