Векторы скалярное произведение векторов: Скалярное произведение векторов — урок. Геометрия, 9 класс.

Скалярное и векторное произведения. Проекция вектора на вектор

В данной статье будут изложены основные инструкции, относительно векторов. С их помощью Вы будете знать что с ними можно делать, а что нет. Поэтому переходим к изучению операций над векторами.

І. Суммой двух -мерных векторов

и называют-мерный вектор , координаты которого равны сумме соответствующих координат векторов — слагаемых:

Например, если ,

то

Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов

ІІ. Произведением числа (скаляра) на -мерный вектор называется -мерный вектор , координаты которого равны произведению числа на соответствующие координаты вектора

Например

Операции сложения векторов и умножения числа на вектор ( — некоторые числа) обладают свойствами:

1)

2)

3)

4)

5)

6)

7) Для произвольного вектора существует противоположный вектор такой, что

ІІІ. Скалярным произведением двух -мерных векторов и называют число, равное сумме произведений соответствующих координат векторов:

Например,

если, то

Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними

Из приведенного выше определения можно получить формулу для вычисления угла между векторами

или в координатной форме

Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого

Из последнего определения вытекают формулы для нахождения проекции вектора на вектор

или в координатной форме

Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.

Алгебраические свойства скалярного произведения векторов:

1)

2)

3)

4)Равенство имеет место при условии

Геометрические свойства скалярного произведения

1)векторы перпендикулярны между собой, если

2) угол между векторами острый в случаях, когда

3) угол между векторами тупой в случаях, когда

ІV.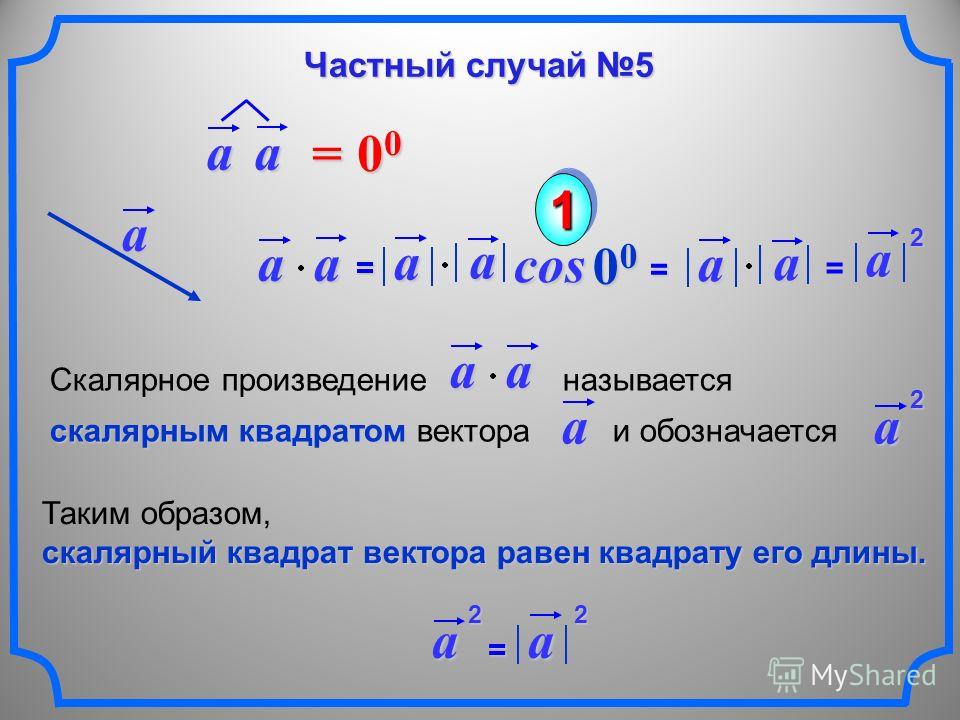 Векторным произведением или двух векторов называется вектор , который отвечает следующим условиям:

1) модуль вектора равен произведению модулей векторов и на синус угла между ними

2) вектор нормальный к плоскости, построенной на векторах и ;

3) вектор направлен так, что с его конца кратчайший поворот от вектора к происходит против часовой стрелки. Иными словами, векторы образуют правую тройку.

Векторное произведение имеет следующие геометрические свойства:

Его модуль равен площади параллелограмма построенного на векторах и

Поэтому площадь треугольника построенного на векторах и равна модулю половины векторного произведения этих векторов

Алгебраические свойства векторного произведения

1) векторное произведение равно нулю в случае коллинеарности векторов или когда один из них нулевой;

2) от перестановки векторов векторное произведение меняет знак на противоположный

3)

4)

На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее

Рассмотрим конкретные примеры для усвоения пройденного материала.

———————————————

Задача 1.

Заданы векторы и

Найти следующие величины

1) сумму векторов

2) скалярное произведение векторов

3) ) векторное произведение площадь треугольника построенного на векторах

4) угол между векторами

5) проекцию каждого из векторов на другой

Решение

1) Проведем вычисления

2) Скалярное произведение будет равно

3) Векторное произведение вычисляем по формуле

Площадь треугольника будет равна

4) Найдем угол между векторами по формуле

В ней скалярное произведение уже найдено поэтому находим длины векторов

Подставляем нужные значения в формулу

Находим значение угла

5) Найдем проекции векторов

Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится

На этом урок окончен. Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.

——————————————————

Посмотреть материалы:

• Длина вектора. Угол между векторами
• Скалярное произведение векторов
• Разложение вектора по базису
• Смешанное произведение векторов
• Деление отрезка в заданном отношении
• Треугольная пирамида

Векторы для чайников. Часть 2. Скалярное и векторное произведение. — Блог

Векторы для чайников. Часть 2. Скалярное и векторное произведение.

18 июня 2021 0 Marina Pashnina

Логическое продолжение статьи «Векторы для чайников.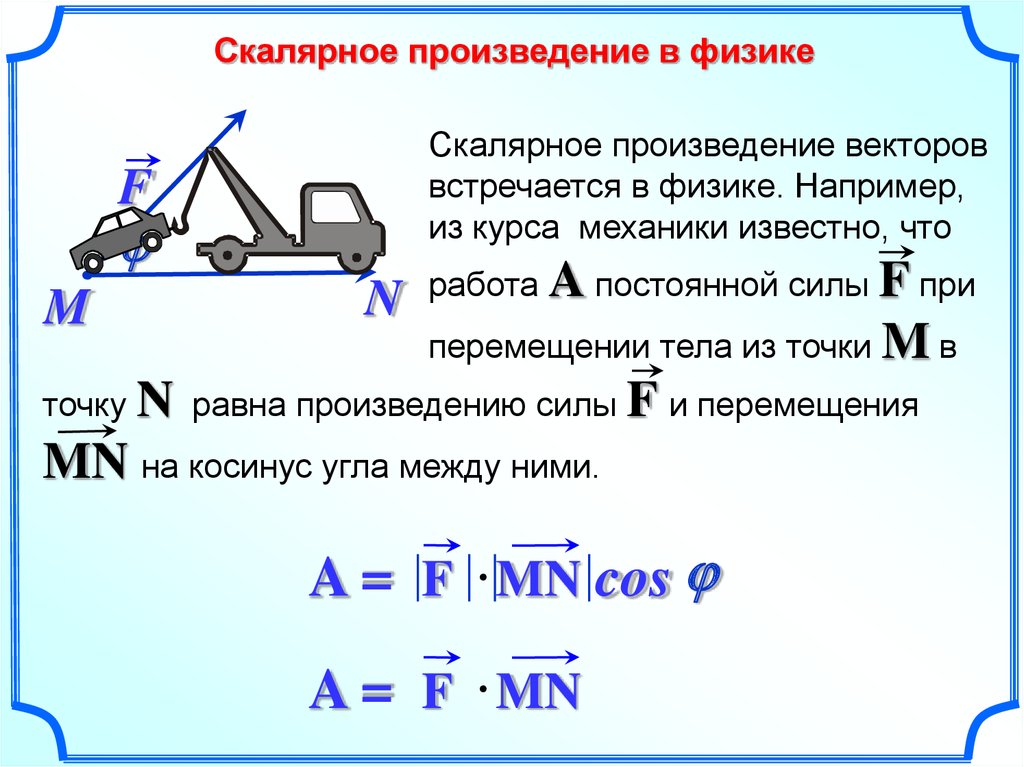 Часть 1″. В первой части рассказывается о том, что такое вектор и о простейших операциях с векторами (сложение и разность векторов, умножении вектора на число).

На этом котики кончаются и начинается злая математика.

 

 

Скалярное произведение векторов

 

Сложение векторов, умножение вектора на число…. Было бы наивным думать, что математикам было это достаточно и они не придумали что-то еще.

Скалярное произведение векторов  ā и b̅ — это ЧИСЛО, которое равно произведению длин векторов ā и b̅ и косинуса угла между ними: 

 

С математической точки зрения скалярное произведение безразмерно — это просто число и все. Скалярное произведение векторов часто применяется в физике и размерность скалярного произведения будет уже зависеть от конкретной задачи. 

Типовая задача при которой используется скалярное произведение — это работа постоянной силы, где в качестве векторов принимаются постоянная сила F, применяемая к какому-то объекту и вектор перемещения s. В этом случае скалярное произведение векторов — это конкретное число — работа силы. Так как работа измеряется в Джоулях и каждый вектор имеет свой физический смысл, то и результат скалярного произведения в данном случае будет измеряться в Джоулях.
 

Векторное произведение векторов

 

Так иногда бывает, что для полного счастья математикам нужно что-то еще, и если скалярное произведение еще может быть знакомо со школы, то векторное произведение чаще всего изучают в ВУЗе на курсах вышмата.

Обрадую всех вас — если все, что происходило до этого работало и в двухмерном и в трехмерном пространстве, то векторное произведение векторов подразумевает работу ТОЛЬКО с трехмерным пространством. (Стало проще, да ведь?)

В данном произведении участвуют также 2 вектора. Отличие от скалярного произведения тех же двух векторов будет в том, что в результате векторного произведения получается ВЕКТОР, а не число.

Формальное определение:
 

Векторным произведением  ā x b̅  неколлинеарных векторов  ā и b̅, взятых в определенном порядке, называется ВЕКТОР ā x b̅ , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ā x b̅  ортогонален векторам  ā и b̅, и направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию.

 

 

Это определение сложное и требует некоторых комментариев:

1. 

Векторы ā и b̅ по определению должны быть неколлинеарны. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Таким образом такие векторы могут называться параллельными, но так называть вектора просто не принято — их называют коллинеарными. Касаемо ситуации с векторным произведением — векторы должны быть, наоборот, непараллельными.

2.

 Важен порядок векторов. От этого зависит направление результата.

3.

Длина результирующего вектора равна площади заштрихованного параллелограмма. 

4.

Результирующий вектор ортогонален векторам  ā и b̅, т.е.  ā ┴ [ā x b̅]  и  b ┴ [ā x b̅]

5.

Результирующий вектор  направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию. 

Мысленно совместите указательный палец с вектором ā и средний палец с вектором b̅. Безымянный палец и мизинец прижмите к ладони. В результате большой палец – результирующий вектор [ā x b̅] будет смотреть вверх. Это правоориентированный базис.

Указательный палец левой руки с тем же вектором  ā, а средний – с вектором b̅. При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис.

Эти базисы не являются чем-то абстрактным. Примером может служить изображение и его отражение в зеркале. Самое обычное зеркало меняет ориентацию пространства, а изображение и зеркальное отражение этого отображения невозможно просто наложить друг на друга (попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются).

 

Что же будет, если вектора  ā и b̅ будут коллинеарны (т.е. параллельны, говоря на простом языке) — все просто, параллелаграм, который образуется этими векторами “складывается” в плоскую прямую, а площадь такой прямой равна нулю, из-за чего и результирующий вектор равен нулевому.  

Скалярное произведение — формула, примеры

Скалярное произведение — это один из способов умножения двух или более векторов. Результат скалярного произведения векторов является скалярной величиной. Таким образом, скалярное произведение также известно как скалярное произведение. Алгебраически это сумма произведений соответствующих записей двух последовательностей чисел. Геометрически это произведение евклидовой величины двух векторов и косинуса угла между ними. Скалярное произведение векторов находит различные применения в геометрии, механике, технике и астрономии. Давайте подробно обсудим скалярный продукт в следующих разделах.

1.	Что такое скалярный продукт?
2.	Формула скалярного произведения
3.	Геометрический смысл скалярного произведения
4.	Матричное представление скалярного произведения
5.	Свойства скалярного произведения
6.	Скалярное произведение единичных векторов
7.	Применение скалярного произведения
8.	Часто задаваемые вопросы о Dot Product

Что такое скалярный продукт?

Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом, отрицательным действительным числом или нулем. 9{n} a_i b_i\)

Формула скалярного произведения для векторов

Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается как \(\overrightarrow a. \overrightarrow b\), который определяется как:

\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\ b|\) cos θ.

Здесь

• \(|\overrightarrow a|\) является величиной \(\overrightarrow a\),
• \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а
• θ — угол между векторами.

Примечание: θ не определено, если либо \(\overrightarrow a\) = 0, либо \(\overrightarrow b\) = 0.

Геометрический смысл скалярного произведения

Скалярное произведение двух векторов строится путем взятия компонента одного вектора в направлении другого и умножения его на величину другого вектора. Чтобы понять векторное скалярное произведение, нам сначала нужно узнать, как найти величину двух векторов и угол между двумя векторами, чтобы найти проекцию одного вектора на другой вектор. 92}\)

Проекция вектора

Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.

Пусть OA = \(\overrightarrow a\), OB = \(\overrightarrow b\), два вектора и θ угол между \(\overrightarrow a\) и \(\overrightarrow b\) . Проведите AL перпендикулярно OB.

Из прямоугольного треугольника OAL , cos θ = OL/OA

OL = OA cos θ = \(|\overrightarrow a|\) cos θ

OL — векторная проекция a на b.

\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ = \(|\overrightarrow b|\) OL

= \(|\overrightarrow b |\) (проекция \(\overrightarrow a\) на \(\overrightarrow b\))

Таким образом, проекция \(\overrightarrow a\) на \(\overrightarrow b = \dfrac{\overrightarrow a. \ overrightarrow b}{|\overrightarrow b|}\)

Аналогично, векторная проекция \(\overrightarrow b\) на \(\overrightarrow a = \dfrac{\overrightarrow a. \overrightarrow b}{|\overrightarrow a|}\)

Угол между двумя векторами с помощью точки Продукт

Угол между двумя векторами рассчитывается как косинус угла между двумя векторами. Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, деленной на произведение величины двух векторов. Формула для угла между двумя векторами выглядит следующим образом. 92}}\)

Рабочее правило для нахождения скалярного произведения двух векторов

Если два вектора выражены через единичные векторы i, j, k вдоль осей x, y, z, то скалярное произведение получается следующим образом:

Если \(\overrightarrow a = a_1\hat i + a_2 \hat j + a_3 \hat k\) и \(\overrightarrow b = b_1 \hat i + b_2 \hat j + b_3\hat k\), тогда

\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + a_2 \hat j + a_3 \hat k)(b_1 \hat i + b_2 \hat j + b_3 \ шапка к)\)

= \((a_1b_1) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1b_3) (\hat i. \hat k) + \\(a_2b_1) ( \hat j. \hat i) + (a_2b_2)(\hat j. \hat j) + (a_2b_3 (\hat j. \hat k) + \\(a_3b_1)(\hat k. \hat i) + ( a_3b_2)(\hat k. \hat j) + (a_3b_3)(\hat k. \hat k)\)

= \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\)

Матричное представление скалярного произведения

Скалярное произведение векторов легко вычислить, если векторы представлены в виде матриц строк или столбцов.

Матрица транспонирования первого вектора получается как матрица-строка. Производится умножение матриц. Матрица-строка и матрица-столбец перемножаются, чтобы получить сумму произведения соответствующих компонентов двух векторов.

Свойства скалярного произведения

Ниже приведены свойства скалярного произведения векторов.

• Коллективное имущество
• Распределительное имущество
• Природная собственность
• Общие свойства
• Векторные тождества

Коммутативное свойство скалярного произведения:

При обычном определении \(\overrightarrow a\). \(\overrightarrow b\) = \(\overrightarrow b\) . \(\overrightarrow a\) , поскольку мы имеем \(|\overrightarrow a||\overrightarrow b|\) cos θ = \(|\overrightarrow b||\overrightarrow a|\) cos θ

Распределение скалярного произведения

Пусть a, b и c — любые три вектора, тогда скалярное произведение является дистрибутивным относительно сложения и вычитания. Это свойство можно распространить на любое количество векторов.

• \(\overrightarrow a. (\overrightarrow b+\overrightarrow c) = \overrightarrow a. \overrightarrow b + \overrightarrow a. \overrightarrow c\)
• \((\overrightarrow a+\overrightarrow b). \overrightarrow c = \overrightarrow a. \overrightarrow c+ \overrightarrow b. \overrightarrow c\)
• \(\overrightarrow a. (\overrightarrow b — \overrightarrow c) = \overrightarrow a. \overrightarrow b — \overrightarrow a. \overrightarrow c\)
• \((\overrightarrow a -\overrightarrow b). \overrightarrow c = \overrightarrow a. \overrightarrow c — \overrightarrow b. \overrightarrow c\)

Природа скалярного произведения

• Мы знаем, что 0 ≤ θ ≤ π.
• Если θ = 0, то a . b = ab [Два вектора параллельны в одном направлении ⇒ θ = 0 ] .
• Если θ = π, a . b = -ab [Два вектора параллельны в противоположных направлениях ⇒ θ = π.
  ].
• Если θ = π/2, то равно . b = 0 [Два вектора перпендикулярны ⇒ θ = π/2]
• Если 0 < θ < π/2, то cosθ положителен и, следовательно, a . b положительный.
• Если π/2 < θ < π, то cosθ отрицательно и, следовательно, равно . b отрицательный.

Другие свойства скалярного произведения

• Пусть a и b — любые два вектора, а λ — любой скаляр. Тогда (λ\(\overrightarrow a). \overrightarrow b\) = λ (\(\overrightarrow a . \overrightarrow b)\)
• Для любых двух скаляров λ и µ λ\(\overrightarrow a\) . μ \(\overrightarrow b\) = (λμ\(\overrightarrow a). \overrightarrow b\) = \(\overrightarrow a\). (λμ \ (\ overrightarrow b \))
• Длина вектора равна квадратному корню из скалярного произведения самого вектора. |\(\перевернуть а\)| = \ (\ sqrt {\ overrightarrow a . \ overrightarrow a} \)
• \(\overrightarrow a.
  \overrightarrow a\) = \(|\overrightarrow a\)| ² (или) можно записать как ²
• Для любых двух векторов a и b \(|\overrightarrow a + \overrightarrow b|\) ≤ |\(\overrightarrow a\)| + |\(\overrightarrow b|\)

Идентичности векторов

• (\(\overrightarrow a + \overrightarrow b\)) ² = \(|\overrightarrow a\)| ² + \(|\overrightarrow b|\) ² + 2 \((\overrightarrow a.\overrightarrow b)\)
• (\(\overrightarrow a — \overrightarrow b\)) ² = \(|\overrightarrow a\)| ² + \(|\overrightarrow b|\) ² — 2 \((\overrightarrow a.\overrightarrow b)\)
• \((\overrightarrow a + \overrightarrow b). (\overrightarrow a — \overrightarrow b) = |\overrightarrow a\)| ² — \(|\overrightarrow b|\) ² ≤ \(|\overrightarrow a\)| + \(|\overrightarrow b|\)

Скалярное произведение единичных векторов

Скалярное произведение единичных векторов изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0,9.0003

\(\шляпа i.\шляпа i\) = \(\шляпа j.\шляпа j\) = \(\шляпа k.\шляпа k\)= 1

\(\шляпа i.\шляпа j \) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0

Применение скалярного произведения

Применение скалярного произведения для расчета работы. Произведение приложенной силы на перемещение называется работой. Если сила приложена под углом θ к смещению, проделанная работа определяется как скалярное произведение силы и смещения как W = f d cos θ. Скалярное произведение также используется для проверки того, являются ли два вектора ортогональными или нет. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos

90º ⇒ \(\overrightarrow a. \overrightarrow b\) = 0

Важные замечания о скалярном произведении:

• Скалярное произведение — это способ умножения двух векторов.
• Геометрически скалярное произведение равно произведению длин векторов на угол косинуса между ними. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|\overrightarrow b|\) cos θ
• Это скалярная величина, не имеющая направления. Его легко вычислить из суммы произведения компонентов двух векторов.
• Если \(\overrightarrow a\) = \(a_1\) i + \(a_2\) j + \(a_3\) k и \(\overrightarrow b\)= \(b_1\) i + \(b_2\ ) j + \(b_3\) k, тогда \(\overrightarrow a. \overrightarrow b = a_1b_1 + a_2b_2+ a_3b_3\)

☛ Связанные темы:

• Сложение векторов
• Произведение векторов
• Типы векторов

Часто задаваемые вопросы о Dot Product

Что такое скалярное произведение двух векторов?

Скалярное произведение двух векторов имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. \(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.

Что такое скалярное произведение двух параллельных векторов?

Скалярное произведение двух параллельных векторов равно произведению модуля двух векторов. Для двух параллельных векторов угол между векторами равен 0°, а Cos0°= 1. Следовательно, для двух параллельных векторов a и b имеем \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|| \overrightarrow b|\) cos 0° = \(|\overrightarrow a|.|\overrightarrow b|\).1 = \(|\overrightarrow a|.|\overrightarrow b|\).

В чем разница между скалярным произведением и перекрестным произведением?

Скалярное произведение — это скалярное произведение, а перекрестное произведение — векторное произведение. Скалярное произведение двух векторов равно \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\)Cosθ, а перекрестное произведение двух векторов равно \(\overrightarrow a \) × \(\overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\) Sinθ.\(\hat{n}\). Результат скалярного произведения двух векторов лежит в той же плоскости, что и два вектора, тогда как результат перекрестного произведения лежит в плоскости, перпендикулярной плоскости, охватывающей два вектора.

Что такое формула скалярного произведения?

Формула скалярного произведения представляет скалярное произведение двух векторов как произведение двух векторов и косинуса угла между ними. Формула скалярного произведения заданных векторов может быть выражена следующим образом. Здесь a и b — два вектора, \(|\overrightarrow a|\) и \(|\overrightarrow b|\) — их соответствующие величины, а θ — угол между двумя векторами a . b = \(|\overrightarrow a||\overrightarrow b|\) cos⁡θ.

Включает ли формула скалярного произведения умножение?

Умножение двух векторов — это не то же самое, что скалярное умножение. Есть два типа умножения с участием двух векторов. Скалярный продукт — это «точечный продукт», а векторный продукт — «перекрестный продукт». Формула скалярного произведения представляет собой скалярное произведение двух векторов как произведение двух векторов и косинуса угла, образованного между ними.

Какова цель формулы скалярного произведения?

Скалярное произведение предназначено для того, чтобы сообщить нам величину вектора силы, приложенного в направлении вектора движения. Скалярное произведение также позволяет нам измерить угол, образованный парой векторов, и относительное положение вектора относительно осей координат.

Что происходит, когда скалярное произведение после использования формулы скалярного произведения равно 0?

Формула скалярного произведения представляет скалярное произведение двух векторов как произведение двух векторов и косинуса угла между ними. Если скалярное произведение равно 0, то мы можем заключить, что либо длина одного или обоих векторов равна 0, либо угол между ними равен 90 градусов.

Где мы используем скалярный продукт?

Концепция скалярного произведения широко используется в физике и технике. Для двух величин, расположенных под углом друг к другу, скалярное произведение дает результат этих двух векторов. Возьмем пример силы, приложенной к телу F, и перемещение тела равно d. Если угол между вектором силы F и вектором смещения d равен θ, то выполненная работа является произведением силы на перемещение. W = FdCosθ.

Как рассчитать скалярный продукт?

Скалярный продукт можно рассчитать в три простых шага. Сначала найдите величину двух векторов a и b, то есть \(|\overrightarrow a|\) и \(|\overrightarrow b|\). Во-вторых, найдите косинус угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косинуса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.

Почему скалярное произведение называется скалярным?

Скалярное произведение является скалярным, поскольку все отдельные составляющие ответа являются скалярными значениями. В \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ, \(|\overrightarrow a|, |\overrightarrow b|\) и Cosθ равны все скалярные значения. Следовательно, скалярное произведение также называют скалярным произведением.

Почему мы используем косинус в скалярном произведении?

Для нахождения скалярного произведения нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы можем найти cosθ в скалярном произведении двух векторов.

Почему скалярное произведение ортогональных векторов равно 0?

Два ортогональных вектора перпендикулярны друг другу, а угол между двумя векторами равен 90°. Поскольку Cos90° = 0, скалярное произведение двух ортогональных векторов равно 0. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).cos90° = \ (|\overrightarrow a|.|\overrightarrow b|\).0 = 0.

Почему скалярное произведение коммутативно?

Скалярное произведение двух векторов равно произведению величины двух векторов и косинуса угла между двумя векторами. И все отдельные компоненты величины и угла являются скалярными величинами. Следовательно, \(\overrightarrow a. \overrightarrow b\) = \(\overrightarrow b. \overrightarrow a\), и скалярное произведение векторов следует коммутативному свойству.

Может ли скалярный продукт быть равен нулю?

Скалярное произведение двух векторов может быть равно нулю, если любой из двух векторов равен нулю или если два вектора перпендикулярны друг другу. Для двух ненулевых векторов скалярное произведение равно нулю, если угол между двумя векторами равен 90º, потому что Cos90º = 0.

Является ли скалярное произведение двух коллинеарных векторов равным 0?

Нет. Это потому, что угол между двумя коллинеарными векторами равен 0, поэтому скалярное произведение двух коллинеарных векторов есть просто произведение их величин (так как cos 0 = 1). Фактически, векторное произведение двух коллинеарных векторов является нулевым вектором.

Понимание скалярного произведения – BetterExplained

Я думаю о скалярном произведении как о направленном умножении. Умножение выходит за рамки повторного подсчета: это применение сущности одного элемента к другому. (Например, сложное умножение — это вращение, а не повторный счет.)

При работе с простыми темпами роста умножение масштабирует одну скорость на другую: большой, чтобы получить 12x»

При работе с векторами («направленный рост») мы можем выполнить несколько операций:

• Добавить векторы: Накопить рост, содержащийся в нескольких векторах.
• Умножить на константу : сделать существующий вектор сильнее (в том же направлении).
• Скалярный продукт: Применение направленного роста одного вектора к другому. Результат — насколько сильнее мы сделали исходный вектор (положительный, отрицательный или нулевой).

Сегодня мы построим наше интуитивное представление о том, как работает скалярное произведение.

Избавьтесь от формулы

Вы повсюду видели уравнение скалярного произведения:

А также обоснование: «Ну, Билли, закон косинусов (ты ведь помнишь это, не так ли? ) говорит, что следующие вычисления одинаковы, так что они есть». Недостаточно хорошо — это не щелкает! Помимо вычислений, что это значит?

Цель состоит в том, чтобы применить один вектор к другому. Уравнение выше показывает два способа сделать это:

• Прямоугольная перспектива: объединить компоненты x и y
• Полярная перспектива: объединить величины и углы

Уравнение «тот материал = тот материал» просто означает «Вот два эквивалентных способа ‘направленного умножения’ векторов».

Восприятие чисел как векторов

Давайте начнем с простого и рассмотрим 3 x 4 как скалярное произведение:

Число 3 означает «направленный рост» в одном измерении (скажем, по оси X), а 4 является «направленным ростом» в том же направлении. 3 x 4 = 12 означает, что мы получаем 12-кратный рост в одном измерении. Хорошо.

Теперь предположим, что 3 и 4 относятся к разным измерениям. Допустим, 3 означает «втрое больше бананов» (ось X), а 4 означает «вчетверо больше апельсинов» (ось Y). Теперь они не одного и того же типа чисел: что произойдет, если применить рост (использовать скалярное произведение) в нашей вселенной «бананы, апельсины»?

• (3,0) означает «Утроить количество бананов, уничтожить апельсины»
• (0,4) означает «Уничтожьте свои бананы, увеличьте количество апельсинов в четыре раза»

Применение (0,4) к (3,0) означает «Уничтожьте рост бананов, увеличьте рост апельсинов в четыре раза». Но у (3, 0) изначально не было оранжевого роста, поэтому конечный результат равен 0 («Уничтожь все свои фрукты, приятель»).

Видите, как мы «применяем», а не просто добавляем? При регулярном сложении мы смешаем векторы вместе: (3,0) + (0, 4) = (3, 4) [вектор, который утроит ваши апельсины, а увеличит ваши бананы в четыре раза].

«Приложение» отличается. Мы мутируем исходный вектор на основе правил второго. И правила (0, 4) таковы: «Уничтожьте рост бананов и увеличьте рост апельсинов в четыре раза». Применительно к чему-то, состоящему только из бананов, например (3, 0), мы остаемся ни с чем.

Конечным результатом процесса скалярного произведения может быть:

• Ноль: у нас нет роста в исходном направлении
• Положительное число: есть некоторый рост в исходном направлении
• Отрицательное число: у нас отрицательный (обратный) рост в исходном направлении

Понимание расчета

«Применение векторов» все еще немного абстрактно. Я думаю: «Сколько энергии/толчка отдает один вектор другому?». Вот как я себе это представляю:

Прямоугольные координаты: перекрытие компонентов

Подобно умножению комплексных чисел, посмотрите, как взаимодействует каждая компонента x и y: х с у, у с у). Поскольку координаты x и y не влияют друг на друга (как держать ведро боком под водопадом — ничего не падает), полное поглощение энергии равно поглощению (x) + поглощению (y):

Полярные координаты: Проекция

Слово «проекция» настолько бесплодно: я предпочитаю «по пути». Сколько энергии на самом деле идет в нашем первоначальном направлении?

Вот как это можно увидеть:

Возьмем два вектора a и b. Поверните наши координаты так, чтобы b стала горизонтальной: она становится (|b|, 0), и все находится на этой новой оси x. Что такое точечный продукт сейчас? (Это не должно измениться только потому, что мы наклонили голову).

Итак, вектор a имеет новые координаты (a1, a2), и мы получаем:

a1 на самом деле «Какова координата x точки a, если предположить, что b является осью x?». Это |a|cos(θ), также известная как «проекция»:

Аналогии скалярного произведения

Общепринятая интерпретация — «геометрическая проекция», но она такая пресная.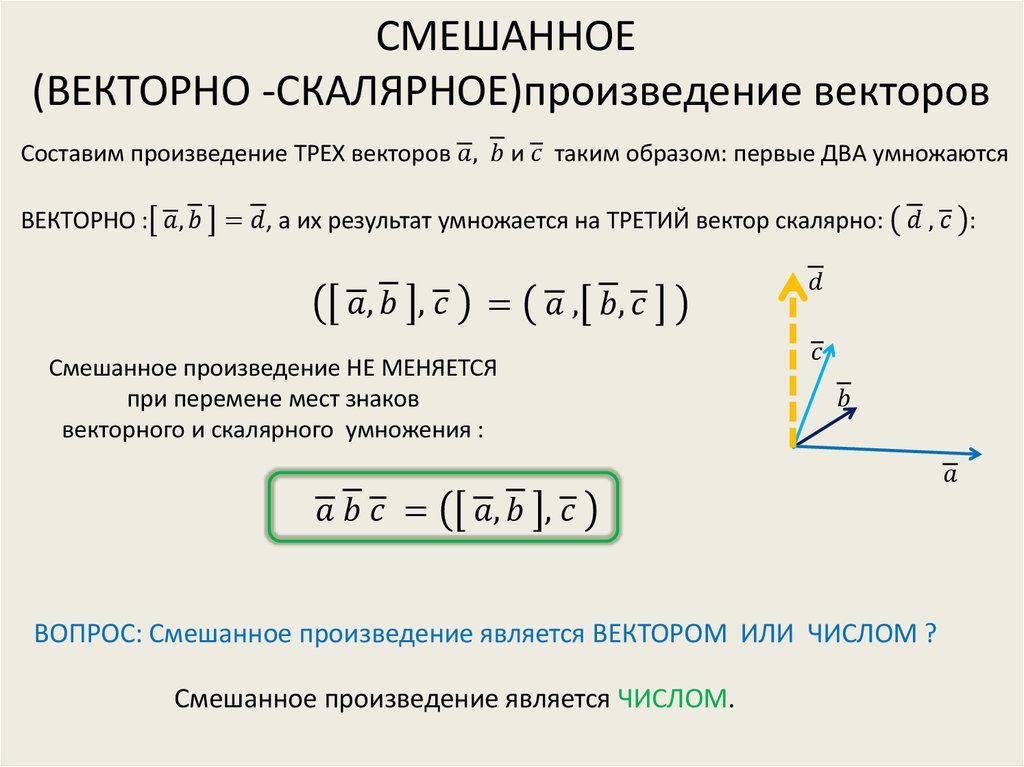 Вот некоторые аналогии, которые меня зацепили:

Поглощение энергии

Один вектор — солнечные лучи, другой — куда указывает солнечная панель (да-да, нормальный вектор). Большие числа означают более сильные лучи или большую панель. Сколько энергии поглощается?

• Энергия = Перекрытие в направлении * Сила лучей * Размер панели

Если вы держите панель боком к солнцу, лучи не попадают (cos(θ) = 0).

Фото предоставлено

Но… но… солнечные лучи уходят от солнца, и панель обращена к солнцу, и скалярное произведение отрицательно, когда векторы противоположны! Сделайте глубокий вдох и помните, что цель состоит в том, чтобы принять аналогию (кроме того, физики все время теряют из виду отрицательные знаки).

Mario-Kart Speed ​​Boost

В Mario Kart на земле есть «ускорители», которые увеличивают вашу скорость (Никогда не играл? Извините.)

Источник фото

Представьте, что красный вектор — это ваша скорость (направление x и y), а синий вектор — это ориентация площадки усиления (направление x и y). Чем больше число, тем больше сила.

Сколько буста вы получите? Для аналогии представьте, что пэд дает бонус к скорости, подобный этому:

• Если вы входите и уходите с 0, вы ничего не получите. (Если вас уронили на площадку, ускорение не будет.)
• Если вы пересечете площадку перпендикулярно, вы получите 0 преимуществ. (Как и при уничтожении банана, в перпендикулярном направлении есть ускорение 0x.)
• Если наше направление и контактная площадка выровнены, наша скорость по оси x увеличивает скорость по оси x, а скорость по оси y увеличивает скорость по оси y:

Аккуратно, да? Другой способ увидеть это: ваша входящая скорость равна $|a|$, а максимальное ускорение равно $|b|$. Процент повышения, который вы фактически получаете (в зависимости от того, как вы выстроились в очередь), составляет $\cos(\theta)$, для общего повышения $|a||b|\cos(\theta)$, что является скалярное произведение.

Аналогия фруктовой лавки

Допустим, в вашем магазине продаются яблоки, бананы и клементины.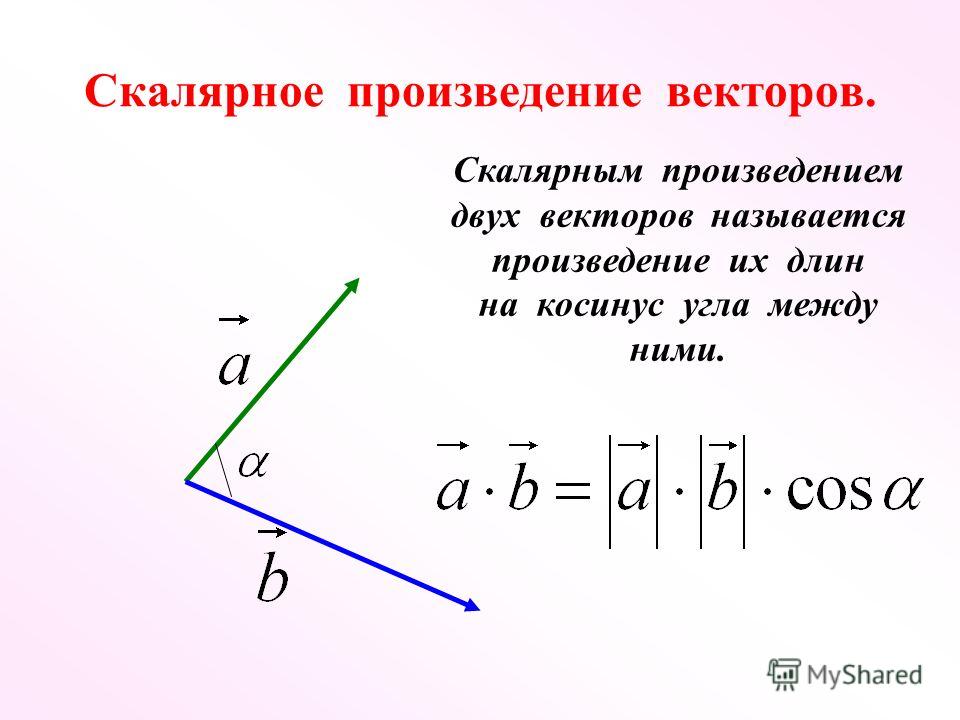 Они стоят \$1, \$2 и \$3 каждый соответственно.

Покупатель хочет купить 2 яблока, 3 банана и 4 клементина. Сколько это стоит?

 стоимость = (количество A) * (цена A) + (количество B) * (цена B) + (количество C) * (цена C)
стоимость = 2*1 + 3*2 + 4*3 = 20
 

Это скалярное произведение между вектором «количество» и вектором «цена»! Мы умножаем совпадающие записи и получаем общее количество. Мы игнорируем записи, умножение которых «не имеет смысла» (почему количество бананов и цена клементина должны влиять друг на друга?).

Физика Физика Физика

Скалярное произведение появляется во всей физике: какое-то поле (электрическое, гравитационное) притягивает какую-то частицу. Мы хотели бы размножаться, и мы могли бы, если бы все было выстроено в ряд. Но это не так, поэтому мы берем скалярное произведение для учета возможных различий в направлении.

Это полезное обобщение: интегралы — это «умножение с учетом изменений», а скалярное произведение — «умножение с учетом направления».